Abstract
Cell migration, a fundamental physiological process in which cells sense and move through their surrounding physical environment, plays a critical role in development and tissue formation, as well as pathological processes, such as cancer metastasis and wound healing. During cell migration, dynamics are governed by the bidirectional interplay between cell-generated mechanical forces and the activity of Rho GTPases, a family of small GTP-binding proteins that regulate actin cytoskeleton assembly and cellular contractility. These interactions are inherently more complex during the collective migration of mechanically coupled cells because of the additional regulation of cell-cell junctional forces. In this study, we adapted a recent minimal modeling framework to simulate the interactions between mechanochemical signaling in individual cells and interactions with cell-cell junctional forces during collective cell migration. We find that migration of individual cells depends on the feedback between mechanical tension and Rho GTPase activity in a biphasic manner. During collective cell migration, waves of Rho GTPase activity mediate mechanical contraction/extension and thus synchronization throughout the tissue. Further, cell-cell junctional forces exhibit distinct spatial patterns during collective cell migration, with larger forces near the leading edge. Larger junctional force magnitudes are associated with faster collective cell migration and larger tissue size. Simulations of heterogeneous tissue migration exhibit a complex dependence on the properties of both leading and trailing cells. Computational predictions demonstrate that collective cell migration depends on both the emergent dynamics and interactions between cellular-level Rho GTPase activity and contractility and multicellular-level junctional forces.
Significance
Cell migration is a fundamental physiological process in which cells sense and move through their surrounding physical environment. Collective cell migration is governed by cell-generated mechanical forces, intercellular junctional forces, and the activity of Rho GTPases. In this study, we use a computational model of collective cell migration to study the interactions between intracellular signaling and these mechanical forces. Significant findings include the prediction of 1) front-to-back and back-to-front Rho GTPase activity waves propagating in the tissue that mediate mechanical tissue synchronization, 2) distinct spatial patterns for cell-cell junctional forces during collective cell migration, with larger junctional forces near the leading edge, and 3) larger junctional force magnitudes associated with faster collective cell migration and larger tissue size.
Introduction
Cell migration is a fundamental physiological process in which cells sense and move through their surrounding physical environment. Adherent cell migration plays a critical role in development and tissue formation, as well as pathological processes, such as cancer metastasis and wound healing (1, 2, 3). The fundamental dynamics of individual cell migration are generally well understood: the front of the cell extends and protrudes, generally mediated by actin polymerization. The cell adheres to the underlying extracellular matrix substrate via integrin binding and the formation of focal adhesions (4). Finally, a cell-generated contractile force retracts the cell back, generating net movement in the direction of migration (5, 6).
At the level of an individual cell, although there are many signaling pathways that regulate the dynamics of lamellipodia and filopodia cellular extensions, Rho GTPases are key drivers of this process. Rho GTPases are small GTP-binding proteins that regulate essential cellular processes and functions, including cellular adhesion, shape, and proliferation. Key members of the Rho GTPase family include Rho, Rac, and Cdc42, each of which have multiple isoforms (7). The Rho GTPase proteins cycle between active GTP-bound and inactive GDP-bound forms (8, 9). Although these proteins are regulators of a host of cellular processes, a primary function of Rho GTPases is the regulation of actin cytoskeleton assembly; thus, these proteins are drivers of cellular contractility (8, 9, 10, 11). Further, there is strong experimental evidence that Rho GTPase activity is critical for cell migration (12, 13).
As Rho GTPase activity drives actomyosin-mediated mechanical forces, mechanical forces also in turn modulate Rho GTPase activity via mechanotransduction: for example, mechanical compression of the cell membrane in human mesenchymal cells has been shown to reduce RhoA activity, mediated by mechanosensitive ion channels (14). Katsumi et al. (15) show that the stretch of vascular smooth muscle cells inhibited Rac and decreased lamellipodia formation. Thus, there is a complex and bidirectional interplay between Rho GTPase activity and mechanical forces at the cellular level (16, 17).
The collective migration of cells is inherently a more complex process, involving the coordination of mechanical and biochemical interactions between both cells and the surrounding substrate and neighboring cells within the tissue (10). Collective migration can be broadly described by different categories, including sheet migration, sprouting and branching, and tumor invasion (1). Coordinated migration generally requires cells to be in physical contact and coupled mechanically via cell-cell junctions. Cell-cell junction forces in turn can regulate key physiological processes, such as proliferation and differentiation (18). However, the interactions between junctional forces and collective migration dynamics are not fully understood.
In this study, we extend a prior model to develop a minimal modeling framework to investigate the interactions between mechanochemical signaling and junctional forces in collective cell migration, investigating directed migration in one dimension. We found in individual cells that migration velocity depends on the feedback between mechanical tension and Rho GTPase activity in a biphasic manner. In mechanically coupled tissue during collective cell migration, waves of Rho GTPase activity mediated mechanical contraction/extension and thus synchronization throughout the tissue. Additionally, we found that junctional forces exhibited distinct spatial patterns during collective cell migration, with larger forces near the leading edge, and further, that larger junctional force magnitudes were associated with faster collective cell migration. The model predicts that collective cell migration depends on both the emergent dynamics and interactions between cellular-level Rho GTPase activity and contractility and multicellular-level junctional forces.
Methods
In this work, we first extend a recently developed minimal cellular model coupling mechanical tension and Rho GTPase signaling to account for the front-back cellular polarity of migrating cells. We then further expand this model to account for mechanical junctions between cells and investigate the properties of collective cell migration.
Individual cell model
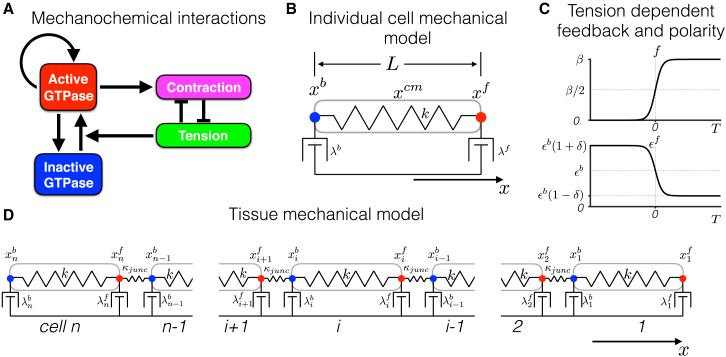
The minimal mechanochemical model that serves as the framework for our study was recently presented by Zmurchok et al. (19). In this model, cellular Rho GTPase activity is coupled with cellular mechanics (Fig. 1 A). Individual cell mechanics are governed by a spring-dashpot system for which a single spring governs extension/contraction of an individual cell and two dashpots at the cell front and back represent viscous coupling with a fixed substrate (Fig. 1 B). As demonstrated by Zmurchok et al.(19), in this model, mechanochemical coupling via several feedback mechanisms can drive periodic cellular contraction and extension. 1) An increase in active Rho GTPase levels promotes actomyosin-mediated cellular contraction which in turn reduces cellular tension. 2) Whereas Rho GTPase activity is self-activated via positive feedback, active Rho GTPase levels are subsequently reduced by the loss of cellular tension. 3) Reduced Rho GTPase activity drives cellular relaxation and extension, increasing cellular tension. 4) Increased cellular tension promotes Rho GTPase activation and increases active Rho GTPase levels, completing the cycle.
Figure 1.
Individual cell and tissue mechanochemical models. (A) A diagram of mechanochemical interactions between active and inactive Rho GTPase levels and mechanical contraction and tension is shown and is adapted from Zmurchok et al. (19). (B) The mechanical model of an individual cell is shown. The model governs the position of the cell front , back , and center of mass ((1d), (1e)). The cell is represented by a Hookean spring, with spring constant k, and dashpots at the cell front and back with constants and , respectively. (C) (Top) Tension-dependent GTPase activation (Eq. 1 b) and (bottom) tension-dependent front-back polarity (Eq. 1 f) are shown as functions of cellular tension T. (D) The mechanical model of n mechanically coupled cells is shown. The model governs the positions of cell fronts and backs for ((2a), (2b), (2c), (2d), (2e)). Key differences between our model and that of Zmurchok et al. (19) include the fact that 1) cell front and back dashpot constants ( and ) are not equal, 2) is cell tension dependent (via Eq. 1 f), and 3) cell-cell mechanical junctions are represented by Hookean springs, with spring constant . To see this figure in color, go online.
Normalized active Rho GTPase signaling (G) is governed by the following:
| (1a) |
where the first term represents a tension-dependent activation rate of inactive Rho GTPase (Ginactive = GT − G), GT is total Rho GTPase levels (i.e., active and inactive forms), b is a basal activation rate, is tension-dependent activation rate, and γ is the Hill equation positive feedback activation rate. The second term represents a constant rate of inactivation. As in the model by Zmurchok et al. (19), time has been normalized relative to the active Rho GTPase residence time (or the inverse of the inactivation rate). Thus, time is presented in normalized units.
The tension-dependent activation is given by the following sigmoidal function of tension:
| (1b) |
where β governs the strength of tension feedback (Fig. 1 C, top). Cellular tension T is given by the difference of cell length L and a Rho GTPase-dependent resting length , that is, T = L − L0 (G). The function produces a switch-like response in Rho GTPase activity in the presence of cellular extension but minimal activation for contraction.
Rho GTPase activity drives cellular contraction by reducing the cell resting length, with the following dependence:
| (1c) |
where l0 is a baseline resting length, and ϕ and Gh are Hill equation amplitude and half-maximal parameters for Rho GTPase dependence on cell resting length, respectively. The maximal cell resting length is l0 = 1; thus, lengths in the spatial dimension are presented in units normalized such that the unit measure is equal to the length of a maximal relaxed cell.
Cellular mechanics are determined by a force balance at each end of the cell, with the position of the cell front and back governed by the following equations, respectively:
| (1d) |
| (1e) |
where k is a Hookian spring constant for the cell, and and are cell front and back viscosities or friction constants, respectively, such that cell length . The cell center of mass is given by .
In the original model formulation by Zmurchok et al. (19), . Here, we introduce a front-back polarity in which the back viscosity is assumed to be fixed, given by , where is a normalized extension/contraction rate. However, the viscosity of the cell front is assumed to be tension dependent, a formulation modified from an approach recently presented by Lopez et al. (20), with , where
| (1f) |
and is a measure of the asymmetry between the front and back of the cell (Fig. 1 C, bottom). Parameter δ can be considered a measure of cellular front-back polarity, which would depend on the strength of a guidance cue (e.g., a chemotactic gradient), where a larger δ corresponds to a larger polarity or gradient. The formulation in Eq. 1 f is based on the following assumptions: 1) during contraction while tension is low, focal adhesions at the cell front are being assembled, and thus there are fewer cell surface-integrin bonds formed, such that friction at the cell front is initially weak (resulting in a large and small ); 2) during cell extension while tension is high, friction at the cell front is larger because of more mature focal adhesion formation (i.e., a small and large ). See Lopez et al. (20) for additional details on this proposed tension-dependent mechanism. We note that in this study, the front-back polarity of an individual cell is specified (and indeed defined by parameter δ). Physiologically, cellular front-back polarity typically emerges in response to a guidance cue (e.g., a wound or a chemotactic gradient). This complex process, which involves the subcellular distributions of GTPases and mechanochemical interactions with the underlying extracellular matrix, has been elegantly studied in several recent computational models (11, 21, 22), and our minimal approach does not account for these aspects of subcellular signaling associated with cellular polarization; however, the focus of our study is on emergent properties of migration that follow from this polarization, and thus for simplicity, we assume a defined front-back polarity for each cell.
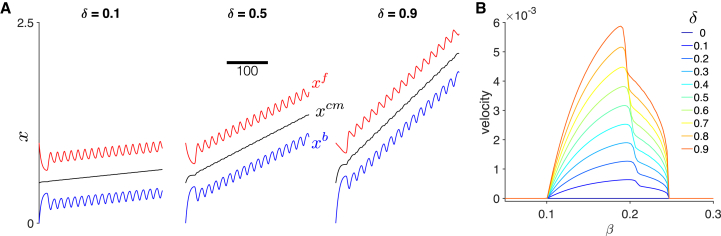
Note for that δ = 0, and thus , as in the original model, resulting in a stationary cell. As shown previously in Zmurchok et al. (19) and shown here in Fig. S1, the long-term behavior of the mechanochemical dynamics depends on the relative strength of the tension-dependent feedback: for small feedback (β = 0.05; Fig. S1 A), the cell remains fixed in a relaxed state, whereas for large feedback (β = 0.3), the cell is fixed in a contractile state. For an intermediate feedback (β = 0.16), the cell state oscillates between contraction and extension, coupled with oscillations in Rho GTPase levels. Note that while the position of the cell front and back extend and contract, the center of the cell remains constant, as expected for δ = 0. Fig. S1 B demonstrates the transition from relaxed (red), to oscillatory (black), to contractile (blue) states as a function of β. Further, we find that in the oscillatory regime, the period of oscillations also depends on the strength of the tension-dependent feedback, such that the period increases as β increases (Fig. S1 C).
Collective cell migration model
We next extend the minimal migrating cell model to represent a one-dimensional tissue of mechanically coupled cells (Fig. 1 D). For each cell i, Rho GTPase activity (Gi) and mechanical forces are represented; in addition to cellular tension, an intercellular mechanical junction between the back of cell i and the front of cell i + 1 is represented by a Hookian spring with spring constant and resting length Ljunc. Thus, the tissue model of n cells is represented by Rho GTPase activity (Gi) and the position of the cell front and back , that is, 3n variables, governed by the following:
| (2a) |
| (2b) |
| (2c) |
| (2d) |
| (2e) |
where cell length and cell tension Ti = Li − L0 (Gi). We assume that cells may have different parameters for front-back polarity (δi) and tension feedback (βi). We note that Zmurchok et al. (19) also consider a one-dimensional array of cells, but they did not represent intercellular mechanical forces transmitted via a spring but rather assumed that the back of cell i and the front of cell i + 1 are the same “node,” which would be the limit of Ljunc = 0 and . Importantly, our formulation enables explicit prediction of intercellular junctional forces throughout the tissue.
All model parameters are given in Table S1. In all individual cell or tissue simulations, initial conditions for Rho GTPase activity G(0) = 1. Initial cell positions were defined such that initial cell lengths were equal to 0.6, with intercellular node spacing such that mechanical junctions were in equilibrium (i.e., front-back cell position differences were equal to the junctional resting length Ljunc). Simulations were performed using the MATLAB (The Mathworks, Natick, MA) stiff ordinary differential equation solver (ode15s). Unless otherwise noted, simulations were run for a duration of 10,000 normalized time units, and analysis was performed on the last 5000 time units.
Results
Individual cell migration depends on tension-dependent feedback and front-back polarity
We first demonstrate how the introduction of front-back cell polarity produces cell migration in an individual cell (Fig. 2 A). For β in the oscillatory range and a small front-back polarity (δ = 0.1), cell front (red) and back (blue) demonstrate periodic extension and contraction (as in the stationary cell case shown in Fig. S1). However, the asymmetry in the cell front friction (specifically more friction, i.e., , during contraction and less friction, i.e., , during extension) produces a gradual net movement in the positive x direction. The position of the cell center (black) illustrates the gradual migration as well. Further, the time course of the cell front, center, and back illustrate that as δ increases, cell migration velocity increases (see Videos S1 and S2). These simulations are consistent with experiments of fibroblast migration, which exhibit oscillations of the cell edge and length and gradual net movement of the cell center (23, 24).
Figure 2.
Dynamics of a migrating individual cell. (A) The time course for cell position (front (red) , center (black) , and back (blue) ) are shown for different values of front-back polarity parameter δ. Cell migration velocity increases for increasing δ. (B) Cell migration velocity is shown as a function of tension-feedback parameter β for different values of δ. Velocity is zero in the nonoscillatory β regime and a biphasic function of β in the oscillatory β regime. Parameters are (A) β = 0.16. To see this figure in color, go online.
(Top) The position of the cell center of mass xcm and Rho GTPase activity G are shown as a function of time. Scale bar = 50. (Middle) Representation of the cell position are shown for different times. Color of the cell corresponds to Rho GTPase activity, with blue denote a low level (0.2) and red denotes a high level (0.5). (Bottom) Position of the cell front (red), center (black), and back (blue) are shown as a function of time. Note time is on the y-axis. Scale bar for middle and bottom panels = 0.5. Video corresponds with results shown in Fig. 2 B. Parameters: β = 0.16, δ = 0.5.
Representation of cell position for individual cells with different values of front-back polarity parameter δ are shown for different times. Note that the color corresponds to the δ value. Scale bar = 0.5. Parameters: β = 0.16.
In Fig. 2 B, we plot the cell migration velocity as a function of β for different values of δ. Velocity is calculated as the slope from a linear regression on the cell center position versus time (using the second half of the simulation for analysis). We find that for any value of β, increasing δ increases migration velocity (consistent with Fig. 2 A). Additionally, the model predicts that cell migration requires periodic extension and contraction and that cells fixed in a relaxed or contractile state are stationary. Thus, the β parameter regimes for oscillations are identical to the regime for nonzero cell migration velocities, and for β values outside the oscillation regime, migration velocity is zero. We also find that for a given value of δ, velocity is biphasic as a function of β, such that there is an optimal β that yields the fastest migration velocity. The optimal β value moderately depends on δ, decreasing as δ increases, demonstrating feedback between cell tension and front-back polarity; however, the β value for the fastest single cell migration velocity is between 0.19 and 0.2 for the full range of δ values.
Collective cell migration depends on individual cell properties and junctional forces
After determining the relationship between tension-dependent feedback and front-back polarity on migration in an individual cell, we next consider these interactions on collective cell migration on mechanically coupled cells. We investigate both homogeneous tissues, in which all cells have the same individual properties, and heterogeneous tissues, in which the front or “leader” cell may have different properties than the back or “trailing” cells in the tissue.
Homogeneous tissues
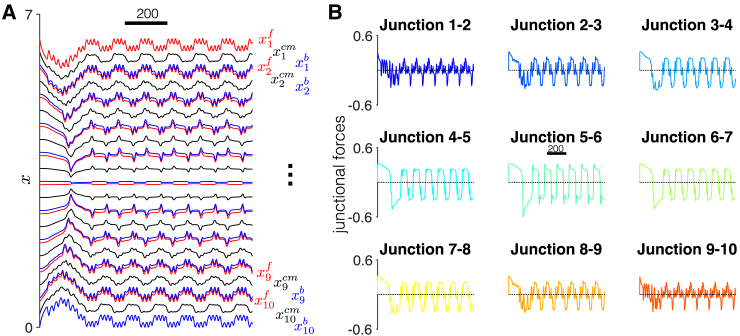
We first consider the case of a homogeneous tissue comprising 10 cells, in which β is in the oscillatory regime for all cells, but has no front-back polarity (δ = 0; Fig. 3). As expected, the collective tissue is stationary; however, individual cells in the front and back of the tissue exhibit periodicity around a stationary position (Fig. 3 A). Thus, cells in the front (e.g., cell 1) and back (e.g., cell 10) exhibit both the higher frequency oscillations, corresponding to periodic extension and contraction, and a slower-frequency oscillation that is an emergent property of the tissue. Toward the interior of the tissue (e.g., cells 4 and 5), oscillations due to extension/contraction are substantially dampened. In this stationary tissue, there is also a symmetry in the time course of the cell positions in that the front of cell 1 mirrors the back of cell 10, the front of cell 2 mirrors the back of cell 9, etc., as might be expected in this symmetrical tissue.
Figure 3.
Dynamics of a stationary tissue. (A) The time course for cell positions (front (red) , center (black) , and back (blue) for ) are shown. The time courses exhibit a front-back symmetry and two distinct frequencies, corresponding to the individual cellular contraction and extension and an emergent frequency from cell-cell mechanical coupling. (B) The time course for each cell-cell junction also exhibits multiple frequencies and periods of both tension and compression. Parameters are tension-feedback β = 0.16 and front-back polarity, δ = 0. To see this figure in color, go online.
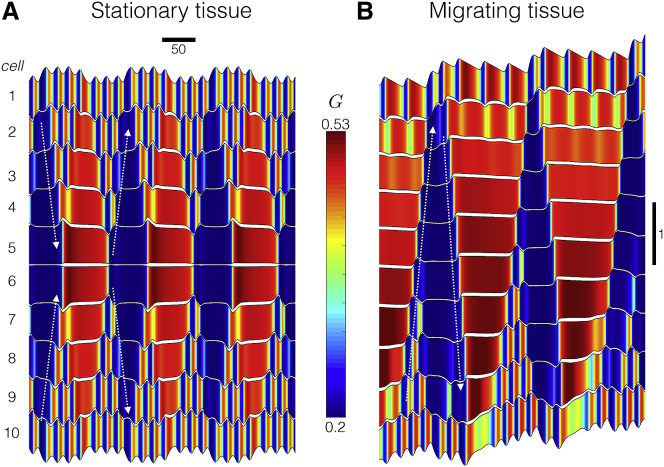
In Fig. 3 B, we investigate the time course of the junctional forces between each cell pair (e.g., between cell 1 and 2, between cell 2 and 3, etc.). The time course for junctional forces demonstrates that the cell junctions exhibit time periods of both tension and compression. Junctional forces on the periphery of the tissue (e.g., junction 1–2 and junction 9–10) also exhibit periodicity associated with both contraction and extension and a slower component associated with tissue movements, as in the cell position plots. The higher frequency associated with cell contraction and extension is similarly dampened in the tissue interior (e.g., junction 5–6). Thus, the stationary tissue simulations predict two key properties: emergent tissue-scale dynamics and a spatial pattern for junctional forces. To investigate the mechanism of the emergent frequency in tissue, we plot Rho GTPase activity in each cell in Figs. 4 and S2. We find that for cells on the periphery (e.g., cells 1 and 10), Rho GTPase activity oscillations are entrained with the cellular contractions and extensions. However, Rho GTPase activity in the interior (e.g., cells 5 and 6) is entrained to the lower frequency oscillations. Further, we observe Rho GTPase activity waves that propagate from the tissue periphery to the interior (see Video S3, dashed arrows), consistent with simulations shown in Zmurchok et al. (19).
Figure 4.
Dynamics of Rho GTPase activity in homogeneous tissue. Kymographs show the time course for cell positions (black), and color indicates Rho GTPase activity in each cell (Gi, for ) in (A) stationary and (B) migrating tissue. Note that time is on the horizontal axis. Parameters are tension-feedback β = 0.16 and (A) front-back polarity, δ = 0, (B) δ = 0.9. To see this figure in color, go online.
(Top) Representation of cell positions in a stationary tissue. Color of the cell corresponds to Rho GTPase activity, with blue denote a low level (0.2) and red denotes a high level (0.53). (Bottom) Position of cell fronts (red), centers (black), and backs (blue) are shown as a function of time. Note time is on the y-axis. Scale bar = 0.5. Video corresponds with results shown in Figs. 3 and 4 A. Parameters: β = 0.16, δ = 0.
We compare these tissue-scale results to the prior results from Zmurchok et al. (19), who also consider a one-dimensional array of cells, but without the presence of intercellular junctions. Periphery-to-interior Rho GTPase activity waves are also present in the Zmurchok et al. (19) model (Fig. S3 A, reproducing Fig. 5 B in (19)), demonstrating that intercellular junctions are not explicitly necessary for this wave behavior. We also compare our results with a variant of both the Zmurchok et al. (19) and adapted models in which we introduce a tissue-scale gradient in the viscosity, such that cells in the tissue front (back) are presented with a lower (higher) viscosity, however, without incorporating tension dependence or cellular front-back polarity. Introduction of a viscosity linear gradient in either the Zmurchok et al. (19) model or the adapted model with intercellular junctions results in the emergence of higher frequency mechanochemical oscillations in the tissue front (Fig. S3, B and C). Interestingly, despite a linear gradient, in both models, Rho GTPase waves still propagate from tissue periphery to interior. Further, the presence of intercellular junctions results in the faster frequency oscillations on the periphery (as in Fig. 4), whereas the multiple frequency oscillations do not occur in the Zmurchok et al. (19) model, suggesting that the intercellular junctions are responsible for higher frequency oscillations at the periphery. Additionally, we note that the introduction of the tissue-scale gradient in viscosity in either model did not result in tissue migration, suggesting that a cellular-scale front-back polarity is necessary for collective migration. Thus, our simulations predict that the tissue-scale emergent dynamics arise because of the interactions between cell-cell coupling and cellular Rho GTPase activity.
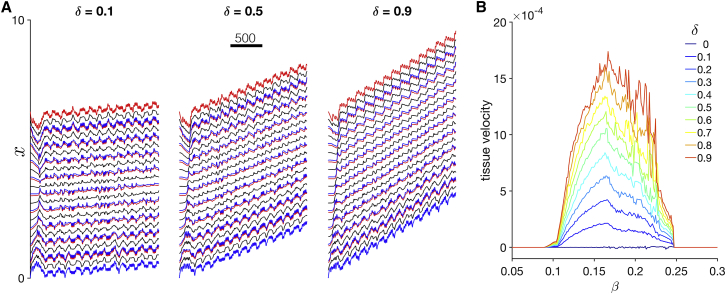
We next investigate simulations of homogeneous tissue in which individual cells do exhibit a front-back polarity (Fig. 5). As in the stationary tissue, the time course of cell positions exhibits complex emergent dynamics, specifically, multiple frequencies, a faster frequency associated with cell contraction and extension, and a slower frequency from tissue movement that emerges because of cell-cell coupling (Fig. 5 A). Further, as in individual cells, increasing the front-back polarity (i.e., increased δ) increases the velocity of the collective cell migration. In Figs. 4 B and S2 B, we plot Rho GTPase activity in the migrating tissue. As in the stationary tissue, Rho GTPase activity in the periphery exhibits high-frequency oscillations associated with cell contraction and extension, whereas the interior exhibits slower-frequency oscillations that are an emergent property of the tissue. Thus, cells at the periphery are regularly extending and contracting, whereas interior cells exhibit much less mechanical activity; interestingly, differences between oscillations at the periphery versus interior are highly sensitive to the individual cellular properties and associated intrinsic oscillation frequencies (also see Fig. 8).
Figure 5.
Dynamics of collective cell migration in homogeneous tissue. (A) The time course for cell positions (front (red) , center (black) , and back (blue) for ) are shown for different values of front-back polarity parameter δ. Collective cell migration velocity increases for increasing δ. (B) Tissue migration velocity is shown as a function of feedback-tension parameter β for different values of δ. Velocity is zero in the nonoscillatory β regime and a generally biphasic but jagged function of β in the oscillatory β regime. Parameters are (A) β = 0.16. To see this figure in color, go online.
Figure 8.
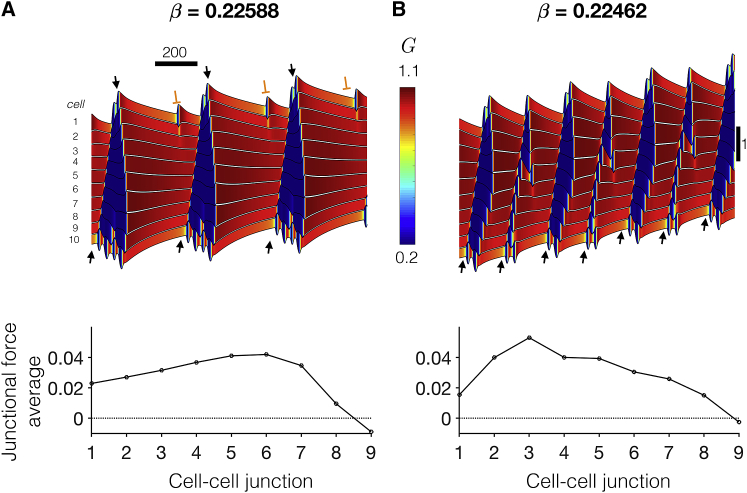
Mechanochemical resonance during collective cell migration. Kymographs show the time course for cell positions (black), and color indicates Rho GTPase activity for two values of tension-feedback parameter β (A and B) that differ by ∼1%. Successful and failed mechanical wave propagation are denoted by black arrows and orange block symbols, respectively. (Bottom) The spatial pattern of junctional force averages for the two examples is shown. Parameters are front-back polarity δ = 0.9. To see this figure in color, go online.
Further, we observe Rho GTPase activity waves propagating in the tissue. However, in contrast with the stationary tissue and previous work (19), Rho GTPase activity waves reorient with the tissue front-back polarity: we observe low Rho GTPase activity wave propagate from tissue back to front and then high Rho GTPase waves propagating front to back (see Video S4, dashed arrows). The timing of these Rho GTPase activity waves corresponds to the beginning and end of the emergent slower frequency, facilitating synchronization across the tissue, again demonstrating that interactions between cell-cell coupling and Rho GTPase activity drive emergent tissue properties.
(Top) Representation of cell positions in a migrating tissue. Color of the cell corresponds to Rho GTPase activity, with blue denote a low level (0.2) and red denotes a high level (0.53). (Bottom) Position of cell fronts (red), centers (black), and backs (blue) are shown as a function of time. Note time is on the y-axis. Scale bar = 0.5. Video corresponds with results shown in Figs. 4 B and 5 C. Parameters: β = 0.16, δ = 0.9.
We summarize the tissue velocity as a function of β for a range of δ values (Fig. 5 B). Velocity of the tissue is calculated as the slope from the linear regression of the first cell center versus time. We find several key similarities and differences between individual cells and tissues: As in individual cells, collective cell migration occurs only for β values within the oscillatory regime, and also similarly, velocity increases as δ increases. Further, we find that for a given β and δ parameter combination, migration velocity of the homogeneous tissue is slower compared to the corresponding individual cell. The general shape of the velocity dependence on β is also biphasic, as in individual cells. However, the velocity versus β traces are “noisy” or jagged in comparison to the smooth traces for individual cells (cf. Fig. 2 B), and this jaggedness is more pronounced for larger δ. This suggests that small changes in cell contractility (i.e., changes in β) can result in quite large changes in collective cell migration velocity, which emerges because of forces imposed at the cell-cell junctions that desynchronize oscillations of mechanically coupled cells, discussed in more detail later. In Supporting Materials and Methods, we plot the tissue velocity against the corresponding individual cell velocity for a given value of β and δ (Fig. S4) and show that, although in general, the tissue and individual cell velocities are proportional, that is not the case for all values of β.
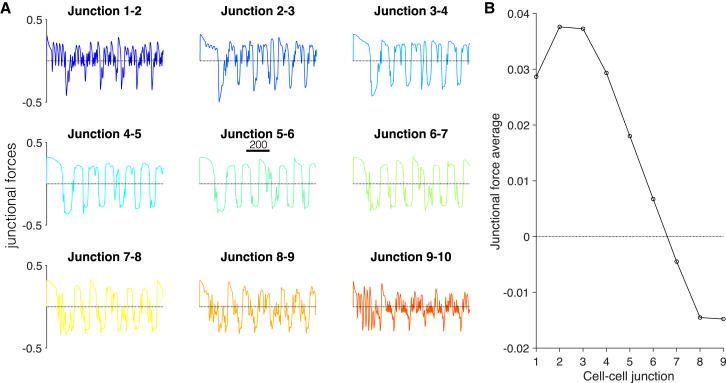
We next investigate junctional forces in collective cell migration (Fig. 6). As in the stationary tissue, the time course of junctional forces exhibits periods of both tension and compression; however, in contrast, forces are not symmetric (Fig. 6 A). We compute the average junctional force for each cell-cell junction and find that junctional forces at the front of migrating tissue are on average tensile, whereas junctional forces at the back of the tissue are on average compressive (Fig. 6 B). The junctional force average exhibits a distinct spatial pattern, with largest forces near, but not at, the tissue front and a gradual decrease toward the tissue back.
Figure 6.
Spatial pattern of junctional forces in collective cell migration. (A) The time course of each cell-cell junction exhibits multiple frequencies, in particular at the tissue periphery. (B) The junction force average is shown as a function of the cell-cell junction (with one corresponding to the cell 1-cell 2 junction at the tissue front). The junctional force average exhibits a maximal near, but not at, the tissue front and then decreases toward the tissue back. Parameters are β = 0.16 and δ = 0.5. To see this figure in color, go online.
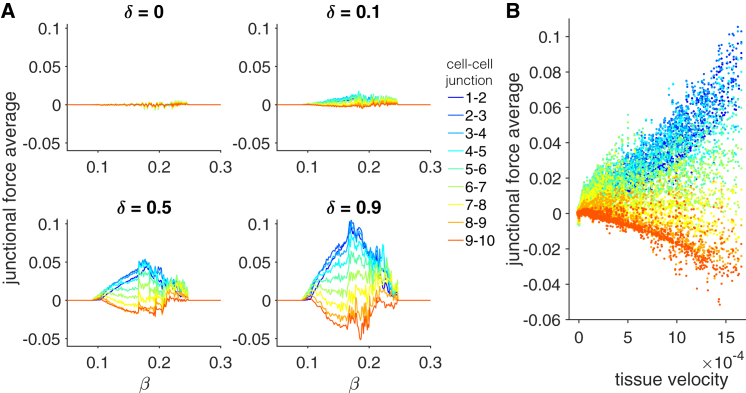
In Fig. 7 A, we plot cell-cell junctional force averages as a function of β for different values of δ. We find that for all migrating tissues (i.e., δ > 0), we find the same general spatial pattern for all values of β: the largest force is near, but not at, the tissue front and decreases toward the tissue back. Further, the magnitude of junctional force averages is generally larger for tissues with faster velocities (cf. Fig. 5 B): the junctional forces are generally “jagged” biphasic functions of β, and junctional force magnitudes increase for increasing δ. A scatter plot of the junctional force averages for the different cell-cell junctions plotted against the corresponding tissue velocity for all values of β and δ further demonstrate that larger magnitude junctional forces in the tissue front and back are associated with faster tissue velocities (Fig. 7 B).
Figure 7.
Spatial pattern of junctional forces depends on tension-feedback and front-back polarity. (A) Junctional force averages are shown for all cell-cell junction pairs as a function of tension-feedback β for different values of front-back polarity δ. For migratory tissues (δ > 0), junctional force averages in general decrease from the tissue front (cell 1-cell 2 junction) to the tissue back. The magnitude of junctional force averages generally increases with increasing δ and follows a jagged biphasic dependence on β. (B) A scatter plot of the junctional force averages for different cell-cell junction pairs (different colors) against the corresponding tissue velocity, calculated from simulations for varying β and δ demonstrate that larger magnitude junctional forces occur for faster collective cell migration. To see this figure in color, go online.
We next investigate the mechanism of steep sensitivity to the feedback tension (β) in collective cell migration. In Fig. 8, we consider two tissues, with β values differing by ∼1%. For β = 0.22588 (Fig. 8 A), we find that the cell position’s time course is comparable to the examples in Fig. 5 A, with oscillations corresponding to cell contraction and extension and slower emergent frequency from mechanical coupling between cells. Further, the time courses also reveal mechanical “waves” that propagate from the tissue back to front and from front to back that arise because of synchronization of individual cell extensions (black arrows). However, there are also several instances in which the mechanical waves “fail” and do not propagate to the tissue front (orange block symbol) because of desynchronization between the individual cells.
For a slightly smaller β = 0.22462 (Fig. 8 B), the oscillation period of individual cells is shorter, such that after an initial transient, all mechanical waves successfully propagate from back to front. Rho GTPase activity facilitates a tissue-wide synchronization such that the emergent tissue frequency is nearly twice that for the slightly larger β value. This synchronization can be described as a “mechanochemical resonance,” in which the individual cell oscillation frequency more closely matches the emergent tissue frequency that results in an increased collective cell migration velocity (see Video S5). As such, the 1% change in β results in an ∼51% change in velocity (0.001142 vs. 0.0005770). The junctional force average spatial patterns are similar to previous examples; however, for the slower migrating tissue, the largest junctional forces are more toward the tissue interior.
Mechanochemical resonance during collective cell migration. Representation of cell positions in migrating tissues with small differences in tension feedback parameter β. Color of the cell corresponds to Rho GTPase activity, with blue denote a low level (0.2) and red denotes a high level (1.1). Scale bar = 0.5. Video corresponds with results shown in Fig. 8. Parameters: δ = 0.9.
Importantly, we should note that measuring such small changes in a cellular property with 1% accuracy is not realistic in an experimental setting. However, these simulations highlight the significance of steep parameter sensitivity that occurs near the bifurcation from an oscillatory to contractile state that occurs in the single cell case for varying β. Near the bifurcation in the single cell, there is steep dependence of the period on β (Fig. S1 C), which alters tissue-wide synchronization, and as a consequence, in this regime, tissue migration velocity is predicted to be highly sensitive to small changes in feedback tension.
Summary plots of tissue velocity for tissues of different sizes are shown in Fig. S5 A. Tissue velocity in general decreases as the size of the tissue increases. We also find the same general trends in all tissue sizes: velocity increases as δ increases, and there is a jagged biphasic dependence on β, although the “peak” β value differs somewhat for different tissue sizes. We also find the same general junctional force average spatial patterns in tissues of different sizes (Fig. S5 B), with the largest forces near, but not at, the tissue front. Additionally, larger magnitude forces are observed in larger tissues.
Heterogeneous tissues
We next investigate collective cell migration in heterogeneous tissues. Specifically, we consider the case in which the properties of the cell at the front of the tissue, the lead cell, has different properties than the other nine trailing cells toward the back of the tissue. Further, we are interested in the case in which the lead cell would individually migrate faster compared to the trailing cells individually (see Fig. 2 B). For simplicity, we limit our study to cases in which either β or δ is the same throughout the tissue. If we consider a single cell simulation with (β, δ) parameters corresponding to a migration velocity near the peak of the biphasic curves in Fig. 2 B, it should be clear that migration velocity may be slower from one of three possible parameter changes: 1) decreasing β (keeping δ constant), 2) increasing β (keeping δ constant), or 3) decreasing δ (keeping β constant).
We show an example of heterogeneous tissue migration in Fig. 9. Parameters for the lead cell are β = 0.16 and δ = 0.9, which an individual cell with corresponding parameters would have a velocity of ∼0.005018. Parameters for the nine trailing cells are such that individual cells would have a migration velocity of 20% of the lead cell individual velocity, ∼0.001004. In Fig. 9 A, the trailing cells parameters are smaller, β = 0.1082, and the same δ = 0.9, and in Fig. 9 B, the trailing cells parameters are a larger, β = 0.2454, and the same δ = 0.9 compared to the lead cell. In both of these examples, the time series of cell positions illustrates that cell contractions and extensions are less pronounced compared to the homogeneous tissues. In Fig. 9 C, the trailing cells parameters are the same, β = 0.16, and a smaller δ = 0.1885. The cell positions exhibit larger cell contractions and extensions compared to the low and high β examples but smaller compared to homogeneous tissues.
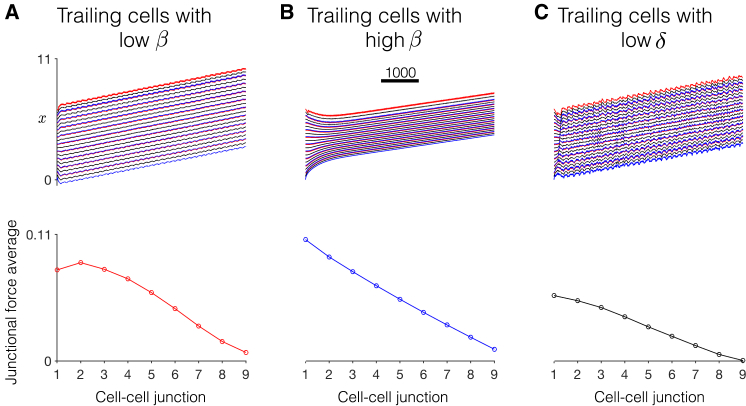
Figure 9.
Dynamics of collective cell migration in heterogeneous tissue. (Top) The time course for cell positions (front (red) , center (black) , and back (blue) for ) are shown for different trailing cell properties, relative to the lead cell, with (A) low β, (B) high β, and (C) low δ trailing cells. See the text for details. (Bottom) The spatial pattern of junctional force averages as a function of the cell-cell junction is shown. Parameters are lead cell: δ = 0.9, β = 0.16. Trailing cells have a scaling factor of 0.2: (A) δ = 0.9, β = 0.1082, (B) δ = 0.9, β = 0.2454, and (C) δ = 0.1885, β = 0.16. To see this figure in color, go online.
Interestingly, we find that the heterogeneous tissue with low β trailing cells has the fastest migration velocity, the tissue with low δ is the next fastest, and the tissue with high β is the slowest. These differences are likely due to the different intrinsic oscillation periods and amplitudes of the trailing cells in each case. For the trailing cells with low β, the amplitude and period of the individual trailing cell’s oscillations are relatively close to the lead cell such that a larger degree of mechanical synchronization occurs as well as a faster resulting tissue velocity. In contrast, for high β trailing cells, the amplitude and period of the trailing cell’s oscillations differ dramatically from the lead cell, resulting in mechanical desynchronization and a slow tissue velocity. In the tissue with low δ trailing cells, although the individual cells have the same intrinsic period, the different front-back polarities introduce some degree of desynchronization, similar to that observed in the homogeneous tissue. The spatial pattern of junctional force averages is similar to previous examples, with the largest forces at or near the tissue front and decreasing toward the tissue back. However, we also find that average junctional forces are positive at the tissue back, in contrast with the homogeneous tissue example in Fig. 6 B. Additionally, we find a less clear correlation between junctional forces and velocity in the heterogeneous tissues, in contrast with homogeneous tissues. The tissue with high β trailing cells, i.e., the slowest tissue, exhibits the largest junctional force averages, whereas the tissue with low δ trailing cells, that is, the second fastest tissue, exhibits the smallest junction force averages.
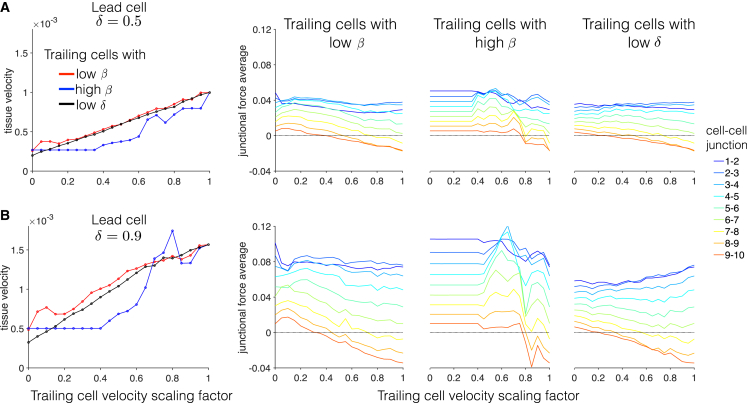
In Fig. 10, we summarize a wide range of similar heterogeneous tissue simulations, measuring tissue velocity and junctional forces as a function of the trailing cell velocity scaling factor (e.g., 0.2 in Fig. 9) for trailing cells with low β, high β, and low δ, relative to the lead cell. For a lead cell with β = 0.16 and δ = 0.5 (Fig. 10 A), tissue velocity increases as the trailing cell velocity scaling factor increases. That is, as might be expected, as the velocity of the individual trailing cells increases and becomes closer to the lead cell velocity, collective cell migration is faster. As in Fig. 9, collective cell migration is faster for trailing cells with low β. Velocity is similar for low δ trailing cells, and velocity is slower for high β trailing cells.
Figure 10.
Summary of heterogeneous tissue cell migration properties. (Left) For lead cells with δ = (A) 0.5 and (B) 0.9, tissue velocity is shown against the trailing cell velocity scaling factor for low β (red), high β (blue), and low δ (black) trailing cells. See the text for details. (Right) Junction force averages are shown for all cell-cell junction pairs as a function of the trailing cell velocity scaling factor. Parameters are lead cell: β = 0.16. The tissue size comprises 10 cells. To see this figure in color, go online.
Spatial patterns of junctional forces for different trailing cell velocity scaling factors demonstrate the junctional force decrease from the tissue front to back, as described above. As in Fig. 9, for small scaling factors, junctional forces are positive at the tissue back. As the scaling factor increases, the magnitude of junctional forces at the tissue front remains fairly constant, whereas junctional forces at the tissue back decrease and become negative for larger scaling factors. Noting that this change in junctional forces occurs in conjunction with increasing tissue velocity suggests that negative average junctional forces at the tissue back promote faster migration.
In Fig. 10 B, we consider a lead cell with δ = 0.9. We observed similar trends as in Fig. 10 A, with larger velocities and larger magnitude junctional forces, consistent with trends in the homogeneous tissue in Figs. 5 and 7, respectively. Interestingly, we find that for high β trailing cells, whereas tissue velocity is generally slow for small scaling factors, for larger scaling factors, tissue velocities are faster than the homogeneous tissue (scaling factor of 1), demonstrating that mechanical synchronization within the tissue of slower individual cells can result in faster migration than weaker synchronization of faster individual cells. We also note that for trailing cell velocity scaling factor of 0, the trailing cells individually are stationary; however, the collective cell migration velocity is still nonzero for all three cases. Thus, the model predicts that a single migratory lead cell can drive collective cell migration of a tissue composed primarily of nonmigratory cells. This is an interesting prediction, although additional details regarding the source and degree of heterogeneity within the cell population are needed to make more conclusive predictions.
Discussion
Summary of main findings
In this study, we adapted a minimal framework for modeling the dynamics of Rho GTPase-mediated migration of individual cells and tissue in one dimension. Individual cell simulations required periodic Rho GTPase activity for migration (Fig. 2), consistent with experiments demonstrating that Rho GTPase-mediated contractility is necessary for migration (12, 13, 25, 26). We find both similarities and differences between individual and collective cell migration. Although mechanical coupling of individual cells with fast migration velocity generally corresponds to faster collective migration, the model predicts that tissue migration velocity is not simply governed by individual migration velocities alone (Figs. 5 and S4). We find that collective migration is governed by propagating waves of Rho GTPase activity that synchronize mechanical waves. As a result, the model predicts high sensitivity to the individual cell tension feedback (Fig. 8) in which small changes can result in large differences in tissue synchronization. We also find that collective migration exhibits a distinct spatial pattern for junctional forces (Fig. 6), with larger forces near the leading edge of the tissue, and further, that larger junctional forces correspond with faster collective migration and large tissues. Finally, we predict in heterogeneous tissues that a single migratory leader cell can drive migration of a tissue composed of slowly migrating trailing cells in a manner that is highly dependent on the properties of the trailing cells (Fig. 9).
Insights from a passive mechanical tissue model
We can derive additional insight into what governs the spatial patterns of junctional forces by considering a purely passive tissue model with comparable geometry. If we neglect the active nonlinear dynamics of individual cell contractility and reduce each individual cell to a node, the one-dimensional tissue can thus be represented by nodes connected by junctional springs with constant ks and resting length Ls, with friction or a viscous element at each node. Further, if we assume that cellular migration is mediated by a constant force Fi applied at each node i, then the dynamics of this n-node passive system are governed by the following:
| (3a) |
| (3b) |
| (3c) |
For the case in which all nodes have the same applied force F, then the position of each node increases constantly in time, with velocity . However, the junctional force between nodes i and i + 1, given by fi = ks (xi − xi+1 − Ls), is equal to zero for all junctions, that is, no junctional forces are present. It is trivially the case that the position of uncoupled nodes, each governed by , would also increase constantly in time with velocity , and thus we see that in this case, the presence of junctional springs has no influence on individual node dynamics.
An additional interesting case is the situation in which F1 = F and Fi = 0 for , that is, a constant force is applied only at the front of the tissue. In this case, the position of each node will also increase constantly in time and after an initial transient, with velocity (Fig. S6 A). Further, it can be shown that at steady state, the junctional force is given by fi = F(1 − i/n) (Fig. S6, B and C). Thus, in the passive model, the junctional force is a linearly decreasing function of the position from the tissue front. Further, junctional forces increase proportionally as the applied force increases.
Comparing the passive model and adapted model presented here illustrates two key insights into the biological significance of Rho GTPase oscillations and the interaction between active and passive tissue properties. For the case of cells that are all moving in response to a constant force, the passive model predicts that mechanically coupling these cells would produce no junctional forces. In contrast, the adapted model with Rho GTPase-mediated contractility does in fact exhibit nonzero junctional forces with distinct spatial patterns and further exhibits that these forces arise because of the fact that individual cells are not driven by a constant force but rather mechanical oscillations. Thus, our results suggest that one critical role of Rho GTPase activity oscillations at the cellular level is to drive migration mediated by periodic contractility (and not a constant force), which in turn drives the formation of junctional forces. These junctional forces further feedback and alter cellular tension, which facilitates tissue-wide Rho GTPase activity synchronization.
For the case of force applied at the tissue front, the passive model demonstrates that the spatial gradient (i.e., higher forces at the tissue front decreasing toward the back) that we observe in the adapted model can be partially explained by the combined effects of an unbalanced net force present at the tissue front and friction with an underlying substrate. However, we note that the spatial patterns observed did not generally strictly follow a linear decrease from front to back (as in the passive model) but typically exhibited a peak near, but not at, the front (e.g., Fig. 6). In some cases, the peak was closer to the tissue back (e.g., Fig. 8), whereas heterogeneous tissues did appear to exhibit a more linear decrease (e.g., Fig. 9, B and C). Thus, the distinct junctional force spatial pattern that is established arises because of both passive mechanical tissue properties and the emergent active properties mediated by cellular contractility.
Prior computational studies of cell migration
There are many prior computational studies of individual and collective cell migration, incorporating a wide range of biophysical detail (20, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36). For example, Zaman and colleagues (27, 28, 29) minimally model individual cell migration, integrating a force-based model of an individual cell with the interactions between cellular and extracellular mechanical forces and extracellular matrix signaling. Other studies have considered a more spatially detailed physical representation of mechanical interactions between individual cells and the extracellular matrix (31, 32). Lopez et al. (20) utilized the same one-dimensional spring representation as we consider here, with cell contraction and extension driven by hysteresis in the cell spring resting length and cell front viscosity terms. Vertex-based models have been developed to study collective migration in a cell sheet or tissue, modeling tissue-scale dynamics such as morphogenesis, which consider mechanical force balance at each node along the boundary of cells and accounting for active and passive mechanical forces (37, 38, 39). Szabó et al. (40) integrated individual cell mechanics into a Cellular Potts framework to predict collective migration in cell sheets. Guven et al. (41) demonstrated that collective migration driven by a chemotactic gradient is primarily governed by chemoattractant secretion and degradation rates.
Whereas these studies focused primarily on the dynamics of cellular and extracellular mechanical interactions, other studies of cell migration have focused more on intracellular and extracellular biochemical signaling. For example, Jilkine et al. (34) investigated multiple possible interaction schemes between the Cdc42, Rac, and Rho GTPase proteins that give rise to physiological spatial polarization. Marée et al. (33) extended a spatially distributed model of Rho GTPase proteins interacting with actin filament dynamics, coupled to a Cellular Potts model accounting for spatial aspects of cellular polarization and protrusion. Merks and colleagues (42, 43, 44, 45) have developed several cellular Potts modeling approaches, coupling cell-cell and cell-extracellular matrix interaction energetic constraints with extracellular biochemical concentrations to study collective cell migration and tissue dynamics in several physiological settings, including angiogenesis and tumor invasion.
Thus, many of these prior studies have accounted for detailed representations of either mechanical or biochemical signaling. Our approach, extended from prior work from Zmurchok et al. (19), represented a compromise between accounting for both mechanical and biochemical signaling and feedback while still utilized a minimal approach that facilitated wide-ranging parameter studies to characterize model behavior. With comparison of our work to this prior study, Zmurchok et al. (19) also observed center-to-periphery Rho GTPase propagating waves in one-dimensional simulations of stationary tissue (comparable to Fig. 4 A), suggesting that junctional forces are not necessary for this mechanochemical synchronization (because junctional forces are not specifically represented in Zmurchok et al. (19)). Interestingly, by accounting for individual cell front-back polarity, we find that the mechanochemical waves also reorient to a tissue back-to-front and front-to-back propagating pattern in a migrating tissue (Fig. 4 B).
Physiological significance
Despite the minimal nature of our model, we can gain useful insights for understanding fundamental in vivo processes involving cell migration, in particular to understand the role of forces in subsets of collective cell migration. For example, chain migration of cells is defined as cells that start as a cluster and delineate away in a single file line toward a chemotactic gradient (46) and has been demonstrated in vivo. The chain migration of neural crest cells, probed in vitro, showed that high cell tension at the periphery inhibits spreading and migration, whereas lower tension in the leader cell promotes leader cell spreading and higher traction forces at later stages of migration (47). Our study predicts that migrating tissue has a high sensitivity to cellular tension feedback, and thus changes in cellular tension at different stages of collective migration may be a biological mechanism for tuning speed of a migrating tissue.
Leader cells have also been shown to be important in cancer metastasis, driving the collective migration of multicellular groups of cancerous cells into the surrounding tissue (48). Interestingly, simulations of heterogeneous tissues predict that a single migratory leading cell can sufficiently drive migration of a tissue composed of slow or stationary trailing cells, suggesting that metastasis may not require a population of primarily motile cancerous cells. Further, our simulations predict that as the migrating tissue size increases, collective migration speed increases. Thus, our simulations suggest that as a tumor grows in size, there may be a critical point at which migrating velocity is sufficient for metastasis, although more physiological details on the heterogeneity within these populations is needed to connect our simulations with experiments.
The presented model may also be compared with physiological branching morphogenesis. In branching morphogenesis occurring in the lung, kidney, vascular system, prostate, mammary gland, and kidney to form tubular branching structures, a leader or “tip” cell responds to a chemotactic or durotactic gradient and protrudes while bringing along follower or “stalk” cells through adhesion junctions. Several studies have shown that mechanically sensitive molecules such as YAP (49), integrin β1 (50), and the TRPV4 ion channel (51) are needed for proper branching morphogenesis, yet measurement of cell-cell force during this process in vivo is limited. Because in vivo collective cell migration is difficult to quantify, especially with respect to cell-cell forces, the presented model provides a method for investigating this fundamental aspect of development and disease and, further, how perturbations, such as dysfunctional cell-cell junction force or enhanced contractility, could alter these processes. Our future work is particularly interested in extending the adapted modeling framework to predict the role in which junctional forces regulate cell division during the morphogenesis process.
Perhaps most relevant to this model is experimental work by Fredberg and colleagues (52) in which measurement of traction forces of migrating sheets of epithelial cells showed significant mechanical forces not only at the leading edge but several rows behind. However, in contrast with most of the model predictions (e.g., Figs. 6 and 7), the traction force measurements of Fredberg and colleagues (52) demonstrate highest cell-cell junction forces for cells far away from the leading edge. Although there are many physical differences between the two-dimensional epithelial sheet migration and one-dimensional migration studied here, these differences could alter tension feedback in subtle ways that result in junctional force spatial patterns comparable to Fig. 8 A, in which larger junctional forces are present away from the leading edge. We are also interested in extending our approach to simulate migration in two and three dimensions, to specifically investigate how these additional degrees of freedom in motion alter the formation of junctional forces.
Limitations
The model formulation used in this study is inherently minimal by design. Specifically, we did not consider interactions between different Rho GTPase proteins, namely, the cross talk and mutual feedback between Cdc42, Rho, and Rac nor the well-established subcellular front-back spatial localization of these proteins during polarization and migration (17, 53). Prior work using detailed multiscale models from Edelstein-Keshet and colleagues (11, 33, 34) has shown that spatial segregation of the Rho GTPase proteins is critical for robust polarization. Similarly, whereas cellular extension, contraction, and migration are inherently a two- or three-dimensional behavior, as focal adhesion formation and integrin binding occurring over a distributed subcellular volume and surface area, respectively, our adapted model minimally represents a single direction or dimension for migration. It would be of interest to consider more spatially detailed representations of these processes; however, an approach accounting for subcellular spatial concentration distributions in a multicellular tissue would be computationally expensive compared to the minimal approach presented here. An interesting compromise would be to account for separate Rho GTPase pools in the cell front and back as recently demonstrated by Holmes et al. (21); we will consider this approach in future work. Finally, the presented model does not consider feedback between junctional forces and intracellular cytoskeletal signaling, such as global rearrangements of the cytoskeleton, which in turn may influence properties of Rho GTPase signaling and/or mechanical properties related to cell contractility or focal adhesion formation. Incorporating these relationships is a natural extension of our work presented here and is an area of interest that we will consider in future work. Our initial focus was to investigate fundamental relationships between key processes governing collective cell migration, specifically intracellular Rho GTPase activity, cellular mechanical forces, and intercellular junctional force interactions.
Conclusions
In this study, model predictions illustrate that collective cell migration is governed by emergent mechanochemical interactions, propagating waves of Rho GTPase activity that synchronize mechanical contraction and extension throughout the tissue. Cell-cell junctional forces exhibit a distinct spatial pattern, with larger forces near the leading edge of the tissue and larger junctional forces associated with faster collective migration. Finally, simulations in both homogeneous and heterogeneous tissue illustrate that collective migration does not depend simply on the velocity of individual cells comprising the tissue but additionally on the mechanochemical interactions that govern intercellular junctional forces and synchronization within the tissue.
Author Contributions
S.H.W. designed the research. J.B. and S.H.W. carried out all simulations and analyzed the data. D.E.C., R.L.H., and S.H.W. wrote the article.
Acknowledgments
This work was supported by the National Institutes of Health via awards R01GM122855 (S.H.W.) and R35GM119617 (D.E.C.).
Editor: Stanislav Shvartsman.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.05.020.
Supporting Material
References
- 1.Rørth P. Collective cell migration. Annu. Rev. Cell Dev. Biol. 2009;25:407–429. doi: 10.1146/annurev.cellbio.042308.113231. [DOI] [PubMed] [Google Scholar]; Rorth, P. 2009. Collective cell migration. Annu. Rev. Cell Dev. Biol. 25:407-429. [DOI] [PubMed]
- 2.Friedl P., Hegerfeldt Y., Tusch M. Collective cell migration in morphogenesis and cancer. Int. J. Dev. Biol. 2004;48:441–449. doi: 10.1387/ijdb.041821pf. [DOI] [PubMed] [Google Scholar]; Friedl, P., Y. Hegerfeldt, and M. Tusch. 2004. Collective cell migration in morphogenesis and cancer. Int. J. Dev. Biol. 48:441-449. [DOI] [PubMed]
- 3.Friedl P., Gilmour D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 2009;10:445–457. doi: 10.1038/nrm2720. [DOI] [PubMed] [Google Scholar]; Friedl, P., and D. Gilmour. 2009. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 10:445-457. [DOI] [PubMed]
- 4.Weinberg S.H., Mair D.B., Lemmon C.A. Mechanotransduction dynamics at the cell-matrix interface. Biophys. J. 2017;112:1962–1974. doi: 10.1016/j.bpj.2017.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]; Weinberg, S. H., D. B. Mair, and C. A. Lemmon. 2017. Mechanotransduction dynamics at the cell-matrix interface. Biophys. J. 112:1962-1974. [DOI] [PMC free article] [PubMed]
- 5.Goehring N.W., Grill S.W. Cell polarity: mechanochemical patterning. Trends Cell Biol. 2013;23:72–80. doi: 10.1016/j.tcb.2012.10.009. [DOI] [PubMed] [Google Scholar]; Goehring, N. W., and S. W. Grill. 2013. Cell polarity: mechanochemical patterning. Trends Cell Biol. 23:72-80. [DOI] [PubMed]
- 6.Mayor R., Etienne-Manneville S. The front and rear of collective cell migration. Nat. Rev. Mol. Cell Biol. 2016;17:97–109. doi: 10.1038/nrm.2015.14. [DOI] [PubMed] [Google Scholar]; Mayor, R., and S. Etienne-Manneville. 2016. The front and rear of collective cell migration. Nat. Rev. Mol. Cell Biol. 17:97-109. [DOI] [PubMed]
- 7.Bishop A.L., Hall A. Rho GTPases and their effector proteins. Biochem. J. 2000;348:241–255. [PMC free article] [PubMed] [Google Scholar]; Bishop, A. L., and A. Hall. 2000. Rho GTPases and their effector proteins. Biochem. J. 348:241-255. [PMC free article] [PubMed]
- 8.Etienne-Manneville S., Hall A. Rho GTPases in cell biology. Nature. 2002;420:629–637. doi: 10.1038/nature01148. [DOI] [PubMed] [Google Scholar]; Etienne-Manneville, S., and A. Hall. 2002. Rho GTPases in cell biology. Nature. 420:629-637. [DOI] [PubMed]
- 9.Hall A. Rho GTPases and the control of cell behaviour. Biochem. Soc. Trans. 2005;33:891–895. doi: 10.1042/BST20050891. [DOI] [PubMed] [Google Scholar]; Hall, A. 2005. Rho GTPases and the control of cell behaviour. Biochem. Soc. Trans. 33:891-895. [DOI] [PubMed]
- 10.Friedl P., Wolf K., Zegers M.M. Rho-directed forces in collective migration. Nat. Cell Biol. 2014;16:208–210. doi: 10.1038/ncb2923. [DOI] [PubMed] [Google Scholar]; Friedl, P., K. Wolf, and M. M. Zegers. 2014. Rho-directed forces in collective migration. Nat. Cell Biol. 16:208-210. [DOI] [PubMed]
- 11.Holmes W.R., Edelstein-Keshet L. Analysis of a minimal Rho-GTPase circuit regulating cell shape. Phys. Biol. 2016;13:046001. doi: 10.1088/1478-3975/13/4/046001. [DOI] [PubMed] [Google Scholar]; Holmes, W. R., and L. Edelstein-Keshet. 2016. Analysis of a minimal Rho-GTPase circuit regulating cell shape. Phys. Biol. 13:046001. [DOI] [PubMed]
- 12.Nobes C.D., Hall A. Rho GTPases control polarity, protrusion, and adhesion during cell movement. J. Cell Biol. 1999;144:1235–1244. doi: 10.1083/jcb.144.6.1235. [DOI] [PMC free article] [PubMed] [Google Scholar]; Nobes, C. D., and A. Hall. 1999. Rho GTPases control polarity, protrusion, and adhesion during cell movement. J. Cell Biol. 144:1235-1244. [DOI] [PMC free article] [PubMed]
- 13.Allena R., Scianna M., Preziosi L. A Cellular Potts Model of single cell migration in presence of durotaxis. Math. Biosci. 2016;275:57–70. doi: 10.1016/j.mbs.2016.02.011. [DOI] [PubMed] [Google Scholar]; Allena, R., M. Scianna, and L. Preziosi. 2016. A Cellular Potts Model of single cell migration in presence of durotaxis. Math. Biosci. 275:57-70. [DOI] [PubMed]
- 14.He L., Tao J., Sun S.X. Role of membrane-tension gated Ca2+ flux in cell mechanosensation. J. Cell Sci. 2018 doi: 10.1242/jcs.208470. 131:jcs208470. [DOI] [PMC free article] [PubMed] [Google Scholar]; He, L., J. Tao, …, S. X. Sun. 2018. Role of membrane-tension gated Ca2+ flux in cell mechanosensation. J. Cell Sci.131:jcs208470. [DOI] [PMC free article] [PubMed]
- 15.Katsumi A., Milanini J., Schwartz M.A. Effects of cell tension on the small GTPase Rac. J. Cell Biol. 2002;158:153–164. doi: 10.1083/jcb.200201105. [DOI] [PMC free article] [PubMed] [Google Scholar]; Katsumi, A., J. Milanini, …, M. A. Schwartz. 2002. Effects of cell tension on the small GTPase Rac. J. Cell Biol. 158:153-164. [DOI] [PMC free article] [PubMed]
- 16.Reffay M., Parrini M.C., Silberzan P. Interplay of RhoA and mechanical forces in collective cell migration driven by leader cells. Nat. Cell Biol. 2014;16:217–223. doi: 10.1038/ncb2917. [DOI] [PubMed] [Google Scholar]; Reffay, M., M. C. Parrini, …, P. Silberzan. 2014. Interplay of RhoA and mechanical forces in collective cell migration driven by leader cells. Nat. Cell Biol. 16:217-223. [DOI] [PubMed]
- 17.Machacek M., Hodgson L., Danuser G. Coordination of Rho GTPase activities during cell protrusion. Nature. 2009;461:99–103. doi: 10.1038/nature08242. [DOI] [PMC free article] [PubMed] [Google Scholar]; Machacek, M., L. Hodgson, …, G. Danuser. 2009. Coordination of Rho GTPase activities during cell protrusion. Nature. 461:99-103. [DOI] [PMC free article] [PubMed]
- 18.Mohan A., Schlue K.T., Conway D.E. Spatial proliferation of epithelial cells is regulated by E-cadherin force. Biophys. J. 2018;115:853–864. doi: 10.1016/j.bpj.2018.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]; Mohan, A., K. T. Schlue, …, D. E. Conway. 2018. Spatial proliferation of epithelial cells is regulated by E-cadherin force. Biophys. J. 115:853-864. [DOI] [PMC free article] [PubMed]
- 19.Zmurchok C., Bhaskar D., Edelstein-Keshet L. Coupling mechanical tension and GTPase signaling to generate cell and tissue dynamics. Phys. Biol. 2018;15:046004. doi: 10.1088/1478-3975/aab1c0. [DOI] [PubMed] [Google Scholar]; Zmurchok, C., D. Bhaskar, and L. Edelstein-Keshet. 2018. Coupling mechanical tension and GTPase signaling to generate cell and tissue dynamics. Phys. Biol. 15:046004. [DOI] [PubMed]
- 20.Lopez J.H., Das M., Schwarz J.M. Active elastic dimers: cells moving on rigid tracks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2014;90:032707. doi: 10.1103/PhysRevE.90.032707. [DOI] [PubMed] [Google Scholar]; Lopez, J. H., M. Das, and J. M. Schwarz. 2014. Active elastic dimers: cells moving on rigid tracks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 90:032707. [DOI] [PubMed]
- 21.Holmes W.R., Park J., Edelstein-Keshet L. A mathematical model coupling polarity signaling to cell adhesion explains diverse cell migration patterns. PLoS Comput. Biol. 2017;13:e1005524. doi: 10.1371/journal.pcbi.1005524. [DOI] [PMC free article] [PubMed] [Google Scholar]; Holmes, W. R., J. Park, …, L. Edelstein-Keshet. 2017. A mathematical model coupling polarity signaling to cell adhesion explains diverse cell migration patterns. PLoS Comput. Biol. 13:e1005524. [DOI] [PMC free article] [PubMed]
- 22.Park J., Holmes W.R., Levchenko A. Mechanochemical feedback underlies coexistence of qualitatively distinct cell polarity patterns within diverse cell populations. Proc. Natl. Acad. Sci. USA. 2017;114:E5750–E5759. doi: 10.1073/pnas.1700054114. [DOI] [PMC free article] [PubMed] [Google Scholar]; Park, J., W. R. Holmes, …, A. Levchenko. 2017. Mechanochemical feedback underlies coexistence of qualitatively distinct cell polarity patterns within diverse cell populations. Proc. Natl. Acad. Sci. USA. 114:E5750-E5759. [DOI] [PMC free article] [PubMed]
- 23.Barnhart E.L., Allen G.M., Theriot J.A. Bipedal locomotion in crawling cells. Biophys. J. 2010;98:933–942. doi: 10.1016/j.bpj.2009.10.058. [DOI] [PMC free article] [PubMed] [Google Scholar]; Barnhart, E. L., G. M. Allen, …, J. A. Theriot. 2010. Bipedal locomotion in crawling cells. Biophys. J. 98:933-942. [DOI] [PMC free article] [PubMed]
- 24.Giannone G., Dubin-Thaler B.J., Sheetz M.P. Periodic lamellipodial contractions correlate with rearward actin waves. Cell. 2004;116:431–443. doi: 10.1016/s0092-8674(04)00058-3. [DOI] [PubMed] [Google Scholar]; Giannone, G., B. J. Dubin-Thaler, …, M. P. Sheetz. 2004. Periodic lamellipodial contractions correlate with rearward actin waves. Cell. 116:431-443. [DOI] [PubMed]
- 25.Plotnikov S.V., Waterman C.M. Guiding cell migration by tugging. Curr. Opin. Cell Biol. 2013;25:619–626. doi: 10.1016/j.ceb.2013.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]; Plotnikov, S. V., and C. M. Waterman. 2013. Guiding cell migration by tugging. Curr. Opin. Cell Biol. 25:619-626. [DOI] [PMC free article] [PubMed]
- 26.Tkachenko E., Sabouri-Ghomi M., Ginsberg M.H. Protein kinase A governs a RhoA-RhoGDI protrusion-retraction pacemaker in migrating cells. Nat. Cell Biol. 2011;13:660–667. doi: 10.1038/ncb2231. [DOI] [PMC free article] [PubMed] [Google Scholar]; Tkachenko, E., M. Sabouri-Ghomi, …, M. H. Ginsberg. 2011. Protein kinase A governs a RhoA-RhoGDI protrusion-retraction pacemaker in migrating cells. Nat. Cell Biol. 13:660-667. [DOI] [PMC free article] [PubMed]
- 27.Harjanto D., Zaman M.H. Matrix mechanics and receptor-ligand interactions in cell adhesion. Org. Biomol. Chem. 2010;8:299–304. doi: 10.1039/b913064k. [DOI] [PubMed] [Google Scholar]; Harjanto, D., and M. H. Zaman. 2010. Matrix mechanics and receptor-ligand interactions in cell adhesion. Org. Biomol. Chem. 8:299-304. [DOI] [PubMed]
- 28.Harjanto D., Zaman M.H. Computational study of proteolysis-driven single cell migration in a three-dimensional matrix. Ann. Biomed. Eng. 2010;38:1815–1825. doi: 10.1007/s10439-010-9970-0. [DOI] [PubMed] [Google Scholar]; Harjanto, D., and M. H. Zaman. 2010. Computational study of proteolysis-driven single cell migration in a three-dimensional matrix. Ann. Biomed. Eng. 38:1815-1825. [DOI] [PubMed]
- 29.Vargas D.A., Zaman M.H. Computational model for migration of a cell cluster in three-dimensional matrices. Ann. Biomed. Eng. 2011;39:2068–2079. doi: 10.1007/s10439-011-0290-9. [DOI] [PubMed] [Google Scholar]; Vargas, D. A., and M. H. Zaman. 2011. Computational model for migration of a cell cluster in three-dimensional matrices. Ann. Biomed. Eng. 39:2068-2079. [DOI] [PubMed]
- 30.Mousavi S.J., Doweidar M.H., Doblaré M. 3D computational modelling of cell migration: a mechano-chemo-thermo-electrotaxis approach. J. Theor. Biol. 2013;329:64–73. doi: 10.1016/j.jtbi.2013.03.021. [DOI] [PubMed] [Google Scholar]; Mousavi, S. J., M. H. Doweidar, and M. Doblare. 2013. 3D computational modelling of cell migration: a mechano-chemo-thermo-electrotaxis approach. J. Theor. Biol. 329:64-73. [DOI] [PubMed]
- 31.Schlüter D.K., Ramis-Conde I., Chaplain M.A. Computational modeling of single-cell migration: the leading role of extracellular matrix fibers. Biophys. J. 2012;103:1141–1151. doi: 10.1016/j.bpj.2012.07.048. [DOI] [PMC free article] [PubMed] [Google Scholar]; Schluter, D. K., I. Ramis-Conde, and M. A. Chaplain. 2012. Computational modeling of single-cell migration: the leading role of extracellular matrix fibers. Biophys. J. 103:1141-1151. [DOI] [PMC free article] [PubMed]
- 32.Dokukina I.V., Gracheva M.E. A model of fibroblast motility on substrates with different rigidities. Biophys. J. 2010;98:2794–2803. doi: 10.1016/j.bpj.2010.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]; Dokukina, I. V., and M. E. Gracheva. 2010. A model of fibroblast motility on substrates with different rigidities. Biophys. J. 98:2794-2803. [DOI] [PMC free article] [PubMed]
- 33.Marée A.F., Jilkine A., Edelstein-Keshet L. Polarization and movement of keratocytes: a multiscale modelling approach. Bull. Math. Biol. 2006;68:1169–1211. doi: 10.1007/s11538-006-9131-7. [DOI] [PubMed] [Google Scholar]; Maree, A. F., A. Jilkine, …, L. Edelstein-Keshet. 2006. Polarization and movement of keratocytes: a multiscale modelling approach. Bull. Math. Biol. 68:1169-1211. [DOI] [PubMed]
- 34.Jilkine A., Marée A.F., Edelstein-Keshet L. Mathematical model for spatial segregation of the Rho-family GTPases based on inhibitory crosstalk. Bull. Math. Biol. 2007;69:1943–1978. doi: 10.1007/s11538-007-9200-6. [DOI] [PubMed] [Google Scholar]; Jilkine, A., A. F. Maree, and L. Edelstein-Keshet. 2007. Mathematical model for spatial segregation of the Rho-family GTPases based on inhibitory crosstalk. Bull. Math. Biol. 69:1943-1978. [DOI] [PubMed]
- 35.Méhes E., Vicsek T. Collective motion of cells: from experiments to models. Integr. Biol. 2014;6:831–854. doi: 10.1039/c4ib00115j. [DOI] [PubMed] [Google Scholar]; Mehes, E., and T. Vicsek. 2014. Collective motion of cells: from experiments to models. Integr. Biol. 6:831-854. [DOI] [PubMed]
- 36.Merchant B., Edelstein-Keshet L., Feng J.J. A Rho-GTPase based model explains spontaneous collective migration of neural crest cell clusters. Dev. Biol. 2018;444(Suppl 1):S262–S273. doi: 10.1016/j.ydbio.2018.01.013. [DOI] [PubMed] [Google Scholar]; Merchant, B., L. Edelstein-Keshet, and J. J. Feng. 2018. A Rho-GTPase based model explains spontaneous collective migration of neural crest cell clusters. Dev. Biol. 444 (Suppl 1), S262-S273. [DOI] [PubMed]
- 37.Okuda S., Inoue Y., Adachi T. Three-dimensional vertex model for simulating multicellular morphogenesis. Biophys. Physicobiol. 2015;12:13–20. doi: 10.2142/biophysico.12.0_13. [DOI] [PMC free article] [PubMed] [Google Scholar]; Okuda, S., Y. Inoue, and T. Adachi. 2015. Three-dimensional vertex model for simulating multicellular morphogenesis. Biophys. Physicobiol. 12:13-20. [DOI] [PMC free article] [PubMed]
- 38.Mathur J., Sarker B., Pathak A. Predicting collective migration of cell populations defined by varying repolarization dynamics. Biophys. J. 2018;115:2474–2485. doi: 10.1016/j.bpj.2018.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]; Mathur, J., B. Sarker, and A. Pathak. 2018. Predicting collective migration of cell populations defined by varying repolarization dynamics. Biophys. J. 115:2474-2485. [DOI] [PMC free article] [PubMed]
- 39.Du X., Osterfield M., Shvartsman S.Y. Computational analysis of three-dimensional epithelial morphogenesis using vertex models. Phys. Biol. 2014;11:066007. doi: 10.1088/1478-3975/11/6/066007. [DOI] [PMC free article] [PubMed] [Google Scholar]; Du, X., M. Osterfield, and S. Y. Shvartsman. 2014. Computational analysis of three-dimensional epithelial morphogenesis using vertex models. Phys. Biol. 11:066007. [DOI] [PMC free article] [PubMed]
- 40.Szabó A., Unnep R., Czirók A. Collective cell motion in endothelial monolayers. Phys. Biol. 2010;7:046007. doi: 10.1088/1478-3975/7/4/046007. [DOI] [PMC free article] [PubMed] [Google Scholar]; Szabo, A., R. Unnep, …, A. Czirok. 2010. Collective cell motion in endothelial monolayers. Phys. Biol. 7:046007. [DOI] [PMC free article] [PubMed]
- 41.Guven C., Rericha E., Losert W. Modeling and measuring signal relay in noisy directed migration of cell groups. PLoS Comput. Biol. 2013;9:e1003041. doi: 10.1371/journal.pcbi.1003041. [DOI] [PMC free article] [PubMed] [Google Scholar]; Guven, C., E. Rericha, …, W. Losert. 2013. Modeling and measuring signal relay in noisy directed migration of cell groups. PLoS Comput. Biol. 9:e1003041. [DOI] [PMC free article] [PubMed]
- 42.Merks R.M., Perryn E.D., Glazier J.A. Contact-inhibited chemotaxis in de novo and sprouting blood-vessel growth. PLoS Comput. Biol. 2008;4:e1000163. doi: 10.1371/journal.pcbi.1000163. [DOI] [PMC free article] [PubMed] [Google Scholar]; Merks, R. M., E. D. Perryn, …, J. A. Glazier. 2008. Contact-inhibited chemotaxis in de novo and sprouting blood-vessel growth. PLoS Comput. Biol. 4:e1000163. [DOI] [PMC free article] [PubMed]
- 43.van Oers R.F., Rens E.G., Merks R.M. Mechanical cell-matrix feedback explains pairwise and collective endothelial cell behavior in vitro. PLoS Comput. Biol. 2014;10:e1003774. doi: 10.1371/journal.pcbi.1003774. [DOI] [PMC free article] [PubMed] [Google Scholar]; van Oers, R. F., E. G. Rens, …, R. M. Merks. 2014. Mechanical cell-matrix feedback explains pairwise and collective endothelial cell behavior in vitro. PLoS Comput. Biol. 10:e1003774. [DOI] [PMC free article] [PubMed]
- 44.Szabó A., Merks R.M. Cellular potts modeling of tumor growth, tumor invasion, and tumor evolution. Front. Oncol. 2013;3:87. doi: 10.3389/fonc.2013.00087. [DOI] [PMC free article] [PubMed] [Google Scholar]; Szabo, A., and R. M. Merks. 2013. Cellular potts modeling of tumor growth, tumor invasion, and tumor evolution. Front. Oncol. 3:87. [DOI] [PMC free article] [PubMed]
- 45.Daub J.T., Merks R.M. A cell-based model of extracellular-matrix-guided endothelial cell migration during angiogenesis. Bull. Math. Biol. 2013;75:1377–1399. doi: 10.1007/s11538-013-9826-5. [DOI] [PMC free article] [PubMed] [Google Scholar]; Daub, J. T., and R. M. Merks. 2013. A cell-based model of extracellular-matrix-guided endothelial cell migration during angiogenesis. Bull. Math. Biol. 75:1377-1399. [DOI] [PMC free article] [PubMed]
- 46.Olson H.M., Nechiporuk A.V. Using Zebrafish to study collective cell migration in development and disease. Front. Cell Dev. Biol. 2018;6:83. doi: 10.3389/fcell.2018.00083. [DOI] [PMC free article] [PubMed] [Google Scholar]; Olson, H. M., and A. V. Nechiporuk. 2018. Using Zebrafish to study collective cell migration in development and disease. Front. Cell Dev. Biol. 6:83. [DOI] [PMC free article] [PubMed]
- 47.Blaue C., Kashef J., Franz C.M. Cadherin-11 promotes neural crest cell spreading by reducing intracellular tension-Mapping adhesion and mechanics in neural crest explants by atomic force microscopy. Semin. Cell Dev. Biol. 2018;73:95–106. doi: 10.1016/j.semcdb.2017.08.058. [DOI] [PubMed] [Google Scholar]; Blaue, C., J. Kashef, and C. M. Franz. 2018. Cadherin-11 promotes neural crest cell spreading by reducing intracellular tension-Mapping adhesion and mechanics in neural crest explants by atomic force microscopy. Semin. Cell Dev. Biol. 73:95-106. [DOI] [PubMed]
- 48.Khalil A.A., de Rooij J. Cadherin mechanotransduction in leader-follower cell specification during collective migration. Exp. Cell Res. 2019;376:86–91. doi: 10.1016/j.yexcr.2019.01.006. [DOI] [PubMed] [Google Scholar]; Khalil, A. A., and J. de Rooij. 2019. Cadherin mechanotransduction in leader-follower cell specification during collective migration. Exp. Cell Res. 376:86-91. [DOI] [PubMed]
- 49.Lin C., Yao E., Chuang P.-T. YAP is essential for mechanical force production and epithelial cell proliferation during lung branching morphogenesis. eLife. 2017;6:e21130. doi: 10.7554/eLife.21130. [DOI] [PMC free article] [PubMed] [Google Scholar]; Lin, C., E. Yao, …, P.-T. Chuang. 2017. YAP is essential for mechanical force production and epithelial cell proliferation during lung branching morphogenesis. eLife. 6:e21130. [DOI] [PMC free article] [PubMed]
- 50.Peters S.B., Nelson D.A., Larsen M. TGFβ signaling promotes matrix assembly during mechanosensitive embryonic salivary gland restoration. Matrix Biol. 2015;43:109–124. doi: 10.1016/j.matbio.2015.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]; Peters, S. B., D. A. Nelson, …, M. Larsen. 2015. TGFβ signaling promotes matrix assembly during mechanosensitive embryonic salivary gland restoration. Matrix Biol. 43:109-124. [DOI] [PMC free article] [PubMed]
- 51.Morgan J.T., Stewart W.G., Gleghorn J.P. The mechanosensitive ion channel TRPV4 is a regulator of lung development and pulmonary vasculature stabilization. Cell. Mol. Bioeng. 2018;11:309–320. doi: 10.1007/s12195-018-0538-7. [DOI] [PMC free article] [PubMed] [Google Scholar]; Morgan, J. T., W. G. Stewart, …, J. P. Gleghorn. 2018. The mechanosensitive ion channel TRPV4 is a regulator of lung development and pulmonary vasculature stabilization. Cell. Mol. Bioeng. 11:309-320. [DOI] [PMC free article] [PubMed]
- 52.Trepat X., Wasserman M.R., Fredberg J.J. Physical forces during collective cell migration. Nat. Phys. 2009;5:426–430. [Google Scholar]; Trepat, X., M. R. Wasserman, …, J. J. Fredberg. 2009. Physical forces during collective cell migration. Nat. Phys. 5:426-430.
- 53.Iden S., Collard J.G. Crosstalk between small GTPases and polarity proteins in cell polarization. Nat. Rev. Mol. Cell Biol. 2008;9:846–859. doi: 10.1038/nrm2521. [DOI] [PubMed] [Google Scholar]; Iden, S., and J. G. Collard. 2008. Crosstalk between small GTPases and polarity proteins in cell polarization. Nat. Rev. Mol. Cell Biol. 9:846-859. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(Top) The position of the cell center of mass xcm and Rho GTPase activity G are shown as a function of time. Scale bar = 50. (Middle) Representation of the cell position are shown for different times. Color of the cell corresponds to Rho GTPase activity, with blue denote a low level (0.2) and red denotes a high level (0.5). (Bottom) Position of the cell front (red), center (black), and back (blue) are shown as a function of time. Note time is on the y-axis. Scale bar for middle and bottom panels = 0.5. Video corresponds with results shown in Fig. 2 B. Parameters: β = 0.16, δ = 0.5.
Representation of cell position for individual cells with different values of front-back polarity parameter δ are shown for different times. Note that the color corresponds to the δ value. Scale bar = 0.5. Parameters: β = 0.16.
(Top) Representation of cell positions in a stationary tissue. Color of the cell corresponds to Rho GTPase activity, with blue denote a low level (0.2) and red denotes a high level (0.53). (Bottom) Position of cell fronts (red), centers (black), and backs (blue) are shown as a function of time. Note time is on the y-axis. Scale bar = 0.5. Video corresponds with results shown in Figs. 3 and 4 A. Parameters: β = 0.16, δ = 0.
(Top) Representation of cell positions in a migrating tissue. Color of the cell corresponds to Rho GTPase activity, with blue denote a low level (0.2) and red denotes a high level (0.53). (Bottom) Position of cell fronts (red), centers (black), and backs (blue) are shown as a function of time. Note time is on the y-axis. Scale bar = 0.5. Video corresponds with results shown in Figs. 4 B and 5 C. Parameters: β = 0.16, δ = 0.9.
Mechanochemical resonance during collective cell migration. Representation of cell positions in migrating tissues with small differences in tension feedback parameter β. Color of the cell corresponds to Rho GTPase activity, with blue denote a low level (0.2) and red denotes a high level (1.1). Scale bar = 0.5. Video corresponds with results shown in Fig. 8. Parameters: δ = 0.9.