Tissue mechanics, an important regulator of development and disease

Abstract

A growing body of work describes how physical forces in and around cells affect their growth, proliferation, migration, function and differentiation into specialized types. How cells receive and respond biochemically to mechanical signals is a process termed mechanotransduction. Disease may arise if a disruption occurs within this mechanism of sensing and interpreting mechanics. Cancer, cardiovascular diseases and developmental defects, such as during the process of neural tube formation, are linked to changes in cell and tissue mechanics. A breakdown in normal tissue and cellular forces activates mechanosignalling pathways that affect their function and can promote disease progression. The recent advent of high-resolution techniques enables quantitative measurements of mechanical properties of the cell and its extracellular matrix, providing insight into how mechanotransduction is regulated. In this review, we will address the standard methods and new technologies available to properly measure mechanical properties, highlighting the challenges and limitations of probing different length-scales. We will focus on the unique environment present throughout the development and maintenance of the central nervous system and discuss cases where disease, such as brain cancer, arises in response to changes in the mechanical properties of the microenvironment that disrupt homeostasis.

This article is part of a discussion meeting issue ‘Forces in cancer: interdisciplinary approaches in tumour mechanobiology’.

1. Introduction

The importance of considering mechanics as an important cell regulator is highlighted in an increasing and rich literature linking changes in mechanics to disruptions in tissue homeostasis and disease progression. This is not surprising, given that mechanics play such an integral role in the development and function of biological systems. During development, growth, differentiation and morphogenesis all depend on cells sensing and exerting forces on their surroundings. The orchestrated morphogenetic cellular movements characteristic of embryonic development require dynamic changes in how cells receive and respond to forces in their microenvironment.

Cells can respond to force through an immediate change in their membrane structure, such as the disassembly of caveolae in response to osmotic pressure [1], and they can also transform mechanical inputs—including stretch, tension, compression and shear forces—into a chemical signal through intracellular molecular signalling cascades that ultimately culminate in altered transcriptional outputs. In addition, increased extracellular matrix (ECM) stiffness has been shown to promote malignant phenotypes in breast cancer [2] and brain cancer [3]. Developmental defects also arise as a result of changes in physical forces. For example, disorders associated with neural tube defects have been shown to be intrinsically linked to mechanics [4]. Cells respond to physical inputs through a process termed mechanotransduction, and the diverse mechanisms by which cells transduce forces will be briefly covered in this review.

As mechanics is increasingly recognized as an important regulator of how tissue homeostasis is achieved and maintained, methods to accurately quantify the contribution of mechanical properties to the function of biological systems have become a significant area of study and permitted a breadth of new methods and techniques to flourish. With these technological advances, comes a new set of challenges in how to compare and interpret studies using different techniques. In this review, we will discuss several of the techniques currently available and the important mechanical properties and parameters to consider for their application and analysis. We will focus on measuring forces throughout the development and maintenance of the central nervous system (CNS), as well as some of the different pathologies that affect it. The technique and parameters chosen should be appropriate to the length-scale of an intended study. Therefore, we will address the methods that are useful at different biological length-scales and discuss the way these techniques have enhanced our understanding of how external forces are transduced intracellularly from the cell surface to the nucleus to alter cell behaviour though transcriptional and epigenetic modifications.

2. Methods to probe and measure cellular and tissue tension

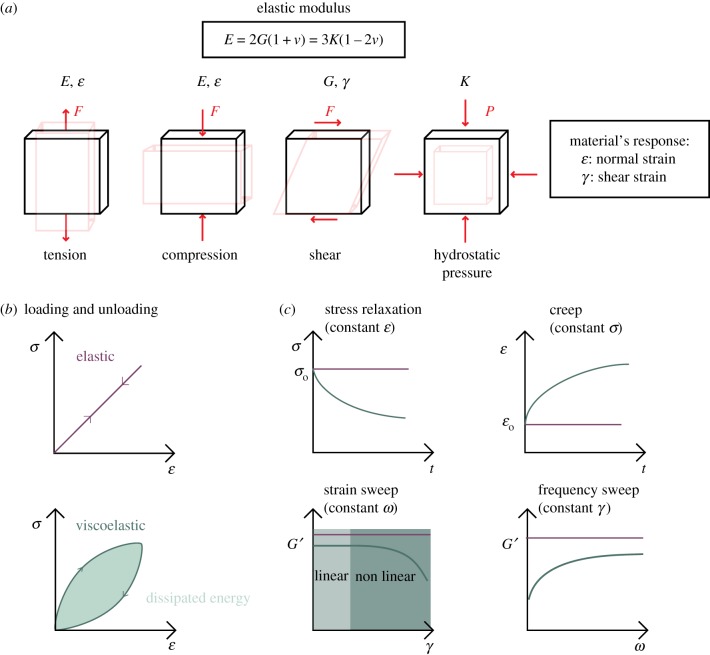
Direct mechanical measurements involve the regional application of a defined physical force (or stress) and quantification of the resulting deformation or strain. The relationship between stress and strain reveals the mechanical properties of the material being studied. For a purely elastic material, under uniaxial deformation (compression or tension), this relationship is defined using Young's modulus (E). Most biological mechanical measurements consider this property; however, an elastic material can also be described using other physical properties. If a material is under shear stress, in which the force applied is in the same plane as the cross-sectional area, the measured property is the shear modulus (G). Another elastic parameter is the bulk modulus (K), which is related to hydrostatic pressure and typically used to make measurements of blood or cerebrospinal fluid (CSF) flow. In an isotropic material, these moduli can be related to each other using Poisson's ratio, υ, a measure of orthogonal deformation to an applied uniaxial stress, where 2G(1 + υ) = E = 3 K(1 – 2υ). Figure 1a summarizes these parameters. Both E and G represent elastic moduli and are proportional (therefore not equal) to the stiffness of materials; however, most biological literature uses E, G, elastic modulus and stiffness interchangeably.

Figure 1.

A summary of mechanical properties deforming under stress. (a) A material resistance to elastic deformation to force (F) or stress (σ) is the elastic modulus. E is Young's modulus, a response to tensile or compressive stress, G is the shear modulus, a response to shear stress, and K is the bulk modulus, a response to hydrostatic pressure. (b) A viscoelastic material dissipates energy upon loading and unloading, whereas an elastic material does not. (c) Different modes of testing the response of viscoelastic materials, which is strain- and frequency-dependent. Viscoelastic materials have an initial linear response to the storage modulus (G′) at low strains followed by a nonlinear response with increasing strain.

Brain tissue is one of the softest tissues in the body, and traditionally seen as a nonlinear viscoelastic material [5]. Elastic materials store energy and the difference between loading and unloading stress–strain curves is negligible. By contrast, viscoelastic materials demonstrate a difference between these curves in the form of dissipated energy (figure 1b). Viscoelasticity is interrogated using rheological analysis, which applies oscillatory stresses and measures the resulting strains to generate a relationship represented by the complex shear modulus G*, composed of the elastic storage modulus G′ and the viscous loss modulus G″. The mechanical behaviour of viscoelastic materials is time- and frequency-dependent [6], that is, dependent on how long the tissue is deformed, the frequency of force application and the rate and amount of deformation (nonlinear response), represented in figure 1c. This presents a challenge when comparing stiffness measurements across different studies due to the high variability of parameters used, including technique, temperature [7], probe geometry and diameter [8], frequency [9], rate of loading, maximum displacement/strain and holding time at surface. In general, applying larger indentation diameters, increasing loading rate, decreasing holding time and increasing indentation depth will increase the perceived stiffness, as exemplified through comprehensive studies that compared the rheology of grey and white matter in the brain [10,11].

The above complications have led to conflicting results when measuring rheological parameters of the same regions of the brain. Several reviews have discussed these parameters in detail along with potential reasons for the different results that have been obtained when attempting to define certain brain biomechanics [12,13]. Franze et al. [12] have compared different experiments employing different strains and concluded that despite apparently disparate results, a trend among them exists; namely, a decrease in the shear modulus with increasing time after strain, characteristic of the stress relaxation behaviour of a viscoelastic material. This highlights the importance of reporting the specific parameters used when comparing measured elastic and shear moduli between studies and techniques.

Moreover, depending on the section of the sample, coronal [10] or sagittal [14], differences in stiffness may appear due to inherent structural anisotropy [11]. White matter is composed of oligodendrocytes and tightly bundled aligned axons, leading to direction-dependent mechanical properties [15] due to anisotropy. Such directional dependence is not as prevalent in grey matter, which represents the least anisotropic region of the brain.

(a). How to measure: size matters

The elastic modulus can be probed across several tissue length-scales. At a macroscale, different regions of the brain, such as the white and grey matter [10], have inherently different stiffnesses. Moreover, within the grey matter, the cortex, hippocampus and caudate regions present unique elastic moduli [16]. Even among different brain pathologies, more aggressive forms of glioma were shown to correlate with elevated stiffness [3], and traumatic brain injuries demonstrate different stiffness as a defining characteristic [17]. At a cellular level, varying stiffness can be observed between neurons and softer glial cells [18], or when comparing soma and axons [19]. Finally, subcellular structures and even single molecules participating in mechanoregulation—such as the microtubule cross-linking τ protein involved in axonal repair [20]—can have their stiffness measured to account for their mechanical contribution to cell and tissue mechanics. Thus, the length-scale is a critical factor to consider when determining suitable techniques and parameters to be applied.

Tissue-level in vitro measurements traditionally used compressive testing [5] or indentation [10]. This requires the measurement of a fresh hydrated post-mortem sample, fixed or snap-frozen. The dependency of the strain rate on these measurements highlighted the presence of the viscous component in the brain, which is better investigated in dynamic frequency sweep protocols, either in shear or tensile/compression mode [13].

Magnetic resonance elastography (MRE) applies acoustic-range waves non-invasively to tissue in order to determine the shear modulus [21,22]. MRE uses the high-frequency range, and as a result of brain viscoelasticity, shear modulus obtained through MRE needs to be viewed in the light of the frequency parameter when compared with conventional indentation and rheology techniques in the low-frequency range [13]. Pogoda et al. [23] found that glioma tissue is not stiffer than the brain at low shear strains when measured in a shear rheometer and in extension mode; however, in compression mode, glioma tissue was stiffer, increasing G′ linearly with strain. This suggested that a mechanism of compression stiffening arises in the brain environment, where increased vascularization and interstitial pressure can compress the brain and affect the mechanical properties of the tissue, as opposed to increase stromal stiffness due to the non-fibrous nature of the brain ECM. Therefore, this complex rheological behaviour of brain tissue requires especial care when comparing results between different complex modulus protocols, such as shear and compression mode.

Higher resolution tissue and cellular measurements often use atomic force microscopy (AFM). In this technique, we measure the deflection of a cantilever after applying a defined force and deforming a sample. Indentation uses a probe with a conical or spherical tip attached to the cantilever. If measuring mechanical properties directly on soft tissues or cells, spherical or blunted pyramidal tips are preferred to avoid excessive stresses due to the sharp probe: E and G′ at deep indentations of a gel were twofold higher with a pyramid tip compared to a spherical one [8,24]. For high-resolution imaging, however, a sharp tip is preferred [8].

To calculate the stiffness of cells with AFM, most studies use the Hertz model, and among its assumptions [25], it considers the cell a linearly elastic material within small deformations (less than 10% of the sample height). However, several studies indicate that cells and cytoskeleton are viscoelastic [18,26], therefore dependent on the rate of deformation, even at small deformations. Nawaz et al. [27] showed that a true elastic response with AFM occurs only when using an optical trap and indenting up to 200 nm with 30 pN force.

While standard force–volume AFM measurements output the elastic modulus, the hysteresis of the approach and retract curves is an approximate proxy of viscoelastic response [28]. Some modifications to standard AFM operations allow precise calculation of rheological parameters, such as multi-harmonic AFM [29] and high-frequency micro-rheology using high-speed AFM [30]. Other microrheological techniques, well reviewed by Chen et al. [31], include actively using particles to probe, such as with magnetic bead twisting rheology [32] and micropipette aspiration [33], or passively measuring fluctuating forces in a material with, for example, image-based tracking [34] and optical tweezers [35].

One group suggested that the viscoelastic character at the cell membrane happens due to the presence of protrusions, corrugations (microvilli, filopodia) and glycocalyx, collectively called the pericellular brush, and that underneath the brush, the membrane is purely elastic [36]. They proposed an additional model to the Hertz, termed the Brush model, in which the contribution of the softer glycocalyx-rich layer is decoupled from the mechanical properties of the stiffer membrane underneath [36], and that their calculated elastic modulus is independent of indentation rate and depth. Cortical neuron measurements indicated that the soma has a stiffness of around 1.5 kPa at 37°C with a brush length of 3–4 µm, dependent on loading speed, but when the contribution of the two layers are considered, the effective elastic modulus is softer and closer to the 50–500 Pa range found in the literature [37–39]. Other groups using multifrequency AFM in a reconstituted model of the lipid bilayer showed that at high cholesterol concentration, the lipid bilayer has both elastic and viscous behaviour. As the cholesterol decreases, the elastic component dominates and softens [40]. Given that a bulky glycocalyx has been implicated in stiffer ECM and increased brain cancer malignancy [41], differences in lipid content, indentation rate and depth could explain some heterogeneities found comparing stiffness between brain tumour studies using AFM [3,41,42] and MRE [43], which has less resolution to discern the contribution of the glycocalyx and cell membrane detectable with AFM [44].

Brillouin scattering, a technique that measures the frequency shift of scattered light interacting with acoustic phonons in the gigahertz range [45], is a non-contact method to three-dimensionally map intra- and extracellular mechanical compressibility with high spatial resolution [46]. The output is the longitudinal elastic modulus M, which, although not directly related and several orders of magnitude higher, correlates to the elastic modulus E measured by AFM. Some studies then used it as a proxy for stiffness, measuring the mechanical contribution of intracellular structures including the nucleoli and the nuclear envelope [47] and the role of cell body density in local tissue stiffness in ruminant retina [48]. However, Wu et al. [49], using a hydrogel model, raised the point that Brillouin measurements are sensitive to a sample's water content and when accounting for this parameter, the correlation between M and E disappears. Scarcelli & Yun's reply [50] pointed out that Wu's polymer model did not have physiologically relevant water content variation, and that, physiologically, cells vary little in their water percentage. But they acknowledged the phenomenological character of the correlation and suggested that a correlation between M and E needs to be calibrated before linking M to stiffness. The brain has a water content of 77% [51], and cellular structures vary in their osmotic behaviour, thus caution must be exerted when comparing M with stiffness measurements in the literature, especially if no calibration has been done in the cell and tissue of interest. However, Brillouin scattering remains a viable technique for measuring compressibility of tissues non-invasively.

While we have been discussing methods to probe cell and tissue mechanical properties, one must always remember that cells inherently exert forces on their surroundings. These forces are transmitted through cell–cell and cell–ECM adhesions, which will be discussed in detail in the next sections.

Early assays to interrogate cytoskeletal contractility involved embedding cells in a three-dimensional floating collagen gel and measuring the contraction of the gel over time [52]. We can more accurately measure the traction forces by using a deformable elastic substrate of defined stiffness, such as polyacrylamide, with fluorescent beads and computationally calculate the displacement of the beads after cells deform the substrate [53]. An adaption of this technique uses polydimethylsiloxane microposts arrays [54]—where contact area can be controlled and, depending on the geometrical properties of the posts, a straightforward measurement of cell forces can be obtained, without the use of computationally complex algorithms like traction force microscopy (TFM). Traction force measurements have given insight into how neuronal growth cones generate weak traction stresses in the order of 30 Pa [55]; microglia exert more force on stiffer substrates than neurons [56]; how during neuronal migration of granule cells, there exists three contraction force centres [57]; and how growth cones of peripheral nervous system neurons exert more forces than those of CNS neurons [58]. Force-calibrated glass microneedles have also been used to measure traction force of neuronal growth cones [59].

On a subcellular level, different strategies allow analysis of mechanical forces on molecular events such as protein unfolding, molecular motors and adhesive forces between molecules. Since typical AFM measurements can detect forces in the 10 pN range and displacement of 0.5 nm [60], one could probe adhesion forces between ligand and receptors by using a functionalized tip [61]. Magnetic and optical tweezers provide higher force resolution and permit the study of forces in less than 1–100 pN range [60], and can be used to study force generation on cell junctions, for instance, during tissue morphogenesis [62]. Laser ablation is another technique that provides valuable information on intracellular tension by measuring the retraction of structures after cutting them with a high-intensity beam over time. Cortical flow of the actomyosin cortex is important for several developmental processes and use of laser ablation in the cell cortex directly linked cortical tension to actomyosin contractility in Caenorhabditis elegans [63].

All of these methods involve measuring tension by applying or perturbing internal stresses with an external force. Techniques to measure local forces include fluorescence resonance energy transfer (FRET), where the efficiency of the energy transfer between molecules depends on their separation. FRET use as an internal force sensor provided insight into vinculin tension across focal adhesions [64] and talin force linkage to integrins during cell adhesion [65].

In addition to these force measuring methods, novel microscopy techniques may give more information regarding pathways involved in mechanosensing and mechanotransduction. Scanning angle interference microscopy (SAIM) [66] is a technique with nanoscale resolution that can shed light on nanotopographical features, such as glycoproteins, and how they affect clustering of integrins into focal adhesions [67]. Super-resolution techniques such as total internal reflection microscopy also give insight into how cell–ECM receptor dynamics are affected by substrate stiffness, using high-refractive index silicone gels with defined stiffness [68].

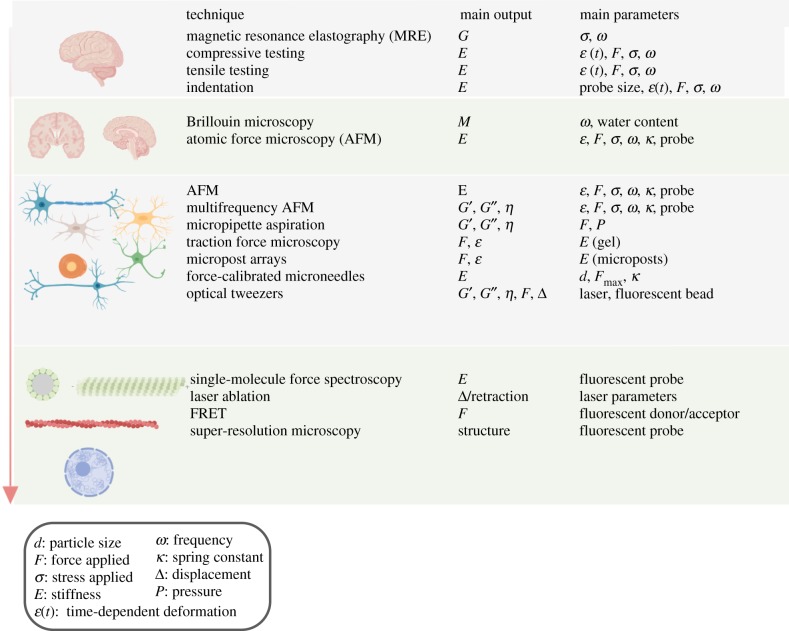
Figure 2 summarizes the methods discussed and in which length-scale they should be used when studying mechanics. In the far-right column, the important parameters of each technique are highlighted and users should refer to the existing literature to properly choose each of these parameters.

Figure 2.

Different techniques used for measuring mechanical properties in the brain and the nervous system divided by length-scale. The far-right column describes some important parameters to consider when choosing to use the technique and compare with different studies.

(b). Mechanical influence of the extracellular matrix

The ECM is an important regulator of homeostasis. During development, direct measurement of changes in tissue stiffness showed that mesoderm stiffening is necessary and sufficient to trigger neural crest cell epithelial–mesenchymal transition (EMT)-induced migration [69]. ECM mechanics are also linked to eye formation, as the early stages of invagination of the underlying surface ectoderm and the optic vesicles (OV), a precursor to the eye, are dependent on a secreted ECM that is stiffer than the cellular OV [70].

ECM stiffness also plays a role in cell-type specification in the nervous system. The use of polyacrylamide gels of defined stiffness showed that mesenchymal stem cells differentiate preferentially to neurogenic phenotypes in soft substrates [71], and soft substrates promote neurogenesis earlier than stiffer substrates [72]. Oligodendrocyte progenitor cells are also sensitive to the substrate stiffness; they migrate more in 700 Pa substrates [73], but differentiate to oligodendrocytes preferentially in a 6.5 kPa substrate [74].

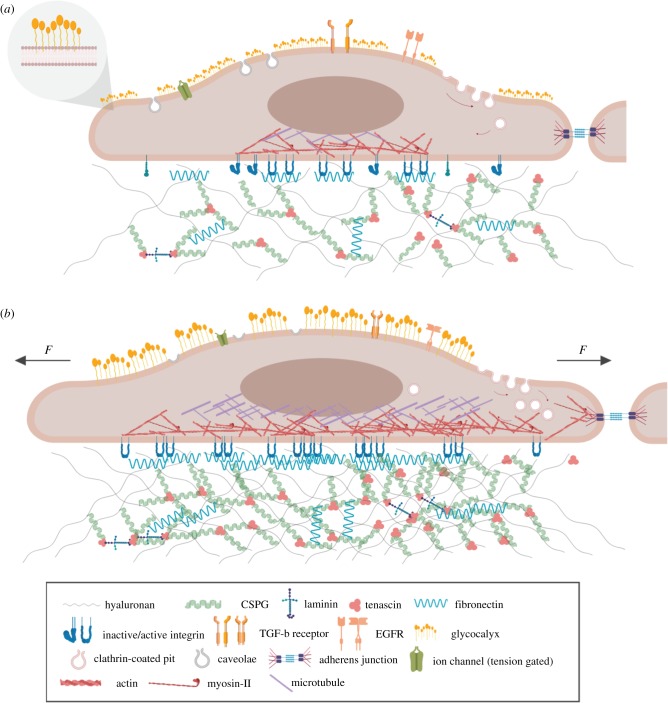
Brain ECM is mostly composed of non-fibrillar glycosaminoglycans, such as hyaluronan, lecticans proteoglycans and tenascin glycoproteins (figure 3). As such, it is compliant, soft and viscoelastic. Perturbations in mechanical signalling, ECM composition and tissue tension can affect brain development as well as result in pathologies such as brain tumours and neurodegenerative diseases such as Alzheimers and Parkinsons. Recent evidence from our laboratory has shown that as brain tumours progress from low to high grade, there is a concurrent increase in the stiffness of the tumour-associated ECM, most likely due to enhanced secretion and deposition of tenascin C by the tumour cells in the matrix [3]. Moreover, this was found to be true within high-grade glioblastomas (GBMs), wherein the less aggressive proneural GBMs can acquire features of the more aggressive mesenchymal GBMs, due to increased mechanical signalling, which in turn facilitates the formation of a bulky glycocalyx and a stem-like phenotype [41]. Previous studies have shown that brain tumours upon recurrence tend to have a more mesenchymal phenotype [75–77]. Thus, mechanical forces can promote a mesenchymal-like transition in less aggressive tumours that can lead to treatment resistance and recurrence.

Figure 3.

Structures present at the cell surface identified as participating in mechanotransduction. Changes in their behaviour are shown in a rest state (a) and when mechanically activated by force (b).

Other structural features such as ECM topography will also affect how forces are sensed by cells. Song et al. [78] created complex topological domains with micropost arrays and regulated EMT—collective and individual cell migration in embryonic tissue. Topographical stimuli can also lead to neuronal polarization [79,80], while fibre diameter has been shown to regulate oligodendrocyte myelin sheath extension [81], which can be studied using engineered nanofibres [82]. In addition, Hall et al. [83] showed that cell forces induce fibre alignment, stiffening the underlying substrate and generating a positive feedback to induce higher cell forces. This could be a mechanism present in several tissue stiffening processes such as tissue morphogenesis, tumour progression and fibrosis.

3. How to sense mechanical cues

Mechanical cues are sensed at the cell membrane through a myriad of structural features and cellular components. In the following sections, we will explore some mechanisms that have been implicated in relaying mechanical input to the cellular interior during the development of the nervous system and the techniques used to study them. We will then explore how this information gets transduced from the cell membrane to the cell interior and transmitted to the nucleus, where translational modifications and epigenetic changes can be driven by mechanics.

(a). Cell membrane

Modifications in the plasma membrane tension can control the dynamics of several important cellular functions, such as cell spreading [84], migration, membrane repair [85], exocytosis [86] and clathrin-mediated endocytosis [87]. Overall membrane tension can be regulated experimentally by swelling cells through osmotic shock or stretching cells in silicone substrates [88]. In addition, membrane tension can form or flatten membrane invaginations such as membrane folds, blebs and caveolae [89]. There is an extensive body of work showing that neurite growth is induced by tension [90] and growth cones have high stiffness [91]. Therefore, it would not be unreasonable to suggest that several processes during development and neuronal function might be regulated by a response to cell tension.

Clathrin and AP2-mediated endocytosis is implicated in several developmental and neuronal processes including neurite extension and maintenance of planarian CNS [92] and in regulating adhesion proteins distribution during migration of young neurons through cell soma translocation [93]. It has also been associated with synaptic plasticity and transmission [94]. In addition, AP-2 has been shown to internalize the cell adhesion molecule L1, a regulator of adhesion and cell migration [95], and mediate endocytosis at rear axonal growth cones, promoting axon outgrowth [96]. Membrane tension determines whether clathrin assembly dynamics are dependent on actin [87], a cytoskeleton filament protein that will be discussed more in the next section. Actin filaments would provide energy to overcome the turgor pressure in yeast [97] in order to deform the membrane [98,99] and promote vesicle budding and scission. Thus, an actomyosin-coupled response to membrane tension via clathrin-mediated endocytosis in neuronal cell types might be proposed.

Caveolins are other mechanosensitive membrane proteins localized mostly to lipid rafts and organized in flask-shaped membrane invaginations named caveolae. Caveolae provide a mechanoprotector role in response to high mechanical stress [100,101], disassembling in response to mechanical tension (hypo-osmotic shock or stretching), in an actin- and ATP-independent cell response [1], shown in the embryonic notochord [102], a precursor to the neural plate. Caveolae protein knockouts have also been correlated with reduced cortical tension, linking the invagination assembly to the ability of cells to structurally build up tension [1,103]. Aside from its role in regulating membrane tension, caveolin-1 also activates and internalizes integrins on soft substrates, contributing to bone marrow mesenchymal stem cell neural lineage specification by inhibiting the BMP-Smad pathway [104].

Integrins are transmembrane receptors involved in cellular adhesion to the ECM and transmitting force and stress from the ECM to the actin cytoskeleton [105,106]. Integrins localize to focal adhesions, and maturation of focal adhesions progresses through integrin clustering, increasing links between integrins and bundled F-actin, eventually recruiting focal adhesion kinase (FAK). The linkage of integrins to F-actin occurs through vinculin and talin. FAK controls the dynamics between actin and focal adhesion by modulating the response to tension [107]. Among other roles, organization of collective cell movements in the Xenopus mesendoderm depends on mediation of tension by FAK [108] and guidance of axonal growth cones through the chemoattractant netrin-1 is also dependent on FAK [109].

Work from our laboratory showed that, independently of actomyosin contractility, a bulky glycocalyx mediates tension promoting integrin clustering [67], indicating a novel mechanosensing role for this carbohydrate-rich structure. The size of the glycocalyx was measured with SAIM, a technique that permits high-resolution visualization of membrane structure. Other mechanotransduction roles for glycocalyx include its response to blood flow in endothelial cells, where it increases the production of nitric oxide by activating transient receptor potential channels in response to stretch [110].

Cadherins promote cell–cell adhesion and are one of the main components of adherens junctions [111]. They have been shown to transduce force in the same order of magnitude as focal adhesions using micropillars [112]. The use of AFM single-cell force spectroscopy showed that, during neurulation, depletion of cadherin-11 promotes single-cell migration of neural crest cells by decreasing the high tension at the leader cells [113].

Mechanosignalling during development also involves other transmembrane receptors including E-cadherin-mediated EGFR signalling [114] and receptors in the TGF-β and BMP family [115]. Other mechanosensing structures include cilia, protrusions in the cell membrane involved in signal transduction. Cilia are composed of a microtubule cytoskeleton and can be classified as motile or non-motile. Motile cilia are present in ependymal cells in ventricles and choroid plexus cells and are important for sensing fluid flow. Conversely, primary cilia are non-motile, present in most brain cells and important during brain development, including left–right specification [116]. Disruptions in ciliary structure and function are connected to several pathologies in neurodevelopment, such as Joubert syndrome and Meckel–Gruber syndrome [117–119].

Cell response to these mechanical inputs will not be necessarily at the site of the application of force. Forces get sensed at the cell membrane, propagated through the cytoskeleton, and a reaction could quickly occur in any of the structures described in this section forming a network with the cytoskeleton, including adherens junctions and focal adhesions. A slower response will happen through intracellular biochemical cascades and transcriptional regulation. We will briefly discuss these mechanisms of mechanotransduction next.

(b). Intracellular mechanotransduction

Migration, morphogenesis and force transduction in the cellular interior relies on the collective contractile behaviour of cytoskeleton proteins, such as actin filaments, myosin motors, intermediate filaments and microtubules, as previously introduced. Each one of these components have different pulling forces, polymerization rates and polarity, which will dictate their function and architecture in the cytoskeleton; these properties will not be discussed as they have been well reviewed elsewhere [120]; instead, we will focus on their role in the nervous system.

Actomyosin contractility is generated by the continuous retrograde flow of actin where filamentous-actin (F-actin) assembly at the leading edge is followed by backwards filament translocation and recycling driven by a myosin-type molecular motor [121,122]. Neurons also depend on the formation of microtubule bundles on the leading edge during migration [123]. In the soma, the nucleus was shown to be encircled by a network of microtubules [123], where myosin-II activity is necessary for nucleokinesis, pulling the centrosome forward during migration [124] via F-actin flow [125] and contracting the cell rear [126].

Developmental processes are tightly controlled by cytoskeleton contractility as they drive tissue morphogenesis [127], tissue stiffening during elongation and neural tube closure [128] and tissue movement through actomyosin control of tissue stiffness in convergent extension [129].

Signals modulating actin organization include the Rho GTPase family, key mediators of mechanotransduction, which coordinate adhesion processes with integrins [130]. During development, RhoA, Cdc42 and Rac1 regulate spontaneous collective migration of neural crest cell clusters through contact inhibition and co-attraction [131]. In addition, substrate stiffness increases RhoA and Cdc42 expression and actomyosin contractility, directly increasing cell stiffness and suppressing neurogenesis during differentiation of neural stem cells [132].

Other signalling pathways involved in mechanotransduction involve BMP-SMAD and TGF-β signalling, pathways involved in neuronal development and differentiation [133]. Neuroectoderm patterning in geometric confinement responds to applied stretch by activating BMP and Wnt signals [115].

(c). Transcriptional regulation by mechanics

Development is a mechanically regulated process, which relies on a tight spatial and temporal regulation of transcription factors that control the various stages of development. Thus, it is logical to hypothesize that the mechanical and transcription machineries potentially engage in crosstalk, which ensures the smooth execution of these developmental steps. External forces generated in the ECM are transmitted through the cytoskeleton into the nucleus of the cells, where these forces can remodel the chromatin structure and regulate transcription factors, in a process called ‘nuclear mechanotransduction’ [134]. Early evidence that cells, upon sensing mechanical cues via the ECM, transmit these forces to the nucleus and change their transcriptional behaviour came from micromanipulating ECM-coated beads using micropipettes and collagen gel contraction assays [135,136].

Since then, a number of studies have uncovered transcription factors and transcriptional regulators whose activity and localization are dictated by the nature of the ECM as well as the mechanical forces exerted on and by the cell. The most well-studied example of transcriptional mechanoresponsiveness is the cytoplasm-to-nuclear translocation of the Yes-associated protein (YAP) and transcriptional coactivator with PDZ-binding motif (TAZ), through sensing of substrate rigidity and cellular geometry and extent of spreading via Rho GTPase and cytoskeletal tension [137]. In the brain, YAP regulates neuronal differentiation in an ECM stiffness-dependent manner [138,139]. Other transcription factors such as nuclear factor κβ (NF-κβ), STAT3 and MAL, sequestered in the cytoplasm under basal conditions, are translocated to the nucleus upon sensing increased cellular or tissue tension [140]. Interestingly, focal adhesions proteins such as zyxin and paxillin also serve as mechanotransducers, sensing ECM stiffness via integrins and the focal adhesion complex, dissociating from the complex to travel to the nucleus. Both these proteins do not have the canonical nuclear localization signals (NLS) and are therefore thought to ‘piggyback’ on other proteins with an NLS or enter the nucleus through other recognition motifs. In the nucleus, paxillin and zyxin act as transcriptional coactivators and can presumably affect steroid hormone receptor activity [141]. The physiological relevance of ECM stiffness causing post-translational modification and translocation was shown by exerting finely tuned mechanical pressure to mouse colon using subcutaneously implanted liposomal magnets. This led to the phosphorylation of β-catenin, causing it to dissociate from the adherens junctions and translocate to the nucleus [142]. Furthermore, one study showed an overall upregulation of transcription upon chromatin stretching in response to local stresses that were applied to integrins and transmitted to the nucleus via the cytoskeleton network [143].

While it is clear that the transcription machinery is regulated by ECM rigidity, how does external force make its presence felt all the way to the nucleus? One of the ways in which the transcriptional machinery is controlled is through nuclear plasticity and shape. The cytoskeleton and the nucleus are linked via an ‘elaborate physico-chemical network’, providing physical and biochemical feedback to one another to maintain cellular function and homeostasis [140]. One such bridge between the nucleus and the cytoplasm is the linker of nucleoskeleton and cytoskeleton (LINC) complex housed within the nuclear envelope, which consist of the transmembrane nesprin proteins. Nesprins act as molecular clips that can bind to the cytoskeletal networks such as actin and tubulin in the cytosol and to the nuclear lamina and chromatin inside the nucleus [134]. Disrupting the LINC complex changes both nuclear shape [144] and transcriptional profile [143], suggesting that transmission of forces is essential to transcriptional homeostasis.

In addition to modulating changes in nuclear shape, external forces can also affect chromatin organization and positioning, thereby affecting transcription. Stem cells are found to contain ‘soft’ mechanically malleable nuclei, whereas ‘stiff’ nuclei are found in more differentiated cells. Interestingly, the chromosomes remain structurally anchored by nuclear scaffolds such as lamin proteins and the nuclear-cytoskeleton network in differentiated nuclei. In stem cell nuclei, the chromosomes lack this structural support, which may begin to explain the plasticity of the nucleus [145]. This plasticity imparts to the genomic content of a stem cell the ability to ‘intermingle’, where these intermingling chromosomes are hotspots for transcriptional regulation, as evidenced by the phosphorylation and localization of RNAPII at these intermingled regions [146]. Furthermore, chromosomes that are closer to the nuclear envelope tend to be more densely packed (heterochromatin) and consequently less accessible to the transcription machinery, when compared with chromosomes that are more central to the nucleus, less densely packed (euchromatin) and more accessible to the transcription machinery [147,148]. Thus, cell and nuclear shape, geometry and extrinsic and intrinsic forces can affect chromosomal positioning within the nucleus (and vice versa), leading to mechanically driven transcriptional reprogramming. Emerging evidence also points to further crosstalk between transcriptional and epigenetic programmes, wherein enhanced mechanical signalling via the Rho kinase (ROCK) led to transcription repression of rRNA transcription, which could be rescued upon chromatin modifying histone deacetylase inhibition [149].

While the role of nuclear topology and chromosomal positioning in transcriptional regulation are still unknown in the context of the brain, recent studies from our laboratory have demonstrated that brain tumour cells (denoted as the GBM proneural cells), when plated on stiff substrates, upregulate a number of transcriptional programmes including cell proliferation, motility and mesenchymal markers, which allow tumour cells to undergo a mesenchymal transition to facilitate local and contralateral invasion, as well as metastasis [41]. This suggests a mechanosensitive switch which regulates the balance between euchromatin and heterochromatin, as well as controlling the transcription factors and chromatin regulating machinery that facilitate this transition.

4. Conclusion

The emergence of mechanics as an important regulator for several biological processes highlights the need for proper appraisal of the several quantitative techniques available. In this review, we commented on the different measurements used when measuring from the intra-cellular level to the organ level. We mentioned some parameters that may lead to conflicting results when comparing different techniques, focusing on the nervous system. These are not comprehensive but may serve as a starting point for researchers interested in assessing the contribution of mechanics. In that sense, we briefly mentioned how the ECM and some cellular structures are involved in the transduction of mechanical signals at the cell surface, particularly in development and in the nervous system, underscoring how mechanosignalling coordinates diverse processes and how much more remains to be studied. Understanding how these structures collectively regulate physiology will be an important blueprint for therapeutical applications. In that sense, we highlighted evidences of how the disruption of tissue mechanics can lead to the emergence of disease in the nervous system, summarized in table 1. Pathologies such as brain cancer and Alzheimer's disease that are linked to a disruption of ECM mechanics will benefit from further understanding in this area by directing more targeted drug discovery.

Table 1.

Pathologies linked with abnormal tissue mechanics and techniques used to probe them.

pathology	technique	type of samples	reference
glioma	shear rheology and compression mode	human glioma cell lines	Pogoda et al. [23]
glioblastoma	atomic force microscopy	human GBM tissue samples, mouse xenograft studies, primary human GBM cells	Miroshnikova et al. [3]
glioblastoma	atomic force microscopy, traction force microscopy, SAIM	human GBM tissue samples, mouse xenograft studies with human GBM cells, primary human cells	Barnes et al. [41]
glioblastoma	multifrequency magnetic resonance elastography	human brain parenchyma (non-invasive) of GBM patients	Streitberger et al. [43]
traumatic brain injury	a custom-built micro-indentation device	P56 mouse brain tissue	MacManus et al. [17]
neurodegenerative diseases (e.g. Parkinson's and Alzheimer's diseases)	three-dimensional magnetic resonance elastography ultrasound hyperechogenecity	human brain (non-invasive)	for review, see Barnes et al. [42]

Data accessibility

This article does not contain any additional data.

Authors' contributions

N.M.E.A. and V.M.W. conceived and planned the review paper. N.M.E.A. and S.K. performed the literature review and drafted the manuscript. V.M.W. made critical revisions to the manuscript. All authors revised and approved the final manuscript.

Competing interests

We declare we have no competing interests.

Funding

Grant support provided by National Institute of Health (grant no. U01CA202241-01), Department of Defense—BCRP, USMRAA (grant no. BC122990) and California Institute of Regenerative Medicine (grant no. RB5-07409) to V.M.W. N.M.E.A. is funded through the UC Berkeley-UCSF Graduate Program in Bioengineering and partially supported by the Schlumberger Foundation Faculty for the Future program.