Spatiotemporally Super-Resolved Volumetric Traction Force Microscopy

Abstract

Quantification of mechanical forces is a major challenge across biomedical sciences. Yet such measurements are essential to understanding the role of biomechanics in cell regulation and function. Traction force microscopy remains the most broadly applied force probing technology but typically restricts itself to single-plane two-dimensional quantifications with limited spatiotemporal resolution. Here, we introduce an enhanced force measurement technique combining 3D super-resolution fluorescence structural illumination microscopy and traction force microscopy (3D-SIM-TFM) offering increased spatiotemporal resolution, opening-up unprecedented insights into physiological three-dimensional force production in living cells.

Living cells continuously generate mechanical forces. Consequently, quantifying these forces is essential for the understanding of their physiological function.^1,2 Traction force microscopy (TFM) is perhaps the most widely used force probing methodology, owing to its versatility in mimicking biological and mechanical conditions, ease of implementation, and reliance on nonspecialist equipment.³⁻⁵ Despite its importance, quantifying cellular force production via TFM remains challenging due to the technical limitations imposed by the measurement system.⁶ Specifically, the limited length scales, time scales, and dimensionality of conventional TFM restrict the application of the technique to biological questions on the micrometer length scale and minute time scale and typically only in two-dimensions.⁶ However, a myriad of cellular processes occur on far smaller length and time scales (i.e., nanometer and subsecond), for example, the engagement of individual receptor ligand complexes during immune cell interactions.⁷ Thus, there is a pressing need to extend the temporal and spatial resolution of TFM to capture the complex mechanical interactions of living cells.

In a typical TFM experiment, a homogeneous, isotropic, and elastic substrate is loaded with fluorescent markers.⁸ Marker displacements tangential to the gel surface applied by the cell in contact with the gel can be imaged using conventional fluorescent microscopy. Using a theoretical model of the elastic surface combined with knowledge of the elastic properties of the gel, the cellular forces responsible for the measured displacements can be calculated.⁹⁻¹¹ Because both the mechanical and molecular properties of the gel surface can be tuned to mimic physiological conditions, TFM offers unique advantages compared to other force quantification modalities, such as FRET based force sensors.¹²⁻¹⁴ Moreover, TFM allows measurement of both the magnitude and direction of the applied forces, which currently remains challenging for other techniques.¹⁵ Note, it should be mentioned that the term “traction” refers to the stresses exerted by the cell at the interface with the gel, while the general term “stress” is used to imply the three-dimensional (3D) stress generating within the body of the gel.

The resolution of TFM is primarily limited by the spatial density at which information within the displacement field can be sampled. Experimentally, this limit is imposed by the finite spatial resolution of the optical fluorescence microscope, as the finite size of the point spread function resulting from each marker bead imposes an upper limit on the spatial density of beads that can be reliably imaged and tracked within the elastic gel. In a recent work, super-resolution stimulated emission depletion (STED) microscopy was combined with TFM to overcome this limit.⁶ The enhanced fluorescent resolution of STED allowed up to 5-fold higher sampling of the displacement field, resulting in an improvement in traction recovery on the submicron scale. Because this improvement relies on STED microscopy, it suffers from limitations inherent to this super-resolution technique; imaging speed is limited by the necessity to scan at each pixel, and the total imaging duration is limited by the high laser intensity required for depletion.¹⁶ While confocal scanning imaging approaches have been employed in combination with 3D-TFM, the necessity to scan at each pixel in all planes makes the imaging speed even slower than single-plane 2D-TFM and/or limits it to small fields-of-view (FOV). (For a 30 × 30 × 10 μm imaging volume with a diffraction limited spatial resolution of 250 nm lateral/500 nm axial, the acquisition time is typically in the order of >1 min per 3D stack of 10 images.)^6,17,18 Similarly, STED microscopy limits itself to acquisition times on the order of >5 min per stack of 10 images due to the required smaller pixel size.

Therefore, to enhance both the spatial and temporal resolution of TFM, a technique is required that allows imaging of a high density distribution of fluorescent beads at high temporal resolution. The live-cell super-resolution technique SIM (structured illumination microscopy) offers resolution doubling in all spatial dimensions compared to confocal laser scanning microscopy, leading to a spatial resolution of 100 nm lateral and 300 nm axial.¹⁹ Because SIM is a wide-field technique, it does not suffer the same limitations as STED microscopy. SIM allows for fast acquisitions times (11 ms per frame, 15 frames per super-resolution image in 3D mode) and exposes the sample to significantly less fluorescence excitation light compared to STED microscopy, maximizing the number of images that can be acquired within a specific time period and minimizing photobleaching effects.²⁰ Notably, confocal spinning disk approaches can achieve acquisition times comparable to 3D-SIM, but at diffraction limited spatial resolution. Crucially, SIM can operate in a 3D mode, allowing for fast, low-light, high resolution, fluorescence imaging in all three spatial dimensions. SIM provides the additional advantage of increased isotropic spatial resolution in both the cell and force imaging, which is lacking in those of comparably fast scanning techniques such as spinning disk microscopy.²¹ The 3D SIM-TFM technique naturally suffers from all of the limitations inherent to SIM experiments,²⁰ and to achieve significant resolution enhancement using 3D-SIM, care must be taken to optimize the imaging conditions, most notably, the imaging depth and the refractive index of the elastic substrate. Substrate thickness should be minimized to reduce detrimental effects of optical aberrations but should be kept sufficiently thick to avoid any mechanical influence of the glass substrate underlying the gel. In the latter case, an objective should be used having an immersion medium that matches the refractive index of the elastic substrate. In this work this is achieved using an elastic substrate that has a refractive index similar to that of glass, permitting the use of a high numerical aperture (NA) oil-immersion objective.²⁰

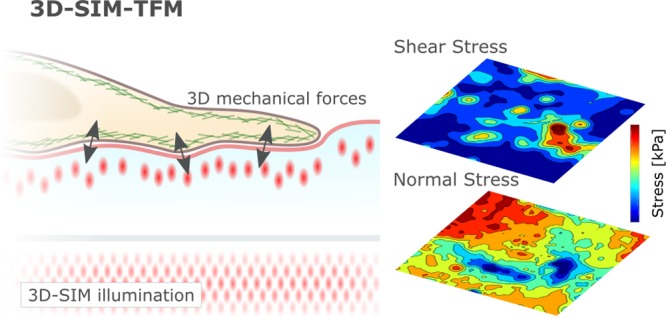
Here, to overcome the technical limitations of conventional TFM, we combine TFM with 3D-SIM (Figure 1a,b). Using a combination of simulations and experiments, we show the increased accuracy in SIM derived 3D-TFM by measuring the rapidly evolving mechanical forces generated during early cell–substrate adherence in cervical cancer HeLa cells. Furthermore, we demonstrate the need for enhanced spatiotemporal sampling of mechanical force production by highlighting the nonlinear evolution of stress in living cells. 3D-SIM-TFM offers physiological, three-dimensional force quantification in live cells at unprecedented spatial-temporal resolution.

Figure 1.

(a) Schematic outlining the application of the 3D-SIM imaging in combination with the 3D-TFM. (b) Representative bead images showing the improvements in the both axial and lateral resolution offered by SIM. Scale bar is 0.5 μm. (c) Schematic describing the finite-element mesh and simulated 3D stress field forming the basis of the computational simulation to analyze the effects of sampling density on the ability to accurately resolve 3D stress fields. (d) Representative displacement of the finite-element mesh under an applied stress field. The mesh displacement has been scaled 10 times to allow better visualization. (e) Interpolation of the displacement field calculated from an applied stress field on the finite-element mesh for a range of bead densities. (f) Stress recovery resulting from an applied 3D stress field for a range of bead densities. Scale bar is 1 μm. (g) Systematic analysis of the relationship between the quality of 3D stress recovery (defined by the DTM), the area of applied stress field and the sampling density of the displacement field. Error bars show standard error.

Higher Bead Density Improves 3D Stress Recovery

To establish the theoretical limits for the accuracy and spatiotemporal resolution of TFM using 3D-SIM, we first performed finite element (FE) simulations to establish the relationship between the sampling density of the substrate displacement and the quality of the stress measurements (force per unit area) in 3D (see Supporting Information).^22,23 The simulations consisted of three stages. (i) A 3D finite element mesh was generated by considering an isotropic and linear elastic gel of size 30 × 30 × 10 μm (in xyz directions) bound to a rigid substrate, mimicking the experimental condition of a silicone gel firmly attached to a glass coverslip. Considering the level of cellular deformations, the chosen gel dimensions minimize both the computational cost and boundary effects. (ii) A stress field was applied at the top surface of the gel, which consisted of a uniform circular stress of a defined radius, with equal stress components in all three spatial dimensions, in plane (S_x, S_y) and normal (S_z) to the gel surface (Figure 1c). Using a linear elastic stress–strain formulation, the resultant displacement field was calculated (Figure 1d) and sampled at a given spatial density corresponding to different bead densities (Figure 1e). (iii) The sampled displacement field for each density was interpolated on the 3D mesh and converted to a 3D stress field using finite element simulations (see Methods section and Supporting Information).

This simulation procedure was performed for a number of bead densities ranging from 0.25 to 15 μm^–2, representing those densities possible using conventional microscopy and super-resolved techniques.⁶ For a given bead density, the radius of the circular stress zone was varied and the resulting recovered stress field was calculated. The difference between the simulated and recovered 3D stress field was then quantified, allowing for the assessment of the information loss for a given stress zone across the range of bead densities, using a metric known as the deviation of traction magnitude (DTM) (see Supporting Information) (Figure 1f,g). The DTM ranged from −1 to 0, where −1 indicates complete loss of stress information in the recovered stress field compared to the simulation and 0 represents a perfect stress recovery. Consistent with previous computational and experimental work in 2D,⁶ the quality of recovered stress was enhanced at high bead densities, allowing spatially smaller 3D stress fields to be more accurately reconstructed, for example, to achieve a DTM of −0.2, a 2 μm traction can be resolved at a bead density of 1 μm^–2, whereas only a 4 μm stress field can be equivalently resolved at a bead density of 0.25 μm^–2

3D-SIM-TFM

To assess the ability of 3D-SIM to experimentally improve the quantification of cell generated mechanical forces, we measured the rapid force evolution during the early adhesion of cervical cancer HeLa cells. We first allowed HeLa cells stably expressing Lifeact-citrine to settle on a 10 kPa silicone substrate functionalized with fibronectin and loaded with red 100 nm fluorescent beads at a density of 1 bead per μm². This bead density was chosen such that at least 80% of beads could be tracked at SIM resolution (compared to <40% in wide-field mode) (see Materials and Methods, Supplementary Figure 1b). By using a silicone substrate with a refractive index close to glass (n = 1.49), we achieved optimal imaging conditions for SIM allowing bead displacements to be accurately quantified at the upper surface of the 20 μm thick gel. Note, FE simulations indicated negligible effects of the glass substrate for displacements on the top face of the gel below 10% of the substrate thickness (2 μm; Supplementary Figure 5).

Ten minutes after deposition of the cells, to capture the cell contact and the 3D motion of the fluorescent beads at the top surface of the gel, a 2 μm stack was initiated at a z-stack rate of 0.1 per second (Figure 2a). Using an exposure time of 11 ms per frame, a two-color (cell and bead fluorescence channels) 2 μm super-resolved z-stack could be acquired in 10 s (z-spacing 142 nm, 14 z-slices per stack). For the acquisition, a total of 420 frames were acquired at each time point (5 phases × 3 angles × 14 z-slices × 2 colors), leading to a total acquisition time of ∼10 s. A single-color 1 μm stack could be acquired every 2 s.

Figure 2.

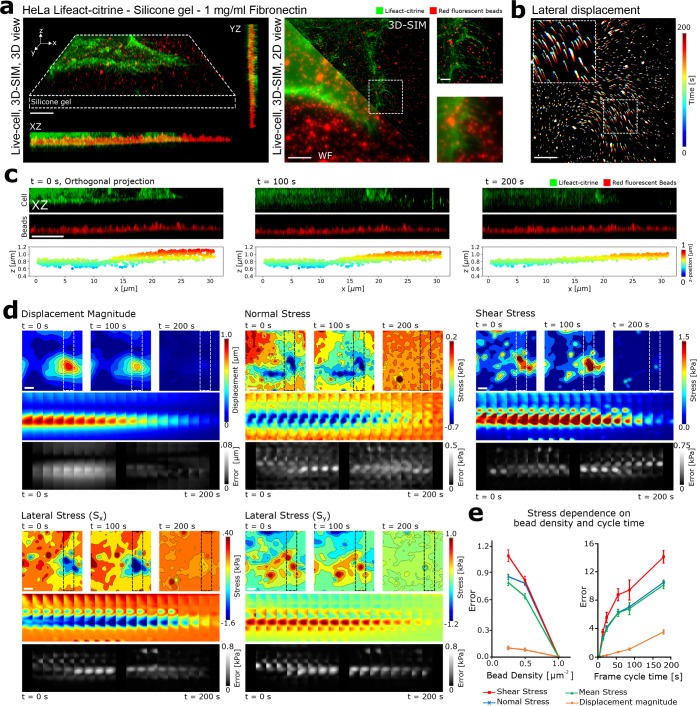
(a) (Left) 3D and orthogonal rendering of the 3D-SIM stack of an adherent HeLa cell expressing Lifeact-citrine attached to the elastic substrate loaded with fluorescent marker beads at a density of 1 bead per μm². (Right) Overlay of 3D-SIM and wide-field imaging of an adherent HeLa cell, indicating the improved resolution of both bead and cell imaging. Scale bars are 5 μm. Zoom in of dashed boxed inset are shown adjacent. Scale bar in the zoom-in image is 1 μm. (b) Temporal projection of the SIM imaged beads, reporting on the lateral displacement of the elastic substrate following the application of cell generated forces. Color-map indicates different time points of the measurement. Scale bar is 5 μm. (c) Dual-color SIM imaging showing the axial cell-induced deformation of the elastic substrate over time measured by the change in axial position of the beads. Scale bar is 5 μm. Lower panels indicate the result of single particle localization and tracking of each of the beads within the 3D stack. (d) Displacement and corresponding recovered stress fields for the adherent HeLa cell were estimated using FE simulations. 3D tracking of the beads allows both lateral (S_x, S_y) and axial (S_z) components of stress to be calculated. Scale bar is 5 μm. The upper panel shows the contour maps of estimated displacement or stress fields at three time points. The middle panel shows the color map of a region of interest over all frames. The lower panel shows the error induced by increasing the sampling time by 10 times relative to the original acquisition time for each frame. Scale bar is 5 μm. (e) (Left) Error in the recovered stress as a function of bead density. Notably, the stress error increases when the bead density is reduced relative to the original acquisition. (Right) Error in the recovered stress as a function of acquisition cycle time. Notably, the stress error increases dramatically when the cycle time is reduced, highlighting the importance of rapid acquisition speed for the accurate reconstruction of cell generated mechanical forces. Error bars show standard error.

To quantify the cell-induced displacements during adhesion to the silicone gel, we utilized a single-particle tracking approach (see Materials and Methods). For each frame within the time lapse, the fluorescent beads were localized within the 3D volume and then linked between frames to form particle trajectories. In the plane of the gel, shear stresses at the gel surface (S_x and S_y) are visible, allowing us to observe both the contraction and relaxation of the gel as the cell contact evolved (Figure 2b and Movies S1–S3). In addition to stresses in the plane of the gel (S_x and S_y), the 3D-SIM imaging allowed us to visualize normal stresses generated by the cell (S_z). Throughout the acquisition, the gel substrate underwent vertical displacements in the range of 1 μm, as illustrated by the representative single-particle tracking in Figure 2c.

To quantify the 3D stresses generated by the cell, finite element calculations were applied to compute the mechanical forces resulting from the experimentally observed 3D displacements of the gel substrate (see Supporting Information). The stress calculation assumed a linearly elastic gel with an elastic modulus of 10 kPa and Poisson ratio of 0.49 (see Materials and Methods). Figure 2d highlights the evolution of the substrate displacements and the corresponding shear and normal stress relative to the final frame (Movies S4–S5). In this case, both normal and shear stress reduced as the cell contact evolved. Notably, individual force profiles could not be averaged across individual cells due to their uniqueness, and hence representative images are displayed, reporting on the general features of force evolution during cell adhesion.

Spatiotemporal Sensitivity of 3D-SIM TFM

Finally, we evaluated the experimental power of 3D-SIM TFM. Simulations highlighted that the ability to accurately recover the stress field from the displacement field critically depended on the sampling density (Figure 1). To investigate this effect experimentally, we reduced the bead density in a range from 1 to 0.25 μm^–2 by randomly removing a fraction of the acquired bead displacements from the finite element calculation, which was equivalent to reducing the acquired bead density. Error calculations were performed for three sets of random nodes at each bead density, showing that the error increased when the bead density was reduced (Figure 2e). In addition, because the forces applied by the cell are evolving on the second time scale, the speed of imaging defined by the number of cycles (number of repeated z-stacks acquired within a specific time) is likely to be critical in resolving the true stress field. To test this, we removed a fraction of the acquired frames in the finite element calculations to artificially increase the cycle time (decrease number of cycles) and estimated the stress fields at each time frame using linear interpolation. Error calculations were performed for three sets of frames for each frame cycle time. Increasing the cycle time also resulted in an increased error, highlighting the nonlinear evolution of stress with time and the importance of acquiring displacement data at appropriately fast speeds (Figure 2e).

Discussion

In this work, we have shown that combining TFM and 3D-SIM can enhance the ability of TFM to capture the rapidly evolving 3D forces during cell adhesion. Many outstanding biological questions are rooted in complex cellular dynamics at submicron length scales and sub minute time scales. Addressing these challenges requires tools that allow for the quantification of such events without impeding the biological process of interest. SIM offers perhaps the best compromise currently available for fast and high spatial resolution cellular imaging at minimal photobleaching and phototoxicity and is therefore well suited for combination with other complementary techniques like TFM. Consequently, 3D-SIM-TFM represents an important advance in the quantification of cellular forces. Consideration should be given to the density and localization of the reference beads embedded within or at the top surface of the silicone gel, which determines the sensitivity of the TFM method.^24,25 We have demonstrated that the right spatiotemporal resolution is critical for the accurate recovery of the underlying force fields. We anticipate that this spatiotemporal enhancement will uncover novel biology, particularly in studying complex cellular interactions, such as cancer cell migration and invasion, where cells are known to rely on small scale and short-lived protrusive and adhesive complexes interacting with ECM and stromal cells that form the extracellular tumor microenvironment.^26,27 This is also true of immune cell interactions where 3D-SIM-TFM allows the stepwise reassembly of specific receptor–ligand interactions, including integrins and costimulatory molecules to address the increasing role being proposed for mechanical force generation.¹

In addition, combining TFM and SIM offers the potential to gain not only increased accuracy and resolution of the forces generated by the cell but also the cellular structures responsible for the force generation. This is of critical importance when correlating cellular structures with zones of force generation, which will likely be critical in uncovering the molecular origin of the observed forces.

SIM is establishing itself as the method of choice for live-cell super-resolution imaging, and thus its combination with established techniques like TFM is timely. Commercially available microscopes that are capable of reproducing the temporal and spatial resolutions shown here are becoming increasingly available, and we anticipate the broad impact of such technologies. Future advances in imaging modalities, such as lattice light sheet based SIM in combination with adaptive optics will offer further opportunities to improve force quantification.

Materials and Methods

Cell Culture

HeLa cells (product 93021013, Sigma-Aldrich; mycoplasma tested) were cultured in sterile DMEM (Sigma-Aldrich) supplemented with 10% FCS (Sigma-Aldrich), 2 mM l-glutamine (Sigma-Aldrich) and 1% penicillin–streptomycin–neomycin solution (Sigma-Aldrich). Cells were maintained at 37 °C and 5% CO₂ during culturing, and handling was performed in HEPA-filtered microbiological safety cabinets

Generation of Stable Cell Lines

HeLa lines stably expressing Lifeact-citrine were generated using a lentiviral transduction strategy. HEK-293T cells were plated in six-well plates at 3 × 10⁵ cells per mL at 2 mL per well in DMEM (Sigma-Aldrich) containing 10% FCS. Cells were incubated at 37 °C and 5% CO₂ for 24 h before transfection with 0.5 μg per well each of the lentiviral packaging vectors p8.91 and pMD.G and the relevant pHR-SIN lentiviral expression vector using GeneJuice (Merck Millipore) as per the manufacturer’s instructions. Forty-eight hours after transfection, the cell supernatant was harvested and filtered using a 0.45 μm Millex-GP syringe filter unit to remove detached HEK-293T cells. In all, 3 mL of this virus-containing medium was added to 1.5× 10⁶ HeLa cells in 3 mL of supplemented DMEM medium. After 48 h, cells were moved into 10 mL of supplemented DMEM and passaged as normal.

Silicone Substrate Preparation

The fabrication of the high refractive index silicone gel substrate was adapted from previously published work.²⁸ Briefly, two components (920A and 920B, Quantum Silicons, Richmond, VA) were combined at a 1:1.1 ratio by weight, respectively. After thorough mixing and degassing, 50 μL of the gel solution was pipetted onto an 18 mm #1.5 glass coverslip and spin coated at 5000 rpm for 10 s to form a 20 μm thick layer. Gels were cured at 100 °C for 2 h, after which gels were stored in PBS at 4 °C. Gels were then functionalized with fluorescent beads and fibronectin. This was achieved by first treating gels with a 10% (v/v) solution of (3-aminopropyl)trimethoxysilane (APTMS) (Sigma-Aldrich) for 5 min. This provided a free amine group on the silicone surface, allowing functionalization via 1-ethyl-3-(3-(dimethylamino)propyl)carbodiimide (EDC) (Sigma-Aldrich), a bifunctional cross-linker that was able to bind the free amine on the gel surface and provide a corboxyl binding group for further functionalization. A solution of 100 nm, red fluorescent (580/605) FluoSpheres carboxylate-modified microspheres (Invitrogen) at a dilution of 1:1000 was combined with EDC in ddH₂O to form a 100 μg/mL solution. The solution was pipetted onto the top surface of the gel at a volume of 100 μL, followed by incubation of 10 min at room temperature. After extensive washing, the process was repeated with a solution of 1 mg/mL fibronectin (Invitrogen) and incubated at room temperature for a further 10 min.

Finite Element Simulations

A commercial finite element (FE) software (ABAQUS, Dassault Systèmes) was used to simulate the mechanical interaction between the cell and the substrate. A detailed description of the FE formulation is provided in the Supporting Information. Briefly, a cuboid section of the substrate was modeled and the domain size selected to be large enough such that the deformations induced by the applied stress field did not reach the borders (semi-infinite condition, Figure S5a). A quadratic tetrahedral 10-node element (C3D10M) with second-order accuracy was employed to mesh the domain (Figure S2). The mesh size was adopted after carrying out mesh sensitivity analysis (Figure S5b–f). A linear elastic constitutive model was used to describe the mechanical behavior of the substrate, and elements were assumed to be nearly incompressible (Poisson’s ratio 0.49). A large deformation formulation was taken into account to consider the effect of geometric nonlinearity (see Supporting Information). For both the direct and inverse problems, boundary conditions applied in three dimensions to nodes located at the bottom surface meant they were constrained in three directions, while no restrictions were applied to the nodes at the side of the domain. Since the displacement vectors were only known at the locations of the fluorescent beads, a cubic interpolation scheme was used to estimate components of displacement vectors at all nodes of the structured finite element mesh located at the top surface of the gel. Considering the application of essential boundary conditions (EBCs), the inverse problem could be inherently solved via FE simulations to estimate unknown stress and strain fields from known displacement and force fields (see Supporting Information). In FE simulations, EBCs were applied to change the stiffness matrix and force vector to create a well-posed problem. Consequently, a dynamic implicit solver could be used to compute traction stress fields in either the direct or inverse problems. The components of stress tensors and deformation vectors were extracted from output files (.odb file) using a custom-written Python script. An image processing toolbox (Matlab, Mathworks) was employed in combination with ImageJ to smoothen and display stress/displacement fields in the region beneath the cell.

3D-SIM

3D-SIM microscopy was performed on a custom built system. Two excitation lasers were used: a 488 nm (MPB Communications Inc. 2RU-VFL-P-500-488-B1R) excitation laser for the actin channel and a 560 nm (MPB Communications Inc. 2RU-VFL-P-500-560-B1R) excitation laser for imaging the fluorescent beads. Excitation light patterns were formed by +1, 0, and −1 diffraction orders, generated by ferroelectric liquid crystal grating (SLM). Orders were focused at the back focal aperture of the objective lens. The excitation beam coming from the laser is collimated and passed through the acousto-optic tunable filter (AOTF, AA Quanta Tech, AOTFnC-400.650-TN). After the beam is expanded and sent to a phase-only modulator, of a polarizing beam splitter, an achromatic half-wave plate (HWP, Bolder Vision Optik, BVO AHWP3), and a ferroelectric spatial light modulator (SLM, Forth Dimension Displays, QXGA-3DM). The SLM displays a grating pattern with parameters matching the excitation wavelength, which is used to generate diffraction patterns. To maximize the pattern contrast, the diffracted light was kept with s-polarization using a polarization rotator. For each frame, the acquisition time was 11 ms. For imaging, a microincubator (H301, Okolabs, Naples, Italy) at 37 °C and 5% CO₂ was used.

Displacement Quantification

Bead displacements were extracted from the 3D-SIM 2 μm z-stack using a Python single-particle tracking library known as trackpy (https://soft-matter.github.io/trackpy/v0.3.2/index.html). Briefly, the algorithm first localized the beads in each z-stack from the time lapse. Next, the localizations were linked into bead trajectories. The ensemble of trajectories was then corrected for sample drift in x/y/z directions using a reference bead away from the cell contact. 3D-SIM-TFM data were acquired in at least 20 individual cells over the course of at least three independent experiments, and the data shown in Figure 2e are representative of the acquired data.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.9b01196.

• Figure S1, quantification of fluorescent bead resolution and tracking; discussion of the FEM; Figures S2–S4, outline of the FEM formulation applied to 3D-SIM-TFM; discussion of DTM calculation, mesh sensitivity analysis, stress calculation, and bead density and frame cycle time error analysis; Figure S5, determination of simulation domain dimensions and mesh sensitivity analysis; Figure S6, effects of bead density and acquisition rate on the accuracy of stress recovery (PDF)

• Movie S1, single-particle tracking showing lateral displacements of the 100 nm beads resulting from 3D-SIM imaging of the silicone gel during HeLa cell adhesion (AVI)

• Movie S2, single-particle tracking showing axial displacements in the XZ plane of the 100 nm beads resulting from 3D-SIM imaging of the silicone gel during HeLa cell adhesion (AVI)

• Movie S3, single-particle tracking showing axial displacements in the YZ plane of the 100 nm beads resulting from 3D-SIM imaging of the silicone gel during HeLa cell adhesion (AVI)

• Movie S4, evolution of the normal stress applied by the adherent HeLa cell to the top surface of the silicone gel (AVI)

• Movie S5, evolution of the shear stress applied by the adherent HeLa cell to the top surface of the silicone gel (AVI)

Author Present Address

^◆ School of Life Sciences, Queen's Medical Centre, University of Nottingham, Nottingham NG7 2UH , United Kingdom.

Author Contributions

^○ These authors contributed equally to this work

The authors declare no competing financial interest.