Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Jun 16;19(7):4702–4711. doi: 10.1021/acs.nanolett.9b01775

Phonon Engineering in Twinning Superlattice Nanowires

Marta De Luca †, Claudia Fasolato †,‡, Marcel A Verheijen §, Yizhen Ren §, Milo Y Swinkels †, Sebastian Kölling §, Erik P A M Bakkers §, Riccardo Rurali ∥,*, Xavier Cartoixà ⊥, Ilaria Zardo †,*
PMCID: PMC6628185  PMID: 31203630

Abstract

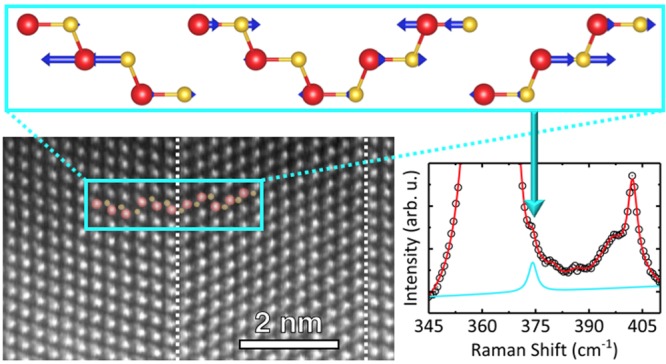
graphic file with name nl-2019-01775a_0006.jpg

One of the current challenges in nanoscience is tailoring the phononic properties of a material. This has long been a rather elusive task because several phonons have wavelengths in the nanometer range. Thus, high quality nanostructuring at that length-scale, unavailable until recently, is necessary for engineering the phonon spectrum. Here we report on the continuous tuning of the phononic properties of a twinning superlattice GaP nanowire by controlling its periodicity. Our experimental results, based on Raman spectroscopy and rationalized by means of ab initio theoretical calculations, give insight into the relation between local crystal structure, overall lattice symmetry, and vibrational properties, demonstrating how material engineering at the nanoscale can be successfully employed in the rational design of the phonon spectrum of a material.

Keywords: Phonon engineering, twinning superlattices, nanowires, Raman spectroscopy, DFT calculations

Designing materials with tailor-made phononic properties is crucial for many open problems within condensed matter and nanoscience, such as engineering efficient thermoelectric materials1,2 and keeping a low thermal budget in nanoelectronics,3 as well as to envisage devices that can use heat for information processing.4−6 Superstructures consisting of a periodic arrangement of two materials, that is, superlattices, can successfully exploit wave interference phenomena, such as the formation of forbidden bandgaps and the modification of the density of states and group velocities of phonons, to control the heat flow by tuning the material’s thermal conductivity.7−10 A connection between the superlattice periodicity and coherent versus incoherent heat transport has been established, outlining two transport regimes dominated either by the corpuscular nature of phonons or by wave interference effects.11,12 Rough or defective interfaces have been shown to significantly reduce the coherence of phonon transport13 and thus much of the rich physics exhibited by phononic superlattices is directly connected to the sharpness of the interfaces defining the superstructure.14 Typical issues that degrade the quality of ordinary heterojunctions, for example, lack of sharpness of the interface, lattice mismatch, and interdiffusion, become negligible or irrelevant in crystal phase superlattices,15−19 which are “homojunctions” where only the crystal structure changes, while the atomic species and the nature of chemical bonding stay the same. This type of superlattices can be realized in nanowires (NWs),20−22 as the great progresses made in recent years in their synthetic growth23 enabled the epitaxial growth of novel crystal phases,24,25 which in bulk can only be observed under extreme conditions of temperature and pressure. The controlled switching between different crystal phases during the growth opened the way to crystal phase engineering where unconventional polytypes can be juxtaposed in an ordered fashion to the most common polymorphs and create crystal phase superlattices. Because of the specific nature of these interfaces, it is of great fundamental and applied interest to assess to what extent one can tune by design the properties of these systems, similarly to what can be achieved with conventional superlattices26,27 or phononic crystals.28

Twinning superlattices (TSLs)29,30 are a limiting case of these crystal phase superstructures, where the only polytype present exhibits a periodic 60° rotation of the crystal lattice. This is a unique metamaterial which locally is constituted by one single crystal phase but has the overall symmetry of a different one and that in III–V compounds has been obtained only with NWs. It is worth noting, however, that since their discovery29,30 none of the functional properties of TSLs has been reported so far. In particular, molecular dynamics simulations of TSL in Si NWs have exposed the possibility to tune the thermal conductivity in these systems by changing the distance between twin planes, namely the period of the superlattice.31,32 In our report, we provide experimental evidence, corroborated and rationalized by ab initio calculations, of such modified properties and of their tunability.

We study GaP TSLs where periodically arranged twin planes with distances L ranging from 4 to 20 nm, separate zincblende (ZB) segments.15 Therefore, although the twin defects themselves can in a way be considered as the shortest possible wurtzite (WZ) inclusion, these NWs are made exclusively of ZB GaP. Yet, the periodic twin arrangement confers a hexagonal symmetry to the NW as a whole. As we will discuss below, this unusual crystal lattice is an excellent test-bed for monitoring how the existence of an overall periodicity affects the phononic properties of the material in terms of number, frequency, and symmetry of the phonon modes arising from the superstructure. Indeed, we show that we can rationally design the phononic properties by tuning the superlattice period. Moreover, we find that the TSL phonons are keeping their coherence over tens of nanometers at room temperature, which is a clear indication that the defect-free and atomically sharp interfaces of TSL NWs make them the ideal superstructure to study coherent phonons and wave interference.

Results

Twinning Superlattice Nanowires

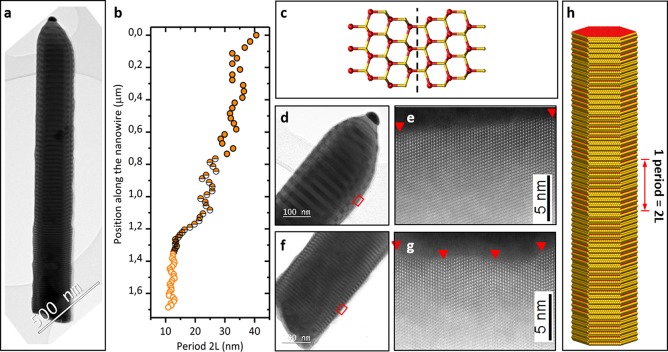
We grow GaP nanowires by metal–organic vapor phase epitaxy using the vapor–liquid–solid growth technique. We analyze the structural properties of the wires by transmission electron microscopy (TEM), which shows that the wires have ZB structure, uniform diameter, and are grown along the ⟨111⟩ direction. Along the nanowire growth direction, regularly spaced twin planes can be observed. Bright-field (BF) TEM images show the ZB segments between consecutive twin planes with different contrast (Figure 1a). A twin acts as a mirror plane, where the stacking of lattice planes ABCABC typical of a pure ZB structure are changed into ABCACBA (Figure 1c). We define the TSL period (2L) as twice the distance between two consecutive twin planes (Figure 1h). By analyzing the variation of the contrast along the NW length, we obtain an estimation of the period. As displayed in Figure 1b, in our sample the period changes along the nanowire length: at the bottom of the NW, a first segment (∼500 nm) exhibits a constant period of about 10 nm; it is followed by a transition region (500–600 nm) with increasing period from 10 to 30 nm; at the end of the NW, a final segment (∼600 nm) has a constant period of about 30–40 nm. All the investigated TSL NWs exhibit very similar structural characteristics. The variation of the twin spacing along the NW length is shown by TEM and high-angle annular dark-field (HAADF) scanning TEM (STEM) images taken at the different location along the NW (Figure 1d–g). Experimental TEM details along with TEM images and periods’ estimation on five NWs are provided in Supporting Information 1.

Figure 1.

Figure 1

Open in a new tab

Nanowire twin superlattice. (a) BF TEM image of a typical TSL nanowire investigated in this study. (b) Relation between position along the NW in (a) and extracted TSL period. (c) Schematic of a twin plane where spheres of different colors represent different types of atoms. (d) BF TEM image acquired at the top of the NW displayed in (a). (e) HAADF STEM image acquired in the position marked by the red square in (d). The red triangles indicate the position of the twin planes. The measured twin period is 32.6 nm. (f) BF high-resolution TEM image acquired at the bottom of the NW displayed in (a). (g) HAADF STEM image acquired in the position marked by the red square in (f). The red triangles indicate the position of the twin planes. The measured twin period is 11.4 nm. (h) Three-dimensional atomic reconstruction of a model TSL nanowire with six TSL periods.

The spatial dependence of the twin spacing characteristic of our NWs enabled us to investigate the phononic properties of TSL NWs for different TSL periods under otherwise identical conditions.

Hexagonal Superstructure

We probed the phonons of TSL NWs by inelastic light-scattering experiments. The expected phonon modes at the Γ-point of the Brillouin zone were computed with ab initio density functional perturbation theory (DFPT) calculations33 within the local density approximation (LDA) with the ABINIT code.34,35 We also computed the corresponding Raman susceptibility tensors and expected theoretical Raman spectra,36 as detailed in the Computational Methods. Polarization-resolved Raman scattering experiments and calculations were performed in backscattering geometry. The incident photon wavevector (ki) is antiparallel to the x-axis and the scattered photon wavevector (ks) is parallel to x. As a consequence, the incident and scattered light polarization vectors, εi and εs, lie in the yz plane, which is the plane of the sample. εi and εs can be separately controlled to obtain the desired scattering geometries. The scattering configuration is expressed in the Porto notation, ki(εi, εs)ks: the outer terms, from left to right, refer to the excitation and scattering direction of the light, respectively, and the inner bracket refers to the excitation and detection polarizations. The main scattering geometries used in this work are the x̅(zz)x, x̅(yy)x, and x̅(zy)x. In the calculations, the nonanalytical corrections suitable to the specific scattering geometry were applied as explained in Supporting Information 2. The single NWs (both TSL and WZ) were placed with the long axis along the z-axis of the reference system. In particular, the WZ [01̅10], [21̅1̅0], and [0001̅] axes were along x, y, and z, and the TSL [011], [21̅1], and [111̅] axes were along x, y, and z. The reference bulk GaP was a (111)B substrate tilted in order to lie in the xz plane and to have the (011) surface lying on the yz plane.

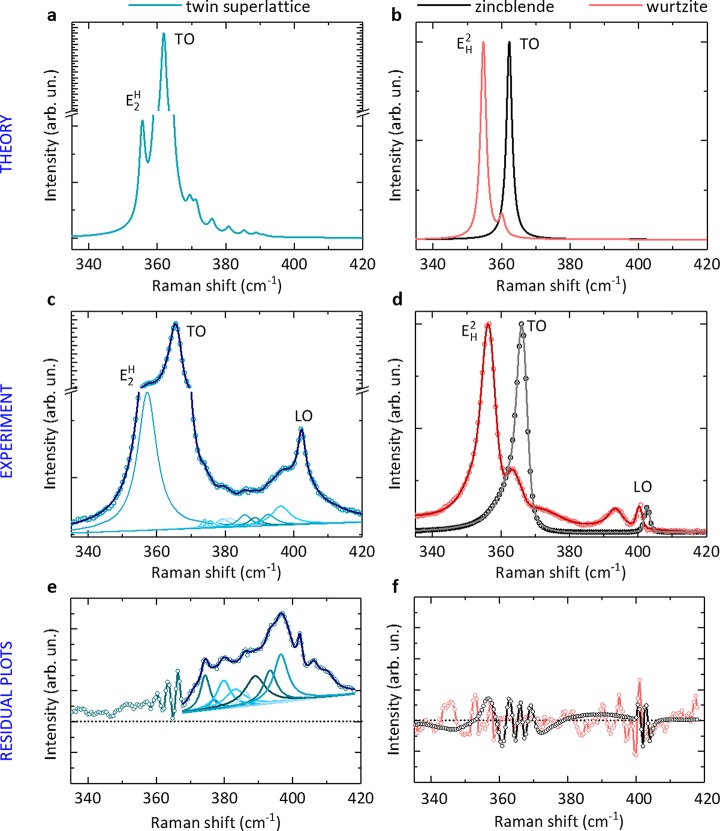
The calculated spectrum of a GaP TSL with 9 nm period length is shown in Figure 2a. For comparison, the reference calculated spectra of bulk ZB and WZ GaP are also shown in Figure 2b. The spectrum of the TSL in Figure 2a features the transversal optical (TO) mode at ∼362 cm–1 similarly to the one of ZB GaP, but it also exhibits a quite pronounced E2H mode, which is characteristic of a hexagonal symmetry like in WZ.37,38 The presence of the E2 mode in the TSL NW is a clear indication that the overall symmetry of a TSL is hexagonal. Indeed, its corresponding space group is P63mc (#186), which is the same as the WZ structure. Notably, the Raman spectrum of the TSL also consists of several phonon modes on the higher wavenumber side of the TO mode, which are neither observed in the ZB nor in the WZ phase but arise from the backfolding of the phonon dispersion due to the different lattice parameter introduced by the superlattice.39−41 According to our calculations, all those modes are transverse optical modes.

Figure 2.

Figure 2

Open in a new tab

Twin superlattice phonon modes and hexagonal symmetry. (a) Calculated spectrum of a GaP twin superlattice with 9 nm period length. (b) Calculated reference spectra of bulk GaP in the ZB (black solid line) and wurtzite (red solid line) crystal phase. (c) Measured spectrum of a GaP twin superlattice nanowire with 9 nm period length (open circles). Deconvoluted Lorentzian components of the data fitting arising from the superlattice are displayed, along with the fit result (solid lines). (d) Measured reference spectra of GaP from a bulk ZB substrate (black circles) and a wurtzite nanowire (red circles) with superimposed fit results (solid lines). All theoretical and experimental spectra were obtained in the x̅(yy)x configuration. All spectra in panels a–d are normalized to the most intense peak contribution. (e) Residual plot (lines + circles) of the fit of the data displayed in panel c performed excluding the modes arising from the superlattice. The fit of the residual plot along with its Lorentzian components (only those arising from the superlattice) are displayed (solid lines). (f) Residual plots (lines + circles) of the fit of the data displayed in (d). The scale of panels e and f goes between −2.5% and 5% of the scale in panels c and d.

Single NWs were transferred on a Si(100) substrate and polarization-dependent spatially resolved measurements were performed at room temperature and at 5.5 K. We performed measurements using two different excitation wavelengths; here, we present results obtained with λexc = 514.5 nm at room temperature (spectra acquired with λexc = 632.8 nm or at 5.5 K, showing consistent results, can be found in the Supporting Information). In Figure 2c,d, we display the experimental spectra corresponding to the theory in Figure 2a,b with the TSL and WZ spectra acquired on NW samples. In the measured spectrum of a GaP TSL NW with 9 nm period length shown in Figure 2c, the TO and E2H modes are clearly visible as in the computed spectrum. Differently from the computed spectrum, the experimental one also exhibits a longitudinal optical (LO) mode at ∼402 cm–1 and a broad shoulder below the LO mode. The latter is ascribed to a surface optical (SO) mode due to the finite size of the NW.42 The LO mode is also present in the reference GaP spectra, acquired on bulk ZB and on the WZ NW and depicted in Figure 2d. This mode is forbidden by selection rules in the adopted scattering geometry and is indeed absent in the theoretical results. The forbidden LO mode arises in both bulk and NW samples from the use of a high NA objective (see Supporting Information 3) and in the case of the WZ and TSL NWs also possibly from size effects responsible for a relaxation of selection rules. The SO mode is also revealed in the spectrum collected from the WZ NW but absent in the spectrum collected from the bulk (011) GaP, confirming its origin. Both of these features (the finite size effects and the high NA of the objective) are not accounted for in the theoretical modeling and thus this disagreement is not surprising. Finally, notice that the TO mode in the experimental spectra of the ZB, WZ, and TSL is broadened to the low-frequency side. This effect, well-known in bulk GaP,43,44 is due to the strong anharmonicity of the material, as further discussed in the Supporting Information 4.

Table 1 displays a comparison between the calculated (first row) and measured (second row) frequencies of the TO, LO, and E2H modes for GaP ZB, WZ, and TSL. Our computed frequencies agree well with the experimental results with a small underestimation which is within 4 cm–1 for all modes with the exception of the LO. The disagreement of the latter is larger because of the known underestimation of the nonanalytical correction to the calculation due to the larger values of the LDA dielectric constant (ε = 12.9) with respect to experiment (ε = 11.1),45 leading to a smaller TO–LO splitting. Indeed, the discrepancy between the calculated and measured LO frequencies decreases if we renormalize the nonanalytical correction using the experimental value of the dielectric constant (see value in parentheses in the table).

Table 1. Calculated and Experimental Frequencies of TO, LO, and E2H modes for GaP ZB, WZ, and TSLa.

  TO (cm–1)
 LO (cm–1)
 E2H (cm–1)
  ZB WZ TSL ZB WZ TSL WZ TSL
theory 362.2 360.1 361.6 391.9 (396.5) 391.2 391.7 354.7 355.6
exp. 366.2 363.0 365.5 402.6 400.2 402.4 356.3 357.3
Open in a new tab
a

Experimental frequencies refer to the samples of Figure 2c,d. The TSL period is 9 nm. The scattering configuration used both for experiments and calculations is x̅(zz)x for the TO and LO modes and x̅(yy)x for the E2H. The error on the experimental values is ±0.5 cm–1. The value between parentheses for the calculated LO frequency of the ZB has been obtained by renormalization of the non-analytical corrections using the experimental value of the dielectric constant.

Because a difference between experimental and theoretical frequencies occurs regardless of the crystal symmetry involved (ZB, WZ, TSL), when comparing theory to experiment we will focus on the relative shift in the frequencies induced by the different crystal symmetries and not on the absolute frequency values. The agreement between theoretical and experimental frequency shifts is indeed very good. In going from the ZB to the WZ phase, TO and LO modes downshift by different, consistent amounts in both the theoretical and the experimental data. The frequencies of the modes in the TSL are in between the ZB and the WZ values, closer to the ZB. The E2H mode, arising from the back-folding of the TO mode in both WZ and TSL, upshifts by ∼1 cm–1 when going from the WZ to the TSL structure. The dependence of TO and E2 frequencies on the TSL period will be discussed in more detail below (see, e.g., Figure 5).

Figure 5.

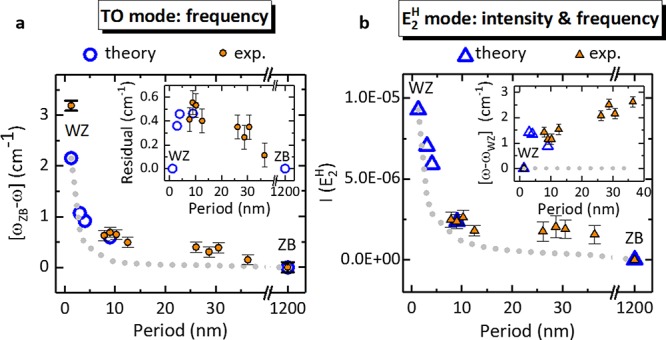
Figure 5

Open in a new tab

Dependence of TO and E2H modes on TSL period. (a) Calculated (open circles) and experimental (filled circles) frequencies of TO mode in the x̅(zz)x configuration for GaP ZB, WZ, and TSL expressed as absolute shifts from the calculated and experimental ZB TO mode. The error bar of experimental frequencies is ±0.1 cm–1 (smaller than the absolute error given by the spectral resolution, which is equal to 0.5 cm–1) because the data were acquired with the same experimental alignment. The dashed gray curve was obtained from a model computing the spectra in TSL as a linear combination of the ZB and WZ phases, weighting each contribution by the corresponding volume ratio: the total volume of one period Vtot is the NW cross section times the period of the TSL; the volume of the WZ Vwz is equal to the NW cross section times 2c, where c is the thickness of an AB segment and 2 is the number of twin defects in every period; the volume of the ZB is derived by difference, Vtot – VWZ. The inset shows the difference between the theoretical and experimental data and the gray curve (open circles and filled circles, respectively). (b) Calculated (open triangles) and experimental (filled triangles) intensity of the E2 mode in the x̅(yy)x configuration for GaP ZB, WZ, and TSL. To allow a fair comparison, because the Raman intensity is not absolute we have rescaled the experimental intensities so that the experimental E2H mode intensity of the NW with the 9 nm period matches the calculated one, as in Figure 3d. The dashed gray curve is the E2 mode intensity obtained with the weighted model. The inset shows the theoretical and experimental E2H frequency with respect to the WZ E2 frequency as a function of TSL period. The dashed gray curve represents the E2H frequency shift provided by the weighted model.

As predicted by the calculations, in the TSL experimental spectrum displayed in Figure 2c, we also detect significant spectral features between the TO and LO modes. Although the finite full width at half-maximum (fwhm) of the phonon modes prevents one from resolving each component of the spectrum by eye, a careful quantitative analysis clearly exposes the presence of numerous, well-defined phonon modes between the TO and LO modes, whose Lorentzian contributions to the spectrum are displayed by solid lines. Figure 2e is particularly revealing in this sense. It shows the residual plot of a fit of data displayed in Figure 2c where we include only the E2H, TO, SO, and LO modes and a broad Gaussian to account for the contribution of the TSL modes between TO and LO modes; for comparison, in Figure 2f we provide also the residual plot of the fit of the data collected on the two reference systems including the E2, TO, LO, and SO modes. In the case of the WZ GaP NW and the bulk ZB GaP, the obtained residual oscillates within 2% of the measured intensity, which confirms that all necessary contributions to the fits were already included in Figure 2d. Instead, the residual of the analysis of the TSL spectrum, including the TSL broad contribution between TO and LO, strongly increases in the range of frequencies between the TO and LO modes and has clearly distinguishable features that can be fitted by Lorentzian peaks, further corroborating the quantitative analysis of Figure 2c.

Tunability of the Phononic Properties

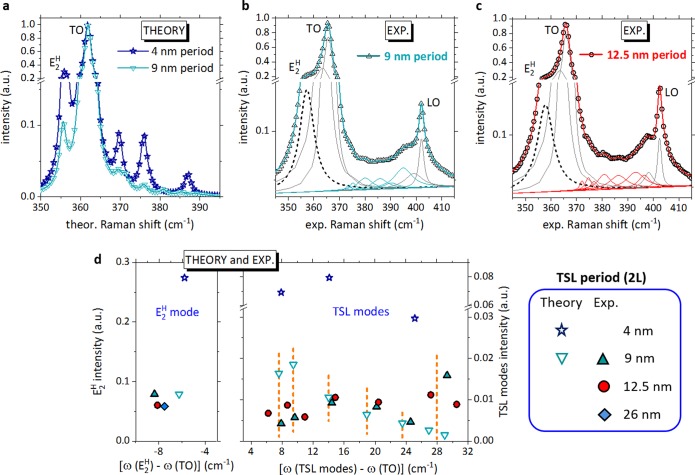
As discussed previously, the spacing between the twin planes varies along the length of the NW, being always shorter at the bottom than near the tip. This feature is especially appealing because it gives access to TSLs with different periods within a single NW. It is worth mentioning here that the probed region of the NW is limited to the laser spot size, and therefore at the two NW ends we probe phonons arising from a constant TSL period. Our computed Raman spectra predict the possibility of tuning the number and intensity of the spectral features with wavenumbers beyond the TO by controlling the period of the TSL. This is shown in Figure 3a, where we compare the computed Raman spectrum of a TSL with a period of 9 nm (the same of Figure 2a) with another with a shorter period of 4 nm. As expected, a shorter period results in fewer peaks.

Figure 3.

Figure 3

Open in a new tab

Tunability of the phononic properties in twin superlattices. (a) Calculated spectra of a GaP TSL with 4 nm (open stars and blue solid line) and 9 nm (open triangles and cyan solid line) period length. (b) Measured spectrum of a GaP TSL nanowire with ∼9 nm period length. Deconvoluted components of the data fitting are displayed (E2H mode in black dashed line, TO, SO, and LO modes in gray solid line). (c) Measured spectrum of a GaP TSL nanowire with ∼12.5 nm period length. Deconvoluted components of the data fitting are displayed. The intensity scales of the spectra in (b,c) are directly comparable. (d) Intensity vs wavenumbers of the calculated (empty symbols) and measured (filled symbols) phonon modes arising from the SL from the spectra displayed in panels a–c. Colors refer to the corresponding period length. Stars are for 2L = 4 nm, triangles are for 2L = 9 nm, circles are for 2L = 12.5 nm, as summarized in the legend. Vertical dashed lines show the good agreement between calculated and experimental phonon frequencies of the TSL with period of 9 nm. This is also evident in Table 2. The blue diamond refers to data acquired on a NW with ∼26 nm period length. All theoretical and experimental spectra were obtained in the x̅(yy)x configuration. In order to allow a fair comparison, all calculated and experimental frequencies are expressed as frequency shifts from the TO mode of the relative sample. Similarly, we have rescaled all the experimental intensities so that the E2 mode intensity retrieved experimentally on NW with the 9 nm period matches the E2H intensity calculated for a TSL with the same period.

The quantitative calculation unveils that the fewer the peaks, the higher their intensity. Indeed, in the limiting case of a vanishing period we retrieve the WZ case where there is only one very intense folded mode (E2H).

Figure 3 also displays the experimental Raman spectra acquired from two NWs with slightly different periods: 9 nm in panel b and 12.5 nm in panel c (see Supporting Information 5 for different scattering configurations and for a discussion of Raman selection rules). It is worth stressing that the twin period has been estimated by TEM measurements performed on the very same wires after Raman measurements. Notice that the period length of the NW in Figure 3b closely compares to one of the cases considered in our theoretical calculations (Figure 3a), thus we compare the frequencies of the modes between the TO and LO modes originated from the back-folding in Table 2. The phonon frequencies are given as a relative shift with respect to the TO mode to get rid of the slight underestimation of phonon frequencies by DFPT. Considering the experimental error, we find a remarkable agreement between theory and experiment. Notice that the peak with 24.6 cm–1 frequency shift is quite broad, and thus it is probably resulting from a convolution of the separate 23.5 and 27.0 cm–1 modes predicted by theory.

Table 2. Calculated and Experimental Frequencies of the Folding-Originated Modes for GaP TSL Expressed as Frequency Shifts from the TO Modea.

  TSL mode 1(cm–1) TSL mode2 (cm–1) TSL mode3 (cm–1) TSL mode 4 (cm–1) TSL mode 5 (cm–1) TSL mode 6 (cm–1) TSL mode 7(cm–1)
theory 7.6 9.5 14.0 18.9 23.5 27.0 29.0
exp. 7.9 9.6 14.4 20.2 24.6 29.3
Open in a new tab
a

Experimental frequencies refer to the spectra displayed in Figure 3b. The TSL period in both theory and experiment is 9 nm. The scattering configuration used both for experiments and calculations is the x̅(yy)x. The error on the experimental values is ±1.5 cm–1.

Let us now compare the spectra recorded on the NWs with slightly different periods (in Figure 3b,c) to demonstrate experimentally the tunability of the phononic properties. The quantitative analysis of these spectra shows that at longer periods, we observe a larger number of spectral features than at shorter periods which is in line with the prediction of the theory. It is interesting to observe that also the E2H peak, which is the other characteristic signature of these TSLs, obeys the rule regarding its intensity, which is stronger for shorter periods. A more quantitative comparison is carried out in Figure 3d, where we plot the intensity as a function of the Raman shift (calculated from the TO of the pertinent sample) of all the measured and computed phonon modes extracted from fitting the spectra reported in Figure 3a–c. The NW with 12.5 nm period shows one more peak between TO and LO than the NW with 9 nm period, which is in agreement with the expectation of an increased number of modes in a longer period TSL, and the E2 mode is more intense in the NW with the shorter period. In the plot of the E2H mode, we also included the results obtained from a TSL period of ∼26 nm. As expected, its intensity slightly decreases due to the increased period length. The relative spectrum and analysis are displayed in Supporting Information 6. We did not perform a quantitative analysis including ∼20 TSL modes between TO and LO because it would be affected by a non-negligible degree of arbitrariness (see Supporting Information 6). The vertical dashed lines in Figure 3d highlight the good agreement between calculated and experimental frequencies of the TSL with 9 nm period.

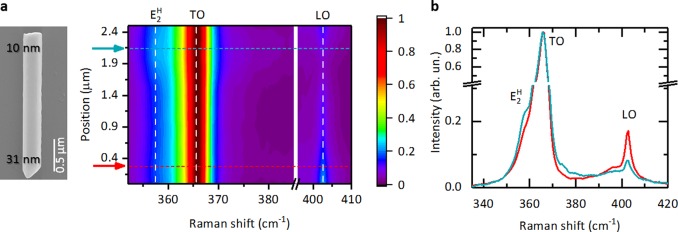
A one-dimensional Raman scan acquired along the length of the TSL NW studied in Figure 2 is displayed in Figure 4. The spatially resolved investigation allows monitoring the changes in the Raman spectrum ensuing from the changes in the period of the TSL. Here, the period length decreases with increasing position in the vertical scale. In Figure 4b, we display two representative Raman spectra extracted from the map in the positions indicated by the arrows in Figure 4a. In the top part, the period is smaller and thus the intensity of the TSL folded-originated modes (E2H and the modes between TO and LO) is higher. In the bottom part, where the gold droplet is located, and the NW is slightly tapered, the LO mode is enhanced. This happens in all our measurements (see, e.g., Supporting Information Figures 6 and 7). The LO enhancement is due the presence of the gold nanoparticle. Indeed, metal nanoparticles can affect the electromagnetic near-field profile in the surrounding region, thus rendering forbidden modes greatly enhanced, a phenomenon very well-known for molecular samples in surface enhanced Raman scattering applications.46 The map confirms that where the period is smaller, the intensity of the TSL folded-originated modes (E2 and the modes between TO and LO) is higher.

Figure 4.

Figure 4

Open in a new tab

Dependence of the TSL phonon modes on the period lengths. (a) Raman map as a function of the position along the NW (step size: 0.15 μm) where the spectrum in Figure 2c was acquired. A SEM image of this NW is displayed on the left side of the map. Period decreases with increasing position, as indicated in the SEM image. The map was recorded in the x̅(yy)x configuration in order to highlight TSL-related features, and each line in the color plot was normalized to its maximum intensity (TO mode). (b) Raman spectra extracted from the map in the positions indicated by the arrows and dashed lines in (a). The x-scale is changed from panel a to panel b for sake of clarity.

The period of the TSL not only determines the number, frequency, and intensity of the folding-originated modes but it also affects the frequency of the “bulklike” modes, namely TO and LO. In Figure 5a, we compare theoretical and experimental frequencies of TO mode as a function of the TSL period. We consider the WZ as a TSL with vanishing period and the ZB as a TSL with asymptotically long period (for the plot we set it equal to 1200 nm, i.e., about twice the laser spot) and plot the absolute frequency shifts from the calculated and experimental TO mode of the ZB as open and filled symbols, respectively. The theory predicts a gradual upshift with increasing period (i.e., decreasing frequency shift with respect to the ZB TO). The experimental values nicely reproduce this behavior. Although the shift of the TO mode with the TSL period is quite small, its observation is an important confirmation that we are probing the phonons of the TSL and that our theory provides an accurate description of the physics involved. For the sake of completeness, we have also considered the hypothetical situation in which the TO shifts arise from the fact that in our scattering volume, we have portions of ZB (namely, the segments sandwiched between two consecutive TSL planes) and portions of WZ (namely, the TSL planes, which can be viewed as WZ inclusions consisting of one single AB bilayer). Therefore, we develop a simple model where we weigh each contribution (ZB and WZ) with the corresponding volume ratio, and the TSL spectrum is computed as a linear combination of the theoretical ZB and WZ spectra. We then analyze the obtained spectra to extract the TO frequency shift as a function of TSL period. The results are displayed by the gray dashed curve in Figure 5a. The inset shows the difference between the data and the curve. By construction, the curve intersects the WZ and ZB theoretical data, while it does not provide an accurate estimate of the TSL TO theoretical frequencies (the difference is indeed about 0.5 cm–1), which were computed by considering the whole TSL crystal with its own symmetry and not as a weighted sum of large ZB and thin WZ portions. The same difference is observed in the experimental data as well. It is worth noticing that for periods around 40 nm, the measured TO mode frequency is very close to the one of the ZB structure and does not differ significantly from the one of the simplified model, whereas the deviations for periods up to 30–35 nm lead us to infer the TSL period up to which we observe coherent phonon effects. However, as the discrepancy between the dashed curve and the TSL theoretical data is quite small, one might still conclude that the simplified model gives a reasonable prediction of the TO frequencies of the TSL. In this respect, it is very important to stress that a similar approach is incapable of predicting other crucial features observed in our experiments and calculations, such as the appearance of spectral features between the TO and the LO mode, which are remarkable and unambiguous signatures of the coherent phonon propagation enabled by the superlattice, as well as the intensity and frequency of the E2H mode. Namely, we have computed with the simple model of weighted crystal phase contributions also the intensity and frequency of the E2 mode (gray dashed curve in Figure 5b and inset, respectively) and compared it with the computed and measured (open triangles and filled circles in Figure 5b, respectively). Only the ab initio calculation of the TSL crystal accounts for the observed intensities, while those resulting from the weighted WZ/ZB segments are lower than the experimental intensities. Even more striking, the model of weighted crystal phase contribution cannot account for a dependence of the frequency of the E2H mode on TSL period (see inset in Figure 5b).

Our results provide evidence that periodic twins with periods up to about 35 nm cannot be regarded as, for example, wurtzite inclusions in a zinc-blende structure and rather confer the crystal with a new symmetry resulting in new properties. On the other hand, we suggest that the model with weighted crystal phase contribution can be a useful tool to predict phononic properties with randomly occurring twins and/or crystal phase mixing where coherent phonon effects do not occur.

Finally, we stress that our experimental results are very sound and reproducible, as testified from the fact that (i) five different TSL NWs with very similar structural characteristics show very similar Raman spectra (see Supporting Information 7); (ii) measurements performed in the same scattering geometry but with different excitation wavelengths on different NWs exhibit consistent spectral features (see Supporting Information 8); (iii) data acquired at 5.5 K on the same NWs measured at room temperature in the same configuration show consistent results (see Supporting Information 9).

The presence of the E2H mode and the other backfolded peaks in the TSL NWs is an important indication that the associated phonons are keeping their coherence over a few TSL periods, namely, that the mean free path of those phonons is longer than the period length. This is clearly the case for the short period part of the NWs but also for the long period part, because also in that region we observe clear, though less intense (as predicted by theory), TSL phonon modes. This observation agrees well with our calculated mean free paths of optical phonons of bulk GaP at room temperature, which can be as long as 50 nm. Noticeably, backfolded phonon modes were observed until now in “conventional” heterostructure superlattices with considerably shorter periods than the twin periods probed in this study.41 The maintenance of coherent phonon propagation over tens of nanometers is the essential requirement for its exploitation in thermal applications based on coherent phonons. Quite remarkably, most of our study, which provides the experimental demonstration of coherent phonons in NWs, was carried out at room temperature, and because already at room temperature we are probing coherent phonons, low temperature conditions, which correspond to a longer phonon mean free path, are not needed to unveil TSL-originated phonon modes.

In conclusion, we have reported on the phononic properties of GaP nanowires twinning superlattices by investigating them with inelastic light scattering. We have observed the E2H mode characteristic of the WZ crystal structure and a number of spectral features beyond the TO mode. The first of these observations was unexpected, because the nanowires investigated locally possessed a ZB structure. However, the twin defect stacking confers an overall hexagonal structure to the system giving rise to this phonon mode. The second observation was a direct result of the folding of the dispersion relation determined by the periodic superstructure. Both of these observations were unambiguously corroborated by ab initio theoretical calculations and by the dependence of these spectral fingerprints on the spacing of the twin planes. This fact supports the tunability of the phonon spectrum of these systems and paves the way toward the achievement of phononic properties by design.31,32,47 We suggest that future heat transport experiments will show that this controlled tuning of the phonon spectrum also results in a measurable modification of the thermal conductivity, because (i) our calculations demonstrate that also acoustic modes undergo the same folding as optical modes (see Supporting Information 10) and (ii) although high frequency optical phonons per se do not contribute significantly to the thermal conductivity, they play an important role in third- and higher-order phonon scattering processes that also involve acoustic phonons.

Methods

Nanowire Growth

The zincblende GaP TSLs NWs were grown in an Aixtron Close Coupled Showerhead MOVPE reactor. Prior to growth, we used soft contact lithography to make regular nanoholes pattern in a SiNx-coated GaP (111)B wafer. Then the Au-catalyzed GaP TSLs were grown by the vapor–liquid–solid mechanism with a V/III ratio of 21.5 at 640 °C.48 Phosphine (PH3) and trimethyl gallium (TMGa) were used as precursors, and hydrogen chloride gas was used to prevent nanowire tapering. The wurtzite (WZ) GaP NWs were grown with the method described in ref (49).

Structural Investigation

TEM studies on NWs were performed using a probe-corrected JEOL ARM 200F transmission electron microscope operated at 200 kV in both BF TEM mode and HAADF STEM mode.

Computational Methods

We have performed ab initio DFPT calculations33 within the LDA with the ABINIT code34,35 of TSLs with a period of 3, 4, and 9 nm. The latter compares directly with a periodicity of the twins found in some of the samples investigated experimentally. We use hexagonal cells, containing N = 10, 12, and 30 monolayers, for the three TSLs studied. Notice that to satisfy periodic boundary conditions an even number of twin defects, placed along the ZB [111] crystal axis, must be included and thus the computational cells used in the calculations contain two twin planes. The Brillouin zone was sampled with a converged grid of 16 × 16 × M, with M taking values of 3, 2, and 1 going from the smallest to the largest cell. The calculations have been performed in a bulk system, as we do not expect the vibrational properties of NWs of these characteristic diameters to be affected by confinement. We compute the Raman susceptibility tensor from the third derivative of the total energy: twice with respect to the application of an electric field (i.e., incident and scattered light polarization vectors) and once with respect to the phonon displacement coordinates, making use of the 2n + 1 theorem.50 Given the sensitivity of the energy derivatives to the quality of the converged wave functions, a high plane wave cutoff of 38 Ha, an energy cutoff for the fine fast Fourier transform of 76 Ha, and a strict convergence criterion of the wave function residual norm of 10–22 were used.

In order to properly account for the scattering geometry used in the experiment, the Raman intensity of each mode n has been calculated as

graphic file with name nl-2019-01775a_m001.jpg

where Rn is the Raman susceptibility tensor calculated ab initio, while εi and εs are the polarization vectors of the incident and scattered light, respectively.51 Once the intensity for each phonon mode has been calculated, Raman spectra are generated by summing up Lorentzian functions, each associated to a calculated mode frequency. The Lorentzian functions have a full width at half-maximum that is chosen to reproduce the experimental one.

Raman Experimental Details

Raman experiments were performed by exciting the samples either with the 633 nm line of a HeNe laser or with the 514.5 nm line of an Ar+Kr+ laser. The incident power was kept below 1 mW to avoid heating or damaging effects. The samples were illuminated with a high numerical aperture (0.95) 100× objective (if not differently specified), which allows a spatial resolution of about 600 nm for the 514.5 nm laser. The polarization of the incident laser light and of the backscattered beam can be controlled and selected by means of polarization optics. The scattered light was collected by a T64000 triple spectrometer in subtractive mode, equipped with a 1.800 g/mm grating and a liquid nitrogen-cooled CCD detector, providing a spectral resolution of 0.5–1 cm–1. T = 5.5 K measurements were performed by loading samples in a He continuous-flow cryostat using the 514.5 nm laser.

Acknowledgments

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement 756365) and from the Swiss National Science Foundation research Grant (Project Grant 200021_165784). R.R. acknowledges financial support by the Ministerio de Economía, Industria y Competitividad (MINECO) under Grant FEDER-MAT2017-90024-P and the Severo Ochoa Centres of Excellence Program under Grant SEV-2015-0496 and by the Generalitat de Catalunya under Grant 2014 SGR 301. X.C. acknowledges financial support by the Ministerio de Economía, Industria y Competitividad under Grant TEC2015-67462-C2-1-R (MINECO/FEDER). The calculations have been performed at the Red Española de Supercomputación (RES) within the project “Phonons dispersion relation in GaP crystal phase superlattices” (FI-2017-1-0026). Solliance and the Dutch province of Noord-Brabant are acknowledged for funding the TEM facility. M.D.L. acknowledges support from the Swiss National Science Foundation Ambizione Grant (Grant PZ00P2_179801). C.F. acknowledges financial support from Sapienza University scholarship “Borsa di Perfezionamento all’Estero 2017–2018”. The authors thank A. Campo and M. Carballido for nanowire manipulation and Z. Azdad for preliminary work.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.9b01775.

  • Further structural characterization of the nanowires, details on computational and spectroscopic methods and analysis, and Raman spectra taken on different nanowires, with different scattering geometries, at low temperature, and with different excitation wavelengths (PDF)

Author Contributions

I.Z. conceived the experiment. M.D.L. and C.F. performed the measurements. M.D.L., C.F., and I.Z. analyzed the experimental results. Y.R. and E.P.A.M.B. grew the samples. S.K. and M.Y.S. prepared the samples for TEM investigation, which was performed by M.A.V., while M.Y.S. took SEM images. R.R. and X.C. performed the theoretical calculations. R.R., I.Z., and M.D.L. wrote the manuscript. All authors discussed the results and commented on the manuscript.

The authors declare no competing financial interest.

Supplementary Material

nl9b01775_si_001.pdf (825.7KB, pdf)

References

  1. Zebarjadi M.; Esfarjani K.; Dresselhaus M. S.; Ren Z. F.; F Z.; Chen G. Perspectives on thermoelectrics: from fundamentals to device applications. Energy Environ. Sci. 2012, 5, 5147. 10.1039/C1EE02497C. [DOI] [Google Scholar]
  2. Benenti G.; Casati G.; Saito K.; Whitney R. S. Fundamental aspects of steady-state conversion of heat to work at the nanoscale. Phys. Rep. 2017, 694, 1. 10.1016/j.physrep.2017.05.008. [DOI] [Google Scholar]
  3. Moore A. L.; Shi L. Emerging challenges and materials for thermal management of electronics. Mater. Today 2014, 17, 163. 10.1016/j.mattod.2014.04.003. [DOI] [Google Scholar]
  4. Terraneo M.; Peyrard M.; Casati G. Controlling the Energy Flow in Nonlinear Lattices: A Model for a Thermal Rectifier. Phys. Rev. Lett. 2002, 88, 094302 10.1103/PhysRevLett.88.094302. [DOI] [PubMed] [Google Scholar]
  5. Li N.; Ren J.; Wang L.; Zhang G.; Hänggi P.; Li B. Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 2012, 84, 1045. 10.1103/RevModPhys.84.1045. [DOI] [Google Scholar]
  6. Volz S.; Ordonez-Miranda J.; Shchepetov A.; Prunnila M.; Ahopelto J.; Pezeril Th.; Vaudel G.; Gusev V.; Ruello P.; Weig E. M.; Schubert M.; Hettich M.; Grossman M.; Dekorsy Th.; Alzina F.; Graczykowski B.; Chavez-Angel E.; Reparaz J. S.; Wagner M. R.; Sotomayor-Torres C. M.; Xiong S.; Neogi S.; Donadio D. Nanophononics: state of the art and perspectives. Eur. Phys. J. B 2016, 89, 15. 10.1140/epjb/e2015-60727-7. [DOI] [Google Scholar]
  7. Maldovan M. Sound and heat revolutions in phononics. Nature 2013, 503, 209. 10.1038/nature12608. [DOI] [PubMed] [Google Scholar]
  8. Maldovan M. Phonon wave interference and thermal bandgap materials. Nat. Mater. 2015, 14, 667. 10.1038/nmat4308. [DOI] [PubMed] [Google Scholar]
  9. Huxtable S. T.; Abramson A. R.; Tien C.; Majumdar A.; LaBounty C.; Fan X.; Zeng G.; Bowers J. E.; Shakouri A.; Croke E. T. Thermal conductivity of Si/SiGe and SiGe/SiGe superlattices. Appl. Phys. Lett. 2002, 80, 1737. 10.1063/1.1455693. [DOI] [Google Scholar]
  10. Li D.; Wu Y.; Fan R.; Yang P.; Majumdar A. Thermal conductivity of Si/SiGe superlattice nanowires. Appl. Phys. Lett. 2003, 83, 3186. 10.1063/1.1619221. [DOI] [Google Scholar]
  11. Luckyanova M. N.; Garg J.; Esfarjani K.; Jandl A.; Bulsara M. T.; Schmidt A. J.; Minnich A. J.; Chen S.; Dresselhaus M. S.; Ren Z.; Fitzgerald E. A.; Chen G. Coherent Phonon Heat Conduction in Superlattices. Science 2012, 338, 936. 10.1126/science.1225549. [DOI] [PubMed] [Google Scholar]
  12. Ravichandran J.; Yadav A. K.; Cheaito R.; Rossen P. B.; Soukiassian A.; Suresha S. J.; Duda J. C.; Foley B. M.; Lee C.-H.; Zhu Y.; Lichtenberger A. W.; Moore J. E.; Muller D. A.; Schlom D. G.; Hopkins P. E.; Majumdar A.; Ramesh R.; Zurbuchen M. A. Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater. 2014, 13, 168. 10.1038/nmat3826. [DOI] [PubMed] [Google Scholar]
  13. Wen Y.-C.; Hsieh C.-L.; Lin K.-H.; Chen H.-P.; Chin S.-C.; Hsiao C.-L.; Lin Y.-T.; Chang C.-S.; Chang Y.-C.; Tu L.-W.; Sun C.-K. Specular Scattering Probability of Acoustic Phonons in Atomically Flat Interfaces. Phys. Rev. Lett. 2009, 103, 264301. 10.1103/PhysRevLett.103.264301. [DOI] [PubMed] [Google Scholar]
  14. Huberman S. C.; Larkin J. M.; McGaughey A. J. H.; Amon C. H. Disruption of superlattice phonons by interfacial mixing. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 155311. 10.1103/PhysRevB.88.155311. [DOI] [Google Scholar]
  15. Caroff P.; Dick K. A.; Johansson J.; Messing M. E.; Deppert K.; Samuelson L. Controlled polytypic and twin-plane superlattices in III–V nanowires. Nat. Nanotechnol. 2009, 4, 50. 10.1038/nnano.2008.359. [DOI] [PubMed] [Google Scholar]
  16. Dick K. A.; Thelander C.; Samuelson L.; Caroff P. Crystal phase engineering in single InAs nanowires. Nano Lett. 2010, 10, 3494. 10.1021/nl101632a. [DOI] [PubMed] [Google Scholar]
  17. Bolinsson J.; Caroff P.; Mandl B.; Dick K. A. Wurtzite–zincblende superlattices in InAs nanowires using a supply interruption method. Nanotechnology 2011, 22, 265606. 10.1088/0957-4484/22/26/265606. [DOI] [PubMed] [Google Scholar]
  18. Assali S.; Gagliano L.; Oliveira D. S.; Verheijen M. A.; Plissard S. R.; Feiner L. F.; Bakkers E. P. A. M. Exploring Crystal Phase Switching in GaP Nanowires. Nano Lett. 2015, 15, 8062. 10.1021/acs.nanolett.5b03484. [DOI] [PubMed] [Google Scholar]
  19. Thelander C.; Caroff P.; Plissard S.; Dey A. W.; Dick K. A. Effects of Crystal Phase mixing on the Electrical Properties of InAs Nanowires. Nano Lett. 2011, 11, 2424. 10.1021/nl2008339. [DOI] [PubMed] [Google Scholar]
  20. Lu W.; Lieber C. M. Semiconductor nanowires. J. Phys. D: Appl. Phys. 2006, 39, R387. 10.1088/0022-3727/39/21/R01. [DOI] [Google Scholar]
  21. Rurali R. Colloquium: Structural, electronic, and transport properties of silicon nanowires. Rev. Mod. Phys. 2010, 82, 427. 10.1103/RevModPhys.82.427. [DOI] [Google Scholar]
  22. Royo M.; De Luca M.; Rurali R.; Zardo I. A review on III–V core–multishell nanowires: growth, properties, and applications. J. Phys. D: Appl. Phys. 2017, 50, 143001. 10.1088/1361-6463/aa5d8e. [DOI] [Google Scholar]
  23. Wang N.; Cai Y.; Zhang R. Q. Growth of nanowires. Mater. Sci. Eng., R 2008, 60, 1. 10.1016/j.mser.2008.01.001. [DOI] [Google Scholar]
  24. Caroff P.; Bolinsson J.; Johansson J. Crystal Phases in III-V Nanowires: From Random Toward Engineered Polytypism. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 829. 10.1109/JSTQE.2010.2070790. [DOI] [Google Scholar]
  25. Glas F.; Harmand J.-C.; Patriarche G. Why Does Wurtzite Form in Nanowires of III-V Zinc Blende Semiconductors?. Phys. Rev. Lett. 2007, 99, 146101. 10.1103/PhysRevLett.99.146101. [DOI] [PubMed] [Google Scholar]
  26. Rozas G.; Winter M. F. P.; Jusserand B.; Fainstein A.; Perrin B.; Semenova E.; Lemaître A. Lifetime of THz Acoustic Nanocavity Modes. Phys. Rev. Lett. 2009, 102, 015502 10.1103/PhysRevLett.102.015502. [DOI] [PubMed] [Google Scholar]
  27. Anguiano S.; Bruchhausen A. E.; Jusserand B.; Favero I.; Lamberti F. R.; Lanco L.; Sagnes I.; Lemaître A.; Lanzillotti-Kimura N. D.; Senellart P.; Fainstein A. Micropillar Resonators for Optomechanics in the Extremely High 19–95-GHz Frequency Range. Phys. Rev. Lett. 2017, 118, 263901. 10.1103/PhysRevLett.118.263901. [DOI] [PubMed] [Google Scholar]
  28. Gorishnyy T.; Ullal C. K.; Maldovan M.; Fytas G.; Thomas E. L. Hypersonic phononic crystals. Phys. Rev. Lett. 2005, 94, 115501. 10.1103/PhysRevLett.94.115501. [DOI] [PubMed] [Google Scholar]
  29. Algra R. E.; Verheijen M. A.; Borgström M. T.; Feiner L.-F.; Immink G.; van Enckevort W. J. P.; Vlieg E.; Bakkers E. P. A. M. Twinning superlattices in indium phosphide nanowires. Nature 2008, 456, 369. 10.1038/nature07570. [DOI] [PubMed] [Google Scholar]
  30. Burgess T.; Breuer S.; Caroff P.; Wong-Leung J.; Gao Q.; Hoe Tan H.; Jagadish C. Twinning superlattice formation in GaAs nanowires. ACS Nano 2013, 7, 8105. 10.1021/nn403390t. [DOI] [PubMed] [Google Scholar]
  31. Xiong S.; Kosevich Y. A.; Sääskilahti K.; Ni Y.; Volz S. Tunable thermal conductivity in silicon twinning superlattice nanowires. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 195439. 10.1103/PhysRevB.90.195439. [DOI] [Google Scholar]
  32. Porter A.; Tran C.; Sansoz F. Intrinsic nanotwin effect on thermal boundary conductance in bulk and single-nanowire twinning superlattices. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 195431. 10.1103/PhysRevB.93.195431. [DOI] [Google Scholar]
  33. Baroni S.; de Gironcoli S.; Dal Corso A.; Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515. 10.1103/RevModPhys.73.515. [DOI] [Google Scholar]
  34. Gonze X.; Amadon B.; Anglade P. M.; Beuken J. M.; Bottin F.; Boulanger P.; Bruneval F.; Caliste D.; Caracas R.; Côté M.; Deutsch T.; Genovese L.; Ghosez Ph.; Giantomassi M.; Goedecker S.; Hamann D. R.; Hermet P.; Jollet F.; Jomard G.; Leroux S.; Mancini M.; Mazevet S.; Oliveira M. J. T.; Onida G.; Pouillon Y.; Rangel T.; Rignanese G.-M.; Sangalli D.; Shaltaf R.; Torrent M.; Verstraete M. J.; Zerah G.; Zwanziger J. W. ABINIT: First-Principles Approach to Material and Nanosystem Properties. Comput. Phys. Commun. 2009, 180, 2582. 10.1016/j.cpc.2009.07.007. [DOI] [Google Scholar]
  35. Veithen M.; Gonze X.; Ghosez Ph. Nonlinear Optical Susceptibilities, Raman Efficiencies, and Electro-Optic Tensors from First-Principles Density Functional Perturbation Theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 125107. 10.1103/PhysRevB.71.125107. [DOI] [Google Scholar]
  36. Fasolato C.; De Luca M.; Djomani D.; Vincent L.; Renard C.; Di Iorio G.; Paillard V.; Amato M.; Rurali R.; Zardo I. Crystalline, Phononic, and Electronic Properties of Heterostructured Polytypic Ge Nanowires by Raman Spectroscopy. Nano Lett. 2018, 18 (11), 7075–7084. 10.1021/acs.nanolett.8b03073. [DOI] [PubMed] [Google Scholar]
  37. Zardo I.; Conesa-Boj S.; Peiro F.; Morante J. R.; Arbiol J.; Uccelli E.; Abstreiter G.; Fontcuberta i Morral A. Raman spectroscopy of wurtzite and zinc-blende GaAs nanowires: Polarization dependence, selection rules, and strain effects. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 80, 245324. 10.1103/PhysRevB.80.245324. [DOI] [Google Scholar]
  38. De Luca M., Zardo I.. Semiconductor Nanowires: Raman Spectroscopy Studies. In Raman Spectroscopy and Applications; Maaz K., Ed.; InTech, 2017. [Google Scholar]
  39. Klein M. V. Phonons in semiconductor superlattices. IEEE J. Quantum Electron. 1986, 22 (9), 1760–1770. 10.1109/JQE.1986.1073174. [DOI] [Google Scholar]
  40. Jusserand B.; Paquet D.; Regreny A. “Folded” optical phonons in GaAs/Ga1-xAlxAs superlattices. Phys. Rev. B: Condens. Matter Mater. Phys. 1984, 30, 6245. 10.1103/PhysRevB.30.6245. [DOI] [Google Scholar]
  41. Jusserand B.; Cardona M.. Raman Spectroscopy of Vibrations in Superlattices. In Superlattices and Other Microstructures, Light Scattering in Solids V; Topics in Applied Physics; Cardona M., Güntherodt G., Eds.; Springer-Verlag: Berlin, 1989, Vol. 66, 49. [Google Scholar]
  42. Gupta R.; Xiong Q.; Mahan G. D.; Eklund P. C. Surface Optical Phonons in Gallium Phosphide Nanowires. Nano Lett. 2003, 3 (12), 1745–1750. 10.1021/nl034842i. [DOI] [Google Scholar]
  43. Barker A. S. Jr. Dielectric Dispersion and Phonon Line Shape in Gallium Phosphide. Phys. Rev. 1968, 165 (3), 917–922. 10.1103/PhysRev.165.917. [DOI] [Google Scholar]
  44. Widulle F.; Ruf T.; Göbel A.; Schönherr E.; Cardona M. Raman Study of the Anomalous TO Phonon Structure in GaP with Controlled Isotopic Composition. Phys. Rev. Lett. 1999, 82 (26), 5281–5284. 10.1103/PhysRevLett.82.5281. [DOI] [Google Scholar]
  45. Authors and editors of the volumes III/17A-22A-41A1a: Gallium phosphide (GaP) dielectric constants. In Group IV Elements, IV-IV and III-V Compounds. Part a - Lattice Properties. Landolt-Börnstein - Group III Condensed Matter (Numerical Data and Functional Relationships in Science and Technology); Madelung O., Rössler U., Schulz M., Eds.; Springer, Berlin, Heidelberg, 2001; Vol. 41A1a.
  46. Moskovits M. Surface-enhanced Raman spectroscopy: a brief retrospective. J. Raman Spectrosc. 2005, 36, 485. 10.1002/jrs.1362. [DOI] [Google Scholar]
  47. Mizuno H.; Mossa S.; Barrat J.-L. Beating the amorphous limit in thermal conductivity by superlattices design. Sci. Rep. 2015, 5, 14116. 10.1038/srep14116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Algra R. E.; Verheijen M. A.; Feiner L.; Immink G. G. W.; van Enckevort W. J. P.; Vlieg E.; Bakkers E. P. A. M. The Role of Surface Energies and Chemical Potential during Nanowire Growth. Nano Lett. 2011, 11, 1259. 10.1021/nl104267p. [DOI] [PubMed] [Google Scholar]
  49. Assali S.; Zardo I.; Plissard S.; Kriegner D.; Verheijen M. A.; Bauer G.; Meijerink A.; Belabbes A.; Bechstedt F.; Haverkort J. E. M.; Bakkers E. P. A. M. Direct Band Gap Wurtzite Gallium Phosphide Nanowires. Nano Lett. 2013, 13, 1559. 10.1021/nl304723c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Gonze X.; Vigneron J.-P. Density-functional approach to nonlinear-response coefficients of solids. Phys. Rev. B: Condens. Matter Mater. Phys. 1989, 39, 13120. 10.1103/PhysRevB.39.13120. [DOI] [PubMed] [Google Scholar]
  51. Turrel G.; Corset J.. Raman Microscopy Developments and Applications, 1st ed.; Academic Press: Malta, 1996. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl9b01775_si_001.pdf (825.7KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES