Questioning the γ-gauche effect: stereoassignment of 1,3-disubstituted-tetrahydro-β-carbolines using ¹H-¹H coupling constants

Abstract

The Pictet-Spengler reaction of tryptophan esters and aldehydes has been widely applied in natural product synthesis and medicinal chemistry. To date, the trans- or cis-configuration of 1,3-disubstituted tetrahydro-β-carbolines (THβCs) formed in this reaction has most often been assigned based on the relative ¹³C chemical shifts of C1 and C3 in the diastereomers. Although the upfield shifts of C1 and C3 in trans-THβCs relative to cis-THβCs has been attributed to steric compression associated with the “γ-gauche” effect, we show that this effect is not borne out experimentally for other carbons that should suffer this same compression. Thus we developed a robust alternative method for stereochemical assignment based on ¹H NMR coupling constants (31 examples) and supported by extensive DFT-based conformational analysis and calculation of ¹H-¹H coupling constants. DFT calculations of ¹³C NMR chemical shifts also cast doubt upon the role of the “γ-gauche” effect on C1 and C3 chemical shifts in trans-THβCs.

Graphical Abstract

Introduction

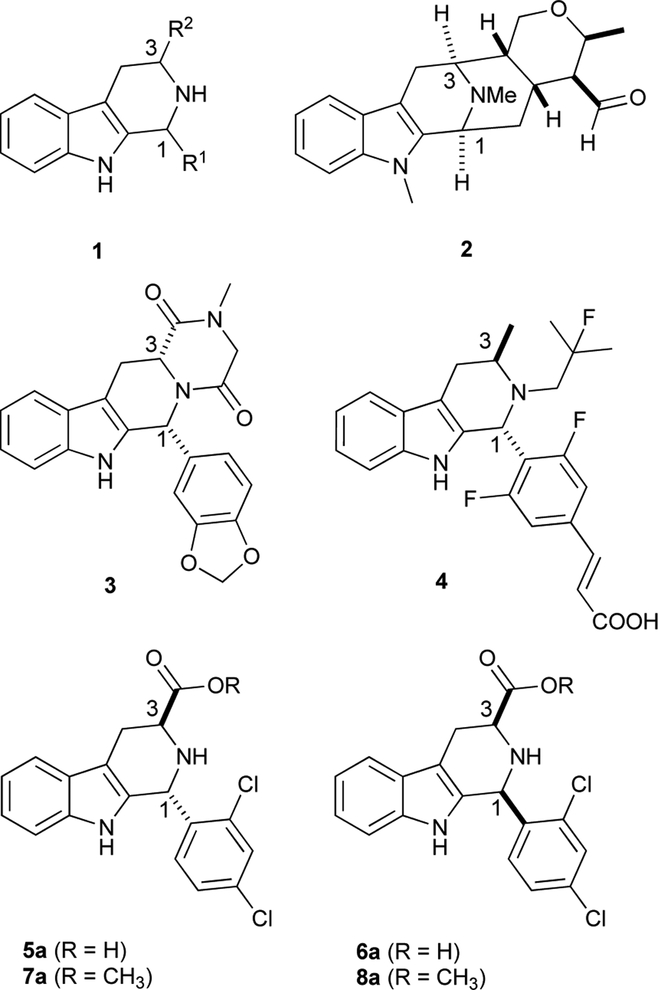
1,3-Disubsubstituted tetrahydro-β-carbolines (THβCs) 1 show a wide spectrum of biological activities,^{1, 2} and serve as synthetic intermediates to the sarpagine/macroline/ajmaline class of natural products,³ such as talcarpine 2 (Figure 1).⁴ They are also prominent in medicinal chemistry as precursors to approved drugs and preclinical drug candidates: representative examples include the erectile dysfunction drug tadalafil (3)⁵ and the anticancer candidate AZD9496 (4, currently in Phase I trials, Figure 1).⁶ A compound of special interest for our group is 5a, also known as MMV008138, which was originally identified⁷ from a screen of a publicly available chemical library (the Malaria Box⁸). Although the configuration of 5a was initially unknown, later studies^9–11 confirmed that 5a is (1R,3S)-configured, and that it is a much more potent antimalarial agent than its cis-diastereomer 6a (and enantiomers ent-5a and ent-6a). Compounds 5a and 6a were prepared by Pictet-Spengler reaction of (S)-Trp-OMe with 2,4-dichlorobenzaldehyde, followed by a separation of the diastereomeric esters 7a and 8a, and hydrolysis.⁹ Ongoing optimization of this scaffold for antimalarial activity requires an accurate assignment of the relative stereochemistry of the ester precursors, and to this point we have used the ¹³C NMR empirical rule of Ungemach et al.¹² In brief, C1 and C3 chemical shifts of trans-1,3- disubstituted THβCs (e.g., 5a, 7a) have been shown to be reliably upfield of those of the corresponding cis-diastereomers (e.g., 6a, 8a). The accuracy of this assignment method has been confirmed in several cases by X-ray crystallography^12–15 and NOESY/ROESY correlations (between H1 and H3 in cis-diastereomers),^{13, 16–18} and appears to be secure. The ¹³C NMR method is based on the so-called “γ-gauche effect,” which attributes upfield shifts of carbons to steric compression resulting from gauche interaction with a γ-substituent.^{19, 20} The γ-gauche effect of sp³-hybridized carbon has been well-documented in decalins,²¹ norbornanes,²² acetonides,²³ and conformationally-locked cyclohexanes.^24–26 It has also been invoked to deduce conformational preferences of conformationally-mobile substituted cyclohexanes,²⁷ and to deduce relative configuration of natural products²⁸ and various acyclic compounds.^29–32 However, in some cases the magnitude of this effect is very small.²² In addition, for sp²-hybridized carbons, γ-gauche substituents can cause both small upfield²⁶ and small downfield^{26, 27} shifts, and the effect on sp-hybridized carbons can also be very small.²⁴ As yet there is no firm consensus that the upfield shift of sp³-carbons possessing a γ-gauche interaction is actually steric in origin,^{19, 33} and a number of observations in our laboratory (detailed below) did not comport with the steric hypothesis. Given these uncertainties, we validated a ¹H NMR coupling constant method, based on firm theoretical grounds, to reliably assign relative configuration in 1,3-disubstituted THβCs (31 examples). Reliance on ¹H NMR coupling constants rather than ¹³C NMR chemical shifts confers several benefits, including reduced sample mass and experiment time requirements. Most significantly, unlike the ¹³C NMR chemical shift method, this method can be applied reliably when only one diastereomer is in hand, as is the case for highly diastereoselective Pictet-Spengler reactions.^{17, 34–36} Use of the ¹³C NMR method in these cases requires further chemical transformation or subsequent synthesis of the other diastereomer. The assignment method presented herein is supported by an extensive density functional theory (DFT)-based conformational analysis and ¹H-¹H coupling constant prediction for two pairs of trans- and cis-diastereomers (7a/8a, 7b/8b). Lastly, DFT calculations of ¹³C chemical shifts of C1 and C3 in these four compounds demonstrate that steric compression associated with the “γ-gauche” effect is not responsible for the upfield shift of C1 in trans-configured Pictet-Spengler adducts.

Figure 1.

1,3-disubsubstituted THβC 1 and related medicinally important compounds. Talcarpine’s (2) atom numbering modified to highlight similarity to other THβCs in the Figure.

Results and Discussion

¹³C and ¹H NMR Analysis of 1,3-disubstituted THβCs

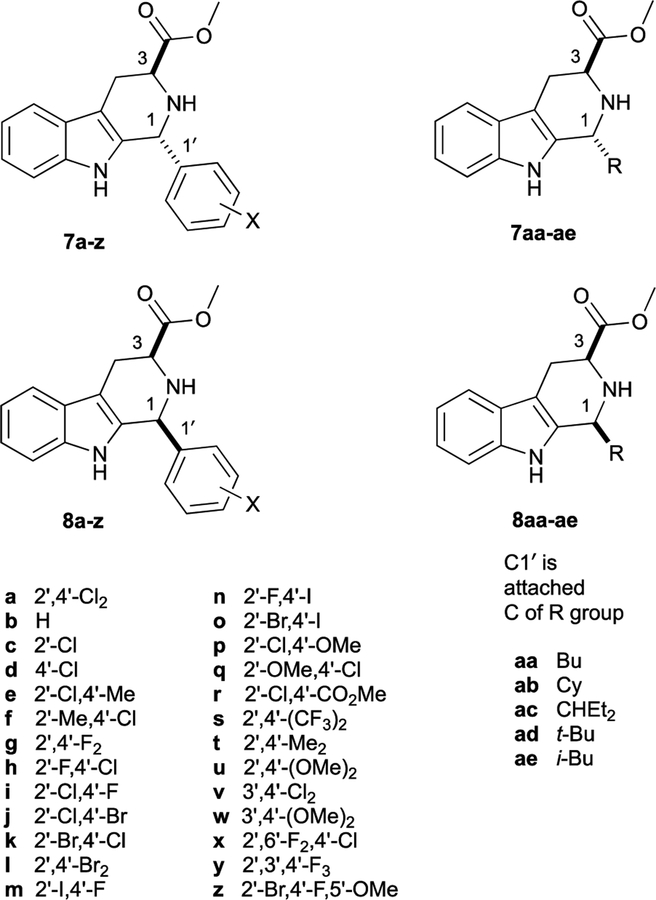
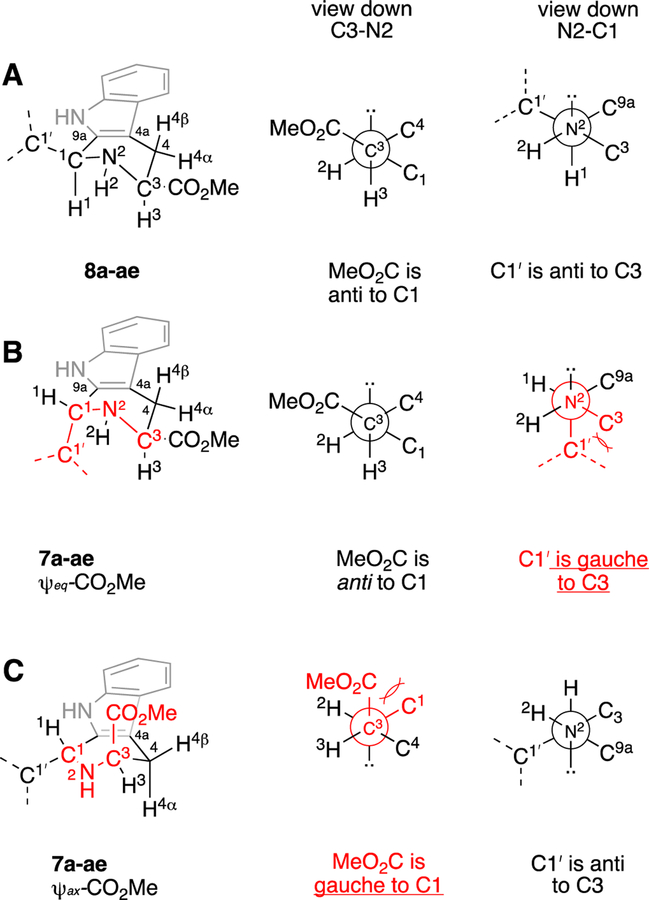
For this study we analyzed the ¹H and ¹³C NMR data of 30 additional pairs of diastereomeric THβC methyl esters related to 7a and 8a. Most of these compounds (7b-z, 8b-z) were previously prepared by Pictet-Spengler reaction of (S)-Trp-OMe with the requisite benzaldehyde;^{9, 37} five additional pairs of diastereomers derived from aliphatic aldehydes were also prepared for this work (7aa-ae, 8aa-ae, Figure 2). Each pair of diastereomers was separated by column chromatography, and their configurations assigned as cis- or trans- using the ¹³C NMR empirical rule¹² (See Table S1). Throughout our previous work, we noted that the cis-isomer was first-eluting in each case, as long as the eluent comprised a mixture of methylene chloride, hexane, and ethyl acetate. In the case of 7a and 8a, the assignment of trans-configuration to diastereomer 7a was confirmed by X-ray crystallography of its methyl amide derivative.⁹ It should be noted that the assignment of the C1 and C3 ¹³C NMR peaks is not always straightforward: the C1 peak may be upfield or downfield of C3, depending on the substitution of the C1-aryl group. Furthermore, in the trans-isomers 7a-z, the ¹³C NMR chemical shifts of C3 and the methoxy carbon are often very close. Thus, the chemical shifts (¹H and ¹³C) of 7a, 8a, and 15 other pairs of diastereomers were confirmed using HSQC, HMBC, and C-DEPT (See Tables S1–S4, Figures S1–S5). Taken together, over 31 pairs of diastereomers, the average C3 chemical shift is 52.5 ± 0.6 ppm for trans- and 56.8 ± 0.2 ppm for cis-, giving an average relative shift of −4.1 ± 0.6 ppm for C3 in 7a-ae relative to 8a-ae (C3 Δδ_7–8, Table 1). Note that the C1 chemical shifts of the trans- and cis-esters 7a-ae and 8a-ae are significantly influenced by the 1-aryl and 1- alkyl substituents, as evidenced by the large standard deviations seen (51.7 ± 3.2 and 54.6 ± 3.4 ppm, for 7a-ae and 8a-ae, respectively). Nevertheless, within a pair of diastereomers, the relative shift of C1 in 7a-ae relative to 8a-ae is quite constant (Δδ_7–8 = −2.9 ± 0.5 ppm). With this data in hand, the possible γ-gauche rationale for the upfield C1 and C3 chemical shifts in 7a-ae relative to 8a-ae (Δδ_7–8, Table 1) can be evaluated. The tetrahydropyridine ring of cis-esters 8a-ae should adopt an all pseudoequatorial conformation A, since the alternative half-chair conformation (not shown) would feature severe 1,3-diaxial interactions between C1’ and CO₂Me (Figure 3). In contrast trans-esters 7a-ae would likely populate two alternative half-chair conformations B and C, each featuring one pseudoequatorial (ψ_eq) and one pseudoaxial (ψ_ax) group.³⁸ As can be seen in the Newman projections in Figure 3 for the cis-isomers 8a-ae, the CO₂Me group on C3 is anti to C1 (view down C3-N2 axis), and C1’ of the C1-substituent is anti to C3 (view down N2-C1 axis). However, in conformer B (ψ_eq-CO₂Me) of 7a-ae, C1’ of the 1-substituent is gauche to C3, while CO₂Me remains anti to C1. Similarly, in conformer C (ψ_ax-CO₂Me) of 7a-ae, the CO₂Me group is gauche to C1, while C1’ remains anti to C3. Thus, if (and only if) both conformations B and C of 7a-ae are populated, will both C1 and C3 of 7a-ae experience steric compression relative to those carbons in 8a-ae, and thus be shifted upfield in the ¹³C NMR spectrum. Logically, such steric compression would also be expected to result in similar upfield ¹³C NMR shifts for those carbons in 7a-ae that interact with C1 and C3 in this γ-gauche relationship, namely the CO₂Me C=O, and C1’. Interestingly however, this reciprocity is not seen. Over 31 pairs of compounds, the C=O ¹³C NMR resonances of 7a-ae are not upfield of those in 8a-ae, but are in fact slightly downfield (Δδ_7-8 = +0.8 ± 0.2 ppm, Table 1). Similarly, in the 16 cases of 1-aryl Pictet-Spengler adducts where we have unequivocally assigned C1’, this resonance is not upfield in the trans- relative to the cis-isomer (Table 1, Δδ_7-8 = +0.9 ± 0.5). These small downfield shifts of the CO₂Me C=O and aryl C1’ carbons in 7aa-ae might be ascribed to some not yet understood insensitivity of sp²-hybridized carbons to the γ-gauche effect. But in the five pairs of 1-alkyl Pictet-Spengler adducts, the sp³-hybridized C1’ carbons are also not shifted upfield in 7aa-ae relative to 8a-ae (Table 1, Δδ_7-8 = +0.7 ± 0.4). The failure of the gauche-oriented C1’ and C3 sp³-carbons in 7aa-ae (Figure 3B) to reciprocally exert upfield shifts on each other (relative to 8a-ae) thus clearly undermines the proposal that “steric compression” determines C1 and C3 chemical shifts in THβCs.

Figure 2.

Pictet-Spengler adduct methyl esters studied in this work.^{9, 37}

Table 1.

Average ¹³C NMR chemical shifts (δ, ppm) of C3, C1, C=O, and C1’ (CDCl₃) in the trans- and cis-Pictet-Spengler adducts (7a-7ae and 8a-8ae, respectively), and average relative shifts of the trans-adducts (Δδ_7–8, ppm).

	δ(7a-ae)	δ(8a-ae)	Δδ7–8a
C3	52.5 ± 0.6	56.8 ± 0.2	−4.1 ± 0.6
C1	51.7 ± 3.2	54.6 ± 3.4	−2.9 ± 0.5
C=O	174.0 ± 0.4	173.3 ± 0.2	+0.8 ± 0.2
Aryl C1’b	134.2 ± 7.8	133.4 ± 8.2	+0.9 ± 0.5
Alkyl C1’c	41.4 ± 4.7	40.7 ± 5.2	+0.7 ± 0.4

^aDefined at each of the carbons as δ for 7 – δ for 8.

^bData from 16 1-aryl Pictet-Spengler analogs for which C1’ was unambiguously assigned.

^cData from 7aa-ae and 8aa-ae.

Figure 3.

Proposed half-chair conformations of the tetrahydropyridine rings in 8a-ae (A) and 7a-ae (B, C), and Newman projections down the C3-N2 and N2-C1 axes. Gauche interactions of ring substituents are highlighted in red.

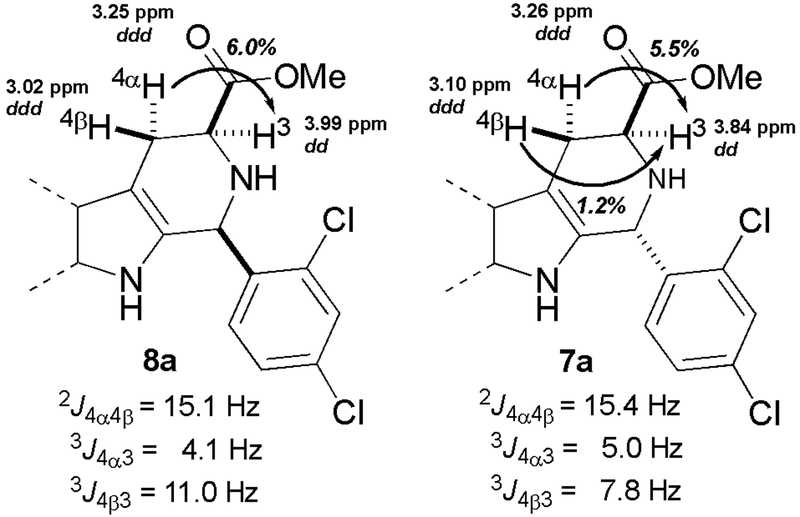
With the rationale of the ¹³C NMR chemical shift assignment method now uncertain, we looked for another method by which to reliably assign relative configuration. As mentioned earlier, NOESY/ROESY has been used periodically to confirm cis-configuration (correlation of H1 and H3),^{13, 16–18} but we favored a method of greater operational simplicity. Two previous studies used the magnitude of vicinal coupling constants as a means of assigning cis- or trans-configuration, albeit for a single pair of diastereomers each.^{13, 16} We sought to validate this method with the 31 additional pairs of diastereomers depicted in Figure 2. Inspection of conformer A for cis-esters 8a-ae suggests that the three-bond coupling constants ³J_4α−3 and ³J_4β−3 should be well differentiated: H4α is approximately gauche to H3, and H4β is approximately anti to H3 (Figure 3). In contrast, if the trans-diastereomers 7a-ae populate both tetrahydropyridine conformations B and C as predicted, then ³J_4β−3 values will not be as well differentiated from the corresponding ³J_4α−3 values, since H4β is approximately anti to H3 in conformer B, but is approximately gauche to H3 in conformer C. For 8a, HSQC identified H4 resonances at 3.25 and 3.02 ppm. Individual irradiation of these two resonances resulted in 6.0% and ~0% NOE enhancement of H3 (3.99 ppm, Figure S5, Table S5), allowing assignment of H4α to the peak at 3.25 ppm, and H4β to the peak at 3.02 ppm. Based on these assignments we measured ³J_4α−3 and ³J_4β−3 as 4.1 and 11.0 Hz, respectively. Thus, a large difference is seen in these coupling constants for 8a, as expected. Similarly, we used 1D NOE experiments to assign H4β and H4α in trans-ester 7a (Figure S4, Table S5). In this case the values of ³J_4α−3 and ³J_4β−3 were much more similar (5.0 and 7.8 Hz, respectively). These findings are summarized in Figure 4. Based on the ¹H chemical shifts and ³J values of 7a and 8a, H4α and H4β were assigned in the other 30 pairs of diastereomers, and the individual coupling constants were determined (Tables S3 & S4). Average ¹H chemical shifts and J values are shown in Table 2. As expected from their distance from the C1-substituent, the ¹H chemical shifts of H3, H4α, and H4β in 7a-ae and 8a-ae fall within very narrow ranges (Table 2, entries 1–3). As can be seen, the average value of ³J_4β−3 in cis-esters 8a-ae is 11.1 ± 0.1 Hz (Table 2, entry 4), suggesting an approximately antiperiplanar arrangement of H4β and H3. In contrast, the average value of ³J_4β−3 in trans-esters 7a-ae is consistently lower (7.3 ± 0.9 Hz), as expected if both conformers B and C were populated.³⁹ These well-differentiated average values of ³J_4β−3 for cis- and trans-diastereomers are very similar to those reported for the two aforementioned pairs of diastereomers noted previously.^{13, 16} Note that the average values of ³J_4α−3 (entry 5) are similar for both 7a-ae and 8a-ae, consistent with a near gauche orientation of H4α and H3 in all three conformers A-C.

Figure 4.

Assignment of diastereotopic protons H4α and H4β in 8a and 7a. Abbreviations used: dd = doublet of doublet, ddd = doublet of doublet of doublet. Note that H4α and H4β are coupled through 5 bonds to H1 (not shown), see Figure 5.

Table 2.

Selected average ¹H chemical shifts and coupling constants in 7a-ae and 8a-ae (CDCl₃).

Entry	Avg	7a-ae	8a-ae
1	δ H3 (ppm)	3.91 ± 0.09	3.94 ± 0.09
2	δ H4α (ppm)	3.23 ± 0.06	3.22 ± 0.04
3	δ H4β (ppm)	3.10 ± 0.05	2.98 ± 0.08
4	3J4β−3 (Hz)	7.3 ± 0.9	11.1 ± 0.1
5	3J4α−3 (Hz)	5.2 ± 0.2	4.1 ± 0.1
6	2J4α−4β (Hz)	15.3 ± 0.1	15.1 ± 0.1
7	5J4β−1 (Hz)	1.5 ± 0.1	2.5 ± 0.1
8	5J4α−1 (Hz)	1.3 ± 0.2	1.8 ± 0.1

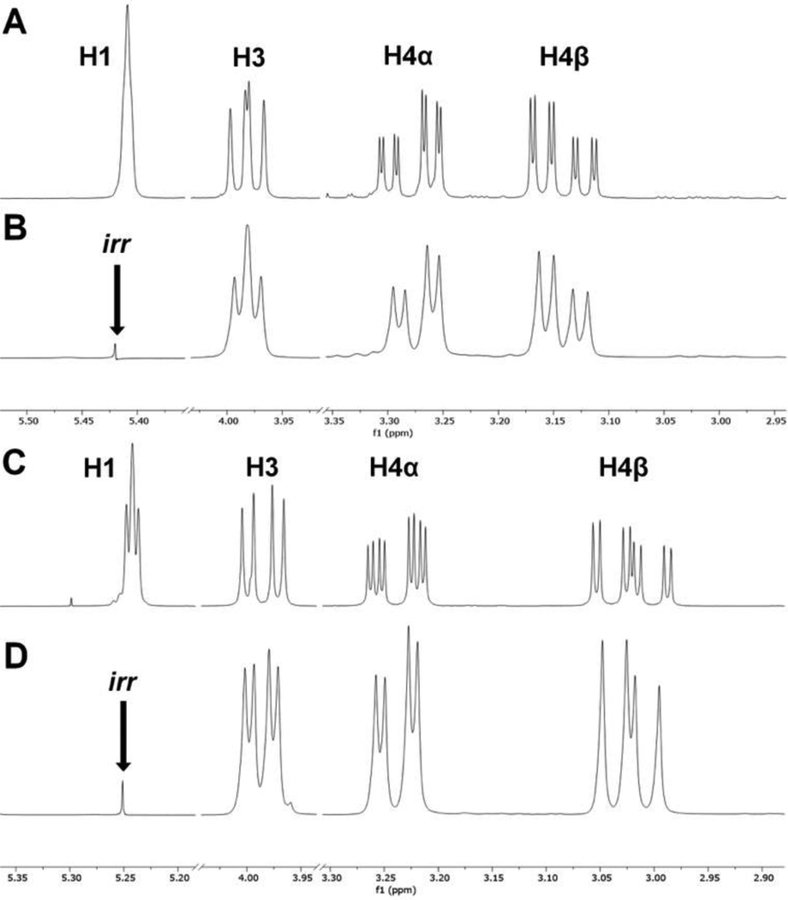
One noteworthy feature of the ¹H NMR spectra of 7a-ae and 8a-ae is the visible 5-bond coupling between H1 and H4α, and between H1 and H4β, as shown for 7b and 8b in Figure 5 (Table 2, entries 7–8). Note that for trans-1-aryl derivatives 7a-z, H1 appears as a broad singlet, as shown for 7b in Figure 5A. That the fine splitting in H4α and H4β is in fact due to 5-bond coupling to H1 was confirmed by single-frequency decoupling (Figure 5B). For cis-1-aryl derivatives 8a-z, 5-bond coupling is occasionally seen at H1, as shown for 8b in Figure 5C. Although 5-bond ¹H-¹H coupling is rare, it is particularly common in cyclohexenes,^{40, 41} (which resemble the tetrahydropyridine ring of 7a-ae and 8a-ae) and has been noted at least once previously in Pictet-Spengler adducts.¹³

Figure 5.

Five-bond coupling of H1 to H4α and H4β in 7b and 8b A) H1, H3, H4α, and H4β resonances in the ¹H NMR spectrum of 7b; B) Single frequency decoupling of H1 in 7b; C) H1, H3, H4α, and H4β resonances in the ¹H NMR spectrum of 8b; D) Single frequency decoupling of H1 in 8b.

Density Functional Theory (DFT) Conformational Analysis of 7a/8a and 7b/8b

As described above, values of ³J_4β−3 effectively distinguish trans-esters 7a-ae from cis-esters 8a-ae. Furthermore, the observed values of ³J_4β−3 in these compounds appear reasonable based on a first-principles conformational analysis (Figure 3). To further substantiate our method for stereochemical assignment we undertook computational studies of the possible conformers of 7a/8a and 7b/8b. Multiple automated conformer searches were performed at the MMFF94 level, starting from at least two initial geometries of each compound. These structures were then optimized at B3LYP/6–31G(d)^{42, 43} to give 16 conformers of 7a, 14 conformers of 8a, and 8 conformers each for 7b and 8b. As shown in Table 3, these conformers can be classified with respect to four structural features, and thus grouped into eight ensembles of conformers.

Table 3.

The number of B3LYP/6–31G(d) potential energy minima found for 7a/8a, 7b/8b within each conformational ensemble.

Conformer	7a	8a	7b	8b
Total	16	14	8	8
ψax-CO2Me	8	6	4	4
ψeq-CO2Me	8	8	4	4
exo-2’-Cl	8	8	-	-
endo-2’-Cl	8	6a	-	-
ax-H2	8	6	4	4
eq-H2	8	8	4	4
H-bondb	12	12	6	6
No H-bondc	4	4	2	2

^aTwo conformers, namely ψ_ax-CO₂Me, endo-2’-Cl, ax-H2, were not found in the initial conformational search, likely due to their expected high energy.

^bIntramolecular H-bonding of H2 to C=O or OMe deduced from H2$\cdots$O distances ranging from 2.3 – 2.7 Å.

^cLack of H-bond deduced from H2$\cdots$O > 3.7 Å.

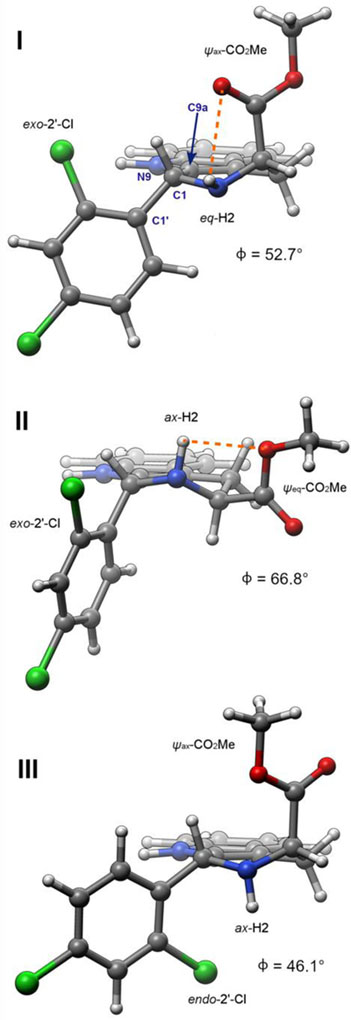
First, the approximate half-chair conformation of the tetrahydropyridine ring can be classified as having a ψ_ax- or ψ_eq-CO₂Me group; representative calculated structures of 7a exhibiting these features are shown in Figure 6 (I and II, respectively). Interestingly, the orientation of the 1-aryl groups in 7a and 7b does not differ significantly among these different tetrahydropyridine conformers. For 7a, the C1’-C1-C9a-N9 dihedral angle φ for II (66.8°) is only slightly larger than that seen in I and III (52.7 and 46.1°, respectively), despite the expectation that the 1-aryl group would be pseudoaxial in II and pseudoequatorial in I and III. The larger than expected φ value in I and III is likely a consequence of allylic strain of the 1-aryl group and N9. Second, the 2’-Cl of 7a and 8a can be oriented exo- or endo- to the tetrahydropyridine ring: see Figure 6 for calculated structures I/II (exo-) vs III (endo-). Note that this isomerism is absent in 7b and 8b, which feature an unsubstituted phenyl ring. Third, the N-H can be axial or equatorial, and fourth, the CO₂Me group can be hydrogen- bound to the NH, or not hydrogen-bound.⁴⁴ These last two features are illustrated in the representative computed structures of 7a in Figure 6. In trans-ester 7a, eight ψ_ax-CO₂Me and eight ψ_eq-CO₂Me conformations were located (cf. B and C, Figure 3). In the cis-isomer 8a, only six ψ_ax-CO₂Me conformers and eight ψ_eq-CO₂Me conformations were found. As expected, the six ψ_ax-CO₂Me conformers of 8a are all much higher in energy than the ψ_eq-CO₂Me conformations, due to 1,3-di-pseudoaxial interaction of the C3-CO₂Me and C1-aryl groups.⁴⁵ As depicted in Figure 6, for 7a and 8a, the 2’-Cl group can adopt an exo- or endo-orientation with respect to the tetrahydropyridine ring. This type of conformational isomerism is not observed in 7b/8b, since they bear an unsubstituted phenyl ring; thus, the number of possible conformations available to 7a/8a is generally double that of 7b/8b. The axial and equatorial orientations of the hydrogen (H2) are roughly equally represented among the conformers. In conformations featuring a ψ_eq-CO₂Me group, both ax-H2 and eq-H2 can hydrogen-bond to the CO₂Me group, via the C=O or OMe oxygen atoms. In contrast, for conformations featuring a ψ_ax-CO₂Me group, only eq-H2 can form an intramolecular H-bond via the C=O or OMe oxygen atoms. In ψ_ax-CO₂Me/ax-H2 conformations, an intramolecular H-bond is geometrically impossible (e.g. structure III, Figure 6). Structures of the lowest energy conformers of 7a, 8a, 7b, and 8b are presented in the Supporting Information (Figures S6 & S7). To calculate free energies of these conformers at 298 K, single point energies were calculated using the mPW1PW91⁴⁷and B3LYP functionals, at a larger basis set (6–311+G(2d,p)), and with PCM⁴⁸ implicit solvation (CHCl₃). As described below, the 6–311+G(2d,p) basis set, mPW1PW91 functional, and PCM solvation model were chosen based on their suitability for ¹³C NMR shift calculations.⁴⁹ In addition, we also calculated single point energies at M06–2X/def2-TZVP (with PCM solvation), since the M06–2X functional^{50, 51} has been recommended for accurate energies of conformers, especially in conjunction with the def2-TZVP basis set.^{52, 53} Free energy corrections (based on B3LYP/6–31G(d) frequencies) were then applied to these single point energies (Tables S6–S13).

Figure 6.

Representative calculated (B3LYP/6–31G(d)) structures of 7a illustrating the orientation of the CO₂Me, NH, and 2’-Cl groups. The C1-C1-C9a-N9 dihedral angle is represented by φ. In conformers I and II, internal hydrogen bonding between H2 and the carbonyl or methoxy O atoms is depicted with orange dashed line. Note that intramolecular hydrogen bonding is geometrically impossible in conformer III. Conformers I, II, and III are described as 7a-01, 7a-09, and 7a-10 respectively in the Supporting Information. Graphics rendered using Chimera.⁴⁶

Boltzmann distributions of the conformers of 7a/8a, 7b/8b calculated using mPW1PW91/6–311+G(2d,p) (PCM, CHCl₃) free energies were very similar to those based on B3LYP/6–311+G(2d,p) (PCM, CHCl₃) free energies (Table S14). M06–2X/def2-TZVP (PCM, CHCl₃) free energy-based Boltzmann distributions largely follow these trends, but for 8a and 8b show a diminished preference for conformers in the ψ_eq-CO₂Me ensemble (e.g. A, Figure 3) vs those in the ψ_ax-CO₂Me ensemble (see Table S14). As a consequence (see below), mPW1PW91 and B3LYP/6–311+G(2d,p)-based Boltzmann distributions give superior prediction of ³J_4β−3, relative to those based on M06–2X/def2-TZVP. Furthermore since calculations at mPW1PW91/6–311+G(2d,p) give improved prediction of ¹³C NMR chemical shifts relative to those based on B3LYP/6–311+G(2d,p), (see below), for simplicity we will base all calculations below on mPW1PW91/6–311+G(2d,p) (PCM, CHCl₃) Boltzmann weights of the conformers. These values were summed to calculate the percentage occupying each of the four pairs of conformational ensembles noted previously (Table 4).

Table 4.

Boltzmann distribution of conformational ensembles, based on mPW1PW91/6–311+G(2d,p) (PCM, CHCl₃)//B3LYP/6–31G(d) free energies at 298 K.

	7a	8a	7b	8b
	[%]	[%]	[%]	[%]
ψax-CO2Me	26.9	2.6	39.8	0.8
ψeq-CO2Me	73.1	97.4	60.2	99.2
exo-2’-Cl	93.0	81.7	–	–
endo-2’-Cl	7.0	18.3	–	–
ax-H2	38.6	47.8	35.9	42.5
eq-H2	61.4	52.2	64.1	57.5
H-bond	95.0	99.5	94.2	99.9
No H-bond	5.0	0.5	5.8	0.1

As anticipated, trans-esters 7a and 7b significantly populate both the ψ_ax-CO₂Me and ψ_eq-CO₂Me conformational ensembles (cf. B and C, Figure 3). For 7a, the lowest energy ψ_ax-CO₂Me conformation (7a-01) is only 0.9 kcal/mol higher in energy than global minimum ψ_eq-CO₂Me structure (7a-08, Table S7, Figure S6). For 7b, the lowest energy ψ_ax-CO₂Me conformation (7b-01) and lowest energy ψ_eq-CO₂Me conformation (7b-05) are within 0.02 kcal/mol of each other (Table S9, Figure S7). In contrast, cis-esters 8a and 8b adopt >97% and >99% ψ_eq-CO₂Me conformations respectively.⁵⁴ For 8a and 8b, the lowest energy ψ_ax-CO₂Me conformations are 3.1 (8a-04) and 4.6 kcal/mol (8b-05) higher in energy than global minimum ψ_eq-CO₂Me structures (8a-01 and 8b-03, Figures S6 & S7, Tables S11 & S13). As discussed at the outset, ψ_ax-CO₂Me conformations of 8a and 8b would be unstable by virtue of 1,3-dipseudoaxial interactions with the ψ_ax-aryl group at C1. Thus, these DFT calculations support the first-principles conformational analysis presented in Figure 3, and the values of ³J_4β−3 reported in Table 2. Other noteworthy features of our calculations are: 1) in 7a and 8a there is a significant preference for the exo-2’-Cl orientation, which appears to be steric in origin; 2) ax-H2 and eq-H2 conformations are similar in energy for all four compounds; 3) intramolecularly H-bonded structures are much more favorable than non-H-bonded structures for all four compounds.

DFT calculations of select ¹H-¹H coupling constants in 7a/8a and 7b/8b

Using mPW1PW91/6–311+G(2d,p) (PCM, CHCl₃) Boltzmann weights we then calculated select ¹H-¹H coupling constants at B3LYP/6–31G(d,p)u+1s//B3LYP/6–31G(d), which has been found to be economical and accurate (RMSD < 0.5 Hz) for a wide range of organic molecules.⁵⁶ As can be seen in Table 5, this method worked very well for 7a/8a and 7b/8b. For the 5 coupling constants previously presented in Table 2, over 4 compounds, excellent accuracy (RMSD < 0.4 Hz, Tables S15,16 ) was obtained. Most importantly, the close correspondence of calculated and observed values of ³J_4β−3 and ³J_4α−3 suggests that the mPW1PW91/6–311+G(2d,p) (PCM, CHCl₃) Boltzmann weights accurately capture the distribution of ψ_ax-CO₂Me and ψ_ax-CO₂Me conformers of the tetrahydropyridine ring in 7a/8a and 7b/8b. For reference, use of the M06–2X/def2-TZVP Boltzmann distributions in these calculations gave less accurate values of ³J_4β−3 for 8a and 8b (8.8 and 10.2 Hz, respectively, Table S16) as a consequence of the diminished energetic difference between the ψ_ax-CO₂Me and ψ_ax-CO₂Me conformers.

Table 5.

Calculated (B3LYP/6–31(d,p)u+1s//B3LYP/6–31G(d))^a vs observed (italics) ¹H-¹H coupling constants for 7a/8a and 7b/8b.

	7a	8a	7b	8b
	(Hz)	(Hz)	(Hz)	(Hz)
3J4β−3	8.3/7.8	10.5/11.0	6.2/6.8	10.7/11.2
3J4α−3	4.5/5.0	3.9/4.1	5.1/5.4	3.9/4.3
2J4α−4βb	15.3/15.4	15.1/15.1	15.3/15.4	15.0/15.2
5J4β−1	1.9/1.5	3.0/2.5	1.9/1.6	3.0/2.6
5J4α−1	1.2/1.2	2.0/1.9	1.8/1.4	2.1/1.9

^aWeighted average over all conformations, based on mPW1PW91/6–311+G(2d,p)//B3LYP/6–31G(d) Boltzmann distribution (298 K).

^b2J_HH values for sp³ C-H are calculated to be negative, as expected;⁵⁵ the absolute values are shown here.

DFT calculations of ¹³C chemical shifts of 7a/8a and 7b/8b

With the B3LYP/6–31G(d) geometries and mPW1PW91/6–311+G(2d,p) (PCM, CHCl₃) Boltzmann distribution of the conformers of 7a/8a and 7b/8b validated by the calculated ¹H-¹H coupling constants in Table 5, we were positioned to determine whether the distinctive C1 and C3 chemical shifts of the cis- and trans-diastereomers could be reproduced by computation. We thus calculated ¹³C NMR chemical shifts (δ) for each conformer of 7a, 7b, 8a, and 8b from the B3LYP/6–31G(d) geometries at the B3LYP/6–311+G(2d,p) (PCM, CHCl₃) and mPW1PW91/6–311+G(2d,p) (PCM, CHCl₃) levels of theory (Table S17–S20). These functionals, basis set, and solvation model were selected based on their excellent performance in a recent study of colchicine.⁴⁹ The weighted average ¹³C NMR chemical shifts of each carbon in 7a, 7b, 8a, and 8b were then calculated using the calculated Boltzmann populations; mean average deviations (MAD) of the calculated chemical shifts from the observed values were calculated to assess the performance of each functional. As seen in Table 6, both functionals predict ¹³C NMR chemical shifts well, giving MAD of ~2 ppm or less. The slightly smaller MAD values seen for 7b/8b relative to 7a/8a is a consequence of inaccurate calculation of the ¹³C chemical shifts for Cl-bearing carbons C2’ and C4’ in 7a and 8a (see Tables S17, S19). However, over the four compounds examined, the mPW1PW91 functional performs better than the B3LYP functional (average MAD = 1.4 ppm vs 1.8 ppm). A recent study of the calculated ¹³C NMR spectrum of colchicine in CDCl₃ also noted improved accuracy of the mPW1PW91 functional relative to B3LYP, and our calculated MAD (1.4 ppm) is even lower than they reported (1.9 ppm).⁴⁹ As can be seen in Table 7, ¹³C NMR chemical shifts for C3, C1, C=O, and C1’ calculated by this method very closely match the observed values (italics) for all four compounds, with deviations generally less than 2 ppm. Looking at the difference in chemical shift for a particular carbon between diastereomers (Δδ_7-8), the congruity is even better. For example, the C1 and C3 Δδ_7-8 values for 7a/8a are predicted to be −4.1 and −2.9 ppm; the observed Δδ_7-8 values are −4.4 and −2.6 ppm, respectively; the correspondences for 7b/8b are also very close. Note that this DFT method also recapitulates the observed slight (+0.5 to +1.3 ppm) downfield shifts of C=O and C1’ in the trans-isomers. These close correspondences are also seen using the B3LYP functional (Table S17–S20). Thus, DFT predicts the observed upfield shifts of C1 and C3 in 7a-b relative to 8a-b, as well as the slight downfield shifts of C=O and C1’.

Table 6.

All-carbon mean absolute deviation (MAD) in calculated ¹³C NMR chemical shifts for 7a, 7b, 8a, and 8b at the indicated levels of theory.

Compound	B3LYP/6–311+G(2d,p) (PCM, CHCl3)// B3LYP/6–31G(d) (ppm)a	mPW1PW91/6–311+G(2d,p) (PCM, CHCl3)// B3LYP/6–31G(d) (ppm)a
7a	2.1	1.7
7b	1.5	1.1
8a	2.0	1.6
8b	1.4	1.0
Averageb	1.8	1.4

^aMean absolute deviation in ¹³C NMR chemical shift for all 19 carbons in each compound.

^bAverage of MAD for compounds 7a, 7b, 8a, and 8b.

Table 7.

Calculated^a vs observed (italics) ¹³C NMR chemical shifts (δ) for select carbons in 7a, 7b, 8a, 8b, and corresponding differences in δ between diastereomers (Δδ_7-8).

Carbon	Compounds	δ(7)	δ(8)	Δδ7–8b
C3	7a, 8a	53.4 / 52.3	57.5 / 56.7	−4.1 / −4.4
	7b, 8b	54.0 / 52.7	57.8 / 57.0	−3.8 / −4.3
C1	7a, 8a	52.9 / 51.3	55.8 / 53.9	−2.9 / −2.6
	7b, 8b	56.6 / 55.1	59.8 / 58.8	−3.2 / −3.7
C=O	7a, 8a	175.3 / 173.8	174.9 / 173.1	+0.4 / +0.7
	7b, 8b	175.8 / 174.3	175.1 / 173.3	+0.7 / +1.0
C1’	7a, 8a	139.2 / 137.9	138.6 / 137.4	+0.6 / +0.5
	7b, 8b	143.8 / 142.1	142.2 / 140.8	+1.6 / +1.3

^aBoltzmann Weighted mPW1PW91/6–311+G(2d,p) (PCM, CHCl₃)//B3LYP/6–31G(d) ¹³C NMR chemical shifts.

^bΔδ_7–8 = δ(7) – δ(8); values in normal font are derived from calculated chemical shifts, values in italics are from observed chemical shifts.

Computational evaluation of the role of steric compression in the ¹³C chemical shifts of C1 and C3 in 7a and 7b

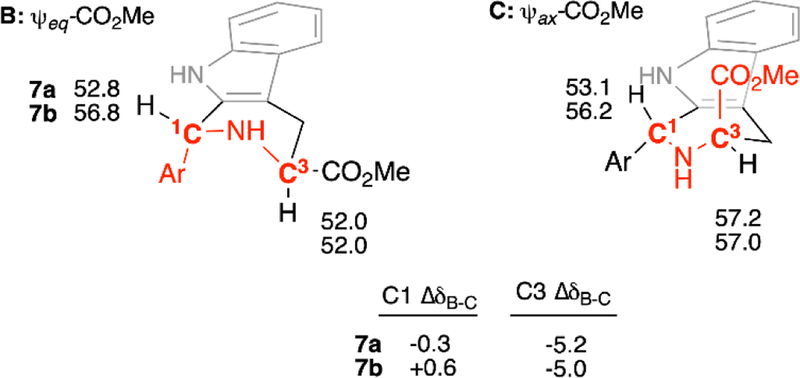
With the accuracy of DFT-derived ¹³C NMR chemical shifts for 7a/8a and 7b/8b now established, we are in a position to ask whether these upfield shifts of C1 and C3 in 7a and 7b relative to 8a and 8b can be attributed to “steric compression.” If so, the chemical shifts of C1 and C3 in 7a and 7b should be dependent on the conformation of the tetrahydropyridine ring. By grouping the individual conformers of 7a and 7b into two overall ψ_eq- and ψ_ax-CO₂Me tetrahydropyridine conformational ensembles (i.e. B and C, Figure 3), and recalculating the weighted average ¹³C NMR chemical shifts at C1 and C3, we can assess the effect of γ-gauche-associated steric compression (Figure 7, Tables S19-S20). As can be seen, the calculated ¹³C chemical shifts of C3 in 7a and 7b in ensemble B are considerably upfield of the values in ensemble C (C3 Δδ_B-C = −5.2 and −5.0 ppm respectively). These calculated upfield shifts could be consistent with steric compression of C3 resulting from γ-gauche interaction with the C1-aryl group in ensemble B (cf. Figure 3). However, no significant differences are seen in the chemical shifts of C1 in 7a and 7b between ensembles B and C (C1 Δδ_B-C = −0.3 and +0.6 ppm, respectively), despite its γ-gauche orientation to the ψ_ax-C3-CO₂Me group in ensemble C. These observations are replicated at the B3LYP/6–311+G(2d,p) (PCM, CHCl₃)//B3LYP/6–31G(d) level (Tabled S22–S22). Thus, the uniform upfield shift of C1 in 7a-ae relative to 8a-ae (Table 1) cannot be attributed to the γ-gauche effect, since the C1 chemical shifts remain unchanged whether the C1-CO₂Me group is gauche (ensemble C) or anti- (ensemble B).

Figure 7.

Weighted (mPW1PW91/6–311+G(2d,p) (PCM,CHCl₃)//B3LYP/6–31G(d)) ¹³C NMR chemical shifts for C1 & C3 of 7a and 7b in the ψ_eq- and ψ_ax-CO₂Me tetrahydropyridine conformational ensembles B and C. Gauche interactions of ring substituents with C1 and C3 are highlighted in red.

Conclusions

In this report we have demonstrated that the trans- or cis-configuration of 1,3-disubstituted THβCs can be reliably assigned by ¹H NMR spectroscopy, based on a particular coupling constant (³J_4β−3). Over 31 cis-esters compounds 8a-ae, the value of ³J_4β−3 is 11.1 ± 0.1 Hz, indicating they exclusively populate a tetrahydropyridine conformational ensemble that features a ψ_eq-CO₂Me group at C3 (A, Figure 3). In contrast for the 31 trans-esters compounds 7a-ae, the value of ³J_4β−3 is 7.3 ± 1.2 Hz, indicating these compounds populate two nearly equienergetic tetrahydropyridine conformational ensembles: one featuring a ψ_eq-CO₂Me group at C3 (B, Figure 3), and one featuring a ψ_ax-CO₂Me group at C3 (C, Figure 3). In every case these assignments match those made by the ¹³C NMR chemical shift method of Ungemach et al,¹² but this ¹H NMR assignment method has several benefits. In addition to reduced sample quantity and experiment time requirements, it can be applied when only one stereoisomer is in hand. Extensive DFT calculations support the conformational analysis undergirding the ¹H NMR assignment method, including accurate (RMSD = 0.4 Hz) calculation of ³J_4β−3 and other ¹H-¹H coupling constants. Furthermore, these calculations show that the presence or absence of a γ-gauche substituent has no effect on the ¹³C NMR chemical shift of C1 in 7a and 7b (Figure 7). This calculated result, combined with the observed failure of C1 and C3 to exert reciprocal upfield shifts of the C=O and C1’ carbons in 7a-ae (Table 1), thus challenge the conceptual foundation of the traditional ¹³C NMR chemical shift assignment method for 1,3-disubstituted THβCs. With this foundation in doubt, one cannot predict scenarios under which the method would fail to properly assign trans- and cis-THBCs. Since biological activity within the medicinally important 1,3-disubstituted-THβC scaffold is typically very sensitive to configuration,^{2, 5, 9, 37} a missed assignment could muddy emerging structure-activity relationships and mislead investigators. In contrast, the sound theoretical foundation of the ³J_4β−3 assignment method described herein allows one to use standard tools of conformational analysis to anticipate conditions under which it might fail. This important feature and the other advantages listed above commend its use to synthetic and medicinal chemists.

Methods

Computational

To extensively probe the conformational space available to compounds 7a, 7b, 8a, and 8b, automated conformer searches (MMFF94) were performed using Spartan ‘16,⁵⁷ starting from at least two different geometries. These MMFF94 minima were then optimized at B3LYP/6–31G(d) using Gaussian 09,⁵⁸ giving the numbers of conformers listed above in Table 4. In each case vibrational frequency analysis (NIMAG=0) confirmed that each stationary point was a minimum. Individual conformers of 7a, 7b, 8a, and 8b are identified in the Supporting Information as 7a-01 to 7a-16, 7b-01 to 7b-08, 8a-01 to 8a-14, 8b-01 to 8b-08, respectively. Single point energies of each conformer were calculated with three different functionals and larger basis sets, as described above: B3LYP/6–311+G(2d,p), mPW1PW91/6–311+G(2d,p) and M06–2X/def2-TZVP each with implicit solvation SCRF=(PCM,Solvent=Chloroform). Free energies were calculated by adding the free energy (298 K) corrections derived from unscaled B3LYP/6–31G(d) frequencies to these single point energies, to derive the corresponding Boltzmann distributions. The overall population of each of the eight conformational ensembles described in Table 4 (and Table S14) were calculated by summing the Boltzmann populations of the appropriate individual conformers.

Calculated J_HH coupling constants shown in Table 5 were obtained using the B3LYP functional with core-augmented 6–31G(d,p) basis set (“6–31G(d,p)u+1s”). Note that only Fermi contact terms were evaluated, and only couplings between the hydrogen atoms of interest (H4β, H4α, H3, H1) were specified for calculation. This approach was selected based on its high accuracy (RMSD <0.5 Hz over a large test set) and low computational cost.⁵⁶ Interestingly, although ¹H chemical shift modeling benefits from inclusion of implicit solvation, this study demonstrated that implicit solvation does not improve the accuracy of calculated J_HH values;⁵⁶ thus we calculated values in the gas phase. The coupling constants (³J_4β−3, ³J_4α−3, ²J_4β−4α, ⁵J_4β−1, ⁵J_4α−1) in each conformer of 7a, 8a, 7b, and 8b, (scaled by the recommend factor of 0.9117) are given in Table S15, which includes a sample Gaussian route section to perform these calculations. To obtain weighted average J_HH coupling constants, the various Boltzmann distributions were applied (Table 5 and S16).

Shielding tensors σ for each carbon in each conformer were calculated from the B3LYP/6–31G(d) geometries at the B3LYP/6–311+G(2d,p) (PCM, CHCl₃) and mPW1PW91/6–311+G(2d,p) (PCM, CHCl₃) levels of theory. These functionals, basis set, and solvation model were selected based on their excellent performance in a recent study of the ¹H and ¹³C NMR solution spectra of colchicine.⁴⁹ The corresponding ¹³C NMR chemical shifts were calculated according to the formula δ = (σ – b)/a, where a = slope and b = intercept.⁵⁹ The values of a and b were taken from the aforementioned study of colchicine,⁴⁹ and were a = −1.043 , b = 181.717 for B3LYP/6–311+G(2d,p) (PCM=CHCl₃), and a = −1.042, b = 186.357 for mPW1PW91/6–311+G(2d,p) (PCM=CHCl₃). The weighted average ¹³C chemical shifts of each carbon were then determined using the calculated Boltzmann distributions, and compared to experimental chemical shifts to obtain the MAD for each compound studied.

Chemistry

All NMR spectra were acquired in CDCl₃. As described above, 1-aryl-substituted Pictet-Spengler adducts 7a-z and 8a-z were prepared previously;^{9, 37 1}H and ¹³C NMR analyses described in this paper were performed on archived samples.

Experimental

Synthesis of 7aa and 8aa

To a mixture of L-tryptophan methyl ester hydrochloride (514 mg, 2.02 mmol), 4Å molecular sieves (1 g, powdered), and pentanal (0.24 mL, 2.26 mmol), CH₂Cl₂ (6 mL) was added under nitrogen. The resulting mixture was stirred at room temperature for 48 hours. TFA (0.3 mL, 3.92 mmol) was added dropwise. Reaction mixture was further stirred at room temperature for additional 24 hours. Reaction was cooled to 0 °C and saturated aqueous solution of NaHCO₃ (6 mL) was added, followed by addition of EtOAc (6 mL). After stirring for 30 min at 0 °C, the molecular sieves were filtered and phases of the filtrate were partitioned and the aqueous layer was extracted with EtOAc (3 × 10 mL). The combined organic layers were washed with saturated aqueous NaCl solution (25 mL), dried over Na₂SO₄ and concentrated in vacuo. Compounds 7aa and 8aa were separated from the crude material by flash chromatography (gradient, from 1:1 CH₂Cl₂ : hexane to 2:2:1 CH₂Cl₂ : hexane : EtOAc) to give 8aa (190 mg, 33%, first-eluting, off-white solid) and 7aa (45 mg, 8%, second-eluting, yellow oil). A mixed fraction of 7aa and 8aa (162 mg, 28% yield) was also obtained.

Methyl (1R,3S)-1-butyl-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (7aa):

¹H NMR (400 MHz, CDCl₃) δ 7.73 (s, 1H), 7.49 (ddd, J = 7.6, 1.4, 0.7 Hz, 1H), 7.31 (ddd, J = 8.0, 1.2, 0.7 Hz, 1H), 7.15 (ddd, J = 8.0, 7.1, 1.4 Hz, 1H), 7.10 (ddd, J = 7.6, 7.1, 1.1 Hz, 1H), 4.24 (dd, J = 8.3, 4.9 Hz, 1H), 3.99 (dd, J = 7.3, 5.3 Hz, 1H), 3.75 (s, 3H), 3.12 (ddd, J = 15.3, 5.3, 1.2 Hz, 1H), 2.99 (ddd, J = 15.3, 7.3, 1.5 Hz, 1H), 1.93 (s, 1H), 1.84 – 1.68 (m, 2H), 1.58 – 1.44 (m, 2H), 1.43 – 1.35 (m, 2H), 0.94 (t, J = 7.2 Hz, 3H). ¹³C NMR (101 MHz, CDCl₃) δ 174.4, 136.0, 135.8, 127.2, 121.7, 119.5, 118.1, 110.8, 107.0, 52.7, 52.2, 50.4, 35.5, 28.5, 25.1, 22.9, 14.2. This compound has been reported previously without full NMR characterization.⁶⁰

Methyl (1S,3S)-1-butyl-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (8aa):

¹H NMR (400 MHz, CDCl₃) δ 7.79 (s, 1H), 7.48 (d, J = 7.7 Hz, 1H), 7.36 – 7.30 (m, 1H), 7.16 (td, J = 8.1, 7.6, 1.3 Hz, 1H), 7.11 (ddd, J = 7.6, 7.2, 1.2 Hz, 1H), 4.20 (ddt, J = 8.3, 4.1, 2.2 Hz, 1H), 3.83 (s, 3H), 3.80 (dd, J = 11.2, 4.2 Hz, 1H), 3.13 (ddd, J = 15.1, 4.2, 1.9 Hz, 1H), 2.82 (ddd, J = 15.1, 11.2, 2.6 Hz, 1H), 2.00 – 1.91 (m, 1H), 1.72 (dddd, J = 13.8, 10.5, 8.1, 5.2 Hz, 1H), 1.52 – 1.44 (m, 2H), 1.39 (dddd, J = 14.2, 8.7, 6.9, 5.4 Hz, 2H), 0.94 (t, J = 7.1 Hz, 3H). ¹³C NMR (101 MHz, CDCl₃) δ 173.9, 136.0, 135.8, 127.3, 121.8, 119.7, 118.1, 110.9, 108.2, 56.6, 52.9, 52.3, 34.7, 27.6, 26.1, 23.1, 14.1. This compound has been reported previously without full NMR characterization.⁶⁰

Synthesis of 7ab and 8ab

The procedure for 7aa/7ab above was followed using L-tryptophan methyl ester hydrochloride (1.281 mg, 5.03 mmol), 4Å molecular sieves (3.5 g, powdered), and cyclohexanecarboxaldehyde (0.58 mL, 5.09 mmol). Following workup, 7ab and 8ab were isolated by column chromatography (5:5:3.5 CH₂Cl₂: hexane: EtOAc) to give 8ab (1.02 g, 65%, first-eluting, pale yellow solid) and 7ab (149 mg, 10% yield, second-eluting, off-white solid). A mixed fraction of 7ab and 8ab (190 mg, 12% yield) was also obtained.

Methyl (1R,3S)-1-cyclohexyl-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (7ab):

¹H NMR (400 MHz, CDCl₃) δ 7.76 (s, 1H), 7.49 (ddt, J = 7.6, 1.5, 0.8 Hz, 1H), 7.31 (dt, J = 8.0, 1.0 Hz, 1H), 7.18 – 7.07 (m, 2H), 4.08 (d, J = 5.2 Hz, 1H), 4.02 (dd, J = 6.9, 5.3 Hz, 1H), 3.72 (s, 3H), 3.10 (ddd, J = 15.3, 5.3, 1.3 Hz, 1H), 3.00 (ddd, J = 15.3, 6.9, 1.5 Hz, 1H), 1.87 – 1.78 (m, 4H), 1.76 – 1.65 (m, 4H), 1.37 – 1.10 (m, 6H). ¹³C NMR (101 MHz, CDCl₃) δ 174.7, 135.9, 134.6, 127.2, 121.7, 119.5, 118.1, 110.8, 107.9, 55.4, 53.5, 52.2, 43.3, 30.4, 28.6, 26.7, 26.5, 26.5, 25.0. mp 150.2–154.8 °C. This compound has been previously reported and both NMR and mp data are consistent with the literature.^{61, 62}

Methyl (1S,3S)-1-cyclohexyl-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (8ab):

¹H NMR (400 MHz, CDCl₃) δ 7.80 (s, 1H), 7.48 (ddd, J = 7.6, 1.4, 0.7 Hz, 1H), 7.34 (dt, J = 8.0, 1.0 Hz, 1H), 7.19 – 7.08 (m, 2H), 4.16 (q, J = 2.3 Hz, 1H), 3.82 (s, 3H), 3.74 (dd, J = 11.2, 4.1 Hz, 1H), 3.11 (ddd, J = 14.9, 4.1, 1.8 Hz, 1H), 2.78 (ddd, J = 14.9, 11.2, 2.6 Hz, 1H), 1.89 – 1.68 (m, 6H), 1.51 – 1.17 (m, 6H). ¹³C NMR (101 MHz, CDCl₃) δ 174.0, 136.1, 134.9, 127.4, 121.7, 119.6, 118.0, 110.9, 109.3, 57.8, 56.6, 52.3, 42.5, 29.8, 27.0, 27.0, 26.7, 26.5, 26.1. mp 132.3–135.3 °C. This compound has been previously reported and both NMR and mp data are consistent with literature.^{61, 62}

Synthesis of 7ac and 8ac

The procedure for 7aa/8aa above was followed using L-tryptophan methyl ester hydrochloride (501 mg, 1.97 mmol) and 2-ethylbutanal (0.27 mL, 2.19 mmol). Purification on column chromatography (5:5:2 CH₂Cl₂: hexane: EtOAc) yielded 8ac (166.4 mg, 28%, first-eluting, yellow glass) and 7ac (34.3 mg, 6%, second-eluting, yellow oil). A mixed fraction of 7ac and 8ac (312.3 mg, 52.8% yield) was also obtained.

Methyl (1R,3S)-1-(pentan-3-yl)-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (7ac):

¹H NMR (400 MHz, CDCl₃) δ 7.74 (s, 1H), 7.49 (ddt, J = 7.5, 1.5, 0.8 Hz, 1H), 7.31 (dt, J = 7.8, 1.1 Hz, 1H), 7.17 – 7.12 (m, 1H), 7.10 (td, J = 7.4, 1.2 Hz, 1H), 4.48 (dt, J = 3.3, 1.8 Hz, 1H), 4.05 (t, J = 5.2 Hz, 1H), 3.68 (s, 3H), 3.12 (dt, J = 5.4, 1.7 Hz, 2H), 1.91 (s, 2H), 1.63 – 1.48 (m, 3H), 1.38 – 1.23 (m, 3H), 1.05 (t, J = 7.2 Hz, 3H), 0.84 (t, J = 7.5 Hz, 3H). ¹³C NMR (101 MHz, CDCl₃) δ 174.7, 136.0, 134.7, 127.4, 121.6, 119.4, 118.0, 110.8, 108.2, 54.1, 52.2, 51.0, 46.7, 24.4, 23.1, 22.7, 12.6, 12.3. HRMS (ESI) [M+H]⁺ calculated for C₁₈H₂₄N₂O₂: 301.1911. Found: 301.1910.

Methyl (1S,3S)-1-(pentan-3-yl)-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (8ac):

¹H NMR (400 MHz, CDCl₃) δ 7.76 (s, 1H), 7.48 (ddt, J = 7.7, 1.5, 0.7 Hz, 1H), 7.33 (ddd, J = 8.0, 1.2, 0.8 Hz, 1H), 7.18 – 7.13 (m, 1H), 7.11 (ddd, J = 7.6, 7.1, 1.2 Hz, 1H), 4.35 (q, J = 2.3 Hz, 1H), 3.82 (s, 3H), 3.74 (dd, J = 11.2, 4.1 Hz, 1H), 3.12 (ddd, J = 15.0, 4.1, 1.9 Hz, 1H), 2.78 (ddd, J = 15.0, 11.2, 2.6 Hz, 1H), 1.69 (s, 1H), 1.63 – 1.53 (m, 3H), 1.37 – 1.24 (m, 2H), 1.04 (t, J = 7.3 Hz, 3H), 0.89 (t, J = 7.5 Hz, 3H). ¹³C NMR (101 MHz, CDCl₃) δ 174.1, 136.0, 135.5, 127.5, 121.7, 119.6, 117.9, 110.9, 109.5, 56.6, 54.6, 52.3, 46.1, 26.2, 23.3, 22.8, 13.2, 12.8. HRMS (ESI) [M+H]⁺ calculated for C₁₈H₂₄N₂O₂: 301.1911. Found: 301.1908

Synthesis of 7ad and 8ad

The procedure for 7aa/8aa above was followed using L-tryptophan methyl ester hydrochloride (514 mg, 2.02 mmol) and trimethylacetaldehyde (0.65 mL, 5.98 mmol). Purification on column chromatography (5:5:2 CH₂Cl₂: hexane: EtOAc) yielded 8ad (1.9 mg, 0.3%, first-eluting, yellow oil) a mixed fraction of 7ad and 8ad (289.7 mg, 50%, yellow oil). Recrystallization of the mixture from EtOAc gave a small quantity of pure 7ad (17.1 mg, 3%, colorless crystals).

Methyl (1R,3S)-1-(tert-butyl)-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (7ad):

¹H NMR (400 MHz, CDCl₃) δ 7.78 (s, 1H), 7.50 (ddt, J = 7.7, 1.5, 0.8 Hz, 1H), 7.35 – 7.28 (m, 1H), 7.18 – 7.13 (m, 1H), 7.10 (ddd, J = 7.7, 7.1, 1.2 Hz, 1H), 4.09 (app. t, J = 5.2 Hz, 1H), 4.07 (t, J = 1.4 Hz, 1H), 3.63 (s, 3H), 3.11 (ddd, J = 15.0, 5.1, 1.5 Hz, 1H), 3.08 (ddd, J = 15.0, 5.3, 1.6 Hz, 1H), 1.08 (s, 9H). ¹³C NMR (126 MHz, CDCl₃) δ 175.1, 135.9, 133.7, 127.0, 121.8, 119.4, 118.1, 110.7, 109.2, 59.4, 54.4, 52.1, 36.8, 27.3, 24.7. HRMS (ESI) [M+H]⁺ calculated for C₁₇H₂₂N₂O₂: 287.1754. Found: 287.1753. mp = 141.3–142.4 °C

Methyl (1S,3S)-1-(tert-butyl)-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (8ad):

¹H NMR (400 MHz, CDCl₃) δ 7.90 (s, 1H), 7.50 (d, J = 8.1 Hz, 1H), 7.33 (dt, J = 8.1, 0.9 Hz, 1H), 7.17 (ddd, J = 8.1, 7.1, 1.3 Hz, 1H), 7.11 (ddd, J = 8.1, 7.1, 1.1 Hz, 1H), 4.03 (s, 1H), 3.83 (s, 3H), 3.68 (dd, J = 11.2, 3.6 Hz, 1H), 3.14 (ddd, J = 14.6, 3.6, 1.5 Hz, 1H), 2.77 (ddd, J = 14.6, 11.2, 2.4 Hz, 1H), 1.13 (s, 9H). ¹³C NMR (101 MHz, CDCl₃) δ 174.0, 136.0, 134.6, 126.9, 121.9, 119.6, 118.0, 110.8, 62.6, 56.5, 52.3, 35.7, 27.1, 26.4. This compound has been previously reported and NMR data are consistent with literature.⁶³

Synthesis of 7ae and 8ae

The procedure for 7aa/8aa above was followed using L-tryptophan methyl ester hydrochloride (502 mg, 1.97 mmol) and 3-methylbutanal (0.23 mL, 2.14 mmol). Purification on column chromatography (5:5:2 CH₂Cl₂: hexane: EtOAc) to give 8ae (152.8 mg, 27%, first-eluting, yellow oil) and 7ae (117.4 mg, 21% yield, second-eluting, yellow oil). A mixed fraction of 7ae and 8ae (225.6 mg, 40% yield) was also obtained.

Methyl (1R,3S)-1-isobutyl-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (7ae):

¹H NMR (400 MHz, CDCl₃) δ 7.74 (s, 1H), 7.48 (ddt, J = 7.7, 1.5, 0.8 Hz, 1H), 7.30 (ddd, J = 8.0, 1.2, 0.8 Hz, 1H), 7.15 (ddd, J = 8.0, 7.1, 1.4 Hz, 1H), 7.10 (ddd, J = 7.6, 7.1, 1.2 Hz, 1H), 4.32 (dd, J = 10.0, 4.2 Hz, 1H), 3.99 (dd, J = 7.4, 5.3 Hz, 1H), 3.75 (s, 3H), 3.13 (ddd, J = 15.4, 5.3, 1.2 Hz, 1H), 3.00 (ddd, J = 15.4, 7.4, 1.5 Hz, 1H), 1.96 (dddt, J = 15.0, 6.6, 4.6, 2.3 Hz, 2H), 1.88 (s, 2H), 1.73 (ddd, J = 13.7, 9.9, 4.8 Hz, 1H), 1.53 (ddd, J = 13.8, 9.4, 4.2 Hz, 1H), 1.04 (d, J = 6.5 Hz, 3H), 1.01 (d, J = 6.7 Hz, 3H). ¹³C NMR (101 MHz, CDCl₃) δ 174.4, 136.0, 135.9, 127.2, 121.7, 119.5, 118.1, 110.8, 106.8, 52.5, 52.2, 48.2, 44.5, 25.1, 24.8, 23.8, 21.7. This compound has been previously reported and NMR data are consistent with literature.⁶⁴

Methyl (1R,3S)-1-isobutyl-2,3,4,9-tetrahydro-1H-pyrido[3,4-b]indole-3-carboxylate (8ae):

¹H NMR (400 MHz, CDCl₃) δ 7.84 (s, 1H), 7.48 (ddt, J = 7.6, 1.5, 0.7 Hz, 1H), 7.33 – 7.30 (m, 1H), 7.19 – 7.14 (m, 1H), 7.11 (ddd, J = 7.1, 1.3 Hz, 1H), 4.23 (ddt, J = 9.0, 4.4, 2.2 Hz, 1H), 3.83 (s, 3H), 3.80 (dd, J = 11.2, 4.2 Hz, 1H), 3.14 (ddd, J = 15.0, 4.2, 1.9 Hz, 1H), 2.83 (ddd, J = 15.0, 11.2, 2.6 Hz, 1H), 2.10 – 1.97 (m, 2H), 1.75 – 1.60 (m, 2H), 1.04 (d, J = 6.6 Hz, 3H), 1.01 (d, J = 6.6 Hz, 3H). ¹³C NMR (101 MHz, CDCl₃) δ 173.9, 136.2, 136.0, 127.4, 121.8, 119.7, 118.1, 110.9, 107.9, 56.6, 52.3, 50.7, 44.5, 26.1, 24.4, 24.0, 21.8. This compound has been previously reported and NMR data are consistent with literature.⁶⁴