Abstract
We investigate the spectral evolution in different metal phthalocyanine molecules on NbSe2 surface using scanning tunnelling microscopy (STM) as a function of the coupling with the substrate. For manganese phthalocyanine (MnPc), we demonstrate a smooth spectral crossover from Yu-Shiba-Rusinov (YSR) bound states to spin-flip excitations. This has not been observed previously and it is in contrast to simple theoretical expectations. We corroborate the experimental findings using numerical renormalization group calculations. Our results provide fundamental new insight on the behavior of atomic scale magnetic/SC hybrid systems, which is important, for example, for engineered topological superconductors and spin logic devices.
Keywords: Magnetic impurity, superconductor, scanning tunneling microscopy (STM), Yu-Shiba-Rusinov state, spin-flip excitation
Precise control of the properties of magnetic impurities on surfaces, such as the spin state and magnetic anisotropy, is one of the ultimate goals in fabricating atomic or molecular scale devices for data storage or computing purposes. However, the properties of magnetic impurities are strongly influenced by the atomic environment. In the extreme case, the interactions with the environment (substrate) can create entirely new electronic states, such as the Kondo effect,1−3 or the formation of Yu-Shiba-Rusinov (YSR) bound states on superconductors.4−8 YSR states have received intense interest as it has become possible to create artificial designer structures, where the interaction between the YSR states gives rise to Majorana modes.9−16 The YSR states are very sensitive to the immediate environment of the impurity spin and give information on the role of the local environment on the exchange interaction J of an impurity spin with a superconductor.3,7,12,15−27 The bulk of recent experimental work on YSR states on superconducting (SC) substrates has demonstrated that the strength of the exchange interaction J can be significantly influenced by a small change in the adsorption site of the impurity or by spacers between the impurity and substrate.3,18,24−32
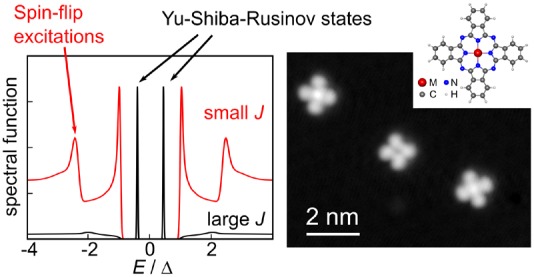
Figure 1a illustrates how the exchange coupling J with the substrate competes with the superconducting (SC) pairing energy Δ. The interaction of the local spin with the Cooper pairs gives rise to a low-lying excited state within the gap of the quasiparticle excitation spectrum.4−8 When J is decreased, the direct interaction of the local spin with the Cooper pairs is reduced and the YSR states merge with the SC coherence peaks. In the simplified theory by Yu, Shiba, and Rusinov, the position of the YSR state is EYSR = Δ(1 – α2)/(1 + α2) with α proportional to J, α = πρJS/2, where ρ is the normal-state density of states of the substrate at the Fermi level and S is the impurity spin. The bound state results from the spin-dependent scattering of Bogoliubov quasiparticles on the impurity and is thus associated with the longitudinal part of the exchange interaction, JSzsz, where s represents the spin-density of the substrate electrons at the impurity position. Furthermore, internal spin transitions in combination with magnetic anisotropy can give rise to symmetric features with respect to EF outside the superconducting gap (Figure 1b).18,30,33−38 These are associated with the spin-flip (SF) events, whereby the spin projection changes by ±1.33,37,38 The renormalization of the magnetic anisotropy, associated with the transverse part of the exchange interaction J(S+s– + S–s+), approximately follows a Deff = D0[1 – β(ρJ)2 + ···] dependence. In the simple picture, the relative magnitudes of these two channels (YSR and spin-flip) are not constrained and, in principle, both of these effects should be observed simultaneously.39,40 Although both YSR states and spin-flip excitations have been observed on the same experimental system, where the exchange coupling is changed by the adsorption site of the magnetic impurity,22 they have not been observed simultaneously in a single configuration. This suggests that the complete picture of the interplay between these two effects is more complicated, requiring a full many-body treatment of the quantum mechanical spin degree of freedom interacting with a (gapped) continuum of electrons.
Figure 1.
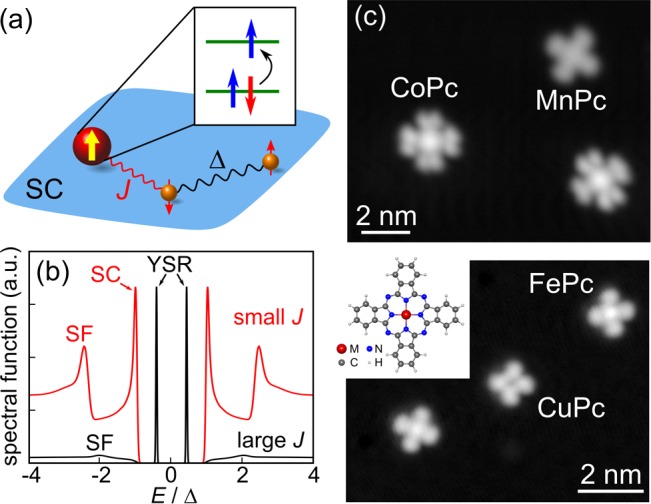
(a) Impurity spin is exchange coupled (strength J) to the superconducting substrate (gap Δ). (b) Impurity induces pairs of bound states symmetric with respect to EF within the gap of the quasiparticle excitation spectrum (black curve, states marked with YSR). Even at vanishing J, for impurities with S ≥ 1, the internal spin degrees of freedom can result in symmetric features with respect to EF outside the SC gap (red curve, spin-flip (SF) excitations). (c) Topographic STM images of the molecules used in this study (imaging set-point 0.5 V/2 pA). Inset: Schematic of a MPc molecule.
Here, we experimentally demonstrate smooth crossover from YSR states to spin-flip excitations in metal phthalocyanine molecules (MPcs) on NbSe2 surface. Using scanning tunneling microscopy (STM), we tune the exchange coupling strength J and follow the spectral evolution from the YSR states to intrinsic quantum spin states characterized by well-developed spin-flip excitations. Our results provide detailed understanding of the low-energy quantum states in magnetic/SC hybrid systems and could have significant ramifications for the design and control of atomic-scale magnetic devices.
Figure 1c shows
topographic STM images of isolated MPc molecules on NbSe2; see Supporting Information (SI) for
details. Their topographic appearance already reflects differences
that allow us to classify them into two groups: the metal ion appears
as a protrusion in FePc, CoPc, and MnPc and as a depression in CuPc
depending on the coupling of the out of plane d-orbitals with the
tip states.41,42 We characterize the spin states
of different MPcs by recording differential conductance spectra (dI/dV curves) with an SC tip (Figure 2a). For CoPc and MnPc, there
are two peaks at symmetric bias voltages within the SC gap. These
subgap peaks are due to the formation of YSR states and indicate a
sizable magnetic interaction with the SC substrate caused by an unpaired
spin in the 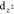 -orbital (see Figure 2b for the spin states
of the molecules).
This orbital is subject to strong coupling with the electronic states
of the substrate due to its symmetry, while the spins on the dxy- and
-orbital (see Figure 2b for the spin states
of the molecules).
This orbital is subject to strong coupling with the electronic states
of the substrate due to its symmetry, while the spins on the dxy- and 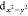 -orbitals are expected to be only
weakly
coupled.42,43 The dI/dV curve taken on CuPc shows an unperturbed SC gap of NbSe2 due to the absence of unpaired spin in the
-orbitals are expected to be only
weakly
coupled.42,43 The dI/dV curve taken on CuPc shows an unperturbed SC gap of NbSe2 due to the absence of unpaired spin in the 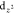 orbital (Figure 2b). As an S = 1/2 system,
CuPc is also not expected to show any spin-flip excitations.
orbital (Figure 2b). As an S = 1/2 system,
CuPc is also not expected to show any spin-flip excitations.
Figure 2.
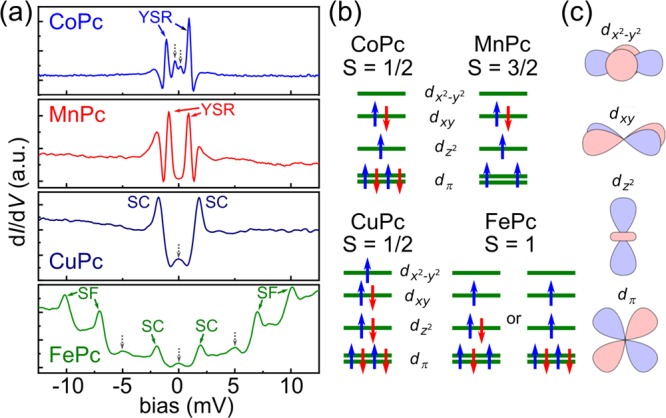
(a) Differential conductance spectra (dI/dV) recorded over the center of the different MPcs with a SC tip. The YSR states and spin-flip (SF) excitations are marked. Gray dotted arrows mark transitions due thermal excitation of carriers across the SC gap.3 (b) The ground state spin configurations of the different MPcs. For FePc, we show two possible spin configurations (having similar energy). (c) Illustration of the different d-orbital symmetries.
Although the dI/dV curves
taken
on FePc do not show YSR states, there are remarkable features outside
the SC gap. Their symmetric appearance points to inelastic excitations.33,44,45 Interestingly, unlike in the
previous studies that required decoupling the magnetic molecules using
an extra organic ligand as a spacer,18,30 we observe
these signals already when the molecule is directly adsorbed on the
SC substrate. Because FePc is also expected to have a dominant 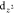 -character, the
molecule–substrate
interaction should be similar to CoPc and MnPc. The surprising absence
of YSR states on FePc suggests that the magnetic interaction with
the SC substrate is actually weak, which would be at odds with an
unpaired spin occupying a
-character, the
molecule–substrate
interaction should be similar to CoPc and MnPc. The surprising absence
of YSR states on FePc suggests that the magnetic interaction with
the SC substrate is actually weak, which would be at odds with an
unpaired spin occupying a  -orbital. FePc has spin triplet S = 1 electronic
ground state and DFT calculations suggest
that FePc on NbSe2 has the same spin as in the gas phase
(SI for details). Two different spin-configurations
separated by 80 meV have been proposed as the ground state46,47 (Figure 2b). The
absence of YSR states is consistent with the predicted lower energy
configuration with two electrons on the
-orbital. FePc has spin triplet S = 1 electronic
ground state and DFT calculations suggest
that FePc on NbSe2 has the same spin as in the gas phase
(SI for details). Two different spin-configurations
separated by 80 meV have been proposed as the ground state46,47 (Figure 2b). The
absence of YSR states is consistent with the predicted lower energy
configuration with two electrons on the 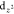 -orbital.46 This
ground state spin configuration can be altered by slight differences
in the molecular ligand field or the interaction with the substrate
as shown by YSR states observed on a related iron porphyrin molecule
on Pb(111) substrate.31
-orbital.46 This
ground state spin configuration can be altered by slight differences
in the molecular ligand field or the interaction with the substrate
as shown by YSR states observed on a related iron porphyrin molecule
on Pb(111) substrate.31
We have verified that the observed transitions result from inelastic spin excitations by acquiring the dI/dV spectra under an external magnetic field (B) perpendicular to the sample surface (see SI for details). The B-field dependence of the energies of the first and second feature is consistent with S = 1 with transverse anisotropy. Fitting the data with a phenomenological spin Hamiltonian Heff = gμBBSγ + DSz2+E(Sx – Sy2), where g is the Landé g factor, μB is the Bohr magneton, and Sγ is the spin component along the field direction, we obtain D = 5.5 meV and E = 1.4 meV indicating easy-plane magnetic anisotropy. The positive value of D is comparable to the bulk value (in contrast to the measurements on oxidized Cu(110) surface giving D < 0).47,48
The exchange coupling between the magnetic impurity and the substrate can be modulated by changing the adsorption site of the molecule.3,18,28−30,49,50 We successfully positioned CoPc and FePc molecules on different adsorption sites through STM manipulation (SI Figure S3), which affects the energy positions of both the YSR states and the inelastic features. On CoPC, the YSR states can even change between particle- or hole-like character depending on the adsorption site, similarly to the reported results on MnPc adsorbed on Pb(111).28 On FePc, adsorption site causes variations of E and D with typical values in the range of 1.2–2.7 and 4.2–9.0 meV, respectively.
Because of the sensitivity
of the YSR states and spin-excitations,
they can be tuned continuously by the force exerted by the STM tip.31,32,51 We expect to have attractive
forces between the tip and the molecule;52,53 this would result in pulling the molecule away from the substrate
and reduction of the exchange coupling between the molecule and the
substrate upon decreasing the tip–molecule distance. Figure 3 shows a series of
tunneling spectra measured at different tip–sample distances
above the central ion of the MPc molecule. The dI/dV spectra on a CoPc molecule, Figure 3a, show a shift of the YSR
resonances toward higher bias. At zoffset ≈ 60 pm, the YSR resonances have merged with the SC coherence
peaks at the gap edge. The dI/dV spectra on MnPc (Figure 3b) also show a clear shift of the YSR resonance toward the
SC gap edge. At zoffset ≈ 240 pm,
as the YSR resonance is merging with the SC coherence peak, a new
symmetric pair of peaks is emerging outside the gap (marked with *).
Finally, on FePc (Figure 3c), the two spin excitation energies monotonously increase
with decreasing tip–sample distance. These variations in the
YSR and spin excitations states of the MPc molecules are caused by
the interaction of the STM tip causing the metal ion to be pulled
toward the STM tip.31,32,51 This has the largest effect on the out-of-plane d-orbitals (dxz/yz and  ), where the
overlap with the substrate
wave function will be strongly affected.
), where the
overlap with the substrate
wave function will be strongly affected.
Figure 3.
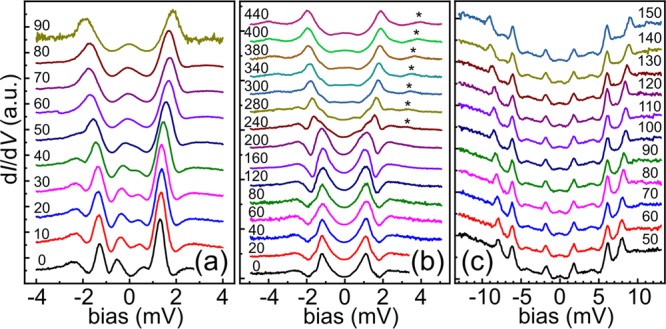
Normalized dI/dV spectra recorded over CoPc (set-point V = 20 mV, I = 300 pA) (a), MnPc (set-point V = 20 mV, I = 200 pA) (b), and FePc (set-point V = 50 mV, I = 200pA) (c) at different tip–sample distances from far (bottom) to close (top). Initial tip–sample distance given by the set-point conditions, then the tip is approached by a distance of zoffset indicated in the figure (values in pm).
With CoPc (S = 1/2), the interaction with
the
tip reduces the coupling between the  -orbital and
the NbSe2 and the
YSR states move to the SC coherence peaks (J decreases)
(Figure 3a). With FePc
(S = 1), in addition to modifying the exchange coupling J, the tip–sample interaction might also affect the
energies of the d-orbitals slightly. This causes the bare magnetic
anisotropy D0, which is an admixture of
low-lying excited states of the molecules,54 to be directly affected by the tip–sample distance. In this
system, it is not possible to distinguish whether the effective anisotropy Deff changes dominantly through the variation
of D0 or J.
-orbital and
the NbSe2 and the
YSR states move to the SC coherence peaks (J decreases)
(Figure 3a). With FePc
(S = 1), in addition to modifying the exchange coupling J, the tip–sample interaction might also affect the
energies of the d-orbitals slightly. This causes the bare magnetic
anisotropy D0, which is an admixture of
low-lying excited states of the molecules,54 to be directly affected by the tip–sample distance. In this
system, it is not possible to distinguish whether the effective anisotropy Deff changes dominantly through the variation
of D0 or J.
With MnPc (S = 3/2), the coupling strength J decreases as the tip–sample distance decreases leading to the migration of the YSR states toward the SC gap edge and the recovery of the SC coherence peaks. When the YSR peaks are close to the gap edges, the spectra also show new symmetric features outside the gap, which are due to spin–flip excitations. In MnPc, at zero external magnetic field the axial magnetic anisotropy splits the spin states Ms = ±1/2 and Ms = ±3/2 by an energy separation of 2D, which corresponds to the observed spin excitation. This gives D ≈ 0.7 meV, which is close to the bulk value55 (more detailed analysis below). There could also be inelastic excitations in this energy range corresponding to molecular vibrations (phonons). We can rule this out by experiments under an external magnetic field which also indicate a positive value of D > 0 (see SI for details).
Conventional picture of the YSR states and spin-flip excitations neglecting quantum fluctuations does not predict a crossover behavior from the YSR states to spin-excitations. These conduction channels should be independent and readily observable at the same time. To resolve this disagreement with our experimental results, we describe the magnetic impurity by a multiorbital Anderson model for the relevant d-shell orbitals.56 This can be reduced in a given charge state to an effective model that takes the form of a Kondo Hamiltonian with the spin degree of freedom, S, only57,58 (see SI for details). Since the total spin operator has contributions from all d-orbitals, it is in general exchange coupled to different symmetry-adapted combinations of states from the substrate with different values of Kondo coupling strength, Ji. These differences are due to the unequal orbital energies and hybridization strengths. Only those Ji that are sufficiently large need to be retained; in the problems considered here, a single orbital is always strongly dominant, as evidenced by the presence of a single pair of subgap YSR peaks. We also take into account the spin–orbit coupling that leads through orbital excitations to residual magnetic-anisotropy terms. We solve the resulting single-channel anisotropic Kondo model with high spin S using the numerical renormalization group (NRG) method giving a numerically exact solution.59−61
Figure 4a shows the calculated spectral functions as a function of the exchange coupling for a magnetic impurity with S = 3/2 (e.g., MnPc). In the absence of anisotropy (D = E = 0), the binding of a Bogoliubov quasiparticle would lead to an emergence of a YSR bound state with the spin reduced by 1/2 (YSR screening from S = 3/2 to S = 1), giving rise to a single pair of YSR peaks. The phenomenology in the isotropic case is similar to that in the classical model, where the impurity is described as a static local magnetic field that binds Bogoliubov quasiparticles of the opposite spin direction. The many-body character of the subgap states is, however, revealed in the presence of magnetic anisotropy, which leads to the splitting of the subgap S = 1 multiplet into the low-energy |Sz = 0⟩ state and the high-energy (1/2)(|Sz = 1⟩ ± |Sz=–1⟩) states.62 For D ≪ Δ, such splitting is directly observable.28 When the anisotropy is large, as is the case here, the high-energy states are pushed instead into the continuum and only the |Sz = 0⟩ subgap state is observable. Furthermore, one finds additional features outside the gap that are related to the transitions within the unscreened S = 3/2 multiplet.18 These spectral steps correspond to the spin-flip excitations, similar to the those in systems with normal-state substrates.35,63 The exchange coupling to the substrate determines the energy shift as well as the lifetime broadening of the excited states.18,64 We model NbSe2 as a soft-gap superconductor with a small but finite concentration of subgap states, hence the excited spin states have even for ωsf = 2D < 2Δ relatively short lifetimes compared to hard-gap superconductors, because the dominant decay channel (emission of particle-hole excitations) is here open. For this reason, a finite value of J leads to significant broadening of the spin-flip excitations. It is difficult to resolve both spectral features, considering the required magnitude of J for the YSR states to be visibly separated from the gap edges.
Figure 4.
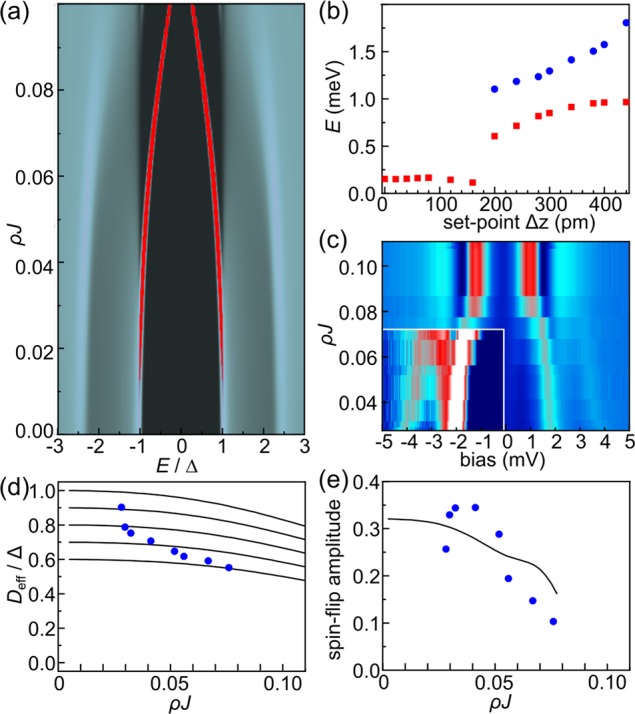
(a) Theoretical spectral functions for a magnetic impurity (S = 3/2) on a superconductor with varying exchange coupling J (spectra normalized by the value at high energy). (b) Extracted energies of the YSR resonances (red squares) and the spin-flip excitations (blue circles) from the experiments shown in Figure 3b. (c) Color-scale plot of the measured tunneling conductance as a function of the exchange coupling ρJ estimated from the energies of the YSR resonances (area inside the white rectangle is shown in enhanced contrast). (d) Comparison between the experimental Deff (symbols) and the calculated values (solid lines with D0/Δ = 0.6–1.0) scaled by the SC gap Δ as a function of the exchange coupling with the substrate. (e) Extracted experimental values (blue circles) and calculation results (black line) of the amplitude of the spin-flip transition as a function of the exchange coupling with the substrate.
The theory curves in Figure 4a can be compared with the experiments shown in Figure 3b. The energies of the YSR peaks and spin-flip excitations extracted from the experimental results are shown in Figure 4b (the SC gap of the tip has been subtracted). At small values of zoffset < 200 pm, only the YSR resonances are visible. As the tip is approached further, the YSR peaks merge with SC gap edges and spin-flip features emerge at a bias voltage between 3 and 4 mV. We can estimate the exchange coupling with the substrate by comparing the theoretical and experimental YSR energies (SI Figure S8). This allows us to convert set-point zoffset to an effective exchange coupling at that tip–molecule separation. The experimental data is replotted as a function of ρJ in Figure 4c, which can be directly compared with Figure 4a (note that the bias axis in Figure 4c still contains the offset due to the superconducting gap of the tip).
We can also plot the renormalized (effective) magnetic anisotropy Deff and the intensity of the spin-flip transitions as a function of the estimated ρJ (Figures 4d,e). This is possible as the energy of the YSR state depends only very weakly on the precise value of D in the experimentally relevant range (SI Figure S8). The comparison with theoretical results (solid lines in Figure 4d) yields a value of D0/Δ ∼ 0.7 for the nonrenormalized (bare) value of the magnetic anisotropy. The experimental values actually deviate from the theoretical trend expected for a fixed value of D0. This is the case for all couplings J but more particularly for small J, which corresponds to the largest tip–molecule interaction in the experiment. It is likely that the interaction with the tip distorts the molecular geometry or induces charge transfer with the metal ion resulting in a change in D0. The presence of the YSR resonances thus allows us to disentangle the two contributions to the variation of Deff. The extracted value D0 as a function of the tip–sample distance is plotted in the SI Figure S9.
The intensity of the spin-flip transition (Figure 4e) shows a monotonous decrease with increasing J (except the first two points, where the reason is again likely to be the tip–molecule interaction). The value at low J is close to the theoretically expected value of 0.4 for pure spin-flip excitations on a normal metal substrate (see SI Figure S10 for details).37,38 Comparing the experimental values with the theoretical predictions again highlights the strong correspondence between theory and experiments.
In conclusion, we have demonstrated coexistence and a smooth evolution from the YSR states to spin-flip transitions in MnPc molecules as the coupling with the NbSe2 substrate is reduced. The excitation energies reveal a significant renormalization of the anisotropy by the exchange coupling and it has a strong effect on the excited spin lifetime. The spin-flip excitations are broadened and washed out at higher values of J making simultaneous detection with the YSR states difficult. Our results provide fundamental new insight on the behavior of atomic scale magnetic/SC hybrid systems. This is important, for example, for the design of engineered topological superconductors consisting of magnetic atoms on SC substrates9,16,65 and achieving long spin life- and coherence times in spin logic devices.66−68
Acknowledgments
This research made use of the Aalto Nanomicroscopy Center (Aalto NMC) facilities and was supported by the European Research Council (ERC-2017-AdG no. 788185 “Artificial Designer Materials”), Academy of Finland (Academy Professor Funding nos. 318995 and 320555, Academy Research Fellow no. 256818, and Postdoctoral Researcher nos. 309975 and 316347), and the Aalto University Centre for Quantum Engineering (Aalto CQE). Our DFT calculations were performed using computer resources within the Aalto University School of Science Science-IT project and the Finnish CSC-IT Center for Science. R.Ž. acknowledges the support of the Slovenian Research Agency (ARRS) under P1-0044 and J1-7259.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.9b01583.
Experimental and computational methods, and additional results (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Li J.; Schneider W.-D.; Berndt R.; Delley B. Kondo Scattering Observed at a Single Magnetic Impurity. Phys. Rev. Lett. 1998, 80, 2893–2896. 10.1103/PhysRevLett.80.2893. [DOI] [Google Scholar]
- Madhavan V.; Chen W.; Jamneala T.; Crommie M. F.; Wingreen N. S. Tunneling into a Single Magnetic Atom: Spectroscopic Evidence of the Kondo Resonance. Science 1998, 280, 567–569. 10.1126/science.280.5363.567. [DOI] [PubMed] [Google Scholar]
- Franke K. J.; Schulze G.; Pascual J. I. Competition of Superconducting Phenomena and Kondo Screening at the Nanoscale. Science 2011, 332, 940. 10.1126/science.1202204. [DOI] [PubMed] [Google Scholar]
- Yu L. Bound State in Superconductors with Paramagnetic Impurities. Acta Phys. Sin. 1965, 21, 75. [Google Scholar]
- Shiba H. Classical Spins in Superconductors. Prog. Theor. Phys. 1968, 40, 435–451. 10.1143/PTP.40.435. [DOI] [Google Scholar]
- Rusinov A. I. On the Theory of Gapless Superconductivity in Alloys Containing Paramagnetic Impurities. Sov. Phys. JETP 1969, 29, 1101–1106. [Google Scholar]
- Yazdani A.; Jones B. A.; Lutz C. P.; Crommie M. F.; Eigler D. M. Probing the Local Effects of Magnetic Impurities on Superconductivity. Science 1997, 275, 1767–1770. 10.1126/science.275.5307.1767. [DOI] [PubMed] [Google Scholar]
- Heinrich B. W.; Pascual J. I.; Franke K. J. Single Magnetic Adsorbates on s-Wave Superconductors. Prog. Surf. Sci. 2018, 93, 1–19. 10.1016/j.progsurf.2018.01.001. [DOI] [Google Scholar]
- Nadj-Perge S.; Drozdov I. K.; Li J.; Chen H.; Jeon S.; Seo J.; MacDonald A. H.; Bernevig B. A.; Yazdani A. Observation of Majorana Fermions in Ferromagnetic Atomic Chains on a Superconductor. Science 2014, 346, 602–607. 10.1126/science.1259327. [DOI] [PubMed] [Google Scholar]
- Ruby M.; Pientka F.; Peng Y.; von Oppen F.; Heinrich B. W.; Franke K. J. End States and Subgap Structure in Proximity-Coupled Chains of Magnetic Adatoms. Phys. Rev. Lett. 2015, 115, 197204. 10.1103/PhysRevLett.115.197204. [DOI] [PubMed] [Google Scholar]
- Pawlak R.; Kisiel M.; Klinovaja J.; Meier T.; Kawai S.; Glatzel T.; Loss D.; Meyer E. Probing Atomic Structure and Majorana Wavefunctions in Mono-Atomic Fe Chains on Superconducting Pb Surface. npj Quantum Inf. 2016, 2, 16035. 10.1038/npjqi.2016.35. [DOI] [Google Scholar]
- Kezilebieke S.; Dvorak M.; Ojanen T.; Liljeroth P. Coupled Yu-Shiba-Rusinov states in molecular dimers on NbSe2. Nano Lett. 2018, 18, 2311–2315. 10.1021/acs.nanolett.7b05050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruby M.; Heinrich B. W.; Peng Y.; von Oppen F.; Franke K. J. Exploring a Proximity-Coupled Co Chain on Pb(110) as a Possible Majorana Platform. Nano Lett. 2017, 17, 4473–4477. 10.1021/acs.nanolett.7b01728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ménard G. C.; Guissart S.; Brun C.; Leriche R. T.; Trif M.; Debontridder F.; Demaille D.; Roditchev D.; Simon P.; Cren T. Two-dimensional Topological Superconductivity in Pb/Co/Si(111). Nat. Commun. 2017, 8, 2040. 10.1038/s41467-017-02192-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruby M.; Heinrich B. W.; Peng Y.; von Oppen F.; Franke K. J. Wave-Function Hybridization in Yu-Shiba-Rusinov Dimers. Phys. Rev. Lett. 2018, 120, 156803. 10.1103/PhysRevLett.120.156803. [DOI] [PubMed] [Google Scholar]
- Kim H.; Palacio-Morales A.; Posske T.; Rózsa L.; Palotás K.; Szunyogh L.; Thorwart M.; Wiesendanger R. Toward Tailoring Majorana Bound States in Artificially Constructed Magnetic Atom Chains on Elemental Superconductors. Sci. Adv. 2018, 4, eaar5251 10.1126/sciadv.aar5251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji S.-H.; Zhang T.; Fu Y.-S.; Chen X.; Ma X.-C.; Li J.; Duan W.-H.; Jia J.-F.; Xue Q.-K. High-Resolution Scanning Tunneling Spectroscopy of Magnetic Impurity Induced Bound States in the Superconducting Gap of Pb Thin Films. Phys. Rev. Lett. 2008, 100, 226801. 10.1103/PhysRevLett.100.226801. [DOI] [PubMed] [Google Scholar]
- Heinrich B. W.; Braun L.; Pascual J. I.; Franke K. J. Protection of Excited Spin States by a Superconducting Energy Gap. Nat. Phys. 2013, 9, 765. 10.1038/nphys2794. [DOI] [Google Scholar]
- Ménard G. C.; Guissart S.; Brun C.; Pons S.; Stolyarov V. S.; Debontridder F.; Leclerc M. V.; Janod E.; Cario L.; Roditchev D.; Simon P.; Cren T. Coherent Long-Range Magnetic Bound States in a Superconductor. Nat. Phys. 2015, 11, 1013–1016. 10.1038/nphys3508. [DOI] [Google Scholar]
- Ruby M.; Pientka F.; Peng Y.; von Oppen F.; Heinrich B. W.; Franke K. J. Tunneling Processes into Localized Subgap States in Superconductors. Phys. Rev. Lett. 2015, 115, 087001. 10.1103/PhysRevLett.115.087001. [DOI] [PubMed] [Google Scholar]
- Ruby M.; Peng Y.; von Oppen F.; Heinrich B. W.; Franke K. J. Orbital Picture of Yu-Shiba-Rusinov Multiplets. Phys. Rev. Lett. 2016, 117, 186801. 10.1103/PhysRevLett.117.186801. [DOI] [PubMed] [Google Scholar]
- Cornils L.; Kamlapure A.; Zhou L.; Pradhan S.; Khajetoorians A. A.; Fransson J.; Wiebe J.; Wiesendanger R. Spin-Resolved Spectroscopy of the Yu-Shiba-Rusinov States of Individual Atoms. Phys. Rev. Lett. 2017, 119, 197002. 10.1103/PhysRevLett.119.197002. [DOI] [PubMed] [Google Scholar]
- Island J. O.; Gaudenzi R.; de Bruijckere J.; Burzurí E.; Franco C.; Mas-Torrent M.; Rovira C.; Veciana J.; Klapwijk T. M.; Aguado R.; van der Zant H. S. J. Proximity-Induced Shiba States in a Molecular Junction. Phys. Rev. Lett. 2017, 118, 117001. 10.1103/PhysRevLett.118.117001. [DOI] [PubMed] [Google Scholar]
- Senkpiel J.; Rubio-Verdú C.; Etzkorn M.; Drost R.; Schoop L. M.; Dambach S.; Padurariu C.; Kubala B.; Ankerhold J.; Ast C. R.; Kern K.. Robustness of Yu-Shiba-Rusinov Resonances in Presence of a Complex Superconducting Order Parameter. arXiv:1803.08726, 2018.
- Etzkorn M.; Eltschka M.; Jäck B.; Ast C. R.; Kern K.. Mapping of Yu-Shiba-Rusinov States from an Extended Scatterer. arXiv:1807.00646, 2018.
- Liebhaber E.; Gonzalez S. A.; Baba R.; Reecht G.; Heinrich B. W.; Rohlf S.; Rossnagel K.; von Oppen F.; Franke K. J.. Yu-Shiba-Rusinov States in the Charge-Density Modulated Superconductor NbSe2. arXiv:1903.09663, 2019. [DOI] [PubMed]
- Schneider L.; Steinbrecher M.; Rózsa L.; Bouaziz J.; Palotás K.; Dias M. d. S.; Lounis S.; Wiebe J.; Wiesendanger R.. Magnetism and In-Gap States of 3d Transition Metal Atoms on Superconducting Re. arXiv:1903.10278, 2019.
- Hatter N.; Heinrich B. W.; Ruby M.; Pascual J. I.; Franke K. J. Magnetic Anisotropy in Shiba Bound States Across a Quantum Phase Transition. Nat. Commun. 2015, 6, 8988. 10.1038/ncomms9988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatter N.; Heinrich B. W.; Rolf D.; Franke K. J. Scaling of Yu-Shiba-Rusinov Energies in the Weak-Coupling Kondo Regime. Nat. Commun. 2017, 8, 2016. 10.1038/s41467-017-02277-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinrich B. W.; Braun L.; Pascual J. I.; Franke K. J. Tuning the Magnetic Anisotropy of Single Molecules. Nano Lett. 2015, 15, 4024–4028. 10.1021/acs.nanolett.5b00987. [DOI] [PubMed] [Google Scholar]
- Farinacci L.; Ahmadi G.; Reecht G.; Ruby M.; Bogdanoff N.; Peters O.; Heinrich B. W.; von Oppen F.; Franke K. J. Tuning the Coupling of an Individual Magnetic Impurity to a Superconductor: Quantum Phase Transition and Transport. Phys. Rev. Lett. 2018, 121, 196803. 10.1103/PhysRevLett.121.196803. [DOI] [PubMed] [Google Scholar]
- Malavolti L.; Briganti M.; Hänze M.; Serrano G.; Cimatti I.; McMurtrie G.; Otero E.; Ohresser P.; Totti F.; Mannini M.; Sessoli R.; Loth S. Tunable Spin-Superconductor Coupling of Spin 1/2 Vanadyl Phthalocyanine Molecules. Nano Lett. 2018, 18, 7955–7961. 10.1021/acs.nanolett.8b03921. [DOI] [PubMed] [Google Scholar]
- Heinrich A. J.; Gupta J. A.; Lutz C. P.; Eigler D. M. Single-Atom Spin-Flip Spectroscopy. Science 2004, 306, 466. 10.1126/science.1101077. [DOI] [PubMed] [Google Scholar]
- Hirjibehedin C. F.; Lutz C. P.; Heinrich A. J. Spin Coupling in Engineered Atomic Structures. Science 2006, 312, 1021. 10.1126/science.1125398. [DOI] [PubMed] [Google Scholar]
- Hirjibehedin C. F.; Lin C.-Y.; Otte A. F.; Ternes M.; Lutz C. P.; Jones B. A.; Heinrich A. J. Large Magnetic Anisotropy of a Single Atomic Spin Embedded in a Surface Molecular Network. Science 2007, 317, 1199. 10.1126/science.1146110. [DOI] [PubMed] [Google Scholar]
- Wiesendanger R. Spin Mapping at the Nanoscale and Atomic Scale. Rev. Mod. Phys. 2009, 81, 1495–1550. 10.1103/RevModPhys.81.1495. [DOI] [Google Scholar]
- Ternes M. Spin Excitations and Correlations in Scanning Tunneling Spectroscopy. New J. Phys. 2015, 17, 063016. 10.1088/1367-2630/17/6/063016. [DOI] [Google Scholar]
- Ternes M. Probing Magnetic Excitations and Correlations in Single and Coupled Spin Systems with Scanning Tunneling Spectroscopy. Prog. Surf. Sci. 2017, 92, 83–115. 10.1016/j.progsurf.2017.01.001. [DOI] [Google Scholar]
- Berggren P.; Fransson J. Spin Inelastic Electron Tunneling Spectroscopy on Local Magnetic Moment Embedded in Josephson Junction. EPL 2014, 108, 67009. 10.1209/0295-5075/108/67009. [DOI] [Google Scholar]
- Berggren P.; Fransson J. Theory of Spin Inelastic Tunneling Spectroscopy for Superconductor-Superconductor and Superconductor-Metal Junctions. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 205438. 10.1103/PhysRevB.91.205438. [DOI] [Google Scholar]
- Lu X.; Hipps K. W.; Wang X. D.; Mazur U. Scanning Tunneling Microscopy of Metal Phthalocyanines: d7 and d9 Cases. J. Am. Chem. Soc. 1996, 118, 7197–7202. 10.1021/ja960874e. [DOI] [Google Scholar]
- Kügel J.; Karolak M.; Krönlein A.; Senkpiel J.; Hsu P.-J.; Sangiovanni G.; Bode M. State identification and tunable Kondo effect of MnPc on Ag(001). Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 235130. 10.1103/PhysRevB.91.235130. [DOI] [Google Scholar]
- Kügel J.; Karolak M.; Senkpiel J.; Hsu P.-J.; Sangiovanni G.; Bode M. Relevance of Hybridization and Filling of 3d Orbitals for the Kondo Effect in Transition Metal Phthalocyanines. Nano Lett. 2014, 14, 3895–3902. 10.1021/nl501150k. [DOI] [PubMed] [Google Scholar]
- Jaklevic R. C.; Lambe J. Molecular Vibration Spectra by Electron Tunneling. Phys. Rev. Lett. 1966, 17, 1139–1140. 10.1103/PhysRevLett.17.1139. [DOI] [Google Scholar]
- Stipe B. C.; Rezaei M. A.; Ho W. Single-Molecule Vibrational Spectroscopy and Microscopy. Science 1998, 280, 1732. 10.1126/science.280.5370.1732. [DOI] [PubMed] [Google Scholar]
- Fernández-Rodríguez J.; Toby B.; van Veenendaal M. Mixed Configuration Ground State in Iron(II) Phthalocyanine. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 214427. 10.1103/PhysRevB.91.214427. [DOI] [Google Scholar]
- Tsukahara N.; Kawai M.; Takagi N. Impact of Reduced Symmetry on Magnetic Anisotropy of a Single Iron Phthalocyanine Molecule on a Cu Substrate. J. Chem. Phys. 2016, 144, 044701. 10.1063/1.4940138. [DOI] [PubMed] [Google Scholar]
- Tsukahara N.; Noto K.-i.; Ohara M.; Shiraki S.; Takagi N.; Takata Y.; Miyawaki J.; Taguchi M.; Chainani A.; Shin S.; Kawai M. Adsorption-Induced Switching of Magnetic Anisotropy in a Single Iron(II) Phthalocyanine Molecule on an Oxidized Cu(110) Surface. Phys. Rev. Lett. 2009, 102, 167203. 10.1103/PhysRevLett.102.167203. [DOI] [PubMed] [Google Scholar]
- Bauer J.; Pascual J. I.; Franke K. J. Microscopic Resolution of the Interplay of Kondo Screening and Superconducting Pairing: Mn-Phthalocyanine Molecules Adsorbed on Superconducting Pb(111). Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 075125. 10.1103/PhysRevB.87.075125. [DOI] [Google Scholar]
- Kügel J.; Karolak M.; Krnlein A.; Serrate D.; Bode M.; Sangiovanni G. Reversible magnetic switching of high-spin molecules on a giant Rashba surface. npj Quantum Mater. 2018, 3, 53. 10.1038/s41535-018-0126-z. [DOI] [Google Scholar]
- Ternes M.; González C.; Lutz C. P.; Hapala P.; Giessibl F. J.; Jelínek P.; Heinrich A. J. Interplay of Conductance, Force, and Structural Change in Metallic Point Contacts. Phys. Rev. Lett. 2011, 106, 016802. 10.1103/PhysRevLett.106.016802. [DOI] [PubMed] [Google Scholar]
- Gross L.; Mohn F.; Moll N.; Liljeroth P.; Meyer G. The Chemical Structure of a Molecule Resolved by Atomic Force Microscopy. Science 2009, 325, 1110–1114. 10.1126/science.1176210. [DOI] [PubMed] [Google Scholar]
- Boneschanscher M. P.; van der Lit J.; Sun Z.; Swart I.; Liljeroth P.; Vanmaekelbergh D. Quantitative Atomic Resolution Force Imaging on Epitaxial Graphene with Reactive and Nonreactive AFM Probes. ACS Nano 2012, 6, 10216–10221. 10.1021/nn3040155. [DOI] [PubMed] [Google Scholar]
- Wang D.-s.; Wu R.; Freeman A. J. First-Principles Theory of Surface Magnetocrystalline Anisotropy and the Diatomic-Pair Model. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 14932–14947. 10.1103/PhysRevB.47.14932. [DOI] [PubMed] [Google Scholar]
- Barraclough C. G.; Gregson A. K.; Mitra S. Interpretation of the Magnetic Properties of Manganese (II) Phthalocyanine. J. Chem. Phys. 1974, 60, 962–968. 10.1063/1.1681174. [DOI] [Google Scholar]
- Georges A.; Medici L. d.; Mravlje J. Strong Correlations from Hund’s Coupling. Annu. Rev. Condens. Matter Phys. 2013, 4, 137–178. 10.1146/annurev-conmatphys-020911-125045. [DOI] [Google Scholar]
- Horvat A.; Žitko R.; Mravlje J. Low-energy Physics of Three-Orbital Impurity Model with Kanamori Interaction. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 165140. 10.1103/PhysRevB.94.165140. [DOI] [Google Scholar]
- Horvat A.; Žitko R.; Mravlje J. Spin-Orbit Coupling in Three-Orbital Kanamori Impurity Model and Its Relevance for Transition-Metal Oxides. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 085122. 10.1103/PhysRevB.96.085122. [DOI] [Google Scholar]
- Wilson K. G. The Renormalization Group: Critical Phenomena and the Kondo Problem. Rev. Mod. Phys. 1975, 47, 773–840. 10.1103/RevModPhys.47.773. [DOI] [Google Scholar]
- Bulla R.; Costi T. A.; Pruschke T. Numerical Renormalization Group Method for Quantum Impurity Systems. Rev. Mod. Phys. 2008, 80, 395–450. 10.1103/RevModPhys.80.395. [DOI] [Google Scholar]
- Hofstetter W. Generalized Numerical Renormalization Group for Dynamical Quantities. Phys. Rev. Lett. 2000, 85, 1508–1511. 10.1103/PhysRevLett.85.1508. [DOI] [PubMed] [Google Scholar]
- Žitko R.; Bodensiek O.; Pruschke T. Effects of Magnetic Anisotropy on the Subgap Excitations Induced by Quantum Impurities in a Superconducting Host. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 054512. 10.1103/PhysRevB.83.054512. [DOI] [Google Scholar]
- Otte A. F.; Ternes M.; von Bergmann K.; Loth S.; Brune H.; Lutz C. P.; Hirjibehedin C. F.; Heinrich A. J. The Role of Magnetic Anisotropy in the Kondo Effect. Nat. Phys. 2008, 4, 847–850. 10.1038/nphys1072. [DOI] [Google Scholar]
- Oberg J. C.; Calvo M. R.; Delgado F.; Moro-Lagares M.; Serrate D.; Jacob D.; Fernández-Rossier J.; Hirjibehedin C. F. Control of Single-Spin Magnetic Anisotropy by Exchange Coupling. Nat. Nanotechnol. 2014, 9, 64. 10.1038/nnano.2013.264. [DOI] [PubMed] [Google Scholar]
- Röntynen J.; Ojanen T. Topological Superconductivity and High Chern Numbers in 2D Ferromagnetic Shiba Lattices. Phys. Rev. Lett. 2015, 114, 236803. 10.1103/PhysRevLett.114.236803. [DOI] [PubMed] [Google Scholar]
- Baumann S.; Paul W.; Choi T.; Lutz C. P.; Ardavan A.; Heinrich A. J. Electron Paramagnetic Resonance of Individual Atoms on a Surface. Science 2015, 350, 417–420. 10.1126/science.aac8703. [DOI] [PubMed] [Google Scholar]
- Paul W.; Yang K.; Baumann S.; Romming N.; Choi T.; Lutz C. P.; Heinrich A. J. Control of the Millisecond Spin Lifetime of an Electrically Probed Atom. Nat. Phys. 2017, 13, 403–407. 10.1038/nphys3965. [DOI] [Google Scholar]
- Natterer F. D.; Yang K.; Paul W.; Willke P.; Choi T.; Greber T.; Heinrich A. J.; Lutz C. P. Reading and Writing Single-Atom Magnets. Nature 2017, 543, 226–228. 10.1038/nature21371. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


