Significance
The cytoskeleton is a remarkable example of an active biomaterial and is at the heart of critically important problems in biology and medicine related to animal cells’ mechanical sensing and function. A satisfying physical understanding of the actomyosin cortex’s complex biophysics and mechanical properties has, however, proven elusive. We measure cytoskeletal motion, forces, and rheology using substrates containing arrays of flexible microscopic posts with high precision and statistical power. Surprisingly, the cytoskeletal networks display highly intermittent fluctuations whose energy content is dominated by rare large events, similar to what is seen in earthquakes or physical systems with avalanches. Our findings suggest that future cytoskeletal models must contain elements that self-organize onto a mechanically marginal state prone to avalanches.
Keywords: cytoskeleton, cell mechanics, cortex, dynamics, active matter
Abstract
The ability of animal cells to crawl, change their shape, and respond to applied force is due to their cytoskeleton: A dynamic, cross-linked network of actin protein filaments and myosin motors. How these building blocks assemble to give rise to cells’ mechanics and behavior remains poorly understood. Using active micropost array detectors containing magnetic actuators, we have characterized the mechanics and fluctuations of cells’ actomyosin cortex and stress fiber network in detail. Here, we find that both structures display remarkably consistent power law viscoelastic behavior along with highly intermittent fluctuations with fat-tailed distributions of amplitudes. Notably, this motion in the cortex is dominated by occasional large, step-like displacement events, with a spatial extent of several micrometers. Overall, our findings for the cortex appear contrary to the predictions of a recent active gel model, while suggesting that different actomyosin contractile units act in a highly collective and cooperative manner. We hypothesize that cells’ actomyosin components robustly self-organize into marginally stable, plastic networks that give cells’ their unique biomechanical properties.
The cytoskeleton has long been recognized as a remarkable active material (1–3) with unusual viscoelastic behavior (4–6), and the seeming ability to change rapidly from fluid to solid and to adjust its stiffness over a wide range. Early attempts to explain these phenomena drew on analogies with other systems, such as the sol−gel transition (7, 8), tensegrity architecture (9, 10), and the soft glassy rheology model of materials such as foams and emulsions (11, 12), but none of these approaches were able to capture the essential phenomena completely. In the last few years, a new approach has sought to derive the cytoskeleton’s mechanics from the physics of polymer networks (13) and the activity of embedded molecular motors. In this view, the cytoskeleton is an active gel (14, 15) of filamentary biopolymers and protein cross-links, stiffened by an internal “prestress” generated by myosin motors (9, 10), and fluctuating due to myosin minifilaments’ uncorrelated, random binding and unbinding (16–19). Despite its successes, however, the active gel model does not correctly predict the observed viscoelasticity of cells, which displays a power law dependence on frequency (4, 5, 20–22), and does not naturally account for the observed highly heterogeneous nature of intracellular fluctuations.
Here we report extensive micromechanical measurements of NIH 3T3 fibroblasts using active micropost array detectors (AMPADs). These microfabricated supports provide a closely spaced array of deformable microposts directly coupled to the cells’ actomyosin machinery (23–28). The posts’ motion can be tracked at high speed with nanometer precision, and they also include embedded magnetic nanowires that can be used to measure the cytoskeleton’s mechanical response to applied force. We find that most posts under the cell are adhered to the basal actomyosin cortex, while a subset of peripheral posts are adhered to contractile actomyosin stress fibers; the 2 can be readily distinguished by mean traction force. The motion of cortical posts resembles weakly polarized, 2D random walks with intermittent large steps, while stress fiber posts display motion that is both highly and persistently anisotropic. Both populations of posts report power law viscoelasticity resembling earlier studies (4, 5, 20, 21, 29), and superdiffusive position fluctuations that superficially resemble those in studies of cytoplasmic tracers (16, 19, 20, 30–33). Closer examination of the data, however, reveals that the mean-squared displacements (MSDs) of both types of posts display broadly distributed amplitudes and superdiffusive behavior that is not naturally explained by the active gel model. We find that the amplitude distribution is fat-tailed, due to intermittent, large step-like displacements resembling avalanches and earthquakes in physical systems (34). Our regular array of detectors also allows us to determine the spatial extent and symmetry of the largest avalanche-like rearrangements in the cortex (35, 36), which are both spatially and temporally complex, resembling those in plastic solids (37, 38). A recent simulation study of soft glassy materials (38) suggests a physical interpretation of our cell data wherein myosin contractile units (CUs) (27) self-organize into marginally stable tensile and plastic networks, whose physics gives rise to cells’ avalanches, superdiffusive motion and power law rheology (35, 38, 39).
Results
AMPAD Arrays Probe Cellular Motion at the Nanoscale.
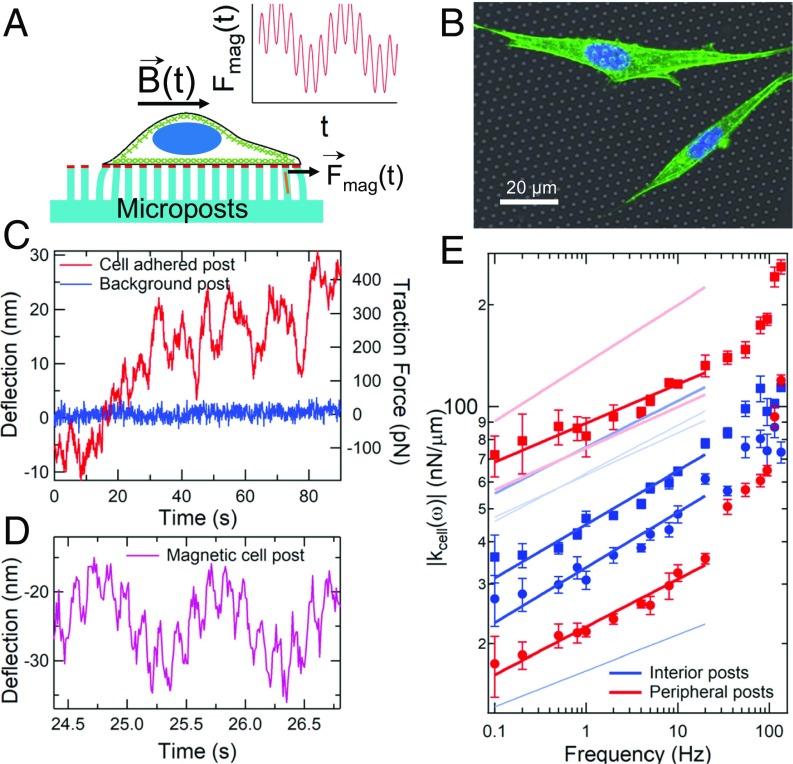
Micropost arrays are an increasingly important approach for quantifying cellular mechanics (23–28). A schematic of a micropost array with a cell attached is shown in Fig. 1A. The arrays contain flexible poly(dimethylsiloxane) (PDMS) microposts that deflect in response to an adherent cell’s fluctuating forces and/or strains. The microposts’ tips were coated with fibronectin to enable cells to form integrin-based focal adhesion linkages to the posts (23, 25, 28), which, in turn, mechanically coupled the microposts directly to the cells’ actomyosin network. Magnetic nickel nanowires embedded in ∼1% of the microposts enabled actuation of those posts with an external magnetic field B(t) (25, 40) to probe the cells’ rheology via forces Fmag(t) applied by the “magnetic” posts to the cell. Fig. 1B shows a confocal image of NIH 3T3 cells attached to a micropost array composed of 1.8-µm-diameter posts with 4-µm spacing in a hexagonal pattern. Brightfield movies of the microposts were recorded at up to 100 frames per s, and a centroid particle-tracking algorithm (41) was used to track the positions of the microposts with spatial resolution of <2 nm. As shown in Fig. 1C, microposts coupled to a cell showed dynamic fluctuations significantly larger than the noise observed on “background” posts that were not engaged with a cell. These fluctuations were observable over a wide range of timescales, from 100 ms to 1,800 s (the duration of data collection for each cell) (SI Appendix, Fig. S1). While many research groups use fluorescence microscopy to facilitate image analysis of micropost motion against the background of the cell, we favor brightfield imaging for its much higher signal to noise and resulting spatial and temporal resolution. While motion of refractile objects within the cell can, in principle, contribute to the observed motion of nearby posts, control measurements reveal that contributions from such effects are detectable but contribute only ∼3 nm of RMS deflection over 60-s timescales (SI Appendix).
Fig. 1.
Microposts can be used to measure cytoskeletal dynamics and viscoelasticity. (A) Cell on a flexible micropost array; micropost tips are coupled to the actomyosin cytoskeleton (green) via fibronectin (red). Posts with magnetic nanowires (orange) exert a double-sinusoidal force Fmag(t). (B) Composite white-light image of post array with fluorescence of 3T3 fibroblasts immunostained for actin (green) and nuclei (blue). Actin stress fibers are concentrated near the cells’ peripheries. (C) Typical displacements of a cell-adhered (red) and a nonadhered (blue) post. (D) Deflection of a cortex-adhered magnetic post, driven at 1 Hz and 7 Hz. (E) The computed local cellular rheology is a weak power law function of frequency (symbols); peripheral posts are in red, interior posts are in blue. As shown in Fig. 2, peripheral posts are associated with stress fibers, and interior posts are associated with the cortex. Error bars were determined as described in SI Appendix, Methods. Solid lines are fits of the form |kcell(ω)| = Aωβ with βinterior = 0.13 ± 0.02 (n = 6) and βperipheral = 0.12 ± 0.02 (n = 4) (±SE for each case). Fits for additional magnetic microposts (data points omitted for clarity) are shown as pale lines. See SI Appendix, Fig. S2 for full dataset.
Spatially Resolved Measurements of Cellular Power Law Rheology.
Characterizing an active matter system like the cytoskeleton requires that one probe both the fluctuations and the mechanical response to applied stress, or rheology (1). We drove the magnetic microposts with sinusoidal magnetic fields from a dual magnetic tweezer system (42), and used digital lock-in techniques (43) to measure the amplitude and phase of the posts’ resulting time-dependent motion to <0.2 nm in amplitude. These measurements showed significant amplitude fluctuations over long timescales (SI Appendix, Fig. S2A), an effect previously attributed to time dependence in the cell’s coupling to the probe (44). To remove such confounding effects, we applied 2 sinusoidal signals simultaneously, one at a frequency that was scanned over a wide range, and another which served as a constant frequency reference (Fig. 1D). Measurements of the ratio of the 2 signals’ amplitudes (44) gave significant reduction in uncertainty for the frequency dependence of the microposts’ mechanical response (SI Appendix, Fig. S2B).
Since both the microposts and the attached cell contribute to the response to magnetic actuation, the system effectively behaves as 2 viscoelastic units connected in parallel (SI Appendix, Fig. S2C), one of which contains the cellular contribution and other that of the post. To extract the cellular stiffness, we measured the viscoelastic response of magnetic microposts while coupled to cells, and then measured each magnetic micropost’s stiffness separately after removing the cells from the AMPAD arrays via treatment with trypsin/ethylenediaminetetraacetic acid (SI Appendix, Fig. S2D). The cellular stiffness was computed from the difference between the 2 measurements. Control measurements showed no measurable difference in background post stiffness before and after trypsinization (SI Appendix, Fig. S2E).
The resulting measurements of the frequency-dependent cellular stiffness kcell(ω) are shown in Fig. 1E. We found a weak power law response, |kcell(ω)| = Aωβ, extending over at least the frequency range 0.1 Hz to 20 Hz. The magnitude of the cellular stiffness, A, varied by over an order of magnitude, while the value of the power law exponent β was found to be independent of the stiffness magnitude. Notably, the exponent of the observed power laws for posts at the cell periphery and in the cell interior were indistinguishable, with βperipheral = 0.12 ± 0.02 and βinterior = 0.13 ± 0.02. This near-elastic response is consistent with previous measurements of cells (4, 19–21, 31, 45). As we discuss below, the peripheral posts were largely associated with actin stress fibers, while interior posts were coupled to the actin cortex. We also observed some additional stiffness (4, 20, 31, 46–49) at the highest frequencies probed; such effects have been hypothesized by several authors to be due to actin filament fluctuations (46–48).
Cellular Fluctuations Are Superdiffusive and Associated with Different Cytoskeletal Structures.
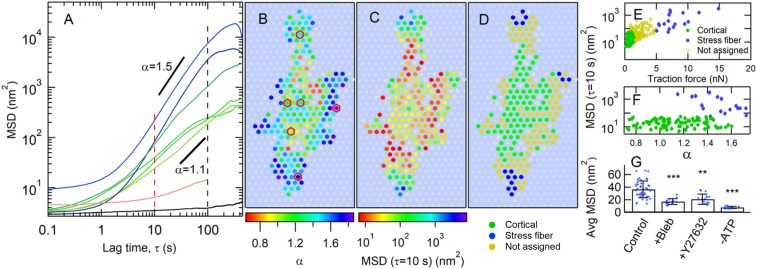
We characterized the motion of the microposts in response to internally generated cellular forces via the posts’ MSDs <Δr2(τ)> = <(r(t+τ) − r(t))2>, where τ is the lag time. Fig. 2A shows a representative set of MSD traces from posts whose locations underneath a cell are indicated in Fig. 2B. For a range of lag times, roughly 1 s < τ < 20 s to 100 s, the MSD curves rise above the short-time noise floor that arises from measurement error, and display power law behavior, <Δr2(τ)> τα, with the exponent α typically being greater than 1. There is a large dispersion of both power law exponents and MSD amplitudes, which does not appear to be due to statistical undersampling, as each MSD is computed from 18,000 measurements. Such superdiffusive behavior in a mostly elastic material indicates the presence of internal nonthermal driving sources (16, 19). The values of the MSD exponent α correlate with micropost position within the cell, as shown in Fig. 2B, with the largest MSD exponents typically located at the cell periphery. The corresponding map of the MSD amplitude variations is shown in Fig. 2C, where, again, posts with larger MSD amplitude were more likely to be peripherally located. These trends were replicated over all untreated cells studied; additional examples are shown in SI Appendix, Fig. S3. Due to the length of the observation period (30 min), it was necessary to account for the effects of cell motility. Only microposts that were engaged mechanically with the cells for the full observation period are shown in the color maps in Fig. 2 and SI Appendix, Fig. S3, and were included in the subsequent analysis. The specific signatures used to identify post engagement with cells are described in SI Appendix, Methods and are illustrated in SI Appendix, Fig. S4. Finally, we estimated the extent to which refraction by different moving cell structures [lipid granules, organelles, actin waves (50–52)] could contribute to the apparent post motions (Fig. 2A, red curve and SI Appendix). While detectably above the noise floor, this was found to be negligibly small so as not to affect our conclusions.
Fig. 2.
Cell fluctuations show spatial variation of amplitude and superdiffusive exponent. (A) MSD vs. lag time τ for individual microposts typically show superdiffusive behavior (∼τα, with α > 1). Red and black dashed lines show τ ranges discussed below. The black trace is the MSD for a post not coupled to a cell, and the red trace shows the background due to fluctuations in cellular optical density (SI Appendix). (B and C) Heat maps of (B), MSD exponent α (for 5 s ≤ τ ≤ 10 s), and (C), MSD amplitude at τ = 10 s for cell-adhered posts. Gray hexagons show posts not engaged with the cell for the full measurement interval. Gray circles indicate background posts. Posts with MSD traces in A are outlined in red in B. (D) Classification of microposts according to traction force: maximum traction force of <2 nN (“cortical” posts with low traction force) in green; average traction force of >5 nN (“stress fiber” posts with high traction force) in blue; remainder of posts in yellow. (E) Scatter plot of MSD magnitude at τ = 10 s vs. average traction force. (F) MSD magnitude at τ = 10 s vs. MSD exponent α for cortical and stress fiber posts (omitting middle case open circles in E). SEs for points in E and F are smaller than the symbol sizes. (G) Myosin inhibition reduces displacement fluctuations in cortical posts. Error bars in G show ±SD. Average MSD magnitude at τ = 10 s for control cells (25 cells), and for cells following treatment with blebbistatin (10 cells), Y27632 (11 cells), or ATP depletion (4 cells); significance via unpaired t test. **P < 0.01; ***P < 0.001.
Given the range of actomyosin structures present in a cell, to analyze our cellular fluctuation data, it is important to identify which cytoskeletal components individual microposts were probing. We found that average traction force magnitude provided a reliable, independent parameter with which to bifurcate our micropost dataset into 2 groups, those coupled to stress fibers and those coupled to the cortex, and that the fluctuation metrics (MSD amplitude and exponent) showed strong correlation with this bifurcation. This procedure is illustrated in Fig. 2 D–F. We segmented the microposts for each cell into a subpopulation with average traction forces larger than 5 nN and a subpopulation with maximum traction force less than 2 nN. The high-traction force posts were concentrated at the cell edges, and the low-traction force posts were more centrally located (Fig. 2D and SI Appendix, Figs. S3 E and F and S5), as is typically seen for contractile cells on such substrates (23, 25, 26, 28). The correlations of the fluctuation metrics with the traction force-based discriminator are illustrated in Fig. 2 E and F. We also note that “caging” effects on the MSDs due to the elastic restoring force of the posts appear to be small on the timescales we consider, at least for the low-traction force posts (SI Appendix).
Chemical interventions confirmed the biophysically distinct character of the 2 micropost subpopulations, and also confirmed that the fluctuations we observed were actomyosin-driven. Following adenosine 5′-triphosphate (ATP) depletion or treatment with the myosin inhibitor blebbistatin or the Rho-associated kinase inhibitor Y27632, microposts in the high-traction force category were no longer found (SI Appendix, Fig. S6), consistent with the known ablation of stress fibers under these conditions (21, 53). The amplitudes of the low-traction force (cortical) posts’ MSDs were reduced by all 3 treatments (Fig. 2G and SI Appendix, Fig. S6), although the fluctuations were not fully ablated. Confocal microscopy of the distribution of subcellular actin structures further supported the identification of the stress fiber-associated and cortically associated micropost groups, as the cells’ peripheries typically showed densely stained actin bundles (Fig. 1B), consistent with the presence of actin stress fibers, while the central regions showed more diffuse actin staining, characteristic of the actin cortex. The peripheral high-density actin bundles were not visible following each of the chemical interventions (SI Appendix, Fig. S6). Overall, these observations confirm that our experiments probed active cytoskeletal dynamics, and that we can separate the posts into biophysically distinct stress fiber-associated and cortically associated cytoskeletal categories (discarding posts having an intermediate traction force).
Micropost MSDs Are Highly Variable.
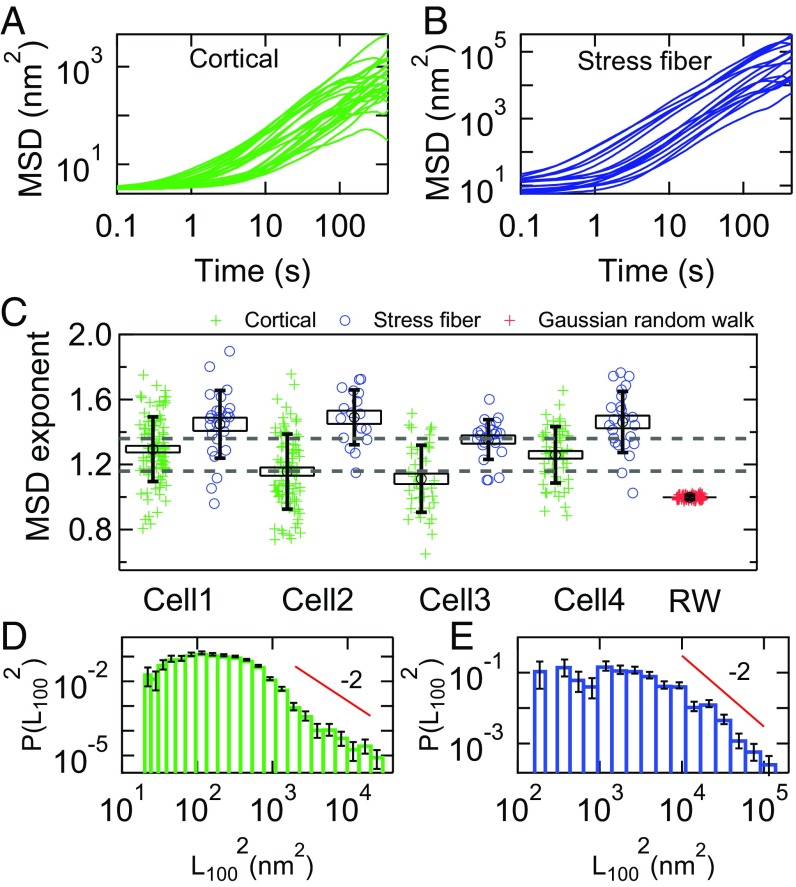
Typical MSDs for both cortical and stress fiber adhered microposts are displayed in Fig. 3 A and B. As seen by other authors for cytoplasmic tracers (19), the MSDs of different posts show striking variations in amplitude and time dependence. Power law fits reveal that the MSD exponents for both cortical- and stress fiber-associated posts, αc and αsf, showed significant dispersion both within a given cell and from cell to cell. Fig. 3C shows the distributions for αc and αsf for 4 representative cells. (The full dataset and accompanying statistical analysis are summarized in SI Appendix, Statistics and Table S1.) The exponents for the stress fibers are systematically higher than those for the cortex. The observed dispersion in αc and αsf is not an experimental artifact arising simply from undersampling. To illustrate this, we show, in Fig. 3C, the dispersion of exponents around α = 1 for a simulated Gaussian random walk that has the same number (18,000) of samples as the experimental trajectories, and which shows a very tight convergence compared with the data. While a simple random walk is not the correct physical model for the cortex, this comparison highlights the anomalous statistics and resulting poor convergence of the post displacement data.
Fig. 3.
(A and B) Spread of MSDs for (A) cortical and (B) stress fiber-associated microposts for a single cell (cell 2 in C). Traces are only shown for one-third of the cortical posts for cell 2 in A for clarity. (C) Dispersion in MSD exponents α for 4 different cells, showing variation both within and between cells. Green crosses (blue circles) show MSD exponents for cortical (stress fiber) microposts. The dashed gray lines show the range αc = 1.26 ± 0.09 (mean ± SD) expected if α = 1 + 2β, given our measured values and cell-to-cell variation of β. Red crosses show data for the dispersion in α for a simulated Gaussian random walk (RW). Boxes show SEs, and vertical bars show SDs. See SI Appendix, Table S1 for information on full dataset, and see SI Appendix, Statistics for details on significance of results quoted in the text. (D and E) Histograms of MSD magnitude at τ = 100 s (black dashed line in Fig. 2A) in (D) cortical posts and (E) stress fiber posts. Solid lines are power laws with exponent −3. Error bars were estimated as for each bin in D and E.
In the active gel model (16–19), such active fluctuations are the result of myosin minifilaments binding, sliding, and unbinding randomly in space, time, and orientation. Making simple assumptions for the myosin activity, the resulting MSD exponent is predicted to have a value equal to α = 1 + 2β, even when the motion is the result of a small number of actomyosin binding events. Based on our measured values of β, one would therefore expect αc = 1.26 ± 0.09 (mean ± SD). This range for αc is shown as dashed lines in Fig. 3C and corresponds to the observed cell-to-cell variations in β. The cell-averaged value of the cortical exponents = 1.17 ± 0.02 (SE, Ncells = 14) is consistent with the α = 1 + 2β prediction to within experimental uncertainty. In contrast, the stress fiber exponent values for individual cells differ from the expected range αsf = 1.24 ± 0.09 (mean ± SD), as does the value averaged across all cells, = 1.47 ± 0.02 (SE, Ncells = 13, P < 0.001). Notably, the SD of the cortical MSD exponents, δαc = 0.2, is significantly larger than expected given the small SD of β values (2δβ = 0.09). This appears to be incompatible with the predictions of the active gel model with a simple picture of temporally and spatially uncorrelated actomyosin filaments deforming a network with power law viscoelasticity.
In addition to the exponent, we can analyze the distribution of MSD amplitudes at τ = 100 s, L1002 = MSD(τ = 100 s), as shown in Fig. 3 D and E. For both the cortical and stress fiber posts, the distributions of L1002 are highly non-Gaussian with a “fat tail” at large amplitudes, with a form that is comparable to an eye guide having a power law form with an exponent of −2. Power law tails can lead to poor convergence to the mean when averaging data together; formally, the mean <x> of power law distributed numbers diverges (54) in the case of a power law tail where P(x) ∼ x−a, for a ≤ 2. The fat tails that we observe in Fig. 3 D and E are, notably, comparable to that threshold, suggesting that the dispersion of MSD amplitudes may be a consequence of non-Gaussian statistics (54) in the microposts’ fluctuations.
Microposts Display Rare Large Displacements and Non-Gaussian Random Motion.
The extreme variability of different cellular tracer MSDs is often attributed to cell “heterogeneity.” That is, the fat tails of large MSD amplitudes in Fig. 3 D and E are typically supposed to be due to a population of microposts that sample parts of the cytoskeleton that are correspondingly softer or have higher amplitudes of myosin activity. In what follows, we analyze the fluctuations of single post trajectories, and find clear evidence in the cortex, at least, that anomalous statistics, and not heterogeneity, are responsible for the large dispersion observed in micropost MSDs.
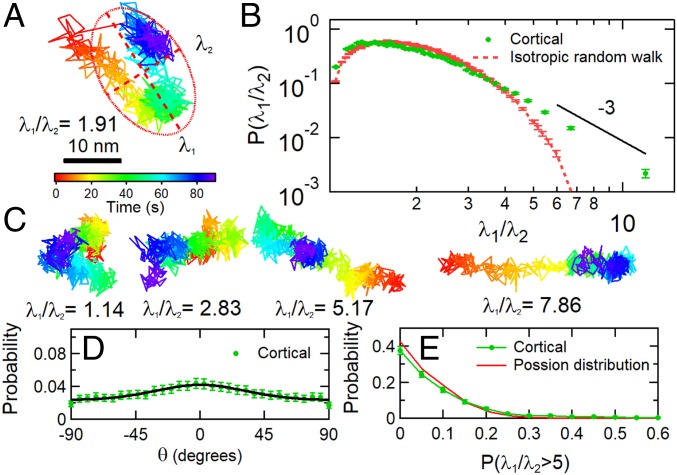
First, we compute a dimensionless anisotropy index of the 2D trajectories of each post via a principal component analysis (as a dimensionless measure, this is, in principle, insensitive to the heterogeneous amplitudes of different MSDs). Each post’s 1,800-s trajectory was broken into 20 segments of 90-s duration, and the 2D moment of inertia tensor I of the trajectory (55) for each segment was computed. As illustrated in Fig. 4A, the ellipse defined by the 2 eigenvalues λ1 and λ2 of I yields an anisotropy index λ1/λ2 ≥ 1 for a post’s motion during that interval. Fig. 4B shows the probability distribution for the anisotropy index of the cortical micropost trajectories. The distribution shows that most trajectories are essentially isotropic (compared with a simulated isotropic random walk), but that there is a highly anisotropic subset forming a power law tail at large λ1/λ2, with an exponent of roughly −3. To understand the nature of the highly anisotropic trajectories in Fig. 4B, we display typical post trajectories with different anisotropies in Fig. 4C. These typically show random and isotropic motion, with amplitude of a few nanometers (corresponding to λ2), superimposed on a large unidirectional displacement (corresponding to λ1) that spans several tens of seconds of time. The major axis of the trajectory (and the large displacement) is only weakly aligned with the mean traction direction, as shown in Fig. 4D, suggesting that it is not due, for example, to the abrupt release of traction from a micropost. To assess whether these large displacements are concentrated among a subset of posts, or are clustered in time, we show, in Fig. 4E, the probability distribution for the fraction of time when a single post’s motion displays highly anisotropic motion (λ1/λ2 > 5); overall, 9.5% of the 90-s-long micropost trajectories satisfied the criterion. The experimental distribution in Fig. 4E closely resembles a Poisson distribution with an expectation value of 0.095, indicating that the large displacement events occur randomly over time and among different cortex-associated posts. The corresponding analysis of stress fiber-associated posts (SI Appendix, Fig. S7), in contrast, shows that their motion is highly anisotropic, persistent in direction and aligned with the same posts’ mean traction direction.
Fig. 4.
Cortical cell fluctuations showed anisotropy. (A) An example of a displacement trajectory of a micropost over a 90-s interval. The red ellipse with semimajor axis λ1 and semiminor axis λ2 illustrates the computation of the anisotropy index λ1/λ2 for this trajectory via principal component analysis (λ1/λ2 = 1.91 in this case.). (B) Probability distribution of the anisotropy index λ1/λ2. Eyeguide highlights a power law tail for highly anisotropic trajectories. (C) Examples of posts with a range of λ1/λ2. (D) Probability distribution of the angle between the major axis of the fitted ellipse’s long axis and the direction of the micropost’s average traction force F. The solid line is a fit with full width 2σ = 107°. See SI Appendix, Methods for details. (E) Probability distribution of the fraction of a post’s fluctuations with λ1/λ2 > 5, measured over 1,800 s in 90-s intervals. Error bars were estimated as for each bin in the probability distributions.
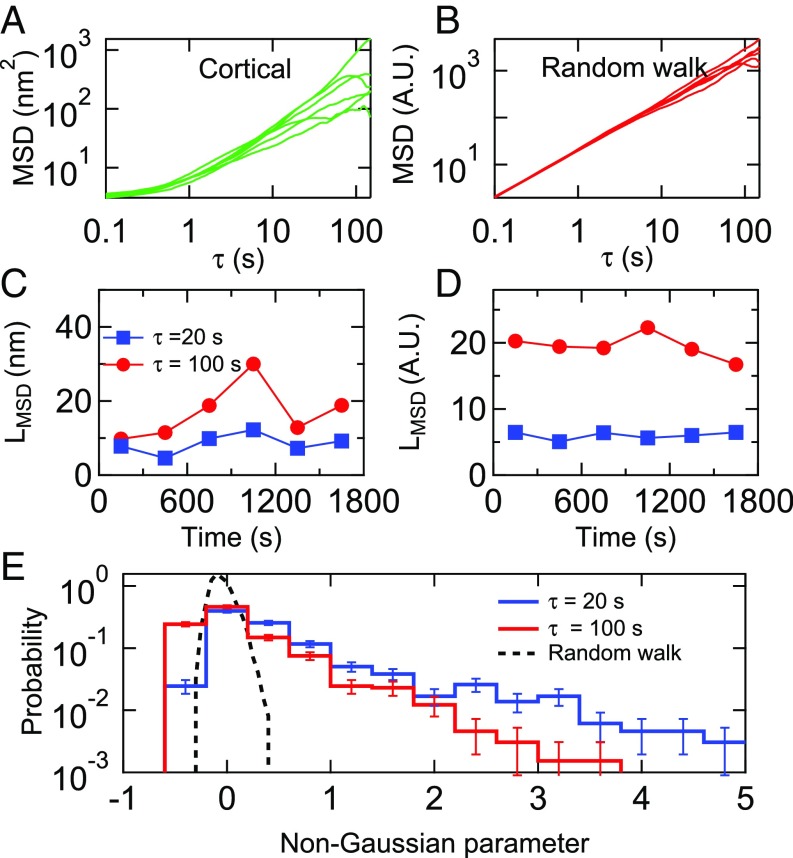
We next examined the time dependence, if any, of the amplitudes of the fluctuations of individual cortical microposts (Fig. 5). Specifically, to understand the statistical fluctuations in a single trajectory, we divided each 1,800-s trajectory into 6 trajectories of 300 s each, and computed the MSD for each (Fig. 5A). Notably, the resulting MSDs show a significant spread in amplitude and power law exponent, even when drawn from a single micropost trajectory, compared with the MSD of a simulated Gaussian random walk with the same number of steps (Fig. 5B). The MSD amplitudes were strongly time-dependent, an effect which is more pronounced at τ = 100 s than at τ = 20 s (Fig. 5C), compared with the Gaussian random walk (Fig. 5D). A standard way of characterizing such intermittent or “bursty” data is via a non-Gaussian parameter, α2, computed by comparing the second and fourth moments of a probability distribution (56) (SI Appendix). The distribution of non-Gaussian parameters for each cortical micropost for Ncells = 14 untreated 3T3 cells is shown in Fig. 5E, and shows a fat tail compared with that expected for a Gaussian process, presumably due to the contribution of the aforementioned large displacements. Corresponding data for the stress fiber microposts, which show qualitatively similar behavior, are shown in SI Appendix, Fig. S8. We note that, as with the dimensionless anisotropy index, the non-Gaussian parameter would not be affected by static post-to-post variations in fluctuation amplitude.
Fig. 5.
Spread of MSDs calculated for (A) a single cortical post over each of the 6 300-s intervals in the 1,800-s measurement window. (B) Simulation showing spread in 6 MSDs for a Gaussian random walk over the same time interval. (C and D) LMSD = [MSD(τ)]1/2 for τ = 20 s and 100 s for the data shown in A and B. (E) Distribution of the non-Gaussian parameter, α2, computed over the full 1,800-s interval for cortical posts for Ncells = 14 cells. The distribution at τ = 20 s (black dashed line) for an 18,000-step Gaussian random walk is shown for comparison. Error bars were estimated as for each bin in the probability distributions.
In summary, detailed analysis of single post trajectories reveals the signature of large displacement events, occurring randomly in time and space. The largest displacements, according to the anisotropy analysis, as implied in Fig. 4B, have a power law distribution of amplitudes, λ1, with a form roughly varying as P(λ1) ≈ λ1−3, (the marginal case leading to a nonconvergent second moment). This distribution corresponds mathematically to the power law tail seen in the MSD amplitudes, and leads to both the observed intermittency and large dispersion of MSD amplitudes and exponents. Combined with the superdiffusive character of the MSD time dependence, these findings are suggestive of a highly non-Gaussian process consisting of random large jumps in time having a fat-tailed distribution of amplitudes (54, 55, 57); here perhaps superimposed upon a background of normal Gaussian fluctuations.
The Cortex Displays Avalanche-like Displacements or “Cytoquakes.”
In physical systems, intermittent and collective motions of particles, having a power law distribution of sizes, are generically called avalanches, like their namesakes in snow or sand. In this context, “size” might refer to different measures of the event, including its amplitude, its spatial extent, or the energy released, as these measures are typically found to be correlated. Were the cortical cytoskeleton prone to such avalanche-like instabilities, e.g., due to intermittent reconfigurations of tensile stress within the network, it would naturally explain the origin of the large displacement events we observe. In this picture, the energy released by the avalanches would scale as the work done on the posts and on the cortex [i.e., ΔE ≈ (kcell + kpost)(L100)2]. We have already seen that the probability distribution P((L100)2) has a fat tail approximating a power law with an exponent of −2. In earthquakes (one example of avalanche-like dynamics), energy release follows a similar power law distribution, termed the Gutenberg−Richter law (58, 59). Indeed, the largest post displacement events we observe are comparable in frequency and amplitude to those seen in a study of the temporal dynamics of individual membrane-bound tracer beads on human airway smooth muscle cells, by Alencar et al. (34), who coined the term “cytoquakes” to describe them. Alencar et al. also showed that the cytoquakes have power law temporal correlations (Omori’s law) resembling those in earthquakes.
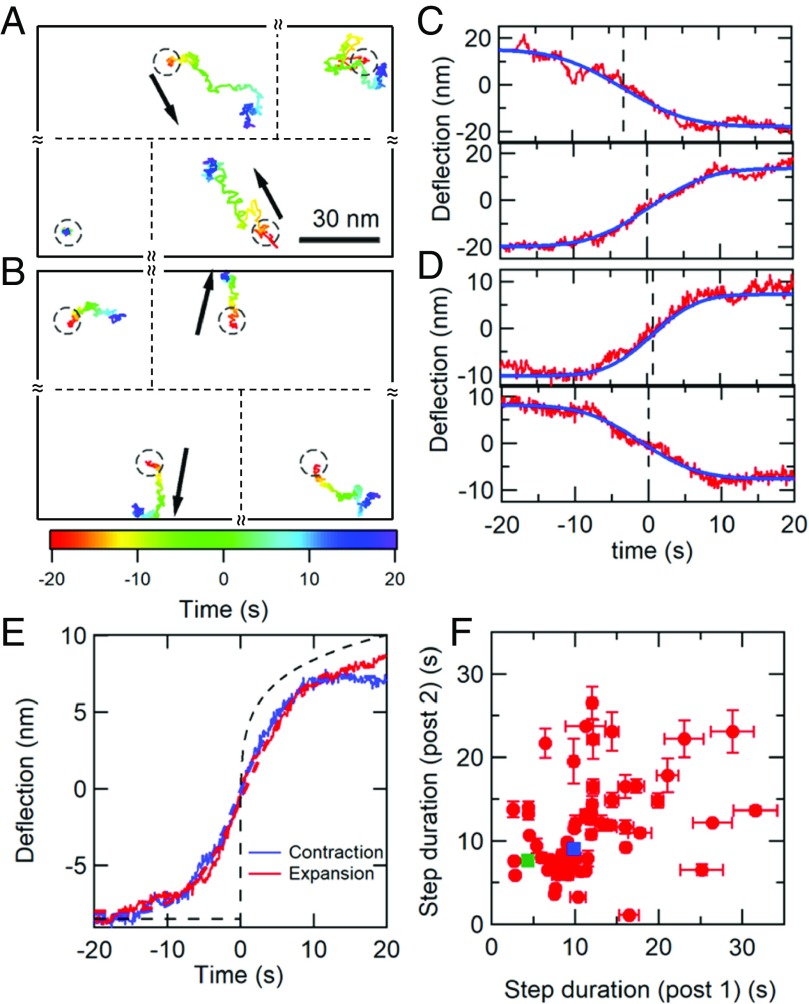
To explore this picture further, we must examine whether the displacements we observe correspond to spatially extended reconfigurations (which we will henceforth call avalanches), and analyze their temporal behavior in greater detail. The parallel and spatially organized high-resolution measurements of cytoskeletal fluctuations enabled by the AMPAD arrays are ideally suited to such analysis. We searched for and isolated the largest spatially extended avalanche events in our dataset by cross-correlating the motions of pairs of nearest-neighbor posts (separated by 4 µm). Specifically, we screened the cortical post deflection dataset, divided into 90-s intervals, for occurrences of large deflections that were antiparallel to each other and aligned with the 2 posts’ line of centers, and which were nearly coincident in time (details in SI Appendix, Methods). As a statistical control, we screened for similar events on cortical posts that were not nearest neighbors. Over our set of 14 cells with 1,800-s data ensembles and 25 additional cells with single 90-s data ensembles, we observed 4,848 nearest-neighbor cortical micropost pairs. Within this dataset, we found 68 avalanche events that were large enough to span across 2 posts, while, on a matched control ensemble, we found only 2 (P < 10−5). (Unfortunately, the much smaller set of stress fiber-associated microposts did not contain enough near-neighbor pairs to give sufficient statistical power for a similar analysis.) Two typical avalanche events are shown in Fig. 6 A and B. We did not observe any temporal correlation between pairs of events, such as expected if contractile events were followed by expanding events on the same pair of posts. Significantly, cells with myosin inhibited by blebbistatin or Y27632 yielded no avalanches (P < 10−5). Similar coincidence detection schemes that looked for correlated (same direction) post motion, or coincident motion transverse to the line of centers, found no events. This statistical analysis provides an independent verification of large-scale reconfiguration of the cortex, in addition to the power law distribution of single-post displacements discussed earlier. The motion of the post trajectories in a single avalanche is quite irregular (as opposed to being linear and directed), consistent with their being driven by multiple microscopic rearrangements of the cytoskeleton that are distributed over space and time (rather than a single rearrangement). The observation that avalanches only display anticorrelated motion parallel to the line of centers is consistent with our expectations that the displacement field should nonetheless display roughly quadrupolar symmetry (16, 60) at the longest length scales (as expected for a 2D viscoelastic sheet), and also rules out several possible confounding explanations, like cortical deadhesion, or out-of-plane motion (e.g., endocytosis or microvillus formation). See SI Appendix, Fig. S9 for details. We also note that waves of actin polymerization (46–48) would be expected to give correlated, parallel transverse displacements of pairs of posts, which we do not observe, suggesting that they are not responsible for our step-like displacements.
Fig. 6.
Antiparallel micropost motions reveal cortical avalanche dynamics. (A and B) Examples of strongly anticorrelated steps in the 2D trajectories of nearest-neighbor micropost pairs. The black arrows indicate each post’s overall direction of motion. The trajectories are color-coded to indicate time. Circles indicate the posts’ resting positions. The relative positions of the posts in the pair and the 2 adjacent posts are shown, but their separations are not to scale. (C and D) Displacements for the posts in the pairs in A and B projected onto the line of centers; experiment (red curves) and error function fit (blue curve). The time t = 0 was set at the peak of the first derivative for the bottom trace. (E) Step profiles averaged over 12 contracting (blue) and 19 expanding (red) pairs. Dashed red and blue lines show fits to error functions to extract average step durations tcontract = 9.5 ± 0.2 s and texpand = 8.8 ± 0.1 s, and average step heights hcontract = 8.2 ± 0.1 nm and hexpand = 8.8 ± 0.2 nm. The ratio of step sizes was restricted to the range 0.7 < h2/h1 < 1.4, with both h1 and h2 > 6 nm. Dashed black line shows calculated viscoelastic creep response to a step stress at t = 0, with deflection ∝ tβ, based on measured cell rheology (Fig. 1E). (F) Scatter plot of step durations for pairs of posts, pooling the contracting and expanding pairs. Determination of error bars on individual points is described in SI Appendix. The blue and green squares correspond to the data in C and D, respectively. The lack of close correlation (Pearson coefficient = 0.4) suggests that avalanches proceed through multiple, nonsynchronous events.
To parameterize the avalanches, we fit each post’s deflection along the line of centers with an error function (Fig. 6 C and D) to extract the amplitude, mean occurrence time, and duration of the avalanche on each post. Surprisingly, the average amplitude and functional form of expanding and contracting events are indistinguishable (Fig. 6E), and both types were seen with roughly equal probabilities. This is unexpected, as the activity of myosin filaments is strictly contractile; experiments with in vitro actomyosin gels (17) show contractile events in the network due to myosin binding and sliding activity on actin filaments, followed by abrupt network expansion events when the myosin unbinds the actin. Notably, the shape of these events is qualitatively different from that expected for the response to a single step in stress, which can be computed from the measured power law rheology (dashed line in Fig. 6E) (61, 62), and is inconsistent with a single microscopic rearrangement event. Moreover, the deflection durations for pairs of neighboring posts were only weakly correlated (Fig. 6F), and the deflection occurrence times were noncoincident in time by 1 s to 2 s compared with a 0.1-s uncertainty. Taken together, all these observations strongly suggest that the avalanches display spatiotemporally complex evolution, e.g., a series of rearrangement events distributed over space and time, rather than motion that is abrupt in time, with a regular quadrupolar form occurring coincidentally in time everywhere, as seen in gels (17).
Discussion
In this paper, we have shown that AMPADs are a versatile tool to understand the dynamics and rheology of the cytoskeleton. This system combines key features comparable to other leading techniques, with a regular array of probes that can map the mechanical response, as is possible with atomic force microscopy (22, 63–65), and measure cellular fluctuations and local rheology simultaneously with high temporal resolution and ligand specificity, as with magnetic twisting cytometry (4, 44, 45). In this study, the use of AMPADs has allowed us to make a detailed examination of the mechanics of the cell cortex and stress fibers. We find that the cortex displays both power law rheology and intermittent fat-tailed fluctuations that are correlated into large avalanche-like displacements spanning at least 4 µm in spatial extent. In isolation, it would be difficult to imagine how a system consisting of simple building blocks could display all these phenomena. However, recent studies describe and explain the origin of rearrangements having a power law amplitude distribution (39), superdiffusive motion and power law rheology (38), and avalanches (35) in gels, emulsions, and sandpiles, respectively, under deformation. The key features these models have in common is that these systems self-organize into a state where many degrees of freedom are near a point of instability, called a marginal solid, and are capable of plastic rearrangements when deformed. The resulting behavior is similar to the common notion of avalanches, in which motion along one unstable degree of freedom can trigger (destabilize) others in a complex chain reaction to form an avalanche (35). In these solid materials, power law rheology is due to stress relaxation due to plastic rearrangements driven by superdiffusive fluctuations (38).
Our cell results suggest a potentially fruitful way of thinking about the architecture of cytoskeletal networks, as our observations could be naturally explained if the cytoskeleton’s constituents self-organize into a mechanically marginal state, akin to jammed (35, 37, 39) and soft glassy materials (11, 12, 37–39). In the cortex, single myosin minifilaments have been found to self-assemble with other proteins into CUs during the cell spreading process that have complex, nonlinear mechanochemical behavior (27) that can be modeled by a collection of 2-state molecular motors (66). In the fully spread cells we studied, we hypothesize that CUs and actin filaments robustly self-organize into tensile networks which are plastic and whose steady states are marginally stable (35), where a small local rearrangement can trigger an avalanche of structural reconfiguration that arrests only when the network reaches a new marginally stable state. The superdiffusive fluctuations that are characteristic of such avalanche dynamics in turn drive plastic rearrangements (38), which, as in soft glassy matter, would then lead to the previously unexplained power law rheology of the cytoskeleton.
As we have shown, high-resolution measurements of cells’ active matter dynamics can offer a powerful window into cellular biophysics. With its combination of integrated, high-precision, and spatially correlated measurements of cytoskeletal fluctuations and local, magnetically driven measurements of cellular rheology, the approach described here has enabled the elucidation of the complex spatial and temporal correlations in the active dynamics of the actomyosin cortex. These results suggest that the physics of jammed materials and plastic deformation may be the origin of cytoskeletal active mechanics, fluctuations, and rheology, with significant implications for future models of the cortex, and for efforts to connect molecular-scale machinery to cellular-scale behavior and dynamics.
Methods
See SI Appendix, Methods for full method details.
AMPAD devices were fabricated in PDMS using replica molding (23, 28). Nickel nanowires with low-field magnetic moment of µ = 0.15 pA⋅m2 were embedded in ∼1% of the posts during fabrication (25, 40). The AMPADs were functionalized to restrict cell adhesion to the tips of the posts. Experiments were carried out with NIH 3T3 fibroblasts (ATCC). The microposts’ dynamics were measured with brightfield video microscopy, and their positions vs. time were determined using a centroid-based particle tracking algorithm (41). AC magnetic actuation in the frequency range 0.1 Hz ≤ f ≤ 135 Hz was carried out with a dual magnetic tweezer system (42), and the resulting micropost motion was measured via digital lock-in analysis (43). The MSD exponents α of the microposts’ trajectories were determined from the MSDs’ time derivatives for lag times in the range 5 s ≤ τ ≤ 10 s after subtracting the MSD noise floor. The condition α < 0.5 was used to identify background posts not attached to cells. Myosin activity was inhibited by 30-min treatment with either 60 nM blebbistatin or 50 nM Y27632, and ATP depletion studies followed published methods (19, 44). Fluorescence microscopy and analysis methods to identify large cortical avalanche-like events are described in SI Appendix, Methods.
Supplementary Material
Acknowledgments
We thank Christopher S. Chen for comments and discussions, and for providing micropost molds, and we thank Yun Chen for assistance with confocal microscopy. This work was supported, in part, by the National Institutes of Health (HL-127087).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1900963116/-/DCSupplemental.
References
- 1.Marchetti M. C., et al. , Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1187 (2013). [Google Scholar]
- 2.Ramaswamy S., The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys. 1, 323–345 (2010). [Google Scholar]
- 3.Prost J., Julicher F., Joanny J. F., Active gel physics. Nat. Phys. 11, 111–117 (2015). [Google Scholar]
- 4.Fabry B., et al. , Scaling the microrheology of living cells. Phys. Rev. Lett. 87, 148102 (2001). [DOI] [PubMed] [Google Scholar]
- 5.Bursac P., et al. , Cytoskeletal remodelling and slow dynamics in the living cell. Nat. Mater. 4, 557–561 (2005). [DOI] [PubMed] [Google Scholar]
- 6.Trepat X., et al. , Universal physical responses to stretch in the living cell. Nature 447, 592–595 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Condeelis J. S., Taylor D. L., The contractile basis of amoeboid movement. V. The control of gelation, solation, and contraction in extracts from dictyostelium discoideum. J. Cell Biol. 74, 901–927 (1977). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Janmey P. A., Hvidt S., Lamb J., Stossel T. P., Resemblance of actin-binding protein/actin gels to covalently crosslinked networks. Nature 345, 89–92 (1990). [DOI] [PubMed] [Google Scholar]
- 9.Ingber D. E., Cellular tensegrity: Defining new rules of biological design that govern the cytoskeleton. J. Cell Sci. 104, 613–627 (1993). [DOI] [PubMed] [Google Scholar]
- 10.Ingber D. E., Tensegrity I. Cell structure and hierarchical systems biology. J. Cell Sci. 116, 1157–1173 (2003). [DOI] [PubMed] [Google Scholar]
- 11.Sollich P., Lequeux F., Hébraud P., Cates M. E., Rheology of soft glassy materials. Phys. Rev. Lett. 78, 2020–2023 (1997). [Google Scholar]
- 12.Sollich P., Rheological constitutive equation for a model of soft glassy materials. Phys. Rev. E. 58, 738–759 (1998). [Google Scholar]
- 13.Bausch A. R., Kroy K., A bottom-up approach to cell mechanics. Nat. Phys. 2, 231–238 (2006). [Google Scholar]
- 14.Gardel M. L., et al. , Elastic behavior of cross-linked and bundled actin networks. Science 304, 1301–1305 (2004). [DOI] [PubMed] [Google Scholar]
- 15.Gardel M. L., et al. , Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl. Acad. Sci. U.S.A. 103, 1762–1767 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lau A. W. C., Hoffman B. D., Davies A., Crocker J. C., Lubensky T. C., Microrheology, stress fluctuations, and active behavior of living cells. Phys. Rev. Lett. 91, 198101 (2003). [DOI] [PubMed] [Google Scholar]
- 17.Mizuno D., Tardin C., Schmidt C. F., Mackintosh F. C., Nonequilibrium mechanics of active cytoskeletal networks. Science 315, 370–373 (2007). [DOI] [PubMed] [Google Scholar]
- 18.MacKintosh F. C., Levine A. J., Nonequilibrium mechanics and dynamics of motor-activated gels. Phys. Rev. Lett. 100, 018104 (2008). [DOI] [PubMed] [Google Scholar]
- 19.Guo M., et al. , Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell 158, 822–832 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hoffman B. D., Massiera G., Van Citters K. M., Crocker J. C., The consensus mechanics of cultured mammalian cells. Proc. Natl. Acad. Sci. U.S.A. 103, 10259–10264 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hoffman B. D., Crocker J. C., Cell mechanics: Dissecting the physical responses of cells to force. Annu. Rev. Biomed. Eng. 11, 259–288 (2009). [DOI] [PubMed] [Google Scholar]
- 22.Hecht F. M., et al. , Imaging viscoelastic properties of live cells by AFM: Power-law rheology on the nanoscale. Soft Matter 11, 4584–4591 (2015). [DOI] [PubMed] [Google Scholar]
- 23.Tan J. L., et al. , Cells lying on a bed of microneedles: An approach to isolate mechanical force. Proc. Natl. Acad. Sci. U.S.A. 100, 1484–1489 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.du Roure O., et al. , Force mapping in epithelial cell migration. Proc. Natl. Acad. Sci. U.S.A. 102, 2390–2395 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sniadecki N. J., et al. , Magnetic microposts as an approach to apply forces to living cells. Proc. Natl. Acad. Sci. U.S.A. 104, 14553–14558 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Geng Y., Wang Z., Review of cellular mechanotransduction on micropost substrates. Med. Biol. Eng. Comput. 54, 249–271 (2016). [DOI] [PubMed] [Google Scholar]
- 27.Wolfenson H., et al. , Tropomyosin controls sarcomere-like contractions for rigidity sensing and suppressing growth on soft matrices. Nat. Cell Biol. 18, 33–42 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fu J., et al. , Mechanical regulation of cell function with geometrically modulated elastomeric substrates. Nat. Methods 7, 733–736 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rigato A., Miyagi A., Scheuring S., Rico F., High-frequency microrheology reveals cytoskeleton dynamics in living cells. Nat. Phys. 13, 771–775 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Caspi A., Granek R., Elbaum M., Enhanced diffusion in active intracellular transport. Phys. Rev. Lett. 85, 5655–5658 (2000). [DOI] [PubMed] [Google Scholar]
- 31.Yamada S., Wirtz D., Kuo S. C., Mechanics of living cells measured by laser tracking microrheology. Biophys. J. 78, 1736–1747 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mak M., Kamm R. D., Zaman M. H., Impact of dimensionality and network disruption on microrheology of cancer cells in 3D environments. PLoS Comput. Biol. 10, e1003959 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Robert D., Nguyen T.-H., Gallet F., Wilhelm C., In vivo determination of fluctuating forces during endosome trafficking using a combination of active and passive microrheology. PLoS One 5, e10046 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Alencar A. M., et al. , Non-equilibrium cytoquake dynamics in cytoskeletal remodeling and stabilization. Soft Matter 12, 8506–8511 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wyart M., Marginal stability constrains force and pair distributions at random close packing. Phys. Rev. Lett. 109, 125502 (2012). [DOI] [PubMed] [Google Scholar]
- 36.Held G. A., et al. , Experimental study of critical-mass fluctuations in an evolving sandpile. Phys. Rev. Lett. 65, 1120–1123 (1990). [DOI] [PubMed] [Google Scholar]
- 37.Nicolas A., Ferrero E. E., Martens K., Barrat J.-L., Deformation and flow of amorphous solids: Insights from elastoplastic models. Rev. Mod. Phys. 90, 045006 (2018). [Google Scholar]
- 38.Hwang H. J., Riggleman R. A., Crocker J. C., Understanding soft glassy materials using an energy landscape approach. Nat. Mater. 15, 1031–1036 (2016). [DOI] [PubMed] [Google Scholar]
- 39.Ferrero E. E., Martens K., Barrat J. L., Relaxation in yield stress systems through elastically interacting activated events. Phys. Rev. Lett. 113, 248301 (2014). [DOI] [PubMed] [Google Scholar]
- 40.Sniadecki N. J., Lamb C. M., Liu Y., Chen C. S., Reich D. H., Magnetic microposts for mechanical stimulation of biological cells: Fabrication, characterization, and analysis. Rev. Sci. Instrum. 79, 044302 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Crocker J. C., Grier D. G., Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 179, 298–310 (1996). [Google Scholar]
- 42.Lin Y. C., Kramer C. M., Chen C. S., Reich D. H., Probing cellular traction forces with magnetic nanowires and microfabricated force sensor arrays. Nanotechnology 23, 075101 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dixon P. K., Wu L., Broad-band digital lock-in amplifier techniques. Rev. Sci. Instrum. 60, 3329–3336 (1989). [Google Scholar]
- 44.Massiera G., Van Citters K. M., Biancaniello P. L., Crocker J. C., Mechanics of single cells: Rheology, time dependence, and fluctuations. Biophys. J. 93, 3703–3713 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Puig-de-Morales M., et al. , Cytoskeletal mechanics in adherent human airway smooth muscle cells: Probe specificity and scaling of protein-protein dynamics. Am. J. Physiol. Cell Physiol. 287, C643–C654 (2004). [DOI] [PubMed] [Google Scholar]
- 46.Gittes F., Schnurr B., Olmsted P. D., MacKintosh F. C., Schmidt C. F., Microscopic viscoelasticity: Shear moduli of soft materials determined from thermal fluctuations. Phys. Rev. Lett. 79, 3286–3289 (1997). [Google Scholar]
- 47.Gisler T., Weitz D. A., Scaling of the microrheology of semidilute F-actin solutions. Phys. Rev. Lett. 82, 1606–1609 (1999). [Google Scholar]
- 48.Palmer A., Xu J., Kuo S. C., Wirtz D., Diffusing wave spectroscopy microrheology of actin filament networks. Biophys. J. 76, 1063–1071 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Deng L., et al. , Fast and slow dynamics of the cytoskeleton. Nat. Mater. 5, 636–640 (2006). [DOI] [PubMed] [Google Scholar]
- 50.Giannone G., et al. , Periodic lamellipodial contractions correlate with rearward actin waves. Cell 116, 431–443 (2004). [DOI] [PubMed] [Google Scholar]
- 51.Gerhardt M., et al. , Actin and PIP3 waves in giant cells reveal the inherent length scale of an excited state. J. Cell Sci. 127, 4507–4517 (2014). [DOI] [PubMed] [Google Scholar]
- 52.Inagaki N., Katsuno H., Actin waves: Origin of cell polarization and migration? Trends Cell Biol. 27, 515–526 (2017). [DOI] [PubMed] [Google Scholar]
- 53.Van Citters K. M., Hoffman B. D., Massiera G., Crocker J. C., The role of F-actin and myosin in epithelial cell rheology. Biophys. J. 91, 3946–3956 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zaburdaev V., Denisov S., Klafter J., Levy walks. Rev. Mod. Phys. 87, 483–530 (2015). [Google Scholar]
- 55.Harris T. H., et al. , Generalized Lévy walks and the role of chemokines in migration of effector CD8+ T cells. Nature 486, 545–548 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Phillies G. D. J., In complex fluids the Gaussian Diffusion Approximation is generally invalid. Soft Matter 11, 580–586 (2015). [DOI] [PubMed] [Google Scholar]
- 57.Weron R., Levy-stable distributions revisited: Tail index > 2 does not exclude the Levy-stable regime. Int. J. Mod. Phys. C 12, 209–223 (2001). [Google Scholar]
- 58.Gutenberg B., Richter C. F., Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 34, 185–188 (1944). [Google Scholar]
- 59.Zargar R., Nienhuis B., Schall P., Bonn D., Direct measurement of the free energy of aging hard sphere colloidal glasses. Phys. Rev. Lett. 110, 258301 (2013). [DOI] [PubMed] [Google Scholar]
- 60.Lemaître A., Caroli C., Rate-dependent avalanche size in athermally sheared amorphous solids. Phys. Rev. Lett. 103, 065501 (2009). [DOI] [PubMed] [Google Scholar]
- 61.Kelly P. A., “Mechanics lecture notes: An introduction to solid mechanics.” http://homepages.engineering.auckland.ac.nz/∼pkel015/SolidMechanicsBooks/index.html. Accessed 19 June 2019.
- 62.Ferry J. D., Viscoelastic Properties of Polymers (Wiley, New York, ed. 3, 1980). [Google Scholar]
- 63.Smith B. A., Tolloczko B., Martin J. G., Grütter P., Probing the viscoelastic behavior of cultured airway smooth muscle cells with atomic force microscopy: Stiffening induced by contractile agonist. Biophys. J. 88, 2994–3007 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kilpatrick J. I., Revenko I., Rodriguez B. J., Nanomechanics of cells and biomaterials studied by atomic force microscopy. Adv. Healthc. Mater. 4, 2456–2474 (2015). [DOI] [PubMed] [Google Scholar]
- 65.Li M., Dang D., Liu L., Xi N., Wang Y., Atomic force microscopy in characterizing cell mechanics for biomedical applications: A review. IEEE Trans. Nanobioscience 16, 523–540 (2017). [DOI] [PubMed] [Google Scholar]
- 66.Lohner J., et al. , Large and reversible myosin-dependent forces in rigidity sensing. Nat. Phys. 10.1038/s41567-019-0477-9 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.