Inter-institutional analysis demonstrates the importance of lower than previously anticipated dose regions to prevent late rectal bleeding following prostate radiotherapy

Abstract

Purpose:

To investigate whether inter-institutional cohort analysis uncovers more reliable dose-response relationships exemplified for late rectal bleeding (LRB) following prostate radiotherapy.

Material and Methods:

Data from five institutions was used. Rectal dose-volume histograms (DVHs) for 989 patients treated with 3DCRT or IMRT to 70–86.4Gy@1.8–2.0Gy/fraction were obtained, and corrected for fractionation effects (α/β=3Gy). Cohorts with best-fit Lyman-Kutcher-Burman volume-effect parameter a were pooled after calibration adjustments of the available LRB definitions. In the pooled cohort, dose-response modeling (incorporating rectal dose and geometry, and patient characteristics) was conducted on a training cohort (70%) followed by final testing on the remaining 30%. Multivariate logistic regression was performed to build models with bootstrap stability.

Results:

Two cohorts with low bleeding rates (2%) were judged to be inconsistent with the remaining data, and were excluded. In the remaining pooled cohorts (n=690; LRB rate=12%), an optimal model was generated for 3DCRT using the minimum rectal dose and the absolute rectal volume receiving less than 55 Gy (AUC=0.67; p=0.0002; Hosmer-Lemeshow p-value, pHL=0.59). The model performed nearly as well in the “hold-out” testing data (AUC=0.71; p<0.0001; pHL=0.63), indicating a logistically shaped dose-response.

Conclusion:

We have demonstrated the importance of integrating datasets from multiple institutions, thereby reducing the impact of intra-institutional dose-volume parameters explicitly correlated with prescription dose levels. This uncovered an unexpected emphasis on sparing of the low to intermediate rectal dose range in the etiology of late rectal bleeding following prostate radiotherapy.

Introduction

Most studies of normal tissue dose-response relationships use data from single institutions. Intra-institutional studies have only a limited variation of dose-volume variables. In essence, variables that can be identified as predictive are effectively restricted to those with sufficient variance in the investigated cohort [1], which is, consequently, closely related to the applied treatment technique, including prescription dose levels and beam arrangements.

Combining data from varied planning protocols has the potential to reduce statistical artifacts related to intra-institutional correlations among dose/volume variables. We hypothesize that combining data across institutions may shed new light on the dose tolerances for normal tissues due to a larger number of patients, and an increased variability in dose-volume histograms (DVHs) due to various treatment and delivery approaches [1]. While data-handling tools to facilitate pooled analyses are readily accessible [2], the feasibility of successfully modeling outcomes across institutions is potentially limited by differences in methods used to measure outcomes [3–6] or any unaccounted for properties of patient populations [5].

To test our hypothesis we combined six datasets from five institutions (n=989) and asked if a generalizable dose-response relationship can be established for late rectal bleeding (LRB) after RT for localized prostate cancer. Late rectal bleeding has the potential to negatively impact quality of life [7]. Previous dose-response efforts for LRB have used data from single cohorts and institutions, or synthesized dose-volume cut points from individual studies into a combined plot [3]. In this study, we first addressed whether data is fundamentally similar enough to be pooled. We then generated a dose-response relationship incorporating patient and treatment characteristics.

Methods and materials

Cohort-specific information

Six cohorts were initially identified for this pooled dose-response analysis of LRB. These cohorts comprised 989 patients treated with primary external-beam RT for localized prostate cancer in 1991–2007 to 70–86.4Gy@1.8–2.0Gy/fraction (Tables 1, S1 and S2). Institutions included the British Columbia Cancer Agency, Canada (Cohort 1 [8]), Aarhus University Hospital, Denmark (Cohort 2 [9]), Memorial Sloan Kettering Cancer Center, USA (Cohorts 3 and 4 [10, 11]), Haukeland University Hospital, Norway (Cohort 5 [12]), and Sahlgrenska University Hospital, Sweden (Cohort 6 [13]). Treatment was typically 3D Conformal Radiotherapy (3DCRT), except in one cohort where intensity-modulated RT (IMRT) had been used (Table S1). Dose was prescribed to the isocenter except in Cohorts 3 and 4, where the prescription dose was given as the minimum isodose surface encompassing the planning target volume. Only in Cohort 2 was image-guidance routinely performed, which consisted of multiple era-specific procedures [9]. Cohorts 3 and 4 included dose/volume data for all treated patients that experienced LRB (cases), but only a subset of the patients that did not (controls): three controls were matched per case based on RT technique and year of RT, (as proposed by Jackson et al [10]), resulting in 72 patients chosen from 369 in Cohort 3, and 68 patients chosen from 601 patients in Cohort 4. In all conducted analyses, each control was, therefore, weighted by the inverse of the sampling frequency (accounting for both RT technique and treatment year). In what follows, quoted LRB rates reflect the rates observed in the complete cohorts.

Table 1.

Characteristics for all individual cohorts and for the pooled cohort.

Cohort [ref.]	LRB definition (grade)	LRB rate	Age [y] LRB	No LRB	Diabetes LRB	No LRB	Hemorrhoids LRB	No LRB	HT LRB	No LRB	Smoking LRB	No LRB	Volume [cm3] LRB	No LRB
1 [8]	≤2 laser coagulations (LRB≥2)	8 (12)	82±7	79±6	17 (2)	19 (25)	0 (0)	7 (9)	58 (7)	63 (83)	33 (4)	51 (67)	90±43	95±42
2 [9]	Blood in stools ≥1–4 times/month (LRB≥m)	12 (24)	69±6	69±5	8 (2)	9 (16)	0 (0)	1 (2)	92 (22)	91 (160)	54 (13)	91 (125)	68±39	70±41
3 [10]	≥ Intermittent LRB (LRB≥2)	5 (18)	68±4	67±6	0 (0)	8 (28)	0 (0)	4 (13)	28 (5)	39 (137)	39 (7)	58 (203)	86±32	126±64
4 [11]*	≥ Intermittent LRB (LRB≥2)	1.5 (17)	70±4	70±7	6 (1)	<1 (10)	18 (3)	<1 (1)	35 (6)	3 (30)	41 (7)	3 (30)	62±21	58±16
5 [12]*	Occasionally >2/w (LRB≥2)	2 (5)	61±5	65±6	N/A	N/A	N/A	N/A	100 (5)	85 (193)	N/A	N/A	103±45	101±50
6 [13]	Red blood in stools ≥1 time/month (LRB≥m)	22 (61)	67±5	66±5	6 (10)	13 (27)	16 (61)	5 (11)	13 (8)	18 (38)	61 (37)	60 (129)	41±21	51±24
Pooled	LRB definitions in cohorts 1–3, 6 (LRB≥2, LRB≥m)	12 (118)	69±7	70±7	9 (10)	8 (71)	9 (10)	4 (35)	37 (42)	42 (116)	53 (61)	60 (524)	59±36	74±45

Note: Age, and Volume are given as the population average±SD; Diabetes, hemorrhoids, hormonal therapy (HT), the rate for the finally selected LRB definitions (Figure 1A; 1^st Results section), and smoking are given as % (n). The two cohorts excluded from the pooled analysis (cohorts 4 and 5) are denoted with *.

To exclude uncertainties in rectal definition, the rectum was manually re-defined in all patients to be the volume within the outer rectal contour (including contents) from the slice below the recto-sigmoid junction to the slice above the anal canal. Pre-treatment rectal preparation protocols were not used on a routine basis.

Assessment of LRB after RT had been performed by patients in two cohorts, and by physicians in four cohorts, using a total of five scoring systems (cf. Table S2 for a complete overview of all LRB assessments being used) [9, 13–16]. The minimum follow-up time criterion was three months (Table S2). Within each scoring system, LRB was defined as the maximum-recorded LRB grade within an individual’s follow-up time. Across all cohorts, the median follow-up time for LRB was 3.0–7.3 year. For physician-assessed scores, LRB was defined as ≥Grade 2 (denoted LRB_≥2). For patient-assessed scores, there were three candidate LRB definitions (≥monthly, ≥weekly, and ≥daily occurrence of LRB, denoted LRB_≥m, LRB_≥w, LRB_≥d, respectively), and we, therefore, investigated each of these three candidate definitions.

Pooling approach

Our approach was to consider whether all datasets were consistent enough to justify pooling, as commonly performed in meta-analyses. As a measure of comparability, we used the commonly reported Lyman-Kutcher-Burman (LKB) model that essentially weights different regions of the DVH according to a power-law [17, 18]. Within the LKB formalism, large heterogeneities in the volume-effect parameter a indicate distinctively different volume-effects: a high value of a indicates that the highest doses in the DVH drive the complication probability, whereas a value of a near 1 indicates the mean dose drives the probability of a complication [3]. The LKB model further includes two additional parameters: the probability of a 50% complication rate (D₅₀), and the slope of the dose-response curve (m). Since both D₅₀ and m depend on the a value of the investigated organ, we assumed that pooling feasibility is primarily determined by the a value rather than focusing on either D₅₀ or m individually.

Prior to DVH extraction and to adjust for differences in fractionation schemes, the dose-distribution for each patient was converted into equivalent doses as if all doses were delivered in 2 Gy fractions, assuming α/β=3 Gy [3, 19].

Best-fit LKB parameters (a, D₅₀, and m) for LRB were initially assessed from rectal DVHs in each cohort using Maximum Likelihood estimation with a grid search (grid size: a=0.001:100 on a logarithmic scale in 55 steps; D₅₀=25:250 in 2 Gy steps; m=0.01:1.1 in 0.02 steps). For the best-fit a in each cohort, 95% confidence intervals were estimated (95%CI_BP) from 95^th percentiles of the fitted values from 1000 bootstrap sample populations [20]. The heterogeneity index I² [21, 22] was then calculated for the cohort-specific a relative to the 95%CI_BP of a in the other cohorts. The I² statistic describes the percentage of total variation across studies that is due to heterogeneity rather than chance, and ranges from 0 to 100%, with lower values indicating no observed heterogeneity [22]. We calculated the I² statistic after omitting each cohort in turn. An I² statistic close to 0% amongst the remaining cohorts, therefore, indicates no residual heterogeneity, and that the omitted cohort was fundamentally different from the remaining cohorts, and should not be pooled.

Subsequently, best-fit LKB parameters were assessed for the remaining pooled cohort. The area under the receiving-operating characteristics curve (AUC) of the related generalized equivalent uniform dose, gEUD [23], was compared to that of the gEUD using the QUANTEC recommended a value of 11 [3]. The AUCs had to be within the 95%Cs (AUC95%CI) of each other for the models to be considered to have same predictive ability [24].

Dose-response modeling

For the pooled cohort, more general multivariate dose-response modeling was performed based on including variables related to rectal dose and geometry, as well as patient characteristics. Dose for each patient was represented by a total of 104 variables (including also gEUD with the best-fit a), geometry by three, and patient characteristics by five variables (Table S3). All analyses were conducted in MATLABv. R2016a, and extraction of dose data was performed in the computational environement for radiotherapy research, CERR [25].

Overall, the modeling approach followed that of the Transparent Reporting of a multivariate prediction model for Individual Prognosis Or Diagnosis (TRIPOD) statement, and further details can be found in [26]. The pooled cohort was randomly split into 70% and 30%; the former was used for model training, and the latter for model testing. Dose-response modeling was based on logistic regression. Within the model building process (training), univariate and multivariate analysis (UVA, MVA) was applied with bootstrap resampling using 1000 sample populations. A backward-forward stepwise selection was used in the MVA with the objective of minimizing the Akaike Information Criterion. A variable was considered a candidate predictor for MVA if presenting with an average p-value<0.20 across all bootstrap samples on UVA. Candidate predictors were then eliminated until no variable had a Spearman’s rank correlation coefficient (|R_s|) ≥0.70 with any other selected variable. In MVA, a model was considered a candidate model if it was selected in ≥10% of the possible 1000 Bootstrap models.

The utility of candidate MVA models was assessed by their discriminative ability (AUC, and logistic regression p-values), and by comparison with observed LRB rates in quintiles (Hosmer-Lemeshow p-values, p_HL [27]); all given as the average ± standard deviation (SD) across the 1000 sample populations. In addition, calibration was represented graphically by plotting the model(s) predictions vs. the observed LRB rates. Finally, the candidate MVA models were evaluated in the testing cohort without any re-fitting applied (AUC, p-values, and p_HL given as one value/metric). An MVA model derived from the 70% training cohort was considered final if it was generalizable in the 30% testing cohort, i.e., if the AUC in the latter cohort was within the average±SD of the AUC in the training cohort for corresponding models, and if p_HL was >0.05.

Ultimately, the performance of the final MVA models in the pooled cohorts was evaluated in each excluded cohort (exclusion based on the I² criterion; cf. Pooling approach). If the performance of the final models was unsatisfactory, excluded cohorts were modeled individually using a similar approach as in the pooled cohort. Where the number of LRB cases was small, validation using a training and testing approach could not be performed.

Results

Pooling investigation based on best-fit Lyman-Kutcher-Burman parameter a

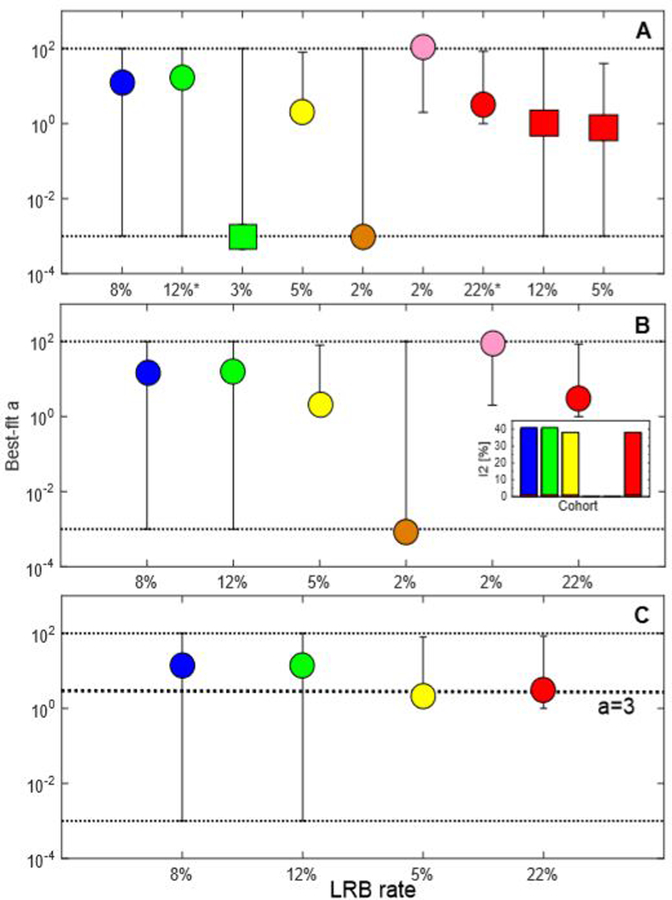
The median best-fit a across all cohorts was 2 (range across cohorts: 0.001–90). For the two cohorts with multiple candidate LRB definitions, best-fit values of a with those from cohorts using LRB_≥2 agreed the most when using LRB_≥m: the median a value across all Bootstrap samples was 10/0.5/0.8 using LRB_≥m/LRB_≥w/LRB_≥d compared to a corresponding a value of 8 for LRB_≥2 in the remaining cohorts (cf. Figure 1A for the median a values and associated 95%CI_BP). In the further analyses, LRB_≥m was, therefore, chosen and considered the finally selected LRB definition for these two cohorts. As summarized in Table S2, LRB_≥2 refers to a combination of ≤2 laser coagulations (Cohort 1), and ≥intermittent/occasional >twice per week LRB (Cohorts 3–5), and LRB_≥m refers to ≥1–4 times/month (Cohorts 2, 6).

Figure 1A–C.

Best-fit a and 95%bootstrap percentile confidence intervals (black dotted lines) for: A Each cohort (Cohort 1 [8]: blue; Cohort 2 [9]: green; Cohort 3 [10]: yellow; Cohort 4 [11]: orange; Cohort 5 [12]: pink; Cohort 6 [13]: red). The green and red circles denote the LRB definitions in the cohorts with multiple LRB definitions considered feasible to pool, i.e., with the median a value closest to that of the remaining cohorts as indicated by * on the x-axis legend (LRB definitions: LRB_≥m for PRO-based and LRB_≥2 for the physician-assessed LRB), and squares the excluded LRB definitions, i.e., LRB_≥w and LRB_≥d. B. Cohorts initially considered for pooling. C. Cohorts ultimately pooled based on the I² assessments. Note: The results from the I² (%) calculations, i.e., the residual heterogeneity by excluding each cohort have been inserted in Figure 1B; Black dashed line in Figure 1C refers to the best-fit a=3 in the pooled cohort.

The I² statistic for the cohort-specific a relative to the 95%CI_BP of a in the other cohorts indicated that the two cohorts with the lowest LRB rates (2% compared to 5–22% in the other four cohorts) should be excluded given I²=0% excluding each of them. One of these excluded cohorts was the only cohort that included patients treated solely with IMRT (Cohort 4). The best-fit a for these two cohorts was close to the boundary points of the investigated grid for a (a=0.001, 90; grid: 0.001:100); a in the other four cohorts was within the grid (a=2–16). Excluding each of the other four cohorts, I² was 38–40% (Figure 1B and C). These four cohorts included a total of 690 patients with a 12% LRB rate and were, thus, considered feasible to pool.

Best-fit (95%CI_BP) LKB model parameters in the pooled cohort were a=3 (2–4); m=0.43 (0.35–0.47); and D₅₀=41 Gy (29–53). Also, a trend that the AUC of the gEUD using the best-fit a being higher than that of using the QUANTEC recommended a was observed: AUC=0.67 vs. 0.62, but AUC_95%CI was 0.06. Patient characteristics for each individual cohort and also for the pooled cohort are given in Table 1.

Pooled cohort: Dose-response modeling

In the training cohort, 38 candidate predictors were suggested and were mostly related to dose (92% of the variables). Of these variables, 32 were highly correlated with any of the remaining six variables that presented with a lower p-value (median |R_s|: 0.87 (range: 0.70–1.00); Figure S1; Table S4). Hence, these six variables were considered final candidate predictors and qualified for MVA (Table 2).

Table 2.

Dose-response modeling results for the final univariate candidate predictors and from multivariate logistic regression analysis in the pooled training cohort (complete univariate logistic regression analysis results are given in Table S4).

Univariate variable	AUC	p	pHL	β0	β1
Vabs<55*	0.66±0.03	0.0004±0.003	0.60±0.03	−1.16	−0.02
Dmin*	0.63±0.03	0.01±0.04	0.59±0.02	−2.56	0.05
Dmax, surr*	0.58±0.04	0.03±0.11	0.62±0.01	−2.72	0.02
Length*	0.62±0.04	0.07±0.16	0.66±0.06	−1.39	−0.09
CSA*	0.59±0.04	0.10±0.18	0.62±0.03	−1.54	−0.04
D45*	0.58±0.04	0.11±0.20	0.62±0.02	−2.91	0.02
Multivariate variable	AUC	p	pHL	β0	β1, βs	Frequency [%]
Vabs<55, Dmin	0.67±0.03	0.0002±0.001	0.59±0.03	−1.51	−0.02, 0.02	47
Dmin	0.62±0.03	0.001±0.06	0.59±0.02	−2.56	0.05, -	25

Note: Variables are sorted in increasing p-value order;

^*included in MVA; AUC, p, and p_HL are given as population average±SD across all Bootstrap samples; regression coefficients (β₁, β₂) and the intercept (β₀) are given without Bootstrapping.

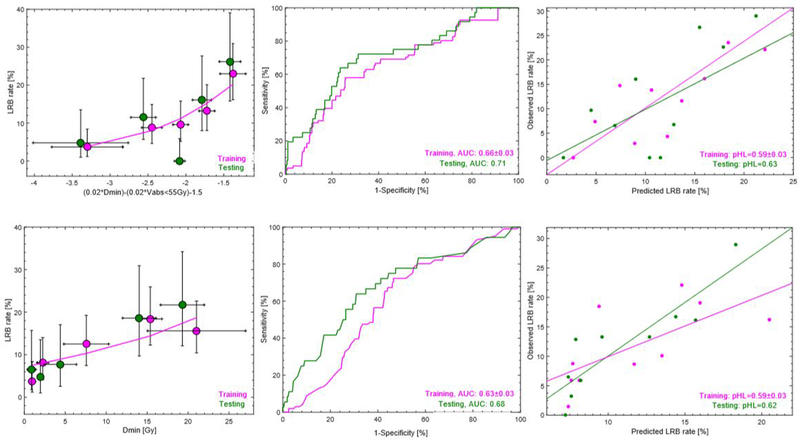
Two final MVA models were suggested (model frequency: 25%, 47%). These were the minimum dose (D_min), with or without the absolute volume receiving <55 Gy (Vabs<55Gy; Table 2). The AUC of the most frequently selected MVA model (Vabs<55Gy and D_min) in the training cohort was 0.67±0.03 (p-value: 0.0002±0.01) and 0.71 (p-value: <0.0001) in the testing cohort (Note: no re-fitting applied in testing; all regression coefficients result from the analysis in training). The corresponding values for the second most frequently selected model (D_min) were 0.63±0.03 (p-value: 0.01±0.06) and 0.68 (p-value: <0.0001; Figure 2; Table 2), respectively. Hence, the AUC of both MVA models was in the near vicinity but slightly larger in the testing compared to in the training cohort. The p_HL of both models indicated good agreement between the observed and predicted rate of LRB in the training and the testing cohort (p_HL: 0.62, 0.63). The population average±SD D_min and Vabs<55Gy in the pooled cohort were 13±8Gy and 37±28cm³ for patients with LRB to 11±8Gy and 50±38cm³ for patients without LRB.

Figure 2.

Dose-response curves for the two final MVA models (left) in the training cohort (magenta) and observed data in the testing cohort (green) with associated receiver-operating characteristics curves (middle) in the training cohort (green) and as applied to the testing cohort (magenta), as well as calibration plots. Note: Confidence intervals for observed LRB (circles) are given as exact 95% binomial confidence intervals.

Excluded cohorts

The performance of the two final MVA models in Cohort 5 was reasonable (AUC: 0.67, 0.85; p: 0.11, 0.01 for Vabs<55Gy and D_min, and D_min, respectively) but poor in Cohort 4, i.e., in the IMRT cohort (AUC<0.50; Figure S2). A separate dose-response modeling in Cohort 4 suggested three final MVA models: hemorrhoids and hormonal therapy with or without Vabs≥5Gy (AUC: 0.67, 0.65; p≤0.0001), and hemorrhoids with the maximum value of the minimum slice-wise rectal dose (D_{max, surr}; AUC: 0.58; p≤0.0001; Table S5). Hemorrhoids and hormonal therapy were more and less common, respectively, in patients with LRB compared to patients without LRB (0.3 % vs. 0.1%; 1% vs. 3%). The population average±SD Vabs≥5Gy and D_{max, surr} was 61±21cm³ and 18±5Gy for patients with LRB, while 56±15cm³ and 17±3Gy for patients without LRB.

Discussion

We hypothesized that combining data across institutions may shed new light on the dose tolerances for normal tissues and investigated clinical outcomes after RT for localized prostate cancer by combining six data sets from five institutions. This included six prescription dose levels, two major treatment techniques, five assessments of the studied clinical outcome, as well as five available patient characteristics. A careful approach was applied to account for these differences. We used the inconsistency index I² [22], which is commonly applied to establish heterogeneity in meta-analyses, together with a best-fit LKB a value estimation [17, 18] in order to assess pooling feasibility across the cohorts. Two-thirds of the data (690/989 patients; all treated with 3DCRT to 70–78Gy) could be pooled with a combined LRB rate of 12%.

Based on single-institutional data, high rectal doses (~65–78 Gy) have been associated with LRB following 3DCRT to 70–80 Gy [3, 5, 28, 29]. Conversely in our pooled cohort, dose-response modeling demonstrated that only dose variables related to sparing were important to understand LRB: the two final MVA models included the minimum dose (D_min) with the inclusion of the absolute volume receiving <55 Gy (Vabs<55Gy), a sparing quantification of the intermediate dose region, or D_min only. Variables related to high-dose irradiation had either a poor predictability (average p>0.20 on UVA across all Bootstrap samples in training), or were highly correlated with other variables (|R_s|≥0.70) that presented with a superior predictability. Thus, by pooling data, a new sparing-related rectal dose-response relationship for LRB was identified. Our best-fit a (3; 95%CI: 2–4) was smaller than the a (11; 95%CI: 7–25) recommended by QUANTEC [3], and placed more emphasis on mid-dose regions [23]. The AUC of the gEUDs from our best-fit a was higher (but not significantly so) than that of QUANTEC (AUC: 0.67 (AUC_95%CI: 0.06) vs. 0.62). The QUANTEC-based a was synthesized from four studies [30–33] with a similar combined LRB rate (13%), treatment technique, and prescription dose levels (3DCRT: 64.0–79.2Gy) as in our pooled cohort. QUANTEC excluded 59% of the patients where LRB had been assessed in combination with three other rectal toxicities [33], which led to no residual heterogeneity, i.e., I²=0 [3]. This could be an indication that the etiological pattern of LRB, i.e., telangiectasia and ulceration of the rectal mucosa [34, 35], is distinctively different from that of other rectal toxicities [36]. The rectal volumes across the pooled (training) cohort ranged between 11–277 cm³ (median: 59 cm³) as can be expected given variable filling due to the general absence of both image-guidance and pre-treatment rectal preparation to a large extent. Further, rectal volume was a candidate predictor (training), with smaller volumes resulting in higher LRB rates (p=0.001; Table S4), but was not considered a final candidate predictor given its strong correlation with Vabs<55Gy that presented with a lower p-value (|R_s|: 095; p=0.0004; Table S4; Figure S1).

Two of the cohorts did not qualify for pooling given that the residual I² was 0% excluding either of them; and their best-fit a values pointed towards the extreme low- or the extreme high dose end (Cohort 4 [11]: a=0.001; Cohort 5 [12]: a=90). The LRB rate in these cohorts was considerably lower than that of the remaining individual and pooled cohorts (2% vs. 5–22% and 12%). Surprisingly, the performance of the final MVA models as applied to Cohort 5 was reasonable (Figure S2), however, there were only five LRB cases in this cohort. Also, even though we redefined the rectal volumes in all cohorts, those in Cohort 5 were significantly larger than those of the pooled cohort (population median: 91 cm³ vs. 61 cm³; p<0.0001, Wilcoxon rank-sum test). Cohort 4 was the only cohort where patients had been treated with IMRT, which has been associated with lower rates of late rectal toxicity compared to after 3DCRT [38, 39]. Our final MVA models were unable to explain this protective effect (Figure S2), and the DVHs for patients with LRB were on average located below those of patients without LRB in the IMRT cohort (Figure S3).

Only one previously published work, a single institutional study by Troeller et al [4], derived a dose-response for late rectal toxicity after 3DCRT and applied it to IMRT. The 3DCRT model overestimated the rate of observed rectal toxicity in the IMRT cohort. In the QUANTEC review, Michalski et al [3] argued that 3DCRT treatments are likely to be more sensitive to rectal motion than IMRT, with the former resulting in considerably larger volumes exposed to intermediate or high doses. Dose-response modeling within our IMRT cohort found MVA models of similar performance as that of our pooled cohort, but final models differed in that the IMRT models included in addition to the maximum isodose that completely surrounds the rectum (on any slice), i.e., a dose sparing variable, also hemorrhoids, hormonal therapy, and the absolute rectal volume ≥5 Gy. Interestingly, parameterizing dose as surface maps, Wortel et al [40], found a similar trend of association (p=0.20) between their 3DCRT and the image-guided IMRT cohort of anorectal doses at the anterior-left 60% of the central axis explaining acute rectal bleeding. Thus, handling the inherently different dose distributions between 3DCRT and IMRT treatments could involve focusing on spatial dose patterns related to rectal sparing [41–43]. However, since our IMRT models were derived from one institution and one cohort, it is not surprising that they included variables different from those included in the final MVA models in our pooled cohort, and, the final IMRT models should, thus, be candidates for exploration in multiple IMRT cohorts.

A challenge of combining data from multiple cohorts and institutions is to re-calibrate the endpoint of interest to better account for differences in reporting. In our study we needed to calibrate LRB definitions from the two cohorts where LRB had been reported by patients with those from cohorts using physician-assessed LRB. The best-fit a in each of these two cohorts showed best agreement with those of the others, i.e., LRB_≥2 using the LRB_≥m definition (best-fit a=10/0.5/0.8 for LRB_≥m/LRB_≥w/LRB_≥d vs. a=8 using LRB_≥2 in the remaining cohorts). This LRB calibration corresponded to a combination of ≤2 laser coagulations (Cohort 1), ≥intermittent/occasional >twice per week LRB (Cohorts 3–5), and LRB ≥1–4 times/month (Cohorts 2, 6). While a difference in rates between patient- and physician-assessed LRB has previously been recognized [3, 5, 6, 37], our study is one of the first dose-volume response-focused studies that addresses and incorporates differences in outcome assessment. A similar analysis should ideally have been conducted in the other four cohorts, but was not possible since these presented only with the LRB_≥2 definition. Even though the minimum follow-up time on LRB across our cohorts was within that considered a late effect, i.e., assessed at a ≥three months after completed RT [3], time-to-LRB analysis was not possible given the cross-sectional LRB assessment used for patient-reported LRB in two cohorts compared to the longitudinal LRB assessment performed by physicians in the remaining cohorts. Baseline LRB status was not available for the cohorts included in the final pooled cohort. Data on the presence of pre-RT hemorrhoids was, however, available in the pooled cohort, but baseline LRB status surrogated by hemmorhoids did not explain LRB in the pooled cohort (p=0.44).

Previous single institution studies including 3DCRT data have implicated that the dose-response relationship for LRB may be confounded by aspirin use [29], diabetes [44, 45], hormonal therapy [46, 47], and previous abdominal surgery [48, 49]. We did not find any of the available patient characteristics (age, diabetes, hemorrhoids, hormonal therapy and smoking) to be associated with LRB in our pooled cohort. On the other hand, all three final MVA models in the IMRT cohort included hemorrhoids with or without hormonal therapy, which increased and decreased, respectively, the risk of LRB. Even though hemorrhoids and hormonal therapy were more common in the pooled cohort compared to in the IMRT cohort (35% vs. 3% and 3% vs. 0.4%), it is possible that the lack of a similar finding in the pooled cohort was due to diversity in the definition and reporting of these variables between institutions. All potentially confounding factors such as aspirin use, abdominal surgery, or intra/inter-fractional rectal motion could, however, not be accounted for.

Correction for multiple hypotheses testing of the 104 investigated variables was not explicitly considered. Principal component analysis demonstrated that four degrees-of-freedom accounted for 96% of the DVH variability, i.e., one extra component for the same variability compared to the study by Söhn et al [50], whereas one degree-of-freedom explained 98% of the rectal geometry and 99% of the patient characteristics. The in total six degree-of-freedom corrected significance level at 0.8% did not influence on our final models given that both D_min and Vabs<55Gy presented with averaged p-values over the 1000 sample populations below this threshold (Table 2).

In adjusting all DVHs for fractionation effects we assumed α/β=3 Gy. This has been the most widely used α/β ratio, and also enabled us to compare our results with those synthesized from the four studies in the rectal-specific QUANTEC report [3]. Estimation of best-fit α/β ratio in the study by Marzi et al [19] for overall rectal toxicity after conventionally fractionated as well as hypfractionated RT, has supported the choice of 3 Gy (best-fit range: 1.0–3.5 Gy).

A novel focus of our study was the investigation of unconventional dose-volume variables related to sparing, e.g., absolute and relative volumes receiving <x Gy (previously ≥x Gy variables only have typically been investigated), and the maximum surrounding rectal isodose. Our results emphasized that rectal sparing is related to LRB over the previously more common high dose focus as summarized in [3]. A likely explanation for this unusual finding in the setting of LRB is that we pooled data across multiple prescription dose levels and institution-specific treatment approaches, reducing the likelihood of identifying spurious variables selected due to strong correlations with prescription dose related variables, such as the relative rectal volume receiving ≥70Gy.

Conclusions

By combining multiple datasets and including a wide range of treatment-related characteristics, we found that previously unappreciated aspects of the rectal dose distribution are important in predicting LRB. In particular, we found that the ‘spared rectal volume’ is important rather than rectal volumes irradiated to high doses as previously suggested by single institution studies. Sparing-related dose-volume variables may previously have gone unnoticed due to strong correlations in dose-volume variables within single institutions, and, thus, pooling data across institutions has shed new light on the dose tolerance for LRB. When pooling data it is important to carefully consider whether datasets are similar enough to be jointly analyzed. Most of our 3DCRT data satisfied our pooling criteria. We found models describing LRB in 3DCRT to be different from those for IMRT, although sparing was important for IMRT also.