Sources of variability and accuracy of performance assessment in the clinical pharmacology quality assurance (CPQA) proficiency testing program for antiretrovirals

Abstract

BACKGROUND:

The Clinical Pharmacology Quality Assurance (CPQA) program provides semi-annual proficiency testing of antiretroviral analytes for eleven U.S. and international clinical pharmacology laboratories to ensure inter-laboratory comparability. In this manuscript, we provide estimates of the main sources of variability and assess the accuracy of the algorithm for the assessment of performance.

METHODS:

Descriptive statistics are reported from thirteen proficiency testing rounds from 2010–2016. Eight of the most common antiretroviral analytes were examined. Variance components analysis was employed to rank the relative contributions of clinical pharmacology laboratories, antiretroviral analyte and concentration category (low, medium and high) to bias and variability using mixed models. Binary classification metrics of the proficiency testing assessment algorithm are calculated in comparison to a model employing 95% prediction limits around estimated regression equations.

RESULTS:

Clinical pharmacology laboratories provided 4,109 reported concentrations of 65 unique samples for each of the eight antiretroviral analytes across 13 proficiency testing rounds. Individual clinical pharmacology laboratory accounted for the greatest amount of total variability (4.4%). Individual clinical pharmacology laboratory and analyte combination (interaction) accounted for the greatest amount of bias (8.1%). Analyte alone accounted for 0.5% or less for total variability and bias. Overall, employing a ±20% acceptance window around the final target, 97% of individual reported concentrations were scored acceptable and 96% of antiretroviral /Round Scores were deemed satisfactory. Comparison with the regression model gave 100% sensitivity but only 34.47% specificity. Narrowing the acceptance window to ±15% improved specificity to 84.47% while maintaining a 99.17% sensitivity.

CONCLUSION:

The current CPQA proficiency testing scoring algorithm which employ a ± 20% acceptance window appears to suffer from a low specificity and may be too lenient. A stricter ±15% acceptance window would increase specificity and overall accuracy while lowering the overall pass rate by only 3%.

Introduction

The Clinical Pharmacology Quality Assurance (CPQA) program was established in 2008 and provides multiple quality-centered activities for all National Institute of Allergies and Infectious Diseases, Division of AIDS (NAIAD/DAIDS) HIV Clinical Trial Networks globally. CPQA was established, in part, to meet the Clinical Laboratory Improvement Act (CLIA) mandate that clinical laboratories participate in and demonstrate satisfactory performance in proficiency testing (PT) programs.¹ CPQA provides a semi-annual proficiency PT program for eleven U.S. and international clinical pharmacology laboratories (CPLs) which support NIAID/DAIDS funded HIV/AIDS clinical pharmacology and clinical trial networks. The PT program has included more than 27 different antiretroviral (ARV) drugs since its inception.

In a previous report,² we developed and tested regression models to longitudinally assess the precision and accuracy of reported concentrations (RCs) by individual CPLs. We compared estimates of error and bias between models in which the assigned nominal concentration (NC) of ARV analytes was set to either the formulated weighed-in-value (WIV) (ie NC=WIV) or to a final-target-value (FTV) comprised of a hybrid of either WIV or the group mean (ie NC=FTV) (The algorithm is specified in the previous report). We further employed analysis of covariance (ANCOVA) models to identify factors associated with program accuracy and precision. We found that use of the NC=FTV algorithm attenuated estimates of bias overall and as a function of concentration magnitude. The NC=FTV algorithm is therefore a better model when ensuring inter-laboratory comparability is the goal. Prediction intervals from the regression of recovery on NC=FTV further suggested that a smaller window of acceptance should be considered. According to the ANCOVA models, we identified that CPL, analyte, and ARV-specific concentration category (low/medium/high for the ARV) as the three factors that exhibited significant associations with bias and/or error, while other factors including PT round and ARV-independent concentration category (WIV in ranges: 30–200, 200–500, 500–1200, 1200–3200, and 200–8000 ng/mL) did not.

Here, we provide a more comprehensive analysis by focusing on results for the eight most frequently tested ARVs including atazanavir (ATV), darunavir (DRV), efavirenz (EFV), emtricitabine (FTC), lopinavir (LPV), nevirapine (NVP), ritonavir (RTV), and tenofovir (TFV), across 13 PT rounds, not previously reported, conducted from 2010 to 2016. Our goal is to provide better estimates of the main sources of variability, to evaluate in more detail the accuracy of the algorithm for the assessment of performance, and to assess the effect of narrowing the acceptance window on acceptance rates.

Methods

PT PROGRAM

The CPQA PT program designs, prepares and distributes two PT exercises (rounds) per year. Blank plasma matrix is spiked with drugs to attain pre-specified concentrations of ARV analytes. These pre-specified concentrations are termed the weighed-in-value (WIV) and are prepared using reference ARVs obtained from the NIH-AIDS Research and Reference Reagent Program.³ Each ARV is provided at five different concentrations, which are appropriate for samples both within the therapeutic range as well as occasional samples above or below said range. ARVs are incorporated into two PT panels; currently nine analytes are included in panel A, six analytes are included in panel C and 1 analyte is included in Panel E. Prepared PT samples are stored at −70 ± 15°C and initially pre-qualified by the CPQA analytical laboratory. Pre-qualification analysis is never used to alter the NC of PT samples but rather used to ensure that gross formulation errors have not occurred. PT samples are then shipped on dry ice to participating CPLs with detailed instructions. Using an online Laboratory Data Management System (LDMS), each laboratory confirms receipt and sample integrity, indicates planned reporting of specific analytes, and submits assay results (ie. RCs). At the end of the submission period, a completeness evaluation is performed to confirm that all planned results are received; discrepancies are queried for resolution.

PT SCORING ALGORITHM

The most common methods for assigning NC in PT programs are based on either a reference value (determined as the formulated weighed in value, WIV) or a consensus value of the participants such as the mean of reported concentrations (group mean, GM).⁴ CPQA PT employs a hybrid of these two methods to assign NC, which we term the final-target-value (FTV). In our algorithm, FTV is set to the WIV by default. The GM rather than WIV is used as the FTV only when the percent deviation of GM (determined after removal of outliers, if any) from the WIV is >5%, the number of laboratories reporting for that sample is large enough (4 or more), and the coefficient of variation between CPLs’ RCs is ≤15%. The GM is also used as the FTV when the number of laboratories reporting is exactly 3 and the coefficient of variation among CPLs is ≤ 15% (regardless of percent deviation of GM from WIV).² Therefore, our independent variable in all analyses was log (FTV).

The PT scoring algorithm reflects US Clinical Laboratory Improvement Act (CLIA) PT regulations.⁵ Each individual RC receives an RC Score of “Acceptable” provided it is within ± 20% of FT.⁶ Concentrations below a CPLs limit of quantitation are assigned a censor code indicating that the sample was either below sensitivity of the assay or undetectable. RCs outside ± 20% receive an RC Score of “Unacceptable”. Each ARV analyte is provided at five different concentrations in each round. These five RC scores reported by a CPL are pooled to determine the CPL’s overall performance for that analyte termed the “ARV/Round Score.” The “Satisfactory” score is assigned when at least 80% of the RCs (4 out of 5 levels for a single analyte) have a RC Score of acceptable. Less than 80% “Acceptable” leads to an “Unsatisfactory” ARV/Round Score for the particular analyte.

Statistical Analysis

DESCRIPTIVE SUMMARY

To describe the characteristics of the PT program, we present an update to the previous report focusing on results from eleven CPLs, across 13 PT rounds (December 2010 to July 2016) and the eight most commonly tested ARVs which were included in all PT rounds: atazanavir (ATV), darunavir (DRV), efavirenz (EFV), emtricitabine (FTC), lopinavir (LPV), nevirapine (NVP), ritonavir (RTV), and tenofovir (TFV). All RCs with an assigned RC score, either acceptable or unacceptable, were retained in the descriptive table. We summarized the number of RCs and the percentage of RCs that achieved an RC Score of “Acceptable” for each analyte/CPL combination, for each analyte pooled over all CPLs, and for each CPL pooled over all analytes. We also summarized the number of ARV/Round Scores, and the percentage of ARV/Round Scores that were “Satisfactory” for each analyte pooled over all CPLs and for each CPL pooled over all analytes. For each analyte, we also summarize: (1) the number of unique samples, (2) the percentage where PD ≤ 5%, (3) the percentage where CV ≤ 15%, and (4) the percentage where FTV = WIV.

COMPARISON OF PT ASSESSMENT WITH PREDICTION LIMITS AROUND ESTIMATED REGRESSION EQUATIONS

An alternate criterion to assign RC scores was based on fitting a linear regression model describing the relationship between the natural log of RCs (dependent variable) to the natural log of FTV concentrations (independent variable). Those RCs falling inside 95% prediction limits around the estimated regression equation were deemed acceptable; the rest were deemed unacceptable.

In order to assess the accuracy of the PT scoring algorithm used, comparisons with the linear regression model were made by the calculation of binary classification metrics including sensitivity, specificity, positive predictive value, negative predictive value and overall accuracy. Sensitivity was defined as probability that the RC was acceptable by the PT program algorithm when it was also acceptable according to the regression model (true acceptable rate). Specificity was defined as probability that the RC was unacceptable by the PT program algorithm when the RC was also unacceptable according to the regression model (true unacceptable rate). Positive predictive value was defined as the probability that when the RC was acceptable in the linear regression model, the RC was also deemed acceptable in the PT program algorithm. Negative predictive value was defined as the probability that when the RC was unacceptable in the linear regression model, the RC was also deemed unacceptable in the PT program algorithm. Accuracy was defined as the overall probability that a RC will be correctly classified.⁷ In order to further examine our previous findings suggesting that a smaller window of acceptance should be considered,² these calculations were made employing an acceptability thresholds of ± 20% and ±15% around the FTV. Furthermore, we illustrate the effect of the threshold on PT performance by plotting the false acceptable and false unacceptable rates for thresholds from 5% to 30%.

VARIANCE-COMPONENTS ANALYSIS

To assess the relative contributions of analyte, CPL and analyte-specific concentration category to the magnitude of assay bias (signed differences between nominal and reported) and variability (absolute values of the differences between nominal and reported concentrations; absolute value ensures that over- and under-estimation of the same absolute magnitude are treated the same), we performed variance-components analyses. In the analysis of variability, for the dependent variable: we first calculated the absolute recovery$, \frac{100\times [FinalTargetValue+abs\left(FinalTargetValue-ResultUsed\right)]}{FinalTargetValue}$, then ranked the absolute recovery, and performed the variance-components analysis by fitting a linear mixed-effects model to the ranks. As we anticipated that bias and variability could be higher for samples at the low and high ends of the concentration spectrum, analyte-specific concentration category (low, medium and high) was treated as a fixed effect. As we wanted to infer about analytes and laboratories in general, analyte, CPL and their interaction were treated as random effects (that is, analytes and CPLs were treated as samples from a (theoretical) larger population). Models specifications are given in the statistical supplement.

Results

DESCRIPTIVES

For the 13 PT rounds, a total of 9,486 RCs for PT specimens were reported by participating laboratories. Of these, 3,002 RCs were excluded from the final report; these RCs are also not considered herein. Reasons that an RC was excluded from the final report include: RC was used for a test panel, for a blank sample or for analytes that the laboratory did not select for PT. Results for a total of 27 analytes were included in the round-specific final reports across the 13 rounds, however, this report focuses on the 8 most clinically relevant analytes that were included in all 13 rounds, for which there were 4,124 RCs. Of these 4,124 RCs, 15 were not scored for PT (result not quantifiable). The remaining 4,109 RCs received scores of either Acceptable or Unacceptable. These 4,109 RCs are included in descriptive analyses herein.

Additional exclusions apply in the model-based analyses herein, where RC is the continuous dependent variable, and the goal is to evaluate analytical variability, not pre-or post-analytical events such as transcription errors. Specifically, the following types of RCs were excluded: 6 RCs were reported as below the lower limit of quantitation, 13 additional RCs where a result was expected but absent, 5 RCs where incorrect units were entered for the upper and lower assay limits, 32 RCs where the percent deviation between the RC and the final target value was above 50% in absolute value, and an additional 4 RCs where the percent deviation was above 20% in absolute value and the lab received an “Unsatisfactory” analyte score for all samples for the analyte due to clerical errors (data-entry transcription, incorrect units reported, etc). Thus 4,049 RCs are retained in the model-based analyses herein.

CHARACTERISTICS OF SAMPLES AND SCORES

For each analyte and CPL combination, Table 1 lists the overall number of RCs, RC Scores and ARV/Round Scores and the percent that received acceptable or satisfactory scores. Column 1 gives the ARV analytes and the range of concentrations formulated into PT samples. The second-to-last row of Table 1 gives the total number of Result Scores for each CPL (pooling analytes) and the CPL-specific percentages of Result Scores that were deemed acceptable, based on the decision rule, “acceptable if within ±20% of FTV”. The number of RCs per lab ranges from 130 (for lab 3) to the maximum of 520 (for lab 2). Only laboratories 3 and 11 reported fewer than 300 concentrations. The percent acceptable scores range from 93% (for lab 9) to 100% (for laboratories 2 and 8). The last row of Table 1 gives the total number of ARV/Round Scores issued for each CPL, which ranges from 26 (for lab 3) to the maximum of 104 (for laboratory 2). The last row also shows laboratory-specific percentages of ARV/Round Scores that were deemed Satisfactory. These range from 89% (for laboratory 9) to 100% (for laboratories 2 and 8).

Table 1:

Overall descriptive characteristics of all Clinical Pharmacology Quality Assurance Proficiency Testing reported concentrations (RC) from 11 individual clinical pharmacology laboratories for 8 antiretroviral analytes during 13 rounds conducted from 2010 through 2016.

	# RCs by CPL (%Acceptable)
ARV (range, ng/mL)	1	2	3	4	5	6	7	8	9	10	11	RC Score (% Acceptable)	ARV/Round Score (% Satisfactory)
ATV (150–12000)	65 (100)	65 (100)		60 (98)	65 (89)	65 (97)	30 (100)	45 (100)	55 (98)	55 (95)		505 (97)	101 (97)
DRV (350–12000)	65 (98)	65 (100)		60 (100)	50 (100)	65 (100)	50 (96)	45 (100)	55 (100)	65 (98)		520 (99)	104 (99)
EFV (230–20000)	65 (100)	65 (100)		55 (95)	65 (100)	65 (100)	65 (100)	45 (100)	60 (98)	50 (100)	50 (92)	585 (99)	117 (98)
FTC (25–4500)	65 (100)	65 (100)	65 (94)	25 (100)	30 (100)	20 (70)		65 (100)	60 (88)	15 (100)		410 (96)	82 (93)
LPV (220–24000)	65 (100)	65 (100)		60 (98)	65 (100)	65 (97)	65 (100)	45 (100)	50 (80)	50 (98)	55 (93)	585 (97)	117 (96)
NVP (225–12000)	65 (100)	65 (100)		55 (91)	65 (100)	65 (89)	50 (96)		60 (90)		54 (96)	479 (95)	96 (96)
RTV (75–5800)	30 (67)	65 (100)		60 (98)	65 (97)	55 (84)	65 (98)	45 (100)	60 (93)	65 (97)	45 (100)	555 (95)	111 (95)
TFV (30–600)	65 (97)	65 (100)	65 (95)	25 (100)	60 (98)		35 (100)	65 (100)	60 (92)	15 (100)	15 (100)	470 (98)	94 (96)
RC Score (% Acceptable)	485 (97)	520 (100)	130 (95)	400 (97)	465 (98)	400 (94)	360 (99)	355 (100)	460 (93)	315 (98)	219 (95)
ARV/Round Score (% Satisfactory)	97 (97)	104 (100)	26 (92)	80 (98)	93 (97)	80 (93)	72 (97)	71 (100)	92 (89)	63 (98)	44 (95)	4109(97)	822(96)

CPL: clinical pharmacology laboratory, ARV: antiretroviral, RC: reported concentration, ATV: atazanavir, DRV: darunavir, EFV: efavirenz, FTC: emtricitabine, LPV: lopinavir, NVP: nevirapine, RTV: ritonavir, and TFV: tenofovir

The second-to-last column gives the total number of Result Scores for each analyte (pooling CPLs) and the analyte-specific percentage of Result Scores that were deemed acceptable. The number of RCs per analyte ranges from 410 (for FTC) to 585 (for EFV and LPV). No single analyte was reported by all 11 CPLs. The second-to- last column also gives analyte-specific percentages of RCs that received acceptable RC Scores. Percent acceptable ranges from 95% (for NVP and RTV) to 99% (for DRV and EFV). The last column gives the total number of ARV/Round Scores issued for each analyte, which ranges from 82 (for FTC) to 117 (for EFV and LPV). Analyte-specific percentages of satisfactory ARV/Round Scores are also shown; these range from 93% (for FTC) to 99% (for DRV).

For each analyte, Table 2 gives the number of unique samples tested, and the percentages where: (1) percent deviation (PD) from WIV ≤ 5%, (2) coefficient of variation (CV) ≤ 15%, and (3) WIV (as opposed to GM) was selected as the final target value. Sixty-five unique samples were analyzed for each of the eight analytes. Among these analytes, percentage of PD ≤ 5% ranges from 34% (DRV) to 80% (TFV), while percentage of CV ≤ 15% shows a smaller range from 92% (FTC) to 100% (DRV). Percentage where FTV = WIV has a similar pattern as percentage of PD ≤ 5% (range: 34% - 78%). Since the variations between the RCs for a specific analyte sample are controlled within a good range for all eight analytes, based on our algorithm to select the FTV, when GM for a specific analyte sample is close to WIV, WIV is selected as the FTV, otherwise GM is selected as the FTV as long as the number of RCs are large enough for that sample.

Table 2:

Characteristics of Samples by Analyte

ARV	No. Unique Samples	% Where PD <= 5%	% Where CV <= 15%	% Where FTV = WIV
ATV	65	71	95	72
DRV	65	34	100	34
EFV	65	57	98	57
FTC	65	68	92	68
LPV	65	75	94	75
NVP	65	46	97	49
RTV	65	77	95	78
TFV	65	80	98	78

PD: Percent deviation, CV: coefficient of variation, FT: final target concentration, WIV: weighed in value, ATV: atazanavir, DRV: darunavir, EFV: efavirenz, FTC: emtricitabine, LPV: lopinavir, NVP: nevirapine, RTV: ritonavir, and TFV: tenofovir.

VARIANCE-COMPONENTS ANALYSIS

Variance-components analyses used mixed effects models to estimate the contribution of each random effect to the total variance of the dependent variable and identify the major contributing factors. Table 3 provides a summary of the variance-components analysis. In the model treating Analyte and CPL as random effects and analyte-specific concentration as a fixed effect with all interaction terms included, CPL accounts for 2.6% of bias and 4.4% of error with a small contribution from analyte and the remaining variation is random. Interactions in the model indicates that interaction between analyte and laboratory (analyte/laboratory combinations) account for 3.4% of error and 8.1% of bias, with much smaller contributions from other combinations. The remaining variation is random.

Table 3.

Summary of variance components analyses (CPL and analyte treated as random effects, analyte-specific concentration category as a fixed effect, all interaction terms included).

Measure	CPL	Analyte	[C]cat	CPL*analyte	Analyte*[C]cat	CPL*[C]cat	CPL*analyte*[C]cat
Bias	2.6%	<0.5%	--	8.1%	<0.5%	<0.5%	2.0%
Error	4.4%	0.5%	--	3.4%	<0.5%	<0.5%	1.0%

CPL; clinical pharmacology laboratory, [C]cat; analyte-specific concentration category

PARAMETER ESTIMATES FROM FITTING REGRESSION MODELS

When WIV is used as the NC, the estimated intercept is negative, and the estimated slope is positive (data not shown). Both estimates are statistically significant. When NC=FTV, the estimated intercept is not significantly different from zero. The estimated slope, while statistically significant (different from the value 1.0), is only different from the (null) value 1.0 at the 1/10,000 decimal place.

ACCURACY OF THE PERFORMANCE ASSESSMENT ALGORITHM

Table 4 compares the PT scoring algorithm with the prediction model using 95% prediction limits around the estimated regression equation at both ±20% and ±15% thresholds. Considering first the ±20% cut-off, the PT scoring algorithm and the prediction model agree for 96.67% accuracy of RCs; 94.91% where both are acceptable and 1.75% where both are unacceptable. There are 3.33% of RCs deemed acceptable by the PT scoring algorithm but unacceptable by the prediction model, while there is no RC discrepant in the other direction.

Table 4:

Binary classification metrics of RC scores of the CPQA PT program compared to the RC scores of the prediction model where the success criterion is within 95% prediction limits around the estimated regression line. The comparison is made where the criterion for acceptable result score (cut-off) is within ±20% or ±15% around the final target.

Comparison group	±20% Cut-off		±15% Cut-off
	Count	Percent	Count	Percent
Both are Acceptable (a)	3843	94.91	3832	94.64
Acceptable in PT program but Unacceptable in Prediction Model (c)	135	3.33	32	0.79
Unacceptable in PT program but Acceptable in Prediction Model (b)	0	0	11	0.27
Unacceptable in PT program and Unacceptable in Prediction Model (d)	71	1.75	174	4.30
Sensitivity (a/(a+b))		100.00		99.71
Specificity (d/(c+d))		34.47		84.47
Positive Predictive Value (a/(a+c))		96.61		99.17
Negative Predictive Value (d/(b+d))		100.00		94.05
Accuracy ((a+d)/(a+b+c+d))		96.67		98.94

When a ±15% threshold window is applied to the PT scoring algorithm, the two methods agree for 98.94% accuracy of RCs; 94.64% where both are acceptable and 4.30% where both are unacceptable. Compared with the ±20% cut-off, at ±15% the agreement where both are acceptable is very similar (94.9% vs. 94.6%), while agreement on unacceptable increases from 1.75% to 4.30%. The percent of RCs acceptable by PT scoring algorithm and unacceptable by the prediction model decreases, from 3.33% to 0.79%, and the percent unacceptable by PT scoring algorithm and acceptable by prediction model very slightly from 0 to 0.27%.

A clearer picture appears in calculating and examining the binary classification metrics. Using a 20% cut-off, the main deficiency of the current PT scoring algorithm is a lack of specificity where only 34.47% (71 out of 206) of unacceptable analyte scores detected by the prediction model are also detected by the PT scoring algorithm which, appears to miss nearly two-thirds of all scores that would be scored unacceptable by the prediction model.

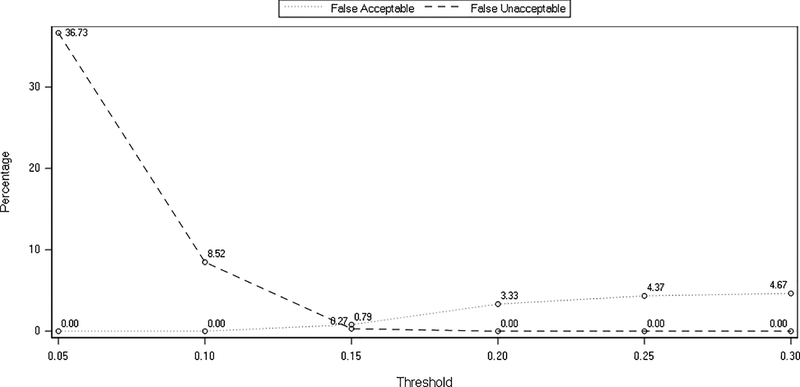
Application of a 15% cut-off greatly increases the specificity of the PT scoring algorithm from 34.47% to 84.47% where 174 of 206 of unacceptable analyte scores detected by the prediction model are also detected by the PT scoring algorithm. The ±15% threshold also increases the overall accuracy from 96.67% to 98.94% and results in only small reductions in sensitivity and negative predictive value. This relationship between false acceptable and false unacceptable rates is illustrated graphically in figure 1. False acceptable rates rise, and false unacceptable rates fall as the acceptance criterion increases from ±5% to ±30%. Values for both parameters clearly reach a common minimum at a ±15% cut-off.

Figure 1:

Effect of acceptance window threshold (±5% to ±30%) on the percentage of false acceptable and the false unacceptable reported concentrations.

Beyond the acceptability of individual RC Scores, the satisfactory performance of a CPL for an ARV analyte, during a PT round, is based on attaining a satisfactory ARV/Round Score. To examine the impact of the low sensitivity of the PT scoring algorithm at a ±20% cut-off on the overall PT program, we calculated the number of ARV/Round Score assignments (satisfactory or unsatisfactory) which would have actually changed as a result of employing a ±15% cut-off. Table 5 shows that of 822 total ARV/Round Scores, 791 (96%) were deemed satisfactory using a ±20% cut-off in contrast to 765 (93%) satisfactory using a ±15% cut-off.

Table 5:

Comparison of analyte scores, using PT algorithm, for result score thresholds of ±20% or ±15% around the final target value.

Criterion for Satisfactory Analyte Score	Number of Satisfactory Analyte Scores	Total number of Analyte Scores	Percent of Analyte Scores that are Satisfactory
Within ±20% of Final Target Value	791	822	96%
Within ±15% of Final Target Value	765	822	93%

Discussion

Previous longitudinal examination of CPQA PT performance used fewer rounds of PT results but a broader spectrum of ARV analytes to conduct longitudinal analysis of PT across multiple CPLs.² We developed and tested statistical models that longitudinally assessed the precision and accuracy of concentrations reported by individual CPLs and determined factors associated with round-specific and long-term assay accuracy, precision, and bias using a new regression model. These analyses helped us determine that our NC=FTV scoring algorithm is tenable compared to a scoring algorithm employing only the formulated WIV. Use of the WIV only, to assign the NC, has the desirable statistical property that it is independent of the dependent RC variable, however it is biased from the true but unknown concentrations in the PT samples and is extremely sensitive to PT sample preparation error. The CPQA PT scoring algorithm is designed to prevent application of the unacceptable NC when there was a preparation error and uses FTV (set by either WIV or GM) to assign NC and to ultimately determine acceptable/unacceptable PT performance. The drawback in using FTV as the independent variable is that, when the GM is substituted, the independent variable is not statistically independent from, but is based on, subsets of RCs (i.e., the dependent variable). In this report, parameter estimates from fitting regression models indicates that, overall, the agreement between RC and NC is better when NC=FTV, with the estimated intercept near zero and the estimated slope near 1.0. Therefore, our independent variable in all analyses was log (FTV).

Our prior univariate analyses² also helped us identify several factors, including CPL, analyte and analyte concentration as the most significant contributors to variability and bias. Here, variance component analyses were done by using mixed effects models to estimate the contribution of analyte and CPL as random effects, and analyte-specific concentration category as a fixed effect, to the total variance of RCs. Although only our final mixed model (2 random error and 1 fixed effect with interactions) is presented here, we examined multiple versions of the models treating all components as random effects both with and without interactions. In all these models, the components of variation were in similar magnitude and rank order and analyte specific concentration category (high/medium/low) was better characterized as a fixed effect. We choose to model analyte concentration as a fixed effect as the accuracy and precision of the liquid chromatography-mass spectrometry (LC-MS) methodologies, and analytical methodologies in general, tend to have distinct patterns of decreased precision and accuracy at the upper and lower limits of the dynamic range. At low concentrations, we expect increased imprecision and decreased accuracy due to low signal-to-noise ratios and the fact that our client CPLs follow FDA guidelines for bioanalytical method validation.⁸ These guidelines allow ±20% deviation and a 20% imprecision (expresses as percent coefficient of variation; %CV) for the lowest calibrations and validation quality control materials as opposed to a 15% limits throughout the remaining analytical range. At upper limits, ion suppression effects and/or decreased ionization efficiency tend to decrease precision and accuracy. Our findings agree with our previous univariate models in that mainly individual CPL, and to a lesser degree ARV analyte, appear to be the main drivers of variability and bias beyond random error.

In order to examine the accuracy of the CPQA PT scoring algorithm, we generated binary classification metrics of the PT scoring algorithm versus scoring using 95% prediction limits around estimated regression equations as the “gold standard” comparator. The current PT scoring algorithm (RC is acceptable within ±20% of FTV) demonstrates 96.67% accuracy with the prediction model yet suffers from a relatively low specificity of only 34.47%. This means that the PT scoring algorithm tends to miss “true” PT failures at the level of individual RCs. Altering the PT scoring algorithm to use a ±15% window greatly increases the specificity to 84.47% and also increases the overall accuracy to 98.94%. This indicates that the current ±20% window may be too lenient. Indeed, our client CPLs have validated their methods to meet ±15% accuracy and 15% imprecision (%CV) thresholds according to FDA guidelines. This is evident in the improved performance metrics for the overall program when a stricter ±15% window is enforced.

Caution, however, should be taken in considering the prediction model as the “gold standard” comparator. There are limitations in the use of prediction limits around the regression model as the “gold standard” for determining the RC score. The model assumes that RCs are log-normally distributed and have a linear relationship with logs of the FTV. Using the 95% prediction limits as thresholds for “Acceptable”, 5.1% of RCs are identified as “Unacceptable” (Table 5); this is the expected percentage of RCs outside the limits under the null hypothesis that all log RCs arise from the same populations (that is, populations with expected values of 0.002 + log (FTV)). Future work may evaluate the performance of the prediction limits as limits of acceptability when specific types of assay problems are postulated. In particular, focused analysis on the effect of a more restrictive acceptance window on PT performance at lower concentrations is warranted. In contrast to our findings that analyte specific concentration category is a not a major source of variability, The International Interlaboratory Quality Control Program for Therapeutic Drug Monitoring of Antiretroviral Drugs in Human Plasma/Serum has reported that concentration range is the only significant predictor of inaccurate results with lower concentrations performing worse than medium or high concentrations.^{9, 10}

Conclusions

The current CPQA PT scoring algorithm employing a ± 20% acceptance window appears to suffer from a low specificity and may be too lenient. A stricter ±15% acceptance window would increase specificity and overall accuracy while lowering the overall PT program pass rate by only 3%.