Abstract
Purpose:
To assess the impact of the number of iterations of compressed sensing (CS) reconstruction on the kinetic parameters and image quality in dynamic contrast-enhanced (DCE)-MRI of the breast, with prospectively undersampled CS-accelerated scans.
Materials and Methods:
Breast examinations including ultrafast DCE-MRI using CS were conducted for 21 patients. Images were reconstructed with different numbers of iterations. The peak enhancement ratio of the aorta and wash-in slope, initial area under the curve, and Ktrans of the breast lesions were measured. The root mean square error and structural similarity between the images using 50 iterations and images with a lower number of iterations were evaluated as criterion for quantitative image evaluation.
Results:
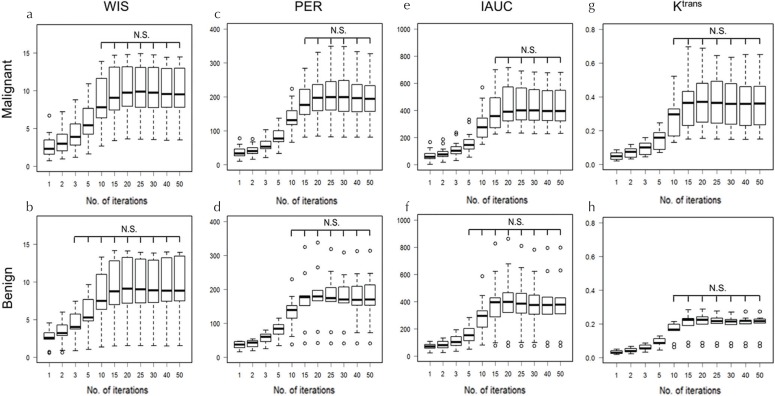
Using an insufficient number of iterations, the contrast-enhanced effect was highly underestimated. In all semi-quantitative parameters, the number of iterations that stabilized the parameters in malignant lesions was higher than that in benign lesions. At least 15 iterations were needed for semi-quantitative parameters. For Ktrans, there were no significant differences between 10 and 50 iterations in both malignant and benign lesions.
Conclusion:
The kinetic parameters using ultrafast DCE-MRI with CS are affected by the number of iterations, especially in malignant lesions. However, if the images are reconstructed with an adequate number of iterations, ultrafast DCE-MRI with CS can be a powerful technique having high temporal and spatial resolution.
Keywords: breast, compressed sensing, iteration, magnetic resonance imaging, ultrafast dynamic contrast-enhanced-magnetic resonance imaging
Introduction
Dynamic contrast-enhanced (DCE)-MRI is widely used as a powerful imaging tool to evaluate breast lesions. For DCE-MRI, a contrast agent is injected into the blood stream before or during the acquisition of a series of T1-weighted images using fast imaging techniques. By analyzing the changes of the MR signal intensity over time, semi-quantitative analyses based on the time-intensity curve (TIC) can be performed, and quantitative parameters can be estimated by fitting pharmacokinetic models. Several studies have shown the benefit of qualitative and quantitative kinetic parameters for distinguishing malignant from benign lesions1–4 and assessing the response of breast cancer to neoadjuvant chemotherapy5 and radiation therapy.6 Detailed kinetic information, particularly for quantitative kinetic parameters, requires high temporal resolutions. On the other hand, morphological assessment of the lesion, another important feature of lesion characterization, requires high spatial resolution. Recently, compressed sensing (CS) has become available for the acceleration of dynamic MRI acquisitions, which is achieved by enabling the reconstruction of subsampled data.7 Along with the promising results from ultrafast DCE-MRI with much shorter acquisition time,8–12 CS is regarded as one of the accelerated methods to use in the clinical setting. Utilization of CS algorithms can improve the temporal/spatial resolution of DCE-MRI, and several works describing retrospective simulations have demonstrated the feasibility of such improvements.9,13,14–16 Many of the reports on DCE-MRI using CS are retrospective studies in which fully sampled raw data sets are downsampled after data collection. Khalsa and Fessler17 showed how the regularization parameters used in CS reconstruction affected the TIC. In many studies for optimizing the parameters used in the CS reconstruction, the calculation of image reconstruction was continued until iterative reconstruction converges to get images that satisfy the L1 minimization problem. However, because many CS reconstruction techniques are computationally intensive, the generation of images using these techniques can take a significant amount of time, this not ideal in a clinical settings. With the number of iterations in the numerical CS optimization typically fixed to avoid prolonged reconstruction times, a careful analysis of its effect on the final results is highly desirable, in particular to minimize the estimation error in lesion-enhancement characteristics. The aim of this study was to assess the impact of the number of iterations used in CS reconstruction on kinetic parameters and the image quality in ultrafast DCE-MRI of the breast, with prospectively undersampled CS-accelerated scans.
Materials and Methods
Patients
The study was approved by the Institutional Review Board with waiver of informed consent, because of the retrospective collection of the clinical breast MRI data. High-temporal CS-accelerated examination was part of the hybrid protocol with conventional DCE-MRI with the same total image acquisition time as our standard clinical breast DCE-MRI protocol. The dataset includes 21 DCE-MRI examinations acquired from 20 female and one male (mean 53.9 years; range 33–82 years) who underwent clinical breast DCE-MRI with a high-temporal CS-accelerated examination for either the evaluation of suspicious lesions on mammography/ultrasonography or preoperative evaluation, from December 2015 to March 2016. The raw data of each CS-accelerated examination were saved and available for prospectively testing various CS reconstruction parameters. The diagnosis was pathologically confirmed based on the histopathology of surgically excised specimens and/or needle core biopsies. There were 18 breast cancers: nine invasive carcinomas of no special type, two invasive lobular carcinomas, one mucinous adenocarcinoma, and six ductal carcinomas in situ (DCISs). There were three benign lesions pathologically confirmed as papilloma (n = 1), fibroadenoma (n = 1), and fibroepithelial neoplasm (n = 1). The remaining five lesions were diagnosed as benign on MRI and followed-up for at least 12 months without showing any sign of malignancy. The study population of the current analysis was partially overlapped with the previous study18 which aimed to visualize breast vessels associated with ipsilateral breast lesions.
MRI acquisition
Bilateral breasts were scanned using a 3T system (MAGNETOM Skyra, Siemens Healthcare, Erlangen, Germany) and an 18-channel dedicated breast coil, with patients in the prone position. The DCE-MRI consisted of ultrafast MRI using the prototype sequence (from 13 s before to 60 s after contrast injection), followed by standard DCE-MRI sequence of initial phase (60–120 s), delayed phase (300–360 s) and high spatial resolution post-contrast images between these two phases (120–300 s). The ultrafast DCE-MRI data used for the current analysis were acquired using a prototypical non-fat-suppressed 3D volumetric interpolated breath-hold examination (VIBE) sequence using a variable-density sampling in the phase-encoding plane obeying a Gaussian distribution with the following imaging parameters: TR = 5.04 ms, TE = 2.46 ms, flip angle (FA) = 15°, slice thickness = 2.5 mm, 60 partitions, matrix size = 384 × 269, FOV = 360 × 360 mm2, CS acceleration = 16.5, and temporal resolution = 3.65 s. DCE-MRI was sequentially acquired at 20 consecutive time points (preceded by 2 s preparing time) with a total acquisition time of 75 s. Thirteen seconds after scan commencement, 0.1 mL/kg gadoteridol was injected at 2 mL/s, followed by 20 mL of saline flush injected at 2 mL/s. For the analysis of the quantitative parameters, pre-contrast T1 maps with B1 field inhomogeneity correction using the dual-FA method (2° and 15°) were acquired.
Compressed sensing image reconstruction
Compressed sensing reconstruction was conducted with the following minimization problem:
| (1) |
where A represents the system matrix including undersampled Fourier transform and coil profiles, x is the reconstructed image, y is the measured k-space data, W is a linear operator that first performs a Haar wavelet decomposition in both spatial and temporal dimension with a regularization parameter, λ. The regularization in this CS reconstruction is done for low- and high-frequency components in wavelet space. In this study, these regularization parameters were chosen for each frequency, 0.002 and 5.000, respectively. The number of iterations for a fast iterative shrinkage-thresholding algorithm19 optimization using a time-averaged starting point = 1, 2, 3, 5, 10, 15, 20, 25, 30, 40, and 50.
The reconstruction was implemented in C++ and integrated into the scanner reconstruction pipeline. Reconstructions with a varying number of iterations were performed retrospectively within the scanner environment on CPU system. Reconstruction time per each number of iterations was recorded and compared.
Data analysis
DCE-MRI parameters
Semi-quantitative parameters were derived voxel by voxel from the TIC and analyzed using a custom-made Matlab (The MathWorks, Inc., Natick, MA, USA) program. The semi-quantitative parameters were as follows: wash-in slope (WIS) between arrival and peak enhancement time, peak enhancement ratio (PER) along the kinetic curve, and initial area under the curve (IAUC), which was defined as the area from contrast arrival to after 5th phase.
From the DCE-MRI data sets, the quantitative parameter Ktrans (the transfer constant of contrast from the plasma to the tissue extracellular extravascular space [EES]) was calculated based on the Tofts20 model using the DCE Tool plug-in for Osirix (http://kyungs.bol.ucla.edu/software/DCE_tool/DCE_tool.html).21 The pharmacokinetic analysis was performed using the population-based arterial input function reported by Walker, et al., modified by Frits-Hansen.22 Semi-quantitative and quantitative parameters were obtained for the selected set of number of iterations.
Quantitative image evaluation
The reconstructed images were evaluated by the root mean square error (RMSE) and structural similarity (SSIM). The RMSE was calculated as follows:
| (2) |
| (3) |
where X are the reference images, which were reconstructed with the maximum number of iterations (in the present study, 50), and Y are the images reconstructed with the other selected number of iterations.
The SSIM index compares local patterns of pixel intensities that have been normalized for luminance and contrast.23 It is based on the idea that the human visual system is good at extracting information based on structure:
| (4) |
where X and Y are the local windows for the reference and reconstructed images, respectively, μX and μY are the averages of X and Y, respectively, σX and σY are the variances of X and Y, respectively, and σXY is the covariance of x and y. c1 = (K1L)2 and c2 = (K2L)2 are the two variables to stabilize the division with a weak denominator, where L is the dynamic range of the pixel-values, K1 = 0.01 and K2 = 0.03. The SSIM index was measured between the images using 50 iterations and the remaining selected iterations by the formula above using a custom-made Matlab program.
Statistical evaluation
All P-values were two-sided and P ≤ 0.05 were considered statistically significant. All statistical analyses were performed with EZR software (Saitama Medical Center, Jichi Medical University, Saitama, Japan), which is a graphical user interface for R (The R Foundation for Statistical Computing, Vienna, Austria). More precisely, it is a modified version of R commander designed to add statistical functions frequently used in biostatistics. The Dunnett’s test was performed to compare DCE-MRI parameters (WIS, PER, IAUC, and Ktrans) and the image evaluation values (RMSE and SSIM) between images using 50 iterations and the remaining selected iterations.
Results
Reconstruction time
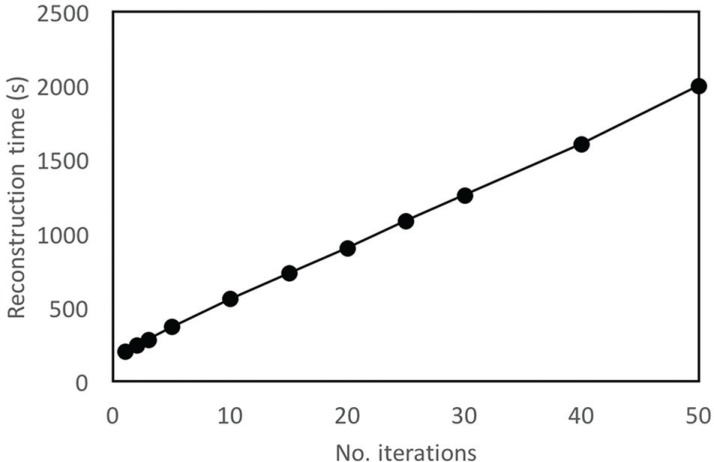
The reconstruction time was prolonged as the number of iterations increases. DCE-MRI images reconstructed using 50 iterations required approximately 35 min (Fig. 1).
Fig. 1.
The reconstruction time with different numbers of iterations. In total, 1200 images (60 slices × 20 phases) were reconstructed with each number of iterations.
Effects of the numbers of iterations on signal intensity
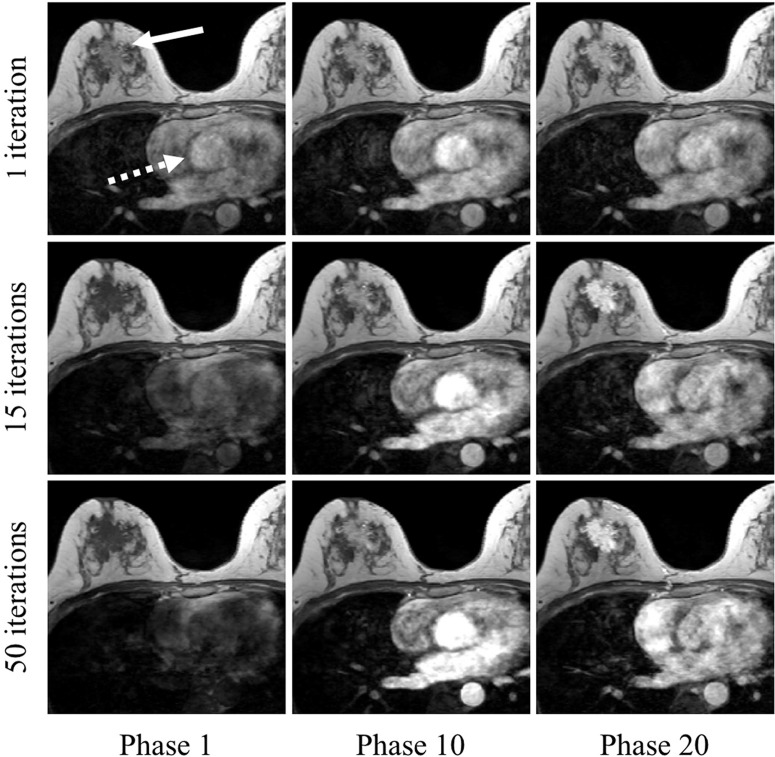
The images of example lesions reconstructed with different numbers of iterations at the different time points are shown in Fig. 2. The signal of the aorta (dashed arrow) using one iteration pre-contrast (Phase 1) was higher than that using 50 iterations. Conversely, the signal of the aorta using one iteration post-contrast (Phases 10 and 20) was lower than that using a higher number of iterations. This tendency was similar in the malignant lesion (arrow).
Fig. 2.
Images reconstructed using different numbers of iterations (top row: one iteration; middle row: 15 iterations; bottom row: 50 iterations) at different time points (left column: phase 1 [pre-contrast]; middle column: phase 10; right column: phase 20). On the pre-contrast images (Phase 1), the signal of the regions of interest, such as aorta (dashed arrow) and malignant lesion (arrow) using one iteration shows high intensity, despite the phase before contrast arrival. On the post-contrast images (Phases 10 and 20), the signal of these regions using one iteration is lower than that using 15 or 50 iterations. compressed sensing (CS) reconstruction used in this study was L1 minimization problem in both spatial and temporal direction. In small number of iterations, the reconstructed images were strongly affected by the regularization in time domain. As a result, the error in pre-contrast phase and the reduction of contrast-enhanced effects occurred.
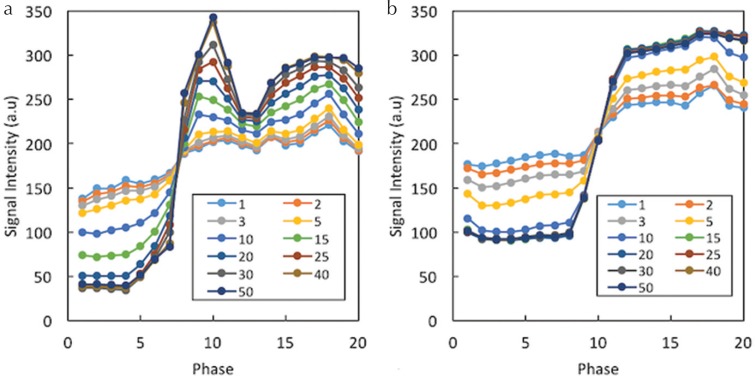
Exemplary results of the TIC for the aorta (a) and malignant lesion (b) for different numbers of iterations are shown in Fig. 3. The signal intensity pre-contrast decreased as the number of iterations increased. In comparison, the signal intensity post-contrast increased as the number of iterations increased. Therefore, the signal difference between the pre- and post-contrast images was higher for the larger numbers of iterations. This effect was greater for the aorta than for the lesion, and the required minimum number of iterations stabilizing the TIC was larger for the aorta.
Fig. 3.
Exemplary results for the time-intensity curves in the aorta (a) and malignant lesion (b) for different numbers of iterations. The signal difference between pre- and post-contrast images is higher for larger numbers of iterations. This effect is larger for the aorta than for the lesion, and the required minimum number of iterations stabilizing the time-intensity curve is larger for the aorta.
DCE-MRI parameters
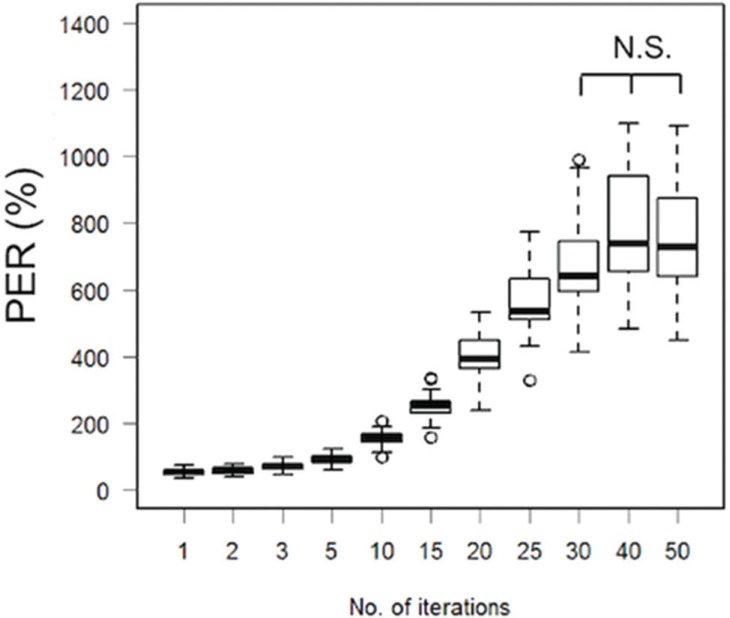
The boxplot of PER for the descending aorta using different numbers of iterations (Fig. 4) demonstrated that the PER values with < 25 iterations were lower than the values using 30 iterations. The PER values were not significantly different among those using 30 iterations or above.
Fig. 4.
Boxplot of the PER in the descending aorta using different numbers of iterations. The PER values with less than 25 iterations are significantly lower compared to the result using 50 iterations. PER, peak enhancement ratio; N.S., not significant.
The boxplots show the values if the semi-quantitative parameters (WIS, PER, and IAUC) obtained using different number of iterations in malignant and benign lesions (Fig. 5a–5f). In all semi-quantitative parameters, the number of iterations, which stabilized the parameters in malignant lesions, was higher than that in benign lesions. For malignant lesions, more than 10, 15, and 15 iterations were required for WIS, PER, and IAUC, respectively. Conversely, in benign lesions, more than 3, 5, and 10 iterations for WIS, PER, and IAUC were required, respectively.
Fig. 5.
Boxplots of semi-quantitative parameters; WIS (a and b), PER (c and d), IAUC (e and f) and Ktrans (g and h) in malignant and benign lesions using different numbers of iterations. In all semi-quantitative parameters, the number of iterations that stabilized the parameters (i.e. minimum number of iterations in which parameters do not show statistically significant difference from those of 50 iterations) in malignant lesions was higher than that in benign lesions. WIS, wash-in slope; IAUC, initial area under the curve; PER, peak enhancement ratio; Ktrans, the transfer constant of contrast from the plasma to the tissue extracellular extra-vascular space. N.S., not significant.
Figure 5g and 5h shows the boxplots of the quantitative parameter Ktrans in malignant and benign lesions with different iterations. There were no significant differences between 10 and 50 iterations in both malignant and benign lesions.
Quantitative image evaluation
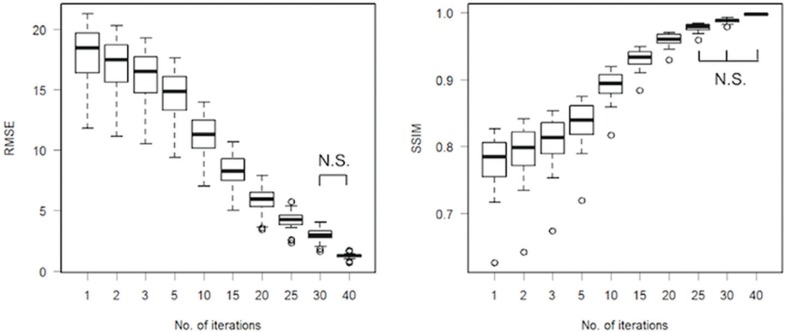
The RMSE and SSIM between the images reconstructed using 50 iterations and images reconstructed using fewer iterations are shown in Fig. 6. The SSIM values between 50 and 40 iterations were above 0.998, and the images were considered approximately equal. There were no significant differences in the RMSE between 30 and 40 iterations, and in the SSIM between 25 and 40 iterations.
Fig. 6.
The root mean square error and structural similarity between images reconstructed using 50 iterations and images reconstructed using fewer iterations. RMSE, root mean square error; SSIM, structural similarity; N.S., not significant.
Discussion
The current analysis demonstrated that DCE-MRI images were strongly affected by the number of iterations. CS reconstruction used in this study was L1 minimization problem in both spatial and temporal direction. In small number of iterations, the reconstructed images were strongly affected by the regularization in time domain. As a result, the error in pre-contrast phase and the reduction of contrast-enhanced effects occurred (Fig. 2). In the quantitative image evaluation, the number of iterations needed was 30 for RMSE and 25 for SSIM. Conversely, the number of iterations that stabilized the kinetic parameters was higher for malignant lesions, likely due to hypervascularity, even though 15 iterations sufficed. The inconsistency of the image evaluation and the kinetic parameters originated from the inclusion of the aorta shows the strongest time dependence and, therefore, required a larger number of iterations to achieve temporal fidelity. As reconstruction time increases linearly with the number of iterations, the latter should be optimized and set according to the target tissue and purpose.
Parallel-imaging (PI) techniques were proposed to accelerate data acquisition in MRI using arrays of receiver coils with spatially varying sensitivities.24–26 Unfortunately, PI is intrinsically associated with a loss in signal-to-noise ratio, due to the reduction of the number of data samples acquired. In 2006, 2D controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) was introduced.27 By modifying the phase-encoding sampling strategy, aliasing is shifted in a way that exploits the underlying receiver array more efficiently. The result is improved the image quality, with a more robust and homogenous reconstruction. Furthermore, CAIPIRINHA-Dixon-time-resolved angiography with interleaved stochastic trajectories (CDT) volumetric interpolated breath-hold examination (VIBE) which is the combination of parallel imaging, view sharing, and Dixon water–fat separation, provided higher temporal resolution (5 s/time point) while preserving diagnostic image quality, in DCE-MRI of the prostate.28
Unlike PI, however, in the CS used in our study, no complementary information is collected. Using a variety of algorithms, medical images can be successfully compressed while preserving diagnostic efficacy, even at compression ratios from 9:1 to 25:1.29
Several reports have demonstrated the usability of CS in breast DCE-MRI. The optimization of undersampling acquisition with 2D Gaussian distribution and radial undersampling was conducted by Wang et al.13 and Chan et al.16 using retrospectively collected data. Sung et al.30 and Raja et al.31 investigated reconstruction methods for solving CS problems. In recent years, studies using prospective data acquisition in clinical settings have begun to be published. Levine et al.32 proposed the combination of a view sharing method and CS. However, view sharing methods sometimes suffer from artifacts related to the point-spread-function of the undersampling scheme, such as ringing for time-resolved imaging of contrast kinetics. Kim et al.33 demonstrated the relationship between reconstruction parameters and Ktrans using the iterative golden-angle radial sparse parallel (iGRASP) MRI technique. The GRASP technique is a unique method, in which data are continuously acquired for a period of time, and image reconstruction is performed with flexible temporal information, such that multiple user-defined temporal resolutions with distinct numbers and positions of temporal frames can be obtained from the same dataset. In addition to breast imaging, studies using GRASP DCE-MRI have reported positive results for head/neck, cardiac, liver, and prostate imaging.34–37
Nevertheless, CS still has several limitations. First, CS reconstruction as an optimization problem is computationally more demanding than conventional reconstructions and, therefore, needs significant computation time. Most of the reports regarding CS referred to undersampling strategy, the sparsifying transform, and reconstruction parameters (especially the regularization parameter), and there are few reports referring to numerical optimization parameters such as the number of iterations. Needless to say, the reconstruction time is prolonged as the number of iterations increases, so the optimization of the number of iterations is of great importance in clinical practice. In this study, DCE-MRI images reconstructed using 50 iterations required approximately 35 min, which is still too long for a clinical routine. Second, images obtained with a CS reconstruction are strongly dependent on the regularization parameters used in the reconstruction, and furthermore, optimal values can be substantially different between situations, i.e., the target organ and purpose of the imaging (MR angiogram, quantitative imaging, and morphological evaluation of the lesion). The specific values apply only for the specific application in which they have been used and optimized.38 The challenge most often noted by researchers is the difficulty of selecting parameters to optimize the performance of CS. In the cases where this challenge has been addressed, pilot studies or multiple iterations of image reconstruction were necessary to select parameters such as the sampling pattern, regularization parameter, and sparsifying transform to optimize results.39
Limitations
This study had several limitations. First, few benign lesions were included in this study since the MRI examination was conducted on patients with high suspicion of malignancy based on prior physical examination, mammography, and ultrasound. Second, the optimal reconstruction parameters can be dependent on the purpose of the imaging study and the target organs; therefore, values reported in this study might not be appropriate for different applications. Third, DCE-MRI scans commenced only 1 min after injection of the contrast agent, and total EES volume (Ve) was not calculated or evaluated in this study. Fourth, we have no ground-truth DCE-MR images for comparison because the patients underwent a single examination using CS DCE-MRI only.
Conclusion
In conclusion, kinetic parameters using ultrafast DCE-MRI with CS are affected by the number of iterations, especially in malignant regions. However, if the images are reconstructed with an adequate number of iterations, ultrafast DCE-MRI with CS can be a powerful technique having high temporal and spatial resolution.
Acknowledgments
This work was supported by a Grant-in-Aid for Scientific Research “Evaluation of Wash in Phase in Breast MRI using Ultrafast Imaging” (Grant Number JP15K09922) and a Grant-in-Aid for Scientific Research on Innovative Areas “Initiative for High-Dimensional Data-Driven Science through Deepening of Sparse Modeling” (MEXT grant numbers 25120002, 25120008).
The authors would like to thank Mami Iima, Akane Ohashi, Rena Sakaguchi, Makiko Kawai, and Ayami Ohno Kishimoto in breast imaging group, Kyoto University Graduate School of Medicine, and Maika Urago in Division of Clinical Radiology Service, Kyoto University Hospital for their knowledgeable support. Authors would like to express our sincere gratitude to Yuta Urushibata and Katsutoshi Murata from Siemens Healthcare K.K. for their technical advice.
Footnotes
Conflicts of Interest
Marcel Dominik Nickel is employed by Siemens Healthcare GmbH, which offered the prototype sequence. The remaining authors declare that they have no conflicts of interest.
References
- 1.El Khouli RH, Macura KJ, Kamel IR, Jacobs MA, Bluemke DA. 3-T dynamic contrast-enhanced MRI of the breast: pharmacokinetic parameters versus conventional kinetic curve analysis. AJR Am J Roentgenol 2011; 197:1498–1505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schabel MC, Morrell GR, Oh KY, Walczak CA, Barlow RB, Neumayer LA. Pharmacokinetic mapping for lesion classification in dynamic breast MRI. J Magn Reson Imaging 2010; 31:1371–1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yabuuchi H, Matsuo Y, Okafuji T, et al. Enhanced mass on contrast-enhanced breast MR imaging: lesion characterization using combination of dynamic contrast-enhanced and diffusion-weighted MR images. J Magn Reson Imaging 2008; 28:1157–1165. [DOI] [PubMed] [Google Scholar]
- 4.Tozaki M, Igarashi T, Matsushima S, Fukuda K. High-spatial-resolution MR imaging of focal breast masses: interpretation model based on kinetic and morphological parameters. Radiat Med 2005; 23:43–50. [PubMed] [Google Scholar]
- 5.Wu J, Gong G, Cui Y, Li R. Intratumor partitioning and texture analysis of dynamic contrast-enhanced (DCE)-MRI identifies relevant tumor subregions to predict pathological response of breast cancer to neoadjuvant chemotherapy. J Magn Reson Imaging 2016; 44:1107–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang CH, Yin FF, Horton J, Chang Z. Review of treatment assessment using DCE-MRI in breast cancer radiation therapy. World J Methodol 2014; 4:46–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med 2007; 58:1182–1195. [DOI] [PubMed] [Google Scholar]
- 8.Abe H, Mori N, Tsuchiya K, et al. Kinetic analysis of benign and malignant breast lesions with ultrafast dynamic contrast-enhanced MRI: comparison with standard kinetic assessment. AJR Am J Roentgenol 2016; 207:1159–1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mann RM, Mus RD, van Zelst J, Geppert C, Karssemeijer N, Platel B. A novel approach to contrast-enhanced breast magnetic resonance imaging for screening: high-resolution ultrafast dynamic imaging. Invest Radiol 2014; 49:579–585. [DOI] [PubMed] [Google Scholar]
- 10.Pinker K, Grabner G, Bogner W, et al. A combined high temporal and high spatial resolution 3 Tesla MR imaging protocol for the assessment of breast lesions: initial results. Invest Radiol 2009; 44:553–558. [DOI] [PubMed] [Google Scholar]
- 11.Pineda FD, Medved M, Wang S, et al. Ultrafast Bilateral DCE-MRI of the breast with conventional fourier sampling: preliminary evaluation of semi-quantitative analysis. Acad Radiol 2016; 23:1137–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Saranathan M, Rettmann DW, Hargreaves BA, Lipson JA, Daniel BL. Variable spatiotemporal resolution three-dimensional Dixon sequence for rapid dynamic contrast-enhanced breast MRI. J Magn Reson Imaging 2014; 40:1392–1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang H, Miao Y, Zhou K, et al. Feasibility of high temporal resolution breast DCE-MRI using compressed sensing theory. Med Phys 2010; 37:4971–4981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gamper U, Boesiger P, Kozerke S. Compressed sensing in dynamic MRI. Magn Reson Med 2008; 59:365–373. [DOI] [PubMed] [Google Scholar]
- 15.Jung H, Sung K, Nayak KS, Kim EY, Ye JC. k-t FOCUSS: a general compressed sensing framework for high resolution dynamic MRI. Magn Reson Med 2009; 61:103–116. [DOI] [PubMed] [Google Scholar]
- 16.Chan RW, Ramsay EA, Cheung EY, Plewes DB. The influence of radial undersampling schemes on compressed sensing reconstruction in breast MRI. Magn Reson Med 2012; 67:363–377. [DOI] [PubMed] [Google Scholar]
- 17.Khalsa KA, Fessler JA. Resolution properties in regularized dynamic MRI reconstruction. in Proceedings of the 4th IEEE Int. Symp. Biomed. Imaging From Nano to Macro, 2007;456–459. [Google Scholar]
- 18.Onishi N, Kataoka M, Kanao S, et al. Ultrafast dynamic contrast-enhanced MRI of the breast using compressed sensing: breast cancer diagnosis based on separate visualization of breast arteries and veins. J Magn Reson Imaging 2018; 47:97–104. [DOI] [PubMed] [Google Scholar]
- 19.Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. Soc Ind Appl Math J Imaging Sci 2009; 2:183–202. [Google Scholar]
- 20.Tofts PS. Modeling tracer kinetics in dynamic Gd-DTPA MR imaging. J Magn Reson Imaging 1997; 7:91–101. [DOI] [PubMed] [Google Scholar]
- 21.Zöllner FG, Weisser G, Reich M, et al. UMMPerfusion: an open source software tool towards quantitative MRI perfusion analysis in clinical routine. J Digit Imaging 2013; 26:344–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Walker-Samuel S, Leach MO, Collins DJ. Evaluation of response to treatment using DCE-MRI: the relationship between initial area under the gadolinium curve (IAUGC) and quantitative pharmacokinetic analysis. Phys Med Biol 2006; 51:3593–3602. [DOI] [PubMed] [Google Scholar]
- 23.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 2004; 13:600–612. [DOI] [PubMed] [Google Scholar]
- 24.Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn Reson Med 1997; 38:591–603. [DOI] [PubMed] [Google Scholar]
- 25.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999; 42:952–962. [PubMed] [Google Scholar]
- 26.Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002; 47:1202–1210. [DOI] [PubMed] [Google Scholar]
- 27.Breuer FA, Blaimer M, Mueller MF, et al. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magn Reson Med 2006; 55:549–556. [DOI] [PubMed] [Google Scholar]
- 28.Othman AE, Martirosian P, Schraml C, et al. Feasibility of CAIPIRINHA-Dixon-TWIST-VIBE for dynamic contrast-enhanced MRI of the prostate. Eur J Radiol 2015; 84:2110–2116. [DOI] [PubMed] [Google Scholar]
- 29.Koff DA, Shulman H. An overview of digital compression of medical images: can we use lossy image compression in radiology? Can Assoc Radiol J 2006; 57:211–217. [PubMed] [Google Scholar]
- 30.Sung K, Daniel BL, Hargreaves BA. Location constrained approximate message passing for compressed sensing MRI. Magn Reson Med 2013; 70:370–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Raja R, Sinha N. Adaptive k-space sampling design for edge-enhanced DCE-MRI using compressed sensing. Magn Reson Imaging 2014; 32:899–912. [DOI] [PubMed] [Google Scholar]
- 32.Levine E, Daniel B, Vasanawala S, Hargreaves B, Saranathan M. 3D Cartesian MRI with compressed sensing and variable view sharing using complementary poisson-disc sampling. Magn Reson Med 2017; 77:1774–1785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kim SG, Feng L, Grimm R, et al. Influence of temporal regularization and radial undersampling factor on compressed sensing reconstruction in dynamic contrast enhanced MRI of the breast. J Magn Reson Imaging 2016; 43:261–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wu X, Raz E, Block TK, et al. Contrast-enhanced radial 3D fat-suppressed T1-weighted gradient-recalled echo sequence versus conventional fat-suppressed contrast-enhanced T1-weighted studies of the head and neck. AJR Am J Roentgenol 2014; 203:883–889. [DOI] [PubMed] [Google Scholar]
- 35.Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med 2010; 64:767–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chandarana H, Feng L, Block TK, et al. Free-breathing contrast-enhanced multiphase MRI of the liver using a combination of compressed sensing, parallel imaging, and golden-angle radial sampling. Invest Radiol 2013; 48:10–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rosenkrantz AB, Geppert C, Grimm R, et al. Dynamic contrast-enhanced MRI of the prostate with high spatiotemporal resolution using compressed sensing, parallel imaging, and continuous golden-angle radial sampling: preliminary experience. J Magn Reson Imaging 2015; 41:1365–1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Runge VM, Richter JK, Heverhagen JT. Speed in clinical magnetic resonance. Invest Radiol 2017; 52:1–17. [DOI] [PubMed] [Google Scholar]
- 39.Jaspan ON, Fleysher R, Lipton ML. Compressed sensing MRI: a review of the clinical literature. Br J Radiol 2015; 88:20150487. [DOI] [PMC free article] [PubMed] [Google Scholar]