Extending Classification Algorithms to Case-Control Studies

Abstract

Classification is a common technique applied to ’omics data to build predictive models and identify potential markers of biomedical outcomes. Despite the prevalence of case-control studies, the number of classification methods available to analyze data generated by such studies is extremely limited. Conditional logistic regression is the most commonly used technique, but the associated modeling assumptions limit its ability to identify a large class of sufficiently complicated ’omic signatures. We propose a data preprocessing step which generalizes and makes any linear or nonlinear classification algorithm, even those typically not appropriate for matched design data, available to be used to model case-control data and identify relevant biomarkers in these study designs. We demonstrate on simulated case-control data that both the classification and variable selection accuracy of each method is improved after applying this processing step and that the proposed methods are comparable to or outperform existing variable selection methods. Finally, we demonstrate the impact of conditional classification algorithms on a large cohort study of children with islet autoimmunity.

Introduction

Matched case-control (MCC) studies are a common design for epidemiological studies due to their potential gains in efficiency and avoidance of confounders. The general design of MCC studies is to group individuals with the outcome of interest (“cases”) and those without (“controls”) based on features such as age and sex. In omics studies, often the goal of MCC studies is to identify biomarkers that are highly correlated with the case/control labels that can lead to a better understanding of the cause of the disease. Despite the large number of studies using this design, the number of methods that account for the pairing has grown very slowly and almost always assume a linear relationship between sample features and the outcome of interest. Furthermore, most of the popular methods used to analyze MCC studies perform poorly when the covariate space is high dimensional or when the effects are highly nonlinear.

Although other methods have been proposed,^1,2 a majority of methods used to analyze MCC studies while controlling for covariate information are based on conditional logistic regression (CLR).³ Conditional logistic regression is similar to standard logistic regression but controls for the matching design by estimating the effects of each covariate conditional on the paired design.⁴ As such, CLR is able to identify covariates whose linear effects are associated with each patient’s case-control status without flagging spurious relationships due solely to the paired nature of the study.

In its original form, CLR was designed to handle modestly sized covariate datasets and is not well suited to handle the volume or veracity of data present in an ’omics-type analysis. To remedy this, several variations of standard CLR have been proposed to deal with high-dimensional datasets.^5–9 However, based on these published results, CLR and its many variants still struggle to accurately differentiate the cases from the controls, particularly when there are nonlinear effects, the noise is sufficiently large or the number of inputs is too large.⁷

Modern classification techniques such as random forests (RF),¹⁰ support vector machine¹¹ (SVM), and naive Bayes (NB) can successfully model such complicated input/output relationships but do not account for the matched design of MCC studies and require modification to be used in these situations. That is, applying these methods without accounting for the paired nature of the study likely accounts for their poor performance relative to CLR, which does account for the pairing.^8,12–15 More recently, Dimou et al¹⁶ proposed a paired SVM approach to identify damaged regions of the brain, but the specialized kernel they proposed is not applicable to general classification problems with binary outcomes.

In this article, we show that by preprocessing the data, any number of linear and nonlinear classification algorithms can be used to appropriately analyze data generated by MCC studies. This method is a general framework which, for the first time, makes a much larger set of classification algorithms available to researchers analyzing MCC study data. The new group of classification algorithms resulting from this method, called conditional classification algorithms, are designed specifically to analyze MCC studies. Using artificially generated data, we show when and by how much the proposed conditional classification algorithms outperform their standard counterparts. We also identify situations in which they will outperform CLR. In the next section, we describe the proposed preprocessing technique. We then demonstrate how classification and variable selection accuracies improve in a simulation study. Finally, we employ our methods along with CLR to a large cohort study on The Environmental Determinants of Diabetes in the Young (TEDDY) to understand the ramifications on messy and high-dimensional real-world ’omics data.

Methods

In this section, we describe the data processing step that defines the proposed set of conditional classification algorithms. The theoretical derivations that prove the validity of the proposed approach are given in the supplemental material. We then describe the methods used to generate and analyze the artificial data. Finally, the TEDDY study is described including the data cleaning steps and how it was analyzed.

Conditional classification algorithms

To make a standard classification algorithm conditional, it must account for the paired structure of the MCC study. We propose centering the within pair data by its mean to address the paired data structure. For example, consider a single protein measured on 4 individuals that are split into 2 case-control pairs. The protein abundance for the case and control in pair 1 is 750 and 500, respectively, while that same protein has abundance 500 and 250, respectively, for pair 2. Because the abundance for the control in pair 1 is the same as the case in pair 2, standard classification algorithms would not identify this protein as significant. After pair correction, however, any classification algorithm would identify this protein as significant because the pair-corrected abundance values are 125 and −125 for the case and control, respectively, in both pairs.

Put mathematically, this is equivalent to the common statistical practice of projecting a feature matrix into the null space generated by the matrix of pair indicators. Let $n$ denote the cohort size, which is composed of $p$ disjoint and equally sized strata, ie, pairs, of MCC subjects. Let $m$ denote the size of each strata and $K$ denote the number of features. Define the matrix of strata indicators $\mathrm{Z}={\mathrm{I}}_{p\times p}\otimes 1_m$, where ${\mathrm{I}}_{p\times p}$ is a $p\times p$ identity matrix, $1_m$ is an m-dimensional column vector of ones and ⊗ is the Kronecker product. Then, $\mathrm{Z}$ is a $n\times p$ matrix where the $(i,j)\mathrm{th}$ element is a 1 if subject $i$ is in strata $j$ and is 0 otherwise. The projection matrix associated with $\mathrm{Z}$ is ${\mathrm{P}}_{\mathrm{Z}}=\mathrm{Z}{({\mathrm{Z}}^T\mathrm{Z})}^{-1}{\mathrm{Z}}^T={\mathrm{I}}_{p\times p}\otimes (1_m{1}_m^T)/m$, which is a $n\times n$ block diagonal matrix with $m\times m$ blocks where every element is $1/m$. To project the $n\times K$ feature matrix $\mathrm{X}$ into the null space of $Z$, pre-multiply $\mathrm{X}$ by ${\mathrm{I}}_{n\times n}-{\mathrm{P}}_{\mathrm{Z}}$. Define the case-control corrected feature matrix ${\mathrm{X}}^{*}$ as ${\mathrm{X}}^{*}=({\mathrm{I}}_{n\times n}-{\mathrm{P}}_{\mathrm{Z}})\mathrm{X}$.

We define any classification algorithm trained using the pair adjusted features ${\mathrm{X}}^{*}$ as a conditional classification algorithm. We refer to training the same classification algorithm on the raw features $\mathrm{X}$ as the standard classification algorithm. In the “Results” section, we empirically compare the conditional and standard classification algorithms. In the context of 1:1 case-control studies, both linear discriminant analysis (LDA) and the Gaussian NB classifier are guaranteed to return one case and one control per strata; no such guarantee exists for the standard versions of those classifiers. In addition, we show that CLR is a special case of the proposed set of paired classification algorithms. We do this by showing the CLR likelihood is unaffected by the pair correction and that the maximizer of the CLR likelihood also maximizes the pair-corrected logistic regression (up to a scaling factor). See the supporting information for details on these two theoretical results.

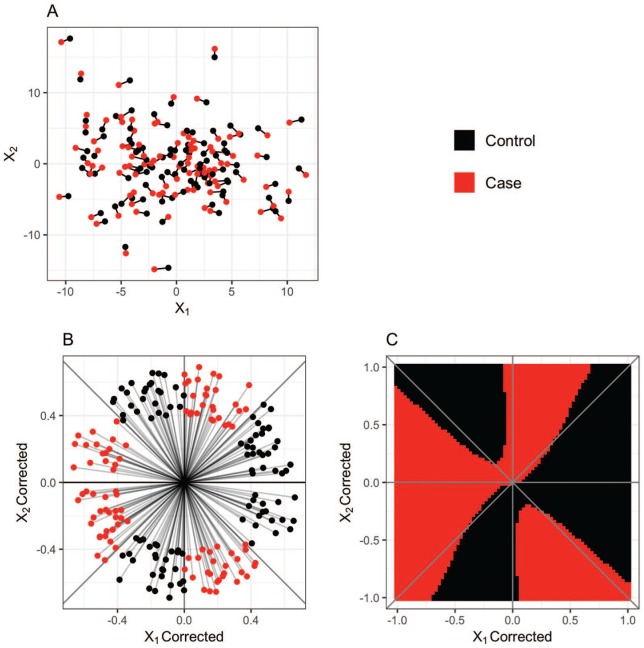
Figure 1 shows a simulated example that clearly demonstrates the value of the conditional classification approach over CLR and standard machine learning for data with complicated structure. This example includes only two features to allow for easy visualization, but could be extended to large feature spaces. Consider a 1:1 case-control dataset with two features, $x_{ijk}$, where $i$ indicates the pair $i=1,\dots ,n$, $j\in \{1,2\}$ indicates the person within each pair and $k\in \{1,2\}$ indicates the feature number. Let $\mathrm{X}$ represent the full feature matrix and ${\mathrm{X}}_i$ be the $2\times 2$ submatrix of $\mathrm{X}$ that has all the information for case-control strata $i$. Each submatrix ${\mathrm{X}}_i$ is created by

Figure 1.

A single dataset from the 2 variable simulation study is plotted in its raw form (A) and after controlling for the case-control design (B). A SVM with a radial-basis kernel function was trained to the pair corrected data, and the decision boundaries closely align with the true boundaries between classes (C). SVM indicates support vector machine.

$$X_i=\left(\begin{array}{c}{x}_{i1}\\ x_{i2}\end{array}\right)=\left(\begin{array}{cc}{x}_{i11}& x_{i12}\\ x_{i21}& x_{i22}\end{array}\right)=\left(\begin{array}{cc}{r}_{i1}\cos ({\varphi }_1)+{\mu }_1& r_{i1}\sin ({\varphi }_1)+{\mu }_2\\ r_{i2}\cos ({\varphi }_1)+{\mu }_1& r_{i2}\sin ({\varphi }_1)+{\mu }_2\end{array}\right)$$

where $r_{i1}\sim \mathrm{Unif}[0.4,0.7]$, $r_{i2}=-r_{i1}$, ${\varphi }_1\sim \mathrm{Unif}[0,2\pi )$, and ${\mu }_k\sim N(0,5)$ $k=1,2$ for $i$. The response label for each individual in pair $y_{ij}$, $0$, is set to ${\varphi }_{i1}$ (control) if $1$ is in the second, fourth, fifth, or seventh octant of the feature space shown in Figure 1B and $x_{ij1}$ (case) otherwise. This design ensures that each pair is composed of one case and one control.

A set of 100 case-control pairs generated in this fashion is plotted in Figure 1A where the dot color indicates case-control status and the black lines connect individuals in the same pair. In its raw form, the data are noisy and difficult to classify. For this dataset, a CLR model with coefficients for $x_{ij2}$, $x_{ij1}{x}_{ij2}$ and $X_1$ returns a misclassification rate of 43%. A standard SVM with a radial basis function performs slightly worse with a misclassification rate of 47%. A large proportion of the errors committed by the SVM are due to the fact that both individuals in each strata are given the same label. However, after the pair correction is applied (Figure 1B), the differences between cases and controls are clearly visible through the dividing boundary between the two strata, which is also clearly nonlinear. In fact, the conditional NB classifier and the conditional SVM with a linear kernel both perform worse than the CLR when applied to the corrected data (misclassification rates greater than 43% for this dataset). A conditional SVM with a radial basis function and a conditional random forest (CRF), however, achieve misclassification rates of 3% and 4%, respectively. In addition, the fitted class labels generated by these methods consist of one case and one control per pair. To illustrate the results of the conditional SVM with a radial basis function, Figure 1C is a plot of the decision boundary learned by the conditional SVM with a radial basis function kernel when applied to this dataset.

In terms of variable importance, the P-values associated with regression coefficients of the CLR indicate that $X_2$ is an important feature, P-value .002, while $p=200$ and the interaction of the two variables are not statistically significant, P-values of .59 and .07, respectively. Conversely, removing either variable from the conditional support vector machine (CSVM) or CRF dramatically decreases model performance, indicating both variables are important in differentiating the cases from the controls. This indicates that CLR is not able to identify important features if their relationship with the outcome of interest is highly nonlinear whereas the CSVM and CRF models are.

Although this is a small toy example, it illustrates the potential gains in classifier accuracy and biomarker discovery by incorporating nonlinear classifiers into the domain. In the next section, we describe a much larger simulation study to empirically investigate the potential gains of conditional classifiers.

Simulation study

The simulation scenario implemented here is motivated by Balasubramanian et al.⁸ Each simulated dataset consists of 200 1:1 case-control pairs and 225 features, thus using the notation from the previous section, $m=2$, $n=400$, $K=225$ and ${\delta }_k$. The first 25 features are significant biomarkers while the remaining 200 features are noise. The features for each pair were drawn from the bivariate normal distribution

$$\left[\begin{array}{c}{x}_{i1k}\\ x_{i2k}\end{array}\right]\sim N_2\left(\left[\begin{array}{c}1\\ 1+{\delta }_k\end{array}\right],\left[\begin{array}{cc}1& {\rho }_k\\ {\rho }_k& 1\end{array}\right]\right)$$

where ${\rho }_k$ and $k=1,\dots ,K$ are the mean shift and within pair correlation, respectively, associated with feature $\left|{\delta }_k\right|\in \{0.125,0.25,0.5\}$. For this study we allowed the magnitude of the mean shift to take 3 possible values $k=1,\dots ,20$ for $0$ and ${\rho }_k\in \{0.0.1.0.4.0.8\}$ otherwise. Within each dataset, the sign of each feature was allowed to be positive or negative with equal probability; therefore, biomarkers that are both over-expressed and under-expressed in the case samples relative to their controls are considered. We considered 4 possible values of the biomarker within pair correlations: $k<=20$ for $0$ and ${\delta }_k$ otherwise. For each combination of ${\rho }_k$ and $g=1,\dots ,5$, 2000 datasets were created and 7 different classification algorithms were fit to each dataset: logistic regression (LR), NB, SVM with a radial basis function kernel (SVM-RBF), SVM with a linear kernel (SVM-Lin), RF, LDA, and random penalized conditional logistic regression (RPCLR).⁸ Random penalized conditional logistic regression is different from the other 6 methods in that only a conditional version exists and it cannot be used to predict an individual’s case/control label. Therefore, we will only compare it to the other 6 methods in terms of variable importance accuracy and not predictive accuracy. Furthermore, because we cannot assess its predictive accuracy in the context of the TEDDY data, it will not be applied to those data.

To assess the impact of the proposed preprocessing step, conditional and standard versions of each method, except RPCLR, were applied to every dataset. See Table 1 for specifics on the implementation of each method. In terms of the tuning parameters associated with each of the algorithms, cross-validation (CV) was used to choose the tuning parameters for the regularized CLR model. The width of the Gaussian kernel used by the SVM-RBF model was set to the median of the squared Euclidean distances between the input features.²¹ The number of trees included in the RF model was set to 500 and the number of variables to consider at each node was the largest integer less than the square root of the total number of features. For RPCLR, the number of variables included in each model was set to 7 and the number of bootstrap replicates was set to 2000, as recommended by the authors.⁸

Table 1.

The 6 classification methods used were implemented in the program R¹⁷; the specific functions (and packages) used are given below as well as the different variable importance methods used for each method.

Method	R Function (package)	Variable importance measure
LDA	lda (MASS18)	Magnitude of the scalings of the discriminant functions
CLR	clogitL1 (clogitL119)	Standardized regression coefficient magnitude
Naive Bayes	naiveBayes (e107120)	KL distance between the conditional distribution of each feature given the target class
Both SVMs	ksvm (kernlab21)	1D sensitivity analysis measure based on average absolute deviation from the median22
RF	ranger (ranger23)	Gini index
RPCLR	GetVarImp (RPCLR24)	Average change in out of bag AIC with and without each variable

Abbreviations: AIC, Akaike information criterion; CLR, conditional logistic regression; KL, Kullback Leibler; LDA, linear discriminant analysis; RF, random forests; RPCLR, random penalized conditional logistic regression; SVM, support vector machines.

We used predictive accuracy to determine which method should be used to identify important biomarkers. In this context, prediction is the labeling of individuals within a group that was not used to estimate the parameter values. The predictive accuracy of each method was quantified by computing the proportion of individuals whose classes were predicted correctly in a 5-fold CV framework. The exact procedure is summarized as follows:

1. Case-control pairs are randomly split into 5 disjoint groups numbered 1 through 5;

2. For each group $g$:

   • (a) Train each classification algorithm using all the data except group g;
   • (b) Predict the class labels for individuals in the testing set, group $[0,1]$.

3. Compare the true class labels to the predicted class labels in 2b to compute the proportion of individuals that were classified correctly.

The significance of each feature was quantified by a variable importance metric computed on each of the training sets and then averaged across the 5 folds. The metrics used depend on the method applied (last column of Table 1). These metrics were used to quantify the importance of each feature. Receiver operating characteristic (ROC) curves based on the true importance labels and the variable importance metrics were created to assess the accuracy of each method, which was summarized using the area under the curve (AUC). Therefore, each method’s variable selection accuracy is measured by this AUC value, which lies in the range ${\log }_2$ with larger values being better, and a value of 0.5 corresponds to an uniformative classifier.

TEDDY study

The TEDDY study²⁵ is a large prospective study with the goal of discovering factors that initiate the autoimmune response and destruction of the pancreatic beta cells, leading to the development of type 1 diabetes (T1D). TEDDY was formulated into a nested case-control study to enable biomarker studies, pairing on: clinical center, sex, and family history of T1D,²⁶ which resulted in 418 case-control pairs for analysis. TEDDY is particularly interested in understanding the environmental factors that trigger islet autoimmunity (IA), thus the metabolomic, lipidomic, and genetic single-nucleotide polymorphism (SNP) data at the time point of autoimmunity are evaluated.

After a $n_{case}$ transformation of the ’omics data, 5 preprocessing steps were applied to each data source that effectively determines a starting number of features: weighted coefficient of variation (CoV),²⁷ percent missingness, near zero variance (NZV), univariate pairwise significance tests, and pairwise correlation. We remove features within a source if the weighted CoV is greater than 200%. We define weighted CoV as

$$\frac{n_{case}*co{v}_{case}+n_{control}*co{v}_{control}}{n_{case}+n_{control}}$$

where $n_{control}$ and $\left|\delta \right|=0.125$ are the number of nonmissing values for cases and control, respectively, within in a time point and

$$co{v}_{case}=|100*\frac{s_{case}}{{\overline{x}}_{case}}|co{v}_{control}=|100*\frac{s_{control}}{{\overline{x}}_{control}}|$$

We also remove any features that were more than 10% missing and use RF imputation²⁸ to impute those that were less than 10% missing. Next, we remove features that had very few unique values relative to the number of samples or a much greater frequency of the most common value relative to the second most common value.²⁹ Before significance tests, the lipid data are handled specially to remove redundant information by eliminating different adducts for the same lipid. For the negatively ionized lipids, we simply removed all Cl– adducts because they tend to ionize poorly. The positively ionized lipids depend on the lipid class in terms of which adduct to keep. For the non-LPC and non-PC classes, we retained the NH₄ adduct because it was consistently greater in peak intensity. For the ceramides class, we used the H adduct as the other (H₂O) adduct is a degradation of the lipid due to in source fragmentation. Finally, for the LPC and PC classes, we used the most common adduct (H) as the other (Na) was rarely noted. Next, for all data types but the SNPs, univariate paired t-tests were applied to each feature and all features with P-value less than .20 were retained.

Four criteria were used to filter the SNPs: missingness, minor allele frequency (MAF), the Hardy-Weinberg test for equilibrium (HWE), and CLR. Missingness, MAF, and HWE testing were performed using PLINK version 1.90.³⁰ SNPs with missingness less than 1%, MAF less than 0.2, P-values from the HWE test less than .001, and conditional logistic regression P-values less than .006 were retained for the analysis. The .006 P-value threshold was chosen to parallel the 0.2 threshold used for the other data sources. That is, because there are roughly 33 times more SNPs than other data types, the SNP threshold was set to 0.2/33 ≈ 0.006. As a final step of the data cleaning procedure, all biomolecules that have pairwise correlations greater than 0.9 were removed one-by-one to minimize redundancy in the final dataset. These steps ensure that each feature does not have an excessive relative variability, does not have an excessive amount of missing data, and contains enough variability and significance to potentially distinguish cases from controls.

The same 5-fold CV approach used in the simulation study was used for the TEDDY data to assess each method’s predictive accuracy. However, instead of implementing 5-fold CV once per dataset, the CV method was repeated 200 times per data source to account for the uncertainty of the CV procedure itself. Feature importance was assessed using a single analysis of the full dataset with each method according to the feature importance metrics reported in Table 1. As mentioned previously, RPCLR will not be applied to these data because we cannot assess its predictive accuracy.

Results

Simulation study

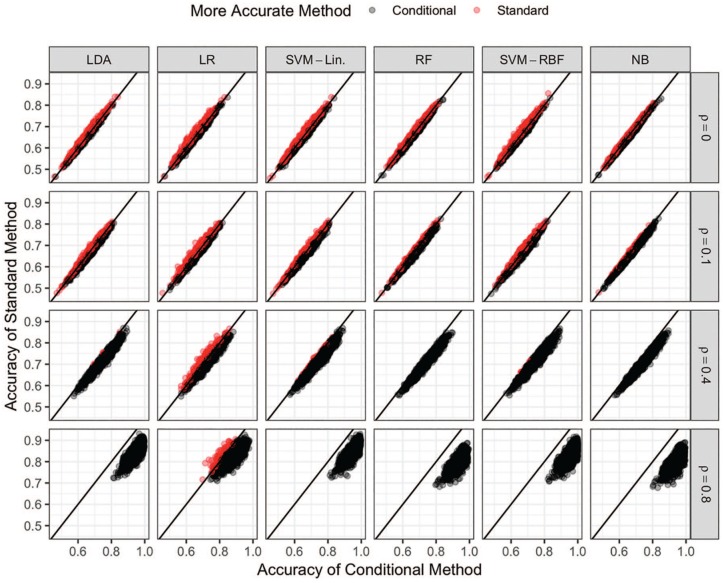
Scatter plots of the 2000 classification accuracy values for each classification method are shown in Figure 2 for $\rho$ and all values of the within pair correlation $\rho$. Random penalized conditional logistic regression cannot be used as a classification algorithm so it is not included. The accuracy values for the conditional and standard versions of each method are plotted on the x- and y-axes, respectively. The red points represent datasets for which the standard version of that method was more accurate than its conditional counterpart while the converse is true for the black points. Within each method, the cloud of points are closest to the identity line when the within correlation is zero or small (top two rows). This indicates the conditional methods behave most similarly to their standard counterparts for small values of $\rho$. As the within pair correlation grows (move down each column), the cloud of points move to the right indicating the conditional methods get more accurate when $\rho$ increases. The cloud of points do not move up; however, indicating the performance of the standard methods do not change as a function of $\rho$.

Figure 2.

Scatter plots of the classification accuracies for all conditional (x-axis) and standard (y-axis) methods and values of $\left|\delta \right|=0.125$ when $\delta$. The color of each point indicates which version, standard (red) or conditional (black), of each method is more accurate for each simulated dataset. LDA indicates linear discriminant analysis; LR, logistic regression; NB, Naive Bayes; RBF, radial basis function; RF, random forests; SVM, support vector machine.

These conclusions are supported by Table 2, which gives the percent of datasets in which the standard method was preferred to the conditional method for each algorithm and combinations of $\rho$ and $\rho$. The number of times the standard method is preferred decreases differently for each of the algorithms. This implies the sensitivity of each algorithm to the paired structure varies depending upon how the algorithm performs classification. In particular, the linear discriminative algorithms (LDA, LR, and SVM-Lin) require a stronger within pair correlation for the conditional method to clearly outperform its standard counterpart. The nonlinear discriminative algorithms (RF and SVM-RBF) separate themselves more quickly and by a larger margin as the correlation increases. Finally, the linear generative algorithm (NB) separates itself from the onset and creates the widest gap for large values of $\delta$.

Table 2.

Percentage of simulated datasets in which the standard version of the classification algorithm outperformed the conditional version in terms of classification accuracy by $\rho$ and $\left|\delta \right|$ combination.

$\rho$	$\left|\delta \right|$	LDA	LR	SVM-Lin.	RF	SVM-RBF	NB
0.125	0	8.8	53.2	14.6	3.4	2.5	0.1
	0.1	6.3	48.5	12.7	2.5	1.9	0.1
	0.4	2.8	29.6	7.4	0.6	0.5	0
	0.8	0.1	0.8	0.2	0	0	0
0.25	0	6.5	12.9	12.4	0.5	0.5	0
	0.1	3.4	7.4	8.2	0.1	0.3	0
	0.4	0.1	0.2	1.1	0	0	0
	0.8	0	0	0	0	0	0
0.5	0	2.2	0	3.9	0	0.1	0
	0.1	0.9	0	1.6	0	0	0
	0.4	0	0	0	0	0	0
	0.8	0	0	0	0	0	0

Abbreviations: LDA, linear discriminant analysis; LR, logistic regression; NB, Naive Bayes; RBF, radial basis function; RF, random forests; SVM, support vector machine.

Also apparent from Table 2 is the relationship between $\left|\delta \right|$ and the conditional method accuracies. In particular, the fact that the standard method is preferred so infrequently with large $\rho$ implies the importance of accounting for the paired structure is more important when the within pair difference is larger, as expected.

An analogous representation of the variable selection accuracy is given in Figure 3. Similar to the classification accuracy results, the conditional and standard methods cluster most closely around the identity line for small values of $\rho$ and then drift to the right, which indicates the conditional method improves in accuracy more quickly than the standard method as a function of $\rho$. Unlike the accuracy results, however, the cloud of points also moves upward as a function of $\rho$, implying the standard method also becomes more accurate at identifying the important biomarkers as $\rho$ increases. Therefore, the standard methods are better able to identify which features should be used to classify the data as $\rho$ increases, but they are no better at performing the actual classification (Figure 2). Finally, the algorithms appear to improve in accuracy at approximately the same rate as a function of $\rho$. That is, there is no clear distinction between the linear and nonlinear discriminative or generative algorithms with respect to accurate variable selection.

Figure 3.

Scatter plots of the variable selection accuracies for all conditional (x-axis) and standard (y-axis) methods and values of $\left|\delta \right|=0.125$ when $\delta$. The color of each point indicates which version, standard (red) or conditional (black), of each algorithm is more accurate for each simulated dataset. LDA indicates linear discriminant analysis; LR, logistic regression; NB, Naive Bayes; RBF, radial basis function; RF, random forests; SVM, support vector machine.

Finally, we compare all of the conditional methods by their average variable selection accuracies in Table 3. As expected, the accuracy of all methods improves when $\rho$ and/or $(\delta =0.125and\rho =0.1)$ increases. One existing method, RPCLR, was the most accurate method in one instance $\left|\delta \right|$ and was in the top 3 in 9 out of 12 scenarios. The proposed conditional Naive Bayes (CNB) and CRF approaches are most frequently in the top 3, followed by the CLDA and CSVM-RBF methods. We can therefore conclude that the proposed methods are comparable or outperform the existing variable selection methods CLR and RPCLR.

Table 3.

Average variable selection accuracy for each method.

Method	$\rho =0$	$\rho =0.1$	$\rho =0.4$	$\rho =0.8$	$\rho$
CLR		0.6573	0.668	0.726	0.883
CLDA		0.653	0.668	0.7423	0.9442
CNB		0.6621	0.6752	0.7432	0.939
CRF	0.125	0.6602	0.6733	0.741	0.934
CSVM-Lin.		0.652	0.667	0.741	0.9442
CSVM-RBF		0.654	0.669	0.7441	0.9521
RPCLR		0.656	0.6811	0.738	0.929
CLR		0.881	0.898	0.937	0.977
CLDA		0.869	0.891	0.945	0.993
CNB		0.9041	0.9251	0.9711	1.0001
CRF	0.25	0.9003	0.9202	0.9682	1.0001
CSVM-Lin.		0.866	0.888	0.942	0.992
CSVM-RBF		0.875	0.898	0.951	0.998
RPCLR		0.9012	0.9113	0.9633	1.0001
CLR		0.980	0.982	0.987	0.993
CLDA		0.959	0.965	0.980	0.996
CNB		0.9991	1.0001	1.0001	1.0001
CRF	0.5	0.9991	1.0001	1.0001	1.0001
CSVM-Lin.		0.956	0.962	0.978	0.996
CSVM-RBF		0.965	0.969	0.981	0.999
RPCLR		0.9991	0.9993	1.0001	1.0001

Abbreviations: CLDA, conditional linear discriminant analysis; CLR, conditional logistic regression; CNB, conditional Naive Bayes; CRF, conditional random forests; CSVM, conditional support vector machine; RBF, radial basis function; RPCLR, random penalized conditional logistic regression.

The top 3 methods for each $\left|\delta \right|$ and $\omega$ combination are denoted with superscripts 1, 2, and 3.

Case study—TEDDY study data

The sample sizes and descriptive feature statistics for each data type are reported in Table 4. The within pair differences and correlation was computed by taking the average absolute difference between features and the average correlation between feature vectors within each pair, respectively. Because the standard classification algorithms do no account for the pairing, we estimated the same quantities for random pairs in the dataset to determine how influential the pairing may be on algorithm performance. To do this, 10 000 random pairs were chosen, the same quantities were computed and then averaged across the chosen pairs. Assuming that the mechanism that differentiates cases and controls in the TEDDY data is similar to the simulation scenario explored in the previous section, then the increased correlation and difference between matched pairs relative to random pairs leads us to believe the conditional methods will outperform their standard counterpart. However, the large correlation in the data as a whole could make the difference between the methods small.

Table 4.

Feature set sizes, summary statistics, within mean absolute pair differences, within correlations (cor.), and random pair differences correlations for each data type based on the 504 samples.

Statistic	Metabolomics	Positive lipidomics	Negative lipidomics	SNPs
# Features (K)	170	277	252	236
Minimum	–0.079	3.585	4.807	0.000
Maximum	23.149	23.564	21.428	2.000
Mean	10.416	14.766	13.097	1.296
Median	9.899	14.432	12.784	1.000
Standard deviation	3.142	2.854	2.211	0.685
Within pair difference	1.880	1.099	1.043	1.519
Random pair difference	1.497	0.549	0.430	0.687
Within pair correlation	0.938	0.984	0.984	–
Random pair correlation	0.749	0.968	0.967	–

Abbreviation: SNP, single-nucleotide polymorphism.

The random pair distance and correlation was computed by randomly sampling 10 000 pairs of random individuals from the dataset and computing their pairwise correlation and mean absolute distance. Within pair correlations for SNPs are not reported because of their discrete nature.

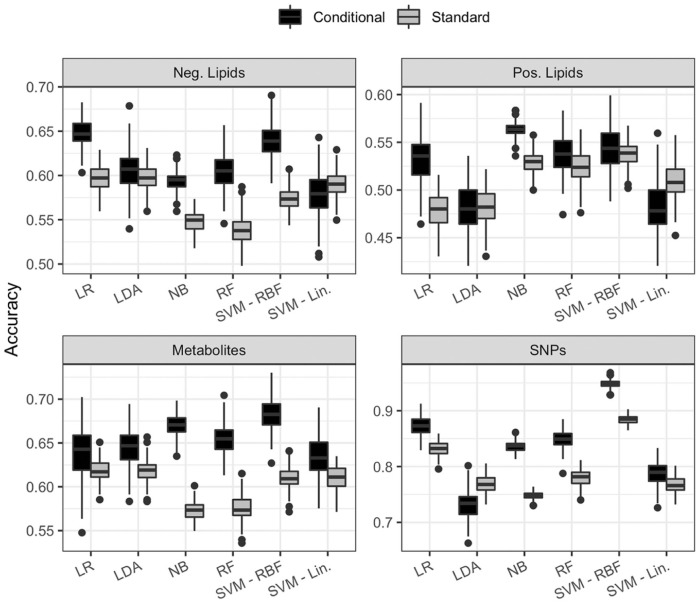
Box plots of the 200 repeated accuracy values are shown in Figure 4 for each method and biomolecule. Overall the conditional method of each algorithm (black boxes) is more accurate than the standard method (gray boxes). That is, the predictive accuracy of each algorithm is improved when the paired nature of the study is taken into account compared to when it is ignored. In 5 of the 24 comparisons performed, the standard method was more accurate than the conditional method: LDA for positive lipids (accuracy difference of 0.0015) and SNPs (0.035), and SVM with a linear kernel for positive lipids (0.029) and negative lipids (0.01). The large correlation between random pairs in both types of lipids could explain the comparable accuracy.

Figure 4.

Box plots of the 200 repeated 5-fold cross-validation accuracies for the 4 different data types and 6 different classification algorithms. LDA indicates linear discriminant analysis; LR, logistic regression; NB, Naive Bayes; RBF, radial basis function; RF, random forests; SVM, support vector machine.

To make recommendations about when each algorithm should be employed in practice, the conditional methods were ranked from most (ranked 1) to least (ranked 6) accurate within each CV replicate. Those ranks were averaged across the 200 replicates and plotted in Figure 5 for the different biomolecules. Paired t-tests comparing the accuracy measures were used within each biomolecule to determine which algorithms performed significantly better than the others in terms of predictive accuracy.

Figure 5.

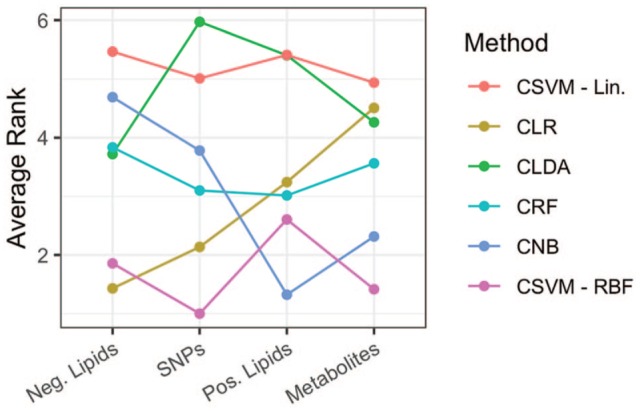
The average rank of each conditional method for each data type where the algorithm with the lowest rank was the most accurate within each repeated cross-validation (CV) run. CLDA indicates conditional linear discriminant analysis; CLR, conditional logistic regression; CNB, conditional Naive Bayes; CRF, conditional random forests; CSVM, conditional support vector machine; RBF, radial basis function; SNP, single-nucleotide polymorphism.

From Figure 5, it is clear that the CSVM-RBF classifier is a reliable method to use regardless of data type. Similar to what was concluded from Figure 4, CLR and CNB are conversely related. That is, CLR is the best method for one type of lipid data (negative), a distant second for the SNPs, and is ranked at least fourth for the remaining two methods. Conversely, CNB is the best method for the other types of lipids (positive), second for metabolites, and at least fourth for the remaining data types. In general, it appears that CLDA and CSVM-Lin are the least favorable for this type of analysis.

To determine which biomolecules were most predictive of the case/control status of each individual, the features were ranked within each source using a variable importance metric appropriate for each classification algorithm (Table 1). A scree plot of the variable importance measures was used to separate the influential from the noninfluential features according to each model. An abridged list of the influential features chosen by the CSVM-RBF and CLR methods along with their ranks, direction of association (+/-), and published literature connecting each biomolecule to IA are given in Table 5.

Table 5.

An abridged list of the influential metabolites and lipids identified by the CSVM-RBF and CLR methods along with notes and references for biomolecules that have been previously linked to T1D and/or IA.

Source	Biomolecule	CSVM-RBF rank	CLR Rank	References
Lipids	Acylcarnitine	—	3(+)	32
	Glccer	—	3(−)	33
	Ceramide	13(−)	—	34
	pc_36_5_4_29_824_54	20(−)	5(−)	35
	fa_16_1_2_71_253_22	6(+)	6(+)	36,37
Metabolites	α-Tocopherol	1(−)	2(−)	38–40
	Adipic acid	2(+)	1(+)	41,42
	Glucose	3(−)	28(−)
	Creatinine	7(+)	3(+)	43
	Heptadecanoic acid	—	4(+)	44
	Hydroxybutanoic acid	8(+)	11(+)	45,46
	Leucine	10(−)	—	47
	Isothreonic acid	20(−)	—	48
	Glycerol galactoside	—	23(−)	49–51
SNP (Gene)	rs7158663 (Meg3)	10(−)	34(−)	52
	rs17388568 (ADAD1)	—	19(−)	53,54
	rs4580644 (CD38)	—	20(+)	55,56

Abbreviations: CLR, conditional logistic regression; CSVM, conditional support vector machine; IA, islet autoimmunity; RBF, radial basis function; SNP, single-nucleotide polymorphism; T1D, type 1 diabetes.

The direction of the association is indicated by the “+” symbol for factors that are larger in the case group relative to controls and “–” when the opposite is true.

Discussion

The conditional NB classifier was the most accurate method in the simulation study and was one of the top two methods for 2 of the 4 data types (Figure 5). We hypothesize this is due to the fact that NB is a generative rather than discriminative algorithm. As described in Ng et al,³¹ generative algorithms have larger asymptotic classification error limits than discriminative classifiers, but have the potential to reach that error limit sooner than their discriminative counterparts. Thus, the consistent performance of the conditional NB algorithm could be due to the rather limited number of individuals in the TEDDY study relative to the complicated biology associated with IA as being learned by noisy ’omics feature sets. Similarly, even though the difference between cases and controls in the simulation study was rather simple, the small number of important features relative to unimportant ones made the signal difficult to detect.

Further evidence to support this hypothesis is that the CSVM-RBF was the second most accurate method in the simulation study and one of the top two classifiers for all data types. Because the SVM-RBF is a nonlinear classifier, it is able to model the complicated ’omics to disease relationship much better than the discriminative methods that rely on linear separators, ie, CLR, CLDA, and CSVM-Lin. This is particularly true for the metabolites in which the difference between the conditional and standard versions of each linear discriminative method is small even though they exhibit the largest between strata discrepancy (Table 4), which is a counterintuitive result given the strong pairing information.

One of the most important components of paired classification methods is the ability to select biomarkers that can lead to a better understanding of the diseases being studied. Unlike standard machine learning, these methods are not designed to predict the class of a single case or control as the model is dependent on the pairing. In terms of the variables selected by the different methods (Table 5), CLR and CSVM-RBF selected the same 2 metabolites as the 2 most important features: α-tocopherol and apidic acid. α-tocopherol is a vitamer of vitamin E whose exact role in the progression of IA is still being studied,⁴⁰ but has been shown to protect against its progression.^38,39 Our results similarly indicate that α-tocopherol is negatively associated with IA progression. The role of adipic acid in type 2 diabetes has previously been studied,^41,42 but this is the first time it has been shown to play an active role in IA. Our results agree and suggest that large amounts of adipic acid are associated with a higher incidence of IA. Both methods found these 2 metabolites to be highly important and agreed on the direction of association is testament to the proposed methods validity with real data.

Both methods indicate that hydroxybutanoic acid is positively correlated with IA, which agrees with previously published studies that indicate it is an early marker for glucose intolerance.^45,46 Creatinine, a waste-product created by the breakdown of muscle, was ranked highly by both methods (CSVM-RBF 7; CLR 3) and is a commonly used marker for kidney function in that higher levels of creatinine in the blood or urine indicate decreased kidney function. Islet autoimmunity and hypoglycemia are closely linked with kidney function; therefore, increased creatinine levels would be expected among individuals with IA relative to healthy control due to compromised kidney function. As such, creatinine could be positively correlated with IA like our analysis suggests.

In terms of lipids, there is less agreement between the 2 methods, but several results consistent with the literature have been identified. Conditional logistic regression found acylcarnitine, identified among the positively ionized lipids, to be highly important to model performance and that it is positively correlated with IA progression. Previous studies also found that C3 and C4 acylcarnitines were significantly more abundant in patients with IA and T2D relative to their controls.³² A highly significant biomarker identified among the positively ionized lipids was hexosylceramide (annotated as glccer), which is negatively associated with IA progression according to both our results and a previous study that found the activation of natural killer T cells by a variant of alpha-galactosylceramide prevents the onset and recurrence of autoimmune IA. It is also possible that the hexosylceramide is a glucosylceramide because both molecules are isobaric and indistinguishable by mass spectrometry. Inhibition of glucosylceramide synthesis has been associated with an improvement of insulin tolerance.⁵⁷ The CSVM-RBF found ceramide to be negatively associated with IA progression, which is supported by the literature.³⁴ In general, high levels of some fatty acids, such as FA (16:1), have been found to be risk factors for IA,^36,37 a result supported by both methods. Finally, some ω-3 polyunsaturated fatty acids, such as pc_36_5_4_29_824_54, have been found to be negatively associated with IA, which is again confirmed by our results.

The SNPs interrogated in this report are from the ImmunoChip, a custom genotyping array based on robust genome-wide association study (GWAS) results obtained from 12 autoimmune diseases. The SNPs listed in Table 5 consistently point to the insulin component of T1D. The CSVM-RBF method highly ranked rs7158663, a SNP located on the maternal expressed gene 3 (Meg3) on chromosome 14q32.2, while CLR ranked it rather low. You et al⁵² showed that the downregulation of Meg3 is associated with impaired glucose tolerance and decreased insulin secretion in mice. Our results are validated in the TEDDY cohort, where decreased Meg3 expression is associated with development of islet autoimmunity or T1D. Conditional logistic regression highly ranked rs17388568 and rs4580644, SNPs that are located in the adenosine deaminase domain containing 1 (ADAD1) gene on chromosome 4q27 and in introns of the cluster of differentiation 38 (CD38) gene on chromosome 4p15.32. The rs17388568 SNP has been identified as a risk factor for T1D in the Wellcome Trust Case Control Consortium⁵³ as well as in a follow-up study.⁵⁴ The rs4580644 SNP is predicted to influence regulation based upon effects on enhancer and histone marks and DNAase hypersensitivity. CD38 plays a key role in insulin secretion and has been shown to differentiate individuals with and without T1D; in particular, anti-CD38 autoantibodies have been suggested as new diagnostic biomarkers in autoimmunity in diabetes.^55,56

On the whole, we have demonstrated that a wide range of classification algorithms can be used to correctly analyze and interrogate features of nested case-control studies provided the study design is accounted for with a prior data transformation. Through a simulation study and analysis of the TEDDY data, we have demonstrated that CLR is limited in the types of relationships it can model and can typically be outperformed by more sophisticated classification algorithms like SVM and NB. In particular, CLR and CSVM-RBF agreed on several potential biomarkers for IA, but the CSVM-RBF identified several other potential markers that have not been previously identified. We believe this demonstrates the potential to identify more meaningful biomarkers through the use of more analytical methods than just CLR.