Dystrophin As A Molecular Shock Absorber

Abstract

Dystrophin is the largest protein isoform (427 kDa) expressed from the gene defective in Duchenne muscular dystrophy, a lethal muscle-wasting and genetically inherited disease. Dystrophin, localized within a cytoplasmic lattice termed costameres, connects the intracellular cytoskeleton of a myofiber through the cell membrane (sarcolemma) to the surrounding extracellular matrix. In spite of its mechanical regulation roles in stabilizing the sarcolemma during muscle contraction, the underlying molecular mechanism is still elusive. Here, we systematically investigated the mechanical stability and kinetics of the force-bearing central domain of human dystrophin that contains 24 spectrin repeats using magnetic tweezers. We show that the stochastic unfolding and refolding of central domain of dystrophin is able to keep the forces below 25 pN over a significant length change up to ~ 800 nm in physiological level of pulling speeds. These results suggest that dystrophin may serve as a molecular shock absorber that defines the physiological level of force in the dystrophin mediated force-transmission pathway during muscle contraction/stretch, thereby stabilizing the sarcolemma.

Table of Contents (TOC)

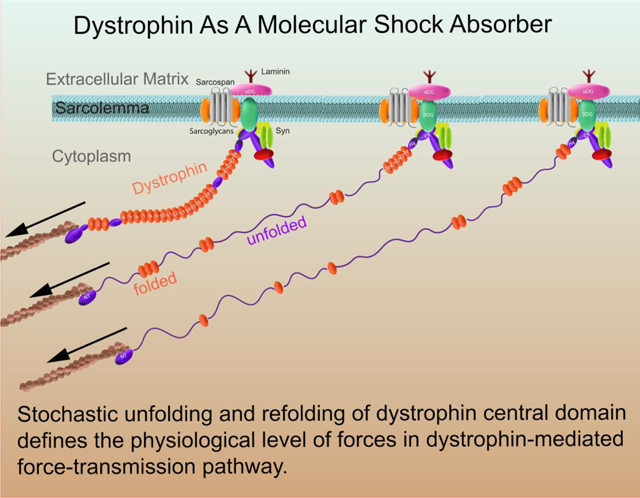
Dystrophin is a 427 kDa (3685 residues) cytoskeletal protein expressed from the DMD gene defective in Duchenne muscular dystrophy, a lethal muscle-wasting disease that afflicts 1 in 3500 live-born males.^1–3 Dystrophin protein is comprised of four major domains: 1), actin-binding domain (ABD) at the amino terminal domain that contains a pair of calponin homology (CH) modules; 2), the central rod domain that consists of 24 triple helical spectrin-like repeats (SR) interspersed with 4 putative hinge domains (H1,…,H4); 3), The cysteine-rich domain that encodes two EF-hand-like modules bounded by WW and ZZ modules; and 4), the carboxy-terminal domain that is unique to dystrophin and its homologues utrophin and the dystrobrevins.^{2, 4–12} The ABD, SR and EF-hand domains are structurally homologous to that present in several other actin binding proteins such as α-actinins and β-spectrins.^{2, 4} The cysteine-rich C-terminus domains of dystrophin are responsible for interacting with sarcospan, α- and β-dystroglycan (DG), dystrobrevins (DB), syntrophins (SYN), and α-, β-, γ-, δ- sarcoglycan complex (SGC).^{2, 4–13} Together, these are now collectively termed as dystrophin-glycoprotein complex (DGC).^{2, 4–12}

Dystrophin, together with its tightly associated complex, is localized within a cytoskeletal lattice termed costameres, which physically couple the sarcolemma and sarcomeres through extensive interacting networks.^{6–11, 14–17} Briefly, the ABD as well as SR11–15 domains of dystrophin link the complex to cytoskeleton through interacting with actin filament; the transmembrane β-DG and peripheral α-DG anchor the DGC to the cell membrane and contact with the ECM such as Laminin.^{6–11, 14–17}

Importantly, studies have established the critical role of dystrophin in stabilizing the sarcolemma against mechanical forces experienced during muscle contraction or stretch.^18–27 For instance, the absence of dystrophin in humans and the mdx mouse (which has a point mutation in DMD gene, resulting in nonfunctional dystrophin protein) leads to costamere disorganization,^28–31 sarcolemma fragility,^{19–20, 32–33} muscle weakness and necrosis.^{21, 34–35} Sarcolemma fragility, muscle weakness and necrosis are all exacerbated by mechanical stress, improved by muscle immobilization, and corrected in the mdx mouse by transgenic expression of full-length dystrophin.^19–27 However, the molecular mechanisms by which the dystrophin plays its mechanical stabilization roles are still elusive.

While the importance of N- and C-termini is apparent as the mechanical linkage of the cytoskeleton and sarcolemma, it has also been demonstrated that localization of dystrophin at the sarcolemma does not require simultaneous presence of the C-terminal domains and the N-terminal ABD domain.^36–39 Importantly, the central rod region (or part of it) is required for high efficiency of rescue of the normal phenotype in mdx mouse, demonstrated by that minidystrophin containing at least 8 SR domains rescues the phenotype more efficiently than microdystrophin containing only 4 SRs.^40–44 All these findings highlight the importance of the long central domain, which was mainly regarded as a scaffolding region previously.

To understand the roles of the central rod domain in mechanical regulation of dystrophin, it is critical to investigate the mechanical stabilities and dynamics of the force-bearing central domains, particularly, the 24 SR domains. Past decades, biophysical studies have advanced our understanding of the SR domains from various SR-containing proteins.^45–49 Importantly, AFM force spectroscopy stretching of the mini-dystrophins has revealed the unfolding force distribution of partial central rod domain.⁴⁵ However, a systematic information of force-dependent unfolding and refolding dynamics of the full 24 SR domains is essential to gain the mechanical picture of the central rod domain, which is yet to be investigated.

In addition, besides the full-length dystrophin in muscle tissues, the DMD gene also contains four internal promoters that drive expression of distinct serially truncated proteins of dystrophin in non-muscle tissues, including Dp260, Dp140, Dp116, and Dp71.⁵⁰ These truncated non-muscle isoforms mainly lack the N-terminal ABD and part of the central rod domain. How they may affect the mechanical regulation is also interesting.

To further reveal the roles of the dystrophin, especially the central rod domain in the mechanical stabilization of the sarcolemma, in this study, we systematically investigated the mechanical stability and the force-dependent unfolding/refolding transition rates of the force-bearing central domain of human dystrophin that contains 24 spectrin-repeats using magnetic tweezers.^51–53 We show that the central domain of dystrophin is able to keep the forces below 25 pN over a significant length change up to ~ 800 nm in physiological level of pulling speeds. Based on these results, we propose that dystrophin may serve as a molecular shock absorber, through force-dependent unfolding and refolding of the SR domains, that defines the physiological level of force in the dystrophin mediated force-transmission pathway with large deformations during muscle contraction/stretch, thereby stabilizing the sarcolemma.

RESULTS AND DISCUSSION

The mechanical stability and transition kinetics of central domain in dystrophin.

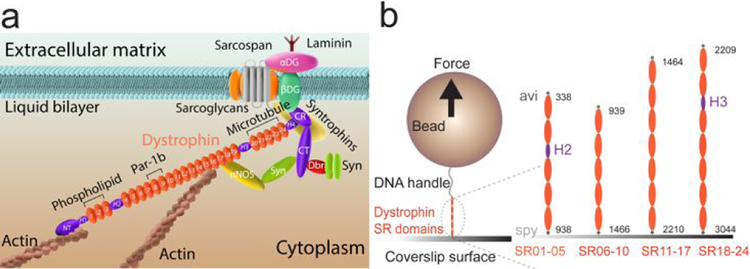
In order to investigate the mechanical stability and kinetics of the central domain in dystrophin, which contains the 24 SR domains (Fig. 1a), we constructed four fragments that cover the central domain: SR01–05, SR06–10, SR11–17, SR18–24, where the SR01–05 contains the H2, and the SR18–24 contains the H3 (Fig. 1, Methods). By stretching each of the constructs, the unfolding/refolding dynamics of each SR domain can be probed and the mechanical properties of these domains can be quantified (Fig. 2&3).

Figure 1. Experimental design of single dystrophin stretching.

(a) Illustration of the dystrophin structure and its localization in vivo. Several important binding partners of dystrophin are indicated in the panel. (b) Illustration of the experimental design of single dystrophin central domain stretching: the central domain of the dystrophin is segmentized into four fragments: SR01–05, SR06–10, SR11–17 and SR18–24. The SR01–05 contains the H2, and the SR18–24 contains the H3. Each protein construct is tagged with biotin-avi at N-terminus and spy at C-terminus. Through the tags, the protein constructs were specifically tethered between a 2.8-μm-diameter paramagnetic bead and a coverslip surface in a flow-channel. Forces on the fragments are controlled, and the resulting extension changes of the fragments are recorded through a magnetic tweezers system.

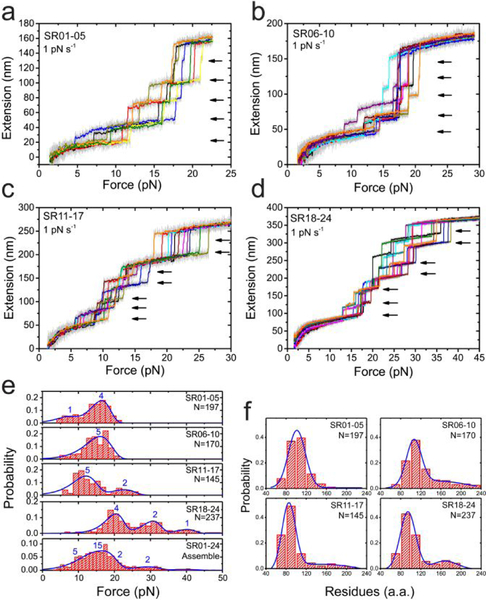
Figure 2. Force-dependent unfolding of the full central rod domain.

(a-d) Typical force-extension curves of the central rod fragments (a: SR01–05, b: SR06–10, c: SR11–17, d: SR18–24) during force-increase scan with a loading rate of 1 pN s⁻¹. Each stepwise extension jump indicates an unfolding event (black arrows). In each panel, multiple (>5) independent scan cycles are indicated by colors (10-points FFT smooth of raw data in gray). (e) Force distributions of the unfolding of the 24 SR in the central rod domain. The blue lines are the best fitting based on Bell’s model. The numbers on the panels indicate the number of SR domains involved in the distribution. (f) Distributions of the number of residues involved in each unfolding events. The blue lines are Gaussian fitting of the distribution. In e&f, “N” indicates the total unfolding events analyzed.

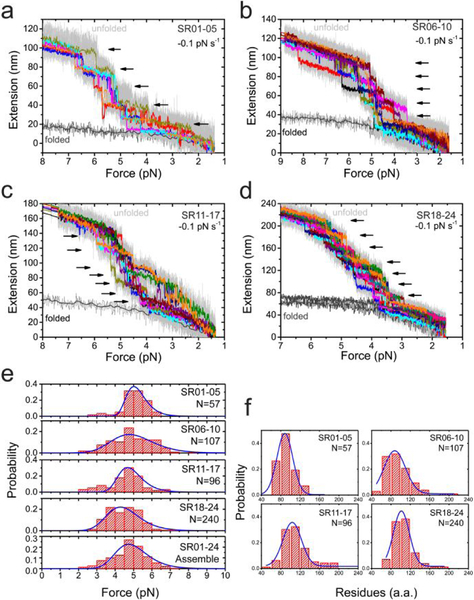
Figure 3. Force-dependent refolding of the full central rod domain.

(a-d) Typical force-extension curves of the central rod fragments (a: SR01–05, b: SR06–10, c: SR11–17, d: SR18–24) during force-decrease scan with a loading rate of −0.1 pN s⁻¹. Each stepwise extension drop indicates a refolding event (black arrows). In each panel, multiple (>5) independent scan cycles are indicated by colors (10-points FFT smooth of raw data in gray). (e) Force distributions of the refolding of the 24 SR in the central rod domain. The blue lines are the best fitting based on Arrhenius law. (f) Distributions of the number of residues involved in each refolding events. The blue lines are Gaussian fitting of the distribution. In e&f, “N” indicates the total refolding events analyzed.

Fig. 2a–d show the unfolding dynamics of the 24 SR domains (SR01–05 in panel a, SR06–10 in panel b, SR11–17 in panel c, and SR18–24 in panel d) during force-increase scans with a force loading rate of 1 pN s⁻¹. Unfolding dynamics at a higher loading rate of of 5 pN s⁻¹ is also provided for comparison (Fig. S1). During the force-increase, each domain underwent unidirectional unfolding. The clear step-wise extension-jump during unfolding of each domain (arrows in the panels) suggests that the unfolding can be understood as a two-state transition overcoming a high energy barrier separating the folded and unfolded states.

Assuming the unfolded state structure is a randomly coiled peptide, the contour length released during an unfolding step can be estimated based on the worm-like chain polymer (WLC) model of unfolded protein peptide with a bending persistence length of 0.8 nm,^54–55 from which the number of residues involved in the unfolding can be calculated based on a contour length of 0.38 nm per residue (Methods).⁵⁶ The distribution of the estimated number of residues involved in the SR unfolding shows a major peak and a minor peak (Fig. 2f). The major peak of ~110 a.a. of residues is consistent with the number of residues in one SR domain. The minor peak of ~200 a.a., is consistent with simultaneous mechanical unfolding of two SR domains, suggesting potential cooperative unfolding of some of the domains.

The unfolding force distribution of all the SR domains at the loading rate are plotted in Fig. 2e. Several different mechanical stability groups of these SR domains can be identified. For SR01–05, there are a major peak at ~ 16 pN, and a minor peak at ~7 pN. These two mechanical stability groups correspond to four and one SR domains, respectively, estimated based on the probability ratio through double Gaussian fitting. For SR06–10, there are a major peak at ~15 pN, corresponding to five SR domains. For SR11–17, there are a major peak at ~12 pN, and a minor peak at ~22 pN, corresponding to five and two SR domains, respectively. For SR18–24, there are a major peak at ~17 pN, and two minor peaks at ~30 pN and ~40 pN, corresponding to four, two and one SR domains, respectively. The unfolding force distributions of the full 24 SR domains is obtained by merging the data from the four constructs (Fig. 2e, bottom panel). Here we note that the similar unfolding force distribution of the domains in the same group suggests similar mechanical stability of these domains, but does not imply cooperative unfolding of the domains.

The fully unfolded SR domains were then allowed to be re-folded during force-decrease scans with a loading rate of −0.1 pN s⁻¹ (Fig. 3a–d). The refolding events of the domains are indicated by the step-wise extension-drops (arrows). In contrast to the unfolding force distribution, the refolding force distribution of all the SR domains shows a single peak at ~5 pN at the loading rate of −0.1 pN s⁻¹ (Fig. 3e). The number of residues estimated based on the force-dependent refolding steps show a single peak of 100 a.a. of residues based on WLC model fitting assuming the unfolded state still exists in a randomly coiled peptide conformation at low forces around 5 pN (Fig. 3f). The consistency between the expected number of residues per SR (100–110 a.a) and the estimated number of residues from refolding step sizes of SRs suggest that refolding transition to the folded SR helix bundle occurs from a disordered peptide chain instead of a chain of three α-helices (Methods). The refolding force distributions of the full 24 SR domains is obtained by merging the data from the four constructs (Fig. 3e, bottom panel).

At forces outside the experimental force range, the force-dependent unfolding and refolding rates of these SR repeats can be estimated through extrapolation based on reasonable physical models. Previous studies have shown that the force-dependent unfolding rate of α-helix-bundle domains can be described by Bell’s model,^{55, 57–60} $k_u^{\text{Bell}}(F)=k_u^0\text{exp}(\beta F\Delta )$, where $\beta =\frac{1}{K_{B}T}$, and Δ is the transition distance and $k_u^0$ is the extrapolated zero-force unfolding the extrapolated zero-force rate. The unfolding force-distributions predicted by Bell’s model at the loading rate 1 pN s⁻¹ can well fit the experimental data (blue lines, Fig. 2e, Methods), which determine the best fitting kinetic parameters for each mechanical stability group (Table 1).

Table 1. The extrapolated parameters of zero-force unfolding/refolding transitions.

Δ is the unfolding transition distance, $k_u^0$ is the extrapolated zero-force unfolding rate, Δ and $k_u^0$ are obtained based on unfolding force distribution fitted by Bell’s model. $l_f^0$ is the contour length of the peptide chain fraction of the refolding transition state, $k_u^0$ is the extrapolated zero-force refolding rate, $l_f^0$ and $k_u^0$ are obtained based on refolding force distribution fitted by Arrhenius law. The error bar is the standard deviation of the values that obtained from bootstrap analysis.

	SR01-05		SR06-10	SR11-17		SR18-24
NSR	1	4	5	5	2	4	2	1
Δ (nm)	1.5 ± 0.2	1.5 ± 0.2	1.0 ± 0.1	1.3 ± 0.1	1.3 ± 0.1	1.6 ± 0.2	1.6 ± 0.2	1.6 ± 0.2
${\mathrm{k}}_{\text{u}}^0$ (s−1)	0.13 ± 0.02	4 ± 0.5 ×10−3	2 ± 0.6 ×10−2	3 ± 0.5 ×10−2	1 ± 0.2 ×10−3	5 ± 1 ×10−4	7.7 ± 1.2 ×10−6	1.6 ± 0.3 ×10−7
${\mathrm{l}}_{\text{f}}^0$ (nm)	14.6 ± 3.4		24.4 ± 4.8		17.1 ± 2.3		20.9 ± 2.6
${\mathrm{k}}_{\text{f}}^0$ (s−1)	22.6 ± 4.7		0.39 ± 0.08		5.0 ± 0.6		0.8 ± 0.2

In contrast to unfolding, refolding of protein domains cannot be described by Bell’s model. This is because the unfolded state is a flexible peptide polymer, whose extension is sensitive to force at which refolding occurs. This leads to a force-dependent transition distance, $\Delta {\text{f}}^{*}(F)$, invalidating the assumption of a constant transition distance in Bell’s model. Therefore, we applied more generous Arrhenius equation, $k_{\text{f}}^{\text{Arrh}}(F)=k_{\text{f}}^0\text{exp}\left[-\beta \Delta {\varphi }^{*}(F)\right]$, where $\Delta {\varphi }^{*}(F)=-{\int }_0^F\Delta {\text{f}}^{*}(f)df$, is the force induced change to the free energy difference between the transition state and the unfolded state. $\Delta {\text{f}}^{*}(F)$ can be calculated based on the force-dependent extension difference between the transition state structure and the unfolded state structure.^61–62 Assuming the transition state is a partially folded structure consisting of a folded core and an unfolded fraction that is modelled as peptide chain. Therefore, $\Delta {\text{f}}^{*}(F)=x^{*,}{}^{\text{WLC}}(F)+x^{*,\text{FJC}}(F)-x_{\text{u}}^{\text{WLC}}(F)$, where x^*,FJC(F) and x^*,WLC(F) are the force-dependent extensions of are the force-dependent extensions of the folded core and the peptide chain of the transition state, respectively, and $x_{\text{u}}^{\text{WLC}}(F)$ is the force-dependent extension of the peptide chain of the unfolded state. As shown in Fig. 3e, the refolding force distribution predicted by this model at the loading rate of −0.1 pN s⁻¹ can well fit the experimental data (blue lines, Fig. 3e, Methods), which give rise to the best fitting kinetic parameters in Table 1.

By applying Bell’s model for unfolding events, and Arrhenius’ law for refolding events, we can estimate the force-dependent transition rates of these 24 SR domains over a range wider than that directly measured in experiments (Fig. 4a).

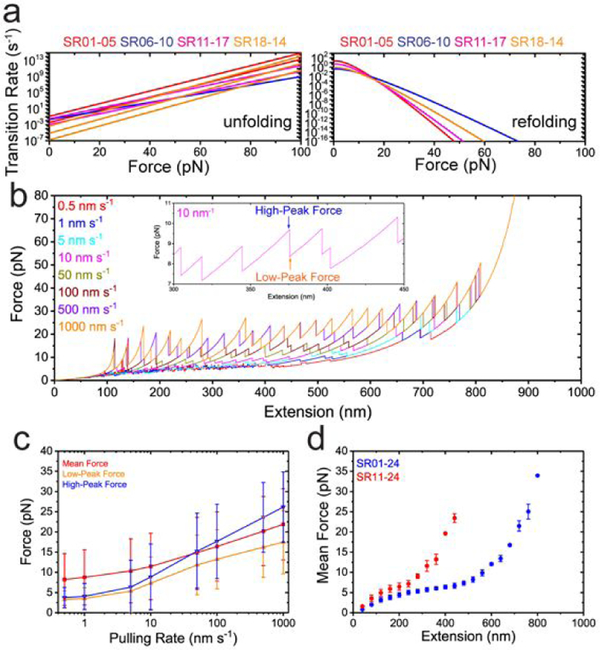
Figure 4. Dystrophin central domain as molecular shock absorber.

(a) The force-dependent unfolding (left) and refolding (right) transition rates based on experimental determined transition parameters. The four colours represent four segments (red for SR01–05, blue for SR06–10, magenta for SR11–17 and orange for SR18–24). There are eight lines for force-dependent unfolding rates for the eight kinetic groups of unfolding – two in SR01–05, one in SR01–10, two in SR11–17, and three in SR18–24. In contrast, there are four lines for force-dependent refolding rates. (b) The force fluctuations of the central domain during the linear extension increase up to 950 nm with various pulling rates (indicated by colors), obtained by Gillespie Kinetics simulation based on the experimental determined transition parameters. Inset shows the zoom-in of the force fluctuation (extension within 300–450 nm with 10 nm s⁻¹ pulling rate). Each sudden force-drop indicates a domain unfolding. The blue arrow indicates the high-peak force, and the orange arrow indicates the low-peak force. (c) The pulling rate dependent forces on central domain. The mean force is calculated as the time average of the forces from the first force peak to the last force peak; The high-peak force refers to the force right before unfolding events, and the low-peak force refers to the force right after the unfolding events. The error bars indicate the standard deviation of the data. Each pulling-rate simulation was performed with 30 repeats. The total number of unfolding/refolding events vary as pulling-rate. (d) The extension dependent forces of the central domain. The symbols indicate the averaged forces at the corresponding extension over 1000 s constant extension clamping, the error bars indicate the standard deviations. The blue data are simulations of full central domain with 24 SRs. The red data are simulations of truncated central domain with 11_th to 24_th SRs.

Dystrophin as a molecular shock absorber, defining the physiological forces.

To estimate the tension in the dystrophin-mediated force transmission pathway during sarcomere contraction and relaxation cycles, we performed kinetics simulation by a revised Gillespie algorithm based on the force-dependent unfolding and refolding rates of the full 24 SR domains (Supporting Text S1).⁶³

Briefly, the 24 rod domains are treated as a one-dimensional lattice model. At a given extension of the rod, the force in the rod is estimated based on the structural states (i.e., folded or unfolded) of the domains in the rod and the force extension curves of the domains in the corresponding states. In addition, the four hinge regions, H2 and H3 in SR01–05 and SR18–24 as well as H1 and H4 at the two ends of the rod, are modeled as flexible chains which follow the WLC model.⁵⁴ In response to the force, each rod domain undergoes stochastic structural transitions based on its force dependent unfolding and refolding transition rates (Fig. 4a). Both the time to the next transition event and the domain involved in that transition are stochastically determined based on transition rates of each domain.⁶³ After each transition, the structural states of the lattice were updated, and the resulting force was recalculated. Iteration of this process results in evolution of the structural states, causing force fluctuation in the rod, at a given extension. In addition, the stochastic kinetics simulation performed on a time varying extension of the rod can predict changes of tension and structural states of the rod domains at different pulling rates (i.e., the rate of total extension change).

Fig. 4b shows the resulting extension-force curves of the full central rod domain including the 24 SR domains and the four hinge regions at various pulling rates covering the range of possible in vivo conditions.⁶⁴ At each pulling rate, the curves exhibit a saw-tooth pattern. Each tension-increase phase is a result of extension increase without structural changes, while each abrupt force-decrease/increase indicates unfolding/refolding of a domain that relaxes/increases the tension (Fig. 4c).

Importantly, over the wide range of pulling rates from 0.5 nm s⁻¹ to 10³ nm s⁻¹, the average forces in the dystrophin is maintained below ~ 20 pN, with peak forces at ~ 5–30 pN, over a large extension range (up to ~ 900 nm, which is ~ 90% of the contour length of fullly unfolded central domain) (Fig. 4b). This extension range is close to the sarcomere length change during sarcomere contraction. Due to the transient nature, the peak forces might not impose a significant influence on the mechanical stability of the dystrophin mediated mechanotransmission. Further, at a constant extension ranging widely from 40 nm to 800 nm, where the dystrophin rod likely contains a mixture of folded and unfolded SRs, the tension fluctuates within 25 pN (Fig. 4d). These results suggest that through the stochastic unfolding and refolding of the force-bearing SR domains, dystrophin has a potential to serve as a molecular mechanical shock absorber that keeps the force within certain level throughout the whole force-transmission pathway it mediates during dynamic sarcomere contraction and relaxation.

Previous studies reported mutants/isoforms of dystrophin that lack some of the SR domains (Fig. 1a). Particularly, dp427c and dp427p1 with mutated or truncated ABD domain, possibly lead to weaker actin filament binding through ABD domain; dp260–1 and dp260–2 with deletion of ABD and SR01–09, can only associate with actin filament through SR10–15, leading to shorter length of the dystrophin. To investigate the effects of these dystrophin isoforms/mutants on the molecular mechanical shock absorber capability, we performed simulations with the corresponding numbers of SR domains as shown in Fig. 4d. The results show that, although the isoforms/mutants are capable of buffering forces within a similar level, they can only do so over a significantly shorter extension range compared to full-length dystrophin.

In this study, we determined the force-dependent stability and kinetics of the 24 SR domains in the central domain of dystrophin. The 24 SR domains provide binding sites to a number of important proteins (Fig. 1a). The currently discovered interactors of the central domains include phospholipid (1_st-3 SRs),^65–68 Par-1b kinase (8_th-9_th SRs),⁶⁹ actin filaments (11_th-17_th SRs),^{6, 70} neuronal nitric oxide synthase (nNOS) (16_th-17_th SRs),⁷¹ microtubule filaments (20_th-24_th).^72–73 However, how force applied to dystrophin may affect these interactions is poorly understood.

Our results show that, the 24 SR domains can be unfolded over a force range from 5 – 40 pN (at loading rates in the order of 1 pN s⁻¹). Therefore, the unfolding/refolding of the 24 SR domains may serve as mechanical switches of their interacting partners. Through unfolding of the SR domains, it turns off the interaction of those that target to the folded SR domain region, while it turns on those that target to the unfolded region of SR domains, and vice versa. Interestingly, it has been reported that mechanical loading regulates NOS expression and its activity in developing and adult skeletal muscle.⁷⁴ Importantly, mechanical activation/deactivation of interactions appears a generic mechanism shared among a number of crucial mechanosensing proteins, such as talin, α-catenin, α-actinin, and titin etc.^{53, 57–59, 75–77} It would be interesting to further investigate how binding partners of the force-bearing regions within dystrophin are regulated by force in the future.

In our body, the dystrophin pulling rate can vary over a wide range. In heart, heart beating involves cyclic stretching with a frequency in the order of 1 Hz and an extension change of sarcomere in the order of 1 μm. Assuming that dystrophin undergoes cyclic stretching-relaxation processes with the similar frequency, and involves an extension change of similar range, the pulling rate of dystrophin in heart tissue can be roughly estimated in the order of 1000 nm s⁻¹. For skeletal muscle, the pulling rates depend on conditions, for example whether the person is doing exercise. Under most of conditions the pulling rates can be considered slower than 1000 nm s⁻¹. Our simulations have been done over a wide range of pulling rate from 0.5 nm s⁻¹ to 1000 nm s⁻¹, which we believe covers most of the physiological pulling rate range of human muscles.

Our simulation results show that dystrophin, particularly its central domain, may serve as a molecular shock absorber that buffers the average forces in dystrophin over a range of ~5–25 pN and peak forces up to 30 pN over a large extension change up to hundreds of nm till all SR unfolded. Therefore, it may play an important role that defines the physiological level of forces in the dystrophin mediated force-transmission pathway during muscle contraction/stretch, thereby stabilizing the connections to sarcolemma and to sarcomere by preventing accumulation of large tension. In addition, the simulation results suggest that shortened dystrophin isoforms/mutants are also capable of buffering forces within similar range. However, the extension range within which the force can be buffered, which is in proportional to the number of repeats, is decreased. Therefore, these shortened isoforms may lose their force buffering function when the deformation exceeds the extension range, impairing the mechanical stability of sarcolemma and sarcomere connections.

A quantitative understanding of force level in each important force-transmission pathway in vivo is crucial for deciphering the molecular mechanisms of mechanosensing proteins. In many important force-transmission pathways, one or more large rod-like proteins consisting of a tandem of repeats of structural domains are involved, such as talin in focal adhesion site, nesprins at nuclear membrane, and dystrophin at sarcolemma. All such large rod-like force-bearing proteins have the potential to buffer force in the force-transition pathways they mediate. Current imaging technologies enable the measurement of the extension fluctuation of such force-bearing large rod-like proteins in living cells.^78–79 Our study shows that the force fluctuation in the molecule can be estimated based on the extension fluctuation, providing the knowledge of force-dependent unfolding and refolding rates of the structural repeats. Therefore, we propose a method to measure the force in a force-transmission pathway in living cells, by combining in vitro measurement of the force-extension relation of the relevant force-buffering protein and in vivo measurement of the extension fluctuation of the corresponding protein. This method is different from the FRET-based force sensor,⁸⁰ providing an alternative approach for force-estimation in vivo with a force range up to tens of pN.

CONCLUSIONS

In summary, we experimentally determined the force-dependent stability of the 24 SR domains in the central domain of dystrophin, and propose that through the stochastic unfolding/refolding of the rod domains, dystrophin may serve as a molecular shock absorber that buffers the average forces in dystrophin over a range of ~5–25 pN and peak forces up to 30 pN over a large extension change. Therefore, it may play an important role that defines the physiological level of forces in the dystrophin mediated force-transmission pathway during muscle contraction/stretch, thereby stabilizing the connections to sarcolemma and to sarcomere by preventing accumulation of large tension.

EXPERIMENTAL METHODS

Plasmids constructs and protein expression.

Four fragments of the dystrophin central rod domain (i.e., SR01–05: 338_th-938_th; SR06–10: 939_th-1466_th; SR11–17: 1464_th-2210_th; SR18–24: 2209_th-3044_th) were synthesized by PCR using plasmid template containing the full-length human dystrophin sequence.⁷⁰ Each of the four DNA fragments was then sub-cloned into expression vectors (pET151-TOPO) with an N-terminal avi-tag and a C-terminal spy-tag using HiFi DNA Assembly (NEBuilder®). Each of the resulting plasmids was co-transformed with a BirA plasmid and expressed in Escherichia coli BL21 (DE3) cultured in LB-media with D-Biotin (Sigma Aldrich), and affinity purified through His-tag.

Single-protein manipulation and analysis.

A vertical magnetic tweezers setup,^{51, 53} was combined with a disturbance-free, rapid solution-exchange flow channel for conducting in vitro protein stretching experiments.⁵² All experiments were performed in solution containing: 1× PBS, 1% BSA, 2 mM DTT, 10 mM Sodium L-ascorbate at 21 °C.

Transition step size to residue number conversion.

The force-extension curve of a folded SR domain is determined by the rigid rotation fluctuation of a characteristic rigid-body with a length b ~ 4.5 nm, estimated from the PDB file of the folded SR domain,⁸¹ which is the distance between the two force-attaching points (i.e. the N- to C-terminal distance in our experiment). This force-extension curve can be described by the freely-jointed chain polymer model with a single segment: $x^{\text{FIC}}(f)=b\left(\text{coth}\left(\frac{fb}{k_{B}T}\right)-\frac{k_{B}T}{fb}\right)$. The unfolded state of a domain can be a flexible peptide chain, and this force-extension curve can be described by the worm-like chain (WLC) polymer model through the Marko–Siggia formula, with a bending persistence length of A ~ 0.8 nm: $\frac{fA}{k_{B}T}=\frac{1}{4{\left(1-\frac{x^{\text{WLC}}(f)}{l}\right)}^2}-\frac{1}{4}+\frac{x^{\text{WLC}}(f)}{l}$, ^54–55 where l = n * l₀ is the contour length of the unfolded domain, n is the number of residues of the domain, l₀ = 0.38 nm is the contour length of per residue.⁵⁶ Hence the unfolding/refolding stepsize is the extension differences of the domain before and after unfolding at the transition (unfolding/refolding) force, i.e., $\Delta x(f)=x^{\text{WLC}}(f)-x^{\text{FJC}}(f)$. Based on the above equations, the contour length l and the number of residues n involved in the transition can be obtained from the measured step-sizes of the transition at a given force.

Unfolding/folding kinetics and force distribution.

The unfolding and refolding force distributions of the SR domains obtained at given loading rates carry the information of the kinetics of the transition. The force-dependent unfolding/refolding kinetics predicts an unfolding/folding force distribution, ρ_r(f), at a given loading r as:

$${\rho }_{\text{r}}(f)=\{\begin{array}{ll}\frac{k(f)}{\text{r}}{e}^{-\underset{f0}{\overset{f}{\int }}(f^{\prime })\frac{\text{d}{f}^{\prime }}{\text{r}}}\hfill & ,\text{r}>0\hfill \\ \frac{k(f)}{\left|\text{r}\right|}{e}^{\underset{f0}{\overset{f}{\int }}(f^{\prime })\frac{\text{d}{f}^{\prime }}{\text{r}}},\hfill & \text{r}=-\left|\text{r}\right|\hfill \end{array}$$

where the f₀ = 0 pN for r > 0, and f₀ is a sufficiently large value (30 at which the folding probability is zero for r < 0. f is the force where transitions occur. Equation on upper panel predicts the unfolding force distribution (r > 0), the bottom panel predicts the refolding force distribution (r = − |r| < 0). In the case of Bell’s model for unfolding transition, ρ_r(f) has a simple analytical solution.⁶⁰ Based on above derived equations, the kinetics parameters of unfolding and refolding of SRs can be determined by maximum likelihood fitting. The standard deviations of the kinetic parameters are obtained by bootstrap analysis (Supporting Text-S2).