Tradeoffs and Constraints on Neural Representation in Networks of Cortical Neurons

Abstract

Neural representation is pivotal in neuroscience. Yet, the large number and variance of underlying determinants make it difficult to distinguish general physiologic constraints on representation. Here we offer a general approach to the issue, enabling a systematic and well controlled experimental analysis of constraints and tradeoffs, imposed by the physiology of neuronal populations, on plausible representation schemes. Using in vitro networks of rat cortical neurons as a model system, we compared the efficacy of different kinds of “neural codes” to represent both spatial and temporal input features. Two rate-based representation schemes and two time-based representation schemes were considered. Our results indicate that, by large, all representation schemes perform well in the various discrimination tasks tested, indicating the inherent redundancy in neural population activity; Nevertheless, differences in representation efficacy are identified when unique aspects of input features are considered. We discuss these differences in the context of neural population dynamics.

Introduction

While the notion that object representation is embedded in sequences of action potentials is fairly well accepted among neuroscientists, there is less agreement concerning the actual representation schemes (i.e., neuronal activity features) that carry stimulus-relevant information at the assembly level. Attempts to address this question range from in vivo measurements combined with psychophysical procedures, to abstract mathematical constructs that are realized (in most cases) in numerical simulations. As it currently stands, in vivo research of neural representation has led to highly region and context-specific answers (deCharms and Zador, 2000). The nature of neural representations in the brain is determined and affected by many factors: anatomy and wiring of the region in interest, ongoing activity, modulations from other brain regions, properties of the stimulus itself and many others. It is difficult, given all these determinants, to understand the origins of the relations obtained in vivo, and to attribute a property of the “neural codes” to its cause. Not the least of the factors that constrain the nature of the neural code is the biophysics of the neural assembly itself: dynamical properties of its elements and connections. This is a more fundamental and generic aspect of the neural representation problem, which is less dependent of the specific region, modality and functional context, and is the primary focus of the present study.

So far, most studies of input representation by generic neural assemblies, or of the input-output relations of such assemblies, were mainly theoretically oriented, and were based on analytic or numeric models of populations of neurons (Mazurek and Shadlen, 2002; Sanger, 2003). While these approaches carry the appealing advantage of reduced modeling, they also suffer from serious shortcomings, resulting from exactly those simplifications and abstractions. By choosing a simplified model of a neuron and a synapse, they leave out most of their internal processes and dynamics, that might have a major impact on the results and their interpretations.

The tradeoff then, is between limited control and multiplicity of intervening factors in in vivo experimental approaches, and unavoidable oversimplifications in theoretical approaches. Here we have followed an intermediate path, that allows considerable control over relevant variables and good sampling capabilities, while maintaining the complexity of individual neurons and synaptic connections practically intact. We describe experiments performed using large scale random networks of cortical neurons, developing in vitro (Marom and Shahaf, 2002; Morin et al., 2005) upon substrate-embedded electrode arrays that allow stimulation at multiple spatial locations while monitoring the spiking activity of many individual neurons.

In this study we map the concepts of representation and input-output relations to this system. Given the dynamics and properties imposed by the biological assembly, we ask: Which representation schemes are plausible and what are the constraints and limitations involved? We compared a number of representation schemes in a series of discrimination tasks, to assess their efficacy in revealing the differences between inputs—namely, the spatial location of the input, and the time elapsed from the previously applied stimulus. Our results show that in general, all the examined representation schemes perform well in these tasks, while differences in their relative advantages become apparent when different tasks are considered.

Materials and Methods

Network preparation.

Cortical neurons were obtained from newborn rats (Sprague Dawley) within 24 h after birth using mechanical and enzymatic procedures described in earlier studies (Marom and Shahaf, 2002). The neurons were plated directly onto substrate-integrated multielectrode arrays and allowed to develop functional and structural mature networks over a time period of 2–3 weeks. The number of neurons in a typical network is in the order of tens to hundreds of thousands; various estimates of connectivity suggest that each neuron is monosynaptically connected to 10–30% of all other neurons in a radius of 600 μm, with ∼20% of the synapses being inhibitory (see (Marom and Shahaf, 2002) for a comprehensive review of the preparation). The preparations were bathed in MEM supplemented with heat-inactivated horse serum (5%), glutamine (0.5 mm), glucose (20 mm), and gentamycin (10 μg/ml), and maintained in an atmosphere of 5% CO₂ and 95% air at 37°C in an incubator as well as during the recording phases. Multielectrode arrays (MEAs) of 60 Ti/Au/TiN electrodes, 30 μm in diameter, and spaced 500 μm from each other (MultiChannel Systems) were used. The insulation layer (silicon nitride) was pretreated with polyethyleneimine.

Measurements and stimulation.

A commercial 60-channel amplifier (B-MEA-1060, MultiChannel Systems) with frequency limits of 150–5000 Hz and a gain of ×1024 was used. The B-MEA-1060 was connected to MCPPlus variable gain filter amplifiers (Alpha Omega) for further amplification. Rectangular 200 μs biphasic 50 μA current stimulation through chosen pairs of adjacent MEA electrodes was performed using a dedicated stimulus generator (MultiChannel Systems). Data were digitized using two parallel 5200a/526 A/D boards (Microstar Laboratories). Each channel was sampled at a frequency of 24 Ksample/s and prepared for analysis using the AlphaMap interface (Alpha Omega). Thresholds (×8 RMS units; typically in the range of 10–20 μV) were defined separately for each of the recording channels before the beginning of the experiment. All the activity recorded in the 60 electrodes was collected and stored for analyses. The data presented here is not spike-sorted. Each electrode in our setup senses ∼1–3 neurons and previous analyses on sample datasets do not show qualitative differences in results between spike sorted and nonsorted spike trains.

Data analysis.

Mature networks (14–21 days in vitro) were chosen for experimentation based on their ability to reliably respond to more than one source of low-frequency (0.1 Hz) stimulation. Reliability is defined as above 50% success in evoking a synchronous population response, denoted “network spike” (NS) as explained in Results (Eytan and Marom, 2006; Thivierge and Cisek, 2008). The first 10 ms following each stimulus were removed from the data, to exclude spikes that were directly evoked by the stimulus itself; this point is further elaborated on in Results, General considerations. Response features were extracted from the neural response, and were standardized before classification analysis. Of the various available methods for estimating the information content of a specific neural response feature with regard to a specific input feature (each regraded as a random variable) (Paninski, 2003; Nelken and Chechik, 2007), we chose the decoding approach, which put a lower limit on the information content (in the sense that an optimal decoder can be only approximated by a real one, hence resulting an underestimation of the information). We use here a support vector machine (SVM) with a nonlinear Gaussian kernel, a general-use state of the art supervised classification algorithm (Ben-Hur et al., 2008). In general, a SVM is an algorithm designed to find an optimal separating hyperplane between two or more groups of points in an Euclidean space. Eighty percent of the available data are used as a training set by the algorithm for the construction of the hyperplane, while the remaining 20% are used for the generalization error evaluation, which is quoted throughout this paper. Specifically, we have used MCSVM1.0 (webee.technion.ac.il/people/koby), a C code package for multiclass SVM (Crammer and Singer, 2001) with Gaussian radial-based function kernel. The kernel width parameter was set to a value in the range [0,10] which gives the maximal accuracy in 5 trials. Each classification was repeated 30 times (for confidence interval estimation), each time with a different randomly selected train and test sets.

Results

General considerations

Various measures of cell physiology, microscopic connectivity statistics and activity dynamics, indicate that in vitro networks of cortical neurons are reasonable models of in vivo neural assemblies, notwithstanding the absence of large-scale morphological features (Marom and Shahaf, 2002; Morin et al., 2005). The main mode of activity in these networks, both spontaneous (van Pelt et al., 2004; Chiappalone et al., 2007) and in response to electrical stimulation is the network spike (NS)—an event of synchronous network activity (Eytan and Marom, 2006; Thivierge and Cisek, 2008; Thiagarajan et al., 2010) lasting tens to hundreds of milliseconds. At the system level (in vivo), the network spike is a universal phenomenon that characterizes responses to sensory objects, regardless of the stimulus modality, stimulus complexity or cortical area involved (Meister et al., 1991; Riehle et al., 1997; Usrey and Reid, 1999); behaviorally relevant objects are believed to be represented by the activity of neurons within the network spike time-amplitude envelope (Keysers et al., 2001; Wesson et al., 2008; Foffani et al., 2009). In recent years, multiple studies have shown that the biophysical nature of the in vivo network spike, as well as its capacity to represent temporal and spatial input features, are preserved in the reduced in vitro model system, enabling well controlled analysis of the network spike's properties in a single, isolated neural network (Marom and Shahaf, 2002).

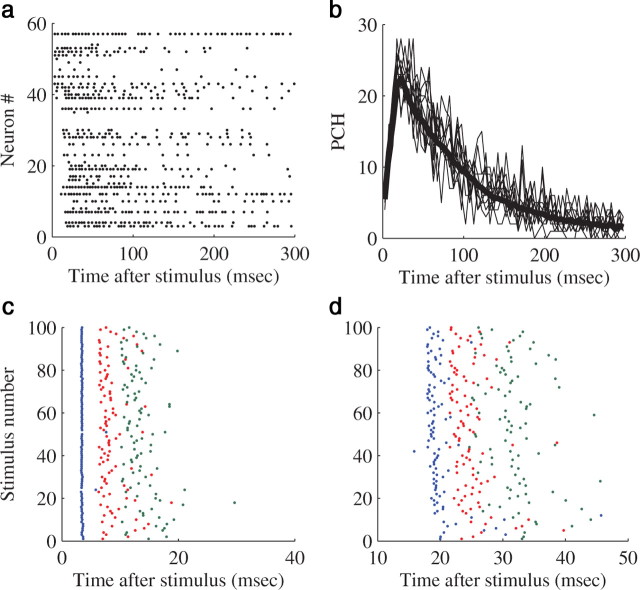
An electrical stimulation of an in vitro network (a current pulse between a pair of electrodes—see Materials and Methods) induces an action potential in a subgroup of neurons (Jimbo et al., 2000). This so-called “immediate response” (or “receptive sheath”) is very precise and reproducible (i.e., repeats itself with low jitter in consecutive trials) (Fig. 1c), involves ∼5–10% of the neurons in the network (estimated by the number of neurons that respond immediately out of the total recorded neurons), and does not involve synaptic transmission; indeed, immediate spikes persist also under total synaptic blockade (data not shown). While the subset of neurons that responds directly to stimulation depends on the identity of the stimulating electrodes, overlap between these subsets does exist.

Figure 1.

The network spike. All the panels are examples from a singe experiment. a, An example of a single, stimulus-evoked NS. Each line is a raster plot of a single electrode. b, Population firing rate profiles of NS (population-count-histogram—PCH). Each thin line is the histogram of a single evoked NS, binned with a 5 ms bin size, the thick black line is the average of 120 responses. All NS are evoked by the same stimulating electrode. c, d, A raster of the first three spikes of two example neurons. Here also it can be seen that while the immediate first spike is very precise, later spikes suffer from a large jitter. c, The raster is elicited from a neuron participating in the immediate response. d, The raster is created from a neuron first firing in the recruitment phase.

Following the immediate response, activity is propagated into the rest of the network by synaptic transmission, and eventually recruits the vast majority of neurons (the so-called “recruitment phase” of the NS). Activity then reverberates across the network and eventually dies out (Eytan and Marom, 2006; Thivierge and Cisek, 2008), creating the characteristic shape of the network spike. An example of a stimulus-evoked NS, with the immediate response, the recruitment phase, followed by a reverberating phase that lasts a couple hundreds of milliseconds (Jimbo et al., 2000; Eytan and Marom, 2006), is provided in Figure 1.

This study focuses on the ways stimulation features affect synaptically mediated activity, beyond the immediate response. The immediate response may last for up to 25 ms following a stimulus, however more then 95% of its spikes are confined to the first 10 ms (Bakkum et al., 2008; Shahaf et al., 2008; supplemental Item 1, available at www.jneurosci.org as supplemental material); therefore, the first 10 ms following each stimulus were excluded from the data. While data beyond this limit might contain, in a very low probability, a small fraction of spikes that were directly activated by the stimulus, we chose not to exclude spikes beyond 10 ms since the data there is made of mostly synaptically mediated response.

In what follows we will denote different stimulating electrodes (that evoke immediate response in different subsets of neurons) as different “spatial sources” representing different input identities. The “output” of the assembly is defined as the spatiotemporal pattern of individual action potentials in the NS (i.e., all the downstream spikes, excluding the immediate response). The questions asked here concern the capacity of this output activity to represent different stimulus features. To that end, our general approach is as follows: network spikes are evoked using stimuli that differ from each other in their spatiotemporal features (i.e., different positions of stimulation, or different temporal patterns from the same input position); population responses to these stimuli are recorded and analyzed with the aim of extracting activity features that may be mapped to the different spatiotemporal features of the input. To avoid trivialization of the results, we only consider the activity of neurons that are broadly tuned—that is, neurons that participate in responses to all of the input sources.

We adhere to an operational interpretation of the “representation scheme” concept—that is, reducing it to the question of transformations that maintain sufficient statistics to allow for categorization of input features. In this respect, a comparison between efficacies of representational schemes is a comparison between different reducing transformations. In search of a common ground for such a comparison, one approach is to use information-theoretic measures to quantify the relation between stimulus and response features. Such methods, however, are impractical when data are limited and large populations of neurons are concerned (Petersen et al., 2002; Sanger, 2003; Nelken et al., 2005). The alternative chosen here is the use of a decoder (Quian Quiroga and Panzeri, 2009) that places a lower limit on the information content of the response by the performance of a supervised classifier, which attempts to determine the stimulus that caused the neural response. In the decoding paradigm, the responses are labeled with a few distinct classes that correspond to specific features of the input (spatial location, interstimulus interval, etc.). Different features of the response are then extracted using predefined reducing transformations (see below), to produce the feature (representation) vectors. The dataset is divided to training and test sets that are used to train and evaluate the decoder (see methods). Here we chose to use as a decoder a general-purpose support vector machine (SVM, see Materials and Methods). The performance of the decoder on the test set (the classification accuracy) places a lower limit on the “real” information content of the representation scheme (feature of the neural response) about the stimulus feature used to label the data.

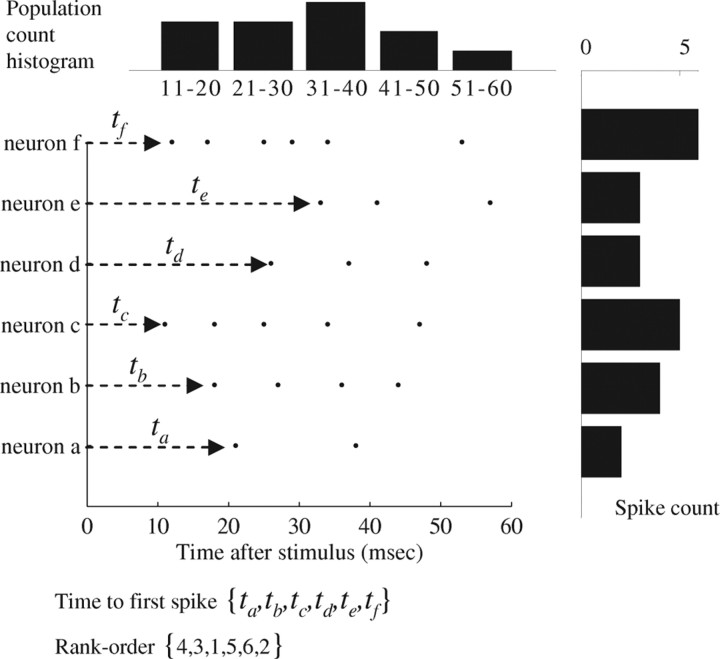
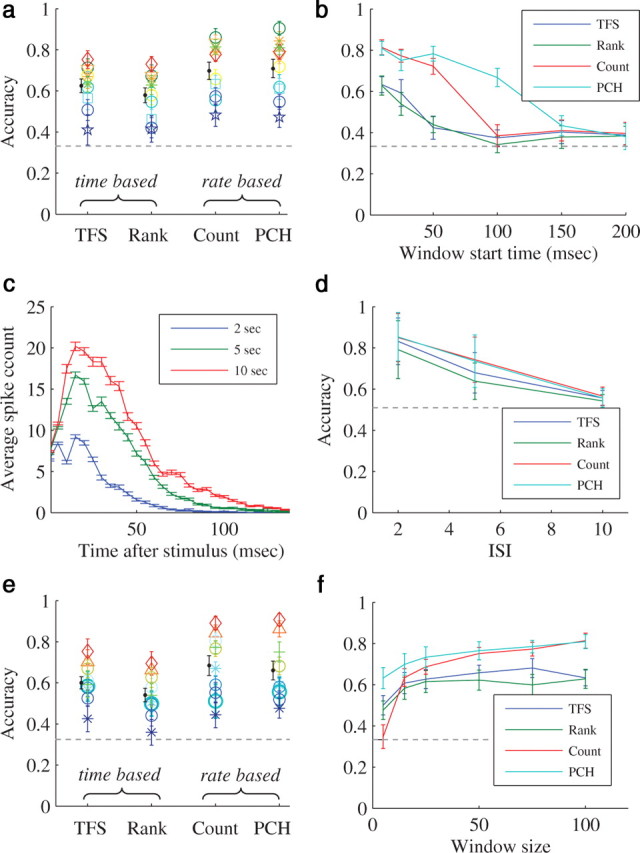
We have tested and compared four typical examples of reducing transformations that are referred to in the neurophysiology literature (Fig. 2), as follows. (1) Population-count-histogram: Here, the individual identities of spiking neurons is omitted, and only the temporal profile of the total spike count, throughout the network, is considered (Schwartz, 1993; Hupé et al., 2001; Fiorillo et al., 2003). (2) Spike-count: The timing of individual spikes is omitted, and only the number of spikes evoked by each (identified) neuron in a predefined time interval is considered (Arabzadeh et al., 2006; Foffani et al., 2009; Jacobs et al., 2009). (3) Time-to-first-spike: The precise time delay from the stimulus to the first spike evoked by each (identified) neuron is considered (Petersen et al., 2001; Foffani et al., 2004; Johasson and Birznieks, 2004; Gollisch and Meister, 2008; Gollisch and Meister, 2008). (4) Rank-order: A vector of recruitment rank order, constructed from time-to-first-spike (Thorpe et al., 2001; Van Rullen and Thorpe, 2001; VanRullen et al., 2005; Shahaf et al., 2008).

Figure 2.

An illustration of the data reduction process. Neurons (a–f) responding to a single stimulation event by evoked spikes (dots). The first 10 ms after stimulus were discarded. The TFS (time-to-first-spike) representation is the precise time of the first spike at each electrode. The rank representation is derived from latencies to first spikes (t_a–t_f). Neurons that fired within the same time bin were ranked according to their alphabet. The count representation is the number of spikes in each electrode in a given time window following the stimulation. The PCH (population-count-histogram) representation is the temporal profile of spike counts of the all neuron in a defined time window.

Of course, other types of representation schemes do exist (e.g., correlation-based, or general spike patterns); however, the above four types seem to cover a wide enough range of response features. The general approach presented here may be extended to include more specific types of schemes. Note that these four reducing transformations may generally be designated as time based (time-to-first-spike and rank-order) or rate based (population-count histogram and spike-count). These transformations are parameterized by a number of parameters (e.g., temporal resolution, temporal window length, number of neurons etc.). The dependence of classifier performance on some of those parameters will also be described.

Representation of stimulus identity

As a first experiment, five spatial input sources (stimulating electrode pairs) were chosen randomly and the efficacy of the four schemes described above in discriminating between the responses was compared. The stimuli were ordered randomly, once every 15 s; a total of 850 stimuli per experiment were applied. Six experiments, performed on six different cultured network preparations, were analyzed. Ideally, one would like to compare the efficacy of the reduced representation schemes to the ability of the decoder to classify the input sources given the entire dataset, before any reducing transformation is applied. Obviously, the dimensionally of the entire data—that is, all spikes that were recorded during the response (lasting ∼300 ms) from all the electrodes (60 electrodes), is too high to be considered. However, even if the spiking activity of 20 neurons, binned at a 5 ms time resolution, is used, the average test set classification accuracy is ∼0.9 (±0.07 SD). In the analysis that follows, we will see that reduction of the data by the various transformations, can maintain similar classification accuracies.

Indeed, as seen in Figure 3a, all four data reduction schemes maintain a sufficient amount of information to allow the classifier to perform well above chance (which is 0.2 for a five input sources). However, it is clear from Figure 3a that time-based schemes outperform rate-based schemes. Of the two time-based schemes, rank-order (which is a further reduction of the time-to-first-spike scheme) captures practically all the information carried by the time-to-first-spike scheme. This is consistent with recently published results (Shahaf et al., 2008). A table of all the results used for construction of Figure 3a is presented in supplemental Item 2 (available at www.jneurosci.org as supplemental material), together with general response statistics of the networks. The better performance of the time-based schemes, that take into account only the first spikes recorded by each electrode, suggests that timing (be it absolute or ranked) of spikes is an informative feature of the response. Interestingly, as shown in Figure 3b, the timing of later spikes (second, third, etc.), recorded as the response progresses, becomes much less informative, suggesting that the significance of exact timing reduces as the temporal duration from stimulation increases.

Figure 3.

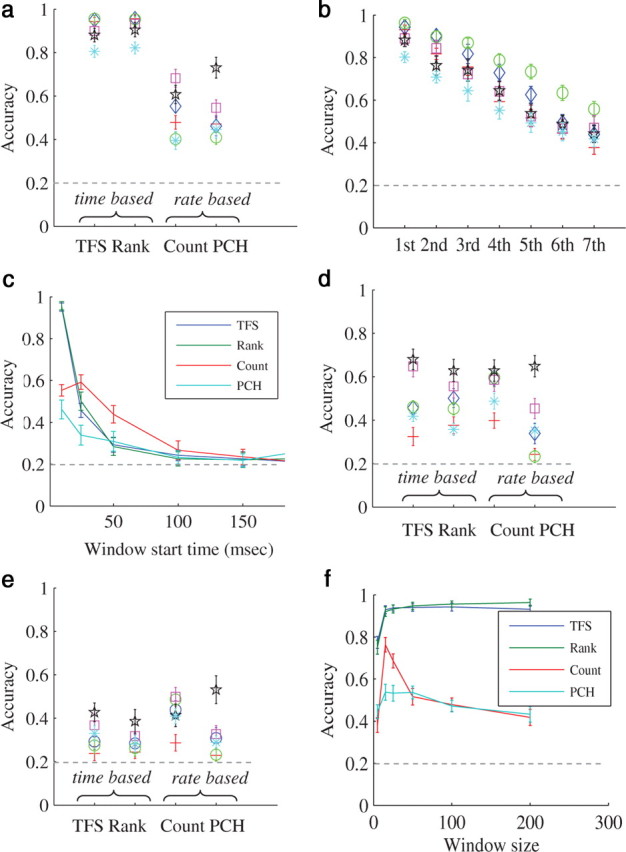
Representation of stimulus identity. Classification accuracy of each representation scheme in spatial experiments. Support vector machine (SVM) algorithm with a Gaussian radial-based function kernel was applied to vectors of training sets (see Materials and Methods). The resulting classifiers were validated using test sets vectors. Confidence interval are calculated over 30 train-test cycles. Horizontal dashed line represents chance level. a, Analysis results on all (n = 6) spatial categorization task experiments. Each color represents a different experiment. Results with response window of length 100 ms which starts 10 ms following the stimulation. b, The classification accuracy of precise time for the first spike in each neuron, the second spike and so on. Each color represents a different experiment. c, An example from one specific spatial experiment, that shows the sensitivity of classification accuracy to the window start time after the stimulus. d, Results with response window of length 100 ms which starts 25 ms following the stimulation. e, Results with response window of length 100 ms which starts 50 ms following the stimulation. f, An example from one specific experiment, that shows the sensitivity of classification accuracy to response window size.

Is this true also for rate-based schemes (meaning, do first spikes contribute more information than subsequent ones)? The analysis of Figure 3a was performed on spikes recorded during a window of 100 ms from stimulation (excluding, as always, the immediate response spikes). We checked how performance is affected when the window's start-time is delayed (keeping its total length fixed), to obtain insights as to the “temporal location” of the information embedded in the network spike. As can be seen in Figure 3c (an example from one experiment), classification accuracy of time-based representation schemes is significantly reduced when only spikes recorded beyond 25 ms from stimulus are considered (in accordance with the previous analysis). Under such conditions, the efficacy of time-based schemes approaches the efficacy of rate-based schemes. Beyond 50 ms, classification accuracy becomes quite low in all schemes. Results from all experiments are summarized in Figure 3e. We have also analyzed the effect of the window size on classification accuracy (Fig. 3f). This analysis shows that there exists an optimal window size, beyond which additional spikes do not improve the performance, and, in the case of rate-based schemes, even reduce it.

Altogether, the results of this section suggest that information about the spatial location of the stimulus (“stimulus identity”) is largely concentrated in the first tens of milliseconds following the stimulation, within the recruitment phase of the NS. As the observation duration increases, the signal becomes contaminated by factors irrelevant to this task. These additional contributions to the response might contain information about other features of the stimulus, the state and ongoing processes of the network, history of input and activity, etc.

Dependency on the physical distance between stimulating electrodes

We have seen that different stimulating electrodes elicit neural responses that differ enough from each other to enable input discrimination. What can be said about the relation between this discrimination capacity and the physical distance between the stimulating electrodes? In other words, is stimulation from electrodes far away from each other is more easily discriminated compared with electrodes that are near to each other? To evaluate this issue we compared the source separation performance for different pairs of stimulation sources in the same preparation. As Figure 4a shows, discrimination is indeed better when spatially remote stimulation sources are used. This can arguably be attributed to a smaller overlap between the groups of immediate-responding neurons (closely located sources entail larger overlaps between immediate responding neuron groups—data not shown). This property can be used to demonstrate a very simplified generalization-like task in our model system. Generalization, that is the capacity to tell that a hitherto unobserved object belongs to a familiar category, is one of the most ubiquitous features of neural systems (Thompson, 1962; Wilson, 2001; Hampton and Murray, 2002). While risking oversimplification of this broad concept, we offer the somewhat naive reduction of the concept to “spatial proximity” of input coordinates, the logic being that objects belonging to the same category activate groups of neurons that overlap. The idea, in our reduced system, is to see how a classifier that was trained to categorize responses to two distant stimuli (A and B) will classify a response from a third source C (Fig. 4b), that can be at various distances from A and B. This (possibly expected) result shows that the classifier tends to classify the responses to the new stimuli as belonging to the closer known source, thus supporting this mapping of the generalization concept.

Figure 4.

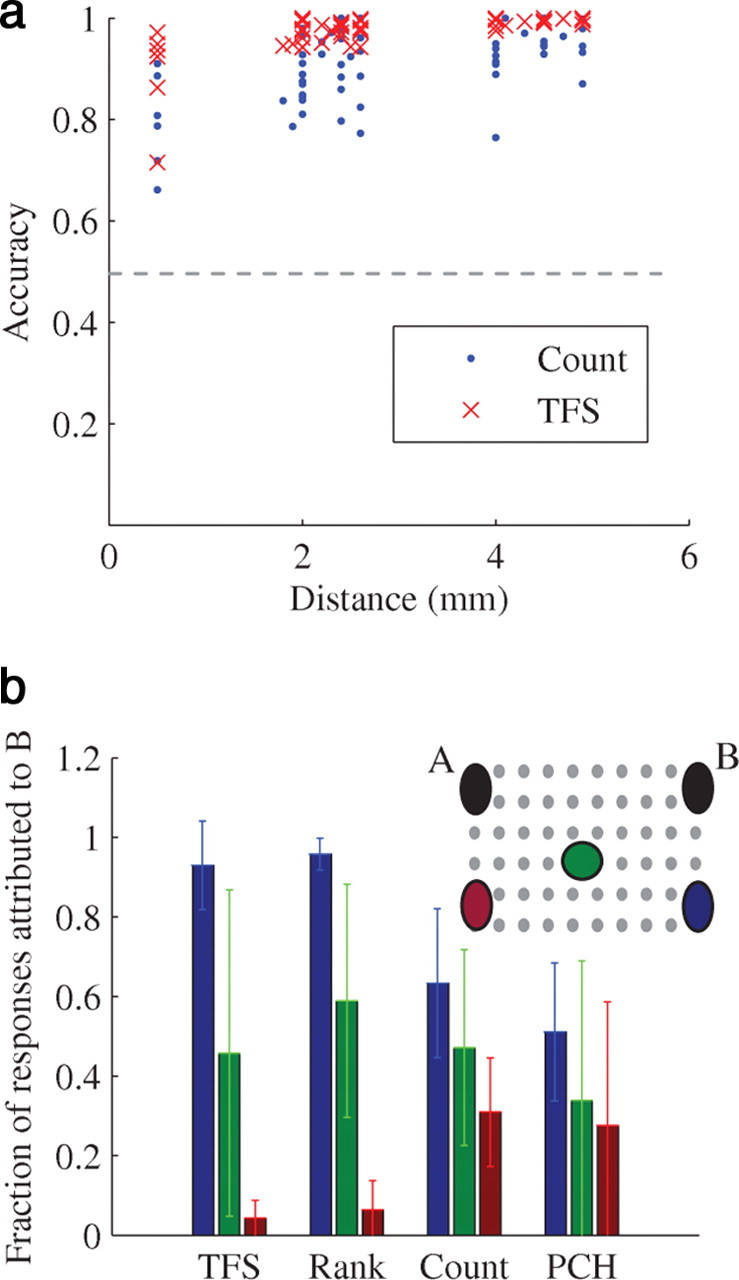
Dependency on the physical distance between stimulating electrodes. a, The classification accuracy between the responses of pairs of stimulation sources as function of the distance between the sources. All spatial discrimination experiments are included in the analysis. Horizontal dashed line represents chance level. b, Inset, An illustration of electrodes selection. The decoder was trained to classify between stimulations given at sites A and B. In the testing phase, it was given responses to stimulation from sites C asking to which site (A or B) the response is classified. Main panel, The average percentage of the responses that were elicited from stimulus of each source C that the SVM was classified as B. Error bars represent SD.

Representation of interstimulus intervals

A neural response to a given stimulus is affected not only by the spatial identity of the stimulus, but also by the history of the stimulation sequence: the temporal pattern of stimulation preceding the current stimulus. How good are the four different representation schemes in distinguishing between temporal input features? We have narrowed this question and operationally phrased it as follows: Given two consecutive stimuli that excite the network from a single identified location, can one tell, based on neuronal responses to the second stimulus, the time interval between the first and the second stimuli? To answer this question, one spatial input source was chosen and the time intervals between subsequent stimuli were randomly varied (2, 5, 10 and 15 s). The classifier in these experiments was trained to distinguish between the different interstimulus intervals. Each interval occurred 200 times; a total of 800 stimuli were delivered in each experiment and 10 experiments in six different preparations were performed. The range of interstimulus intervals (ISI) used reflects the relevant regimes: The lower limit (∼1 s) was dictated by our need to guarantee a reasonable level of network responsiveness to any given stimulus in the series. The upper ISI limit (∼20 s), reflects our attempt to entrain the network and thus avoid interference of spontaneous activity.

Our analysis revealed that the responses to 10 and 15 s intervals were practically indistinguishable (data not shown), therefore the analysis below pertains only to interval sizes 2, 5 and 10 s. This analysis showed that overall performance in this task was quite low as compared classifier performance in spatial categorization tasks, and the variance between different experiments was substantial. Nevertheless, in all the experiments, in contrast to spatial categorization tasks, rate-based schemes performed slightly better (Fig. 5a). A table of all the results used for construction of Figure 5a is presented in supplemental item 2 (available at www.jneurosci.org as supplemental material), together with general response statistics of the networks. The advantage of rate-based schemes in temporal categorization remains stable even when the data are extracted from relatively late responses to the stimulus (Fig. 5b,e). Figure 5c provides some intuition as to this effect: there seems to be an overall reduction in the network response for shorter interstimulus intervals. This effect lasts for tens of milliseconds following response onset, and is not present when responses from different spatial sources are compared. It complies with a well established result regarding the adaptation of the network response to stimulation frequency (Eytan et al., 2003). Note that the time duration within which firing rates are integrated, considerably affects the quality of categorization: The longer the duration, the better the performance, indicating that, in contrast to discrimination of the stimulus spatial identity, the late phases of the response clearly contains information about the stimulation interval. The classification accuracy also depends on the size of the difference between the intervals: the larger the difference, the better the discrimination becomes. This is shown in Figure 5d, where the discrimination performance for time intervals of 15 s and all the other intervals (2, 5 and 10 s) is compared.

Figure 5.

Representation of interstimulus intervals. Classification accuracy of each representation scheme in temporal experiments. Support vector machine (SVM) algorithm with a Gaussian radial-based function kernel was applied to vectors of training sets (see Materials and Methods). Horizontal dashed line represents chance level. a, Analysis results on all (n = 10) spatial categorization task experiments. Each color represents a different experiment. Results with response window of length 100 ms which starts 10 ms following the stimulation. The black line is the mean ± SD of the classification accuracy in all the experiments. b, An example from one specific temporal experiment, that shows the sensitivity of classification accuracy to the window start time after the stimulus. c, The response envelope. An example from one specific experiment. The average network spikes of all the responses of specific interval as a function of the time after the stimulus (5 ms time bin). Color represents interstimulus interval, error bars represent SEM. Shorter intervals result lower population responses. d, The sensitivity of classification accuracy to the size of the difference between the interstimulus intervals. The average of the classification accuracy between 15 s interstimulus interval and all the remaining intervals (2, 5 and 10) in all of the experiments. Error bars represent SD. The response window is of length 100 ms and starts 10 ms following the stimulation. e, Results with response window of length 100 ms which starts 25 ms following the stimulation. The black line is the mean ± SD of the classification accuracy in all the experiments. f, An example from one specific experiment, that shows the sensitivity of classification accuracy to response window size.

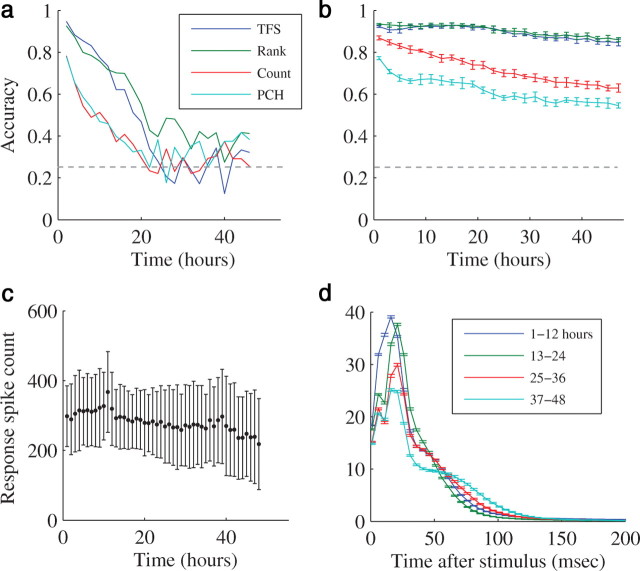
Long-term dynamics of representations

In the experiments described so far (lasting several hours), all responses were lumped and analyzed together, regardless of when they were recorded during the experiment. But neural responses, both in vivo and in vitro, tend to change over long-time scales (Sterna et al., 2001; Wagenaar et al., 2006). How are these dynamics manifested in the classification ability of each of the analyzed schemes? Are there response features which are stable enough to maintain representations over long-durations? To answer these questions, we repeated the spatial categorization experiments with four spatial input sources, over a 48 h period. To study the temporal stability of a given representation, the classifiers were trained on data taken from the first 2 h of the experiment, then tested on the entire dataset. As shown in Figure 6a, the performance of all schemes deteriorated over time (with a timescale of ∼10 h) up to the point where discrimination power vanished. In other words, the distribution of responses changed over time and as it did the separating hyperplane was no longer discriminative between the inputs. This does not indicate however, whether a hyperplane that separates the responses recorded over long-time periods, could be found. To check this, we compared the efficacy of the different representation schemes on experiment segments of different durations. One hundred fifty responses from each source were randomly chosen from the first 2 h, the first 4 h and so on. The efficacy of population-count-histogram, spike-count, time-to-first-spike, and rank-order transformations over each of those datasets (divided as usual to train and test sets) is compared. As shown in Figure 6b, while classification accuracy gradually degraded with longer durations, time-based representation schemes degraded only moderately, maintaining high classification accuracy even after 2 d. In contrast, the classification accuracy of rate-based schemes deteriorated significantly, implying that these response features are less stable and more susceptible to long-term dynamical changes. This result is in accord with the result of the previous sections, showing that rate-based features are more informative with regard to the history of the input, while time-based features are more time invariant and hence more reliable in representing the spatial location (or identity) of the input.

Figure 6.

Long-term dynamics of representations. The classification accuracy of each representation scheme over 48 h. An example from a single experiment. Horizontal dashed line represents chance level. a, The SVM classifier was trained to classify between responses taken from the first 2 h of the experiment. In the testing phase, responses from every following 2 h were classified according to the separation hyperplane elicited in the training phase. b, Mean ± SD classification accuracy of 10 train-test cycles of 150 responses from each sources chosen randomly from the first 2 h, then from the first 4 h and so on. c, Network response dynamics over a 48 h long-experiment. The number of spikes (mean ± SD) in the responses of the entire network every hour. d, The response envelope. The experiment was divided into four 12 h periods. The figure depicts the average network spikes of all the responses of a specific period as a function of the time after the stimulus (5 ms time bin). Color represents different period. Error bars represent SEM. It is evident that while not identical, the response envelope and the spike count in the entire network do not differ significantly. In particular, there is no significant “drift” in the mean spike count.

Discussion

In this study, using generic networks of cortical neurons as a model system, we follow the path of a stimulus–reconstruction approach to compare the representational efficacy of four types of popular schemes, two rate-base and two time-based: population-count-histogram (Schwartz, 1993; Hupé et al., 2001; Fiorillo et al., 2003), spike-count (Arabzadeh et al., 2006; Foffani et al., 2009; Jacobs et al., 2009), time-to-first-spike (Petersen et al., 2001; Foffani et al., 2004; Johasson and Birznieks, 2004; Gollisch and Meister, 2008; Gollisch and Meister, 2008), and rank-order (Thorpe et al., 2001; Van Rullen and Thorpe, 2001; VanRullen et al., 2005; Shahaf et al., 2008). Notwithstanding limitations associated with the stimulus–reconstruction approach in relation to brain function, it served us well in the present context as a mean for estimating the total information content, embedded in a given response feature, about an input. This is a statistical question; our choice to use a nonlinear classifier subserved the need to extract as much information as possible from the data. Simpler classifiers might be more suitable when one is interested in the decoding procedure itself (simplicity, plausibility, cost, etc.), but this is not the case here.

We found that the nature of response in neural populations dictates strong correlations between different response features, which are a priori independent [e.g., rank order of first events and population time histogram are completely orthogonal features of a set of general spike trains (Marom et al., 2009), resulting in high redundancy in response features. This can give an observer the freedom to choose between different “schemes,” without loosing much information. Having said that, we have shown that while rate-based schemes do perform well, their efficacy is significantly reduced compared with time-based measures in classifying the spatial location of a stimulus. We have also found that overlap between groups of receptive sheath neurons (neurons that directly respond to the stimulus and serve as a source for the assembly excitation) is translated to similarity in response pattern, and can be thought of as a form of generalization. Time-based representation schemes are also more stable over long-periods of time, under changes induced by the long-term dynamics of the neural assembly. On the other hand, when classification between temporal features of a given stimulus source is sought, there is an advantage to rate-based representation schemes, which are more sensitive to adaptation processes, and hence contain information with regard to the history of stimulation.

This study offers a unique approach to the issue of neural representation in the model system chosen. Networks of cortical neurons developing in vitro (Marom and Shahaf, 2002; Morin et al., 2005) can provide insights to the well studied field of neural representation, insights that cannot be derived using numerical simulations or data from in vivo experiments. In its essence, this approach is closest to simulation models, where generic questions are asked, but with the advantage of using real neurons and connections instead of reduced computational models. This is an advantage when addressing questions regarding constraints imposed by cellular and synaptic physiology on the plausibility of different neural representation schemes, and the tradeoffs involved when one chooses which features to extract from neural responses. For example, “real” responses to stimulation are highly variable (Arieli et al., 1996), partly due to noise and intervening input, but also due to the intrinsic complex dynamics of multiple processes at all levels (Marom, 2010). This variability is difficult to reproduce in simulation, yet it is critical to the understanding of neural representation. We show here that while time-based schemes are more invariant under these long-term changes, and better represent stimulus identity (spatial localization), rate-based schemes can use regularities in this variability to represent history-dependent features.

While the constraints imposed by the “real” biological components are evidently present in vivo, there are several drawbacks to this level: the ability to stably record from multiple neurons and to stimulate at arbitrary patterns is reduced, and anatomical and region-specific effects are considerable making it difficult to derive general insights. Furthermore, the on-going neural activity, inputs from other brain regions and the changing chemical milieu, confound and interfere with the ability to study the effects of the input parameters on representation, as was done here.

It is important to emphasize that the in vitro system suffers from several drawbacks and limitations, and the conclusions drawn here must be kept in the correct context. The most severe of these are the bias that arises from the free and unconstrained development, which may lead to topological and activity features that do not necessarily represent those that exist in the brain (Quartz and Sejnowski, 1997). The in vitro system is offered here as a complementary model to the more conventional approaches, which may contribute unique insights, and be used to study aspects and questions that are mostly inaccessible using standard methods.

While it would be interesting to see how the results presented here regarding the redundancy of representation schemes and the differential effect of adaptation processes can be extrapolated to in vivo models and incorporated into simulation studies, this research opens the door for studying intriguing questions using the in vitro system that were mostly unachievable until now. One of the main advantages of the in vitro system is the ability to perform long, practically open ended experiments (Potter and DeMarse, 2001). We expect that systematic study of the dynamics of different response features, the dependency between features, and the timescales of change can give valuable insights that are mostly unavailable by standard methods.

Long-experiments can also be used to study developmental effects on neural representation. Specifically it would be interesting to study the effect of stimulation patterns during development on the ability to distinguish between them at later times, and the time course of the efficacy in discrimination. It would also be possible to study the effect of stimulation history more systematically and further into the past. Finally, perhaps the most intriguing aspects of the representation question is its plasticity (Recanzone et al., 1993; King et al., 2000), and the way it is modulated by neural signals external to the assembly. In vitro studies may include modulation and plasticity (Chiappalone et al., 2008) of representation by various methods, such as closed loop electrical stimulation and selective application of neuromodulators.