Pinna Cues Determine Orienting Response Modes to Synchronous Sounds in Elevation

Abstract

To program a goal-directed orienting response toward a sound source embedded in an acoustic scene, the audiomotor system should detect and select the target against a background. Here, we focus on whether the system can segregate synchronous sounds in the midsagittal plane (elevation), a task requiring the auditory system to dissociate the pinna-induced spectral localization cues. Human listeners made rapid head-orienting responses toward either a single sound source (broadband buzzer or Gaussian noise) or toward two simultaneously presented sounds (buzzer and noise) at a wide variety of locations in the midsagittal plane. In the latter case, listeners had to orient to the buzzer (target) and ignore the noise (nontarget). In the single-sound condition, localization was accurate. However, in the double-sound condition, response endpoints depended on relative sound level and spatial disparity. The loudest sound dominated the responses, regardless of whether it was the target or the nontarget. When the sounds had about equal intensities and their spatial disparity was sufficiently small, endpoint distributions were well described by weighted averaging. However, when spatial disparities exceeded ∼45°, response endpoint distributions became bimodal. Similar response behavior has been reported for visuomotor experiments, for which averaging and bimodal endpoint distributions are thought to arise from neural interactions within retinotopically organized visuomotor maps. We show, however, that the auditory-evoked responses can be well explained by the idiosyncratic acoustics of the pinnae. Hence basic principles of target representation and selection for audition and vision appear to differ profoundly.

Introduction

Natural acoustic environments typically contain a mixture of multiple sound sources, from which the auditory system needs to select behaviorally relevant information to program a response. Target selection has been addressed extensively in the visuomotor literature (Becker and Jürgens, 1979; Findlay, 1982; Ottes et al., 1984, 1985; Chou et al., 1999; Aitsebaomo and Bedell, 2000; Watanabe, 2001; Arai et al., 2004; Nelson and Hughes, 2007). When two visual targets are presented in spatial–temporal proximity, saccadic eye movements often terminate between the two target locations (averaging). Varying target features (salience, onset asynchrony, spatial disparity, size), task constraints (instruction), or saccade reaction times systematically affects response endpoint distributions (Findlay, 1982; Ottes et al., 1984, 1985). This behavior is thought to arise from neural interactions within spatially organized maps, like in midbrain superior colliculus (Ottes et al., 1984; Lee et al., 1988; van Opstal and Van Gisbergen, 1990; Glimcher and Sparks, 1993; Kim and Basso, 2008).

In contrast to the retinotopic organization of the visual system, the auditory system is tonotopic. Hence sound locations are derived from implicit acoustic cues. Interaural time and level differences determine sound source azimuth (Middlebrooks and Green, 1991; Blauert, 1997); pinna-related spectral-shape cues encode elevation (Shaw, 1966; Blauert, 1969; Wightman and Kistler, 1989; Middlebrooks, 1992; Hofman and van Opstal, 1998, 2002; Kulkarni and Colburn, 1998; Langendijk and Bronkhorst, 2002). Two simultaneous sounds at different azimuth locations induce the percept of one phantom source at the so-called summing location (Blauert, 1997). For example, identical sounds symmetrically presented left and right of the listener are perceived as a single sound source at straight ahead. Its location systematically varies with relative intensities and timings of the speakers, which can be understood from sound wave interference at the ear canals.

Here, we test whether similar principles apply to elevation, as the effect of spatial summation for complex spectral-shape cues is far from obvious. The only study addressing this issue focused on discriminating sounds in virtual acoustic space and noted that listeners could not segregate sounds in the midsagittal plane (Best et al., 2004). As previous research did not address sound localization performance, we took a different approach, by characterizing free-field sound localization with head saccades evoked by two simultaneous, but different, sounds in the midsagittal plane: a broadband buzzer (BZZ) (target) and a Gaussian white noise burst (GWN) (nontarget). Both sounds were perceptually easily distinguishable and localizable when presented alone. We presented the two sounds synchronously and systematically varied their locations, relative level, and spatial disparities over a large range.

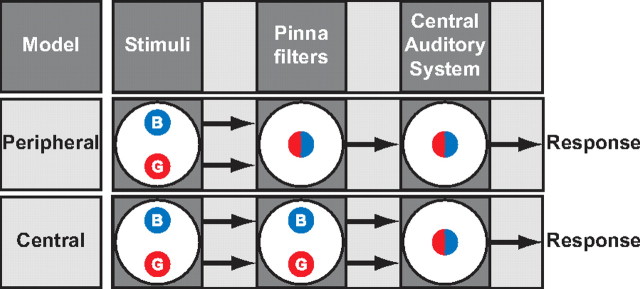
Figure 1 considers two hypotheses to explain localization percepts in case of averaging. In the peripheral model, the two sounds (blue and red circle) interfere with each other at the pinnae, creating a new amplitude spectrum that depends on the relative sound levels (mixed symbol). In contrast, the central model states that the sound spectra are both preserved at the periphery and along the ascending auditory pathway (blue and red circles). Interactions between the two sound percepts then take place in the central auditory system (mixed symbol). Note that the two models predict identical averaging behavior. Yet the two schemes are mutually exclusive. If the subject's behavior can be fully explained by peripheral acoustics, central interactions cannot account for the results, as information of the individual sound sources is not transmitted to higher centers. If, however, peripheral acoustics are not sufficient to explain averaging behavior, one must assume a neural integration stage.

Figure 1.

Two competing accounts for perceiving a phantom sound source at a weighted-average location in the midsagittal plane. Top, In the peripheral-interaction model, the double-sound spectra of BZZ (B) and GWN (G) yield an amplitude spectrum corresponding to the weighted-averaged location (symbolized by mixed circle). The interactions of the two sound sources take place at the level of the pinna, and their identities are lost in the CNS. Bottom, In the neural-interaction scheme, the periphery preserves spectral shape of either source (blue and red circle at the pinna stage). A weighted-averaged percept emerges through neural interactions in an audiospatial representation (mixed circle at the central auditory system stage). Both models predict the same behavior, yet they are mutually exclusive.

Our data indicate that, except when BZZ intensity well exceeded GWN, listeners were unable to ignore the nontarget, regardless of response reaction times and spatial disparity. Interestingly, simulations with a pinna-based similarity model indicate that observed response patterns may be fully understood from idiosyncratic pinna acoustics. These results suggest a marked difference between target selection mechanisms for vision and audition.

Materials and Methods

Listeners

Four listeners (ages, 29–32; three males, one female) with normal hearing as indicated by their audiometric curves (hearing threshold ≤20 dB between 250 and 11,300 Hz; 11 0.5 octave steps) participated in the experiments. Two of the authors (P.B., M.W.) served as listeners, and the other two listeners were naive about the purpose of the study. Before the actual experiments, the two authors performed in several pilot experiments to find the best range of parameters in the present study. The naive subjects did not participate in any of these pilot experiments and did not receive any feedback during or after their performance in the experimental series.

Experiments were conducted after subjects gave their full understanding and written consent. The experimental procedures were approved by the Local Ethics Committee of Radboud University Nijmegen and adhered to the Code of Ethics of the World Medical Association (Declaration of Helsinki), as printed in British Medical Journal (July 18, 1964).

Apparatus and sound generation

All experiments were performed in a dark 3 × 3 × 3 m room lined with acoustic foam (UXEM Flexible Foams) that attenuated sound reflections >500 Hz. Background noise level was 30 dBA. Sounds were presented from a total of 29 speakers (SC 5.9; Visaton; art. no. 8006) mounted on a vertical motorized circular hoop, 2.5 m in diameter. Loudspeakers were mounted in 5° increments from −55 to 85° on the front (double-polar coordinates) (see below). The listener was seated in the center of this hoop (head-centered) on a straight-back chair. In the present study, the hoop was always aligned with the midsagittal plane.

For easier visualization, target locations and head movement responses were transformed to double-polar coordinates (Knudsen and Konishi, 1979). The vertical location is given by the elevation coordinate ε [i.e., the angle formed by the center of the hoop (listener's head), sound source/response location, and the horizontal plane]. Positive (negative) elevation values indicate locations above (below) the listener's interaural axis. The horizontal location is given by the azimuth coordinate α, which is the angle formed by the center of the hoop, the sound source, and the median plane. In the current study, the speaker azimuth was always at α = 0°.

Speaker selection was done with a custom-made program written in C++ running on a PC (2.8 GHz Intel Pentium D; Dell). The same program was used to record head saccades (see below, Behavioral testing and paradigms), directional transfer functions (see below, Directional transfer functions), and sound playback. For the presentation of stimuli, a stored wav file made off-line with MatLab (Mathworks) was sent to a real-time processor (RP2.1 System3; Tucker-Davis Technologies) at a sampling rate of 48.828 kHz. After attenuation by custom-built amplifiers, the audio signal was sent to the selected speaker. In a given trial, either one or two speakers could be selected to play the stimuli. Transfer characteristics of the speakers differed by <0.3 dB (root mean square) from 1 to 15 kHz. Accordingly, no attempt was made to correct for these small speaker differences.

To ensure microsecond timing precision, relevant trial information was sent from the PC to a custom-made microcontroller that initiated and controlled events in the trial.

Stimuli

All sounds had 50 ms duration, including 5 ms smooth sine/cosine-squared onset/offset ramps. We used two different sounds in the localization experiments: a GWN (0.5–20 kHz bandwidth) and a periodic quasinoise burst (BZZ) that had the same amplitude spectrum as the GWN, but differed in its temporal structure (Zwiers et al., 2001). The quasinoise had a fixed periodicity of 20 ms (making it sound like a 50 Hz buzzer). Sound levels were varied between 35 and 55 dBA in 5 dB steps for the GWN and from 32 to 52 dBA in 5 dB steps for the BZZ (measured with Brüel & Kjær BK2610 sound amplifier and Brüel & Kjær BK4144 microphone; at the location of the listener's head). In double-sound trials (see below, Behavioral testing and paradigms), we always held either the BZZ or the GWN constant at 42 or 45 dBA, respectively, while varying the level of the other sound. This resulted in a total of nine different combinations, for which the level difference, ΔL, could assume the values −13, −8, −3, +2, and +7 dB. Positive/negative differences indicate that the BZZ/GWN is louder. In additional trials, we created summed sounds that were constructed by linearly adding the GWN and the BZZ temporal waveforms at all different level combinations. These combined sounds were always played from one randomly selected speaker and served as a control (see Fig. 2C,D). The different combinations of these stimuli were ordered as indicated by the following example: B₃₂G₄₅, contains a BZZ at 32 dBA and GWN at 45 dBA (i.e., ΔL = −13 dB). Its numerical order on the scale between BZZ-only (number 1) to GWN-only (number 11) is 10. B₅₂G₄₅ is number 2, etc.

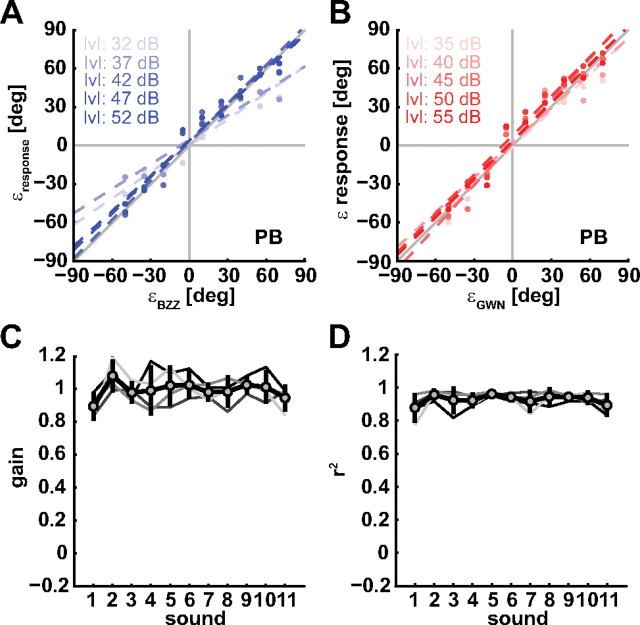
Figure 2.

Standard localization behavior of listener P.B. to single-speaker sounds at five levels (BZZ: 32, 37, 42, 47, 52 dBA; GWN: 35, 40, 45, 50, 55 dBA). A, B, Stimulus–response plots for BZZ (A) and GWN (B). The different color shades indicate different levels. Gains and correlation coefficients are close to 1, and biases close to 0°, indicating good localization performance. The dashed lines indicate linear regression lines. C, Gains for all single speaker sounds. Subscript numbers indicate the level of BZZ (1) and GWN (11) and the summed sounds (for details, see Materials and Methods). The lines in different shades of grays are from different listeners. The thick black line with gray circles is the average over all four listeners. Error bars denote 1 SD. D, Correlation coefficients obtained for single-sound stimulus–response plots. Both gains and correlations are close to 1, indicating high localization accuracy and precision, respectively.

Behavioral testing and paradigms

The behavioral testing procedure required the listeners to orient a head-fixed laser pointer toward the perceived location of the BZZ “as quickly and as accurately as possible.” If no BZZ was perceived, the listener simply had to localize the presented sound. The laser pointer (LQB-1-650; World Star Tech) was attached to a modified lightweight sunglasses frame (glasses were removed) and projected its red beam onto a small, frame-attached disk (diameter, 1 cm) at ∼30 cm in front of the listener's nose. This assured that no visual cues (e.g., reflections on the wall and hoop) influenced the localization behavior of the listeners. Head movements were measured with the magnetic search coil technique (Robinson, 1963). To that end, a small custom-made coil was wound around the laser pointer and connected to an eye monitor (EM7; Remmel Labs) that was also used to drive three pairs (horizontal, vertical, frontal) of field coils mounted alongside the edges of the experimental chamber. The demodulated data were A/D-converted at 1000 Hz (RA16 System3; TDT) and stored on disk for further off-line analysis.

To calibrate the head coil, a calibration session was performed before each experiment. The listener was asked to orient the laser pointer toward light-emitting diodes (LEDs) mounted in front of the loudspeakers on the hoop. A total of 56 points distributed in the frontal hemisphere was sufficient to calibrate the horizontal and vertical components of head movements to within 0.6°.

In the experimental session, a trial started with a green fixation LED at α = 0° and ε = 0°. The listener aligned his head with this fixation LED, after which he initiated the trial sequence by a button press. In a trial, one of the following three stimulus types could be presented.

Single-sound trials.

The sound—either the GWN or the BZZ—was emitted from one single speaker with varying level (see above, Stimuli) at one of nine locations (ε = [−50, −35, −20, …, 70] degrees) on the frontal midsagittal plane. This amounted to a total of 45 single-target trials per stimulus type (in total, 90 trials). The responses toward these stimuli were used to assess the listener's standard localization behavior.

Double-sound test trials.

Two speakers emitted the test sounds simultaneously. Speaker locations were identical with the single-sound locations. The separation between the two speakers could thus vary between 15 and 120° elevation in steps of 15°. For example, holding speaker 1 at −50°, the following eight locations were used for speaker 2: −35, −20, −5, 10, 25, 40, 55, and 70°. Additionally, we varied the level difference as described above (see Stimuli). All possible spatial (N = 9 × 8) and level configurations (N = 5) were tested for each stimulus type (N = 2), leading to a total of 720 trials per listener.

Double-sound control trials.

A single speaker emitted the linear sum of BZZ and GWN at the same level differences as in the double-speaker trials. Ninety trials were performed with these stimuli (9 locations × 5 levels × 2 types).

In total, a measurement session contained 900 localization trials and lasted for ∼1 h.

Note that the three largest spatial disparities in double-sound trials had only a limited amount of possible spatial combination per level difference (90° = 6 trials; 105° = 4 trials; 120° = 2 trials). Therefore, listeners M.W. and P.B. performed an additional experiment in which the level difference in double-sound trials was fixed at −3 dB and spatial disparity for the double-sound trials was limited to 90, 105, and 120° (total of 528 trials per listener).

Data analysis

Head orientation was calibrated using the data obtained in the calibration experiment. Combinations of raw data (AD values horizontal, vertical, and frontal components) and known LED locations (azimuth and elevation in degrees) were used to train two three-layer neuronal networks for azimuth and elevation, respectively. The networks were trained by the Bayesian regularization implementation of the backpropagation algorithm (MatLab; Neural Networks Toolbox) to avoid overfitting (MacKay, 1992). In addition to a linear mapping from AD values to degrees, the networks also accounted for small inhomogeneities in the fields and cross talk between the three channels. The thus trained networks were then used to calibrate the experimental data.

A custom-written MatLab script was used to automatically detect saccades in the calibrated data by using a preset velocity criterion (15°/s) to saccade onset and offset. Detected saccades were visually inspected for errors and corrected if necessary. Saccades with a reaction time <150 ms were discarded as anticipatory responses.

Response normalization

For the data analysis shown in Figures 7 and 8, the head saccade endpoints in double-sound trials were normalized by the following:

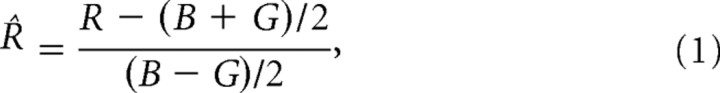with B and G, the elevation of BZZ and GWN stimuli, respectively, and R, the head movement response elevation. For a response directed to the GWN nontarget (R = G), R̂ = −1, whereas for a response to the target BZZ (R = B), R̂ = +1.

Figure 7.

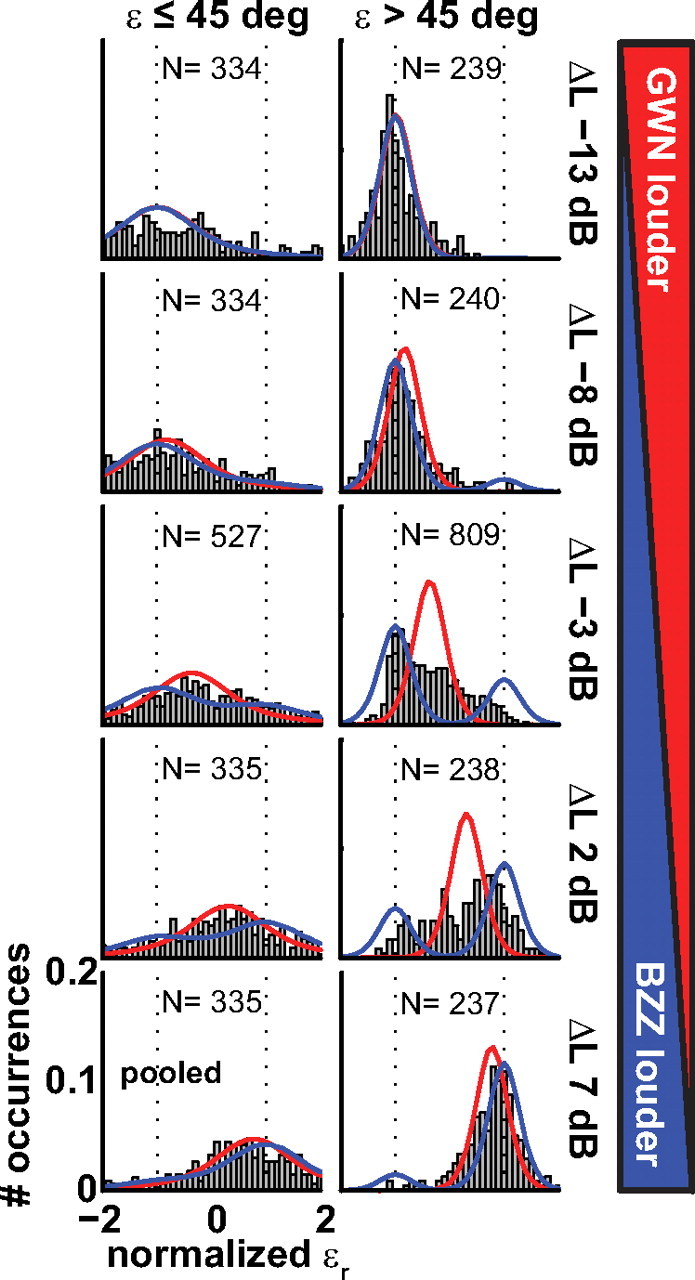
Normalized saccade-endpoint distributions for the five ΔL values (rows), pooled over all listeners. Data are separated in Δε ≤ 45° (left column) and Δε > 45° (right column). The black dotted lines indicate normalized target locations, with 1.0 denoting the BZZ and −1.0 denoting GWN. The red line indicates a simulated weighted-averaged target prediction (μ = ε_AVG, σ = 12°, N = 10⁴). The blue line shows a simulated bimodal prediction (μ₁ = w_BZZ·ε_BZZ, μ₂ = w_GWN·ε_GWN, σ = 12°, N = 10⁴).

Figure 8.

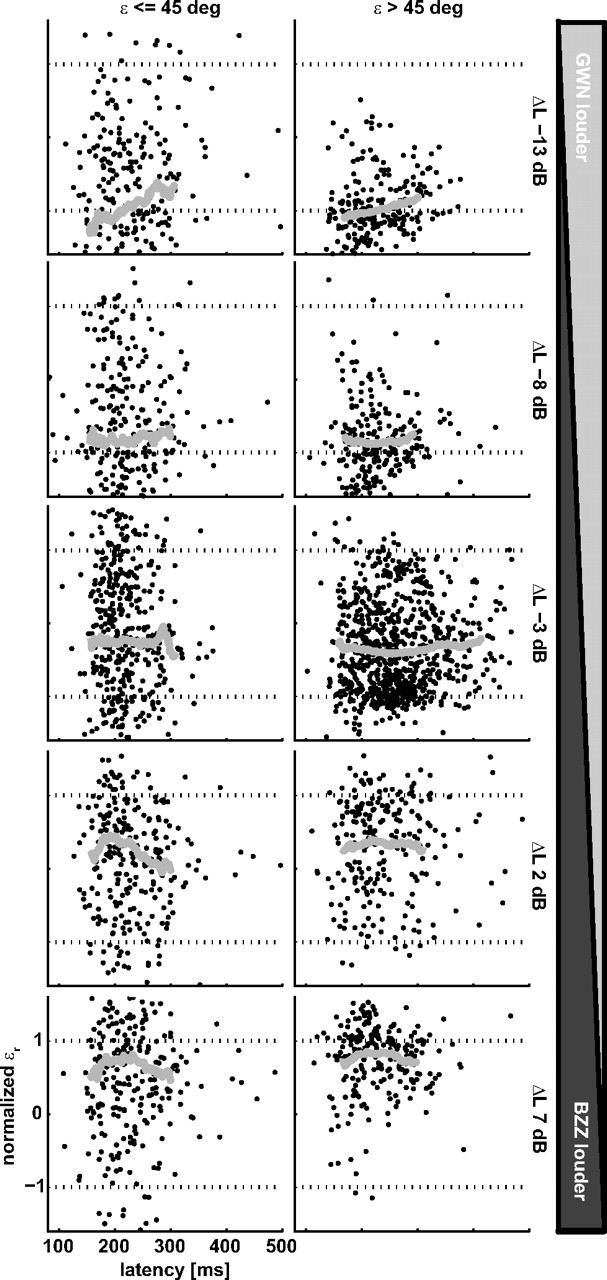
Normalized head-saccade endpoints as a function of saccade latency for the five ΔL values (rows), pooled over all listeners. Data are separated in conditions in which Δε ≤ 45° (left column) and Δε > 45° (right column). BZZ and GWN locations are indicated by the dotted black lines at 1 and −1, respectively. The thick gray line indicates the running average.

Regression analysis and statistics

In all regression analyses, parameters were found by minimizing the mean squared error (Press et al., 1992).

We performed a linear regression analysis on the stimulus–response relationship to quantify localization behavior in elevation as follows:

with R and T response elevation and target elevation, respectively. The slope, a, is the response gain, and offset, b (in degrees), the response bias. To determine the goodness of fit, we calculated the correlation coefficient between fit and data.

To test whether responses could be described by a weighted average of the locations of BZZ, T_BZZ, and GWN, T_GWN, we first determined the optimal weights, separately for each ΔL, as described by weighted-average formula as follows:

where w_B and 1 − w_B are the dimensionless weights of BZZ and GWN, respectively. R_AVG is the weighted-average prediction for the response. Weights were found by minimizing the mean-squared error with the MatLab routine fmins (Nelder–Mead simplex). Then, we evaluated to what extent the measured responses in the entire data set (pooled over all ΔL per listener) could be best described by either the BZZ location (i.e., the target), the GWN location (i.e., the nontarget), the weighted-average prediction, R_AVG, of Equation 3, or the level difference by using a normalized (z-transformed) multiple linear regression analysis according to the following:

with X̃ ≡ (X − μ_x)/σ_x, the dimensionless z-score of variable X (μ_X mean; σ_X SD); R, the response elevation; R_AVG, the weighted-average response prediction of Equation 3; ΔL, the level difference; and p, q, w, and m, the dimensionless regression parameters (partial correlation coefficients).

To obtain confidence limits of the coefficients, we used a bootstrap method. To that end, 1000 data sets, randomly drawn from the responses (with replacement), were generated and subjected to the regression analysis of Equation 4. The SD of the resulting set of 1000 coefficients was used to estimate the confidence levels of the partial correlation coefficients.

Directional transfer functions

For all listeners, we measured their directional transfer functions (DTFs) simultaneously from both ears. To that end, we sampled 360 locations in the frontal hemisphere. A small probe microphone (Knowles EA1842) connected to a small rubber tube (1.5 mm outer diameter; length, 5.5 cm) was positioned at the entrance of the external auditory meatus of each ear and fixed with tape without obstructing or deforming the pinnae. The listener's interaural axis was aligned with α = 0° and ε = 0°, and the head was supported in this position by a neck rest. As a probe stimulus, a periodic flat spectrum Schroeder-phase signal (Schroeder, 1970) was used, which consisted of 20 periods with duration of 20.5 ms each (total duration, 410 ms). The probe was presented at a sound pressure level of 50 dBA. The first and last periods were sin²/cos²-ramped (5 ms) and were discarded in the analysis. The same measurements were also performed without the listener in place. In that case, the two microphones were positioned at the location of the listener's interaural axis. These latter measurements were used to correct for speaker and microphone characteristics as well as location-specific reflections from the measured transfer functions.

The recorded microphone signal was preamplified (custom-built amplifiers), amplified (Luxman Stereo Integrated Amplifier A-331), bandpass filtered (Krohn-Hite 3343; passband, 0.2–20 kHz), and sampled at 48.828 kHz (RP2.1 System 3; TDT). The subsequent off-line analysis was performed in MatLab. First, the average signal over Schroeder periods 2–19 was calculated (1024 samples) for listener and microphone measurements. Subsequently, the magnitude spectra were computed by means of the fast Fourier transform (512 bins). The obtained spectra were smoothed using a simple Gaussian filter with a constant Q factor of 8 (Algazi et al., 2001) and converted to sound level. Then the microphone measurements were subtracted for all locations. Finally, the DTFs were obtained by subtracting the mean spectrum of the whole data set from each measurement. In that way, only the direction dependent information from the pinnae remained (Middlebrooks, 1992).

Similarity model of sound localization

Since acoustic pressure waves add linearly at the ear, we reconstructed the sensory spectrum for a given BZZ/GWN combination by first adding the corresponding measured sensory spectra of the same single targets. To that end, the two selected DTFs (on linear magnitude scale) were filtered (i.e., multiplied) with the magnitude spectrum of BZZ and GWN and corrected for the actual levels used in the experiment. These operations were performed in the frequency domain before log-(dB) transformation. After summation, we performed a log-transformation on the combined amplitude spectrum to approximate the neural input spectrum for the double sound (here termed “double DTF”). For simplicity, in this analysis we only used the right-ear DTFs measured at azimuth 0°.

We then calculated the SD over a frequency range from 3 to 12 kHz of the difference between the double DTF (considered as the sensory input), and all measured single DTFs (presumed to be stored in the brain as neural templates). This SD is taken as a measure of similarity (Langendijk and Bronkhorst, 2002), rather than the correlation coefficient between sensory spectrum and DTFs (Middlebrooks, 1992; Hofman and van Opstal, 1998). The resulting similarity index (SI) was scaled so that it ranged from 0 (no similarity) to 1 (identical). The idea behind this procedure is that a conceptually similar analysis is thought to be performed by the ascending auditory pathway to estimate the most likely elevation angle, given the sensory spectrum (Middlebrooks, 1992; Hofman and van Opstal, 1998, 2003; Kulkarni and Colburn, 1998; Langendijk and Bronkhorst, 2002). According to this model, the DTF template (with its associated location) that yields the highest similarity index has also the highest probability for being the real location of the source.

Correction procedure

We assessed the quality of the SI as a predictor of behavior by determining the SI that corresponded to a given response. Note that the SI analysis is based entirely on the acoustics and does not account for a potential response bias in the head motor response (the gain, a, and offset, b, in Eq. 2). Since some listeners could display a significant response bias, we corrected responses (for both single- and double-sound trials) by using the mean gain and bias obtained from all single-sound trials (data shown in Fig. 2). In this way, the double-sound responses were normalized with respect to the single-target localization results. Since our SI maps had a finite resolution, we calculated the distance between response location and all sampled DTF locations and selected the closest location. Finally, we binned the dimensionless SI values (bin width, 0.1), after which the resulting histograms were normalized by the maximal number of occurrences (Figs. 9, 10).

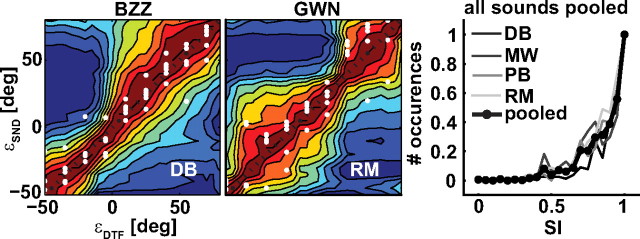
Figure 9.

SI of single-sound DTFs and Schroeder-DTF templates (colored patches) and normalized single-sound head-movement responses (white dots) for BZZ (listener D.B.; left) and GWN (listener R.M.; center) as a function of target location. Responses and areas of highest similarity (warm colors) between template and target DTF coincide with response location. Right, Normalized histograms of the SIs obtained at the response locations pooled across all 11 single sounds for all four listeners (different shades of gray). The thick line with markers indicates average across listeners.

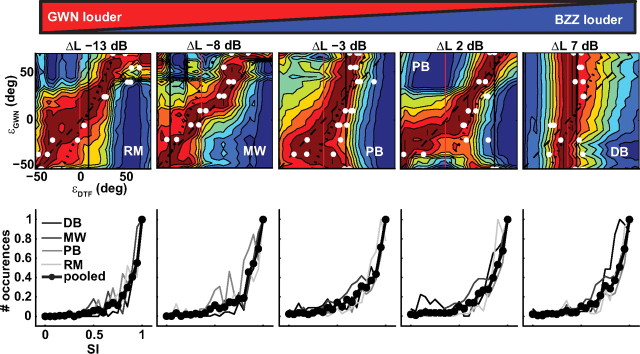
Figure 10.

SI of double-sound DTFs and Schroeder-DTF templates (colored patches) as a function of GWN location, and the template location for all five ΔL values and four different listeners (top row). The listener's responses are indicated as white dots. In each plot, the buzzer location was held constant at the location indicated by the solid black line. The dashed-black line indicates the GWN location (unity), and the dotted-black line indicates a prediction based on the weighted average of buzzer and GWN location. The warm colors indicate small differences between template and simulated double-DTF, and cold colors indicate large differences. Bottom row, Normalized histograms of SI obtained at response locations for all ΔL values pooled across Δε conditions for all listeners (different shades of gray). The thick line with markers denotes average across listeners.

Results

Single-sound localization

We first assessed localizability of BZZ and GWN by analyzing the stimulus–response relationships for all single-sound trials. In these trials, either the BZZ or the GWN were presented alone, or superimposed, at all nine combinations used in the double-sound trials (see Materials and Methods). Figure 2 shows representative stimulus–response plots for listener P.B. In this figure, response elevation for the BZZ (Fig. 2A) and for the GWN (Fig. 2B) are plotted against target elevation for all levels tested (different shades). The gains for the BZZ at low sound levels (32 and 37 dBA) were somewhat lower (0.69 and 0.64) than at higher sound levels. These levels were close to the background noise of ∼30 dBA that was always present in the experimental chamber, so that the signal-to-noise ratio (SNR) was low too. This effect of low SNR on elevation localization gain has been reported previously (Zwiers et al., 2001; van Wanrooij et al., 2009). Note that, at the other levels, elevation gain was close to 1, and the biases were close to 0° for both BZZ and GWN, indicating excellent localization performance. Figure 2, C and D, shows gains and correlation coefficients for BZZ, GWN, and the summed control sounds for the four listeners (different shades of gray) and the average across listeners (thick black line with gray circles). Both gain and r² are close to 1 and do not depend systematically on stimulus level. These data demonstrate that listeners localized the BZZ and GWN, as well as the summed control sounds, with high precision.

Double-sound localization

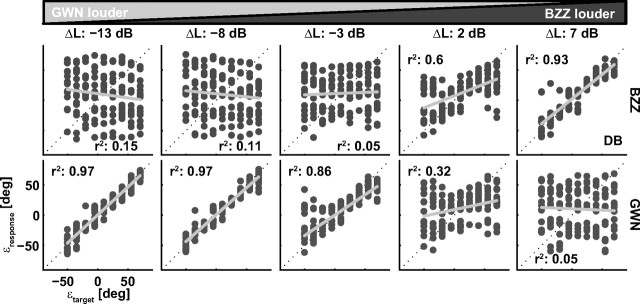
The listener's task in the double-sound trials was to localize the BZZ and to ignore the GWN. To test how well listeners performed in this task, we plotted the listener's localization response of all double-sound trials as a function of the actual BZZ location. The results of this analysis for listener D.B. are shown in Figure 3, top row. Each column shows the data for a given ΔL (left: −13 dB, GWN is much louder than BZZ; right: +7 dB, BZZ is louder than the GWN). It is apparent that, for negative ΔL, the responses do not correlate with the actual BZZ location. However, when BZZ levels start to exceed the GWN (ΔL + 2 dB), responses start to be directed toward the BZZ location. Only at a ΔL of +7 dB 93% of the variance in the response data can be explained by the BZZ location. In other words, the listener could not perform the task when the BZZ sound level was comparable with, or lower than, the GWN level.

Figure 3.

Localization behavior of listener DB in double-speaker trials. Each column shows stimulus–response data for one level difference between BZZ and GWN. Top row, Responses plotted against BZZ location. Bottom row, Responses plotted versus GWN location.

One may therefore wonder whether in these cases the listener, instead of localizing the BZZ, actually localized the GWN. The bottom row of Figure 3 replots the responses as a function of GWN location, which shows that the response pattern is now reversed. When the GWN stimulus was much louder than the BZZ (ΔL = −13 and −8 dB), the nontarget GWN location explained 97% of the responses variance. Only for the case of a much louder BZZ target (ΔL = +7 dB), responses cannot be accounted for by the GWN location.

Interestingly, although at the extreme-level differences, responses were directed to either the GWN (large negative ΔL) or the BZZ (large positive ΔL), at near equal levels of ΔL = −3 dB and +2 dB, the correlation coefficient decreased appreciably. We therefore wondered whether, as in the visuomotor system, a weighted average of the stimulus locations (Eq. 3) could perhaps better explain the entire set of responses.

To obtain the weights for the two targets at each ΔL, we first performed a multiple linear regression analysis for each listener (Eq. 3). The variables in the regression were the respective locations of BZZ and GWN. Note that, because of the large range of stimulus disparities used in the experiments, a potential spurious correlation between BZZ and GWN locations was eliminated. We then used the optimal weights (w_B and 1 − w_B) from this regression analysis to calculate the weighted-averaged target locations for linear regression (Eq. 2) with the listener's responses.

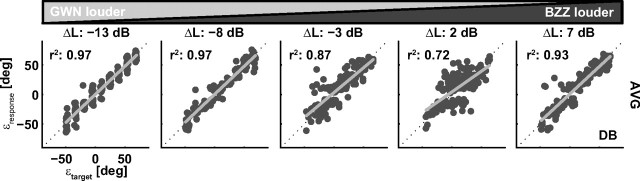
Figure 4 shows the results of the weighted-average predictions for listener D.B. Note that the data correlate much better with the averaged locations over the entire range of ΔL values than with the actual target positions (compare Fig. 3). At extreme ΔL values, the correlation coefficients of the weighted-average prediction are identical with the corresponding BZZ/GWN single target result. Importantly, however, the weighted-average estimate also accounts significantly better for the data variance at the smaller level differences (ΔL, −3 and 2 dB) than either the BZZ or the GWN locations.

Figure 4.

Localization behavior of listener DB in double-speaker trials as a function of a weighted-average target prediction (Eq. 3) of BZZ and GWN location for five level differences.

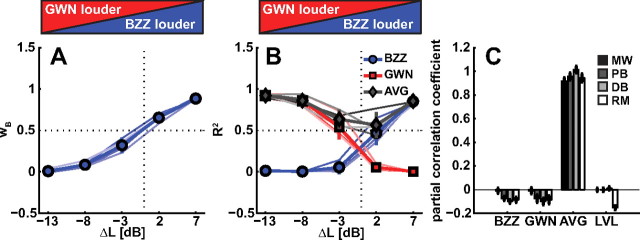
The resulting weight of the BZZ, w_B (Eq. 3), for all listeners are shown in Figure 5A as function of ΔL (individual, thin blue lines; average, thick line). It is obvious that the contribution of the BZZ to the responses strongly depends on ΔL. For example at ΔL = +7 dB, the BZZ dominates with a weight close to 1. The opposite can be seen at ΔL = −13 dB, for which the BZZ has a weight close to 0. The reverse behavior holds for the GWN since w_G = 1 − w_B. The crossing point [i.e., the point at which both targets contribute equally (0.5)] is at a ΔL close to 0.

Figure 5.

A, Partial correlation coefficients for BZZ location on localization response obtained with regression analysis of Equation 3. The weight of the GWN is 1 − w_b. The thin lines indicate data from individual listeners; the thick lines with markers show pooled data. The influence of a target depends in a sigmoid manner on the level difference. Note that the point of equal contribution (weight = 0.5) is at ΔL = 0 dBA. B, Correlation coefficients obtained from the linear regression shown in Figure 2. The color convention is as in A. The coefficients for the weighted-average prediction are depicted in gray colors. For BZZ and GWN stimuli, the correlation decreases with decreasing level of the corresponding single target. The correlation coefficient of the weighted-average prediction is equal to the single target values at extreme level differences. At ΔL of −3 and +2 dBA, however, the weighted-average prediction correlates better with the responses than either BZZ or GWN. C, Partial correlation coefficients of Equation 4 for all four listeners (M.W., P.B., D.B., R.M.). Most of the data can be explained by the weighted-averaged prediction, with coefficients >0.8 for all four listeners.

The superiority of the weighted-average prediction can also be seen in Figure 5B, which shows the r² values (variance explained) of the linear regression (Eq. 2) as a function of ΔL (individual data, thin lines; mean across listeners, thick lines with markers). It can be seen that the correlation coefficients for the single stimuli decrease toward 0 with decreasing level of that respective stimulus. In contrast, the goodness-of-fit for the weighted-averaged locations is high throughout the entire ΔL range, but drops slightly for the smallest ΔL values of −3 and 2 dB (to ∼0.6) (see below) (two-sample t test, p = 0.0084).

To assess that the weighted averaging model captures the essence of the data best, we performed an extended multiple linear regression analysis (Eq. 4), in which the variables were the actual BZZ and GWN locations, the weighted-average target prediction (from Eq. 3), and ΔL. Results for each listener are shown as bars in Figure 5C. This analysis makes clear that the responses can indeed best be explained by the weighted-average prediction, since the partial correlation coefficients for this variable exceeded 0.8 for all four listeners.

Yet the regression results for the weighted-average prediction shown in Figure 5A–C deviated significantly from the optimal value of 1. Note, however, that these results were based on pooled target conditions, in which we included all spatial disparities, Δε. Possibly, target averaging breaks down at large spatial disparities, in which case also the averaging model would provide a poor predictor for the data.

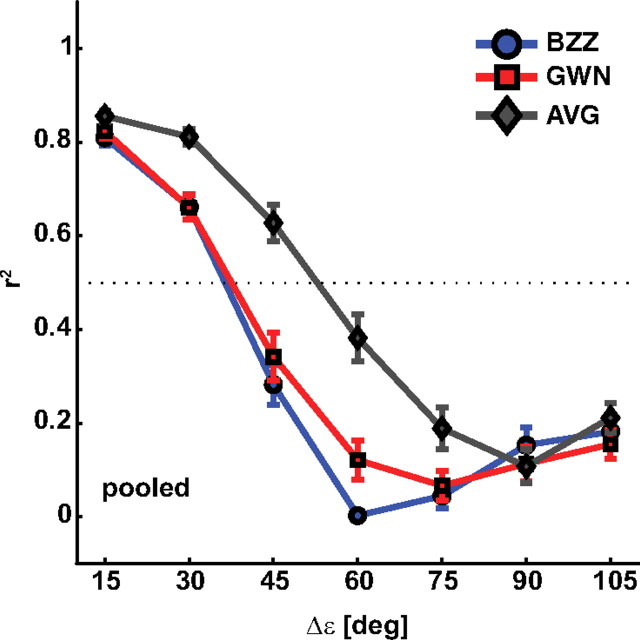
To test for this possibility, we reevaluated the correlation coefficients for BZZ, GWN, and weighted-average prediction (Eq. 2), but now for each of the tested Δε separately. In this analysis, we combined the three largest Δε values (90, 105, and 120°) for the linear regression analysis, as we had only two target configurations for Δε = 120° (see Materials and Methods). Figure 6 shows the results pooled across listeners (same color conventions as in Fig. 5). Values decline rapidly for BZZ and GWN, and they drop below 0.4 at Δε > 45°. In contrast, the coefficients obtained with the weighted-averaged prediction are higher than the single-target coefficients for all Δε < 90°. Only for the largest Δε values (90, 105, and 120°), BZZ, GWN, and average prediction are indistinguishable from each other (all are close to 0.1–0.2). This indicates that, at larger Δε values, none of the three regression models is able to predict the responses.

Figure 6.

Linear regression gains (Eq. 2) for BZZ (blue), GWN (red), and weighted-averaged prediction (gray) as a function of Δε pooled across all four listeners. Data at Δε = 105° are averaged over Δε = (90, 105, and 120°). Error bars denote 1 SD.

To further study what happens at the large spatial disparities, we divided the data into two sets: Δε ≤ 45° and Δε > 45°. At this criterion, the weighted-averaged model could explain at least 60–65% of the data variance (Fig. 6). Figure 7 shows the probability distributions (pdfs) of normalized (Eq. 1) head-saccade endpoints pooled across listeners. The data are shown separately by level difference, ΔL (rows; GWN loudest top; BZZ loudest bottom) and spatial separation, Δε (columns; Δε ≤ 45°, left; Δε > 45°, right). A value of +1.0 indicates a response to BZZ, a value of −1.0 to GWN (see Materials and Methods). In addition to the measured endpoints, we performed numerical simulations based on the weighted-average prediction (red lines) and on a bimodal prediction (blue lines). In these simulations, we used SD = 12° of single-sound responses to generate Gaussian response distributions and simulated 10⁴ double-sound responses for each condition in the experiments. At large ΔL values (top and bottom rows), the weighted-average simulations and measured data are in good agreement regardless of Δε and show a unimodal distribution. However, a marked difference between measurements and weighted-average simulation is seen for the ΔL = −3 and +2 dB data. At Δε values ≤45°, the response distribution is single peaked so that the weighted-average model seems to fit the data better than the bimodal model. The pattern observed at Δε values >45° is more complex, as the responses are clearly not single peaked. Accordingly, the weighted-average model is not in good agreement with the data. Interestingly, however, neither is a simple bimodal model: although the main response peak lies closest to the location of the louder sound, and a secondary peak is found near the softer sound, either peak appears to lie between the two actual sound locations at +1 and −1.

As listeners were instructed to ignore the GWN nontarget, we wondered whether their localization behavior might have benefited from longer reaction times, which has been shown to be the case in visuomotor experiments (Becker and Jürgens, 1979; Ottes et al., 1985). Figure 8 shows the normalized response location as a function of head-saccade latencies (pooled across listeners). For graphical purposes, we restricted the ordinate to range from −1.5 to 1.5. We divided the data set according to ΔL (rows) and Δε ≤ 45° versus Δε > 45° (columns), as in Figure 7. The gray line in each panel indicates the running average through all data. This analysis demonstrates no systematic influence of response latency on localization behavior. Thus, response accuracy did not improve when listeners postponed their responses, although their auditory system could have accumulated more evidence for the actual target location.

DTF similarity model

The response patterns described so far appear to resemble those found in the visuomotor literature. In what follows, our analysis will be guided by the two opposing hypotheses described in Introduction (Fig. 1). According to the peripheral hypothesis averaging and bimodal response behavior arise as a result of acoustic interactions at the pinnae. In the case of averaging responses, the auditory system has no way of retrieving the original source locations because the averaging location is already encoded by the double DTF at the pinna filtering stage.

To test for this hypothesis, we applied the similarity analysis of recorded DTFs to the localization data (see Materials and Methods). As a consistency check, we first calculated the SI maps of the single-sound trials on which we superimposed the listener's head movement responses (compare Fig. 2). Figure 9 shows the results obtained with listeners D.B. (left panel) and R.M. (center panel). The gain and bias-corrected elevation responses of the listeners are plotted as white dots (ordinate, target location; abscissa, response location), and the SI of the different DTFs is shown color encoded. The warm colors indicate high similarity between template DTF and filtered single DTF; the cold colors indicate poor similarity. As DTFs were obtained from broadband flat-spectrum Schroeder sweeps, and the single sounds used in this experiment had similar long-term amplitude spectra, the SI map is expected to show a single strip of high correlation along the main diagonal. The figure shows that this is indeed the case, which indicates that the listener's DTFs are unique for each elevation angle and therefore contain unambiguous elevation information. The left-hand panel shows data for BZZ (listener D.B.), and the center panel, for GWN (listener R.M.). In line with Figure 2, the listeners were well able to localize the single targets, so that all responses lie close to the black-dashed identity line with little variability. Importantly, as all responses fall on the dark-red patches that indicate high similarity (close to 1.0) between template and sensory DTFs, locations of high similarity thus correlate well with response location. This finding was also obtained without the gain-bias correction of single-sound responses (data not shown).

The right-hand panel shows the pooled histograms of the similarity indices obtained for the single-sound responses of all listeners (gray-coded lines) pooled across all 11 single-target conditions. The thick solid line shows the average for all conditions and listeners. Clearly, the SI peaks sharply at a value 1.0, with little variability, indicating that sound localization responses to a single broadband sound in the midsagittal plane are highly reproducible and can be well explained by perceived similarity between the sensory spectrum and the internally stored representation of pinna filters.

Figure 10 shows the results of the similarity analysis for the double-sound conditions in the same format as Figure 9. We selected examples from all four listeners (top row), for each of the applied ΔL values (left to right). To give an overview of the data, we selected one BZZ location for each case (positioned at the black solid line) and plotted the SI (colored patches) and the listener's responses (white dots) as a function of GWN location (corresponding with the black-dashed identity line). Note that the situation is now more complex than for the single-sound conditions of Figure 9, as the sensory spectra deviate significantly from the single DTFs obtained with Schroeder sweeps. In the bottom row of Figure 10, we show the pooled histograms of the SIs obtained at the response location for all Δε values and all four listeners (different shades of gray). The average across the listeners is indicated as a black line with markers.

In the left-hand panel of the top row, the GWN is 13 dB louder than the BZZ, and the response endpoints (gain and bias corrected) (see Materials and Methods) are distributed close to the dark-red patch parallel to the central diagonal that corresponds to the GWN location (listener R.M.). The bottom-left panel shows the pooled histograms for the individual listeners and the mean for this condition. The histogram peaks close to the highest value of SI = 1.0. The same is seen for the ΔL = −8 dB condition of listener MW. On the right side of Figure 10, we show results of the ΔL = +7 dB condition for listener D.B. (top), and the resulting SI histograms (bottom), which indicate localization responses that are dominated by the BZZ location (which in this figure is positioned at ε_BZZ = +10°). More interesting are the near-equal ΔL conditions (−3 and +2 dB) shown in the central panels for listener P.B. (top). Especially at large spatial disparities (bottom half of the top panels), the responses became bimodal, whereas for small spatial disparities (top half of the panels), we obtained weighted averaging responses (ΔL = +2 dB data align with the dotted-black line with a slope of ∼2.0). Again, for both response modes, the head-pointing responses fall on or very near to the dark-red patches of high similarity. Thus, when sounds of equal ΔL are spatially well separated, the acoustic periphery preserves major features of individual DTF characteristics. However, when they are closer together (within ∼45°), highest similarity is found for the weighted-averaged elevation. The listener's responses are guided by these acoustic similarities. This is shown in the histograms (central bottom panels), which demonstrate that these results were obtained for all listeners and for all Δε values.

Discussion

Summary

When confronting the auditory system with two broadband sounds presented synchronously in the midsagittal plane, the perceived location is determined by sound level differences and spatial disparity, but not by task requirements (target vs nontarget), or reaction time. Our data reveal three different response modes of the sound localization system in this situation. When level differences exceeded ∼5 dB, the loudest sound determined perceived location, regardless of spatial disparity. However, when sound levels were about equal, we observed two response modes that depended on spatial disparity. For spatial separations within 45°, we obtained weighted-averaged responses, with unimodal distributions. Larger spatial separations resulted in bimodal response distributions, in which the listener oriented to either the target location or the nontarget. However, even in this case, responses were drawn toward the location of the competing stimulus (Fig. 7).

We show that all observed response patterns may be understood from pinna-induced spectral cues. Our results therefore favor the hypothesis in which auditory spatial percepts to synchronous stimuli are guided by acoustic interactions at the pinnae (Fig. 1).

Averaging and bimodality in the auditory system

Response averaging in azimuth is a well established phenomenon (stereophony) and, for simple sounds like a pure tone presented from two speakers in the free field, can be fully explained by interference of sound waves at each ear canal. A similar percept, however, can be obtained through dichotic stimulation (e.g., binaural beats), in which case sounds cannot interact at the ear canals, and hence a neural cause for the perceived intracranial location is more likely. Two localization cues underlie the percept of sound-source azimuth. Interaural time differences (ITDs) operate at low frequencies (<1.5 kHz), as the relationship between ongoing phase difference and azimuth is unambiguous. Interaural level differences (ILDs) arise from the head shadow effect and functions at high frequencies (>3 kHz). Both cues are processed by independent brainstem pathways that involve the medial and lateral superior olive, respectively (Yin, 2002). Interestingly, imposing a conflicting ILD in combination with a given ITD under dichotic listening induces a weighted-averaged intracranial location (time–intensity trade-off). Also in this case, the percept must arise from neural integration of binaural inputs. In short, spatial averaging in azimuth may have both a peripheral (for very simple sounds) and a central (for complex sounds) origin.

Note that, for synchronous broadband stimuli in the midsagittal plane, the emergence of response averaging is not obvious. The elevation percept is thought to be determined by the amplitude spectrum of the direction-dependent pinna filter impulse response, the so-called DTF (Wightman and Kistler, 1989). The direction-dependent phase characteristic of the pinna filter is considered irrelevant. When two sounds are presented simultaneously, sound waves add linearly at the pinnae as follows:

with h_D(τ), the total pressure wave at the eardrum in response to two impulses presented synchronously at locations 1 and 2. The respective DTFs at the locations are described by their amplitude spectra, R₁(ω) and R₂(ω). However, since spectra are complex variables, H(ω) = R(ω) exp(−i Φ(ω)), with Φ(ω) the direction-dependent phase spectrum, the combined amplitude spectrum is not simply the linear superposition of the respective amplitude spectra [i.e., R_D(ω) ≠ R₁(ω) + R₂(ω)], but the following:

which relies on the amplitude and phase spectra of either DTF. Given the complexity of spectral-shape functions, it is not immediately clear form Equation 6 that the (weighted) combination of two sounds yields an amplitude spectrum that best corresponds to the weighted-averaged location (or to two shifted locations, for widely separated stimuli) (Fig. 7). Interestingly, the data in Figure 10 indicate that this is indeed the case.

Note that listeners were able to perceptually distinguish the conditions in which only one sound (either BZZ or GWN) was presented, or a double sound (BZZ plus GWN). Thus, they could report reliably whether or not the target sound was presented together with a nontarget. Yet they invariably reported to always perceive a single, mixed sound source coming from one location, even when their responses resulted in bimodal distributions.

Does this all mean that the auditory system is not capable to segregate auditory objects in elevation? We believe the answer is “yes” for synchronous sounds. However, introducing a brief (few and even submillisecond) onset asynchrony in either azimuth or elevation has been shown to immediately shift the localization percept toward the first sound (the precedence effect) (Litovsky et al., 1999; Yin, 2002; Dizon and Litovsky, 2004). This clearly indicates the involvement of neural processing that weeds out secondary acoustic input to enable localization. Our results hint at the interesting possibility that this temporal filter may be functionally imperative: if the secondary signal were not filtered out, the auditory system cannot segregate different sound sources in the midsagittal plane.

Comparison with other studies

The different response modes in our experiments are quite reminiscent of previous reports from visuomotor experiments, in which two visual targets evoked saccadic eye movements (Becker and Jürgens, 1979; Findlay, 1982; Ottes et al., 1984, 1985; Chou et al., 1999; Aitsebaomo and Bedell, 2000; Watanabe, 2001; Arai et al., 2004; Nelson and Hughes, 2007). Those studies revealed that the visuomotor system typically responds with averaging saccades when stimuli are presented in spatial–temporal proximity, and when the response reaction time is fast. Responses become bimodal when the spatial separation increases beyond ∼30°. However, in both cases, the saccadic system can optimize accuracy in a target/nontarget paradigm by prolonging reaction times (Becker and Jürgens, 1979; Ottes et al., 1985): whereas early saccades invariably end at averaged locations, or in many cases at the distractor, late saccades can all be directed toward the task-imposed target.

Our auditory-evoked head saccades differ from these visuomotor response properties in two major respects. First, auditory response patterns did not evolve over time, since localization accuracy did not improve with increasing reaction time (Fig. 8). Second, in visuomotor experiments, visual stimuli were well separable, both at the retina, and in early sensory responses of neurons within the visuomotor pathways. This holds also for example for the midbrain superior colliculus (SC), a crucial sensorimotor interface for the programming and generation of eye–head orienting responses (Arai et al., 2004; Kim and Basso, 2008). The actual visual response selection leading to either averaging or bimodal responses is therefore attributable to neural processing, rather than to visual peripheral limitations. It has been hypothesized that such response selection could take place within topographically organized neural maps, as in SC, in which target locations are mapped onto spatially separated neural populations. Competition between different populations, combined with local-excitatory/global-inhibitory interactions, shapes the population that represents the saccade goal. Task constraints and stimulus saliency help favor neurons that represent the target to win this competition, yet also averaging may be the result of this competition (van Opstal and Van Gisbergen, 1990; Glimcher and Sparks, 1993; Arai et al., 2004; Kim and Basso, 2008).

Our data indicate that such selective processes do not occur in the audiomotor system for synchronous stimuli, since acoustic interactions at the level of the auditory periphery appear to impose the auditory goal. The spectral shapes of sounds are only preserved when they have about equal loudness and are widely separated in the midsagittal plane (Fig. 10), leading to bimodal response distributions. However, even under those conditions, listeners do not perceive two segregated auditory objects. In a pilot experiment, subjects also listened to the double sounds without making head saccades, but instead indicated whether they perceived two distinct auditory events. In all trials, they perceived only one acoustic event (data not shown). The differences in temporal fine structure between BZZ and GWN were therefore not sufficient to separate the sounds. Interestingly, we also obtained weighted-averaging responses when temporal fine structure and spectral content of the stimuli were very different (two male voice utterances of the same duration). Again, subjective reporting indicates the percept of only one (mixed) sound source that emanated from one, averaged, location (data not shown).

DTF model

Our SI analysis follows previous studies that correlated DTFs with sound localization (Middlebrooks, 1992; Hofman and van Opstal, 1998, 2003; Langendijk and Bronkhorst, 2002). These studies assume that the sensory spectrum is somehow compared with internally stored templates that are related to elevation after a learning process (Hofman et al., 1998; van Wanrooij and van Opstal, 2005). The template with highest similarity to the sensory input is selected and mapped to the source location. Our data show that sound localization responses faithfully follow the DTF similarity map that is based on a representation on single broadband sounds, as head-saccade endpoints are clustered at locations with high similarity values. Similar findings have been reported for cats, who were shown to rely on their spectral cues for localization (pinna-related notches) when presented with illusory localization cues in the two-dimensional free field (Tollin and Yin, 2003).

Although the neural representations of templates and the associated mapping stages in the auditory pathway are still not known, dichotic and free-field perceptual experiments showed that DTFs can be smoothed substantially without hampering spatial percepts (Kulkarni and Colburn, 1998; Hofman and van Opstal, 2002). Additional study is required to assess the relative contributions of acoustic variables, task constraints, temporal asynchronies, and combined azimuth/elevation cues, to the segregation and selection of multiple sounds. The present experiments provide a first step toward that goal.