Abstract
Local groups of neurons engaged in a cognitive task often exhibit rhythmically synchronized activity in the gamma band, a phenomenon that likely enhances their impact on downstream areas. The efficacy of neuronal interactions may be enhanced further by interareal synchronization of these local rhythms, establishing mutually well timed fluctuations in neuronal excitability. This notion suggests that long-range synchronization is enhanced selectively for connections that are behaviorally relevant. We tested this prediction in the human motor system, assessing activity from bilateral motor cortices with magnetoencephalography and corresponding spinal activity through electromyography of bilateral hand muscles. A bimanual isometric wrist extension task engaged the two motor cortices simultaneously into interactions and coherence with their respective corresponding contralateral hand muscles. One of the hands was cued before each trial as the response hand and had to be extended further to report an unpredictable visual go cue. We found that, during the isometric hold phase, corticomuscular coherence was enhanced, spatially selective for the corticospinal connection that was effectuating the subsequent motor response. This effect was spectrally selective in the low gamma-frequency band (40–47 Hz) and was observed in the absence of changes in motor output or changes in local cortical gamma-band synchronization. These findings indicate that, in the anatomical connections between the cortex and the spinal cord, gamma-band synchronization is a mechanism that may facilitate behaviorally relevant interactions between these distant neuronal groups.
Introduction
Neuronal oscillations entail rhythmic fluctuations in the excitability of groups of neurons. These excitability fluctuations have been hypothesized to mechanistically affect the efficiency of interactions between connected neuronal groups (Fries, 2005). In particular, when oscillations in two neuronal groups are mutually coordinated (i.e., when the oscillations are coherent), efficient interaction is likely to occur (Womelsdorf et al., 2007). Activated groups of neurons often show oscillatory activity in the gamma band (Gray et al., 1989; Fries et al., 2001). These oscillations are modulated during cognitive tasks and have therefore been implicated to subserve a functional role in cognition and behavior (Tallon-Baudry et al., 1997; Womelsdorf et al., 2006). Together, this led to the hypothesis that long-range gamma-band synchronization facilitates neuronal communication between behaviorally relevant neuronal groups.
The interpretation of estimates of interareal sychronization based on noninvasive recordings is difficult because of volume conduction effects, although modern source localization techniques alleviate this interpretational problem to a certain extent (Schoffelen and Gross, 2009). These techniques have yielded valuable insight into the recruitment of synchronized networks of brain regions (Gross et al., 2002; Jerbi et al., 2007). Here, we studied long-range neuronal interactions in the human corticospinal system. In particular, we measured brain activity in sensorimotor regions with magnetoencephalography (MEG) and motor unit activity with electromyography (EMG), thus bypassing the problem of volume conduction effects altogether. In previous work, we successfully used the corticospinal system as a model system to show that gamma-band synchronization leads to effective neuronal communication (Schoffelen et al., 2005). However, in that study, only one corticospinal connection was assessed. Therefore, we were not able to test a key prediction of the hypothesis. This prediction states that, in order for neuronal synchronization to be instrumental for neuronal communication, it should be selectively modulated between neuronal groups, depending on the behavioral relevance of these groups for the task at hand.
In this study, we used a bimanual motor task to test this selectivity prediction. We studied the neuronal interactions between sensorimotor regions in the brain and α motorneurons innervating respective contralateral forearm muscles. We selectively modulated the behavioral relevance of one of these corticospinal connections by presenting a response cue, indicating the hand with which the subjects had to respond on an imperative go cue.
We hypothesized gamma-band corticomuscular coherence to be selectively increased in the behaviorally relevant corticospinal connection (i.e., between a motor effector and the corresponding contralateral sensorimotor cortex, when this motor effector was cued, compared with when it was not cued to respond). The results of our analysis support this hypothesis. We found selective changes in long-range synchronization, both spatially confined to the relevant corticospinal connection and spectrally confined to the gamma band. In contrast, analysis of local synchronization revealed a readiness effect in the beta band in sensorimotor cortices.
These findings suggest that long-range gamma-band synchronization is selectively increased in behaviorally relevant neuronal connections and thus subserves a functional role in cognition by linking the relevant nodes in a neuronal network.
Materials and Methods
Subjects.
Eleven healthy subjects (five females; mean age, 24 years; range, 21–28; four left-handed) participated in the experiment. All subjects gave written informed consent according to the Declaration of Helsinki.
Experimental paradigm.
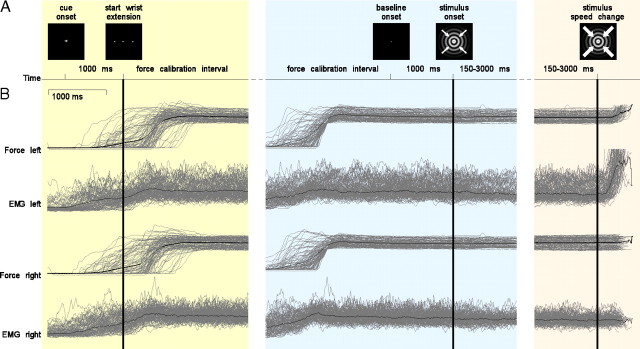
The subjects were seated comfortably with their forearms in a relaxed position, supported by cushions on the armrests of the MEG chair. Figure 1A schematically shows the paradigm. At the beginning of a trial, subjects were asked to fixate on a small cueing stimulus that was projected on a screen in front of them. This cue consisted of a little white triangle pointing either to the left or to the right and was presented for 1 s. Subsequently, the cueing stimulus was replaced by a white fixation dot, and the subjects had to extend both their wrists against two compliant levers connected to two force transducers and to keep the measured force within a specified window, which was defined between 1.1 and 1.5 N. The lower boundary of the force window was selected based on visual inspection of EMG traces obtained during a few pilot sessions, in which clear tonic EMG activity was observed once the wrist extension was sufficient to cross this boundary. Subjects received feedback about the exerted force by the color of two dots, presented to either side of the fixation dot, which turned from red to green as soon as the required force level at the respective side was reached. This force calibration interval ended when the force exerted by both wrists was within the prespecified window for >1 s. The disappearance of the colored dots marked the beginning of a 1 s baseline interval, in which only the fixation dot was presented to the subject. The fixation dot was continuously present on the screen in the time interval between the offset of the cueing stimulus and the onset of the visual stimulus. The stimulus was a concentrically contracting sinusoidal grating (diameter, 5 deg; spatial frequency, 2 cycles/deg; contrast, 100%; velocity, 0.8 deg/s). The subjects' task was to react as fast as possible to a speed change of the stimulus that could occur at any moment between 150 and 3000 ms after stimulus onset. Subjects had to respond by increasing the extension of the left or right wrist, corresponding with the previously cued direction. Importantly, the subjects had to maintain a constant extension of the noncued wrist until the end of the response interval.
Figure 1.
Experimental paradigm and motor output for an example subject. The timeline of a trial with its key events are shown in A. Motor output as measured with strain gauges (force signal) and surface EMG is shown in B. Only trials that required a response with the left hand are shown. The gray lines show time courses of single trial activity; the black lines represent the average. The three columns represent the physiological data time locked to three key events in the trial [i.e., the start of the wrist extension (left column), the onset of the visual stimulus (middle column), and the speed change of the stimulus (right column)]. The key events are denoted by the solid vertical lines.
A trial was considered successful if (1) the subject responded with the cued wrist within 600 ms after the speed change of the stimulus; (2) the applied force was within the specified window until the speed change of the stimulus for the cued side, and until the end of the response interval for the noncued side. As soon as the applied force on one of the levers drifted out of the specified window before the speed change, the trial was aborted. To maximize the amount of trials suitable for analysis, we used an increasing hazard rate. This means that the instantaneous probability of the stimulus' speed change increased with time. For more information, see Schoffelen et al. (2005). Approximately 10% of the trials were catch trials, in which no speed change occurred and which ended after 3 s of visual stimulation.
Each subject performed a sequence of 300 trials, divided into six blocks. The response cues were randomly pointing to the right or to the left. The subjects received feedback about their responses. There was a 1 s interval between the end of the response feedback and the onset of the cue stimulus of the following trial, allowing for eye blinks.
Before the experimental recording session, subjects performed two blocks of unimanual contractions. These blocks consisted of 20 trials of 8 s each, in which subjects were asked to extend either their right or left wrist while fixating on a colored fixation cross. The color changed from red to green as soon as the force applied to the lever was within the specified window between 1.1 and 1.5 N. The data in these blocks were used to select sensors for a region of interest analysis.
Data acquisition.
The force applied to the levers was measured by strain gauges. Apart from being digitized and recorded in parallel with the electrophysiological data, the force signals were also fed into a second, separate A/D converter, and a software window discriminator was implemented to detect whether the force was within the specified window.
MEG was acquired with a 151-sensor axial gradiometer system (Omega 2000 whole head MEG system; CTF Systems). Bipolar surface EMG was recorded from the left and right musculus extensor carpi radialis longus using two Ag/AgCl electrodes, which were placed over the muscles with a 3 cm interelectrode distance, with the proximal electrodes placed 4 cm distal to the external epicondyle of the humerus. The electrooculogram (EOG) was recorded from a bipolar electrode pair placed above and lateral to the outer canthus of the left eye. The impedance of the EMG and EOG electrodes was <20 kΩ. The data were low-pass filtered at 300 Hz and digitized at 1200 Hz. Before and after the MEG recording, the subject's head position relative to the gradiometer array was determined using coils positioned at the subject's nasion and at the bilateral external auditory meatus.
EMG/MEG preprocessing.
All analyses were done with FieldTrip, an open-source Matlab toolbox for neurophysiological data analysis (Oostenveld et al., 2011).
Only data segments between the start of a trial and the speed change of the stimulus were analyzed. Segments that were contaminated by eye movements, muscle activity, or jump artifacts in the superconducting quantum interference devices were discarded. The power line interference was removed by estimating and subtracting the 50, 100, and 150 Hz components in the MEG data, using a discrete Fourier transform on 5 s data segments including the artifact-free data segments of interest.
To estimate the EMG amplitude, we high-pass filtered the raw EMG at 10 Hz (Kilner et al., 2000) and computed the absolute value of the Hilbert transform of the filtered signals. This procedure gives a time-dependent estimate of the total power of the signal generated by the muscular units and hence provides information with respect to the timing of spiking activity of the motorneurons. This is exactly the information that is relevant for the estimation of corticomuscular coherence (Halliday and Farmer, 2010). Taking the absolute value of the Hilbert transform is a nonlinear transformation of the signal that is closely related to the commonly used full rectification of the high-pass filtered EMG signal (Myers et al., 2003). Recent work using simulated EMG activity reopened the debate questioning rectification to be an appropriate processing step for the optimal estimation of corticomuscular coherence (Halliday and Farmer, 2010; Neto and Christou, 2010). Empirically, however, rectification does not negatively affect the estimated coherence (Yao et al., 2007), and simulations that take the spiking times of motor units into account show a clear benefit of applying a nonlinear transformation to the EMG signal (Myers et al., 2003). In the following, we will use the term “EMG” for the preprocessed EMG signal.
The data were divided into four subsets, according to the cued response side, and according to the presence of the moving stimulus. In the following, we will use the terms “condition left” and “condition right” to denote the trials according to the cued response side. We will use the term “prestimulus interval” for the 1 s interval before the onset of the visual stimulus. We will use the term “stimulus interval” for the periods between onset of the moving stimulus and the speed change. For the stimulus interval, we only took data into account starting 300 ms after stimulus onset, to avoid activity that is locked to the onset of the stimulus. As a consequence, we discarded the trials for additional analysis in which the speed change of the stimulus occurred earlier than 700 ms after stimulus onset (because of our 400 ms analysis window) (see below).
The measured axial gradients of the magnetic field were transformed into planar gradients using a nearest neighbor interpolation (Knosche, 2002). This facilitates the averaging of the MEG topographies across subjects.
Spectral analysis.
Power spectra and cross-spectra were computed using the multitaper method (Mitra and Pesaran, 1999). The data were cut into nonoverlapping 0.4 s segments. Each data segment was tapered using a set of discrete prolate spheroidal sequences (Slepian functions). We used two sets of tapers to achieve different amounts of spectral concentration, thus maximizing sensitivity for effects in the beta- and gamma-frequency bands. For the frequency bins up to 30 Hz, we used three tapers, which resulted in a spectral smoothing of ±5 Hz around each frequency bin. The physiological beta band has a bandwidth of ∼10 Hz, and therefore the spectral concentration of ±5 Hz nicely captures this frequency band. For the frequency bins beyond 30 Hz, we used nine tapers, resulting in a spectral smoothing of ±12.5 Hz around each frequency bin. This choice was motivated by band-limited effects in the gamma band usually having a bandwidth on the order of 25 Hz. Each tapered data segment was Fourier transformed, and the horizontal and vertical planar gradients were recombined, by projecting the planar gradient data onto the direction in which the power was maximized, without distorting the phase relationship between the signals. This was achieved by singular value decomposition of the real part of the cross-spectral density between the horizontal and vertical planar gradient, and using the first singular vector to project the data.
Power spectra and cross-spectra were computed according to the following:
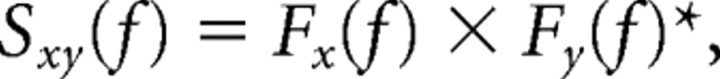 |
where Fx(f) denotes the Fourier transform of signal x at frequency f, and * denotes the complex conjugate. When x ≠ y, Sxy denotes the cross-spectrum between signal x and signal y. When x = y, Sxy reduces to Sxx, which represents the power spectrum of signal x. Single segment power spectra and cross-spectra were obtained by averaging across the tapers. Coherence was computed according to the following:
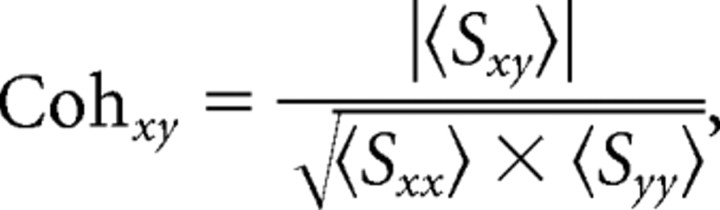 |
where 〈·〉 denotes the mean across segments. Power spectra were averaged across segments and log10 transformed. The log10 transformation was applied to stabilize the variance to facilitate the stratification (see below).
Statistical analysis: sensor level.
We compared different sets of data segments and computed t spectra (Bauer et al., 2006; Lange et al., 2011) (for the comparison of power, to account for differences in absolute power between the subjects because of variability in the subject's exact position with respect to the sensor array) and z spectra (Bokil et al., 2007; Maris et al., 2007) (for the comparison of coherence, to account for the differences in the bias, introduced by different numbers of data segments across subjects), for each individual subject.
Unpaired t statistics were computed for each signal and each frequency bin according to the following:
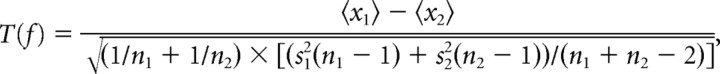 |
where 〈xa〉 denotes the average power in condition a, na is the number of observations, and sa2 is the variance of the power in condition a.
Z spectra for the difference in coherence between MEG-EMG channel pairs and each frequency bin were computed according to the following:
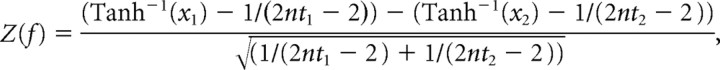 |
where xa denotes the coherence in condition a, nta is the numbers of tapers applied in condition a, and Tanh−1 is the inverse hyperbolic tangent.
For the group statistics, we pooled the individual subjects' t and z spectra. We used these pooled t or z values as first-level test statistic, but based the statistical inference on a nonparametric permutation test (Nichols and Holmes, 2002; Maris and Oostenveld, 2007). In the case of the t and z spectra, exchanging the conditions is equivalent to swapping the sign of the values in the spectrum. By recomputing the average spectrum, after having swapped the sign of the individual spectra in a random subset of subjects, an observation under the null hypothesis is obtained. A reference distribution is generated by repeating this step multiple times and the likelihood of the observed data is computed by comparing it with the reference distribution. To control the false alarm rate, we applied a clustering algorithm (Maris and Oostenveld, 2007). This was done in the following way. For each channel and frequency bin, we computed two critical t values (in the case of coherence, z values) by comparing the observed value with the reference distribution obtained at that channel frequency bin. The critical values were taken such that 2.5% of the highest values obtained by permuting the single subjects' observations exceeded the positive critical value, and 2.5% of the lowest values were smaller than the negative critical value (this corresponds to a two-sided p value of 0.05, uncorrected). Subsequently, the observed and permuted data were thresholded at these critical values and spatiospectral clusters were formed consisting of threshold exceeding channel frequency points neighboring in frequency space and in physical space. For each cluster, a second-level test statistic was computed by summing the suprathreshold (or infrathreshold) t values (z values). The reference distributions of the cluster-based test statistic were obtained by taking the most extreme value of the test statistic in each permutation. The cluster-based test statistics in the observed data were tested against these reference distributions to obtain a corrected p value for each cluster.
Sensors of interest analysis of corticomuscular coherence.
Brain signals that are coherent to the EMG are typically picked up at sensors overlying contralateral motor regions. We therefore constrained our initial analysis of corticomuscular coherence to two subsets of sensors. We selected two subsets of 10 MEG sensors overlying both motor regions. These sensors were selected from the spatial topography of the corticomuscular coherence based on the preexperiment unimanual contraction data. Artifact-free data segments were cut into 0.4 s nonoverlapping segments, and corticomuscular coherence spectra were computed with a spectral smoothing of ±5 Hz. For each subject and frequency bin, we applied a spatial normalization step to achieve an equal weighing across the subjects. For a given frequency bin, we subtracted the mean coherence value across all MEG sensors and divided the resulting value by the SD across the sensors. Subsequently, we averaged the spatially standardized coherence spectra across the subjects and frequency bins. For each of the unimanual contraction conditions, we selected the 10 MEG sensors that displayed the highest standardized coherence with the EMG.
Z spectra of the difference in corticomuscular coherence were analyzed in two runs, using different multitaper settings. For frequencies <30 Hz, we used a spectral smoothing of ±5 Hz, and for frequencies >30 Hz, we used a spectral smoothing of ±12.5 Hz. For each subject and region of interest, the spectra were averaged across the 10 MEG sensors, and the regions of interest were combined for each subject, according to the following formula:
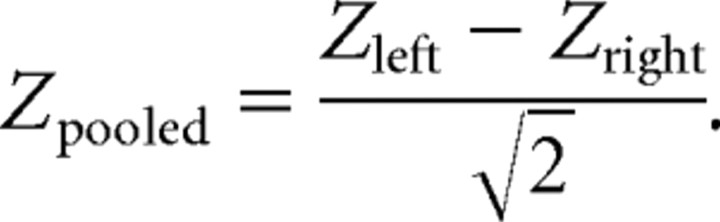 |
The resulting spectra were pooled across subjects, and a nonparametric permutation test was performed.
Source analysis.
For the analysis of the neuronal sources, we used a beamformer method, DICS (Dynamical Imaging of Coherent Sources) (Gross et al., 2001). Each subject's brain volume was divided into a regular grid. The grid positions were obtained by a linear transformation of the grid positions in a canonical 8 mm grid. This canonical grid was based on a template brain (Montreal Neurological Institute), and for each subject, we computed the linear transformation optimally aligning the subject's brain volume to the template brain, using SPM2 (http://www.fil.ion.ucl.ac.uk/spm). We applied the inverse of this linear transformation to the grid positions of the canonical grid to obtain subject-specific dipole grids. This procedure facilitates the group analysis, because no spatial interpolation of the volumes of reconstructed activity is required.
For each grid position, we constructed spatial filters. These filters have the property that they optimally pass activity from the location of interest, while other activity, which is present in the data, is suppressed. The filter weights are calculated with the following formula:
where L(r) is the forward model for the location r of interest (the lead field matrix), C(f) is the cross-spectral density (CSD) matrix between all MEG signal pairs at the frequency f, λ is a regularization parameter, and I is the identity matrix.
To compute the lead field matrices, we used a single-shell volume conduction model, based on the shape of the inside of the skull (Nolte, 2003). The inside of the skull was derived from each individual subject's structural magnetic resonance image, which was spatially aligned to the MEG sensors. Despite the fact that, in this volume conduction model, there is no truly magnetically silent direction, we excluded the most silent direction from the lead fields, since this direction potentially picks up a lot of noise.
To analyze the location of the sources accounting for the significant sensor level effects, we computed the CSD matrix between all MEG sensor pairs from the Fourier transforms of the tapered data epochs at the frequencies of interest. As we had found significant sensor-level effects in the beta and gamma bands, those two bands were subjected to source level analysis. For each subject, and within each of the frequency bands, we identified the frequency bin that yielded the most extreme t value (for power comparisons), or z value (for coherence comparisons), averaged across sensors. Spatial filters were constructed for each grid location, based on the identified frequency bin, and the Fourier transforms of the tapered data epochs were projected through the spatial filters, using the following formula:
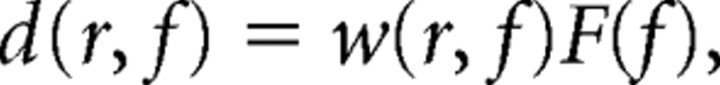 |
where F is an N×M matrix, containing the Fourier coefficients at frequency f, of N channels and M single tapered data epochs. The matrix d represents the Fourier coefficients in three orthogonal directions (3×M matrix) for a dipole at location r. We estimated the orientation in which the power of the dipole was maximal, by singular value decomposition of the real part of the dipole-level cross-spectral and projected the Fourier coefficients on this direction, yielding a 1×M fast Fourier transform vector. This vector represents the Fourier coefficients for the dipole with an orientation in the direction of maximal power. T statistics (for the comparison of power) and z statistics (for the comparison of coherence) at each voxel were subsequently computed in the same way as it was computed at the sensor level.
The individual functional statistical volumes were combined across subjects. We used a nonparametric permutation test to assess significance and correct for multiple comparisons in the same way as described for the sensor level statistical analysis (Nichols and Holmes, 2002; Maris and Oostenveld, 2007).
Stratification.
Our experimental procedures aimed at keeping the motor output constant while modulating motor preparation as a function of time (visual stimulation vs prestimulus period) or effector side (right vs left wrist cued). However, the motor output was not under direct control of the experimenter and the motor output produced by the subjects could not be constrained within an arbitrarily narrow window (Fig. 1B). To minimize effects of small changes in motor output, we therefore performed a post hoc stratification of the data based on the EMG amplitudes. The goal of the stratification was to obtain, from each of the two conditions, a subset of trials such that the distribution of EMG power values across the trials constituting the subsets was identical for each of the two conditions. This approach has been adjusted from Roelfsema et al. (1998) and a similar strategy has been successfully applied to control for EMG fluctuations (Schoffelen et al., 2005). The following procedure was applied to the single subject data and for each frequency bin separately.
We binned the observations in each condition according to the log10-transformed power estimates of both EMG signals. The bin centers were obtained for each EMG signal separately by dividing the range of all EMG power values into eight equally spaced bins. In this way, each of the observations fell within one of 64 (i.e., 8 × 8) bins, formed by the joint distribution of the power values of the left and right EMG. For each of these 64 bins, we selected a subset of observations such that across the two conditions, the number of observations was identical. From the condition with the lowest number of observations in a given bin, all N observations constituting that particular bin were selected for the stratified sample. From the other condition, a subset of N observations was randomly drawn from the observations constituting that particular bin.
Results
On average, an experimental session yielded 260 (SEM, 14) 400 ms artifact-free data segments for condition left, and 269 (SEM, 10) data segments for condition right. The stratification procedure, in which we aimed at equalizing the motor output across the two conditions, yielded on average 202 (SEM, 9) data segments for both conditions. In addition, we analyzed the time segments before the onset of the visual stimulus. An experimental session delivered on average 231 (SEM, 7) data segments in the baseline interval for condition left, and 228 (SEM, 5) for condition right. Figure 1B illustrates the motor behavior of an example subject for all trials in condition left. Single trials have been time-locked to different events to illustrate the effects of these key events on motor output. Note that, for some traces, the three time axes partially overlap because of variability in the duration of the different temporal intervals.
Selection of region of interest sensors
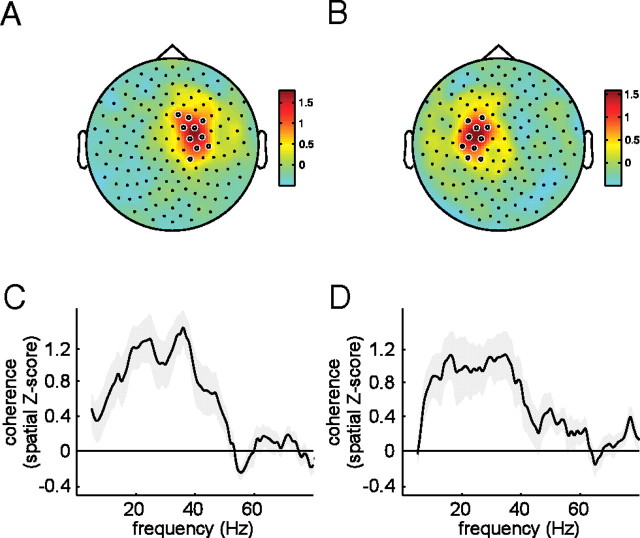
Figure 2, A and B, shows spatial topographies of the corticomuscular coherence between the left EMG and all MEG sensors (Fig. 2A), and between the right EMG and all MEG sensors (Fig. 2B), spatially z scored and averaged across subjects and the frequency range between 10 and 40 Hz. From these topographies, constructed from data obtained during a preexperimental recording session, two sets of 10 MEG sensors were selected for the region of interest analysis for corticomuscular coherence (white circles). Figure 2, C and D, shows the spatially z scored coherence spectra averaged across the selected 10 MEG sensors, for the connection between the left EMG and the set of right hemisphere sensors (Fig. 2C), and for the connection between the right EMG and the set of left hemisphere sensors (Fig. 2D).
Figure 2.
Selection of sensors of interest for corticomuscular coherence analysis. Spatial topographies (A, B) and spectral signatures (C, D) of corticomuscular coherence obtained during a preexperiment recording with unimanual contractions, for the left wrist extension (A, C) and the right wrist extension (B, D). Coherence spectra were spatially Z scored before averaging across subjects. Selected sensors of interest are shown as white circles on the topographies.
Condition left versus condition right during stimulus interval: coherence
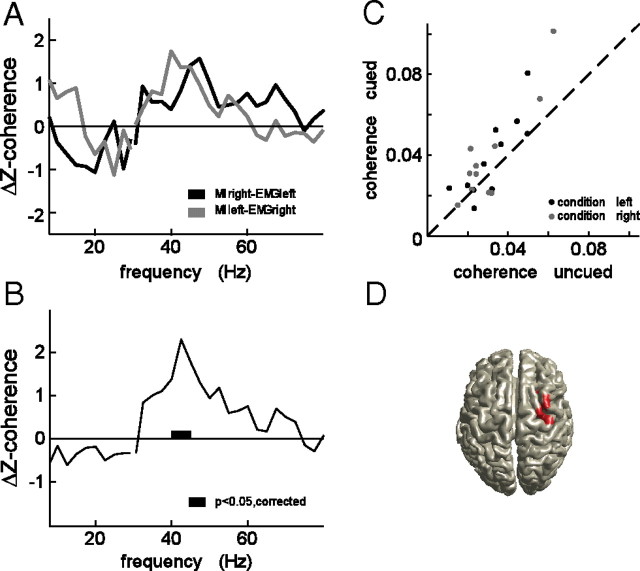
Figure 3 shows the effect of the response cue on corticomuscular coherence during the stimulus interval, for a single representative subject. Figure 3, A and C, shows the coherence for the corticospinal connection to the left arm muscle, for the response left condition (Fig. 3A) and the response right condition (Fig. 3C). Figure 3, B and D, shows the coherence in the same conditions, but now for the corticospinal connection to the right arm muscle. The corticospinal connection mediating the cued response (Fig. 3A,D) shows long-range gamma-band coherence. This gamma-band coherence was attenuated when the same connection was not cued (Fig. 3B,C). Figure 3E shows, for each of the corticospinal connections, the spatially selective readiness effect, which we defined as the Z-transformed difference in coherence between the cued and uncued conditions.
Figure 3.
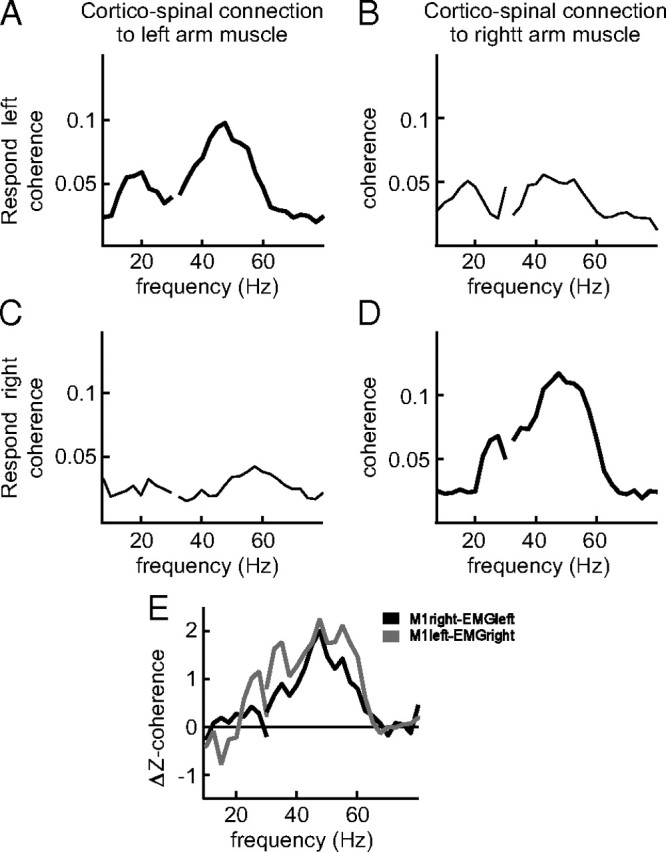
Spatially specific readiness effect on corticomuscular coherence in a representative single subject. Raw coherence spectra are shown for the two corticospinal connections [right primary motor cortex (M1) to left arm muscle (A, C) and left M1 to right arm muscle (B, D)] in the two response conditions [response left (A, B) and response right (C, D)]. The thick black lines represent the situation in which the respective corticospinal connection was cued for the response. E, Z-transformed coherence difference between the cued and uncued conditions, for the left response side (gray line) and the right response side (black line).
Figure 4 shows the spatially selective readiness effect, pooled across all subjects, after stratifying for EMG power. Figure 4A shows the readiness effect for the coherence in the corticospinal connection to the right arm muscle (gray line), and for the coherence in the corticospinal connection to the left arm muscle (black line). Gamma-band corticomuscular coherence between the right EMG and the left hemisphere sensors was significantly increased (p < 0.05, nonparametric permutation test, corrected) but did not reach significance on the other side (p < 0.1, nonparametric permutation test, corrected). Figure 4B shows the readiness effect pooled across hemispheres. There is a significant increase in corticomuscular coherence in the frequency band between 40 and 45 Hz (p < 0.05, nonparametric permutation test, corrected). We did not find a significant effect of handedness on the readiness effect (results not shown). Figure 4C shows for each of the corticospinal connections tested the corticomuscular coherence averaged between 35 and 52 Hz for the cued versus the uncued conditions. In the cued condition, coherence was enhanced by a median of 25% compared with the uncued condition (p < 0.02, paired sign test).
Figure 4.
Spatially specific readiness effect on corticomuscular coherence across subjects. Z-transformed differences in corticomuscular coherence between the cued and uncued conditions for the left response side (gray line) and the right response side (black line), pooled across subjects (A). Results of statistical analysis across subjects after pooling the left and right response sides (B). Scatterplot showing for each of the corticospinal connections the corticomuscular coherence (averaged between 35 and 52 Hz) for the cued versus the uncued conditions (C). Source analysis results of the readiness effect on gamma-band corticomuscular coherence, showing the statistically significant cluster (D).
We further tested the spatial specificity of this effect, and performed a beamformer analysis to analyze which regions in the brain showed a significant readiness effect (Fig. 4D). To this end, we computed Z-transformed coherence differences in gamma-band corticomuscular coherence between each of the EMGs and the brain, when the EMG was on the cued side versus when it was not on the cued side. For each subject, the Z volume of coherence between the right EMG and the brain was subsequently mirrored in the sagittal plane and pooled with the Z volume of coherence between the left EMG and the brain. Figure 4D shows that the significant increase in gamma-band corticomuscular coherence is confined to cortical regions in the vicinity of primary motor cortex contralateral to the cue side.
Condition left versus condition right during stimulus interval: power
To investigate whether the changes found in corticomuscular coherence could be confounded by changes in oscillatory brain activity, we computed T spectra of the power difference between condition left and condition right. Statistical analysis revealed two significant clusters of sensors, overlying left and right sensorimotor cortices. The frequency range contributing to the significant effect was confined to the beta band (17.5–25 Hz in the left hemisphere cluster, and 15–27.5 Hz in the right hemisphere cluster), and the sign of the effect indicated that this beta-band activity is decreased in sensorimotor cortex contralateral to the cued response hand compared with the ipsilateral cortex. Figure 5A shows the t spectra, averaged across the sensors contributing to each of the clusters, which are shown in the topography (red line: cluster in left hemisphere, p < 0.05, nonparametric permutation test, corrected; blue line: cluster in right hemisphere, p < 0.05, nonparametric permutation test, corrected). Analysis of the neuronal sources accounting for this finding revealed bilateral sensorimotor cortices. Figure 5B shows the clusters of significant voxels projected onto a template brain (p < 0.05, nonparametric permutation test, corrected). We did not observe condition-specific modulations of cortical oscillatory activity in the gamma-frequency band.
Figure 5.
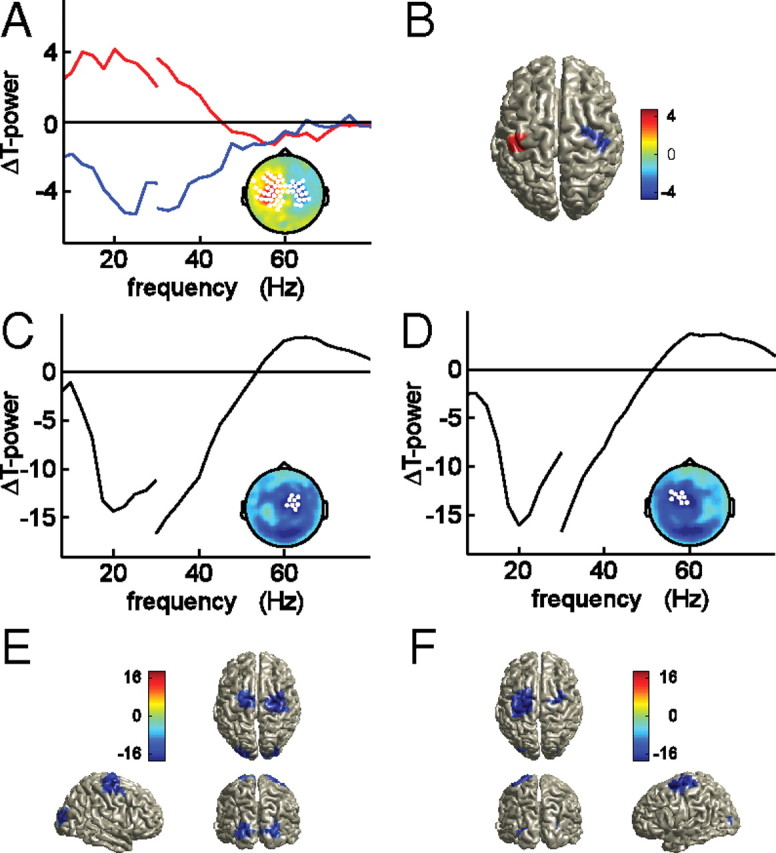
Response cue induced changes in beta-band activity after spectral stratification for the EMG power. A, Pooled t spectra of the power difference between cue left and right conditions during the stimulus interval, averaged across significant clusters of sensors (p < 0.05, corrected), as highlighted in the topography (inset). Red line, Left hemisphere cluster. Blue line, Right hemisphere cluster. Source analysis results of the response cue induced modulation in beta-band (20 Hz) activity (B). Visual stimulus induced changes in beta-band activity for the cue left condition (C, E) and the cue right condition (D, F), suggestive of a cue-dependent asymmetric decrease in beta-band oscillatory activity. Pooled t spectra were averaged across the highlighted sensors in the corresponding topographies (C, D). Source analysis results of stimulus-induced changes in oscillatory activity at 20 Hz (E, F).
Prestimulus versus stimulus interval: power
To further investigate the readiness effect on cortical beta-band oscillatory activity, we compared the condition-specific stimulus intervals with their respective condition-specific prestimulus intervals. The onset of the visual stimulus elicited a broadband decrease in oscillatory activity in almost all MEG sensors (data not shown), with a frequency between 8 and 30 Hz. Statistical analysis revealed a significant cluster of sensors consisting of almost all MEG sensors in each condition (p < 0.0005, corrected). This broadband decrease appeared to consist of several separate spatio-spectral minima, in the alpha- and beta-frequency bands. The topography of the decrease in beta-band activity was condition specific and involved sensors overlying sensorimotor regions. We therefore focused on the beta band in the following. Figure 5C–F show the difference in beta-band activity between the prestimulus interval and the stimulus interval, for condition left (Fig. 5C,E) and condition right (Fig. 5D,F). Onset of the visual stimulus led to a widespread decrease in beta-band activity (16–30 Hz), with a minimum over central MEG sensors. This decrease was lateralized for the conditions, being stronger in the hemisphere that was cued to respond. Figure 5C shows the topographical distribution for the beta-band decrease for condition left with the average t spectrum of the eight sensors showing the strongest decrease in this frequency band. Figure 5D shows the same effect, but then for condition right. Next to the lateralized beta-band decrease in central MEG sensors, the topographies show a clear decrease in beta-band oscillatory activity in posterior MEG sensors. Source reconstruction of the stimulus-induced beta decrease revealed significant effects in motor regions, contralateral to the cued response side, and in visual regions (Fig. 5E,F).
Discussion
In this study, we used the corticospinal connection as a model connection to test for selectivity of cognitive modulations of long-range gamma band synchronization. Subjects had to maintain a bilateral wrist extension in anticipation of an imperative go cue. We aimed at selectively manipulating the subjects' readiness to respond with one of their hands, by providing a directional cue before each trial, indicating the side of the required response. We analyzed corticomuscular coherence during the interval in which the isometric contractions were maintained, and we observed that low gamma-band (40–47 Hz) corticomuscular coherence between the nodes of the cued long-range connection was selectively increased. Also, we found that the onset of the visual stimulus induced a more profound decrease in beta-band activity in sensorimotor regions of the cued hemisphere. All of these changes were observed in the absence of significant changes in motor output.
Past work has shown that gamma-band corticomuscular coherence leads to effective neuronal communication (Schoffelen et al., 2005). In that study, a temporal augmentation in readiness to respond was accompanied by an increase in long-range gamma-band coherence. A study using a very similar paradigm showed a corresponding increase in corticomuscular excitability via transcranial magnetic stimulation (van Elswijk et al., 2007). Yet Schoffelen et al. (2005) tested only one connection, between the left motor cortex and the spinal motorneurons connected to a right forearm muscle. Therefore, we could not exclude that the changes were unspecific and reflecting temporal modulations in global alertness. The present setup allowed for simultaneous measurement of the synchronization in two long-range connections and enabled us to specifically address the selectivity issue.
Gamma-band corticomuscular coherence has been reported in various experimental paradigms. It has been observed during strong isometric contractions (Brown et al., 1998), phasic movements (Brown et al., 1998; Omlor et al., 2007), and during movement preparation (Schoffelen et al., 2005). The occurrence of gamma-band corticomuscular coherence during phasic movements and movement preparation, and its dependence on cognitive factors, make it a phenomenon that is likely of functional relevance. We add evidence to this hypothesis by showing here that gamma-band corticomuscular coherence is modulated by task requirements in a spatially specific manner.
Here, we studied neuronal synchronization in a network engaged in the preparation of a motor response. Oscillations in the beta-frequency range are a prominent feature of neuronal activity in the motor system (Murthy and Fetz, 1996; Baker et al., 2001; Courtemanche et al., 2002; Brovelli et al., 2004; Jensen et al., 2005). These oscillations have been shown to relate to movement preparation (Crone et al., 1998; Pfurtscheller and Lopes da Silva, 1999; Neuper and Pfurtscheller, 2001) and response selection (Kaiser et al., 2001; Doyle et al., 2005). In the present study, we found cue-specific differences in the amplitude of stimulus-induced local beta-band desynchronization in sensorimotor cortices. These findings are in line with converging evidence that beta-band oscillations in the motor system favor the existing motor state (Chen et al., 1998; Gilbertson et al., 2005). Yet we did not find an effect of the response cue on long-range beta-band synchronization. Corticomuscular beta-band coherence is a robust phenomenon that has been extensively studied (Conway et al., 1995; Gross et al., 2000; Baker et al., 2003; Pohja et al., 2005; Witham et al., 2010) and that has been shown to vary with task requirements (Kilner et al., 2000) and performance (Kristeva et al., 2007). In a recent study, van Wijk et al. (2009) used a cued choice response task to study corticomuscular phase synchronization. They reported a relative increase in beta-band phase synchronization between the uncued motor effector and the corresponding motor regions. The reason for this discrepancy may lie in the differences with respect to specific details of the experimental design and/or in the way the data could be analyzed. The main differences were that, in our setup, the response cue was given at the beginning of each trial, and the go cue occurred at an unpredictable moment. Response cue effects on long-range beta-band synchronization became apparent when the synchronization was expressed relative to the precue interval (van Wijk et al., 2009). Our design did not allow for such an analysis because in our setup the cue was given before each trial, and therefore we did not obtain a time interval in which the subject was not cued, while at the same time already performing the isometric muscle contractions. Conversely, the unpredictable go cue in our experiment may have engaged the motor system in such a way that it enabled us to observe long-range gamma-band synchronization (Schoffelen et al., 2005).
Corticomuscular coherence has been found to be not solely mediated by the efferent connection between cortical regions and the spinal cord (Kilner et al., 2004; Riddle and Baker, 2005; Patino et al., 2008), and studies of the direction of information flow between the cortex and the spinal cord suggest a bidirectional flow of information (Mima et al., 2001; Witham et al., 2010) during simple motor behavior. However, future work is needed to address the question of directionality in our data, possibly using nonlinear analysis methods (Jin et al., 2010).
Another interesting question is whether the implications of our finding can be generalized to long-range corticocortical interactions as well. In fact, several studies reported on long-range corticocortical gamma-band synchronization (Saalmann et al., 2007; Gregoriou et al., 2009). These studies used microelectrode recordings in awake monkeys to investigate connections between neurons with overlapping receptive fields in lateral intraparietal cortex (area LIP) and area MT (Saalmann et al., 2007), and connections between the frontal eye fields (FEFs) and area V4 (Gregoriou et al., 2009). Using a visual attention paradigm, it was shown that spatial attention to a location inside the receptive fields of the recorded neurons led to an increase in gamma-band synchronization. Yet other studies report oscillations in lower frequency bands (beta band) to be synchronized between area LIP and FEFs (Buschman and Miller, 2007), and between dorsal premotor cortex and the parietal reach region (Pesaran et al., 2008). In our study, the frequency band showing a significant effect across the population is a relatively narrow band and low in frequency compared with the cortical band-limited effects in the gamma-frequency range typically reported in visual, somatosensory, or motor activation studies (Bauer et al., 2006; Hoogenboom et al., 2006; Cheyne et al., 2008). The specificity of the frequency band may thus be related to the experimental task and (the spatial extent of) the activated network.
In conclusion, we found that a directional response cue selectively increases long-range gamma-band synchronization in the neural connection that needs to be established for a specific cognitive task. This finding supports the hypothesis that gamma-band synchronization has a role in shaping cognition by allowing for efficient neural communication between relevant nodes of a neural network.
Footnotes
This work was supported by grants from the Netherlands Organization for Scientific Research (P.F., J.-M.S.), the European Science Foundation European Young Investigator Award Program (P.F.), and the BrainGain Smart Mix Programme of the Netherlands Ministry of Economic Affairs and the Netherlands Ministry of Education, Culture and Science (J.-M.S., R.O.).
References
- Baker SN, Spinks R, Jackson A, Lemon RN. Synchronization in monkey motor cortex during a precision grip task. I. Task-dependent modulation in single-unit synchrony. J Neurophysiol. 2001;85:869–885. doi: 10.1152/jn.2001.85.2.869. [DOI] [PubMed] [Google Scholar]
- Baker SN, Pinches EM, Lemon RN. Synchronization in monkey motor cortex during a precision grip task. II. Effect of oscillatory activity on corticospinal output. J Neurophysiol. 2003;89:1941–1953. doi: 10.1152/jn.00832.2002. [DOI] [PubMed] [Google Scholar]
- Bauer M, Oostenveld R, Peeters M, Fries P. Tactile spatial attention enhances gamma-band activity in somatosensory cortex and reduces low-frequency activity in parieto-occipital areas. J Neurosci. 2006;26:490–501. doi: 10.1523/JNEUROSCI.5228-04.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bokil H, Purpura K, Schoffelen JM, Thomson D, Mitra P. Comparing spectra and coherences for groups of unequal size. J Neurosci Methods. 2007;159:337–345. doi: 10.1016/j.jneumeth.2006.07.011. [DOI] [PubMed] [Google Scholar]
- Brovelli A, Ding M, Ledberg A, Chen Y, Nakamura R, Bressler SL. Beta oscillations in a large-scale sensorimotor cortical network: directional influences revealed by Granger causality. Proc Natl Acad Sci U S A. 2004;101:9849–9854. doi: 10.1073/pnas.0308538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown P, Salenius S, Rothwell JC, Hari R. Cortical correlate of the Piper rhythm in humans. J Neurophysiol. 1998;80:2911–2917. doi: 10.1152/jn.1998.80.6.2911. [DOI] [PubMed] [Google Scholar]
- Buschman TJ, Miller EK. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science. 2007;315:1860–1862. doi: 10.1126/science.1138071. [DOI] [PubMed] [Google Scholar]
- Chen R, Yaseen Z, Cohen LG, Hallett M. Time course of corticospinal excitability in reaction time and self-paced movements. Ann Neurol. 1998;44:317–325. doi: 10.1002/ana.410440306. [DOI] [PubMed] [Google Scholar]
- Cheyne D, Bells S, Ferrari P, Gaetz W, Bostan AC. Self-paced movements induce high-frequency gamma oscillations in primary motor cortex. Neuroimage. 2008;42:332–342. doi: 10.1016/j.neuroimage.2008.04.178. [DOI] [PubMed] [Google Scholar]
- Conway BA, Halliday DM, Farmer SF, Shahani U, Maas P, Weir AI, Rosenberg JR. Synchronization between motor cortex and spinal motoneuronal pool during the performance of a maintained motor task in man. J Physiol. 1995;489:917–924. doi: 10.1113/jphysiol.1995.sp021104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courtemanche R, Pellerin JP, Lamarre Y. Local field potential oscillations in primate cerebellar cortex: modulation during active and passive expectancy. J Neurophysiol. 2002;88:771–782. doi: 10.1152/jn.2002.88.2.771. [DOI] [PubMed] [Google Scholar]
- Crone NE, Miglioretti DL, Gordon B, Sieracki JM, Wilson MT, Uematsu S, Lesser RP. Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. I. Alpha and beta event-related desynchronization. Brain. 1998;121:2271–2299. doi: 10.1093/brain/121.12.2271. [DOI] [PubMed] [Google Scholar]
- Doyle LM, Yarrow K, Brown P. Lateralization of event-related beta desynchronization in the EEG during pre-cued reaction time tasks. Clin Neurophysiol. 2005;116:1879–1888. doi: 10.1016/j.clinph.2005.03.017. [DOI] [PubMed] [Google Scholar]
- Fries P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn Sci. 2005;9:474–480. doi: 10.1016/j.tics.2005.08.011. [DOI] [PubMed] [Google Scholar]
- Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- Gilbertson T, Lalo E, Doyle L, Di Lazzaro V, Cioni B, Brown P. Existing motor state is favored at the expense of new movement during 13–35 Hz oscillatory synchrony in the human corticospinal system. J Neurosci. 2005;25:7771–7779. doi: 10.1523/JNEUROSCI.1762-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray CM, König P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338:334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
- Gregoriou GG, Gotts SJ, Zhou H, Desimone R. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science. 2009;324:1207–1210. doi: 10.1126/science.1171402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Tass PA, Salenius S, Hari R, Freund HJ, Schnitzler A. Cortico-muscular synchronization during isometric muscle contraction in humans as revealed by magnetoencephalography. J Physiol. 2000;527:623–631. doi: 10.1111/j.1469-7793.2000.00623.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Kujala J, Hamalainen M, Timmermann L, Schnitzler A, Salmelin R. Dynamic imaging of coherent sources: studying neural interactions in the human brain. Proc Natl Acad Sci U S A. 2001;98:694–699. doi: 10.1073/pnas.98.2.694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Timmermann L, Kujala J, Dirks M, Schmitz F, Salmelin R, Schnitzler A. The neural basis of intermittent motor control in humans. Proc Natl Acad Sci U S A. 2002;99:2299–2302. doi: 10.1073/pnas.032682099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halliday DM, Farmer SF. On the need for rectification of surface EMG. J Neurophysiol. 2010;103:3547; author reply 3548–3549. doi: 10.1152/jn.00222.2010. [DOI] [PubMed] [Google Scholar]
- Hoogenboom N, Schoffelen JM, Oostenveld R, Parkes LM, Fries P. Localizing human visual gamma-band activity in frequency, time and space. Neuroimage. 2006;29:764–773. doi: 10.1016/j.neuroimage.2005.08.043. [DOI] [PubMed] [Google Scholar]
- Jensen O, Goel P, Kopell N, Pohja M, Hari R, Ermentrout B. On the human sensorimotor-cortex beta rhythm: sources and modeling. Neuroimage. 2005;26:347–355. doi: 10.1016/j.neuroimage.2005.02.008. [DOI] [PubMed] [Google Scholar]
- Jerbi K, Lachaux JP, N′Diaye K, Pantazis D, Leahy RM, Garnero L, Baillet S. Coherent neural representation of hand speed in humans revealed by MEG imaging. Proc Natl Acad Sci U S A. 2007;104:7676–7681. doi: 10.1073/pnas.0609632104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin SH, Lin P, Hallett M. Linear and nonlinear information flow based on time-delayed mutual information method and its application to corticomuscular interaction. Clin Neurophysiol. 2010;121:392–401. doi: 10.1016/j.clinph.2009.09.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser J, Birbaumer N, Lutzenberger W. Event-related beta desynchronization indicates timing of response selection in a delayed-response paradigm in humans. Neurosci Lett. 2001;312:149–152. doi: 10.1016/s0304-3940(01)02217-0. [DOI] [PubMed] [Google Scholar]
- Kilner JM, Baker SN, Salenius S, Hari R, Lemon RN. Human cortical muscle coherence is directly related to specific motor parameters. J Neurosci. 2000;20:8838–8845. doi: 10.1523/JNEUROSCI.20-23-08838.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilner JM, Fisher RJ, Lemon RN. The coupling of oscillatory activity between muscles is strikingly reduced in a deafferented subject compared with normal controls. J Neurophysiol. 2004;92:790–796. doi: 10.1152/jn.01247.2003. [DOI] [PubMed] [Google Scholar]
- Knosche TR. Transformation of whole-head MEG recordings between different sensor positions. Biomed Tech (Berl) 2002;47:59–62. doi: 10.1515/bmte.2002.47.3.59. [DOI] [PubMed] [Google Scholar]
- Kristeva R, Patino L, Omlor W. Beta-range cortical motor spectral power and corticomuscular coherence as a mechanism for effective corticospinal interaction during steady-state motor output. Neuroimage. 2007;36:785–792. doi: 10.1016/j.neuroimage.2007.03.025. [DOI] [PubMed] [Google Scholar]
- Lange J, Oostenveld R, Fries P. Perception of the touch-induced visual double-flash illusion correlates with changes of rhythmic neuronal activity in human visual and somatosensory areas. Neuroimage. 2011;54:1395–1405. doi: 10.1016/j.neuroimage.2010.09.031. [DOI] [PubMed] [Google Scholar]
- Maris E, Oostenveld R. Nonparametric statistical testing of EEG- and MEG-data. J Neurosci Methods. 2007;164:177–190. doi: 10.1016/j.jneumeth.2007.03.024. [DOI] [PubMed] [Google Scholar]
- Maris E, Schoffelen JM, Fries P. Nonparametric statistical testing of coherence differences. J Neurosci Methods. 2007;163:161–175. doi: 10.1016/j.jneumeth.2007.02.011. [DOI] [PubMed] [Google Scholar]
- Mima T, Matsuoka T, Hallett M. Information flow from the sensorimotor cortex to muscle in humans. Clin Neurophysiol. 2001;112:122–126. doi: 10.1016/s1388-2457(00)00515-0. [DOI] [PubMed] [Google Scholar]
- Mitra PP, Pesaran B. Analysis of dynamic brain imaging data. Biophys J. 1999;76:691–708. doi: 10.1016/S0006-3495(99)77236-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behavior. J Neurophysiol. 1996;76:3949–3967. doi: 10.1152/jn.1996.76.6.3949. [DOI] [PubMed] [Google Scholar]
- Myers LJ, Lowery M, O'Malley M, Vaughan CL, Heneghan C, St Clair Gibson A, Harley YX, Sreenivasan R. Rectification and non-linear pre-processing of EMG signals for cortico-muscular analysis. J Neurosci Methods. 2003;124:157–165. doi: 10.1016/s0165-0270(03)00004-9. [DOI] [PubMed] [Google Scholar]
- Neto OP, Christou EA. Rectification of the EMG signal impairs the identification of oscillatory input to the muscle. J Neurophysiol. 2010;103:1093–1103. doi: 10.1152/jn.00792.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuper C, Pfurtscheller G. Event-related dynamics of cortical rhythms: frequency-specific features and functional correlates. Int J Psychophysiol. 2001;43:41–58. doi: 10.1016/s0167-8760(01)00178-7. [DOI] [PubMed] [Google Scholar]
- Nichols TE, Holmes AP. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum Brain Mapp. 2002;15:1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nolte G. The magnetic lead field theorem in the quasi-static approximation and its use for magnetoencephalography forward calculation in realistic volume conductors. Phys Med Biol. 2003;48:3637–3652. doi: 10.1088/0031-9155/48/22/002. [DOI] [PubMed] [Google Scholar]
- Omlor W, Patino L, Hepp-Reymond MC, Kristeva R. Gamma-range corticomuscular coherence during dynamic force output. Neuroimage. 2007;34:1191–1198. doi: 10.1016/j.neuroimage.2006.10.018. [DOI] [PubMed] [Google Scholar]
- Oostenveld R, Fries P, Maris E, Schoffelen JM. FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput Intell Neurosci. 2011;2011:156869. doi: 10.1155/2011/156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patino L, Omlor W, Chakarov V, Hepp-Reymond MC, Kristeva R. Absence of gamma-range corticomuscular coherence during dynamic force in a deafferented patient. J Neurophysiol. 2008;99:1906–1916. doi: 10.1152/jn.00390.2007. [DOI] [PubMed] [Google Scholar]
- Pesaran B, Nelson MJ, Andersen RA. Free choice activates a decision circuit between frontal and parietal cortex. Nature. 2008;453:406–409. doi: 10.1038/nature06849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfurtscheller G, Lopes da Silva FH. Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol. 1999;110:1842–1857. doi: 10.1016/s1388-2457(99)00141-8. [DOI] [PubMed] [Google Scholar]
- Pohja M, Salenius S, Hari R. Reproducibility of cortex-muscle coherence. Neuroimage. 2005;26:764–770. doi: 10.1016/j.neuroimage.2005.02.031. [DOI] [PubMed] [Google Scholar]
- Riddle CN, Baker SN. Manipulation of peripheral neural feedback loops alters human corticomuscular coherence. J Physiol. 2005;566:625–639. doi: 10.1113/jphysiol.2005.089607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roelfsema PR, Lamme VA, Spekreijse H. Object-based attention in the primary visual cortex of the macaque monkey. Nature. 1998;395:376–381. doi: 10.1038/26475. [DOI] [PubMed] [Google Scholar]
- Saalmann YB, Pigarev IN, Vidyasagar TR. Neural mechanisms of visual attention: how top-down feedback highlights relevant locations. Science. 2007;316:1612–1615. doi: 10.1126/science.1139140. [DOI] [PubMed] [Google Scholar]
- Schoffelen JM, Gross J. Source connectivity analysis with MEG and EEG. Hum Brain Mapp. 2009;30:1857–1865. doi: 10.1002/hbm.20745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoffelen JM, Oostenveld R, Fries P. Neuronal coherence as a mechanism of effective corticospinal interaction. Science. 2005;308:111–113. doi: 10.1126/science.1107027. [DOI] [PubMed] [Google Scholar]
- Tallon-Baudry C, Bertrand O, Delpuech C, Permier J. Oscillatory gamma-band (30–70 Hz) activity induced by a visual search task in humans. J Neurosci. 1997;17:722–734. doi: 10.1523/JNEUROSCI.17-02-00722.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Elswijk G, Kleine BU, Overeem S, Stegeman DF. Expectancy induces dynamic modulation of corticospinal excitability. J Cogn Neurosci. 2007;19:121–131. doi: 10.1162/jocn.2007.19.1.121. [DOI] [PubMed] [Google Scholar]
- van Wijk BC, Daffertshofer A, Roach N, Praamstra P. A role of beta oscillatory synchrony in biasing response competition? Cereb Cortex. 2009;19:1294–1302. doi: 10.1093/cercor/bhn174. [DOI] [PubMed] [Google Scholar]
- Witham CL, Wang M, Baker SN. Corticomuscular coherence between motor cortex, somatosensory areas and forearm muscles in the monkey. Front Syst Neurosci. 2010;4 doi: 10.3389/fnsys.2010.00038. pii:38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Womelsdorf T, Fries P, Mitra PP, Desimone R. Gamma-band synchronization in visual cortex predicts speed of change detection. Nature. 2006;439:733–736. doi: 10.1038/nature04258. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- Yao B, Salenius S, Yue GH, Brown RW, Liu JZ. Effects of surface EMG rectification on power and coherence analyses: an EEG and MEG study. J Neurosci Methods. 2007;159:215–223. doi: 10.1016/j.jneumeth.2006.07.008. [DOI] [PubMed] [Google Scholar]