Direct Corticospinal Control of Force Derivative

Abstract

During simultaneous generation of static and dynamic forces, motor cortical signals only predict the dynamic components, suggesting a key role in the coding of force changes. However, such a role is obscured by uncertainties regarding the representation of dynamic force signals in corticospinal outputs. We used transcranial magnetic stimulation (TMS) of the motor cortex in humans during a task that dissociated the direction of instantaneous net force and that of force derivative. The direction of TMS-evoked force outputs was closely associated with that of the force derivative, and had no relationship with that of the net force generated simultaneously, even though the magnitude of the instantaneous net force largely exceeded that of the force derivative. This observation supports the hypothesis that during dynamic force generation, the motor cortex and the corticospinal system assume a pivotal role in coding the direction of force changes, through selective recruitment of spinal motoneurons.

Introduction

Anatomical, physiological, and clinical observations accrued for more than one century have established the important role of the motor cortex in force production. Yet, the exact role of the motor cortex in force and movement generation remains incompletely clarified and is subject to contrasting points of view (Georgopoulos and Ashe, 2000; Moran and Schwartz, 2000; Scott, 2000; Todorov, 2000). There are numerous sets of experimental data supporting both a role in high-level motor control (kinematic, motor memory, serial order …) and a lower-level, more direct, control of muscles (force) (Ashe, 1997). The role of the motor cortex in higher-level control is questioned because most observations are based on recordings of single-cell activity in relation to behavior, which do not establish a causal relationship between the measured variable and the motor effect (Cheney et al., 1988; Fetz et al., 1989; Wise, 1993). One approach to infer a causal role is to observe the behavioral effects induced by electrical stimulation of the motor cortex (Churchland and Shenoy, 2007). We recently reported that transcranial magnetic stimulation of the motor cortex reproduces the voluntary motor outputs, allowing the study of motor cortical outputs to transcranial magnetic stimulation (TMS) in relation to dynamic force production in human subjects (Cros et al., 2007).

Force, a physical time-dependent magnitude, may be considered static (time-invariant) or dynamic (time-varying). The neural activity in the motor cortex correlates with dynamic forces (Humphrey et al., 1970; Smith et al., 1975; Georgopoulos et al., 1992; Boline and Ashe, 2005), but also with static forces and many kinematic variables (Ashe, 1997). In dynamic force paradigms, motor cortical signals predict only the direction of force change or its derivative (Georgopoulos et al., 1992), having no bearing on the direction of the static force generated simultaneously. Thus, during dynamic force generation, the motor cortex assumes a central role in specifying force changes, indicating a dependence on the behavioral context of force production. It remains unanswered how those signals are expressed in the cortical outputs to the spinal cord. In this study, we examined the stimulation-evoked force pulse (“twitch,” T) with single-pulse TMS of the motor cortex in a paradigm that achieves an orthogonal dissociation between the instantaneous net force and its first derivative, to establish the relationships between the force pulses evoked by TMS and the voluntary forces.

Materials and Methods

Subjects and experimental setup.

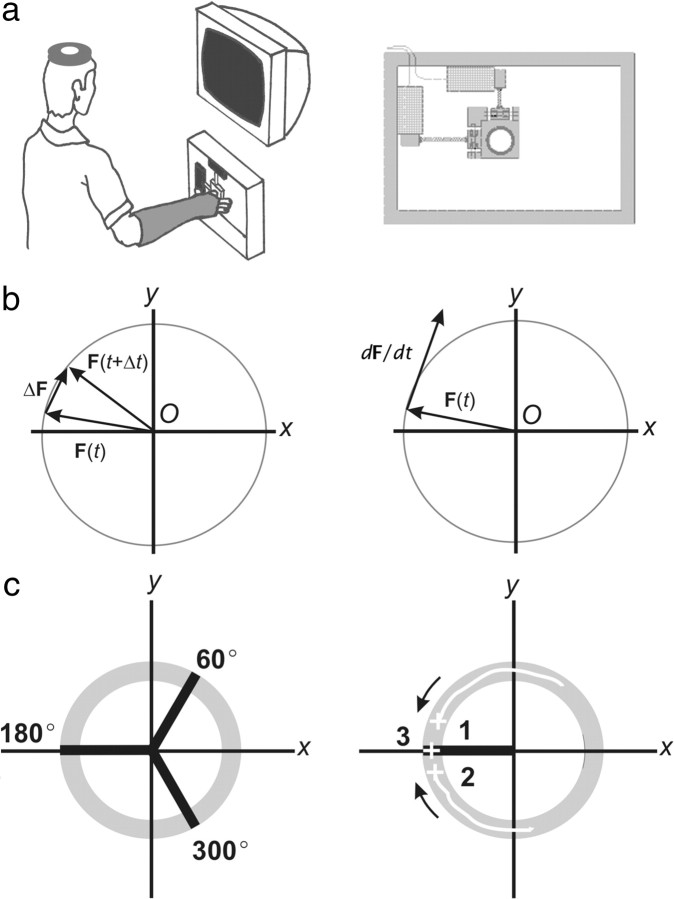
Five right-handed healthy adults participated in the study (ages 30–47). The Institutional Review Board of the Massachusetts General Hospital approved the study. Each subject gave informed consent in writing. The experimental setup consisted of a rigid ring attached to two orthogonally arranged load cells (Minibeam, Interface), allowing us to record isometric force exerted at the second metacarpophalangeal joint of the right hand. We built a rigid cast customized for each subject around the hand and forearm to obtain mechanical isolation from forces acting at neighboring joints. A Magstim Model 200 single pulse stimulator was used in all experiments. A PC computer was used for data acquisition, display, and triggering of the magnetic stimulator. The force signal was digitized and acquired at a frequency of 500 Hz and instantly displayed on a computer monitor at eye level placed 1 m in front of the subject (Fig. 1a). The tip of the net force exerted was represented as a yellow position cursor. The spatial references for task performance and a two-dimensional Cartesian coordinate reference system were represented over a black background. Force input was calibrated so that rest corresponded to the origin of the coordinates. A 90-mm-diameter circular coil was centered over the vertex, at the optimal position to stimulate the hand area. It was kept horizontal and the side was chosen to induce a current flow from back to front over the left hemisphere. The minimum intensity at which a muscle twitch >0.2 N was evoked at rest in 3/6 trials was considered the resting threshold, which was the intensity used in all experiments. Each stimulus is a square pulse of maximum duration of 1 ms, which induces a charge density of similar temporal profile in the target tissue.

Figure 1.

a, Experimental setup and behavioral paradigms. Left, Experimental setup; right, force-recording device. b, Force composition of the paradigm at any time interval (left) and instantaneously (right). c, Left, Experimental sets instructed (60°, 180°, and 300°); right, in response set at 180°, the position of the cursor is illustrated within the annulus: 1 and 2 indicate dynamic trials, CCW and CW, respectively, and 3 indicates static trials. Stimuli were applied at the direction of the set (180° in this case).

Behavioral task.

The dynamic task was set to achieve a maximal dissociation between the directions of the net force exerted and that of the force change. Let the force F(t) be a vector function of the scalar variable t (time). If the vector F(t) is drawn from a fixed origin O, and the scalar t is allowed to vary, the tip of F(t) will describe a curve in space. Let ΔF(t) be a time-dependent vector joining the tips of F(t) at two different times, t and t + Δt. F(t + Δt) is the resultant of the vectorial summation of F(t) and ΔF(t). As Δt approaches zero (Δt→0), the line of action of ΔF(t) becomes increasingly tangent to the curve, becoming its first derivative, dF/dt. The resolution of the vector analysis was set at 1 ms, which corresponds to the duration of the TMS pulse. At that resolution, ΔF(t) and dF/dt are virtually identical and were not further distinguished. Similarly, the net force F(t + Δt) becomes virtually identical to the instantaneous F(t) (Fig. 1b).

The task consisted of a cursor displacement within a displayed ring-shaped figure (annulus) centered at the origin of coordinates. The subjects had to move the cursor within the inner and the outer radii of the annulus at a self-determined, comfortable rate (dynamic trials), or to hold it still (static trials). The annulus was centered at the resting position, and the inner and outer radii corresponded to force magnitudes of 11.5% and 18.5%, respectively, of the maximum voluntary contraction (MVC) exerted in a specific center-out direction. The intersection between the annulus and its radius was considered an experimental set. We acquired data in three sets that were evenly distributed in force space (60°, 180°, and 300°). In each set, the data acquisition program randomly instructed the subjects to displace the cursor within the annulus either clockwise (CW) or counterclockwise (CCW), or to hold it static (Fig. 1c). In dynamic trials, whenever the cursor position fell within the annulus in a 40 ms epoch before reaching the set location, a magnetic stimulus was delivered. In each set, we obtained 30 dynamic (15 CW and 15 CCW) and 20 static trials.

Differentiation and selection criteria.

We smoothed force data using a 7 Hz low-pass filter (Mottet et al., 1994) and approximated their first and second derivatives numerically with seven-point Lagrange polynomials (Beyer, 1982). We defined T onset time as the first data point following TMS (t₀) ≥ the mean magnitude of the second derivative of force + 2 SD in the epoch t₀ ±10 ms. We used d²F/dt data to calculate the twitch onset time because we allowed small variations of dF/dt (coefficient of variation, CV, ≤15%), which could hypothetically affect the correct determination of the twitch onset time. Given the central and peripheral transmission delay, in the dynamic trials the onset of T lagged behind the time of the application of the TMS pulse. The time of maximum twitch tension was defined as the first point of smallest dF/dt magnitude following twitch onset. F(t) and dF/dt were computed at the point of T onset. We defined valid dynamic trials according to two conditions: (1) The rate of force change (dF/dt) during the 50 ms epoch preceding the twitch ought to be approximately constant (CV ≤ 15%). With this condition, we forced the motor system to accomplish the simplest task that dissociated instantaneous force and its first derivative, minimizing higher-order force changes. (2) The magnitude of dF/dt induced by TMS represented an increase ≥50% over the mean magnitude dF/dt in the 50 ms preceding epoch. This condition was set to avoid detecting fluctuations in the force output as stimulation-evoked twitches. Compliance with these conditions was determined blinded to the direction of T.

Geometrical and statistical analysis.

For graphical display, in each subject and set we computed mean vectors of CCW, CW, and static trials separately. The variability in the points of origin of vectors was expressed with standard ellipses, while their directional variability was expressed with confidence intervals computed nonparametrically (Bastchelet, 1981; Efron and Tibshirani, 1993). The analyzed parameters were the direction of F(t), dF/dt, and T, and the magnitude of F(t) and dF/dt. We compared the directions of T and dF/dt vectors computing the angular difference in each vector pair (corresponding to a single trial) and normalizing the result for the trajectory of dynamic force (i.e., all CW) and direction of the set (i.e., as if all had been collected within the same set). We used the Watson test to examine the pooled directions of all dynamic trials for differences from the uniform distribution and clustering around 0° (Bastchelet, 1981). We used t tests to compare mean vector magnitudes. Descriptive statistics represent mean ± SD. Significance was set at p < 0.05.

Results

We obtained 292 valid dynamic trials and 281 static trials. Examples of rejected trials are shown as supplemental data. The mean magnitude of F(t) did not differ significantly between static and dynamic trials (|F(t)| = 3.81 ± 0.74 N in the static condition; |F(t)| = 3.86 ± 0.79 N in the dynamic condition; p = 0.462). In the dynamic condition, the mean magnitude of dF/dt was significantly smaller (approximately two orders of magnitude) than that of F(t), in all subjects (Table 1). In any given set, the point of origin of mean T vectors was roughly similar in static and dynamic conditions, indicating that the magnitude and direction of instantaneous force, F(t), at the time of T onset were also similar under both conditions. In the static condition, T pointed in the same direction as the voluntarily exerted F(t) (Fig. 2), indicating that the excitability changes associated with static force generation were reflected in the output to stimulation (Cros et al., 2007). However, in the same experimental set in the dynamic condition, T was codirectional with dF/dt only, losing the directional association with the F(t) vector that was present in static trials (Figs. 2, 3). In all experimental sets, changing the trajectory of dynamic force from CW to CCW or vice versa resulted in a complete reversal in the direction of T (Fig. 2a). An occasional deviation from the close directional association between T and dF/dt was observed in some direction sets in some subjects, which may represent instances in which TMS fails to achieve a uniform stimulation of the active neuronal ensemble. The population of angular distances between the directions of dF/dt and T was both significantly different from the uniform distribution and clustered around 0° (p < 0.001) (Fig. 2b), indicating directional similarity.

Table 1.

Average parameters of F(t), dF/dt, and T during dynamic trials

Subject	Trials (n)	Force magnitudes at stimulation instanta,b		dF/dt magnitudec [(N/s)/CV]	Angular velocityc (°/s)	T onset latency/peak (ms)	TMS-induced increase in dF/dtc (%)
		F(t)	dF/dt
1	47	14.9	0.03***	29.37/0.09	425 ± 82	25.25/28.18	280
2	54	13.2	0.05***	42.26/0.09	606 ± 42	21.26/45.60	230
3	52	14.8	0.03***	30.62/0.09	506 ± 144	25.0/34.56	297
4	74	14.9	0.04***	34.87/0.07	541 ± 124	26.27/47.03	305
5	65	14.8	0.04***	39.02/0.08	553 ± 113	22.18/94.66	397

n, Number of analyzed trials.

***p < 0.0001.

^aNormalized for 0.15 × MVC in the direction of the set.

^bMagnitude of dF/dt vector computed at 1 ms resolution (duration of TMS pulse).

^cComputed for the 50 ms epoch before TMS-induced twitch (T).

Figure 2.

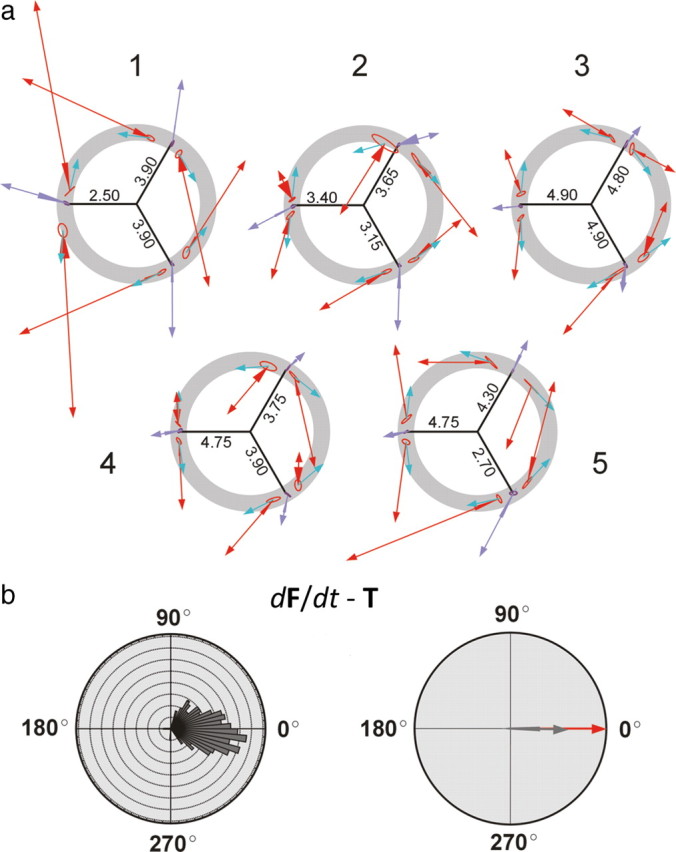
a, Polar plots summarizing the force data per subject (labeled 1–5). The annulus is plotted in the background. The radii indicate the force magnitude (in newtons) corresponding to 15% of the MVC in that direction and calibrate vectors within that set. Mean T vectors in dynamic trials are represented in red. Their origin is slightly shifted because of transmission delay following cortical stimulation. Mean T vectors in static conditions are represented in purple. The ellipse at the base of each mean vector represents the variability of the points of origin of the vectors. The triangle at the base of each T vector represents the 90% confidence interval for the mean vector direction. Blue vectors indicate the mean dF/dt vectors. For display, they are represented of 2 N arbitrary magnitude since their actual magnitude would be too small to visualize. To simplify the graphic, the mean F(t) vector has been omitted from display. b, Left, Frequency distribution of pooled directions representing the angular distance between individual dF/dt and T pairs in the dynamic paradigms (bin width 5 degrees). Right, Plot of the mean angular distance of the same data (dark gray) with 90% confidence interval of that population. Note that the direction of 0° (red vector) is included within the confidence interval.

Figure 3.

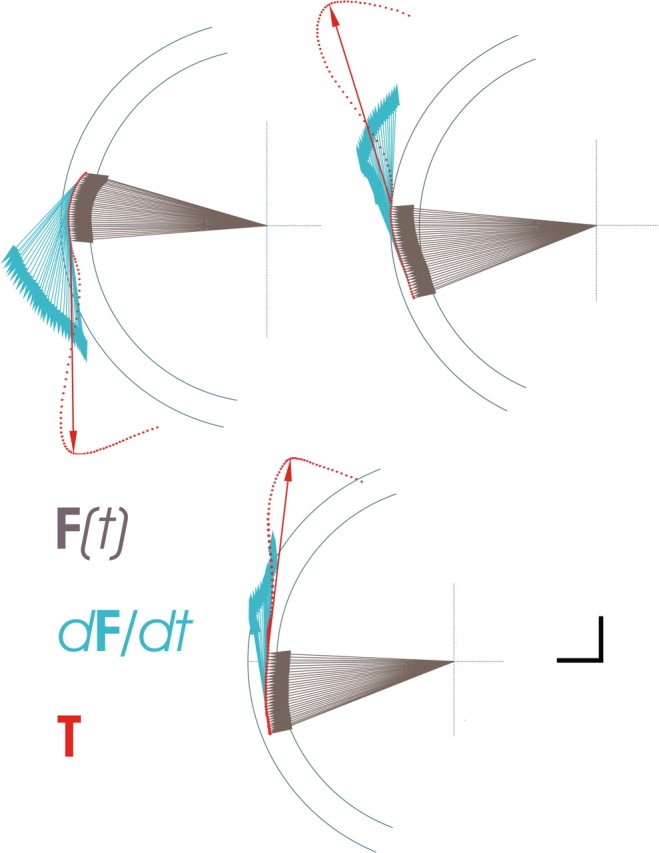
Detailed force composition in three individual trials over time (every 2 ms), showing data points and T vector, and illustrating F(t) and dF/dt in the epoch immediately before T onset. Calibration: vertical and horizontal bars = 1 N, applies to magnitude of T and F(t). Magnitude of dF/dt is arbitrary [enhanced for illustration purposes; actual magnitude is considerably smaller (see Table 1)].

Discussion

Although the number of subjects was small, we studied each of them in conditions that support the generalization of our results: (1) the experimental paradigm was reproduced for opposite directions within each set, and (2) each set corresponded to three completely different positions in force space, indicating no relationship of TMS outputs to activation of specific muscles or muscle patterns, but rather a fundamental dependence on the underlying force composition of the paradigm. We rejected a high number of dynamic trials, blindly to the directions of vectors, based on excessive fluctuations of voluntary force and on insufficient size of the evoked force vectors. We deliberately rejected small T vectors, to completely discard force increases not evoked by the stimulus. We believe the possibility of mislabeling background force changes as TMS-evoked is highly unlikely based on the following additional reasons: (1) The mean latency of the evoked twitch onset was ∼20 ms for all subjects, well below the expected minimum reaction time of a voluntary response or a startle response to the click of the stimulus. Additionally, the low variability of the latency is inconsistent with the known high variability of human reaction times. (2) The twitch onset was defined by a rapid increase in dF/dt, indicating a synchronous recruitment of many motor units. (3) In pilot experiments with sham stimulation (stimulation coil held at 2 cm from the scalp), we failed to identify such increases. (4) Single cortical magnetic stimuli have been shown to interrupt and delay the execution of a voluntary movement (Day et al., 1989a), indicating that the evoked twitch was uncontaminated from continuing voluntary force generation.

Different output channels or differential excitability for instantaneous net force versus force derivative?

In our dynamic paradigm, at any point in time the magnitude of instantaneous force remains constant: the only ongoing change is in force direction. New motoneurons are constantly recruited, but only those to be subsequently recruited are selectively excited by TMS. Those already recruited remain inaccessible to the cortical stimulus. This dissociated output suggests a differential neural control of net force and force changes, which may be coded and transmitted along different channels or through a differential modulation of excitability or timing in the same channel, or both.

TMS is well suited to detect changes in corticospinal excitability with different motor behaviors (Hess et al., 1987; Datta et al., 1989; Flament et al., 1993; Nielsen et al., 1993), and its output may reproduce voluntary activation (Cros et al., 2007). The increased excitability to TMS during voluntary contractions depends on cortical and spinal mechanisms (Mazzocchio et al., 1994; Ugawa et al., 1995; Di Lazzaro et al., 1998). It represents the contribution of active neurons (Lemon et al., 1995) but also subthreshold excitatory synaptic activity (Baldissera et al., 2002; Cros et al., 2007). At the cortex, the induced electrical field excites corticospinal output neurons both directly and indirectly. Indirect excitation involves activation of cortical networks that have either excitatory or inhibitory effects on corticospinal neurons. These may fire repeatedly in response to a single TMS pulse. The indirect excitation of cortical output neurons is favored at low stimulation intensities (Day et al., 1989b; Burke et al., 1993; Berardelli et al., 1994; Fujiki et al., 1996; Rothwell, 1997), which may hypothetically enhance the ability of this technique to reproduce physiological processing (Cros et al., 2007). Increased cortical excitability during voluntary static contractions is evidenced as an increased size of descending corticospinal volleys compared to rest (Di Lazzaro et al., 1998). Furthermore, during dynamic contractions the corticospinal excitability to TMS (as measured by the amplitude of the evoked twitch) increases markedly compared to static contractions, and does so linearly with the rate of force change (Cros et al., 2007). In a delayed cued task, the activity of spinal interneurons is modulated preceding movement according to parameters of the upcoming movement (Prut and Fetz, 1999), a mechanism that may contribute to changes in the excitability of motoneuronal populations to TMS.

A possible explanation for our findings would be that populations of cells in the motor cortex control force change as a sequential specification of net force vectors over time, such that F(t) generated at a later time could be specified in advance relative to the actual F(t). In that case, a separate control of dF/dt need not be postulated. However, at the rates of force change generated by the subjects in our dynamic experiments, producing force vectors orthogonal to those actually generated would take 150–200 ms, much longer than the 5–10 ms it takes cortical neurons to physiologically influence the activity of spinal motoneurons, as measured with spike-triggered averaging methods in nonhuman primates (Cheney and Fetz, 1985). Alternatively, it could be postulated that F(t) and dF/dt are controlled by the same cortical cells, but signals controlling dF/dt overrule those of F(t) in the TMS response. For that to occur, some physiological difference either in the neuronal activation or in the transmission of those signals must exist, making the excitability of elements coding for dF/dt to TMS much higher than that of elements coding for F(t). Such a difference could be a physiological delay in the transmission of F(t) compared to dF/dt signals, but the target spinal motoneuronal populations for either signal differ markedly, which is inconsistent with the same elements controlling simultaneously both force components. A more plausible explanation is that during static contractions the role of the motor cortex in force generation is accessory, while during dynamic contractions it assumes a central role in force production, most importantly in the control of force changes. Signals controlling the net force, originating from other motor system structures or from a different motor cortical neuronal population than that controlling force derivative, would then be transmitted in parallel to the most relevant motor cortical signals, either nonpreferentially along the corticospinal pathways or through other spinal descending pathways.

Furthermore, our findings can be viewed under the magnitude–direction of force coding framework. In relation to force, many studies of motor cortical activity indicate that directional signals are strong predictors of activity, whereas magnitude signals are present but to a more limited extent (for review, see Ashe, 1997). Whether both signals are separately coded is still uncertain, but recordings during dynamic force generation indicate that they are to some degree embedded in the activity of cortical neurons (Boline and Ashe, 2005). However, our data would indicate that magnitude of net force is not a relevant signal transmitted along the corticospinal system, since in our simple paradigm the magnitude of net force is much larger that the magnitude of force derivative, suggesting that signals for force magnitude and force trajectory are coded and transmitted along different channels.

Selective coding of force trajectory vectors

Our results are complementary to those describing the relation between force derivative and population motor cortical activity with vectorial methods (Georgopoulos et al., 1992; Schwartz, 1994; Georgopoulos, 1995). During a dynamic force paradigm, single neurons in the motor cortex are tuned to the direction of force derivative even when a constant force bias is exerted in a different direction. The population activity of the cortical ensemble, computed as the population vector, points accurately in the direction of the dynamic force pulse generated, but not in that of the net force (Georgopoulos et al., 1992). Such context dependency of both the cortical activity (Georgopoulos et al., 1992; Schwartz, 2007) and the outputs to stimulation (our experiments) suggests that the relevant signals transmitted in the population activity along the corticospinal system relate to geometrical aspects of the force trajectory. Because of the nonfocal nature of the stimulus in our experiments, neuronal recruitment is achieved by diffuse stimulation of the cortical networks (Rathelot and Strick, 2006), and modulated neurons likely contribute most to the output. The functional linkage between the stimulation and the evoked output is evident. Furthermore, functionally relevant motor synergies may be specified at a cortical level, as shown for muscle activity (Holdefer and Miller, 2002; Morrow et al., 2007), accounting for a selective recruitment of motoneuronal subsets implementing the first derivative of force. Indeed, selectivity in the recruitment of motor units is linked to the direction of isometric force, even within the same motoneuronal pool (Flanders and Soechting, 1990; Theeuwen et al., 1994; Herrmann and Flanders, 1998). Along this framework, we postulate that during our dynamic paradigm subsets of motor units receive inputs from the motor cortex coding for force change, while other motor unit populations with different directional tuning properties and different premotoneuronal inputs generate the remaining forces.