Spike-Train Communities: Finding Groups of Similar Spike Trains

Abstract

Identifying similar spike-train patterns is a key element in understanding neural coding and computation. For single neurons, similar spike patterns evoked by stimuli are evidence of common coding. Across multiple neurons, similar spike trains indicate potential cell assemblies. As recording technology advances, so does the urgent need for grouping methods to make sense of large-scale datasets of spike trains. Existing methods require specifying the number of groups in advance, limiting their use in exploratory analyses. I derive a new method from network theory that solves this key difficulty: it self-determines the maximum number of groups in any set of spike trains, and groups them to maximize intragroup similarity. This method brings us revealing new insights into the encoding of aversive stimuli by dopaminergic neurons, and the organization of spontaneous neural activity in cortex. I show that the characteristic pause response of a rat's dopaminergic neuron depends on the state of the superior colliculus: when it is inactive, aversive stimuli invoke a single pattern of dopaminergic neuron spiking; when active, multiple patterns occur, yet the spike timing in each is reliable. In spontaneous multineuron activity from the cortex of anesthetized cat, I show the existence of neural ensembles that evolve in membership and characteristic timescale of organization during global slow oscillations. I validate these findings by showing that the method both is remarkably reliable at detecting known groups and can detect large-scale organization of dynamics in a model of the striatum.

Introduction

Identifying similarities between spike trains is a key element in understanding neural coding and computation. With single neurons, similar spike patterns evoked by stimuli are evidence of common coding or neuronal properties. The reliability of spike timing across trials in vitro is dependent on the oscillating frequency of injected current (Fellous et al., 2001; Schreiber et al., 2004; Galán et al., 2008), and currents comprising multiple frequencies (Fellous et al., 2004) or white noise (Mainen and Sejnowski, 1995) can elicit multiple reliable patterns of spike timing. Demonstrations of reliable, precise spike timing of single neurons in vivo include the responses of area MT neurons to precisely repeated dot-motion patterns (Bair and Koch, 1996), of fly H1 cells to variable velocity stimuli (de Ruyter van Steveninck et al., 1997), and of auditory cortex neurons to transient tones (DeWeese et al., 2003). In each case, finding common spike-train patterns reveals the encoding of a repeating component of the stimulus.

Simultaneously recorded neurons with similar spike trains are potential cell assemblies, sharing a common coding or computation (Harris et al., 2003; Fujisawa et al., 2008). Ensembles of hippocampal neurons reactivate in sequence during both sleeping (Wilson and McNaughton, 1994) and waking (Foster and Wilson, 2006), encoding sequences of just-experienced places; ensemble reactivation has also been reported in striatum (Pennartz et al., 2004) and prefrontal cortex (Peyrache et al., 2009). Spontaneous formation of switching cell assemblies has been reported in both hippocampal CA3 (Sasaki et al., 2007) and striatal (Carrillo-Reid et al., 2008) slices, suggesting that ensemble encoding is an inherent property of many neural circuits. In each case, grouping common activity patterns has been key to detecting the existence of putative assemblies.

Existing grouping methods typically require specification of the number of groups at the outset (Fellous et al., 2004; Slonim et al., 2005), limiting their usefulness for exploring datasets. Moreover, most methods require specification of some dimensionless parameter that is found by trial and error or intuition. I present a new method, derived from the problem of “community detection” in arbitrary networks, that solves these key difficulties: it self-determines the number of groups in any set of spike trains and groups them accordingly; and the only free parameter is the timescale of spike-train comparisons.

Freed from these constraints, we can detect hidden structure in datasets that would be difficult to find any other way. I analyze single-unit data from substantia nigra pars compacta (Coizet et al., 2006), recorded during repeated pain stimuli with and without bicuculline in the superior colliculus, and find previously undetected spike patterns that suggest that superior colliculus input causes a variable resetting of these neurons' pacemaker currents. I analyze multineuron recordings from the cat cortex and show that spontaneous activity, globally alternating between quiet “down” states and active “up” states, comprises neural ensembles that evolve over time in both membership and characteristic timescale of organization. Finally, I use model spike data to show that the algorithm reliably detects known groups, scales to large datasets, and can detect subtle changes in dynamical states.

Materials and Methods

At its most general, the algorithm for detecting patterns among spike trains follows a two-step procedure. First, some measure of comparison between each pair of spike trains is computed. For all N spike trains, we compare all N(N − 1)/2 unique pairs, resulting in a comparison matrix C with entry C_ij = C_ji being the comparison measure between spike trains i and j. The comparison can be made using any of a wide variety of correlation, distance, or similarity metrics, of which there is a vast choice. Moreover, there are a number of well known metrics specifically designed for pairwise comparisons of spike trains (Victor and Purpura, 1996; van Rossum, 2001; Fellous et al., 2004). Here I focus on similarity metrics, as my algorithm requires comparisons in this form.

Second, some method acts on the comparison matrix to identify spike trains that form groups based on their shared properties: for example, in the simplest case, if there is a strong similarity within each of the spike-train pairs (A, B), (A, C), and (B, C), then the triplet {A, B, C} forms a group. Applied to the entire dataset, the algorithm thus seeks to group the data into sets of spike trains that are more related to each other than with the remaining trains. With this in mind, I outline the details of my specific algorithm. A MATLAB toolbox for running the algorithm and control analyses on spike-train time series is available from me and from http://www.abrg.group.shef.ac.uk/code/.

Specifying the clustering algorithm

Timescales and the choice of comparison measures.

Comparisons between spike trains can look for events at many timescales, from common recurring single spikes on the scale of a few milliseconds to common slow oscillations on the scale of seconds. Spike trains are thus preprocessed into representations suitable for detecting events at different timescales. This preprocessing falls broadly into either “binned” forms that discretize time or “binless” forms that focus on the individual spike. The disadvantages of using binned representations of spike trains for analyses are well documented (see, e.g., Kruskal et al., 2007; Grün, 2009; Paiva et al., 2010); indeed, I demonstrate in the Results (see Fig. 4) that basing our method on binless representations is always superior. Nonetheless, as the computation time for the algorithm is often an order of magnitude or more faster using binned representations, I often found the binned representations invaluable for preliminary analyses, and for guiding the choice of analysis timescales.

Figure 4.

Robust clustering on synthetic spike-pattern data over increases in noise and number of groups. A, Mutual information scores for the best clustering based on the binned representation of the spike trains. Each point is an average over the 30 datasets for that noise level, with bars giving ±1 SD. For each dataset the bin size giving the greatest mutual information score was retained. Dashed lines here and in B indicate the upper bound on the best-case mutual information scores for random assignment of the spike trains to the correct number and size of groups (the dashed lines are the mean mutual information over 1000 realizations, plus 1 SD). The clustering was robust to increasing noise and across increasing number of groups for each noise level, falling to random chance performance only at noise level 7 (X = 20 extra spikes, J = 30 ms of jitter). B, Clustering using the binless representations of the spike trains performed similarly well, retaining near 100% accuracy up to noise level 4 (X = 4, J = 5 ms) regardless of the number of groups. C, Plotting the difference in mean mutual information (MI) for the binless and binned spike-train representations shows clearly that the binless representation is substantially more reliable for intermediate levels of noise.

The binned preprocessing focused on the pattern of activity. For each spike train, I divided time into discrete bins of width δt seconds, and in each bin recorded a 1 for the presence of any spikes, and a 0 for the absence. The resulting binary vector thus simply recorded the pattern of activity and inactivity for the neuron. For each pair of binary vectors, I computed the normalized Hamming distance h, the proportion of bins that differed between the two vectors. I took ĥ = 1 − h as my similarity measure: hence ĥ approaches 1 as the vectors become equal. Therefore, I used C_ij = C_ji = ĥ to construct the comparison matrix from binned representations of the spike trains.

The binless preprocessing focused on the reliability of spike timing. I convolved each spike with a Gaussian function of width σ seconds (Fellous et al., 2004), resulting in a continuous vector representation of the spike train (down to the spike-train quantization step, which was 1 ms throughout). I used the cosine of the angle between pairs of vectors as a measure of similarity (Schreiber et al., 2003; Fellous et al., 2004):

where g⃗_i and g⃗_j are the vectors of the ith and jth spike train convolved with a Gaussian, the numerator is a dot product, and the denominator is the product of the vector norms. Again s_ij is a similarity measure: s_ij goes to 1 as the vectors become equal, and goes to 0 as they become orthogonal. Therefore, I used C_ij = C_ji = s_ij to construct the comparison matrix from binless representations of the spike trains.

When using both binned and binless forms, I first selected a set of discrete bins {δt} based on the interspike interval statistics of the entire spike train dataset. I then followed Kruskal et al. (2007) and used equivalent Gaussian widths of σ_i = δt_i/$\sqrt{12}$, for the ith discrete bin size. Regardless of how each C was constructed, all diagonal entries were set C_ii = 0, as strictly applying the similarity measures so that C_ii = 1 prevents successful clustering as each spike train is always more similar to itself than any other, so that the clustering tends to place each spike train in its own group.

Other choices of similarity metrics could be applied in principle, though I have not the space to examine them here. For binned preprocessing, the Hamming similarity is the most natural choice for binary vectors, and emphasizes spike-train pairs that are both coactive and cosilent; applying other similarity metrics to the binary representations would give similar results. If we wished to emphasize not just the pattern but also the correlation between the fluctuations in the magnitude of activity, then the comparison matrix could be constructed by counting spikes in each bin and applying a continuous metric, such as a rectified correlation coefficient or the cosine similarity (Eq. 1). For the Gaussian-window preprocessing, any other form of general similarity metric could be applied, and we would expect the results to be qualitatively similar. It would be also interesting to examine the use of other spike-train-specific comparison metrics (Victor and Purpura, 1996; van Rossum, 2001), after suitable conversion into a similarity measure.

Choice of grouping method: network modularity.

Standard data clustering techniques, such as K-means and its various extensions, can be used to find clusters within the comparison matrix C, but these are limited because the user must define the number of clusters in advance (Fellous et al., 2004; Fortunato, 2010); they also require some post hoc measure of clustering success to decide the number of clusters to retain, and for which timescale of analysis. Similarly, standard spectral-clustering or graph partitioning algorithms could be applied to a network created from C, but require prior specification of the size of the resulting partitioned groups—see Newman (2006a) and Fortunato (2010) for discussion. These techniques are thus difficult to use for any kind of exploratory data analysis.

My first step was to interpret the comparison matrix as describing a graph or network [for a review of network theory applications in neuroscience, see Bullmore and Sporns (2009)]. Finding an unspecified number of groups or “communities” in arbitrary networks is a prominent problem (Girvan and Newman, 2002; Fortunato, 2010). I propose here a novel application of a powerful, fast “community detection” method (Newman, 2006a,b). My further key advances are generalizing this method both to work on arbitrary weighted networks and to split the network into a unique set of groups in one step.

I begin by outlining how the established method could be used to find spike-train groups by splitting a network repeatedly in two (Newman, 2006b), as this builds a more intuitive picture, and is itself a reasonable approach for detecting spike-train groups (Humphries et al., 2009b); in the next section, I then describe how my new method uses its core ideas, but extends them to both keeping all entries of C and finding all groups simultaneously.

Imagine that we apply a thresholding function A = f(C) to the comparison matrix, defining what is and what is not a “strong” similarity: any similarity greater than threshold is assigned a 1, and any below threshold is assigned a 0 (Fig. 1A). The resulting adjacency matrix A fully describes an undirected network: the network has as many nodes as spike trains; the links between nodes are defined by the ones in the entries of A; and the links are symmetric, hence the network is undirected. Many recent approaches to dividing such networks into clusters attempt to maximize a benefit function

often called “modularity” (Girvan and Newman, 2002), over all possible subdivisions of the network. That is, the division that maximizes Q creates the clearest division of the network into sets of nodes, with more connections within them, but fewer connections between them, than expected (Fig. 1A).

Figure 1.

Network theory concepts. A, An arbitrary comparison matrix showing pairwise similarities between 10 spike trains (spectrum scale, red: high similarity; blue: low similarity; note that the diagonal is set to zero for convenience). Two groups are embedded within this matrix. If we threshold this matrix, we create an adjacency matrix of zeros (white) and ones (black), which describes a network. The network has 10 nodes, corresponding to the 10 spike trains, and the entries in the adjacency matrix describe the links between them: we draw the network here as a ring lattice. The problem of “community detection” in a network is to group the nodes together so that most links are formed within communities, and few links between communities. When we cluster this network using a community detection algorithm, we see the two groups of four (red) and six (blue) nodes placed in the original comparison matrix: they contain most links within them but few between them (node order on the ring lattice is rearranged to show the groups). B, The choice of threshold is crucial to the clustering process: too low, and the network is too dense; too high, and the network is too sparse. In both cases, the clustering algorithm returns an incorrect grouping: too dense, and the nodes are in the wrong groups; too sparse, and there are too many groups. C, In my new algorithm, I treat the comparison matrix as describing a weighted network: all nodes are connected, but links have different weights (indicated by line thickness). My algorithm can correctly group these nodes such that strong links are within groups, and weak links are between groups. Thus, one advantage of my new algorithm is that it can find the correct grouping—as in A—but without needing to guess the appropriate threshold.

Existing methods focus on maximizing Q by iteratively splitting the network into two parts (Newman, 2006a). Thus, we define a vector s, with entry s_i ∈ {−1, 1} denoting to which of the two groups node i belongs (the actual assignment of entries is dealt with below in Eq. 9). The number of links within the two communities is then

where ^T is the transpose operator. Key here is quantification of the “expected number of links” within each community, which is encapsulated in the null-model network P. Following Newman (2006a), we use here the null model

where m is the total number of links in network A, and d_i (d_j) is the degree of node i (j): the number of links made by node i (j) in A. This null model is closely related to the so-called “configuration” model: it essentially forms a random network with the same expected degree sequence as the network being analyzed. Thus the expected number of links within the two communities is

Substituting Equation 3 and Equation 5 into Equation 2, we get the form for Q

where B = A − P is the so-called “modularity” matrix, whose entries

denote the difference between the number of links A_ij connecting nodes i and j and the expected number of links P_ij.

If we compute the eigenvalues λ_i and the eigenvectors u_i of B for all n nodes, and order the eigenvalues so that λ₁ ≥ λ₂ ≥ … ≥ λ_n, then it turns out that we can use the leading eigenvector u₁ to partition the nodes into two groups:

We can then use the resulting vector s to compute modularity Q from Equation 6: if Q is positive, we retain the split; if it is negative, we do not split. We need only do this once, as the sum in Equation 6 is maximized by the choice of Equation 9 (Newman, 2006a). To divide the original network into multiple groups, we can take each subnetwork resulting from the first split and repeat the process, iterating through each subsequent split until no split yields Q > 0.

However, directly applying this method to spike-train data would inevitably lose information (Fig. 1B). Only adjacency matrices (entries all 1 or 0, describing a network) can be handled, in which case we must introduce the further, dimensionless threshold parameter (Humphries et al., 2009b), on which the clustering critically depends (Fig. 1B). Furthermore, only the leading eigenvector is retained, dividing the network in two, but other groups, once unintentionally bisected, can never be recovered (Newman, 2006a). Thus, I sought to extend this method in two ways: first, by making use of all positive eigenvectors so that all groups could be found simultaneously; and, second, by using the full comparison matrix, to avoid losing information and introducing a further parameter.

A novel algorithm for clustering spike trains.

My new method is outlined in Figure 2. I began from the basis that if η is the number of positive eigenvalues (and corresponding eigenvectors) of B, then the maximum number of possible groups is M = η + 1 (Newman, 2006a). In this case, if we attempt to find multiple groups, we define a matrix S of group membership to replace the vector s (Eq. 9):

Then by analogy with Equation 6, we maximize (Newman, 2006a)

where Tr is the matrix trace function, the sum of all diagonal elements.

Figure 2.

Flow diagram of full spike-train clustering algorithm. The algorithm broadly follows a two-step procedure. First, some measure of similarity between each pair of n spike trains is computed, resulting in an n × n comparison matrix C. As common events can occur at many timescales, and between single or multiple spikes, the spike trains must be put into an appropriate representation before comparison—here I look at discretely binning the spike trains or convolving each spike with a Gaussian (a “binless” representation). Second, I interpret the comparison matrix as describing a weighted network: the problem of finding an unspecified number of groups or “communities” in networks is well studied. We can thus use a “community detection” method to find groups within our comparison matrix. The best division is that maximizing a benefit function called “modularity,” Q = [number of links within communities] − [expected number of such links]. We compute Q as shown: a null model (“expected”) matrix is subtracted from the comparison matrix, resulting in a modularity matrix B. The positive entries of B denote stronger than expected similarity between a pair of spike trains, and negative entries denote weaker than expected similarity. We find the division that maximizes Q in two steps. First, we find the eigenvalues of B; the maximum number of groups M is one more than the number of positive eigenvalues. Second, we take the M − 1 eigenvectors corresponding to the positive eigenvalues, and use K-means clustering with K = 2 … M to find all groups within the eigenspace defined by the eigenvectors (as the eigenvectors are each n entries long, each set defines coordinates for every spike train; and the closer the coordinates of a pair of spike trains, the greater the overlap of their respective sets of pairwise similarities with other spike trains, including each other). For each K, we compute Q: we then keep the clustering that maximizes Q, and hence automatically retrieve the number of groups in the original spike-train data.

We now work directly on the comparison matrix: we interpret this as a fully connected, weighted network (Fig. 1C), and make the replacement A_ij←C_ij in Equation 8 so that B = C − P. Hence the degree d_i becomes the total similarity between node i and all others, and the total number of links m becomes the total similarity in matrix C. We use the null model as defined above (Eq. 4): then P is a model of the expected pairwise similarity between spike trains, given the total similarity each spike train has with all others. The key difficulty is to then solve the problem of assigning all nodes to groups simultaneously in S, while also exploring the range of possible groups. My solution was the following algorithm:

1. Retain the η eigenvectors of B corresponding to the η positive eigenvalues. These define an η-dimensional eigenspace: coordinates of the ith node—the ith spike train—in this eigenspace are given by ith entry in each of the eigenvectors. The closer the coordinates of a pair of spike trains, the greater the overlap of their respective sets of pairwise similarities with other spike trains, including each other.

2. Iterate over j = 1 … η, spanning the complete range of possible groups from 2 to η + 1. (a) Run K-means clustering on the retained eigenvectors, using K = j + 1 to find the K clusters of nodes that correspond to the j + 1 potential groupings. The K-means algorithm is initialized using the K-means++ algorithm (see Appendix) to improve reliability. (b) Compute Q for that clustering, assigning each cluster found by the K-means clustering to the appropriate column of S as defined in Equation 10. (c) Repeat steps a and b for robustness, resulting in a set of Q values: we retain Q_j, the highest Q, as the modularity value for that potential number of groups and its corresponding group membership S. Typically I repeated the clustering 20 times, starting from different cluster centers chosen using the K-means++ algorithm (see Appendix).

We finally keep the group membership S with the maximum modularity score found over all numbers of groups j = 1 … η tested: I notate this as Q_max^t = max_jQ_j, for the particular bin size t = δt or Gaussian width t = σ. The algorithm was repeated for each bin or window size I used for a particular dataset, thus giving a set of {Q_max^t}.

In principle, we could take the maximum of this set Q_max = max_t{Q_max^t} as indicating the timescale at which the spike trains were most obviously structured, that is, having the strongest similarities within groups, and least similarity between groups. However, we must take care to eliminate the possibility of spurious results arising from the detection of “patterns” that are just statistical fluctuations inherent in any large-scale dataset of neural activity (Ikegaya et al., 2004; Mokeichev et al., 2007; Ikegaya et al., 2008; Roxin et al., 2008; Grün, 2009). Intuitively, the chance of finding a spurious grouping based on pairwise comparisons will depend on both the number of spike trains and the choice of timescale (δt or σ), and hence so too will the modularity score Q_max^t. Increasing the number of spike trains simply increases the probability of randomly occurring correlations between pairs of trains; the interplay of the distributions of spike-train rates and irregularities within the dataset will tend to increase randomly occurring correlations at a particular timescale. In the Appendix, I demonstrate that both of these factors can lead to spurious clusterings, and determine the resulting value of Q_max.

To control for random groupings, I generated matched sets of shuffled control data for each dataset of spike trains, and grouped them. For each experimental condition of single-unit data, consisting of a single spike train recorded while a stimulus is repeated, I randomly shuffled interspike intervals (ISIs) while keeping stimulus presentation times the same. For the multiple neuron data, each spike train's ISIs were shuffled into a random order. In both cases, the control data matched both the first and second moments of the ISI distribution of each real spike train, but eliminated correlations between trains.

I ran each set of shuffled spike trains through the clustering algorithm using the same set of bin sizes {δt} or Gaussian widths {σ} as the data, recording the maximum modularity score Q_ctrl^t for each. I repeated the shuffling 20 times, to get a set of 20 Q_ctrl^t values for each t. From each set of Q_ctrl^t, I used the maximum value found as my upper confidence bound Q_C^t, then computed ΔQ^t = Q_max^t − Q_C^t: the difference, for that timescale (δt or σ), between the maximum modularity score for the data and the upper confidence limit. If at least one ΔQ^t > 0, then I took the maximum of these (ΔQ) as indicating the timescale at which spike-train patterns were most obviously structured.

From my algorithm, we gain two advantages over other time-series clustering methods. First, because of the form of Equation 10, we can guarantee that Q_j is not simply a monotonically increasing function of the number of groups. Hence, Q_max^t uniquely identifies the grouping that maximized modularity over all possible groupings for that timescale, leaving us free to examine a range of timescales of our choosing, with no arbitrary parameters. Second, either Q_max^t ≤ 0 or ΔQ^t ≤ 0 is direct evidence that there are no groups in the data at that timescale—my method can hence give the equally useful null result.

Nonetheless, as with any unsupervised clustering method, one must exercise caution when interpreting the output of the algorithm. Like many combinatorial problems, optimizing Q is an NP-complete problem (Brandes et al., 2006): computing an individual solution is quick (polynomial time), but finding an optimal solution may require superpolynomial time, making the computation impracticable even for small problems (Fortunato, 2010). Hence, any practically useful solution is heuristic—in this case, based on eigenvector decomposition—and cannot guarantee that the partition optimizing Q has been found.

Even if the optimal partition could be found, in some cases this would not guarantee the final clustering has been found. Fortunato and Barthélemy (2007) showed that, for undirected, unweighted networks, modularity has a resolution limit problem: given the total number of links in the network m, if a detected group contains less than ∼$\sqrt{m}$ links, then it is possibly two or more groups combined. Note that this pertains only to groups that are already small on the scale of the network. An equivalent condition has not been derived for weighted networks, as used here, but Berry et al. (2009) have shown that weighted networks have a higher resolution limit than that of unweighted networks—that is, detectable groups are smaller. I find here that, even if we were to interpret the limit $\sqrt{m}$ directly as a weighted equivalent $\sqrt{W}$, given the total weight W of the entire network, the detected groups in my dataset analyses exceed this by at least an order of magnitude. Nonetheless, the potential need to check very small detected groups for subgroups should be borne in mind for future applications of this method.

Synthetic spike-train data for assessing clustering

Specification of synthetic spike-train data.

I tested the clustering algorithm using surrogate data created by Fellous et al. (2004) (available from http://cnl.salk.edu/fellous/data/JN2004data/data.html). Each set of synthetic spike train contained a known number of clusters G, and each cluster had 35 spike trains. Each cluster was defined by E ∈ {4, 5, 6} spike-event times chosen uniformly at random within a 1 s interval. Each spike train of that cluster inherited these spike times, which simulated the common patterns across trials or across multiple neurons. Noise was then added to each spike train: a 15% probability of each spike event not being inherited; each spike-event time jittered by an amount drawn from a Gaussian distribution of mean 0 and SD J ms; and X extra “nonpatterned” spikes added at times sampled uniformly at random from the 1 s interval. The clusters were combined into a single spike-train dataset and their order shuffled to obscure the patterns.

In the complete surrogate data, this was done 30 times for each combination of {G, J, X} from the sets: G ∈ {2, 3, 5} clusters per dataset; J ∈ {0, 1, 3, 5, 10, 15, 20, 30, 40, 50} ms jitter; and X ∈ {0, 2, 3, 4, 8, 11, 15, 20, 25, 35} extra spikes. In this paper, I show the results of simultaneously incrementing J and X, as this provides the most stringent test of the algorithm. I refer to each increment as a “noise level,” which ranges from 0 (J = 0 ms, X = 0) to 9 (J = 50 ms, X = 35). Figure 3A shows an example of a resulting spike-train dataset for G = 3 clusters, and noise level 1 (J = 1 ms and X = 2).

Figure 3.

Example clustering of synthetic spike-pattern data. A, Raster plot of the original dataset, containing G = 3 groups of 35 trains each, each train modified with the smallest amount of noise used here: X = 2 extra spikes, J = 1 ms of jitter (noise level 1). B, Binless clustering of the dataset in A (with σ = 0.0044 s) correctly assigns every spike train to its group. C, Comparison of binned and binless performance on this spike-train dataset over changes in bin size and equivalent Gaussian width (plotted against bin size here). Comparing spike trains in a binless representation gives more robust and more gracefully degrading accuracy over different timescales than using the binned representation. A normalized mutual information score of 1 indicates that the found grouping of spike trains corresponded exactly to the real grouping.

Quantifying comparative clustering of spike-train data.

I quantified the performance of the clustering algorithm on the synthetic data by computing the normalized mutual information I(A, B) between the found group structure 𝔸 and the real group structure 𝔹 (Danon et al., 2005). This measures the amount of information that knowledge of group structure 𝔸 gives us about group structure 𝔹, and vice versa. I first constructed a confusion matrix F, in which element F_ij is the number of nodes in the ith group of 𝔸 that are also in the jth group of 𝔹. I then found the normalized mutual information

where n_A and n_B are the number of groups in partitions 𝔸 and 𝔹, respectively, N_i and N_j are the sums over the ith row and jth column of the confusion matrix, and N is the sum over the whole matrix. I(A, B) = 1 if the two group structures are identical, and I(A, B) = 0 if the two groups structures are completely independent (including if one structure has no groups). I used this measure because it gracefully handles the cases where the clustering method finds too few or too many groups, as well as incorrect assignment of nodes. I computed Equation 12 for every bin size or Gaussian width tested, and kept the maximum found for each synthetic spike-train dataset. (I also used the normalized mutual information to assess the consistency of group structure over time for the multineuron datasets—this is discussed further in the Results.)

I computed lower bounds for mutual information scores. The assignment of no groups gives I(A, B) = 0; so the best case for a lower bound was assigning the same number of groups of the same size, but with nodes randomly assigned to each. For the synthetic data, I took a sample dataset from each of G = {2, 3, 5}, randomly assigned each spike train to a group, and computed I(A, B) between the random assignment and the real grouping. I repeated this 1000 times to get a mean and SD of I(A, B) for best-case random performance.

Neurophysiological data

Single-unit data from substantia nigra pars compacta.

I analyzed in detail a single substantia nigra pars compacta (SNc) neuron from the study of Coizet et al. (2006), whose aim was to characterize putative dopaminergic neuron responses to pain stimuli, and the role of the superior colliculus in modulating this response. The study used urethane-anesthetized, female, Hooded Lister rats, and extracellular single unit recordings were made using glass microelectrodes from SNc neurons located contralaterally to the stimulated hindpaw. The single neuron I analyzed contained a complete set of 244 trials across three conditions: a control condition of a repeated hindpaw stroke (28 trials); the baseline condition of 2 ms duration, 3.0–5.0 mA amplitude footshock applied every 2 s (60 trials); and a modulation condition of the same footshock applied every 2 s, but after bicuculline was injected into the superior colliculus (156 trials). In the latter condition, the 156 SNc neuron trials I used were all taken after a reliable response to footshock could be elicited in the superior colliculus, indicating that bicuculline had diffused completely. See Coizet et al. (2006) for further details of the experimental protocol.

Multineuron data from cortical areas 17 (V1) and 18 (V2).

I analyzed in detail 54-contact polytrode recordings of spontaneous activity in cat V1 and V2 (Blanche, 2005; Blanche et al., 2005). All neural data were recorded by Tim Blanche in the laboratory of Nicholas Swindale, University of British Columbia, and downloaded from the National Science Foundation-funded Collaborative Research in Computational Neuroscience data sharing website (http://crcns.org/). The downloaded dataset contains spike trains sorted from the polytrode recordings according to the methods detailed by Blanche (2005) and Blanche et al. (2005). The data I used were obtained from a single session of recording from paralyzed and anesthetized (N₂O and isoflurane) cats in the absence of visual stimuli. The V1 dataset contained 25 spike trains, recorded from a polytrode inserted down the medial bank of V1 (so putatively recording from a single layer): I used the initial 120 s of recording in which all spike trains were present. The V2 dataset contained 50 spike trains, recorded from a polytrode inserted vertically (so putatively recording across layers II–VI): I used the period between 22 and 321 s (299 s of data in total) in which all spike trains were present.

Further data analyses.

Having detected groups, I performed additional analyses of their interactions and internal structure, to further elucidate the organization detected by the clustering method. To look at activity for a population of spike trains in the cortical data, I plot the sum of the convolved spike trains—at the Gaussian width chosen by the clustering—giving us an effective moving-window average of the total number of spikes in the chosen population. For frequency-domain analyses, I computed multitaper power spectra directly from the spike-train time series; I also computed multitaper coherency and phase between the population activity vectors, with 95% confidence intervals. Both spectra and coherency (and their confidence intervals) were computed using functions from the Chronux toolbox (Jarvis and Mitra, 2001; Bokil et al., 2010) (http://chronux.org) for MATLAB, using parameters of time-bandwidth product TW = 4 and 9 tapers.

Results

The algorithm reliably and robustly finds repeating spike patterns

My method aims to partition spike-train datasets into groups such that the similarity between each pair of spike trains within each group is maximized and across groups is minimized. Each spike train is preprocessed by discrete binning or convolving each spike with a Gaussian. We then construct a comparison matrix comprising the similarity scores between every pair of spike trains in the dataset. This matrix is interpreted as a fully connected, weighted network: our task then becomes a generic problem of “community detection” in networks, where each community is a group of spike trains. The partition we seek thus corresponds to maximizing the “modularity” score Q = [number of links within communities] − [expected number of such links]. My extended algorithm for computing this score (see Materials and Methods) uniquely allows us to find all groups simultaneously, while working directly with the comparison matrix. We can then repeat the whole method for each choice of bin size δt or Gaussian width σ, and compare Q scores to find the timescale(s) at which the partition is clearest.

I first analyzed a large set of synthetic data to test the algorithm's detection of known spike train patterns. Both binned and binless spike-train preprocessing were used so I could compare their performance when looking for patterns formed by reliable timing of individual spikes. Each spike-train dataset was analyzed with seven bin or window sizes in equally spaced intervals. I found that basing the bin sizes on the ISI statistics of the dataset generally yielded excellent results. The largest bin size was set as the median ISI from the dataset—using the median ensures that skewed ISI distributions are handled well. The smallest bin size was set as the ISI corresponding to the first percentile in the ISI distribution. The corresponding Gaussian widths for binless preprocessing were then based on these values (see Materials and Methods).

The algorithm could successfully cluster spike trains into the correct groups using either binned or binless processing. Figure 3 shows the successful clustering of a G = 3 spike-train dataset using binless preprocessing. Even with the small amount of noise added to this dataset, it is not immediately obvious to the eye that there are three groups in the original raster plot; the algorithm nonetheless extracted these with complete accuracy. This example also demonstrates how binless preprocessing generally both improved the robustness of the algorithm's accuracy and allowed it to degrade more gracefully with changes in timescale compared to the binned preprocessing.

Nonetheless, if we look at the most accurate clustering on each spike-train dataset for either preprocessing method, both performed better than chance up to a very high level of added noise (Fig. 4). Further, performance for a given level of noise was not strongly degraded by increasing the number of groups. Performance at chance levels only occurred for the clustering of some spike-train datasets at noise level 7, corresponding to 20 extra spikes (compared to 4–6 spikes in the repeating pattern) and 30 ms of jitter per spike train. With this much added noise, it is arguable that this is correct performance: in some sense, the spike patterns no longer existed in these datasets because the repeating spikes were jittered on the same timescale as the typical interspike interval for the dataset—with ∼25 spikes per train, the expected ISI was 40 ms, and the jitter had an SD of 30 ms.

There was a clear advantage of using convolved Gaussians to look for patterns made by individual spikes. Figure 4C shows that clustering using the binless representation was consistently more accurate than using the binned representation as noise levels increased. The performance of the two representations was approximately the same without noise or with so much noise that the patterns were obliterated. At all intermediate noise levels, however, the clustering using binless representations recovered more information about the underlying group structure.

Differentiating hidden SNc cell responses to pain stimuli

I applied these insights from the surrogate data and looked for spike-train patterns in data from a single SNc neuron responding to multiple, repeated stimuli (Coizet et al., 2006). I looked separately at three sets of trials. In control trials, the rat received repeated strokes of the hindpaw. In baseline response trials, hindpaw footshock was applied at 2 s intervals. In modulation trials, the footshock was applied at the same intervals, but after the injection of the GABA antagonist bicuculline into the superior colliculus had diffused sufficiently for the collicular neurons to respond to the footshock as well. For each set of trials, I took the 2 s of spike train following each stimulus application, aligned them to the stimulus presentation, and looked for spike-train patterns across trials. I used only binless representations, as my analyses of the surrogate data suggested that this was the best approach for detecting spike-train patterns on the scale of single spikes. Also following my approach to the synthetic data, I determined 10 equally spaced bin sizes between the minimum ISI and the median ISI of all spike trains in a set of trials and converted these bin sizes into Gaussian widths. Finally, for each condition, I generated many sets of control data by shuffling the ISIs of the neuron during that condition, then redividing the spike train at the stimulus times used in the experiment; I thus removed any correlation between the stimuli and the spike train, while still respecting the spike-train statistics. All shuffled datasets were clustered using the algorithm, using the same set of Gaussian widths: taking the maximum modularity of the data Q_max^σ and the maximum across all the shuffled datasets Q_C^σ, I considered the groupings of the data to be significant only if the difference between the two (ΔQ^σ) was greater than zero.

No false positive groupings for SNc responses to control stimuli

The control stimulus had no effect on the firing pattern of the SNc neuron, which showed typical pacemaker-like firing of ∼4 spikes/s throughout (supplemental Fig. 2A, available at www.jneurosci.org as supplemental material). Applying the clustering algorithm to the 28 spike-train sections found no groups at any of the Gaussian widths: ΔQ^σ was less than zero for each width. This shows that my method does not find groups in arbitrary datasets: it can give clear null results, which are just as important as the ability to find groups.

Baseline response to pain stimulation drifts over experimental session

A clear response to the painful stimulus was evident in the set of baseline response trials. The poststimulus time histogram (PSTH) shows that application of the stimulus reliably caused an elongated pause in firing, and that the first poststimulus spike at the end of this pause occurred within a very narrow time window of ∼60 ms (Fig. 5A; in supplemental Fig. 2B, available at www.jneurosci.org as supplemental material, I replot around the stimulus application time to make clear the extent of the pause). Thereafter, reliable, regular firing returned. The clustering algorithm robustly finds two groups in the baseline trials, with the best grouping (the maximum ΔQ^σ) found for σ = 0.0095 s. Color coding the group membership in trial order over the experiment makes it immediately clear that the two groups correspond to a drift in the typical ISI over the experimental session (Fig. 5A), an effect not visible in the PSTH or initial raster plot.

Figure 5.

Clustering algorithm shows previously undetected SNc neuron responses to pain stimuli. Both columns show the same analyses of the two different conditions: raster plot of the original spike-train data, aligned at the onset of the stimulus at 0 s; corresponding PSTH; spike trains color-coded by group, and plotted in trial order; spike trains color-coded by group, and plotted in group order. A, In the baseline condition, both raster and PSTH show clear responses after stimulus: a pause, a peak of activity, and then resumption of typical SNc pacemaker firing. But even in this highly robust response, the algorithm reliably found two groups (groups plotted for maximum ΔQ^σ found with a Gaussian width of σ = 0.0095 s). When plotted in trial order, it is clear that the two groups correspond to a drift in response over the experiment. B, In the modulation (postbicuculline) condition, a clear pause then activity peak also occurred after stimulus. Compared to the baseline condition, the PSTH shows an irregular firing patterns after the peak. The clustering algorithm reliably found three groups (groups plotted for maximum ΔQ^σ found for σ = 0.0307 s). These correspond to three different phases of spike response after stimulation. Trial-order plotting shows that these were intermingled throughout. Plotting the three groups found by the clustering algorithm clearly shows that, after application of bicuculline in superior colliculus, individual trial responses were comparable to the baseline condition: a clear pause after stimulus, followed by highly regular firing.

Postbicuculline response to pain stimulation is unexpectedly reliable

The injection of the GABA_A antagonist bicuculline into the superior colliculus changed the response to the pain stimulus. The PSTH shows that a clear pause in firing was followed by a period of poststimulus activation (Fig. 5B; supplemental Fig. 2C, available at www.jneurosci.org as supplemental material, replots around the stimulus application time to make clear the extent of the pause), but after this response, the PSTH is relatively flat, suggesting irregular firing compared to the highly structured PSTH of the baseline condition.

The algorithm shows that this is not the case. It finds three groups, with the best grouping found for σ = 0.0307 s. These groups correspond to different resets of the SNc neuron's firing after the initial poststimulus activation: spike trains from individual trials returned to pacemaking after the poststimulus peak that followed the pause in firing. However, the resumption of regular firing did not occur with the same delay after stimulus, as it did on the baseline trials, and hence was obscured in the PSTH (Fig. 5B). The individual PSTHs for each of the three groups, plotted in supplemental Figure 3 (available at www.jneurosci.org as supplemental material), nicely illustrate that for individual trials there was a highly reliably firing after the stimulus was applied, but that the firing was not reliably resumed at the same delay after the pause in activity on each trial.

Detecting groups in simultaneous multineuron recordings

Analyzing simultaneous multineuron recordings brings additional problems. The long timescales of simultaneous recordings sessions lead inevitably to nonstationary spike-train time series, and hence patterns—here, putative cell assemblies—that fluctuate over time. Such large datasets also present strong challenges simply because of their size: we wish to detect groups made up of large numbers of neurons and over timescales of seconds. I show here that my algorithm rises to these challenges. In the Appendix, I show how the algorithm's output (Q, number of groups) and computation time are expected to scale with changes in the size of the dataset, the timescale chosen for analysis, and the distribution of firing rates within the dataset. While the size of dataset and choice of timescale predominantly dictate the computation time, the time for a complete analysis (including all controls) remains reasonable—on the order of minutes to hours—even up to very large N and very large timescales for the Gaussian windows.

Correlation structure of cat V2 spike trains evolves under anesthesia

I analyzed polytrode recordings of spontaneous activity in cortical area V2 from a paralyzed and anesthetized cat, made by Tim Blanche at the Swindale laboratory (see Materials and Methods). I used the algorithm to search for patterns across all 50 spike trains in a sliding window of 50 s, applied every 10 s—the sliding window allowed me to look at nonstationary structure over such a long, continuous recording. As these recordings were under isoflurane anesthetic, I decided to look for large timescale structure of the spontaneous activity, potentially locked to slow (<1 Hz), cortex-wide oscillations (Ferron et al., 2009). Supplemental Figure 4 (available at www.jneurosci.org as supplemental material) confirms that the power spectra of spike trains in both V1 and V2 were dominated by <1 Hz components throughout the recordings used here. Thus, in each window, I tested 10 Gaussian widths equally spaced between 0.029 and 0.29 s, corresponding to discrete bin sizes between 0.1 and 1 s. Here I report my analyses using Gaussian-convolved spike trains; in supplemental Figure 5 (available at www.jneurosci.org as supplemental material), I show that my preliminary analyses using discretely binned representations also revealed spike-train groups on these timescales.

I again applied control analyses to avoid the detection of spurious groups through the chance occurrence of shared patterns across spike trains (see Materials and Methods): I constructed 20 control datasets for each 50 s window by randomly shuffling the ISIs of each spike train, thus conserving both the first and second moments of the ISI distribution for each train; each control dataset was then grouped using the same set of Gaussian widths. Taking the maximum modularity of the data Q_max^σ and the maximum across all the shuffled datasets Q_C^σ, I considered the groupings of the data to be significant only if the difference between the two (ΔQ^σ) was greater than zero. I took the maximum over all ΔQ^σ as indicating the timescale at which the most evident structure could be found [that is, ΔQ = max_σ{ΔQ^σ}].

I found clear group structure throughout the V2 spontaneous activity, which evolved over tens of seconds. Figure 6A shows that both maximum Q_max^σ and maximum ΔQ^σ were always positive and varied over time, indicating that spike-train groups existed even after controlling for potential rate and Gaussian width confounds. These maximum ΔQ^σ were found for Gaussian widths between 0.116 and 0.289 s (corresponding to bin sizes between 0.4 and 1 s) in each window (Fig. 6B), consistent with the detected correlated activity following the <1 Hz slow-wave oscillations under isoflurane (Ferron et al., 2009). The number of groups giving maximum ΔQ^σ was predominantly two, and occasionally three or four (Fig. 6C). The nonstationary correlation structure of cortical activity is most evident when we compare the grouping of spike trains in each time window to the grouping in the seventh window (centered on 85 s), which had the maximum ΔQ over all windows (Fig. 6D). While the group memberships and sizes fluctuated over time, the organization could repeat: the second peak in Figure 6D, at window 20 (centered on 215 s), only differed from window 7 in the assignment of 3 neurons. Furthermore, the mutual information scores between window 7 and all the others always considerably exceeded the upper bound given by randomly assigning those windows' spike trains to groups of the same size, indicating that a consistent core set of spike trains were always grouped together.

Figure 6.

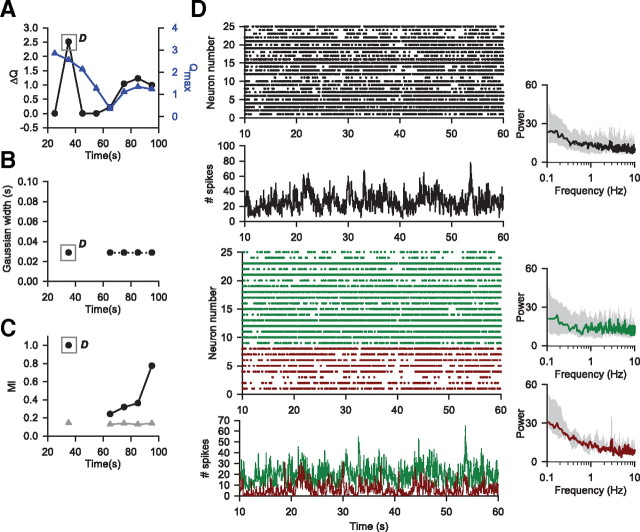
The clustering algorithm revealed evolving spontaneous neural activity in cat area V2 under anesthesia. I ran the algorithm on all 50 spike trains using a 50 s sliding window, applying the window every 10 s within the 299 s of retained recording. I show here analyses using pairwise comparisons of Gaussian-convolved spike trains. A, The maximum modularity scores Q_max indicate an evolving group structure over the recording; plotting ΔQ shows this evolution was consistent even after controlling for the detection of spurious groups. Gray boxes here and in B–D indicate the 50 s windows plotted in detail in Figure 7, A and B. B, ΔQ in each window was consistently found for Gaussian widths between 0.116 and 0.289 s. C, The number of groups changed over the course of the recording. D, Changes in group membership over the recording. Here I plot the normalized mutual information between each window's grouping and the grouping found in the window with maximum ΔQ (the 7th window, centered on 85 s). This always considerably exceeded the upper bound given by randomly assigning those windows' spike trains to groups of the same size, indicating that a consistent core set of spike trains were always grouped together [gray line and symbols, plotting the mean plus 2 SD of 1000 samples from randomly generated I(A, B)s for each window, where A was the group structure in window 7, and B was a random assignment of the spike trains into the same size of groups found for the window].

Looking closer at the individual time windows, we see that ΔQ and corresponding timescale σ reflect the organization of spikes within each group, and their relationship to a range of slow oscillations in neural activity. Figure 7A shows the breakdown of the group activity for the window with the highest ΔQ (window 7), which was on the timescale of σ = 0.289 s. The whole population's spike trains were dominated by the <1 Hz activity, consistent with the transitions between quiet “down” states and active “up” states characteristic of spontaneous cortical activity (Steriade et al., 1993; Kerr et al., 2005; Luczak et al., 2007; Ferron et al., 2009). Both detected groups of spike trains in this window were also strongly dominated by <1 Hz oscillations, one group substantially more than the other. The less-dominated group also had occasional brief periods of simultaneous spiking, and a sustained period of spiking lasting >10 s. The population activities of the two groups' were anti-phase at very low frequencies (<0.4 Hz), but in phase at the slightly higher frequencies (0.5–1 Hz) that normally comprise the peaks in cortical EEG/LFP spectra (Ferron et al., 2009). Thus, the detected groups at this timescale correspond to neurons with an anti-phase, very slow oscillation, upon which is superimposed the widely reported in-phase ∼1 Hz slow-oscillation.

Figure 7.

Breakdown of V2 spontaneous activity in individual time windows with highest (A) and lowest (B) ΔQ. From top to bottom, I plot the following for these 50-s-long windows: the raster plot of the spike trains; the corresponding population activity as the sum over the convolved spike trains at the chosen timescale; the raster plot sorted by group membership; and the corresponding population activity of the groups. At the bottom, coherency and phase are plotted between the red and green group population activities (see below)—the line gives the 95% significance level for coherence; the gray shading gives 95% confidence interval for the phase. To the right, I also plot the median (line) and interquartile range (gray shading) of the individual spike trains' power spectra, taken over the whole population (black) or over the groups (color-coded). A, The breakdown of group activity from the window with the maximum ΔQ (window 7, centered on 85 s, σ = 0.289 s). The whole population shows <1 Hz slow oscillation in activity. Two groups were detected by the algorithm: one group (green) contained many spike trains with strong <1 Hz oscillations, but with no specific peak frequency in the population. The second group (red) had comparatively less <1 Hz power in the spike-train oscillations but shared firing patterns, particularly a sustained plateau of activity between ∼85 and 95 s into the recording. The coherency and phase between the two groups' population activities show that they were anti-phase at very low frequencies (<0.4 Hz), but in phase at the higher frequencies (0.5–1 Hz). B, The window with minimum ΔQ (window 12, centered on 135 s; σ = 0.144 s) had lower power at very low frequencies, but a more evident peak of sustained ∼1 Hz oscillation in the population activity. The three groups detected by the algorithm can be distinguished by the relative amounts of power at very low frequencies, with the smallest group (blue) containing only substantial oscillations at ∼1 Hz. The green and red groups show a wider range of slow oscillations in their population activities, which phase shift around the center of the window (dashed vertical line): in the first half, the population activities are anti-phase when coherent; at ∼135 s, the populations become in phase, showing a high-degree of coherency across a wide range of low frequencies.

Compare this with the breakdown of group activity in Figure 7B for the window with the lowest ΔQ (window 12, σ = 0.144 s). In this window, three groups were detected: one dominated by very low-frequency oscillations (red), one with no such oscillations (blue), and one intermediate (green). In contrast to the activity in window 7, the whole population activity, and each of the groups, contained a peak in power around 0.8–1 Hz. The two main detected groups (red and green) showed an intriguing phase shift about halfway through this 50 s window: in the first half, the population activities were strongly anti-phase at the coherent frequencies; but at ∼135 s, there was a clear switch to coherent, in-phase activity between the populations, across a broad range of low frequencies. Thus, the change in ΔQ is reflected in the changes of intergroup synchronization and their coupling to the global oscillatory activity at the sub-1 Hz timescale.

Transient correlation structure of cat V1 spike trains

My equivalent analysis of recordings from cortical area V1 under the same conditions illustrated two further points of contrast: that groups need not be found at all, and that group structure under anesthesia need not be tied to any global oscillation. Group structure for the spike trains were found in two separate periods, and only clearly emerged toward the end of the recordings (Fig. 8A,C). Two groups were found throughout, and consistently had maximum ΔQ^σ for a Gaussian width of σ = 0.0144 s (Fig. 8B), and hence the detected structure was always at different timescales than those in V2. Again, the groupings fluctuated between time windows, but retained a consistent core set of commonly grouped spike trains when compared to the window with maximum ΔQ (Fig. 8C). Looking in detail at this time window (Fig. 8D) shows that the different timescales of V1 patterning compared to V2 are reflected in the timescale of synchronized spikes. Both groups had spike trains with irregularly occurring synchronized firing in the absence of a dominant underlying oscillation, despite the individual spike trains' spectra clearly being dominated by <1 Hz components, both in this window and throughout the recording (supplemental Fig. 4, available at www.jneurosci.org as supplemental material). One group (green) contained spike trains with substantial power at frequencies up to 10 Hz, while the other (red) contained spike trains with a clear peak frequency around 3 Hz. This suggests that putative cell assembly activity among this set of neurons was not tied to the sub-1 Hz global oscillation.

Figure 8.

Analysis of spontaneous activity in V1 of isoflurane-anesthetized cat. I ran the algorithm on all 25 spike trains within a 50 s sliding window, applying the window every 10 s within the 120 s of recording. All analyses are the same as those of the V2 data in Figures 6 and 7. A, I found that detectable structure was split into two discrete periods; three of the time windows had no ΔQ^σ > 0 for any of the 11 Gaussian widths tested. The clearest structure only emerged toward the end of the recording period. B, All windows with ΔQ > 0 had ΔQ for the smallest Gaussian width tested. C, The spike-train grouping in the second window (the one with maximum ΔQ) was most completely repeated in the final window; but in all windows with ΔQ > 0, the grouping was significantly more related to the grouping in window 2 than to the best-case random assignment of spike trains to the groups (gray lines and symbols; see Fig. 6C). D, Breakdown of activity in window 2 (centered on 35 s). Two groups were found, both showing periods of synchronized activity, and both containing <1 Hz oscillations, but with no dominant frequencies; the distinction between the two in the frequency domain is the relative contributions of the >1 Hz frequencies: the green group contains spike trains with a broad range of higher-frequency activity; the red group contains spike trains with a peak frequency around 3 Hz.

The detection of large timescale structure in large datasets

I analyzed the output of a large-scale model of the rat striatum to look at the detection of cell assembly activity across thousands of spike trains. Whereas the previous sections demonstrated using the clustering algorithm for exploring data, here I demonstrate how it can apply to analysis of model dynamics, and hence insights into neural computation. The striatum is principally composed of GABAergic projection neurons (SPNs), which typically have spontaneous rates well below 1 spike/s in vivo, and sporadically show phasic activity locked to behavioral events (for review, see Kreitzer, 2009). The recent demonstration that NMDA activation of a striatal slice can spontaneously generate multiple SPN cell assemblies (Carrillo-Reid et al., 2008) suggests that the striatal network can self-organize its activity, potentially via local inhibition between SPNs.

I previously codeveloped a model that simulates all the GABAergic neurons and the connections between them in a given volume of striatal tissue (Humphries et al., 2009b), using spiking models of the dominant SPNs and rarer fast-spiking interneurons (FSIs). We previously showed that such a network could spontaneously generate cell assemblies, but were most evident in an SPN-only network (Humphries et al., 2009b)—Ponzi and Wickens (2010) have also demonstrated cell assembly formation in a random network of SPN-like neurons. With the FSIs included, our network showed some evidence of cell assemblies, but its dynamics were difficult to characterize. In related work, Zillmer et al. (2009) showed that complex, edge-of-chaos dynamics are common in large networks of inhibitory spiking neurons. Hence, I used my algorithm to reexamine the large-scale striatal model for similar, subtly shifting dynamical states.

To look at cell assembly formation, I simulated 10 s of spontaneous activity within a 250 × 250 × 250 μm cube of striatum, hence containing 1359 SPNs and 41 FSIs (Humphries et al., 2009b), driven by background cortical activity of ∼500 spikes/s arriving at each neuron (Blackwell et al., 2003; Wolf et al., 2005; Humphries et al., 2009b). The algorithm was then applied to the spike trains of the 1344 SPNs that fired more than one spike during the simulation. I looked for structure on the timescale of the average firing rate by convolving the spike trains with a range of five Gaussian widths equally spaced between 0.045 and 0.16 s, corresponding to discrete bin sizes equally spaced between the 10th and 50th percentiles of the ISI distribution. Again I controlled for spurious groupings by applying the algorithm to 20 sets of matched control spike trains for each Gaussian width, and comparing the maximum modularity obtained to that from the original dataset.

The algorithm reported multiple timescales with significant modularity (i.e., ΔQ^σ > 0), with the clearest grouping structure found for the two largest Gaussian widths tested (Fig. 9A,B). Though three groups were detected at both widths, these group structures were distinct between the two widths (normalized mutual information between the structures was 0.022), suggesting that network states of the model were changing at different timescales for different neurons. These were hidden when examining the activity of the whole projection neuron population, which showed no clearly identifiable repeating states (Fig. 9C). I confirmed this by examining the transition matrices of the individual groups at both widths. Figure 9D shows that, for the smaller width (σ = 0.126 s), two of the groups had irregularly recurring activity states unique to either early or late in the simulation; the other group had a unique set of activity states around 5 s, which did not recur before or after that time. In contrast, Figure 9E shows that, for the larger width (σ = 0.16 s), two of the groups showed regularly recurring activity states across the whole simulation. Thus, the grouping algorithm separated irregularly and regularly repeating network states at different timescales for different neurons.

Figure 9.

Detection of structure in large-scale sets of multineuron spike train data. Here I analyzed 10 s of simulated spontaneous activity from a one-to-one scale model of the striatum's GABAergic microcircuit; the model simulated a cube of striatum 250 μm on the side, containing 1359 projection neurons and 41 fast-spiking interneurons, all driven for 10 s by background cortical input of ∼500 spikes/s, the minimum required to reliably fire the projection neuron (Humphries et al., 2009a). Analyses of the projection neuron spike trains are shown here; the interneuron population had no detectable groups. A, The largest ΔQ, indicating the most evident group structure, was found for large Gaussian widths of 0.126 and 0.16 s. B, At these widths, three groups of projection neurons were found. C, The transition matrix of the whole projection neuron population. The spike trains were divided into 200 ms bins, and each bin was assigned a 1 if it contained at least one spike, or a 0 otherwise. Between all pairs of the resulting 40 binary vectors, I then computed the Hamming similarity—the proportion of entries that were the same—with values close to 1 indicating a repeating network state. The matrix for the whole population shows no evidence of either unique or repeated network states. D, Breakdown of activity for the three groups found with σ = 0.126 s. The total activity of the three groups (top) shows that at this timescale two groups (red and green) were consistently anti-phase, except where the third (blue) had a period of enhanced activity centered around 5 s. Computing transition matrices separately for each of the groups shows that there were changes in the network state: in group 1, the network states around 5 s irregularly repeated thereafter, and recurred more often than any other; in group 2, the network state before 6 s recurred many times, compared with after 6 s; in group 3, the peak of activity around 5 s comprised a sequence of dissimilar network states, that did not occur before or after this time. E, Breakdown of activity for the three groups found with the largest Gaussian width of σ = 0.16 s. The transition matrices show that groups 2 and 3 both had regularly repeating network states.

Discussion

I have described a new method for detecting spike-train ensembles with two advantages: it self-determines the most likely number of groups in the data; and its only free parameter is the timescale of pairwise comparison—which is determined by the questions asked of the data.

Analyses of single-unit data

The analyses of the synthetic data demonstrated that my method reliably self-determines the number of groups in each set of spike-train data, and that basing the timescale of the pairwise comparisons on spike-train statistics worked well. Moreover, the assignment of spike trains to each group was robust to noise. Noticeable deviation from 100% accuracy only occurred after jittering each patterned spike by ∼10 ms and doubling the number of additional spikes per train. I also demonstrated the advantage of making pairwise comparisons between binless rather than discretely binned representations of spike trains.

Using these insights, I analyzed single-unit data from a rat SNc neuron in response to hindpaw stimulation. The pacemaker firing of SNc neurons in vivo is well established (Grace and Bunney, 1984; Guzman et al., 2009). Prior studies report that aversive stimuli inhibit the firing of dopaminergic neurons (Ungless et al., 2004; Brischoux et al., 2009). Coizet et al. (2006) showed that this inhibition is a pause in the SNc neurons' pacemaker firing—with my algorithm, I found unsuspected further decompositions of this pattern.

The neuron showed no response to brushes of the hindpaw, my method reporting no groups within spike-train periods aligned to this stimulus—confirming that the method can give an equally useful null result. Consistent with Coizet et al. (2006), I found that the hindpaw footshock caused a pause followed by a reliably timed spike, the neuron reverting to regular, pacemaker-like firing thereafter, but with a subtle elongation of the ISI over the experimental session (Fig. 5A). One possibility is that change in anesthetic depth over the session had a subtle effect on the slow oscillation of the membrane potential that drives the pacemaking (Wilson and Callaway, 2000; Guzman et al., 2009).

More striking was my new finding that the application of footshock after bicuculline injection in the superior colliculus led to equally reliable poststimulus pacemaker firing, but that this firing did not restart at a consistent time (Fig. 5B). This suggests that the monosynaptic input from the superior colliculus to SNc neurons (Comoli et al., 2003) can variably reset these neurons' pacemaker currents, and that the “inhibition” caused by aversive stimuli is best understood as a variable resetting of the SNc neuron's membrane potential oscillation.

Analyses of multineuron data

Slow spontaneous transitions between active “up” and quiet “down” states occur in single cortical neurons both in vivo (Steriade et al., 1993; Mahon et al., 2001) and in vitro (Sanchez-Vives and McCormick, 2000). The strong correlations with slow oscillations in surface electroencephalogram (Steriade et al., 1993; Mahon et al., 2001) and local field potentials (Destexhe et al., 1999) suggest there are globally coherent changes in neural activity across cortex. However, recent work has provided evidence that, during such spontaneous activity, simultaneously recorded neurons have diverse firing patterns at up-state transitions (Luczak et al., 2007), and the set of neurons making up the population activity is both sparse and continually changing (Kerr et al., 2005). Here I have shown directly that spontaneous cortical activity contains neural ensembles evolving over time in composition and synchronization.

For spike trains from V2 of isoflurane-anesthetized cat, I found that the modularity scores ΔQ of 50-s-wide overlapping windows varied over the whole recording, reflecting changes in the underlying organization of spike trains over time. In the 50 s window with the highest ΔQ, I found two groups, whose population activity was in phase around 0.8–1 Hz—suggesting a globally coherent oscillation—yet was anti-phase at lower frequencies (<0.4 Hz). The window with the lowest ΔQ had a distinct grouping of the same neurons. I found one group containing neurons dominated by a ∼1 Hz oscillation. The other two groups' population activity initially oscillated anti-phase at sub-1 Hz frequencies, but then phase shifted and became coherent across low frequencies (∼0.4–1.2 Hz). Furthermore, in data from V1, I found that significant group structure was transient, occurring in only five of the eight windows I examined. These findings directly confirm that individual neurons change their contribution to the population activity over time, and that, as a consequence, both ensemble and individual firing patterns are unique.

Despite the changes in group synchronization and oscillation, the groups contained a consistent core on a subset of timescales. A subset of the spike-train grouping found in the window with the highest ΔQ was repeated above chance levels in all other windows (Figs. 6D, 8C). In the V2 data, maximum modularity (ΔQ) in each window was found for Gaussian widths between 0.144 and 0.289 s, suggesting that the synchronization timescale in V2 often followed the <1 Hz oscillations. By contrast, spike-train groups in V1 were consistently found for a width of 0.0289 s, on the timescale of individual spikes, and consistent with the dominance of higher-frequency power in this population. My findings show that the correlation structure of spike trains within neural ensembles can differ between V1 and V2, consistent with a recent voltage-sensitive dye imaging study showing adjacent regions of mouse cortex need not be strongly correlated during spontaneous slow oscillations (Mohajerani et al., 2010). Taken all together, my results show neural ensembles within spontaneously active cortex, which fluctuate in organization over timescales of tens of seconds, and which alter their internal correlation structure independently of each other.

The dynamics embedded within large-scale ensemble recordings or the output of large-scale computational models are difficult to extract. I showed that my algorithm could detect unsuspected organization in the output of a large-scale model of the rat striatum (Humphries et al., 2009b). The model generated spontaneous cell assemblies in response to unstructured, background input, consistent with the spontaneous emergence of cell assemblies reported in vitro (Carrillo-Reid et al., 2008). Moreover, my algorithm provided evidence for complex dynamics of these assemblies, organized on different timescales for different neurons: on one timescale, the neurons in two of the groups showed a distinct shift in their irregular repetition of a network state; on the other timescale, the neurons in two of the groups showed a regular repetition of a network state. These dynamics are distinct from irregular, unrelated firing of the neurons, and from regular, stable oscillations in neural activity.

Challenges and extensions

While I have demonstrated the algorithm's robustness and applications, as with any unsupervised clustering method I exercise caution in interpreting the output. Hence, I have been careful throughout to interpret detected groups by their global features (Figs. 6–9), to check the consistency of multineuron data grouping, and to compare groupings to random assignment (e.g., Fig. 6D).

It is nonetheless possible that spike trains could be placed in “wrong” groups (Fig. 4), or do not belong to any group. Soft clustering of spike trains may be useful here, and also has distinct applications (Slonim et al., 2005; Peyrache et al., 2010), including analysis of cell assembly reactivation across sleep–wake cycles (Peyrache et al., 2009) because of the difficulty of guaranteeing that the same neurons have been recorded throughout. An implementation of soft clustering could use the distance of a spike train from each centroid in the K-means clustering stage to define its relative group membership. Alternatively, an iterative removal of groups (Zhao et al., 2010) could avoid problems with “background” spike trains.

A further challenge will be interpreting the meaning of detected groups during ongoing behavior, to understand when a group is defined functionally (i.e., coappears consistently) or effectively (i.e., correlates with specific events). Furthermore, group interactions could be physical or functional: groups with anti-correlated population activities (e.g., Figs. 7A, 9D) are not necessarily physically antagonistic—the particular firing sequence could be a stable state of the system, and hence reflects a functional relationship.

Extensions to temporal and directional correlations could address these questions. For temporal correlations, one could find correlation coefficients between pairs of spike trains at a range of delays, and use the maximum found as the entry in the comparison matrix. Causal inference techniques, such as Granger causality (Barnett et al., 2009), could determine directional correlations. The resulting directed comparison matrix would require using community-detection techniques for directed networks (Leicht and Newman, 2008). This breadth of possible extensions illustrates the fruitfulness of using community-detection ideas for developing analyses of large-scale neural data.

Appendix

K-means++ algorithm

Repeating the K-means clustering from a different set of initial cluster centers each time is required to overcome the problem of the K-means algorithm becoming stuck in local minima. I further improved the reliability of the clustering by using the K-means++ algorithm (Arthur and Vassilvitskii, 2007) to choose these initial cluster centers: (1) Choose one node i uniformly at random from among the n nodes; the coordinates of the first cluster center are then the coordinates of that node: the ith entry in each of the j eigenvectors. (2) For each node x, compute D(x), the distance between x and the nearest center that has already been chosen. (3) Add one new node at random as a new center, chosen with probability proportional to D(x)². (4) Repeat steps 2 and 3 until K centers have been chosen. (5) Proceed with standard K-means clustering using the chosen centers.

Scaling properties of the new algorithm

Here I examine how the output and time course of the new clustering algorithm depend on both the parameters of the dataset and the choice of timescales that are examined.

Cortex-like synthetic spike-train data

In all cases, I created N gamma-distributed spike trains of 50 s duration, sampling ISIs from the gamma distribution Γ(a, b), where a = 1/CV_ISI² and b = x̄_ISI/a given the mean (x̄_ISI) and coefficient of variation (CV_ISI) of the ISIs. These were sampled for each spike train from log-normal probability density functions matching the statistics of cortical recordings; the resulting spike trains thus match the firing statistics of a population of cortical pyramidal cells, while omitting specific correlations between the spike trains. For a given combination of N, Gaussian widths σ (or bin size δt), and ISI and CV_ISI probability distributions, I generated 20 datasets and ran each through my grouping algorithm.

Anesthetized cortex.

From the anesthetized cat V2 data of Tim Blanche (see main text), I extracted the log-normal x̄_ISI density function L(−1.47, 1.32), and the log-normal CV_ISI density function L(0.62, 0.33) over the 50 spike trains in the dataset. These functions are plotted in Figure 10D, and used to generate the results in Figure 10A–C.

Figure 10.

Scaling of algorithm output and time with data and analysis parameters, when applied to cortex-like spike-train datasets without built-in correlations between spike trains. I plot medians and interquartile range (where appropriate) of all quantities. A, Using Gaussian-convolved trains, Q_max^σ scales monotonically like a power law with increasing numbers of spike trains N, for any width σ. There is also a monotonic scaling of Q_max^σ with Gaussian width for all dataset sizes greater than N ≈ 50. B, Binned spike trains scale similarly, but with consistently higher modularity scores than their binless counterparts. C, Computation time for the complete algorithm appears to scale slightly faster than a power-law—i.e., is superpolynomial—for large N datasets (plotted here for a Gaussian width of 0.144 s; note that the range bars are too small to see on this scale). D, Log-normal probability density functions for sampling the mean ISI and CV of each spike train in the datasets for A–C; fits were extracted from the data on V2 of anesthetized rat (see Appendix text). E, For a fixed size of dataset (N = 250), Q_max^σ rises to a plateau with increasing Gaussian width. F, At the same time, the number of groups giving Q_max^σ typically falls with increasing Gaussian width. G, For small Gaussian widths, the time taken for completion of the algorithm remains constant, but increases approximately linearly for larger Gaussian widths, despite the algorithm ultimately returning a smaller number of groups. H, Log-normal probability density functions for sampling the mean ISI and CV of each spike train in the datasets for E–G, given for typical values of activity in waking-state sensory cortex (see Appendix text). I, For a fixed size of dataset (N = 250), moving from a narrow (σ_L = 1) to a broad (σ_L = 2) distribution of ISIs decreases Q_max^σ for small Gaussian widths, but has no consistent effect for large widths. The movement from a narrow to broad distribution in this case corresponds to an increase in the number of low-rate spike trains. J, The number of groups stays relatively constant for a given Gaussian width, except for the combination of large widths and increasing numbers of low-rate spike trains (interquartile range bars are omitted here for clarity). For most choices of σ_L, the number of groups decreases with increasing width, similar to F. K, For each dataset, the time taken to complete the algorithm using all Gaussian widths falls monotonically with a broadening of the ISI distribution. L, The tested set of log-normal probability distribution functions for the ISI distribution, simulating a range of plausible distributions for awake cortex; the CV distribution was the same as in H.

Awake cortex.

I also tested scaling with a range of datasets mimicking the firing statistics of waking-state sensory cortex. The log-normal ISI density function L(−0.057, 1.72) was extracted from auditory cortex data presented by Hromádka et al. (2008); the log-normal CV_ISI density function L(−0.5, 0.5) approximates the range of CV_ISI reported for both areas MT and V1 by Softky and Koch (1993). These functions are plotted in Figure 10H, and used to generate the results in Figure 10E–G. Based on these data-derived functions, I also tested the effects of changing the ISI distribution width σ_L, using 11 different distributions L(−0.057, σ_L) with σ_L equally spaced in the interval [1, 2]. This set of functions is plotted in Figure 10L, and used to generate the results in Figure 10I–K.

All times were collected on a PC with a Xeon 2.27 GHz quad-core processor and 12 GB RAM, running Windows 7; all code was written and run under MATLAB 2007b.

Scaling of algorithm output

Spurious groupings of spike trains are dependent on two factors, the number of spike trains and the choice of timescale (Gaussian width or bin size) at which the spike trains are compared. The greater the number of spike trains, the greater the number of randomly occurring correlations simply because of the increased sample size. The timescale dependency need not be monotonic: the distribution of spike-train rates and irregularity across the dataset dictate the occurrence rates of two spike trains being active at the same time by chance. Figure 10, A and B, illustrates that the modularity score Q_max^t indeed shows these dependencies on both the number of spike trains and timescale of comparisons when clustering synthetic datasets of uncorrelated spike trains. Focusing on a specific size of dataset, in Figure 10, E and F, we see that Q_max^σ rises to a plateau with increasing width, but the number of groups that gives Q_max^σ falls. Hence the need for stringent controls, to ensure that the number and quality of the detected clusterings in the data correspond to more than just the combined effect of the size of the dataset and the choice of timescale.

Figure 10, I and J, shows that, for a fixed size of dataset, changing the distribution of firing rates within it changes the algorithm's output in a more complex fashion. Broadening the distribution, so introducing more lower-rate spike trains, lowers Q_max^σ, but only for small Gaussian widths. Broadening the distribution also disrupts the strong inverse relationship between the number of groups found and the Gaussian width. Hence the specific distribution of rates in a dataset affects the performance of the algorithm.

Scaling of algorithm time

To give some idea of computation time, I collated run-time statistics for these scaling studies. These times include the complete algorithm: convolution of all spike trains with the Gaussian window, construction of the similarity matrix, and clustering. I found that computation time increases faster than a power law with increasing size of dataset N (Fig. 10C). However, the times involved are still practical: for a 0.144 s Gaussian window, the largest 50-s-long dataset of 1000 trains took ∼36 min to complete. In Figure 10G, we see that, when looking at each Gaussian width in turn, the smaller widths take approximately the same amount of computation time to complete, but that time increases (roughly) linearly with larger widths. This is despite the algorithm ultimately returning fewer groups for these larger widths (Fig. 10F). Hence, looking at timescales corresponding to large-scale structure in the spike trains substantially increases the computation time. Finally, in Figure 10K, we see that increasing the width of the firing rate distribution decreases the overall run time of the algorithm, taken over all tested Gaussian widths; however, the decrease is small on the scale of the total time, so the specific statistics of the dataset do not contribute substantially to differences in the algorithm run time.

I also note that, overall, the time to run a complete analysis is dominated by the need to run a large number of control clusterings, and the computation time for this in turn is dependent on the size of the dataset and the choice of timescales for analysis. Thus, improving the efficiency of this algorithm is more dependent on finding more efficient choices of control than on altering the central algorithm—for example, it may be possible to replace the null model P (Eq. 4), currently derived from the dataset, with a null model derived from control sets of spike trains, and hence not require the clustering of the control data.