Efficient Encoding of Vocalizations in the Auditory Midbrain

Lars A Holmstrom; Lonneke B M Eeuwes; Patrick D Roberts; Christine V Portfors

doi:10.1523/JNEUROSCI.1964-09.2010

. 2010 Jan 20;30(3):802–819. doi: 10.1523/JNEUROSCI.1964-09.2010

Efficient Encoding of Vocalizations in the Auditory Midbrain

Lars A Holmstrom ^1,^✉, Lonneke B M Eeuwes ², Patrick D Roberts ^1,³, Christine V Portfors ²

PMCID: PMC6633079 PMID: 20089889

Abstract

An important question in sensory neuroscience is what coding strategies and mechanisms are used by the brain to detect and discriminate among behaviorally relevant stimuli. There is evidence that sensory systems migrate from a distributed and redundant encoding strategy at the periphery to a more heterogeneous encoding in cortical structures. It has been hypothesized that heterogeneity is an efficient encoding strategy that minimizes the redundancy of the neural code and maximizes information throughput. Evidence of this mechanism has been documented in cortical structures. In this study, we examined whether heterogeneous encoding of complex sounds contributes to efficient encoding in the auditory midbrain by characterizing neural responses to behaviorally relevant vocalizations in the mouse inferior colliculus (IC). We independently manipulated the frequency, amplitude, duration, and harmonic structure of the vocalizations to create a suite of modified vocalizations. Based on measures of both spike rate and timing, we characterized the heterogeneity of neural responses to the natural vocalizations and their perturbed variants. Using information theoretic measures, we found that heterogeneous response properties of IC neurons contribute to efficient encoding of behaviorally relevant vocalizations.

Introduction

Most animals face a complex sensory environment from which they have to extract behaviorally relevant cues for survival. A key question in sensory neuroscience is how the brain detects and discriminates among these cues. Sensory systems often use broadly tuned neurons with overlapping receptive fields at the periphery, resulting in a distributed and redundant encoding of stimuli. This encoding strategy helps overcome the stochastic responses of individual neurons but is subject to interneuron correlations and overlapping representations of similar and/or simultaneous stimuli, complicating discrimination among these external events (Sompolinsky et al., 2001; Shamir and Sompolinsky, 2004; Averbeck et al., 2006). It has been hypothesized that ascending sensory pathways overcome these limitations through efficient encoding strategies driven by selectivity to complex features (Linsker, 1988; Rolls and Treves, 1990; Atick, 1992; Chelaru and Dragoi, 2008). One manifestation of such a strategy is population diversity, in which neurons with heterogeneous receptive fields contribute to an encoding that minimizes response correlations and maximizes information throughput (Gawne and Richmond, 1993; Bell and Sejnowski, 1995; Shamir and Sompolinsky, 2006; Chelaru and Dragoi, 2008). Evidence of heterogeneous encoding has been documented in various cortical structures (Hubel and Wiesel, 1962; Ringach et al., 2002; Haupt et al., 2004). Understanding where heterogeneity emerges in sensory pathways is vital for understanding the neural mechanisms that drive efficient encoding of behaviorally relevant stimuli. In this study, we examined whether heterogeneous receptive fields driven by selectivity to acoustic features in conspecific vocalizations results in efficient encoding in the inferior colliculus (IC).

The IC is the main nucleus in the auditory midbrain, receiving ascending input from the majority of brainstem nuclei (Adams, 1979) and descending projections from auditory cortex (Saldaña et al., 1996). Efficient encoding of conspecific vocalizations may be facilitated by neurons in the IC that respond to specific acoustic features found in vocalizations such as frequency modulations (Woolley and Casseday, 2005; Andoni et al., 2007), amplitude modulations (McAlpine, 2004; Woolley and Casseday, 2005), duration (Brand et al., 2000; Pérez-González et al., 2006), and/or combination sensitivity (Portfors and Wenstrup, 1999; Portfors, 2004). Although previous studies focused on feature selectivity by individual neurons to synthetic stimuli or token vocalizations, it is unknown whether the IC uses heterogeneity and/or selectivity to efficiently encode natural stimuli.

In this study, we characterized neural responses to four behaviorally relevant vocalizations in the mouse IC. We used a novel stimulus design methodology based on a harmonic state space model and the extended Kalman smoother that enabled us to manipulate the time-varying frequency, amplitude, duration, and harmonic structure of each vocalization (Holmstrom et al., 2009). Based on measures of both spike rate and timing, we measured the heterogeneity of neural responses to the natural vocalizations and their perturbed variants. Using information theoretic measures, we found that heterogeneous response properties of IC neurons contribute to efficient encoding of behaviorally relevant vocalizations.

Materials and Methods

Animals

Twenty-four female CBA/CaJ mice, 7–27 weeks of age, were used in this experiment. The animals were housed with littermates of the same gender until the surgical procedure was performed. The mice were kept under a reversed 12 h light/dark regimen so that the electrophysiological recordings occurred during their awake period. Food and water were provided ad libitum. All animal care and experimental procedures were in accordance with the guidelines of the National Institutes of Health and approved by the Washington State University Institutional Animal Care and Use committee.

Surgical procedures

The surgical procedures used in this study have been described previously in detail (Felix and Portfors, 2007). Briefly, mice were anesthetized with isoflurane inhalation, and a midline incision was made in the scalp. The skin was reflected laterally, and lidocaine gel was applied topically to exposed tissue. The positions of the left and right IC under the skull were located using stereotaxic coordinates and marked with India ink to guide the subsequent craniotomy. A tungsten ground electrode was inserted into the cerebral cortex, and a hollow metal rod was cemented onto the skull. The animal was allowed to recover from general anesthesia for at least 1 h before the electrophysiology experiment began. Typically, experiments were conducted 1 d after surgery.

At the start of electrophysiological recordings, the mouse was given a mild sedative (acepromazine, 5 mg/kg, i.p.) and restrained in Styrofoam molded to the animal's body. The headpin was bolted to the custom-designed stereotax in a sound-attenuating chamber. Using the stereotaxic coordinates, a craniotomy was made over one IC and the dura was removed. A glass micropipette electrode (impedance, 8–20 MΩ) filled with 1 m NaCl was positioned over the IC. Electrode advancement through the IC was controlled by a hydraulic micropositioner (model 650D; David Kopf Instruments) located outside the sound-attenuating chamber. To protect the brain from dehydration, the hole in the skull was covered with petroleum jelly during and between recording sessions. A supplemental dose of acepromazine (2.5 mg/kg, i.p.) was given to animals that continued to struggle or showed other signs of discomfort. Animals that showed continued discomfort were removed for the day, but most mice remained calm throughout a recording session. Each session typically lasted 4–8 h. Data were collected from the same animal on 2 or 3 consecutive days but never more than twice in the same-side IC.

Acoustic stimulation

Stimulus generation was controlled by custom-written software on a personal computer located outside of the sound-attenuating chamber. The stimuli were fed into a high-speed analog-to-digital converter (400,000 samples per second; Microstar Laboratories), a programmable attenuator (model PA5; Tucker Davis Technologies), a power amplifier (model HCA-1000A; Parasound), and a leaf tweeter speaker (Infinity). Acoustic stimuli were presented in free field; the speaker was positioned 10 cm from the ear contralateral to the IC under investigation. The speaker output was calibrated using a ¼ inch condenser microphone (model 4135; Brüel and Kjær) placed at the position that would normally be occupied by the ear of the animal. Sound pressure levels (SPLs) were obtained for frequencies between 6 and 100 kHz at 0 and 10 dB attenuation. Sound pressure levels showed a gradual decline of 3.2 dB per 10 kHz. In our data analysis, a correction was applied based on this decline. A fast Fourier transform of the acoustic signals was done to check for harmonic distortion in the output signals. Distortion products were buried in the noise floor (>50 dB below signal level) and therefore considered negligible.

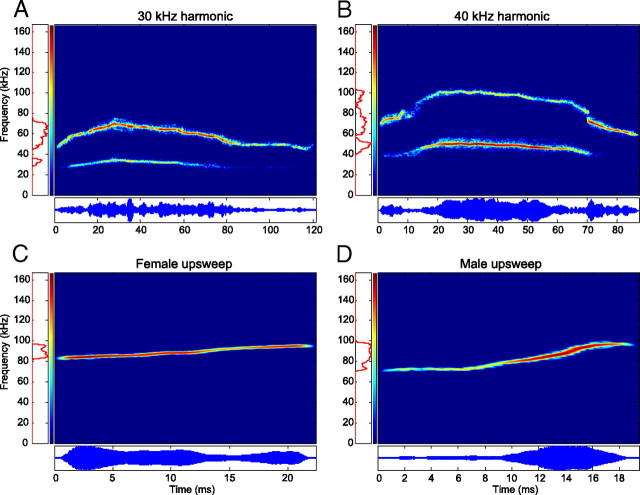
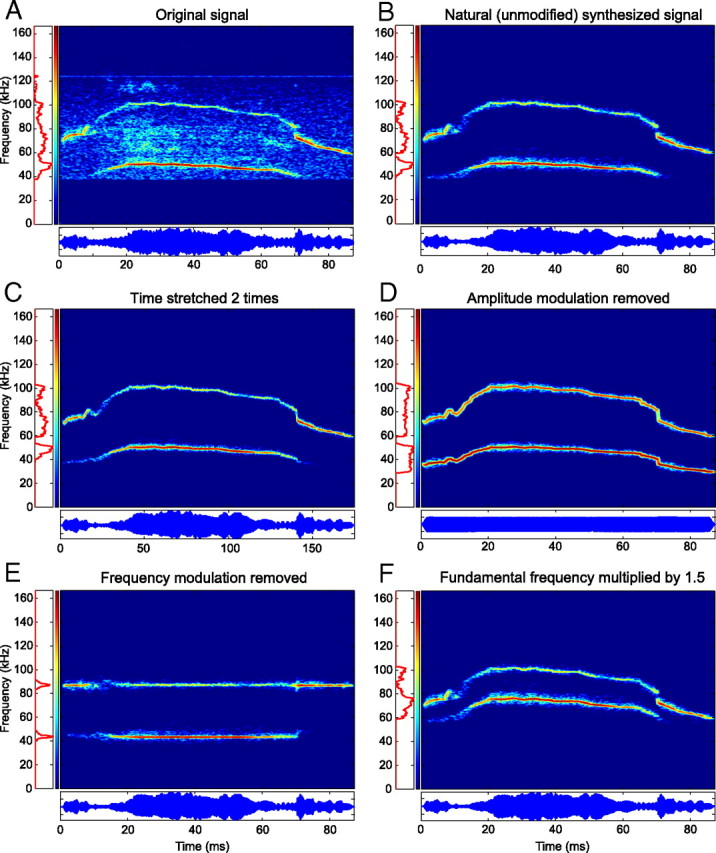
For this study, four representative vocalizations (Fig. 1) commonly emitted by adult CBA/CaJ mice during social interactions were chosen from a collection of calls recorded in our laboratory (Portfors, 2007). The 30 kHz harmonic, 40 kHz harmonic, and male upsweep vocalizations were recorded during male–female pairings and are most likely emitted by the male. The female upsweep vocalization was recorded from a female directly after her litter was removed from the nest. The 30 kHz harmonic vocalization (Fig. 1A) spans a frequency range of 28–74 kHz and is 118 ms in duration. The first (and only) harmonic contains significantly more power than the fundamental. The frequency contour of the vocalization starts low, builds to a peak at ∼30 ms, and slowly falls until the vocalization terminates. The 40 kHz harmonic vocalization (Fig. 1B) spans a frequency range of 40–103 kHz and is ∼85 ms in duration. This vocalization also has a single harmonic and has a low–high–low frequency contour. The majority of the spectral power, however, is found in the fundamental for the middle 66 ms of the vocalization. These two vocalizations were chosen because they were similar in duration and spectral structure but had different frequency ranges. The female upsweep vocalization (Fig. 1C) spans a frequency range of 82–98 kHz and is 22 ms in duration. There is no harmonic structure, and the frequency rises linearly. The male upsweep vocalization (Fig. 1D) spans a frequency range of 70–100 kHz and is 19 ms in duration. There is no harmonic structure, the frequency remains constant for the first 7 ms and then rises linearly, and most of the spectral power lies between 80 and 100 kHz. These two vocalizations were chosen because they are more simple than the harmonic vocalizations, are very similar in spectrotemporal content to one another (with the exception of differences in amplitude modulation), and are emitted by opposite genders of CBA/CaJ mice.

Figure 1. — Spectrograms (top) and oscillograms (bottom) of the natural ultrasonic mouse vocalizations used in the study. A, B, and D were recorded during male–female pairings and were most likely emitted by the male, whereas C was emitted by a female in isolation after her pups were removed. All vocalizations were synthesized from the original recordings to remove excessive background noise.

These vocalizations were analyzed by extracting the time-varying frequency, amplitude, and phase information of their fundamental and harmonic (if present) components with custom-written Matlab code implementing a harmonic state-space signal model and the extended Kalman smoother (Holmstrom et al., 2009). This enabled the synthesis of the original vocalizations in the absence of background noise (Fig. 2A,B). These synthesized yet unmodified vocalizations are referred to as the natural vocalizations throughout this study. Furthermore, by manipulating the extracted parameter values, a set of variants were generated for each vocalization. Vocalizations were upshifted or downshifted in frequency by 5, 10, 15, and 20%. Duration was doubled and halved (Fig. 2C), amplitude modulation (AM) was removed (Fig. 2D), and frequency modulation (FM) was removed (Fig. 2E). For two vocalizations, harmonic structure was disrupted by removal of either the fundamental or the harmonic frequency components. In addition, the fundamental component was upshifted by 5–25% in 5% increments relative to the harmonic frequency while holding the harmonic component constant, or the harmonic frequency was downshifted in identical steps while the fundamental frequency was kept constant (Fig. 2F).

Figure 2. — Analysis and synthesis of the 40 kHz harmonic vocalization. A, Background noise and small recording artifacts are present in the original recording. B, Synthesis of the signal faithfully regenerated the harmonic content of the vocalization in the absence of the noise present in the original recording. C, Duration doubled without altering the frequency. D, AM removed without altering the FM. E, FM removed without altering the AM. F, An inharmonic vocalization generated by multiplying the fundamental frequency by 150%.

Data acquisition and analysis

Extracellular action potentials were recorded from well isolated single units. All units were assumed to be located in the central nucleus of the IC based on the stereotaxic coordinates and penetration depth of the recording sites. Before digitization (10,000 samples per second; Microstar Laboratories), spikes were amplified (model 2400; Dagan), and bandpass filtered (Butterworth 600 Hz to 6 kHz; model 3364; Krohn-Hite). Data collection software was custom written and provided real-time displays of spike trains, poststimulus time histograms (PSTHs), raster plots, and statistics. Raw waveforms were stored for offline analysis and examined after recordings to ensure that only well isolated single units were included in the data analysis. Pure tones varying between 6 and 60 kHz (100 ms duration, 1 ms rise–fall time) at intensities of 10–70 dB SPL were used as search stimuli. Once a single unit was isolated, characteristic frequency (CF) and minimum threshold were determined audiovisually. CF was defined as the frequency that evoked spikes to 50% of the stimulus presentations at the lowest intensity, and minimum threshold was defined as the lowest intensity that evoked spikes to 50% of the stimulus presentations at CF. Tone burst stimuli (50–150 ms duration, 1 ms rise–fall time, 3–4 Hz repetition rate, 200–300 ms recording window) from 6 to 100 kHz were presented in 1–2 kHz steps at 10, 30, and 50 dB above threshold to construct frequency response areas (FRAs). Each frequency–intensity pair was presented 20 times.

All vocalization variants (2 ms rise–fall time, 20 repetitions at a rate of 3–4 Hz, 200–300 ms recording window) were then presented to the neurons at 60–80 dB SPL in 10 dB increments. This range was chosen because the vocalizations are emitted at these intensities in laboratory settings. To classify a neuron as being responsive to a particular stimulus, the neuron had to fire in response to at least 50% of the stimulus presentations, and these spikes could not be attributable to spontaneous activity (determined audiovisually).

Spike metrics.

Three metrics were chosen to objectively evaluate neural responses to the natural versus perturbed vocalizations: one for measuring temporal consistencies among the responses of a neuron to repeated presentations of an identical stimulus, one for measuring temporal similarities between the responses of a neuron to two different stimuli, and the other for measuring firing rate similarities between the responses of a neuron to two different stimuli.

The first, based on the temporal encoding hypothesis, assumes that the timing of spikes conveys important information. This hypothesis is grounded in observations of phase-locked responses throughout the auditory system, originating in the auditory nerve (Galambos and Davis, 1943) and extending to auditory cortex (Steinschneider et al., 1999). Information theoretic analyses of real and simulated sensory neurons have quantified how variability in spike timing reduces the information content of the neural code (Bialek et al., 1991; Rieke et al., 1993, 1995; Rokem et al., 2006; Shamir et al., 2007). We assumed that a neuron that was selective to a particular vocalization would generate responses with the least amount of spike time variability (jitter) across repeated presentations.

The “correlation-based similarity measure” (R_X), as proposed by Schreiber et al. (2003) and used by Wang et al. (2007) and Huetz et al. (2009), measures how well two binary spike trains of equal duration are temporally correlated. The temporal similarity between two binary spike trains, $\vec{b_{1}}$ and $\vec{b_{2}}$ , is found by first convolving each spike train with a Gaussian kernel with mean 0 and SD σ. The correlation between the two filtered spike trains, $\vec{x_{1}}$ and $\vec{x_{2}}$ , can then be calculated as follows:

This results in a temporal similarity measure that is bound between 0 and 1 and is dependent on σ. A value of 0 indicates that the responses are uncorrelated, whereas a value of 1 indicates perfect correlation (the timing of the spikes in the two responses are identical). Two spike trains with zero spikes each are assumed to be uncorrelated and assigned a value of 0. As σ increases from 0, the metric becomes less and less sensitive to differences in spike timing. In this study, σ was set equal to 3 ms. This value was chosen partially based on the results of Wang et al. (2007). In our own analysis, smaller values of σ consistently resulted in negligible values of R_X even for similar spike trains. Higher values of σ, conversely, were not sensitive enough to temporal spike jitter and reduced the contrast between responses that were phase locked and those that were not.

Because a single vocalization was presented a total of N times to a neuron, generating N spike trains, the response consistency for each neuron was calculated as follows:

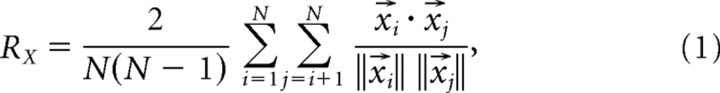graphic file with name zns00310-7510-m02.jpg

which is equal to the mean of all possible distinct and nonredundant correlations of the N spike trains and excludes all self-comparisons (i ≠ j). This metric is again bound between 0 and 1 and indicates how similar the N responses were. A perfectly consistent response indicates that each presentation of the vocalization evoked spikes that all occurred at exactly the same time.

Because two distinct vocalizations were each presented N times to a single neuron, the cross-correlation metric for each neuron was calculated as follows:

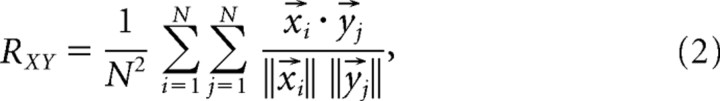graphic file with name zns00310-7510-m03.jpg

which is equal to the mean of all possible cross-correlations between the two sets of N spike trains and is again bound between 0 and 1. This metric provides insight into whether the temporal characteristics of the responses to different stimuli can be used for discriminating between different vocalizations.

For classification purposes, it was important to specify a condition for which the response of a neuron to one vocalization was considered temporally different from the response to a different vocalization. Because a high spontaneous rate to either variant may result in a high response similarity, a simple threshold on R_XY does not satisfy this requirement. Based on a combination of response consistency and response similarity, our temporal similarity measure was defined as follows:

graphic file with name zns00310-7510-m04.jpg

This measure addresses bias implicit in R_XY when neurons have high spontaneous firing rates. Our objective classification rule for determining whether a response to vocalization X was temporally altered relative to vocalization Y was given by the following:

and resulted in very similar classification results as those obtained audiovisually.

Other metrics for comparing the temporal qualities of binary spike trains were also investigated, such as the Victor–Purpura spike timing metric (Victor and Purpura, 1996) and the van Rossum spike distance (van Rossum, 2001). We chose the correlation-based spike metrics because they are normalized. This quality is important for the current study because a primary goal was to calculate these metrics across populations of neurons with differing response properties.

The third metric, based on the rate encoding hypothesis, assumes that the total number of spikes generated by a neuron conveys important information about the acoustic stimuli. This hypothesis is grounded in observations of rate encoding originating in the auditory nerve (Galambos and Davis, 1943) and is the foundation of the ubiquitous frequency response area, a measure of neural selectivity for pure tone stimuli used in all auditory nuclei. Information theoretic analysis of real and simulated neurons have also measured the information capacity of neurons using a rate code (Stein et al., 1972; Bialek et al., 1991). From this point of view, we predicted that a neuron that is selective to a particular variant of a vocalization would generate the most spikes in response to this variant.

The “selectivity index” (Wang and Kadia, 2001; Philibert et al., 2005; Pincherli Castellanos et al., 2007) was chosen to quantify whether a neuron fired more often in response to a natural vocalization as opposed to one of its variants. This metric completely disregards the temporal qualities of the neural response $\vec{b}$ and was calculated using the estimated spike rate r of $\vec{b}$ over the complete recording window. The selectivity index d was given by the following:

graphic file with name zns00310-7510-m06.jpg

where r₁ is the spike rate of the response to the natural vocalization, and r₂ is the spike rate of the response to the modified vocalization. This metric is equal to the normalized spike rate difference and is bound between −1 and 1. A value of 1 indicates that the neuron responded only to the natural vocalization, a value of −1 indicates that the neuron responded only to the modified vocalization, and a value of 0 indicates no difference in the spike rate between the two responses. If both r₁ and r₂ are 0, they are assumed not to differ and are assigned a value of 0.

Because two distinct vocalizations were each presented N times to a neuron, the selectivity index for the responses of the neuron was calculated as follows:

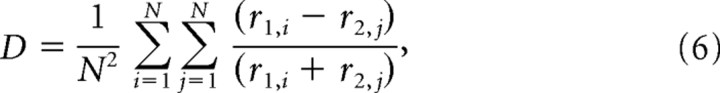graphic file with name zns00310-7510-m07.jpg

which is equal to the mean spike rate distance between the two sets of N spike trains and is bound between −1 and 1. A value above 0 indicates an elevated spike rate in response to the natural vocalization.

Population spike metrics.

Using the above spike metrics, three measures were used to quantify and compare the population response characteristics to each vocalization variant: the median response consistency to the natural vocalization, R̄_X^N, the median response consistency to each modified variant, R̄_X^M, and the mean selectivity index for each modified variant, D̄. The median was used to characterize R_X^N and R_X^M because of the presence of outliers and the non-normality of these distributions. The bootstrap method was used to place 95% confidence intervals on the estimate of the medians. Nonparametric, two-sample Kolmogorov–Smirnov tests were performed to determine whether distributions of R_X values were statistically different. To determine whether the distributions of D were statistically different from the responses to the natural vocalization, two-tailed, two-sample t tests were used. The SD of the distribution was used to generate the confidence intervals.

Predicting responses to complex stimuli from responses to pure tones.

One of the goals of the study was to measure whether responses in the IC to complex vocalization stimuli are more heterogeneous than responses in lower auditory nuclei. Our method for performing this comparison is based on results that show that responses to these stimuli in lower nuclei can be accurately predicted by the pure tone responses of individual neurons (Bauer et al., 2002; Pollak et al., 2003). Using the pure tone responses of neurons in the IC, we can therefore predict how a neuron with the same FRA would respond in a lower nuclei and compare this modeled response with the recorded response of the neuron.

For each neuron, a model was optimized to approximate the relationship between the pure tone input and the resulting firing rate of the neuron, as approximated by the PSTH. The model was a discrete (in both frequency and time) linear finite impulse response filter h_i such that:

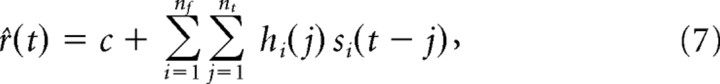graphic file with name zns00310-7510-m08.jpg

where r̂(t) was the predicted time-varying firing rate, c was the spontaneous firing rate of the neuron, i was the frequency band index of the stimulus, j was the time lag index, s_i(t) was the discrete time–frequency representation of the time-varying stimulus, n_f was the number of frequency bands, and n_t was the number of time lag indices. The parametrization of h_i can be interpreted as a spectrotemporal receptive field (STRF) (Aertsen and Johannesma, 1981; Eggermont et al., 1983; Theunissen et al., 2001; Gill et al., 2006). After fitting the model, arbitrary stimuli (e.g., complex vocalizations) can be converted into a spectrographic representation and convolved with the filter, generating a predicted response. Details of the applied modeling methodology can be found in the study by Holmstrom et al. (2007).

Discrimination efficiency among vocalization variants by individual neurons.

To address how efficiently individual neurons discriminated among the modified variants of a vocalization, we asked the following question: provided a single spike train recorded from a given neuron, can we correctly classify which vocalization variant generated it? To quantify the discrimination efficiency of the encoding strategy used by the IC, we used a measure of information transfer between stimuli and neural responses based on a classification task (Victor and Purpura, 1996; Huetz et al., 2009). Given all of the responses of a neuron to each variant of a vocalization, a single response was removed from this set. Classification was then performed by measuring which responses of the vocalization variant were, on average, most similar to the held-out spike train based on the similarity measure S_XY defined in Equation 3, in which the correlation of the single held-out spike train R_X was set equal to 1. This similarity measure was used instead of R_XY because it addresses bias implicit in R_XY when either or both of the responses had a high spontaneous firing rate. By iterating over each spike train from each of the N_vocs vocalization variants, a confusion matrix M was generated. Each element of this matrix, M_i,j, indicated how many spike trains generated from vocalization i were classified as being more similar to the responses generated by vocalization j. In the case of a tie, an equal value was added to each tying entry in M, summing to 1. Using this confusion matrix, the information transfer H of the neuron was calculated as follows:

where M_total was the total number of spike trains being classified, and H was bound between 0 and log₂N_vocs. If the responses of the neuron to each vocalization variant were temporally consistent yet distinct (low similarity values S_XY), spike trains were relatively easy to classify, M approached a diagonal matrix, and H was maximized. If spike trains were difficult to classify because of weak or highly correlated responses, the values of M_i,j approached a uniform distribution, and H was minimized. For each neuron, a different value of H was calculated to indicate how efficiently it discriminated among the variants of a specified vocalization.

To assess how well the population of neurons could discriminate among the set of vocalizations, a similar experiment was performed in which, for a given stimulus, a composite response was generated consisting of one response from each neuron. Because 20 recording were made from each neuron to each stimulus, we created 20 composite population responses to each stimulus. The information transfer of these composite responses, H_pop, could then be calculated to measure the efficiency of the population encoding as a whole at the task of discriminating among the vocalization variants.

Estimating bias in the information transfer.

To correct for the bias H_bias inherent in the calculation of H using a finite amount of recorded data, H_bias was estimated using a shuffling technique (Victor and Purpura, 1997; Huetz et al., 2009). The spike trains for a given neuron were randomly assigned to the different vocalization variants, and the information transfer analysis was performed as described above. This shuffling process was repeated 100 times to calculate the mean (H̄_bias) and SD of H_bias. Only information transfer values greater than H̄_bias + 2 SD were considered significant.

Quantification of response heterogeneity across IC neurons.

A similar information theoretic analysis was performed to address the heterogeneity of responses to stimuli across the neural population. This analysis focused on the following question: ‘provided a single spike train recorded in response to a given vocalization, can we correctly classify which neuron it was recorded from? If the responses of all neurons to a given vocalization were weak or redundant, classification was difficult and the information transfer H was low. As the heterogeneity of the responses increased, so did H. The methodology for this analysis was similar to the vocalization discrimination efficiency analysis performed above. In this case, however, one value of H was calculated for each vocalization variant presented in the study (instead of one for each neuron in the study). H was bound between 0 and log₂N_neurons, where N_neurons was the number of neurons responding to the vocalization class (e.g., 30 kHz harmonic) being analyzed.

The single-unit recording techniques used in this study allow us to focus on the intertrial signal correlations that occur when neurons with overlapping receptive fields respond to the same stimuli. Future studies with multielectrode recordings will allow us to address the effect of heterogeneity of the within-trial noise correlations of a neural population in IC.

Results

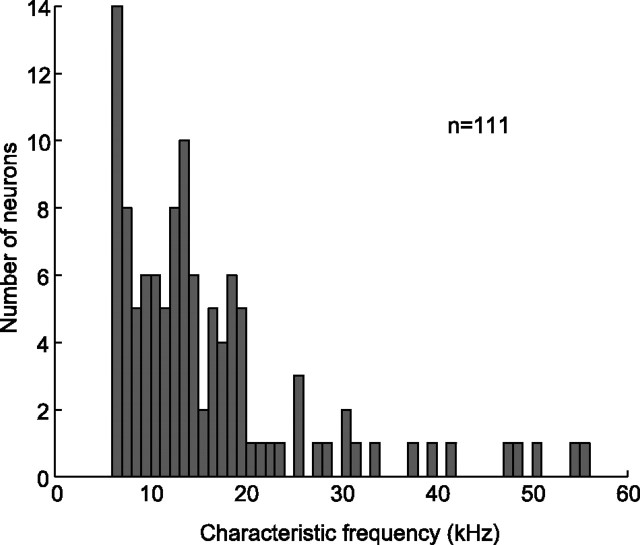
In this study, we were interested in understanding how biologically relevant, complex sounds are encoded in the IC. Mice are a model system for studying this because they possess a typical mammalian auditory system and they emit a wide repertoire of vocalizations under various social contexts (Panksepp et al., 2007; Wang et al., 2008). Despite the ubiquity and behavioral relevance of mouse ultrasonic (>20 kHz) vocalizations, we found an under-representation of neurons with CFs that matched the spectral content of the vocalization stimuli (25–102 kHz). Moreover, of the 111 neurons included in this report, 54% (n = 60) responded to one or more of the natural and/or modified variants, although the majority (n = 45) had a CF below 25 kHz (Fig. 3). Fourteen neurons that responded to the vocalizations did not respond to pure tones above 25 kHz.

Figure 3. — Distribution of characteristic frequencies. Only 10% (n = 12) of the neurons had characteristic frequencies in the range of the ultrasonic vocalizations presented in this study, yet 54% (n = 60) of the neurons responded to one or more vocalizations (natural or modified).

The natural 30 kHz harmonic (n = 28) and 40 kHz harmonic (n = 9) vocalizations elicited responses in neurons across tonotopic layers, whereas the CFs of the neurons that responded to the natural female upsweep (n = 8) were clustered around 15 kHz despite the high spectral content (82–98 kHz) of this vocalization. The median response consistency of neurons responding to the natural female upsweep (R̄_X^N = 0.56 ± 0.21) was higher than that of neurons responding to the natural 30 kHz harmonic and 40 kHz harmonic vocalizations (R̄_X^N = 0.27 ± 0.04 and 0.28 ± 0.11) for a similar median spike rate (r̄ = 15.0 ± 5.1, 18.7 ± 5.5, and 14.0 ± 3.6 spikes/s, respectively). This indicates that the discharge patterns of neurons responding to the natural female upsweep showed less temporal variability than those responding to either natural harmonic vocalization, although the short duration of this vocalization contributes to this effect. The natural male upsweep vocalization failed to elicit substantial responses in our sample of IC neurons, although both the spectral content and duration are similar to that of the female upsweep (Fig. 1C,D).

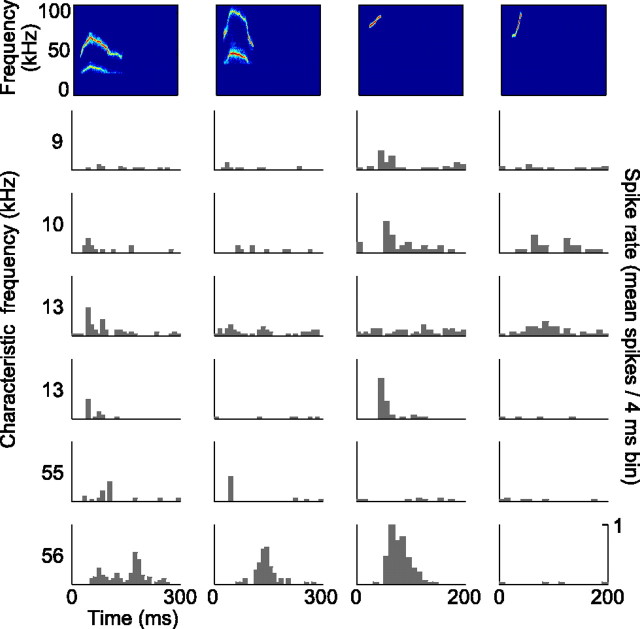
The different natural vocalizations evoked a heterogeneous pattern of responses in our neural population with respect to discharge rate and temporal firing pattern. In addition, the natural 30 kHz harmonic, 40 kHz harmonic, and female upsweep vocalization elicited responses in different subsets of neurons. There was moderate overlap between the subsets; of the 31 neurons that responded to the natural vocalizations, 12 responded to more than one. Neurons with similar CFs and/or FRAs did not always respond to the same natural vocalizations (Fig. 4) (FRAs not shown). Besides diversity in the degree of selectivity for the natural vocalizations across our population, we found response heterogeneity within individual neurons that responded to multiple vocalizations. Some neurons encoded the various vocalizations with different discharge rates, some with different discharge patterns, and some displayed differences in both. An example of a neuron that responded to multiple natural vocalizations with diverse discharge rates and patterns is shown in the bottom row of Figure 4.

Figure 4. — PSTHs of six representative neurons in response to the natural vocalizations. The spectrograms of the vocalizations are displayed at the top. The characteristic frequency of each neuron is indicated on the left of each row of responses. Each of the vocalizations elicited a response in a subset of the neurons, and the responses were heterogeneous with respect to discharge rates and patterns. Even neurons with similar CFs responded differently to the vocalizations (middle rows).

Predicting responses to complex stimuli from responses to pure tones

STRF models were created for all neurons in the experiment using the pure tone responses of each neuron. The normalized mean squared error (NMSE) on the training (pure tone) data was 0.43, with an SD of 0.16. NMSE is normalized by the variance of the target data (the pure tone responses) such that any value below 1 is an improvement on a predicted response equal to the mean firing rate of each neuron. In most cases, the resulting model provided a good fit between the pure tone stimulus and responses across the full range of frequencies and intensities.

The models were then used to predict the responses to the vocalization stimuli. These predictions approximated the responses of neurons in lower auditory nuclei with the same FRAs. The NMSE on these predictions was 0.92, with an SD of 0.3. Although the NMSE was higher than that of the training data (as would be expected from generalizing the model to novel complex stimuli), the predictions were often qualitatively similar to the actual responses to the harmonic vocalizations. The models captured the delay and magnitude of onset responses, adaptation, inhibitory rebounds, and sideband inhibition. This is attributable to the overlap between the spectral content of these vocalizations and the FRAs of many of the neurons in the study. In some cases, however, the predictions deviated significantly from the recorded responses, even when the model fit the pure tone responses accurately. Furthermore, the models incorrectly predicted no response to the female upsweep vocalization variants, except for a few cases in which the frequency downshifted variant did overlap with the FRA of neurons. This provides evidence that the encoding strategy of the IC can be predicted by pure tone responses in some cases but must be dependent on other mechanisms at other times.

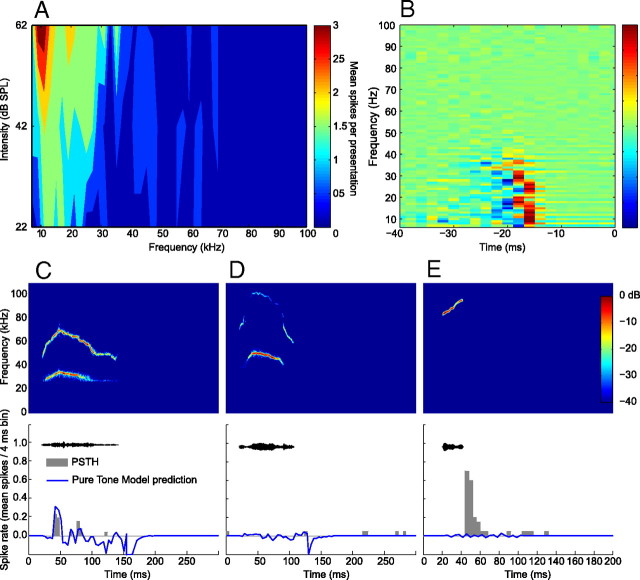
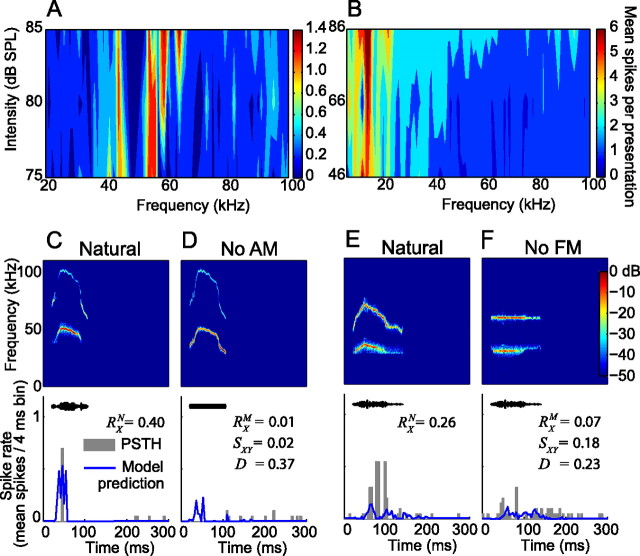
Figure 5 provides an example of the recorded and modeled responses of a neuron to the natural variants of the 30 kHz harmonic, 40 kHz harmonic, and female upsweep vocalizations. The FRA of the neuron ranged between 7 and 35 kHz (Fig. 5A). Using the pure tone responses of this neuron, a model was generated that was the best linear transfer function between the spectrotemporal characteristics of the pure tone training data and the neural responses (Fig. 5B). The vocalization stimuli were converted into a spectrographic representation and convolved with the model to generate the predicted responses. The prediction to the 30 kHz harmonic vocalization closely matched the recorded response (Fig. 5C). This close fit suggests that the encoding of this vocalization could be approximated by a linear summation of independent responses to different frequency components of the vocalization. The lack of overlap between the FRA of the neuron and the spectral content of the 40 kHz harmonic vocalization resulted in negligible recorded and predicted responses (Fig. 5D). The model cannot explain, however, the pronounced response to the female upsweep vocalization (Fig. 5E). This suggests that a different encoding strategy was used that is not based on linear or nonlinear summations of the frequency components of the vocalization.

Changing the spectral content of vocalizations altered neural responses

It was common that neurons that were unresponsive to the natural vocalizations showed a response to their modified variants. This was the case for 24, 22, 5, and 7 neurons for the 30 kHz harmonic, 40 kHz harmonic, female upsweep, and male upsweep vocalizations, respectively. For both harmonic vocalizations, the increase in the number of responsive neurons could to some extent be explained by changes that occurred in the spectral content of these vocalizations after perturbing their acoustic parameters.

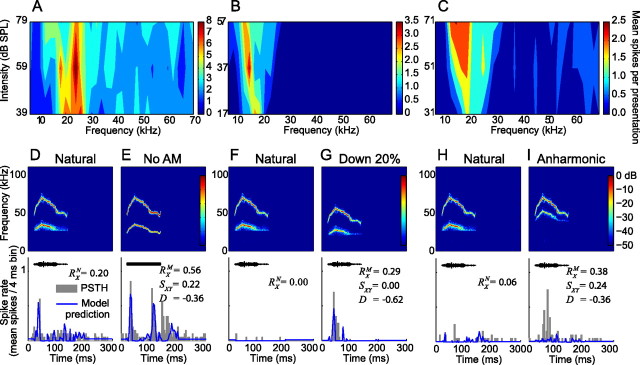
The effect of altering the spectral content of a vocalization on neural responsiveness is illustrated in Figure 6. In these examples, there was little (Fig. 6A) or no overlap (Fig. 6B,C) between the FRAs of the neurons and the spectral content of the natural 30 kHz harmonic vocalization. This is reflected in the weak (Fig. 6D) or absent (Fig. 6F,H) response to this vocalization. Removal of the AM makes the intensity of each harmonic equal to the mean intensity of the harmonic through the entire duration of the vocalization. This resulted in increased energy in the lower frequency tail of the 30 kHz harmonic vocalization, shifting it into the FRA of the neuron shown in Figure 6A. As a result, this neuron drastically increased its discharge rate (D = −0.36 ± 0.14) and thereby also altered its temporal response pattern (S_XY = 0.22 ± 0.08) (Fig. 6E). This response was accurately modeled by the pure tone model. Similarly, downshifting the 30 kHz harmonic vocalization in frequency increased the overlap between its spectral content and the FRA of the neuron in Figure 6B, causing a response (Fig. 6G). The transition from unresponsive to the natural vocalization (R_X^N = 0.00 ± 0.01) to highly responsive to a variant with increased energy in lower frequencies is again reflected in the higher response consistency (R_X^M = 0.29 ± 0.08), low response similarity (S_XY = 0.00 ± 0.02), and negative selectivity index (D = −0.62 ± 0.16). Once more, this response was accurately predicted by the pure tone model. In contrast to the vocalization variants shown in Figure 6, E and G, the spectral content of the inharmonic variant in Figure 6I has shifted away from the FRA of this neuron (Fig. 6C) yet generates a consistent response (R_X^M = 0.38 ± 0.08), whereas the natural vocalization does not (R_X^N = 0.06 ± 0.02; D = −0.36 ± 0.10). Furthermore, the pure tone model predicts the absence of a response to this variant (Fig. 6I). This apparent discrepancy may be attributable to the nonlinear amplification of sounds with multiple frequency components in the cochlea. The distortion product with the highest intensity generated through this mechanism (f₂ − f₁) falls within the FRA of this neuron, perhaps causing its response. Neural sensitivity to cochlear distortion products has been documented previously throughout the auditory system (Goldstein and Kiang, 1968; McAlpine, 2004; Abel and Kössl, 2009; Portfors et al., 2009) and has been proposed as a mechanism for providing sensory cues in communication (Portfors et al., 2009; Warren et al., 2009).

Removal of AM or FM from the vocalizations altered neural responses

The majority of neurons that responded to a natural vocalization or a no-AM variant (32 of 40) changed their discharge rate, discharge pattern, or both when the AM was removed. The discharge rate decreased in 31% [27 of 87 (Table 1)] and increased in 40% [35 of 87 (Table 1)] of the responses. Likewise, the majority of neurons that responded to a natural vocalization or a no-FM variant (25 of 31) changed their discharge rate, discharge pattern, or both when the FM was removed. The discharge rate decreased in 34% [31 of 87 (Table 1)] and increased in 32% [28 of 87 (Table 1)] of the responses. This indicates that both AM and FM are important acoustic features in creating selectivity to natural vocalizations within individual IC neurons. Figure 7 displays two such cases.

Table 1.

Modifying acoustic parameters of vocalizations altered neural responses in a heterogeneous manner

	↑	↑/Δ	↓	↓/Δ	Δ	∼
30 kHz harmonic
AM removed	9	11	9	2	2	13
FM removed	8	6	13	2	2	15
Time compressed	9	3	13	4	3	18
Time stretched	10	10	9	1	3	12
Harmonic removed	4	5	5	6	2	15
Fundamental removed	5	3	9	6	1	14
40 kHz harmonic
AM removed	6	7	7	1	1	6
FM removed	10	2	7	1	1	7
Time compressed	5	2	7	3	2	11
Time stretched	4	5	10	1	2	6
Harmonic removed	4	0	5	4	0	9
Fundamental removed	5	0	4	2	2	9
Female upsweep
AM removed	2	0	0	8	0	3
FM removed	2	0	2	6	0	3
Time compressed	3	0	4	3	0	3
Time stretched	4	2	1	0	1	5

Open in a new tab

Number of neurons that altered their spike rate or timing to each modification of each natural vocalization. Only neurons responding to one or more variant of each vocalization are included. ↑ indicates that the number of spikes increased by >20%. ↓ indicates that the number of spikes decreased by >20%. Δ indicates that the temporal pattern changed significantly, as determined by the classification rule defined in Equation 4. ∼ indicates that no significant changes occurred in either spike rate or temporal pattern.

Figure 7. — AM and FM are important features for creating selective neural responses. A, B, The FRAs of two neurons. C, This neuron consistently responded to the natural 40 kHz harmonic vocalization (R_X^N = 0.40), which was predicted by the pure tone model. D, The lack of response to the no-AM variant is indicated by the reduced R_X^M value, low response similarity (*S_XY* = 0.02), and large, positive selectivity index (D = 0.37). The predicted response was also attenuated as a result of increased power introduced into the inhibitory sideband captured by the model. E, This neuron showed a robust response to the natural 30 kHz vocalization, which was not captured by the model because the spectral power of the vocalization lies outside the FRA of the neuron. F, The response was significantly reduced after removal of the FM from this vocalization.

The FRA of the first neuron (Fig. 7A) overlapped with the spectral content of the 40 kHz harmonic vocalization, resulting in a consistent response (R_X^N = 0.40 ± 0.13) that was predicted by the pure tone model (Fig. 7C). After removal of the AM, the recorded response disappeared and the modeled response was significantly reduced (Fig. 7D) (R_X^M = 0.01 ± 0.03). Response selectivity for the natural vocalization translated into a positive selectivity index (D = 0.37 ± 0.10) and low response similarity (S_XY = 0.02 ± 0.02). The no-AM variant of this vocalization had more energy in the 30–52 kHz band at onset and triggered sideband inhibition that was captured by the model. The second neuron showed selectivity to the natural variant of the 30 kHz harmonic vocalization, although its FRA did not overlap with the frequency content of the vocalization (Fig. 7B). The pure tone model did not predict the strong response to the natural variant (Fig. 7E). Removal of the FM diminished the response (R_X decreased from 0.26 ± 0.08 to 0.07 ± 0.02), generating a positive selectivity index (D = 0.23 ± 0.10) and low response similarity (S_XY = 0.18 ± 0.06). The prediction of a weak response to the no-FM variant remains relatively unchanged (Fig. 7F) because the spectral content of the variant is above the FRA of this neuron. These results suggest that the FM in the vocalization is responsible for evoking the neural response, although the frequency content of the vocalization is outside the FRA of the neuron. This neuron may be responding to cochlear distortions generated by the FM sweep as we have shown previously to occur in IC neurons (Portfors et al., 2009).

Vocalization duration modulated neural responses

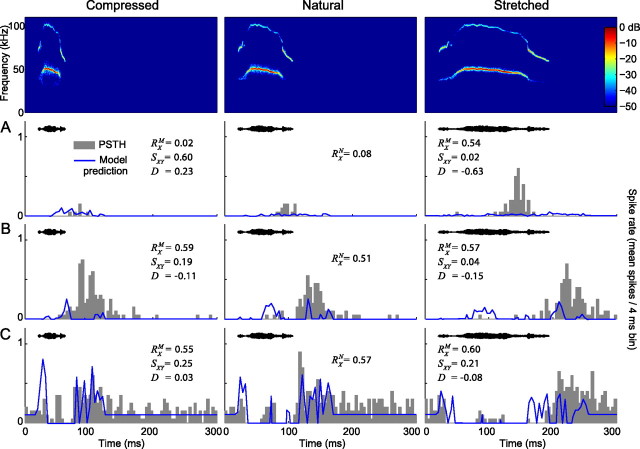
As with removal of AM or FM, modifying the duration of the vocalizations changed the responses in the majority of the recorded neurons. For the most part, neurons decreased their discharge rate in response to the compressed vocalizations and increased their discharge rate in response to the stretched vocalizations (Table 1). To illustrate the response heterogeneity across our neural population, several ways that neurons modulated their response to duration-altered variants of the 40 kHz harmonic vocalization are shown in Figure 8. The neuron in Figure 8A was selective to the time-stretched variant. The response consistency R_X of this neuron for the compressed, natural, and stretched vocalization were 0.02 ± 0.01, 0.08 ± 0.02, and 0.54 ± 0.10, respectively. This indicates that the response pattern to the stretched version had the least temporal variability during repeated presentations of the stimulus. Furthermore, the selectivity index (D = −0.63 ± 0.18) signifies an increased discharge rate in response to the stretched vocalization. The strong response to the stretched variant was not predicted by the pure tone model, indicating that a mechanism other than facilitory frequency interaction may be contributing to the robust response.

Figure 8. — Vocalization duration modulates the responses of neurons in the IC. ***A–C***, Responses to the time compressed (half as long; left column), natural (middle column), and time-stretched (twice as long; right column) 40 kHz harmonic vocalization are shown for three neurons. The neuron in A was selective for the stretched variant (R_X^M = 0.54 and D = −0.63), although the pure tone model predicts no response to this variant. The neurons in B and C displayed consistent responses regardless of the duration of the stimulus (*R_X* ranges from 0.55 to 0.60), resulting in low values of D. However, both of these neurons shifted the timing of the response in accordance with the duration of the vocalization (*S_XY* ≤ 0.25). Note that the neuron in C displayed a sustained inhibitory response and that the inhibitory rebound is most apparent in response to the natural vocalization.

The high response consistencies (R_X = 0.55 ± 0.14 to 0.60 ± 0.12) together with the selectivity indices close to 0 (D = −0.015 ± 0.07 to 0.03 ± 0.01) of the neurons shown in Figure 8, B and C, suggest that these neurons do not prefer one duration-altered variant over another. When the response similarity is taken into account, however, it becomes clear that the temporal response patterns changed from one variant to the next in both neurons (S_XY ≤ 0.25). This encoding scheme would be particularly useful for discriminating between vocalization variants with different durations.

Population responses

By characterizing responses to natural vocalizations and perturbed variants of these vocalizations, we have shown that the selectivity of the individual neurons can be created through sensitivity to particular acoustic parameters of the vocalizations. In some cases, this sensitivity can be explained by the pure tone responses of the neurons, whereas in other cases, it cannot. Here, we address whether there were trends in selectivity across the population of responding neurons. This population analysis was performed for each vocalization independently by focusing on the subset of neurons that responded to the vocalization or one of its variants. Of the 60 neurons that responded to our suite of vocalization stimuli (including all natural vocalizations and their variants), 52 responded to the 30 kHz harmonic, 31 to the 40 kHz harmonic, 13 to the female upsweep, and 7 to the male upsweep vocalizations.

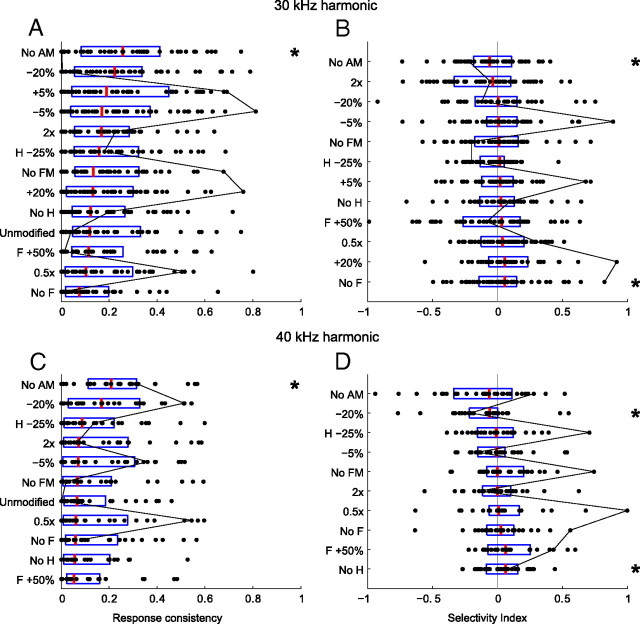
For the two harmonic vocalizations, we found a heterogeneous mixture of responses to the natural and modified vocalizations (Fig. 9). The evoked response consistencies for each vocalization variant were distributed broadly, with many neurons having low response consistencies and fewer having high values (Fig. 9A,C). The evoked selectivity indices for each vocalization variant were also distributed broadly (Fig. 9B,D), and this metric was approximately distributed normally. Individual neurons often varied significantly in their response consistencies and selectivities across the set of variants, as exemplified by the black line in Figure 9, following the values of a single neuron.

Figure 9. — A, C, Population response consistencies (*R_X*) for neurons responding to at least one variant of the 30 kHz (A) or 40 kHz (C) harmonic vocalization, sorted from most consistent (top) to least consistent (bottom). B, D, Population selectivity indices (D), sorted from least selective to the natural vocalization (top) to most selective (bottom). Box plots indicate the range of the second and third quartile of the distribution along with the median. The black line connects the metric values for a single neuron across the vocalization variants, indicating how variable a single neuron may be to perturbations in the vocalization characteristics. There is evidence of significant heterogeneity in the responses to the vocalizations from both a spike timing (A, C) and a spike rate (B, D) perspective. Except for the no-AM variant, mean response consistencies did not differ significantly from the responses to the natural vocalizations (similar temporal jitter), nor was there a significant difference in mean spike rate between the responses to the natural vocalizations and most modified vocalizations. * indicates distributions that were significantly different from the distribution of the natural variant (two-sample Kolmogorov–Smirnov test, α = 0.05).

The median response consistency was highest to the no-AM variant, and the distribution of these response consistencies (R_X^M) was statistically larger than the distribution of response consistencies (R_X^N) to the natural vocalizations (two-sample Kolmogorov–Smirnov test, α = 0.05). All other variants evoked distributions of response consistencies that were not statistically different from the responses to the natural vocalization. Because the overlap between the spectral content of the no-AM variants and the FRAs of the neurons are larger than for any other variant, almost half of the neural population increased their discharge rate in response to these vocalizations (Table 1). This led to a statistically significant increase in discharge rate (D̄ = −0.09 ± 0.10; two-tailed, two-sample t test, α = 0.05) for the 30 kHz harmonic vocalization variant without AM. Similarly, downshifting the 40 kHz harmonic vocalization increased the overlap between spectral content and FRAs, which resulted in a statistically significant increase in discharge rate (D̄ = −0.11 ± 0.09; two-tailed, two-sample t test, α = 0.05).

Disrupting the harmonic structure resulted in an overall decrease in discharge rate. This decrease was significant (two-sample Kolmogorov–Smirnov test, α = 0.05) for the variant with the fundamental removed for the 30 kHz harmonic vocalization (D̄ = 0.09 ± 0.05) and the variant with the harmonic removed for the 40 kHz harmonic vocalization (D̄ = 0.10 ± 0.08). For the no-fundamental variant of the 30 kHz vocalization, this is probably primarily attributable to a decrease in spectral energy within the FRAs of the neurons. However, removal of the harmonic from the 40 kHz vocalization does not affect overlap between FRAs and spectral content, indicating that the harmonic structure is important for generating a response.

These results indicate no selectivity for the natural variant of each vocalization. On the contrary, they indicate that nearly all perturbations of the harmonic vocalizations resulted in similarly robust responses from both a spike timing and spike rate perspective. Each variant, however, was encoded very differently, with different subsets of neurons responding to each variant or significantly different responses by individual neurons responding to multiple variants.

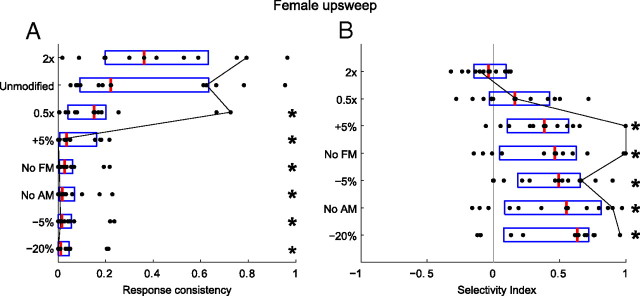
In contrast to responses to the harmonic vocalizations, responses to the female upsweep displayed strong selectivity to the natural vocalization (Fig. 10). With the exception of the time-stretched variant, the median response consistency and mean discharge rates were highest to the natural variant (R_X^N > R_X^M and D̄ > 0). This suggests that the female upsweep is encoded by neurons that are very sensitive to the spectrotemporal properties of this vocalization and that similar stimuli may be filtered out precortically.

Figure 10. — A, Population response consistencies (*R_X*) for neurons responding to at least one variant of the female upsweep vocalization, sorted from most consistent (top) to least consistent (bottom). B, Population selectivity indices (D), sorted from least selective to the natural vocalization (top) to most selective (bottom). Box plots indicate the range of the second and third quartile of the distribution along with the median. The black line connects the metric values for a single neuron across the vocalization variants. There is significant evidence of population selectivity to the natural vocalizations from both a spike timing (A) and a spike rate (B) perspective. With the exception of the stretched variant, response consistency values differed significantly from the responses to the natural vocalizations (more temporal jitter), and there were significant differences in mean spike rate between the responses to the natural vocalizations and the modified vocalizations. * indicates distributions that were significantly different from the distribution of the natural variant (two-sample Kolmogorov–Smirnov test, α = 0.05).

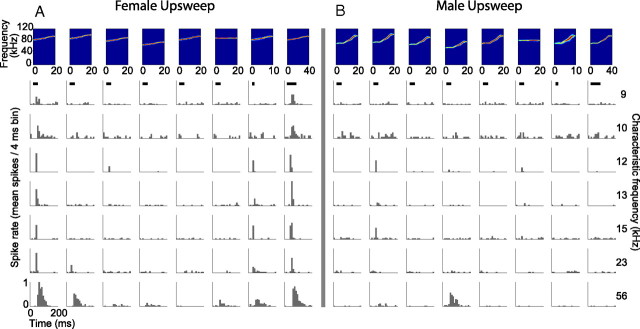
This result is particularly striking when considering how similar the male and female upsweep vocalizations are with respect to frequency and duration (Fig. 1C,D). The only noteworthy differences between these two vocalizations are AM and FM, suggesting that the subpopulation of neurons that respond to the female upsweep are highly AM or FM selective. However, the time-stretched variant of the male upsweep is very similar to the natural female upsweep (with respect to FM sweep rate, range, and bandwidth) yet does not elicit responses in neurons that do respond to the female upsweep vocalization. This finding suggests that selectivity to AM or AM rate is the underlying reason for the differences in responses to the two vocalizations. Again, the spectral content of the upsweep vocalization is outside the FRA of the neurons. One possible explanation for these responses is that AM can create cochlear distortion products that evoke responses in IC neurons even when the carrier frequency of the signal is outside the neural FRA (McAlpine, 2004). Consequently, when AM is removed, the cochlear distortions are not generated and no response is elicited.

The differences in selectivity to the female upsweep vocalization (Fig. 11A) compared with the male upsweep vocalization (Fig. 11B) are displayed for seven representative neurons. As can be seen in the first column of Figure 11A, the responses to the natural female upsweep vocalization showed very little variability in the presence and timing of spikes across stimulus presentations. This results in a high R̄_X^N. Responses to the time-stretched variant (Fig. 11A, last column) were similar in temporal pattern but were often slightly higher in discharge rate. This accounts for the negative value of D̄ for this variant (Fig. 10) (data not significant). Changes in AM, FM, and frequency shifting evoked little or no response from the neurons, resulting in low values of R̄_X^M and high values of D̄. Figure 11B shows the responses of the same neurons to the male upsweep vocalization. At best, the neurons responded weakly to the modified vocalizations, resulting in the low values of R̄_X^N, R̄_X^M, and D̄ (data not shown).

Figure 11. — Specific examples of responses to variants of the female (A) and male (B) upsweep vocalizations showing that the neural population was selective to the natural (A, first column) and time-stretched (A, last column) variants of the female upsweep vocalization. The spectrograms of the vocalizations are displayed across the top in the following order: natural, +5%, −5%, −20%, no AM, no FM, time compressed, time stretched. The characteristic frequency of each neuron is displayed on the right. Neurons with a wide range of CFs responded to the female upsweep vocalization, although its spectral content is far outside the FRA of each neuron and the pure tone models predicted no response. Despite the similarity in duration and spectral content to the female upsweep vocalization, the natural male upsweep vocalization did not elicit substantial responses in the neuron population, and very few neurons responded to any of its variants.

Efficiency of vocalization discrimination in the IC

A primary motivation behind this study was to objectively test whether the IC encodes information more efficiently than lower auditory nuclei by increasing the heterogeneity of the neural responses to complex vocalization stimuli. This hypothesis is based on evidence that the IC is the first site in the ascending auditory system that shows selectivity to complex features found in vocalizations (Klug et al., 2002) and that increasing the heterogeneity of neural responses results in a theoretical increase in information throughput (Gawne and Richmond, 1993; Bell and Sejnowski, 1995; Shamir and Sompolinsky, 2006; Chelaru and Dragoi, 2008).

For each neuron in the study, the information transfer H was calculated to quantify how efficiently the neuron could discriminate among the variants of each natural vocalization (e.g., 30 kHz harmonic). If a particular neuron had weak or correlated responses to each variant of a vocalization, then it was difficult to classify what vocalization was responsible for a particular response and H was low for the neuron. If the responses were highly heterogeneous, then classification was possible and H was increased.

It has been shown that the pure tone response characteristics of neurons from lower auditory nuclei are sufficient to estimate their responses to complex vocalization stimuli (Bauer et al., 2002; Pollak et al., 2003). To approximate how the neurons in our study of the IC would respond if they had been in a lower auditory nucleus, we used a pure tone spectrotemporal modeling methodology (see Materials and Methods) to predict their responses to our vocalization stimuli. The output of the model was an estimated PSTH with a bin width of 2 ms (chosen to approximate the refractory period of the neuron). We were then able to generate simulated spike trains for each neuron and vocalization by interpreting these modeled PSTHs as the probability of finding a spike within each 2 ms window. Using this method, we generated a set of simulated spike trains of equal number to the recorded data (20 spike trains per stimulus) and performed an identical assessment of the information transfer, H, of each neuron for each vocalization class. This enabled us to directly compare the discrimination efficiency of neurons in the IC with the discrimination efficiency of neurons from lower auditory nuclei. Figure 12 summarizes the results of this analysis.

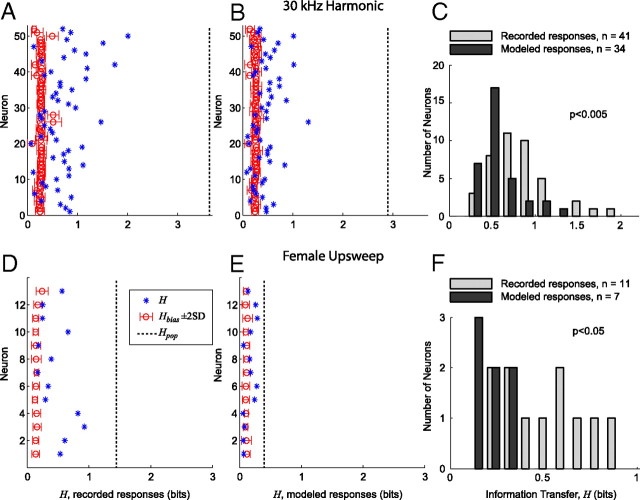
Figure 12. — IC neurons use a more efficient encoding strategy for discrimination among vocalizations than an encoding strategy based on modeled responses by lower auditory nuclei. A, Information transfer (H) between stimuli and responses for each neuron that responded to at least one of the 30 kHz harmonic vocalization variants. The open circle and error bars indicate H̄_bias + 2 SD. The x-axis spans the bounds of H [(0 log₂N_vocs) bits]. The dashed line indicates H_pop, the information transfer of the neural population as a whole. B, H for each neuron measured from the modeled responses to the 30 kHz harmonic vocalization variants. C, Histogram comparing the recorded and modeled distributions of H for the neurons with significant information transfer (H̄_bias + 2 SD). H for the recorded data is significantly greater than H for the modeled data (two-sample Kolmogorov–Smirnov test, p < 0.005). D, H between stimuli and response for each neuron that responded to at least one of the female upsweep vocalization variants. E, H for each neuron measured from the modeled responses to the female upsweep vocalization variants. F, Histogram comparing the recorded and modeled distributions of H for the neurons with significant information transfer (H̄_bias + 2 SD). H for the recorded data is significantly greater than H for the modeled data (two-sample Kolmogorov–Smirnov test, p < 0.05).

For the 30 kHz harmonic vocalization (Fig. 12A–C), the 52 neurons that responded to at least one variant of this vocalization were included in the analysis. H and H̄_bias ± 2 SD were calculated for both the recorded data (Fig. 12A) and the modeled data (Fig. 12B). The maximum information transfer possible was log₂N_vocs = 3.7 bits, which is attainable if each spike train could unambiguously be matched with the associated vocalization using the similarity measure S_XY. For the recorded data, 41 of the 52 neurons had significant values of H (H > H̄_bias ± 2 SD). The maximum information transfer H_max was 2.01 bits, and the mean information transfer H̄ was 0.83 bits. For the modeled data, 34 of the 52 neurons had significant values of H: H_max = 1.31 bits and H̄ = 0.57 bits. The distributions of H for the recorded and modeled data (Fig. 12C) were significantly different (two-sample Kolmogorov–Smirnov test, p < 0.005). When taken a whole, as if they fired in synchrony to each vocalization stimuli, the information transfer of the neural population, H_pop, was 3.62 bits for the recorded data and 2.91 bits for the modeled data. This result shows that the set of 52 neurons could almost perfectly classify each vocalization (2.6% error rate). This result also shows that the increased heterogeneity of the recorded responses led to a more efficient population encoding than the less heterogeneous modeled responses.

For the female upsweep vocalization (Fig. 12D–F), the 13 neurons that responded to at least one variant were included in the analysis. H and H̄_bias ± 2 SD were calculated for both the recorded data (Fig. 12E) and the modeled data (Fig. 12F). The maximum information transfer possible was log₂N_vocs = 3 bits. There were fewer vocalizations in this analysis because frequency upshifted variants were not included and the female upsweep is not harmonically structured. For the recorded data, 11 of the 13 neurons had significant values of H (H > H̄_bias ± 2 SD). The maximum information transfer H_max was 0.92 bits, and the mean information transfer H̄ was 0.51 bits. For the modeled data, 7 of the 13 neurons had significant values of H: H_max = 0.28 bits and H̄ = 0.22 bits. The distributions of H for the recorded and modeled data (Fig. 12F) were significantly different (two-sample Kolmogorov–Smirnov test, p < 0.05). For this vocalization, H_pop was 1.40 bits for the recorded data and 0.37 bits for the modeled data. This again shows that the increased heterogeneity of the recorded responses led to a more efficient population encoding than the less heterogeneous modeled responses. Because these responses were not as heterogeneous as the responses to the 30 kHz harmonic vocalization, however, it was not possible to uniquely determine the source vocalization using our recorded neural population and classification methodology.

Both of these cases indicate that individual neurons encoded the 30 kHz harmonic and female upsweep vocalizations such that they provided useful information for discriminating among the variants of these vocalizations. Although the modeled responses to the 30 kHz harmonic vocalization variants were often qualitatively similar to the recorded responses, significantly more information was available within the recorded responses for the task of discriminating among the vocalization variants. Furthermore, the analysis based on the recorded responses of the neural population resulted in more neurons with significant values of H than did the analysis based on the responses generated by the pure tone model of each neuron (n = 41 vs n = 34 for the 30 kHz harmonic vocalization and n = 11 vs n = 7 for the female upsweep vocalization), meaning that a higher percentage of the neural population contributed to the encoding of this vocalization. This suggest that the actual responses were further modulated by the system to increase their heterogeneity and information throughput. For the female upsweep vocalization, the differences between the recorded and modeled H populations were even more significant because the models almost always predicted the absence of any response. Classification between the natural, time-compressed, and time-expanded variants was difficult because of the correlation of these responses (Fig. 11A), however. In this case, most of the information transfer can be attributed to the ease of classifying between the set of variants that elicited a response and the set of those that did not.

Heterogeneity of responses across the neural population

Although the previous efficiency measure was focused on the heterogeneity of responses from a single neuron to a suite of vocalization stimuli, another efficiency measure is based on the heterogeneity of responses across the neural population to individual vocalizations. An increase in this type of heterogeneity has been shown theoretically to increase information throughput of neural populations by reducing within-trial noise correlations (Shamir and Sompolinsky, 2006; Chelaru and Dragoi, 2008) and intertrial signal correlations (Gawne and Richmond, 1993; Bell and Sejnowski, 1995; Chechik et al., 2006).

For each vocalization variant in the study, the information transfer H was calculated to quantify how heterogeneous the responses were across the whole neural population. If each neuron in the study had weak or correlated responses to a particular vocalization variant, then it would be difficult to classify which neuron a given response could be attributed to and H would be low for the vocalization variant. If the responses were highly heterogeneous, then classification was possible and H was high. Figure 13 summarizes the results of this analysis.

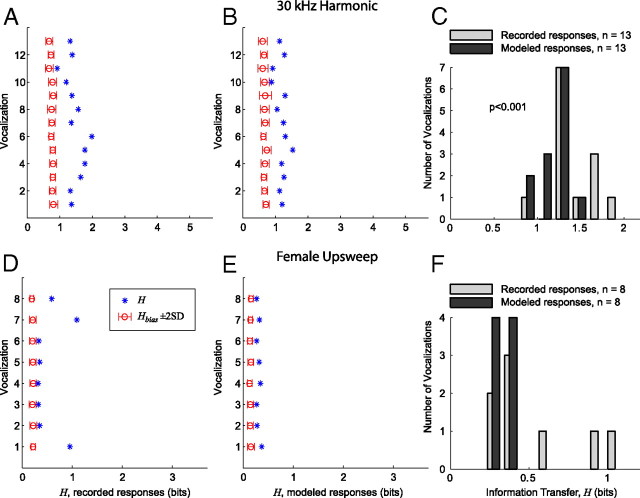
Figure 13. — IC responses are more heterogeneous to a given vocalization than is predicted by modeled responses from lower auditory nuclei. A, Information transfer (H) for each variant of the 30 kHz harmonic vocalization, measured across all neurons that responded to at least one of the variants. The open circle and error bars indicate H̄_bias + 2 SD. The x-axis spans the bounds of H [(0 log₂N_neurons) bits]. B, H for each variant of the 30 kHz harmonic vocalization using the responses modeled from the pure tone response properties of each neuron. C, Histogram comparing the recorded and modeled distributions of H for the vocalization variants with significant information transfer (H̄_bias + 2 SD). H for the recorded data is significantly greater than H for the modeled data (two-sample Kolmogorov–Smirnov test, p < 0.001). D, Information transfer (H) for each variant of the female upsweep vocalization, measured across all neurons that responded to at least one of the variants. The three variants with the elevated values of H are as follows: natural (bottom), time stretched, and time compressed (top). E, H for each variant of the female upsweep vocalization using the responses modeled from the pure tone response properties of each neuron. F, Histogram comparing the recorded and modeled distributions of H for the vocalization variants with significant information transfer (H̄_bias + 2 SD). H for the recorded data and H for the modeled data are not significantly different. This is primarily attributable to the small sample size (n = 8).

For the 30 kHz harmonic vocalization (Fig. 13A–C), the 52 neurons that responded to at least one variant were included in the analysis. H and H̄_bias ± 2 SD were calculated for both the recorded data (Fig. 13A) and the modeled data (Fig. 13B). The maximum information transfer possible was log₂N_neurons = 5.2 bits, which occurs if each spike train could unambiguously be matched with the associated neuron using the similarity measure S_XY defined in Equation 3. For both the recorded and modeled data, all 13 vocalization variants had significant values of H (H > H̄_bias + 2 SD). The recorded data had a maximum information transfer H_max = 1.98 bits and a mean information transfer H̄ = 1.46 bits. For the modeled data, H_max = 1.53 bits and H̄ = 1.17 bits. The distributions of H for the recorded and modeled data were significantly different (two-sample Kolmogorov–Smirnov test, p < 0.001).

For the female upsweep vocalization (Fig. 13D–F), the 13 neurons that responded to at least one variant were included in the analysis. H and H̄_bias ± 2 SD were calculated for both the recorded data (Fig. 13D) and the modeled data (Fig. 13E). The maximum information transfer possible was log₂N_neurons = 3.5 bits. For both the recorded and modeled data, all eight vocalization variants had significant values of H (H > H̄_bias + 2 SD). The recorded data had a maximum information transfer H_max = 1.09 bits and a mean information transfer H̄ = 0.54 bits. For the modeled data, H_max = 0.39 bits and H̄ = 0.33 bits. The distributions of H for the recorded and modeled data were not significantly different in this case (two-sample Kolmogorov–Smirnov test), although the data indicate that H was greater for the recorded responses. The lack of statistical significance is primarily attributable to the small number of samples (n = 8).

Although the modeled responses to the 30 kHz vocalization captured many of the salient features of the recorded responses, they were not as heterogeneous, resulting in lower values of H for every vocalization and a less efficient encoding. For the female upsweep vocalization, H was very low for the five vocalization variants that elicited insignificant responses in the population for both the recorded and modeled responses. Although the recorded responses to the natural, time-compressed, and time-expanded variants were highly correlated across the neurons (Fig. 11A), it was still often possible to classify which neuron generated a particular response based on small differences in the temporal pattern of the response, resulting in higher values of H for these vocalizations.

Both of these cases again indicate that neurons in the IC have responses that are more heterogeneous to a given vocalization than would be expected in lower auditory nuclei, resulting in a more efficient encoding.

Discussion

Our results shows that, based on measures of both spike rate and spike timing, neurons in mouse IC have heterogeneous receptive fields. This heterogeneity leads to a decrease in signal correlation across the neural population, thereby increasing the encoding efficiency for behaviorally relevant stimuli (relative to lower auditory nuclei).

Heterogeneous response properties in the IC

In this study, we used a novel stimulus design methodology based on a harmonic state space model and the extended Kalman smoother that enabled us to manipulate specific acoustic features in natural mouse vocalizations and to generate a set of modified vocalizations. Altering a single vocalization and testing for selectivity among the variants revealed that the responses of IC neurons changed in many different ways.

The 30 and 40 kHz harmonic vocalizations used in our study are four to six times longer than the upsweep vocalizations and have significant AM and FM variability. These vocalizations generated responses in large subsets of neurons: 47% (n = 52) and 28% (n = 31), respectively. The populations that responded to each variant had highly heterogeneous mixtures of spike rates and temporal response consistencies. Whereas the distributions of spike rates and temporal consistencies were similar for the variants of each vocalization, the responses of individual neurons often varied significantly with each perturbation. These results show that the IC is highly sensitive to perturbations of acoustic features in these stimuli, resulting in a distinct neural representation of each vocalization.

Response heterogeneity has been reported in numerous cortical structures (Chelaru and Dragoi, 2008). In primary visual cortex, there is a broad diversity of neural selectivity for complex stimuli across all cortical layers (Hubel and Wiesel, 1962; Ringach et al., 2002). Similarly, the somatosensory cortex has substantial variability of receptive field size, overlap, and position across layers and within layers (Haupt et al., 2004). Our results suggest that heterogeneity in receptive fields and response types is already present in precortical auditory pathways.

In contrast to the harmonic vocalizations, the female and male upsweep vocalizations used in our study are short in duration and have monotonic FM, no harmonic structure, and simple AM envelopes. We found significant differences between the encoding of these and the harmonic vocalizations. Only 13 and 7 neurons responded to variants of the female and male upsweep vocalizations, respectively. We found strong evidence of neural selectivity for the natural and duration modified variants of the female vocalization. Although the median number of spikes present in the response of each neuron to the natural variant of this vocalization was not significantly different than the harmonic vocalizations (r̄ = 15.0 ± 5.1 vs 18.7 ± 5.5 and 14.0 ± 3.6 spikes/s for the 30 kHz and 40 kHz harmonic vocalizations), the timing precision was significantly greater (R̄_X^N = 0.56 ± 0.21 vs 0.27 ± 0.04 and 0.28 ± 0.11). All other variants of the vocalization elicited negligible responses. This suggests an encoding of this vocalization that filters out all similar, and possibly irrelevant, stimuli.

These results are in agreement with those reported by Liu and Schreiner (2007) in mouse primary auditory cortex A1, who found that the timing of spikes, and not just the average spike count, is an important aspect of the neural encoding of vocalizations. Furthermore, they observed selectivity for the natural versions of their ultrasonic vocalization stimuli, which were simple in structure and similar to the female upsweep vocalization we used.

Selectivity for the natural variants of conspecific vocalizations has been reported in the auditory cortex (Gehr et al., 2000; Wang and Kadia, 2001; Grace et al., 2003; Wang et al., 2005; Amin et al., 2007) and the IC (Pincherli Castellanos et al., 2007) of mammals and birds. Contradictory results have been reported, however, in both the auditory thalamus (Philibert et al., 2005; Huetz et al., 2009) and the IC (Suta et al., 2003) using anesthetized animals. This has led to speculation that selectivity may be species, state, and nuclei specific (Philibert et al., 2005). Our finding of neural population selectivity only for the simple vocalizations indicates that both strategies are present in the IC and that these previous results are not necessarily contradictory.

Despite being very similar in frequency and duration, the natural variant of the male upsweep vocalization did not generate substantial responses in the neural population. It is possible that our sample set of neurons did not include any neurons that responded to this vocalization. Alternately, it is possible that this vocalization is filtered out by this stage of processing, thereby simplifying the discrimination task for higher-level processing.

Different neural mechanisms likely underlie the heterogeneous responses to vocalizations seen in the IC. In the simplest case, some neurons respond to all vocalizations that have energy within the frequency tuning curve of the neuron. In other cases, inhibition sculpts selective responses to vocalizations (Andoni et al., 2007; Holmstrom et al., 2007). In addition, individual neurons may be selective to different acoustic features found in vocalizations such as AM, FM, duration, and spectral content (Brand et al., 2000; Portfors and Wenstrup, 2002; Portfors and Felix, 2005; Woolley and Casseday, 2005; Pérez-González et al., 2006; Andoni et al., 2007). By independently manipulating these acoustic features, we showed that the response of each neuron was modulated in a different way. Finally, IC neurons may use cochlear distortions that are generated by combinations of ultrasonic frequencies in vocalizations to generate responses even when the spectral content of the vocalization is outside the FRA of the neuron (Portfors et al., 2009). Thus, by using a variety of different mechanisms across the neural population, the IC is able to generate a unique representation of each vocalization.

Efficient encoding in the IC

Our finding that neurons in the IC have heterogeneous responses to vocalizations supports the idea of efficient encoding in the mammalian midbrain. Peripheral sensory neurons are often coarsely tuned and stochastic, yet subtle discrimination among stimuli is critical for the survival of many species. One approach for overcoming the noisy responses of individual neurons is through population encoding in which sensory information is redundantly distributed across a large number of neurons. The benefits of population encoding at the periphery have been hypothesized in the visual (Lee et al., 1988), motor (Georgopoulos et al., 1986), and auditory (Wever, 1933) systems. However, correlations in neural responses limits the effectiveness of this approach (Sompolinsky et al., 2001; Shamir and Sompolinsky, 2004; Averbeck et al., 2006) and distributed encoding schemes make discrimination among similar and/or simultaneously encountered stimuli difficult because of overlapping neural representations.

It has been hypothesized that sensory systems facilitate the discrimination task by implementing a factorial code in which information with considerable redundancy and correlation (as is true for most naturalistic stimuli) is recoded such that distinct stimulus events are represented with little or no statistical interdependence (Nadal and Parga, 1994). This process may be the result of an evolutionary optimization that maximizes the efficiency of the neural code and is subject to the physical constraints of neural networks and the statistical and behavioral qualities of the stimuli (Barlow, 1960; Linsker, 1988; Bialek et al., 1991; Atick, 1992). This results in the migration from a redundant encoding at the periphery to an efficient, heterogeneous encoding in higher-level processing that is driven by feature extraction. Evidence of this migration has been documented in sensory modalities as diverse as taste (Rolls and Treves, 1990) and vision (Rolls and Tovee, 1995). This encoding strategy also dictates that higher-level neural representations match the statistical and behavioral qualities of the stimuli (Barlow et al., 1989). Stimuli that are not often encountered may be encoded less efficiently than stimuli that are repeatedly encountered.

Our information theoretic analysis compared the efficiency of the encoding of vocalization stimuli in the IC with an encoding that was predicted by the pure tone responses of each neuron. We used the pure tone response model as our reference because previous studies show that the IC is the first site in the ascending auditory pathway in which neural responses to vocalizations cannot be predicted by neural responses to pure tones alone (Bauer et al., 2002; Klug et al., 2002; Pollak et al., 2003). Our results showed that the mouse IC encodes vocalizations more efficiently than an encoding predicted by the pure tone model. Information transfer was significantly improved by increasing the heterogeneity of the responses across the neural population. Other studies have shown that increasing the heterogeneity of the receptive fields of individual neurons increases the information contained in the population response attributable to the decrease in neural correlation (Gawne and Richmond, 1993; Bell and Sejnowski, 1995; Chechik et al., 2006; Shamir and Sompolinsky, 2006; Chelaru and Dragoi, 2008).

The responses to the female and male upsweep vocalizations showed a different extreme of a factorial code. The female vocalization, perhaps because of its simple spectrotemporal structure and lack of natural variability, was encoded by a small number of highly precise neurons. Most perturbations to this vocalization resulted in little or no response. Because the pure tone model for each neuron predicted no response from this vocalization, our information theoretic analysis showed that the encoding used by the IC was more efficient than our reference encoding. The male vocalization, conversely, did not generate responses in any of our 111 neurons despite its similarity to the female vocalization, perhaps indicating that it was filtered out by this level of auditory processing because it was not often encountered or was behaviorally irrelevant to our subject mice.

Our findings suggest that the IC plays a critical role in the efficient encoding of auditory information by facilitating the discrimination of behaviorally relevant sounds. Considering that mice emit a much more extensive repertoire of vocalizations than were used as stimuli in this study, we expect that the IC is even more heterogeneous in its responses to complex sounds in the natural environment.

Footnotes

This work was supported by National Science Foundation Grants IOS-0620560 and IOS-0920060 (C.V.P.) and Collaborative Research in Computational Neuroscience Grant IIS-0827722 (P.D.R.). We also thank the anonymous reviewers for their helpful comments.

References

Abel C, Kössl M. Sensitive response to low frequency cochlear distortion products in the auditory midbrain. J Neurophysiol. 2009;101:1560–1574. doi: 10.1152/jn.90805.2008. [DOI] [PubMed] [Google Scholar]
Adams JC. Ascending projections to the inferior colliculus. J Comp Neurol. 1979;183:519–538. doi: 10.1002/cne.901830305. [DOI] [PubMed] [Google Scholar]
Aertsen AM, Johannesma PI. The spectro-temporal receptive field: a functional characteristic of auditory neurons. Biol Cybern. 1981;42:133–143. doi: 10.1007/BF00336731. [DOI] [PubMed] [Google Scholar]
Amin N, Doupe A, Theunissen FE. Development of selectivity for natural sounds in the songbird auditory forebrain. J Neurophysiol. 2007;97:3517–3531. doi: 10.1152/jn.01066.2006. [DOI] [PubMed] [Google Scholar]
Andoni S, Li N, Pollak GD. Spectrotemporal receptive fields in the inferior colliculus revealing selectivity for spectral motion in conspecific vocalizations. J Neurosci. 2007;27:4882–4893. doi: 10.1523/JNEUROSCI.4342-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Atick J. Could information theory provide an ecological theory of sensory processing? Network. 1992;3:213–251. doi: 10.3109/0954898X.2011.638888. [DOI] [PubMed] [Google Scholar]
Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nat Rev Neurosci. 2006;7:358–366. doi: 10.1038/nrn1888. [DOI] [PubMed] [Google Scholar]
Barlow HB. Current problems in animal behaviour. Cambridge, UK: Cambridge UP; 1960. The coding of sensory messages; pp. 331–360. [Google Scholar]
Barlow HB, Kaushal TP, Mitchison GJ. Finding minimum entropy codes. Neural Comput. 1989;1:412–423. [Google Scholar]
Bauer EE, Klug A, Pollak GD. Spectral determination of responses to species-specific calls in the dorsal nucleus of the lateral lemniscus. J Neurophysiol. 2002;88:1955–1967. doi: 10.1152/jn.2002.88.4.1955. [DOI] [PubMed] [Google Scholar]
Bell AJ, Sejnowski TJ. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995;7:1129–1159. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
Bialek W, Rieke F, de Ruyter van Steveninck RR, Warland D. Reading a neural code. Science. 1991;252:1854–1857. doi: 10.1126/science.2063199. [DOI] [PubMed] [Google Scholar]
Brand A, Urban R, Grothe B. Duration tuning in the mouse auditory midbrain. J Neurophysiol. 2000;84:1790–1799. doi: 10.1152/jn.2000.84.4.1790. [DOI] [PubMed] [Google Scholar]
Chechik G, Anderson MJ, Bar-Yosef O, Young ED, Tishby N, Nelken I. Reduction of information redundancy in the ascending auditory pathway. Neuron. 2006;51:359–368. doi: 10.1016/j.neuron.2006.06.030. [DOI] [PubMed] [Google Scholar]
Chelaru MI, Dragoi V. Efficient coding in heterogeneous neuronal populations. Proc Natl Acad Sci U S A. 2008;105:16344–16349. doi: 10.1073/pnas.0807744105. [DOI] [PMC free article] [PubMed] [Google Scholar]
Eggermont JJ, Aertsen AM, Johannesma PI. Prediction of the responses of auditory neurons in the midbrain of the grass frog based on the spectro-temporal receptive field. Hear Res. 1983;10:191–202. doi: 10.1016/0378-5955(83)90053-9. [DOI] [PubMed] [Google Scholar]
Felix RA, 2nd, Portfors CV. Excitatory, inhibitory and facilitatory frequency response areas in the inferior colliculus of hearing impaired mice. Hear Res. 2007;228:212–229. doi: 10.1016/j.heares.2007.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Galambos R, Davis H. The response of single auditory-nerve fibers to acoustic stimulation. J Neurophysiol. 1943;6:39–57. [Google Scholar]
Gawne TJ, Richmond BJ. How independent are the messages carried by adjacent inferior temporal cortical neurons? J Neurosci. 1993;13:2758–2771. doi: 10.1523/JNEUROSCI.13-07-02758.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gehr DD, Komiya H, Eggermont JJ. Neuronal responses in cat primary auditory cortex to natural and altered species-specific calls. Hear Res. 2000;150:27–42. doi: 10.1016/s0378-5955(00)00170-2. [DOI] [PubMed] [Google Scholar]
Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science. 1986;233:1416–1419. doi: 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]
Gill P, Zhang J, Woolley SM, Fremouw T, Theunissen FE. Sound representation methods for spectro-temporal receptive field estimation. J Comput Neurosci. 2006;21:5–20. doi: 10.1007/s10827-006-7059-4. [DOI] [PubMed] [Google Scholar]
Goldstein J, Kiang N. Neural correlates of the aural combination tone 2f1–f2. Proc IEEE. 1968;56:981–992. [Google Scholar]
Grace JA, Amin N, Singh NC, Theunissen FE. Selectivity for conspecific song in the zebra finch auditory forebrain. J Neurophysiol. 2003;89:472–487. doi: 10.1152/jn.00088.2002. [DOI] [PubMed] [Google Scholar]
Haupt SS, Spengler F, Husemann R, Dinse HR. Receptive field scatter, topography and map variability in different layers of the hindpaw representation of rat somatosensory cortex. Exp Brain Res. 2004;155:485–499. doi: 10.1007/s00221-003-1755-3. [DOI] [PubMed] [Google Scholar]
Holmstrom L, Roberts PD, Portfors CV. Responses to social vocalizations in the inferior colliculus of the mustached bat are influenced by secondary tuning curves. J Neurophysiol. 2007;98:3461–3472. doi: 10.1152/jn.00638.2007. [DOI] [PubMed] [Google Scholar]
Holmstrom L, Kim S, McNames J, Portfors C. Stimulus design for auditory neuroethology using state space modeling and the extended kalman smoother. Hear Res. 2009;247:1–16. doi: 10.1016/j.heares.2008.09.012. [DOI] [PubMed] [Google Scholar]
Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
Huetz C, Philibert B, Edeline JM. A spike-timing code for discriminating conspecific vocalizations in the thalamocortical system of anesthetized and awake guinea pigs. J Neurosci. 2009;29:334–350. doi: 10.1523/JNEUROSCI.3269-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Klug A, Bauer EE, Hanson JT, Hurley L, Meitzen J, Pollak GD. Response selectivity for species-specific calls in the inferior colliculus of Mexican free-tailed bats is generated by inhibition. J Neurophysiol. 2002;88:1941–1954. doi: 10.1152/jn.2002.88.4.1941. [DOI] [PubMed] [Google Scholar]
Lee C, Rohrer WH, Sparks DL. Population coding of saccadic eye movements by neurons in the superior colliculus. Nature. 1988;332:357–360. doi: 10.1038/332357a0. [DOI] [PubMed] [Google Scholar]
Linsker R. Self-organization in a perceptual network. Computer. 1988;21:105–117. [Google Scholar]
Liu RC, Schreiner CE. Auditory cortical detection and discrimination correlates with communicative significance. PLoS Biol. 2007;5:e173. doi: 10.1371/journal.pbio.0050173. [DOI] [PMC free article] [PubMed] [Google Scholar]
McAlpine D. Neural sensitivity to periodicity in the inferior colliculus: evidence for the role of cochlear distortions. J Neurophysiol. 2004;92:1295–1311. doi: 10.1152/jn.00034.2004. [DOI] [PubMed] [Google Scholar]
Nadal JP, Parga N. Nonlinear neurons in the low noise limit: a factorial code maximizes information transfer. Network. 1994;5:565–581. [Google Scholar]
Panksepp JB, Jochman KA, Kim JU, Koy JJ, Wilson ED, Chen Q, Wilson CR, Lahvis GP. Affiliative behavior, ultrasonic communication and social reward are influenced by genetic variation in adolescent mice. PLoS ONE. 2007;2:e351. doi: 10.1371/journal.pone.0000351. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pérez-González D, Malmierca MS, Moore JM, Hernández O, Covey E. Duration selective neurons in the inferior colliculus of the rat: topographic distribution and relation of duration sensitivity to other response properties. J Neurophysiol. 2006;95:823–836. doi: 10.1152/jn.00741.2005. [DOI] [PubMed] [Google Scholar]
Philibert B, Laudanski J, Edeline JM. Auditory thalamus responses to guinea-pig vocalizations: a comparison between rat and guinea-pig. Hear Res. 2005;209:97–103. doi: 10.1016/j.heares.2005.07.004. [DOI] [PubMed] [Google Scholar]
Pincherli Castellanos TA, Aitoubah J, Molotchnikoff S, Lepore F, Guillemot JP. Responses of inferior collicular cells to species-specific vocalizations in normal and enucleated rats. Exp Brain Res. 2007;183:341–350. doi: 10.1007/s00221-007-1049-2. [DOI] [PubMed] [Google Scholar]
Pollak GD, Klug A, Bauer EE. Processing and representation of species-specific communication calls in the auditory system of bats. Int Rev Neurobiol. 2003;56:83–121. doi: 10.1016/s0074-7742(03)56003-2. [DOI] [PubMed] [Google Scholar]
Portfors CV. Combination sensitivity and processing of communication calls in the inferior colliculus of the moustached bat Pteronotus parnellii. An Acad Bras Cienc. 2004;76:253–257. doi: 10.1590/s0001-37652004000200010. [DOI] [PubMed] [Google Scholar]
Portfors CV. Types and functions of ultrasonic vocalizations in laboratory rats and mice. J Am Assoc Lab Anim Sci. 2007;46:28–34. [PubMed] [Google Scholar]
Portfors CV, Felix RA., 2nd Spectral integration in the inferior colliculus of the cba/caj mouse. Neuroscience. 2005;136:1159–1170. doi: 10.1016/j.neuroscience.2005.08.031. [DOI] [PubMed] [Google Scholar]
Portfors CV, Wenstrup JJ. Delay-tuned neurons in the inferior colliculus of the mustached bat: implications for analyses of target distance. J Neurophysiol. 1999;82:1326–1338. doi: 10.1152/jn.1999.82.3.1326. [DOI] [PubMed] [Google Scholar]
Portfors CV, Wenstrup JJ. Excitatory and facilitatory frequency response areas in the inferior colliculus of the mustached bat. Hear Res. 2002;168:131–138. doi: 10.1016/s0378-5955(02)00376-3. [DOI] [PubMed] [Google Scholar]
Portfors CV, Roberts PD, Jonson K. Over-representation of species-specific vocalizations in the awake mouse inferior colliculus. Neuroscience. 2009;162:486–500. doi: 10.1016/j.neuroscience.2009.04.056. [DOI] [PubMed] [Google Scholar]
Rieke F, Warland D, Bialek W. Coding efficiency and information rates in sensory neurons. Europhys Lett. 1993;22:151–156. [Google Scholar]
Rieke F, Bodnar DA, Bialek W. Naturalistic stimuli increase the rate and efficiency of information transmission by primary auditory afferents. Proc Biol Sci. 1995;262:259–265. doi: 10.1098/rspb.1995.0204. [DOI] [PubMed] [Google Scholar]
Ringach DL, Shapley RM, Hawken MJ. Orientation selectivity in macaque v1: diversity and laminar dependence. J Neurosci. 2002;22:5639–5651. doi: 10.1523/JNEUROSCI.22-13-05639.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rokem A, Watzl S, Gollisch T, Stemmler M, Herz AV, Samengo I. Spike-timing precision underlies the coding efficiency of auditory receptor neurons. J Neurophysiol. 2006;95:2541–2552. doi: 10.1152/jn.00891.2005. [DOI] [PubMed] [Google Scholar]
Rolls ET, Tovee MJ. Sparseness of the neuronal representation of stimuli in the primate temporal visual cortex. J Neurophysiol. 1995;73:713–726. doi: 10.1152/jn.1995.73.2.713. [DOI] [PubMed] [Google Scholar]
Rolls ET, Treves A. The relative advantages of sparse versus distributed encoding for associative neuronal networks in the brain. Network. 1990;1:407–421. [Google Scholar]
Saldaña E, Feliciano M, Mugnaini E. Distribution of descending projections from primary auditory neocortex to inferior colliculus mimics the topography of intracollicular projections. J Comp Neurol. 1996;371:15–40. doi: 10.1002/(SICI)1096-9861(19960715)371:1<15::AID-CNE2>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
Schreiber S, Fellous JM, Whitmer D, Tiesinga P, Sejnowski TJ. A new correlation-based measure of spike timing reliability. Neurocomputing. 2003;52–54:925–931. doi: 10.1016/S0925-2312(02)00838-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shamir M, Sompolinsky H. Nonlinear population codes. Neural Comput. 2004;16:1105–1136. doi: 10.1162/089976604773717559. [DOI] [PubMed] [Google Scholar]
Shamir M, Sompolinsky H. Implications of neuronal diversity on population coding. Neural Comput. 2006;18:1951–1986. doi: 10.1162/neco.2006.18.8.1951. [DOI] [PubMed] [Google Scholar]
Shamir M, Sen K, Colburn HS. Temporal coding of time-varying stimuli. Neural Comput. 2007;19:3239–3261. doi: 10.1162/neco.2007.19.12.3239. [DOI] [PubMed] [Google Scholar]
Sompolinsky H, Yoon H, Kang K, Shamir M. Population coding in neuronal systems with correlated noise. Phys Rev E Stat Nonlin Soft Matter Phys. 2001;64 doi: 10.1103/PhysRevE.64.051904. 051904. [DOI] [PubMed] [Google Scholar]
Stein RB, French AS, Holden AV. The frequency response, coherence, and information capacity of two neuronal models. Biophys J. 1972;12:295–322. doi: 10.1016/S0006-3495(72)86087-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Steinschneider M, Volkov IO, Noh MD, Garell PC, Howard MA., 3rd Temporal encoding of the voice onset time phonetic parameter by field potentials recorded directly from human auditory cortex. J Neurophysiol. 1999;82:2346–2357. doi: 10.1152/jn.1999.82.5.2346. [DOI] [PubMed] [Google Scholar]
Suta D, Kvasnák E, Popelár J, Syka J. Representation of species-specific vocalizations in the inferior colliculus of the guinea pig. J Neurophysiol. 2003;90:3794–3808. doi: 10.1152/jn.01175.2002. [DOI] [PubMed] [Google Scholar]
Theunissen FE, David SV, Singh NC, Hsu A, Vinje WE, Gallant JL. Estimating spatio-temporal receptive fields of auditory and visual neurons from their responses to natural stimuli. Network. 2001;12:289–316. [PubMed] [Google Scholar]
van Rossum MC. A novel spike distance. Neural Comput. 2001;13:751–763. doi: 10.1162/089976601300014321. [DOI] [PubMed] [Google Scholar]
Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol. 1996;76:1310–1326. doi: 10.1152/jn.1996.76.2.1310. [DOI] [PubMed] [Google Scholar]
Victor JD, Purpura KP. Metric-space analysis of spike trains: theory, algorithms and application. Network. 1997;8:127–164. [Google Scholar]
Wang H, Liang S, Burgdorf J, Wess J, Yeomans J. Ultrasonic vocalizations induced by sex and amphetamine in m2, m4, m5 muscarinic and d2 dopamine receptor knockout mice. PLoS ONE. 2008;3:e1893. doi: 10.1371/journal.pone.0001893. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang L, Narayan R, Graña G, Shamir M, Sen K. Cortical discrimination of complex natural stimuli: can single neurons match behavior? J Neurosci. 2007;27:582–589. doi: 10.1523/JNEUROSCI.3699-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang X, Kadia SC. Differential representation of species-specific primate vocalizations in the auditory cortices of marmoset and cat. J Neurophysiol. 2001;86:2616–2620. doi: 10.1152/jn.2001.86.5.2616. [DOI] [PubMed] [Google Scholar]
Wang X, Lu T, Snider RK, Liang L. Sustained firing in auditory cortex evoked by preferred stimuli. Nature. 2005;435:341–346. doi: 10.1038/nature03565. [DOI] [PubMed] [Google Scholar]
Warren B, Gibson G, Russell IJ. Sex recognition through midflight mating duets in culex mosquitoes is mediated by acoustic distortion. Curr Biol. 2009;19:485–491. doi: 10.1016/j.cub.2009.01.059. [DOI] [PubMed] [Google Scholar]
Wever EG. The physiology of hearing: the nature of response in the cochlea. Physiol Rev. 1933;13:400–425. [Google Scholar]
Woolley SM, Casseday JH. Processing of modulated sounds in the zebra finch auditory midbrain: responses to noise, frequency sweeps, and sinusoidal amplitude modulations. J Neurophysiol. 2005;94:1143–1157. doi: 10.1152/jn.01064.2004. [DOI] [PubMed] [Google Scholar]

[B1] Abel C, Kössl M. Sensitive response to low frequency cochlear distortion products in the auditory midbrain. J Neurophysiol. 2009;101:1560–1574. doi: 10.1152/jn.90805.2008. [DOI] [PubMed] [Google Scholar]

[B2] Adams JC. Ascending projections to the inferior colliculus. J Comp Neurol. 1979;183:519–538. doi: 10.1002/cne.901830305. [DOI] [PubMed] [Google Scholar]

[B3] Aertsen AM, Johannesma PI. The spectro-temporal receptive field: a functional characteristic of auditory neurons. Biol Cybern. 1981;42:133–143. doi: 10.1007/BF00336731. [DOI] [PubMed] [Google Scholar]

[B4] Amin N, Doupe A, Theunissen FE. Development of selectivity for natural sounds in the songbird auditory forebrain. J Neurophysiol. 2007;97:3517–3531. doi: 10.1152/jn.01066.2006. [DOI] [PubMed] [Google Scholar]

[B5] Andoni S, Li N, Pollak GD. Spectrotemporal receptive fields in the inferior colliculus revealing selectivity for spectral motion in conspecific vocalizations. J Neurosci. 2007;27:4882–4893. doi: 10.1523/JNEUROSCI.4342-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] Atick J. Could information theory provide an ecological theory of sensory processing? Network. 1992;3:213–251. doi: 10.3109/0954898X.2011.638888. [DOI] [PubMed] [Google Scholar]

[B7] Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nat Rev Neurosci. 2006;7:358–366. doi: 10.1038/nrn1888. [DOI] [PubMed] [Google Scholar]

[B8] Barlow HB. Current problems in animal behaviour. Cambridge, UK: Cambridge UP; 1960. The coding of sensory messages; pp. 331–360. [Google Scholar]

[B9] Barlow HB, Kaushal TP, Mitchison GJ. Finding minimum entropy codes. Neural Comput. 1989;1:412–423. [Google Scholar]

[B10] Bauer EE, Klug A, Pollak GD. Spectral determination of responses to species-specific calls in the dorsal nucleus of the lateral lemniscus. J Neurophysiol. 2002;88:1955–1967. doi: 10.1152/jn.2002.88.4.1955. [DOI] [PubMed] [Google Scholar]

[B11] Bell AJ, Sejnowski TJ. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995;7:1129–1159. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]

[B12] Bialek W, Rieke F, de Ruyter van Steveninck RR, Warland D. Reading a neural code. Science. 1991;252:1854–1857. doi: 10.1126/science.2063199. [DOI] [PubMed] [Google Scholar]

[B13] Brand A, Urban R, Grothe B. Duration tuning in the mouse auditory midbrain. J Neurophysiol. 2000;84:1790–1799. doi: 10.1152/jn.2000.84.4.1790. [DOI] [PubMed] [Google Scholar]

[B14] Chechik G, Anderson MJ, Bar-Yosef O, Young ED, Tishby N, Nelken I. Reduction of information redundancy in the ascending auditory pathway. Neuron. 2006;51:359–368. doi: 10.1016/j.neuron.2006.06.030. [DOI] [PubMed] [Google Scholar]

[B15] Chelaru MI, Dragoi V. Efficient coding in heterogeneous neuronal populations. Proc Natl Acad Sci U S A. 2008;105:16344–16349. doi: 10.1073/pnas.0807744105. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B16] Eggermont JJ, Aertsen AM, Johannesma PI. Prediction of the responses of auditory neurons in the midbrain of the grass frog based on the spectro-temporal receptive field. Hear Res. 1983;10:191–202. doi: 10.1016/0378-5955(83)90053-9. [DOI] [PubMed] [Google Scholar]

[B17] Felix RA, 2nd, Portfors CV. Excitatory, inhibitory and facilitatory frequency response areas in the inferior colliculus of hearing impaired mice. Hear Res. 2007;228:212–229. doi: 10.1016/j.heares.2007.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B18] Galambos R, Davis H. The response of single auditory-nerve fibers to acoustic stimulation. J Neurophysiol. 1943;6:39–57. [Google Scholar]

[B19] Gawne TJ, Richmond BJ. How independent are the messages carried by adjacent inferior temporal cortical neurons? J Neurosci. 1993;13:2758–2771. doi: 10.1523/JNEUROSCI.13-07-02758.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B20] Gehr DD, Komiya H, Eggermont JJ. Neuronal responses in cat primary auditory cortex to natural and altered species-specific calls. Hear Res. 2000;150:27–42. doi: 10.1016/s0378-5955(00)00170-2. [DOI] [PubMed] [Google Scholar]

[B21] Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science. 1986;233:1416–1419. doi: 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]

[B22] Gill P, Zhang J, Woolley SM, Fremouw T, Theunissen FE. Sound representation methods for spectro-temporal receptive field estimation. J Comput Neurosci. 2006;21:5–20. doi: 10.1007/s10827-006-7059-4. [DOI] [PubMed] [Google Scholar]

[B23] Goldstein J, Kiang N. Neural correlates of the aural combination tone 2f1–f2. Proc IEEE. 1968;56:981–992. [Google Scholar]

[B24] Grace JA, Amin N, Singh NC, Theunissen FE. Selectivity for conspecific song in the zebra finch auditory forebrain. J Neurophysiol. 2003;89:472–487. doi: 10.1152/jn.00088.2002. [DOI] [PubMed] [Google Scholar]

[B25] Haupt SS, Spengler F, Husemann R, Dinse HR. Receptive field scatter, topography and map variability in different layers of the hindpaw representation of rat somatosensory cortex. Exp Brain Res. 2004;155:485–499. doi: 10.1007/s00221-003-1755-3. [DOI] [PubMed] [Google Scholar]

[B26] Holmstrom L, Roberts PD, Portfors CV. Responses to social vocalizations in the inferior colliculus of the mustached bat are influenced by secondary tuning curves. J Neurophysiol. 2007;98:3461–3472. doi: 10.1152/jn.00638.2007. [DOI] [PubMed] [Google Scholar]

[B27] Holmstrom L, Kim S, McNames J, Portfors C. Stimulus design for auditory neuroethology using state space modeling and the extended kalman smoother. Hear Res. 2009;247:1–16. doi: 10.1016/j.heares.2008.09.012. [DOI] [PubMed] [Google Scholar]

[B28] Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B29] Huetz C, Philibert B, Edeline JM. A spike-timing code for discriminating conspecific vocalizations in the thalamocortical system of anesthetized and awake guinea pigs. J Neurosci. 2009;29:334–350. doi: 10.1523/JNEUROSCI.3269-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B30] Klug A, Bauer EE, Hanson JT, Hurley L, Meitzen J, Pollak GD. Response selectivity for species-specific calls in the inferior colliculus of Mexican free-tailed bats is generated by inhibition. J Neurophysiol. 2002;88:1941–1954. doi: 10.1152/jn.2002.88.4.1941. [DOI] [PubMed] [Google Scholar]

[B31] Lee C, Rohrer WH, Sparks DL. Population coding of saccadic eye movements by neurons in the superior colliculus. Nature. 1988;332:357–360. doi: 10.1038/332357a0. [DOI] [PubMed] [Google Scholar]

[B32] Linsker R. Self-organization in a perceptual network. Computer. 1988;21:105–117. [Google Scholar]

[B33] Liu RC, Schreiner CE. Auditory cortical detection and discrimination correlates with communicative significance. PLoS Biol. 2007;5:e173. doi: 10.1371/journal.pbio.0050173. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B34] McAlpine D. Neural sensitivity to periodicity in the inferior colliculus: evidence for the role of cochlear distortions. J Neurophysiol. 2004;92:1295–1311. doi: 10.1152/jn.00034.2004. [DOI] [PubMed] [Google Scholar]

[B35] Nadal JP, Parga N. Nonlinear neurons in the low noise limit: a factorial code maximizes information transfer. Network. 1994;5:565–581. [Google Scholar]

[B36] Panksepp JB, Jochman KA, Kim JU, Koy JJ, Wilson ED, Chen Q, Wilson CR, Lahvis GP. Affiliative behavior, ultrasonic communication and social reward are influenced by genetic variation in adolescent mice. PLoS ONE. 2007;2:e351. doi: 10.1371/journal.pone.0000351. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B37] Pérez-González D, Malmierca MS, Moore JM, Hernández O, Covey E. Duration selective neurons in the inferior colliculus of the rat: topographic distribution and relation of duration sensitivity to other response properties. J Neurophysiol. 2006;95:823–836. doi: 10.1152/jn.00741.2005. [DOI] [PubMed] [Google Scholar]

[B38] Philibert B, Laudanski J, Edeline JM. Auditory thalamus responses to guinea-pig vocalizations: a comparison between rat and guinea-pig. Hear Res. 2005;209:97–103. doi: 10.1016/j.heares.2005.07.004. [DOI] [PubMed] [Google Scholar]

[B39] Pincherli Castellanos TA, Aitoubah J, Molotchnikoff S, Lepore F, Guillemot JP. Responses of inferior collicular cells to species-specific vocalizations in normal and enucleated rats. Exp Brain Res. 2007;183:341–350. doi: 10.1007/s00221-007-1049-2. [DOI] [PubMed] [Google Scholar]

[B40] Pollak GD, Klug A, Bauer EE. Processing and representation of species-specific communication calls in the auditory system of bats. Int Rev Neurobiol. 2003;56:83–121. doi: 10.1016/s0074-7742(03)56003-2. [DOI] [PubMed] [Google Scholar]

[B41] Portfors CV. Combination sensitivity and processing of communication calls in the inferior colliculus of the moustached bat Pteronotus parnellii. An Acad Bras Cienc. 2004;76:253–257. doi: 10.1590/s0001-37652004000200010. [DOI] [PubMed] [Google Scholar]

[B42] Portfors CV. Types and functions of ultrasonic vocalizations in laboratory rats and mice. J Am Assoc Lab Anim Sci. 2007;46:28–34. [PubMed] [Google Scholar]

[B43] Portfors CV, Felix RA., 2nd Spectral integration in the inferior colliculus of the cba/caj mouse. Neuroscience. 2005;136:1159–1170. doi: 10.1016/j.neuroscience.2005.08.031. [DOI] [PubMed] [Google Scholar]

[B44] Portfors CV, Wenstrup JJ. Delay-tuned neurons in the inferior colliculus of the mustached bat: implications for analyses of target distance. J Neurophysiol. 1999;82:1326–1338. doi: 10.1152/jn.1999.82.3.1326. [DOI] [PubMed] [Google Scholar]

[B45] Portfors CV, Wenstrup JJ. Excitatory and facilitatory frequency response areas in the inferior colliculus of the mustached bat. Hear Res. 2002;168:131–138. doi: 10.1016/s0378-5955(02)00376-3. [DOI] [PubMed] [Google Scholar]

[B46] Portfors CV, Roberts PD, Jonson K. Over-representation of species-specific vocalizations in the awake mouse inferior colliculus. Neuroscience. 2009;162:486–500. doi: 10.1016/j.neuroscience.2009.04.056. [DOI] [PubMed] [Google Scholar]

[B47] Rieke F, Warland D, Bialek W. Coding efficiency and information rates in sensory neurons. Europhys Lett. 1993;22:151–156. [Google Scholar]

[B48] Rieke F, Bodnar DA, Bialek W. Naturalistic stimuli increase the rate and efficiency of information transmission by primary auditory afferents. Proc Biol Sci. 1995;262:259–265. doi: 10.1098/rspb.1995.0204. [DOI] [PubMed] [Google Scholar]

[B49] Ringach DL, Shapley RM, Hawken MJ. Orientation selectivity in macaque v1: diversity and laminar dependence. J Neurosci. 2002;22:5639–5651. doi: 10.1523/JNEUROSCI.22-13-05639.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B50] Rokem A, Watzl S, Gollisch T, Stemmler M, Herz AV, Samengo I. Spike-timing precision underlies the coding efficiency of auditory receptor neurons. J Neurophysiol. 2006;95:2541–2552. doi: 10.1152/jn.00891.2005. [DOI] [PubMed] [Google Scholar]

[B51] Rolls ET, Tovee MJ. Sparseness of the neuronal representation of stimuli in the primate temporal visual cortex. J Neurophysiol. 1995;73:713–726. doi: 10.1152/jn.1995.73.2.713. [DOI] [PubMed] [Google Scholar]

[B52] Rolls ET, Treves A. The relative advantages of sparse versus distributed encoding for associative neuronal networks in the brain. Network. 1990;1:407–421. [Google Scholar]

[B53] Saldaña E, Feliciano M, Mugnaini E. Distribution of descending projections from primary auditory neocortex to inferior colliculus mimics the topography of intracollicular projections. J Comp Neurol. 1996;371:15–40. doi: 10.1002/(SICI)1096-9861(19960715)371:1<15::AID-CNE2>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]

[B54] Schreiber S, Fellous JM, Whitmer D, Tiesinga P, Sejnowski TJ. A new correlation-based measure of spike timing reliability. Neurocomputing. 2003;52–54:925–931. doi: 10.1016/S0925-2312(02)00838-X. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B55] Shamir M, Sompolinsky H. Nonlinear population codes. Neural Comput. 2004;16:1105–1136. doi: 10.1162/089976604773717559. [DOI] [PubMed] [Google Scholar]

[B56] Shamir M, Sompolinsky H. Implications of neuronal diversity on population coding. Neural Comput. 2006;18:1951–1986. doi: 10.1162/neco.2006.18.8.1951. [DOI] [PubMed] [Google Scholar]

[B57] Shamir M, Sen K, Colburn HS. Temporal coding of time-varying stimuli. Neural Comput. 2007;19:3239–3261. doi: 10.1162/neco.2007.19.12.3239. [DOI] [PubMed] [Google Scholar]

[B58] Sompolinsky H, Yoon H, Kang K, Shamir M. Population coding in neuronal systems with correlated noise. Phys Rev E Stat Nonlin Soft Matter Phys. 2001;64 doi: 10.1103/PhysRevE.64.051904. 051904. [DOI] [PubMed] [Google Scholar]

[B59] Stein RB, French AS, Holden AV. The frequency response, coherence, and information capacity of two neuronal models. Biophys J. 1972;12:295–322. doi: 10.1016/S0006-3495(72)86087-9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B60] Steinschneider M, Volkov IO, Noh MD, Garell PC, Howard MA., 3rd Temporal encoding of the voice onset time phonetic parameter by field potentials recorded directly from human auditory cortex. J Neurophysiol. 1999;82:2346–2357. doi: 10.1152/jn.1999.82.5.2346. [DOI] [PubMed] [Google Scholar]

[B61] Suta D, Kvasnák E, Popelár J, Syka J. Representation of species-specific vocalizations in the inferior colliculus of the guinea pig. J Neurophysiol. 2003;90:3794–3808. doi: 10.1152/jn.01175.2002. [DOI] [PubMed] [Google Scholar]

[B62] Theunissen FE, David SV, Singh NC, Hsu A, Vinje WE, Gallant JL. Estimating spatio-temporal receptive fields of auditory and visual neurons from their responses to natural stimuli. Network. 2001;12:289–316. [PubMed] [Google Scholar]

[B63] van Rossum MC. A novel spike distance. Neural Comput. 2001;13:751–763. doi: 10.1162/089976601300014321. [DOI] [PubMed] [Google Scholar]

[B64] Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol. 1996;76:1310–1326. doi: 10.1152/jn.1996.76.2.1310. [DOI] [PubMed] [Google Scholar]

[B65] Victor JD, Purpura KP. Metric-space analysis of spike trains: theory, algorithms and application. Network. 1997;8:127–164. [Google Scholar]

[B66] Wang H, Liang S, Burgdorf J, Wess J, Yeomans J. Ultrasonic vocalizations induced by sex and amphetamine in m2, m4, m5 muscarinic and d2 dopamine receptor knockout mice. PLoS ONE. 2008;3:e1893. doi: 10.1371/journal.pone.0001893. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B67] Wang L, Narayan R, Graña G, Shamir M, Sen K. Cortical discrimination of complex natural stimuli: can single neurons match behavior? J Neurosci. 2007;27:582–589. doi: 10.1523/JNEUROSCI.3699-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B68] Wang X, Kadia SC. Differential representation of species-specific primate vocalizations in the auditory cortices of marmoset and cat. J Neurophysiol. 2001;86:2616–2620. doi: 10.1152/jn.2001.86.5.2616. [DOI] [PubMed] [Google Scholar]

[B69] Wang X, Lu T, Snider RK, Liang L. Sustained firing in auditory cortex evoked by preferred stimuli. Nature. 2005;435:341–346. doi: 10.1038/nature03565. [DOI] [PubMed] [Google Scholar]

[B70] Warren B, Gibson G, Russell IJ. Sex recognition through midflight mating duets in culex mosquitoes is mediated by acoustic distortion. Curr Biol. 2009;19:485–491. doi: 10.1016/j.cub.2009.01.059. [DOI] [PubMed] [Google Scholar]

[B71] Wever EG. The physiology of hearing: the nature of response in the cochlea. Physiol Rev. 1933;13:400–425. [Google Scholar]

[B72] Woolley SM, Casseday JH. Processing of modulated sounds in the zebra finch auditory midbrain: responses to noise, frequency sweeps, and sinusoidal amplitude modulations. J Neurophysiol. 2005;94:1143–1157. doi: 10.1152/jn.01064.2004. [DOI] [PubMed] [Google Scholar]

PERMALINK

Efficient Encoding of Vocalizations in the Auditory Midbrain

Lars A Holmstrom

Lonneke B M Eeuwes

Patrick D Roberts

Christine V Portfors

Abstract

Introduction

Materials and Methods

Animals

Surgical procedures

Acoustic stimulation

Figure 1.

Figure 2.

Data acquisition and analysis

Spike metrics.

Population spike metrics.

Predicting responses to complex stimuli from responses to pure tones.

Discrimination efficiency among vocalization variants by individual neurons.

Estimating bias in the information transfer.

Quantification of response heterogeneity across IC neurons.

Results

Figure 3.

Figure 4.

Predicting responses to complex stimuli from responses to pure tones

Figure 5.

Changing the spectral content of vocalizations altered neural responses

Figure 6.

Removal of AM or FM from the vocalizations altered neural responses

Table 1.

Figure 7.

Vocalization duration modulated neural responses

Figure 8.

Population responses

Figure 9.

Figure 10.

Figure 11.

Efficiency of vocalization discrimination in the IC

Figure 12.

Heterogeneity of responses across the neural population

Figure 13.

Discussion

Heterogeneous response properties in the IC

Efficient encoding in the IC

Footnotes

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases