Visuomotor Coordination Is Different for Different Directions in Three-Dimensional Space

Abstract

In most visuomotor tasks in which subjects have to reach to visual targets or move the hand along a particular trajectory, eye movements have been shown to lead hand movements. Because the dynamics of vergence eye movements is different from that of smooth pursuit and saccades, we have investigated the lead time of gaze relative to the hand for the depth component (vergence) and in the frontal plane (smooth pursuit and saccades) in a tracking task and in a tracing task in which human subjects were instructed to move the finger along a 3D path. For tracking, gaze leads finger position on average by 28 ± 6 ms (mean ± SE) for the components in the frontal plane but lags finger position by 95 ± 39 ms for the depth dimension. For tracing, gaze leads finger position by 151 ± 36 ms for the depth dimension. For the frontal plane, the mean lead time of gaze relative to the hand is 287 ± 13 ms. However, we found that the lead time in the frontal plane was inversely related to the tangential velocity of finger. This inverse relation for movements in the frontal plane could be explained by assuming that gaze leads the finger by a constant distance of ∼2.6 cm (range of 1.5–3.6 cm across subjects).

Introduction

Gaze shifts in a natural environment require binocular eye movements with both directional and depth components. When playing tennis, a player has to track the ball with the eyes to estimate its movement direction in 3D space before he/she can hit the ball at the proper position at the proper time. This task requires ball tracking with conjugate (saccadic and smooth pursuit) and disconjugate (vergence) eye movements to adjust fixation to the ball at varying distances relative to the subject.

Almost all studies in eye–hand coordination have been done for movements in a frontal plane, implicitly assuming that the characteristics of eye–hand coordination are identical for all movement directions. Recently, Van Pelt and Medendorp (2008) tested the accuracy of pointing movements to remembered target positions and found that changes in vergence led to errors in memory-guided reaches that were based on the new eye position and on the depth of the remembered target relative to that position. These findings demonstrate that eye position affects hand position in pointing. This result and the finding that directional changes in gaze by saccades are much faster than depth changes in gaze (Chaturvedi and Gisbergen, 1998) raise the question as to whether eye–hand coordination during tracking a moving target or tracing a shape in 3D is similar for the directional and depth components.

When tracking an object moving in the frontal plane, the trajectories of the eye and hand almost superimpose, whereas the eye leads the hand during tracing a complex shape (Gielen et al., 2009). This illustrates that eye–hand coordination is task dependent, in agreement with previous observations that eye–hand coordination changes during learning (Sailer et al., 2005) and that directional and variable errors of the eye and hand change differently according to the task (Sailer et al., 2000).

To investigate any differences between eye–hand coordination in the frontal plane (only conjugate eye movements) and in depth (also requiring vergence eye movements), we have measured 3D eye movements of subjects in two eye–hand coordination tasks. These tasks used stimulus paths in the frontal plane and the same paths rotated along the horizontal axis inducing variations in depth. In the first task, subjects were asked to track a target moving along a curved 3D path with their finger. We investigated whether the observation that gaze almost perfectly follows a target moving in the frontal plane (Fuchs, 1967) also applies to the depth component for targets moving in 3D by presenting the same stimulus path in the frontal and oblique orientation. In the second task, subjects had to move their finger along a curved path in 3D. In this task, each new fixation point is located at a different depth, resulting in combined fast, conjugate saccades and disconjugate vergence eye movements. Based on the different dynamics for gaze changes in direction and in depth (Chaturvedi and Gisbergen, 1998), we expect differences in eye–hand coordination in the frontal plane and for eye–hand movements in 3D space.

Materials and Methods

Subjects.

Five human subjects (three males) aged between 23 and 56 years participated in the experiment. All subjects were right-handed and had normal or corrected-to-normal visual acuity. None of the subjects had any known neurological or motor disorder. Furthermore, all subjects had participated in previous eye-tracking experiments with scleral coils and reported that they had no problems in perceiving depth in the presented anaglyph stimuli. One subject (one of the authors) was aware of the purpose of the experiment, whereas the others were naive. All subjects gave informed consent. The experimental procedures were approved by the local Ethics Committee of the Radboud University Nijmegen.

Experimental setup.

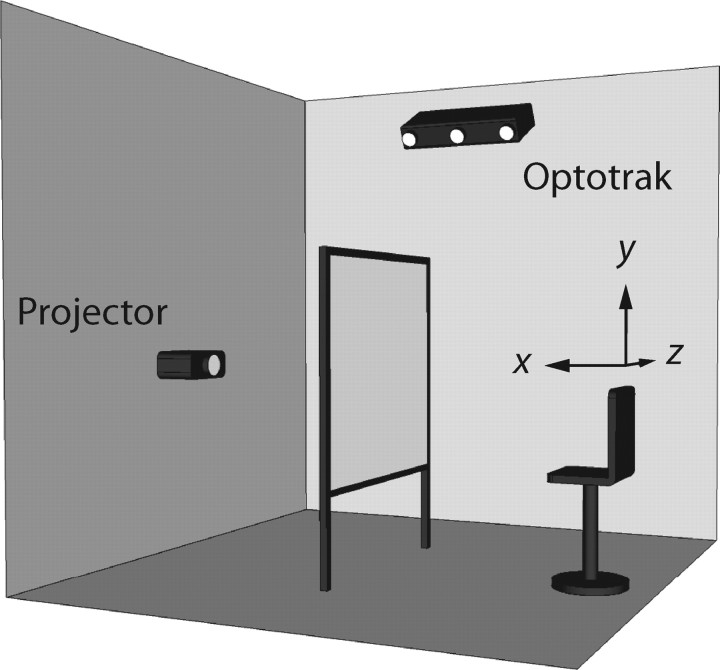
Subjects were seated in a chair with a high backrest in front of a 2.5 × 2 m² rear-projection screen in a completely darkened room (Fig. 1). The subject's eyes were positioned at a distance of ∼70 cm to the screen. The height of the chair was adjusted to align the subject's cyclopean eye with the center of the projection area. Head movements were restrained by a helmet fixed to the chair.

Figure 1.

Experimental setup. Red-green anaglyph stimuli (123 × 92 cm²) were projected with an LCD projector (Philips ProScreen 4750) on a 2.5 × 2 m² rear-projection screen. The subject was seated in an adjustable chair to align the subject's cyclopean eye with the center of the projection area, ∼70 cm in front of the screen. Finger movements were measured with an Optotrak 3020 system. A Cartesian coordinate system was defined with its center located at the subject's cyclopean eye, its x-axis pointing toward the screen, its y-axis pointing upward, and its z-axis pointing in horizontal direction, to the subject's right.

Visual stimuli were rear projected on the screen with an LCD projector (Philips ProScreen 4750) with a refresh rate of 60 Hz. The size of the computer generated image was 123 × 92 cm². A red–green anaglyph stereoscopic system was used to create a red and green copy of the stimulus. Subjects wore anaglyph stereo glasses with red and green filters to ensure that each eye received input from either the red or green stimulus, respectively. The disparity between the red and green images provided the perception of depth. Although the anaglyph stimuli produced discrepancies between accommodation and vergence, the subjects had an accurate percept of stimulus depth (see Figs. 4, 5), in agreement with previous studies in the literature. For a subject-invariant perception of the 3D stimuli, the perspective transformations had to take into account the distance between the eyes and the distance from the cyclopean eye to the screen. Therefore, inter-pupil distance and distance to the screen were measured before the experiment. Typical distances were 6.5 cm for the inter-pupil distance and 70 cm for the distance to the screen.

Figure 4.

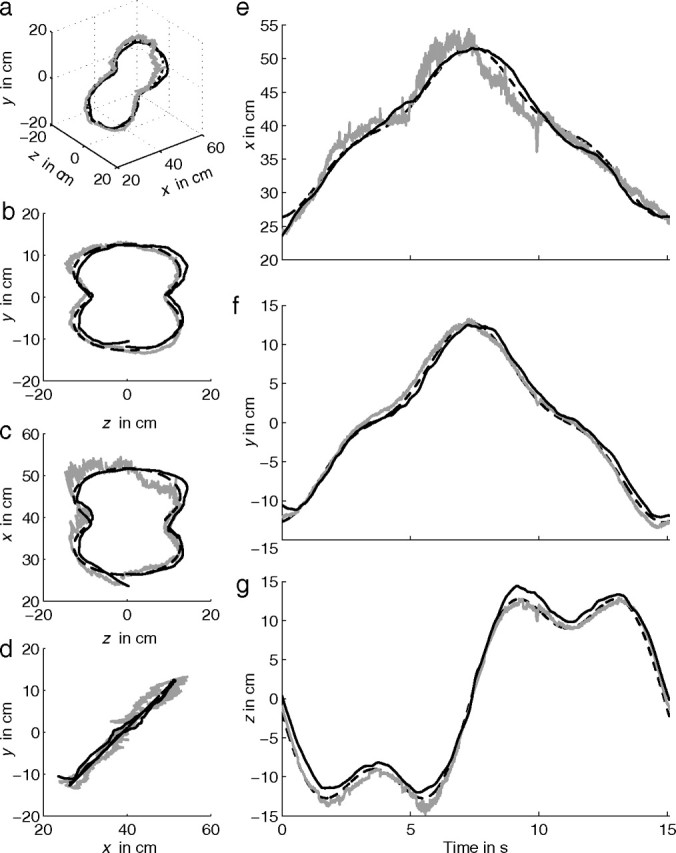
Stimulus (dashed line), gaze (gray line), and finger position (solid black line) of subject S5 tracking the oblique Cassini shape. Data of one cycle are shown. Quasi 3D view (a), frontal view (b), top view (c), and side view (d). e–g show the corresponding time traces for x, y, and z direction, respectively.

Figure 5.

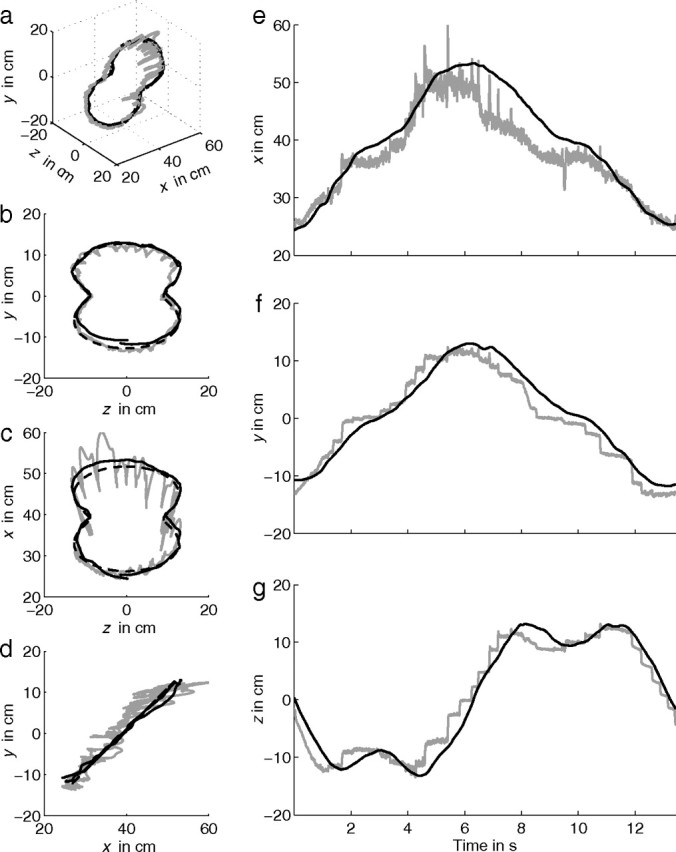
Stimulus (dashed line), gaze (gray line), and finger position (solid black line) of subject S5 moving the finger (tracing) along an oblique Cassini shape. a–g as in Figure 4. Small panels on the right show expanded time traces (e–g).

Finger position was measured with an Optotrak 3020 system (Northern Digital) at a sample frequency of 120 Hz. The Optotrak cameras were located at the upper right corner with respect to the subject, tilted down at an angle of 30°, to track the position of strobing infrared light-emitting diodes (ireds) with an accuracy better than 0.15 mm in all dimensions. An ired was placed at the tip of the right index finger, oriented toward the cameras. In addition, an ired was placed next to the right eye to control for any unintended head movements (see below).

Gaze was measured using scleral coils (Skalar) in both eyes simultaneously in a large magnetic field (Remmel Labs). The three orthogonal components of this magnetic field, with frequencies of 48, 60, and 80 kHz, were produced by a 3 × 3 × 3 m³ cubic frame. The subject's head was fixated by a helmet in the center of the frame in which the magnetic field is most homogeneous. No instructions were given to the subject regarding eye movements during the experiment. The signals from both coils were filtered by a fourth-order low-pass Bessel filter (3 dB cutoff frequency at 150 Hz) and then sampled at 120 Hz.

To relate finger, gaze, and stimulus position to each other, a right-handed Cartesian laboratory coordinate system was defined (Fig. 1). Its origin was located at the subject's cyclopean eye. The positive x-axis pointed forward, i.e., orthogonal to the screen away from the subject, the positive y-axis upward, and the positive z-axis in horizontal direction to the subject's right. Note that the x, y, and z directions correspond approximately to depth, elevation, and azimuth, respectively.

Experiments.

The experiment started with a calibration trial to calibrate the scleral coils. Subjects were instructed to fixate at 3 × 3 × 3 small spherical targets (radius of 3 mm) with a spacing of 15 cm along each axis, resulting in a total of 27 targets spanning a cube with a volume of 30 × 30 × 30 cm³. Its center was located at x = D − 25 cm, with D the distance between the subject's cyclopean eye and the screen (∼70 cm). During the calibration, the frame of the cube was visible. Targets were sequentially presented from left to right, top to bottom, and front to back, starting at the upper left vertex of the frontal plane. Subjects had to fixate on the target, press a button, and maintain fixation for 1 s for sampling of the coil data.

Stimuli were presented in three blocks. In the first block of eight trials (trials 1–8), stimuli were presented in two different conditions (“tracking” or “tracing”), two different velocities (slow or fast), and two different orientations (frontal or oblique, rotated over 45°). In the tracking condition (trials 1, 3, 5, and 7), subjects were asked to track a dot (diameter of 1.7 cm at x = 70 cm) moving along an invisible 3D path with their right index finger. In the tracing condition (trials 2, 4, 6, and 8), the entire path (width of 0.8 cm at x = 70 cm) was visible and subjects were asked to trace the path with their right index finger at approximately the same speed as in the tracking condition. The path was defined by a so-called Cassini shape, given by the following:

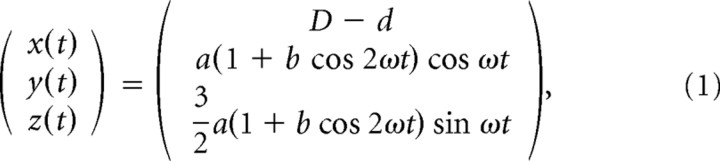with D the distance between the subject's cyclopean eye and the screen (70 cm), d = 30 cm, a = 20 cm, and b = 0.5. The dot started at the top and moved along this path in four cycles, with ω = $\frac{2\pi }{15}$ or ω = $\frac{2\pi }{10}$ rad/s, resulting in a movement duration of 15 s per cycle (slow trials: 1 and 5) or 10 s per cycle (fast trials: 3 and 7). Note that, for the tracing condition, there is no moving stimulus because the complete path is visible. Therefore, in the tracing condition (trials 2, 4, 6, and 8), subjects were instructed to move their finger along the shape with a velocity approximately equal to the velocity in the previous tracking trial. Equation 1 defines the frontal orientation with the path in the y–z plane (trials 1–4). The oblique orientation was obtained by rotating this path 45° left-handed along the z-axis (trials 5–8) such that the lower part of the Cassini shape is closer to the subject than the upper part. This transformation from the frontal orientation (x, y, z) to the 45° tilted orientation (x′, y′, z′) is given by the following:

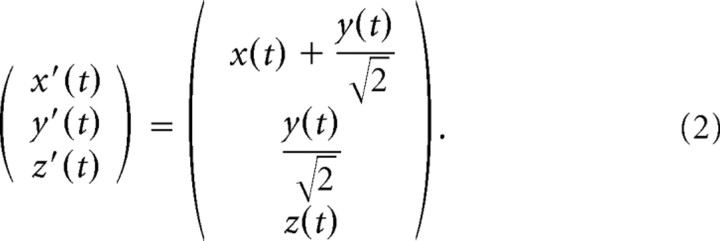In the second block of four trials (trials 9–12), the shape of the stimuli was given by a helix with four windings, two different orientations (long axis along the z- or x-axis) and two different sizes (small or large). All trials in this block were performed in the tracing condition, in which the complete path of the helix was visible. Subjects were asked to follow the shape back-and-forth three times. A helix with the z orientation (trials 9 and 11) had its long axis along the z-axis, and the data points of the helix were defined by the following:

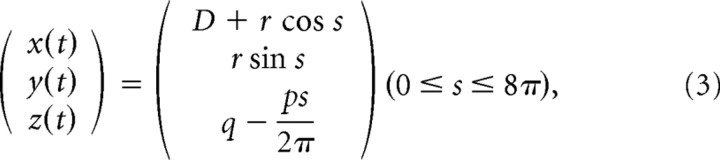with D the distance between the subject's cyclopean eye and the screen (70 cm), p = 9 cm (pitch) and q = 18 cm. Helices with the long axis along the x-axis (trials 10 and 12) were obtained by swapping the x- and z-axis and setting q = −12 cm. For both orientations, the small helix was defined by r = 6 cm (trials 9 and 10) and the large helix by r = 10 cm (trials 11 and 12). In this block, no particular instructions on finger velocity were given. However, it is known that the tracing velocity decreases as curvature increase (Lacquaniti et al., 1983). Therefore, the radius of the helix implicitly imposes the finger velocity, resulting in slow trials (trials 9 and 10) and fast trials (trials 11 and 12).

The last block of eight trials (trials 13–20) was identical to the first block, except that the stimulus shape was given by a Limaçon shape instead of a Cassini shape. The Limaçon shape in the frontal orientation (trials 13–16) was defined as follows:

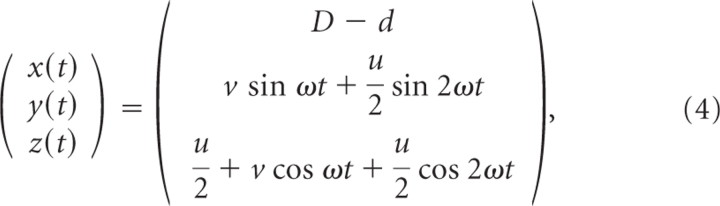with D the distance between the subject's cyclopean eye and the screen (70 cm), d = 30 cm, u = 20 cm, and v = 10 cm. The oblique orientation (trials 17–20) was obtained by rotating this path 45° left-handed about the z-axis (Eq. 2).

Each experiment took ∼40 min including the application of eye coils and infrared markers (8 min), instructions (2 min), calibration (3 min), first block with trials 1–8 (10 min), second block with trials 9–12 (5 min), third block with trials 13–20 (10 min), and removing of eye coils and markers (2 min).

Data calibration.

The Optotrak system measures the 3D coordinates of the markers in Optotrak coordinates. The transformation into the laboratory coordinates [i.e., the same coordinate system defined for the stimuli (see Fig. 1)] involves a rigid body transformation, which translates the origin of the Optotrak coordinate system to the origin of the laboratory coordinate system and rotates the Optotrak coordinate axes to align with the laboratory coordinates axes. A procedure described by Challis (1995) was used to determine the rigid body transformation parameters (i.e., a rotation matrix and a translation vector).

Precise mapping of gaze position requires calibration of the eye coils. Commonly, a neural network is trained to obtain a proper mapping of the voltage signals of each coil to azimuth and elevation (Goossens and Van Opstal, 1997). This approach works well for 2D gaze positions in the frontal plane but appeared to be less accurate in the depth direction as a result of small errors in vergence that give rise to relatively large errors in 3D gaze position, especially if the fixation point is relatively far from the subject. Therefore, we used a novel calibration method introduced by Essig et al. (2006). With this approach, azimuth and elevation could be determined with an accuracy ≤0.3°. This accuracy allowed us to estimate gaze position in depth (i.e., the x-coordinate) with an accuracy of 5 cm when the fixation point was relatively far from the subject (x = 55 cm) and up to 1 cm for near fixation points (x = 15 cm). Note that this accuracy reflects a variable (“noise”) error, which still allows us to determine distances in depth more accurately by averaging over time, which is what a cross-correlation achieves.

Data preprocessing.

Data were analyzed using Matlab (MathWorks). Two trials (2% of the data) were discarded because of technical problems discovered during the data analysis. To skip initial transients in tracking and tracing (Mrotek et al., 2006), data analysis started 5 s after the start of each trial. In addition, for the tracing data, the analysis stopped 5 s before the end of each trial. Occasionally, the marker on the finger was not visible for the Optotrak cameras. One trial was discarded because the marker was not visible for >700 ms. In seven trials, the marker was not visible for 42–633 ms. For these trials, missing values were interpolated using a cubic spline. The result was validated by comparing the interpolated finger position with the finger position in the previous and/or next cycles within the same trial. For all these trials, the interpolated finger position did not substantially differ from the measured finger position of the previous and/or next cycles within that trial.

During the data analysis, we sometimes found relatively large errors between the median values of gaze and finger position for the x, y, and z components. Analyses of these trials revealed that this error originated from multiple sources, including head movements, calibration errors, and the pointing accuracy of the subjects. It is important to have an accurate estimate of gaze and finger position, because small deviations lead to large errors in lead time estimation. Therefore, trials in which the median of eye and finger position differed by >2 cm were discarded (25% of the data).

Average lead time.

The lead time of gaze relative to finger position was calculated for the x, y, and z components separately. First, for each component of gaze, the mean position of that component was subtracted from the corresponding gaze data. Similarly, the mean finger position was subtracted from the finger position time traces. Then, a Hann (also called Hamming) window (Jenkins and Watts, 1968) was applied to all components of the gaze and finger time traces. The average lead time of gaze relative to finger position was defined as the time of the peak of the cross-covariance between the gaze and finger time trace. A positive lead time means that gaze leads finger position. This procedure was repeated for all trials and all subjects. Additionally, for the tracking condition, the lead time between gaze and stimulus position and between finger and stimulus position was calculated. Gaze shifts in azimuth direction have the same dynamics as gaze shifts in elevation direction, and, therefore, the lead times of the y and z component were pooled for averaging. We will refer to the y and z directions as the frontal direction and the x direction as the depth direction. We used a Mann–Whitney U test at the 5% significance level to test for significant differences between lead times for the frontal and oblique orientation of the Cassini and Limaçon shapes (helices were not included in this statistical analysis). In addition, we used a two-sample t test at the 5% significance level to test for significant differences between the following two variables: lead time in frontal direction versus depth for gaze–finger lead time in frontal direction for tracking versus tracing and gaze–finger lead time in depth for tracking versus tracing.

Effect of saccades on lead time.

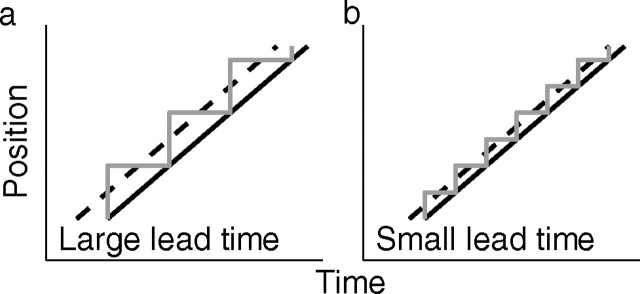
During tracing, gaze moves along the stimulus shape by a sequence of saccades (Reina and Schwartz, 2003) (see Results). The effect of saccades on the estimate of lead time between gaze and finger position is illustrated in Fig. 2. Suppose that a subject moves the finger along a straight line at a constant velocity. If saccades move gaze to a new position on the line and if gaze remains at this position until the hand has reached that position, the mean lead time of gaze, as obtained by cross-covariance, is larger for long fixation times (Fig. 2a, large saccades) than for short fixation times (Fig. 2b, small saccades).

Figure 2.

Illustration of the relation between fixation interval between saccades and time delay between gaze and finger position. a, Assume that a subject is instructed to move the finger along a straight line at a constant velocity and that the subject does so by a sequence of saccades (gray line) with constant fixation times between saccades. Also assume that gaze moves to a new position as soon as the finger (solid black line) reaches the gaze position. A relatively small number of fixations (3 in this example) with long fixation times between saccades results in a relatively large effective lead time (dashed line) of gaze relative to finger position. b, A relatively large number of fixations (6 in this example) with short fixation times results in a relatively small effective lead time of gaze relative to finger.

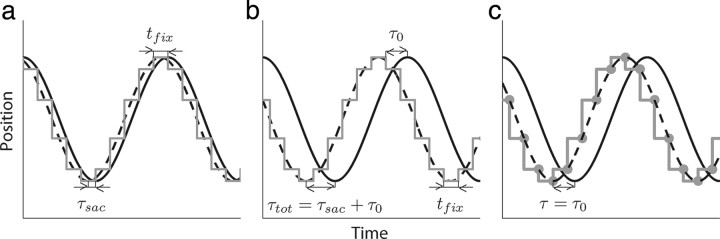
In this study, we investigate the relative timing of gaze and finger position when subjects move their finger along a closed, curved trajectory. As an example, Figure 3 shows simulations of gaze and finger position (gray and solid black line, respectively) for movements along a circle in the frontal (y–z) plane, assuming a constant finger velocity and assuming that the finger moves perfectly along the circle. Furthermore, let us assume that gaze jumps to a new position at time t and that this new position is equal to the finger position at time t + t_fix (Fig. 3a). Moreover, assume that gaze stays at this future finger position until the finger has reached that position. The lead time of gaze with respect to finger position corresponds to the time shift that gives the best overlap between gaze and finger position, indicated by the dashed line in Figure 3a. Because this lead time emanates from the fact that gaze leads the finger by a sequence of saccades, we call this the saccadic lead time τ_sac.

Figure 3.

Schematic illustration of the analysis to calculate lead time of gaze relative to hand. a, Graphical representation of one directional component of gaze position (gray line) and finger position (solid black line) while tracing a circle in the frontal (y–z) plane at a constant velocity. t_fix is the subject's fixation time between saccades, which is constant in this example. In that case, maximum overlap between gaze and finger position, which corresponds to the time of the peak of the cross-covariance function between gaze and hand position, occurs when finger position is shifted by a time τ_sac, indicated by the dashed line. b, Same as a, but now gaze position leads hand position by an additional time τ₀. Maximum overlap occurs when finger position is shifted by a time τ_tot = τ_sac + τ₀ toward the left (dashed line). c, Same as b, but the saccade onsets (gray dots) are interpolated by a cubic spline (dashed line). Maximum overlap between this dashed line and finger position occurs when finger position is shifted by τ = τ₀.

If we assume a constant fixation time between saccades, the saccadic lead time equals half the fixation time (i.e., τ_sac = $\frac{1}{2}$ t_fix), because this corresponds to the time shift that gives the best overlap between gaze and finger position (Fig. 3a, dashed line). Similarly, if there would be one single fixation with a duration t_fixⁱ, its corresponding individual saccadic lead time τ_sacⁱ would be equal to $\frac{1}{2}$ t_fixⁱ. In general, fixation times are not constant. To find an average saccadic lead time τ_sac of a trial, each individual saccadic lead time τ_sacⁱ should be weighted according to the corresponding fixation time τ_fixⁱ, resulting in the following:

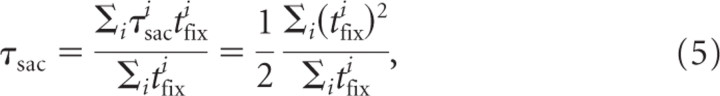which simplifies to τ_sac = $\frac{1}{2}$ t_fix if all fixations have the same duration t_fix.

Next, we extend the model by assuming an additional lead time τ₀ (Fig. 3b). Thus, each saccade at time t brings gaze to a new position that is equal to the gaze position at time t + t_fix + τ₀. This implies that gaze jumps to a new position before the finger has reached the previous gaze position. Figure 3b shows that, in this model, the total lead time τ_tot is equal to the saccadic lead time plus τ₀. We will call τ₀ the primary lead time.

The model described above gives us the total lead time but is insufficient to quantify the contribution of the saccadic and primary lead time separately from the data. Therefore, we determined all saccade onsets for each directional component (y and z). These saccade onset points were interpolated by a cubic spline (Fig. 3c, dashed line). One trial (1% of the data) was discarded because the number of saccade onset points was too small to produce a reliable interpolation curve. It is obvious that the primary lead time τ₀ corresponds to the difference in time between the measured finger position (solid black line) and interpolated line (dashed line), which can easily be determined by cross-covariance. This method also allows us to estimate the average lead time, because this is equal to the difference between the total lead time and primary lead time.

Effect of finger velocity on primary lead time.

The analyses described in the previous section provide the total lead time of gaze relative to finger position and its two components: a saccadic lead time, which is a function of the fixation times between saccades, and a primary lead time. Although the primary lead time is independent of fixation time, it may depend on finger velocity (Gielen et al., 2009). Therefore, we propose two hypotheses regarding the effect of finger velocity on the gaze–finger lead time. Our null hypothesis is that the primary lead time is constant and independent of finger velocity. Alternatively, we hypothesize that gaze leads the finger by a constant distance. Therefore, we plotted the primary lead time as a function of mean tangential finger velocity v = $\sqrt{v_x^2+v_y^2+v_z^2}$ and calculated the correlation between primary lead time and mean finger velocity.

If the latter hypothesis is true, the primary lead time τ₀ is equal to lead distance Δs divided by the mean tangential finger velocity, and, therefore, the primary lead time τ₀ as obtained from the cross-correlation should decrease for higher tangential finger velocities. We applied three different methods to obtain an estimate for Δs. The mean lead distance was obtained by fitting τ_o = $\frac{\Delta s}{v}$ for each subject by variation of Δs (method I). We used the bootstrap method (n = 100) to compute the SD. In a second approach, we calculated Δs = vτ₀ for each trial, which gives the mean lead distance and SD for each subject and for all data (method II). In addition, we determined the lead distance directly for every trial as the mean distance between gaze and finger position at each saccade onset (method III). We used a two-sample t test at the 5% significance level to test for significant differences between the lead distance distribution obtained by methods I and II and a Mann–Whitney U test at the 5% significance level to test for significant differences between methods I and III and between methods II and III.

Results

Behavior during tracking

Figure 4a shows a quasi 3D view of stimulus (dashed line), gaze (gray line), and finger position (solid black line) for subject S5 tracking a target moving along the oblique Cassini shape. The dashed line is hard to distinguish from the solid line because of the almost perfect tracking by the subject. Figure 4b–d shows the corresponding frontal, top, and side views, respectively, for one repetition of the stimulus. In the tracking condition, gaze follows the moving target quite well by smooth pursuit in three dimensions. Gaze and finger trajectories deviate more from the stimulus path in the depth direction (x) than in the frontal direction (y and z; Fig. 4, compare b, c). In addition, gaze occasionally deviates from the target during blinks and small saccades. Data in Figure 4 are representative for all subjects.

Figure 4e–g shows the corresponding time traces of stimulus (dashed line), gaze (gray line), and finger position (solid black line) for the x, y, and z components, respectively. The time traces show that gaze is superimposed almost perfectly on hand position in the y and z directions. In the x direction (depth) (Fig. 4e), the noise is larger than in the y and z directions as a result of small errors in measurement and calculation of vergence (see Materials and Methods). These results demonstrate that subjects are able to perceive the anaglyph stimuli correctly and that they have an accurate percept of the position of the moving target in 3D. In addition, the time traces show that gaze leads finger position by a small amount of time. This will be quantified in more detail later.

Behavior during tracing

Figure 5a shows a quasi 3D view of stimulus (dashed line), gaze (gray line), and finger position (solid black line) of the same subject (S5) for tracing the very same shape as in Figure 4. Figure 5b–d shows the corresponding frontal, top, and side views, respectively. For tracing, the azimuth and elevation components of gaze move along the completely visible shape by a sequence of saccades. During a saccade, gaze deviates from the stimulus path as a result of transient divergence (Fig. 5c,e). This divergence originates from an asymmetry between abducting and adducting saccadic eye movements. Because the abducting eye has a higher acceleration in a horizontal saccade and is on-target somewhat earlier than the adducting eye, the binocular fixation point shows an outward-looping trajectory in depth during a saccade (Collewijn et al., 1997). In the x direction (depth), these deviations can be as large as 5 cm for large saccades and are disproportionately larger for far than for near targets as a result of the nonlinear relation between vergence and distance.

Figure 5e–g shows the corresponding time traces of gaze (gray line) and finger position (solid black line) for the x, y, and z component, respectively. In the x direction, changes in gaze are slightly noisy but otherwise smooth as usual for vergence eye movements, except for the transient divergence during saccadic gaze shifts (see expanded time trace in Fig. 5e). In contrast to the tracking condition, the y and z components of gaze are not smooth but consist of a sequence of saccades. Gaze jumps to a new position on the shape and fixates there until the finger is close to this position. As soon as the finger is close to that position, a new saccade brings gaze to a next position on the shape (see expanded time trace in Fig. 5f,g). Gaze position clearly leads finger position for the y and z direction. Similar results were obtained for the Limaçon shapes and helices.

Lead times in gaze–finger coordination

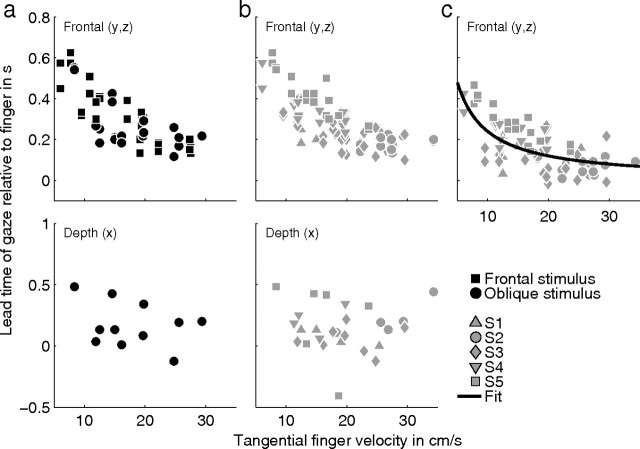
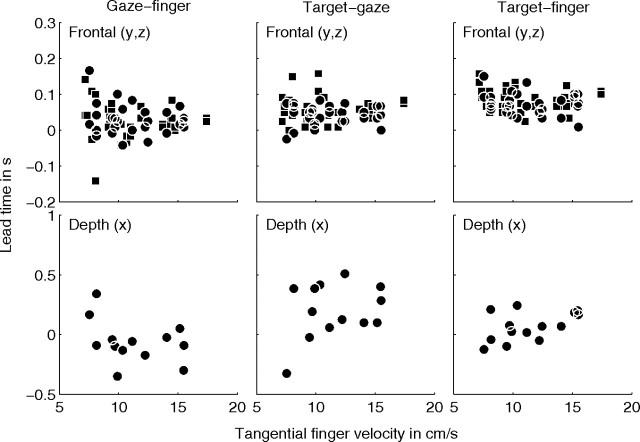
As explained in Materials and Methods, the time of the peak of the cross-covariance between gaze and finger position gives a measure of the mean lead time of gaze relative to finger position. Figure 6a shows the mean lead time of gaze relative to the finger (corresponding to time of the peak of the cross-covariance function) in the y and z direction (top panel) and depth (x) direction (bottom panel). Data of all subjects are shown, but only trials with the Cassini and Limaçon stimulus shapes are included (no helices). Squares and circles in Figure 6a represent lead times for the frontal and oblique stimulus orientations, respectively. The lead times shown here represent the total lead time (Fig. 3b). The lead times of gaze relative to the finger for the components in the frontal plane are not significantly different for the frontal and oblique stimulus orientations. This means that any depth components in the path do not affect the lead times for the components of gaze and hand in the frontal plane. We also tested whether lead times in the y and z direction (top panel) were different for Cassini and Limaçon shapes with the frontal orientation (squares) versus the shapes with the oblique orientation (circles). We did not find a significant difference (Mann–Whitney U test, p = 0.34).

Figure 6.

Lead times of gaze relative to finger for the tracing condition. The top and bottom show values for the frontal directions (y and z) and the depth direction (x), respectively. a, Time of the peak of the cross-covariance function between gaze and finger position as a function of the mean tangential finger velocity. Only data for the Cassini and Limaçon stimulus shapes are shown. Squares and circles represent data for the frontal and oblique stimulus orientations, respectively. The lead times shown here represent the total lead time (see Fig. 3b). b, Same as a, but lead times of trials with the helices as stimulus shape are included as well. Different gray symbols refer to data from different subjects. c, Time of the peak of the cross-covariance function between gaze position after interpolation of the saccade onsets with a cubic spline and finger position. The lead times shown here represent the primary lead time (see Fig. 3c). Different gray symbols refer to data from different subjects. The black line shows the best fit of τ_o = $\frac{\Delta s}{v}$ over all subjects.

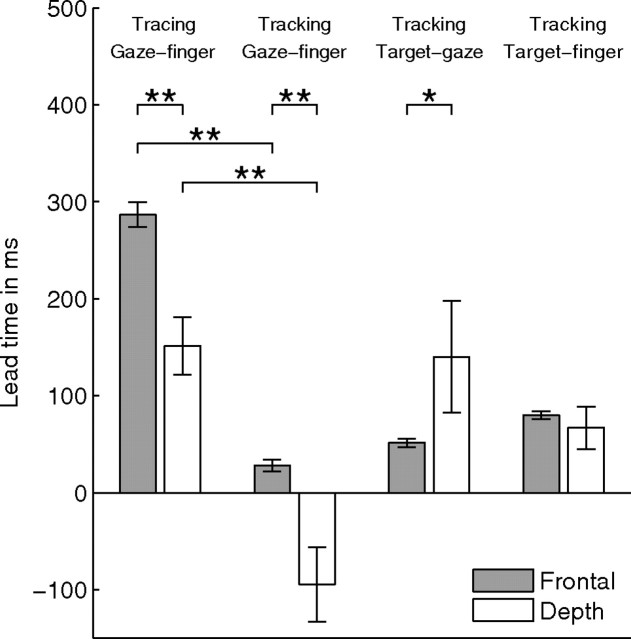
When saccades are involved in eye–hand coordination like in tracing, the time of the peak of the cross-covariance function depends on the fixation time between saccades and may depend on the velocity of tracing. To investigate this in detail, Figure 6b shows the same data as in Figure 6a, but lead times of trials with the helices as stimulus shape are included as well. Different gray symbols refer to data from different subjects. For the y and z directions (frontal plane), there is a significant correlation between lead time and tangential finger velocity (r = −0.72, p < 0.01) (Fig. 6b, top). This correlation is not significant in depth (p = 0.91) (Fig. 6b, bottom). Thus, a lower tracing velocity of the finger results in a larger lead time of gaze with respect to finger for the frontal plane but not for the depth direction. The mean ± SE gaze–finger lead time is 287 ± 13 ms (n = 84) in the frontal plane and 151 ± 36 ms (n = 28) in depth (Fig. 7). The difference between the lead times in the frontal plane and depth is significant (p < 0.01).

Figure 7.

Lead time of gaze relative to finger (for tracing and tracking), target relative to gaze (tracking), and target relative to finger (tracking) in the frontal direction (gray bars) and depth (white bars). Values were obtained by averaging over all trials and subjects. Because the data show mean values over trials and subjects, we provide the SE (error bars) as a measure of the error in the estimate of the mean. Significant differences are indicated by *p < 0.05 and **p < 0.01. The negative gaze–finger lead time in depth for the tracking condition means that gaze lags behind finger position.

These results for tracing are different from the results obtained for tracking. For tracking, we calculated the lead time of gaze relative to finger position, of target relative to gaze position, and of target relative to finger position, in the frontal and the depth direction (Fig. 8). We subdivided the lead times in the frontal plane into trials for shapes in the frontal orientation (Fig. 8, squares) and in the oblique orientation (circles). Because we did not find a significant difference between frontal and oblique stimulus orientation (Mann–Whitney U test, p > 0.1) for all three lead times, data for both stimulus orientations were pooled. We calculated the correlation between the lead time of gaze relative to finger and mean tangential finger velocity for the frontal and depth directions. For both directions, this correlation was small and did not appear to be significant (r = −0.12, p = 0.37 for the frontal direction and r = −0.35, p = 0.22 for the depth direction). We also calculated the lead times averaged over all trials and subjects for the frontal and the depth direction. In the tracking condition, gaze and finger lag behind the moving target. For gaze, the mean ± SE delay is 51 ± 4 ms (n = 60) in the frontal plane and 140 ± 57 ms (n = 14) in depth. For the finger, the mean ± SE delay is 80 ± 4 ms (n = 60) in the frontal direction and 67 ± 22 ms (n = 14) in depth. As a result, gaze leads the finger on average by 28 ± 6 ms (n = 60) in the frontal plane but lags behind the finger by 95 ± 39 ms (n = 14) in depth. The mean lead times of gaze relative to the finger in the tracking condition are significantly different from the mean lead times in the tracing condition (p < 0.01) both for the frontal and depth components (Fig. 7). In Discussion, we will further elaborate on these findings.

Figure 8.

Time of the peak of the cross-covariance function between gaze and finger position (first column), target and gaze position (second column), and target and finger position (third column), as a function of the mean tangential finger velocity in each trial for the tracking condition. The top and bottom row show values for the frontal directions (y and z) and the depth direction (x), respectively. Squares and circles represent data for the frontal and oblique orientations, respectively, for the Cassini and Limaçon shapes.

Effect of saccades on gaze–finger timing

In the previous section, we have shown that the lead time between gaze and finger position for tracing is on average 287 ms in the frontal direction (Fig. 7) and that this lead time varies with tangential finger velocity in the frontal plane (Fig. 6b, top). Moreover, the mean lead time for the frontal direction is significantly different from the value for depth (151 ms) (Fig. 7). In this section, we will investigate the effect of saccades on the relative timing of gaze and finger position.

As illustrated in Figure 3, we hypothesize that the lead time of gaze relative to the finger in the frontal direction in the tracing condition is a combination of a saccadic lead time and a primary lead time. To test this hypothesis, we interpolated all saccade onsets with a cubic spline, as illustrated in Figure 3c. Next, we calculated the mean gaze–finger lead time from the cross-covariance between the spline function and finger position for the frontal direction. The results are shown by the symbols in Figure 6c. Different symbols refer to data from different subjects. Figure 6c gives the primary lead time as a function of tangential finger velocity in the frontal plane. The mean ± SE value for the primary lead time is 166 ± 12 ms, which is significantly smaller (Mann–Whitney U test, p < 0.01) than the total mean lead time (287 ms) (Fig. 6b, top) of gaze relative to finger in the tracing condition. The correlation between primary lead time and finger velocity is significant (r = −0.61, p < 0.01).

In the previous section, we found that the gaze–finger lead time in depth is 151 ± 36 ms (mean ± SE), which is significantly different from the total lead time of 287 ± 13 ms in the frontal direction (Fig. 7, first two bars). However, after correction for the saccadic lead time, the mean primary lead time in the frontal direction is 166 ± 12 ms, which is not significantly different from the mean lead time in depth (Mann–Whitney U test, p = 0.71).

The difference between total lead time (Fig. 6b) and primary lead time (Fig. 6c) corresponds to the saccadic lead time (method I). Table 1 shows the saccadic lead time in milliseconds. Values are given as mean ± SD over all tracing trials. The saccadic lead time for the five subjects ranges from 93 to 142 ms. Figure 9 shows the histograms of the fixation times for all trials per subject (S1–S5), as well as the distribution of fixation times for all subjects. The solid and dashed line in each histogram indicate the median and mean value, respectively. The median fixation times for the five subjects range from 233 to 267 ms. As explained in Materials and Methods, the saccadic lead time is related to the length of the fixations in a trial (Eq. 5). As a check for consistency, we have also calculated the saccadic lead time from the individual fixations in each trial according to Equation 5 (Table 1, method II). For this method, the saccadic lead time for the five subjects ranged from 119 to 169 ms, which is larger than the corresponding lead times found by method I. This difference is significant (Mann–Whitney U test) for subjects S2, S4, and S5 and for all subjects pooled. We will give an explanation for this difference in Discussion.

Table 1.

Saccadic lead times in milliseconds calculated as the difference between total lead time and primary lead time (method I) and obtained from fixation times according to Equation 5 (method II)

Subject	Method I	Method II
S1	93 ± 50	119 ± 29
S2	123 ± 18	172 ± 61
S3	125 ± 56	149 ± 21
S4	107 ± 20	146 ± 23
S5	142 ± 27	169 ± 23
All subjects	121 ± 39	154 ± 37

Values are given as mean ± SD over all tracing trials.

Figure 9.

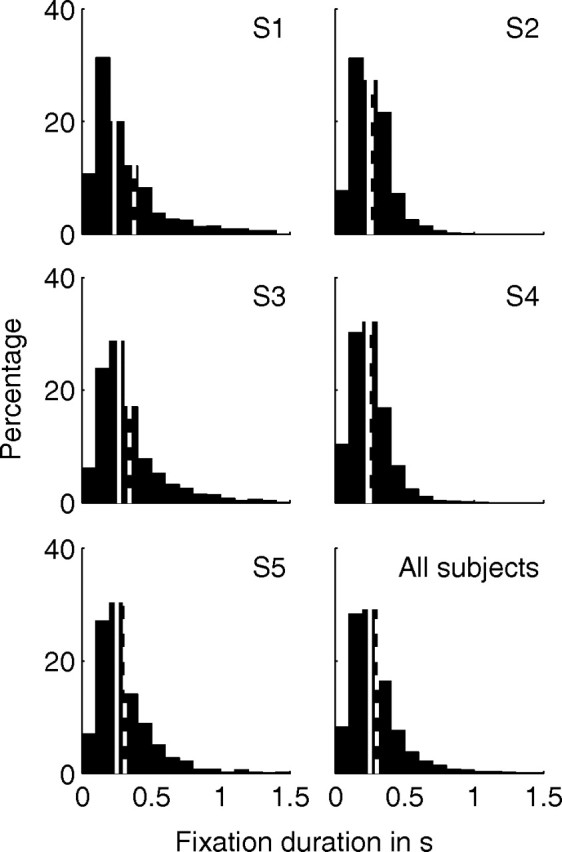
Distribution histograms of the fixation times for subjects S1–S5 and across all subjects. Values are obtained from individual fixations of each tracing trial. Solid and dashed lines indicate the median and mean value over all values in the histogram, respectively. The distribution of fixation times is given as a percentage of the total number of fixations.

The general notion in the literature is that gaze leads finger position in time. Our null hypothesis was that this lead time should be constant and independent of velocity of the finger, yet, after correction for the saccadic lead time, we still find a significant negative correlation between the gaze–finger lead time and mean finger velocity. The data in Figure 6c suggest an inverse relationship between lead time and tangential finger velocity. This inverse relationship is qualitatively in agreement with the hypothesis that gaze leads finger position by a constant displacement. This predicts τ_o = $\frac{\Delta s}{v}$, where τ₀ is the primary lead time, Δs is the mean lead distance of gaze relative to finger position, and v is the tangential finger velocity.

To test the hypothesis that gaze leads the finger by a constant displacement, we fitted the relation τ_o = $\frac{\Delta s}{v}$ to the data in Figure 6c by varying Δs. The best fit over all subjects for the primary lead time is shown by the solid line in Figure 6c and corresponds to a mean ± SD lead distance of 2.6 ± 0.1 cm. Fits for each subject separately reveal that the range of lead distances is between 1.5 and 3.5 cm (Table 2, method I).

Table 2.

Lead distance of gaze relative to finger position in centimeters computed as follows: I, the best fit of τ_o = $\frac{\Delta s}{v}$ (SD obtained by bootstrap procedure with n = 100); II, the product of finger velocity v and primary lead time τ₀; and III, the distance between gaze and finger position at each saccade onset

Subject	Mean ± SD (cm) [median (cm)]
	Method I	Method II	Method III
S1	2.2 ± 0.3	2.5 ± 1.0 [2.6]a	3.8 ± 2.5 [3.1]b
S2	1.5 ± 0.2	1.7 ± 1.0 [1.6]	2.9 ± 2.3 [2.2]b,c
S3	1.5 ± 0.2	1.8 ± 1.7 [1.5]	3.0 ± 1.9 [2.6]b,c
S4	2.9 ± 0.2	3.3 ± 0.8 [3.3]a	4.2 ± 2.5 [3.9]b
S5	3.5 ± 0.1	3.6 ± 0.6 [3.6]	3.7 ± 2.3 [3.3]
All subjects	2.6 ± 0.1	2.6 ± 1.4 [2.7]	3.6 ± 2.4 [3.1]b,c

^a,b,cSignificant difference (p < 0.05) between the lead distance distribution obtained by methods I and II, methods I and III, and methods II and III, respectively.

Another method to determine the mean lead distance of gaze relative to finger is to calculate Δs = vτ₀ using the primary lead time and the mean tangential velocity of each trial. The results demonstrate that the mean ± SD lead distance of gaze relative to finger position in the frontal plane for the tracing condition is 2.6 ± 1.4 cm with a range between 1.7 and 3.6 cm for all subjects (Table 2, method II). For subjects S2, S4, and S5 and for the pooled dataset, the lead distance found by this method is close to the value obtained by the best fit to the data (method I) and is not significantly different from the value obtained by the best fit.

Alternatively, the lead distance is obtained directly by calculating the distance between gaze and finger position at each saccade onset for all tracing trials. The median lead distance obtained by this method has a range between 2.2 and 3.9 cm (Table 2, method III). Compared with method II, method III gives significant differences for subjects S2 and S3 and for the pooled dataset. Compared with the value obtained by the best fit (method I), method III yields significantly different results for the mean lead distance for all subjects, except subject S5. The median values obtained by method III are smaller (range of 2.2–3.9 cm) than the mean values (range of 2.9–4.2 cm; see Discussion). The analyses indicate that not lead time, but lead distance, is approximately constant, resulting a lead time that is inversely proportional to the finger velocity.

Discussion

The dynamics of saccades and smooth pursuit, which are involved in the control of gaze in the frontal plane, are very different from that of the vergence system. This led us to suggest that the lead time of gaze relative to the finger is different in the frontal plane and in depth. Our results revealed that the lead time of gaze relative to the finger was not constant for tracing but inversely related to tangential velocity of the hand. The lead time is relatively large (∼500 ms) for small velocities and decreases to ∼200 ms for finger velocities of ∼30 cm/s (Fig. 6b). After correction for a saccadic lead time, the remaining lead time still decreases inversely with finger velocity (Fig. 6c). Our results can be explained by assuming that gaze leads finger position by a constant distance of ∼2.6 cm.

The lead time of gaze relative to the finger was obtained from the cross-covariance between gaze and finger position. Because the lead time of gaze varied with tangential velocity and because the tangential velocity varied along the Cassini and Limaçon shapes, the peak of the cross-covariance reflects the mean lead time over a range of velocities in a trial.

For tracing, the gaze–finger lead time has two components: a saccadic and a primary lead time. The saccadic lead time reflects the contribution of saccades to the total lead time and therefore depends on the fixation time between saccades. We estimated the saccadic lead time by taking the difference between total lead time and primary lead time (method I) and from the individual fixation times according to Equation 5 (method II). The values found by method II are larger than for method II (Table 1). This difference can be explained by considering Figure 3a. In this figure, the fixation end points (or saccade onsets) are located exactly at the finger position curve (black line). However, in general, the fixation end points will not perfectly superimpose on the finger position time trace because of measurement errors, motor noise, and limited pointing accuracy of the subject. As a consequence, the fixation duration of a particular fixation will be slightly shorter or longer compared with the hypothetical situation in Figure 3a. Assuming that the difference between the measured and hypothetical fixation time is ±ϵ with equal probability, Equation 5 becomes

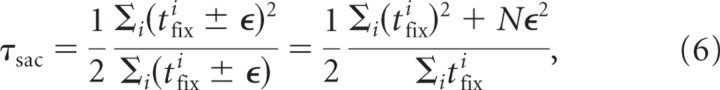with N the number of fixations. This equation shows that the saccadic lead time estimated from detected fixations is biased toward larger values (because of the term Nϵ²). However, the noise does not affect the value of the saccadic lead time obtained by cross-covariance (method I). Thus, methods I and II give the same results only if the fixation end points exactly superimpose on the finger position (Fig. 3a) or on the finger position shifted in time (Fig. 3c). If not, method II will yield systematically larger saccadic lead times than method I.

The distribution of measured fixation times (Fig. 9) reveals a sharp peak for values <250 ms with a mean value exceeding 250 ms. For all subjects, the mean value exceeds the median value. This can be attributed to the fact that fixation times can only be positive. Therefore, any outliers correspond to large positive values, which implies that the mean value is biased toward larger values. This positive bias also affects the median value but to a smaller extent.

Another consideration is that finger velocity and saccade interval might be related. For example, a higher movement velocity might imply a more rapid sequence of saccades with shorter intervals. If so, the inverse correlation between lead time of gaze and finger velocity might be an artifact of the inverse correlation between finger velocity and fixation time. To investigate this in more detail, we calculated the correlation between finger velocity and fixation duration for each subject. This correlation appeared to be small (range of 0 to −0.3). In addition, we did not find a significant correlation between mean fixation interval and mean finger velocity (p > 0.3). Finally, the mean finger velocity was not significantly correlated to the number of saccades per second. Therefore, we conclude that our result of an inverse relation between lead time and tangential hand velocity is not an artifact of a hidden correlation between hand velocity and saccade frequency.

The results in Figure 7 show that the mean lead times for tracking of gaze relative to the finger (28 and −95 ms for the frontal plane and depth, respectively) are much smaller than the corresponding lead times for tracing. In addition, Figure 5 shows that gaze position deviates from the stimulus shape more for depth than for direction in the tracing condition. This is not attributable to an erroneous percept of stimulus depth. The almost perfect match between stimulus position, gaze, and finger position for tracking indicates that subjects perceive the anaglyph stimulus quite well. Because the complete stimulus is visible in the tracing condition, it is highly unlikely that the percept of the stimulus path is inferior in the tracing condition. The less accurate match between stimulus path and gaze position in depth is in agreement with previous studies (Admiraal et al., 2003, 2004), which have shown that fixation accuracy on targets is less when visual information is available on target position relative to the environment, especially for the depth component. Moreover, Gonzalez et al. (1998) reported that the perceived depth of random dot stereograms is not affected by vergence, which suggests that imperfections of gaze in depth do not affect the accuracy of pointing in depth.

After correction for the saccadic lead time, we found a mean primary lead time of gaze relative to the finger in the frontal plane, which is close to the lead time for depth (166 and 151 ms, respectively). This might suggest that the underlying mechanisms may be similar. This is not true because the lead time of gaze varies with tangential finger velocity in the frontal plane but not for depth. Moreover, the different results for tracking (i.e., a lead time of gaze of 28 ms in the frontal plane but a lag of 95 ms in depth) suggest different mechanisms for tracking in the frontal plane and in depth.

Our results clearly demonstrate differences in the coordination of gaze and finger position for the frontal plane and depth. There is some evidence from the literature supporting this result. For example, several studies have demonstrated that direction and depth are processed separately as independent variables during updating across eye movements (Ghez et al., 1997; Henriques et al., 1998; Van Pelt and Medendorp, 2008). Moreover, there is evidence that target depth and direction are processed in functionally distinct visuomotor channels (Flanders et al., 1992; DeAngelis, 2000; Cumming and DeAngelis, 2001; Vindras et al., 2005). Another difference is that gaze leads finger position in the tracking condition by 28 ms in the frontal plane but lags behind the finger in depth by 95 ms. Although the lag between target and gaze depends on the predictability of the moving target (Collewijn and Tamminga, 1984), it seems highly unlikely that anticipation or predictability would be different for the frontal plane and for depth. It is also highly unlikely that the velocity of the moving target or the finger velocity (typically <30 cm/s, corresponding to ∼15°/s in this study) is too fast for the vergence system to track. This follows from results by Erkelens et al. (1989), who showed that errors between gaze and a moving target are <1° in the depth direction for movement velocities in the range between 10 and 40°/s. Therefore, we conclude that the different lead time of gaze relative to the finger for the frontal plane and for depth reflects differences in the dynamics of visuomotor control for version and vergence.

The results of our study suggest that feedforward and (internal) feedback transformations, which are thought to be part of the servo-control system for eye–hand coordination (Wolpert et al., 1995), should not only deal with time delays in internal and sensory feedback loops but also with spatial aspects. The latter seems obvious, but our study is the first to demonstrate that the visuomotor transformations generate a constant lead of gaze in space by ∼2.6 cm. This distance is relatively small and may be a compromise between a distance that which is small enough to have a sharp percept of target and finger position and long enough for planning the finger trajectory. If the aim is to lead the finger such that both the target and finger position are sharply represented on the retina, then it might be retinal eccentricity rather than distance in space that is relevant. In that case, the distance of 2.6 cm, which corresponds to ∼2° in our study, will become smaller or larger if the distance of the stimulus shape is nearer or farther away, respectively.