Abstract
Motion is a potent cue for the perception of three-dimensional (3D) shape in primates, but little is known about its underlying neural mechanisms. Guided by recent functional magnetic resonance imaging results, we tested neurons in the fundus of the superior temporal sulcus (FST) area of two macaque monkeys (Macaca mulatta, one male) using motion-defined surface patches with various 3D shapes such as slanted planes, saddles, or cylinders. The majority of the FST neurons (>80%) were selective for stimuli depicting specific shapes, and all the surfaces tested were represented among the selective FST neurons. Importantly, this selectivity tolerated changes in speed, position, size, or between binocular and monocular presentations. This tolerance demonstrates that the 3D structure-from-motion (3D-SFM) selectivity of FST neurons is a higher-order selectivity, which cannot be reduced to a lower-order speed selectivity. The 3D-SFM selectivity of FST neurons was unaffected by removal of the opposed-motion cue that supplemented the speed gradient cue in the standard stimuli. When tested with the same standard stimuli, fewer neurons in the middle temporal/visual 5 (MT/V5) area were selective than FST neurons. In addition, selective MT/V5 neurons represented fewer types of surfaces and were less tolerant of stimulus changes than FST neurons. Overall, these results indicate that FST neurons code motion-defined 3D shape fragments, underscoring the central role of FST in processing 3D-SFM.
Introduction
The extraction of three-dimensional (3D) shape is a fundamental challenge for the visual system of animals living and behaving in a three-dimensional world. Behavioral studies have established that optical motion is one of the primary sources of information for the perception of 3D shape in human and nonhuman primates (Siegel and Andersen, 1988, 1990; Todd and Norman, 2003) and that this information is useful over a wider range of conditions than binocular disparity. Little is known, however, about the underlying neural mechanisms of 3D shape extraction based on motion cues. Some previous studies have examined the responses of middle temporal/visual 5 (MT/V5) neurons while monkeys made judgments about an ambiguous direction of motion in a rotating transparent cylinder (Bradley et al., 1998; Dodd et al., 2001). This task reveals mechanisms related to the monkey's perception of relative order in depth, but it requires no judgment about 3D shape (Born and Bradley, 2005).
The estimation of 3D shape-from-motion (3D-SFM) requires the detection of at least second-order gradients in velocity, which can be directly associated with different types of intrinsic surface structures, such as cylindrical, ellipsoidal, or saddle-shaped regions (Lappin and Craft, 2000). Neurons in MT/V5 have been shown to be selective for depth (zero-order) from motion (Nadler et al., 2008), and neurons in areas MT/V5 and dorsal medial superior temporal area (MSTd) selective for first-order (i.e., linear) variations in image velocity have also been reported (Treue and Andersen, 1996; Xiao et al., 1997a; Sugihara et al., 2002). In MSTd, it has been shown that speed gradients that give rise to 3D-SFM can be superimposed on any direction pattern (Duffy and Wurtz, 1997) and, conversely, that selectivity for flow components depends only on the direction pattern (Tanaka et al., 1989; Orban et al., 1995). However, no investigation has thus far discovered any neurons selective for the higher-order patterns of relative motion that are necessary for the estimation of surface curvature. Recent studies using functional magnetic resonance imaging (fMRI) in monkeys (Vanduffel et al., 2002; Nelissen et al., 2006) have provided some indication that these cells might be located in the fundus of the superior temporal sulcus (FST) area, a satellite of MT/V5 (Ungerleider and Desimone, 1986). Little is known about the properties of FST neurons, except for the larger receptive fields (RFs) and weaker direction selectivity compared with MT/V5 neurons (Desimone and Ungerleider, 1986; Rosenberg et al., 2008).
If FST plays a prominent role in the extraction of 3D-SFM, we can make the following predictions: (1) a high proportion of FST neurons should be selective for 3D-SFM stimuli, (2) neurons should be selective for a wide range of representative surface shapes, (3) the selectivity should tolerate changes in mean speed, position, or size of the stimuli to guarantee operation of higher-order mechanisms, and, finally, (4) selectivity and this tolerance should be enhanced in FST compared with its main input area, MT/V5. The present experiments bear out these four predictions.
Materials and Methods
General procedures
All experimental procedures were in accordance with the national and European guidelines and were approved by the Katholieke Universiteit Leuven ethical committee. Two rhesus monkeys [Macaca mulatta; “I” (male, 7–8 kg) and “M” (female, 3.5–4.5 kg)] were implanted, under isoflurane anesthesia, with a head post and a recording chamber over the posterior superior temporal sulcus (STS). FST (see Fig. 1B) was localized using landmarks visualized with MRI. Additional functional criteria included neuronal RF sizes and locations as characterized by previous single-cell studies (Desimone and Ungerleider, 1986; Hikosaka et al., 1988) and fMRI-based retinotopic maps (Nelissen et al., 2006; Kolster et al., 2009). Most RFs were located within a polar angle of 45 ° from the horizontal meridian (HM) (supplemental Fig. S1, available at www.jneurosci.org as supplemental material), indicating that we recorded mainly from the middle part of FST, to which the HM projects (Kolster et al., 2009). In monkey M, the RFs in the most lateral penetrations were located close to the upper vertical meridian in agreement with the fMRI-based retinotopic map of FST (Kolster et al., 2009). Thus, in both monkeys, the RFs avoided the lower vertical meridian, which marks the boundary between FST and ventral MST. In monkey M, the RFs also shifted to larger eccentricities rostrally, typical of FST (Nelissen et al., 2006; Kolster et al., 2009). The linear regression line relating the square root of the RF area to eccentricity was given by the equations RF size = 1.3 × eccentricity + 11.7° (monkey I) and RF size = 1.0 × eccentricity + 9.9° (monkey M), which lies between the values for MT/V5 neurons and neurons from the three different subdivisions of MST (Tanaka et al., 1993). We also recorded 64 neurons from area MT/V5 in the same two subjects. Anatomical position, strong direction selectivity, smaller RF sizes, and an inverse caudorostral eccentricity gradient compared with FST (Ungerleider and Desimone, 1986) provided clear evidence that these recordings were made in MT/V5.
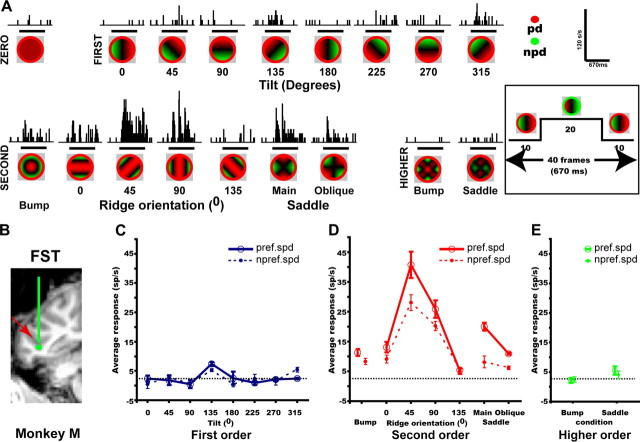
Figure 1.
Example FST neuron. A, Poststimulus time histograms showing the average response of neuron MD182_F (eccentricity 4.5°, direction 0°), recorded at the estimated position indicated in B, to the 3D-SFM (fast speed) stimuli. Stimulus surfaces are portrayed as a color code, in which hue indicates direction during the initial 10 frames (see insets) and saturation the speed. Calibration bars: 120 spikes/s, 670 ms. B, Coronal section of anatomical MR showing the recording site in FST (red arrow) of monkey M. C–E, Response plotted as a function of tilt (C), second-order stimuli (D) [d′ = 4.21; separability index (r2) 3D shape–speed = 0.99] and higher-order stimuli (E) for preferred speed (solid lines) and nonpreferred (dashed lines) speeds. Horizontal lines, Baseline activity.
Subjects' eye movements were recorded at 60 or 120 Hz using an infrared camera (Iscan). Subjects maintained fixation within a small window (1.2 × 1.2° for monkey M; 1.4 × 1.4° for monkey I) centered on a 0.15° fixation target throughout the trial and were rewarded with apple juice at the end of the trial. Extracellular recordings (Sawamura et al., 2006) were made using tungsten microelectrodes (in situ impedance of ∼1 MΩ at 1 kHz; FHC), advanced inside a guiding tube. Signals were amplified and filtered, and spike times, stimulus, and behavioral events were stored for offline analysis.
The display (60 Hz; 29.25 × 21.95 °) was positioned at a distance of 75 cm from the eyes. Random-dot stimuli (∼50% black dots; white, 39.5 cd/m2; black, 0.5 cd/m2; dot sizes, 0.03–0.1°) were presented on a uniform gray (24 cd/m2) background. After 500 ms of fixation, a static pattern (the first frame of the sequence) was presented for 1000 ms before movement commenced. These motion stimuli had variable durations depending on the specific test used and were always followed by a 300 ms static display of the last frame of the motion sequence. All stimuli were presented binocularly, except when stated otherwise.
Preliminary testing
We first estimated the RF center using squares (2.5°, 4.5°, and 6.5°), containing random dots moving horizontally or vertically at 4°/s, presented at a series of positions tiling the entire screen. Motion began rightward or upward, reversed at frame 10 (167 ms), then reversed again at frame 30, such that the first and the last frames of the 40 frame (667 ms) sequence were identical. At the estimated RF center, we positioned a circular patch (4 or 12° diameter) of random dots moving coherently in eight directions of translation (45° intervals; duration, ∼333ms) to estimate the preferred direction of the neuron. Finally, we presented a 6 × 8 mosaic of 3.5° squares, containing random dots moving coherently in the preferred direction for ∼333 ms, covering most (28 × 21°) of the screen. These positions, plus one additional square in the exact center, were presented randomly for a total of 49 conditions, providing a detailed mapping of the receptive field. RF size was defined as the square root of the RF area, measured at 50% of maximum response, following Raiguel et al. (1995).
Many FST neurons were also tested, after the main test was completed, in a speed test in which the random-dot pattern (4 or 12° diameter) moved for 667 ms in the optimal direction at five different speeds from 1 to 16°/s in 1 octave steps. Median number of repetitions was seven (quartiles 7–8).
Motion-defined depth–structure stimuli and main test
Motion-defined depth–structure stimuli
The stimuli in these experiments were similar to those used in numerous human psychophysical experiments (van Damme et al., 1994; Phillips and Todd, 1996; Perotti et al., 1998). Their design was motivated by basic principles of differential geometry with which it is possible to decompose smooth surfaces into qualitatively distinct patches based on the relative patterns of curvature in different directions (Koenderink, 1990). These patch types are defined in a principled manner by their levels of differential structure. For example, consider the depth map of a slanted plane. The first spatial derivative in the direction of slant will be nonzero, but all higher-order spatial derivatives will be zero. Thus, slanted planes are referred to as first-order surfaces. Second-order surfaces are those whose depth maps have nonzero second spatial derivatives. These can be subdivided into three distinct classes based on the product of the two principal curvatures, which can be positive (as on a sphere), negative (as on a saddle), or zero (as on a cylinder). It is also possible to define more complex surface patches whose depth maps have nonzero higher-order spatial derivatives. Because of the evidence that human observers can successfully identify these different types of patch structures (van Damme et al., 1994; Phillips and Todd, 1996; Perotti et al., 1998), they were chosen to characterize the neural encoding of 3D surface shape in the present experiments.
The stimuli depicted 3D surface patches textured with random-dot patterns. Their 3D structures were optically specified by patterns of motion parallax under orthographic projection. In natural vision, motion parallax is most commonly produced by rotations of a surface in depth relative to the point of observation, but equivalent patterns to those produced by small angle rotations can also be created by shearing surface patches about an axis in the image plane (Todd and Perotti, 1999). The advantage of this approach for experimental purposes is that it does not result in some parts of a surface being occluded by others. Some example stimuli that were generated with this procedure are presented in the supplemental Movies M1–M7 (available at www.jneurosci.org as supplemental material). Because these displays were rendered under orthographic projection, the signs of the surface slants or curvatures are mathematically ambiguous. However, many observers have a strong bias toward perceiving ambiguous curved surfaces as convex rather than concave. The displays were viewed binocularly, except when otherwise mentioned. Although this binocular presentation created a nominal conflict between the stereo and motion cues for 3D shape, explicit testing revealed no effect of such a conflict (see Results).
The range of speeds within the motion patterns was equal across stimuli for a given mean speed, and we tested two mean speeds (slow, 1.25°/s; fast, 2.5°/s; range, 0–8 and 0–16°/s). All of the surface patches were shown inside a circular aperture and oscillated back and forth beginning in the preferred direction. In any given motion pattern, many more pixels moved at a speed close to zero than at the fastest speed in the range, explaining why the mean is low compared with the fastest value. The mean speed equaled exactly 1.25°/s for the linear gradients using the slow range of speeds. For the higher-order surfaces, the mean speed deviated slightly from this nominal value (range, 1.10–1.41°/s). The two speed ranges selected represent a compromise between the perceptual requirements of SFM, which requires slow speeds (Todd and Norman, 1991), and the preference of neurons in MT/V5 and its satellites for fast speeds (Orban, 1997). Todd and Norman (1991) manipulated the speed range and observed that, for excessively slow speed ranges, the motion percept became discontinuous, whereas for overly fast speeds, the display became nonrigid. Extrapolating from their frame range to the 40 frame sequence used here (see below) yields an optimal speed range of 0–2.5°/s. Thus, our speed ranges fall between this optimum and the threshold for nonrigid motion. Similarly, the speeds in a recent motion parallax study of MT/V5 neurons (Nadler et al., 2008) ranged from 0 to 5°/s. Because the 3D surfaces were sheared about an axis in the image plane, regions behind that plane moved opposite to those in the front, although the particular directions that corresponded to front and back were mathematically ambiguous. Each 3D-SFM stimulus consisted of 40 frames (duration, ∼667 ms). During the first 10 frames, the surface regions in front of the fixation plane moved in the preferred direction of the cell, whereas the surface regions behind this plane moved in the nonpreferred direction (Fig. 1A). The motion direction then reversed for 20 frames and reversed again for the last 10 frames.
We used two sizes of 3D-SFM stimuli with 4° (small) and 12° (large) apertures. Because all stimuli had to be prepared in advance, only two sizes could be tested. These apertures were surrounded by an annulus (of widths 0.4 and 1.2° for small and large stimuli), in which random dots translated at a constant speed of 2°/s. This annulus ensured that the only differences between the 3D surfaces and the background were motion differences. The motion direction inside the annulus was the same as that of the surface regions in front of the fixation plane. Thus, these dots initially moved in the preferred direction and then reversed at frames 10 and 30. It is important to note that the patterns of accretion and deletion at the boundary between a surface and its surrounding annulus was determined solely by the local directions of motion and provided no valid information about relative depth orders. Note also that, for any given main test, the surround annulus was identical for all stimuli.
Depth orders
First-order stimuli were planes slanted in depth, specified by a linear change in speed over distance (supplemental Movie M1, available at www.jneurosci.org as supplemental material). We used eight values of tilt in steps of 45° (Fig. 1). Smoothly curved surfaces with regions of concavity and convexity defined the second-order stimuli. The surfaces (supplemental Movies M2–M4, available at www.jneurosci.org as supplemental material) could either be oriented ridges (four orientations in steps of 45°), a bump in which the sign of curvature was the same in all directions, and saddles in which the sign of curvature in one direction was opposite to the curvature in the orthogonal direction. We used two orientations of saddles. In the “main” saddle stimulus, the principal curvatures were oriented along the horizontal and vertical axes. Rotating this display 45° generated the “oblique” saddle stimulus. Thus, we used a total of seven second-order stimuli. Higher-order stimuli included a complex bump and a complex saddle with multiple regions of concavities and convexities, similar to their respective second-order depth structures (supplemental Movies M5, M6, available at www.jneurosci.org as supplemental material). Finally, a zero-order stimulus (Fig. 1A) (supplemental Movie M7, available at www.jneurosci.org as supplemental material) with coherent dot motion inside the circular aperture but possessing no speed gradient was included as a control (2D control). Dot speed in this control condition equaled the nominal mean speed of the non-zero-order stimuli, with two different mean speeds (1.2 and 2.5°/s) tested. Again, motion was initially in the preferred direction, reversing at frames 10 and 30.
Main test: conditions.
For the vast majority of the FST neurons (261 of 317) and for all 64 tested MT/V5 neurons, the main test included 18 depth–structure conditions: eight tilt values, four ridge orientations, a bump, saddles in two orientations, a complex bump, a complex saddle, and one zero-order stimulus, presented at two mean speeds (fast and slow). These 36 conditions were presented in random order. However, in 56 of 317 cells tested in FST, we used only the main saddle, resulting in 34 stimuli (17 depth–structure conditions × 2 speeds) in the main test. All neurons were tested at the center of the RF, using one of two sizes (4 or 12° diameter), depending on RF size. The median number of repetitions for the main test was eight (quartiles 8–10).
Main test: statistical analysis of the neuronal responses
All analyses were performed on gross responses during the 667 ms stimulus presentation (shifted 50 ms to account for response latency). Responsiveness was assessed separately for each order by comparing the firing rates during stimulus presentation with those before using a split-plot ANOVA (with baseline–stimulus period as repeated within-trial factor and stimulus–condition as between-trial factor) and required that p < 0.0167 (0.05/3) to correct for multiple comparison (n = 3 orders). We next performed a two-way ANOVA using gross responses to the stimuli of each order (8, 7, or 2 depth–structure conditions × 2 speeds). For each of the three orders, a cell was considered selective if the main effect of depth–structure condition was significant (two-way ANOVA, p < 0.0167, correction for multiple comparisons).
Measures of selectivity: d′ and area under the receiver operating characteristic curve
The degree of selectivity of the neurons for different 3D-SFM stimuli within each order was quantified using a d′ index (Vogels and Biederman, 2002), defined as follows:
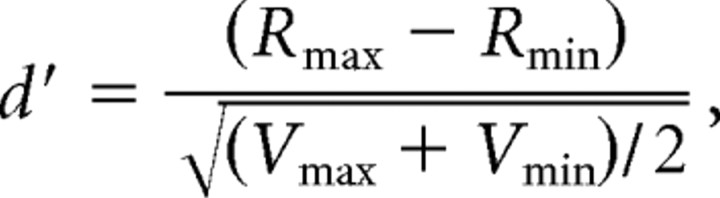 |
where Rmax and Rmin are the average gross responses for the 3D-SFM stimulus eliciting the maximum response (preferred) and the 3D-SFM stimulus eliciting the least responses (nonpreferred) within each order. Vmax and Vmin are the between-trial variances of the neuronal responses to preferred and nonpreferred 3D-SFM stimuli, respectively. A similar index was also used to define the selectivity of FST neurons in the speed test (comparing “best” and “worst” speeds).
Receiver operating characteristic (ROC) analysis (Green and Swets, 1966; Vogels and Orban, 1990) was used as alternative means of quantifying the difference between responses to the preferred and nonpreferred stimuli. The area under the ROC (auROC) curve was used as metric of selectivity. This analysis uses all the information contained in the response distributions, whereas the d′ uses only the mean and SD. Conversely, d′ has a greater range than auROC. Whatever the distance between two nonoverlapping distributions, auROC never exceeds a value of 1, whereas d′ will further increase with the distance between distributions.
Comparison of response levels at the two speeds of the main test
To compare response levels at the two mean speeds, we first averaged the tuning for the different orders of 3D-SFM over speed and derived the optimal stimulus from this average. This optimal stimulus was then used to calculate the index according to the formula (RF − RS)/(RF + RS), where RF and RS are responses at fast and slow speeds, respectively.
Additional control tests
Position and size tolerance tests
To test the position tolerance of 3D-SFM selectivity, we repeated the main test at a nonpreferred location within the RF. We tested 63 selective FST cells by displacing either the large or the small stimulus by 1–10° (median, 2.6°; quartiles 1.8–5.1) depending on RF size and 18 MT/V5 neurons with shifts ranging from 0.5 to 2.4° (median, 1.1°) using the 4° stimuli. In addition, we tested 25 FST and four MT/V5 neurons by repeating the same test using the nonpreferred size of 3D-SFM stimuli.
Depth cue test in FST
Because the 3D-SFM stimuli in the main test contained opponent motion in addition to a speed gradient, we also tested with 3D-SFM controls containing speed gradients or opponent motion alone, using the preferred mean speed indicated by the main test. Conditions were presented in random order and were of the same duration as those in the main test (∼667 ms).
First-order control test (n = 29 neurons).
Three types of stimuli were presented with the eight tilt values used in the main test: the original slanted planes (supplemental Movie M1, available at www.jneurosci.org as supplemental material), slanted planes generated by speed gradients alone (pure gradients) (supplemental Movie M8, available at www.jneurosci.org as supplemental material), and “opponent-motion” stimuli without speed gradients (supplemental Movie M9, available at www.jneurosci.org as supplemental material). In pure-gradient stimuli, surround annuli were static, whereas in the opponent-motion stimuli, the surround annulus was the same as in the original slanted plane condition.
Second-order control test (n = 27).
We used only four ridge orientations at two speeds to search for ridge-orientation-selective neurons. We tested ridge-selective cells with four orientations of the original ridges, pure-gradient ridges (surfaces defined solely by speed gradients), and opponent-motion ridges (motion direction as in the original ridges but with no speed gradient). Speeds were defined exactly as for the first-order stimuli.
Monocular controls test in FST
To test the effect of the conflict between stereo and motion in the standard binocular displays, 32 FST cells were tested both binocularly and monocularly using the conditions of the main test, randomly choosing to use either both eyes or only the right eye for the first of the two tests. A median of eight runs (quartiles 8–10) were collected per test. In 30 of the 32 cells, we also repeated the original presentation.
Comparison of response levels
For all control tests, we compared response levels for the two values at which the main test had been performed. To that end, we used the response index comparing the difference in the responses to the optimal stimulus to the sum of these responses, as indicated above for the speed comparison in the main test. Table 1 indicates the numerators for each of the response indices.
Table 1.
Median and quartiles of the response indices of responsive FST neurons
| Comparison | Orders of 3D-SFM | Number of cells | Median | Quartiles (1st–3rd) | p valuea |
|---|---|---|---|---|---|
| Speed, fast–slow | First | 301 | 0.05 | −0.03 to 0.18 | < 10−8 |
| Second | 304 | 0.09 | −0.01 to 0.22 | < 10−9 | |
| Higher | 283 | 0.05 | −0.07 to 0.18 | < 10−4 | |
| Position, central–peripheral | First | 63 | 0.06 | 0 to 0.25 | < 0.002 |
| Second | 63 | 0.05 | −0.05 to 0.19 | < 0.007 | |
| Size, small–large | First | 25 | 0.18 | 0.03 to 0.43 | < 0.007 |
| Second | 25 | 0.10 | −0.13 to 0.44 | NS | |
| Ocularity, binocular–monocular | First | 29 | 0.09 | −0.13 to 0.22 | NS |
| Second | 29 | 0.10 | −0.06 to 0.18 | NS | |
| Cues, regular–pure | First | 29 | 0.02 | −0.13 to 0.2 | NS |
| Second | 27 | 0.02 | −0.14 to 0.07 | NS | |
| Cues, regular–opponent motion | First | 29 | −0.03 | −0.19 to 0.09 | NS |
| Second | 27 | 0.05 | −0.18 to 0.14 | NS |
aWilcoxon's sign rank test.
Index of separability
Within each order (first or second), we used the separability measure (Mazer et al., 2002; Kayaert et al., 2005; Yamane et al., 2008) to quantify how well the neuron retained its 3D shape preference across the different mean speeds, positions, sizes, ocularity, and defining cues. First, the gross responses of each selective cell were tabulated in an m × n response matrix (M) with m and n corresponding to the different 3D shapes and to the stimulus transform variable (speed or position, etc.), respectively. We then computed the singular value decomposition (M = USV′) of the response matrix. The predicted response was reconstructed from the first principal components, i.e., the product of the first columns of U and V of the singular value decomposition. The separability index equals the squared correlation (r2) between the actual responses and the predicted responses.
Two statistical tests with opposite null hypotheses were performed on the separability index. In the first test, the null hypothesis was nonseparability. We randomly permuted the mean neuronal responses for different 3D shapes (e.g., for eight values of tilt) within each tested speed, position, or size and computed a separability index for the reshuffled responses. Permuting the responses within but not across speed, position, or size ensured that the mean permuted response averaged across 3D shapes for a given speed or position was the same as the mean observed response. Permutations were performed 1000 times. If the separability index value obtained experimentally exceeded the 95th percentile of the distribution of separability indices for the reshuffled responses, the neuron was deemed to have a separability index significantly different from zero.
In the second test, the null hypothesis was perfect separability. First, the ratio between the two marginals of the response matrix for the stimulus transform variable was calculated for the actual data. This ratio was used to generate a new response matrix by keeping the actual response distributions (over the number of trials tested) of one value of the stimulus transform variable and then predicting the distributions for the other value by bootstrapping from the actual response distributions for the first value. From this response matrix, a separability index was calculated. This procedure was repeated 1000 times, 500 times for each of the two values of the stimulus transform variable. If the separability index obtained experimentally was smaller than the fifth percentile of the bootstrapped separability index distribution, the neuron was deemed to have an index significantly different from one.
Random line test in FST
We tested FST neurons using random line (RL) segments, either rotating in depth (RL rotation) or translating in a 2D plane (RL translation) in the horizontal direction, which Nelissen et al. (2006) used previously to assess MR sensitivity to SFM. The RL stimuli were the same bitmap sequences used in the fMRI study by Nelissen et al. (2006) but tested with three different speeds. To lower the speed, we simply repeated frames, which resulted in different stimulus durations across speeds. However, for any given speed, the duration was the same for RL rotation or RL translation. For the fast speed, each frame was displayed once. The RL rotated or translated rightward for the first nine frames (150 ms), then to the left in the next 18 frames (300 ms), and finally to the right in the last nine frames (150 ms). Mean speeds were 4.6°/s for RL rotation and 4.3°/s for RL translation. In the medium (2.3°/s) and slow (1.15°/s) speed conditions, each bitmap was displayed two or four times, respectively, and motion duration correspondingly increased to 1200 and 2400 ms. At all speeds, the movement of the translating RL was restricted to within 0.6° of the RF center.
Five RL patterns (supplemental Movie M10, available at www.jneurosci.org as supplemental material) rotated and translated at three speeds, yielding 30 conditions presented randomly in this test. Only FST neurons (n = 42) tuned to horizontal directions were tested. Because fMRI activations reflect cell populations, we averaged gross responses across all sampled cells within each condition.
Statistical testing of population response selectivity
Repeated-measures ANOVA was used to assess the effect of a stimulus variable on the population responses. The input of this ANOVA was the mean of the responses of each neuron to each of the stimulus values.
Results
Selectivity of FST neurons for SFM stimuli
We recorded from single FST neurons (Fig. 1) in two awake, behaving monkeys (M. mulatta) while they observed planes slanted in depth (first-order stimuli), bumps, ridges, and saddles (second-order stimuli) presented at multiple orientations and surfaces with multiple regions of concavity and convexity (higher-order stimuli). Before presenting these stimuli in the main test, the RF size and location as well as the preferred direction of the neuron were determined quantitatively. In addition, speed test data were obtained for many neurons. Figure 1 shows the responses of an FST neuron to the 4° stimuli in the main test. The poststimulus time histograms (PSTHs) document the responses to the preferred (mean) speed (2.5°/s), whereas the stimulus–response curves are plotted for both preferred and nonpreferred speeds. Note that the neuron did not respond to first- or higher-order stimuli but responded to second-order stimuli, with a preference for the 45° ridge. It was selective for second but not first- or higher-order stimuli in that the main effect of shape in the two-way ANOVA (factors shape and speed; see Materials and Methods) was significant for second order (p < 0.00001) but not for first or higher order. The interaction between shape and speed for second-order stimuli was not significant (p = 0.025, NS). Four additional example FST cells (Fig. 2) illustrate selectivity for a slanted plane with a 90° tilt, a main saddle, a higher-order saddle, plus a combined selectivity for the 135° tilt and 0° ridge. In all four cases, the main effect of shape was significant (p < 0.0001 or better) for the relevant order(s) but not for the others. In none of these neurons was the interaction between speed and shape significant. The fifth neuron in Figure 2 illustrates FST neurons selective for first- and second-order stimuli (both significant main effect of shape, p < 0.001 or better) but with an interaction between speed and shape (both significant interaction, p < 0.016 or better).
Figure 2.
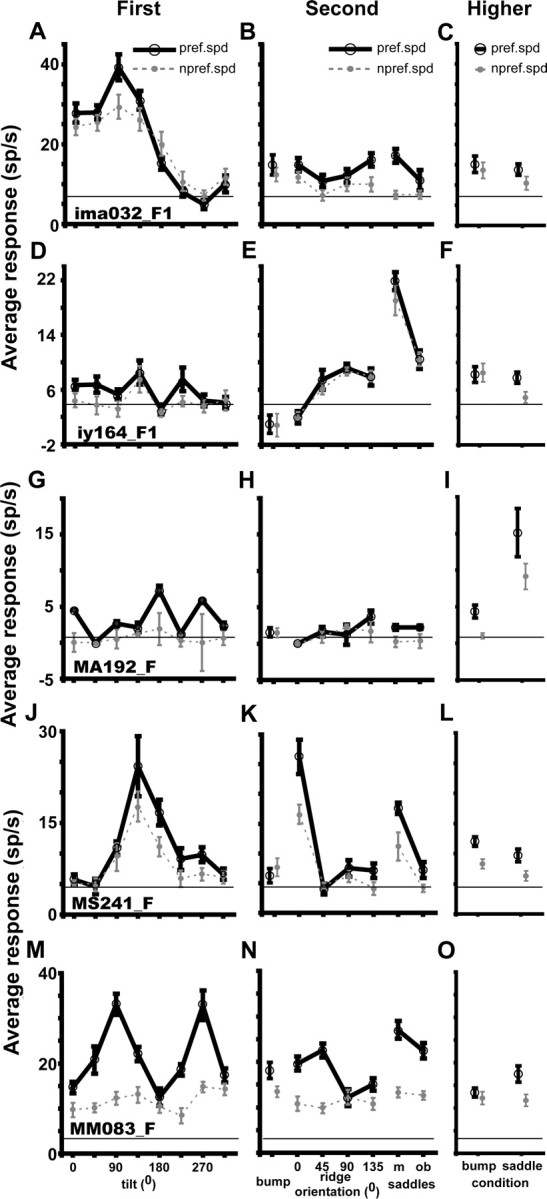
Tuning curves for tilt, second-order and higher-order structure at preferred (black solid lines) and nonpreferred (gray dashed lines) speeds of five FST neurons (A–O); all five neurons preferred the fast mean speed (2.5°/s). A–C, Neuron (Ima032_F1, eccentricity 4.8°, stimulus size 12°) selective for first-order stimuli (d′ first-order = 3.85, first-order separability r2 shape–speed = 0.99; two-way ANOVA, main effect of tilt, p < 10−4; interaction of tilt and speed, NS; other main effects, NS). D–F, Neuron (Iy164_F1, eccentricity 3.6°, stimulus size 4°) selective for the oblique saddle (d′ second-order = 5.48, separability r2 shape–speed = 0.99; two-way ANOVA for main effect of second order, p < 10−6; interactions between speed and second order, NS). G–I, Neuron (MA192_F, eccentricity 4.8°, stimulus size 12°) selective for the higher-order saddle (d′ higher-order = 2.12; two-way ANOVA, main effects of higher order, p < 10−4; interaction between speed and higher order, NS). J–L, Neuron (MS241_F, eccentricity 1.7°, stimulus size 4°) selective for both first-order (first-order d′ = 3.42; separability r2 shape–speed = 0.97) and second-order (second-order d′ = 3.87; separability r2 shape–speed = 0.97) stimuli [two-way ANOVA, main effects of condition, p < 10−7 and interaction of condition and speed was nonsignificant for both first and second order; main effect of condition for higher order was nonsignificant. M–O, Neuron (MM083_F, eccentricity 2.4°, stimulus size 4°) selective for first-order (d′ = 3.3 and separability r2 speed shape = 0.78) and second-order (d′ = 2.7 and separability r2 speed shape = 0.69) stimuli but with speed interaction (two-way ANOVA, main effects of condition, p < 10−6 and p < 10−3 for first and second order, respectively, and interaction between shape and speed, p < 10−3 and p < 0.012 for first and second order).
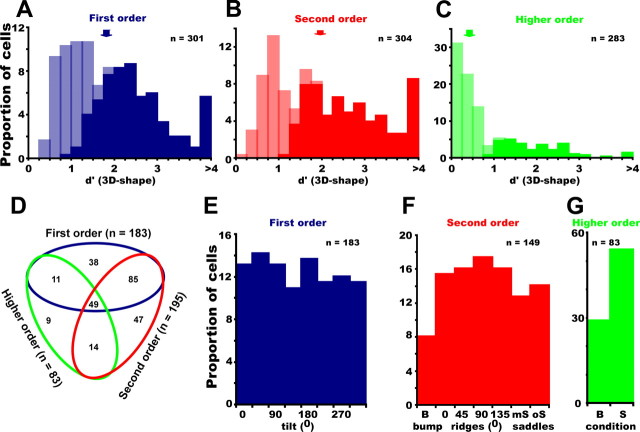
Analyzing the responses of 317 FST neurons (monkey I, n = 121; monkey M, n = 196) showed that the vast majority (306, 97%) were responsive to stimuli of at least one order of speed gradient. Of these 306 responsive neurons, 183 (60%) were selective (i.e., a significant main effect of shape; p < 0.0167, two-way ANOVA) for first order, 195 (64%) for second order, and 83 (27%) for higher order (Fig. 3A–C). In addition, 45 neurons (15%) showed a significant interaction between shape and speed for first order, 65 (21%) for second order, and 21 (7%) for higher order. Only a few neurons [nine first order (3%); eight second order (3%); 11 higher order (4%)] showed an interaction between speed and shape without a main effect of shape. Considering all orders, 253 (83%) of the responsive FST neurons were selective for at least one order. Many neurons were selective for more than one order, and only approximately one-third were selective for just one order (Fig. 3D). Interestingly, although a substantial number of neurons were selective for only first- or second-order stimuli, a mere nine neurons (3% of the responsive FST neurons) were selective only for higher-order stimuli. These latter stimuli were included in the main test to investigate how well first- and second-order stimuli capture the selectivity of FST neurons for 3D-SFM. The small proportion of neurons requiring higher-order stimuli, although likely underestimated, indicates that first- and second-order stimuli are adequate for testing the selectivity of FST neurons.
Figure 3.
Selectivity of FST neurons: A–C, Distributions of d′ for first-order (A), second-order (B), and higher-order (C) responsive FST neurons; light and dark hatching indicates selective and nonselective neurons, respectively, based on two-way ANOVA (p < 0.0167). D–G, Stimulus preferences: number of neurons selective for the three orders of stimuli (D). A neuron can be selective for multiple orders. E–G, Distribution of optimal stimuli for first-order (E), second-order (F), and higher-order (G) selective FST neurons. B, Bump; S, saddle.
The degree of selectivity in FST neurons was measured by the d′ index for each order separately. This index relates the difference between responses to the best and the worst stimuli to the average SD of these responses (Fig. 3A–C). The d′ values were computed for each order for which the neuron showed a significant response. As expected, the selective neurons had larger d′ values than nonselective but responsive neurons, and d′ did not depend on eccentricity for any order of stimuli (correlations between d′ and eccentricity were nonsignificant). The median d′ was 1.79 (quartiles 1.05–2.48, n = 301) for first-order stimuli, 1.98 (1.0–2.9, n = 304) for second-order stimuli, and 0.39 (0.16–1.0, n = 283) for higher-order stimuli. Thus, for first and second order, the average d′ was close to 2, indicating that the difference in the response to the best and worst stimulus was about two times the average SD. ROC analysis confirmed the strong selectivity of FST neurons for the first- and second-order stimuli (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). Median auROC values were 0.91 (quartiles 0.79–0.98), 0.92 (quartiles 0.79–1), and 0.62 (quartiles 0.54–0.82) for first-, second-, and higher-order stimuli, respectively.
The selectivity of FST neurons could not be explained by differences in eye movements between stimulus conditions (supplemental Figs. S3, S4, available at www.jneurosci.org as supplemental material), nor could the selectivity of these neurons for 3D-SFM be explained by their lower-order speed selectivity (Fig. 4). The effect of speed (range, 1–16°/s) was tested in a substantial number of neurons (n = 189) using a zero-order random-dot pattern moving in the preferred direction. The correlations between the d′ for the different orders of 3D shape and the d′ for speed were small but statistically significant: r2 = 0.05, p < 0.003 (first order), r2 = 0.06, p < 0.001 (second order), r2 = 0.02, p < 0.05 (higher order). From the plots (Fig. 4), however, it is clear that many neurons with low speed selectivity could exhibit a sharp, statistically significant selectivity for first-, second-, or higher-order stimuli. Thus, the FST selectivity for 3D-SFM cannot simply be explained by lower-order speed selectivity.
Figure 4.
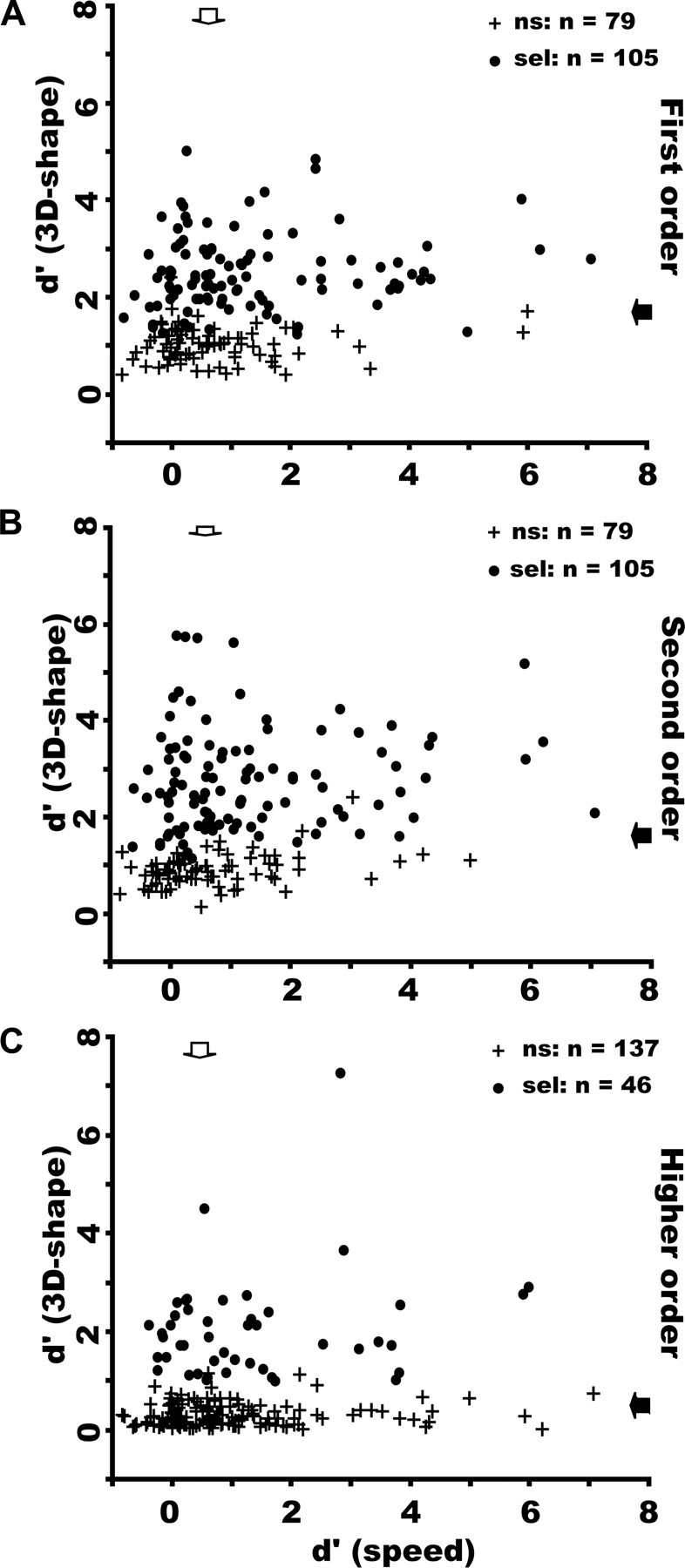
d′ for 3D-SFM plotted as a function of d′ for mean speed in FST neurons responsive to first-order (A), second-order (B), and higher-order (C) stimuli. ns, Nonselective (crosses); sel, selective (dots). The correlation was weak but significant in each order: r2 = 0.05, p < 0.003 (A), r2 = 0.06, p < 0.001 (B), r2 = 0.02, p < 0.05 (C). Arrows indicate median values.
Preferred stimuli of selective FST neurons
The FST neurons that were selective for one of the orders of 3D-SFM exhibited uniform preferences for all the stimuli within that order (Fig. 3E–G), except for the bump that was underrepresented among second-order (χ2 = 8.92, p < 0.02) and higher-order (χ2 = 9.82, p < 0.001) stimuli. Because many neurons were tuned to both the orientation of first-order slanted surfaces and second-order ridges, the question arises as to whether or not the second-order selectivity simply reflected the first-order selectivity. To that end, we performed the following analysis on the FST neurons showing selectivity for ridge orientation. We selected those neurons for which a two-way ANOVA of the responses to the four ridges using ridge orientation and speed as factors had shown a main effect of ridge orientation. After aligning the preferred ridge orientations, responses were averaged as a function of ridge orientation relative to the preferred orientations of the neurons. This yielded, by definition, a sharply tuned function over the ±90° range (Fig. 5A). We then plotted the responses of these neurons to first-order planes as a function of the orientation matching that of the ridge surfaces. Note that responses to planar surfaces differing by 180° are averaged together because both correspond to a single ridge orientation. If the first-order selectivity contributes to the selectivity for ridge orientation, then the curve for the averaged planar orientations should also be tuned. In fact, it is flat (Fig. 5A), and the repeated-measure ANOVA of these responses was not significant. Requiring that the ridge selective neurons were also selective for tilt orientation produced a similar nonsignificant effect of ridge orientation with regard to first-order responses. Thus, the selectivity of FST neurons for ridge orientation cannot be explained by concomitant first-order selectivity.
Figure 5.
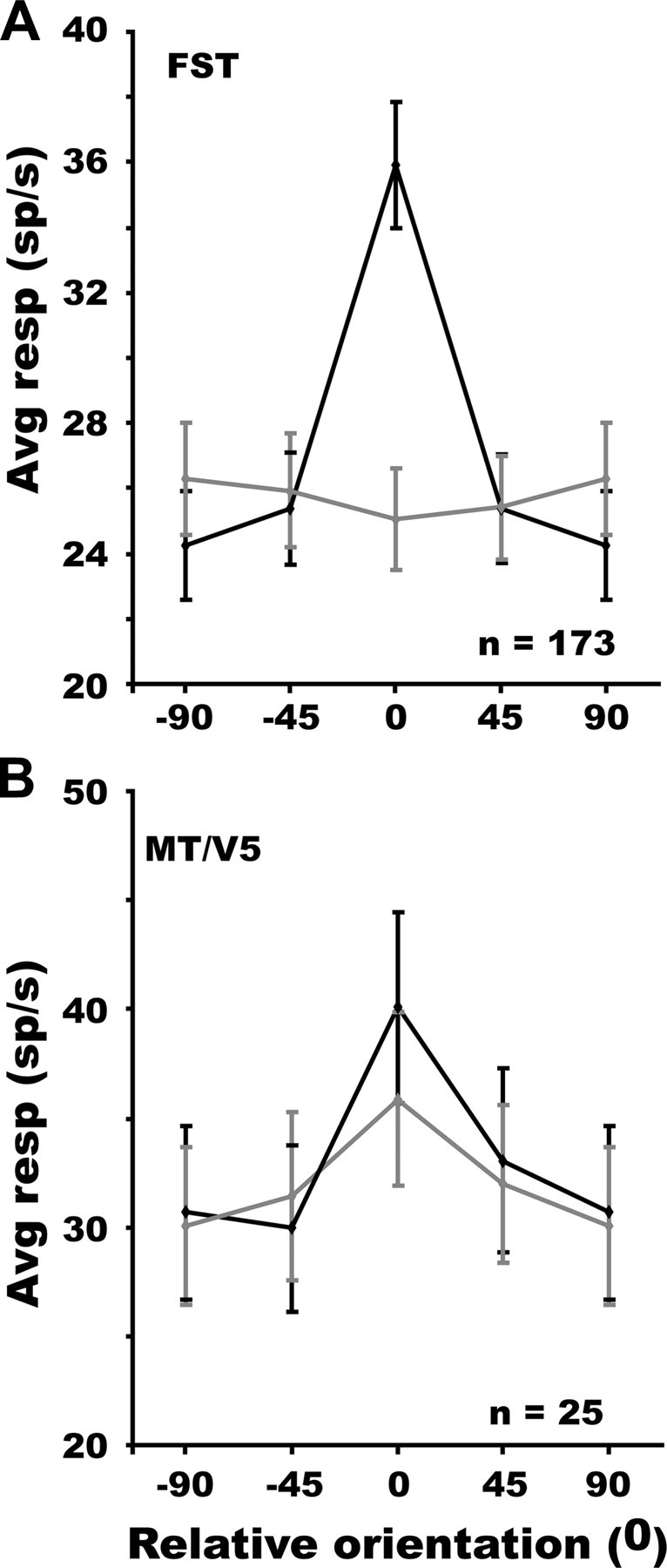
Average gross responses of FST neurons (n = 173, A) and MT/V5 neurons (n = 25, B) selective for ridge orientation, to matched ridges (black) and planar surfaces (gray) plotted as a function of the relative orientation of the ridges. Tuning for tilt orientation was nonsignificant (repeated-measures ANOVA) in A but significant in B (F(3,72) = 4.51, p < 0.002).
Tolerance of FST selectivity for 3D-SFM for changes in speed, position, and size
Having verified our first two predictions, we now turn to the prediction of tolerance for stimulus changes. The aim of these tests was to distinguish between higher-order selectivity for 3D shapes and lower-order speed selectivity. Because we tested tolerance for several stimulus changes, we restricted the study to two values for each transform variable. More values will have to be tested to fully characterize tolerance for each of the variables. The test for speed tolerance was incorporated in the main test, which included conditions at two mean speeds. The tolerance of the 3D-SFM selectivity for speed was assessed at both the population and the single-cell levels. Before testing whether or not the stimulus preference depended on speed, we compared the response levels at the two mean speeds used in the main test. To that end, we computed the response index relating the difference in response levels at slow and fast speeds to their sum for each of the three orders. The median index was only slightly positive but differed significantly from zero (Table 1). Thus, the average response was 10–20% greater for the fast mean speed compared with the slow one in the main test.
The population analysis of selectivity for the first-order stimuli is based on orientation being a single circular dimension, allowing the responses to be plotted as a function of the orientation difference with respect to the preferred orientation. The preferred orientation was defined for each neuron using the preferred speed. If the population tolerates speed changes, the curves for the preferred and nonpreferred speeds should be similar and the curve for the nonpreferred speed should differ significantly from a flat curve, which can be tested by a repeated-measure ANOVA of the data for the nonpreferred speed curve. The population analysis of selectivity for the second-order stimuli is based on a ranking of the stimuli according to the responses to the preferred speed and using this same rank for the responses to the nonpreferred speed. As for the first-order stimuli, tolerance to the speed change can be tested by a repeated-measures ANOVA on the ranked data of the nonpreferred speed. The result of this population analysis for first- and second-order selective neurons is shown in Figure 6, A and B. For both the first- and second-order selective neurons, the tuning of the nonpreferred speed curve proved significant (repeated-measures ANOVA; F(7,1274) = 26.86, p < 10−7; and F(5,970) = 49.79, p < 10−8, respectively). Because not all neurons were tested with the oblique saddle, the ranking in Figure 6B was performed on the responses to six second-order stimuli. Results were similar when this procedure was applied to the subpopulation of neurons tested with all seven second-order stimuli (n = 149; data not shown). A similar result (repeated-measures ANOVA, F(1,82) = 71.28, p < 10−8) was also obtained for higher-order selective neurons (supplemental Fig. S5, available at www.jneurosci.org as supplemental material). The ranking procedure concentrates on similarities in the preferred values for the two speeds but allows for differences in gain between the speeds. This is different from the ANOVA in which the absence of an interaction requires that the two curves differ only by a vertical shift. Thus it is not surprising that the ranking procedure indicates speed tolerance even for the populations of neurons with interactions between shape and speed in the ANOVA (supplemental Fig. S6, available at www.jneurosci.org as supplemental material). The latter populations clearly show a difference in gain between the two speeds, whereas those without interaction exhibit curves that are more parallel. However, even the neurons without interaction still show some gain change.
Figure 6.
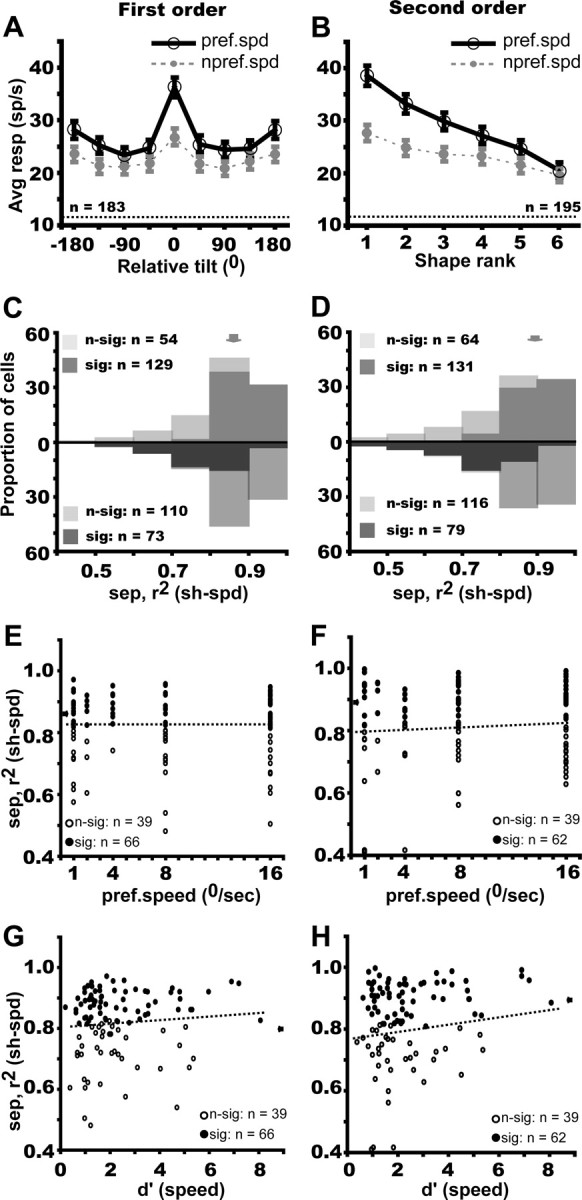
Speed tolerance of FST neurons selective for first-order (blue, A, C, E, G) and second-order (red, B, D, F, H) stimuli. A, B, Average gross responses for preferred (black solid lines) and nonpreferred (gray dashed lines) speeds plotted a function of relative tilt and rank in descending order of preference (both determined at preferred speed). C, D, Distribution of the (3D shape–speed) separability index for first- and second-order selective neurons; light and dark hatching indicates, respectively, nonsignificant and significant neurons according to the permutation test (top row) and bootstrapping test (bottom row). Arrows indicate median values. E, F, Separability index plotted as a function of preferred speed: r2 = 0.0006, NS and r2 = 0.009, NS, respectively. G, H, Separability index plotted as a function of d′ for speed: r2 = 0.012, p < 0.02 and r2 = 0.054, NS, respectively. Contrary to the prediction, the speed tolerance slightly increases with d′ for speed.
At the single-cell level, we computed a separability index reflecting the fraction of the response variance explained by the full speed-tolerance hypothesis: the higher the index, the more speed tolerant the shape preference of the neuron. The median separability (between 3D shape and speed) index was 0.87 (quartiles 0.79–0.91) for first-order selective neurons and 0.89 (quartiles 0.75–0.93) for second-order neurons, indicating strong tolerance for a twofold change in mean speed (Fig. 6C,D). This was confirmed by the large fraction of neurons (more than two-thirds) for which the separability index was significantly different from zero, as tested by a permutation test (Fig. 6C,D, upper distributions). Conversely, the separability index differed significantly from one in less than half (40%) of the neurons (Fig. 6C,D, lower distributions). It is important to note that the distributions of separability indices of neurons with and without interaction in the ANOVA differ little from one another, despite the fact that separability as defined here (see Materials and Methods) implies an interaction. This may be explained by the fact that the neurons without speed–shape interaction in the ANOVA still exhibited some gain change (supplemental Fig. S6, available at www.jneurosci.org as supplemental material).
Because the mean speeds in the gradients were relatively slow, one might conjecture that neurons that were selective for faster speeds might be less speed tolerant. Also, the shape preferences of neurons more selective for speed might be less speed tolerant than the less selective neurons. To examine these possibilities, we tested the correlation of the separability index for shape and speed with the preferred speed and with d′ for speed, using the 189 FST neurons for which speed response curves had been measured. The correlation between separability and the speed characteristics proved significant for neither the first- nor second-order selective neurons (Fig. 6E–H). Thus, the speed tolerance of the 3D-SFM selectivity of FST that we have documented here was independent of the speed characteristics of the neurons.
To further test the tolerance of the 3D-SFM selectivity, we performed additional critical control tests on a subpopulation of neurons, investigating position and size tolerance. In these tests, the main test was repeated with the stimuli shifted to a different position in the RF or using the alternate size stimuli. The 3D-SFM selective FST cells, despite the expected but modest change in response level (Table 1), retained their depth–structure preferences even when tested at a nonpreferred position within the RF, as shown by the population analysis in Figure 7, A and B: the responses at the nonpreferred position depended significantly on the rank or relative tilt, just as with the nonpreferred speed (Fig. 6A,B). Because the curves were aligned on the preferred values for the preferred positions, the similarity of the tuning obtained with the nonpreferred position demonstrates the tolerance. The separability (between 3D shape and position) indices were again close to 0.9 with medians of 0.86 (quartiles 0.78–0.93) and of 0.89 (quartiles 0.79–0.94) for first- and second-order selective neurons, respectively (Fig. 7C,D). More than 60% of the neurons had indices significantly different from zero. Conversely, 43% of the neurons had an index differing significantly from one. Although only two positions were tested, this position tolerance is the more remarkable in that shifts in position of up to 10° were tested, and, critically, separability indices did not depend on the absolute value of the position shift (Fig. 7E,F) nor on the size of the shift relative to the RF size (Fig. 7G,H). Neither did the separability indices depend on the percentage overlap between the stimuli in the original and shifted positions: r2 = 0 (p > 0.95) for first order and r2 = 0.01 (p > 0.55) for second order.
Figure 7.
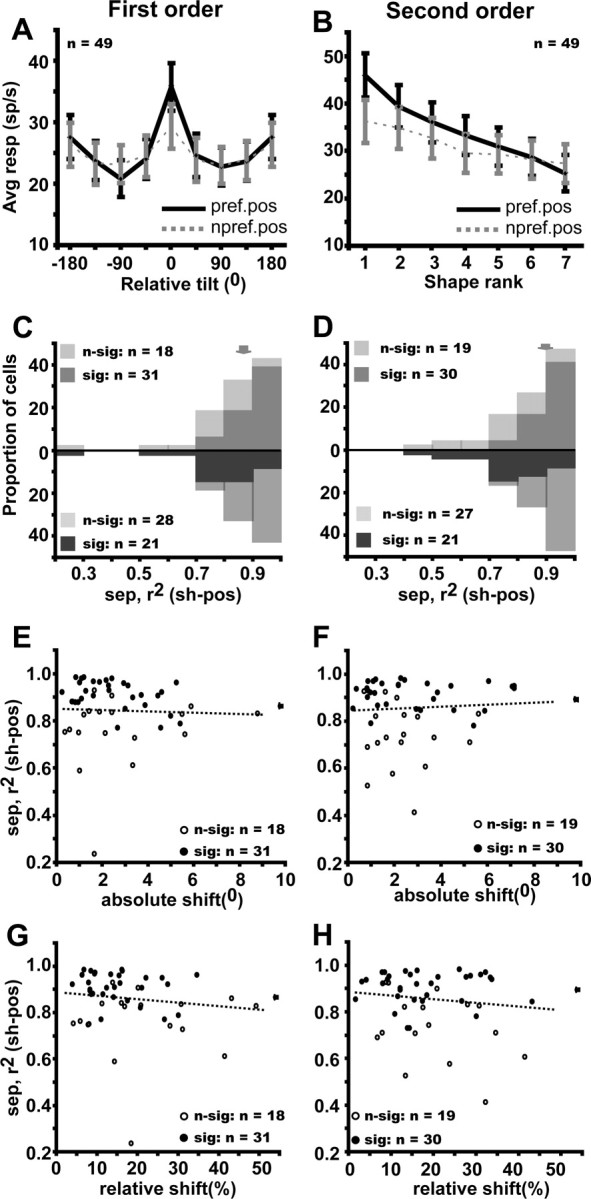
Position tolerance of FST neurons selective for first-order (A, C, E, G) and second-order (B, D, F, H) stimuli. A, B, Average gross response at preferred (black solid lines) and nonpreferred (gray dashed lines) position plotted as a function of relative tilt and rank in descending order of preference (both determined at preferred position). The tuning for nonpreferred position is significant: repeated-measures ANOVA, F(7,336) = 5.19, p < 10−3 and F(6,258) = 12.13, p < 10−7 for first and second order. C, D, Distribution of the (3D shape–position) separability index for first- and second-order selective neurons; light and dark hatching, respectively, indicate nonsignificant and significant neurons according to the permutation test (top row) and bootstrapping test (bottom row). Arrows indicate median values. E, F, Separability index plotted as a function of absolute shift: r2 = 0.002, NS and r2 = 0.003, NS, respectively. G, H, Separability index plotted as a function of relative shift (proportion of RF size): r2 = 0.04, NS and r2 = 0.03, NS, respectively.
Very similar results were obtained with regard to stimulus size. Both the population analysis and the individual neuron analysis (Fig. 8A–D) revealed a tolerance of 3D SFM selectivity, despite modest changes in the response level (Table 1). Again the separability index did not depend on the value of the size change relative to RF size (supplemental Fig. S7, available at www.jneurosci.org as supplemental material). The population analysis also confirmed the position and size tolerance of higher-order selective FST neurons (supplemental Fig. S5, available at www.jneurosci.org as supplemental material). Selective FST cells are thus not only speed but also position and size tolerant. The latter two tolerances clearly demonstrate that selectivities are not the trivial consequences of local RF heterogeneities (Treue and Andersen, 1996) in (zero-order) speed tuning but reflect the operation of higher-order mechanisms (Xiao et al., 1997b) capturing the depth–structure itself.
Figure 8.
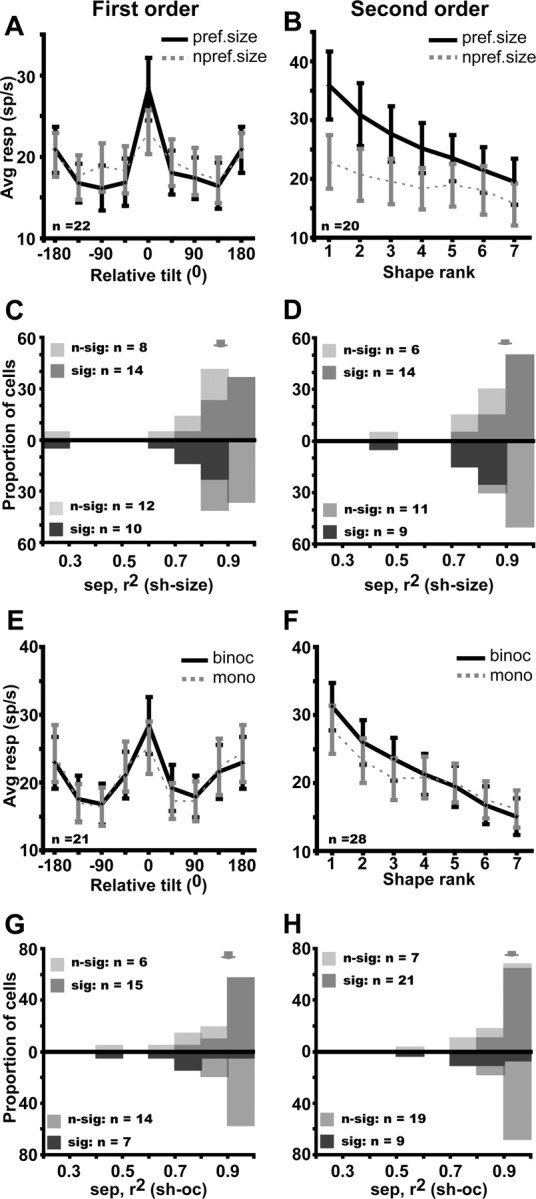
Size tolerance (A--D) and tolerance for ocularity (E–H) of FST neurons selective for first-order (A, C, E, G) and for second-order (B, D, F, H) stimuli. A, B, Average gross response for preferred (black solid lines) and nonpreferred (gray dashed lines) size plotted a function of relative tilt and rank in descending order of preference (both determined using preferred size). The tuning for the nonpreferred size is significant: repeated-measures ANOVA, F(7,147) = 3.49, p < 0.002 and F(6,114) = 4.58 p < 0.002 for first and second order. C, D, Distribution of the (3D shape size) separability index for first- and second-order selective neurons: median (quartiles), 0.87 (0.82–0.93) and 0.90 (0.83–0.96), respectively; light and dark hatching indicates, respectively, nonsignificant and significant neurons according to the permutation test (top row) and bootstrapping test (bottom row). Arrows indicate median values. E, F, Average gross response for preferred (black solid lines) and nonpreferred (gray dashed lines) ocularity plotted a function of relative tilt and rank in descending order of preference (both determined using preferred ocularity). The tuning for the nonpreferred ocularity is significant: repeated-measure ANOVA, F(7,140) = 8.43, p < 10−7 and F(6,162) = 18.48, p < 10−8 for first and second order. G, H, Distribution of the (3D shape ocularity) separability index for first- and second-order selective neurons: median (quartiles), 0.90 (0.81–0.93) and 0.93 (0.85–0.96), respectively, as indicated by arrows; light and dark hatching, respectively, indicate nonsignificant and significant neurons on the permutation and bootstrapping tests.
Tolerance of FST selectivity for 3D-SFM for changes in ocularity
The strongest tolerance of FST selectivity for 3D-SFM was obtained by comparing monocular and binocular presentations. The population curves were very similar for monocular and binocular presentations, and the separability indices averaged 0.9 or more (Fig. 8E–H). Thus, the conflict with the stereo information present in the standard binocular conditions influenced neither the FST selectivities nor the response levels (Table 1).
Selectivity of FST neurons for pure speed gradients
The 3D-SFM stimuli used in the main test were complex in nature and included not only speed gradients but also opponent motion (Sáry et al., 1994; Tyler et al., 2006). To investigate the contribution of each cue individually, 3D-SFM-selective FST neurons were tested with surfaces defined by a single cue (Fig. 9A,B) (supplemental Movies 8, 9, available at www.jneurosci.org as supplemental material). For both orders, the response levels were hardly altered (Table 1), but selectivity was reduced with the pure speed gradient and the opponent-motion stimuli (filled and open arrows along the ordinate in Fig. 9C,D) compared with the original stimuli (filled arrows along abscissa), but it was only for the neurons selective for second-order that such differences reached significance. For these neurons, the difference in d′ for pure-gradient and opponent-motion almost reached significance when correcting for multiple comparisons (Wilcoxon's matched pair test, p < 0.04). Consistent with the decrease in d′, the proportion of selective cells was reduced. Of 29 neurons selective for first order, 21 retained this selectivity for the pure-gradient and the opponent-motion stimuli. Of 26 neurons selective for second order, 19 remained selective for pure-gradient stimuli and 18 for opponent-motion stimuli. Furthermore, for first-order neurons, the correlations between the selectivity for the single cue and the original stimuli were weak but were stronger (r2 exceeding 0.3) for second-order selective neurons. Thus, selectivity was generally similar for the two cues.
Figure 9.
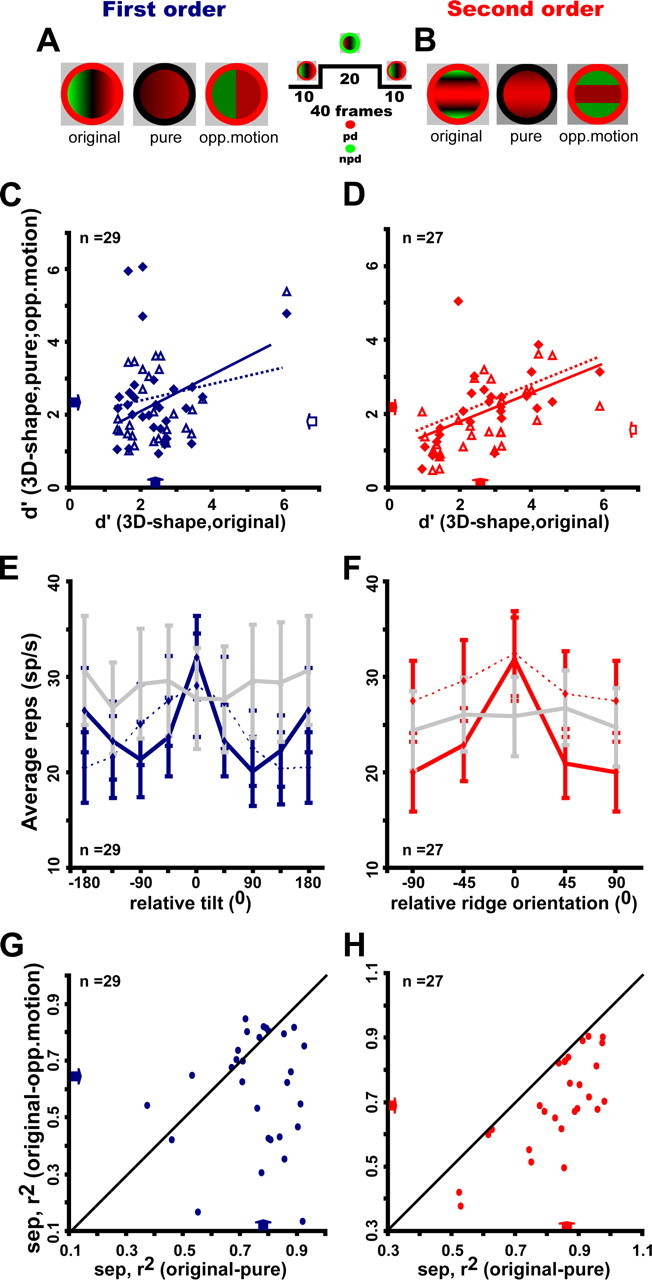
Selectivity for single cue stimuli of FST neurons selective for first-order (A, C, E, G) and second-order (B, D, F, H) stimuli. A, B, Color plots of first-order (A) and ridge (B) stimuli: “original” are the original 3D-SFM stimuli, “pure gradients” include only a speed gradient, and “opponent-motion” stimuli contain only opposite directions of motion without speed gradients. C, D, d′ for 3D shape in the pure-gradient (filled symbols) and opponent-motion (open symbols) stimuli plotted as a function of d′ for 3D shape in the original stimuli; median values for first-order, original, 2.4 (1.7–2.71); pure-gradient, 2.2 (1.6–2.2); opponent-motion, 1.89 (1.5–3.0) [distribution differences, Wilcoxon's matched pair test, all NS: correlation original vs pure-gradient, r2 = 0.018, NS and original vs opponent-motion: r2 = 0.2, p < 0.02; median values for second order: original, 2.7 (1.5–3.2); pure-gradients, 2.15 (1.3–2.5); opponent-motion, 1.5 (1.1–2.5); distribution differences, Wilcoxon's matched pair test: original vs pure (Z = 3.1, p < 0.002), original vs opponent-motion (Z = 3.7, p < 0.0003); pure-gradients vs opponent-motion (Z = 2.07, ns), correlation original vs pure-gradient, r2 = 0.3 p < 0.004 and original vs opponent-motion, r2 = 0.36 p < 0.001]. E, F, Average gross response for original stimuli (dark solid lines) pure-gradient stimuli (dashed lines) and opponent-motion stimuli (light solid lines) plotted a function of relative tilt and rank in descending order of preference (both determined for the original stimuli). G, H, Separability index for the pair original–opponent-motion plotted as a function of separability index for the pair original–pure-gradients [median (quartiles) values for first order: 0.79 (0.71–0.86) for original–pure-gradient and 0.65 (0.43–0.78) for original–opponent-motion; distributions significantly different, Wilcoxon's matched pair test (Z = 2.78, p < 0.01); median values for second order: 0.86 (0.79–0.92) for original– pure-gradient and 0.69 (0.62–0.82) for original–opponent-motion; distributions significantly different on Wilcoxon's matched pair test (Z = 4.54, p < 0.2 10−5]. Arrows indicate median values.
Tolerance analysis, however, did reveal a difference at both the population (Fig. 9E,F) and single-cell (Fig. 9G,H) levels. Indeed, in the population analysis, the curves for opponent-motion stimuli, aligned to the preference for the original stimuli, did not exhibit significant tuning (repeated-measures ANOVA, NS), whereas those for pure speed gradients did (ANOVA; F(7,196) = 10.7, p < 10−6; and F(3,78) = 4.3, p < 0.005 for first and second order, respectively). Similarly, the separability indices were significantly larger for the pair original pure-gradient stimuli than for the pair original opponent-motion stimuli, and correspondingly most points in Figure 9, G and H, lie below the diagonal. These findings were very similar for first- and second-order selective neurons. Thus, one can conclude from this analysis that both the selectivity and the preferred stimuli were similar for the original and pure speed gradient stimuli, underscoring the role of speed gradients in the processing of 3D shape from motion.
Responses of FST neurons to random line stimuli
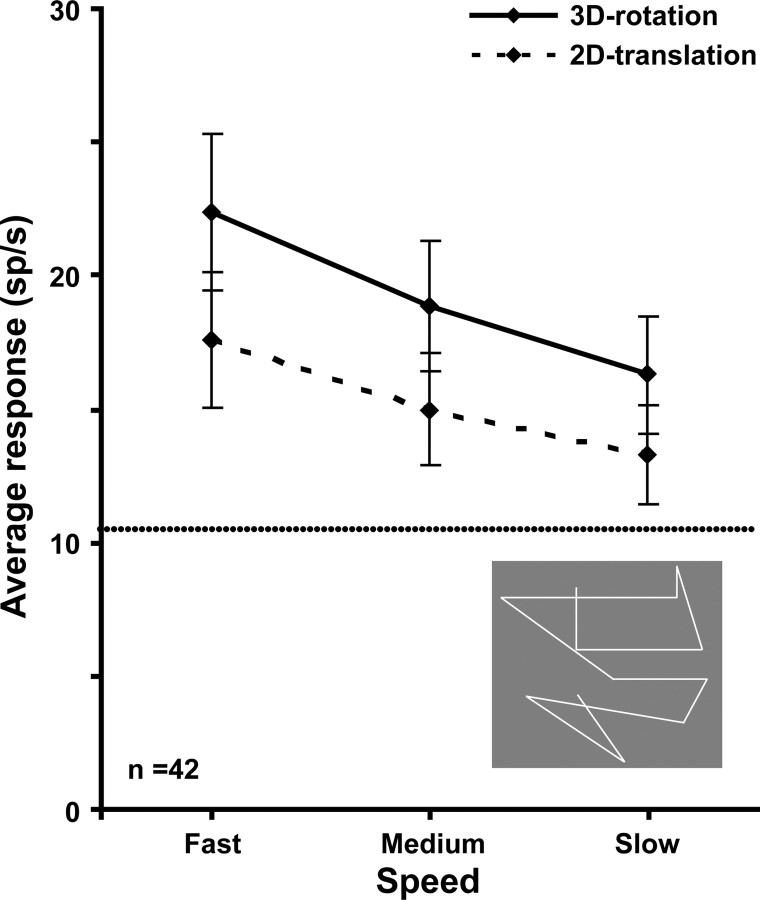
Previous monkey fMRI studies (Vanduffel et al., 2002; Nelissen et al., 2006) revealed stronger MR activity in FST for randomly connected lines (RL) rotating in depth as opposed to translating in the frontoparallel plane. We measured responses to such RL stimuli at three speeds (see Materials and Methods) in 42 FST neurons. Within this subsample, 90% of the neurons were selective for at least one order of the random-dot 3D-SFM stimuli, a proportion similar to that of the overall sample. Responses for rotating RL were, on average, significantly stronger than for RL translating in a plane (Fig. 10). A repeated-measures ANOVA yielded a significant (F(41,1) = 22.1, p < 0.0005) main effect of condition (rotation vs translation) and of speed (F(82,2) = 26.3, p < 10−6), as well as a significant interaction (F(82,2) = 4.9, p < 0.01). Post hoc Bonferroni's tests of the differences between rotation and translation were significant (p < 10−6) at all three speeds. An increase in firing rate of ∼30% was observed with the rotation RL, a value similar to the change in MR activity observed in the fMRI experiments (Nelissen et al., 2006). These findings suggest that the results of the RL test, used to investigate the extraction of 3D-SFM using fMRI, reflect the actual responses of the local neurons.
Figure 10.
Average gross responses of 42 FST neurons to 3D rotating and 2D translating random lines presented at three speeds. Horizontal lines, Average spontaneous activity. Difference between rotation and translation proved significant: repeated-measures two-way ANOVA, main effect of depth structure, F(1,47) = 26.48, p < 10−6. Inset, Single frame of random lines stimuli taken from Nelissen et al. (2006).
Comparison of FST and MT/V5 neurons
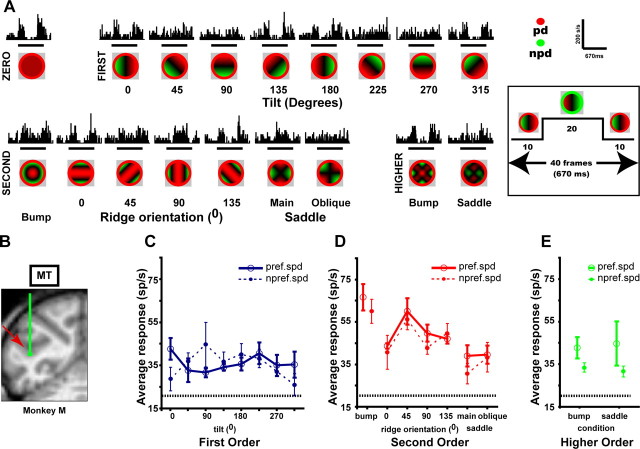
Because FST receives its major input from MT/V5 (Desimone and Ungerleider, 1986; Ungerleider and Desimone, 1986; Distler et al., 2002) and because some MT/V5 neurons are selective for linear speed gradients (Treue and Andersen, 1996; Xiao et al., 1997a), we wanted to examine how much 3D-SFM selectivity is already present in MT/V5. We therefore tested 64 neurons in MT/V5 of the same subjects (Fig. 11). We found MT/V5 neurons to be selective not only for first-order gradients, in agreement with Xiao et al. (1997a) and Nguyenkim and DeAngelis (2004), but also for second-order gradients. An example MT/V5 neuron, selective for second-order structure with a preference for the bump, is shown in Figure 11.
Figure 11.
MT/V5 neuron (io152_F, eccentricity 5.2°) selective for second-order stimuli. A, Recording site in MT/V5 of monkey M. B, PSTHs plotting average responses to the 18 depth–structure conditions of the main test (2.5°/s, 4° size). C–E, Tuning curves for the different orders of depth structure at preferred (2.5°/s, solid line, same data as in B) and nonpreferred (1.25°/s, dashed line) speeds: main effect of condition, two-way ANOVA, p < 10−8; interaction between speed and second order, NS (second-order d′ = 1.98; separability index (r2) 3D shape–speed = 0.92). Main effects condition of other orders NS. Same conventions as in Figures 1 and 2.
The main and position tolerance tests, however, revealed seven distinctions between the two areas seen in comparing the MT/V5 sample with an FST sample of matched RF eccentricity. First, MT/V5 neurons did demonstrate selectivity for the 3D-SFM stimuli (as indicated by a significant main effect of shape in the two-way ANOVA with speed and shape as factors), but their proportions were smaller in MT/V5 than in FST. Forty-four percent of the MT/V5 neurons were selective for first order compared with 60% in FST. For second order, the proportions were 45% in MT/V5 and 65% in FST and for higher order 15 and 28%. Overall, 58% of the MT/V5 neurons were selective for at least one order compared with 82% of the FST neurons. All these differences were significant on a binomial test (p < 0.003 or better on binomial tests). Second, the selective neurons in MT/V5 responded very strongly to the zero-order controls, unlike FST neurons. This is captured by the large and significant (Mann–Whitney U test, p < 10−6 for both orders) shift in the index comparing these two responses (the difference of the responses divided by their sum) from a median value of 0.06 in MT/V5 to one of 0.42 in FST neurons (both orders) (Fig. 12A,B).
Figure 12.
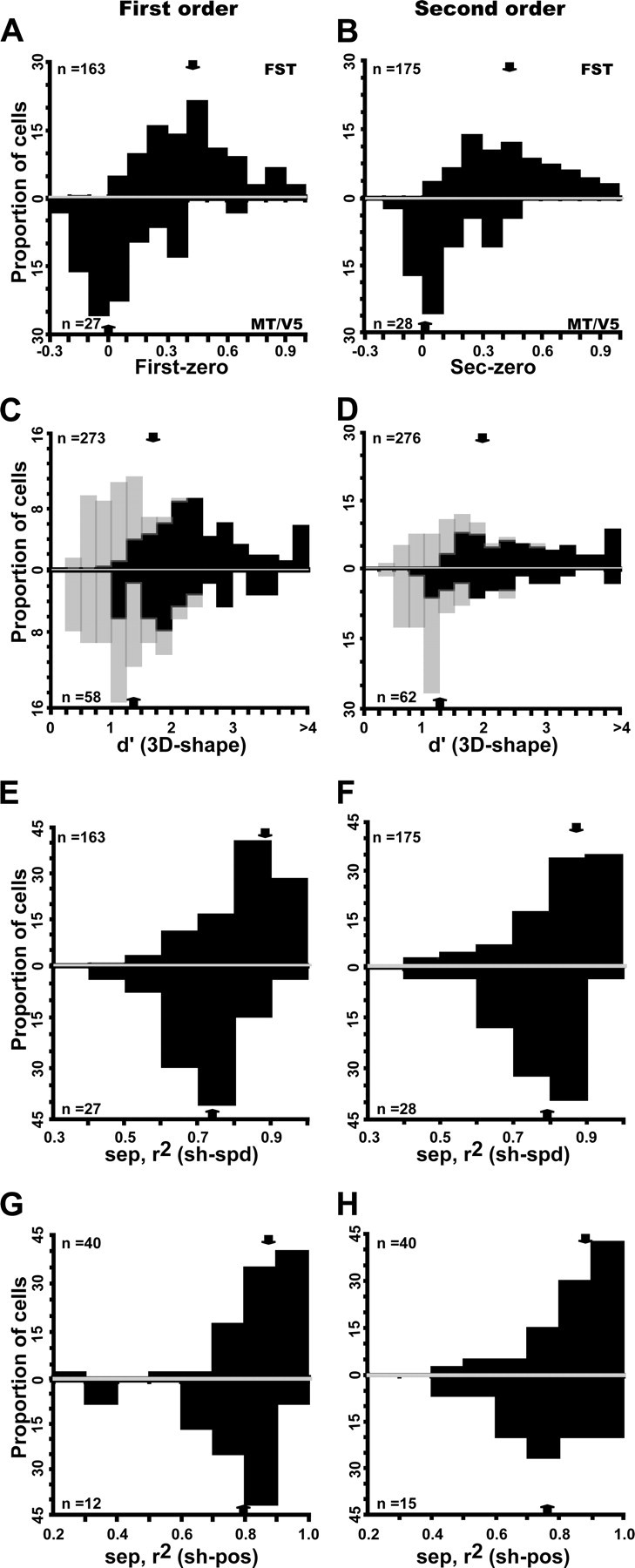
Comparison of MT/V5 (below) and FST (above) neurons selective for first-order (A, C, E, G) and second-order (B, D, F, H) stimuli. A, B, Distribution of index [(Rnz − Rz)/(Rnz + Rz)], where Rnz and Rz are responses to nonzero and zero order, respectively; first-order FST median, 0.42 (0.27–0.58); MT/V5 median, 0.06 (−0.06 to 0.12). Distribution significantly higher for FST (Z = 7.05, p < 10−7, Mann–Whitney U test); second-order FST median, 0.42 (0.28–0.62); MT/V5 median, 0.06 (−0.02 to 0.23). Distribution significantly higher for FST (Z = 6.06, p < 10−5, Mann–Whitney U test). C, D, Distribution of d′ (for 3D shape): light and dark hatching indicate nonselective and selective according to ANOVA): first-order FST median, 1.7 (1.05–2.44); MT/V5 median, 1.43 (0.98–1.9); second-order FST median, 1.9 (1.34–2.9); MT/V5 median, 1.27 (1.02–2.1). E, F, Distributions of 3D shape–speed separability index; first-order FST median, 0.87 (0.79–0.90); MT/V5 median, 0.74 (0.67–0.86); second-order FST median, 0.88 (0.75–0.92); MT/V5 median, 0.80 (0.78–0.85). G, H, Distributions of 3D shape–position separability index: first-order FST median, 0.88 (0.82–0.93); MT/V5 median, 0.8 (0.7–0.89); distribution difference NS; second-order FST median, 0.88 (0.79–0.95); MT/V5 median, 0.78 (0.7–0.84). Difference significant (Mann–Whitney U test, Z = 1.98, p < 0.05). Arrows indicate median values.
Third, MT/V5 neurons were less selective than FST neurons, especially for neurons responsive to second-order gradients (Fig. 12C,D). The median d′ was 1.7 for first-order responsive FST neurons compared with only 1.43 for their MT/V5 counterparts (Mann–Whitney U test, Z = 2.56, p < 0.02), whereas the median was 1.9 for second-order responsive FST neurons compared with 1.27 for their MT/V5 counterparts (Mann–Whitney U test, Z = 4.06, p < 0.0001). Despite the fact that we mainly used the small stimuli to test MT/V5 neurons (75% of the neurons), the SFM stimuli were larger, relative to the RF size, for MT/V5 neurons than for the FST neurons. This raises the issue of a possible mismatch between the stimulus size and the RF to the disadvantage of the MT/V5 neurons and that might explain their reduced selectivity. Because one would expect the degree of mismatch to be inversely correlated with RF size, this issue can be addressed by measuring the relationship between d′ and RF size. The correlation was computed for both MT/V5 and FST neurons, separately for each stimulus size and depth order, but in none of these 12 cases did the d′ depend significantly on RF size. Thus, it is unlikely that the weaker selectivity of MT/V5 neurons compared with FST neurons reflect the differences in the degree of mismatch between stimulus and RF sizes in the two areas.
Fourth, although the distribution of stimulus preferences for first-order selective neurons were uniform in both MT/V5 and FST, this was true for FST neurons but not MT/V5 neurons selective for second-order stimuli. Indeed, most (23 of 28, 82%) MT/V5 neurons selective for second order preferred a ridge, whereas the distribution was more uniform in FST, in which only 64% of the second-order selective neurons preferred a ridge. This difference was highly significant (χ2 = 31.8, p < 10−9). Fifth, selectivity for second-order ridges of neurons in MT/V5, unlike that of FST neurons, could be explained by the first-order selectivity of the neuron (Fig. 5). Furthermore, 93% (23 of 25) of the MT/V5 neurons tuned for ridges were also selective for first-order tilt, whereas this was the case for only 66% (106 of 161) of the FST neurons. This difference was highly significant (χ2 = 38.7, p < 10−9).
Sixth, the 3D-SFM selective MT/V5 neurons were less tolerant of incidental stimulus changes than selective neurons in FST. For both speed and position tolerance, the average separability indices were lower in MT/V5 than in FST (Fig. 12E,H), but the difference reached significance only for the 3D shape–speed separability index of first-order neurons (Mann–Whitney U test, Z = 3.5, p < 0.005) (Fig. 12E) and for the 3D shape–position separability index of second-order selective neurons (Mann–Whitney U test, Z = 1.98, p < 0.05) (Fig. 12H). More importantly, the proportion of neurons with separability indices significantly different from zero was significantly larger in FST than in MT/V5 (χ2 test). This held true for the separability between mean speed and 3D shape for both first order (69 vs 30%, χ2 = 27.3, p < 10−4) and second order (65 vs 32%, χ2 = 19.62, p < 0.0005). It also applied to the separability between position and 3D shape for both first order (68 vs 25%, χ2 = 8.1, p < 0.04) and second order (67 vs 27%, χ2 = 8.16, p < 0.05). The weak position tolerance among the selective neurons in MT/V5 is consistent with the existence of non-uniform surrounds (Xiao et al., 1997b) participating in the local extraction of 3D-SFM (Born and Bradley, 2005; Orban, 2008).
Because we mainly used the small stimuli to test MT/V5 neurons (75% of the neurons compared with 55% in FST), the differences in selectivity or tolerances for speed and position changes may reflect these differences in size. Therefore, we reanalyzed the differences between MT/V5 and FST neurons restricting the analysis to neurons with matched RF eccentricities and tested with small stimuli. As shown in Figure 13, the differences between the two areas with regard to their relative response to higher-order stimuli, selectivity as measured by d′, and tolerance for changes in speed and position were all significant.
Figure 13.
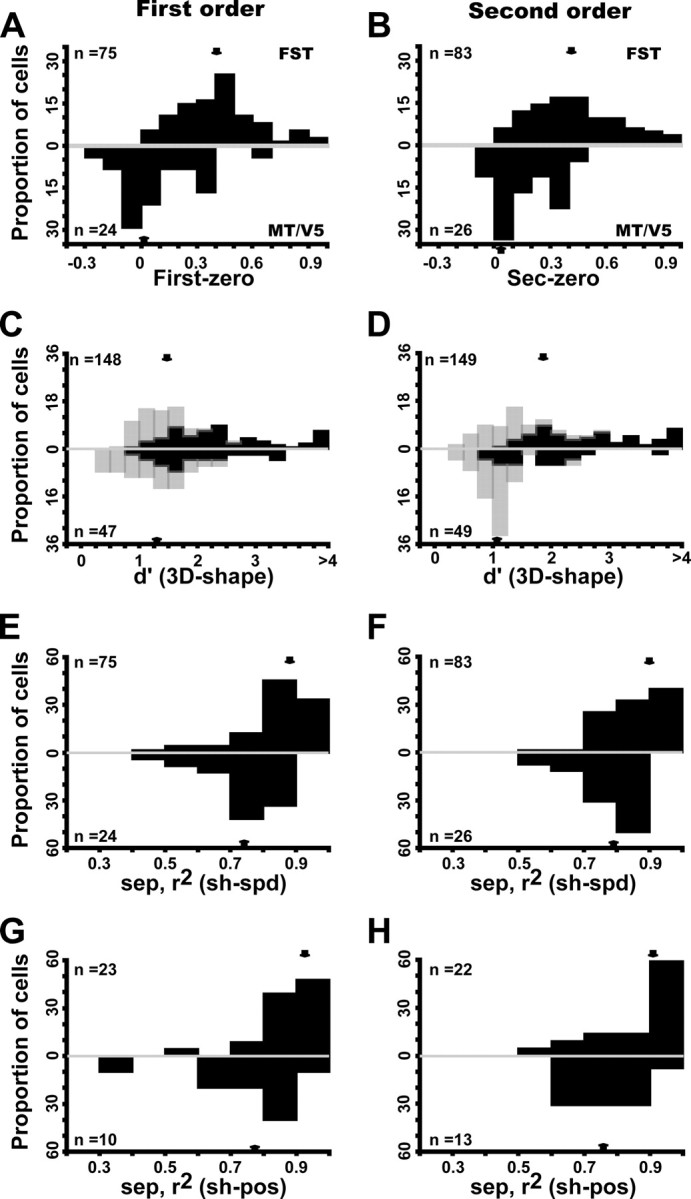
Comparison of MT/V5 (below) and FST (above) neurons tested with small stimuli and selective for first-order (A, C, E, G) and second-order (B, D, F, H) stimuli. A, B, Distribution of index [(Rnz − Rz)/(Rnz + Rz)], where Rnz and Rz are responses to nonzero and zero order, respectively; first-order FST median, 0.40 (0.28–0.56); MT/V5 median, 0.04 (−0.03 to 0.24). Distribution significantly higher for FST (Z = 5.5, p < 10−6, Mann–Whitney U test); second-order FST median, 0.40 (0.26–0.58); MT/V5 median, 0.15 (−0.05 to 0.30). Distribution significantly higher for FST (Z = 4.1, p < 10−3, Mann–Whitney U test). C, D, Distribution of d′ (for 3D shape): light and dark hatching indicate nonselective and selective according to ANOVA: first-order FST median, 1.66 (1.18–2.37); MT/V5 median, 1.47 (0.99–1.96); distribution significantly higher for FST (Z = 2.16, p < 0.03, Mann–Whitney U test); second-order FST median, 1.8 (1.26–2.78); MT/V5 median, 1.12 (0.96–1.47). Distribution significantly higher for FST (Z = 4.6, p < 10−5, Mann–Whitney U test). E, F, Distributions of 3D shape–speed separability index; first-order FST median, 0.88 (0.80–0.92); MT/V5 median, 0.75 (0.70–0.81); distribution significantly higher for FST (Z = 4.47, p < 10−5, Mann–Whitney U test); second-order FST median, 0.86 (0.80–0.93); MT/V5 median, 0.79 (0.71–0.84); distribution significantly higher for FST (Z = 3.88, p < 10−3, Mann–Whitney U test). G, H, Distributions of 3D shape–position separability index: first-order FST median, 0.92 (0.84–0.96); MT/V5 median, 0.79 (0.66–0.90); distribution significantly higher for FST (Z = 2.48, p < 0.02, Mann–Whitney U test); second-order FST median, 0.92 (0.79–0.95); MT/V5 median, 0.76 (0.69–0.80); distribution significantly higher for FST (Z = 2.04, p < 0.05, Mann–Whitney U test). Arrows indicate median values.
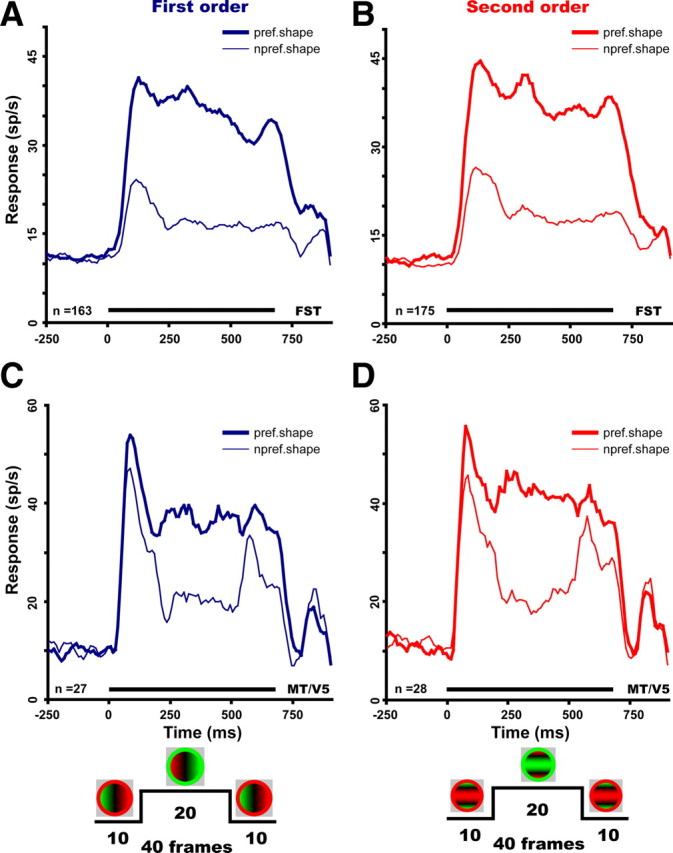
Finally, the time course of the emergence of selectivity differed markedly in MT/V5 and FST (Fig. 14). For both first and second order, MT/V5 neurons responded earlier to the stimuli than did FST neurons (40 ms onset latency on average compared with 50 ms), consistent with the known motion processing hierarchy (Felleman and Van Essen, 1991). However, 3D-SFM selectivity, as assessed by a paired t test between preferred and nonpreferred population responses (10 ms bin width), emerged 40 ms earlier in the 3D-SFM selective FST population compared with that in MT/V5. Indeed, selectivity was apparent in FST from the very onset of the response, whereas it emerged only at 90 ms after response onset in MT/V5. Furthermore, selectivity in FST was stable over the entire duration of the stimulus presentation, unlike that in MT/V5 (Fig. 14). The difference in selectivity of MT/V5 neurons for the middle period compared with the first 10 and last 10 frames reflects differences in the summation of the central speed distribution with the motion in the surrounding annulus for the preferred and nonpreferred directions. Indeed, the majority of MT/V5 neurons have antagonistic surrounds, which overlaps to a large degree with the excitatory RF. Because the average ratio of stimulus to RF size, taken at 50% of maximum responses (see Materials and Methods), equaled 1 for both first- and second-order MT/V5 neurons, the annulus was located in the majority of MT/V5 neurons over the surround near its point of maximum sensitivity (Raiguel et al., 1995). Because the motion in the annulus was always presented together with the speed patterns over the central part of the RF, this annulus motion thus exerted its effect through the surround mechanism in the majority of MT/V5 neurons. This so-called antagonistic surround is direction selective sharing the same preferred direction as the excitatory center (Tanaka et al., 1986; Orban, 1997). Hence, during the middle period when the dots in the annulus moved in the nonpreferred direction (Fig. 14, insets), this annulus motion had little or no effect. This middle period thus represents the reference situation, corresponding to the speed gradients acting on their own.
Figure 14.
Population response as a function of time for preferred (thick line) and nonpreferred (thin line) values of first-order (A, C) and second-order (B, D) depth–structure in FST (A, B) and MT/V5 (C, D) selective neurons. Numbers are indicated. Curves are smoothed (boxcar smoothing, 50 ms). In FST, the difference (paired t test, 2 consecutive bins also significant, p < 0.05) between preferred and nonpreferred stimulus became significant at 50 ms compared with 90 ms in MT/V5. Differences between preferred and nonpreferred responses remained significant throughout the stimulus duration (including during the direction reversal) in FST but not in MT/V5. Insets at the bottom show the time courses of the stimulation for a first-order gradient on the left and a second-order gradient (ridge) on the right.
Because responses in MT/V5 were more selective in this middle period (Fig. 14C,D), responses in FST and MT/V5 were compared in the window defined by frames 10–30, shifted 50 ms to account for latency. Although the distributions of the separability indices for changes in speed and position still differed significantly between these two areas, the selectivity captured by the d′ was no longer significantly different between the two areas (supplemental Fig. S8, available at www.jneurosci.org as supplemental material). Conversely, the proportion of selective neurons was still significantly larger in FST compared with MT/V5. For first- and second-order selectivity, these proportions were 54% compared with 42% and 57% compared with 47%, respectively. Both differences were significant (p < 0.05, binomial test). Overall, 82% of FST neurons were selective for any order of SFM compared with only 60% in MT/V5, a highly significant difference (p < 10−5, binomial test). Thus, even within the middle period of the stimulation, during which MT/V5 neurons are the most selective, significant differences between the FST and MT/V5 populations remain.
Figure 14, C and D, also shows that, in MT/V5, neuronal selectivity for 3D-SFM was strongly reduced when the dots in the annulus moved in the preferred direction, i.e., the 10 first and 10 last frames of the stimulation. It has been shown recently that the effect of the surround can switch from suppressive to facilitatory, depending on the strength of the response to the central stimuli (Huang et al., 2008). From these results, one would predict that the response to the preferred speed gradients over the center will be reduced by the annulus motion in the preferred direction, although the much weaker response to the nonpreferred gradients would be enhanced. This is exactly what is shown in Figure 14, C and D, although the reduction of the response to the preferred gradient is small at best. Hence, MT/V5 neurons can be selective for a restricted set of gradients when these gradients are tested on their own, but this selectivity will be strongly modulated by the presence of nearby motion, if it happens to be in the preferred direction of the neurons. Conversely, this dependence no longer applies to FST neurons (Fig. 14A,B), which are farther along in the hierarchy. Thus, the annulus in the present experiments served as a proxy for motion that is likely to occur in the vicinity of 3D objects under 3D-SFM conditions. The presence of the annulus in our stimuli therefore revealed an additional difference between FST and MT/V5, which would otherwise have gone undetected. It is also worth noting that, although the SFM stimuli used here were ambiguous with respect to the sign of curvature, they do not change in sign when the direction of motion reverses. On the contrary, the perceived sign of curvature is stable for long periods despite direction reversals in the stimulus and after such switches at random instants again remains stable regardless of direction changes (see supplemental movies, available at www.jneurosci.org as supplemental material). Hence, the behavior of FST neurons matches the perception better than the MT/V5 neurons, assuming that monkeys perceive the stimuli like humans (Siegel and Andersen, 1990).
Discussion
Area FST has been known for >20 years, yet its contribution to visual processing has remained essentially unknown. This underscores the advantages of the present approach in which single-cell studies are guided by fMRI (Tsao et al., 2006). Previous fMRI studies (Vanduffel et al., 2002; Nelissen et al., 2006) had revealed MR activity in area FST in response to 3D-SFM and opponent-motion stimuli. Here, we demonstrate that the neurons of this area indeed respond to 3D-SFM stimuli and, more importantly, that they do so in a selective manner. Furthermore, FST neuronal responses, like the MR signals in FST, are stronger for RL rotating in depth than RL translating in a plane. In addition, the difference is ∼30% for both types of measurements.
Selectivity of FST neurons for 3D-SFM
The main result of the present study is the selectivity for at least one order of 3D-SFM observed in the large majority of FST neurons. Several lines of evidence indicate that this is a genuine higher-order selectivity, which cannot be reduced to a lower-order speed selectivity. Indeed, the degree of 3D-SFM selectivity depended little on speed selectivity, and many neurons without speed selectivity still showed 3D-SFM selectivity. Selectivity for 3D-SFM tolerated a twofold change in the mean speed and that tolerance was unrelated to the speed–response characteristics of the neurons. A far stronger argument for higher-order selectivity is the demonstration of position tolerance (Lagae et al., 1994; Janssen et al., 1999; Bridge and Cumming, 2008). Indeed, the FST selectivity for all orders of 3D-SFM tolerated shifts between two positions, and this tolerance was essentially independent of the absolute or relative size of the shift or the degree of overlap between the stimuli at the two positions. Finally, FST selectivity for 3D-SFM was also shown to tolerate a threefold size change in a manner unrelated to the relative magnitude of that change. Thus, the FST selectivity for 3D-SFM reflects the higher-order characteristics of the stimuli such as speed gradients and opposed-motion rather than some local speed preference within a particular part of the RF. Furthermore, direct comparison of the tunings for the original and the single-cue stimuli indicated that speed gradients were the predominant higher-order cue generating FST selectivity for first- and second-order 3D SFM stimuli. Because we explored only two mean speeds, two positions, and two sizes, additional work is needed to fully characterize the tolerance of FST neurons.
Extraction of 3D-SFM in two stages
FST receives input from MT/V5, V3A, V3 dorsal, and V4 (Boussaoud et al., 1990). Because MT/V5 neurons are strongly selective for motion direction and those of V3A are not, it is generally accepted (Boussaoud et al., 1990) that FST inherits its motion responses from MT/V5. The present results when considered together with previous work (Xiao et al., 1997a; DeAngelis et al., 1998; Nadler et al., 2008) indicate that depth structure is extracted from motion in two stages, successively in MT/V5 and FST. MT/V5 neurons extract predominantly first-order and single curvature second-order speed gradients through their non-uniform surrounds (Xiao et al., 1995, 1997b). Because on average the stimulus size equaled the RF size and the surround overlaps the excitatory RF (Raiguel et al., 1995), the speed gradients stimulated the surround of most MT/V5 neurons. The critical surround feature seems to be simply its non-uniformity, in addition to relative speed sensitivity (Xiao et al., 1997a,b).The distinction between single and double suppressive zones seems less important, because most (25 of 28) MT/V5 neurons were selective for both first- and second-order gradients. The spatial overlap of the surround and the excitatory RF may explain why SFM selectivity in MT/V5 exhibited some tolerance for changes in position or size and for direction reversals. Thus, speed gradient selectivity of MT/V5 neurons seems to be a more global RF property than pattern selectivity (Majaj et al., 2007).
By convergence of multiple selective MT/V5 neurons onto single FST neurons, RFs will increase in size, increasing the tolerance of the selectivity, including that for motion direction reversals (Fig. 14), and allowing selectivity for doubly curved second-order stimuli (bumps and saddles) to emerge and the second-order ridge selectivity to become dissociated from first-order selectivity. Additionally, we conjecture that input from V4 into FST may add opponent-motion signals, because V4 neurons are selective for such stimuli (Mysore et al., 2006). The convergence of the second cue at the level of FST neurons will enhance selectivity for SFM stimuli and will also reduce the responses to zero-order stimuli. At present, it is unclear how the convergence of multiple MT/V5 neurons onto a single FST neuron increases position tolerance, but the process might be similar to that operating between MT/V5 and MSTd for optic flow components (Tanaka et al., 1989; Lagae et al., 1994) or along the ventral stream (Riesenhuber and Poggio, 2000). The longer latency in the MT/V5 population might partially reflect feedback but may also be a consequence of the stronger motion onset signals in MT/V5 compared with FST and the weaker temporal coherence between the less selective MT/V5 neurons compared with FST neurons. Thus, we suggest that, unlike the emergence of selectivity for flow components, which is a single step process in MSTd (Lagae et al., 1994), the extraction of 3D-SFM occurs in two stages, involving MT/V5 and FST. This may be needed because both speed and direction signals contribute to selectivity for SFM stimuli (Roy et al., 1992), whereas direction signals alone suffice for flow components selectivity (Tanaka et al., 1989; Orban et al., 1995). Nevertheless, at the level of FST, the automatic extraction of 3D shape from the sole motion cue is primarily complete. This follows from (1) the large proportion (83%) of selective neurons, (2) the thoroughness of the analysis, including all orders of 3D-SFM and all values within those orders, (3) the tolerance of the selectivity for changes in speed, position, size, cue, and duration, and (4) the early onset of the selectivity. These findings confirm our predictions and cast FST in a pivotal role in the processing of 3D-SFM information, although MT/V5 participates significantly in the process.
Processing of 3D shape signals beyond FST
FST projects to lateral intraparietal area and ventral intraparietal area in the intraparietal sulcus (Bullier et al., 1996) and later studies have reported projections to anterior intraparietal area (AIP) (Borra et al., 2008). FST also projects to the more rostral parts of the upper and lower banks of the STS (Boussaoud et al., 1990). AIP and rostral STS have been implicated in 3D shape processing by single-cell and fMRI studies (Janssen et al., 1999, 2000; Durand et al., 2007; Yamane et al., 2008; Joly et al., 2009; Srivastava et al., 2009). Thus, FST is connected with other areas known to be involved in 3D shape processing. The parietal component of this network is enhanced in humans (Vanduffel et al., 2002). Indeed, the projection of 3D-SFM signals to AIP might be crucial for the manipulation of objects, especially articulated objects such as tools, explaining its enhancement in humans (Vanduffel et al., 2002; Peeters et al., 2009).
Given these anatomical connections, the FST motion signals may converge on the IT neurons described by Yamane et al. (2008) to build a multifragment 3D shape representation using motion as the cue. Additionally, FST might project to body- and face-selective patches (Tsao et al., 2003), some of which are located in the general vicinity of FST. Indeed, ridges might portray body parts, particularly limbs (Marr and Nishihara, 1978), fingers, and, to a lesser extent, the lips and nose (Susskind et al., 2008). Saddles may portray the skin surface of articulations, e.g., between the index and thumb or the inside of the elbow, but also parts of the face (e.g., the bridge of the nose). It would be advantageous to build a 3D body and face representation from motion, insofar as the body, and to a lesser degree the face, is highly mobile. In this respect, additional studies may reveal that FST neurons not only exhibit position tolerance in their 3D shape tuning but are tuned for additional parameters of ridges (e.g., curvature or size) or saddles (e.g., relative size and curvature in the orthogonal directions). In addition, there is growing evidence (Lange and Lappe, 2006; Vangeneugden et al., 2009) that action descriptions are derived at least partially (Giese and Poggio, 2003) from the temporal derivatives of shape; thus, it is conceivable that, by taking temporal derivatives of ridge and saddle signals, one could generate action-selective neurons. In this respect, it worth noting that fMRI has revealed an exquisite sensitivity to the sight of others' actions in areas MT/V5 and FST (Nelissen et al., 2006). Additional work is required to explore how 3D-SFM is processed further in these higher-order areas, preferably using fMRI-guided single-cell studies.
Conclusion
The present study provides conclusive evidence that FST is heavily involved in the extraction of 3D-SFM, building on the initial processing in area MT/V5. In this manner, we have attributed at least one well defined function to area FST, which had so far been assigned no clear role in visual processing.
Footnotes
This work was supported by Grants EF05/014, IUAP6/29, GSKE. The help of P. Kayenbergh, G. Meulemans, M. De Paep, W. Depuydt, I. Puttemans, M. Docx, as well as the comments of S. Lisberger, B. Cumming, and W. Vanduffel on a previous version of this manuscript are kindly acknowledged.
References
- Born RT, Bradley DC. Structure and function of visual area MT. Annu Rev Neurosci. 2005;28:157–189. doi: 10.1146/annurev.neuro.26.041002.131052. [DOI] [PubMed] [Google Scholar]
- Borra E, Belmalih A, Calzavara R, Gerbella M, Murata A, Rozzi S, Luppino G. Cortical connections of the macaque anterior intraparietal (AIP) area. Cereb Cortex. 2008;18:1094–1111. doi: 10.1093/cercor/bhm146. [DOI] [PubMed] [Google Scholar]
- Boussaoud D, Ungerleider LG, Desimone R. Pathways for motion analysis: cortical connections of the medial superior temporal and fundus of the superior temporal visual areas in the macaque. J Comp Neurol. 1990;296:462–495. doi: 10.1002/cne.902960311. [DOI] [PubMed] [Google Scholar]
- Bradley DC, Chang GC, Andersen RA. Encoding of three-dimensional structure-from-motion by primate area MT neurons. Nature. 1998;392:714–717. doi: 10.1038/33688. [DOI] [PubMed] [Google Scholar]
- Bridge H, Cumming BG. Representation of binocular surfaces by cortical neurons. Curr Opin Neurobiol. 2008;18:425–430. doi: 10.1016/j.conb.2008.09.003. [DOI] [PubMed] [Google Scholar]
- Bullier J, Schall JD, Morel A. Functional streams in occipito-frontal connections in the monkey. Behav Brain Res. 1996;76:89–97. doi: 10.1016/0166-4328(95)00182-4. [DOI] [PubMed] [Google Scholar]
- DeAngelis GC, Cumming BG, Newsome WT. Cortical area MT and the perception of stereoscopic depth. Nature. 1998;394:677–680. doi: 10.1038/29299. [DOI] [PubMed] [Google Scholar]
- Desimone R, Ungerleider LG. Multiple visual areas in the caudal superior temporal sulcus of the macaque. J Comp Neurol. 1986;248:164–189. doi: 10.1002/cne.902480203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Distler C, Mustari MJ, Hoffmann KP. Cortical projections to the nucleus of the optic tract and dorsal terminal nucleus and to the dorsolateral pontine nucleus in macaques: a dual retrograde tracing study. J Comp Neurol. 2002;444:144–158. doi: 10.1002/cne.10127. [DOI] [PubMed] [Google Scholar]
- Dodd JV, Krug K, Cumming BG, Parker AJ. Perceptually bistable three-dimensional figures evoke high choice probabilities in cortical area MT. J Neurosci. 2001;21:4809–4821. doi: 10.1523/JNEUROSCI.21-13-04809.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffy CJ, Wurtz RH. Medial superior temporal area neurons respond to speed patterns in optic flow. J Neurosci. 1997;17:2839–2851. doi: 10.1523/JNEUROSCI.17-08-02839.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durand JB, Nelissen K, Joly O, Wardak C, Todd JT, Norman JF, Janssen P, Vanduffel W, Orban GA. Anterior regions of monkey parietal cortex process visual 3D shape. Neuron. 2007;55:493–505. doi: 10.1016/j.neuron.2007.06.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felleman DJ, Van Essen DC. Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex. 1991;1:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- Giese MA, Poggio T. Neural mechanisms for the recognition of biological movements. Nat Rev Neurosci. 2003;4:179–192. doi: 10.1038/nrn1057. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal detection theory and psychophysics. New York: Wiley; 1966. [Google Scholar]
- Hikosaka K, Iwai E, Saito H, Tanaka K. Polysensory properties of neurons in the anterior bank of the caudal superior temporal sulcus of the macaque monkey. J Neurophysiol. 1988;60:1615–1637. doi: 10.1152/jn.1988.60.5.1615. [DOI] [PubMed] [Google Scholar]
- Huang X, Albright TD, Stoner GR. Stimulus dependency and mechanisms of surround modulation in cortical area MT. J Neurosci. 2008;28:13889–13906. doi: 10.1523/JNEUROSCI.1946-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssen P, Vogels R, Orban GA. Macaque inferior temporal neurons are selective for disparity-defined three-dimensional shapes. Proc Natl Acad Sci U S A. 1999;96:8217–8222. doi: 10.1073/pnas.96.14.8217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssen P, Vogels R, Orban GA. Three-dimensional shape coding in inferior temporal cortex. Neuron. 2000;27:385–397. doi: 10.1016/s0896-6273(00)00045-3. [DOI] [PubMed] [Google Scholar]
- Joly O, Vanduffel W, Orban GA. The monkey ventral premotor cortex processes 3D shape from disparity. Neuroimage. 2009;47:262–272. doi: 10.1016/j.neuroimage.2009.04.043. [DOI] [PubMed] [Google Scholar]
- Kayaert G, Biederman I, Op de Beeck HP, Vogels R. Tuning for shape dimensions in macaque inferior temporal cortex. Eur J Neurosci. 2005;22:212–224. doi: 10.1111/j.1460-9568.2005.04202.x. [DOI] [PubMed] [Google Scholar]
- Koenderink JJ. Solid Shape. Cambridge, MA: Massachusetts Institute of Technology; 1990. [Google Scholar]
- Kolster H, Mandeville JB, Arsenault JT, Ekstrom LB, Wald LL, Vanduffel W. Visual field map clusters in macaque extrastriate visual cortex. J Neurosci. 2009;29:7031–7039. doi: 10.1523/JNEUROSCI.0518-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagae L, Maes H, Raiguel S, Xiao DK, Orban GA. Responses of macaque STS neurons to optic flow components: a comparison of areas MT and MST. J Neurophysiol. 1994;71:1597–1626. doi: 10.1152/jn.1994.71.5.1597. [DOI] [PubMed] [Google Scholar]
- Lange J, Lappe M. A model of biological motion perception from configural form cues. J Neurosci. 2006;26:2894–2906. doi: 10.1523/JNEUROSCI.4915-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lappin JS, Craft WD. Foundations of spatial vision: from retinal images to perceived shapes. Psychol Rev. 2000;107:6–38. doi: 10.1037/0033-295x.107.1.6. [DOI] [PubMed] [Google Scholar]
- Majaj NJ, Carandini M, Movshon JA. Motion integration by neurons in macaque MT is local, not global. J Neurosci. 2007;27:366–370. doi: 10.1523/JNEUROSCI.3183-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marr D, Nishihara HK. Representation and recognition of the spatial organization of three-dimensional shapes. Proc R Soc Lond B Biol Sci. 1978;200:269–294. doi: 10.1098/rspb.1978.0020. [DOI] [PubMed] [Google Scholar]
- Mazer JA, Vinje WE, McDermott J, Schiller PH, Gallant JL. Spatial frequency and orientation tuning dynamics in area V1. Proc Natl Acad Sci U S A. 2002;99:1645–1650. doi: 10.1073/pnas.022638499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mysore SG, Vogels R, Raiguel SE, Orban GA. Processing of kinetic boundaries in macaque V4. J Neurophysiol. 2006;95:1864–1880. doi: 10.1152/jn.00627.2005. [DOI] [PubMed] [Google Scholar]
- Nadler JW, Angelaki DE, DeAngelis GC. A neural representation of depth from motion parallax in macaque visual cortex. Nature. 2008;452:642–645. doi: 10.1038/nature06814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelissen K, Vanduffel W, Orban GA. Charting the lower superior temporal region, a new motion-sensitive region in monkey superior temporal sulcus. J Neurosci. 2006;26:5929–5947. doi: 10.1523/JNEUROSCI.0824-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyenkim JD, DeAngelis GC. Macaque MT neurons are selective for 3D surface orientation defined by multiple cues. Soc Neurosci Abstr. 2004;368:12. [Google Scholar]
- Orban GA. Visual processing in macaque area MT/V5 and its satellites (MSTd and MSTv) In: Rockland KS, Kaas JH, Peters A, editors. Cerebral cortex. New York: Plenum; 1997. pp. 359–434. [Google Scholar]
- Orban GA. Higher order visual processing in macaque extrastriate cortex. Physiol Rev. 2008;88:59–89. doi: 10.1152/physrev.00008.2007. [DOI] [PubMed] [Google Scholar]
- Orban GA, Lagae L, Raiguel S, Xiao D, Maes H. The speed tuning of medial superior temporal (MST) cell responses to optic-flow components. Perception. 1995;24:269–285. doi: 10.1068/p240269. [DOI] [PubMed] [Google Scholar]
- Peeters R, Simone L, Nelissen K, Fabbri-Destro M, Vanduffel W, Rizzolatti G, Orban GA. The representation of tool use in humans and monkeys: common and uniquely human features. J Neurosci. 2009;29:11523–11539. doi: 10.1523/JNEUROSCI.2040-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perotti VJ, Todd JT, Lappin JS, Phillips F. The perception of surface curvature from optical motion. Percept Psychophys. 1998;60:377–388. doi: 10.3758/bf03206861. [DOI] [PubMed] [Google Scholar]
- Phillips F, Todd JT. Perception of local three-dimensional shape. J Exp Psychol Hum Percept Perform. 1996;22:930–944. doi: 10.1037//0096-1523.22.4.930. [DOI] [PubMed] [Google Scholar]
- Raiguel S, Van Hulle MM, Xiao DK, Marcar VL, Orban GA. Shape and spatial distribution of receptive fields and antagonistic motion surrounds in the middle temporal area (V5) of the macaque. Eur J Neurosci. 1995;7:2064–2082. doi: 10.1111/j.1460-9568.1995.tb00629.x. [DOI] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T. Models of object recognition. Nat Neurosci. 2000;3(Suppl):1199–1204. doi: 10.1038/81479. [DOI] [PubMed] [Google Scholar]
- Rosenberg A, Wallisch P, Bradley DC. Responses to direction and transparent motion stimuli in area FST of the macaque. Vis Neurosci. 2008;25:187–195. doi: 10.1017/S0952523808080528. [DOI] [PubMed] [Google Scholar]
- Roy JP, Komatsu H, Wurtz RH. Disparity sensitivity of neurons in monkey extrastriate area MST. J Neurosci. 1992;12:2478–2492. doi: 10.1523/JNEUROSCI.12-07-02478.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sáry G, Vogels R, Orban GA. Orientation discrimination of motion-defined gratings. Vision Res. 1994;34:1331–1334. doi: 10.1016/0042-6989(94)90207-0. [DOI] [PubMed] [Google Scholar]
- Sawamura H, Orban GA, Vogels R. Selectivity of neuronal adaptation does not match response selectivity: a single-cell study of the FMRI adaptation paradigm. Neuron. 2006;49:307–318. doi: 10.1016/j.neuron.2005.11.028. [DOI] [PubMed] [Google Scholar]
- Siegel RM, Andersen RA. Perception of three-dimensional structure from motion in monkey and man. Nature. 1988;331:259–261. doi: 10.1038/331259a0. [DOI] [PubMed] [Google Scholar]
- Siegel RM, Andersen RA. The perception structure from visual motion in monkey and man. J Cogn Neurosci. 1990;2:306–319. doi: 10.1162/jocn.1990.2.4.306. [DOI] [PubMed] [Google Scholar]
- Srivastava S, Orban GA, De Mazière PA, Janssen P. A distinct representation of three-dimensional shape in macaque anterior intraparietal area: fast, metric, and coarse. J Neurosci. 2009;29:10613–10626. doi: 10.1523/JNEUROSCI.6016-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugihara H, Murakami I, Shenoy KV, Andersen RA, Komatsu H. Response of MSTd neurons to simulated 3D orientation of rotating planes. J Neurophysiol. 2002;87:273–285. doi: 10.1152/jn.00900.2000. [DOI] [PubMed] [Google Scholar]
- Susskind JM, Lee DH, Cusi A, Feiman R, Grabski W, Anderson AK. Expressing fear enhances sensory acquisition. Nat Neurosci. 2008;11:843–850. doi: 10.1038/nn.2138. [DOI] [PubMed] [Google Scholar]
- Tanaka K, Hikosaka K, Saito H, Yukie M, Fukada Y, Iwai E. Analysis of local and wide-field movements in the superior temporal visual areas of the macaque monkey. J Neurosci. 1986;6:134–144. doi: 10.1523/JNEUROSCI.06-01-00134.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka K, Fukada Y, Saito HA. Underlying mechanisms of the response specificity of expansion/contraction and rotation cells in the dorsal part of the medial superior temporal area of the macaque monkey. J Neurophysiol. 1989;62:642–656. doi: 10.1152/jn.1989.62.3.642. [DOI] [PubMed] [Google Scholar]
- Tanaka K, Sugita Y, Moriya M, Saito H. Analysis of object motion in the ventral part of the medial superior temporal area of the macaque visual cortex. J Neurophysiol. 1993;69:128–142. doi: 10.1152/jn.1993.69.1.128. [DOI] [PubMed] [Google Scholar]
- Todd JT, Norman JF. The visual perception of smoothly curved surfaces from minimal apparent motion sequences. Percept Psychophys. 1991;50:509–523. doi: 10.3758/bf03207535. [DOI] [PubMed] [Google Scholar]
- Todd JT, Norman JF. The visual perception of 3-D shape from multiple cues: are observers capable of perceiving metric structure? Percept Psychophys. 2003;65:31–47. doi: 10.3758/bf03194781. [DOI] [PubMed] [Google Scholar]
- Todd JT, Perotti VJ. The visual perception of surface orientation from optical motion. Percept Psychophys. 1999;61:1577–1589. doi: 10.3758/bf03213119. [DOI] [PubMed] [Google Scholar]
- Treue S, Andersen RA. Neural responses to velocity gradients in macaque cortical area MT. Vis Neurosci. 1996;13:797–804. doi: 10.1017/s095252380000866x. [DOI] [PubMed] [Google Scholar]
- Tsao DY, Freiwald WA, Knutsen TA, Mandeville JB, Tootell RB. Faces and objects in macaque cerebral cortex. Nat Neurosci. 2003;6:989–995. doi: 10.1038/nn1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsao DY, Freiwald WA, Tootell RB, Livingstone MS. A cortical region consisting entirely of face-selective cells. Science. 2006;311:670–674. doi: 10.1126/science.1119983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyler CW, Likova LT, Kontsevich LL, Wade AR. The specificity of cortical region KO to depth structure. Neuroimage. 2006;30:228–238. doi: 10.1016/j.neuroimage.2005.09.067. [DOI] [PubMed] [Google Scholar]
- Ungerleider LG, Desimone R. Cortical connections of visual area MT in the macaque. J Comp Neurol. 1986;248:190–222. doi: 10.1002/cne.902480204. [DOI] [PubMed] [Google Scholar]
- van Damme WJ, Oosterhoff FH, van de Grind WA. Discrimination of 3-D shape and 3-D curvature from motion in active vision. Percept Psychophys. 1994;55:340–349. doi: 10.3758/bf03207604. [DOI] [PubMed] [Google Scholar]
- Vanduffel W, Fize D, Peuskens H, Denys K, Sunaert S, Todd JT, Orban GA. Extracting 3D from motion: differences in human and monkey intraparietal cortex. Science. 2002;298:413–415. doi: 10.1126/science.1073574. [DOI] [PubMed] [Google Scholar]
- Vangeneugden J, Pollick F, Vogels R. Functional differentiation of macaque visual temporal cortical neurons using a parametric action space. Cereb Cortex. 2009;19:593–611. doi: 10.1093/cercor/bhn109. [DOI] [PubMed] [Google Scholar]
- Vogels R, Biederman I. Effects of illumination intensity and direction on object coding in macaque inferior temporal cortex. Cereb Cortex. 2002;12:756–766. doi: 10.1093/cercor/12.7.756. [DOI] [PubMed] [Google Scholar]
- Vogels R, Orban GA. How well do response changes of striate neurons signal differences in orientation: a study in the discriminating monkey. J Neurosci. 1990;10:3543–3558. doi: 10.1523/JNEUROSCI.10-11-03543.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao DK, Raiguel S, Marcar V, Koenderink J, Orban GA. Spatial heterogeneity of inhibitory surrounds in the middle temporal visual area. Proc Natl Acad Sci U S A. 1995;92:11303–11306. doi: 10.1073/pnas.92.24.11303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao DK, Marcar VL, Raiguel SE, Orban GA. Selectivity of macaque MT/V5 neurons for surface orientation in depth specified by motion. Eur J Neurosci. 1997a;9:956–964. doi: 10.1111/j.1460-9568.1997.tb01446.x. [DOI] [PubMed] [Google Scholar]
- Xiao DK, Raiguel S, Marcar V, Orban GA. The spatial distribution of the antagonistic surround of MT/V5 neurons. Cereb Cortex. 1997b;7:662–677. doi: 10.1093/cercor/7.7.662. [DOI] [PubMed] [Google Scholar]
- Yamane Y, Carlson ET, Bowman KC, Wang Z, Connor CE. A neural code for three-dimensional object shape in macaque inferotemporal cortex. Nat Neurosci. 2008;11:1352–1360. doi: 10.1038/nn.2202. [DOI] [PMC free article] [PubMed] [Google Scholar]