The Absence of Eye Muscle Fatigue Indicates That the Nervous System Compensates for Non-Motor Disturbances of Oculomotor Function

Abstract

The physical properties of our bodies are subject to change (due to fatigue, heavy equipment, injury or aging) as we move around in the surrounding environment. The traditional definition of motor adaptation dictates that a mechanism in our brain needs to compensate for such alterations by appropriately modifying neural motor commands, if the vitally important accuracy of executed movements is to be preserved. In this article we describe how a repetitive eye movement task brings about changes in eye saccade kinematics that compromise accurate motor performance in the absence of a proper compensatory response. Surgical lesions in animals and human patient studies have previously demonstrated that an intact cerebellum is necessary for the compensation to arise and prevent the occurrence of hypometric movements. Here we identified the dynamic properties of the eye plant by recording from abducens motoneurons responsible for the required movement and measured the muscle response to microstimulation of the abducens nucleus in rhesus monkeys. The ensuing results demonstrate that the muscular periphery remains intact during the fatiguing eye movement task, while internal sources of noise (drowsiness, attentional modulation, neuronal fatigue etc.) must be responsible for a diminished oculomotor performance. This finding leads to the important realization that while supervising the accuracy of our movements, the nervous system takes additionally into account and adapts to any disruptive processes within the brain itself, clearly unrelated to the dynamical behavior of muscles or the environment. The existence of this supplementary mechanism forces a reassessment of traditional views of cerebellum-dependent motor adaptation.

Introduction

While quickly ascending a flight of stairs, one heavily relies on the ability of her CNS to produce motor commands that will accurately guide the limb to the desired target at each step. After extensive physical exercise and with fatigued limb muscles, the individual is still able to perform the climbing task with identical accuracy, albeit with slower displacements. This is because our motor commands are continuously adjusted to produce accurate movements while the properties of our body change; a neural mechanism called motor adaptation. Previous experimental investigations of motor adaptation have almost exclusively been concerned with the ability to adapt motor behavior to novel dynamics of the body or external environment, by for instance imposing force fields to ongoing arm movements (Shadmehr and Mussa-Ivaldi, 1994; Li et al., 2001).

Suppose now that the person climbs up the flight of stairs after having performed mentally exhausting nonphysical work. This would intuitively lead to slower movement kinematics even though the physical dynamics of the limb being displaced are unaltered. This example highlights our contention that, as opposed to peripheral physical changes, movement accuracy can additionally be compromised by central cognitive processes that deteriorate the reliability of converting the desired displacement plan into the actual movement. We then further argue that the concept of motor adaptation needs to be extended to include the ability of the CNS to cope not only with external physical changes but with disruptive sources of noise present within the brain itself. The existence of this supplemental compensatory mechanism seems to be of even higher importance; because the manifestation of such central disturbances during a person's daily activities are ostensibly more recurrent than modifications of the motor periphery.

Here we provide the first conclusive evidence that during a motor task, a neural mechanism actively compensates for changes unspecific to the muscular periphery that would otherwise cause movements to become inaccurate. We trained rhesus monkeys to perform a strenuous task during which the oculomotor system, due to extensive repetitive use, undergoes significant physiological changes as reflected by progressively slower saccadic eye movements. Accuracy is however maintained because of a compensatory upregulation of movement duration. Previous investigations of the effects of repetitive eye movements on oculomotor performance (Brozek, 1949; Bahill and Stark, 1975; Schmidt et al., 1979; Fuchs and Binder, 1983; Straube et al., 1997; Chen-Harris et al., 2008; Xu-Wilson et al., 2009) were all based on psychophysical measures and the reached conclusions about the origin of fatigue remained suggestive at most. We demonstrate from single motor unit recordings in the monkey abducens nucleus that the system dynamics of the peripheral eye plant remain unaltered during the “fatigue” experiment. This result indicates that the slower eye kinematics are not the consequence of a muscular fatigue, but supports our hypothesis that cognitive factors (i.e., mental fatigue) are degrading the oculomotor functioning and are being successfully compensated to preserve accurate movements.

Materials and Methods

Animals

Three rhesus monkeys (Macaca mulatta) were prepared for eye position recording using the magnetic scleral search coil technique (Judge et al., 1980). To painlessly immobilize the monkeys' heads, a titanium pole was attached to the skull with titanium bone screws. Titanium was used for its high biocompatibility and for compatibility in functional magnetic resonance imaging settings. Recording chambers (also titanium) were implanted over the posterior part of the skull to gain access to the abducens nuclei for extracellular recordings by advancing electrodes through the cerebellum (Prsa et al., 2009). All surgical procedures were conducted under general anesthesia (introduced with ketamine and maintained by inhalation of isoflurane and nitrous oxide, supplemented by remifentanil) with control of vital parameters (body temperature, CO₂, O₂, blood pressure, ECG), followed the guidelines set by the National Institutes of Health and national law and were approved by the local committee supervising the handling of experimental animals. After the surgery, monkeys were supplied with analgesics until full recovery.

Behavioral tasks

During all behavioral tasks, the monkeys sat head-fixed in a primate chair in total darkness. They were trained to make saccadic eye movements to a white target dot (0.2° diameter) displayed on a monitor screen positioned 43 cm in front of the animals. The eye position signal measured by the scleral search coil method was calibrated and sampled at 1 kHz. The monkey received an automatic liquid reward at the end of a successful trial. A trial counted as successful, if the animal maintained gaze inside an eye position window (±1.5°) during initial fixation until the target jump, and displaced the eyes back inside the window in its new position and maintained fixation no later than 300 ms after the jump.

Saccadic fatigue paradigm.

The monkeys were trained to execute large numbers of visually guided eye saccades from a central fixation point toward a peripheral target in the horizontal direction. During each experiment the target always appeared at the same eccentricity but was varied from session to session anywhere between 8° and 24°, with 10–12° being the most frequent amplitude range (Fig. 1C). The central point was fixated for 400–500 ms, after which the peripheral target appeared with the simultaneous disappearance of the fixation target. After the saccadic eye movement, the monkeys had to fixate the peripheral target for 250–400 ms. To maximize the rate of consecutive saccades, the intertrial interval was set to zero (the next trial was initiated as soon as the previous one finished).

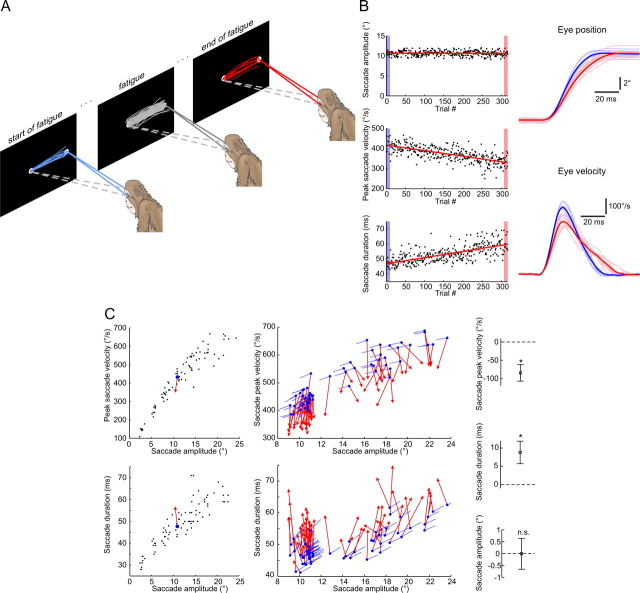
Figure 1.

Typical changes in eye saccade kinematics during saccadic fatigue. A, Illustrative depiction of the fatigue experiment. The selected convention was to define the first and last 10 trials as the start and end of fatigue. B, Saccade peak velocity and duration, but not amplitude, progressively change during the fatigue experiment. Left, Lines are least-squares linear fits to the three saccade metrics plotted for each consecutive trial. Right, Eye position and eye velocity individual (thin) and mean (bold) traces at the start (blue) and end (red) of the fatigue experiment. C, Eye saccade kinematics move away from their pre-fatigue main sequences. Left, Average data points at the start (blue dots) and end (red arrowheads) of one fatigue session with the pre-fatigue peak saccade velocities and durations plotted against amplitude (black dots). Middle, Same average data points for all 62 fatigue sessions. Blue lines indicate the direction of change predicted by the corresponding pre-fatigue main sequences. Right, Mean ± SD changes in peak saccade velocity and duration across all fatigue sessions were statistically different from zero (t tests, *p < 10⁻³⁰) while the mean amplitudes did not significantly (n.s.) change (t test, p = 0.91).

Amplitude tuning paradigm.

To test for the tuning of cells to saccades of different amplitudes, before the fatigue experiment, the animals executed visually guided saccades from a central fixation point toward targets at eight different peripheral eccentricities (from 2.5° to 20° in 2.5° steps) in the horizontal direction. Ten saccades on average (but never less than six) were performed for each eccentricity. The central and peripheral fixation times in this paradigm were 900–1000 ms and 500–700 ms. The intertrial interval was varied between 100 and 500 ms and the target amplitude was randomly chosen for each trial. The post-fatigue amplitude tuning had the same fixation and intertrial interval durations as in the saccadic fatigue paradigm, and was performed as an immediate continuation of the latter.

Electrophysiology and microstimulation

Postsurgical MRI was used to facilitate the anatomic localization of the abducens nucleus. The identification of this area was confirmed by extracellular recordings characterized only by the typical burst-tonic discharge patterns during ipsilateral saccades of single isolated units and more often of a noisy multiunit background response, which could be continuously kept on the electrode signal for long tuning distances (up to 2 mm). We therefore exclude the possibility of having recorded from neurons with similar responses in the immediately adjacent nucleus prepositus and medial vestibular nuclei, which additionally harbor neurons with distinctly different discharge patterns that were never encountered. Furthermore, we attempted to map the limits of the abducens nucleus by slightly modifying each time the coordinates of the penetrating electrode inside the recording chamber. An effort was then made to record from the central portion of the abducens nuclei to avoid the units innervating nontwitch muscle fibers lying around its periphery (Büttner-Ennever et al., 2001).

All extracellular action potentials were recorded with commercially available enamel-coated tungsten microelectrodes (Frederick Haer) with 1–10 MΩ nominal impedances that were driven to the brainstem by means of a high precision motor (1 μm movement steps). Single units were isolated on-line with the Multi Spikes Detector software (Alpha Omega Engineering) by detecting and sorting waveforms according to shape. Only well isolated waveforms, clearly distinguishable from the ever present background activity, were considered for further recording.

In the abducens microstimulation manipulations, the stimulus consisted of a sequence of constant current biphasic pulses (each phase lasting 0.2 ms) and was applied for 100 ms at four different frequencies (300 Hz, 400 Hz, 500 Hz and 600 Hz). The current intensity was varied between 25 and 35 μA between different sessions but was held constant throughout each individual session. For the purpose of the stimulation experiments, one monkey was trained to fixate a central fixation point for a random time interval (700–1000 ms) after which the point was extinguished and a gap interval of 500 ms followed before a peripheral target appeared randomly in any of eight peripheral directions. The stimulation was applied 50–200 ms into the gap period in 20–30% of the trials randomly interleaved, at least four times for each of the four stimulus frequencies. A liquid reward was delivered to the monkey each time it successfully made a saccade toward the final peripheral target.

System identification and data analysis

All analyses were performed off-line with custom programs compiled in Matlab (MathWorks). The recorded horizontal eye position signals were sampled at 1 kHz, smoothed with a Savitzky–Golay filter (window = 10 points, polynomial degree = 4) and velocity traces were computed by taking digital derivatives. We used the 20 °/s velocity criterion for detecting saccade onset and end. Saccades with maximal velocity below 100 °/s or with durations longer than 100 ms were discarded. We estimated the instantaneous firing rate of the recorded neurons with a continuous spike density function, generated by convoluting the spike train with a Gaussian function of width σ = 5 ms.

The parameters of the two models in Equations 1 and 2 were evaluated for each recorded neuron using a system identification technique similar to the one previously developed for the analysis of pontine burst neurons (Cullen et al., 1996) and also applied to the discharges of abducens neurons (Sylvestre and Cullen, 1999). Briefly, each of the model formulations in the continuous time domain was first mapped into discrete time using the finite differences transform and assuming an output-error model structure. The parameters of the discrete time formulation were then evaluated using a prediction error method with preprogrammed functions available in the Matlab System Identification Toolbox. The method consists of an iterative numerical search for a parameter set that minimizes the distance between the predicted outputs (according to the parameter set at each iteration) and the actual measured outputs. The iterative update of each parameter is done according to the damped Gauss–Newton method (Ljung, 2002). This was preferred to a linear regression algorithm because of the partially correlated inputs (position, velocity, acceleration) and the dependence of the current on the previous output values in the second-order model. Only the saccadic portions of eye movements and spike density functions (traces between saccade onset and end) were used and data from multiple trials (always N/2 of the total set of N trials (see below); N = 80 on average) were merged for the identification analysis. Because the burst of spikes in abducens units leads saccade onset by a few milliseconds (Fig. 2A), the spike density functions had to be shifted forward in time to be aligned with the movement of the eyes. This lead time was evaluated both subjectively and by the dynamic estimation method (Cullen et al., 1996). The latter consists of repeating the identification for a range of lead times and choosing the one the gives the highest goodness of fit measure. The initial conditions were always taken from the measured data.

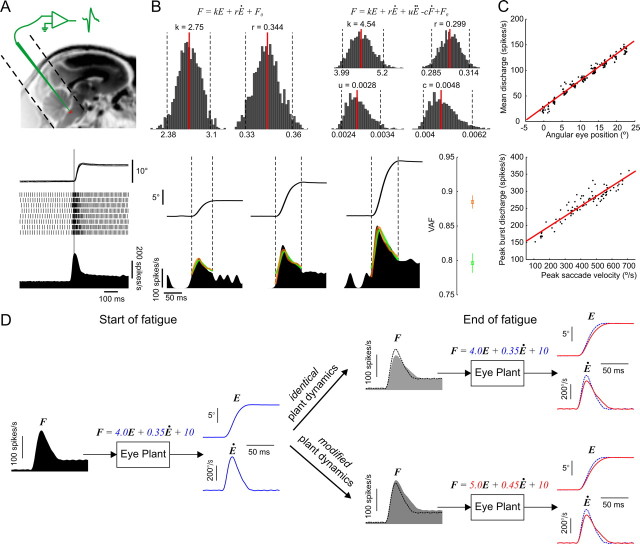
Figure 2.

Characterization of abducens neurons' activity. A, Recording neurons from the abducens nucleus. Top, Approximate anatomical location of the abducens nucleus in an MRI image of a rhesus monkey. Dotted lines reveal the placement and orientation of the recording chamber. Bottom, A typical saccade-related discharge pattern of an abducens neuron. The superimposed eye traces, detected action potentials and the average spike density function are aligned on saccade onset (vertical line). B, Quantitative assessment of abducens discharges. Top, Spiking rates were fitted with the two model formulations and bootstrap histograms were computed for each model parameter. Median values (red lines) and limits of the 95% confidence intervals (dotted lines) are provided. Bottom, Examples of eye traces and spike density functions recorded during three saccades of increasing amplitude. The VAF measure (mean ± SD) was used to evaluate how well the models fit the data. The predicted activity is superimposed on the actual one for the first-order (green) and second-order (orange) model fits. Dotted vertical lines indicate the onset and end of each saccade. C, Position and velocity sensitivity measures. Data from the same example neuron with least-squares linear regression fits (red lines). D, Simulation of eye plant dynamics with the first-order model showing changes in firing rates of abducens motoneurons that would be expected under the muscular and nonmuscular fatigue hypotheses. Left, Simulated motoneuron spike density profile (F) given the pre-fatigue eye position (E) and velocity (Ė) traces (in blue) with the indicated model parameters. Right, Same simulation with a slower and longer post-fatigue eye saccade (in red) in the two cases where the eye plant parameters are either modified or remain unchanged. The simulated pre-fatigue data (dotted traces) are superimposed for comparison purposes. With identical plant dynamics, the expected changes in firing rates parallel those in eye saccade kinematics, whereas in the case of modified dynamics they do not. In the latter case, the neuron's sensitivity to eye position and velocity (as measured in C) would be altered, and attempting to predict the firing rate with the pre-fatigue eye plant dynamics (as in B) would underestimate the actual rate.

A bootstrap analysis provided confidence intervals for each evaluated model parameter (Fig. 2B) and allowed a statistical comparison between the pre-fatigue and post-fatigue estimates for individual neurons (Fig. 3). It consisted of repeating the system identification for each neuron 1300 times on different subsets of the data each time. The different subsets were formed by taking at random, without replacement, N/2 trials from the total set of N trials (for N = 80 trials, 10²³ such combinations are possible). The models were then validated at each repetition on the other, independent, N/2 half of the trials by computing the variance accounted for (VAF). The VAF is calculated as {1 − [var(F_est − F_m)/var(F_m)]} where F_m is the measured and F_est the estimated firing rate, and provides a normalized measure of how much of the variability in a unit's discharge is explained by the model.

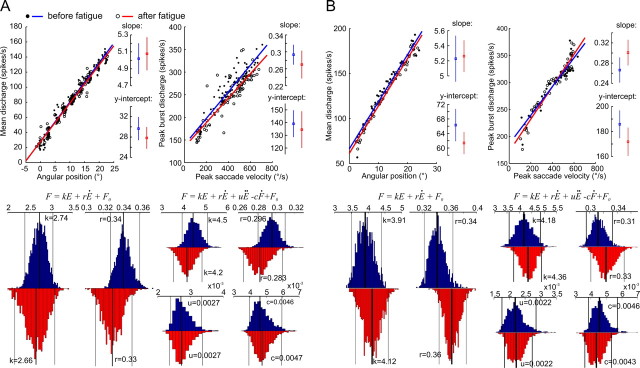
Figure 3.

Eye plant dynamics are not altered by saccadic fatigue. A, Comparison of pre-fatigue and post-fatigue discharge properties of a single abducens neuron. Top, Position and velocity sensitivity data with their least-squares linear regression fits before and after the fatigue experiment. Insets provide the slopes and y-intercepts (with their 95% confidence intervals) of the regression lines. Bottom, Bootstrap distributions of the first- and second-order model parameters evaluated before (blue) and after (red) fatigue. On each histogram, the median values (thick lines) with their 95% confidence intervals (thin lines) are provided. B, Comparison of pre-fatigue and post-fatigue saccade-related properties of a population response of 62 neurons. Same measures as in A. The population activity was computed by dividing the range of saccade amplitudes into equally sized bins of 0.5°. Eye position traces and the associated spike density functions were then assigned to their corresponding bins and average saccades and firing rates were then computed across all trials and all neurons for each bin.

The population activity of all neurons (Fig. 3B) was computed by dividing the range of saccade amplitudes into equally sized bins of 0.5°. Eye position traces and the associated spike density functions were then assigned to their corresponding bins and average saccades and firing rates were then computed across all trials and all neurons for each bin.

The duration versus amplitude main sequence was fit with a straight line and that of the peak velocity versus amplitude with an exponential function. The direction of change predicted by the main sequences during fatigue (Fig. 1C, blue lines) was then evaluated as the tangent to these two fitting curves evaluated at the relevant data points. The peak burst discharge and the mean discharge during fixation were evaluated respectively as the spike density function (after being shifted by its lead time) maximum value between saccade start and end, and its mean value in an interval of 400 ms, 50 ms after/before saccade end/start.

We performed paired or unpaired Student's t tests whenever we wished to evaluate whether two data samples came from distributions with equal means. Normality of data was tested with the Kolmogorov–Smirnov test. We deemed the difference to be statistically significant when the probability (p value) of having distributions with equal means did not surpass the 5% level.

Results

Fatiguing the oculomotor system

We trained three rhesus monkeys to execute large numbers of visually guided eye saccades from a central fixation point toward a peripheral target at a very fast rate (Fig. 1A). Each experiment consisted of 500 saccades on average, performed at a mean rate of 1 saccade every 2 s. Changes in saccade kinematics are readily observed throughout the course of such an experiment; peak velocity decreases while accuracy is maintained because duration increases in a fully compensatory manner (Fig. 1B).

Eye saccades are otherwise considered to be very stereotypical movements. Their velocity traces typically have bell-shaped profiles and a precise nonlinear association exists between peak saccade velocity and amplitude on the one hand, and a linear relation between saccade duration and amplitude on the other; referred to as the “saccadic main sequence.” The main sequence dictates that higher amplitude saccades become increasingly both longer and faster. Our results show that fast repetitive eye movements largely skew the velocity profiles (Fig. 1B) and cause the saccade kinematics to move away from their main sequence (Fig. 1C). Explicitly put, the slower saccades caused by the fatigue should normally be indicative of a neural command leading to smaller amplitude movements, yet a late extension in movement duration brings the saccade to the intended target and keeps amplitude constant. Both saccade duration and velocity change, while the amplitude remains constant; the fatigue experiment therefore disrupts the normal mode of operation of saccadic eye movements. The increase in saccade duration seems furthermore to be reflective of a compensatory cerebellum-dependent mechanism, since it is only present in healthy subjects, whereas it does not accompany the drop in peak velocity in cerebellar patients (Golla et al., 2008; Xu-Wilson et al., 2009) and monkeys with cerebellar lesions (Barash et al., 1999) and hence does not prevent the expected hypometric saccades in those cases. Therefore, the preservation of accuracy despite a breakdown of ordinary motor behavior during saccadic fatigue is clearly indicative of an adaptive neural process.

We look next at whether the compensation observed during saccadic fatigue falls into the traditional definition of motor learning alluded to in the introduction. In other words, does the cerebellum-dependent mechanism adapt to changes in the dynamic properties of the peripheral eye plant (i.e., muscular fatigue) or to some other physiological changes in the oculomotor system?

Identification of eye plant dynamics

The abducens nucleus located in the pontomedullary brainstem just beneath the floor of the fourth ventricle (Fig. 2A) harbors mainly two functional cell groups; motor neurons and internuclear neurons. The axons of motor neurons give rise to the sixth cranial nerve and innervate the lateral rectus muscle of the eye. The internuclear neurons project axons to the subgroup of motor units in the contralateral oculomotor nucleus which directly innervate the medial rectus muscle of the other eye. Therefore, a burst of spikes in neurons of the abducens nucleus is translated into muscle force and then into eye movement in a fairly direct way. It has the effect of rotating the ipsilateral eye temporally and the contralateral eye nasally, effectively producing a horizontal ipsiversive binocular eye movement.

A typical abducens neuron discharge during ipsiversive saccades displays a strong phasic burst of spikes during the saccade, followed by a constant tonic firing rate that lasts throughout peripheral fixation (Fig. 2A). The phasic burst accelerates the eyes during the saccadic component of movement against the viscous forces acting on the eye globe, and the tonic discharge holds the eyes fixed at the peripheral position by counteracting the elastic forces that pull the eye back toward midline. This typical phasic-tonic pattern of discharge reflects the dynamic properties of the “eye plant” (production of muscle force and the action of that force on the eye globe and supporting orbital tissues) that need to be overcome to produce the desired saccadic eye movement (Robinson, 1964, 1970). The eye plant dynamics thus seem to be dominated by its viscoelastic properties and can be modeled as a first-order system (Eq. 1) between the firing rate of abducens neurons (F) at input and instantaneous eye position (E) at output (k, elasticity constant, r, viscosity constant, F₀, bias term).

In a notable study evaluating a number of different eye plant model formulations (Sylvestre and Cullen, 1999), the first-order model in Equation 1 was indeed shown to be an adequate descriptor of motor neuron discharges during saccades. A second-order formulation (Eq. 2) including an acceleration term (uË) and a slide term (−cḞ), was however shown to significantly improve the quality of fit and best account for the dynamics between firing rate and the saccadic eye movement.

Before the fatigue experiment, we recorded single neurons in the abducens nucleus while the monkeys made saccades to targets of varying amplitudes (80 saccades on average between 2.5° and 20°). We used these data to run a system identification analysis of the two model formulations in Equations 1 and 2, obtained bootstrap confidence intervals of each evaluated parameter and validated the identified models on an independent set of data (see Materials and Methods for details). The identification and validation results are provided for one example neuron in Figure 2B. The mean (±SD) percentage of variance in the firing rates of the recorded neurons that could be accounted for (VAF) by the first- and second-order model fits were 0.63 (±0.1) and 0.67 (±0.1) respectively. From the same data, we also computed the traditional velocity and position sensitivity tuning curves (relationship between peak saccade velocity and peak burst discharge, and between eye position and firing rate during fixation) for each recorded neuron (Fig. 2C). The latter provides an additional, more qualitative, description of the relationship between abducens neuron discharges and eye saccade metrics.

We then continuously kept recording the same neurons throughout the fatigue experiment and repeated the above task and identification analysis immediately after. The muscular fatigue hypothesis predicts that after the fatigue experiment, the system identification should yield significantly larger parameters of eye plant dynamics as well as increased slopes of the position and velocity sensitivity curves compared with before fatigue. The model simulations in Figure 2D describe the expected changes in the firing rates of abducens motoneurons under the muscular and nonmuscular fatigue hypotheses. We recorded a total of 62 neurons from three monkeys (31 from monkey R, 9 from monkey N and 22 from monkey H) and present the obtained results in the following section.

Eye plant dynamics are not altered by fatigue

The single example in Figure 3A illustrates the consistent finding that the dynamics of the eye plant, evaluated from single neuron data by the traditional first-order and a more complex second-order model, did not show any significant changes as a result of fatigue. The corresponding pairs of model parameters, evaluated with the pre-fatigue and post-fatigue data separately, systematically showed an overlap between their 95% confidence intervals. A distribution of each parameter evaluated from all 62 different neurons, showed a marginally significant increase after fatigue in the mean value of the r parameter in the first-order model, while the difference remained highly insignificant for the distributions of all other parameters (Table 1). Moreover, the neurons' sensitivities to peak saccade velocity and static eye position did not change after the fatigue experiment, as revealed by the single cell example (Fig. 3A) and a paired comparison between the distributions of the sensitivity curves' slopes and y-intercepts of all neurons evaluated before and after fatigue (Table 1).

Table 1.

The parameters of the evaluated models as well as the position and velocity sensitivity curves did not change as a result of fatigue for the population of abducens neurons

	Parameter	Before fatigue	After fatigue	Paired t test (p value)
First-order model	k	5.3 (7.6, 3.9)	5.6 (7.6, 3.5)	0.47
	r	0.35 (0.43, 0.3)	0.37 (0.45, 0.3)	0.035
VAF (mean ± SD)		0.63 ± 0.1	0.62 ± 0.1
Second-order model	k	5.8 (8.2, 2.6)	5.6 (9.4, 2.9)	0.49
	r	0.52 (0.82, 0.27)	0.5 (0.79, 0.28)	0.63
	u	0.014 (0.02, 0.009)	0.015 (0.021, 0.011)	0.62
	c	0.037 (0.043, 0.03)	0.036 (0.046, 0.027)	0.92
VAF (mean ± SD)		0.67 ± 0.1	0.67 ± 0.1
Position sensitivity	slope	5.61 ± 2	5.61 ± 2.2	0.99
	y-intercept	53.3 ± 43.6	52.7 ± 39.4	0.78
Velocity sensitivity	slope	0.32 ± 0.16	0.33 ± 0.16	0.41
	y-intercept	194.6 ± 84.3	191 ± 90.6	0.49

Values followed by parenthetical values are medians (upper/lower quartile). Values followed by ± values are means ± SD.

Extraocular muscles however do not contract in response to a discharge from a single abducens neuron but from a population of many neurons. It is then conceivable that changes in the properties of eye plant dynamics due to muscular fatigue appear in the responses of single neurons in absolute terms only but never reach significant levels. We therefore computed a population response where each average saccadic eye movement was now associated with an average discharge of as many as 62 abducens neurons (see Materials and Methods for details). The identification of eye plant dynamics was then repeated with the population response computed with both the pre-fatigue and post-fatigue sets of data. A comparison of the 95% confidence intervals of the system parameter estimates still revealed large overlaps for all parameters between the two independently evaluated sets (Fig. 3B). The velocity and position sensitivity curves based on these average discharges were also not significantly modified by the fatigue sessions.

We next looked at whether any changes of the oculomotor periphery became apparent during the course of the saccadic fatigue experiment itself. As previously noted, the fast repetitive series of eye saccades brought about significant changes in movement kinematics. For all 62 fatigue sessions during which individual abducens units were being recorded, the monkeys produced the typical pattern of reduced peak saccade velocity and increased duration, all while the amplitude of saccades remained constant. Accordingly, each fatigue experiment moved the relationship between saccade amplitude and each of the two movement metrics (peak velocity and duration) away from their characteristic pre-fatigue main sequences (Fig. 1C). The relationship between the firing rates of abducens neurons and these altered saccade kinematics however did not change. First, the drop in peak velocity was accompanied by a decreased peak discharge as predicted by the neuron's velocity sensitivity curve (Fig. 4A). When normalized by their corresponding velocity sensitivity regression fits evaluated with the pre-fatigue data, the average peak discharge values plotted against the average peak velocity, at the start and end of the fatigue sessions, fell along the normalized line of unity slope passing through the origin (Fig. 4A). The lines connecting the average data points of the first and last 10 trials of the fatigue experiment had a mean (±SD) slope of 0.91 (±0.59) which was not significantly different from one (t test, p = 0.25). Second, the previously computed dynamic model fits for each neuron could fit equally well both the abducens discharges at the start of fatigue, and those that eventually give rise to the saccades with slower kinematics (Fig. 4B). Had the physical dynamics of the eye plant progressively changed during the fatigue experiments, one would expect the identified models to ever more underestimate the actual motor neuron discharges, thus increase the residual variance (variance of the difference between actual and predicted signals) and lead to significantly lower VAF values. No significant differences were however found between the distributions of mean VAF values at the start and end of fatigue for both the first- and second-order models (t test, p = 0.13 and p = 0.44 respectively) for the entire population of 62 neurons.

Figure 4.

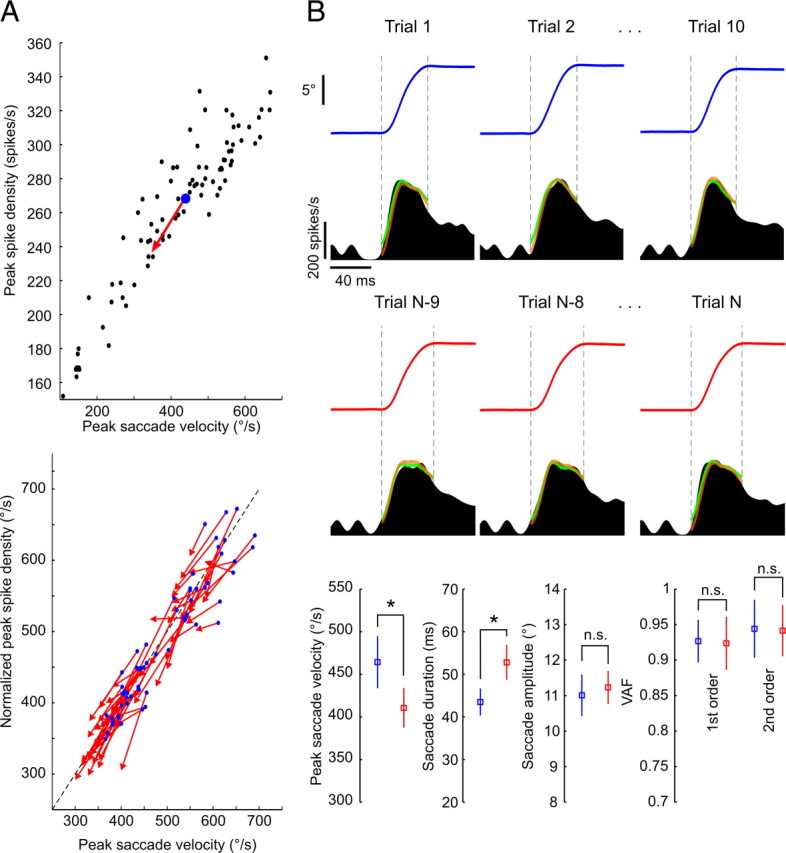
No changes in eye plant dynamics occur during the course of fatigue. A, Progressively slower eye saccades are accompanied by parallel decreases in peak discharges of abducens neurons. Top, Average data points at fatigue start (blue dots) and end (red arrowheads) with pre-fatigue peak discharges plotted against saccade peak velocity (black dots) for one example neuron. Bottom, Same average data points for all 62 neurons normalized to the unity-slope line (dotted line) with their respective pre-fatigue velocity sensitivity regression fits [Y_n = (Y − b)/a, where Y_n is the normalized version of the peak spike density measure Y, and a and b are, respectively, the slope and y-intercept of the velocity sensitivity regression line]. B, The evaluated models predicted the activity of abducens neurons equally well throughout fatigue. Top, Eye traces and corresponding abducens neuron spike density functions of an example neuron, with superimposed first (green)- and second (orange)-order model fits, for three trials taken from the start (blue) and end (red) of a fatigue experiment. Bottom, Between the start (blue) and end (red) of the fatigue, mean (±SD) values of peak saccade velocity and duration showed significant changes (*) (t tests, p = 0.0004 and p = 0.00003, respectively), whereas those of saccade amplitude (p = 0.36) and the VAF by the first (p = 0.85)- and second (p = 0.88)-order model fits did not (n.s.).

Our results indicate that the observed changes in eye saccade kinematics were accompanied by parallel changes in the discharge rates of abducens neurons; the dynamic relationship between the two was sustained. The physiological changes that disrupt habitual saccadic performance therefore originate upstream of the abducens nucleus, away from the oculomotor periphery.

Confirming the absence of muscular fatigue by microstimulation

As an additional control experiment we electrically stimulated the abducens nucleus before and after the long repetitive sequence of saccades. We applied a stimulating current of constant intensity and duration at four different frequencies through the electrode's tip located in the abducens nucleus while the monkey held its gaze fixed in the straight-ahead position (see Materials and Methods for details). The amplitudes and peak velocities of the ipsilaterally evoked saccades were then compared between three different stimulation periods; before the fatigue experiment, immediately after, and following a rest period which allowed voluntary saccades to regain their pre-fatigue velocity and duration levels. If the fatigue sessions caused a weakening of eye muscles, then the current applied at the same site with identical parameters should evoke significantly slower and/or lower amplitude saccades compared with the before fatigue and after rest periods.

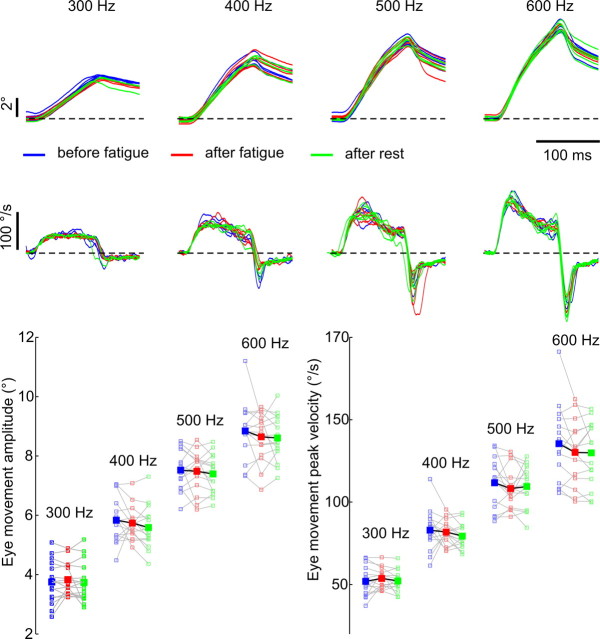
We repeated the above described sequence of stimulation experiments during 15 sessions in one monkey, each time at a different site within the abducens nucleus. While increasing the stimulation frequency consistently evoked faster and larger eye movements, no discernable differences could be observed between the three different stimulation periods (Fig. 5). A two-way ANOVA analysis (the two factors being stimulus frequency and stimulation period) confirmed that across the 15 individual sessions, there was a significant main effect of stimulus frequency on peak velocities (p = 0) and amplitudes (p = 0) of the evoked movements. The null hypothesis that either saccade amplitudes or peak velocities were equal for the three stimulation periods could however not be rejected at a significant level (p = 0.5 and p = 0.52 respectively). There were also no significant interactions between the two factors for either the amplitude (p = 0.99) or the peak velocity (p = 0.96) measures. It therefore seems that the rectus muscles of the eye respond without change to microstimulation of their motor neurons following a fatiguing eye movement task.

Figure 5.

Microstimulation of the abducens nucleus confirms the absence of muscular fatigue. Top, Eye position (first row) and velocity (second row) traces of the stimulation-evoked eye movements at four different stimulus frequencies were highly similar before (blue) and after (red) a fatigue session, and after a subsequent rest period (green). The traces are aligned on saccade onset. Bottom, Mean amplitudes and peak velocities of the stimulated saccades for all 15 experimental sessions (small open squares) together with their average values (large filled squares).

Discussion

In traditional views of motor adaptation, the neural control of movement is continuously adapted to compensate for any changes in the physical properties of the body or the external environment (due to age, injury, muscular fatigue, carrying weighty objects etc.). The first descriptions of adaptive changes in eye movement control adhered to this view; the observed adaptive processes were implied to compensate for alterations in the oculomotor plant (Kommerell et al., 1976; Abel et al., 1978; Optican and Robinson, 1980; Optican and Miles, 1985; Grossberg, 1986; Scudder and McGee, 2003) and were moreover shown to depend on the cerebellum (Optican and Robinson, 1980; Scudder and McGee, 2003). In studies of arm displacements under external force fields, the ability to learn to move accurately with novel limb dynamics also depends on an intact cerebellum (Smith and Shadmehr, 2005). The prevalent theory suggests that the nervous system adapts to the external perturbation by computing/updating an internal model of either inverse (Shadmehr and Mussa-Ivaldi, 1994; Wolpert and Miall, 1996) or forward dynamics (Wolpert and Miall, 1996) of the actual physical plant. The progressive regulation of eye saccade kinematics during the fatigue experiment that we described is a characteristic example of a cerebellum-dependent motor adaptation that preserves accurate movements (Barash et al., 1999; Golla et al., 2008; Xu-Wilson et al., 2009). A number of early (Brozek, 1949; Bahill and Stark, 1975; Schmidt et al., 1979; Fuchs and Binder, 1983) and more recent (Straube et al., 1997; Chen-Harris et al., 2008; Xu-Wilson et al., 2009) investigations have already speculated that when subjects were engaged in repetitive eye movements, cognitive processes such as mental tiredness might be responsible for a diminished oculomotor performance. By a direct electrophysiological identification of eye plant dynamics, we here provide the first conclusive evidence that the oculomotor periphery remains intact during an exhausting eye movement task. Consistent with in vitro studies suggesting that preparations of extraocular muscles of rabbit (Frueh et al., 1994) and mouse (Kaminski and Richmonds, 2002) are particularly fatigue resistant, our results show that even in natural behaviors, primate extraocular muscles do not display any fatigue characteristics analogous to those of skeletal muscles. More remarkable is the implication that saccadic fatigue must be of premotor origin, reflecting altered saccade commands due to modified cognitive modulation or to neuronal adaptation; factors which collectively tend to deteriorate the precision and reliability of the conversion of the initial saccade plan into the actual movement. This deterioration due to “non-motor” noise is prevented by a compensatory mechanism in the cerebellum, which does not subscribe to the above description of classical motor adaptation.

The origin of fatigued saccades is necessarily a corruption of the neural encoding of the planned movement. For instance, the reliability by which the desired displacement is eventually encoded in the superficial and intermediate layers of the superior colliculus (SC) (Schiller et al., 1980; Hanes and Wurtz, 2001) might be gradually diminished during fatigue. This could be caused by either a neuronal habituation to the consequences of the same repeating visual stimulus or by modulation from cortical areas reflecting a state of “mental tiredness” (reduced alertness, motivation, attention etc.) of for instance neurons in the SC which have been found to reflect arousal or attentive states (Sparks and Mays, 1980). As a result, the SC deep layers would provide a command to the saccade generator in the pons (Raybourn and Keller, 1977; Keller et al., 2000) to move the eyes with inappropriately reduced amplitude, naturally associated with a lower velocity than the initial nonfatigued saccades. The oculomotor cerebellum, which integrates eye movement information from all key cortical and subcortical areas (Thielert and Thier, 1993), then actively increases saccade duration and prevents this inaccuracy by prolonging the saccade-related discharges via its notable projections to the pontine brainstem area (Noda et al., 1990). This plausible hypothesis makes testable predictions which could and should be verified by further electrophysiology and modeling studies of the oculomotor system. What remains certain however is that the typical pattern of cerebellum-dependent changes in saccade kinematics during fatigue is not attributable to a modification in the dynamic properties of the eye plant. In agreement with more recent models of the saccadic system (Quaia et al., 1999; Glasauer, 2003), this observation suggests that instead of solely adapting for long-term alterations in the oculomotor periphery (e.g., weakening of eye muscles), the cerebellum continuously monitors the progress of each movement and passively compensates for sources of inaccuracy regardless of their origin. Alternatively, the cerebellum could actively discriminate between the different potential errors in movement accuracy, estimate the sources of these errors, and adapt to each independently.