Aberrant Frontal and Temporal Complex Network Structure in Schizophrenia: A Graph Theoretical Analysis

Abstract

Brain regions are not independent. They are interconnected by white matter tracts, together forming one integrative complex network. The topology of this network is crucial for efficient information integration between brain regions. Here, we demonstrate that schizophrenia involves an aberrant topology of the structural infrastructure of the brain network. Using graph theoretical analysis, complex structural brain networks of 40 schizophrenia patients and 40 human healthy controls were examined. Diffusion tensor imaging was used to reconstruct the white matter connections of the brain network, with the strength of the connections defined as the level of myelination of the tracts as measured through means of magnetization transfer ratio magnetic resonance imaging. Patients displayed a preserved overall small-world network organization, but focusing on specific brain regions and their capacity to communicate with other regions of the brain revealed significantly longer node-specific path lengths (higher L) of frontal and temporal regions, especially of bilateral inferior/superior frontal cortex and temporal pole regions. These findings suggest that schizophrenia impacts global network connectivity of frontal and temporal brain regions. Furthermore, frontal hubs of patients showed a significant reduction of betweenness centrality, suggesting a less central hub role of these regions in the overall network structure. Together, our findings suggest that schizophrenia patients have a less strongly globally integrated structural brain network with a reduced central role for key frontal hubs, resulting in a limited structural capacity to integrate information across brain regions.

Introduction

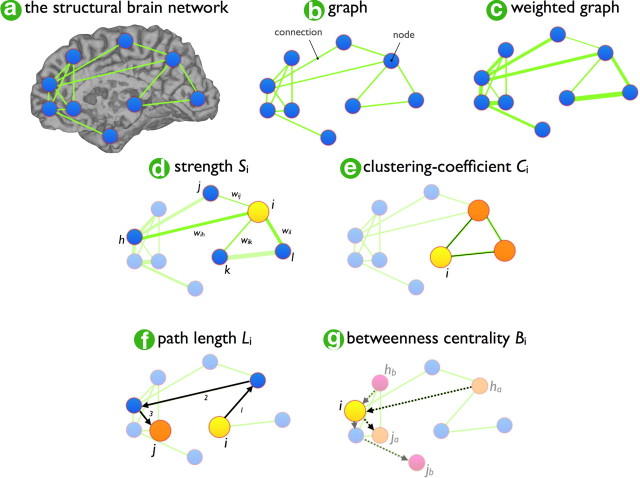
The human brain is a complex network of interacting regions. Recent pioneering studies have probed the organization of the brain network using “graph theory” (Sporns and Zwi, 2004; Achard et al., 2006; Hagmann et al., 2007; van den Heuvel et al., 2008a; Stam et al., 2009), a mathematical framework in which the brain is represented as a network of nodes, reflecting the different brain regions, and connections between the nodes, representing white matter tracts (for review on brain networks, see Reijneveld et al., 2007, Bullmore and Sporns, 2009); Figure 1 shows the graph measures used in this paper. These studies showed that the human brain network is organized according to a highly efficient small-world topology (Watts and Strogatz, 1998) combining a high level of segregation with a high level of global efficiency (Bullmore and Sporns, 2009); it is an organization critical for effective integration of information between brain regions (Kaiser and Hilgetag, 2006) and cognitive fitness (Bassett et al., 2009; Li et al., 2009; van den Heuvel et al., 2009a).

Figure 1.

The brain network, a graph, and graph organizational measurements. Each individual structural brain network was represented as a graph (a). A graph is a mathematical description of a network (b), consisting of a collection of nodes (blue dots) and a collection of connections between the nodes (green lines). A weighted graph (c) is a network in which the strength of the connections is taken into account, expressing a tighter connection between two nodes as one with a higher weight. From a graph, a number of key organizational characteristics can be computed describing the local and global organization of the connections and the overall structure of the network. The connectivity strength S_i of a graph (d) is measured as the sum of the weights of each node i and reflects how strong node i is connected to the rest of the network. The node-specific clustering coefficient C_i (e) is computed as the weight intensities of the local subnetwork G_i of node i in ratio of the total number of possible connections and provides information about how strongly node i is connected locally in the graph. Furthermore, the node-specific travel distance L_i (f) reflects the average distance from node i to every other node in the network. L_i is computed as the shortest travel distance between node i and j in the network, averaged over all nodes j, i.e., all connections that have to be crossed to travel from node i to node j in the network. In a weighted graph, the shortest distance between node i and node j is typically defined as the sum of the inverse of the weights of the connections that have to be passed to travel from node i to node j. The betweenness centrality B_i of node i (g) is computed as the number of shortest routes between two nodes h and j in the graph that pass through node i, expressing how central node i is located in the network. Finally, measures of overall organization can be computed by averaging the node-specific values S_i, C_i, and L_i, over all nodes i in the network.

Schizophrenia, a psychiatric disorder characterized by hallucinations, delusions, loss of initiative, and cognitive impairments, has long been suggested to be related to a reduced capacity to integrate information between the different regions of the brain (Kraepelin, 1919; Friston, 1998). Magnetic resonance imaging (MRI) studies have shown morphological abnormalities of frontal and temporal gray matter structures in patients (Wright et al., 2000; Hulshoff Pol and Kahn, 2008; Arnone et al., 2009; Ellison-Wright and Bullmore, 2010). Furthermore, studies using diffusion tensor imaging (DTI), a technique that enables the examination of white matter tracts of the brain, have revealed reduced white matter microstructural integrity of specific frontal and temporal white matter structures (Kanaan et al., 2005; Kubicki et al., 2007; Ellison-Wright and Bullmore, 2009; Voineskos et al., 2010). It remains unknown, however, whether the overall brain network infrastructure is affected in schizophrenia. Here, we studied the complex brain networks of 40 schizophrenia patients and 40 matched healthy controls constructed from DTI data. Within a weighted graph approach, one can incorporate additional information on the strength of the connections on a continuous scale, enabling a more detailed examination of the organization of a network. Fractional anisotropy (FA) values, subtracted from the DTI measurements, provide information on the general microstructural organization of white matter, incorporating information on fiber orientation and fiber structure. However, a more intuitive and direct measure for the connectivity strength of white matter tracts is their level of myelination, as myelin is known to play a crucial role in facilitating fast information transport along axonal bundles (Bozzali and Wrabetz, 2004). We therefore combined DTI with magnetic transfer imaging (MTR), a technique that is sensitive to the level of macromolecules (including myelin) present in brain tissue. Key graph organizational properties of the individual MTR-weighted brain networks were computed and compared between the patient and healthy control groups. As control conditions, brain networks were also examined in an FA-weighted fashion and an unweighted fashion to provide additional information on the underlying fiber connectivity structure of the brain network.

Materials and Methods

Subjects

A group of 40 patients with schizophrenia and 40 healthy participants participated in this study (matched for age, gender, handedness, and parental education) (Mandl et al., 2008), after obtaining written informed consent as approved by the Medical Ethics Committee for Research in Humans (METC) of the University Medical Center Utrecht, Utrecht, The Netherlands. The study was performed according to the directives of the Declaration of Helsinki (amendment of Edinburgh, 2000). Healthy participants were recruited by means of local newspaper advertisements. Healthy controls had no first-degree relative with any mental illness or a second-degree family member with a psychotic disorder. Patients were diagnosed in the presence of a psychiatrist with the Comprehensive Assessment of Symptoms and History (CASH) (Andreasen et al., 1992), leading to a Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition (American Psychiatric Association, 1994) diagnosis for schizophrenia. “Age of onset of illness” was defined as the age of which the participants started to experience psychotic symptoms for the first time, as obtained by the CASH. At time of scanning, all patients were receiving typical or atypical antipsychotic medication. To assess drug use of patients and healthy controls, the Composite International Diagnostic Interview (CIDI) (Robins et al., 1988) was used. Four patients and one healthy participant met criteria for drug abuse and one patient met criteria for drug dependency, including the use of cannabis (in all six subjects) and others (three subjects). For demographics, see Table 1.

Table 1.

Demographic data of the group of schizophrenia patients and group of matched healthy participants

	Schizophrenia patients	Matched healthy participants
N	40	40
Male/female	30/10	29/11
Age: range, mean (SD) (years)	20–41, 26.8 (5.8)	18–45, 28.0 (7.7)
Handedness: right/left/ambidextrous	37/3/0	35/5/0
Level of education: mean (SD) (years)	10.4 (2.5)♠	13.8 (2.2)
Parental level of education mean (SD) (years)	13.6 (2.7)	13.6 (3.2)
Age at first symptoms: range, mean (SD) (years)	16.9–38.4, 27.7 (5.6)
Duration of illness: mean (SD) (months)	25.1 (17.4)
Medication at time of the scan♦
Typical antipsychotics: N, median (range) haldol equivalent	40, 3.5 (4.7)
Atypical antipsychotics: N, median (range) haldol equivalent	29, 7.1 (12)
Cumulative medication♣
Typical antipsychotics: N, mean	1,106.5
Atypical antipsychotics: N, mean (SD)	22, 36208.4 (6830.9)
Typical and atypical antipsychotics N, mean (SD)	13, 10956.2 (9640.3)
PANSS positive symptoms: mean (SD)	15.7 (5.6)
PANSS negative symptoms: mean (SD)	15.6 (5.7)
PANSS general symptoms: mean (SD)	31.0 (7.2)
PANSS total score: mean (SD)	62.3 (15.8)
PANSS general symptoms: mean (SD)	14.4 (7.9)

See supplemental materials for a detailed description of symbols. PANSS, Positive and negative symptom scale.

Image acquisition and processing

Acquisition

All participants underwent a 35 min scanning session in which well validated DTI, MTR, and anatomical T1 images were acquired. MRI scans were made on a 1.5 tesla Philips Intera clinical scanner at the University Medical Center Utrecht. For each subject, first a three-dimensional anatomical T1 image was acquired for anatomical reference (acquisition: spoiled gradient T1 weighted, coronal, echo time (TE) = 4.6 ms, repetition time (TR) = 30 ms, flip angle = 30, 160–180 contiguous slices covering whole brain, 1 × 1 × 1.2 mm³ voxels, SENSE: 1.5/1.5). After the T1 image, two sets of DTI images were acquired, each consisting of 32 diffusion-weighted volumes with different noncollinear diffusion directions, all with a b-factor = 1000 s/mm² and eight diffusion-unweighted volumes with a b-factor = 0 s/mm² (acquisition: TE = 88 ms, TR = 9822 ms, SENSE: 2.5; flip angle = 90, 60 slices of 2.5 mm voxels, covering whole brain). Third, directly after acquiring the two DTI sets, an MTR scan was acquired to get information on the level of myelination of white matter consisting of two images (acquisition: TE = 3.7 ms, TR = 37.5, SENSE: 2.5, flip angle = 8, 60 slices of 2.5 mm voxels, covering whole brain), with the second MTR image acquired with an additional off-resonance prepulse (three-lobe sync-shaped, frequency offset 1100 Hz, 620°), designed to excite macromolecules, including myelin (Wolff and Balaban, 1994; van Buchem, 1999).

Image preprocessing

DTI, MTR, and T1 images were preprocessed as follows.

DTI preprocessing.

First, the two DTI sets were realigned and corrected for common gradient-induced distortions (Andersson and Skare, 2002). Second, within each voxel the diffusion profile was fitted a tensor using the two sets of 32 weighted images and the average B = 0 image. From the resulting tensor, the main diffusion direction in each voxel was selected as the principal eigenvector resulting from the eigenvalue decomposition of the fitted tensor, marking the preferred diffusion direction in each voxel. For each voxel the FA, indicating the level of anisotropic diffusion, was computed (Beaulieu and Allen, 1994; Basser and Pierpaoli, 1996).

MTR preprocessing.

For each dataset, the MTR images were realigned to correct for possible small head movements using mutual information. For each voxel, the MTR value, marking the level of macromolecules present was computed as the percentage of the signal lost due to the application of the prepulse by computing the normalized difference between the prepulsed volume I_mt (volume with prepulse) and the nonprepulsed volume I₀ (first acquired volume without prepulse). Formally:

Registration

For each subject individually, the anatomical reference T1 image was realigned to the B = 0 image (rigid transformations using mutual information), and the MTR images were realigned (rigid) with the DTI images, taking the B = 0 images as a target and the I_o MTR image. To enable group comparison, the anatomical images were normalized to standard space, using nonlinear transformation of the subject's T1 image to the standard MNI305 space (Collins et al., 1994).

Fiber tract reconstruction

Next, for each individual dataset, white matter tracts of the brain network were reconstructed using the fiber assignment by continuous tracking (FACT) algorithm (Mori and van Zijl, 2002). This enabled the reconstruction of each white matter tract in the brain, often referred to as fibers or tracts (Van den Heuvel et al., 2008b, 2009b). Fibers were reconstructed by starting eight seeds in each voxel and following the main diffusion direction of each voxel (as selected as the principal eigenvector) until the fiber tract entered a voxel with a low level of diffusion preference (FA < 0.1) or made an unexpected high angular turn (angle > 45 degrees), or when the fiber followed a highly different path from the diffusion profiles of its surrounding voxels (angle > 45 degrees). Within a graph theoretical setting, one can incorporate information on the strength (referred to as weight) of the connections, defining the strength of a structural connection between brain regions on a continuous scale. An intuitive measure for the strength of a white matter connection is its level of myelination, as measured by MTR, as higher levels of myelination have been linked to higher transportation speeds along the axonal connections (Wolff and Balaban, 1994; van Buchem, 1999). Therefore, the strength of each reconstructed fiber was labeled with its corresponding MTR value by assigning each point of the fiber tract with the MTR value of the voxels along the three-dimensional (3D) path of the fiber (Mandl et al., 2008, 2010; van den Heuvel et al., 2008b, 2009b). Finally, to enable examination of these fibers on a group level, individual fibers were normalized to standard space using the normalization parameters of the individual T1 image to the normalized T1 MNI305 space (Mandl et al., 2008).

Graph theory: construction of structural brain networks

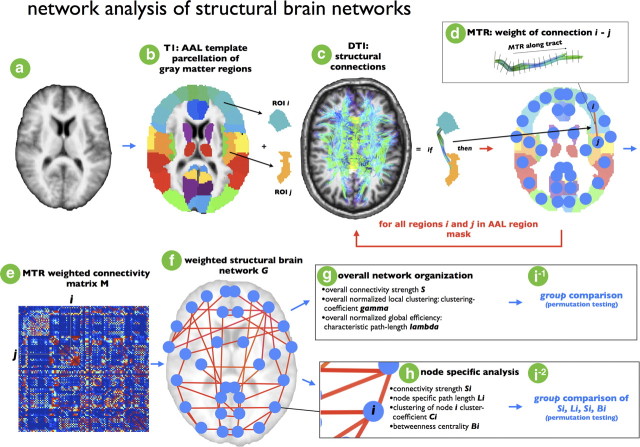
Using the collection of all reconstructed DTI fiber tracts, a structural brain network was constructed for each individual dataset by using a validated graph theoretical framework (Hagmann et al., 2007; van den Heuvel et al., 2008a, 2009a; Bullmore and Sporns, 2009). This procedure included the following steps, illustrated one-by-one in Figure 2a–i. A graph G = (V,E) consists of a collection of nodes V and a collection of connections E, determining the level of connectivity between the nodes. First, brain regions (i.e., the nodes of the graph G) were defined on basis of the T1 image (Fig. 2a) and the automatic anatomical label (AAL) template (Fig. 2b), an anatomical label map that corresponds to the normalized T1 anatomical template brain (Collins et al., 1994; Tzourio-Mazoyer et al., 2002), parcellating the brain into 108 unique regions (Fig. 2b). Next, each individual DTI connectivity dataset was represented as a graph G, with the brain regions defined as the nodes of the graph and the edges between nodes i and j (i.e., brain region i and region j) reflecting a reconstructed white matter tract. For each pair of two regions in the AAL template, it was determined whether the two regions were connected by a white matter pathway by selecting the fibers that touched both region i and j in the total collection of reconstructed tracts, if any (Van den Heuvel et al., 2008b, 2009b) (Fig. 2c,d). This procedure was repeated for all regions i and j in the template map (Fig. 2c,d, red loop). Next, for each connection in G (Fig. 2d) the strength of a connection was taken as the average level of MTR (believed to reflect the level of myelination of the tract) of the selected fiber tracts (Fig. 2d) and filled in the weighted connectivity matrix M (Fig. 2e). This resulted in a matrix representation of the undirected weighted brain network, with weighted connections between brain regions that are structurally connected and the strength of the connections expressed by the level of MTR (Fig. 2f).

Figure 2.

Schematic overview of formation of individual structural brain networks. For each individual dataset, a structural brain network was constructed. First, for each dataset (a) from the AAL template consisting of 108 unique brain regions (54 each hemisphere), two regions, i and j, were selected (b). From the total collection of reconstructed white matter tracts (based on the DTI data), the white matter fibers interconnecting region i and region j were selected by selecting those tracts that touched both region i and region j. If this selection procedure revealed fibers between i and j (c), node i and node j in the brain network were interconnected by a connection. Furthermore, the weight w_ij of the connection between node i and j was selected as the MTR value along the selected fibers, reflecting the level of myelination of the selected tract (d), and w_ij was included in cell c_ij of the weighted connectivity matrix M. If no tract was found between region i and j, no connection was included in graph G, resulting in c_ij value of 0 in M. These steps were repeated for all regions i and j in the AAL template (e), resulting in a filled weighted connectivity matrix M, representing a weighted undirected graph G (f). Next, from the resulting brain network overall organizational characteristics (g) and node-specific organizational characteristics (h) (see supplemental materials and Fig. 1) were computed and compared between patients and healthy controls (i).

Graph theory: computation of the graph organizational characteristics, overall organization and node-specific measures

The topology of the weighted structural brain networks of the patients and the healthy controls were examined using graph theory. For each individual dataset, the organization of the structural brain networks was examined by computing the overall level of connectivity S, normalized clustering-coefficient gamma, and normalized characteristic path length lambda (Fig. 2g), together with an exploratory analysis of the behavior of each node in the network specifically, including the regional measures weighted degree of strength S_i, the path length L_i, the clustering coefficient C_i, and the betweenness centrality B_i (see Fig. 1 for illustration). The graph organizational measures were computed as follows (Brain Connectivity Toolbox, http://www.brain-connectivity-toolbox.net) (Rubinov and Sporns, 2010).

First, for each individual connectivity matrix M, the weights of the connections were normalized to the maximum of M, normalizing for individual overall differences in connectivity strength:

For each of the individual brain networks it was ensured that the graph was connected, meaning that none of the brain regions were disconnected from the graph.

Weighted connectivity strength S.

Next, the connection strength S_i of each node i in the network was computed as the sum of the weights of all the connections of node i, providing information on the total level of (weighted) connectivity of a node (Fig. 1d). Formally:

In turn, the total connection strength S of the graph G was computed as the sum of S_i for all nodes N in G:

As the weights of the connections were taken as the level of MTR (as a marker for their level of myelination), whole-brain S expresses an overall level of MTR of the connectivity brain network.

Weighted clustering coefficient C.

The weighted clustering-coefficient C_i of node i was computed, expressing the likelihood that the neighbors of node i are interconnected, providing information on how strong node i and its direct neighbors are clustered (Fig. 1e), formally (Rubinov and Sporns, 2010):

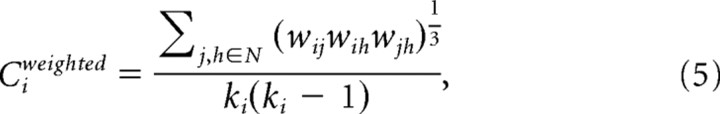with w_ij the weight between node i and node j in the network. Leaf nodes (nodes with only one connection) were assigned a C_i of 0. The overall clustering-coefficient C of G was computed as the average of C_i over all voxels i in G:

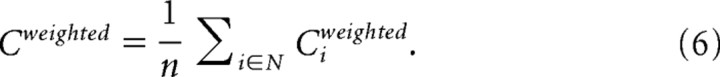Weighted characteristic path length L.

The weighted path length L_i of each node i was computed as the average minimal travel distance d(i,j) between node i and all nodes j in the network (Fig. 1f), measured as the inverse of the weights of the connections that have to be crossed to travel from node i to node j in the graph. Formally:

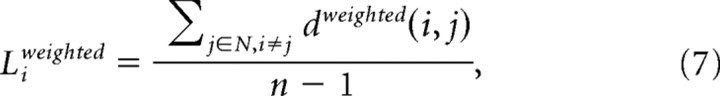with

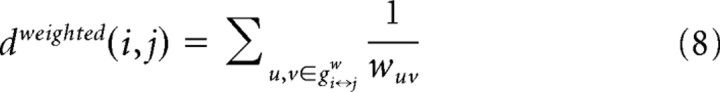and with g_i↔j^w the shortest weighted distance between node i and j in the graph, crossing on the way nodes u and v, with w_uv defined as the weight of the connection between node u and region v (i.e., normalized MTR value of the fiber tract interconnecting region u and region v). In turn, the weighted characteristic path length L of the entire network, expressing how well the overall network is connected, was computed as the mean over all L_i for all i in G:

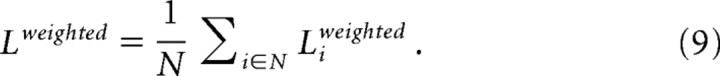Weighted betweenness centrality B.

The level of centrality (Fig. 1g) of a node provides information on how central node i is located in the overall network, expressing the importance of a node i in facilitating communication between the different regions of the brain network. The level of weighted betweenness centrality B_i for node i in the network was computed as the number of shortest paths between any two nodes h and j in the network that pass through node i (Rubinov and Sporns, 2010):

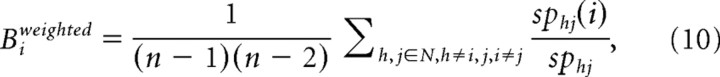with sp_hj(i) the number of shortest path between h and j that passes through node i. B_i was computed for all nodes i in the network and for datasets, both patients and healthy participants.

Identification of hubs.

“Hub nodes” or “hubs” take a central position in a network. They can be easily reached by most of the nodes of the network due to their central position, playing a crucial role in fast transport and efficient integration of information across the network (Sporns et al., 2007; Bullmore and Sporns, 2009). Several metrics can be used to identify hubs. Hub nodes generally display an above average high number of connections, a high level of (betweenness) centrality, a short average distance towards the other nodes of the network, and a low clustering coefficient (Sporns et al., 2007; Bullmore and Sporns, 2009). The structural hubs of the healthy brain network were identified by computing a level of “hubness” for each node in the average brain network of the group of healthy controls, determining whether a node belonged to: (1) the top 20% of nodes showing the highest level of connectivity S_i; (2) the top 20% of nodes showing the highest level centrality B_i; (3) the top 20% of nodes showing the lowest L_i; and/or (4) the top 20% nodes showing the lowest C_i. Each node was assigned a score between 0 and 4, determined by the total number of hub criteria fulfilled. Regions showing a hub-score of 2 or higher were marked as hub nodes.

To determine how a graph is organized locally and globally, the clustering coefficient C and path length L of a graph are typically compared with the (weighted) clustering coefficient C^random and (weighted) characteristic path length L^random of a random network. Therefore, for each individual brain network a set of 100 comparable random networks with similar degree sequence and symmetric adjacency matrix were formed, and C^random and L^random were defined as the average clustering coefficient and characteristic path length, respectively, over these random networks. Small-world networks are characterized by a clustering-coefficient C, which is >C^random, or a ratio gamma defined as C/C^random >1 and an average path length that is around the same order as that of the comparable random graph, expressed by L ∼ L^random or a ratio lambda defined as L/L^random of ∼1 (Bullmore and Sporns, 2009).

Statistics

Whole-brain group network analysis.

Differences in overall organizational graph characteristics between the group of patients and the group of healthy controls were examined using permutation testing (Bassett et al., 2008) (Fig. 2i-1). First, for each individual brain network the graph parameters (S, gamma, and lambda) were computed (as described above). Second, between-group differences on S, gamma and lambda were computed between the group of patients and healthy controls. Third, in the permutation step, each subject was randomly assigned to one of two random groups consisting of the same number of subjects as the original patient and control groups (n = 40). Next, differences between the parameters S, gamma and lambda of the two random groups were computed. This procedure was repeated for 10,000 permutations, resulting in a sampled between-group difference null distribution for each graph metric. Finally, for the S, lambda, and gamma parameters, the observed patient versus control between-group effect (step 2) was assigned a p value by computing the proportion of the total number of 10,000 entries resulting from the permutation that was greater than (or smaller than if the effect was negative) the observed patient versus control group effect. A significance threshold of α = 0.05 (uncorrected) was used for testing the overall connectivity strength S, normalized clustering gamma, and normalized path length lambda measures.

Node-specific group analysis.

Second, the role of each individual node in the network (i.e., each region in the brain network) was examined by comparing each node-specific weighted S_i, L_i, C_i,, and B_i values between patients and controls for all nodes i (i.e., for all brain regions) (Fig. 2i-2). This analysis was conducted to examine whether the role of region i in the overall organization of the brain network was changed in patients. To investigate between-group differences in node-specific S_i, C_i, L_i, and B_i values between patients and controls, a permutation test was used. This procedure followed the same steps as the permutation test of the whole-brain graph measures (10,000 permutations; see above, Whole brain group network analysis), resulting in a null distribution for each node-specific parameter and a p value for each between-group difference in S_i, L_i, C_i, and B_i for each of the 108 nodes of the brain network. A significance threshold of α = 0.05 (uncorrected) was used. To address the problem of multiple comparisons (i.e., the problem of multiple testing >108 brain regions for multiple graph metrics), effects were tested on whether they survived a false discovery rate (FDR) threshold of q = 0.05 (Benjamini and Hochberg, 1995) determined over all node-specific parameters together, providing good control over false positives. FDR correction was used, but future studies are needed to determine the optimal methodology to control for multiple testing in a network setting. Alternative correction methods have been suggested (Zalesky et al., 2010).

Graph modeling

Graph measures can be strongly related to each other; for example, a node with more connections is likely to have a shorter path length and a higher centrality. To get a better understanding of whether possible between-group differences in L_i and B_i effects are the result of “just” changing connectivity strength (i.e., changed number of connections or weighted connectivity strength Si) or whether they reflect organizational differences, an exploratory “graph modeling” analysis was conducted (Stam et al., 2009). In this modeling analysis, observed between-group changes in connectivity strength (S_i) were simulated in the brain networks of the healthy control group by taking the brain network G of the healthy controls and replacing the weights of each node in G at which a significant schizophrenia-linked effect on S_i was observed (see Results) by the weights of the connections from the brain networks of the patients, arriving at a new graph G*. Graph metrics L_i, B_i, and C_i of G* were computed and compared with the metrics of G. When comparing G* with G resulted in similar properties for both networks (i.e., differences that are smaller than effects found in the patient population), this would suggest that (at least) part of the schizophrenia-related L_i or B_i differences are the result of disorganization of connections and, to a lesser extent, just the loss of connections or connectivity strength of the brain networks of patients. In detail, the graph modeling consisted of the following steps. First, the structural brain network Gn-con from subject n from the group of N healthy controls was selected. Second, the structural brain network Gm-pat from a randomly selected patient m from the group of M patients was selected. Third, within Gn-con the weights of the nodes that were found to have a significantly changed S_i profile in patients (see Results) were replaced with the weights of Gm-pat, arriving at an adjusted graph Gn-con*. Fourth, the graph metrics L_{i and} B_i were computed for Gn-con*. Steps 1–4 were repeated for all subjects n in the group of N healthy controls. Each subject n was assigned a randomly selected patient m, with no duplicates (i.e., each n was matched to a unique patient m). Fifth, differences in L_i and B_i between Gn-con and Gn-con* were computed. For computational reasons, normal theory (t statistics) were used instead of permutation testing (as done in the main analysis). To be as conservative as possible about possible S_i-induced differences between L_i and B_i, an uncorrected α of 0.05 was used. Finally, as the group of patient was group matched to the group of healthy controls and not case-matched m, step 5 was repeated 1000 times, each iteration randomly “matching” subject n to a randomly selected patient m for all N.

Unweighted network analysis

In the main analysis a MTR-weighted graph approach was used. To test the role of the MTR weighting on possible organizational differences between the brain networks of patients and healthy controls, an additional test was performed in which the MTR weighting was omitted from the analysis. For each individual dataset, all nonzero weights (i.e., all connections) were set to 1, resulting in an unweighted version of G (i.e., graph representation of the structural brain network). Graph characteristics were computed and compared between the two groups.

FA-weighted network analysis

Within the main analysis the weights of the connections were taken by the level of MTR of the white matter tracts, assessing the level of myelination of the tracts (Foong et al., 2001; Kubicki et al., 2005b). An alternative measure for connectivity strength could be the level of fractional anisotropy, as FA values are regularly used as a measure of white matter microstructural organization and as a marker for white matter integrity in patient studies (Sun et al., 2003; Beaulieu et al., 2005; Kim et al., 2007; Mori et al., 2007; Van den Heuvel et al., 2008b; Chiang et al., 2009). Therefore, an additional analysis was performed in which FA values were used as a measure of connectivity strength. In this additional analysis, a similar weighted graph analysis was performed (Fig. 2, as described above), but with the difference that this time the weight of the connections were defined as the FA values of the interconnecting white matter tracts rather than the MTR values. Similar to the MTR analysis, overall graph organizational properties S, C, L, and node-specific measures S_i, C_i, L_i, and B_i were computed and compared between groups.

Results

Overall topology of the structural brain network

Both patients and healthy controls showed a small-world organization of the structural brain networks expressed by a gamma >1 (mean: SD; patients: 1.9664|0.1675, healthy participants: 1.9576| 0.1368) and lambda ∼1 (mean|SD; patients:1.0992|0.0146, healthy participants: 1.0989|0.0172). The overall level of connectivity S did not differ between patients and healthy controls (p = 0.19, permutation testing), reflecting no significant difference in overall connectivity strength (i.e., overall MTR level) between patients and controls. Furthermore, looking at the overall organization characteristics of the brain networks of patients, the normalized clustering coefficient gamma did not differ between patients and healthy controls (p = 0.45, permutation testing) (Fig. 3a), nor did the overall normalized path length lambda (p = 0.46, permutation testing, Fig. 3b). In summary, patients displayed gamma and lambda values close to the values of the brain networks of the healthy controls, suggesting an intact overall organization of the structural brain network in schizophrenia, supporting previous findings (Bassett et al., 2008).

Figure 3.

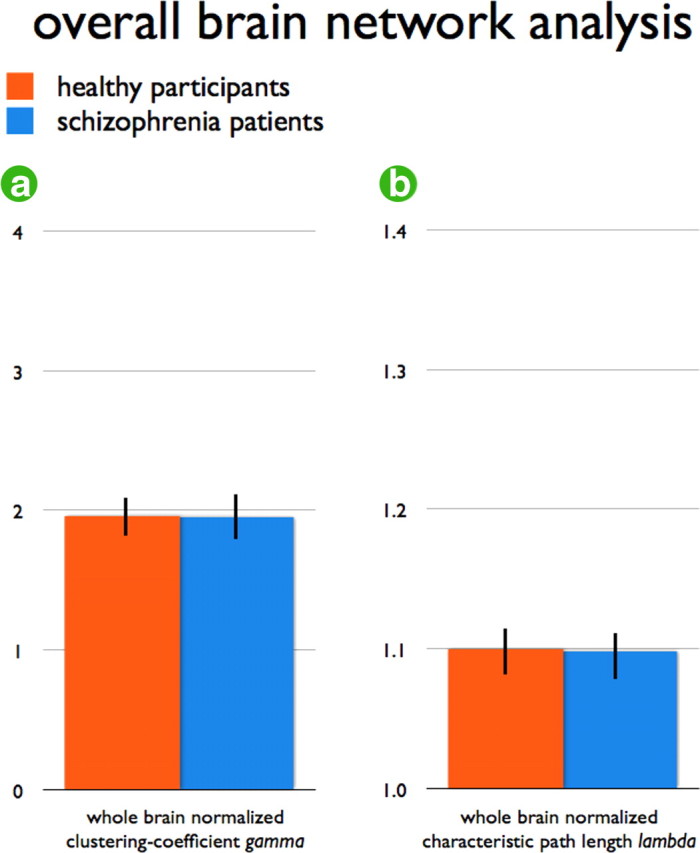
Overall graph organizational measures S, gamma and lambda values of controls and schizophrenia patients. Overall measures of normalized clustering coefficient gamma (a) and normalized path length lambda (b) of the patient and healthy control group. Bars express standard deviation over the group of subjects. Figure shows no significant differences in overall organization of the brain networks of schizophrenia patients and healthy participants on gamma or lambda.

Node-specific analysis

Identification of hubs

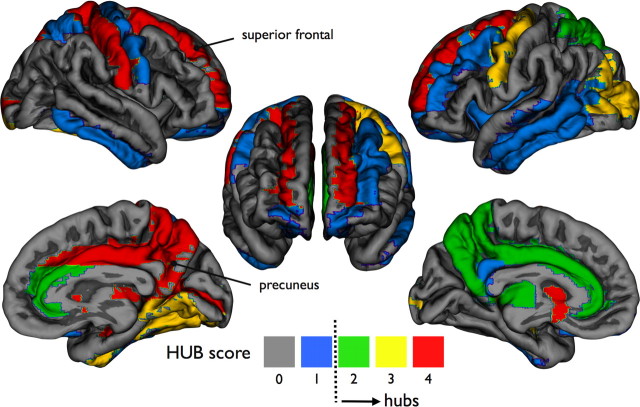
Examining the properties of the individual nodes of the brain network identified a central network role for the following areas in the healthy brain network: bilateral caudate (maximum hub scores of 4 and 4, respectively), bilateral superior frontal cortex (4,4), right middle cingulum (4, left middle cingulum scored 2), bilateral hippocampus (3,3), right precuneus (4, left precuneus scored 2), bilateral putamen (4,4), and the right thalamus (4, left thalamus scored 2). Figure 4 illustrates the cortical region-specific hub-scores.

Figure 4.

Node-specific hub scores. Figure illustrates region-specific “hub scores” of the average brain network of the group of healthy controls. Hub scores were computed as the number of times a node belonged to the 20% of nodes having a high K_i, a high B_i, a low C_i, and/or a low L_i. High scores mark nodes that take a central position in the brain network (see Materials and Methods). Hubs are also shown in supplemental Movie 1.

Between-group differences in node strength S_i

Group comparison revealed a reduced level of connectivity strength S_i in left and right inferior frontal cortex (p = 0.012 and p = 0.0092, respectively; all p values, permutation testing), left middle frontal cortex (p = 0.0449), left superior frontal cortex (p = 0.0497), right insula (p = 0.0470), and left and right pallidum (p = 0.0315, p = 0.0422), left precentral gyrus (p = 0.0366), right anterior cingulate cortex (p = 0.0181), and right superior temporal pole (p = 0.0035). Effects did not survive FDR correction. The absence of S_i effects marks the fact that schizophrenia does not strongly affect the connectivity strength of the brain network, indicating that possible effects on graph metrics are likely to be related to organizational effects rather than just “reduced connectivity.” Node-specific S_i values of all regions are depicted in supplemental Figure 2b.

Between-group differences in node-specific global path length L_i

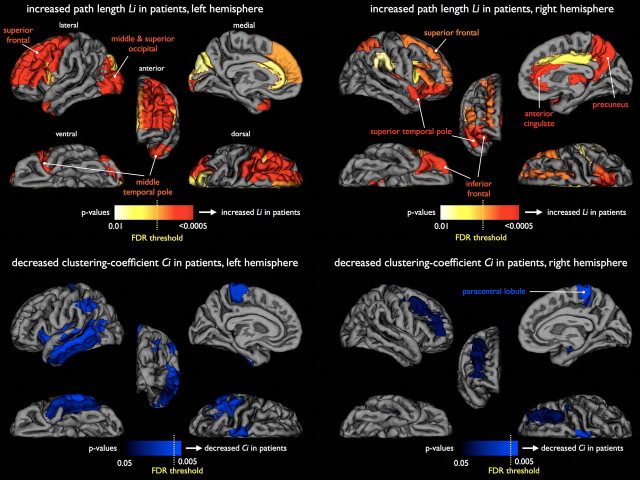
Group comparison revealed an increased path length L_i of frontal and temporal regions in patients (Fig. 5a, left hemisphere, b, right hemisphere). Specifically, patients showed longer structural path lengths L_i of the right anterior cingulate (p = 0.0259, all permutation testing), right superior temporal pole (p = 0.0273), right inferior orbitofrontal (p = 0.0088), and inferior frontal gyrus (p = 0.0320), left middle frontal (p = 0.0458), right insula (p = 0.0225), right pallidum (p = 0.0364), left precentral gyrus (p = 0.0224), and left middle temporal pole (p = 0.0198). A decrease in path length in patients was found in the left superior parietal lobule (p = 0.0287).

Figure 5.

Group differences of node-specific L_i and C_i values between healthy controls and schizophrenia patients. Upper figures show p values of significant between-group increases in node-specific L_i (corrected for within group S_i) for the left and right hemisphere respectively, marking significantly increased path length L_i of olfactory, medial, and superior frontal, occipital, and medial temporal pole brain regions in patients with schizophrenia compared with brain networks of the matched healthy controls (see also supplemental Movie 2). Lower figures mark significantly decreased node-specific clustering coefficient C_i values in patients with schizophrenia, with significantly decreased clustering coefficient of right paracentral lobule and right hippocampus. The L_i effects, together with the low number of C_i effects, tend to suggest that schizophrenia merely affects the global organization of the brain network, leaving the local organization relatively intact. Yellow dotted line expresses the critical FDR threshold (q = 0.05; see Materials and Methods).

S_i correction

It is important to note that the number of connections can have a strong inverse relation with path length (i.e., less connections generally results in a higher path length). Therefore, an additional analysis was performed in which L_i values were corrected for the total connectivity weight S_i of node i, regressing out the interaction between S_i and L_i within each group separately (patients and controls) and rerunning the group comparison. Using this correction, a group difference in the corrected L_i can be interpreted as a difference in the interaction between S_i and L_i between the two groups. Reducing the within-group variance revealed more pronounced, longer path length L_i effects in patients in frontal and temporal brain regions of interest: left and right anterior/middle cingulate cortex (p = 0.0098 and p < 0.0002*, respectively, permutation testing; * indicates region survived critical FDR threshold for multiple comparisons, see Materials and Methods), right superior temporal pole (p = 0.0004*), right inferior (p < 0.0002*) and superior orbitofrontal cortex (p = 0.0347), left precentral gyrus (p < 0.0002*), right insula (p < 0.0002*), right pallidum (p < 0.0002*), left middle temporal pole (p = 0.0012*), and left superior parietal cortex (decreased path length, p < 0.0002*). After correction, patients also showed longer path lengths of right middle orbitofrontal cortex (p = 0.0011*), left and right superior medial frontal cortex (p = 0.0040*, p = 0.016), left and right superior frontal cortex (p < 0.0002*, p = 0.0028*, * indicates region survived FDR threshold), right precuneus region (p < 0.0002*), left middle and left superior occipital lobe (p < 0.0002* and p = 0.0086*, respectively) and left and right superior temporal pole (p = 0.0018*, p = 0.024). Furthermore, correcting for the interaction between S_i and L_i, patients showed a decrease in path length of right fusiform gyrus (p = 0.0044*), right lingual gyrus (p = 0.0011*), right paracentral lobule (p = 0.0036*), and right hippocampus (p = 0.0156). Node-specific values L_i of all regions are presented in supplemental Figure 1a.

Between-group differences in node-specific clustering clustering-coefficient C_i

Patients did not show strong alterations in local clustering. As depicted in Fig. 5c (left hemisphere) and d (right hemisphere), group comparison revealed a decreased clustering-coefficient of the right hippocampus (p = 0.0021*, permutation testing;* indicates region survived FDR correction), left cerebellum (p = 0.0426), left insula (p = 0.0439), right middle frontal (p = 0.0263), left middle and left inferior temporal gyrus (p = 0.0070, p = 0.0307), left inferior parietal (p = 0.0271), right and left paracentral lobule (p = 0.0026*, p = 0.0276) and an increase in C_i of the left inferior occipital gyrus (p = 0.0320). Not finding strong effects on C_i suggests that local connectivity is relatively intact in schizophrenia. Node-specific values C_i of all regions are presented in supplemental Figure 1b.

Between-group differences in node-specific level of centrality betweenness B_i

Group comparison revealed decreased betweenness centrality B_i of left and right anterior cingulates (p = 0. 0300 and p = 0.0157 respectively, permutation testing), left middle frontal cortex (p = 0.0337), left superior frontal gyrus (p = 0.0376), and left frontal olfactory cortex (p = 0.0281) and increased centrality of right fusiform gyrus (p = 0.0119), left superior parietal cortex (p = 0.0201), left hippocampus (p = 0.0393), and parahippocampal cortex (p = 0.0492). Correcting for the interaction of S_i on B_i, (see above, S_i correction) showed decreased betweenness centrality in left and right anterior cingulate (p = 0.0152, p = 0.0046*; * indicates region survived FDR correction), left middle frontal cortex (p = 0.0136), left superior frontal gyrus (p = 0.0162), and left frontal olfactory cortex (p = 0.0201). Increased centrality was found in right fusiform gyrus (p = 0.0021*), left superior parietal cortex (p = 0.01), left hippocampus (p = 0.0276), and parahippocampal cortex (p = 0.041) (Fig. 6). Furthermore, correcting for S_i on B_i revealed additional decreases in centrality of right inferior frontal cortex (p = 0.0112), left middle frontal cortex (p = 0.0129), left inferior orbital frontal cortex (p = 0.0487), left medial frontal cortex (p = 0.0495), and left fusiform gyrus (p = 0.0270) and increased centrality of the left cerebellum (p = 0.0224), left insula (p = 0.0240), left superior parietal (p = 0.0108), and left superior temporal cortex (p = 0.0101) in patients. These additional effects did not survive FDR correction. Node-specific values B_i of all regions are presented in supplemental Figure 2a.

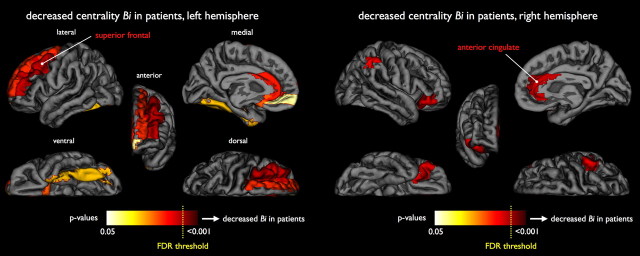
Figure 6.

Group differences of node-specific B_i between healthy controls and schizophrenia patients. Figure shows p values of node-specific decreases of B_i (corrected for within group S_i) in patients for the left and right hemisphere (left and right image), illustrating decreased betweenness centrality B_i of bilateral superior frontal and anterior cingulate regions in patients with schizophrenia (see also supplemental Movie 3). Yellow dotted line expresses the critical FDR threshold (q = 0.05; see Materials and Methods).

Clinical effects

No significant correlations were found between clinical scores [positive and negative symptom scale scores (Kay et al., 1987)/cumulative medication] and the graph organizational characteristics S, gamma, and lambda in the patient group or with the node-specific graph metrics using an FDR of q = 0.05 or even an exploratory uncorrected threshold of α <0.01. Furthermore, we did not find significant associations between dosage of antipsychotic medication intake and graph organizational measures. From this, we carefully conclude that antipsychotic medication did not explain our findings. Studies set up to specifically examine the influences of antipsychotic medication on structural network topology are needed, however, before more definite conclusions can be drawn regarding the influence of antipsychotic medication on brain network topology.

Graph modeling

To further examine whether the increased L_i and decreased B_i of frontal and temporal brain regions found in patients were the effect of coinciding reductions in S_i in these regions or whether they resulted from local disorganization, a graph modeling approach was used. The reductions in S_i were modeled in the healthy control networks, resulting in an adjusted healthy brain network G* (see Materials and Methods). Comparing G* and G only revealed significant increases in L_i in the temporal pole (p = 0.031) and inferior orbitofrontal cortex (p = 0.029), but no significant differences in graph metrics were found in the other reported brain regions that showed an increase in L_i and/or a decrease in B_i in patients. This suggests that these between-group differences reflect disorganizational effects rather than (or not explainable by) a loss of connectivity strength.

Control conditions: unweighted graph analysis

To test the role of the MTR weighting on the observed L_i effects, an additional test was performed in which the MTR weighting was omitted from the analysis, setting all connections in the connectivity matrix to 1, resulting in an unweighted version of G, for each individual dataset. Similar to the MTR analysis, no differences in gamma, lambda or K (i.e., number of connections) were found. Moreover, the unweighted node-specific results showed overlap with the MTR weighted analysis, with increased path length L_i of right inferior frontal cortex (p = 0.010, permutation testing; corrected for K_i), right insula (p = 0.003), left middle occipital gyrus (p = 0.006), left middle temporal pole (p = 0.001) and right superior temporal pole (p = 0.001), shorter L_i of left superior parietal cortex (p = 0.001) and decreased B_i of right anterior cingulate (p = 0.017, corrected for K_i) and left superior frontal cortex (p = 0.018). However, in contrast to the MTR-weighted analysis, no significant differences in L_i were found in left anterior cingulum, right middle cingulum, left inferior frontal cortex, and right superior frontal cortex.

Control conditions: FA-weighted graph analysis

An additional weighted graph analysis was performed in which the weight of the connections were taken as the FA values of the interconnecting white matter tracts rather than the MTR values. In general, FA weighting revealed similar results as those of the MTR-weighted analysis, supporting the results of a reduced structural connectivity of frontal and temporal brain regions in schizophrenia. Similar to the MTR analysis, no significant difference in overall FA connectivity strength S (p = 0.46, permutation testing; 10,000 permutations), normalized clustering coefficient gamma (p = 0.31), or normalized path length lambda (p = 0.34) were found. Furthermore, looking at the network role of the individual nodes, the FA-weighted analysis showed significant higher node-specific path length L_i of frontal regions, including right inferior frontal (p = 0.003, permutation testing; corrected for S_i), right middle frontal (p = 0.023), and a trend-like higher L_i of the right temporal pole p = 0.051) supporting the MTR results. However, in contrast to the MTR-weighted results, no significant between-group L_i differences were found in left and right superior frontal regions, left and right anterior cingulum, right middle cingulum, right and left inferior and middle frontal cortex, right insula, right occipital and left superior occipital, right superior parietal, right superior temporal pole, or left superior temporal gyrus. Overlapping the centrality results of the MTR weighted analysis, the FA-weighted analysis did show a reduction in B_i of left superior frontal regions in patients, but this effect did not reach significance (p = 0.079, permutation testing).

Discussion

The main finding of this study is a less strongly integrated structural brain network in patients with schizophrenia, with a reduced central role of key frontal hubs. Although schizophrenia patients showed an overall intact small-world topology, a significant decrease of network connectivity of frontal and temporal areas was found. Specifically, patients displayed a significantly increased path length (i.e., higher L_i) (Fig. 5a) of olfactory, medial, and superior frontal regions, anterior cingulate, medial temporal pole, and superior occipital regions. As the path length of a node expresses how close it is connected globally to other nodes of the network, with shorter path lengths reflecting higher levels of efficient access to information (Latora and Marchiori, 2001; Achard and Bullmore, 2007), our findings suggest a reduced global efficiency of frontal, temporal, and occipital brain regions in schizophrenia. Furthermore, as patients did not show strong changes in connectivity strength S_i or local clustering C_i, our findings tend to suggest that schizophrenia affects the global organization of the brain network and, to a lesser extent, general connectivity strength or local organization. Indeed, the affected superior frontal and cingulate regions were identified as key structural connectivity hubs (Fig. 4) (Bassett et al., 2008; Hagmann et al., 2008), suggesting that an increased path length of these regions is likely to have a strong impact on global information integration in patients. This is further supported by the centrality findings, showing a decreased centrality B_i of superior frontal and anterior cingulate regions in patients. These findings tend to suggest a decreased hub role of frontal regions in the brain network of patients with schizophrenia (Fig. 7). As higher integration efficiency has been linked to cognitive fitness of the brain (Bassett et al., 2009; Li et al., 2009; van den Heuvel et al., 2009a), this may suggest that schizophrenia impacts the capacity of frontal brain regions to efficiently integrate information across the brain network. Interestingly, exploratory centrality analysis also revealed an increase of B_i of left superior parietal, fusiform, and (para)hippocampal regions and a decrease in path length of right paracentral lobule and fusiform gyrus, brain regions that have been reported to show morphological and functional changes in patients (e.g., Ellison-Wright and Bullmore, 2010; Boos et al., 2007). However, the impact of these results remains unclear. Increased B_i and decreased L_i of parietal and hippocampal/fusiform regions may indicate a shift to more temporal brain regions as a possible compensatory mechanism for decreased centrality of frontal regions (Bassett et al., 2008); however, our results did not show a consistent change in graph metrics (i.e., combined B_i and L_i effects) in these regions. Future studies are therefore needed to further examine a possible increased centrality and hypothesized increased hub role of parietal and medial temporal regions in schizophrenia.

Figure 7.

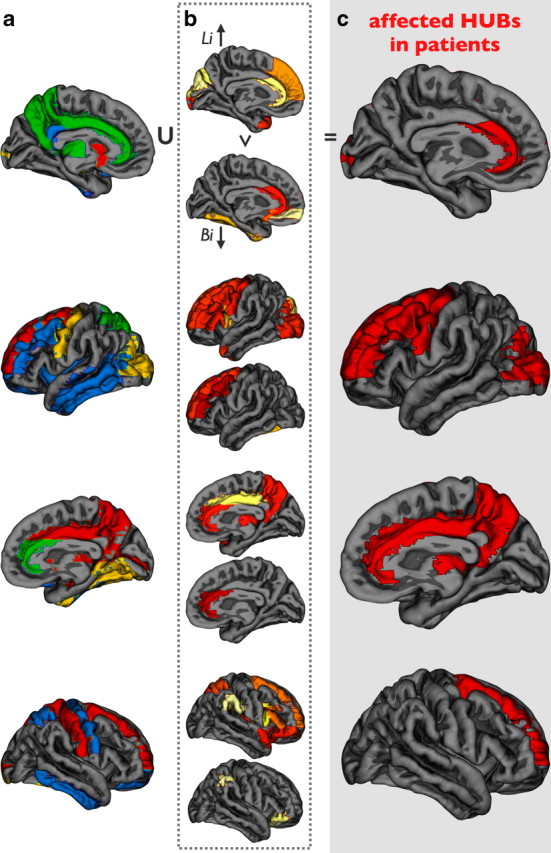
Overlap between hub nodes and brain regions affected by schizophrenia. c shows the intersection between the collection of hub regions (hub-score 2 and more) (a) and the union of the brain regions that showed a significant increase in path length L_i (b, upper parts) and/or a decrease in centrality B_i (b, lower parts). Overlap marks the hub regions that are impacted by disease.

The finding of an affected frontal network organization is in line with previous studies. Bassett et al. examined inter-regional covariation in cortical volume (Bassett et al., 2008) and, in addition to reporting on an intact overall small-world organization (overlapping our MTR-weighted results), schizophrenia patients showed a reduced hierarchical organization and increased connectivity distance of multimodel brain regions together with a loss of frontal hubs, which is coherent with our current DTI findings. However, differences can also be reported. Cortical network organization of patients displayed an increased hub role of (among others) the insula, and inferior frontal and temporal brain regions (Bassett et al., 2008), whereas we found a decrease in centrality of inferior frontal brain regions and an increase in more medial/posterior temporal brain regions (hippocampal/fusiform gyrus). Interestingly, Lynall et al. recently reported on the aspects of functional brain networks of patients with schizophrenia (Lynall et al., 2010), examining resting-state functional MRI recordings, showing that patients have less strongly integrated functional brain networks with less dominant hubs. These functional results support our current structural findings, revealing a decreased structural hub-role of frontal regions in patients.

The neurological process that lead to the observed network alterations remains, however, unclear. From the current analysis it is hard to draw conclusions about the underlying neuropathophysiology, and future studies examining underlying cytoarchitectural changes and their progressive character (Rapoport et al., 2005) are needed. However, there is room for speculation. MTR-weighted analysis revealed changes in network topology distributed diffusely across the frontal lobe. The unweighted and FA-weighted control conditions revealed overlapping results, but interestingly the MTR-weighted conditions were more pronounced, especially in temporal, superior frontal, and anterior cingulate regions. Because MTR is marker for the level of myelination of white matter (Wolff and Balaban, 1994; van Buchem, 1999), this may suggest a subtle but crucial demyelination of widespread tracts linking the frontal and temporal cortex with the rest of the brain network (Kubicki et al., 2005a,b; Ellison-Wright and Bullmore, 2009). Furthermore, as the MTR network analysis mostly revealed decreases in global connectivity profile, rather than effects on local organization, the effects might be concentrated to more long-range tracts. Indeed, structural DTI studies have reported reduced integrity of the cingulum tract in patients, which interconnects the frontal lobe with the parietal lobe, and the unscinate fasciculus, a key tract connecting the frontal lobe with the temporal lobe (Ellison-Wright and Bullmore, 2009; Voineskos et al., 2010). This may lead to reduced global integration of information between widespread brain regions, as functional studies have reported less strongly globally connected and less organized functional brain networks in patients (Micheloyannis et al., 2006; Liu et al., 2008; Lynall et al., 2010). Future studies examining the properties of long-range tracts in schizophrenia and their specific impact on structural and functional brain network topology are needed.

Morphological MRI studies have evidently shown decreased integrity of frontal and temporal gray matter regions (e.g., Wright et al., 2000; Hulshoff Pol et al., 2004; Whitford et al., 2007; Ellison-Wright and Bullmore, 2009). As studies have reported a progressive character of these morphological brain changes (for review see Rapoport et al., 2005; Hulshoff Pol and Kahn, 2008), it is of high interest to start examining how network disconnectivity progresses over time using a longitudinal study design.

As mentioned, our findings are supported by recent DTI studies reporting on reduced integrity of specific structural white matter tracts in patients (Ellison-Wright and Bullmore, 2009), including the cingulum tract and the uncinate fasciculus (Fujiwara et al., 2007; Mori et al., 2007; Rosenberger et al., 2008; Voineskos et al., 2010). Indeed, we recently reported an increase in MTR along the uncinate fasciculus (Mandl et al., 2008). The current network analysis now shows that although the specific connections within a frontal-temporal subnetwork may show increased connectivity (i.e., increased MTR), the level of global connectivity of these frontal and regions toward the other regions of the brain network is still reduced. In this context, we speculate that patients may have a more isolated frontal-temporal subnetwork, possibly with increased communication between frontal and temporal brain regions at the “cost” of reduced external access to information, leading toward reduced global connectivity. Examination of the node-specific clustering coefficient C_i indeed revealed an increase in local connectedness of the right medial frontal cortex and superior temporal pole, but these effects were not significant (p = 0.0739 and p = 0.0892, permutation testing). A possible isolated network position of frontal regions is supported by functional MRI studies that report on increased and more isolated activity of the frontal cortex during cognitive tasks (Kircher et al., 2002; Sommer et al., 2003; Weiss et al., 2006) and aberrant connectivity during rest (Meda et al., 2009; Mannell et al., 2010; Sigurdsson et al., 2010). Structural and functional connectivity are related (Hagmann et al., 2008; Van den Heuvel et al., 2008b, 2009; Greicius et al., 2009; Honey et al., 2009, 2010). and recent studies have suggested both aberrant functional as well as diminished structural connectivity of specific frontal and hippocampal regions in schizophrenia (Zhou et al., 2008; Camchong et al., 2009). Future studies examining the exact link between complex structural and functional brain networks are needed (Bullmore and Sporns, 2009).

Some points should be taken into account when interpreting our results (see supplemental materials for a detailed description). First, the used tracking algorithm needs sufficient directional information at each point along the tract. If the directional information is, however, not univocal, at some point the algorithm is limited in reconstructing the fiber tract (Mori and van Zijl, 2002; Jones, 2008). However, this is unlikely to influence the examination of network differences between two groups, as studies have not reported general tractography differences between patients with schizophrenia and healthy controls. Second, using the AAL template, regions are very different in size, which is likely to have an effect on the degree of the nodes; bigger regions generally have more connections (supplemental Fig. 3). However, because an identical template was used in both groups, this is unlikely to bias between-group differences. To verify this, a post hoc analysis was performed in which the association between the node size (i.e., size of a region in the AAL template) and the between-group effect sizes of the graph metrics was examined. As expected, no strong associations were found between-group effects and region size (supplemental Fig. 4).