Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2010 Jan 27;30(4):1250–1257. doi: 10.1523/JNEUROSCI.1623-09.2010

Gamma-Phase Shifting in Awake Monkey Visual Cortex

Martin Vinck 1,*, Bruss Lima 2,*, Thilo Womelsdorf 1, Robert Oostenveld 1, Wolf Singer 2,3, Sergio Neuenschwander 2, Pascal Fries 1,4,✉
PMCID: PMC6633799  PMID: 20107053

Abstract

Gamma-band synchronization is abundant in nervous systems. Typically, the strength or precision of gamma-band synchronization is studied. However, the precise phase with which individual neurons are synchronized to the gamma-band rhythm might have interesting consequences for their impact on further processing and for spike timing-dependent plasticity. Therefore, we investigated whether the spike times of individual neurons shift systematically in the gamma cycle as a function of the neuronal activation strength. We found that stronger neuronal activation leads to spikes earlier in the gamma cycle, i.e., we observed gamma-phase shifting. Gamma-phase shifting occurred on very rapid timescales. It was particularly pronounced for periods in which gamma-band synchronization was relatively weak and for neurons that were only weakly coupled to the gamma rhythm. We suggest that gamma-phase shifting is brought about by an interplay between overall excitation and gamma-rhythmic synaptic input and has interesting consequences for neuronal coding, competition, and plasticity.

Introduction

Neuronal gamma-band synchronization has been found in several different species, in many different brain structures, and under numerous stimulation, motor, or cognitive conditions (Gray et al., 1989; Bragin et al., 1995; Fries et al., 2001, 2008a; Brosch et al., 2002; Pesaran et al., 2002; Schoffelen et al., 2005; Hoogenboom et al., 2006). Correspondingly, gamma-band synchronization has been implicated in several functions (Gray et al., 1989; Bragin et al., 1995; Wehr and Laurent, 1996; Fries et al., 2001; Fell et al., 2001; Pesaran et al., 2002; Buschman and Miller, 2007). Models that try to explain how gamma-band synchronization subserves different functions typically focus on the precision or strength of gamma-band synchronization (Singer and Gray, 1995; Engel et al., 2001; Salinas and Sejnowski, 2001; Börgers and Kopell, 2008), but the phase of gamma-band synchronization might be another important aspect, as has been proposed numerous times (Buzsáki and Chrobak, 1995; Maass and Natschläger, 1997; Börgers et al., 2005; Schneider et al., 2006; Nikolić, 2007; Fries et al., 2007; Tiesinga et al., 2008; Quian Quiroga and Panzeri, 2009) but so far not yet demonstrated (Ray et al., 2008).

Gamma-band synchronization within a local group of neurons entails rhythmic inhibition through the local inhibitory interneuron network (Csicsvari et al., 2003; Hasenstaub et al., 2005; Vida et al., 2006; Buzsáki, 2006; Bartos et al., 2007; Morita et al., 2008). The gamma-rhythmic inhibition constitutes a gamma cycle that might impact neuronal processing (Fries et al., 2007). Neurons that are strongly activated might spike early in the gamma cycle, i.e., there might be gamma-phase shifting. The spike phase in the gamma cycle would thereby provide an instantaneous analog representation of neuronal excitation. Gamma-phase shifting could have important consequences, endowing early spikes with enhanced impact on postsynaptic neurons (Börgers et al., 2005; Börgers and Kopell, 2008) and with an enhanced chance to potentiate synapses through spike timing-dependent plasticity (STDP) (Markram et al., 1997; Bi and Poo, 1998; Caporale and Dan, 2008) (for more details, see Discussion).

Therefore, as a first step, we set out here to test whether gamma-phase shifting exists in awake monkey visual cortex. We recorded spikes and local field potentials (LFPs) simultaneously from several electrodes in monkey primary visual cortex during stimulation with gratings of different orientations. We found strong evidence for gamma-phase shifting and some indication that it is brought about by the interplay between overall neuronal excitation and gamma-rhythmic synaptic input.

Materials and Methods

Experimental procedures.

Experiments were performed on three adult rhesus monkeys (Macaca mulatta) and followed the guidelines of the European Community for the care and use of laboratory animals (European Union Directive 86/609/EEC) with approval by the appropriate local committee on animal welfare (Regierungspräsidium Hessen, Darmstadt, Germany). After an initial training period, each monkey was surgically implanted with a titanium bolt for stabilizing head position, a scleral search coil for measuring eye position, and a titanium recording chamber (internal diameter, 6 mm) that allowed microelectrode access to primary visual cortex V1. The titanium pieces were fixed to the skull by means of orthopedic screws (Synthes). All surgical procedures were conducted under aseptic conditions with isoflurane anesthesia (Baxter) assisted by a pressure-controlled ventilation unit (1.8 L/min N2O and 0.8 L/min O2; Julian unit; Dräger Medical). Recordings were made from the opercular region of V1 (receptive field centers: 2.0–5.0° of eccentricity) and, in some occasions, from the superior bank of the calcarine sulcus (8.0–12.0° of eccentricity). Electrodes were inserted independently into the cortex via transdural guide tubes (diameter: 300 μm; Ehrhardt Söhne), assembled in a customized recording device (designed by one of the authors, SN). This device comprised five precision hydraulic microdrives mounted onto an x–y stage (MO-95; Narishige), which was secured onto the recording chamber by means of a threaded adapter, providing high recording stability. Quartz-insulated tungsten–platinum electrodes (diameter: 80 μm; Thomas Recording) with impedances from 0.3 to 1.0 MΩ were used to record simultaneously the extracellular activity from three to five sites. Spiking activity of small groups of neurons [multiunit activity (MUA)] and the LFP were obtained by amplifying (1000×) and bandpass filtering (MUA: 0.7–6.0 kHz; LFP: 0.7–170 Hz) the recorded signals using a customized 32 channel head stage and preamplifier (head stage HST16o25; head stage and preamplifier from Plexon). Additional 10× signal amplification was done by on-board amplifiers (E-series acquisition boards; National Instruments). The signals were digitized and stored using a LabVIEW-based acquisition system developed in our laboratory (SPASS, written by SN). Local field potentials were acquired with a resolution of 1.0 ms. Spikes were detected by amplitude thresholding, which was set interactively after online visualization of the spike waveforms (typically 2 to 3 SDs above the noise). Spike events and corresponding waveforms were sampled at 32 kHz, and spike waveforms were recorded for a duration of 1.2 ms.

Visual stimulation.

Stimuli were presented as movies at 100 or 120 frames per second using a standard graphical board (GeForce 6600-series; NVIDIA). The cathode ray tube monitor used for presentation (CM813ET; Hitachi) was gamma corrected to produce a linear relationship between output luminance and gray values and subtended a visual angle of 36° × 28° (1024 × 768 pixels). At the beginning of each recording session, receptive fields were mapped using an automatic procedure, in which a bar was moved across the screen in 16 different directions (n = 160 trials). Receptive field position was estimated from the global maximum of a response matrix, at a resolution of ∼6 min of arc. Subsequently, monkeys passively viewed drifting gratings during fixation of a small central fixation spot. Gratings had spatial frequencies ranging from 0.5 to 2.0 cycles/° and velocities ranging from 0.5 to 3.0°/s. Grating drift directions were generated randomly from a total of 16 directions (steps of 22.5°). The stimuli were centered over the receptive fields within a circular aperture of ∼8.0°. After the monkey acquired fixation, there was a prestimulus baseline of 800–1000 ms after which the stimulus was presented for a duration of 800–1500 ms. For the present analysis, we used only data from this time period. If not mentioned otherwise, we excluded the first 250 ms after stimulus onset because of response onset transients. Monkeys were required to hold stable gaze for 3000 ms, during which additional test stimuli were shown (plaids composed of two grating components) and to respond to a color change of the fixation point. To obtain a reward, monkeys had to release the lever within 500 ms after the color change of the fixation point. Trials were aborted when early or late lever releases occurred or whenever fixation was interrupted and were followed by a blank screen period. Eye position was monitored continuously by a search coil system (DNI; Crist Instruments) with a temporal resolution of 2 ms.

Spike sorting.

Offline spike sorting was performed using principal component analysis (Offline Sorter; Plexon). We used the following criteria to include a single unit in our sample: it had to be well isolated from the multiunit (MUA) on at least one of the first two principal component analysis scores of the waveforms, its isolation had to be stable across time, and a clear refractory period had to be visible in the interspike interval distribution.

Spike–LFP phase locking and spike phase analysis.

Around each spike recorded from one electrode, a 150 ms data segment of the LFPs recorded on other electrodes was cut out. Each LFP data segment was multiplied by a Hanning window before Fourier transforming it, giving the spike-triggered LFP spectrum, as follows:

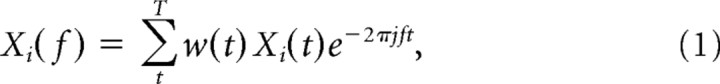graphic file with name zns00410-7572-m01.jpg

where xi(t) is the time series of the LFP data segment around the spike i, i = 1,2 …, N, and w(t) the Hanning window. The 150 ms segment length allowed a frequency resolution of 6.67 Hz. We averaged across the M LFPs from the other electrodes (i.e., not the one on which the spike was recorded) by the following:

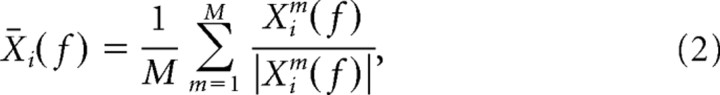graphic file with name zns00410-7572-m02.jpg

where X̄i(f) is now a complex number. By means of Equation 2, the magnitude of the spike-triggered LFP spectrum is ignored in the computation of the spike phase. The spike phase is now simply given by θi = arg(X̄i(f)). We measured phase consistency by means of the spike–LFP phase-locking value, which is defined as follows:

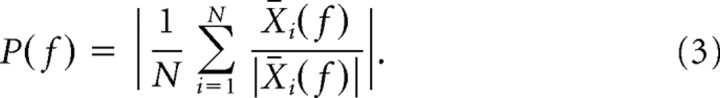graphic file with name zns00410-7572-m03.jpg

The spike–LFP phase-locking value is a biased measure with respect to the number of spikes that are entered in the computation. Therefore, we always entered the same fixed number of spikes into Equation 3 when we compared between samples with a different number of elements. Furthermore, we reduced the statistical variance of our spike–LFP phase-locking value by means of a bootstrapping procedure. For every repetition, we drew the fixed number of spikes without replacement from all the spikes that were in the sample. For each bootstrapped sample drawn, we determined the spike–LFP phase-locking value. Subsequently, we averaged these spike–LFP phase-locking values across all bootstrapped samples, giving our “unbiased” phase-locking value. The statistical significance of the “biased” phase-locking value was assessed by means of the Rayleigh test (α = 0.001).

Relationship of spike phase and orientation.

We investigated whether stimulus orientation determines the spike phase in the gamma cycle. Nonpreferred orientations typically have a small number of spikes that are only weakly gamma-band phase locked. Thus, the estimate of their mean spike phase suffers from high variance. To reduce this variance, at the potential cost of a reduced effect size, we determined the four orientations with the lowest firing rate and pooled these together as the nonpreferred orientations. Similarly, we pooled together the two orientations with the highest firing rate together as the preferred orientations. This ensured that both conditions had a sufficiently large number of spikes. In addition, we only included neurons for which each condition contained >30 spikes.

Relation between spike density and spike phase.

To estimate neuronal activation on short timescales, we determined for each individual spike the density of temporally neighboring spikes by convolving the spike train with a Gaussian kernel with a length of ±125 ms and an SD of 50 ms. Importantly, spike density is a linear predictor variable, whereas spike phase is a circular variable. Hence, their relationship cannot be studied properly with the standard linear regression model, because this model minimizes a linear error term and not a circular one. To address the linear–circular case, we used a linear–circular regression model (Fisher and Lee, 1992). In this model, an arc-tangens link function maps the linear predictor variable to the circle, giving the following model:

graphic file with name zns00410-7572-m04.jpg

where Xi, i = 1,2 …, N, is the independent variable containing N data points, β is the regression coefficient we wanted to estimate, and εi is described by a von Mises distribution VM(μi,κ). To determine the parameter set (β, μ, κ), we maximized the likelihood as follows:

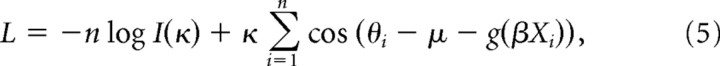graphic file with name zns00410-7572-m05.jpg

using an iterative least-squares algorithm. An SE of our regression parameter was computed, and a p value was obtained by comparing the t statistic, as follows:

graphic file with name zns00410-7572-m06.jpg

against the standardized normal distribution. To directly determine the spike phases associated with different spike densities at the group level, we binned spike densities into nonoverlapping bins and calculated the corresponding mean spike phases, averaged across all neurons, for every bin. We only included neurons that had at least 30 spikes in every spike density percentile. The relationship between spike density percentile and spike phase was statistically quantified using linear–circular regression.

Relationship between strength of phase locking and gamma-phase shifting.

To quantify the relationship between the degree of gamma-phase shifting and the strength of phase locking, we removed several potential confounds from our data.

(1) An obvious confound is that weak and strong phase-locked neurons might have different spike numbers. Therefore, we used the bootstrapping bias-correction procedure as explained above, choosing a fixed number (100) of spikes to determine our spike–LFP phase-locking value.

(2) A more complicated potential confound is that stronger gamma-phase shifting will correspond to a higher dispersion of spike phases and will thus result in a lower spike–LFP locking by definition. Therefore, we introduced a new measure of phase locking, which measures the spike dispersion relative to the estimated phase shift or, in other words, which subtracts the phase shift and then estimates the phase locking as the resultant length of residual error terms (Eq. 3). This new phase-locking value is now calculated on the error terms as follows:

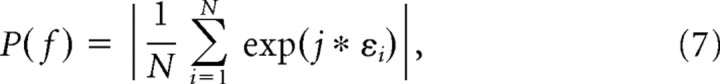graphic file with name zns00410-7572-m07.jpg

where εi is derived from Equation 4. This procedure removed the shifting mean phase in the gamma cycle from the data.

(3) Different animals might have different distributions of the strength of spike-field phase locking. To normalize for this, we used a Z-score standardization for our phase-locking values relative to the mean phase locking within each animal.

After removing these potential confounds, we then sorted neurons into weakly and strongly locked units by using a Z-score value of 0 as our cutoff value. For these two groups, we calculated the corresponding mean spike phases in the gamma cycle, averaged across all neurons. The relationship between spike density percentile and mean phase was quantified by means of linear–circular regression.

Relationship between LFP gamma-band power and phase shifting.

We obtained an indirect measure of the strength of gamma-rhythmic synaptic input by determining the gamma-band power of the spike-triggered LFP spectra. We then used this gamma power to sort, for each neuron, the trials into low-, medium-, and high-gamma trials. Within those three groups of trials, we then determined the dependency of spike phase in the gamma cycle on the spike density percentile. It is expected that trials with a higher LFP gamma-band power will correspond to a higher degree of gamma-band phase locking.

Results

In three monkeys (monkeys J, L, and N), we recorded a total of 106 visually responsive isolated single neurons (25 from monkey J, 23 from monkey L, and 58 from monkey N). The spikes of each of the single units were then related to the average LFP recorded simultaneously from separate electrodes spaced at 1–3 mm distance. During visual stimulation, these spike–LFP pairs showed clear phase locking in the gamma-frequency band (Fig. 1). The gamma-frequency band was different in the three monkeys, peaking at ∼67 Hz in monkey J and ∼40 Hz in monkeys L and N. These three bands are within the range of gamma frequencies described in previous studies in monkeys (Friedman-Hill et al., 2000; Maldonado et al., 2000; Fries et al., 2008a,b) and humans (Hoogenboom et al., 2006; Wyart and Tallon-Baudry, 2008; Muthukumaraswamy et al., 2009). These monkey-specific peak frequencies were used for further analyses, unless full spectra are shown. Further analyses were restricted to those units that showed significant gamma-band spike–LFP phase locking (62 of the 106 units).

Figure 1.

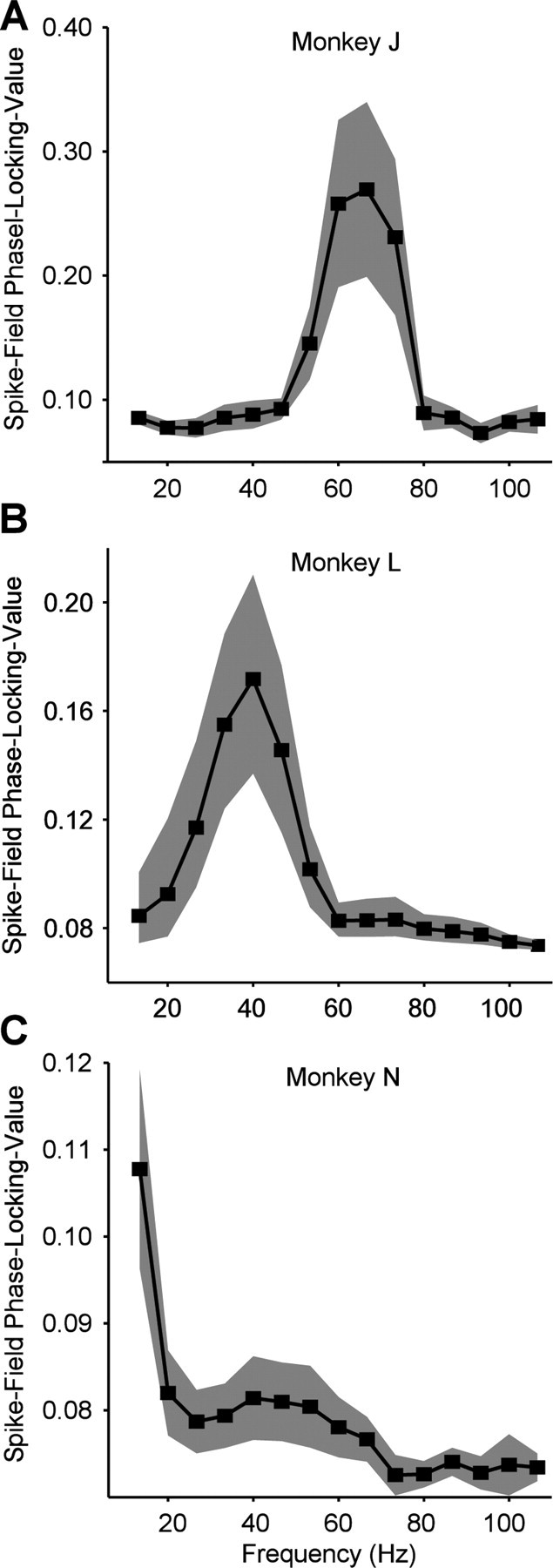
Figure 1.

Open in a new tab

Spike–LFP phase-locking spectra. A, Monkey J. Average spike–LFP phase-locking value plotted as function of frequency. Shaded regions indicate 95% confidence intervals around the mean. A gamma-band peak is visible at ∼67 Hz. B, Monkey L. Same conventions as in A. A gamma-band peak is visible at ∼40 Hz. C, Monkey N. Same conventions as in A. A gamma-band peak is visible at ∼40–53 Hz.

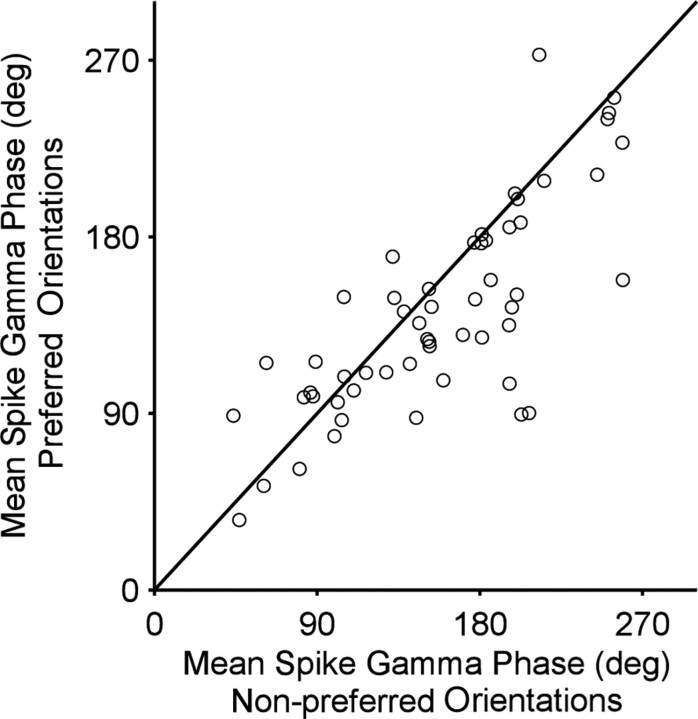
Spikes could be locked to different phases of the gamma cycle. Early phases occurred when the neuron was strongly activated (example shown in Fig. 2A). Neuronal activation was strongly determined by stimulus orientation. Correspondingly, stimulus orientation determined spike phases in the gamma cycle. The spikes of the example neuron (Fig. 2A,B) shifted from 205.6 ± 11.3° [95% confidence interval (c.i.)] for the nonpreferred orientation to 91.0 ±11.3° (95% c.i.) for the preferred orientation. Such orientation-dependent gamma-phase shifting was significant across the population of neurons (p = 0.0027, two-sided paired-sample sign test), although the orientation-dependent shift was smaller in the average than in the example (Fig. 3). On average, spikes shifted from 158.5 ±14.3° (95% c.i.) for nonpreferred orientations to 137.22 ±17.9° (95% c.i.) for preferred orientations.

Figure 2.

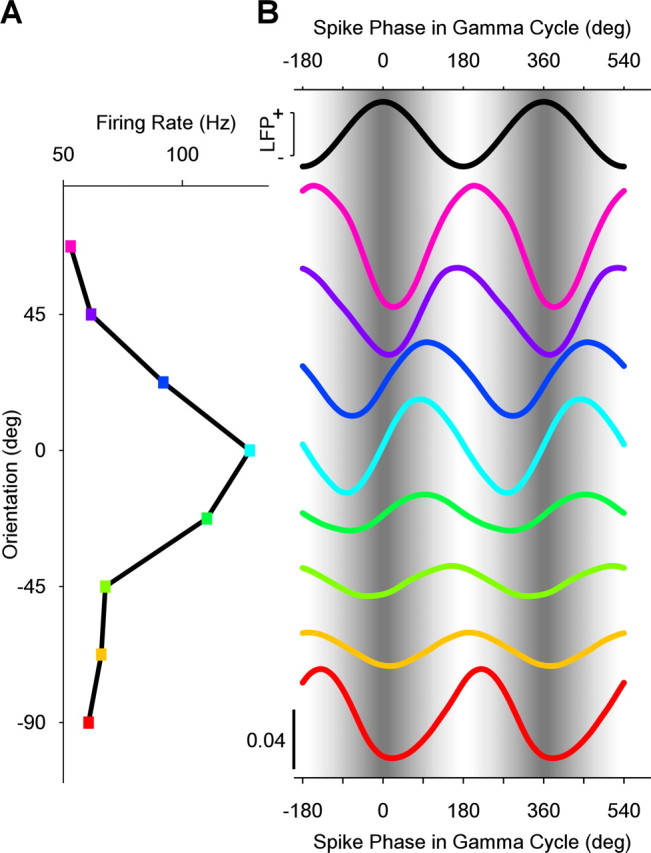
Figure 2.

Open in a new tab

Match between stimulus orientation and neuronal orientation preference determines spike phase in the gamma cycle. A, B, Data from one example neuron. A, Firing rate as a function of stimulus orientation. B, The black sine wave at the top and the sinusoidal gray shading in the background illustrate the LFP gamma phase. The colored lines show spike densities as a function of phase in the gamma cycle. The colors correspond to the colors used in the firing rate panel on the left. All spike density curves are probability densities, normalized such that the mean value of each curve is 1/2π (bottom left calibration bar applies to all curves, and curves are offset along the y-axis to correspond to A).

Figure 3.

Figure 3.

Open in a new tab

Population results for orientation-dependent phase shift. Scatter plot of mean spike phase for the four least preferred orientations (x-axis) versus mean spike phase for the two most preferred orientations (y-axis). Every dot represents a single unit.

Neuronal activation was not only determined by stimulus orientation but also by other factors. One such factor was the time after stimulus onset. Stimulus onset typically induces initial strong activation that then declines gradually. Furthermore, time after stimulus onset determined the exact position of the drifting grating over the receptive field of the recorded neuron. The corresponding dynamic modulations in neuronal activation modulated the spike phase in the gamma cycle (Fig. 4).

Figure 4.

Figure 4.

Open in a new tab

Temporal evolution of spike density and spike phase during the trial. A–C, Data from one example neuron. A, Spike density as a function of time after stimulus onset, calculated in 250 ms rectangular windows. The fluctuations in spike density are predominantly driven by the onset transient and the position of the drifting grating over the receptive field of the neuron. B, Same analysis but for the spike phase in the gamma cycle. C, Same data as in A and B but now showing spike phase directly as a function of spike density.

The rapid dynamics visible in Figure 4 suggest that the spike phase in the gamma cycle is determined by neuronal activation on short timescales. To estimate neuronal activation on short timescales, we determined for each individual spike the density of temporally neighboring spikes by convolving the spike train with a Gaussian kernel with an SD of 50 ms. The example neuron in Figure 5A demonstrates that high spike densities led to early (low) phases in the gamma cycle. This is evident in the negative linear–circular regression slope. Negative slopes were observed for the majority of neurons (80.65% negative slopes, of which 42% individually significant at α = 0.05) (Fig. 5B). The average slope was −0.60 ±0.13°/Hz of spike density (p = 1.8e−06, Wilcoxon's signed-rank test). This finding was consistent for monkey J (average slope: −0.76 ± 0.21; average t statistic: −1.6 ± 0.37; p = 2.6e−04), monkey L (average slope: −0.48 ± 0.14; average t statistic: −1.65 ± 0.69; p = 0.01), and monkey N (average slope: −0.56 ± 0.29; average t statistic: −0.76 ± 0.28; p = 0.01). The dependence of spike phase on spike density was specific for the respective gamma-frequency bands of the three monkeys (Fig. 5C–E).

Figure 5.

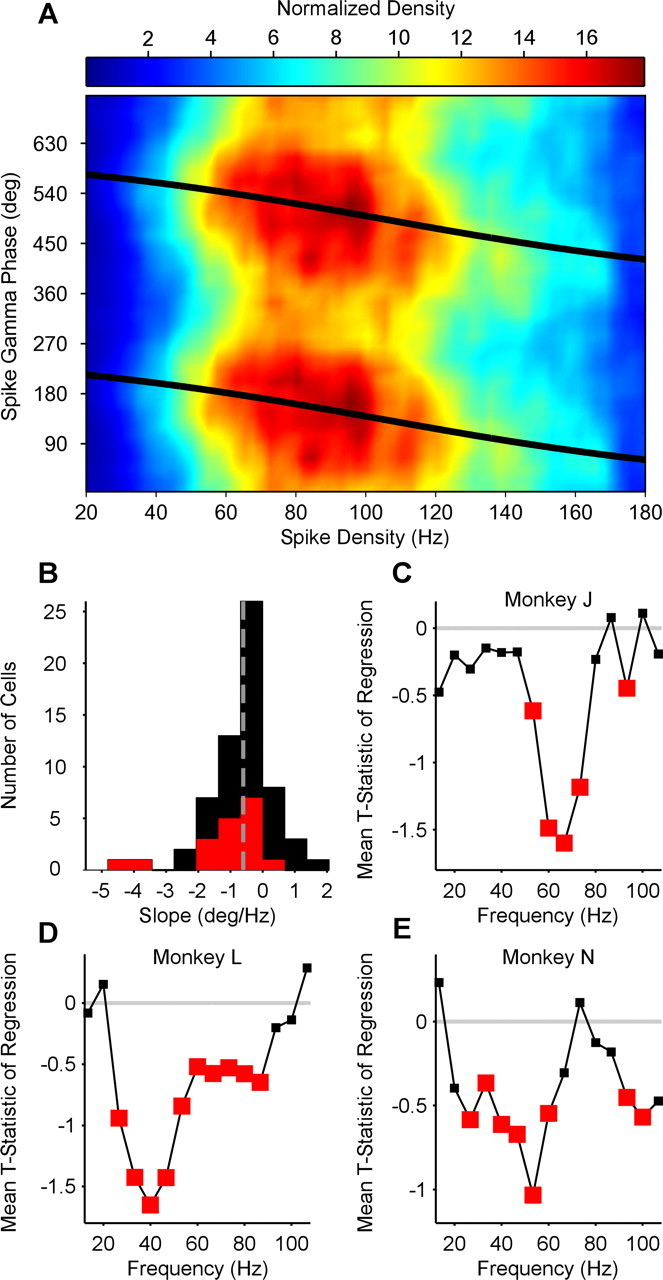
Figure 5.

Open in a new tab

The relationship between spike density and spike phase. A, Example neuron. Spike phase in the gamma cycle plotted as a function of spike density. Colors represent normalized density. B, Group result. Distribution of linear–circular phase-shift regression parameter across neurons. Red bars indicate significant regression weights. Distribution is clearly skewed to the left. C–E, Comparison of frequencies. Average t statistic of spike phase onto spike density regression plotted as a function of frequency. For each monkey, gamma-phase shifting is most significant in that monkey's individual gamma-frequency band (compare with Fig. 1). Red squares indicate significant mean t statistic values (two-sided t test).

To directly determine the spike phases associated with different spike densities, we binned spike densities and calculated the corresponding mean spike phases in the gamma cycle, averaged across all neurons. Those mean spike phases are shown as a function of the spike density percentile in Figure 6A. On average, spikes shifted from 157.2 ± 13.3° for the lowest spike density percentile to 127.1 ± 17.8° for the highest spike density percentile. This is reflected in a clear negative linear–circular regression (regression slope, −0.37 ± 0.10°/spike density percentile; p = 0.0010, two-sided t test).

Figure 6.

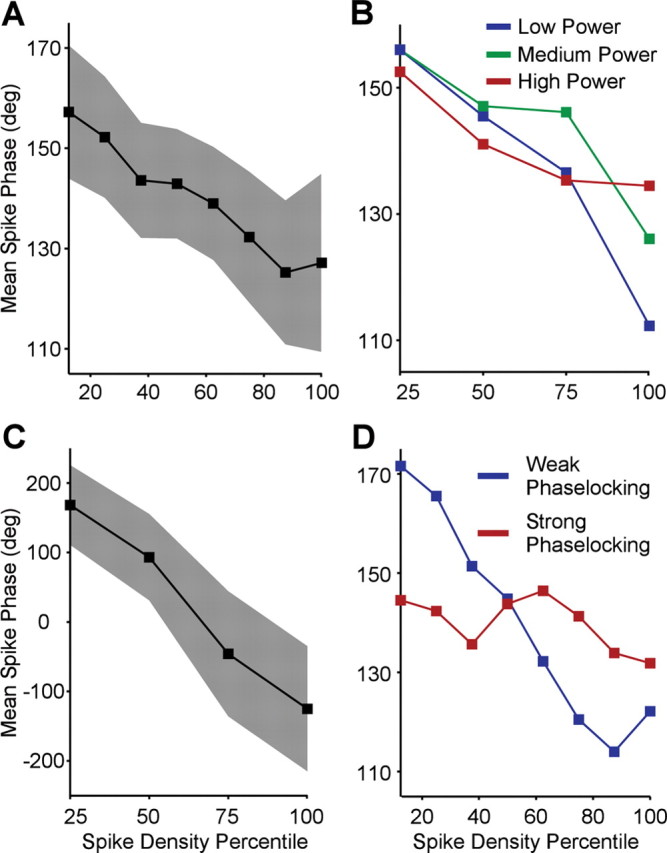
Figure 6.

Open in a new tab

Relationship between strength of rhythmic input and gamma-phase shifting. A, Group result. Mean spike phase in gamma cycle averaged across all neurons plotted as a function of spike density percentile. Filled region indicates 95% confidence intervals. B, Group result. Relationship between spike density percentile and spike phase in gamma cycle for trials with high power (red) versus trials with low power (blue). C, Mean spike phase in gamma cycle during fixation baseline period averaged across all neurons plotted as a function of spike density percentile. Filled region indicates 95% confidence intervals. D, Relationship between spike density percentile and spike phase in gamma cycle separate for neurons with strong phase locking (red) versus weak phase locking (blue).

Together, the results so far show that, within the gamma cycle, spikes occur earlier when the neurons are more strongly activated. The overall neuronal excitation level appears to interact with the gamma-rhythmic component of synaptic input such that higher excitation levels surpass rhythmic membrane potential modulation earlier. If this model is correct, then one might hypothesize that stronger rhythmic input constrains spike times more, i.e., stronger rhythmic input might lead to less activation-dependent shifting of spikes in the gamma cycle, because it might focus the spikes on the peaks of the depolarization cycle. We tested this hypothesis in three ways.

First, we tested whether the amount of phase shifting is related to the strength of rhythmic input in a given trial. We estimated the strength of gamma-rhythmic synaptic input indirectly by determining the gamma-band power of the LFP (Frost, 1967; Mitzdorf, 1985; Schroeder et al., 1995). We then used the gamma power to sort, for each neuron, the trials into low-, medium-, and high-gamma trials. Within those three groups of trials, we then determined the dependence of spike phase in the gamma cycle on the spike density percentile. Figure 6B shows that strong neuronal activation shifted spike phases less during high compared with low gamma-band power. Regression slopes were more negative during low gamma-band power than high gamma-band power (two-sided paired-sign test, p = 0.0396).

Second, we tested whether the activation-dependent phase shift was larger when gamma-band power was very weak in the absence of visual stimulation, during the fixation baseline. We analyzed the baseline period and confirmed that the average spike phase shift as a function of spike density was much larger during the baseline than during visual stimulation (Fig. 6C) (−7.72 ± 3.0999°/spike density percentile; p = 0.0064, two-sided t test).

Third, we used the fact that different neurons phase lock to the gamma rhythm to widely varying degrees. This variation might be attributable to either differences in how strongly a neuron is targeted by gamma-rhythmic input or how responsive to this input it is. We determined for each neuron how strongly it was, on average, phase locked to the gamma rhythm. For this particular analysis, we used a phase-locking measure that compensated for the effects of phase shifting on phase locking by essentially subtracting the estimated phase shift (for details, see Materials and Methods). We then used this shift-corrected metric of gamma-phase locking to sort neurons into weakly and strongly locked units. Figure 6D shows that activation-dependent gamma-phase shifts were much bigger in weakly (−0.71 ± 0.16°/spike density percentile; p = 6.55e−06, two-sided t test) compared with strongly gamma-locked units (−0.10 ± 0.125°/spike density percentile; p = 0.21, two-sided t test).

Discussion

To summarize, we found that neurons spike earlier in the gamma cycle of the LFP when they are more strongly activated, i.e., we observed gamma-phase shifting. We observed gamma-phase shifting first for different activation levels induced by different stimulus orientations. It held true when the activation level around each spike was estimated by the immediately surrounding spike density. We hypothesized that this gamma-phase shifting is brought about by the interaction of varying excitation levels with gamma-rhythmic synaptic input. In support of this, we found that gamma-phase shifting was particularly strong (1) during conditions when LFP gamma-band power was weak and (2) for neurons that were only loosely locked to the gamma rhythm. These latter results are consistent with the hypothesis that weak phase shifting is caused by strong gamma-rhythmic synaptic input, although the correlative evidence does not prove a causal relation.

One potential concern is that the observed changes in spike phase are trivial byproducts of changes in neuronal activation. Neuronal activation is measured by determining postsynaptic spike density, and increased spike numbers will reduce the variance of the phase estimate. However, spike number will not affect the mean of the phase estimate. Increased neuronal activation is also often associated with enhanced LFP power and improved spike–LFP locking (Friedman-Hill et al., 2000; Frien and Eckhorn, 2000; Frien et al., 2000), but the same reasoning holds: whereas the variance of the phase estimate is affected, the mean is not.

Another concern relates to the sorting of neurons into groups with weak and strong gamma-band phase locking. We found that neurons with weak locking shift more. It might be argued that this finding reflects a circularity, because neurons that shift much would have a low phase locking, by definition. We accounted for this by first estimating the phase shift with a regression and then determining the phase locking from the residual errors around the shifting mean phase (for a more elaborate account, see Materials and Methods). Thereby, the shifting mean phase is removed from the data before the phase locking is determined. Even with this correction, low phase-locking was related to large phase shifts.

Our findings complement the work on theta phase precession in the hippocampus (O'Keefe and Recce, 1993; Mehta et al., 2002; Harris et al., 2002) by demonstrating phase shifting for the gamma-frequency band in the awake monkey visual cortex. However, we emphasize one important difference: in hippocampal theta-phase precession, as spikes shift to earlier phases, the precision of theta-band synchronization decreases (Mehta et al., 2002). In contrast, in visual cortical gamma-phase shifting, spikes shift to earlier phases during stronger neuronal activation, and this enhanced activation is typically correlated with an enhanced precision of gamma-band synchronization (Friedman-Hill et al., 2000; Frien and Eckhorn, 2000; Frien et al., 2000). The reason for this discrepancy might be the more local generation of cortical gamma compared with hippocampal theta (Buzsáki, 2006). The theta-rhythmic inhibition that impinges on a given hippocampal neuron stems, at least to a substantial part, from distant and/or widespread neuronal networks (Buzsáki, 2002) whose activation is relatively independent of the local network of the respective neuron. Increased activation of the local network will therefore lift excitation such that it exceeds inhibition not only earlier but also longer in the theta cycle. Longer firing during the theta cycle gives more spike dispersion relative to the theta cycle, i.e., less precise spike–LFP theta phase locking. In contrast, the gamma-rhythmic input that impinges on a given cortical neuron stems predominantly from the local neuronal network whose activation is influenced and highly correlated with the activation of the respective neuron. Thus, increased activation of the local network will not only lift excitation, but it will also increase gamma rhythmic input. This increased rhythmic input will constrain neuronal spiking and thereby lead to stronger spike–LFP gamma phase locking.

It should be noted that, in rat hippocampus, neuronal spiking is locked not only to the theta rhythm but also to the gamma rhythm (Bragin et al., 1995). One study described different classes of hippocampal pyramidal cells that are locked to different phases of the gamma cycle (Senior et al., 2008). These phases differ for different phases of the theta rhythm, but the study did not investigate whether there is a systematic gamma-phase shifting.

One previous study investigated fine time shifts between MUAs recorded from electrodes in primary visual cortex of anesthetized cats (König et al., 1995). Cats were stimulated with drifting bars of varying orientation that activated different MUAs to different degrees. Strongly driven MUAs fired few milliseconds before weakly driven MUAs. These findings are consistent with ours, but our present results extend them in several respects. First, rather than relating two MUAs to each other, we related isolated single neurons to the LFP. This latter approach is used for the investigation of hippocampal theta-phase precession and thereby makes the two phenomena comparable. Second, König et al. studied the position of the central peak in cross-correlograms. This demonstrates a lead or lag in time, but it does not establish a frequency-specific phase shift, i.e., the earlier analysis could not establish gamma-phase shifting. Third, the spectral specificity attained through our approach enabled us to make a close link to models of gamma-band synchronization that prominently entail gamma-rhythmic inhibition (Bartos et al., 2007; Börgers and Kopell, 2008; Morita et al., 2008). Finally, our data were obtained in the awake monkey, demonstrating that gamma-phase shifting exists in the awake state and in the best available invasive model for the human brain.

One recent study investigated spike and LFP recordings from awake monkey secondary somatosensory cortex during tactile stimulation with varying levels of intensity (Ray et al., 2008). The authors set out to test the hypothesis put forward by us previously, stating that stronger activation of cortical neurons should lead to gamma-phase shifting (Fries et al., 2007). In short, the study failed to find evidence for this hypothesis, but this failure is most likely explained by a confound in the recorded signals. The study used spikes and LFPs recorded through the same electrode. The rapid extracellular potential fluctuations associated with action potentials are spectrally broad and therefore contribute also to the LFP. For this reason, previous studies that used spikes and LFPs from the same electrode explicitly removed the spike contribution to the LFP (Pesaran et al., 2002; Jacobs et al., 2007). These spike contributions to the LFP rise with frequency with the same spectral profile as the spectral energy that Ray et al. (2008) take as gamma-band activity (their Fig. 4). Thus, the signal components of the LFP, which Ray et al. consider to be gamma-band activity, reflect the spike itself. They record the spike also in the conventional way, i.e., through high-pass filtering and thresholding, and find that these conventionally recorded spikes have a fixed phase to their high-frequency LFP components. Because both signals reflect the same spiking events, it is self-evident that they do not shift relative to each other.

The potential consequences of gamma-phase shifting are at least twofold (Fries et al., 2007). (1) Excitatory neurons will likely have a bigger impact on their target neurons when they spike early in the gamma cycle. Gamma-rhythmic output typically entrains neuronal target groups (Börgers and Kopell, 2008). Those target groups are therefore undergoing rhythmic inhibition. This rhythmic inhibition will affect inputs least that arrive particularly early in the cycle. The precise arrival time of synaptic inputs depends also on the conduction delays, which, for distant neuronal groups, might be large relative to the phase shift. Therefore, the detailed sequence of neuronal firing in two (distant) interacting neuronal groups is an interesting issue for future research. Regardless of the precise timing relation between synaptic inputs and the phase of the ongoing gamma rhythm of the target group, early input spikes are in the position to trigger additional inhibition in the target group that will in any case diminish the impact of later spikes, thereby exerting a winner takes all mechanism. (2) Activity-dependent changes of synaptic efficacy are sensitive to the precise relative timing of presynaptic and postsynaptic activity, a phenomenon that is called spike timing-dependent plasticity (Markram et al., 1997; Bi and Poo, 1998; Caporale and Dan, 2008). It has been proposed that STDP might be enabled by gamma-band synchronization because the latter focuses neuronal activity in sufficiently short time windows (Wespatat et al., 2004). However, simple cofiring of presynaptic and postsynaptic neurons within short time windows does not lead to systematic STDP. Rather, STDP requires that the presynaptic neuron is either leading or lagging the postsynaptic neuron by a few milliseconds. This is achieved through gamma-phase shifting, because it translates different neuronal activation levels into different spike times during the gamma cycle. Intriguingly, during high-gamma states, spikes shifted less. Such small shifts should lead to maximal synaptic changes, because STDP is stronger for shorter delays between presynaptic and postsynaptic spiking. These predicted consequences of gamma-phase shifting should in principle apply to any two neuronal groups that are gamma-band synchronized, whether they are located within the same or different brain areas/structures (Womelsdorf et al., 2007).

To conclude, gamma-phase shifting is clearly present in awake monkey V1. It will be an important target for future research to test whether it leads to the predicted consequences. If so, gamma-phase shifting could be a very important phenomenon given the widespread occurrence of gamma-band synchronization in different species and brain regions and its relation to numerous cognitive functions (Fries, 2009).

Footnotes

This research was supported by The European Science Foundation European Young Investigator Award Program (P.F.), The Netherlands Organization for Scientific Research (P.F.), Max Planck Society, and the Ernst Strüngmann Institute. We thank C. Bosman for helpful comments.

References

  1. Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat Rev Neurosci. 2007;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
  2. Bi GQ, Poo MM. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci. 1998;18:10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Börgers C, Kopell NJ. Gamma oscillations and stimulus selection. Neural Comput. 2008;20:383–414. doi: 10.1162/neco.2007.07-06-289. [DOI] [PubMed] [Google Scholar]
  4. Börgers C, Epstein S, Kopell NJ. Background gamma rhythmicity and attention in cortical local circuits: a computational study. Proc Natl Acad Sci U S A. 2005;102:7002–7007. doi: 10.1073/pnas.0502366102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bragin A, Jandó G, Nádasdy Z, Hetke J, Wise K, Buzsáki G. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brosch M, Budinger E, Scheich H. Stimulus-related gamma oscillations in primate auditory cortex. J Neurophysiol. 2002;87:2715–2725. doi: 10.1152/jn.2002.87.6.2715. [DOI] [PubMed] [Google Scholar]
  7. Buschman TJ, Miller EK. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science. 2007;315:1860–1862. doi: 10.1126/science.1138071. [DOI] [PubMed] [Google Scholar]
  8. Buzsáki G. Theta oscillations in the hippocampus. Neuron. 2002;33:325–340. doi: 10.1016/s0896-6273(02)00586-x. [DOI] [PubMed] [Google Scholar]
  9. Buzsáki G. Rhythms of the brain. Oxford: Oxford UP; 2006. [Google Scholar]
  10. Buzsáki G, Chrobak JJ. Temporal structure in spatially organized neuronal ensembles: a role for interneuronal networks. Curr Opin Neurobiol. 1995;5:504–510. doi: 10.1016/0959-4388(95)80012-3. [DOI] [PubMed] [Google Scholar]
  11. Caporale N, Dan Y. Spike timing-dependent plasticity: a Hebbian learning rule. Annu Rev Neurosci. 2008;31:25–46. doi: 10.1146/annurev.neuro.31.060407.125639. [DOI] [PubMed] [Google Scholar]
  12. Csicsvari J, Jamieson B, Wise KD, Buzsáki G. Mechanisms of gamma oscillations in the hippocampus of the behaving rat. Neuron. 2003;37:311–322. doi: 10.1016/s0896-6273(02)01169-8. [DOI] [PubMed] [Google Scholar]
  13. Engel AK, Fries P, Singer W. Dynamic predictions: oscillations and synchrony in top-down processing. Nat Rev Neurosci. 2001;2:704–716. doi: 10.1038/35094565. [DOI] [PubMed] [Google Scholar]
  14. Fell J, Klaver P, Lehnertz K, Grunwald T, Schaller C, Elger CE, Fernández G. Human memory formation is accompanied by rhinal-hippocampal coupling and decoupling. Nat Neurosci. 2001;4:1259–1264. doi: 10.1038/nn759. [DOI] [PubMed] [Google Scholar]
  15. Fisher NI, Lee AJ. Regression models for an angular response. Biometrics. 1992;48:665–677. [Google Scholar]
  16. Friedman-Hill S, Maldonado PE, Gray CM. Dynamics of striate cortical activity in the alert macaque. I. Incidence and stimulus-dependence of gamma-band neuronal oscillations. Cereb Cortex. 2000;10:1105–1116. doi: 10.1093/cercor/10.11.1105. [DOI] [PubMed] [Google Scholar]
  17. Frien A, Eckhorn R. Functional coupling shows stronger stimulus dependency for fast oscillations than for low-frequency components in striate cortex of awake monkey. Eur J Neurosci. 2000;12:1466–1478. doi: 10.1046/j.1460-9568.2000.00026.x. [DOI] [PubMed] [Google Scholar]
  18. Frien A, Eckhorn R, Bauer R, Woelbern T, Gabriel A. Fast oscillations display sharper orientation tuning than slower components of the same recordings in striate cortex of the awake monkey. Eur J Neurosci. 2000;12:1453–1465. doi: 10.1046/j.1460-9568.2000.00025.x. [DOI] [PubMed] [Google Scholar]
  19. Fries P. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu Rev Neurosci. 2009;32:209–224. doi: 10.1146/annurev.neuro.051508.135603. [DOI] [PubMed] [Google Scholar]
  20. Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
  21. Fries P, Nikolić D, Singer W. The gamma cycle. Trends Neurosci. 2007;30:309–316. doi: 10.1016/j.tins.2007.05.005. [DOI] [PubMed] [Google Scholar]
  22. Fries P, Scheeringa R, Oostenveld R. Finding gamma. Neuron. 2008a;58:303–305. doi: 10.1016/j.neuron.2008.04.020. [DOI] [PubMed] [Google Scholar]
  23. Fries P, Womelsdorf T, Oostenveld R, Desimone R. The effects of visual stimulation and selective visual attention on rhythmic neuronal synchronization in macaque area V4. J Neurosci. 2008b;28:4823–4835. doi: 10.1523/JNEUROSCI.4499-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Frost JD., Jr Comparison of intracellular potentials and ECoG activity in isolated cerebral cortex. Electroencephalogr Clin Neurophysiol. 1967;23:89–90. [PubMed] [Google Scholar]
  25. Gray CM, König P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338:334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
  26. Harris KD, Henze DA, Hirase H, Leinekugel X, Dragoi G, Czurkó A, Buzsáki G. Spike train dynamics predicts theta-related phase precession in hippocampal pyramidal cells. Nature. 2002;417:738–741. doi: 10.1038/nature00808. [DOI] [PubMed] [Google Scholar]
  27. Hasenstaub A, Shu Y, Haider B, Kraushaar U, Duque A, McCormick DA. Inhibitory postsynaptic potentials carry synchronized frequency information in active cortical networks. Neuron. 2005;47:423–435. doi: 10.1016/j.neuron.2005.06.016. [DOI] [PubMed] [Google Scholar]
  28. Hoogenboom N, Schoffelen JM, Oostenveld R, Parkes LM, Fries P. Localizing human visual gamma-band activity in frequency, time and space. Neuroimage. 2006;29:764–773. doi: 10.1016/j.neuroimage.2005.08.043. [DOI] [PubMed] [Google Scholar]
  29. Jacobs J, Kahana MJ, Ekstrom AD, Fried I. Brain oscillations control timing of single-neuron activity in humans. J Neurosci. 2007;27:3839–3844. doi: 10.1523/JNEUROSCI.4636-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. König P, Engel AK, Roelfsema PR, Singer W. How precise is neuronal synchronization? Neural Comput. 1995;7:469–485. doi: 10.1162/neco.1995.7.3.469. [DOI] [PubMed] [Google Scholar]
  31. Maass W, Natschläger T. Networks of spiking neurons can emulate arbitrary Hopfield nets in temporal coding. Netw Comput Neural Syst. 1997;8:355–372. [Google Scholar]
  32. Maldonado PE, Friedman-Hill S, Gray CM. Dynamics of striate cortical activity in the alert macaque. II. Fast time scale synchronization. Cereb Cortex. 2000;10:1117–1131. doi: 10.1093/cercor/10.11.1117. [DOI] [PubMed] [Google Scholar]
  33. Markram H, Lübke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science. 1997;275:213–215. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
  34. Mehta MR, Lee AK, Wilson MA. Role of experience and oscillations in transforming a rate code into a temporal code. Nature. 2002;417:741–746. doi: 10.1038/nature00807. [DOI] [PubMed] [Google Scholar]
  35. Mitzdorf U. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiol Rev. 1985;65:37–100. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
  36. Morita K, Kalra R, Aihara K, Robinson HP. Recurrent synaptic input and the timing of gamma-frequency-modulated firing of pyramidal cells during neocortical “UP” states. J Neurosci. 2008;28:1871–1881. doi: 10.1523/JNEUROSCI.3948-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Muthukumaraswamy SD, Edden RA, Jones DK, Swettenham JB, Singh KD. Resting GABA concentration predicts peak gamma frequency and fMRI amplitude in response to visual stimulation in humans. Proc Natl Acad Sci U S A. 2009;106:8356–8361. doi: 10.1073/pnas.0900728106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Nikolić D. Non-parametric detection of temporal order across pairwise measurements of time delays. J Comput Neurosci. 2007;22:5–19. doi: 10.1007/s10827-006-9441-7. [DOI] [PubMed] [Google Scholar]
  39. O'Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993;3:317–330. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
  40. Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat Neurosci. 2002;5:805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
  41. Quian Quiroga R, Panzeri S. Extracting information from neuronal populations: information theory and decoding approaches. Nat Rev Neurosci. 2009;10:173–185. doi: 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
  42. Ray S, Hsiao SS, Crone NE, Franaszczuk PJ, Niebur E. Effect of stimulus intensity on the spike-local field potential relationship in the secondary somatosensory cortex. J Neurosci. 2008;28:7334–7343. doi: 10.1523/JNEUROSCI.1588-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Salinas E, Sejnowski TJ. Correlated neuronal activity and the flow of neural information. Nat Rev Neurosci. 2001;2:539–550. doi: 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Schneider G, Havenith MN, Nikolić D. Spatiotemporal structure in large neuronal networks detected from cross-correlation. Neural Comput. 2006;18:2387–2413. doi: 10.1162/neco.2006.18.10.2387. [DOI] [PubMed] [Google Scholar]
  45. Schoffelen JM, Oostenveld R, Fries P. Neuronal coherence as a mechanism of effective corticospinal interaction. Science. 2005;308:111–113. doi: 10.1126/science.1107027. [DOI] [PubMed] [Google Scholar]
  46. Schroeder CE, Steinschneider M, Javitt DC, Tenke CE, Givre SJ, Mehta AD, Simpson GV, Arezzo JC, Vaughan HG., Jr Localization of ERP generators and identification of underlying neural processes. Electroencephalogr Clin Neurophysiol Suppl. 1995;44:55–75. [PubMed] [Google Scholar]
  47. Senior TJ, Huxter JR, Allen K, O'Neill J, Csicsvari J. Gamma oscillatory firing reveals distinct populations of pyramidal cells in the CA1 region of the hippocampus. J Neurosci. 2008;28:2274–2286. doi: 10.1523/JNEUROSCI.4669-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
  49. Tiesinga P, Fellous JM, Sejnowski TJ. Regulation of spike timing in visual cortical circuits. Nat Rev Neurosci. 2008;9:97–107. doi: 10.1038/nrn2315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Vida I, Bartos M, Jonas P. Shunting inhibition improves robustness of gamma oscillations in hippocampal interneuron networks by homogenizing firing rates. Neuron. 2006;49:107–117. doi: 10.1016/j.neuron.2005.11.036. [DOI] [PubMed] [Google Scholar]
  51. Wehr M, Laurent G. Odour encoding by temporal sequences of firing in oscillating neural assemblies. Nature. 1996;384:162–166. doi: 10.1038/384162a0. [DOI] [PubMed] [Google Scholar]
  52. Wespatat V, Tennigkeit F, Singer W. Phase sensitivity of synaptic modifications in oscillating cells of rat visual cortex. J Neurosci. 2004;24:9067–9075. doi: 10.1523/JNEUROSCI.2221-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
  54. Wyart V, Tallon-Baudry C. Neural dissociation between visual awareness and spatial attention. J Neurosci. 2008;28:2667–2679. doi: 10.1523/JNEUROSCI.4748-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES