Targeted Motion Estimation and Reduction (TAMER): Data Consistency Based Motion Mitigation for MRI using a Reduced Model Joint Optimization

Abstract

We introduce a data consistency based retrospective motion correction method, TArgeted Motion Estimation and Reduction (TAMER), to correct for patient motion in MRI. Specifically, a motion free image and motion trajectory are jointly estimated by minimizing the data consistency error of a SENSE forward model including rigid-body subject motion. In order to efficiently solve this large non-linear optimization problem, we employ reduced modeling in the parallel imaging formulation by assessing only a subset of target voxels at each step of the motion search. With this strategy we are able to effectively capture the tight coupling between the image voxel values and motion parameters. We demonstrate in simulations TAMER’s ability to find similar search directions compared to a full model, with an average error of 22%, vs. 73% error when using previously proposed alternating methods. The reduced model decreased the computation time 17x fold compared to a full image volume evaluation. In phantom experiments, our method successfully mitigates both translation and rotation artifacts, reducing image RMSE compared to a motion-free gold standard from 21% to 14% in a translating phantom, and from 17% to 10% in a rotating phantom. Qualitative image improvements are seen in human imaging of moving subjects compared to conventional reconstruction. Finally, we compare in vivo image results of our method to the state-of-the-art.

I. Introduction

PATIENT motion during magnetic resonance imaging scans causes image artifacts that degrade diagnostic utility, often requiring repeated scans, patient callbacks, or lost diagnostic potential [1]. A 2015 paper examining the economic costs of motion at a US hospital found that 20% of MR scans were repeated due to patient motion, including 29% of inpatient and/or ED scans [2]. Motion also represents a challenge in pediatric imaging, where sedation or full general anesthesia are often required, increasing costs and posing increased risk to patients [3].

Because of the prevalence and impact of motion in MRI, many techniques have been developed to detect and correct for patient motion [4]. These techniques can be categorized broadly as either prospective or retrospective. In prospective methods, the imaging coordinate system defined by the MR scanner is updated based upon estimates of the patient movement throughout the scan [5]. Prospective techniques require repeatedly measuring the patient motion during the acquisition. This can be accomplished using external detectors [6], [7], image space navigators [8], [9], and FID navigators [10]. However, all of these methods add complexity to the exam. External markers require placement and calibration, and navigators can be disruptive to the acquisition sequence timing. If the scanner coordinate system is changed on the fly, the motion sensor must also be highly accurate to avoid introducing erroneous motion into the acquisition. Together, these problems have limited the use of prospective correction in the clinic.

Retrospective techniques have attempted to utilize external position tracking systems or navigator data to correct motion artifacts after the k-space data have been acquired. This lessens the concern of imperfect motion information corrupting the acquisition, since standard reconstructions can always be chosen if they give better results. Retrospective techniques include a priori motion information into a physical model to describe the effect of patient motion on the k-space data. By incorporating the effect of the measured motion into the forward model, they account for motion and reconstruct a motion free image, for example using a matrix formulation [11]. Studies have used a priori motion information both from MR navigators [12], [13], or from external tracking devices [14]. Periodic motion models for cardiac and respiratory imaging have also been applied to retrospective motion mitigation in body imaging by binning data into different motion states [15]–[17].

Determining motion directly from the k-space data offers an alternative to using measured motion information from navigators or tracking devices. In this case, only the raw k-space data is used to search for the motion parameters by either minimizing an image quality metric associated with motion, or by jointly estimating the motion parameters and image based on data consistency. In autofocusing [18], the image entropy or a similar criteria was minimized. Autofocusing techniques have been implemented for rigid [19], multirigid [20], and nonrigid [21] motion correction. Joint optimization of the image and motion has also been explored in the context of retrospective motion correction in PET/CT and PET/MR [22], [23].

In this work and others [24]–[28], a data consistency approach is taken. This approach utilizes the intrinsic encoding of motion within multi-channel array coils [29]. The motion information is then extracted from the k-space data by estimating both the rigid-body position parameters present for each shot of the image acquisition and the image itself via the forward model inversion. This has been previously done using an alternating minimization approach, either with an initial estimate of the motion from external sensors as in the GRICS method [24], or in a completely retrospective fashion [25], [26]. In our work, we introduce a reduced image reconstruction model to improve the joint-optimization procedure. In the TArgeted Motion Estimation and Reduction (TAMER) method, we address the computational challenge of the joint image-motion optimization by limiting intermediate motion search steps to targeted subsets of the image, which have been carefully chosen based on model separability. This approach is similar to reduced model approaches used for fast auto-calibration of gradient trajectories for wave-CAIPI MRI reconstruction [30].

II. Theory

A. Mathematical Description

The SENSE [31] based rigid-body motion forward model describes the signal acquired in a 2D multishot imaging sequence:

$$\mathit{s}={\mathit{E}}_{\theta }\mathit{x}$$ (1a)

$${\mathit{E}}_{\theta }=\left[\begin{array}{c}\hfill {{\mathit{E}}_{\theta }}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {{\mathit{E}}_{\theta }}_{N_{sh}}\hfill \end{array}\right]$$ (1b)

where x is a N × 1 column vector of the N image voxel values, E_θ is the NC × N forward model operator (encoding matrix) for a given M × 1 patient motion trajectory θ, and s is the NC × 1 multichannel signal data from C coils. E_θ is the concatenation of the encoding model for each of the N_sh shots (M = 6N_sh for the six rigid-body motion parameters at each shot). The encoding model for each individual shot, l, can be described as:

$${\mathit{E}}_{{\theta }_l}={\mathit{U}}_l{\mathit{FCT}}_{xy,l}{\mathit{T}}_{z,l}{\mathit{R}}_l$$ (2)

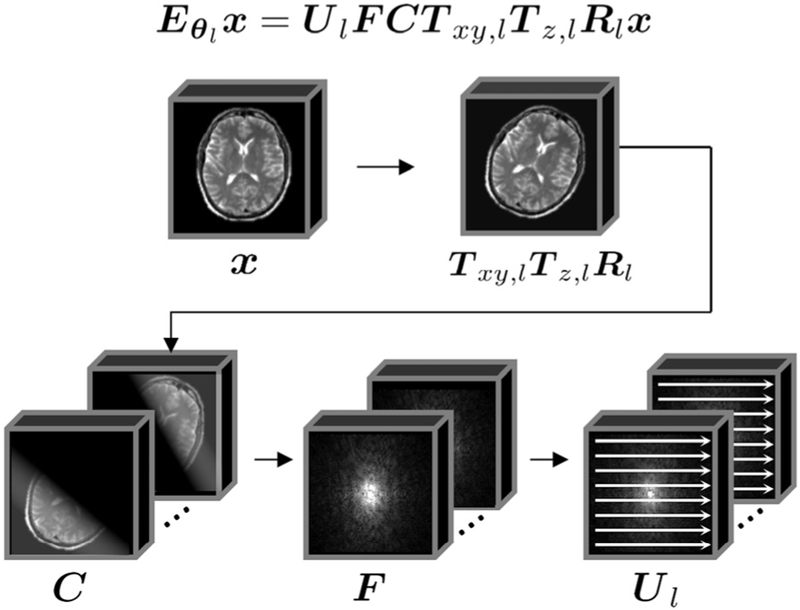
where for shot l, R_l is the rotation operator, T_z,l is the through-plane translation operator, T_xy,l is the in-plane translation operator, C contains the spatially varying coil sensitivities, F is the Fourier encoding operator, and U_l is the nC × NC undersampling operator, where n is the number of k-space samples acquired per shot (N_shn = N). See Fig. 1 for an illustration of the motion forward model, and Appendix A (Supplementary Materials) for a more detailed description of the motion terms.

Fig. 1.

Illustration of the Forward Model. The k-space data for a given shot lis related to the 3D image volume to be reconstructed, x, through the following operators: (1) image motion, which includes rotations, R_l, through-plane translation, T_z,l, and in-plane translations, T_xy,l (2) weighting by the coil sensitivity matrix C (3) Fourier encoding operator F (4) k-space data for the individual shots are created using the undersampling operator U_l.

The goal of this work is to jointly optimize the motion trajectory θ and the image volume x by minimizing the data consistency error:

$$[\widehat{\theta },\widehat{\mathit{x}}]={\text{argmin}}_{\theta ,x}\Vert \mathit{s}-{\mathit{E}}_{\theta }\mathit{x}{\Vert }_2$$ (3)

B. Motivation for Reduced Model

In a typical forward model based image reconstruction, a least-squares objective function ∥s-Ex∥₂ would be minimized to estimate x, e.g. using the conjugate gradient method. Typically, the unknowns would only appear in x, whereas in the TAMER optimization problem (3), the additional motion unknowns appear in E_θ. This corresponds to a more difficult non-linear estimation that requires repeated evaluation of linear least-squares objectives based upon motion trajectories of interest. To ameliorate the computational challenge of this joint optimization, we introduce a model reduction scheme.

Solving this large computational problem has been explored using an alternating optimization approach [25], [26]. In that work, the algorithm alternates between performing a full-volume reconstruction of the image and then taking a single (or very small number) of optimization steps to update the motion estimates. A strength of this approach is that it breaks a difficult joint optimization problem up into two smaller ones. The benefit of this division depends on the separability of the two types of optimization variables (voxel values and motion parameters). For example, the first step to search for the motion variables occurs after a full solve of all the voxel unknowns, and is thus likely to pursue an accurate initial search direction that will improve the objective function. For subsequent iterative steps estimating motion parameters, the quality of the search directions (∇ in Eqn. 8 below) might degrade if tight coupling exists between the two types of optimization variables. In this case subsequent motion parameter estimates are not as accurate which will not allow for the objective to be improved. At this point the alternating algorithm will re-estimate the voxel values using the most recent motion estimate. If the alternating algorithm can only take a few steps before switching to the other variable type, the efficiency is reduced. The reduced efficiency is primarily expected to impact computational speed, yet we note that the variable separation approach as implemented in [26] performs well and quickly. Their approach also makes effective use of reduced spatial resolution image data to speed up both searches and an analytic gradient calculation for the motion search direction.

Because there are uncertainties about the coupling between the voxel and motion parameters and open questions on the effect of using low spatial resolution versions of the data during the optimization, we sought an alternative approach that does not rely on complete uncoupling of the variables. Here, we employ a reduced model of the image reconstruction which can be repeated quickly for every estimation of the motion variables. In this scenario, the trade-off between accuracy and computation time is based on the number of target voxels used when searching for the motion. The data consistency of the reduced data set is evaluated for each potential motion step, capturing the effect of coupling between the variables. A hypothesis of the approach is that the search directions for the motion parameters are improved by this regular update of the chosen subset of voxel intensities. After the motion estimate has converged, a full volume solve (estimation of all the voxels) is performed to generate the final image. It is important to note that neither method (alternating nor TAMER) however can guarantee convergence to a global minimum, due to the properties of the non-linear problem being solved. It is also important to note that hybrid methods which use both alternating minimization and reduced data models could be formed.

C. Model Reduction Using Target Voxels

The vector of image voxel values, x, is broken into two parts to decrease the size of the reconstruction at any given iteration. Specifically, the vector is broken into: x_t, a small targeted subset of voxels (typically ~5%), and x_f, a fixed subset of voxels that is temporarily set constant to values associated with the best previous motion estimate iteration. By fixing a large portion of the voxels to constant values, the number of parameters to be minimized in (3) can be reduced by an order of magnitude. The indices of x_t are determined based on the structure of the encoding matrix, E_θ. See Section II-E for a detailed discussion of target voxel selection.

This voxel separation allows for the linear encoding model to be broken down into two encoding submatrices E_θ(t) and E_θ(f) which operate on the target and fixed voxels, respectively:

$${\mathit{E}}_{\theta }\mathit{x}=({\mathit{E}}_{\theta }(t){\mathit{E}}_{\theta }(f))\left(\frac{{\mathit{x}}_t}{{\mathit{x}}_f}\right)$$ (4)

This separation of x and E_θ can be done for any choice of target and fixed voxels. We can now separate the signal, s, into two terms: s_t, the signal contribution from the target voxels, and s_f, the signal contribution from the fixed voxels.

$${\mathit{E}}_{\theta }\mathit{x}={\mathit{E}}_{\theta }(t){\mathit{x}}_t+{\mathit{E}}_{\theta }(f){\mathit{x}}_f={\mathit{s}}_t+{\mathit{s}}_f$$

Both s_t and s_f are the same length as s, NC × 1, but they contain signal from the different voxel sets. To isolate the signal contribution of the target voxels, s_t, we can subtract the contribution of the fixed voxels from the total signal s:

$${\mathit{s}}_t=\mathit{s}-{\mathit{E}}_{\theta }(f){\mathit{x}}_f={\mathit{E}}_{\theta }(t){\mathit{x}}_t$$ (5)

The optimization can now be reduced to fitting the signal contribution of the target voxels s_t to the correct target voxel values x_t and the correct motion θ. The non-linear joint optimization of the motion and target voxels is now the following:

$$[\widehat{\theta },{\widehat{x}}_t]={\text{argmin}}_{\theta ,{\mathit{x}}_t}\Vert {\mathit{s}}_t-{\mathit{E}}_{\theta }(t){\mathit{x}}_t{\Vert }_2$$ (6)

Here, E_θ(f)x_f (a large, slow operation) is evaluated only once for each motion estimate θ. The repeated evaluations of E_θ(t)x_t necessary to find x_t using conjugate gradient are fast, due to the small size of x_t and the ability to cache many of the operators illustrated in Fig. 1.

D. TAMER Algorithm

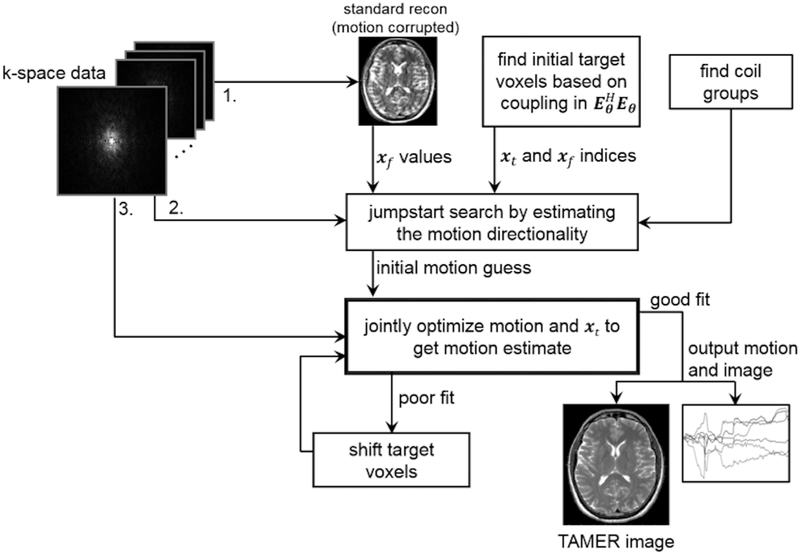
The TAMER method is comprised of three stages: (1) an initial SENSE reconstruction across the complete volume (assuming all motion parameters are zero), followed by the target voxel selection and channel grouping, (2) jumpstart of the motion parameter search to improve convergence of the optimization, and (3) efficient search for motion parameters using the reduced model joint optimization. A schematic overview of the method is described in Fig. 2.

Fig. 2.

TAMER overview. (1) Raw k-space data is used to reconstruct a motion corrupted image, a target voxel pattern is selected to be jointly optimized along with the motion parameters, and the coils on which to run TAMER are grouped based on observed motion artifacts (2) jumpstart of the motion parameters through a coarse grid search, and (3) joint optimization of motion parameters and spatially varying target voxels.

1). Initialization: Image Estimate, Select Target Voxels, & Group Channels:

First, we perform an initial reconstruction of the full image volume, x₀, assuming all motion parameters are zero. Here we calculate x₀ by minimizing the least squared error of the forward model with zero motion by solving the system

$$\left({\mathit{E}}_0^{\mathit{H}}{\mathit{E}}_0\right){\mathit{x}}_0=\left({\mathit{E}}_0^{\mathit{H}}\mathit{s}\right)$$

using conjugate gradient, where E₀UFC, and ${\mathit{E}}_0^{\mathit{H}}$ denotes the conjugate transpose of E₀. The sensitivity maps in C are found using the ESPIRiT method provided as part of the Berkeley Advanced Reconstruction Toolbox [32]. Note that the sensitivity maps in the TAMER forward model are considered to be spatially fixed and independent of any coil loading differences that arise through patient movement.

Next, the indices of the initial target voxels (i.e. the voxel coupling pattern) are selected using the locality of interaction properties contained in the encoding matrix. This can be done without a priori knowledge of the k-space data or underlying image. They are determined solely by the sequence parameters and coil sensitivities (see Section II-E for a detailed discussion of target voxel selection).

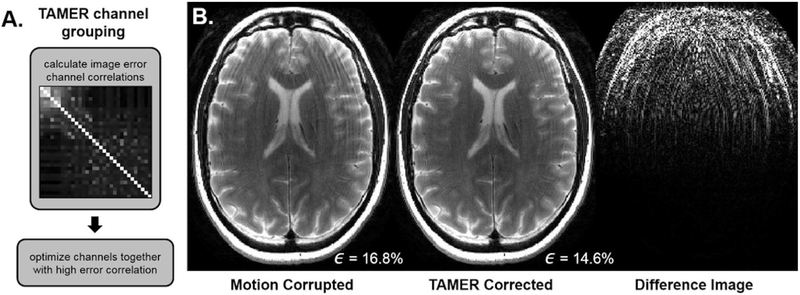
Prior to jointly estimating the motion and voxels based on data consistency, the channels are grouped by their motion artifact properties. This grouping is formed by comparing the data consistency error between the measured k-space data and the forward model with no motion, F⁻¹{s – E₀x₀}. The 2D correlation coefficient of this metric is computed across all channels, and coils with similar motion artifacts will have high correlation. During the iterations to find the motion and image estimates, only the coil group with the largest correlated artifacts is used. After convergence the final motion time course is applied to the data from these coils, and a final image is reconstructed. The correlation across channels was investigated for all data sets used here, and this process can be automated by employing standard clustering algorithms [33].

2). Jumpstart of Motion Parameter Search :

To provide an initial guess of the patient motion for the joint optimization, the data consistency metric is evaluated over a coarse range of values for each motion parameter independently. These values can be quickly calculated in parallel, and the best value for each motion parameter is used to construct the initial search direction for the joint optimization. In our experience, generic optimization packages such as that used in this work can struggle to get out of a trivial initial search position due to lack of tuning of the optimization parameters. Here we used rotation angles within ±5°, with a step size of 1° and the translation ranges were chosen similarly but in units of voxel shifts (not degrees).

3). Joint Optimization of Motion Trajectory and Imaging Volume Using a Reduced Model Search:

After determining the initial target voxels, motion estimate, and coil groupings, the reduced model joint optimization (6) is performed using a quasi-Newton search [34]. Specifically, we use the standard MATLAB (Mathworks, Natick, MA) unconstrained non-linear optimization tool, fminunc, for ease of implementation, but algorithm performance could be improved with a custom descent algorithm such as the one used in [26]. In the TAMER method, we limit our search to only consider an optimal subset of voxel values for any given motion estimate. Thus, the motion trajectory, θ, contains the M optimization variables, and when evaluating the data consistency of any given motion estimate, only target voxels are reconstructed to find an estimate of the joint data consistency error.

For a given motion trajectory estimate at search step i (i.e. θ⁽ⁱ⁾), the reconstructed target voxels, ${\mathit{x}}_t^{(i)}$, are found using conjugate gradient by solving the system:

$$\left({\mathit{E}}_{{\theta }^{(i)}}^{\mathit{H}}(t){\mathit{E}}_{\theta }^{(i)}(t)\right){\mathit{x}}_t^{(i)}={\mathit{E}}_{{\theta }^{(i)}}^{\mathit{H}}(t){\mathit{s}}_t^{(i)}$$

${\mathit{s}}_t^{(i)}$ is found using (5), where the initial values of x_f are the values of x₀ at the corresponding indices. Once ${\mathit{x}}_t^{(i)}$ is calculated, the estimated data consistency error for step i can be evaluated using the full forward model:

$${ϵ}^{(i)}={\Vert \mathit{s}-{\mathit{E}}_{{\theta }^{(i)}}{\mathit{x}}^{(i)}\Vert }_2$$ (7)

This represents one evaluation of the objective function for input motion trajectory θ⁽ⁱ⁾.

To calculate the gradient at step i across all M motion parameters θ⁽ⁱ⁾, we find the change in data consistency error for a small change in θ⁽ⁱ⁾, keeping x⁽ⁱ⁾ constant.

$${\nabla }^{(i)}={ϵ}^{(i)}-{\Vert \mathit{s}-{\mathit{E}}_{{\theta }^{(i)}+\delta \theta }{\mathit{x}}^{(i)}\Vert }_2$$

The new motion estimate is updated using this finite difference gradient approximation

$${\theta }^{(i+1)}={\theta }^{(i)}+{\nabla }^{(i)}$$ (8)

As the joint optimization progresses, the target voxel pattern is shifted across the image. Voxel values at the previous target indices are updated in x_f. The search continues until the maximum number of steps has been taken, or the data consistency converges. It is possible that the high frequency portions of k-space are not resolved in the joint optimization, due to the dominance of the low k-space error in the data consistency minimization. To overcome this potential problem, the joint optimization in (6) can be modified such that the high k-space errors are weighted more heavily in the minimization (such as with an inverse Gaussian filter).

This reduced model search allows for a fast evaluation of many motion trajectories, while also ensuring the motion estimates have high data fidelity by reconstructing the target image volume. TAMER can also be parallelized in several ways. The conjugate gradient call (step 3b) can be parallelized to solve for ${\mathit{x}}_t^{(i)}$ at each step, or different target voxel sets can be optimized in parallel. The gradient evaluation (step 3d) can be computed in parallel as well.

E. Target Voxel Selection – Correlation Matrix Method

The reduced model optimization in (6) is most effective when voxels that are coupled strongly to each other are optimized together. Voxel coupling in MRI occurs whenever there is ambiguity in the encoding of the MRI signal, e.g. undersampled and/or motion corrupted Cartesian acquisitions and many non-Cartesian acquisitions. For example, in a motion free Cartesian R = 2 SENSE image reconstruction, voxels that are located FOV/2 apart in the phase encode direction are coupled to each other.

Mathematically, voxel coupling is described using the correlation matrix, E^HE. The correlation matrix is very large and is typically never explicitly calculated in full. However, the coupling seen by an individual voxel can be easily computed by applying the forward operator, E, and then the adjoint operator, E^H, to a delta function, i.e. (E^HE) δ_j = (E^HE)_j. The magnitude of the entries in this column of the correlation matrix represent the strength of interaction of each voxel on the voxel j, (i.e. x_j). We will refer to this voxel, x_j, as the “root voxel” which will be used to form the target voxel pattern. For a fully sampled, motion-free Cartesian acquisition, each voxel is only coupled to itself, and the correlation matrix would be diagonal.

The first column of Fig. 3 shows an example of a subset of E^HE for no motion, measured patient motion, and random motion, all for RARE [35] imaging with R = 2 undersampling and echo train length (ETL) of 8, which represents the number of k-space lines collected per shot (ETL is also referred to as the turbo factor). For the no motion case, only two voxels in each column are non-zero, because only two voxels are coupled as a result of the R = 2 undersampling in k-space. However, when the encoding matrix includes patient movement, the correlation matrix shows an increased level of voxel coupling. When random motion is used instead of a patient’s measured motion, the observed coupling pattern is similar. Thus, we utilize random motion as a proxy to the unknown motion trajectory in order to easily determine the most likely coupling pattern for the voxels.

Fig. 3.

Target Voxel Selection. First Column: Correlation matrix (${\mathit{E}}_{\theta }^{\mathit{H}}{\mathit{E}}_{\theta }$) for the voxels shown in the white outlined ROI on the left (log scale). Second Column: For a given root voxel (i.e. one row of the correlation matrix), the correlation of the other voxels to the root voxel is plotted (linear scale). Third Column: The magnitude of each voxel’s correlation to the root voxel is plotted in image space (log scale). Fourth Column: The target voxels are chosen for a given region of correlated voxels using thresholding. The motion values used in the second row are from the motion trajectory measured during an fMRI scan of a patient with Alzheimer’s disease.

The second column of Fig. 3 shows a single column of the correlation matrix, (E^HE)_j, for no motion, patient motion, and random motion. A single column of the correlation matrix represents the magnitude of coupling between a root voxel and each of the other imaging voxels. For this example, the root voxel is shown with a black “X” on the image in Fig. 3. These values are plotted in image space in the third column of Fig. 3. As one would expect for the two motion cases, the spacing between coupled voxels in image space is the FOV/ETL. This is because for RARE imaging, each shot can be thought of as an individual motion free image that is highly undersampled. The aliasing pattern from this type of undersampling will alias voxels spaced by FOV/ETL in the phase encode direction, leading to the coupling properties seen in Fig. 3.

To create a specific target voxel pattern, a “root” voxel is chosen, and the column of the correlation matrix with the same index as the root voxel is computed. For all the examples presented in this paper, the center image voxel was used as the “root” voxel. The voxel coupling values are then thresholded and smoothed to create the target voxel set (fourth column of Fig. 3). This target voxel pattern can then be used in the reduced model optimization.

The target voxels are changed throughout the optimization by shifting the initial target voxels perpendicular to the phase encode (and therefore voxel coupling) direction. This follows a similar procedure to that of domain decomposition for solving linear systems of equations [34]. Specifically, in order to converge to the global solution for a fully coupled problem, the boundary conditions for any subset of voxels needs to be correct. Thus, we shift the target voxel pattern across the imaging region during each step of the optimization. We shift the target voxels perpendicular to the phase encode direction by roughly the diameter of the disks show in Fig. 3. Once the pattern has done a full “sweep” across the FOV, we shift the pattern along the readout direction and repeat. To create 3D target voxel subsets, we consider the target voxel regions to be uniform across all slices. Thus, the circular target voxel subsets shown for a single slice example in Fig. 3 are cylinders extending across all slices for a multi-slice imaging volume.

Note that the target voxels for a true motion trajectory and a random motion trajectory are very similar, hence we do not need to know the patient motion a priori to create an accurate target voxel subset. This technique is applicable to many other acquisition types when bulk rigid motion occurs, but the method’s performance for non-rigid body motion has not been investigated in this work, although the target voxel approach might be useful in non-rigid motion models.

III. Experiments

The ability of the TAMER optimization to mitigate motion artifacts was tested using simulations, phantom data, and human subject data. Simulations were performed to verify TAMER’s ability to correct for motion, to compare its search accuracy to an alternating implementation, and to compare different target voxel subsets. Validation also included acquiring corrupted data from a translating anthropomorphic head phantom, a rotating pineapple phantom, and in vivo brain data from a healthy adult subject. To compare to the work in [26], we have reconstructed a subset of their provided neonate motion-corrupted data, and compared the image results.

A. Simulations

1). TAMER Method Validation:

The validation data were acquired on a 3T Siemens Trio scanner (Siemens Healthcare, Erlangen, Germany) with the standard Siemens 32-channel head array coil. T₂-weighted RARE images were acquired with 224 × 224 mm² field of view, resolution 0.5 × 0.5 × 3.0 mm³, TR = 6.1 s, TE = 98 ms, flip angle 150°, and R = 1. For the simulation experiments a single slice from the data was down-sampled to a 128 × 128 matrix size (1.75 × 1.75 mm² resolution) and used as the ground truth k-space data.

A modified version of the forward model in Eqn. (2) was applied to the motion-free dataset to generate a dataset with motion effects where the gold-standard motion-free image was also known (note the term for the coil sensitivities (C) was omitted since we apply the motion-corrupting forward model to individual coil data). The simulated motion time-course was from an Alzheimer’s disease patient’s motion trajectory found using motion alignment of functional MRI timeseries data [36]. We selected a segment of the full motion trajectory that included both in-plane rotation and in-plane translation, but no through-plane motion, to investigate motion effects on a single slice.

The 2D version of the TAMER algorithm was then applied to the slice of motion corrupted k-space data assuming standard protocol parameters, R = 2 undersampling, and turbo factor = 16. Reconstructed images were compared to the ground truth no motion images to verify the algorithm’s ability to converge to the ground truth motion.

The TAMER reduced model allows for motion transformations to be performed across small regions of the 3D FOV, and restricts the regions that FFTs need to be applied and would allow for specific cached DFT matrices to be used. These properties hold as we continuously shift the target voxel pattern across the volume during TAMER. To investigate the computational cost of the target voxel updates vs. full volume reconstruction, we performed repeated evaluations of the objective function for the reduced and full model using the 128 × 128 image, but without the use of cached local DFTs. We used ~5% of the voxels in the image for the reduced model, and with this size reduction we were able to create a fast, cached motion operator implementation. 1000 objective function calls were performed for the two methods (cached reduced model and full model), and the average computation time of each operation in the forward model (add motion, weight by coil sensitivities, Fourier transform, sampling operation) was measured.

2). Targeted vs. Alternating Motion Parameter Search Accuracy:

We demonstrate using simulations the potential advantages of a reduced model joint minimization over an alternating minimization. We implemented an alternating minimization where at each step we calculated: (1) the search direction of an alternating method with no voxel updates (2) the search direction when updating a small subset of target voxels, and (3) the full model search direction that would be determined after performing a full-volume solve (which can be thought of as the ground truth search direction). The alternating motion gradient’s and the targeted motion gradient’s directionalities were then compared to that of the full model.

3). Comparison of Voxel Selection Methods:

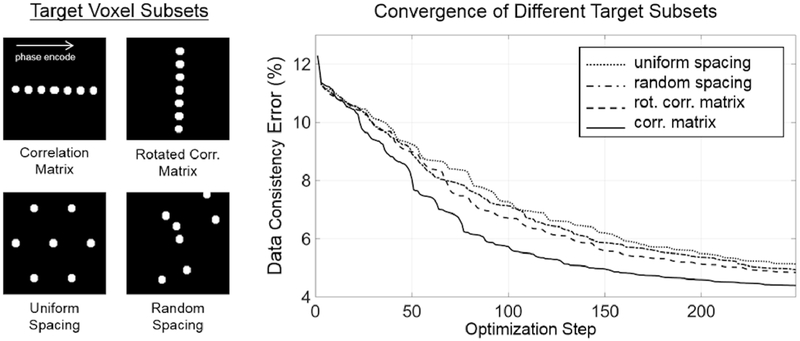
To investigate TAMER’s dependence on voxel coupling properties, the convergence for various target voxel subsets were investigated. Three different voxel subsets were compared to the correlation matrix method: (1) a rotated correlation matrix (i.e. voxels along the readout direction instead of the phase encode direction are used), (2) uniformly spaced voxel disks (of the same size as the disks used in the correlation matrix method), and (3)randomly spaced voxel disks. The convergence curves of each method were compared, as well as their respective output images. Note that these voxel selection methods were used here for comparison only, and all proceeding experiments use the correlation matrix method for voxel selection as described in Section II-E.

B. Phantom Experiments

To test the ability of TAMER to mitigate translational movement, an anthropomorphic head phantom was placed on a translation stage and moved intermittently throughout the scan in the anterior-posterior direction. Data were acquired on a 3T Siemens Trio scanner with a 12-channel birdcage array coil using a standard Siemens 2D T₂-weighted RARE sequence. Sequence parameters include TR = 3.0 s, TE = 99 ms, ETL = 11, 220 × 220 mm² FOV, 12 slices, resolution 0.9 × 0.9 × 3 mm³, and R = 1. The target voxels were 3-4% of the total voxels depending on the slice. Each slice of the volume was reconstructed independently using the 2D version of TAMER since the motion was restricted to in-plane.

TAMER’s ability to suppress rotation artifacts was examined by reconstructing phantom data from a pineapple that was rotated in-plane throughout the scan using a motion actuator. Data were acquired on a 1.5 T Siemens Avanto scanner with a 12-channel head matrix coil using a standard Siemens 2D T₂-weighted RARE sequence. Sequence parameter were ETL = 16, 230 × 208 mm² FOV, 0.6 × 0.6 mm² in-plane resolution, 5 mm slice thickness, TR = 3.8 s, TE = 93 ms, refocus angle = 150°, and R = 1. The coil data was automatically compressed to eight channels by the vendor hardware. The target voxels were 2.7% of the total voxels. 2D TAMER was first performed on this dataset as described in equation (6). The objective function was then minimized again using the first result as a starting point, but with an inverse Gaussian filter weighting high frequency k-space components. This seems to have been helpful in resolving fine structures in the image. Given the noise promotion of this reweighting, we choose to denoise the final image using Tikhonov regularization, although this step may be excluded if desired, and does not affect the motion estimates (i.e. Tikhonov regularization was not used in the minimization objective function).

C. In Vivo Experiments

The TAMER optimization was tested on a human adult subject who was asked to shake their head during the middle of the scan to create motion artifacts. The 2D version of TAMER motion correction was applied here for in-plane motion only on a single slice. The instructions given to the subject were to “nod no” and the axial slice prescription was chosen to create mainly in-plane motion effects; however, unlike the phantom experiments, the experiment is not fully controlled, and it is possible that through-plane motion might also have occurred. The data were acquired using ETL = 11, 220 × 220 mm² FOV, 0.9 × 0.9 mm² resolution, 3 mm slice thickness, TR = 3.0 s, TE = 99 ms, refocus angle = 150°, and R = 1 on a 3T Siemens Trio scanner with a 32-channel head array coil. The target voxels were 2.4% of the total voxels.

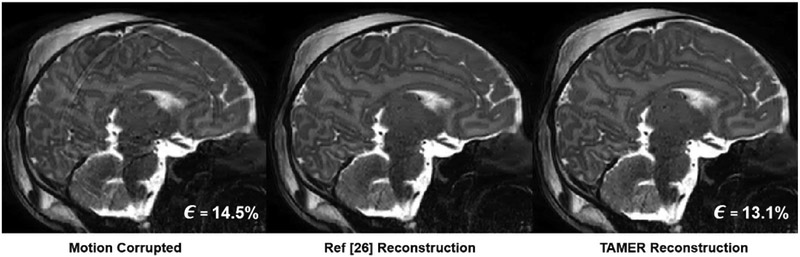
To validate the image quality of our method compared to the state-of-the-art, we reconstructed the data provided with [26] from https://github.com/mriphysics/multiSliceAlignedSENSE/releases/tag/1.0.1. The data set provided was for a neonatal subject with uncontrolled motion, and the dataset was down sampled in the slice direction to remove the slice oversampling. Five slices were then reconstructed using TAMER 3D motion correction and the method in [26], performing both in-plane and through-plane motion correction on the R = 2.49 undersampled data. To provide similar image results, the settings for the reconstruction in [26] were also altered to turn off outlier rejection, slice smoothing, and Gibbs filtering.

IV. Results

We present results showing the ability of the TAMER optimization to mitigate motion artifacts. Simulation results show the algorithm’s accuracy when a ground truth motion trajectory is known. In addition, simulations are used to compare the search direction of a targeted vs. alternating approach, and to compare the convergence between various voxel selection methods. Experimental results include reconstructing motion corrupted data from a translating anthropomorphic head phantom, a rotating pineapple phantom, and in vivo brain data from both a healthy adult subject and a neonatal dataset provided in the accompany code of [26].

A. Simulation Results

1). TAMER Method Validation:

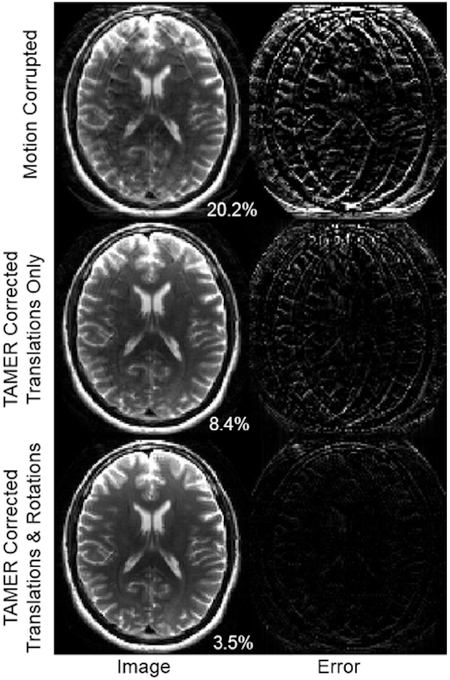
Figure 4 shows the results of applying the TAMER method to simulated motion data. This k-space data was corrupted by both translations and rotations, resulting in an image RMSE of 20.2% compared to a ground truth image. The image improves when jointly optimizing the image and translational motion parameters, resulting in an 8.4% image RMSE. The image is further improved by correcting both translation and rotation motion parameters, resulting in a 3.5% image RMSE.

Fig. 4.

TAMER results in data with simulated motion. (Top) Motion corrupted image. Right column shows difference image formed from the gold standard (uncorrupted) image. (Middle) Image reconstructed using TAMER when only correcting for translations. (Bottom) Image reconstructed when optimizing for both in-plane translation and rotation. Percentages in bottom right correspond to image space RMSE compared to ground truth.

Using this simulated example again (128 × 128 image matrix size, single slice), we measured an overall 17x computational speedup when using target voxel updates compared to the full volume solves, with a speedup for each of the individual steps of: motion operators 82x, coil sensitivities 4x, Fourier transform 5x, and the sampling operator 4.5x.

2). Targeted vs. Alternating Search Accuracy:

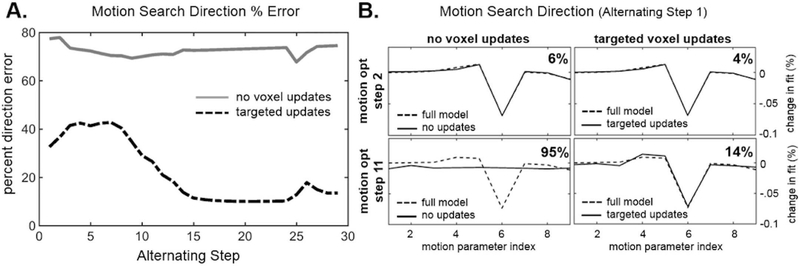
Figure 5 shows the motion search direction accuracy of the motion parameters relative to the “gold standard” search direction. The motion search direction (∇ in Eqn. 8) is the difference between the motion estimates at each step of the search (i.e. θ⁽ⁱ⁺¹⁾ = θ⁽ⁱ⁾+∇⁽ⁱ⁾). The “gold standard” is taken as the search direction found after a full volume solve of the image voxels. In this assessment, a full volume solve of all the voxels is done, followed by 13 iterations of the motion parameter search. This process is then repeated 30 times. If no update of the voxel information occurs during the motion iterations, this would represent an alternating optimization with 13 motion iterations per spatial solve. By construction, the error is 0% for the first of the 13 motion iterations, but grows as the motion search progresses in the absence of updated voxel information, so we plot the average error of the 13 iterations. Fig. 5-A (solid gray curve) shows that the average search error over the 13 motion steps is relatively constant at about 73% for the 30 alternations when no voxel information is updated. In the dotted curve in Fig. 5-A, the first motion search direction is computed the same way; based on the full volume solve of the voxel data. But the remaining 12 motion estimate iterations are informed by an evaluation of the target voxels. In this case, the average search direction error is lowered by the continuous re-evaluation of the target voxels. Fig. 5-B displays the actual motion search direction across the nine motion parameters (for this in-plane simulation with three shots, we had three rotations parameters and six translation parameters for translation in each of the two in-plane directions, i.e. M = 9). Early in the search (motion optimization step 2), both methods find the proper search direction. However after 11 of the 13 steps, the alternating approach was highly inaccurate (95% error), whereas the targeted approach had 14% error.

Fig. 5.

Motion Search Direction Accuracy. Here we compare the accuracy of the motion search direction (∇ in Eqn. 8, which is the difference between the motion estimates at each step of the search, i.e. θ⁽ⁱ⁺¹⁾ = θ⁽ⁱ⁾ + ∇⁽ⁱ⁾), when updating a subset of target voxels, versus assuming the image is constant (no voxels updates). A. The motion search direction error is plotted as a function of the alternating step (i.e. how many times the image volume has been reconstructed). B. The motion search direction is plotted for the no voxel updates and target voxel updates method. The first row shows the search direction at step 2 of the motion optimization, and the second row shows the search direction at step 11 of the motion optimization. Each method (solid) is compared to the full model search direction (dotted), and the average % difference is shown in the top right of each plot.

3). Comparison of Voxel Selection Methods:

Figure 6 shows the convergence of the TAMER optimization for various target voxel selection methods. The data consistency error is plotted as a function of optimization step (i.e. number of motion trajectories tested). The initial data consistency error of the motion-free ground truth SENSE reconstruction used in the simulations was 4.15% (some amount of model error is expected due to coil sensitivity inaccuracies along with image noise). With simulated motion corruption, the data consistency error increased to 12.3%, showing the additional disagreement between the multichannel data and the forward model when assuming no patient motion. The correlation matrix method converged most quickly, followed by the rotated correlation matrix, then random voxel locations, and finally uniformly spaced locations.

Fig. 6.

Comparison of Target Voxel Selection Methods. (Left) Four target voxel masks were used in TAMER optimizations: the correlation matrix mask, the rotated correlation matrix mask, uniformly spaced disks, and randomly spaced disks. (Right) The convergence of TAMER when using each of the target subset masks is shown by plotting the data consistency error as a function of the optimization step (i.e. the number of motion trajectories tested).

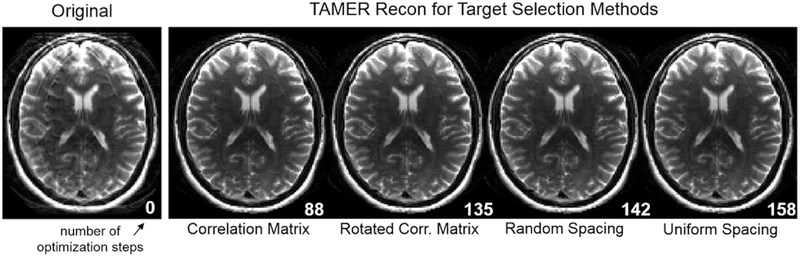
Figure 7 shows each method’s image once it has reached a data consistency error below 6%, with the number of steps required shown in the bottom right. To achieve this degree of motion artifact mitigation, 88 optimization steps were required with the correlation matrix method, and 135, 142, and 158 steps were required for the rotated correlation matrix, random spacing, and uniform spacing, respectively.

Fig. 7.

Image Results for Target Voxel Selection Methods. (Left) Simulated motion corrupted image. (Right) TAMER images for each target voxel selection method. The white number in the bottom right of each image shows the number of steps taken to arrive at the image (all corresponding to 6% data consistency RMSE).

B. Phantom Results

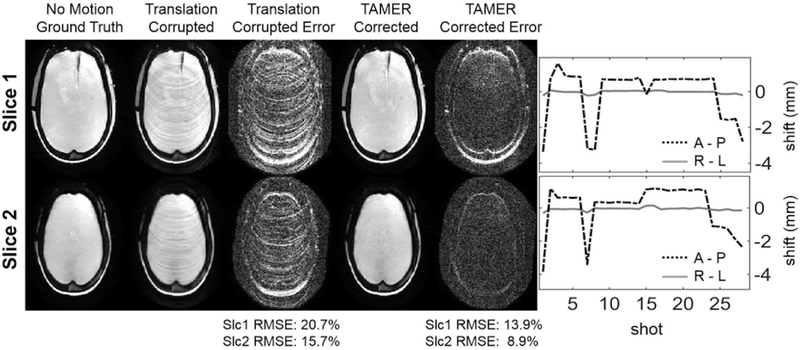
Results from the translation experiment can be seen in Fig. 8. Two representative slices are shown where TAMER mitigates the effects of motion on the final image. Ringing artifacts are removed, and the image space RMSE for the two slices decreases from 20.5% and 15.4% to 15.1% and 10.7%, respectively. The output motion trajectories found using TAMER only show displacement in the A-P direction (axis of translation stage movement), with no significant motion detected in the R-L direction, in agreement with the orientation of the translation stage. Similar motion trajectories are seen for the two slices, consistent with rigid-body motion. For the top slice in Fig. 8, TAMER took 50 minutes running on a Dual Intel Xeon E5-2690 v4 CPU. Source code and data for this figure has been uploaded to https://github.com/mwhaskell/tamer_mri.

Fig. 8.

TAMER Translation Phantom Results. (Left) Comparison of corrupted and motion corrected anthropomorphic phantom images from RARE acquisition with resolution 0.9 × 0.9 × 3 mm³ (error scaled by 7×). Motion was created using a 1D physical translation stage along the A-P direction. (Right) Estimated motion trajectories found using TAMER.

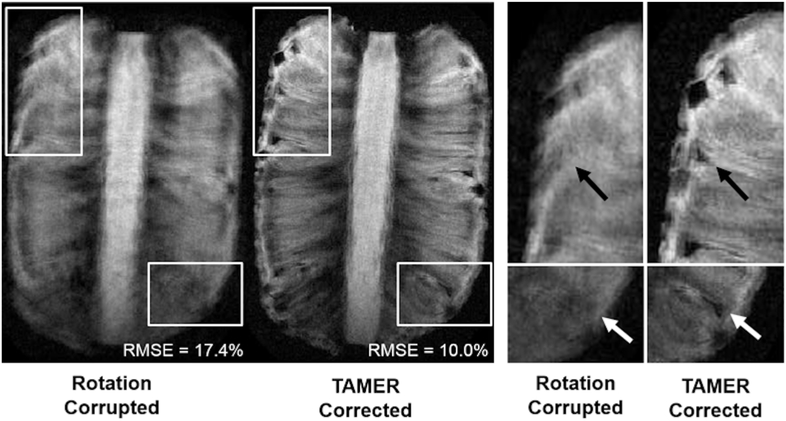
Figure 9 shows rotation corrupted and TAMER corrected images for a rotating pineapple. Blurring has been reduced using TAMER, and fine detailed structures that were indiscernible in the motion corrupted image are resolved, although signs of blurring remain. Image RMSE compared to a no motion ground truth was 17.4% using standard (motion corrupted) reconstruction, and 10.0% using TAMER. The data consistency RMSE was initially 27.6% for the motion corrupted scan, improved to 25.0% following the first TAMER pass, and decreased to 24.5% after the second (i.e. weighted) TAMER pass (for comparison, a no motion acquisition of the same phantom with the same settings had a data consistency RMSE error of 23.4%).

Fig. 9.

TAMER Rotation Phantom Results. A pineapple was rotated in-plane throughout the scan using a motion actuator, with estimated magnitudes of rotation up to ±3°. After TAMER correction, the high frequency components of the object were restored that were previously not visible due to rotation corruption. RMSE compared to a no motion ground truth was calculated for each image.

C. In Vivo Results

Figure 10 shows the results of motion corrupted and TAMER corrected in vivo data. Fig. 10-A shows the correlation coefficients of the image space error of each individual coil. High error correlation was present in the anterior coils, while other channels contained few motion artifacts and were considered to measure mostly non-motion corrupted data. Fig. 10-B shows ringing was reduced by TAMER, while maintaining the high-resolution content of the image. The data consistency error dropped from 16.8% in the original motion corrupted reconstruction to 14.6% using the TAMER method, demonstrating the motion model’s ability to better fit the acquired data.

Fig. 10.

In Vivo Results. A. The image-space data consistency error correlation across the 32 coils was calculated. Channels with high error correlation were grouped together in the TAMER optimization, those with little data consistency error were assumed to have zero motion. B. (Left) Motion corrupted image (Middle) TAMER corrected image. (Right) Difference image displayed at 10×. Data consistency error, ϵ, shown in bottom right.

The clustering produced nine coils that were highly correlated with large data-consistency errors, which were uncorrelated to the remaining channels that showed low data consistency error. The rigid-body model employed in this work will not accurately describe data that has these attributes and we think it may be a result of confounding effects, e.g. spin history. By restricting motion correction to this group of channels we were able to achieve better image quality improvement than an optimization across all channels. For the other experiments, we did not observe disjointed groups when the coil artifacts were analyzed, and all the channels were placed in a single group.

In order to validate the accuracy of our approach to [26], we modified the alternating based optimization package provided as part of that work to closely coincide with the optimization objective shown in (3). Fig. 11 show the image results when using an alternating method similar to the one found in [26] and when using TAMER. The TAMER data consistency error decreased from 14.5% to 13.1%. The code provided with [26] used image space error as a stopping criteria (described in [25] App. A), and therefore the data consistency error was not provided as an output of the algorithm. The TAMER method is able to produce comparable image quality to that of the alternating method.

Fig. 11.

In Vivo TAMER Results Compared to State-of-the-Art. (Left) A motion corrupted sagittal slice. (Middle) Motion correction using an alternating reconstruction by modifying the code provided in [26]. (Right) TAMER motion corrected reconstruction.

V. Discussion and Conclusion

In this work we present TArgeted Motion Estimation and Reduction (TAMER), a reduced model joint optimization to correct for patient motion during MRI scans. TAMER retrospectively corrects for motion during reconstruction by minimizing the data consistency error between the acquired data and a SENSE plus motion forward model. TAMER relies on information about the motion trajectory that has been encoded by the coil array into the k-space data. By minimizing the data consistency, we do not rely on proxy metrics for image quality, such as gradient entropy or total variation, to drive our motion search. In order to efficiently perform this joint minimization, we have introduced a reduced model, where we perform only small reconstructions of target voxel subsets while searching for the motion parameters. TAMER only operates on the full volume data twice (image initialization and final reconstruction). This significantly reduces the computation of the joint optimization (motion parameters and image voxels).

Since TAMER is a retrospective approach which does not alter the acquisition procedure, it has the potential to be easily integrated into current clinical MRI scans. Here we presented results of the TAMER optimization applied to 2D RARE images, one of the most common clinical scans. Our approach can be extended to several other commonly used 2D and 3D clinical sequences. Unlike prospective motion correction techniques [5], TAMER requires no modifications to the acquisition pulse sequence (gradient updates and navigators) nor to the clinical workflow (motion tracking hardware). Nonetheless, if data motion tracking hardware or MR navigator information is available, it could be incorporated into the TAMER optimization. Finally, this retrospective technique will allow for a direct comparison of the TAMER reconstructed image to the standard reconstruction, which is not possible when using prospective correction.

By construction, TAMER requires multichannel data (even for a fully sampled k-space acquisition) since the motion parameters cannot be found without the additional degrees of freedom afforded through multichannel acquisition, and much of the motion information itself likely comes from the intensity and phase patterns incurred from motion within the fixed detector array. In this work we assumed static coil profiles that do not change with patient motion due to changes in coil loading, but for larger motion examples the model could be extended to include dynamic coil profiles as the subject moves through the field of view.

The objective function of our reduced model (6) can be modified by adding a weighting to the L₂ norm or by adding spatial smoothness penalties (as utilized in compressed sensing). In this work, we employed a weighing on the L₂ norm to reconstruct our rotation phantom data (Fig. 9), where after a first pass of an unweighted objective function, we performed a second pass where we weighted the higher regions of k-space more heavily. This was done in an attempt to promote high frequency information in the optimization, as the initial result from TAMER did not adequately resolve fine structures. The weighting was not necessary for other datasets, and we attribute this to the spectral content of this object and the large amount of rotational motion applied in the experiment. Further work must be done to automate this feature of TAMER in future versions.

The main benefit of the more accurate search direction provided with a reduced model (see Fig. 5) will be a more efficient search of the motion parameters, but it will not guarantee a more accurate final motion estimate. In Fig. 11 both TAMER and the code provided in [26] ran until convergence, and the final image quality appears very similar. The fact that TAMER completely eliminates motion artifacts in synthetically corrupted data such as Fig. 4, where gold standard data was corrupted using the same motion forward model used in the motion reconstruction, suggests that residual motion artifacts in the in vivo motion case, or moving phantoms, arises from an incomplete forward model. There are several sources that can contribute to residual data consistency error. In the case of standard parallel imaging, there can be error due to sensitivity map inaccuracies and noise in the individual channel data. Depending on the image SNR this alone can be over 5%. In the presence of motion, additional model inaccuracies can contribute to final data consistency RMSE level. The most likely sources of model error for the remaining artifacts are through-plane motion in the cases where it was not included in the model, spin history effects, and intra-shot motion. In future work, more sophisticated motion models are likely needed to allow full motion mitigation without requiring ancillary techniques which go beyond data consistency, such as the acquisition of oversampled data, reliance on outlier rejection, or regularization or assumptions of through-plane smoothness.

For ease of implementation we consider the target voxel regions to be uniform across all slices in this work. Thus, the circular target voxel subsets shown for a single slice example in Fig. 6 were transformed to cylinders extending across all slices for a multi-slice imaging volume (such as in Fig. 11). However, it is likely to be more efficient to use smaller target voxel subsets that consider the restricted nature of voxel coupling in the through plane or 3D direction, in which case the target voxel subsets would be shortened in the slice direction, for example, shorter cylinders (only across a subset of slices) or spheres.

Our target voxel approach using the correlation matrix showed the fastest convergence compared to other voxel selection methods, however we would expect that due to the strong coupling along the phase encode direction that the rotated correlation matrix of Fig. 6 would not perform well. It seems that all of the patterns which provided rapid convergence also overlapped with areas of elevated data consistency error.

An important area of future work will be to create an efficient implementation of the TAMER algorithm. Our current implementation relies on standard MATLAB motion operations and optimization algorithms, which significantly increases overall computation time. We think it could be beneficial to incorporate implementation strategies used in [26], such as analytical gradient calculations for the motion, a custom non-linear optimization algorithm, and employment of GPU based computation.