Variability of Visual Responses of Superior Colliculus Neurons Depends on Stimulus Velocity

Abstract

Visually responding neurons in the superficial, retinorecipient layers of the cat superior colliculus receive input from two primarily parallel information processing channels, Y and W, which is reflected in their velocity response profiles. We quantified the time-dependent variability of responses of these neurons to stimuli moving with different velocities by Fano factor (FF) calculated in discrete time windows. The FF for cells responding to low-velocity stimuli, thus receiving W inputs, increased with the increase in the firing rate. In contrast, the dynamics of activity of the cells responding to fast moving stimuli, processed by Y pathway, correlated negatively with FF whether the response was excitatory or suppressive. These observations were tested against several types of surrogate data. Whereas Poisson description failed to reproduce the variability of all collicular responses, the inclusion of secondary structure to the generating point process recovered most of the observed features of responses to fast moving stimuli. Neither model could reproduce the variability of low-velocity responses, which suggests that, in this case, more complex time dependencies need to be taken into account. Our results indicate that Y and W channels may differ in reliability of responses to visual stimulation. Apart from previously reported morphological and physiological differences of the cells belonging to Y and W channels, this is a new feature distinguishing these two pathways.

Introduction

Sensory systems transform external information of all modalities into electrical signals. The reliability of this process depends on the precision of coding at different stages of information processing. Variability of cell responses may originate at any level from molecular to network (Paninski et al., 2007; Faisal et al., 2008). Several measures were proposed for quantification of neural variability (Perkel et al., 1967; Gabbiani and Koch, 1998; Dayan and Abbott, 2001; Shinomoto et al., 2009). Interspike intervals variability is typically quantified with the coefficient of variation (Holt et al., 1996; Chelvanayagam and Vidyasagar, 2006), whereas spike count distributions used in estimation of trial-to-trial variability are quantified with the Fano factor (FF) (Fano, 1947).

In the visual system, variability was studied extensively in the geniculate pathway, from the retina, through the dorsal lateral geniculate nucleus to visual cortex (for review, see Lestienne, 2001; Field and Chichilnisky, 2007). It was shown that, when stepping up the levels of the hierarchy of the geniculate visual pathway, the variability of neuronal signal increases (Kara et al., 2000). To our knowledge, there are no available data on the variability of spike trains in the superior colliculus, the first stage of information processing in the extrageniculate visual pathway relaying information through the second-order thalamic nuclei to the higher-order visual areas.

Superior colliculus (SC), the main retinorecipient nucleus of the mammalian midbrain, is involved in visually guided behavior and orientation response directing eyes and head toward the object of interest. SC neurons receive direct inputs from only two classes of retinal ganglion cells: Y and W, which innervate predominantly distinct SC layers (for review, see Waleszczyk et al., 2004). These two inputs shape the characteristic properties of SC neurons, including their velocity preference (Hoffmann, 1973; Waleszczyk et al., 1999, 2007; Wang et al., 2001). The cat SC cells receiving principal input from the Y channel have relatively high background and evoked activity and respond to stimuli at low spatial and high temporal frequencies. These last two features imply that cells driven exclusively by Y inputs respond only to fast stimuli. On the other hand, collicular cells with W inputs respond well to stimulation by slowly moving objects, whereas their “spontaneous” and evoked activities are lower.

The aim of our present study was to analyze how distinct patterns of projection to the SC of the two channels (Y and W) influence the variability of responses of collicular neurons to visual stimulation. To measure response variability, we calculated the FF, compared its changes along with the firing rate, and verified hypothesis using stochastic modeling approach. One would expect that, during the response, the variability would decrease, as the cell should then transmit maximum information about the stimulus. This expectation proved to be true for responses to fast-moving stimuli, when information is transmitted via the Y pathway, but not in the case of the activation by slowly moving stimuli, transmitted via the W channel.

A preliminary report of these findings has been published previously in abstract form and conference materials (Mochol et al., 2008a,b).

Materials and Methods

Surgical procedures

Acute experiments were performed on anesthetized adult cats of either sex. All experimental procedures were performed to minimize the number and the suffering of the animals and followed the European Communities Council Directive of November 24, 1986 (S6 609 EEC) and National Institutes of Health guidelines for the care and use of animals for experimental procedures. The experimental protocol was approved by the Local Ethics Committee at the Nencki Institute of Experimental Biology. Typically, experiments lasted 4 d, during which neuronal activity from the superficial layers of the superior colliculus was recorded continuously with short breaks needed for track changes. On the day preceding the experiment, cats were given dexamethasone phosphate (0.3 mg/kg, i.m.; Dexamethasone; Eurovet Animal Health BV) to reduce the possibility of brain edema. During the experiment, the animals were initially anesthetized with a mixture of xylazine (3 mg/kg, i.m.; Xylavet; ScanVet), propionylpromazine (1 mg/kg, i.m.; Combelen; Bayer), and ketamine (20 mg/kg, i.m.; Ketanest; Biovet) injected intramuscularly with atropine sulfate (0.1 mg/kg; Atropinum Sulfuricum; Warszawskie Zakłady Farmaceutyczne Polfa). Tracheal and cephalic vein cannulations were performed to allow, respectively, artificial ventilation and infusion of paralyzing drugs. Bilateral sympathectomy was performed to further minimize eye movements. During the recording session, anesthesia was maintained with a gaseous mixture of N₂O/O₂ (2:1) and isoflurane (0.5–1%). Antibiotic (enrofloxacin, 5 mg/kg; Baytril; Bayer), dexamethasone phosphate (0.3 mg/kg), and atropine sulfate (0.1 mg/kg, to reduce mucous secretion) were injected intramuscularly daily. Paralysis was induced with intravenously injection of 20 mg of gallamine triethiodide (Sigma) in 1 ml of sodium lactate solution and maintained with continuous infusion of gallamine triethiodide (7.5 mg · kg⁻¹ · h⁻¹, i.v.) in a mixture of equal parts of 5% glucose and sodium lactate solutions. Animals were artificially ventilated, and body temperature was automatically maintained at ∼37.5°C with an electric heating blanket. Expired CO₂ was continuously monitored and maintained at 3.5–4.5% by adjusting the rate and/or stroke volume of the pulmonary pump. The electrocorticogram (ECoG) from the occipital lobe and the heart rate were also monitored continuously. Slow-wave synchronized cortical activity and heart rate below 220 beats/min were maintained by adjusting the isoflurane level in the gaseous mixture. Atropine sulfate (1–2 drops, 0.5% Atropinum Sulfuricum; Warszawskie Zakłady Farmaceutyczne Polfa) and phenylephrine hydrochloride (1–2 drops, 10% Neo-Synephrine; Winthrop-Breon Laboratories) were applied daily on the cornea to dilate the pupils and retract the nictitating membranes. Air-permeable zero-power contact lenses were used to protect the corneas.

A fiber optic light source was used to project the optic discs onto a screen (Pettigrew et al., 1979). The positions of the areae centrales were plotted by reference to the optic discs (Bishop et al., 1962).

Recording and visual stimulation

Extracellular single-unit recordings were made from neurons located in superficial, retinorecipient layers of the SC. For recordings, a plastic cylinder was mounted and glued around the craniotomy (Horsley–Clarke coordinates P1–A5 and L0–L5) above one of the SC. The cylinder was filled with 4% agar gel and sealed with warm wax. Action potentials of single SC neurons were recorded extracellularly with a tungsten or stainless-steel microelectrode (6–10 MΩ; FHC Inc.), conventionally amplified, monitored via a loudspeaker, and visualized on oscilloscope. Recorded signals were digitized and fed to a personal computer for online display, analysis, and data storage with the use of CED 1401 Plus and Spike2 software (Cambridge Electronic Design). Signals containing spike waveforms were bandpass filtered between 0.5 and 5 kHz and digitized at a sampling rate of 50 kHz. The ECoG was bandpass filtered between 0.1 and 100 Hz and digitized at a sampling rate of 1 kHz. The responsiveness of a neuron to visual stimulation and origin of its input from ipsilateral and/or contralateral eye were determined with black or white hand-held stimuli, and the excitatory contralateral and/or ipsilateral receptive fields (minimum discharge fields) of recorded neurons were plotted. The ocular dominance was first determined by listening to neuronal responses via loudspeaker with spikes converted into standard pulses (transistor–transistor logic), and the dominant eye was chosen on this basis for visual stimulation (with the other eye covered). If conditions allowed, i.e., registered signal was stable with well isolated single-unit activity, responses were also recorded to stimulation of the second eye, and ocular dominance class was determined quantitatively following commonly used criteria (Distler and Hoffmann, 1991; Waleszczyk et al., 1999; Hashemi-Nezhad et al., 2003).

To determine velocity response profiles and trial-to-trial variability, we recorded responses of single SC neurons to multiple sweeps of a light rectangles of 1° × 2° or 0.5° × 1° (4–6 cd/m² luminance against 0.5–1 cd/m² background) moving with constant velocity. A slide projector under computer control was used to project stimuli onto a spherical concave screen located at a distance of 0.75 m in front of the cat's eyes and covering an area of 70° in diameter of visual field. The center of the screen was adjusted to overlap the receptive field center of the recorded neuron. The stimulus moved through the receptive field center along its horizontal or vertical axis with velocity ranging from 2 to 1000°/s, the chosen values being approximately uniformly distributed on the logarithmic scale. Movement of the stimulus on the screen was achieved by computer control of the mirror attached to the axle of galvanometer. Voltage changes transferred to galvanometer were generated with Spike2 software and digital-to-analog converter CED 1401 Plus (Cambridge Electronic Design). To ensure smoothness of the stimulus movement, single sweep with full amplitude of 50° was achieved in 500 steps of voltage changes for the fastest stimulus used (1000°/s) up to 5000 steps for the slowest stimulus (2°/s). One trial consisted of motion in one direction, followed by a 1 s waiting period, and then motion in the reverse direction with the same velocity, also followed by 1 s waiting time. The number of trials was proportional to stimulus velocity (from 10 for 2°/s to 100 for 1000°/s).

Localization of recording sites

At the end of recording sessions, small electrolytic lesions were made. The animals were killed with overdose of sodium pentobarbitone (intravenously; Nembutal Sodium Solution, Abbott Laboratories). Brains were removed and immersed in 4% paraformaldehyde in 0.1 m phosphate buffer, pH 7.4. The electrode tracks were reconstructed from 50 μm coronal sections stained with cresyl violet.

Data analysis

Of 140 recorded collicular cells for the study of variability, we chose 35 neurons for which we were sure that every spike was correctly classified during offline discrimination. Thus, for the analysis, we chose these recordings in which signal-to-noise ratio was at least 2. As signal-to-noise ratio, we took peak amplitude of the spike divided by the maximal amplitude of background activity (e.g., spike amplitude of next unit). Spike sorting was based on waveform analysis and performed with Spike2 software (Fig. 1A–C). In all cases, correctness of the single-unit discrimination was confirmed by the presence of an absolute refractory period in the autocorrelogram or interspike interval histogram (Fig. 1C). In one case, two units were discriminated from a simultaneous recording by one electrode. Spike2 software was used to perform offline conversion of single-unit activity waveforms into discrete times of spike occurrence.

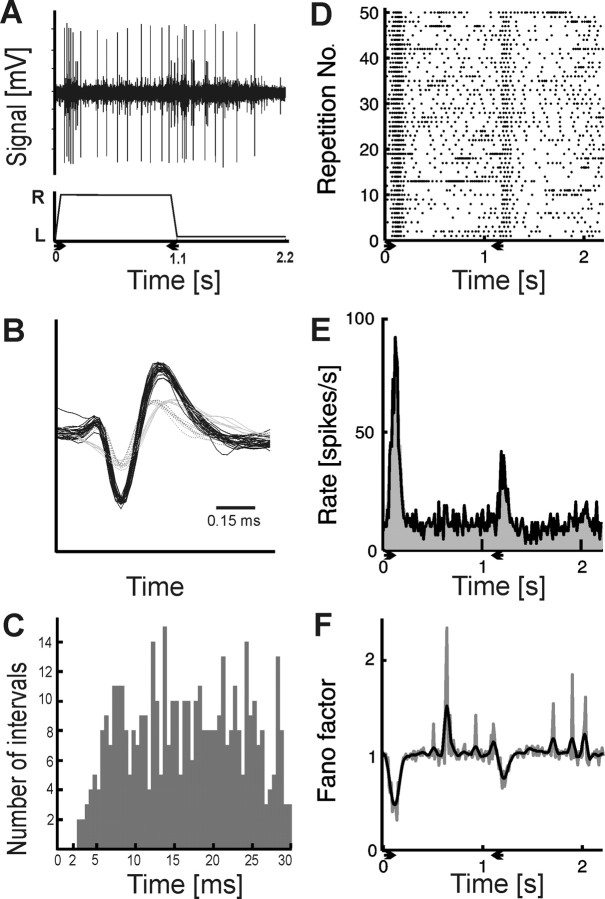
Figure 1.

An example of extracellular recording from a cat superior colliculus cell responding to high velocity motion and a scheme of data analysis method. A, Top shows responses of SC cells to visual stimulus: a bar of light moving back and forth through the receptive field of the neurons with velocity of 500°/s. Bottom represents position of the stimulus on the screen in time. The first slope denotes the stimulus movement from the left side of the screen (L) to the right (R); the second corresponds to the movement in the reverse direction. Horizontal lines correspond to the time when the stimulus remains stationary outside the receptive field. B, Waveforms of three spike types selected from the record presented in A. Only the unit of the highest amplitude (black solid line) was considered for further analysis. Horizontal black bar indicates the timescale; 0.15 ms is the time from minimum to maximum of black spike waveform. C, Interspike intervals histogram for the selected unit confirming correctness of spike discrimination by a clear presence of the refractory period. D, Raster plot of responses of the selected cell to 50 repetitions of stimulus, as in A. The cell responded to stimulus movement in both directions with a preference of movement from left to right. E, PSTH of the responses for the same cell and stimulus parameters as in D. Black line represents raw PSTH, and gray histogram shows firing rate smoothed with a Gaussian kernel. F, Raw (gray line) and smoothed FF (black line) as a function of time for the same data. In each of nonoverlapping 200 bins, mean and variance of spike count were computed. The ratio of these two quantities, known as Fano factor, was used as a measure of trial-to-trial variability. Arrows indicate duration and direction of stimulus motion in every plot in this and subsequent figures.

For later numerical analysis, we used sets of single spike trains corresponding to the stimulus motion in one direction and backward separated by waiting periods (Fig. 1A). After each sweep across the screen, the stimulus was outside the receptive field for 1 s. This waiting time was needed to observe delayed response components, especially in the case of very fast movements. The peristimulus time histograms (PSTHs) were constructed from the responses to all repetitions of a given stimulus whose number varied from 10 for slow to 100 for fast stimuli (Fig. 1D,E, black line). We made similar analysis in two paradigms. In the first case, the time base was divided into 200 bins regardless of the duration of the trial. This approach resulted in different bin lengths depending on the stimulus velocity. In the second paradigm, we used a sliding window of length ranging from 10 to 100 ms shifted with resolution of 1 ms. In both cases, the PSTHs were smoothed using a Gaussian filter extending over six bins (Fig. 1E, gray histogram). The records during 500 ms preceding stimulus movement, when the stimulus was outside the receptive field, were used for background activity estimation. The maximum or minimum (for excitation or suppression, respectively) of the firing rate with respect to the mean background activity was taken as the response level (presented in the form of tuning curves in Fig. 2A).

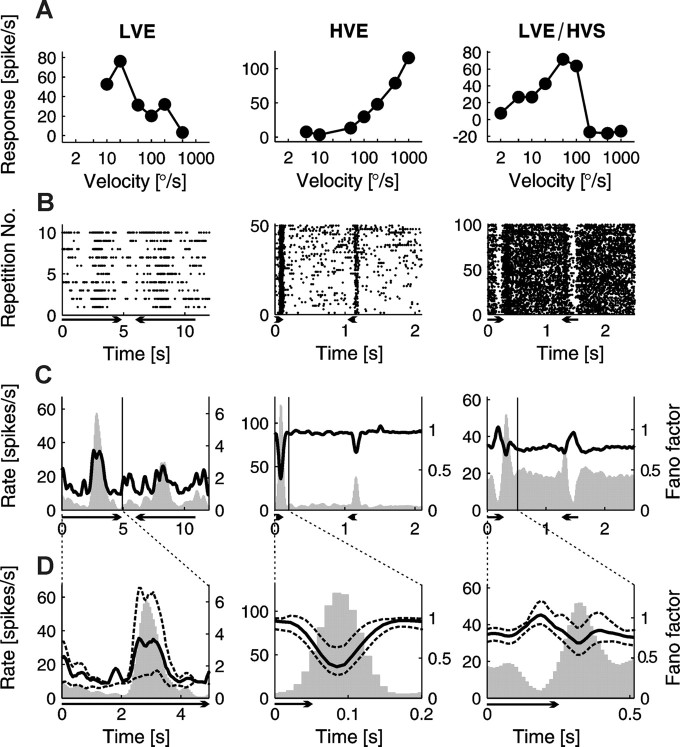
Figure 2.

Responses and FFs calculated for three SC neurons showing different velocity response profiles. Each column represents different type of collicular cell. From left to right, An LVE cell, an HVE cell, and an LVE/HVS cell. A, Velocity tuning curves. As a response level, the difference between the peak of response (maximum discharge rate in case of excitation) or trough (minimum in case of suppression) and background activity was taken. The horizontal axis is in logarithmic scale. B, Raster plots of neuronal responses during all repetitions of stimulus moving with exemplary velocity for a particular cell. One row represents a single response to stimulus movement in both directions. Each dot corresponds to the occurrence of a single spike. Length of the arrow indicates duration of the stimulus and its head the direction of motion. Velocity of the stimulus for the LVE cell is 10°/s, for HVE cell is 1000°/s, and for the LVE/HVS cell is 200°/s. C, Relationship between firing rate (gray histogram) and FF (black solid line) for responses shown in the form of raster plot in B. The left vertical axes indicate the firing rate level, and the right vertical axes indicate the value of FF. Time base of the full PSTH and FF was divided into 200 bins. The region between the “rate” axis and the vertical black line including the time of response is expanded in D. D, Expanded part of cell activity presented in C. Gray histogram is the firing rate, and the black line denotes the FF with black dotted lines standing for error bars. Broad extent of confidence intervals in the case of low velocity excitatory response (left plot) is the effect of the higher trial-to-trial variability. The time axis begins with the stimulus onset. Each plot presents responses to the preferred direction.

All numerical analysis and simulations were performed using Matlab software (MathWorks).

Fano factor.

Trial-to-trial variability was quantified using the FF (Fano, 1947) defined as the variance of spike counts normalized by its mean, where the variance and mean were taken over repetitions:

where t_k is discretized time in kth bin, and N_k is the number of spikes in kth bin. The FF was estimated as a discrete function of time to overcome the apparent nonstationarity of the data. In each bin, the variance and the mean of spike counts were calculated separately giving FF locally in time (Fig. 1F, gray line, raw estimates; black, smoothed FF). In bins with no activity, we put FF equal to 1 to indicate the assumed Poissonian character of low-rate firing. Confidence intervals for FF were computed using bootstrap technique for 1000 samples with replacement (Efron, 1979). The resulting time-dependent FF and its error bars were smoothed using Gaussian filter in the same way as PSTHs.

Correlation coefficient.

To quantify the dependence between the variability and intensity of neuronal response, we calculated the Pearson's correlation coefficient between FF and firing rate values (with subtracted means) for response period. The response period was defined as the longest continuous time interval during which firing rate exceeded the cutoff level for each PSTH. The cutoff level was taken at 10% of response above the background activity for excitation or 10% of response below background activity for suppression. The positive correlation coefficient indicates simultaneous increase (or decrease) of both FF and firing rate during the response period, whereas a negative correlation coefficient means the opposite behavior: increase of one with decrease of the other.

Surrogate data.

To find out how much the observed phenomena depend on the probabilistic structure of the recorded spike trains, the experimental results were compared with the results of the analysis of surrogate data. We used a stochastic modeling approach: the experimental spike trains were treated as realizations of a point process under the assumption that such a process is completely characterized by the conditional intensity function (Johnson, 1996; Brown et al., 2002) defined as the probability to observe a spike at time t given the spiking history H_t up to t:

where N(t) is the number of spikes up to t in a given realization. The above definition can be expressed in terms of the spike time probability density p(t|H_t), as follows:

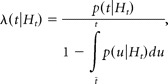where t̃ is the time of the last spike before t. Given the conditional intensity function λ(t|H_t) and the spike history up to t(H_t), the probability of spike occurrence in a small interval Δt is approximately λ(t|H_t) · Δt.

The first model we used was inhomogeneous Poisson process (IP process) (Perkel et al., 1967; Dayan and Abbott, 2001) in which the conditional intensity function does not depend on the history λ(t|H_t) = λ(t). This means that the firing probability at any time depends only on the stimulus and spike occurrences are independent. In this case, λ(t) could be estimated from the empirical firing rate r(t) (that is smoothed PSTH) calculated in discrete bins (in our case 1 ms). Then, the probability to generate a spike in the kth bin was r(t_k) · Δt.

There are several useful generalizations of the IP process (Barbieri et al., 2001; Kass and Ventura, 2001; Truccolo et al., 2005; Soteropoulos and Baker, 2009). We used the family of inhomogeneous renewal processes (Gerstner and Kistler, 2002) also called inhomogeneous Markov interval processes (IMI processes) (Kass and Ventura, 2001) in which the whole spiking history is reduced to the time from the last spike τ, where τ = t − t̃ and λ(t|H_t) = λ(t,τ). To simplify model estimation, we further assumed the multiplicative form of the conditional intensity function λ(t|H_t) = λ₁(t) · λ₂(τ).

In the multiplicative IMI process, the first component λ₁(t) describes the time-dependent modulation of the spiking activity of the neuron reflecting its responsiveness to different stimuli (Berry and Meister, 1998; Brown et al., 2003; Schaette et al., 2005). The second component λ₂(τ), which might be called “postimpulse probability” following Poggio and Viernstein (1964), reflects the membrane properties of the neuron including its refractory periods.

We used two versions of the model in which λ₂(τ) was obtained through parametric (assuming gamma distribution) or nonparametric (kernel smoothing) fits to interspike interval distribution p(τ) estimated from the background activity. Under stationary condition, λ₁(t) is constant and can be set to unity. From p(τ), the component λ₂(τ) was computed as follows:

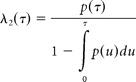Given λ₂(τ), we could calculate the modulatory factor λ₁(t). To do so, the time of experiment was divided into bins of length Δt short enough that there would be at most one spike per bin. Given N repetitions of stimulus, we estimated λ₁(t_k) in kth bin as follows:

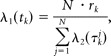where r_k was the rate in kth bin: $\frac{1}{\Delta t}·\frac{N_k}{N}$; N_k was the number of trials in which we observed a spike in the kth bin, and τ_k^j was the interval between current time and the time from the last spike in jth repetition. Details of the estimation technique have been presented previously (Wójcik et al., 2009).

Given conditional intensity function, surrogate data were generated using the thinning method (Dayan and Abbott, 2001; Press et al., 2007). Each set of surrogate data had the same structure (time duration and the repetition number) as the corresponding experimental dataset.

Goodness-of-fit between the proposed models and spike train data series was assessed on the basis of the time-rescaling theorem (Brown et al., 2002). If the assumed model is correct, then the experimental intervals τ_k rescaled via conditional intensity function $\underset{0}{\overset{\tau \kappa }{\int }}$ λ(t,τ)dτ are independent exponential variables with the mean equal to unity. One can then transform the rescaled intervals to uniform distribution through z = 1− exp (τ̃_k) and use the Kolmogorov–Smirnov (K–S) test to quantify the quality of estimation (Brown et al., 2002).

Results

We studied trial-to-trial response variability of neurons recorded from upper (retinorecipient) layers of SC (stratum zonale, stratum griseum superficiale, stratum opticum, and upper part of stratum griseum intermediale). For each neuron, we recorded responses to a visual stimulus moving at constant velocity in a range from 2 to 1000°/s along a horizontal or vertical axis of the receptive field. Responses of 35 neurons for which there was no doubt that every spike was correctly sorted during offline discrimination (see Materials and Methods) were taken for analysis. The cells were recorded from the rostral half of the superior colliculus, which contains binocular representation of the visual field (Feldon and Kruger, 1970; Lane et al., 1974). All cells had binocular inputs. Assuming five classes of eye dominance, 54% of cells (14 of 26 cells for which we could quantitatively determine relative intensity of responses via both eyes) could be classified as belonging to group 3 (equal magnitude of response recorded via the contralateral and ipsilateral eye), 19% (5 of 26) showed contralateral eye dominance (group 2), and 27% (7 of 26) showed ipsilateral eye dominance (group 4). Eye dominance of neurons in our sample was similar to those recorded in previous studies (Bacon et al., 1998; Waleszczyk et al., 1999; Hashemi-Nezhad et al., 2003). In most cases, responses to stimulation of the dominant eye (usually contralateral) were analyzed, but for some neurons (n = 6), we also analyzed data obtained during stimulation of the other eye. No qualitative differences in the response properties of cells or results of later analysis of variability were observed between responses evoked via the ipsilateral and contralateral eye.

On the basis of velocity tuning curves, cells were separated into four groups according to the criteria established in our previous experiments (Waleszczyk et al., 1999). Thus, eight cells that were responsive only to slow stimulus movement (≤200°/s) constituted the low velocity excitatory (LVE) group, six neurons that responded exclusively to velocities above 10°/s constituted the high velocity excitatory (HVE) group, and 13 cells that were excited in a broad range of velocities constituted the LVE/HVE group. Finally, the activity of eight cells was increased at low and suppressed at high velocity of stimulus movement (LVE/HVS group).

Quantification of trial-to-trial variability of responses to different stimulus velocities

Figure 2 shows velocity tuning curves (Fig. 2A), responses to several repetitions of one velocity movement in the form of raster plots (Fig. 2B), and PSTHs (Fig. 2C, gray histograms) for exemplary cells from three groups: an LVE cell (left), an HVE cell (middle), and an LVE/HVS cell (right). The smoothed PSTHs were compared with the time-dependent FFs (Fig. 2C, black lines) considered as a measure of trial-to-trial variability. In D, we show extended parts of Figure 2C, including neuronal responses, FFs, and additionally 95% confidence bounds for FFs.

We found that the relation between the firing rate and FF did not depend on the cell type but rather on the stimulus velocity and the character of response. In the case of activation evoked by slow stimuli, an increase of firing rate during the response was accompanied by the increase of FF (Fig. 2C,D, left panels). This effect was observed for excitatory responses at low velocities in LVE, LVE/HVE, and LVE/HVS cells.

In contrast, during excitatory responses evoked by rapid stimuli, we observed a decrease of FF when the firing rate increased. Such behavior was observed in both the HVE (Fig. 2C,D, middle panels) and LVE/HVE groups. Also for LVE/HVS neurons in the high velocity range, in which neuronal activity was suppressed by fast stimulus, clear negative correlation between the firing rate and FF was found. In this case, however, the decrease of the firing rate was accompanied by the increase of FF (Fig. 2C,D, right panels). It is worth mentioning that, in the case of LVE/HVE cells, we observed both an increase in variability of excitatory responses to low velocity stimulation (Fig. 3A) and a decrease in variability during vigorous responses evoked by high velocity stimuli (Fig. 3B).

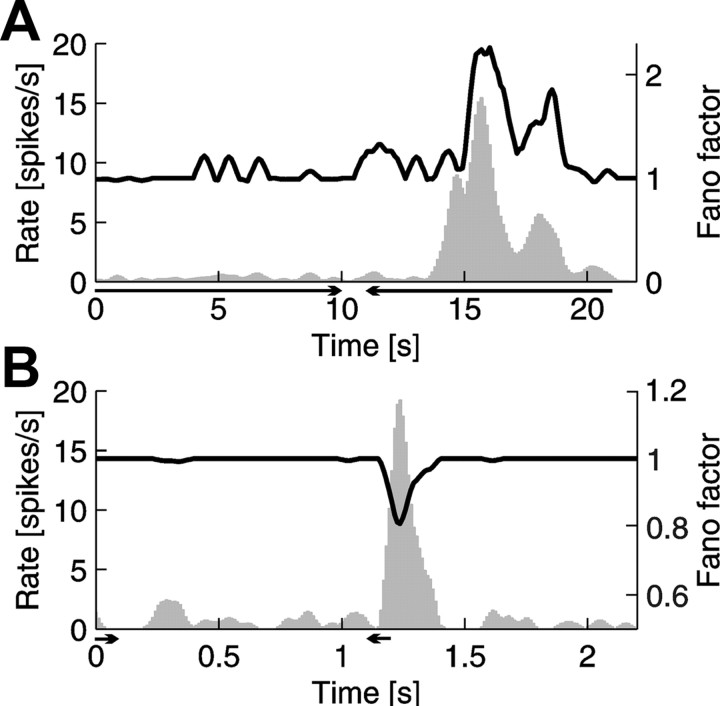
Figure 3.

An example of the relationship between the firing rate and FF for a collicular cell responding in a broad range of stimulus velocities (LVE/HVE cell). Each plot shows the PSTH in the form of gray histogram, with scale given on the left vertical axis. Black lines represent the changing values of the FF with scale given on the right vertical axis. Lengths of the horizontal arrows below the time axis indicate duration of the stimulus, and their heads show the direction of motion. A, Response to low velocity (5°/s) stimulus. During response increase of variability (FF) coincided with an increase of the rate. B, Response to high velocity (500°/s) stimulus. During response, decrease of variability (FF) coincided with an increase of the rate. Notice that, in the case of A and B, peak values of firing rate were similar.

We noted large width of the confidence bounds for FF during response to slow stimuli for which we had fewer repetitions than for fast stimuli (Fig. 2D, left plot). To find out whether the effect was attributable to limited statistics or a consequence of large variability, we performed additional bootstrap analysis for responses to high velocity using a subset of data with the same number of repetitions as for low velocity responses. There were no significant differences in confidence intervals calculated for the truncated and the original dataset of responses at high velocities. Thus, the broader range of confidence bounds for low velocity responses is a consequence of the higher variability of data.

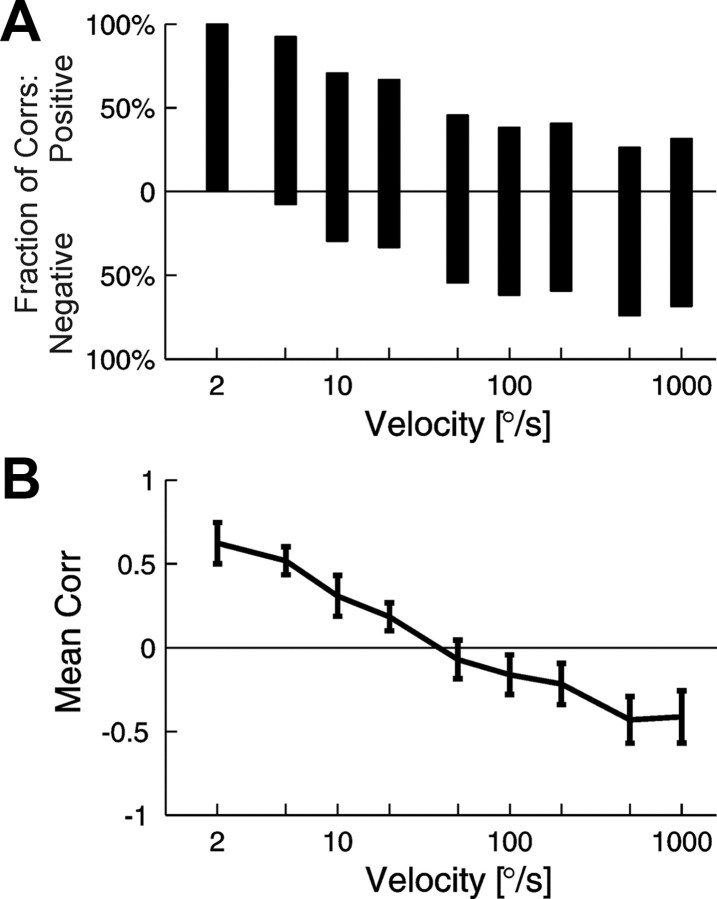
To quantify the observed effects, we calculated the Pearson's correlation coefficient between the FF and the firing rate during the response period (see Materials and Methods). Summary results of dependence of the correlation between firing rate and FF on velocity for the whole set of experimental data are presented in Figure 4. For very slow stimuli, the correlation coefficients were found to be almost exclusively positive (Fig. 4A, 2 and 5°/s). However, in a range of moderate velocities, we found both positive and negative correlation coefficients with a negative trend for higher velocities. For fast stimuli, most coefficients were negative. These observations are supported by the graph presented in Figure 4B, in which for each velocity the mean correlation coefficient is shown. The crossover velocity for LVE/HVE or LVE/HVS cells (that is, a velocity at which the correlation coefficient changed sign) spans between 20 and 200°/s. For the whole dataset, the mean correlation coefficients between rate and FF were positive at low velocities of stimulus movement, up to 20°/s, and negative for velocities above 50°/s.

Figure 4.

Correlation coefficient between the firing rate and FF as a function of stimulus velocity. Pearson's correlation coefficients for experimental data were computed only for periods of responses to visual stimulation. A, Fraction of positive (above the 0 baseline) and fraction of negative (below the 0 baseline) correlation coefficients for a given velocity of stimulus for the whole cell population. B, Mean correlation coefficients for particular velocities obtained by averaging over the responses of all cells. Error bars correspond to SEM values. The firing rate and the FF values were computed in 200 bins for each velocity.

Other factors potentially affecting calculated trial-to-trial variability

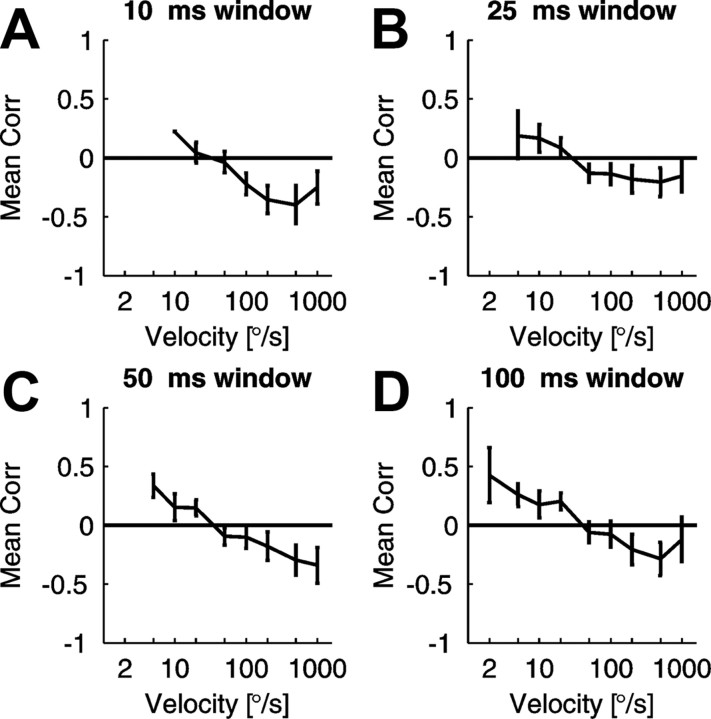
Two factors in the above analysis could potentially affect variability measure and thereby give rise to opposite behavior of FF in the case of low and high velocity responses. One is the different bin size used for FF estimation (Teich et al., 1997). To test the putative influence of bin size on FF, we performed the whole analysis using a fixed number of bins for every response (200) or using fixed size sliding windows shifted with 1 ms resolution regardless of stimulus duration and velocity (see Materials and Methods) for the whole set of collected responses. Regardless of the window size (10, 25, 50, or 100 ms), we observed a monotonous decrease of the firing rate − FF correlation coefficient with increasing velocity (Fig. 5), similar to the fixed-number-of-bins analysis.

Figure 5.

Mean correlation coefficients between firing rate and FF as a function of stimulus velocity calculated in sliding windows with different window lengths: 10 ms (A), 25 ms (B), 50 ms (C), and 100 ms (D). Error bars correspond to SEM values.

Another aspect broadly described in the literature (Softky and Koch, 1993; Holt et al., 1996; Kara et al., 2000) is the influence of the level of activity (magnitude of firing rate) on the trial-to-trial variability: the higher the firing rate, the lower the FF. A simple approach to examine this effect is to generate surrogate data with comparable activity but without any higher-order temporal dependencies between action potentials. We used the IP process to generate reference spike trains. In the Poisson process, generation of an action potential depends only on the mean firing rate and trial-to-trial variability is equal to unity for an infinite number of repetitions. However, for an experimentally feasible number of repetitions, one expects fluctuations of FF, which in principle might be related to the changes in rate. The model data had the same length and the same number of repetitions as the experimental sets, and all the analyses were conducted in the same manner as for the responses of the SC neurons (Fig. 6). Whereas the firing rate of IP surrogate data was almost the same as the experimental rate and the response pattern was not very different, the surrogate FF curves only slightly fluctuated around 1, the theoretical value of the Poisson process. Such an effect was observed both for low and high velocities (Fig. 6B,E, bottom plots). We therefore concluded that the effects observed experimentally could not result from simple variation of rate or from limited statistics.

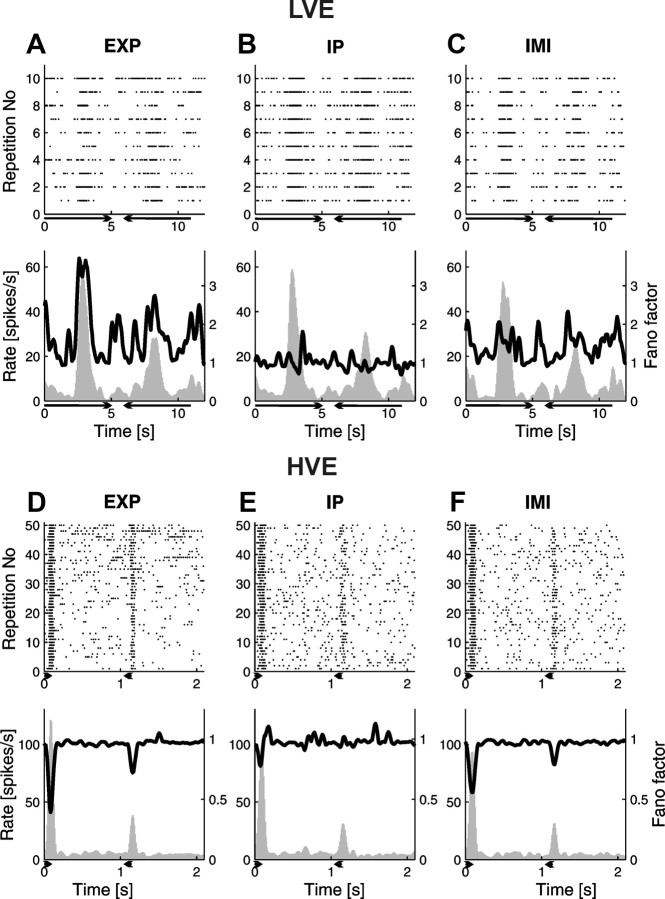
Figure 6.

Comparison of experimental and surrogate data results for two cells: one from the LVE group (A–C) and the second from the HVE group (D–F). In the left column (A, D), experimental data (EXP) are presented. In the middle column (B, E), surrogate data generated with the IP process are presented. In the right column (C, F), surrogate data generated with the IMI process are presented. Each dataset is presented as a raster plot (top) and PSTH (below, gray histogram with scale set on the left vertical axis). The black solid line superimposed on every PSTH is the FF as a function of time (with scale set on the right vertical axis). Lengths of the horizontal arrows below the time axis indicate duration of the stimulus, and their heads show the direction of motion. A, Experimental data. Responses of an LVE cell to slowly moving stimulus (10°/s). Variability of response increases together with the increase of the rate. B, Surrogate data from the IP model. The model was estimated from smoothed experimental firing rate of neuron responses presented in A. In this case, FF oscillates around 1, which is the theoretical value for the Poisson process. Notice that no increase in FF during response can be seen. C, Surrogate data from the IMI model estimated from the responses presented in A. FF in the peak of the response does not reach the value of FF obtained for experimental data. D, Experimental data. Responses of an HVE cell to high velocity (1000°/s) stimulus. Notice that changes in FF are negatively correlated with changes of firing rate during the response. When the rate increases, the variability of response (FF) goes down. E, F, Surrogate data generated with IP and IMI models, respectively. Parameters of models were estimated from responses presented in D. In the case of IP data, FF oscillates around 1, with only slight decrease at peak response, whereas for IMI data, dependency of changes of FF and firing rate replicates experimental results. In all the plots, the number of bins on the time axis was 200.

Inclusion of spiking history in simulations of neural spiking activity in different groups of collicular cells

To better understand stochastic properties of the experimental results, we went one step further in modeling the data and incorporated first-order temporal dependencies between action potentials. Using the IMI model (Berry and Meister, 1998; Kass and Ventura, 2001), in which the probability of generating a spike was a product of two terms, stimulus-dependent and spike-history components, we generated a second family of surrogate data (see Materials and Methods). As for the IP model, the resulting PSTHs for IMI processes were very similar to experimental ones for both low and high stimulus velocities (Fig. 6, compare A, D with C, F, bottom plots). The IMI model reproduced well the observed dependency of the FF and firing rates in the case of high velocity responses (Fig. 6F, bottom plot) but did not mimic the experimental results for low velocity responses (Fig. 6C, bottom plot).

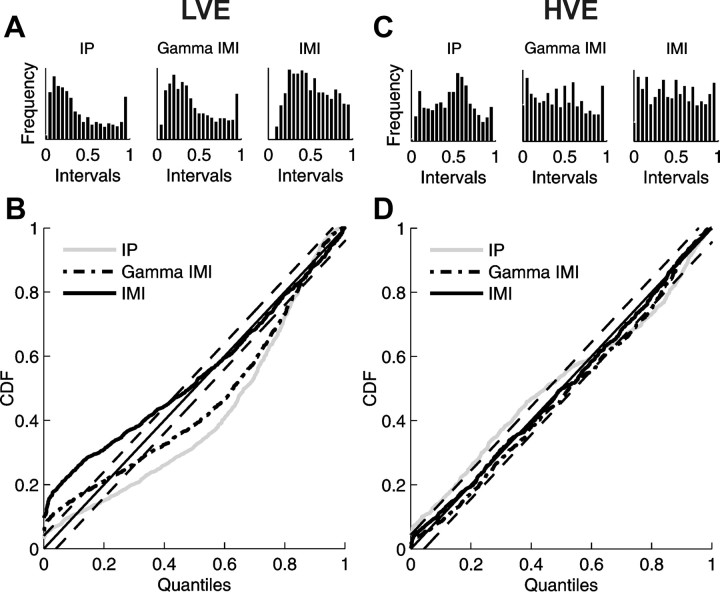
Goodness-of-fit between the proposed model and the experimental data was assessed on the basis of time-rescaling theorem and Kolmogorov–Smirnov statistics (Brown et al., 2002; Truccolo et al., 2005; Czanner et al., 2008). For a good model of the data, experimental interspike intervals, rescaled and transformed using the model conditional intensity, should be uniformly distributed random variables on the interval [0,1]. Histograms of rescaled times and the K–S plots for different models of exemplary responses are presented in Figure 7. A and C show histograms of rescaled interspike intervals obtained for conditional intensity functions estimated with the IP model or IMI models (parametric gamma and nonparametric) for low and high velocity examples, respectively. For high velocity data, the most uniform distribution of the rescaled interspike intervals is obtained for the nonparametric IMI model. In the case of the low velocity example, however, neither model leads to a uniform distribution of the rescaled interspike intervals.

Figure 7.

Comparison of the goodness-of-fit of different models using histograms of rescaled interspike intervals (A, C) and the K–S plots (B, D) for exemplary responses to stimuli of low (A, B) and high (C, D) velocity presented in Figure 6. Histograms and K–S curves were obtained by appropriate rescaling of interspike intervals (see Materials and Methods) with conditional intensity estimated for the IP model (histograms in the left panels, gray lines in K–S plots), the parametric gamma IMI model (histograms in the middle panels, dash–dotted lines in K–S plots), and the nonparametric IMI model (histograms in the right panels, thick solid lines in K–S plots) and then transformed to a uniform distribution on interval [0,1]; vertical axis indicates values of cumulative distribution function (CDF). Diagonals (thin solid lines) correspond to a perfect model of data, and the two parallel thin dashed lines demarcate 95% confidence bounds. The distance of every curve from the diagonal is a measure of the quality of a given model. Notice the poor behavior of all the models for the low velocity example.

Similarly, the curves in the K–S plots (Fig. 7B,D) were obtained by appropriate rescaling of interspike intervals using conditional intensity functions estimated with either the IP model (gray curve) or IMI models (nonparametric, thick solid line; parametric gamma, dash–dotted line). Diagonal (thin solid line) corresponds to the perfect model of data for which rescaled interspike intervals are uniformly distributed. The distance from the diagonal can be used as a measure of the quality of the model. All models describe data obtained for high velocity responses (Fig. 7D) much better than those for low velocities (Fig. 7B). In the low velocity example (Fig. 7B), performance of the IP and parametric IMI models is worst in the range of medium intervals. The nonparametric IMI model seems most adequate except at short intervals. All three models seem to account reasonably well only for the longest interspike intervals because all the K–S curves in this range lie within the 95% confidence bounds (Fig. 7B,D, two parallel thin dashed lines). For the high velocity example, the IP model provides the worst description of the data. The IMI models give a much better description, with K–S curve for the nonparametric IMI model lying entirely within the 95% confidence bounds.

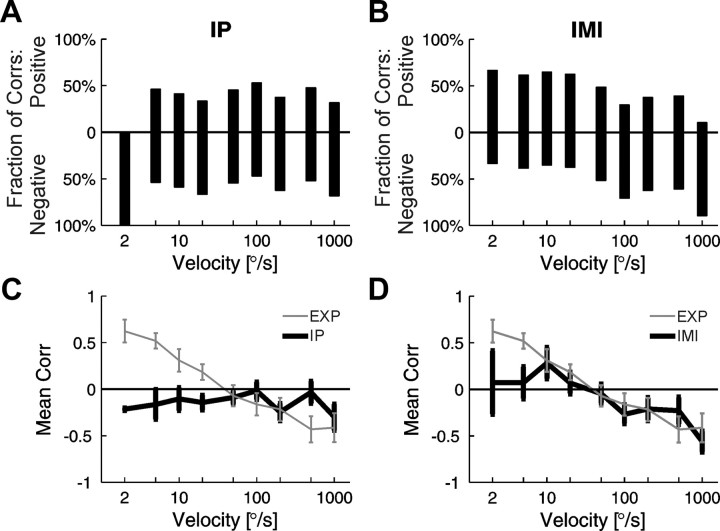
As for the experimental data, Pearson's correlation coefficients between the firing rate and the FF were calculated for the surrogate data generated for the IP model and for the parametric and nonparametric multiplicative IMI models. Summary results concerning velocity dependence of correlation between firing rate and FF for the whole set of surrogate data are shown in Figure 8. Data generated using the IP model are presented in the left column, and data for the nonparametric IMI model are shown in the right column. The correlation coefficients for IP surrogate data do not show any clear dependence on velocity (Fig. 8A,C). For almost all velocities, there was a slightly higher fraction of negative than positive correlations (Fig. 8A), which resulted in mean correlation coefficients below zero (Fig. 8C). The mean correlation coefficients of the IMI surrogate dataset show a similar dependence on velocities as for the experimental data (Fig. 8D) only in the range of moderate and high velocities. At low velocities, correlation coefficients fluctuated around zero (Fig. 8B). The conclusions from the above analysis are similar to those obtained from K–S plots. The IP model seems to be completely inadequate in the description of our data, whereas the IMI models seem to adequately describe the firing of collicular neurons, including variability of responses, in the range of moderate to high stimulus velocities.

Figure 8.

Velocity dependence of correlations between firing rate and FF for surrogate data for the whole population of cells. Data generated using the IP model are presented in the left column (A, C). Data from the nonparametric IMI model are shown in the right column (B, D). Mean Pearson's correlation coefficients between the firing rate and FF were computed over periods corresponding to the response to visual stimulation in the original experimental data (EXP). A, B, Fraction of positive (above the 0 baseline) and fraction of negative (below the 0 baseline) correlation coefficients for a given velocity in the whole population of cells. C, D, Means of correlation coefficients for a given velocity; error bars correspond to SEM values. Results for surrogate data (for IP and IMI, respectively) are presented in black. For comparison, the experimental results are plotted in gray (compare with Fig. 4).

Discussion

In this study, we showed that trial-to-trial response variability of cells in cat's retinorecipient layers of SC strongly depends on velocity of visual stimuli. For cells responding to fast moving stimuli (receiving Y-retinal input), the time-dependent FF correlated negatively with the firing rate. The trial-to-trial variability dropped during excitatory responses and increased during suppression. These findings agree with the intuition that, at high firing rates, responses are less variable and are in line with the previous reports for the visual geniculate pathway (Tolhurst et al., 1983; Kara et al., 2000; Carandini, 2004; Gur and Snodderly, 2006). However, during excitatory responses to slow stimuli (information conveyed by the W channel), variability increased with the firing rate. We know only one such report: bursting responses recorded from the cat's lateral geniculate nucleus (Kara et al., 2000).

Our results indicate that Y and W channels may differ in reliability of responses to visual stimulation. Apart from previously reported morphological and physiological differences of cells belonging to Y and W channels (for review, see Stone, 1983; Burke et al., 1998; Casagrande and Xu, 2004), this is a new feature distinguishing these two pathways.

Factors influencing observed differences

Firing rate dependence

Trial-to-trial variability may depend on magnitude of the firing rate. At high activation level, refractory period limits response irregularity (Berry and Meister, 1998; Kara et al., 2000). Moreover, because FF is the variance normalized by the mean, despite no change in the response variance, the increase of mean rate results in the decrease of FF. This could explain the increase of FF during suppressive responses for high-velocity stimuli. However, in cells responding well in a broad range of velocities (convergence of W and Y channels), the distinct behavior of FF at low and high velocities did not result from different magnitude of the firing rate (Fig. 3).

To explain this effect, one should take into account not only the differences in the levels of evoked but also in background activity of SC cells. Azouz and Gray (1999) argue that the intensity of visually evoked responses in V1 positively correlates with the background membrane potential immediately preceding the visual response. The opposite holds for the latency of evoked response. Thus, the membrane potential preceding the visual response influences its reliability and precision (for review, see Tiesinga et al., 2008). In our experiments, the LVE cells were characterized by both relatively low peak discharge rate and low or virtually absent background activity. This might suggest that these cells operated well below spike generation threshold in the spontaneous state and close to the threshold level when activated with visual stimuli, which resulted in high variability of their responses.

Dependence on dynamics of stimulus features

Several in vivo studies performed on different levels of the visual pathway showed that dynamic stimulation elicited more reliable response than slowly varying stimuli (Bair and Koch, 1996; Berry et al., 1997; de Ruyter van Steveninck et al., 1997; Buracas et al., 1998) (but see Warzecha and Egelhaaf, 1999). This is consistent with intracellular in vitro (Mainen and Sejnowski, 1995) and in vivo (Azouz and Gray, 1999) studies connecting the reliability of cortical cell responses with the dynamics of membrane voltage changes, which associated the highest precision of the action potential generation with rapid membrane depolarization. Also the spike generation threshold was shown to depend on the rate of changes of membrane voltage just before the action potential and was lower when preceded by a brief depolarization (Azouz and Gray, 1999). Thus, it is likely that the spike generation mechanism, which acts as a high-pass filter, favors high velocity visual stimuli that induce rapid changes of membrane voltage and transforms information about such stimuli more precisely.

Differences between cell classes

Response variability may also originate from intrinsic cellular membrane properties (for review, see Tiesinga et al., 2008), such as types of voltage-gated conductances and their distributions through dendritic and somatic membranes, varying in different cell classes. Thus, the diversity of the morphological types of neurons in the superficial layers of the SC (for review, see May, 2006) may be the cause of the found differences in the response variability. Several studies compared the variability of responses between different cell classes in different visual structures (Sestokas and Lehmkuhle, 1988; Hartveit and Heggelund, 1994; Gur and Snodderly, 2006; Andolina et al., 2007; Victor et al., 2007). Although the available results are vague, two studies showing striking similarities to our results are worth mentioning. In the studies of parasol retinal ganglion cells in the macaque monkey (homologs of cat's Y cells) (Crook et al., 2008), spike count variance across trials was much lower than its mean (Uzzell and Chichilnisky, 2004). The finding was inconsistent with Poisson statistics but matched a model that included the relative refractory period. In the in vitro study on neurons from the nucleus of the optic tract (Prochnow et al., 2007), one group of cells, spontaneously active in the in vitro preparation and giving regular responses to current injections, preferred high velocity visual stimuli, as identified previously in the in vivo experiments. The other cells, not spontaneously active and responding in an irregular manner, preferred low stimulus velocities.

Network and modulatory influence

Several reports indicate that modulatory (not spike generating) inputs may affect response reliability (Hartveit and Heggelund, 1994; Andolina et al., 2007; Mitchell et al., 2007). Collicular cells that receive W- or/and Y-type input may also constitute parts of different neural networks within SC and be under the influence of different modulatory inputs. Comparison of laminar distribution of retinal Y and W inputs in the SC (Berson, 1988) and terminals of different cortical areas (for review, see Dreher, 1986; Harting et al., 1992) suggests that collicular cells receiving distinct retinal inputs are also activated by many, rather distinct, populations of cortical neurons.

Moreover, it was suggested that collicular W-input cells have more complex local network of GABAergic interneurons then Y-input cells (Mize, 1996), which is in line with studies showing much stronger influence of the suppressive surround for SC cells responding to slowly moving stimuli (Waleszczyk et al., 1999). GABAergic influence was suggested to increase response variability (Softky and Koch, 1993) (but see Hu et al., 2002); thus, the specific impact of cortical inputs and local GABAergic networks onto SC cells receiving W or Y retinal input might explain their differences in variability.

Data modeling perspective

On the basis of the present data, we cannot settle which of the factors above caused the observed differences between Y and W channels. However, modeling the data under different assumptions, we were able to investigate and exclude some of them. If the firing rate was the only meaningful aspect of the data, the IP process should reproduce the results, including fluctuations of time-dependent FF. Because it failed, we incorporated a spike-history component reflecting the membrane properties of the neuron, including refractory period, in a multiplicative IMI model. This provided adequate description of responses to fast stimuli but failed at low velocities. One may wonder which features of the low velocity data make them so difficult to model in the considered framework and how this framework should be modified. One possibility is to include long-term fluctuations in rate level not related directly to the stimulus, and another is to use population approach considering network influences (Pillow et al., 2008). This will require further studies.

Coding of information and functions of W and Y channels in the SC

Reich et al. (1997) suggested that “the mode of information transmission may switch from detection (in a regime in which spike trains are imprecise and timing is not used to convey information) to discrimination (in a regime in which spike times are precise)”. Thus, the increase of FF during responses to slowly moving stimuli would indicate that W channel does not convey information in a temporally precise spike pattern. This suggestion meshes with the general functions postulated for the W channel, such as ambient vision (Stone et al., 1979) or local movement detection (Rowe and Cox, 1993), and also with the function of the SC in spatial localization of sensory stimuli and orienting behavior, in which detection of stimulus is more important than discrimination of its features.

In contrast, participation of the SC in visuomotor behavior, particularly in reflex adjustment of head and eyes, which often has to be performed in the shortest possible time, indicates the need for fast and reliable transmission of information about the visual environment. The pathway from retina through the superficial and then deep layers of the SC to the oculomotor nuclei (for review, see Munoz 2002) contains few synapses, is relatively short, and is therefore appropriate for fast orientating response to visual stimuli. The Y channel with fast transmission of information (Burke et al., 1998) and low variability of responses to rapid changes in the environment seems to fulfill such demands.

Our results are merely the first indication of the possible differences in coding between Y and W channels or between different groups of collicular cells. Clearly, a deeper analysis of coding in the SC requires more sophisticated measures applied to responses to more complex stimuli (de Ruyter van Steveninck et al., 1997; Shinomoto et al., 2009).