Predictive Coding as a Model of Response Properties in Cortical Area V1

Abstract

A simple model is shown to account for a large range of V1 classical, and nonclassical, receptive field properties including orientation tuning, spatial and temporal frequency tuning, cross-orientation suppression, surround suppression, and facilitation and inhibition by flankers and textured surrounds. The model is an implementation of the predictive coding theory of cortical function and thus provides a single computational explanation for a diverse range of neurophysiological findings. Furthermore, since predictive coding can be related to the biased competition theory and is a specific example of more general theories of hierarchical perceptual inference, the current results relate V1 response properties to a wider, more unified, framework for understanding cortical function.

Introduction

Predictive coding (PC) provides an elegant theory of how bottom–up evidence is combined with top–down priors to compute the most likely interpretation of sensory data. Specifically, PC proposes that an internal representation of the world generates predictions that are compared with stimulus-driven activity to calculate the residual error between the prediction and the sensory evidence. A number of previous proposals for how PC could be implemented in cortical circuitry have all suggested that cortical feedback connections carry predictions and that these act on regions at preceding stages along an information processing pathway to calculate the residual error, which is then propagated via cortical feedforward connections (Mumford, 1992; Barlow, 1994; Rao and Ballard, 1999; Murray et al., 2004; Friston, 2005, 2009; Jehee et al., 2006; Kilner et al., 2007).

An alternative implementation of PC, the PC/BC model (Spratling, 2008a,b), proposes that the calculation of the residual error is performed by connections intrinsic to each cortical region, rather than via feedforward and feedback connection between cortical regions. When viewed in this way, PC can be interpreted as a mechanism of competition between different representations of the sensory world. PC/BC makes particular predictions about the mechanism of competition operating within each cortical area. Specifically, this interpretation of PC requires that neurons that represent predictions (presumed to be pyramidal cells) suppress the inputs to neighboring prediction neurons within a cortical region. This is in contrast to most other models of cortical inhibition, which presume that neurons suppress the outputs of other neurons. Furthermore, PC/BC requires that the strength with which a prediction neuron suppresses a particular input should be proportional to the strength of the afferent connection that that prediction neuron receives from that input. This has the consequence that the strength of competition between two prediction neurons is proportional to the degree of overlap between their receptive fields (RFs).

The effects of competitive interactions between cortical neurons have been most extensively studied in primary visual cortex. Hence, to determine whether the particular mechanism of competition proposed by the PC/BC model is consistent with competitive mechanisms known to operate in cortex, PC/BC was used to simulate the competition between neurons in a population of V1 simple cells. The model was presented with stimuli identical with those used in physiological investigations of V1 response properties. Crucially, the model remained fixed across all the experiments. Hence the model was tested in a manner analogous to V1 with only the parameters for the stimulus (contrast, grating wavelength, presentation time, etc.) under the experimenter's control. The behavior of the model is in good agreement with a wide range of classical and nonclassical RF properties of neurons in cortical area V1. This suggests that the PC/BC version of predictive coding is consistent with the mechanism of competition implemented in primary visual cortex and hence that many of the varied response properties observed in V1 neurons may simply be a by-product of the cortex performing predictive coding.

Materials and Methods

The PC/BC model.

Spratling (2008a) introduced a nonlinear model of predictive coding (nonlinear PC/BC), illustrated in Figure 1, which is implemented using the following equations:

where superscripts of the form Si indicate processing stage i of a hierarchical neural network, e^Si is a (m by 1) vector of error-detecting neuron activations, y^Si is a (n by 1) vector of prediction neuron activations, W^Si is a (n by m) matrix of synaptic weight values normalized such that the sum of each row is equal to ψ, Ŵ^Si is a matrix representing the same synaptic weight values as W but such that the rows are normalized to have a maximum value of ψ, ε₁, ε₂, and ç are parameters, and ∅ and ⊗ indicate element-wise division and multiplication, respectively. These equations are evaluated in the order 1, 2, 3, and the values of y^Si given by Equation 3 are then substituted back into Equations 1 and 2 to recursively calculate the changing neural activations at each time step.

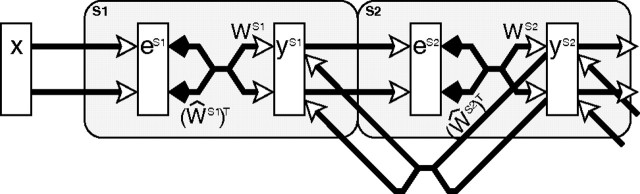
Figure 1.

The PC/BC model: a reformulation of predictive coding (Rao and Ballard, 1999) that can be interpreted as a form of biased competition model. The rectangles represent populations of neurons, with y labeling populations of prediction neurons and e labeling populations of error-detecting neurons. The open arrows signify excitatory connections, the filled arrows indicate inhibitory connections, the crossed connections signify a many-to-many connectivity pattern between the neurons in two populations, the parallel connections indicate a one-to-one mapping between the neurons in two populations, and the large shaded boxes with rounded corners indicate different cortical areas or processing stages.

A value of ψ equal to 1 has been used in previous work (Spratling, 2008a; De Meyer and Spratling, 2009; Spratling et al., 2009). Changing the value of this particular parameter has no effect on the behavior of the model, except to scale the activation values of the error-detecting neurons by $\frac{1}{\text{ψ}}$. In these experiments, a value of ψ equal to 5000 was used to produce error neuron activations of the same order of magnitude as the prediction neuron activations (see supplemental material, available at www.jneurosci.org).

Equation 1 describes the calculation of the neural activity for each population of error-detecting neurons. These values are a function of the activity of the prediction neurons in the preceding cortical area divisively modulated by a weighted sum of the outputs of the prediction neurons in the current area (Spratling et al., 2009). The activation of the error-detecting neurons can be interpreted in two ways. First, e can be considered to represent the residual error between the input to the current processing stage (y^Si−1) and the reconstruction of the input ((Ŵ^Si)^Ty^Si) generated by the prediction neurons at the current processing stage. The values of e indicate the degree of mismatch between the top–down reconstruction of the input and the actual input (assuming ε₂ is sufficiently small to be negligible). When a value within e is greater than $\frac{1}{\text{ψ}}$, it indicates that a particular element of the input is underrepresented in the reconstruction; a value of less than $\frac{1}{\text{ψ}}$ indicates that a particular element of the input is overrepresented in the reconstruction; and a value of $\frac{1}{\text{ψ}}$ indicates that the top–down reconstruction perfectly predicts the bottom–up stimulation. A second interpretation is that e represents the inhibited inputs to a population of competing prediction neurons. Each prediction neuron modulates its own inputs, which helps stabilize the response of the prediction neurons, since a strongly (or weakly) active prediction neuron will suppress (magnify) its inputs and hence reduce (enhance) its own response. Prediction neurons that share inputs (i.e., that have overlapping RFs) will also modulate each other's inputs. This generates a form of competition between the prediction neurons, such that each neuron effectively tries to block other prediction neurons from responding to the inputs that it represents.

Equation 2 describes the updating of the prediction neuron activations. The response of each prediction neuron is a function of its activation at the previous iteration and a weighted sum of afferent inputs from the error-detecting neurons. Equation 3 describes the effects on the prediction neuron activations of top–down inputs from prediction neurons at the next stage in the neural hierarchy. These top–down inputs are a weighted sum of the activity of the prediction neurons at the subsequent processing stage and have a purely modulatory effect on the current processing stage. This feedback allows predictions generated by neurons higher up a processing hierarchy (which have larger receptive fields) to influence the strength of each prediction made at the current processing stage. Equivalently, feedback can be interpreted as influencing the outcome of the competition occurring between prediction neurons at the current processing stage. Hence the PC/BC model can also be interpreted as an implementation of the biased competition model of cortical function (Spratling, 2008a,b).

The V1 model.

This article is concerned with modeling a single cortical region, V1, in isolation. Hence only a single processing stage will be modeled (Fig. 2). Furthermore, all top–down, modulatory, inputs to this area are ignored (i.e., y^V1+1 = 0), and hence Equation 3 can also be ignored. Since there is only one processing stage in the model, the superscripts will be dropped, and the input to V1 will be described by a vector, x = y^V1−1, of inputs coming from a model of the lateral geniculate nucleus (LGN) (see below). The model can thus be simplified to the following two equations:

These equations describe the competition occurring within one processing stage (cortical area) of the PC/BC model. This mechanism of competition is called divisive input modulation (DIM) and has been shown to have excellent pattern recognition abilities on an artificial task (Spratling et al., 2009).

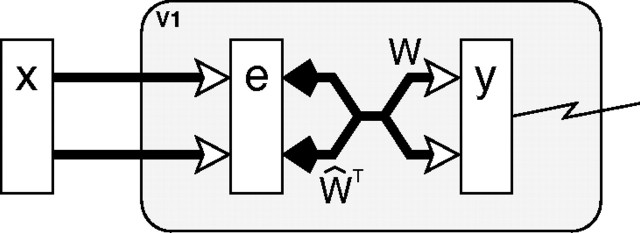
Figure 2.

The model of V1 implemented using PC/BC. The prediction neurons (labeled y) are assumed to correspond to V1 simple cells and the response of one of these neurons is recorded. The RFs of these prediction neurons are determined by the definition of the weight matrix W. Prediction neurons compete to represent the input stimulus x via divisive feedback, which acts on the error-detecting neurons (labeled e) and is carried by connections from the prediction neurons to the error-detecting neurons, which have strength proportional to the corresponding reciprocal weights from the error-detecting neurons to the prediction neurons.

Despite the simplicity of the model, simulating a large population of neurons receiving input from a reasonably large image is computationally demanding using the matrix multiplication method described by Equations 4 and 5. Furthermore, individually specifying the synaptic weight values for a large population of neurons can be inconvenient. For an application, like a model of V1, in which neurons have RFs restricted to a small fraction of the input image, and in which the same patterns of weights are repeated at different spatial locations, it is possible to implement DIM in a more tractable manner using linear filtering and convolution, as follows:

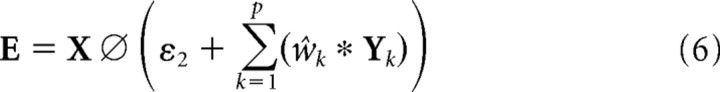Where E, X, and Y_k are two-dimensional arrays equal in size to the input image that represent the error-detecting neuron responses, the input stimulus, and the prediction neuron responses, respectively; w_k is a two-dimensional kernel representing the synaptic weights for a particular class (k) of neuron; p is the total number of kernels; ★ represents cross-correlation (which is equivalent to convolution without the kernel being rotated 180°); and * represents convolution (which is equivalent to cross-correlation with a kernel rotated by 180°). Note that Equation 7 represents a family of equations, one for each kernel.

The RF of a simple cell in primary visual cortex can be accurately modeled by a two-dimensional Gabor function (Daugman, 1980, 1988; Marcelja, 1980; Jones and Palmer, 1987; Lee, 1996). Hence the Gabor function was used to define the weights of each kernel w_k. A definition of a Gabor function of the form proposed by Lee (1996) was used, which includes a term to remove the DC response of the filter as follows:

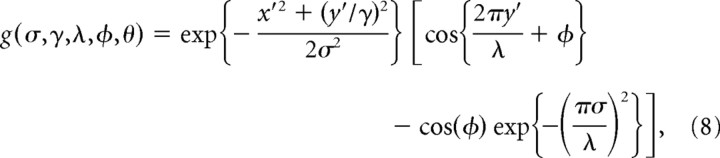where σ = 4 (pixels) was a constant that defined the SD of the Gaussian envelope (which determines the spatial extent of the RF), γ=$\frac{1}{\sqrt{\text{2}}}$ was a constant that defined the aspect ratio of the Gaussian envelope (which determines the ellipticity of the RF), λ = 6 (pixels) was a constant that defined the wavelength of the sinusoid, ϕ was the phase of the sinusoid, and x′ = x cos(θ) + y sin(θ) and y′ = −x sin(θ) + y cos(θ), where θ defined the orientation of the RF. Note that the size of the RF of a model neuron is measured in pixels. This value should have a direct linear relationship with the size of the RF of a cortical cell measured in degrees of visual angle. Different neurophysiological experiments are performed with cells that have different RF sizes. To simulate these different experiments, it would be possible to scale parameters σ and λ to fit the model to each specific cortical neuron. Alternatively, it is possible to keep the model fixed and change the size of the image. The latter approach was taken in the simulations reported in this article.

A family of 32 Gabor functions (Fig. 3a) with eight orientations (θ = 0–157.5° in steps of 22.5°) and four phases (ϕ = 0, 90, 180, and 270°) were used to define the RFs of the neurons in the model. The cross-correlation and convolution performed in Equations 6 and 7 mean that neurons with these RFs are reproduced at every pixel location in the image, and consequently, that the size of the population of V1 cells simulated varies with image size. For an a × b pixel image, the model simulates the response of 32ab prediction neurons (for the experiments reported in Results, an image is typically 51 × 51 pixels, so ∼80,000 prediction neurons were simulated).

Figure 3.

The synaptic weights used in the PC/BC model of V1. a, A family of 32 Gabor functions (8 orientation and 4 phases) used to define the RFs of the neurons in the model. b, The actual synaptic weights of the model neurons were created by separating the positive and negative parts of the Gabor function into separate (non-negative) ON and OFF weights (shown for the bottom right Gabor function only). Each Gabor kernel is 21 × 21 pixels, and hence each prediction neuron in the model receives 21 × 21 × 2 = 882 synaptic weights.

The PC/BC model requires non-negative weights. Hence the weights were separated into distinct ON and OFF channels, which represented the positive and negative parts of the Gabor function using separate sets of non-negative weights (Fig. 3b). These separate channels result in the model illustrated in Figure 4 and described by the following equations:

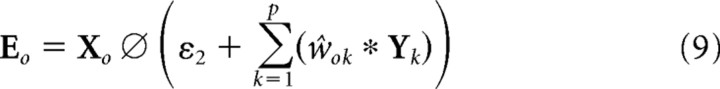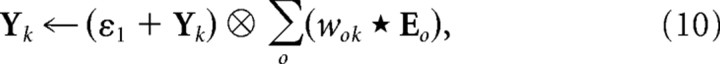where o ϵ [ON,OFF]. The kernels w_ON,k and w_OFF,k were normalized so that sum of all the weights in both the ON and OFF channel was equal to ψ, and ŵ_ON,k and ŵ_OFF,k were normalized so that the maximum value across both the ON and OFF channel was equal to ψ.

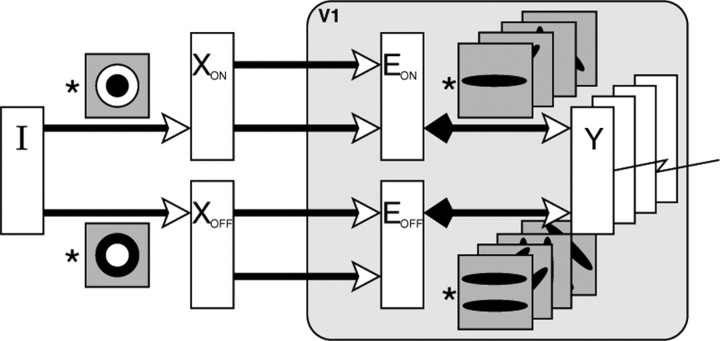
Figure 4.

The PC/BC model of V1 implemented using convolution and with separate ON and OFF channels. The input image I is preprocessed by convolution with a circular-symmetric on-center/off-surround kernel (to generate the input to the ON channel of the V1 model) and a circular-symmetric off-center/on-surround kernel (to generate the input to the OFF channel of the V1 model). The prediction neurons (labeled Y), which represent V1 simple cells, generate the responses that were recorded during the experiments. These responses were generated by convolving the outputs of the (ON and OFF channels of the) error-detecting neurons (labeled E) with (the ON and OFF channels of) a number of kernels representing V1 RFs. This convolution process effectively reproduces the same RFs at every pixel location in the image. The responses of the error-detecting neurons are influenced by divisive feedback from the prediction neurons, which is also calculated by convolving the prediction neuron outputs with the weight kernels.

For each new input image, the prediction neuron responses (Y) were initialized to zero, and then the above equations were iterated to record the response of Y for a number of iterations (t). This recording time, t, was the only parameter (apart from the input image) that was varied during the experiments reported in Results. The response of the prediction neurons on the first iteration is given by the following:

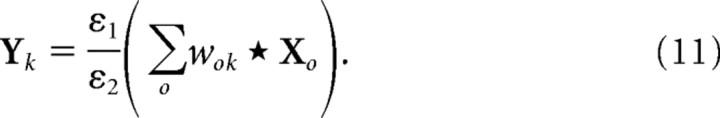The bracketed term on the right-hand side of Equation 11 represents the output produced by a set of linear filters when applied to the image. This initial, linear, response is scaled by the ratio $\frac{{\epsilon }_1}{{\epsilon }_2}$. To ensure that this initial transient did not dominate the recorded responses, values of ε₁ = 0.0001 and ε₂ = 50 were used. Given the large value of ψ used here, these values are similar to those used previously to simulate the interactions between attention and long-range lateral connections in V1 (De Meyer and Spratling, 2009).

Results from neurophysiological studies are generally presented by showing how the mean evoked firing rate of the recorded neuron changes as a particular parameter of the input stimulus is varied. Results from the model were generated in the same way by recording the activity of a single prediction neuron, in response to each input image, for a number of iterations (t) of the PC/BC algorithm. The average response was then calculated by simply taking the mean activity of the recorded prediction neuron over the t iterations that the stimulus was presented. As for typical physiological experiments, the stimulus parameters other than the one being varied during the experiment were matched to the preferred parameters of the neuron under test (e.g., the stimulus was centered over the RF at the preferred orientation, spatial frequency, temporal frequency, etc., of the recorded neuron). Furthermore, the range of grayscale values in the input image I were set equal to the fractional Michelson contrast used for the presentation of stimuli in the corresponding physiological experiment, if this value was reported.

The LGN model (image preprocessing).

The input to the model of V1, described above, was an input image (I) preprocessed by convolution with a LoG (Laplacian-of-Gaussian) filter (l) with SD equal to 1. This is virtually identical with the DoG (difference-of-Gaussians) filter that has traditionally been used to model circular RFs in LGN. The output from this filter was subject to a saturating nonlinearity, such that

The positive and rectified negative responses were separated into two images X_ON and X_OFF simulating the outputs of cells in retina and LGN with circular-symmetric on-center/off-surround and off-center/on-surround RFs. This preprocessing is illustrated in Figure 4. Consistent with neurophysiological data (Reid and Alonso, 1995), the ON-center LGN neurons provided input to the ON subfield of the model V1 simple cells, whereas the OFF-center LGN neurons provided input to the OFF subfield of the model V1 neurons.

In most experiments, static stimuli were used. Hence I and the values of X_ON and X_OFF remained constant throughout each experiment. However, in some experiments, it was necessary to simulate moving stimuli. To do this, the input image was changed, and new X_ON and X_OFF values were calculated, for each iteration of the PC/BC algorithm. The amount the input image changed between consecutive iterations reflected the speed of the temporally changing stimulus. For example, to simulate an object moving at 10 pixels per iteration, the object would be displaced by 10 pixels in one image compared with the previous one. Since moving stimuli in the experiments reported here were sinusoidal gratings, speed was measured in cycles per iteration, where the number of cycles refers to the phase shift between sinusoids in consecutive images.

Code.

Software, written in MATLAB, which implements the PC/BC model described above is available at http://www.corinet.org/mike/code.html.

Results

The following sections present simulations of a number of experiments performed to assess the response properties of cells in V1. These experiments cover basic tuning preferences (orientation tuning, size tuning, spatial frequency tuning, and temporal frequency tuning), suppression attributable to additional stimuli appearing within the classical receptive field (cross-orientation suppression) and outside the classical receptive field (surround suppression, and suppression attributable to textured surrounds), and facilitation attributable to flankers.

Basic tuning properties

Simple cells in V1 are selective for a number of stimulus properties such as color, orientation, direction of motion, spatial frequency, temporal frequency, eye of origin, binocular disparity, and stimulus size and location. The model presented here is restricted to grayscale pixel values coming from a single image and has no mechanism for distinguishing direction of motion. However, it generates behavior that closely matches typical tuning properties of V1 cells for those properties that it does model, namely, orientation, spatial frequency, temporal frequency, and size.

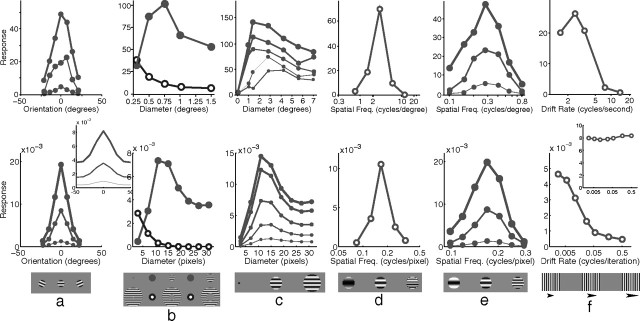
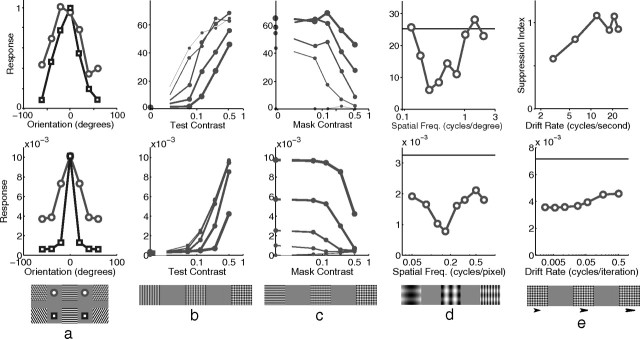
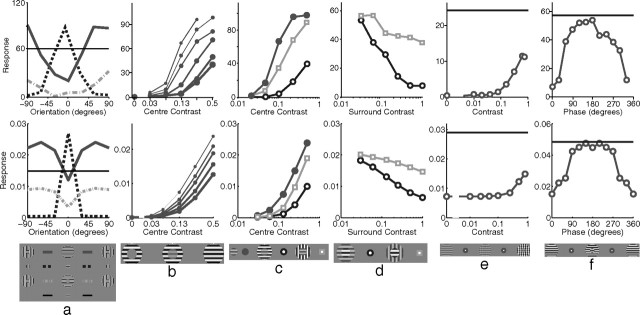
Orientation tuning was measured by presenting, at various orientations, a sinusoidal grating centered over the RF of the recorded neuron (Fig. 5a). Both the V1 neuron and the model neuron showed selectivity for a particular stimulus orientation, with the response falling quickly as the orientation of the stimulus diverged from the preferred orientation. This selectivity was unaltered by stimulus contrast, with a stimulus far from the preferred orientation producing a weak response even when presented at high contrast. Orientation tuning in the model was partially attributable to the alignment of the strongest afferent weights along a specific orientation. However, tuning was sharpened by the competition occurring between neurons in the model. This can be seen by observing the orientation tuning produced when competition was removed from the model (Fig. 5a, inset). Without competition, the neuron had the same orientation preference but was much more broadly tuned producing a strong response (>42% of the maximum) at all orientations, even at 90° from the preferred orientation (data not shown).

Figure 5.

Basic tuning properties. The top row shows neurophysiological data from representative single cells in V1, and the bottom row shows corresponding simulation results. a, Response as a function of grating orientation relative to the preferred orientation of the neuron. Neurophysiological data for a simple cell in cat V1 [adapted from Skottun et al. (1987), their Fig. 3a]. The thickness of each line corresponds to the contrast of the stimulus used as follows: 5% (thin), 20% (medium), and 80% (thick). The inset to the simulation data shows the response of the model without competition, created by recording the linear response generated at the first iteration of the algorithm (see Materials and Methods). b, Response as a function of the diameter of a circular grating (filled circles) and as a function of the inner diameter of an annular grating (open circles). Neurophysiological data for a cell in primate V1 [adapted from Jones et al. (2001), their Fig. 1]. c, Response as a function of grating diameter with variable grating contrast. Shown are neurophysiological data for a cell in primate V1 [adapted from Cavanaugh et al. (2002a), their Fig. 8]. The thickness of each line corresponds to the contrast of the stimulus used as follows: 6% (thinnest), 13, 25, 50, and 100% (thickest). d, Response as a function of grating spatial frequency. Shown are neurophysiological data for a cell in primate V1 [adapted from Webb et al. (2005), their Fig. 2a]. e, Response as a function of grating spatial frequency with variable grating contrast. Shown are neurophysiological data for a simple cell in cat V1 [adapted from Skottun et al. (1987), their Fig. 4a]. The thickness of each line corresponds to the contrast of the stimulus used as follows: 5% (thin), 20% (medium), and 80% (thick). f, Response as a function of grating temporal frequency. Shown are neurophysiological data for a cell in cat V1 [adapted from Freeman et al. (2002), their Fig. 3c]. The inset to the simulation data shows the response summed over all neurons within 11 pixels of the neuron recorded in the main figure.

Both V1 and the model show the same pattern of results when tested with circular sinusoidal gratings of various diameters (Fig. 5b). At small stimulus diameters, the response increased with increasing stimulus size. However, it reached a peak at a certain diameter, defining the summation field (SF) (Angelucci et al., 2002), after which the response became increasingly suppressed before reaching a plateau at large stimulus diameters. In the model, the initial increase in response with stimulus size is attributable to more of the RF of the recorded neuron being stimulated. However, as the stimulus becomes larger, more neurons neighboring the recorded neuron also become stimulated. These neurons engage in a competition to represent the input, and this ongoing competition reduces the recorded response. The plateau is reached when all the neighboring neurons that have RFs that overlap with the recorded neuron are stimulated by the input. For both V1 and the model, response decreased as the inner diameter of an annular grating increased (Fig. 5b). In both cases, response converged to a minimum at a diameter slightly larger than the diameter of the SF. In the model, this behavior is caused by the partial activation of the RF of the recorded neuron at small diameters, and a reduction in the area of the RF stimulated with increasing diameter. In V1, the extent of the SF is known to change with contrast (Fig. 5c, top). The model shows a similar pattern of response (Fig. 5c, bottom), but the expansion of the SF in the model is much smaller than in V1.

Spatial frequency tuning was measured by presenting optimally oriented sinusoidal gratings with different wavelengths. The model produced behavior in close agreement with the empirical data (Fig. 5d), with a sharp peak in response to intermediate spatial frequencies. The weak response of the model neuron at low spatial frequencies is attributable to weak input from the LGN since center-surround cells produce little response to small contrast gradients. The small response at high spatial frequencies results from the stimulus only partially matching the RF of the recorded neuron and hence only partially activating it. The high-frequency stimulus also partially activates more neurons, and hence there is increased competition further suppressing the recorded response. In both V1 and the model, spatial frequency preference was unaffected by stimulus contrast (Fig. 5e).

Increasing the temporal frequency of a drifting grating reduced the response of a neuron both in V1 and in the model (Fig. 5f). In the model, this effect is attributable to a fast moving grating only matching the RF of the recorded neuron part of the time and hence producing a weaker temporally averaged response. A fast-moving grating also activates many other neurons (since the stimulus matches the RFs of different neurons at different times), and hence there is increased competition further suppressing the response of the recorded neuron. In effect, the response to the stimulus becomes distributed across many neurons and the sum of the responses of all neurons in the model remains almost constant with changing drift rate (Fig. 5f, inset).

Cross-orientation suppression

The previous section considered behavior when a single grating was present in the RF of the recorded neuron. When a second grating (the mask) is superimposed on the stimulus, this leads to partial suppression of the response (Fig. 6a). For both V1 and the model, suppression was weakest for mask orientations close to the preferred orientation of the neuron, and strongest for masks presented at orientations that did not evoke a response when such a grating was presented in isolation. In the model, neurons representing different orientations at the same spatial location have overlapping RFs and hence compete to respond to stimuli appearing within this overlapping region. When the stimulus consists of two gratings with significantly different orientations, the two sets of neurons representing these orientations are both active, but the ongoing competition to respond to the inputs they share reduces the response of neurons in both sets. When the stimulus consists of two gratings at similar orientations, competition is even stronger as the neurons representing similar orientation at the same location have RFs that overlap more. However, the effective contrast of the stimulus also increases, and hence the recorded neuron receives a stronger afferent input, which increases its response despite the competition.

Figure 6.

Cross-orientation suppression. The top row shows neurophysiological data from representative single cells in V1, and the bottom row shows corresponding simulation results. a, Response as a function of the orientation of a single grating (squares) and as a function of the orientation of a mask grating additively superimposed on an optimally orientated grating (circles). Shown are neurophysiological data for a cell in cat V1 [data from Bonds (1989); figure adapted from Schwartz and Simoncelli (2001), their Fig. 5]. b, Response as a function of the contrast of the optimally orientated grating for several different orthogonal mask contrasts. The thickness of each line corresponds to the contrast of the mask grating as follows: 0% (thinnest), 6, 12, 25, and 50% (thickest). Shown are neurophysiological data for a cell in cat V1 [adapted from Freeman et al. (2002), their Fig. 2]. c, The data in b replotted to show response as a function of the contrast of the orthogonal mask grating for several different optimally oriented grating contrasts. The thickness of each line corresponds to the contrast of the optimally oriented grating as follows: 0% (thinnest), 6, 12, 25, and 50% (thickest). d, Response as a function of the spatial frequency of an orthogonal mask grating. Shown are neurophysiological data for a simple cell in cat V1 [adapted from DeAngelis et al. (1992), their Fig. 3b]. The horizontal lines show the response to the optimally oriented grating presented in isolation. e, Response as a function of the temporal frequency of an orthogonal mask grating. Shown are neurophysiological data for a cell in cat V1 [adapted from Freeman et al. (2002), their Fig. 3e]. Note that the physiological data are presented in the form of a suppression index: a value of 0 corresponds to no suppression and values >0 correspond to stronger suppression. For the model data, the horizontal line shows the response to the optimally orientated gating in the absence of the mask; hence the mask generates strong suppression across a range of temporal frequencies, consistent with the neurophysiological data.

Figure 6, b and c, show the effects of changing the contrasts of two superimposed orthogonal gratings. In both V1 and the model, increasing the contrast of the optimally orientated grating increases the response, and the response rises more quickly for lower mask contrasts. Equivalently, increasing the contrast of the mask reduces the response. In the model, the former effect is attributable to increasing the afferent input to the recorded neuron as the contrast of the grating at the preferred orientation increases. The latter effect is attributable to increased competition from other neurons that receive increased afferent input as the contrast of the mask increases.

Changing the spatial frequency of an orthogonal mask also affects the strength of the suppression generated (Fig. 6d). In the model, neurons show spatial frequency tuning (Fig. 5d). Hence neurons selective to the orientation of the mask were only stimulated, and hence only generated suppression, when the spatial frequency of the mask was close to the preferred spatial frequency of those neurons.

Stimuli presented at high temporal frequencies also generate weak responses in the model and in V1 (Fig. 5f). It might therefore be expected that a mask presented at a high temporal frequency would be ineffective (Carandini et al., 2002). However, this is not the case (Fig. 6e). Even when the temporal frequency of the mask grating was high, the response to the plaid stimulus was much weaker than the response to the optimal grating, and hence there was strong cross-orientation suppression. This occurred even at temporal frequencies in which the mask, presented alone, produced very little response in a neuron tuned to the orientation of the mask (Fig. 5f). However, the total activity across all neurons remains approximately constant with temporal frequency (Fig. 5f, inset); hence the total inhibition received also remains approximately constant. The current model thus suggests that it is only the distribution of the source of suppression, rather than its total strength, that changes with temporal frequency and this argues against suggestions that cortex is not a source of the suppression generated by high temporal frequency stimuli (Carandini et al., 2002; Li et al., 2006; Priebe and Ferster, 2006).

The experiments described above consider the effects of a non-optimally oriented grating on the response to a grating at the preferred orientation of the recorded neuron. Figure 7 shows the effects of a mask on the response to a grating at a range of orientations, not just the preferred orientation. For both V1 and the model, the response to the plaid is approximately the average of the responses generated by each grating when presented in isolation. In the model, this effect is attributable to the competition that occurs between neurons tuned to different orientations at the same spatial location. These neurons are both activated by the plaid stimulus but they compete to respond to that part of the input that they both represent. This competition reduces the response of both neurons compared with their responses when only a single grating is presented. When the contrasts of the two gratings are unequal, the response to the plaid is biased toward that generated when the higher contrast grating is presented in isolation (Fig. 8). In the model, this effect is attributable to the neurons representing the higher contrast grating receiving the stronger input and being able to more effectively compete to represent the stimulus.

Figure 7.

Cross-orientation suppression with varying orientation. Response as a function of grating orientation for two gratings presented in isolation (dashed lines) and for both gratings presented simultaneously (solid lines). The top row shows responses from a single cell in tree shrew V1 [adapted from MacEvoy et al. (2009), their Fig. 4], and the bottom row shows responses from the model. The angle between the two gratings increases from left to right: 22.5° (left column), 45, 67.5, and 90° (right column).

Figure 8.

Cross-orientation suppression with varying orientation and contrast. Response as a function of grating orientation for two gratings presented in isolation (dashed lines) and for both gratings presented simultaneously (solid lines). The top row shows population responses measured using intrinsic signal optical imaging in tree shrew V1 [adapted from MacEvoy et al. (2009), their Fig. 3], and the bottom row shows responses from a single neuron in the model. The angle between the two gratings was 90°. One grating was presented at a lower contrast than the other: for the left column, the contrasts were 0.5 and 0.25, and for the right column, the contrasts were 0.5 and 0.125.

Surround suppression

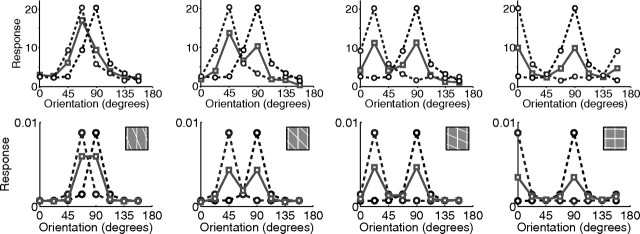
Another form of suppression that has been widely studied in V1 is that attributable to one grating surrounding (rather than being superimposed on) another. The effects of such surrounds can be either suppressive or facilitatory. Jones et al. (2002) observed five distinct patterns of behavior (Fig. 9). “Orientation contrast suppression” and “non-orientation-specific suppression” occurred most frequently when the center-surround border was within the RF of the recorded neuron. “Mixed general suppression” occurred most frequently when the border diameter matched, or was smaller than, the diameter of the RF. “Orientation alignment suppression” was most common when the border diameter matched, or was larger than, the diameter of the RF. Finally, “orientation contrast facilitation” occurred most frequently when the center-surround border was outside the RF. In these experiments, the RF was measured by taking the maximum value found using a variety of techniques, including the measurement of the SF. At the contrast used for the simulations (50%), the model neuron had a SF diameter of ∼12 pixels (Fig. 5c). The diameter of the border between the center and surround used to simulate each of these classes of behavior (Fig. 9) thus correlates well with the diameters at which the different behaviors were most frequently observed in the neurophysiological data. Note, however, that in the model the facilitation attributable to a non-iso-oriented surround at the largest diameter is much weaker than that recorded for the V1 cell.

Figure 9.

Surround suppression with variable surround orientation. The top row shows neurophysiological data from representative single cells in primate V1 [adapted from Jones et al. (2002), their Fig. 1], and the bottom row shows corresponding simulation results. a–e, Each column shows a different pattern of behavior identified by Jones et al. (2002) as follows: orientation contrast suppression (a), non-orientation-specific suppression (b), mixed general suppression (c), orientation alignment suppression (d), and orientation contrast facilitation (e). In each case, response is plotted as a function of grating orientation relative to the preferred orientation of the neuron for a central grating presented in isolation (dashed lines) and as a function of the orientation of a surrounding annulus in the presence of an optimally oriented central grating (solid lines). Note that for the neurophysiological data in a, but not the other plots, only the response at 0° is shown for the condition in which the center is presented in isolation (circular marker). The results for the model were generated using a center diameter of the following: 7 pixels (a), 11 pixels (b), 13 pixels (c), 17 pixels (d), and 19 pixels (e). The inner diameter of the surrounding annulus was equal to the center diameter in each case.

The pattern of results generated by the model can be explained as follows. The values of the dashed lines at 0° orientation correspond to the different points along the size tuning curve (Fig. 5b). Hence, moving from Figure 9a–e, there is a rise and fall in the size of the peak as the diameter of the grating increases. In each case, as the orientation of the grating deviates from the preferred orientation of the recorded neuron, so the response falls. When the surround is iso-oriented, the stimulus is effectively a single large grating at the preferred orientation of the neuron. Hence the values of the solid lines at 0° orientation correspond to the plateau of the size tuning curve (Fig. 5b), and the response is approximately constant with changing diameter. When the surround is not iso-oriented, the response increases as the diameter of the center increases (Fig. 9, from a to e). This is attributable to the afferent excitation received by the recorded neuron increasing as the center diameter increases.

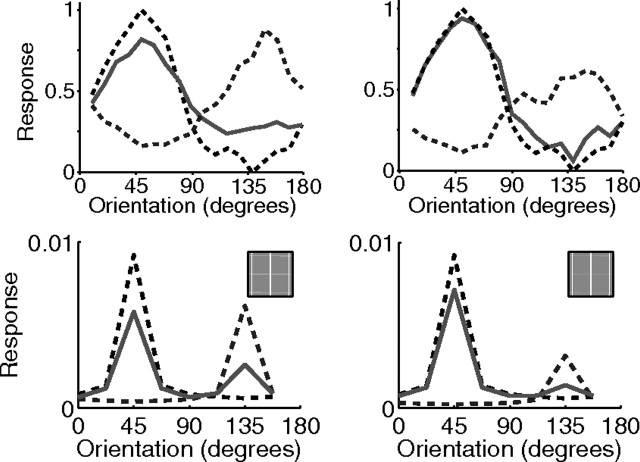
Reducing the contrast of the center stimulus, in relation to the contrast of the surround stimulus, can affect the orientation selectivity of surround suppression. Specifically, Levitt and Lund (1997) found that for 21% of cells surround suppression occurred over a wider range of surround orientations when using a low-contrast center, even though the same cell was subject to surround suppression only with a near iso-oriented surround when the center was presented at high contrast (Fig. 10a, top). The same behavior is observed in the model (Fig. 10a, bottom). This is attributable to the low-contrast center stimulus when presented in isolation, at the preferred orientation, still producing a strong response from the recorded neuron (Fig. 5a). However, in the presence of a high-contrast surround at any orientation, the neurons representing this high-contrast surround receive a stronger input and are more effective at competing to represent the stimulus and so are more effective at suppressing the response of the recorded neuron. As for 75% of the recorded cells (Levitt and Lund, 1997), the orientation of the surround that generated the greatest suppression in the model was the same for high- and low-contrast centers.

Figure 10.

Surround suppression with variable contrast and variable surround phase. The top row shows neurophysiological data from representative single cells in V1, and the bottom row shows corresponding simulation results. a, Response plotted as a function of grating orientation relative to the preferred orientation of the neuron for a central grating presented in isolation (dashed line), as a function of the orientation of a surrounding annulus in the presence of an optimally oriented central grating (solid line), and as a function of surround orientation for a center contrast much smaller than the surround contrast (dash-dot line). The horizontal lines show the response to the low-contrast center stimulus presented alone at the preferred orientation. Shown are neurophysiological data for a cell in primate V1 [adapted from Levitt and Lund (1997), their Fig. 1d]. b, Response as a function of the contrast of the central grating in the presence of an iso-oriented surround. Shown are neurophysiological data for a cell in primate V1 [adapted from Cavanaugh et al. (2002a), their Fig. 5b]. The thickness of each line corresponds to the contrast of the grating in the annular surround: 0% (thinnest), 3, 6, 12, 25, and 50% (thickest). c, Response as a function of the contrast of the central grating with no surround (filled circles), an iso-oriented surround (open circles), and an orthogonal surround (squares); in the latter two cases, the surround contrast was fixed at 50%. Shown are neurophysiological data for a simple cell in primate V1 [adapted from Cavanaugh et al. (2002b), their Fig. 5a]. d, Response as a function of the contrast of the surround grating with an iso-oriented surround (circles), and an orthogonal surround (squares); in both cases, the center contrast was fixed at 40%. Shown are neurophysiological data for a cell in primate V1 [adapted from Webb et al. (2005), their Fig. 6]. e, Response as a function of the contrast of an orthogonal surround grating superimposed on an iso-oriented surround grating in the presence of an optimally oriented center. Shown are neurophysiological data for a cell in cat V1 [adapted from Walker et al. (2002), their Fig. 2b]. The contrast of the center and the iso-oriented surround were fixed at 30%. The horizontal lines indicate the response to the central grating in isolation. f, Response as a function of the phase of the grating in the surround. Shown are neurophysiological data for a cell in primate V1 [adapted from Xu et al. (2005), their Fig. 2a]. The horizontal lines indicate the response to the central grating in isolation.

For both V1 and the model, the strength of response increases with the contrast of the center in the presence of an iso-oriented surround (Fig. 10b). This is unsurprising since the strength of the afferent stimulation received by the recorded neuron increases with contrast. As the contrast of the surround increases, so does the suppression (Fig. 10b). In the model, this is attributable to increased competition from neurons representing the surround partially suppressing the response of the recorded neuron. For both V1 and the model, at all center contrasts an orthogonal surround produces weaker suppression than that produced by an iso-oriented surround (Fig. 10c). In the model, this behavior is attributable to the recorded neuron having an RF that overlaps less with neurons representing the orthogonal surround compared with neurons representing the iso-oriented surround. Hence the recorded neuron is suppressed less in the former condition than the latter. For both V1 and the model, suppression increases with surround contrast and suppression attributable to an orthogonal surround is weaker than suppression attributable to an iso-oriented surround (Fig. 10d). As in the preceding experiment, this is attributable to the recorded neuron having an RF that overlaps less with neurons representing the orthogonal surround compared with neurons representing the iso-oriented surround. In either condition, increasing the contrast of the surround increases the afferent input to neurons representing the surround and hence increases the strength of suppression.

The suppressive influence of an iso-oriented surround can be reduced by superimposing on the surround a second grating with an orthogonal orientation (Fig. 10e). For both V1 and the model, the degree of suppression varies with the contrast of the orthogonal surround grating. Suppression is strongest (weakest) when the contrast of the orthogonal surround is lower (higher) than the contrast of the iso-oriented surround. In the model, this effect is attributable to the neurons responding to the iso-oriented surround (which most strongly suppress the response of the recorded neuron) being themselves suppressed by the responses of neurons to the orthogonal surround at high contrast (there is cross-orientation suppression between the neurons responding to the surround).

The strength of surround suppression is also influenced by the phase of an iso-oriented surround grating (Fig. 10f). For both V1 and the model, the suppression is weakest when the surround is out of phase with the center stimulus and strongest when the surround and center gratings are in phase. In the model, there is strong competition between neurons with collinear RFs at overlapping locations. When the surround is at the same phase as the center, neurons with RFs collinear with the recorded neuron are activated and suppress its response. In contrast, when the surround is out of phase with the center, neurons with RFs collinear to the recorded neuron are not activated by the surround stimulus; they thus do not inhibit the recorded neuron, which generates a stronger response.

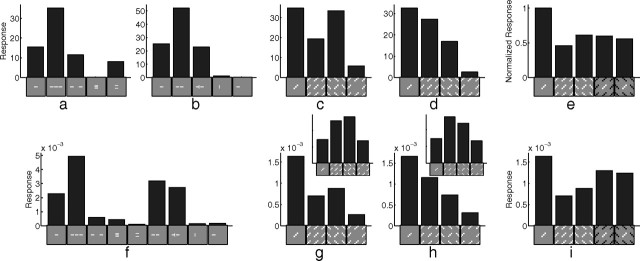
Flankers and textured surrounds

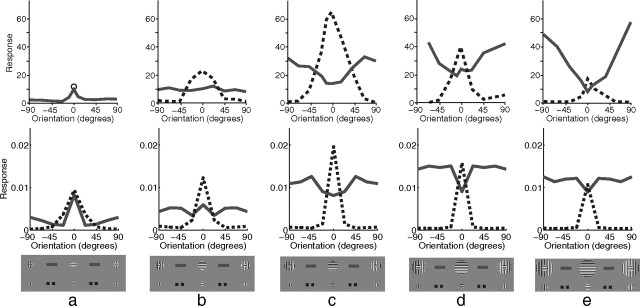
The interaction between center and surround has also been explored using isolated bars rather than gratings (Fig. 11a,b). A pair of collinear flankers, or a single collinear flanker, increases the response to a bar presented at the center of the RF, even though these flanking stimuli produce little response when presented alone. Furthermore, the enhancement attributable to a collinear flanker can be blocked by a perpendicular bar separating the central bar from the flanker. In contrast to collinear flankers, parallel flankers suppress the response to the central bar. The model produces behavior that is mostly consistent with the physiological data (Fig. 11f). The results of the model can be explained as follows. The collinear flankers partially activate the RF of the recorded neuron, and hence its response is enhanced because of increased afferent input. Hence the model suggests that some nonclassical RF effects may result from the inadvertent stimulation of the classical RF. The collinear flankers when presented in isolation are much better represented by other neurons, and hence the response of the recorded neuron is suppressed. When a collinear flanker is presented together with an orthogonal flanker, the recorded neuron receives greater afferent input, but there is also stronger competition to represent that input (from neurons selective for the orthogonal bar) so this configuration has little overall effect on the response. Finally, the parallel flankers activate neighboring neurons, which compete with the recorded neuron, suppressing its response. In the neurophysiological data, the effects were highly dependent on the positioning of the contextual stimuli relative to the central stimulus (Kapadia et al., 1995, 2000). The model shows a similar dependence (data not shown): the facilitation generated by a collinear flanker is reduced and is eventually abolished as (1) the spacing between the flanker and the central stimulus increases, (2) the flanker is tilted relative to the central stimulus, and (3) the flanker is laterally offset from the central stimulus.

Figure 11.

The effect of flankers and textured surrounds on neural response. a, Response to one set of flanker configurations of a single cell in primate V1 [adapted from Kapadia et al. (2000), their Fig. 7a]. b, Response to a second set of flanker configurations of a different cell in primate V1 [adapted from Kapadia et al. (1995), their Fig. 11a]. c, Average response of 28 cells in primate V1 that were classified as orientation contrast cells [adapted from Nothdurft et al. (1999), their Fig. 4a]. d, Average response of 14 cells in primate V1 that were classified as uniform cells [adapted from Nothdurft et al. (1999), their Fig. 4b]. e, Average response of 124 cells in primate V1 to textured surrounds with varying contrast [adapted from van der Smagt et al. (2005), their Fig. 4a]. f, Response of a model neuron to both sets of flanker configurations shown in a and b. g, Response of a model neuron to texture patterns like those in c and d, in which the spacing between bars was 1.6 times the bar length. h, Response of a model neuron to similar texture patterns created using a spacing of two times the bar length. The insets to g and h show the linear response of the model for the two different texture spacings. i, Response of a model neuron to texture patterns with varying contrast, as used in e. Note: The icons used to represent the stimulus configurations in c–e and g–i show only the central portion of the actual images used in the experiments.

Rather than using single bars, experiments have also been performed using surrounding textures created from many equally spaced bars (Knierim and van Essen, 1992; Nothdurft et al., 1999; Hegdé and Felleman, 2003). Nothdurft et al. (1999) observed two different patterns of behavior: for “orientation contrast” cells, the response to a central, optimally oriented, bar was suppressed by an iso-oriented surrounding texture, but not an orthogonal surround (Fig. 11c); for “uniform” cells, the response to the central bar was suppressed by textures at either orientation, but most strongly by an orthogonal surround (Fig. 11d). The model can produce results consistent with both these behaviors by using different spacings between the bars in the stimuli (Fig. 11g,h). The spacings used in the model are consistent with the range of spacings used in the neurophysiological experiments. Nothdurft et al. (1999) report that changing texture spacing affects the strength of suppression but do not report a correlation between texture spacing and the orientation contrast and uniform patterns of suppression. The behavior of the model can be explained by the overlap of the surrounding texture with the RF of the recorded neuron. The initial, linear, response of the model to the texture with smaller spacing (Fig. 11g, inset) shows that the iso-oriented texture provides slightly less afferent input to the recorded neuron than the orthogonal texture, whereas for the texture with larger spacing the initial, linear, response (Fig. 11h, inset) shows that the iso-oriented texture provides more afferent input than the orthogonal texture. In the full model, there is strong competition to represent the contextual stimuli, which results in a weaker response from the recorded neuron. However, the average response still reflects the relative magnitudes of the initial, linear, responses to each texture configuration. When the surrounding texture is presented alone, the recorded neuron is a poor representation of the input, so it quickly loses the competition and produces a very weak response.

Differences between the center and surround along other feature dimensions, such as contrast polarity, have also been found to diminish the suppression caused by a textured surround (Fig. 11e). Consistent with the empirical data, the model shows (Fig. 11i) that center-surround differences in both dimensions (orientation and contrast polarity) do not generate a greater reduction in suppression than that generated by a single dimension. In the model, changing the contrast polarity of the surround only has the effect of changing the identity of those neurons that are most strongly activated by that surround. The two sets of neurons activated by the surround at each contrast polarity both have RFs that overlap with the RF of the recorded neuron to a similar degree, and hence both conditions generate a similar degree of suppression in the recorded neuron.

Discussion

Previous work (Rao and Ballard, 1999) has shown that PC is capable of modeling end-stopping behavior (similar to the result shown in Fig. 5b) and texture “pop out” (similar to the result shown in Fig. 11g). However, this previous work did not explore whether PC could account for other V1 response properties, perhaps because that work assumed that predictions arise from feedback from extrastriate areas and hence are only likely to be involved in nonclassical RF properties. The interpretation of PC described in this article assumes that predictions arise within V1 and that PC can be viewed as a form of competition. This interpretation suggests that PC should also account for classical, as well as nonclassical, RF properties, as has been demonstrated here.

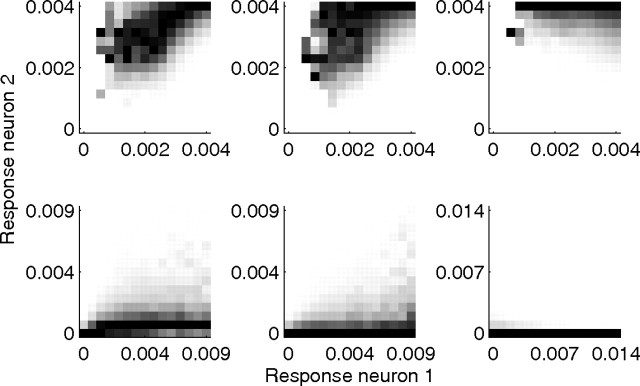
The specific predictive coding model implemented in this article (PC/BC) employs a divisive mechanism to calculate the residual error between the predictions and the sensory input. This mechanism can be interpreted as a form of divisive normalization like that proposed by the normalization model (Albrecht and Geisler, 1991; Heeger, 1991, 1992; Carandini and Heeger, 1994; Wainwright et al., 2001). However, unlike the normalization model, in PC/BC the normalization pool for each neuron is restricted to the population of neurons that have overlapping RFs, and the normalization is applied to the inputs to the population of competing neurons rather than the outputs. The normalization model is capable of simulating a subset of the results presented here (Heeger, 1994; Heeger et al., 1996; Schwartz and Simoncelli, 2001) and has also been recently extended (Reynolds and Heeger, 2009) to model a subset of the attentional data that can be simulated by PC/BC (Spratling, 2008a). However, since the weights used to pool the responses, and so calculate the strength of normalization, are not specified by the normalization model, it has many more free parameters than PC/BC. As with the normalization model (Schwartz and Simoncelli, 2001; Wainwright et al., 2001), PC/BC reduces redundancy between neural representations (Fig. 12).

Figure 12.

Conditional probability histograms of responses to a natural image. In each histogram, a column indicates the probability that neuron 2 generates an output of the given magnitude given that neuron 1 has generated an output of the magnitude shown on the abscissa. A dark pixel indicates a high conditional probability. Each column in each histogram has been independently rescaled to fill the full range of intensity values. The top row shows histograms for the initial linear response of the model (without competition). The bottom row shows histograms for the model including inhibition. Histograms in the left-hand column are for two neurons tuned to the same orientation but 2 pixels apart, so that RFs are parallel. Histograms in the middle column are for two neurons tuned to the same orientation but 6 pixels apart, so that RFs are parallel. Histograms in the right-hand column are for two neurons tuned to orthogonal directions at the same location. It can be seen that, without competition, the responses are correlated such that the higher the response at the first neuron, the higher the response is likely to be from the second neuron. It is also the case that all neurons tend to generate strong responses. After competition has occurred, the responses are much more sparse (fewer neurons generate strong responses), and the dependency between different neurons is substantially reduced, and for neurons at the same location (bottom-right histogram) the correlation is eliminated. The image used to generate these histograms was image number 23 from the still image database used in the study by van Hateren and van der Schaaf (1998).

There are many other models that can simulate individual results presented here (Douglas and Martin, 1991; Ben-Yishai et al., 1995; Somers et al., 1995; Carandini and Ringach, 1997; Troyer et al., 1998; Adorján et al., 1999; Dragoi and Sur, 2000; Stetter et al., 2000) (for review, see Ferster and Miller, 2000; Seriès et al., 2003), and many of these models employ mechanisms similar to those used by PC/BC. However, the PC/BC model differs from these previous models in providing a computational explanation for the behavior of V1 neurons as well as providing a unified account of a number of processes that are currently considered, and modeled, in isolation. The model also makes testable predictions that are described in the supplemental material (available at www.jneurosci.org).

Consistent with previous models and neurophysiological results (Pei et al., 1994; Sompolinsky and Shapley, 1997; Xing et al., 2005), orientation tuning in the PC/BC model results from broadly tuned afferent excitation being sharpened by intracortical competition. This is also consistent with evidence that blocking inhibitory effects across a local population of cortical cells greatly reduces orientation selectivity (Sillito, 1975; Tsumoto et al., 1979; Sato et al., 1996). In the model, blockade of inhibition from neurons with a specific orientation preference should cause neighboring prediction neurons to show increased response to that orientation, rather than simply causing a general disinhibition to all orientations. Such effects have been recorded in V1 (Crook et al., 1998), and analogous data have been obtained from cortical area TE (Wang et al., 2000). The current model is also consistent with neurophysiological evidence that the strength of lateral inhibition peaks for stimuli presented at the preferred orientation of the recorded cortical cell (Ferster, 1986; Douglas et al., 1991; Sato et al., 1996; Sompolinsky and Shapley, 1997). In the model, the strength of inhibition between any two prediction neurons is proportional to the degree of overlap between the RFs. Those neurons with orthogonal orientation preferences at a specific location overlap less than neurons with similar orientation preferences and consequently produce less inhibition.

In the PC/BC model, inhibition from neurons tuned to near orthogonal orientations is still significant and gives rise to cross-orientation suppression. Evidence that suppression occurs for masks with a high temporal frequency has cast doubt on the idea that intracortical inhibition is responsible for cross-orientation suppression (Carandini et al., 2002). This is because the very weak responses evoked by high-frequency stimuli seem insufficient to produce strong suppression. However, the current model does show strong suppression for masks presented at high temporal frequencies. This is attributable to the many neurons weakly activated by the high-frequency mask generating similar suppression as the few neurons strongly activated by the mask when it is presented at a low temporal frequency. In V1, strong cross-orientation suppression requires that both the optimally oriented grating and the mask grating be presented to the same eye even for binocular cells (DeAngelis et al., 1992; Walker et al., 1998). Such behavior is consistent with neurons competing to receive inputs, rather than to produce outputs, as is proposed by the PC/BC model.

Influences from neurons responding to stimuli placed outside the RF of the recorded neuron enable PC/BC to simulate nonclassical RF effects, such as surround suppression, and contextual modulation by flankers and textures. Rather than explaining these behaviors in terms of cortical feedback, which is not supported by the biological evidence (Hupé et al., 2001), the PC/BC model explains these behaviors in terms of competition to represent inputs that are common to the RFs of the recorded neuron and those neurons representing the contextual stimulation.

The extent of the long-range horizontal projections from a V1 cell are commensurate with the size of the SF of that cell measured with a low-contrast grating (Angelucci et al., 2002; Angelucci and Bullier, 2003), which is in turn two to four times larger than the SF measured at high contrast (Sceniak et al., 1999; Angelucci et al., 2002). For the model implemented for this article, the region of the image from which a prediction neuron receives connections with nonzero synaptic weights has a diameter of 21 pixels, which is approximately double the high-contrast SF diameter (Fig. 5b). Thus, the model is compatible with the idea that the long- and short-range lateral connections in V1 are responsible for performing the type of competition proposed by the PC/BC model.

The current model does not incorporate mechanisms to simulate many properties of V1 such as selectivity for color, direction of motion, and disparity. However, the model should be easy to extend by simply including prediction neurons with RFs selective for these additional stimulus properties. The model is also deficient in certain specific aspects of its behavior [e.g., it fails to show adaptation to a stationary input, it fails to produce sufficiently strong orientation contrast facilitation (Fig. 9e), and it does not show sufficient expansion of the SF at low contrast (Fig. 5c)]. These deficiencies may be more challenging to overcome and are likely to require modification to the mathematics of the model. Another limitation of the current implementation is that it models V1 as a completely homogeneous sheet of processing units. No account is taken of variations between individual neurons in their RF properties (such as RF size, exact orientation preference, etc.). Furthermore, no account has been taken of changes in V1 RF properties across cortical layers, between locations in the cortical map, with eccentricity from fovea, species, or age. Including such factors in the model might enable it to account for a greater range of empirical data. Despite this, the model produces a remarkably good fit to a wide range of data (taken from different species, cortical layers, etc.), suggesting that PC is a ubiquitous property of V1. Another omission from the current implementation is feedback connection from extrastriate cortical areas. The model has operated without receiving any top–down or contextual predictions from other parts of the cortex. The influence of such connections is defined by Equation 3 and hence could easily be simulated. The inclusion of predictive inputs from other parts of the cortex may enable to model to simulate nonclassical RF effects that occur for contextual inputs placed sufficiently far from the RF of the recorded neuron that they cannot be explained using the mechanisms implemented in the current model.

In conclusion, this article has shown that the mechanism of competition proposed by the predictive coding model can account for a very wide range of V1 response properties. This suggests that many of the diverse behaviors observed in V1 may simply be explained as a consequence of V1 performing predictive coding: minimizing the error between the observed sensory input and the expectations stored in the synaptic weights of V1 cells.