Endogenous Neuromagnetic Activity for Mental Hierarchy of Timing

Abstract

The frontal-striatal circuits, the cerebellum, and motor cortices play crucial roles in processing timing information on second to millisecond scales. However, little is known about the physiological mechanism underlying human's preference to robustly encode a sequence of time intervals into a mental hierarchy of temporal units called meter. This is especially salient in music: temporal patterns are typically interpreted as integer multiples of a basic unit (i.e., the beat) and accommodated into a global context such as march or waltz. With magnetoencephalography and spatial-filtering source analysis, we demonstrated that the time courses of neural activities index a subjectively induced meter context. Auditory evoked responses from hippocampus, basal ganglia, and auditory and association cortices showed a significant contrast between march and waltz metric conditions during listening to identical click stimuli. Specifically, the right hippocampus was activated differentially at 80 ms to the march downbeat (the count one) and ∼250 ms to the waltz downbeat. In contrast, basal ganglia showed a larger 80 ms peak for march downbeat than waltz. The metric contrast was also expressed in long-latency responses in the right temporal lobe. These findings suggest that anticipatory processes in the hippocampal memory system and temporal computation mechanism in the basal ganglia circuits facilitate endogenous activities in auditory and association cortices through feedback loops. The close interaction of auditory, motor, and limbic systems suggests a distributed network for metric organization in temporal processing and its relevance for musical behavior.

Introduction

Neural mechanisms for encoding timing intervals on different scales have been extensively studied in animals and humans. Intervals of seconds to minutes involve the corticostriatal circuits, in which basal ganglia detect neural oscillations, whereas millisecond timing may rely on motor cortices and cerebellum (for review, see Buhusi and Meck, 2005). Human neuroimaging showed the involvement of these areas in addition to frontal and parietal lobes (Sakai et al., 1999; Schubotz and von Cramon, 2001; Coull et al., 2004; Pastor et al., 2004) even without a motor task (Grahn and Brett, 2007; Chen et al., 2008).

Humans prefer isochrony and relative timing based on integer ratios (e.g., 2:1, 3:1) over non-integer ratio timings (e.g., 2.7:1) in production and perception (Martin, 1972; Handel and Lawson, 1983; Essens, 1986; Collier and Wright, 1995). Such metric hierarchy manifests in music (Lerdahl and Jackendoff, 1983) as listeners use acoustic cues and previous musical knowledge (Hannon and Trehub, 2005) to establish a sense of beat and meter such as march, waltz, or bossa nova. Auditory memory (Palmer and Krumhansl, 1990; Jones et al., 2002) and synchronized movements (Repp, 2007) are facilitated on downbeat (the count one) compared with offbeat or upbeat (the beat preceding downbeat), perhaps by automatic top-down expectation (Jones and Boltz, 1989). Thus, an internal meter representation likely governs human temporal and sensorimotor processing.

Current evidence for neural mechanism of meter is scarce. Anterior temporal lobe lesions resulted in impaired metric judgment compared with preserved non-metric judgment (Liégeois-Chauvel et al., 1998). Neuroimaging revealed that encoding of metric and non-metric patterns for production involved distinct activation of premotor cortex and cerebellum (Sakai et al., 1999), whereas a similar comparison without a task resulted in enhanced but not differential activities for metric rhythms in basal ganglia and anterior superior temporal gyri (STG) (Grahn and Brett, 2007). Furthermore, little is known about time courses of activity in these areas. Sounds violating metric expectation elicit mismatch responses from auditory cortex at latency of 100–150 ms (Vuust et al., 2005), similar to any violation of rule-based context (Näätänen et al., 2007), indicating that a metric-based anticipatory process has access to auditory information quite early.

Processing incoming sound is reflected in the auditory evoked responses, found with human intracranial recording in primary and secondary auditory cortices (Godey et al., 2001), frontal and parietal lobes (Baudena et al., 1995; Halgren et al., 1995a), basal ganglia (Bares and Rektor, 2001), amygdala, hippocampus, and medial temporal lobe (McCarthy et al., 1989; Halgren et al., 1995b). Thus, we hypothesized that the subjective metric context would be reflected in contributions from these areas to the auditory evoked response. Using magnetoencephalography (MEG), we showed that listening to identical metronome clicks in march or waltz context resulted in different time courses of auditory evoked response with latencies of 80–300 ms, in hippocampal area, basal ganglia, precentral gyrus, and auditory and association cortices, suggesting distributed networks to comprise the hierarchical metric system.

Materials and Methods

Participants.

The data from 13 healthy, right-handed musicians (eight males; 18–42 years of age, mean of 28.2 years) after excluding five as a result of technical failures and movement artifacts are reported here. All had extensive musical training (11–30 years, mean of 20.9 years) and no history of psychological or neurological disorders. All participants provided informed consent in written form. The study had been approved by the Research Ethics Board at Baycrest Centre for Geriatric Care.

Tasks and MEG data recording.

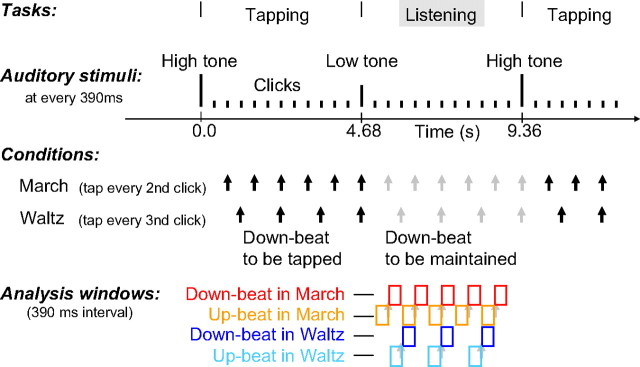
The steady beat with a 390 ms interval was induced by a train of 11 clicks (250 Hz tone of 10 ms duration), followed by a 1000 Hz tone and a 500 Hz tone (50 ms duration) alternately that cued tapping and listening intervals (Fig. 1). One block lasted for 400 s and contained about 42 consecutive finger tapping and listening intervals. The participants were instructed to tap their right index finger on a response button to every second click (“march” condition) in four blocks and every third click (“waltz” condition) in the other four blocks. In each condition, the position of the tapping target tone and its logical continuation was designated as the “downbeat”; the tone preceding the downbeat was considered the “upbeat.” The order of the alternating conditions was balanced between subjects. The timing of the button presses and the electromyogram (EMG) were recorded simultaneously with the MEG. For EMG, Ag/AgCl electrodes were placed on the first dorsal interosseous muscle in the right hand, the knuckle of the index finger, and the ground electrode on the wrist.

Figure 1.

Stimuli and task. Auditory stimuli were short tones presented every 390 ms. Changes in pitch cued the beginning and end of the tapping interval. After a high-pitched tone, the subjects tapped at every second click in the march condition or at every third click in the waltz condition, in separate experimental blocks. Subjects stopped tapping at the low pitch tone and listened to the stimuli. The black arrows indicate the downbeats at which the subjects were tapping in each condition. The gray arrows indicate the subjectively maintained downbeat positions during the listening interval. Upbeats were the clicks immediately preceding the downbeat stimuli. The color-coded boxes indicate the time interval (0–390 ms from stimulus onset) of analyzed MEG data for the four conditions: downbeat in march (red), upbeat in march (orange), downbeat in waltz (blue), and upbeat in waltz (light blue), respectively. The audio file of the stimulus trains is accessible as supplemental data (available at www.jneurosci.org as supplemental material).

The MEG was recorded with a 151 channel neuromagnetometer (VSM Medtech) with a sampling rate of 1250 Hz continuously for each block. Participants were seated upright, with their head resting inside the helmet-shaped MEG sensor. Sounds were delivered binaurally through insert earphones E3A (Etymotic Research). All participants were instructed to sit still and avoid any head movement during each block. Compliance of the subjects was monitored through video cameras.

Data analysis.

The data analysis was focused on auditory evoked responses to stimuli presented during the listening period (Fig. 1). Sporadic finger movements during this time interval were identified by EMG signals exceeding 20 μV in amplitude or 20 μV/s in its first derivative, and corresponding MEG epochs were excluded from additional analysis. The data were corrected for other artifacts such as eye movements using principal component analysis (PCA). Any component exceeding 1.5 pT was subtracted from the MEG data. Thereafter, epochs of MEG data related to the onset of each click stimulus were averaged using a 390 ms of poststimulus window. Separate averages were calculated for metric conditions (march or waltz meter) and accents (downbeat or upbeat) across blocks except the first block, which was considered as training.

Neuromagnetic source activities were estimated using synthetic aperture magnetometry (SAM) (Robinson and Vrba, 1999), a beam-former algorithm that defined a spatial filter on the MEG data in the 0–50 Hz frequency range on a 5 × 5 × 5 mm mesh covering the brain. The SAM computation was based on the single-trial data at a window of −400 to 800 ms (time 0 at the downbeat position, within the listening period) such that the spatial filter was constructed from the whole data length that included upbeat, downbeat, and the next beat (the upbeat in march and the count two in waltz). This resulted in the same time window used for march and waltz conditions in total. Note that no artifact removal algorithm was applied to the single-trial data used for the computation of covariance matrices. This avoids that the rank of the covariance matrix would have been reduced when using either PCA or independent component analysis.

A common head model was derived for all participants based on a template brain magnetic resonance image (MRI) (Montreal Neurological Institute, Montreal, Quebec, Canada) for constructing the spatial filter. We applied the standard procedures as provided by the CTF-SAM package (SAMsrc). These use a multi-sphere head model, i.e., for each MEG sensor a local sphere was approximated to the head shape, which was obtained from the template brain. In the SAM computation (Robinson and Vrba, 1999), the noise term for obtaining the normalized source power (pseudo-Z statistics) is calculated from a singular value decomposition of the MEG signal under the assumption that the smallest eigenvector contained noise only. The activity at each node is represented by three dipole components with the directions according to the head-based coordinate system. The software package provided the geometric mean (i.e., the signal power of a single dipole with the mean direction).

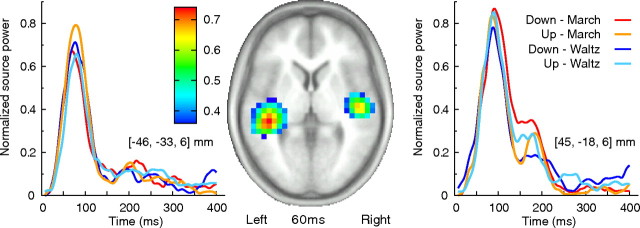
The spatial filter was then applied to the time-domain-averaged evoked magnetic field data obtained under the four experimental conditions. The output was the time courses of normalized source power for each volume element across the entire time interval. This approach, called event-related SAM (ER-SAM), proposed by Cheyne et al. (2006), has been shown to be successful in reliably localizing evoked activities in motor cortex (Cheyne et al., 2006), auditory cortices (Ross et al., 2009a,b), or deeper source as hippocampus (Riggs et al., 2009) and fusiform face area and amygdala (Cornwell et al., 2008). Although previous studies, which were based on a different physiological assumption of changes in the power spectrum between an “active” poststimulus and the prestimulus “control” interval, suggested that the SAM image might be disadvantaged in localizing auditory evoked fields (Herdman et al., 2004), the ER-SAM approach used by Ross et al. (2009a) has demonstrated that the time-averaged transient auditory evoked fields, in particular its long-latency components (80–300 ms), are successfully localized in auditory areas on the superior temporal plane bilaterally and that different subareas reflect separate processing for onset and offset of tones. In all of these studies mentioned above including the present study, ER-SAM images are obtained through the spatial filter using the whole-head sensor data, not just a subgroup of channels. The data in all conditions indeed show activities of comparable size in bilateral auditory cortices as indicated in Figure 2.

Figure 2.

Bilateral auditory evoked activities. The map (middle) shows the mean response of the four conditions in an axial slice at 60 ms latency. The left and right show time course of the evoked response in each of four conditions in the left and right auditory cortex.

The obtained ER-SAM four-dimensional maps were downsampled in time by the factor of eight for data reduction, which resulted in volumetric maps at every 6.4 ms. The individual maps in the four conditions (downbeat in march, downbeat in waltz, upbeat in march, upbeat in waltz) were transformed onto the Talairach standard coordinates using AFNI (National Institute of Mental Health, Bethesda, MD). The voxels, which contained significant activation elicited by the auditory stimuli, were identified by two-sided t tests comparing the mean source power in the first half of the interval and that in the second half by using averaged data across all four conditions. The voxels with p < 0.05 were taken into the subsequent partial least square (PLS) analysis. There was no correction for multiple comparisons at this step because statistical inference was made using multivariate analysis described below.

Significant contrasts in spatial–temporal patterns of source activities across the four conditions were examined by multivariate PLS analysis (McIntosh et al., 1996). As a multivariate technique similar to PCA, the PLS is suitable to identify the relationship between one set of independent variables (e.g., the experimental design) and a large set of dependent measures (e.g., neuroimaging data). PLS has been successfully applied to time series of multielectrode event-related potential (Lobaugh et al., 2001) and functional MRI (fMRI) data (McIntosh et al., 2004). The input of PLS is a cross-block covariance matrix, which is obtained by multiplying the design matrix (an orthonormal set of vectors defining the degrees of freedom in the experimental conditions), and the data matrix (time series of brain activity at each location as columns and subjects within each experimental condition as rows). The output of PLS is a set of latent variables (LVs), obtained by singular value decomposition applied to the input matrix. Similar to eigenvectors in PCA, LVs account for the covariance of the matrix in decreasing order of magnitude determined by singular values. Each LV explains that a certain pattern of experimental conditions (design score) (Fig. 2) is expressed by a cohesive spatial–temporal pattern of brain activity.

The significance of each LV was determined by a permutation test using 500 permuted data with conditions randomly reassigned for recomputation of PLS. This yielded the empirical probability for the permuted singular values exceeding the originally observed singular values. An LV was considered to be significant at p < 0.05. For each significant LV, the reliability of the corresponding eigenimage of brain activity was assessed by bootstrap estimation using 500 resampled data with subjects randomly replaced for recomputation of PLS, at each time point at each location. The ratio of the activity to its SE estimated through the bootstrap approximately corresponds to a Z score.

Each point in time and space for which the absolute value of the bootstrap ratio was >4.0 (corresponding to p < 0.001) was accepted as significantly contributing to the identified contrast for each LV. Summaries of the spatiotemporal patterns of brain activities identified as the eigenimages for the first and second LVs are indicated in supplemental Figures 1 and 2 (available at www.jneurosci.org as supplemental material), respectively, with series of maps downsampled in both space (every 15 mm in anteroposterior direction) and time (every 40 ms).

To extract parsimonious information from these spatiotemporal data while avoiding redundancy and complexity, we selected representative areas that contributed the contrast between the PLS-identified conditions most substantially. In addition to the statistical results provided by the PLS analysis described above, we considered the differences between the observed source activities in march and waltz for LV1 and between upbeat and downbeat in waltz for LV2 for all voxels with bootstrap ratio larger than 4.0 and termed the differences in source activity the “contrast strength.” Here we report the locations of local maxima in the contrast strength with some constraints. A minimum distance of 20 mm between peaks was required based on the assumption of limited spatial resolution of SAM filtered data (Ross et al., 2009a). Local maxima with less than five adjacent significant voxels in space or with significance observed continuously only within <32 ms in time were assumed as likely representing spurious noise rather than an evoked response. The Talairach coordinates of the final selection of spatial locations are reported in Tables 1 and 2 together with the observed bootstrap ratio. The Talailarch anatomical labels for each location were extracted according to the stereotaxic coordinates.

Table 1.

Stereotaxic brain atlas coordinates for the metric contrast (march vs waltz) revealed by the first latent variable (LV1)

Location (Brodmann area)	Hemisphere	Talairach coordinates (mm) (L–R, P–A, I–S)	PLS bootstrap ratio	Contrast strength
Temporal lobe
HG (BA 40/41) and insula (BA 13)	R	45, −23, 11	5.32	1.48
STG (BA 21/22) and insula (BA 13)	R	45, −1, −3	4.32	0.86
STG (BA 41/42)	L	−56, −28, 11	4.54	0.31
STG (BA 41/42)	R	60, −33, 6	5.49	0.17
STG (BA 21/22)	L	−61, −7, 7	5.26	0.66
Insula (BA 13)	L	−41, 9, 2	4.33	0.23
MTG	R	65, −23, −4	5.76	0.63
MTG (BA 21)	R	50, −17, −14	4.18	0.79
MTG (BA 38)	R	40, 1, −39	6.55	1.09
MTG (BA 21/38)	R	50, 0, −34	4.89	0.41
Hippocampus and parahippocampal gyrus	R	30, −38, 0	5.94	0.65
Parahippocampal gyrus and amygdala	L	−30, 0, 13	7.06	0.57
Fusiform gyrus	R	45, −27, −15	6.27	0.12
Frontal lobe
Precentral gyrus (BA 6/4)	R	60, −2, 27	5.52	0.38
Precentral gyrus (BA 4)	R	55, −8, 22	4.29	0.39
Precentral gyrus (BA 43)	L	−46, −8, 22	4.89	0.92
Basal ganglia
Claustrum, insula, and putamen	R	35, −1, 2	5.63	1.30
Claustrum and caudate body	L	−25, 18, 8	4.95	0.66
Lentiform nucleus, putamen, and globus pallidus	L	−30, −17, −4	5.11	0.93
Lentiform nucleus and putamen	L	−30, −13, 11	4.48	0.35

L, Left; R, right. Talairach coordinates: L–R, left–right; P–A, posterior–anterior; I–S, inferior–superior.

Table 2.

Stereotaxic brain atlas coordinates for the accent contrast (downbeat vs upbeat) in waltz context, revealed by the second latent variable (LV2)

Location (Brodmann area)	Hemisphere	Talairach coordinates (mm) (L–R, P–A, I–S)	PLS bootstrap ratio	Contrast strength
Temporal lobe
Insula (BA 13) and HG (BA 41)	R	45, −18, 16	5.32	1.02
Insula	R	40, −2, 17	7.22	0.76
Insula (BA 13)	L	−36, −13, 16	5.11	0.82
STG (BA 21/22)	R	55, −38, 10	6.27	0.82
STG	L	−36, −33, 6	5.26	0.57
STG	R	65, −7, 2	4.86	0.69
MTG (BA 21)	R	65, −12, −4	6.55	0.23
MTG (BA 20/21)	R	50, −17, −14	4.18	0.80
MTG (BA 21/38)	R	45, 5, −34	5.67	0.53
ITG (BA 20/21)	R	45, −4, −44	4.74	0.42
Parahippocampal gyrus	R	25, −33, −5	5.94	0.88
Parahippocampal gyrus	L	−20, −32, −10	5.71	0.82
Amygdala, lentiform nucleus, and putamen	R	30, −1, −8	6.91	0.40
Frontal lobe
IFG (BA 47)	R	35, 19, −7	5.13	0.55
Precentral gyrus (BA 44)	L	−46, 4, 7	5.99	0.25
Precentral gyrus (BA 6/4)	R	−51, −2, 17	5.45	0.52
IPL (BA 40)	L	−51, −29, 31	5.83	0.23
Basal ganglia
Lentiform nucleus and putamen	L	−30, −12, 1	4.87	0.56
Claustrum	L	−25, 18, 8	4.95	0.27
Claustrum and putamen	L	−36, −17, −4	4.14	0.27
Cerebellum
Culmen	L	−56, −41, −31	4.41	0.24

L, Left; R, right; IPL, inferior parietal lobule; ITG, inferior temporal gyrus. Talairach coordinates: L–R, left–right; P–A, posterior–anterior; I–S, inferior–superior.

Results

We obtained time series of source activity for all nodes of a 5 mm lattice spanning the whole brain by spatially filtering the auditory evoked magnetic fields elicited by each click stimulus during the listening period (Fig. 1). In all of the four conditions (downbeat in march, downbeat in waltz, upbeat in march, upbeat in waltz), bilateral auditory cortex showed strong evoked response at left and right STG locations, which shows spatial peaks at ∼60 ms after stimulus onset (Fig. 2). The comparison across the four conditions by multivariate PLS analysis (McIntosh et al., 1996; McIntosh and Lobaugh, 2004) extracted LVs that defined spatiotemporal activation patterns associated with a particular contrast across experimental conditions. Nonparametric permutation tests examined the significance of the LVs yielded by PLS and identified two as significant.

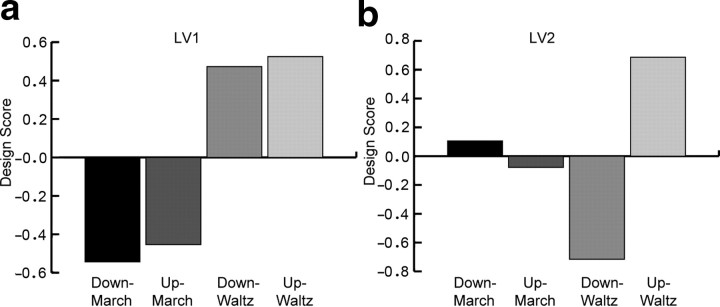
The first LV (p < 0.0001) explained 51.8% of covariance and expressed the contrast between the metric conditions march and waltz (Fig. 3). The second LV (p < 0.029) explained 31.3% of covariance and corresponded to the contrast between the downbeat and upbeat in the waltz (Fig. 3). These contrasts indicate two key findings: first, the overall spatiotemporal patterns of brain activity were different between the march and the waltz, and second, the contrast between downbeat and upbeat was present in the waltz only.

Figure 3.

Contrast revealed by the PLS between march and waltz accounted for by the first latent variable (a) and between upbeat and downbeat in waltz for the second latent variable (b).

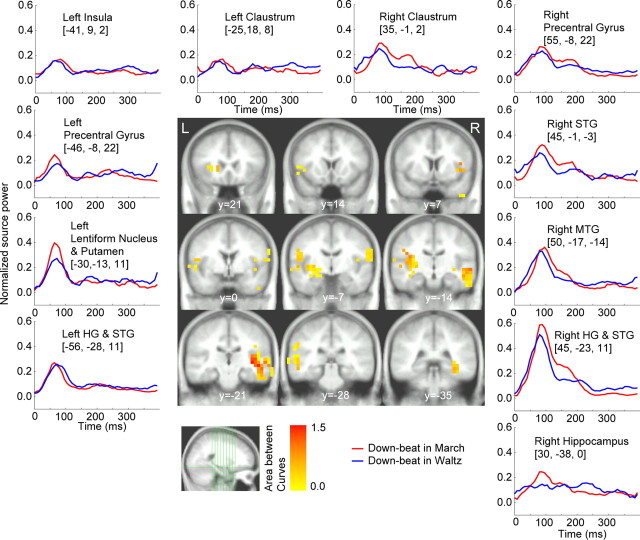
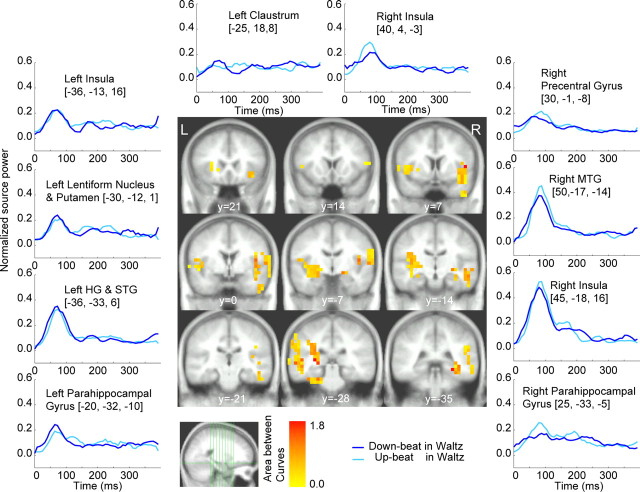
Figure 4 shows the grand-averaged time course of responses to the downbeats in the march and waltz conditions at the source locations for which the bootstrap test (see Materials and Methods) revealed a robust contrast between march and waltz regardless of whether downbeat or upbeat. The color-coded map represents the contrast strength overlaid onto the template MRI. The areas included Heschl's gyrus (HG), superior temporal gyrus (STG), middle temporal gyrus (MTG), insula, precentral gyrus, claustrum, caudate, globus pallidus, and putamen, as indicated in Table 1. The temporal lobe activities were predominant in the right hemisphere. Characteristics of the metric contrasts were as follows: (1) the right hippocampal region showed differential responses to downbeats in march and waltz, with 80 ms peak latency for the march and 250 ms for the waltz, (2) the initial peak at 80 ms was enhanced at left striatum for the march compared with waltz, and (3) primary and nonprimary auditory areas in the right hemisphere exhibited larger responses for the march than the waltz between 80 and 200 ms, with an additional peak at ∼180 ms that was absent in the left hemisphere. Note that, if there is difference in the time course between the sources, it should be interpreted as activity resulting from a different source, as shown by EEG data using the imaginary part of coherence measure (Nolte et al., 2004).

Figure 4.

The brain areas, which contributed to the contrast between march and waltz at the downbeat position (middle). The color-coded voxels belong to an area surrounding a local maximum in the maps of significant results of nonparametric testing the PLS results. The color represents the contrast strength, calculated as the accumulated source power difference across time points at which difference was found as significant by bootstrapping accompanied with PLS. At selected brain areas, the time series of the mean of source power within the group of adjacent voxels is shown in the surrounding panels. The anatomical labels are taken from the center of gravity of each group of connected voxels. L, Left; R, right.

The difference between the downbeat and the upbeat within the waltz context, identified by the second LV, is illustrated in Figure 5. The activities were manifested in similar areas but with more left hemispheric activities, particularly in the basal ganglia and the thalamus (Table 2). Right hemispheric regions commonly showed larger peaks at ∼80 ms latency for the upbeat compared with the downbeat. Furthermore, different response patterns between the left and right hemispheres were present again at hippocampal sites. The peak activity at 80 ms latency was observed in the left hippocampus with an earlier peak for the downbeat compared with the upbeat, whereas the right hippocampal area showed multiple distinct peaks after 150 ms for the upbeat in the waltz condition.

Figure 5.

Maps of contrast strength between downbeat and upbeat within the waltz context (middle). Time series of source power are shown at selected voxels (surrounding panels). L, Left; R, right.

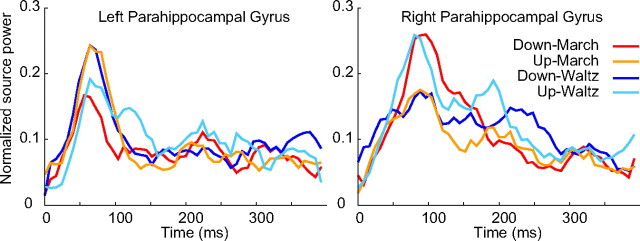
The responses in all four conditions obtained from bilateral parahippocampal gyri under the four conditions are presented in Figure 6. Bilateral hippocampal activity showed a dominant peak before 100 ms for all conditions, with somewhat earlier latency in the left hemisphere compared with the right. It is noteworthy that the time course of activities in the time interval 150–300 ms in the right hippocampal region clearly distinguishes the four conditions.

Figure 6.

Time series of the mean responses in the left and right parahippocampal areas for all four conditions.

Discussion

Our MEG data show that a subjective meter context leads to spatiotemporal modulation of neural activities in hippocampus and surrounding areas in addition to basal ganglia, premotor, auditory, and association cortices, and insula. Multivariate analysis identified a largest effect of the metric contrast between waltz and march. Although the activity in motor-related areas, especially the premotor cortex and inferior frontal gyrus (IFG) [Brodmann area 44 (BA 44)], can be explained partly by the established association of sound and action (Kohler et al., 2002), during our task, the accent contrast, obtained for waltz only, was not as strong as the metric contrast between march and waltz. Thus, the overall difference between march and waltz explained by the first LV is the primary evidence of internal metric organization rather than the accent contrast. This is by large in line with our musical experience in that the downbeat in march has a different feel from the downbeat in waltz. The same is true for the upbeat. Perhaps this is why a musical piece of one meter (march) induces a different feeling continuously at any beat from that by the piece of another meter (waltz). This clearly speaks for the significance of metric contrast observed robustly in space and time across the various brain areas.

The hippocampus appears to play a unique and significant role in maintaining meter, a deeper involvement than observed previously in maintaining of memory for auditory sequences biased by the inferred metrical framework (Essens, 1986; Palmer and Krumhansl, 1990; Sakai et al., 1999; Phillips-Silver and Trainor, 2005). The long-latency response in hippocampal area indexes both meter and accent at different peak latencies and is likely related to anticipating the incoming stimulus sequence based on the encoded metric framework. Similar long-latency endogenous responses at ∼200–300 ms in the same area have been found previously with human intracranial recording when subjects detected a target auditory stimulus embedded in a sequence of repeated standard stimuli (McCarthy et al., 1989; Halgren et al., 1995b). Such processing requires a reference memory for both the acoustic features of sound objects as well as the timing information within the sequence. Damage to the hippocampal system in rats did not eliminate time perception but altered the memory for the duration of a timing interval when required to reproduce it (Meck et al., 1987). Together, hippocampal function seems to be involved in encoding a temporal structure, preferably as a metric-based representation, and using it for anticipation, comparison, and reproduction.

Previously, music theorists have predicted that an internal clock (Povel and Essens, 1985) or a hierarchy of multiple oscillators (Large and Kolen, 1994) is necessary for representation of meter. Corresponding neural substrates have been suggested as the combination of different timing properties of neural firing or oscillations existing in thalamic–cortical–striatal network, hippocampus, and cerebellum (Mauk and Buonomano, 2004; Buhusi and Meck, 2005; Dragoi and Buzsáki, 2006). Modulation of these circuits by auditory stimulation (Aitkin and Boyd, 1975; Brankack and Buzsáki, 1986; Gardiner and Kitai, 1992) seems to be a plausible mechanism that could lead to the generation of endogenous activities observed here. Because the current analysis examined the phase-locked response to the stimulus only, additional analysis should address the exact nature of additional oscillatory activities, which are further crucial components in temporal processing involving connections between cortex and basal ganglia (Matell and Meck, 2004).

In contrast to the response in the hippocampal area, the left basal ganglia showed an enhanced early peak for the march condition (Fig. 4). The striatum receives auditory information through projections from auditory cortex (Yeterian and Pandya, 1998; Borgmann and Jurgens, 1999) as well as auditory (LeDoux et al., 1984) and multimodal thalamic (Matsumoto et al., 2001) nuclei. The former thalamic connection also provides information to the limbic system through the amygdala, whereas the latter is involved in activating the attention system. Graybiel (1997) suggested the role of the basal ganglia as cognitive as well as motor pattern generators. Together with its ability in temporal interval encoding, the basal ganglia might be also involved in generating hierarchy of interval patterns. The larger responses for march than waltz may be associated with the perceptual advantage of binary meter (march-type hierarchy) over trinary (waltz) or more complex metric structures, possibly attributable to the symmetrical nature of our locomotion system or musical experience in Western culture, in which binary meter is more prevalent. The observed pattern of brain activity points to considerably different processing of march and waltz. Likely this can be generalized to the population grown up with Western music, because cultural influence to metric perception is strongly evident even in infancy (Hannon and Trehub, 2005). Behavioral evidence from samples of Western population show that children and adults with no musical training, and even trained musicians, have better performance in production of march-type rhythms than waltz-type rhythms, although the bias was smallest in trained musicians (Drake, 1993). Therefore, the mental representation for metric structure in trained musicians like our participants would not be much different from the untrained population. We tested musicians to minimize performance variability during finger tapping, because musicians perform tapping with higher accuracy and less variability than untrained individuals (Repp and Doggett, 2007). Thus, our hypothesis was that their precisely time-locked neural activities would continue to be consistent across the group in the subsequent listening interval.

Our results are widely consistent with human lesion studies, showing contributions of the anterior temporal lobe (BA 21/38) to metric judgment (Liégeois-Chauvel et al., 1998) and of insula to auditory temporal processing (Bamiou et al., 2006), as well as previous neuroimaging, showing involvement of caudate, putamen, STG, premotor cortex, and IFG in metric processing (Grahn and Brett, 2007). Multiple factors could explain the absence of observed cerebellar contribution: (1) because of the complex cerebellum anatomy, evoked magnetic fields may have been canceled out (Hämäläinen et al., 1993), (2) phase-locking of cerebellum activity may not have been sufficient because animal studies showed various latency pattern of single-unit spike activities, perhaps attributable to different cell types and connections from different peripheral and subcortical auditory relays (Aitkin and Boyd, 1975; Altman et al., 1976; Woody et al., 1999), and (3) cerebellar function might be more significant for processing non-metrical timing (Sakai et al., 1999).

One advantage of investigating neuromagnetic evoked activity in MEG over neuroimaging using fMRI or positron emission tomography is that it provides the temporal dynamics of the responses for all areas of interest on a millisecond scale. The modulation of auditory evoked response in the auditory cortex and surrounding areas occurred chiefly at latencies between 80 and 200 ms. These are the latencies of the N1m and P2m waves of auditory evoked responses (magnetic counterparts of negative and positive vertex scalp voltage peaking at ∼100 and 200 ms, respectively) (Hari et al., 1980). It is widely accepted that N1m and P2m are generated from multiple areas of the superior temporal plane around the auditory cortex, as seen in agreement between human intracerebral and MEG recordings (Godey et al., 2001). These components are sensitive to short- and long-term experience (Pantev et al., 1998; Kuriki et al., 2006; Ross and Tremblay, 2009) and acoustic contents (Ackermann et al., 1999) and show task-related lateralization effect during discrimination (Poeppel et al., 1996). These findings suggest that various cortical and subcortical inputs modulate auditory cortical activity in this latency range according to task demands and relevance. Because the modulation in our data is purely endogenous on identical stimuli, it is interesting to speculate possible pathways that may underlie the modulatory effects in this time range. First, neural circuits within the auditory cortex generating long-latency endogenous activity specific to time processing have been shown in rats (Buonomano, 2003). Cortical input from the observed cross-modal association areas (insula, middle, and inferior temporal gyrus, claustrum, premotor cortex, and inferior parietal lobule) are other reasonable candidates. Finally, multiple subcortical structures could be important modulators. The non-lemniscal thalamocortical projections from the medial geniculate body (MGB) relays auditory information with other sensory and limbic information to auditory cortex (de la Mothe et al., 2006). The descending corticofugal pathway in the non-lemniscal MGB supports gating of auditory input as a feedback loop (Suga and Ma, 2003). These connections are thought to allow neurons in the auditory cortex to adapt rapidly depending on different states of attention and task context (Fritz et al., 2003). Such adaptation could facilitate auditory perception at the exact time point of the anticipated downbeat in the metric structure (Jones and Boltz, 1989; Palmer and Krumhansl, 1990).

The present data highlight the significance of the metric principle in human temporal information processing, which orchestrates distributed networks into coherent time course of neural activities. Specifically, this metric principle supports our abilities of encoding into hierarchies, anticipating, and producing temporal patterns efficiently. The close interaction between auditory, motor, and limbic systems supporting the emergence of metric representation found here may give a biological foundation for the emergence of our musical communal behaviors, such as dancing and chorusing, because meter is one of the most distinctive factors defining music cultural styles and associated social contexts (Lomax, 1978).