Abstract
As long as we only focus on kinematics, rhythmic movement appears to be a concatenation of discrete movements or discrete movement appears to be a truncated rhythmic movement. However, whether or not the neural control processes of discrete and rhythmic movements are distinct has not yet been clearly understood. Here, we address this issue by examining the motor learning transfer between these two types of movements testing the hypothesis that distinct neural control processes should lead to distinct motor learning and transfer. First, we found that the adaptation to an altered visuomotor condition was almost fully transferred from the discrete out-and-back movements to the rhythmic out-and-back movements; however, the transfer from the rhythmic to discrete movements was very small. Second, every time a new set of rhythmic movements was started, a considerable amount of movement error reappeared in the first and the following several cycles although the error converged to a small level by the end of each set. Last, we observed that when the discrete movement training was performed with intertrial intervals longer than 4 s, a significantly larger error appeared, specifically for the second and third cycles of the subsequent rhythmic movements, despite a seemingly full transfer to the first cycle. These results provide strong behavioral evidence that different neuronal control processes are involved in the two types of movements and that discrete control processes contribute to the generation of the first cycle of the rhythmic movement.
Introduction
In everyday behavior, discrete movements, such as reaching or kicking, and rhythmic (continuous) movements, such as clapping or walking, are ubiquitous. As long as we only focus on kinematics, discrete movement appears to be a truncated rhythmic movement, and rhythmic movement appears to be a concatenation of discrete movements. Nevertheless, recent studies have doubted that the control processes of both classes of movements can be combined and/or truncated in such a way. Instead, the question was raised as to whether different neural processes are involved in the generation of both movements (Hogan and Sternad, 2007).
Specifically, previous studies have examined the following three alternative hypotheses. The first hypothesis proposes that discrete movements are fundamental, whereas rhythmic movements are mere concatenations of discrete movements (Feldman, 1980; Shadmehr and Wise, 2005). In contrast, the second hypothesis states that rhythmic movements are fundamental, whereas discrete movements are truncated rhythmic movements (Schöner, 1990; Mottet and Bootsma, 1999). The third hypothesis assumes that rhythmic and discrete movements are two different (or partially different) classes of movements (Sternad et al., 2000; Buchanan et al., 2003). These hypotheses have been examined from behavioral (Buchanan et al., 2003; van Mourik and Beek, 2004), theoretical (Schöner, 1990; Huys et al., 2008; Ronsse et al., 2009), and neuronal (Spencer et al., 2003, 2007; Schaal et al., 2004) perspectives. The current consensus is that rhythmic movements are not mere concatenations of discrete movements (i.e., the first hypothesis has been ruled out). However, it is still largely unknown as to which of the remaining two hypotheses are valid. For example, the movement speed–accuracy tradeoff was different in the two classes of movements (Smits-Engelsman et al., 2002), which seems to support the third hypothesis. On the other hand, a theoretical study suggested that discrete movement can be constructed from rhythmic movement (i.e., supporting the second hypothesis) by imposing timekeeper mechanisms on the controller (Huys et al., 2008).
To address the issue of how the control of rhythmic and discrete movements are related, we have adopted a different approach. Schaal et al. (2004), by using a functional magnetic resonance imaging (fMRI), demonstrated that discrete movements engaged activities of much broader brain areas than rhythmic movements, even when the same wrist movement was performed. Considering the intimate link between the neural processes of motor control and learning (Li et al., 2001; Paz et al., 2003), we assumed that such distinct brain processes for movement control should be reflected in a difference in motor learning. In particular, if the discrete and rhythmic movements are produced on the basis of identical neural processes, the learned discrete movements should be substantially transferred to rhythmic movement and vice versa. On the other hand, if these two types of movements are generated by (partially) independent processes, the transfer of motor learning should be negligible or partial. To test the possibilities, we examined the transfer of learned visuomotor rotations (Krakauer et al., 2000; Tong and Flanagan, 2003) between discrete and rhythmic movements.
Materials and Methods
Participants
Fifty-six neurologically normal volunteers (14 females and 42 males, aged 19–42 years) participated in the experiments. All participants except for two males were right handed as assessed by the Edinburgh Handedness Inventory (Oldfield, 1971). Participants were randomly assigned to one of seven experimental groups (i.e., eight participants in each group; each participant participated in only one experiment). All participants were naive to the purpose of the experiments and signed an institutionally approved consent form. All experiments were approved by the ethical committee of the Graduate School of Education, The University of Tokyo.
Apparatus
The experiments were performed in a darkened room. The participants sat on a straight-backed chair while grasping the handle of a robotic manipulandum with their right hand (Phantom Premium 1.5HF, SensAble Technologies). A spring simulated by the Phantom device (1.0 N/mm) generated a virtual horizontal plane on which the handle movement was restricted. A projector was used to display the position of the handle with a white circle cursor (diameter 8 mm) on a horizontal screen (45 cm × 60 cm) placed ∼13 cm above the virtual plane and ∼15 cm below the shoulder level. Thus, the screen board prevented the participants from directly seeing their arm and handle. The participants controlled the cursor by performing discrete or rhythmic out-and-back movements (the details will be shown in the next section) between a start position (8 mm diameter) and a target (8 mm diameter), which were also displayed on the screen. The start position was located ∼25 cm in front of the body in a mid-sagittal plane, and the target was 7 cm away from it. The start point and the cursor were always visible. The position and velocity of the handle were A/D converted by 500 Hz and stored for the offline analysis later.
Procedure
The participants were instructed to move the cursor between the start position and the target by performing straight, fast, and uncorrected out-and-back movements with a sharp reversal at the target. Before each trial, they needed to place the cursor at the start point after which the target appeared. In the discrete task condition, they performed a single out-and-back movement (Krakauer et al., 2000) within 1 s after the target appearance (the target disappeared after that). In the rhythmic task condition, the participants performed the same out-and-back movements repeatedly (without any break between cycles) until the target disappeared. They were instructed not to make any deliberate correction within each cycle. Slight correction of the movement was allowed only at the turnaround point at which the inward movement turned outward to avoid excessive drift of the turnaround point. In both discrete and rhythmic conditions, they were asked to make the peak velocities of the outward and inward movements as constant as possible over trials and cycles. To accomplish this, the experimenter demonstrated discrete and rhythmic movements (with a frequency of ∼2.5 Hz) and instructed the participants to perform the movements with similar velocity and tempo. In addition, the participants adequately practiced both discrete (∼100 trials) and rhythmic movements (∼300 cycles) under normal visuomotor conditions before each experiment.
Experiment 1.
This experiment was designed to examine the transfer of motor learning (visuomotor rotation) from discrete to rhythmic movement and vice versa. This experiment comprised two sessions: baseline and rotation sessions (3 min rests were taken between the sessions). In the baseline session, the cursor was displayed just above the handle position, while in the rotation session, the cursor was displayed at the position obtained by rotating the handle position around the start position by 30° in the counterclockwise (CCW) direction.
In each session, the participants performed both the discrete and rhythmic tasks in succession (7 s were taken for the transition time between the tasks). In the discrete task, the intertrial interval (ITI) was set to ∼2 s by presenting the target every 2 s. The Rhy-Dis2s group (n = 8) performed the rhythmic task first, while the Dis2s-Rhy group (n = 8) performed the discrete task first. The rhythmic task comprised continuous rhythmic out-and-back movements for 40 s (baseline) or for 100 s (rotation), while the discrete task involved 20 (baseline) or 50 (rotation) discrete out-and-back movements. It should be noted that the duration of the discrete task was almost equivalent to that of the rhythmic movement with this ITI (e.g., in the rotation session, 50 discrete movements took 100 s, which was equal to the duration of a rhythmic set).
Experiment 2.
This experiment was designed to examine how the motor learning of visuomotor rotation progressed with the repetition of the sets of rhythmic movements. The Rhy group (n = 8) successively performed several sets of the rhythmic movements. The first baseline session consisted of the rhythmic movements for 40 s without any visual rotation. Then, the participants performed two sets of 100 s rhythmic movements under the presence of 30° CCW visual rotation, followed by 23 sets of 15 s rhythmic movements. The duration of the first two sets in the rotation session was set to 100 s, by which we can compare the result with that of experiment 1 (Exp. 1). The time interval between the sets was 7 s, and 3 min rests were taken after the second and 14th sets in the rotation session to avoid fatigue among participants.
Experiment 3.
As long as we only focus on kinematics, the rhythmic movements appear to be a continuous version of the discrete movements, so we can expect that reducing the ITI of the discrete movements should make the movement more “rhythm-like.” This experiment was designed to examine how the ITI of the discrete task influenced the motor learning transfer from the discrete to the rhythmic movements. The procedure was almost identical to that in experiment 1, except that a shorter ITI [1 s: Dis1s-Rhy group (n = 8)] or longer ITI [4 s: Dis4s-Rhy group (n = 8)] was adopted for the discrete task. The duration of the discrete session was set to be equal to that of experiment 1 (40 and 100 s for the baseline and rotation session, respectively). According to the changes in the ITI, thus, the number of discrete trials performed by the Dis1s-Rhy group was increased to 40 and 100 for the baseline and rotation session, respectively. Similarly, the number of discrete trials performed by the Dis4s-Rhy group was decreased to 10 and 25 for the baseline and rotation session, respectively. The duration of the rhythmic task was set to 40 and 60 s for the baseline and rotation session, respectively.
Experiment 4.
This experiment was designed to examine how motor learning transfer was influenced when the random ITI was interleaved between discrete training trials. The experimental procedure was almost the same as that of experiment 3. One difference was that the participants [DisRand-Rhy group (n = 8)] performed 25 discrete movements in which the ITI was set to a random variable drawn from the following values: 5, 6, 7, 8, 9, and 10 s.
Experiment 5.
This experiment was designed to examine how motor learning transfer was influenced when a much more thorough discrete training was performed. To this end, the number of movements for the discrete training (ITI = 7 s) was increased to 100 (note that it was 25 for the Dis4s-Rhy group in Exp. 3). The experimental procedure was similar to that of experiment 3, except that the 3 min resting periods were taken after the 30th, 60th, and 90th discrete training trials to maintain the participants' [Dis7s-Rhy group (n = 8)] concentration and prevent fatigue.
Data analysis
The data of the handle position and velocity were low-pass filtered using the fourth-order Butterworth filter with a cutoff frequency of 30 Hz (Winter, 2004). We calculated the position at which the peak outward handle velocity was observed for each trial (discrete task) or for each cycle (rhythmic task). In the rhythmic task, we also detected the turnaround position for each cycle, where the direction of the handle movement switched from inward to outward. Ideally, this turnaround position should be at the start position, but there was often a slight shift due to the difficulty faced by the participants in returning the handle to the start position. The movement direction and the target direction were obtained as the direction from the start position (discrete task) or the turnaround position (rhythmic task) to the position at the handle's peak outward velocity and the target position, respectively. Movement performance was evaluated by the directional error defined as the angular difference between the movement and target directions for each trial (discrete task) and for each cycle (rhythmic task).
Unless otherwise noted, data values were reported as means ± SD calculated for all the participants. A repeated-measures ANOVA was conducted to detect significant differences across cycles or trials and across experimental tasks within each group. A between-group ANOVA was used to detect significant differences across experimental groups. In addition, post hoc Ryan's tests were used to reveal the significant differences across cycles or trials, across experimental tasks, and across experimental groups. The statistical threshold was set at p < 0.05.
Results
Experiment 1: motor learning transfer between discrete and rhythmic movements
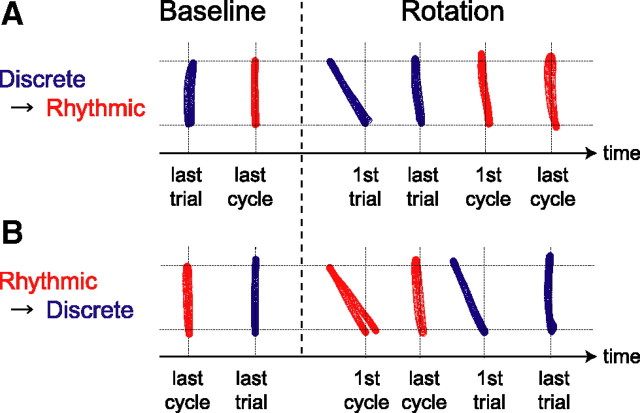
Figure 1 indicates a typical example of the cursor trajectories for a participant of the Dis2s-Rhy group (A) and for a participant of the Rhy-Dis2s group (B). The first movement in the rotation session was perturbed in 30° CCW direction due to the imposed visual rotation for both participants. However, both participants could compensate for the imposed visual rotation after 50 discrete (Fig. 1 A) and 319 rhythmic (Fig. 1 B) movements. For the Dis2s-Rhy participant, this adaptation to the visual rotation was maintained for the subsequent rhythmic movements. On the contrary, for the Rhy-Dis2s participant, considerable deviation of the trajectory from the target reappeared for the subsequent first discrete movement. These results indicate that the visuomotor adaptation acquired through the discrete movements was almost fully transferred to that through the rhythmic movements, while the motor learning transfer from the rhythmic to discrete movements was very small.
Figure 1.
Changes in cursor paths for a representative participant of the Dis2s-Rhy (A) and Rhy-Dis2s (B) groups. The blue and red trajectories represent the cursor paths for the discrete and rhythmic movements, respectively. After the baseline session (20 discrete movements and 40 s rhythmic movement), the participants performed 50 discrete movements and 100 s rhythmic movement under the presence of 30° counterclockwise visual rotation (rotation session). In each session, the Dis2s-Rhy group performed the discrete movement trial first, while the Rhy-Dis2s group performed the rhythmic movement trial first. Both participants were able to move the handle toward the target properly by the end of the first part of the rotation session. This appropriate movement direction was maintained in the following rhythmic cycles for the Dis2s-Rhy participant (A), but the cursor path of the first discrete trial after the rhythmic movement training was largely deviated from the target direction for the Rhy-Dis2s participant (B).
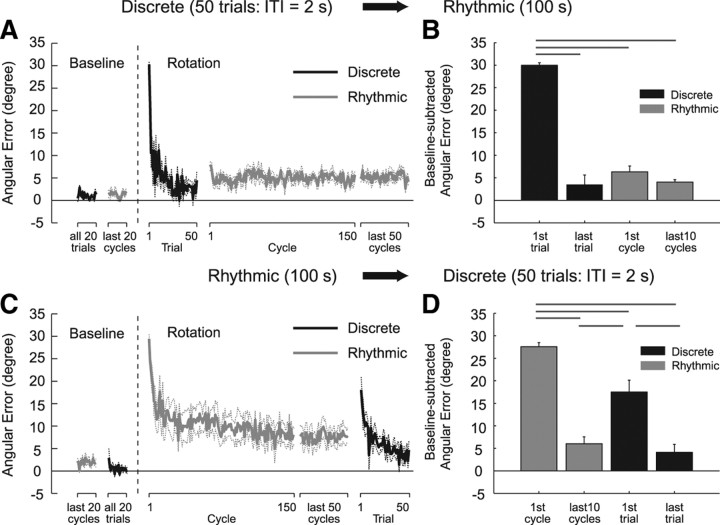
Such asymmetric motor learning transfer between rhythmic and discrete movements was consistently observed for all participants (Fig. 2). For the Dis2s-Rhy group, the angular error evaluated at the peak outward velocity was gradually decreased to the baseline level with discrete movement training (50 trials), and the level of the error remained at the same level (last discrete trial vs first or last 10 rhythmic cycles, p > 0.05) for the subsequent rhythmic movement (Fig. 2 A,B). However, for the Rhy-Dis2s group, although they performed five times the number of movements (267.6 ± 36.8 rhythmic cycles), the significantly larger angular error (last 10 rhythmic cycles vs first discrete trial, p < 0.001) reappeared for the subsequent discrete task (Fig. 2 C,D).
Figure 2.
Learning curve quantified by angular error and their statistical summaries for Dis2s-Rhy (A, B) and Rhy-Dis2s (C, D) groups. The black and gray lines/bars represent the errors of the discrete and the rhythmic movements, respectively. The data were averaged across all participants, and the dash lines and error bars represent ±1 SE. The bar graphs show the residual angular errors calculated by subtracting the baseline error. The horizontal lines above the bar graphs indicate statistically significant differences. As was shown in Figure 1, the averaged data also demonstrate the almost full adaptation transfer from discrete to rhythmic movements (B) but only a small amount of transfer from rhythmic to discrete movements (D).
As for the kinematics of the hand trajectory, the peak velocity of the outward movement in the baseline sessions was not significantly different (paired t test, p > 0.05) between the rhythmic (595 ± 60 mm/s) and discrete movements (580 ± 69 mm/s). However, the peak velocity of the inward movement was significantly larger (paired t test, p < 0.05) for rhythmic movement (596 ± 65 mm/s) than for discrete movement (495 ± 71 mm/s). The peak acceleration of the outward movement was significantly (paired t test, p < 0.05) larger for rhythmic movements (10,523 ± 2307 mm/s2) than for discrete movements (6994 ± 1676 mm/s2), while no significant difference was found in the peak acceleration of the inward movement (discrete movement: 9352 ± 2508 mm/s2; rhythmic movement: 10,154 ± 2117 mm/s2; paired t test, p > 0.05).
Experiment 2: motor learning with repeated sets of rhythmic movements
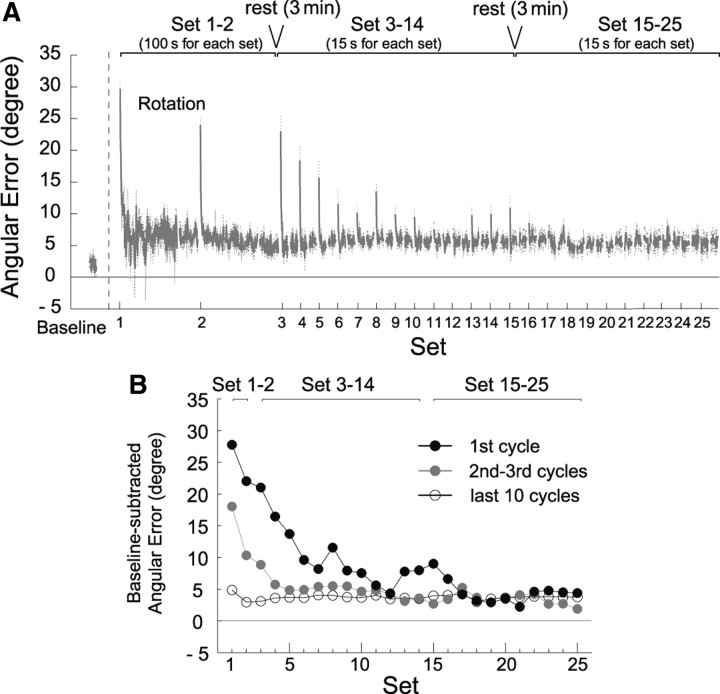
In experiment 1, we observed the unexpected phenomenon that the significant angular error in the discrete movement appeared after the adaptation by the rhythmic movement. We conducted experiment 2 to examine how the adaptation pattern changed when the rhythmic movement sessions were repeated. Figure 3 A indicates the changes in the angular error with the repetition of the rhythmic sets. Although the participants adapted to the visual rotation by the end of the first rhythmic movement set, a significant angular error appeared for the first cycle of the second set, as was observed in experiment 1 (Rhy-Dis2s group) (Fig. 2 C). Similarly, every time a new set was started, the significant angular error was observed for the first cycle in the following sets although the magnitude was gradually decreased (Fig. 3 B).
Figure 3.
Angular errors change with the repetition of rhythmic cycles. A, The errors of the first 150 and the last 50 cycles in sets 1–2 and the errors of the first 20 and the last 20 cycles in sets 3–25. The data were averaged across all participants and the dash lines represent ±1 SE. B, The angular errors for the first rhythmic cycle (black circle), the errors averaged across the second and third cycles (gray circle), and those across the last 10 cycles (open circle) as a function of the rhythmic movement set. The data represent the residual errors after subtracting the baseline error. Significant differences between the first cycle and the last 10 cycles and between the second and third and the last 10 cycles were found until the 15th (except for the 10th, 11th, and the 12th set) and third sets, respectively.
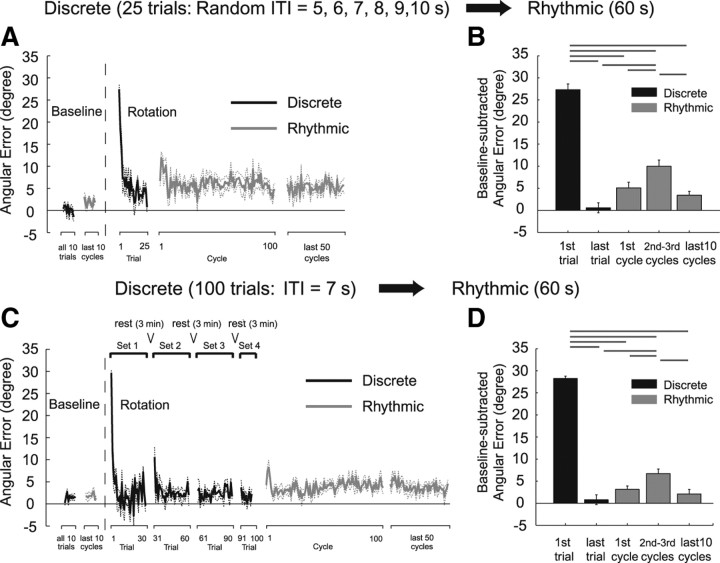
Experiment 3: influence of ITI of the discrete movement on motor learning
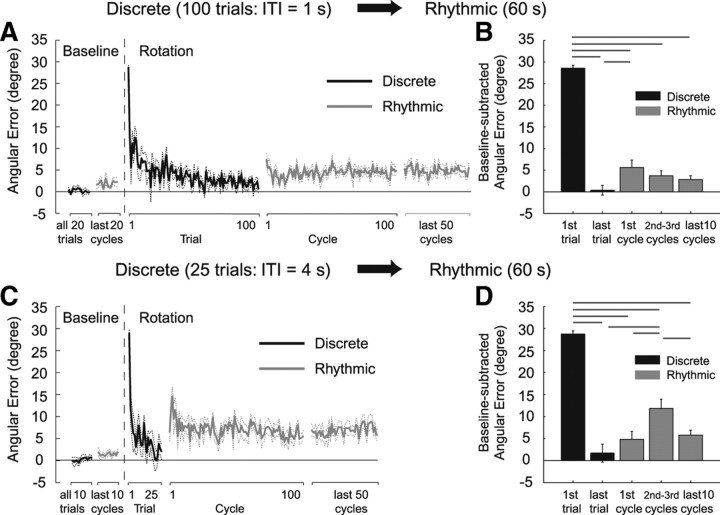
Figure 4 shows participant-averaged learning curves when the ITI was reduced to 1 s (A) (Dis1s-Rhy group) and when the ITI was increased to 4 s (C) (Dis4s-Rhy group). For the Dis1s-Rhy group, the first cycle of the rhythmic task after the discrete movement training exhibited slight but significant (last discrete trial vs first rhythmic cycle, p < 0.01) increase in the angular error (Fig. 4 A,B). On the other hand, for the Dis4s-Rhy group, the angular error of the first cycle of the rhythmic task after the discrete movement training was not significantly different from that of the last discrete movement (last discrete trial vs first rhythmic cycle, p > 0.05). However, in the second and third cycles of the rhythmic task, the angular error significantly larger than that of the first cycle (first rhythmic cycle vs second and third rhythmic cycles, p < 0.01) reappeared (Fig. 4 C,D).
Figure 4.
Learning curve quantified by angular error and the statistical summaries for Dis1s-Rhy (A, B) and Dis4s-Rhy (C, D). The black and gray lines/bars represent the errors of the discrete and the rhythmic movements, respectively. The data were averaged across all participants and the dash lines and error bars represent ±1 SE. The bar graphs show the residual angular errors calculated by subtracting the baseline error. The horizontal lines above the bar graphs indicate significant differences. The error of the first rhythmic cycle was maintained at a small level, as in experiment 1 (Fig. 2), although the difference from the last discrete trial was significant for the Dis1s-Rhy group (B). However, for the Dis4s-Rhy group, a significantly large error reappeared in the second and third cycles (D).
Figure 5 summarizes the results of motor learning transfer from the different training conditions (rhythmic task and discrete tasks with ITI = 1, 2, and 4 s) to the subsequently performed rhythmic movements obtained from experiments 1, 2, and 3. Figure 5 B shows the change in the error from the last trial (discrete task: ITI = 1, 2, and 4 s) or the last 10 cycles (rhythmic task) of the first training set to the first cycle of the following rhythmic movement (see Δ1 in Fig. 5 A). Only after the training was performed with rhythmic task was drastic error increment in the first cycle of the subsequent rhythmic movements observed. Figure 5 C shows the change in the error from the first cycle to the second and third cycles of the rhythmic movements performed after the first training set (see Δ2 in Fig. 5 A). After the first training was performed with the rhythmic movements or with the discrete movements with an ITI of 1 and 2 s, the change in the error showed a negative value. This indicated that the handle movement in the second and third cycles was modified to the direction to decrease the errors. On the contrary, when the ITI was 4 s, the change in the error showed a positive value, indicating that the handle movement in the second and third cycles was pulled back to the direction to increase the errors.
Figure 5.
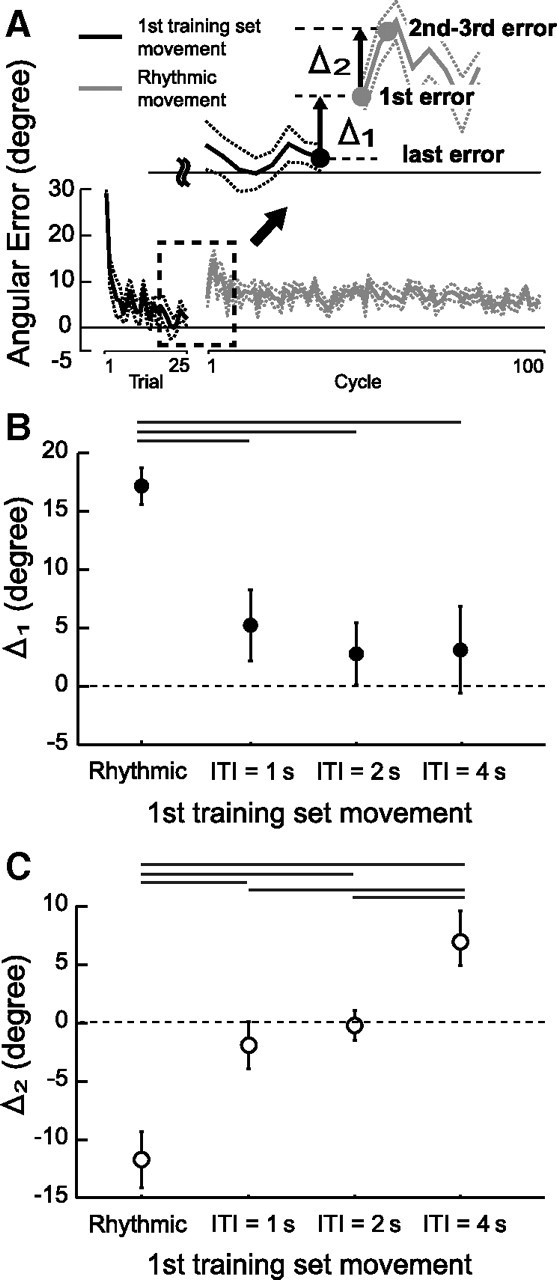
Effect of the type of movement in the first training set (rhythmic movement training or discrete movement training with ITI = 1, 2, or 4 s) on the angular error behavior in the subsequent rhythmic movements. A, To evaluate the effect, we calculated the following two quantities; the change in the error from the end of the first training set (the last discrete trial or the last 10 rhythmic cycles) to the first cycle of the following rhythmic movement (Δ1), and the change in the error from the first cycle to the second and third cycles of the rhythmic movement (Δ2). Positive values of these quantities indicate the increases in the movement error. B, Effect of the type of movement in the first training set on the Δ1. A drastic increase in the error was observed only after the rhythmic movement training. C, Effect of the type of movement in the first training set on the Δ2. Quite naturally, after the rhythmic training or the discrete training with ITI = 1 and 2 s, the error of the subsequent rhythmic movement set decreased in the second cycle compared to the first cycle as indicated by a negative Δ2. However, after the discrete training with ITI = 4 s, a reappearance of the error was observed in the second cycle as indicated by a positive Δ2. The data in B and C were averaged across all participants and error bars represent ±1 SE. The horizontal solid lines indicate statistically significant differences.
Experiments 4 and 5: motor learning transfer when the degree of “discreteness” of the discrete training is increased
For the Dis4s-Rhy group in experiment 3, we observed an incomplete transfer from discrete to rhythmic movements where a significantly larger error appeared in the second and third rhythmic cycles despite a seemingly full transfer to the first cycle (Fig. 4 C,D). We conducted two additional experiments (experiments 4 and 5) to verify that the reappearance of the error in the second and third rhythmic cycles could be observed when the degree of “discreteness” of the discrete training was increased.
In experiment 4, the ITI between the discrete trials was randomly chosen from the values of 5, 6, 7, 8, 9, and 10 s. In experiment 5, the ITI and number of discrete movements were increased to 7 s and 100, respectively (note that they were 4 s and 25 movements for the Dis4s-Rhy group in Exp. 3). In both experiments, as observed in the Dis4s-Rhy group (Fig. 4 C,D), a significantly larger error reappeared in the second and third cycles (Fig. 6), although the error of the first rhythmic cycle stayed at a low level after the discrete training (last discrete trial vs first rhythmic cycle, p > 0.05).
Figure 6.
Learning curve quantified by angular errors and their statistical summaries for experiments 4 (A, B) and 5 (C, D). The black and gray lines/bars represent the errors of discrete and rhythmic movements, respectively. The data were averaged across all participants, and the dash lines and error bars represent ±1 SE. The bar graphs show the residual angular errors calculated by subtracting the baseline error. The horizontal lines indicate significant differences. In both experiments 4 and 5, a significantly large error reappeared in the second and third cycles as observed in the Dis4s-Rhy group of experiment 3 (Fig. 4 C,D), although the error of the first rhythmic cycle stayed at a low level after the discrete training.
Discussion
In this study, we hypothesized that distinct neural control processes for different behavioral contexts will result in separate motor learning for each behavior. For example, partially distinct representation in MI for unimanual and bimanual movements (Donchin et al., 2002; Rokni et al., 2003) would explain why there is only a partial transfer of learning within the same limb across unimanual and bimanual tasks (Nozaki et al., 2006; Nozaki and Scott, 2009). Based on this hypothesis, we tried to clarify the differences in control processes between discrete and rhythmic movements by investigating how motor learning of visual rotation was transferred between them. We found that motor learning was almost fully transferred from discrete to rhythmic movement, not vice versa (experiment 1).
Effects of the amount of training and kinematics
Before concluding that such asymmetric transfer is substantial, we need to consider the influence of two factors: the amount of training and kinematics. The amount of training may not account for the results, because the rhythmic training consisted of approximately five times the number of movements of the discrete training, which should have resulted in the opposite result: larger learning transfer from rhythmic to discrete movement. Differences in kinematics were also unlikely, because (1) the outward peak velocities for rhythmic and discrete movements were almost identical, and (2) the differences in the outward peak acceleration and in the peak inward velocity were too small to explain the asymmetric transfer (Kitazawa et al., 1997). Furthermore, the larger peak outward acceleration and peak inward velocity indicate that the rhythmic movement was mechanically more demanding, which should have resulted in greater motor learning transfer from rhythmic to discrete movement.
Discrete movement control for the first cycle of the rhythmic movement
Figure 3 demonstrated that every time a new rhythmic set was started, significant movement error appeared for the first cycle (Exp. 2). In addition, the first cycle error progressively decreased with the sets, similar to the decrease in the errors with discrete trials. Thus, the training effects of 25 sets of rhythmic movements on their first cycles appear similar to those of 25 discrete trials. These results lead to a hypothesis that the first cycle of rhythmic movements is mainly produced by a discrete movement control process (discrete process), whereas the rest of cycles are produced by a rhythmic movement control process (rhythmic process).
Based on the kinematic differences, van Mourik and Beek (2004) have also made a similar assertion. We also observed a significant but small difference in the outward peak velocity between the first cycle (527.6 ± 85.9 mm/s) and the ongoing cycles (598.7 ± 62.3 mm/s) of rhythmic movements (paired t test, p < 0.05). However, such a subtle difference cannot explain the drastic increase in error from the end of the first set to the first cycle in the second set (Fig. 3), as discussed in the previous section. Thus, our result suggests substantial differences in movement control between the first and remaining cycles.
Effect of the ITI of the discrete movement training
Even when the ITI of the discrete training was reduced to 1 s (Exp. 3), the following first rhythmic cycle did not show a large error increase (Fig. 4 A,B) [although the increase was significant (p < 0.01)]. This was considerably different from the pattern in experiment 2 showing the drastic error increase in the first cycle of the second set (Fig. 3). Thus, even when the discrete task was closer to the rhythmic task in terms of the ITI, the characteristics of motor learning as a discrete task remained almost unchanged (Fig. 5 B). Similarly, after the discrete training with a longer ITI (4 s) or with random ITI (5–10 s), the error in the first cycle of the rhythmic movement was not significantly different from that in the last discrete movement (Figs. 4 D, 6 B).
These results seem to indicate that a sufficient amount of the discrete training would lead to a complete learning transfer to the following rhythmic movement. However, this may not be the case. A significantly larger error reappeared in the second and third cycles despite the absence of the first cycle error when the ITI of the discrete training was 4 s (Figs. 4 C,D, 5) or random (Fig. 6 B). The small number of discrete training trials for the Dis4s-Rhy group (25 trials) might not account for the error reappearance, because similar error reappearance was observed in experiment 5, where the number of discrete training trials was 100 (Fig. 6 D). Another explanation might be that the second and third cycles would be in a “transient” state of the dynamics of the neural circuits and the limb's biomechanics before stable rhythmic movements were achieved. However, this explanation is also unlikely, because such error reappearance was never observed in the Dis1s-Rhy, Dis2s-Rhy, and Rhy groups (Fig. 5 C).
Thus, the error reappearance in the second and third rhythmic cycles following discrete training might reflect the presence of control processes specific to rhythmic movement. One possible rational explanation for the error reappearance observed only after discrete training with longer ITI is that the larger the ITI, the larger the contribution of the discrete process. For example, after the discrete training with 4 s ITI, the discrete process had almost fully adapted to the visual rotation, whereas the rhythmic process had adapted little. According to our hypothesis, the first rhythmic cycle is produced by discrete process, and the contribution of the rhythmic process is increasing with the subsequent cycles. Thus, although the first cycle error was maintained at a small level, the error of the second and third rhythmic cycles might reappear due to the absence of the learning of the rhythmic process. To the contrary, when the ITI was shorter (1 or 2 s), even the rhythmic process adapted to the rotation during discrete training, and this may be the reason why the reappearance of the error was not observed for these ITI conditions.
There might be still another possibility that our results can be explained by the differences in the adaptation process rather than by those in the control process. Recent studies have demonstrated that the motor learning of reaching movement is poorer for smaller ITI (Bock et al., 2005; Francis, 2005), possibly due to decreased error sensitivity with the reduction of the ITI (Huang and Shadmehr, 2007). Indeed, our results (Figs. 2 –4) indicate that, for the smallest ITI (i.e., rhythmic movements), the motor learning was worse with respect to the rate of error reduction and the converged plateau. However, such ITI influence was unlikely to explain the error increase in the first discrete trial after the rhythmic movement training (Fig. 2 C,D). If the rhythmic and discrete movement control processes are identical, the error level of the following discrete task, which was initiated only 7 s after the termination of the rhythmic training, should have been maintained at the same level. Thus, a considerable amount of error increase in the first discrete trial after rhythmic movement training implies the existence of a separate discrete movement control process.
Distinct neuronal processes between discrete and rhythmic movements
Using an fMRI, Schaal et al. (2004) concluded that the discrete process almost fully includes the rhythmic process: rhythmic movement engaged less cortical areas probably due to the function of some rhythmic pattern generator (Brown, 1914). The brain areas specific to discrete process involved higher-level movement planning areas such as premotor, supplementary motor, and posterior parietal area. The asymmetric motor learning transfer shown here seems congruent with their conclusion, especially considering the association of the posterior parietal area with the adaptation to the novel visuomotor environment (Krakauer et al., 2004).
Although the effect was tiny, we found incomplete motor learning transfer from discrete movement to rhythmic movement (Fig. 5 C), suggesting the existence of the control processes specific to rhythmic movement. Previous brain imaging studies have not reported the activated brain region specific to rhythmic movement, but it is still possible that the temporal activity differs. Furthermore, if a spinal pattern generator is more involved in rhythmic movement, then part of the motor learning may occur in the spinal cord (Wolpaw and Tennissen, 2001; Ung et al., 2005). Further studies are required to clarify the neural correlates for incomplete motor learning transfer from discrete to rhythmic movements.
The present study aimed to test the following three alternative hypotheses: (1) discrete movements are fundamental, (2) rhythmic movements are fundamental, and (3) they are two (partially) independent classes of movements. We have shown that the motor learning was almost fully transferred from discrete to rhythmic movement, but that the transfer from rhythmic to discrete movement was small. Such asymmetric motor learning transfer provides strong behavioral evidence that distinct neuronal processes are involved in discrete and rhythmic movements. Thus, from the viewpoint of neural control, a discrete movement is not merely a truncated rhythmic movement, and conversely, a rhythmic movement is not merely a concatenation of discrete movements, supporting the third hypothesis described above. This may have a practical impact on and implications for the way in which a motor skill is learned in sports and rehabilitation.
Footnotes
This work was supported by KAKENHI (#20670008) and a Casio Science Promotion Foundation to D.N. We thank Yoshiharu Yamamoto and members of the Nozaki laboratory for their helpful comments.
References
- Bock O, Thomas M, Grigorova V. The effect of rest breaks on human sensorimotor adaptation. Exp Brain Res. 2005;163:258–260. doi: 10.1007/s00221-005-2231-z. [DOI] [PubMed] [Google Scholar]
- Brown TG. On the nature of the fundamental activity of the nervous centers; together with an analysis of rhythmic activity in progression, and a theory of the evolution of function in the nervous system. J Physiol. 1914;48:18–46. doi: 10.1113/jphysiol.1914.sp001646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchanan JJ, Park JH, Ryu YU, Shea CH. Discrete and cyclical units of action in a mixed target pair aiming task. Exp Brain Res. 2003;150:473–489. doi: 10.1007/s00221-003-1471-z. [DOI] [PubMed] [Google Scholar]
- Donchin O, Gribova A, Steinberg O, Mitz AR, Bergman H, Vaadia E. Single-unit activity related to bimanual arm movements in the primary and supplementary motor cortices. J Neurophysiol. 2002;88:3498–3517. doi: 10.1152/jn.00335.2001. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Superposition of motor program—I. Rhythmic forearm movements in man. Neuroscience. 1980;5:81–90. doi: 10.1016/0306-4522(80)90073-1. [DOI] [PubMed] [Google Scholar]
- Francis JT. Influence of the inter-reach-interval on motor learning. Exp Brain Res. 2005;167:128–131. doi: 10.1007/s00221-005-0062-6. [DOI] [PubMed] [Google Scholar]
- Hogan N, Sternad D. On rhythmic and discrete movements: reflections, definitions, and implications for motor control. Exp Brain Res. 2007;181:13–30. doi: 10.1007/s00221-007-0899-y. [DOI] [PubMed] [Google Scholar]
- Huang VS, Shadmehr R. Evolution of motor memory during the seconds after observation of motor error. J Neurophysiol. 2007;97:3976–3985. doi: 10.1152/jn.01281.2006. [DOI] [PubMed] [Google Scholar]
- Huys R, Studenka BE, Rheaume NL, Zelaznik HN, Jirsa VK. Distinct timing mechanisms produce discrete and continuous movements. PLoS Comput Biol. 2008;4:e1000061. doi: 10.1371/journal.pcbi.1000061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitazawa S, Kimura T, Uka T. Prism adaptation of reaching movements: specificity for the velocity of reaching. J Neurosci. 1997;17:1481–1492. doi: 10.1523/JNEUROSCI.17-04-01481.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krakauer JW, Pine ZM, Ghilardi MF, Ghez C. Learning of visuomotor transformations for vectorial planning of reaching trajectories. J Neurosci. 2000;20:8916–8924. doi: 10.1523/JNEUROSCI.20-23-08916.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krakauer JW, Ghilardi MF, Mentis M, Barnes A, Veytsman M, Eidelberg D, Ghez C. Differential cortical and subcortical activations in learning rotations and gains for reaching: A PET study. J Neurophysiol. 2004;91:924–933. doi: 10.1152/jn.00675.2003. [DOI] [PubMed] [Google Scholar]
- Li CS, Padoa-Schioppa C, Bizzi E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron. 2001;30:593–607. doi: 10.1016/s0896-6273(01)00301-4. [DOI] [PubMed] [Google Scholar]
- Mottet D, Bootsma RJ. The dynamics of goal-directed rhythmical aiming. Biol Cybern. 1999;80:235–245. doi: 10.1007/s004220050521. [DOI] [PubMed] [Google Scholar]
- Nozaki D, Scott SH. Multi-compartment model can explain partial transfer of learning within the same limb between unimanual and bimanual reaching. Exp Brain Res. 2009;194:451–463. doi: 10.1007/s00221-009-1720-x. [DOI] [PubMed] [Google Scholar]
- Nozaki D, Kurtzer I, Scott SH. Limited transfer of learning between unimanual and bimanual skills within the same limb. Nat Neurosci. 2006;9:1364–1366. doi: 10.1038/nn1785. [DOI] [PubMed] [Google Scholar]
- Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia. 1971;9:97–113. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- Paz R, Boraud T, Natan C, Bergman H, Vaadia E. Preparatory activity in motor cortex reflects learning of local visuomotor skills. Nat Neurosci. 2003;6:882–890. doi: 10.1038/nn1097. [DOI] [PubMed] [Google Scholar]
- Rokni U, Steinberg O, Vaadia E, Sompolinsky H. Cortical representation of bimanual movements. J Neurosci. 2003;23:11577–11586. doi: 10.1523/JNEUROSCI.23-37-11577.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronsse R, Sternad D, Lefèvre P. A computational model for rhythmic and discrete movements in uni- and bimanual coordination. Neural Comput. 2009;21:1335–1370. doi: 10.1162/neco.2008.03-08-720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaal S, Sternad D, Osu R, Kawato M. Rhythmic arm movement is not discrete. Nat Neurosci. 2004;7:1136–1143. doi: 10.1038/nn1322. [DOI] [PubMed] [Google Scholar]
- Schöner G. A dynamic theory of coordination of discrete movement. Biol Cybern. 1990;63:257–270. doi: 10.1007/BF00203449. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Wise SP. Cambridge, MA: MIT; 2005. The computational neurobiology of reaching and pointing: a foundation of motor learning. [Google Scholar]
- Smits-Engelsman BCM, Van Galen GP, Duysens J. The breakdown of Fitts' law in rapid, reciprocal aiming movements. Exp Brain Res. 2002;145:222–230. doi: 10.1007/s00221-002-1115-8. [DOI] [PubMed] [Google Scholar]
- Spencer RMC, Zelaznik HN, Diedrichsen J, Ivry RB. Disrupted timing of discontinuous but not continuous movements by cerebellar lesions. Science. 2003;300:1437–1439. doi: 10.1126/science.1083661. [DOI] [PubMed] [Google Scholar]
- Spencer RMC, Verstynen T, Brett M, Ivry R. Cerebellar action during discrete and not continuous timed movements: an fMRI study. Neuroimage. 2007;36:378–387. doi: 10.1016/j.neuroimage.2007.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sternad D, Dean WJ, Schaal S. Interaction of rhythmic and discrete pattern generators in single-joint movements. Hum Mov Sci. 2000;19:627–664. [Google Scholar]
- Tong C, Flanagan JR. Task-specific internal models for kinematic transformation. J Neurophysiol. 2003;90:578–585. doi: 10.1152/jn.01087.2002. [DOI] [PubMed] [Google Scholar]
- Ung RV, Imbeault MA, Ethier C, Brizzi L, Capaday C. On the potential role of the corticospinal tract in the control and progressive adaptation of the soleus H-reflex during backward walking. J Neurophysiol. 2005;94:1133–1142. doi: 10.1152/jn.00181.2005. [DOI] [PubMed] [Google Scholar]
- van Mourik AM, Beek PJ. Discrete and cyclical movements: unified dynamics or separate control? Acta Psychol (Amst) 2004;117:121–138. doi: 10.1016/j.actpsy.2004.06.001. [DOI] [PubMed] [Google Scholar]
- Winter DA. Biomechnics and motor control of human movement. Ed 3. Hoboken, NJ: Wiley; 2004. [Google Scholar]
- Wolpaw JR, Tennissen AM. Activity-dependent spinal cord plasticity in health and disease. Annu Rev Neurosci. 2001;24:807–843. doi: 10.1146/annurev.neuro.24.1.807. [DOI] [PubMed] [Google Scholar]