Oscillatory Dipoles As a Source of Phase Shifts in Field Potentials in the Mammalian Auditory Brainstem

Abstract

A popular model of binaural processing, proposed by Jeffress (1948), states that external interaural time delays (ITDs) are compensated by internal axonal delays allowing ITD to be spatially represented by a population of coincidence detectors in the medial superior olive (MSO). Isolating single-neuron responses in MSO is difficult because of the presence of a strong extracellular field potential known as the neurophonic, so that few studies have tested Jeffress's key prediction. Phase delays in the nucleus laminaris neurophonic in owls have been observed and are consistent with a Jeffress-like model. Here, we recorded neurophonic responses in cat MSO to monaural tones at locations along its dendritic axis. Fourier analysis of the neurophonic was used to extract amplitude and phase at the stimulus frequency. Amplitude, as a function of depth, showed two peaks separated by a dip. A half-cycle phase shift was observed at depths close to the dip, over a wide frequency range. Current source density analysis for contralateral (ipsilateral) stimulation shows a current source close to the neurophonic amplitude peak and a sink a few hundred micrometers ventromedially (dorsolaterally). These results are consistent with a dipole configuration: contralateral (ipsilateral) excitation causes a current sink at the ventromedial (dorsolateral) dendrites and a source at the soma and dorsolateral (ventromedial) dendrites. Incorporating these results in a dipole model explains the phase and amplitude patterns observed. We conclude that the half-cycle phase shift is consistent with a current dipole, making it difficult to derive measurements of axonal delays from the neurophonic.

Introduction

In 1948, Jeffress proposed a model for binaural processing (Jeffress, 1948) involving axonal delay lines and coincidence detection. He proposed that interaural time delays (ITDs) are compensated by axonal delay lines, allowing sound signals to arrive coincidentally at the first site of binaural interaction: the medial superior olive (MSO). MSO neurons would function as coincidence detectors and only fire when receiving input from both ears coincidently. By virtue of an orderly arrangement of delay lines, the ITD at which maximum coincidence occurs (best delay) varies systematically along the long axis of the MSO. Thus, a core prediction of Jeffress is a map of best delays in the MSO.

Goldberg and Brown (1969) showed that MSO neurons are sensitive to changes in ITD, that they have a best delay, and that ITD sensitivity can be understood as a coincidence detection process, confirming one prediction of Jeffress. Separate studies in different mammals (Yin and Chan, 1990; Spitzer and Semple, 1995) confirmed this. However, Jeffress's prediction of a map of delay remains mostly untested (Joris and Yin, 2007). By pooling data across animals, Yin and Chan (1990) showed a significant correlation between the rostrocaudal position of a MSO neuron and its best delay. Consistent with this relationship and the proposed delay lines, tracing studies (Smith et al., 1993; Beckius et al., 1999) showed that spherical bushy cell axons innervate the MSO with ladder-like branching patterns.

Jeffress's predictions are difficult to test because MSO extracellular single-unit recording is challenging. MSO action potentials are small (Scott et al., 2005, 2007) and are masked by an extracellular field potential known as the neurophonic. Neurophonics are AC signals that represent the phase coherent phase-locked activity of a population of neurons. They are found at different locations in the brainstem (Galambos et al., 1959; Boudreau, 1965; Marsh et al., 1970; Snyder and Schreiner, 1984). In the MSO, neurons are arranged tonotopically (Guinan et al., 1972b) with their dendrites stacked in parallel (Stotler, 1953; Schwartz, 1977; Smith, 1995). This arrangement facilitates an “open field” (Lorente De Nó, 1947; Biedenbach and Freeman, 1964), which allows postsynaptic potentials to summate, creating the neurophonic. Thus, the neurophonic contains information on MSO processing and possibly on the proposed map of delay. Studies in the barn owl (Sullivan and Konishi, 1986; Wagner et al., 2005) and chicken (Schwarz, 1992a,b; Köppl and Carr, 2008) measured delays in the nucleus laminaris (avian homolog of the MSO) neurophonic and concluded that there are axonal delay lines and a map of ITD. A study measuring delays in cat neurophonic (Bojanowski et al., 1989) also concluded that there were Jeffress-like delay lines.

Here, we examine the neurophonic along the short dimension of the MSO of cats and find phase shifts similar to those reported in the barn owl, chicken, and cat. However, we find that these shifts are consistent with a dipole phase shift rather than with a time shift caused by delay lines.

Materials and Methods

Surgical preparation.

Adult cats were anesthetized with a mixture of acepromazine (0.2 mg/kg) and ketamine (20 mg/kg). A venous cannula allowed infusion of Ringer's solution and sodium pentobarbital at doses sufficient to maintain an areflexic state. A laryngopharyngectomy was performed, and a tracheal tube was inserted. The basioccipital bone was exposed after resection of the prevertebral muscles. The pinnas were removed, and the bullas were exposed and vented with polyethylene tubing. The animal was placed in a double-walled soundproof room (Industrial Acoustics Company). The trapezoid body (TB) was exposed by drilling a longitudinal slit as close as possible to the medial wall of the bulla. A micromanipulator was used to support a five-channel microdrive with quartz/platinum–tungsten electrodes (TREC; 2–4 MΩ). The electrodes were guided with tubes aligned in one plane and separated by 1 mm. The microdrive also contained built-in broadband preamplifiers (0.04 Hz to 20 kHz, 26 dB gain). The electrodes were positioned in the TB under visual control, just lateral or medial to the rootlets of the abducens nerve. The angle of penetration ranged from 15 to 30° mediolaterally relative to the midsagittal plane. The aim was to penetrate the low-frequency region of the MSO along its dendritic (short) axis (see Fig. 4). Most often, the electrode array was aligned such that the array was parallel to the long rostrocaudal axis of the MSO (i.e., so that electrode 1 would penetrate the MSO at its rostral pole and electrode 5 at its caudal pole). Our motivation for using a linear array of electrodes is to examine whether rostrocaudal changes (i.e., changes across electrodes) are observed that are indicative of the delay lines proposed by Jeffress (1948) (see Introduction). However, in the present study, we restrict ourselves to an analysis of changes in neurophonic along individual electrode tracks. After placing the electrodes in the TB, the basioccipital bone was covered with warm 2% agar.

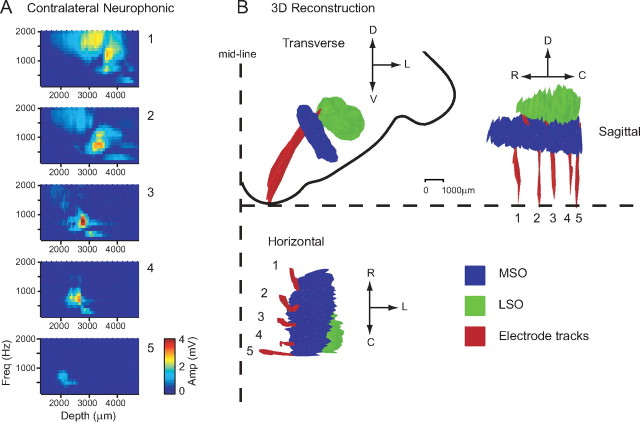
Figure 4.

Histological reconstruction of electrode tracks penetrating the MSO. A, The amplitude of the neurophonic to contralateral stimulation is shown as a function of frequency and depth for each electrode. The amplitude color code is indicated by the calibration bar. B, The electrodes were coated with fluorescent dye allowing tracing and reconstruction of the electrode tracks (red). The outlines of MSO and LSO are shown in blue and green. D, Dorsal; V, ventral; L, lateral; R, rostral; C, caudal.

Stimulus generation and signal sampling.

Dynamic speakers (Super Tweeter; Radio Shack) were connected to a hollow Teflon earpiece that fit in the transversely cut ear canals. Custom software, run on a personal computer, was used to calculate the stimuli and control the digital hardware (PD1 system 2; Tucker-Davis Technologies). The neural signal was amplified (100×), filtered (10–10,000 Hz) (EX1 and EX4–400; Dagan), and sampled (RX8 system 3; Tucker-Davis Technologies; 50 kHz sampling frequency per channel).

Stimuli and data collection.

Monaural tone bursts (100–2500 Hz, 50 or 100 Hz steps, 2000 ms duration, one repetition, 2500 ms repetition interval, 50–70 dB) were played to the contralateral ear and then repeated with a 10 Hz difference (110–2510 Hz) to the ipsilateral ear. Within an experiment, the stimulus level was fixed at 70 dB sound pressure level (SPL) (with the exception of one penetration where 55 dB SPL was used). These same stimuli were also played binaurally (containing a 10 Hz beat). The 10 Hz difference was included in the monaural stimuli to allow a direct comparison between monaural and binaural responses. However, neither the binaural responses nor their comparison with the monaural responses are considered in this paper. The electrodes were advanced through the MSO, along its dendritic axis (see Figs. 4, 5), and a coarse sampling of the neurophonic was performed. The electrodes were judged to be correctly angled if a strong neurophonic response was obtained to both ipsilateral and contralateral stimulation on at least three electrodes. Otherwise, the electrodes were retracted and repositioned. Once the electrodes were in the correct position, the response was measured to monaural ipsilateral and contralateral stimulation at intervals of 50 or 100 μm steps, either while advancing or retracting the electrodes. Zero penetration depth was set when the electrodes touched the brainstem, just before the first penetration. Swelling of the brainstem often occurred after some time, so that in some cases the electrodes had to be retracted to “negative” depths to reach the brainstem surface on withdrawal (see Fig. 1). We normally recorded first from the right MSO and, if time allowed, then moved to the left MSO, using the same stimuli and recording procedures.

Figure 5.

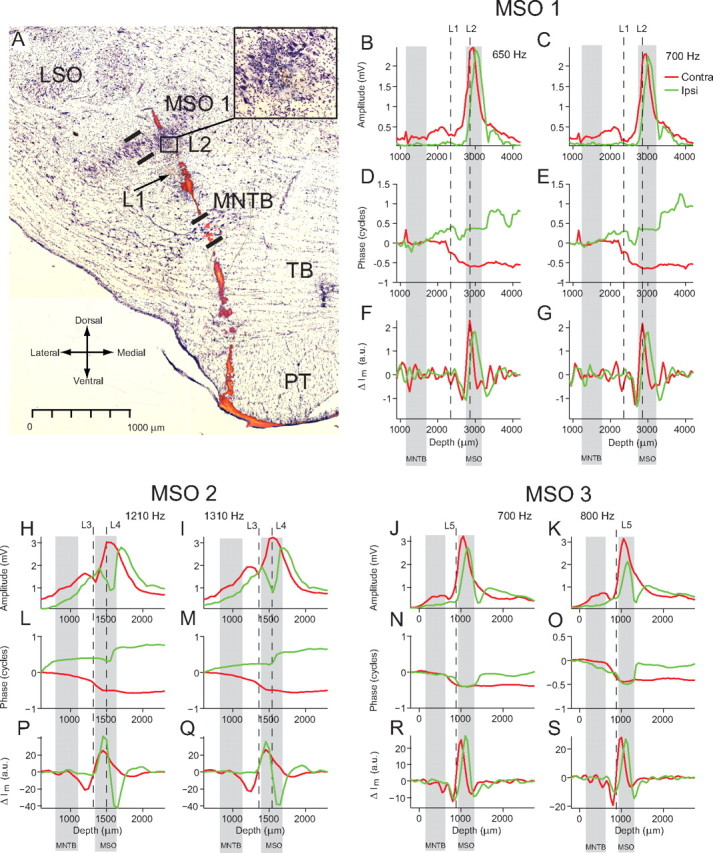
Composite photograph of stained section and electrode track marked by electrolytic lesions and fluorescent dye. A, cresyl violet staining revealing the principal nuclei and two lesions (L1, L2). Superimposed is the fluorescent dye (DiI) of the electrode track, extracted from images taken with a fluorescence microscope from a number of sections before staining. MSO, Medial superior olive—thick lines indicate borders of nucleus; MNTB, medial nucleus of the trapezoid body—thick lines indicate borders of nucleus; LSO, lateral superior olive; TB, trapezoid body; PT, pyramidal tract. B–G show data from the electrode track in A. Red, Contralateral data; green, ipsilateral data. The positions of L1 and L2 are marked by the vertical dashed lines. The extent of the MNTB and MSO, determined from the section, are marked by the gray bands. B, C, Amplitude depth profiles for contralateral and ipsilateral stimulation at 650 and 700 Hz. D, E, Corresponding phase depth profiles. F, G, Current sink and source locations are revealed as minima and maxima in the change in transmembrane current (ΔI_m). H–S, The analysis shown in B–G is repeated for lesions and neurophonic recordings made in the MSO of two additional cats.

Figure 1.

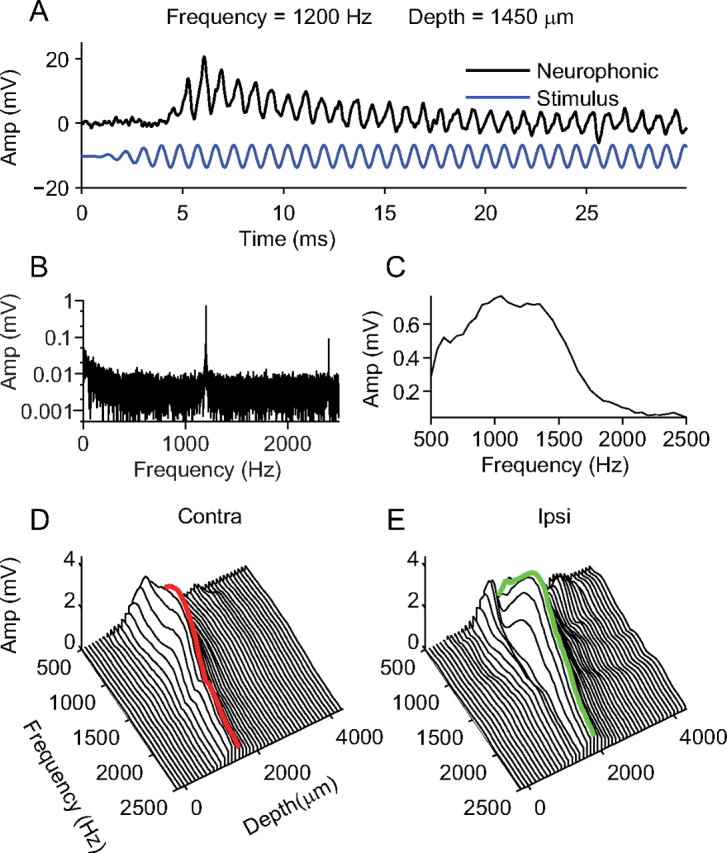
Measurement and Fourier analysis of the neurophonic. A, A 1200 Hz tone played to the contralateral ear (blue line) and the resulting neurophonic response (black line) at a penetration depth of 1450 μm. B, The amplitude spectrum of the neurophonic response shown in A. There is a strong component at the stimulus frequency (1200 Hz) and a weaker harmonic component (2400 Hz). C, The Fourier amplitude at the stimulus frequency is plotted as a function of stimulus frequency for contralateral stimulation at 1450 μm. There is broad frequency tuning in the neurophonic response. D, The analysis shown in C is repeated for a range of penetration depths for contralateral stimulation, showing clear tuning with depth. The red line indicates the depth at which the maximum amplitude was measured. E, The analysis shown in D is repeated for ipsilateral stimulation. The green line indicates the depth at which the maximum amplitude was measured.

Histology and three-dimensional reconstruction.

To allow for visualization of the electrode tracks after the experiment, the electrodes were coated with a fluorescent dye, 1,1′-dioctadecyl-3,3,3′,3′-tetramethyl-indocarbocyanine perchlorate (DiI) (Invitrogen) (DiCarlo et al., 1996), for some penetrations. After the experiment, the cats were killed with an overdose of sodium pentobarbital and perfused transcardially with 10% formalin solution. After cryoprotection in a 30% sucrose solution, the brainstem was frozen using dry ice and sectioned (50 μm) transversely using a sliding microtome (HM430; Microm).

A three-dimensional reconstruction of the electrode tracks and the MSO was made using a Neurolucida (MicroBrightField) tracing system connected to a microscope (BX61; Olympus). Before staining, we visualized and photographed the electrode tracks using fluorescence microscopy and traced their outlines together with the complete outline of the brainstem. The sections were then stained using conventional cresyl violet staining, which removed the DiI, but allowed for visualization of the MSO. The outline of the MSO and the lateral superior olive (LSO) were then added to the tracing of each section and a three-dimensional representation of the electrodes in the superior olivary complex was rendered using the Neurolucida software.

In addition to coating the electrodes with fluorescent dye, lesions were also made at penetration depths of interest, for example at a depth location where there was a peak or a dip in the neurophonic amplitude. To make the lesion, 10 μA of negative current was passed through the electrode for between 10 and 20 s. After staining with cresyl violet, the sites of the lesions were visible and could be added to the reconstruction.

Results

Data presented here were collected from 14 MSOs in nine cats. In this paper, we focus on the changes in neurophonic obtained when traversing the short, mediolateral axis of the MSO. The results are presented in five separate sections as follows: (1) We report the results of a Fourier analysis of the neurophonic response to contralateral and ipsilateral stimulation. (2) The histology and reconstruction are presented and linked to the results of the Fourier analysis. (3) Based on the known MSO architecture and our results, we explain why the neurophonic can be interpreted in terms of a dipole field. (4) A current source density (CSD) analysis of the neurophonic reveals the location of the current sinks and sources generating the neurophonic. (5) A modeling study confirms that the neurophonic can be interpreted in terms of a dipole field.

Fourier analysis: neurophonic phase and amplitude

Figure 1A shows a typical neurophonic response (black line) to a contralateral tone (blue line) of 1200 Hz at 70 dB SPL. The neurophonic response begins after a short delay (<5 ms). Two components are visible. An alternating component locked to the stimulus frequency is sustained throughout the duration of the stimulus: this frequency-following component is the subject of the present paper. A slowly decaying onset response is superimposed on the frequency-following response. The high-pass filtering (10 Hz) in our recording setup precludes full characterization of this component. A discrete Fourier transform (fft; Matlab; The MathWorks) was performed on the complete neurophonic response. The resulting amplitude spectrum is shown is Figure 1B. A strong component is clearly visible at the stimulus frequency (1200 Hz) and a smaller harmonic component is also visible at 2400 Hz. At this depth (1450 μm), for contralateral stimulation, the neurophonic response to a range of stimulus frequencies was collected. An amplitude spectrum was calculated for each response and the amplitude of the component at the stimulus frequency is plotted in Figure 1C. The neurophonic shows tuning to a broad range of frequencies between 500 and 1800 Hz with a peak at 1050 Hz. In this penetration, the neurophonic response to contralateral stimulation was collected at depth intervals of 50 μm between penetration depths of −200 and 4350 μm. Figure 1D shows the same analysis as in Figure 1C but repeated at different penetration depths (for clarity of illustration, only data at depth intervals of 100 μm are shown). The neurophonic response to ipsilateral stimulation was also collected at depth intervals of 50 μm, and these data are shown in Figure 1E (again only at intervals of 100 μm). Figure 1, D and E, shows that for both contralateral and ipsilateral stimulation the neurophonic response is tuned in both frequency and depth. Both the ipsilateral and contralateral neurophonic responses are tuned quite broadly in frequency and show the strongest responses for frequencies between 1000 and 1500 Hz. One key difference between the contralateral and ipsilateral responses is the tuning in depth. As reported previously (Tsuchitani and Boudreau, 1964; Guinan et al., 1972b), the response to contralateral stimulation consistently peaks at a shallower depth than that of ipsilateral stimulation. In the example shown here, the contralateral response peaks at 1450 μm (Fig. 1D, red line), whereas the response to ipsilateral stimulation peaks at 1800 μm (Fig. 1E, green line).

To reveal features in the response profiles not immediately obvious from Figure 1, D and E, the data can be displayed as a function of depth for individual stimulus frequencies. Data collected from a different cat are shown in such a representation in Figure 2A for a restricted range of frequencies (1400–1600 Hz; light to dark shades of red) for contralateral stimulation. The amplitude responses for this range of frequencies all show a similar pattern. There is clear tuning in depth with two peaks in amplitude (750 and 1250 μm) separated by a dip in amplitude. The amplitude responses for ipsilateral stimulation to the same range of frequencies (1400–1600 Hz; light to dark shades of green) are shown in Figure 2B. Here, we observe the same amplitude pattern of two peaks (850 and 1300 μm) separated by a dip in amplitude. Again, there is clear tuning in depth, and, as with the data in Figure 1, the ipsilateral response amplitudes are tuned to slightly deeper depths.

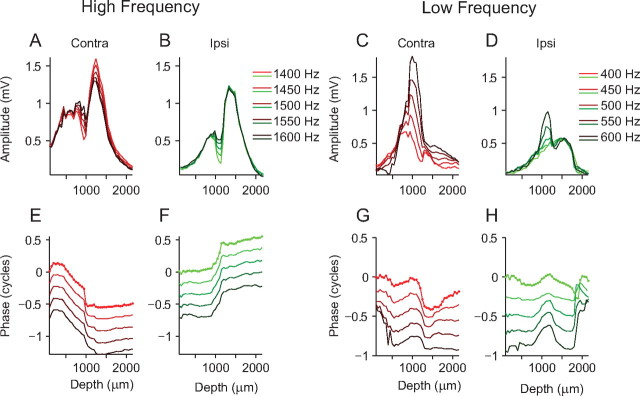
Figure 2.

Amplitude dips and phase shifts in the neurophonic. A, B, The analysis as shown in Figure 1D is replotted for a different dataset for contralateral (A) and ipsilateral (B) amplitude over a range of frequencies (1400–1600 Hz, indicated by different shades of red and green). C, D, Same electrode penetration as A and B but for a lower range of stimulus frequencies (400–600 Hz). E, F, Phase measurements, derived from Fourier analysis of the neurophonic at each depth, for contralateral (E) and ipsilateral (F) stimulation. The dots on the upper line mark individual measurement depths (50 μm intervals). Zero phase was taken as the phase of the lowest stimulus frequency at the first depth measurement. G, H, Same as E and F but for a lower range of frequencies.

We are interested in delays of the neurophonic and so also analyzed the phase spectrum obtained from the Fourier analysis. As with the amplitude analysis, the phase of the component at the stimulus frequency was extracted. In Figure 2E, one line plots this phase measurement, for one stimulus frequency, as a function of depth. The dots on the upper line represent individual phase measurements spaced 50 μm apart. Phase measurements extracted using Fourier analysis are restricted to one stimulus cycle (2π). However, the neurophonic may have delays that are >2π. Delays >2π can be extracted by “unwrapping” phase (i.e., by changing phase jumps between two consecutive penetration depths of greater than or equal to π to their 2π complement). We used a two-step unwrapping procedure to unwrap all phase components. Zero phase was taken as the phase of the lowest stimulus frequency at the first depth measurement for all phases shown in one figure panel. The phases for different frequencies at this depth were then unwrapped (step 1) (unwrap; Matlab; The MathWorks) (i.e., jumps greater than or equal to π are changed to their 2π complement). This determined the starting phase for each stimulus frequency. Using these starting phase measurements, the phase measurements for each stimulus frequency were then unwrapped (step 2) along the depth dimension. For each stimulus frequency, there is a phase shift of around one-half a cycle that occurs between the two peaks in the amplitude response (Fig. 2E). Before and after this half-cycle shift, phase changes with a shallower slope or remains relatively constant. Figure 2F shows the same analysis but now for ipsilateral stimulation. Here, there is also a half-cycle phase shift at all frequencies but in the opposite direction. Again, this occurs between the two peaks in the amplitude response.

Figure 2, C, D, G, and H, shows the same analysis of neurophonic responses recorded on the same electrode penetration as Figure 2, A, B, E, and F, but for a lower range of frequencies (400–600 Hz). For both contralateral and ipsilateral stimulation, the amplitude maxima occur at more superficial depths than for stimulation at higher frequencies. The pattern of the double peaks separated by a dip is less apparent but is still present for some frequencies (Fig. 2C,D). Steep phase shifts are still apparent near these dips, but the general patterns are more complex than at higher frequencies.

The example shown in Figure 2 is typical for most penetrations (including the one penetration collected at 55 dB SPL). At higher frequencies (>1000 Hz), we generally observed a clear half-cycle shift in the phase profile and two peaks in the amplitude profile separated by a dip. For stimulation at lower frequencies, the half-cycle phase shift is still present but is often embedded in a more complex phase profile and the dip in the amplitude profile is often less prominent.

Figure 3 shows data collected on all five electrodes during one penetration for a wide range of frequencies (1000–2000 Hz, in 50 Hz steps). Figure 3A–E shows the contralateral (red) and ipsilateral (green) amplitude profiles for each electrode (1–5). Electrode 1 is the most rostral, and 5, the most caudal. The amplitude of the neurophonic on electrode 5 was very small compared with the other electrodes, and the histology confirmed that electrode 5 passed along the caudal border of the MSO (see below, Histology and reconstruction) (note that Fig. 3 is not the same recording as shown Fig. 4). The amplitude pattern of two peaks separated by a dip is present on all electrodes for both contralateral and ipsilateral stimulation, except on electrode 4 to contralateral stimulation. Figure 3F–J shows the unwrapped phase profiles calculated in the same way as those shown in Figure 2E–H. Displaying phase profiles in this way shows that, for all frequencies, there is a clear and consistent half-cycle phase shift for contralateral stimulation on electrodes 1–4. A clear half-cycle shift in the opposite direction is also visible for ipsilateral stimulation, but there is more variation in the pattern across electrodes. To facilitate a more straightforward comparison across different electrodes and frequencies, the phase difference was calculated by subtracting the ipsilateral from the contralateral phase (Fig. 3K–O). Each blue line shows the interaural phase at one stimulus frequency on one electrode. Plotting the phase in this way reveals a very consistent shift of one full cycle (i.e., one contralateral half-cycle shift and one ipsilateral half-cycle shift in the opposite direction) at all stimulus frequencies on all electrodes that pass through the MSO. These phase patterns are strikingly similar to the one reported in nucleus laminaris of the barn owl (Sullivan and Konishi, 1986), where they were interpreted to reflect pure time delays caused by axonal delay lines. However, we do not think that the large half-cycle delay in the monaural neurophonic in the cat is caused by a delay line. A delay line as postulated by Jeffress would cause a constant time delay in the neurophonic. This would result in a smaller phase delay at low frequencies than at high frequencies, but that is not what we observe. For example, a constant time delay causing a half-cycle phase shift at 1000 Hz would cause a full-cycle phase shift at 2000 Hz. This is clearly not the pattern of phase shifts we observe. The interaural phase change in Figure 3K–N is a full cycle regardless of the stimulus frequency (i.e., a constant phase delay and not a constant time delay). This suggests that the half-cycle phase shift is caused by a dipole configuration as described below (see Interpreting the neurophonic in terms of a dipole) and is not related to a delay line mechanism.

Figure 3.

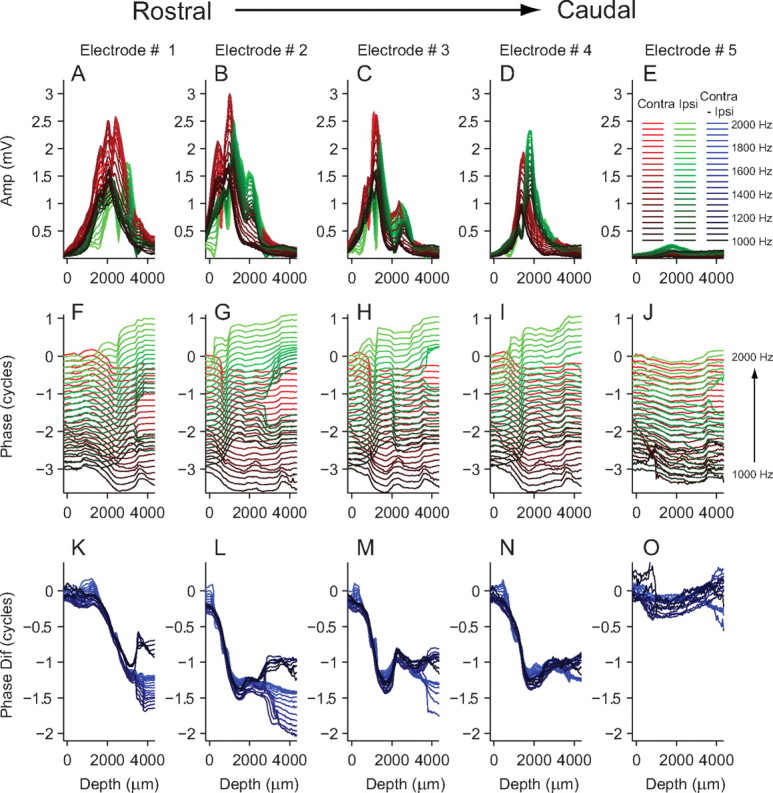
Neurophonic amplitude and phase across five electrodes in one MSO. A–E, Neurophonic amplitude as a function of depth for ipsilateral (green) and contralateral (red) stimulation for a range of frequencies (1100–1500 Hz). F–J, Corresponding phase values. In each panel, zero phase for both ipsilateral and contralateral stimulation was taken as the phase of the lowest stimulus frequency at the first depth measurement. K–O, Difference in phase calculated by subtracting ipsilateral phase from contralateral phase.

Histology and reconstruction

To confirm that the electrodes passed through the MSO and to allow us to link the results of the neurophonic analysis to a specific location in the brainstem, histology was carried out on five animals (eight MSOs). Using the procedure described in Materials and Methods, reconstructions of all eight MSOs together with the LSOs and electrode tracks were made. Figure 4B shows the results of one such reconstruction. The transverse view shows the electrodes (red) clearly passing through the dorsomedial region of the MSO (blue) and entering the LSO (green). Guinan et al. (1972b) have shown that this region of the MSO is tuned to low frequencies. On the horizontal view, all five electrode tracks are visible, and it is again clear that they penetrate the medial, low-frequency region of the MSO. The sagittal and horizontal views show that electrodes 1–5 cover most of the rostral-caudal extent of the MSO, with electrode 5 passing just within the caudal border of the MSO. For each of the electrodes, Figure 4A shows the amplitude of the neurophonic response for contralateral stimulation. The same Fourier analysis described previously is used but here the amplitude of the component at the stimulus frequency is shown as a color (dark red, 4 mV; dark blue, 0 mV), with the stimulus frequency on the y-axis and the penetration depth shown on the x-axis. Electrodes 2–5 are all tuned to ∼700 Hz and show narrow frequency tuning, whereas electrode 1 shows a response to a broader and higher range of frequencies. Electrode 5, passing the caudal border of the MSO, shows the weakest response. The MSO is further from the ventral surface of the brainstem at its rostral edge than at its caudal edge. This explains why the peak in amplitude occurs at deeper depths on electrode 1 (most rostral) than on electrode 5 (most caudal).

Figure 5A is a photograph of a section stained with cresyl violet where the left MSO is visible as a denser region of neurons running from dorsomedial to ventrolateral. The electrode was coated with DiI and left a clearly visible track on the unstained sections. Before staining, the track was visualized and photographed using a fluorescence microscope. The electrode track marked by DiI (Fig. 5A, colored red and orange) was then superimposed on a photograph of the stained section. The sectioning plane was oblique to the plane of the electrode track so that the DiI track was visible across a number of sections. Thus, Figure 5A shows DiI tracks photographed from a number of different sections superimposed on one cresyl violet-stained section. Lesions were made in this penetration at depths of 2350 and 2850 μm, marked as L1 and L2, respectively. L2 is just on the ventral edge of the MSO and L1 is ∼500 μm ventromedially. Figure 5, B and C, shows the amplitude profiles for ipsilateral (green) and contralateral (red) stimulation at frequencies of 650 and 700 Hz (two frequencies that caused the strongest responses). The location of the lesions (vertical dashed lines) shows that the peak of both the contralateral and ipsilateral neurophonic occurs close to the center of the MSO. The borders of the MSO and medial nucleus of the trapezoid body (MNTB) are marked by thick lines on Figure 5A and are shown as gray bands across Figure 5B–G. For contralateral stimulation, the half-cycle phase shift begins ∼500 μm ventromedially from the center of the MSO and stops at the center of the MSO (Fig. 5D,E). The phase profiles for ipsilateral stimulation show a more complex pattern. However, one clear phase shift of approximately one-half a cycle occurs ∼500 μm dorsolaterally to the center of the MSO. Figure 5, F and G, shows the current source density analysis, which is explained in the following section.

The results for the same histological analysis for two different MSOs are shown in Figure 5H–S. Again, most of the large phase shifts take place within or near to the boundaries of the MSO as do the peaks in the amplitude of the neurophonic. A total of 29 lesion sites was identified on 19 electrode penetrations in seven different MSOs (four cats), and all are consistent with the examples shown here.

In general, we found that the frequency at which the maximal neurophonic response occurred was dependent on the penetration angle, such that steeper penetration angles (electrode tip more medially positioned) resulted in lower frequency neurophonic recordings than shallower penetration angles (electrode tip positioned more laterally), which resulted in higher frequency neurophonic responses. This is in agreement with the MSO tonotopic map shown in Guinan et al. (1972b). The histological results also support this finding; more medial penetrations of the MSO had stronger low-frequency responses than penetrations of the more lateral penetrations, which showed stronger high-frequency responses. These observations support the assumption that the neurophonic reflects the activity of a local population of neurons.

Interpreting the neurophonic in terms of a dipole

The concept of a dipole is important in neuroscience and is particularly useful when interpreting electric fields generated in the brain. An electric (charge) dipole can be defined as a pair of equal but opposite charges separated by a small distance. The results of the histological reconstructions combined with the amplitude dips and phase shifts found in the Fourier analysis and our general knowledge of the configuration of inputs to the MSO suggested to us that the neurophonic is generated by a dipole configuration. Figure 6A schematically shows the excitatory and inhibitory inputs to an MSO neuron. For monaural contralateral stimulation, an MSO neuron receives excitatory input on the ventromedial dendrite and inhibitory input on the soma. Considering just the excitatory input, current flows into the neuron on the dendrite creating a current sink (i.e., a flow of positive charge from extracellular space into intracellular space through a specific location on the cell membrane). If current flows into the cell at one location, it must flow out at another, creating a current source located more dorsolaterally near the soma or opposite dendrite (i.e., a flow of positive charge out of the neuron from intracellular space into extracellular space). A current sink and source pair constitute a current dipole (for the distinction between a current and a charge dipole, see below, Modeling study) and will generate a dipole field (Fig. 6C). Figure 6, D and E, shows the amplitude and phase of the potential generated by a current dipole, measured along the dashed line in Figure 6C. Near the current sink a peak in the absolute amplitude of the potential will be measured, followed by a dip to zero as the zero potential line is crossed and a second peak in amplitude near the current source. The phase of the potential will show a sharp phase shift of exactly one-half a cycle when the zero equipotential line is crossed. These phase shifts and amplitude dips are similar to those measured in the neurophonic.

Figure 6.

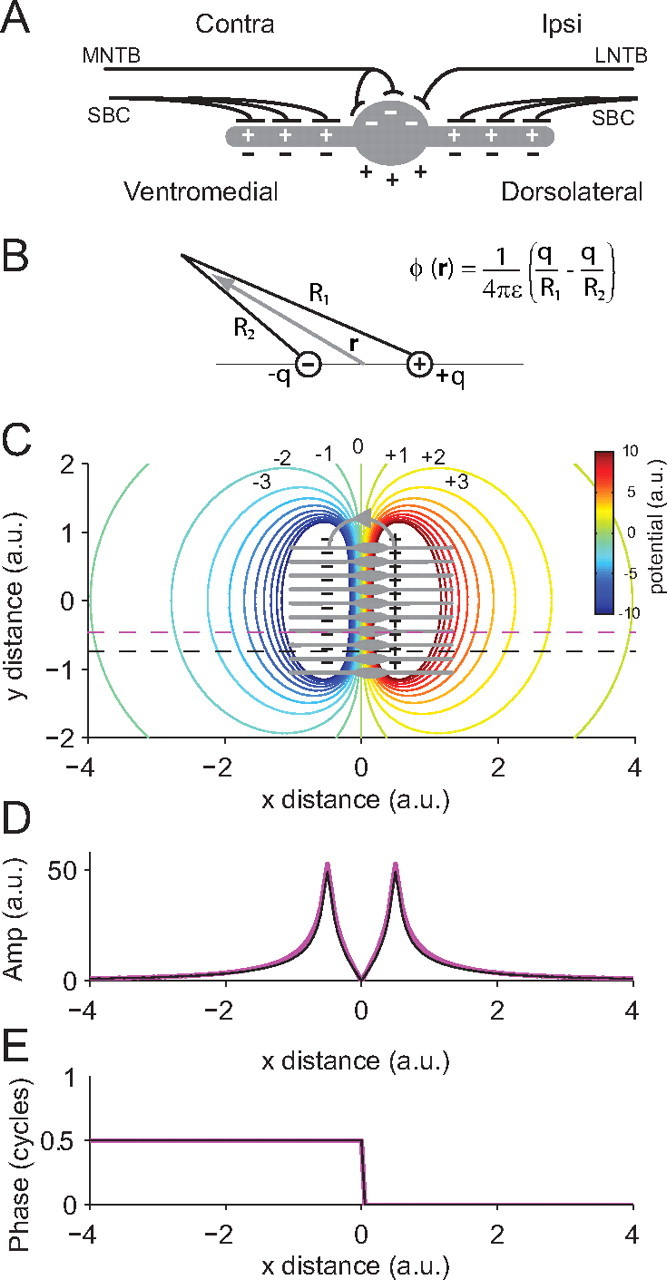
Interpreting the neurophonic in terms of a dipole field. A, The gray object represents an MSO neuron with excitatory inputs from contralateral spherical bushy cells (SBC) on the medial dendrite and excitatory inputs from ipsilateral SBC on the lateral dendrite. Inhibitory input from the contralateral MNTB and the ipsilateral LNTB is present on the soma. The pluses and minuses show the direction of change in intracellular (white) and extracellular (black) potential when an EPSP (SBC input) or IPSP (MNTB or LNTB input) is elicited. B, The charge dipole equation (Eq. 4) can be used to calculate the potential (ϕ) at any given location attributable to a dipole with equal and opposite charges (q) at each pole. ε is the permittivity. C, The gray objects represent a two-dimensional stack of MSO neurons. Contralateral stimulation on the excitatory input on the medial dendrite causes a localized current sink and a corresponding current source near the soma. The current source and sink result in a dipole field. Note that the inhibitory input would also contribute to this source–sink configuration. Here, we used a two-dimensional stack for ease of illustration, but in practice we assume that this pattern will be repeated in the z direction creating a three-dimensional block of orderly arranged MSO neurons. These current dipoles are represented as the black pluses and minuses and the direction of extracellular current flow is marked by the gray line with the arrow. The colored contours show the resulting dipole field (i.e., the equipotential lines calculated by modeling each current dipole using Eq. 5 and summing their individual contributions). D, The amplitude of the potential of the dipole field at the locations marked by the purple and black dashed lines in C are both shown. Note that potential amplitude distributions are almost identical even though their y positions are different. This simulation gives weight to the assumption that the potential is relatively stable in the y and z directions, as we also assume that this stacked arrangement of MSO neurons will be repeated in the z direction. Thus, a reasonable estimation of the transmembrane current can be calculated by simply taking the second derivative in the x direction (see Eqs. 2, 3). E, Phase of the dipole field at the two locations marked by the dashed lines in B. As with the amplitude distributions, the phase is identical at both y locations.

Current source density analysis

Pinpointing the location of current sinks and sources is useful in helping to understand the origin of electric fields, such as the neurophonic, within the brain. However, typical extracellular recordings measure the alternating potential rather than current of these electric fields. To test the conjecture that the neurophonic is generated by a dipole configuration, we performed a CSD analysis. CSD analysis can be used to gain temporal and spatial information about the location of current sources and sinks in the brain and can give significantly better temporal and spatial resolution of neural events than conventional analysis of the measured field potentials (Freeman and Nicholson, 1975; Nicholson and Freeman, 1975; Manis and Brownell, 1983). We postulated that, if the neurophonic is generated by a dipole in MSO neurons, CSD analysis should reveal a current sink located on the dendrites and a current source somewhere near the somata, and that this configuration should be mirror symmetric for ipsilateral and contralateral stimulation. Because our recordings do not provide information on DC, our analysis and its conclusions are necessarily tentative but they are nonetheless consistent with the dipole hypothesis.

If the region of interest contains a high degree of symmetry, as the MSO and its dendrites do, the transmembrane current attributable to one neuronal element (i_m) can be related to the CSD (I_m) using the following simple expression:

where v is the density per unit area of the neuronal elements passing through a given plane. A formal derivation of this expression is shown in the study by Nicholson and Freeman (1975), their Equation 7 and Appendix I. The main assumption that allows us to apply Equation 1 is that the neuronal elements are oriented in an orderly fashion along the same direction, an assumption that is valid in the MSO.

It can be shown that the CSD is related to the second spatial derivative of the extracellular field potential (Nicholson and Freeman, 1975) (expressed here in rectangular Cartesian coordinates) as follows:

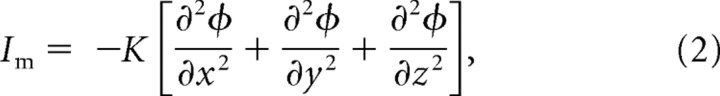where ϕ is the field potential, and K is the conductivity constant. To calculate the location of current sinks and sources using Equation 2, the potential must be sampled along all three principal axes. However, in the MSO, the largest changes in potential will take place along the dendritic axis, which we refer to as the x direction. Neighboring MSO neurons, which are aligned in an orderly arrangement (in both the y and z directions), will show similar changes in potential along the dendritic axis. Thus, changes in potential in a direction perpendicular to the dendritic axis (i.e., along the y or z axes) will be limited (Fig. 6). Thus, assuming that potential only changes along one dimension (along the MSO dendritic axis) and that the conductivity is constant, the CSD can be calculated by simply taking the second spatial derivative along that direction as follows:

This makes the calculation of I_m relatively simple because the electrode penetration direction is also along the dendritic axis. If we assume that v in Equation 1 (i.e., the density of neuronal elements) remains constant throughout the MSO, then the CSD will be linearly related to the transmembrane current. Thus, an estimation of the transmembrane current can be obtained by taking the second spatial derivative of the measured potential (i.e., the neurophonic).

Taking the derivative of a signal decreases its signal-to-noise ratio. Because we used a periodic stimulus, we can improve the signal-to-noise ratio by simple averaging modulo 2π: we divided the waveform into segments of one cycle in length and took the average of these segments. Figure 7A shows the averaged neurophonic signal for contralateral stimulation at 1000 Hz for a range of penetration depths (−100 to 1750 μm). For each depth, there is an averaged neurophonic with a length equal to one cycle of the stimulus frequency: 25 samples/cycle in the example shown in Figure 7A, indicated by the dots at the most superficial depth. The half-cycle phase change with depth, discussed in Figures 2 and 3, is also apparent in Figure 7A: the trough at 0 μm near 0.8 cycles becomes a peak at depths >600 μm. Figure 7C shows exactly the same data as Figure 7A, the averaged contralateral neurophonic, but now replotted as a function of depth. Each gray line in Figure 7C represents one point in the stimulus cycle. The points in the cycle indicated by the two vertical red lines on Figure 7A are shown by the red lines on Figure 7C. Taking the second spatial derivative along the depth dimension of one red line in Figure 7C gives an estimate of the mean instantaneous transmembrane current, I_m, at that specific point in the cycle (Fig. 7D, one red line). This calculation is repeated for every point in the cycle giving I_m as a function of depth for all points in the cycle (Fig. 7D, all gray lines). The red lines (same point in the cycle as red lines in Fig. 7A,C) show the depth profile yielding the maximal I_m (I_mMax) and its counterpart separated by one-half a cycle (I_mMax+π). Subtraction of these two profiles captures the magnitude of changes in I_m during one cycle (ΔI_m), shown by the thick black line in Figure 7D. A current sink–source pair is visible: when the current is maximally negative at 450 μm, the current is maximal positive at 650 μm and one-half a cycle later this pattern is reversed. For each depth, calculated current, I_m, can now be replotted as a function of one stimulus cycle (Fig. 7G). Thus, Figure 7A shows how the voltage changes during one stimulus cycle at each depth, and Figure 7G shows how the current changes during the same stimulus cycle at each depth. The vertical red lines mark the same points in the cycle as in Figure 7A. As emphasized by others (Freeman and Nicholson, 1975; Nicholson and Freeman, 1975; Richardson et al., 1987; Johnston and Wu, 1995), the current is much more spatially localized than voltage (Fig. 7, compare C, D).

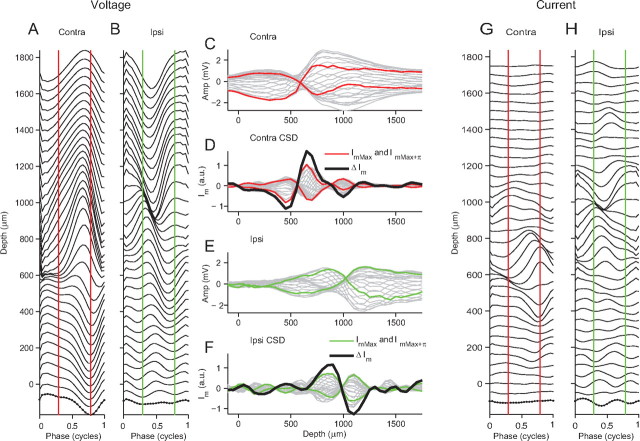
Figure 7.

CSD analysis of the neurophonic revealing current sources and sinks. A, The neurophonic response to contralateral stimulation (1000 Hz) was averaged over one stimulus cycle for all depths. The dots (bottom trace) indicate individual sample points. B, Same analysis for ipsilateral stimulation. C, The averaged contralateral neurophonic shown in A is replotted as a function of depth. D, Taking the second spatial derivative of the contralateral averaged neurophonic gives an estimate of the transmembrane current (I_m) during one complete stimulus cycle (gray lines). The change in transmembrane current (ΔI_m, thick black line) is calculated by finding the point in the cycle with the maximum transmembrane current (I_mMax, red line) and subtracting from this the transmembrane current one-half a cycle later (I_mMax+π, red line). The red lines indicate the same point in the cycle in A and C. The same analysis is applied in E and F for the averaged ipsilateral neurophonic shown in B. I_m for contralateral (D) and ipsilateral (F) stimulations replotted as a function of stimulus cycle for each depth in G and H.

This analysis is repeated for ipsilateral stimulation and the results are shown in Figure 7B, E, F, and H. Again a clear current sink–source pair is visible (Fig. 7F) but at deeper depths than for contralateral stimulation: when the current is maximally negative at 1100 μm, the current is maximally positive at 850 μm and approximately one-half a cycle later this pattern is reversed. The pattern is thus consistent with a dipole that alternates in polarity during every stimulus cycle.

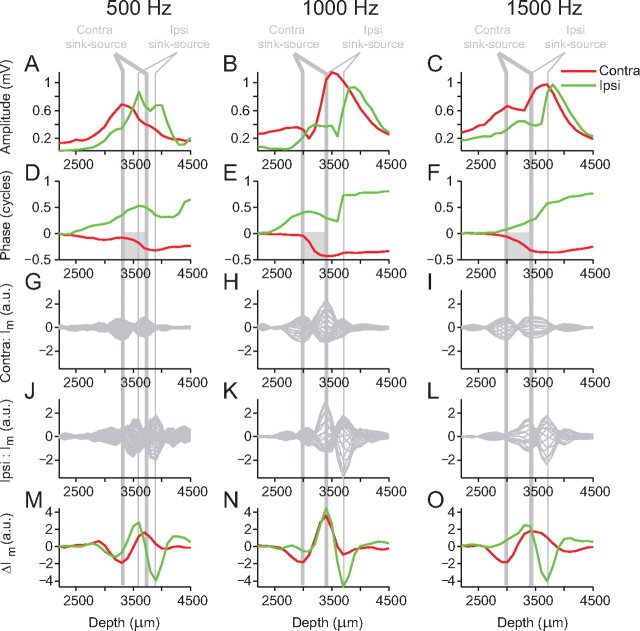
A prediction of the dipole model is that the half-cycle phase shift and the dip in amplitude should occur between the two poles of the dipole configuration (Fig. 6C,D). To examine the spatial relationship between the sinks and sources and the phase shift and amplitude, Figure 8 shows the transmembrane current (I_m and ΔI_m) with the amplitude and phase analysis along one electrode penetration for three different stimulus frequencies (500, 1000, and 1500 Hz). Figure 8A–C shows the contralateral amplitude (red line) and ipsilateral amplitude (green line) profiles, and Figure 8D–F shows the phase profiles. Figure 8G–I shows the transmembrane current, I_m, at all points in one stimulus cycle for contralateral stimulation for the three different stimulus frequencies, and Figure 8J–L shows the same data for ipsilateral stimulation. Figure 8M–O shows ΔI_m for both contralateral and ipsilateral stimulation. For both contralateral and ipsilateral stimulation, at all frequencies, two depths can be defined at which there are large antiphasic oscillations so that a current sink at one location is accompanied by a current source at the other location. We refer to this as a sink–source pair. Moreover, the configuration tends to be such that, for contralateral stimulation, the maximal sink is found at a more superficial depth than the maximal source (Fig. 8G–I), and vice versa for ipsilateral stimulation (Fig. 8J–L). The thick gray vertical lines mark the position of the contralateral sink–source pairs, and the thin gray vertical lines mark the position of the ipsilateral sink–source pairs, based on the maximal ΔI_m values (Fig. 8M–O). For contralateral stimulation at all frequencies, the half-cycle phase changes occurs between the current sink–source pair (Fig. 8D–F, gray boxes) as do the amplitude dips when present (not present at 500 Hz). These observations are consistent with the idea that the contralateral neurophonic is generated by a dipole configuration. For ipsilateral stimulation at 1000 and 1500 Hz, large phase shifts and amplitude dips also occur between the sink–source pair. At 500 Hz, there is a more complex phase profile and a more complex ΔI_m profile with two relatively large minima. This hints at a more complex sink–source configuration generating the neurophonic response at this frequency.

Figure 8.

Location of current sink–source pairs. A–C, Amplitude profiles for contralateral (red) and ipsilateral (green) stimulation at 500, 1000, and 1500 Hz. D–F, Corresponding phase profiles. The gray boxes indicate contralateral half-cycle phase shift. G–I, Estimated contralateral transmembrane current (I_m) calculated by taking the second spatial derivative (i.e., along the depth dimension) of the averaged neurophonic. J–L, Estimated ipsilateral transmembrane current. M–O, Corresponding changes in transmembrane current (ΔI_m) are calculated by subtracting I_mMax from I_mMax+π, where I_mMax is the maximal I_m depth profile in J–L and I_mMax+π is the I_m depth profile occurring one-half a cycle later. The thick gray vertical lines indicate the depths of the contralateral sink–source pair, derived from the largest minima and maxima of the contralateral ΔI_m. The thin gray vertical lines indicate the depths of the ipsilateral sink–source pair, derived from the largest minima and maxima of the ipsilateral ΔI_m.

Based on the bipolar morphology of an MSO neuron and the segregation of the excitatory inputs onto opposite dendrites (Fig. 6A), we interpret these sink–source pairs in the following way. Within each stimulus cycle, a volley of synaptic excitation is followed by an absence of synaptic drive. A volley of contralateral excitation on the ventromedial dendrite (encountered at smaller depths) causes current to flow into the MSO neuron at that location, creating a current sink. If current flows into the neuron on the dendrite, it must flow out of the neuron somewhere else, probably on the soma and/or opposite dendrite, creating a current source. This source is encountered at greater depths (Fig. 7D). For ipsilateral stimulation, the depth profile is reversed: excitatory inputs create a current sink on the dorsolateral dendrite (encountered at the deepest depths) and a current source at shallower depths (Fig. 7D).

The histological reconstruction with lesion sites shown in Figure 5 adds weight to this interpretation. Figure 5, F and G, shows the CSD analysis and relate this to the sites of the lesions and the boundaries of the MSO. For contralateral stimulation lesion 2, made slightly medial to the center of the MSO nucleus, occurs at the same depth as one pole of the contralateral current sink–source pair. The other pole of the sink–source pair occurs ventromedially to the MSO where we expect the medial dendrites with their contralateral excitatory input. Examples of how lesion sites compare with the CSD analysis in another two animals are shown in Figure 5H–S. As mentioned previously, a total of 29 lesions was made on 19 electrode penetrations in seven different MSOs (four cats). When all these lesion sites were compared with the CSD analysis, they were consistent with the examples shown here: one pole of the sink–source pair was located close to the center of the MSO and the other at the edge of the MSO or outside its boundary, as defined by the somata of its Nissl-stained neurons.

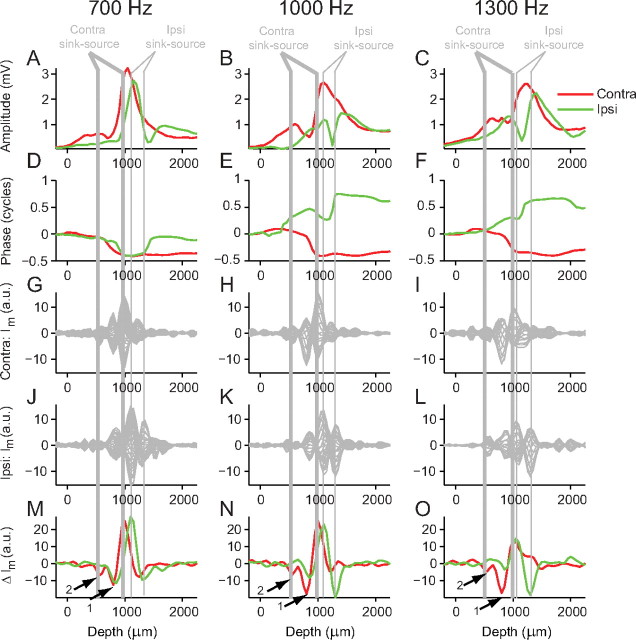
Figure 9 shows amplitude, phase, and CSD (I_m and ΔI_m) analysis from one electrode penetration in the MSO of a different cat for a range of stimulus frequencies (700, 1000, and 1300 Hz). Figure 9M–O shows ΔI_m for this penetration: for contralateral stimulation (red lines), there are two sinks (indicated by arrows) followed by one common source. The amplitude dips and the largest phase shifts occur between the sink and source (thick gray vertical lines). For ipsilateral stimulation, more complex phase profiles are seen but again the amplitude dips and large phase shifts (Fig. 9A–F, red lines) tend to occur between the sink–source pair (thin gray vertical lines). An interpretation of these more complex patterns of sink–source pairs follows in the modeling study.

Figure 9.

Location of current sink–source pairs for a different penetration. See Figure 8 for explanation. The arrows in M–O indicate locations of two current sinks.

Neurophonic recordings in all 14 MSOs (nine cats) showed similar results to those reported in Figures 8 and 9. CSD analysis of the neurophonic response to contralateral stimulation always revealed a sink–source pair located at a more superficial depth than the sink–source pair for ipsilateral stimulation. In general, the locations of the sink–source pairs for both contralateral and ipsilateral stimulation showed minimal variation in depth across the full range of stimulus frequencies (100–2500 Hz).

We calculated the distance between the source and the closest sink (in Fig. 9, this would be the sink indicated by the arrow labeled “1”) for the stimulus frequency that caused the strongest response within the penetration. For contralateral stimulation, the mean sink–source distance was 243 ± 94 μm (±SD), and for ipsilateral stimulation, it was 225 ± 86 μm. These distances correspond well with the known dimensions of MSO neurons and their dendrites (see Discussion). This finding adds weight to the interpretation that the sink may be located on the dendrite of the MSO neuron and the source on, or near, the soma. However, some sinks are located at relatively large distances from the source (Fig. 9, arrow 2). These larger sink–source separation distances may arise because we are measuring the activity of a population of MSO neurons that have a staggered arrangement and/or because the penetration crosses the MSO obliquely.

As is generally the case in the study of field potentials, their generators cannot be positively identified from the study of the potentials themselves. This requires additional knowledge, mainly from anatomy. Despite the reasonable correspondence between anatomy and physiology in our data, our interpretation regarding the source of the generators remains necessarily tentative. A first complicating but interesting factor is the presence of inhibitory inputs on and near the soma. These inputs are expected to contribute to the current source and to increase the amplitude of the neurophonic (see Discussion). It is interesting to observe in Figure 7A that, to contralateral stimulation, the positive deflections beyond 600 μm lead in phase with respect to the negative deflections at shallower depths. One possible explanation for this lead is that a current source caused by inhibitory inputs leads a current sink caused by excitatory inputs. A lead in inhibition relative to excitation has been observed in some neurons of the lateral superior olive (Tsuchitani, 1988; Joris, 1996; Tollin and Yin, 2005) and has been surmised to play a key role in ITD sensitivity in the MSO (Brand et al., 2002; Grothe, 2003; Pecka et al., 2008). A second complicating factor in the CSD analysis is that our recordings do not allow distinction between a dipole for which sink and source are fixed in position and are modulated in amplitude at the stimulus frequency, versus a dipole for which sink and source are not only modulated in amplitude but which also alternate in position. In the traces as in Figure 7, D and F, the sink–source configuration appears to reverse in time (i.e., the sink become a source and the source a sink). One red line shows a sink followed by a source at deeper depths. The other red line shows a reversed pattern one-half a cycle later; the sink becomes a source and vice versa. This reversal may reflect a real reversal of the direction of current [e.g., because of an afterhyperpolarization (undershoot) of the membrane potential of the cell subsequent to a volley of the excitatory inputs]. Alternatively, the reversal is only apparent and reflects a difference in baseline (which we cannot derive from our measurements). For example, a fixed dipole configuration in which the sink fluctuates between a maximum negative current and no current and the source between a maximum positive current and no current, could also generate the patterns observed. In summary, the CSD analysis reveals localized currents that oscillate in counterphase and that we interpret in terms of current sinks and sources generated by phase-locked inputs.

Modeling study

In this section we show that a simple model of the neurophonic, based on a dipole equation, can account for the salient features in the amplitude and phase depth profiles. The potential (ϕ) attributable to a charge dipole at vector location (r) is described by the following equation:

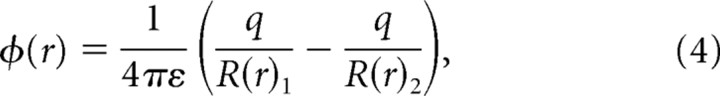where ε is the permittivity, q is the equal but opposite charge at each pole, and R(r)₁ and R(r)₂ are the respective distances from each pole to vector location r where ϕ will be calculated. Distances R₁ and R₂ can be expressed in any convenient coordinate system; we used Cartesian coordinates. Thus, Equation 4 describes the dipole field resulting form two static point charges. However, in the MSO, we are dealing with a current dipole where the current changes in time. Therefore, to more accurately describe this time-varying current dipole, Equation 4 must be modified. The change in current with time will also produce a magnetic field. However, in brain tissue for frequencies <1 MHz, it is safe to assume that the electrical and magnetic fields are uncoupled and the effects of magnetic induction can be neglected (Nunez and Srinivasan, 2006a). Using this quasistatic approach, a mathematically equivalent formula for a current dipole can be derived as follows (Nunez and Srinivasan, 2006b):

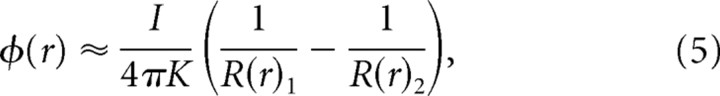where t is time, K is the conductivity, and I is the current. In the model, the time course of I at one pole is described by a sine wave, I(t) = Asin(2πtf + θ), and I at the other pole has the same time course but is always exactly one-half a cycle out of phase. The following equation now describes the time course of the potential at any location in space attributable to such a current dipole:

f is frequency, A is the amplitude current (equal for both poles), and θ is the starting phase. In the model, K is always arbitrarily set to 1 as only the relative amplitude of the potential is calculated. Thus, the time course of the modeled neurophonic measured by an electrode passing close to this dipole can be calculated. Fourier analysis is then used to calculate the amplitude and phase profile attributable to this dipole.

Figure 10A shows the CSD analysis for one case of contralateral stimulation (one electrode penetration at one stimulus frequency), which was used to get input parameters for the model. The x-coordinate of the location of the two poles of the first dipole was taken as the depth indicated by the vertical orange and black lines numbered 1 in Figure 10A. For all dipoles, the y-coordinate and z-coordinate were always zero. The amplitude A was taken as ΔI_m measured at black line 1. To get the phase of the dipole at the depth indicated by black line 1, average I_m was plotted for one cycle (Fig. 10A, inset, black line). The function was fit with a sine wave to estimate the I_m phase at that depth (0.64 cycle, marked above the black line on Fig. 10A, inset, and also to the left of dipole 1 on Fig. 10A). This measured phase was now used as the starting phase, θ, of the first model dipole. Note that the phase measured at the location of the second pole (R₂) is almost exactly out of phase (0.13 cycle) with the first pole (Fig. 10A, inset, orange line). In the model, the two poles are always exactly antiphasic by virtue of their opposite sign (Eq. 4). The time course of the potential attributable to this dipole was calculated for an electrode at depths (x-coordinate) from 0 to 4000 μm in 50 μm steps. The z-coordinate of the electrode track was always zero and the y-coordinate was always 50 μm to avoid directly passing through the poles (dipole y- and z-coordinates were always fixed at zero). The light blue lines on Figure 10, B and C, show the respective modeled amplitude and phase depth profiles attributable to this one dipole. The model amplitude profile shows two peaks of equal height separated by a dip that goes to zero and the model phase profile shows a shift of exactly one-half a cycle occurring at the same depth as the amplitude dip. This is the same as the amplitude and phase profile of a dipole field shown in Figure 6, D and E, respectively. The actually measured amplitude and phase profiles, for the data shown in Figure 10A, are shown in Figure 10, D and E. The gradual half-cycle phase shift is not well matched by the modeled phase profile, and the modeled amplitude does not capture the difference in peak heights seen in the measured amplitude profile.

Figure 10.

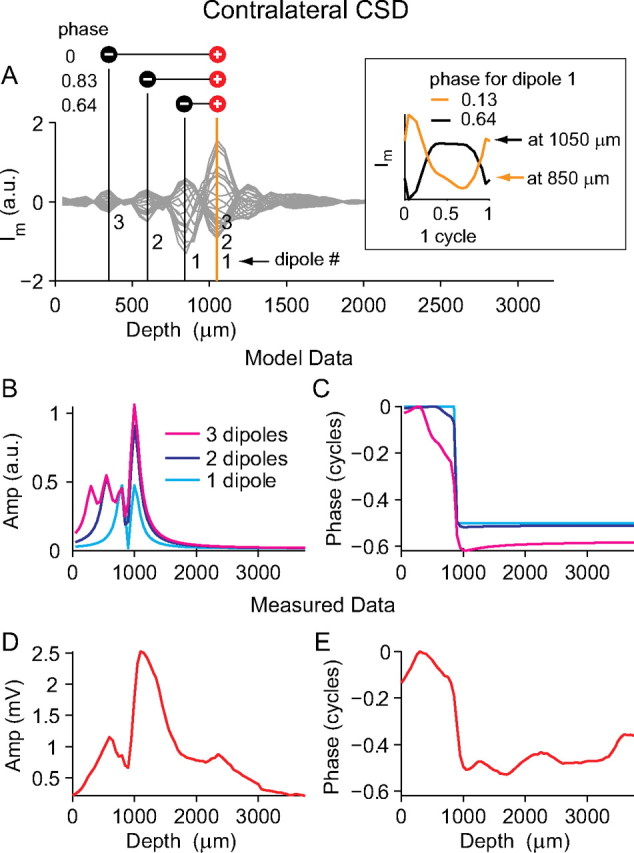
Simple dipole model of the neurophonic. A, The gray lines show transmembrane current (I_m) calculated from the contralateral response using CSD analysis. The location of three sink–source pairs are marked by vertical orange and black lines and the phases of I_m at the pole indicated by the black line are shown to the left of the dipoles. The inset plots I_m for one cycle at the depths of the first sink–source pair (orange and black lines). A sine function is fitted to get the phase measurement. B, C, Amplitude and phase profiles of the modeled neurophonic resulting from one, two, and three dipoles (light blue, dark blue, and magenta, respectively). Model parameters were extracted from the CSD analysis in A. D, E, Actual amplitude and phase profiles measured from the data shown in A, which are reasonably well matched by the model data for three dipoles. Importantly, these three dipoles are situated at different spatial locations and differ in phase.

The poles of dipole 1 in the model were placed at the depths where the CSD analysis shows that the largest changes in I_m occur. However, there are other depths at which local maxima in ΔI_m occur. This indicates that there may be more than one sink–source pair generating the neurophonic, and so a second dipole was added to the model. The second dipole is marked on Figure 10A (orange and black lines 2), and the model parameters were extracted (R₁, R₂, A, and θ) in the same way as described above. The time course of the potential attributable to these two dipoles was now calculated for the same electrode track by simply summing the contributions of each individual dipole. The dark blue lines on Figure 10, B and C, show the respective amplitude and phase depth profiles attributable to both dipoles. The second dipole is at a slightly different phase with the first dipole (compare 0.83 and 0.64). They have one pole at a common location (1000 μm), but the other pole is at different locations (550 vs 800 μm). The location of the poles results in the amplitude profile showing two smaller peaks at more superficial depths, which are not well separated, and one larger peak at the common pole. The amplitude dip no longer reaches zero because the dipoles have a slightly different phase. The fact that the dipoles have a slightly different phase also means that the phase profile shows more gradual shifts (Fig. 10C, dark blue line). A third dipole is now added to the model, and amplitude and phase profiles attributable to the three dipoles are shown as the magenta lines in Figure 10, B and C. The more subtle features of the measured amplitude and phase profiles are now reasonably captured by the modeled amplitude and phase profiles: a smaller amplitude peak at shallower depths separated by a dip from a larger peak at deeper depths and a phase shift of approximately one-half a cycle that is slower at shallower depths and sharper at deeper depths.

How necessary are the spatial and temporal differences between dipoles to create the amplitude and phase profiles of Figure 10, B and C? Figure 11 uses the same model input data as shown in Figure 10, but we now systematically constrain two of the model parameters: dipole spatial location (R₁ and R₂) and dipole starting phase (θ). In Figure 11, A and B, all three dipoles have exactly the same spatial location and starting phase. Neither the measured phase nor amplitude profiles are well described. All three dipoles simply sum together to give the same amplitude and phase patterns seen with only one dipole. In Figure 11, C and D, the dipoles have different spatial locations but the same starting phase. The measured amplitude profile now shows an asymmetry as seen in the physiological data, but the slow phase changes are not reproduced. In Figure 11, E and F, the dipoles have the same spatial location but different starting phases. This configuration cannot account for the slow phase changes measured nor for the complex amplitude patterns seen: the three dipoles just add to a net dipole that is smaller than the net dipoles is Figure 11, A and C.

Figure 11.

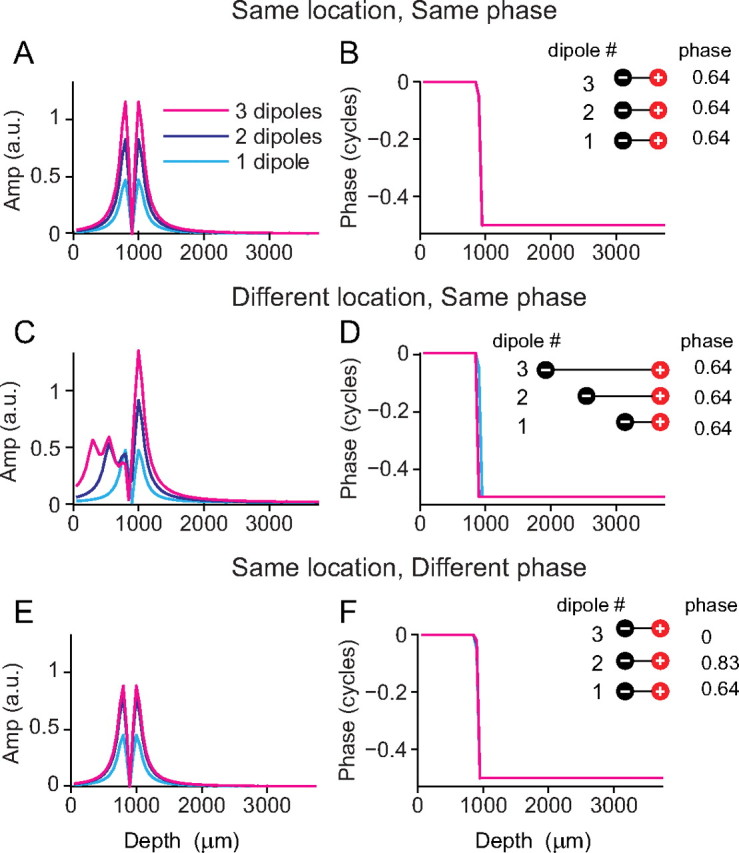
A configuration of dipoles at different spatial locations and with different phases is necessary to match the measured neurophonic phase and amplitude profiles. A–F, Amplitude and phase profiles resulting from one, two, and three dipoles (light blue, dark blue, and magenta, respectively) are shown for the following configurations: at the same spatial location and with the same starting phase (A, B), at different spatial location and with the same starting phase (C, D), and at the same spatial location and with different starting phase (E, F).

In summary, several features of the empirically observed amplitude and phase changes with depth are inconsistent with a single dipole: the unequal amplitude maxima separated by a trough that does not reach 0 V, and the gradual phase shift between these maxima. Our simple model shows that the amplitude features can be accounted for by having a number of dipoles at different spatial locations (and for this the phase relationship between the dipoles is not important) (Fig. 11C). To also reproduce the slow phase changes measured across the MSO, a number of dipoles at different spatial locations and with different starting phases is necessary (Fig. 10C).

The model shown in Figures 10 and 11 is based on only three dipoles. Its simplicity makes the results easy to interpret. We recalculated this model with a stacked dipole configuration similar to that shown in Figure 6C. This spatial arrangement of dipoles is closer to that which we expect to find in the MSO. Twenty dipoles were placed at each of the three x-coordinate locations shown in Figure 10A, and they were evenly spaced along the y-dimension as shown in Figure 6C. The shape of the resulting amplitude and phase profiles differed only very slightly from those shown in Figures 10 and 11, and thus the conclusions remain unchanged. However, both the models described here are a gross simplification of the actual processes generating the neurophonic. They reduce current flow in the entire MSO to a small number of isolated points and do not take into account how the cell bodies and dendrites will affect current flow, and make abstraction of the presence of multiple types of inputs and of multiple contributing neurons, which may differ in characteristic frequency or in other respects. Despite this, the simplest three dipole model still captures the salient features of the neurophonic response and thus serves as a useful tool to illustrate the point that the amplitude and phase profiles measured in the MSO can be accounted for by a basic dipole configuration generating the neurophonic, and that a number of dipoles are required at different spatial locations and that slightly differ in phase.

Discussion

We made penetrations through the short axis of the MSO while recording neurophonic responses to monaural, pure-tone stimuli, and observed double-peaked amplitude profiles and gradual phase shifts as a function of depth, over a range of frequencies. CSD analysis of the data showed a current sink–source pair for contralateral stimulation, which is spatially segregated from the sink–source pair for ipsilateral stimulation. Histological reconstruction confirmed that, for both ipsilateral and contralateral stimulation, one pole of the sink–source pair is located near the MSO center. For ipsilateral stimulation, the second pole of the sink–source pair is located a few hundred micrometers dorsolaterally of the MSO center, whereas for contralateral stimulation the second pole is a few hundred micrometers ventromedially of the MSO center. We interpret these sink–source configurations using the known anatomy of the MSO. The dendrites of MSO cells have a bipolar anatomy, with dendrites on the dorsolateral side receiving ipsilateral input and dendrites on the ventromedial side receiving contralateral input (Fig. 6A). For contralateral stimulation, strongly phased-locked excitation (Joris et al., 1994a,b; Louage et al., 2005) on the ventromedial dendrites causes phased-locked EPSPs, which create a current sink on the ventromedial dendrites. This gives rise to a source located somewhere on the soma or possibly the dorsolateral dendrites. Excitatory ipsilateral stimulation would give rise to a current sink on the dorsolateral dendrites with a corresponding source on the soma or ventromedial dendrites. Note that glycinergic inputs from the MNTB and lateral nucleus of the trapezoid body (LNTB) are predominantly placed near the soma (Helfert et al., 1989; Adams and Mugnaini, 1990; Cant and Hyson, 1992; Kapfer et al., 2002) and cause an outward current. Although the MNTB shows excellent phase locking (Smith et al., 1991, 1998; Joris and Yin, 1998; Paolini et al., 2001; Tollin and Yin, 2005; Mc Laughlin et al., 2008), the situation is less clear for the LNTB. This nucleus also receives the strongly phase-locked input from globular bushy cells (Tolbert et al., 1982; Smith et al., 1991) and contains low-frequency neurons (Tsuchitani, 1977), but we are not aware of any direct physiological evidence for phase locking in the LNTB. No phase-locked responses were reported in LNTB by Guinan et al. (1972a,b), but it is unclear whether their sample included low-frequency neurons. To the extent that the inhibitory inputs are phase-locked and that their phase locking is coherent with the excitatory inputs, inhibitory inputs will reinforce the source near the soma and sink on the dendrites generated by the excitatory inputs. If the excitation and inhibition were exactly out of phase, the currents would no longer reinforce each other.

Although we modeled the dipoles as sine waves, the actual currents are “peakier” (Figs. 7G,H, 10A, inset). This may reflect the timing of afferent inputs to the MSO, which feature narrow period histograms (Joris et al., 1994a,b; Smith et al., 1998). Another factor that affects the cyclic shape of the neurophonic is the relative timing and degree of phase locking of inhibitory versus excitatory inputs, which is currently a matter of interest (Brand et al., 2002; Pecka et al., 2008). Peak doubling, which would be expected for “peaky” out-of-phase excitation and inhibition, is not a feature of the data (Figs. 1, 7G,H, 10A, inset). This observation, combined with the sheer magnitude of the neurophonic, suggests that excitation and inhibition are close in phase and that their dipoles reinforce each other. However, the data do not allow stronger, quantitative statements. Without independent manipulation of excitation and inhibition, it is impossible to isolate their relative contributions to the neurophonic.

In the cat MSO, Stotler (1953) reports dendritic lengths of 200 μm, whereas, in the guinea pig, Smith (1995) shows dendrites of up to 400 μm in length. A recent study by Rautenberg et al. (2009) reports dendritic lengths of between 150 and 300 μm in the gerbil. The sink–source pairs reported here can be separated by up to 500 or 600 μm (Figs. 8, 9), greater than the largest reported dendrite tip-to-soma distances. There are a number of reasons why the sink–source pairs may have these larger separation lengths. The neurophonic reflects the activity of a population of neurons and the location of their somata and dendrite endings are staggered (Scheibel and Scheibel, 1974), giving a longer effective “population” dendrite length. Penetrating this population obliquely would also add to the apparent dendrite length.

Using a dipole equation to model the neurophonic, we obtained amplitude and phase profiles that capture the essential features of the measured data. As expected, model responses based on a single dipole showed a sharp half-cycle phase shift and two amplitude peaks separated by a dip to zero (Fig. 10C,B, light blue line). The CSD analysis suggests that there is usually more than one sink–source pair generating the neurophonic. Incorporating the effects of these additional dipoles into the model yielded phase and amplitude responses that were similar to the measured data. A key finding of the modeling study is that the measured complex amplitude and phase patterns can only be reproduced when multiple dipoles, at different locations, are used in the simulation (Fig. 10C, magenta line). To reproduce the slow half-cycle phase shift, in addition to the dipoles being at different locations, they must also be slightly out of phase (Fig. 10C, magenta line). It is unclear whether these different dipoles correspond to spatially distinct groups of MSO neurons with different phases or to different inputs at different positions along the dendrites of MSO neurons, or both.

Fourier analysis was used to extract the phase component at the stimulus frequency of the neurophonic response to contralateral stimulation at a number of different depths. This phase of the neurophonic to contralateral stimulation, when plotted as a function of depth, showed a consistent half-cycle shift. This phase shift was found to be one-half a cycle for every stimulus frequency. A pure time delay, as postulated in the axonal delay line by Jeffress (1948), would result in a phase shift that increases with stimulus frequency. The fact that the phase shift we observe is one-half a cycle, across all stimulus frequencies, indicates that it cannot be caused by a pure time delay from an axonal delay line. The neurophonic response to ipsilateral stimulation showed a similar shift in the opposite direction. The ipsilateral response was not as consistent as the contralateral response and often showed more complex patterns, particularly at low frequencies (<1000 Hz). This is perhaps related to the anatomical finding, from tracing studies (Smith et al., 1993; Beckius et al., 1999), that the spherical bushy cell axons innervate the MSO in an orderly way on the contralateral side, whereas the innervation on the ipsilateral side is more complex, with axons often looping across the MSO toward the midline before looping back to the MSO on the ipsilateral side, and a less uniform distribution of branches rostrocaudally.

The phase shifts associated with a dipole field complicate the use of neurophonic delays to draw conclusions about axonal delay lines. Phase and time shifts in the mammalian neurophonic have been reported previously. Biedenbach and Freeman (1964) described a reversal in polarity of the potential evoked by clicks in cats. Bojanowski et al. (1989), also working with cats, reported a phase shift in the neurophonic, measured along the dendritic axis of the MSO, to monaural tones and concluded that this phase shift was caused by a delay line. Here, we found a similar phase change but our conclusions regarding the origins of the phase shift are markedly different. We used CSD analysis to show that results are consistent with spatially segregated current sources and sinks in the MSO. This configuration of sources and sinks results in a dipole field. The modeling study shows that this dipole configuration generates phase and amplitude profiles similar to those measured. Therefore, most of the phase change across the short axis of the cat MSO can be understood as a feature of that field without the need for a delay line. It is important to note that this does not preclude the possibility that the neurophonic may contain additional smaller phase shifts from other sources of delay such as axonal delay lines. However, the dipole phase shift is large (one-half a cycle at 500 Hz is 1 ms) compared with the axonal delays proposed by Jeffress (1948) (a few 100 μs). Understanding that the half-cycle phase shift in the neurophonic is caused by a dipole and not an axonal delay line may make it possible to use the neurophonic to derive information about other sources of delay in the MSO that are of functional significance.

A number of studies in birds have also measured neurophonic delays in the nucleus laminaris (Carr and Konishi, 1988; Köppl and Carr, 2008). Sullivan and Konishi (1986) reported one full cycle of change in interaural phase (contralateral–ipsilateral) across the short axis of nucleus laminaris in the barn owl, as we also report (Fig. 3K–N). They concluded that this phase change was the result of a delay line but our dipole interpretation may also apply to the owl data. The study by Sullivan and Konishi (1986) did not report amplitude data and was restricted to single frequencies: phase shifts at single frequencies as shown in their report could reflect either dipoles or delay lines. However, it should be noted that there are key differences in the anatomy of the owl nucleus laminaris and cat MSO. One important difference is that the cat MSO consists of a relatively thin sheet of neurons (three or four) (Stotler, 1953), whereas nucleus laminaris in the barn owl is composed of a thick sheet of neurons (Carr and Konishi, 1990). Thus, a map of delay running across the short axis of nucleus laminaris is a more likely possibility than a map of delay across the MSO short axis. Another key difference is that, at high frequencies, nucleus laminaris neurons have very short stubby dendrites (Smith and Rubel, 1979; Carr and Konishi, 1990), so that the dipole configuration present in the cat may not be present in the barn owl.