Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2010 Oct 20;30(42):14173–14181. doi: 10.1523/JNEUROSCI.0945-10.2010

Decision Time, Slow Inhibition, and Theta Rhythm

Anteo Smerieri 1, Edmund T Rolls 2,3, Jianfeng Feng 4,5,✉
PMCID: PMC6634784  PMID: 20962238

Abstract

In this paper, we examine decision making in a spiking neuronal network and show that longer time constants for the inhibitory neurons can decrease the reaction times and produce theta rhythm. We analyze the mechanism and find that the spontaneous firing rate before the decision cues are applied can drift, and thereby influence the speed of the reaction time when the decision cues are applied. The drift of the firing rate in the population that will win the competition is larger if the time constant of the inhibitory interneurons is increased from 10 to 33 ms, and even larger if there are two populations of inhibitory neurons with time constants of 10 and 100 ms. Of considerable interest is that the decision that will be made can be influenced by the noise-influenced drift of the spontaneous firing rate over many seconds before the decision cues are applied. The theta rhythm associated with the longer time constant networks mirrors the greater integration in the firing rate drift produced by the recurrent connections over long time periods in the networks with slow inhibition. The mechanism for the effect of slow waves in the theta and delta range on decision times is suggested to be increased neuronal spiking produced by depolarization of the membrane potential on the positive part of the slow waves when the neuron's membrane potential is close to the firing threshold.

Introduction

The functions of both low- and high-frequency oscillations in the brain have been the subject of considerable investigation (Buzsaki, 2006). Low-frequency theta oscillations (4–8 Hz) have been observed to increase the phase-locked discharge of single neurons in a visual memory task (Lee et al., 2005). In the hippocampus, the phase of the theta rhythm influences the timing of pyramidal neuron firing, long-term potentiation (theta peaks), and depotentiation (theta troughs) (Hölscher et al., 1997). In this way, theta rhythm may influence synaptic plasticity and the maintenance of memory. It is speculated that recent examples of coupling between gamma amplitude and theta phase (theta-nested gamma) (Canolty et al., 2006) might provide an effective combination for neuronal populations to communicate and integrate information during visual processing and learning, and might provide a process of temporal segmentation that can maintain multiple working memory items (Broadbent, 1975; Lisman and Idiart, 1995; Cowan, 2001; Lee et al., 2005; Jensen, 2006; Lisman and Buzsaki, 2008; Rolls and Deco, 2010), although the same can be accomplished more simply with several local attractor networks (Rolls and Deco, 2010). Oscillatory synchronization can also increase synaptic gain at postsynaptic target sites, thereby potentiating responses to learned stimuli (Fries et al., 2001; Fries, 2005).

There has been an interest in the relation between brain rhythms (Lindsley, 1952) and reaction time for some time. Lansing (1957) reported that simple reaction time to a flash of light was shorter if the flash was delivered in the positive phase of the occipital alpha waves, and suggested that excitability was higher in this phase. Green and Arduini (1954) reported that hippocampal theta usually occurs together with desynchronized EEG in the neocortex, and hypothesized that the theta is related to arousal. There is still debate as to what functional role is played by the theta rhythm. Some human EEG recording studies have reported that theta phase, rather than amplitude, is correlated with cognitive processes, the so-called phase reset model (Rizzuto et al., 2003; Buzsaki, 2006), whereas other studies on the frontal and temporal lobes have placed more importance on the theta amplitude (Canolty et al., 2006).

In this paper, we modify a widely used spiking neuronal attractor network model by introducing a second population of GABA neurons with a long time constant so that it produces theta. We find that the reaction time is considerably reduced. The reduction of the reaction time is associated with a drift upward of one of the specific pools in the period just before and when the decision cues are applied; this provides a mechanism for the faster performance. The results apply equally to decision making and to memory recall, in that memory recall can be understood as a decision in an attractor network about the state it enters based on the input cues (Rolls and Deco, 2010). The same underlying processes and mechanisms apply to the perception of ambiguous patterns (Blake and Logothetis, 2002; Maier et al., 2005), in which the perceptual state can be thought of as a state influenced by the sensory inputs, but also by the stochastic effect of the randomness in the neuronal spiking times (Rolls and Deco, 2010).

Materials and Methods

Network architecture.

For our experiments, we used three variations on the basic architecture proposed by Wang (2002) and extensively explored by Rolls and Deco (2010). The important aspect of cortical architecture for effects of the type we describe is recurrent collateral connections, and these are found throughout the neocortex (Miller et al., 2003; Wong and Wang, 2006; Rolls, 2008). We have described previously how different types of decision making appear to be implemented in different cortical areas by this type of architecture (Rolls and Deco, 2010). In addition, we note that in fact much of the work on decision making that may be related to reaction times is performed on a premotor cortical area, the ventral premotor cortex, and many areas connected to this (Romo et al., 2004; Deco et al., 2010). We further note that a part of the ventral medial prefrontal cortex area 10 has now been implicated in choice decision making between rewards (Behrens et al., 2008; Grabenhorst et al., 2008; Boorman et al., 2009).

The three versions differed only in the properties of the inhibitory neurons. The task of the attractor network is to reach either attractor state A, representing decision A, or attractor state B, representing decision B. The evidence for decision A is applied to the neurons of attractor A, and the evidence for decision B is applied to the neurons of attractor B. A typical task is the comparison of two different stimuli, e.g., vibrotactile stimulation frequency (Deco and Rolls, 2006).

The network is composed of 1000 neurons, 800 of which are excitatory and 200 inhibitory (Fig. 1, top). The current and membrane potential of each neuron are calculated using the leaky integrate and fire model described below. Two pools of 80 neurons each, taken from the 800 excitatory neurons, are taken to be the specialized A and B pools, which receive additional inputs as described above; the remaining 640 excitatory neurons form the nonspecific pool.

Figure 1.

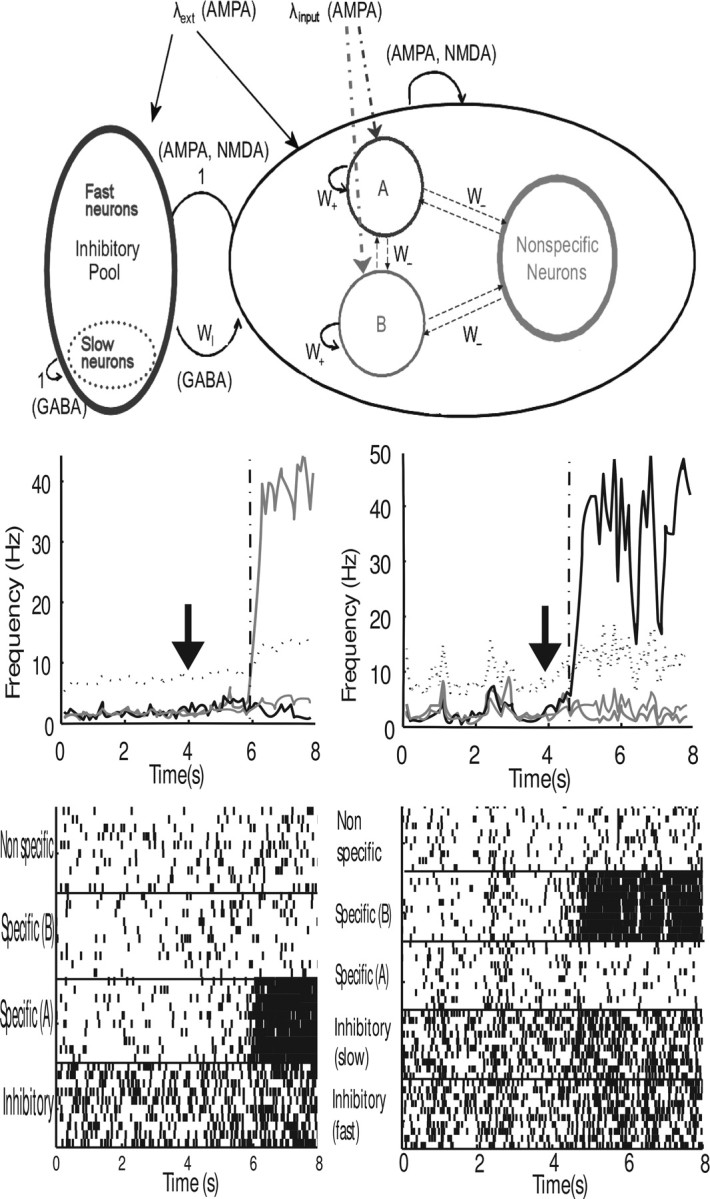
Figure 1.

Open in a new tab

Top, Diagram of the two-pool network model used for the simulations. All connections from the excitatory neurons (the A, B, and nonspecific pools on the right) are AMPA- and NMDA-mediated. The fast and slow models have only one inhibitory pool, in which all the neurons have the same τGABA. The connections from inhibitory neurons shown on the left are GABA-mediated. The letters or numbers next to the arrows specify the synaptic weights. Middle, left, Firing rates for all the pools for sample trials of the original model. Thick gray line, specific pool A; thick black line, specific pool B; thin gray line, nonspecific pool; dotted black line, inhibitory fast pool; dotted gray line, inhibitory slow pool. Input cues are switched on at t = 4 s (arrows). The vertical dashed line marks the moment where the decision was taken, as measured by the criterion described in the text. Bottom, left, Rastergrams for the same two trials, showing the spiking activity for 10 randomly chosen neurons from each population. Middle and bottom, right, Same as with middle and bottom, left, but with the two-pool model.

Neuron model.

The model chosen to represent a single neuron is the leaky integrate and fire model, defined by the equation

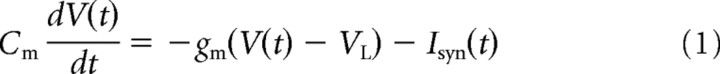graphic file with name zns04210-8989-m01.jpg

where V(t) is the membrane potential of the neuron, Cm is the membrane capacitance, Isyn is the synaptic input received by the neuron, and gm is the leak current conductance. When no input is present, the membrane potential drifts to the rest value VL (−70 mV); if the membrane potential reaches a threshold Vth (−50 mV), the neuron is said to have spiked and the potential is reset to a reset value Vre (−55 mV). The potential is then clamped to the reset value for a brief refractory period τref.

When a neuron spikes, it applies excitatory (driving toward 0 mV) or inhibitory (driving toward −70 mV) synaptic inputs to all the other neurons. Excitatory neurons generate fast AMPA-mediated currents and slower NMDA-mediated currents, whereas inhibitory neurons generate GABA-mediated currents. The total synaptic input to a single neuron is the sum of these currents.

graphic file with name zns04210-8989-m02.jpg

where IAMPA,ext is the current due to external inputs to the network, again AMPA-mediated, described in more detail below.

The GABA- and AMPA-mediated currents follow first-order kinetics, described by

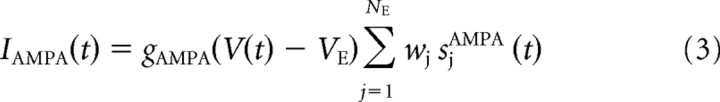graphic file with name zns04210-8989-m03.jpg
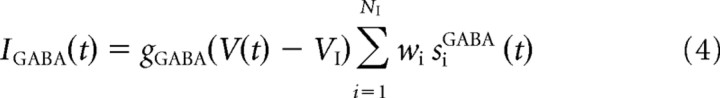graphic file with name zns04210-8989-m04.jpg
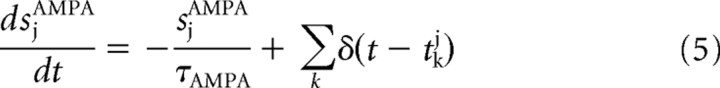graphic file with name zns04210-8989-m05.jpg
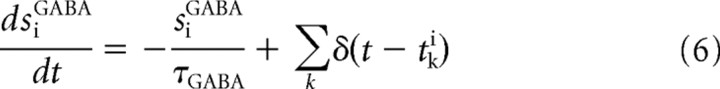graphic file with name zns04210-8989-m06.jpg

where gAMPA and gGABA are the synaptic conductances, s is the fraction of open channels, VI and VE are the reversal potentials for GABA and AMPA currents, wj is the synaptic weights, NI and NE are the numbers of inhibitory and excitatory neurons, and tjk is the time when the j-th neuron emits its k-th spike. The values of these parameters are reported in Table 1 and were taken from Deco and Rolls (2006), in which they were calculated with a mean field analysis to obtain a network with stable decision states.

Table 1.

Parameters used for the simulations

All neurons Excitatory neurons Network parameters
VL = −70 mV Cm = 0.5 nF w+ = 2.2
Vth = −50 mV gm = 25 nS w− = 0.8444
Vre = −55 mV gAMPA,ext = 2.08 nS wi = 1.015
VE = 0 mV gAMPA = 0.104 nS wmedium = 1
VI = −70 mV gNMDA = 0.327 nS Next = 800
τtre = 2 ms gGABA = 1.287 nS Two-pool model only
τAMPA = 2 ms Inhibitory neurons τGABA,slow = 100 ms
τNMDA,rise = 2 ms Cm = 0.2 nF S = 0.25
τNMDA,decay = 100 ms gm = 20 nS f = 0.3077
τGABA = 10 ms gAMPA,ext = 1.62 nS slow model only
α = 0.5 ms−1 gAMPA = 0.081 nS τ̄GABA = 32.5 ms
β = 6.2 · 10−5 V−1 gNMDA = 0.258 nS f = 0.3077
γ = 3.57 gGABA = 1.002 nS
Open in a new tab

Equations for the NMDA currents are slightly different to account for the voltage-dependent magnesium block and the non-negligible rise time.

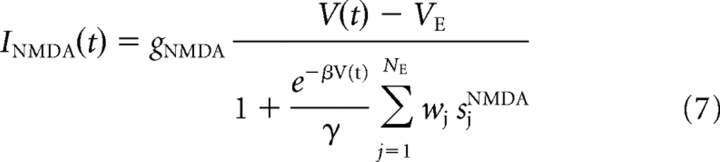graphic file with name zns04210-8989-m07.jpg
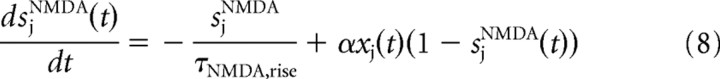graphic file with name zns04210-8989-m08.jpg
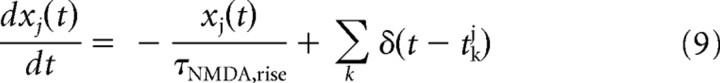graphic file with name zns04210-8989-m09.jpg

where α, β, and γ are numerical parameters with values reported in Table 1. Every neuron receives inputs in the form of excitatory AMPA current spikes, following a Poisson distribution, from Next independent external synaptic connections. In the absence of any input, the frequency is 3 Hz for every synapse for all the neurons in the network. An input to the network is simulated by increasing the frequency of the input to the specific pool neurons A and B. The equations that describe the external current input, for each neuron, are as follows:

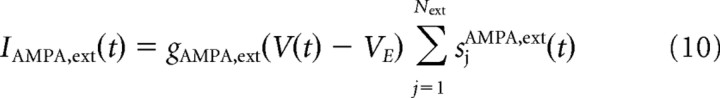graphic file with name zns04210-8989-m10.jpg
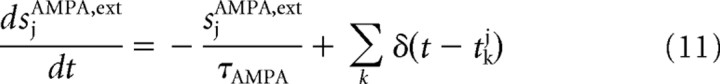graphic file with name zns04210-8989-m11.jpg

where Next is the number (800) of external synaptic connections onto each neuron.

In this model, every neuron is connected to every other neuron. The weights of the synaptic connections are assumed to be generated by a Hebbian learning process. There is a strong connection between neurons of the same specialized pool (w+), a weak connection between neurons of different subsets or between specialized and nonspecialized neurons (w−), a dedicated weight mediates the interaction from the inhibitory neurons to the excitatory neurons (wi), and a medium weight (wmedium) covers all the other cases.

Different versions of the network.

In the original model, all the inhibitory neurons shared the same parameters. To generate theta band activity, however, we needed to have two different populations of inhibitory neurons (White et al., 2000; Kendrick et al., 2009).

We created, therefore, a modified version of the network, in which a fraction S of the inhibitory neurons have a GABA spike decay time constant of τGABA,slow = 100 ms. To keep constant the amount of inhibition in the network, we scaled the GABA conductances for all neurons by a compensating factor f, because fast and slow inhibitory neurons should have the same amplitude of conductance change (White et al., 2000). We kept constant the average amount of inhibition in the network by choosing f so that the average time-integrated change of conductivity caused by a GABA spike remained constant, i.e.,

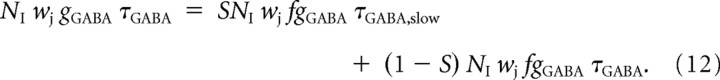graphic file with name zns04210-8989-m12.jpg

Solving for f, this leads to

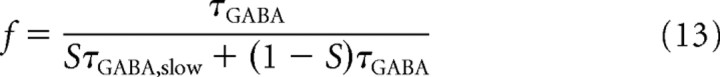graphic file with name zns04210-8989-m13.jpg

which can be read as f being the ratio between the original τGABA value and the new average time constant of the inhibitory neurons.

To check whether any difference in the network performance is due to having two different inhibitory neuronal populations, or is due to a different average τGABA value in the network, we also compared the results with ones taken from a third version of the network, with the same f value and a new value for τ̄GABA = SτGABA,slow + (1 − S)τGABA, equal to the average value in the two inhibitory pool model.

Simulations and frequency analysis.

The model equations were evolved with an Euler algorithm with a step size of 0.05 ms, using MATLAB scripts and C language .mex files. The usual protocol for a trial was to run the simulation for 4 s with no inputs to the specific pool, then add the input and run it for 4 further seconds. Each neuron received a 3 Hz excitatory spike Poisson distribution on each of its 800 external synaptic connections for the whole duration of the simulation. The addition of the input was simulated by bringing the Poisson rate to 3.04 Hz for all 800 external synapses of the neurons in both specialized (decision making) pools. This increase is enough to allow the network to go into a decision state, in which one of the pools has a firing rate ∼40 Hz and the other is almost silent. During a simulation run, the average membrane potential across every neuron in a pool, and the firing times for every neuron in each pool, were recorded. The average firing rates of neurons were then calculated using 100 ms bins. We defined the decision time on each trial as the time from the moment the decision-related inputs were applied until the winning pool reached a firing rate halfway between its spontaneous rate and the final firing rate when in the decision state (averaged over the last 2 s). The winning decision pool was chosen as the one that had the higher firing frequency in the last second of the simulation. The parameters used for the model (Deco and Rolls, 2006) (chosen with a mean-field analysis) are such that, in the period before the decision cues are applied, the noise can occasionally trigger a transition to one of the high-firing rate attractors; any such trials were excluded from the analyses.

Frequency analysis and filtering of the average membrane potentials were performed with a continuous wavelet transform, using a Morlet wavelet in a range of frequencies between 1.5 and 100 Hz, with software in the MATLAB wavelet toolbox.

Results

All the experiments we report in this paper were conducted as comparisons between the original version of the network, where all the inhibitory neurons have τGABA = 10 ms, which we refer to as the fast or original model; a network where a fraction S = 0.25 of the inhibitory neurons have τGABA = 100 ms and the rest have τGABA = 10 ms, referred to as the two-pool network; and a network where all the neurons have τGABA = 32.5 ms, which is the average GABA relaxation time for the two-pool network, referred to as the slow network.

The performance of the network is illustrated in Figure 1, middle and bottom. The average firing rates of the neurons in each pool and rastergrams of 10 randomly selected neurons on the same trial are shown for a typical trial in the original model (Fig. 1, middle left) and for the two-pool model (Fig. 1, bottom right).

Reaction times

Reaction times were measured for a batch of 1000 trials for each network. We note that the decision cues were of equal strength, that is, ΔI = 0 (which signifies that there is no difference in the decision cues applied to each of the two decision-related populations of neurons A and B). During these trials, the inputs were turned on at a random instant between 2 and 4 s to avoid any systematic contribution by possible low-frequency oscillations to the reaction times. Our data showed no correlation, however, between the input injection time and the reaction times of the network.

Binning the reaction times for each model in 100 ms bins yields the distributions plotted in Figure 2, top. As can be seen in the figure, the distribution of reaction times is skewed toward longer reaction times for all three models. The average reaction times were 0.96 s for the fast model, 0.86 s for the slow model, and 0.71 s for the two-pool model, with statistically different values according to the Wilcoxon rank sum test (p < 0.001, n = 1000 for each pair of distributions of reaction times). The median reaction times for the three models are, in the same order, 0.91, 0.82, and 0.65 s. The average reaction time for the fast model is consistent with those reported by Deco and Rolls (2006). Thus, making the inhibition longer can decrease the reaction times of this model of decision making, even when the parameters of the inhibition are selected to provide the same integrated opening of the GABA-activated ion channels, and the mean firing rate when in the attractor was similar between the three models.

Figure 2.

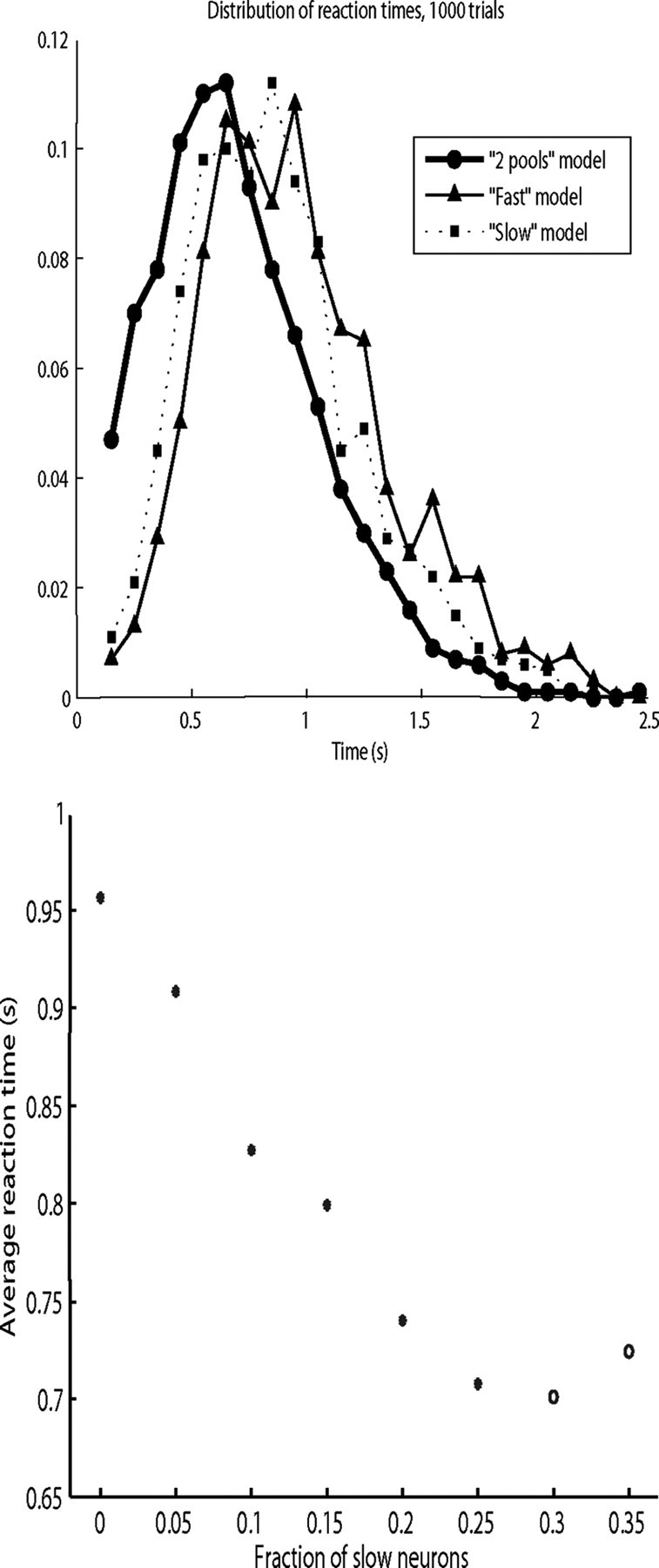
Figure 2.

Open in a new tab

Top, Distribution of the reaction times for the three different models. The distribution was measured using 1000 trials, and the distribution is shown with 100 ms bins. Circles, two-pool model; triangles, fast model; squares, slow model. Bottom, Two-pool model average reaction time as a function of the fraction of slow versus fast neurons in the inhibitory pool. Open circles mark the cases where the spontaneous state is unstable, i.e., the values for which >50% of the trials showed a transition to the decision state before the decision cues are applied. The point for a fraction = 0 corresponds to the fast or original model. The point for a fraction = 0.25 corresponds to the two-pool model.

Influence of the proportion of slow neurons in the two-pool model on the decision times

We showed in Figure 2, top, that the two-pool model has faster reaction times than the other two models. We investigated the relationship between the proportion of slow neurons in the model and reaction times by varying the fraction S of slow neurons in the two-pool model. For each ratio we ran 500 trials, with randomized decision input injection times as described above. The results shown in Figure 2, bottom, indicate a clear decrease in the reaction time as the proportion of slow neurons increases. Thus, having a small proportion (<25%) of the inhibitory neurons with a long time constant can decrease the reaction times. (When the proportion of slow neurons is increased >25%, there is no further decrease in the average reaction time, and the spontaneous state becomes less stable. The spontaneous state was relatively stable when S was <25%, in that the network entered an attractor state in the absence of decision input cues in 2–5% of trials; and when S = 0.3 we had to reject 75% of the trials. For S = 0.35, the proportion of rejected trials with unstable spontaneous activity was >90% of the total).

Average firing rates

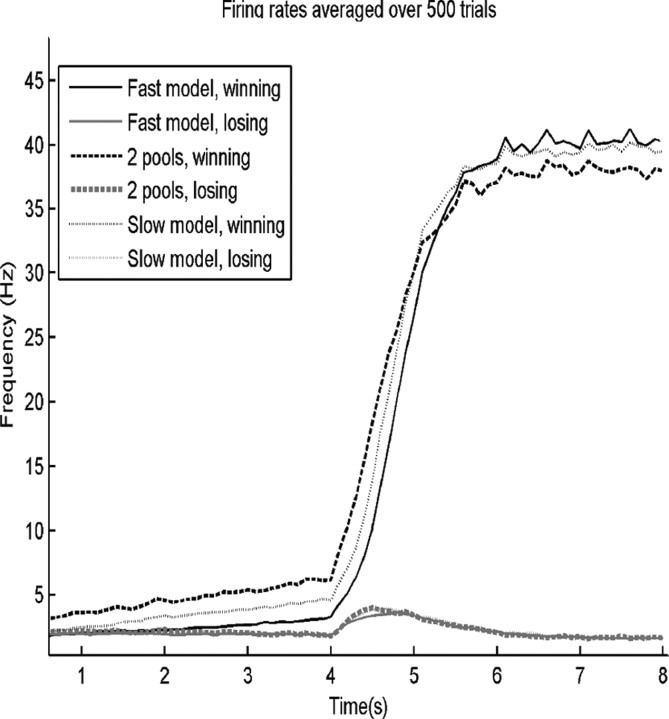
The average firing rate for the winning and the losing selective pools as a function of time is plotted in Figure 3. After the decision cues are applied, there is little difference in the firing rates in the three models. However, before the decision cues are applied, there is an interesting slow increase of firing rate evident for the pool that will win when all the trials are averaged from t = 1 s until t = 4 s, when the decision cues are applied. That is, the average firing rate for several seconds before the decision cues are applied is on average a predictor of which selective pool will win the competition. Further, the two-pool model shows in this period before the decision cues are applied a higher firing rate, on average, for the pool that will win than the slow model, and this in turn has higher firing rates at the end of the spontaneous period when the decision cues are applied than the fast model (Fig. 3).

Figure 3.

Figure 3.

Open in a new tab

Average firing rates for the winning and losing pools over 500 trials for the three models for ΔI = 0. The decision cues were started at 4 s. (Firing rates averaged over 500 trials, winning and losing).

Thus, the decision is anticipated or influenced by the slow change in the average firing rate for several seconds before the decision cues are applied, and the magnitude of this precue drift is greater for the models with faster reaction times. When the decision cues are applied, the pool that is already showing an upward drift (on average) will be likely to win the competition, and will have less far to go when the decision cues are applied and the strong nonlinear dynamics caused by the positive recurrent collateral feedback fully engages. In short, if the firing rate is already (on average across trials) a little up before the cues are applied, the transition to the winning attractor will be easier, and this will produce, on average, shorter reaction times.

This hypothesis was tested as follows. An unequal bias was applied to the two selective pools, and we reasoned that by chance on some trials the pool biased to win will have spontaneous activity that will facilitate the decision, but on other trials drift in the wrong direction will facilitate winning by the incorrect attractor, especially in the two-pool model. Five hundred such simulations were performed using a mean firing rate onto each synapse of 3.05 Hz to pool A, and 3.03 Hz to pool B (which corresponds to ΔI = 16 Hz per neuron given that there are 800 synapses for external inputs on each neuron). The prediction was verified, with 21% margin of error for the two-pool model, 17% for the slow model, and 12% for the fast model. Thus, the increased drift in the two-pool models can contribute to more errors when the drift is against the cues biasing the decision, in line with the hypotheses described in this paper.

Average membrane potential

The findings described indicate that the activity in the period before the decision cues are applied is different for the three models, and is related to the shorter reaction times with ΔI = 0. We investigated this further by analyzing the average membrane potential, Va, of all neurons in the pool in the 4 s precue period for each pool. Figure 4 shows the three distributions for the selective pools that won the competition after the decision cues were applied, although we found very similar distributions for the other pools. As can be seen from Figure 4, the three models have very similar mean and peak Va values, but the two-pool model has a distribution skewed toward increased depolarization. Two-sample Kolmogorov–Smirnov tests confirmed that all three distributions are different from each other (p < 0.001). The skewed distribution toward greater depolarization of the two-pool model before the decision cues are applied is consistent with more activity in this model before the decision cues are applied, contributing to some faster reaction times.

Figure 4.

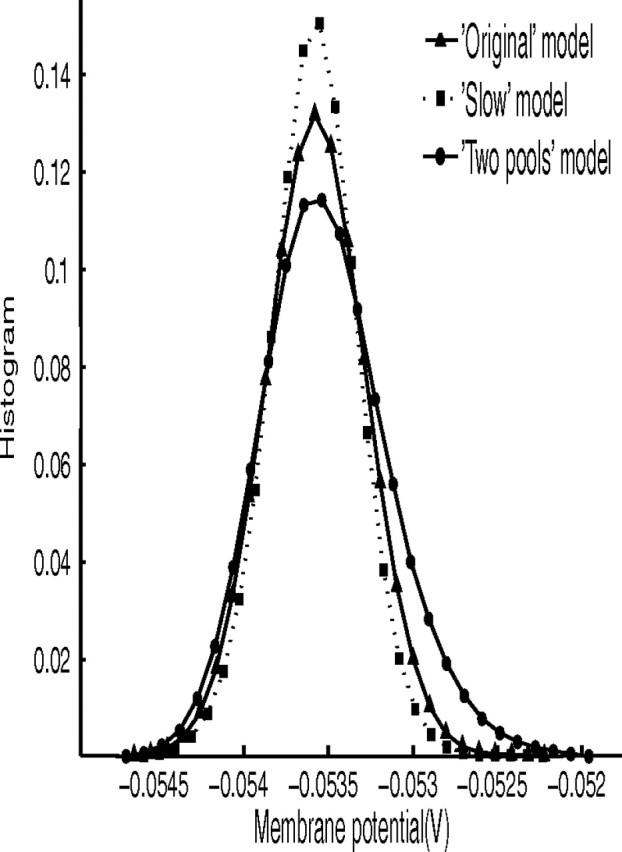
Figure 4.

Open in a new tab

Distribution of average membrane potentials Va values in the specialized winning pool before the cue injection for the three models, using 30 bins. Triangles, fast model; squares, slow model; circles, two-pool model.

Frequency spectra for the average membrane potential and theta-filtered membrane potential

To provide further evidence of the underlying mechanisms for the faster reaction times of the two-pool model, we investigated the frequency spectra of the average membrane potential of the three models. Inter alia, this is expected to give insight into the level and frequency distribution of the noise in the different models, and shows whether some of the models may have theta period activity. Continuous wavelet transform (CWT) of the local field potential was used to analyze the role of activity in different bands, sampling 80 points in the frequency space ranging from 1.5 to 100 Hz. Figure 5, top, shows the power spectra for the three different models. The spectra were obtained by averaging the square value of the CWT coefficients for the whole of the spontaneous period from a single trial, normalizing this (by setting the area under the curve to 1) to obtain a distribution of the power at different frequencies, and then averaging these power spectra across 10 trials for each model.

Figure 5.

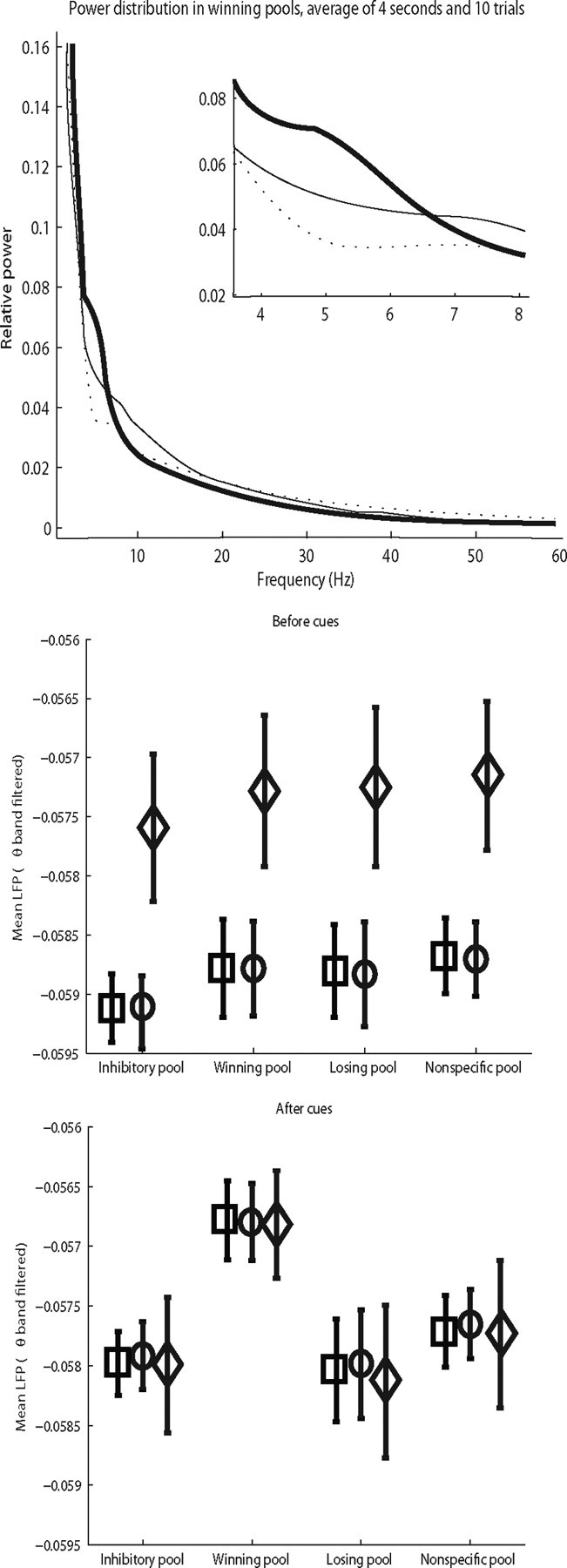
Figure 5.

Open in a new tab

Top, Power spectra as calculated from the continuous wavelet transform of the average membrane potential over the 1.5–100 Hz range. Inset, Detail of the spectra for the 4–8 Hz region. Individual spectra were taken by squaring and normalizing the CWT coefficients for each time point, then averaging the result over the whole 4 s of simulation. Data shown in the plot are the average of 10 such spectra for each model. Dotted line, fast model; thin line, slow model; thick line, two-pool model. Middle and bottom, Mean values and SDs of the theta-filtered average membrane potentials Va, before (middle) and after (bottom) the cue injection for all pools and for the three models. The values reported are the average across 200 trials for each model. Circles, fast model; squares, slow model; diamonds, two-pool model.

Figure 5, top, shows the power spectra for the average membrane potential in the spontaneous period of the selective pool that eventually wins the competition for the three models (the spectra from the other pools were qualitatively similar). Figure 5, top, shows that in the theta frequency range, 4–8 Hz, the power is greatest for the two-pool model, followed by the slow and then the fast model; that is, the same order as the reaction times. We note that these effects extended to even lower frequencies, as low as 2 Hz, which is within the delta band [which extends from 1.5–4 Hz (Buzsaki, 2006)], so that the results described in this paper apply to a range of low frequencies that includes theta and delta. It could be that the theta somehow causes faster reaction times. Or it could be that the altered, slower inhibition in the slow and fast models has the effect of emphasizing low-frequency power, but that the mechanism for the faster reaction times is in fact the greater precue firing rate found on winning trials, greater for the models in the same order as shown in Figure 3. We return to this point in the Discussion, below.

To further investigate the role of theta band activity in the decision processes, we filtered the Va values for single trials using a rectangular filter set to 1 in the range 4–8 Hz, and to 0 previously. This was implemented using a continuous wavelet transform with 40 samples in the 4–8 Hz range. Figure 6 shows that, for the two-pool model, such filtered Va records for three individual trials (upper) and the average of 200 trials (lower). The results indicate that there was no phase reset phenomenon produced by the decision cues; that is, the signals did not develop, for example, peaks at the same time after the decision cues were applied.

Figure 6.

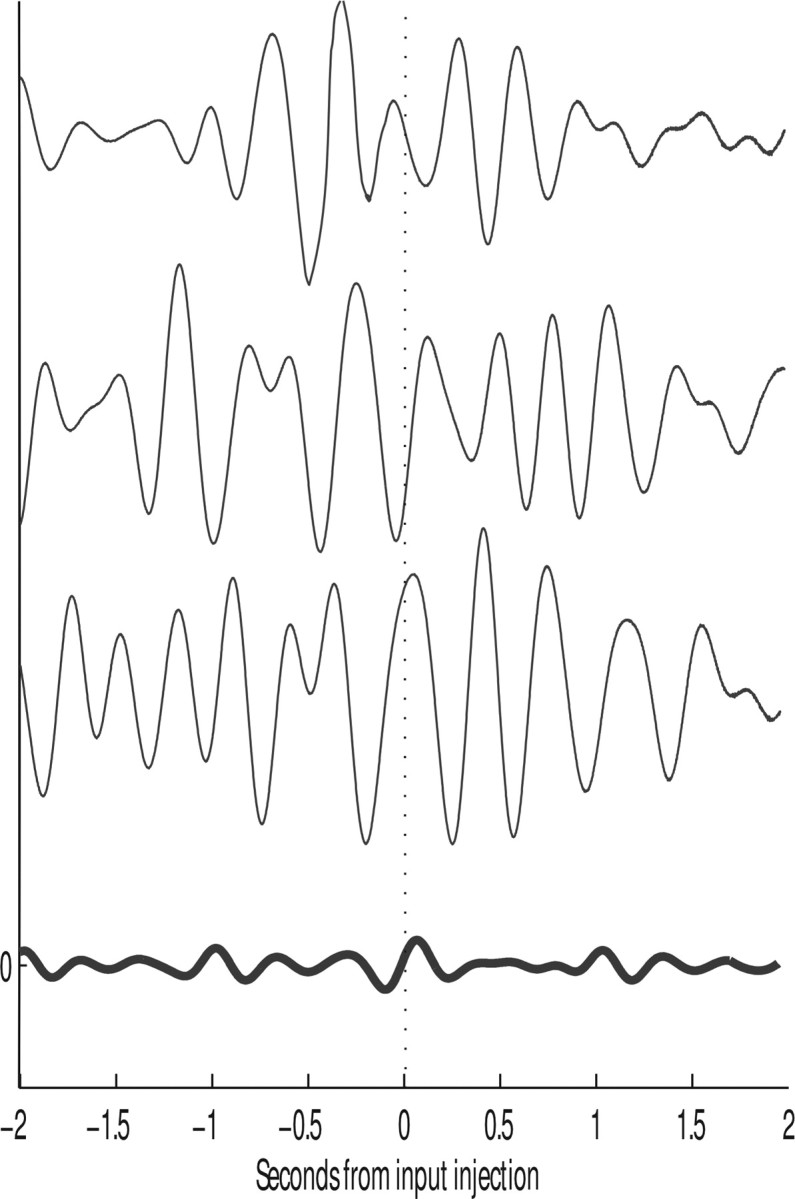
Figure 6.

Open in a new tab

Three different trials, randomly chosen, of theta-filtered average membrane potentials Va obtained using the slow model (top three lines), and the average of the theta-filtered Va over 200 trials (bottom, thick line) for the same model, for 2 s of simulation before and after the input injection. No phase-reset phenomenon is discernible.

In additional investigations, no significant correlation was found between the phase of theta oscillation at the moment of cue injection and the reaction time for a particular trial. As effects of the phase of slow waves at which stimuli are delivered may influence reaction times (Callaway and Yeager, 1960; Dustman and Beck, 1965) and whether a visual stimulus close to threshold is detected (Busch et al., 2009) in some empirical studies, future investigations with the present approach might consider whether such effects can be found in the model if the degree of slow-wave modulation is larger.

We also investigated whether there was a difference in the average membrane potential Va between the different models. There was a small effect for Va to be more depolarized in all pools in the two-pool model than in the slow or original (fast) model in the spontaneous, pre-decision cue period, but this was revealed clearly when Va filtered as above in the range 4–8 Hz was measured, which is what is shown in Figure 5, bottom. In the spontaneous period, the filtered Va indicated greater depolarization. After the decision cues were applied there were no differences in the filtered Va for the three models or in the firing rates.

Discussion

The reaction time distributions in Figure 2, top, show that the model with a small fraction of slower inhibitory neurons, and GABA conductances modified accordingly, has shorter reaction times than the original model with fast (10 ms) synaptic conductances shown in Deco and Rolls (2006). Comparison with the slow model decision time distribution shows that an important factor is the presence of two inhibitory neuron populations. The slow model has the same time-integrated change of GABA conductance as the two-pool model and the same average τGABA value, but its reaction times are considerably longer than the two-pool model. The impact of the slow neurons is shown clearly in Figure 2, bottom: decision time decreases linearly with the proportion of slow neurons until the spontaneous state becomes unstable. The critical proportion of slow neurons is between 25 and 30% of the total.

We suggest that the mechanism for the faster reaction times of the models with slow or two-pool inhibition is that, in the predecision period of spontaneous firing, there is a tendency for the firing rate of one of the pools to drift upward. This drift is greater for the models in the order of two-pools > slow pool > fast pool (Fig. 3), so that when the decision cues are applied, the pool that is already showing an upward drift (on average) will be more likely to win the competition, and will have less far to go when the decision cues are applied and the strong nonlinear dynamics caused by the positive recurrent collateral feedback fully engages. If the firing rate is already (on average across trials) a little up before the cues are applied, this will produce (on average) shorter reaction times.

We tested this hypothesis by applying an unequal bias to the two selective pools, using ΔI = 16, and there were more error trials for the two-pool then for the slow than for the fast models. The implication is that the prestimulus drift in the spontaneous activity is important, and that this is facilitated with slow inhibition and even more by two-pool inhibition.

We suggest that the drift is caused by activity in the recurrent collateral connections, which allow a form of integration of changes produced by the Poisson noise introduced into the network by the spike-firing times of each neuron. This integration is enhanced in the slow and two-pool models. We suggest that a possible mechanism for the less effective inhibition in the two-pool and slow models that leads to increased drift of the firing of the neurons in the model is that the longer the decay time for the inhibition, the greater the chance that it will be lost due to the refractory period of the excitatory neurons, as the excitatory neurons that have just fired will be insensitive to any inhibition in their refractory period.

We further note that if a network changes from asynchronous (desynchronized) to oscillatory activity, the net amount of inhibition will become smaller due to more being lost by the refractory period effect. In more detail, the inhibition will be greatest just after the inhibitory neurons fire, as the ion channels they open in the excitatory neurons are maximally open; and, if the excitatory neurons are firing at this part of the oscillatory cycle, a large amount of inhibition will be lost as they will relatively frequently be in a refractory state. Thus, oscillations could produce a net increase in the excitatory activity in a network.

Consistent with this slower or enhanced processing of slow changes in the slow and two-pool models, there was more power in the low-frequency (4–8 Hz) bands (low theta range) in the precue period of the models (two-pool > slow > fast models) (Fig. 5, top). The theta may reflect these dynamics altered toward slow state changes (increased power at low frequencies), but does not, per se and independently of the altered firing rate in the precue period, appear to contribute to the faster reaction times, for there was no evidence of any relation of theta phase to the reaction time, or for phase reset of the theta at the time the decision cues were applied (Fig. 6).

Frequency analysis shows that having two populations of inhibitory neurons with different time constants enhances theta activity in the model, as has been observed experimentally (Tort et al., 2007, 2008, 2009; Kendrick et al., 2009). Averaging the theta-filtered traces across trials shows that the decision making process does not entail phase reset; the oscillations of the single trials are ∼1 order of magnitude wider than the ones in the averaged trials, whereas, if phase resetting was the case, we would expect at some point oscillations that survive the averaging process.

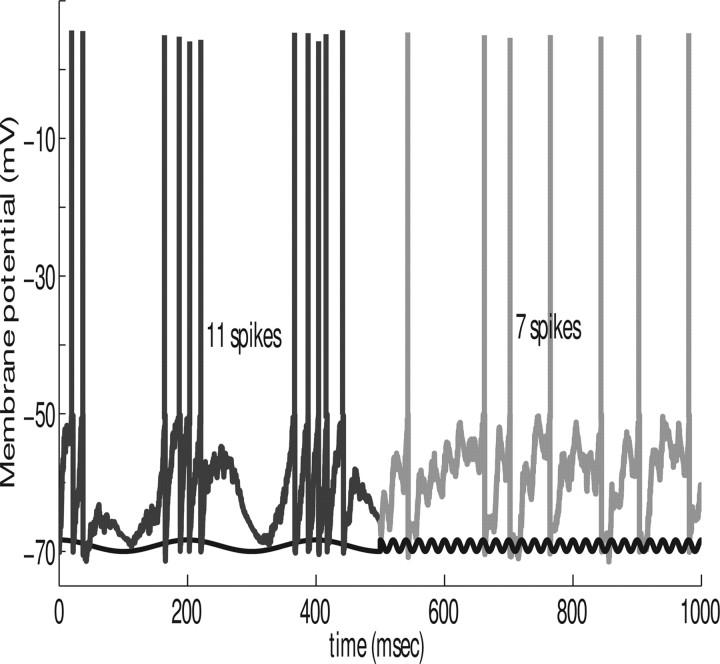
In this paper, we show that slow inhibition, or a mixture of slow and fast inhibition, can speed reaction times in a decision-making network. We suggest that slow drift in the firing rates before the decision cues are applied contributes to this effect, especially with the two-pool and slow models. We suggest part of the mechanism of the increased drift of the spontaneous firing rates before the decision cues are applied is related to a decrease in the overall inhibition being produced. Part of the mechanism for this may be that more of the neurons are in their refractory period when the inhibition is being received in the slow models, as the inhibition is being applied over a longer period in the slow and two-pool models. We tested this by decreasing the refractory period in the model to zero and found that the faster reaction times of the slow and two-pool models remained. We therefore suggest that the mechanism is as described next. In Figure 7, we plotted the membrane potential of a single integrate-and-fire neuron of the type specified in Equation 1 in response to currents applied as Isyn at slow (5 Hz) and at fast (50 Hz) frequencies and with identical amplitudes. The membrane time constant Cm/gm was 20 ms. Figure 7 shows that the membrane potential shows a larger modulation with the low- than with the high-frequency input. This effect is produced by the filtering effect produced by the membrane time constant, which acts as a low-pass filter, with smaller effects produced by the higher frequency of 50 Hz. Depending on the operating or average membrane potential, the larger modulation may produce more action potentials with the low than with the high frequencies, as illustrated in Figure 7. A further analysis of these dynamics is provided by Kang et al. (2010). Therefore, our hypothesis about the effects described in this paper is that an increase in slow excursions of the membrane potential produced by altering the nature of the inhibition in the network (having slow or two inhibitory populations of inhibitory neurons) can result in more action potentials being produced. This increase in the firing rate can then increase the reaction times of the network, which is sensitive to the excitability of the neurons in the network. The excitability is an important factor in the reaction times, as shown by previous research in which the excitability can be altered by, for example, changes in w+, as shown in Figure 1 (Brunel and Wang, 2001; Wang, 2002; Deco and Rolls, 2006; Rolls and Deco, 2010). Thus, our account of the findings described in this paper, that reaction times can be affected by low-frequency modulations (or oscillations) in neural activity, is that these modulations can be translated into effects on firing rates, which in turn influence the dynamics and reaction times of the networks.

Figure 7.

Figure 7.

Open in a new tab

The membrane potential of a single integrate-and-fire neuron of the type specified in Equation 1 in response to currents applied as Isyn at slow (5 Hz) and at fast (50 Hz) frequencies and with identical amplitudes. The frequency was changed at time = 500 ms, and its time course is shown by the sinusoidal waveform (black line). The membrane time constant gL was 20 ms. The membrane potential shows a larger modulation with the low than with the high-frequency input. This effect is produced by the filtering effect produced by the membrane time constant, which acts as a low-pass filter, with smaller effects therefore produced by the higher frequency of 50 Hz. Depending on the average membrane potential produced by other inputs to the neuron, the larger modulation of the membrane potential produced by low frequencies may produce more action potentials with the low than with the high frequencies, as illustrated. In the case illustrated, the main input to the neuron was the sinusoidal input, and VL was −70 mV.

Footnotes

A.S. and J.F. were partially supported by the Future and Emerging Technologies program within the Seventh Framework Programme for Research of the European Commission, under the FET-OPEN grant agreement BION, number 213219.

References

  1. Behrens TE, Hunt LT, Woolrich MW, Rushworth MF. Associative learning of social value. Nature. 2008;456:245–249. doi: 10.1038/nature07538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Blake R, Logothetis NK. Visual competition. Nat Rev Neurosci. 2002;3:13–21. doi: 10.1038/nrn701. [DOI] [PubMed] [Google Scholar]
  3. Boorman ED, Behrens TE, Woolrich MW, Rushworth MF. How green is the grass on the other side? Frontopolar cortex and the evidence in favor of alternative courses of action. Neuron. 2009;62:733–743. doi: 10.1016/j.neuron.2009.05.014. [DOI] [PubMed] [Google Scholar]
  4. Broadbent DE. The magic number seven after fifteen years. In: Kennedy A, Wilkes A, editors. Studies in long term memory. New York: Wiley; 1975. pp. 3–18. [Google Scholar]
  5. Brunel N, Wang XJ. Effects of neuromodulation in a cortical network model of object working memory dominated by recurrent inhibition. J Comput Neurosci. 2001;11:63–85. doi: 10.1023/a:1011204814320. [DOI] [PubMed] [Google Scholar]
  6. Busch NA, Dubois J, VanRullen R. The phase of ongoing EEG oscillations predicts visual perception. J Neurosci. 2009;29:7869–7876. doi: 10.1523/JNEUROSCI.0113-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Buzsaki G. New York: Oxford UP; 2006. Rhythms of the brain. [Google Scholar]
  8. Callaway E, 3rd, Yeager CL. Relationship between reaction time and electroencephalographic alpha phase. Science. 1960;132:1765–1766. doi: 10.1126/science.132.3441.1765. [DOI] [PubMed] [Google Scholar]
  9. Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, Berger MS, Barbaro NM, Knight RT. High gamma power is phase-locked to theta oscillations in human neocortex. Science. 2006;313:1626–1628. doi: 10.1126/science.1128115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cowan N. The magical number 4 in short-term memory: a reconsideration of mental storage capacity. Behav Brain Sci. 2001;24:87–114. doi: 10.1017/s0140525x01003922. discussion 114–185. [DOI] [PubMed] [Google Scholar]
  11. Deco G, Rolls ET. Decision-making and Weber's Law: a neurophysiological model. Eur J Neurosci. 2006;24:901–916. doi: 10.1111/j.1460-9568.2006.04940.x. [DOI] [PubMed] [Google Scholar]
  12. Deco G, Rolls ET, Romo R. Synaptic dynamics and decision-making. Proc Natl Acad Sci U S A. 2010;107:7545–7549. doi: 10.1073/pnas.1002333107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dustman RE, Beck EC. Phase of alpha brain waves, reaction time and visually evoked potentials. Electroencephalogr Clin Neurophysiol. 1965;18:433–440. doi: 10.1016/0013-4694(65)90123-9. [DOI] [PubMed] [Google Scholar]
  14. Fries P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn Sci. 2005;9:474–480. doi: 10.1016/j.tics.2005.08.011. [DOI] [PubMed] [Google Scholar]
  15. Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
  16. Grabenhorst F, Rolls ET, Parris BA. From affective value to decision-making in the prefrontal cortex. Eur J Neurosci. 2008;28:1930–1939. doi: 10.1111/j.1460-9568.2008.06489.x. [DOI] [PubMed] [Google Scholar]
  17. Green JD, Arduini AA. Hippocampal electrical activity in arousal. J Neurophysiol. 1954;17:533–557. doi: 10.1152/jn.1954.17.6.533. [DOI] [PubMed] [Google Scholar]
  18. Hölscher C, Anwyl R, Rowan MJ. Stimulation on the positive phase of hippocampal theta rhythm induces long-term potentiation that can be depotentiated by stimulation on the negative phase in area CA1 in vivo. J Neurosci. 1997;17:6470–6477. doi: 10.1523/JNEUROSCI.17-16-06470.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Jensen O. Maintenance of multiple working memory items by temporal segmentation. Neuroscience. 2006;139:237–249. doi: 10.1016/j.neuroscience.2005.06.004. [DOI] [PubMed] [Google Scholar]
  20. Kang J, Robinson HP, Feng J. Diversity of intrinsic frequency encoding patterns in rat cortical neurons: mechanisms and possible functions. PLoS One. 2010;5:e9608. doi: 10.1371/journal.pone.0009608. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kendrick KM, Zhan Y, Fischer H, Nicol AU, Zhang X, Feng J. Learning alters theta-nested gamma oscillations in inferotemporal cortex. Nat Precedings. 2009. Available at http://hdl.handle.net/10101/npre.2009.3151.2. [DOI] [PMC free article] [PubMed]
  22. Lansing RW. Relation of brain and tremor rhythms to visual reaction time. Electroencephalogr Clin Neurophysiol. 1957;9:497–504. doi: 10.1016/0013-4694(57)90037-8. [DOI] [PubMed] [Google Scholar]
  23. Lee H, Simpson GV, Logothetis NK, Rainer G. Phase locking of single neuron activity to theta oscillations during working memory in monkey extrastriate visual cortex. Neuron. 2005;45:147–156. doi: 10.1016/j.neuron.2004.12.025. [DOI] [PubMed] [Google Scholar]
  24. Lindsley DB. Psychological phenomena and the electroencephalogram. Electroencephalogr Clin Neurophysiol. 1952;4:443–456. doi: 10.1016/0013-4694(52)90075-8. [DOI] [PubMed] [Google Scholar]
  25. Lisman J, Buzsáki G. A neural coding scheme formed by the combined function of gamma and theta oscillations. Schizophr Bull. 2008;34:974–980. doi: 10.1093/schbul/sbn060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lisman JE, Idiart MA. Storage of 7 ± 2 short-term memories in oscillatory subcycles. Science. 1995;267:1512–1515. doi: 10.1126/science.7878473. [DOI] [PubMed] [Google Scholar]
  27. Maier A, Logothetis NK, Leopold DA. Global competition dictates local suppression in pattern rivalry. J Vis. 2005;5:668–677. doi: 10.1167/5.9.2. [DOI] [PubMed] [Google Scholar]
  28. Miller P, Brody CD, Romo R, Wang XJ. A recurrent network model of somatosensory parametric working memory in the prefrontal cortex. Cereb Cortex. 2003;13:1208–1218. doi: 10.1093/cercor/bhg101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Rizzuto DS, Madsen JR, Bromfield EB, Schulze-Bonhage A, Seelig D, Aschenbrenner-Scheibe R, Kahana MJ. Reset of human neocortical oscillations during a working memory task. Proc Natl Acad Sci U S A. 2003;100:7931–7936. doi: 10.1073/pnas.0732061100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Rolls ET. Oxford: Oxford UP; 2008. Memory, attention, and decision-making: a unifying computational neuroscience approach. [Google Scholar]
  31. Rolls ET, Deco G. Oxford: Oxford UP; 2010. The noisy brain: stochastic dynamics as a principle of brain function. [DOI] [PubMed] [Google Scholar]
  32. Romo R, Hernández A, Zainos A. Neuronal correlates of a perceptual decision in ventral premotor cortex. Neuron. 2004;41:165–173. doi: 10.1016/s0896-6273(03)00817-1. [DOI] [PubMed] [Google Scholar]
  33. Tort AB, Rotstein HG, Dugladze T, Gloveli T, Kopell NJ. On the formation of gamma-coherent cell assemblies by oriens lacunosum-moleculare interneurons in the hippocampus. Proc Natl Acad Sci U S A. 2007;104:13490–13495. [Google Scholar]
  34. Tort AB, Kramer MA, Thorn C, Gibson DJ, Kubota Y, Graybiel AM, Kopell NJ. Dynamic cross-frequency couplings of local field potential oscillations in rat striatum and hippocampus during performance of a T-maze task. Proc Natl Acad Sci U S A. 2008;105:20517–20522. doi: 10.1073/pnas.0810524105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Tort AB, Komorowski RW, Manns JR, Kopell NJ, Eichenbaum H. Theta-gamma coupling increases during the learning of item-context associations. Proc Natl Acad Sci U S A. 2009;106:20942–20947. doi: 10.1073/pnas.0911331106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wang XJ. Probabilistic decision making by slow reverberation in cortical circuits. Neuron. 2002;36:955–968. doi: 10.1016/s0896-6273(02)01092-9. [DOI] [PubMed] [Google Scholar]
  37. White JA, Banks MI, Pearce RA, Kopell NJ. Networks of interneurons with fast and slow gamma-aminobutyric acid type A (GABAA) kinetics provide substrate for mixed gamma-theta rhythm. Proc Natl Acad Sci U S A. 2000;97:8128–8133. doi: 10.1073/pnas.100124097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Wong KF, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. J Neurosci. 2006;26:1314–1328. doi: 10.1523/JNEUROSCI.3733-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES