A Novel Form of Presynaptic Plasticity Based on the Fast Reactivation of Release Sites Switched Off during Low-Frequency Depression

Abstract

Repetitive firing of neurons at a low frequency often leads to a decrease in synaptic strength. The mechanism of this low-frequency depression (LFD) is poorly understood. Here, LFD was studied at Aplysia cholinergic synapses. The absence of a significant change in the paired-pulse ratio during LFD, together with the facts that neither the time course nor the extent of LFD were affected by the initial release probability, suggests that LFD is not related to a depletion of the ready-to-fuse synaptic vesicles (SVs) or to a decrease in the release probability, but results from the silencing of a subpopulation of release sites. A subset of SVs or release sites, which acquired a high release probability status during LFD, permits synapses to rapidly and temporarily recover the initial synaptic strength when the stimulation is stopped. However, the recovery of the full capacity of the synapse to sustain repetitive stimulations is slow and involves spontaneous reactivation of the silent release sites. Application of tetanic stimulations accelerates this recovery by immediately switching on the silent sites. This high-frequency-dependent phenomenon underlies a new form of synaptic plasticity that allows resetting of presynaptic efficiency independently of the recent history of the synapse. Microinjection of a mutated Aplysia synapsin that cannot be phosphorylated by cAMP-dependent protein kinase (PKA), or a PKA inhibitor both prevented high-frequency-dependent awakening of release sites. Changes in the firing pattern of neurons appear to be able to regulate the on–off status of release sites via a molecular cascade involving PKA-dependent phosphorylation of synapsin.

Introduction

The frequency modulation during the firing of action potentials by neurons is a key element for information processing within neural networks. At the presynaptic level, one of the most common consequences of increasing the spiking frequency is a decrease in the quantity of neurotransmitter released at each stimulus. This ubiquitous form of homosynaptic presynaptic plasticity is referred to as synaptic depression. However, this term covers multiple situations distinguishable by the frequency of stimulation that induces them and/or the mechanisms involved. Synaptic depression has been shown to result from depletion of the readily releasable pool (RRP) of synaptic vesicles (SVs) (Foster and Regehr, 2004), inhibition of presynaptic calcium channel (Xu et al., 2007), or failure of action potential propagation (Brody and Yue, 2000). Moreover, increases in the frequency of neuronal activity can also convert presynaptic release sites from an active to a silent status in a reversible manner (Royer et al., 2000; Gover et al., 2002; Moulder et al., 2006, 2008).

How the functional status of a release site can be blocked on a change in the firing rate remains an open question. At Aplysia synapses, disabling the function of synaptic vesicle proteins (such as the GTPase Rac or synaptobrevin) and plasma membrane-associated proteins (such as the phospholipase D1) inhibits exocytosis by decreasing in the number of active release sites and not by changing the probability of release (Doussau et al., 2000; Humeau et al., 2001b, 2002, 2007). This suggests that the fusiogenic status of docked SVs as well as that of the plasma membrane at the fusion site determines the “on–off” functional status of the release site. Along the same line, although the number of docked SVs is not affected in boutons that had been silenced by chronic depolarization at hippocampal synapses, the number of ready-to-fuse SVs is reduced, suggesting that blockade of a step during SV priming underlies synapse silencing (Moulder et al., 2006). Moreover, awakening of the release sites previously silenced by impairing Rac function could be produced by the application of a short burst of high-frequency stimuli (Humeau et al., 2007), indicating that silencing/awakening relies on the frequency and timing of the neuronal firing pattern.

Here, we investigated the mechanisms underlying low-frequency-induced depression (LFD) at identified cholinergic synapses of Aplysia. We found that LFD is not related to a depletion of ready-to-fuse SVs or to a decrease in the probability of release, but is attributable to switching off of the functional status of release sites. Spontaneous awakening of release sites silenced during LFD occurs within ∼40 min, but the application of short bursts of stimulation can almost immediately switch on the sites. This burst-dependent reactivation of silent synapses is a new form of synaptic plasticity that resets the presynaptic strength to the level observed before LFD induction. The presynaptic phosphoproteins synapsins have been implicated in the control of synaptic strength when the firing patterns of neurons changes (Fdez and Hilfiker, 2006). Here, we found that the burst-dependent awakening of the sites silenced during LFD requires phosphorylation of synapsin by protein kinase A (PKA).

Materials and Methods

Acetylcholine release and electrophysiological recordings at Aplysia synapses

Aplysia californica were purchased from the University of Florida (Miami, FL). Electrophysiological experiments were performed at identified, chloride-dependent, inhibitory cholinergic synapses in dissected buccal ganglia of Aplysia as described previously (Doussau et al., 2000; Humeau et al., 2001a,b, 2002). Presynaptic neurons (B4 and B5) and one postsynaptic neuron (either B3 or B6) were impaled with two glass microelectrodes (3 m KCl, Ag/AgCl₂, 2–10 MΩ). Action potentials were alternately evoked every 20 s in B4 or B5 using an AxoClamp 2B amplifier (Molecular Devices) (i.e., each presynaptic neuron was stimulated every 40 s; 0.025 Hz). The ensuing evoked, chloride-dependent IPSCs were recorded using the conventional two-electrode voltage-clamp technique (Geneclamp-500 amplifier and Digidata 1322A from Molecular Devices). Their reversal potential V_rev, was determined every 5 min. IPSCs were recorded at a holding potential V_h hyperpolarized 30 mV from V_rev. To express the IPSC amplitude as a value proportional to the amount of released ACh, but independent of the driving force for Cl⁻ ions, IPSC amplitude (I) was converted to apparent membrane conductance changes (G), according to the equation G = I/(V_h − V_rev). Although this has the dimension of a membrane conductance (nanosiemens), we refer to it in this paper as the IPSC amplitude.

Extracellular media and intraneuronal injection

Dissected buccal ganglia were maintained at 22°C using a Peltier-plate system and superfused continuously (10 ml · h⁻¹) with a physiological medium containing the following (in mm): 460 NaCl, 10 KCl, 33 CaCl₂, 78 MgCl₂, 10 HEPES, pH 7.5, as previously described (Humeau et al., 2001b, 2002, 2007). The very high concentration in divalent cations that we used prevented spontaneous neuron firing activity, which otherwise may induce undesired forms of short-term plasticity. This medium corresponds to a [Ca²⁺]/[Mg²⁺]_e ratio of 0.42. When necessary, [Ca²⁺]/[Mg²⁺]_e was modified as described previously (Humeau et al., 2001b). Intraneuronal injection of recombinant proteins and peptides was performed as detailed previously (Humeau et al., 2001b, 2002, 2007). Since the injected volume was in the range of 1–2% of the cell body volume, we assumed that the final intraneuronal concentration was ∼1% of that in the injection micropipette.

Quantal analysis parameters

Consider a synapse or a group of synapses as an array of n independent release sites (i.e., morphological sites), each potentially capable of releasing only one quantum at a time, and with its own individual p, and consider that p is compound resulting from the product of two terms: pA (the chance that a readily releasable quantum is available at the site), which defines the eligibility status of the site for exocytosis (i.e., its functional status), and p_o, the output probability (the chance that the site releases a quantum if a quantum is available) (for review, see Quastel, 1997). According to this view, the product N = n · pA corresponds to the number of functional release sites. Thus, any event modifying the number of morphologically defines sites or eligibility status is susceptible to induce changes in N. We discussed previously the possibility that the fusogenic status of docked SVs may determine the eligibility or functional status of the release site, and pA is likely not a stochastic parameter (Humeau et al., 2007).

If the release of one SV content produces a postsynaptic response of fixed amplitude q, according to the binomial statistics, at a release site, the average postsynaptic response amplitude is as follows: μ = p · q, with variance, Var = p · (1 − p) · q². Now, consider the N functional release sites, P, the average of individual output probability p_o, and Q, the average amplitude of the quantum of response, and assume that the release process at each site is independent of that at the other sites and quanta sum up linearly. The mean amplitudes and variances at the N sites add linearly, and the mean amplitude of the compound response is as follows: I_mean = Σ_i = _1→Nμ_i. This can be rearranged as follows: I_mean = N · P · Q. The fluctuations of the responses around the mean have a variance of the form: Var = N · P · (1 − P) · Q². Analyzing the relationship between I_mean and Var allows getting insights into N, P, and Q (Silver et al., 1998; Reid and Clements, 1999; Humeau et al., 2001b, 2002, 2007; Scheuss et al., 2002; Clements, 2003; Silver, 2003; Foster and Regehr, 2004).

Although the above simplified expressions do not take into account the intrasite and intersite variability in quantum amplitude and the heterogeneity in p at the N sites, which contribute to the fluctuation in amplitude of the postsynaptic response (Clements, 2003; Silver, 2003), the general form of the relationship between Var and I_mean is preserved (Humeau et al., 2002, 2007). Therefore, from the two above equations, it can be deduced that when only P is modified, Var = f(I_mean) is a parabola: Var = Q · I_mean − I_mean²/N. This can be used to estimate P (see below). Our previous work at the studied cholinergic Aplysia synapse has shown that the Var = f(I_mean), obtained by manipulating [Ca²⁺]/[Mg²⁺]_e, is almost a simple parabola, indicating that the other sources of variability have no or modest effect at this preparation. Note that parameter N deduced by variance–mean analysis is a functional parameter and refers to the number of release sites able to experience SV fusion, as defined above (Humeau et al., 2001b, 2002, 2007). Thus, N does not take into account long-lasting silent sites.

Determination of the average release probability at various [Ca²⁺]/[Mg²⁺]_e

The Var = f(I_mean) was built at the studied Aplysia cholinergic synapses by manipulating [Ca²⁺]/[Mg²⁺]_e (Humeau et al., 2002) (see Results). To pool the Var and I_mean data obtained from distinct experiments, individual Var = f(I_mean) plots were normalized to the maximum Var (Var_max) and the corresponding I_mean (I_mean-to-Var_max) was determined by fitting the Var = f(I_mean) plot from each experiment by a quadratic function of the following form: y = y₀ + a · x + b · x², with all parameters left free, using the nonlinear regression procedure running with SigmaPlot 10 (Systat Software) (Humeau et al., 2007). Although the above described normalization of Var and I_mean data did not permit a determination of Q and N from initial slope and parabola extent, the corresponding P could be evaluated. Indeed, when the normalized Var = f(I_mean) is a parabola, similar as in non-normalized plots, Var_max is reached at p = 0.5, and thus P can be determined at each point of the parabola (e.g., when I_mean = I_max/4, p = 0.25, and when I_mean = I_max/2, p = 0.5).

Application of short trains at high frequency

Typically, posttetanic potentiation (PTP) was initiated by two trains (50 Hz for 2 s) (Humeau et al., 2001a). Twenty seconds after the second 50 Hz train terminated, the stimulation rate was returned to the initial rate (i.e., 0.025 Hz). The extent of PTP was expressed by normalizing the amplitude of the maximal IPSC during PTP to the “basal IPSC amplitude” as determined by averaging the amplitudes of the 10 IPSCs preceding the application of the conditioning 50 Hz trains.

Approximation of the time course of LFD, LFD after rest, and posttetanic potentiation during depression

Time constants of LFD, LFD after rest (LFD_AR), and posttetanic potentiation during depression (PTP_LFD) were obtained by fitting the I = f(t) plots using SigmaPlot (Systat Software) using the following equations: I(t) = y₀ + ω_I · exp(−t/τ_I) + ω_II · exp(−t/τ_II) (for LFD) or I(t) = y₀ + ω_fast · exp(−t/τ_fast) + ω_I · exp(−t/τ_I) + ω_II · exp(−t/τ_II) (for LFD_AR and PTP_LFD), where y₀ is either the control plateau at 0.025 Hz or the plateau of LFD, τ_I and τ_II, the time constants of depression during LFD and LFD_AR, and τ_fast, the time constant of the disappearance of the superimposed facilitation observed at depressed synapses during LFD_AR. We imposed the following constraints to the weighting factors: ω_I + ω_II = 100 (for LFD); ω_fast + ω_I + ω_II = 100 (for LFD_AR and PTP_LFD).

Use of the paired-pulse ratio as a measure of release probability

Rationale.

The analysis of the paired-pulse ratio (PPR) between the amplitudes of two postsynaptic responses induced by twin stimuli separated by a short (<1 s) time interval (PPR = I₂/I₁) allows one to gain insight into changes in release probability. Albeit in certain preparations, other mechanisms can produce PPR changes, such as fast inactivation of postsynaptic receptors or of presynaptic P/Q-type Ca²⁺ channels (Bellingham and Walmsley, 1999; Heine et al., 2008), at the studied Aplysia synapse, the extent of PPR is mostly, if not exclusively, determined by P (Doussau et al., 1998; Humeau et al., 2007). The rationale for using PPR to probe changes in P is the following: the extent of the I₂/I₁ ratio is determined by the balance between a facilitatory component and a depression component both activated by the conditioning stimulus. The facilitatory component, which affects P, is probably the consequence of a Ca²⁺-dependent conditioning of the release machinery (Zucker and Regehr, 2002) and the saturation of cytosolic Ca²⁺ buffers (Felmy et al., 2003). The depression component is likely to result from incomplete refilling of the SV pool consumed by the conditioning stimulus (Zucker and Regehr, 2002; Singer and Diamond, 2006).

PPR determination.

Paired postsynaptic responses were evoked by presynaptically applying two brief depolarizing pulses of 5 ms separated by an interval of 40 ms. Since the mean decay time of the evoked postsynaptic responses recorded at 22°C at the cholinergic synapses used in this study varies with the postsynaptic cell and the preparation, the postsynaptic responses partially overlapped. Thus, the amplitude measured at the peak of IPSC₂ was corrected by the exponential residual of I₁, as described previously; this corrected amplitude is referred as to I₂ (Doussau et al., 1998).

PPR modeling.

Let us say that the number of quanta released at the first stimulus of a pair is N₁ · P₁, where N₁ is the number of active (i.e., eligible) sites, and P₁ is the output probability of release at stimulus 1. Thus, on average, I₁ = N₁ · P₁ · Q₁. At the time of stimulus 2, N₂ is the number of release-ready SVs not consumed at stimulus 1 [i.e., N₁ · (1 − P₁)] plus the number of SVs that have been replaced (refilling) and/or acquired fusion competence during the interpulse interval. This fraction depends on the number of SVs (N₁ · P₁) that fused at stimulus 1. Therefore, N₂ = N₁ · ((1 − P₁) + (k_(t) · N₁ · P₁) = N₁ · (1 + ((k_(t) − 1) · P₁)), where k_(t) is the fraction of refilling with the interpulse. Because of the accumulation of Ca²⁺ ions at stimulus 1, P₂ ≥ P₁. On average, I₂ = N₂ · P₂ · Q₂, and when expressed as a function of N₁ and P₁, I₂ = N₁ · (1 + ((k_(t) − 1) · P₁)) · P₂ · Q₂. If we assume that quantal size Q does not change between the two paired stimuli, (Q₁ = Q₂), I₂/I₁ = (1 + ((k_(t) − 1) · P₁)) · P₂/P₁. This means that PPR is independent of N. Accordingly, any change in PPR should indicates a modification of the release probability P. Conversely, no change in PPR when synaptic strength is modified should indicate that modification of N is responsible for changing the amplitude of the postsynaptic responses.

If (but see below) P₂/P₁ and k_(t) are independent of [Ca²⁺]_e, the relationship between I₂/I₁ and P₁ (made by changing [Ca²⁺]_e) is simple and has the following form: y = y₀+ a · x with y₀ = P₂/P₁, and a negative slope, a = −[(P₂/P₁) · (1 − k_(t))]. Also, the relationship between I₂/I₁ and I₁ becomes linear with same y₀, but with a negative slope, a′ = −[(P₂/P₁) · (1 − k_(t))]/I_1max, where I_1max is the amplitude of I₁ when P₁ = 1 (i.e., I_1max = N₁ · Q).

However, it is rather unlikely that P₂/P₁ and k_(t) are independent of [Ca²⁺]_e over a wide range of [Ca²⁺]_e and the linear function provided above corresponds to the tangent of PPR = f(I₁) at a given [Ca²⁺]_e. This relationship can be also used to provide a linear approximation of a limited portion of the PPR = f(I₁) plot. At the studied Aplysia cholinergic synapse, PPR = f(I₁) plots made by a 10-fold change in the [Ca²⁺]/[Mg²⁺]_e (from 2.1 to 0.21) display a large almost linear portion, albeit they significantly deviate from linearity at the lowest and highest [Ca²⁺]/[Mg²⁺]_e [Humeau et al. (2007), their Fig. 1] (see also Fig. 2). This suggests that, at this Aplysia synapse and under the physiological conditions used ([Ca²⁺]/[Mg²⁺]_e between 0.21 and 2.1), P₂/P₁ and k_(t) can be considered to be nearly independent of [Ca²⁺]_e.

Figure 1.

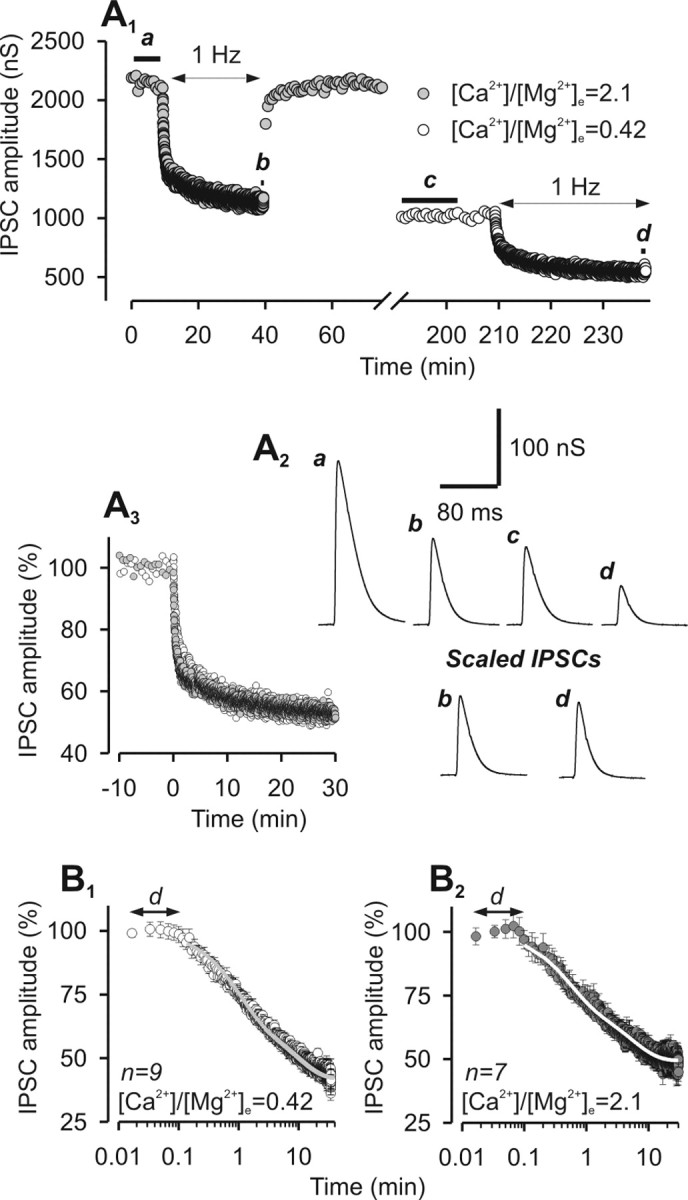
Time course and plateau of LFD are independent of the initial release probability. A₁, Representative experiment of IPSC amplitude plotted against time before and after the induction of LFD at high and low [Ca²⁺]/[Mg²⁺]_e. A₂, Top traces (a–d), Average traces of at least 10 successive IPSCs recorded during the corresponding period indicated by thick horizontal lines on A₁. Bottom traces, Traces b and d corresponding to the plateau of LFD at high and low [Ca²⁺]/[Mg²⁺]_e, respectively, were normalized with respect to the mean value of IPSCs recorded during the plateau at 0.025 Hz. A₃, Superimposition of normalized IPSCs amplitude during LFD monitored at low and high Ca²⁺-containing medium (same symbols as in A₁). IPSC amplitudes were normalized with respect to the mean IPSC value recorded during the plateau at 0.025 Hz. Time 0 denotes the start of 1 Hz stimulation. B, Time course of LFD at low (B₁) and high (B₂) Ca²⁺-containing medium was determined by averaging normalized IPSCs from n experiments as indicated on the graphs. The solid gray and white lines represent the biexponential decay curves fitted to the data. The duration of the delay (d) before the actual induction of depression is represented by the black arrows. Error bars indicate SEM.

Figure 2.

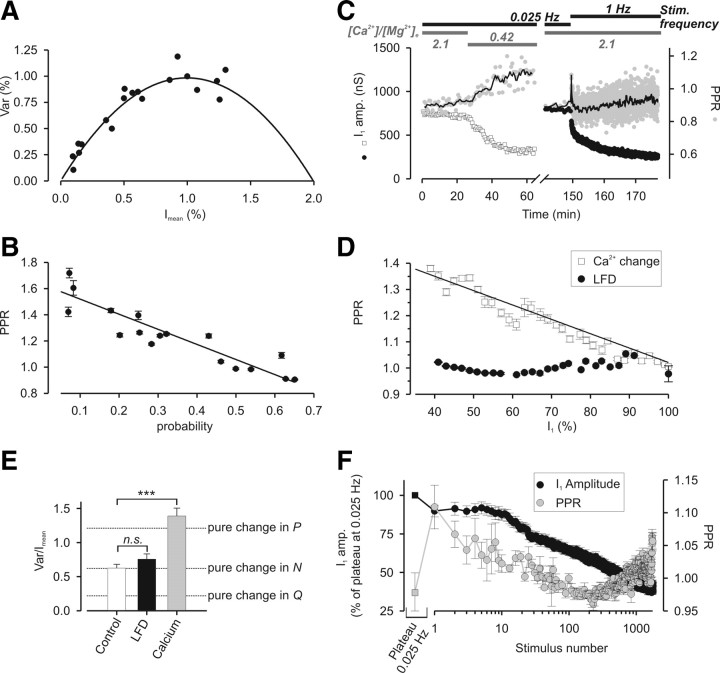
LFD is not attributable to a decrease in P. A, B, PPR is inversely proportional to the probability of release at Aplysia cholinergic synapses. A, Stationary analysis of the fluctuations in IPSC amplitude when release probability is modified by changes in [Ca²⁺]/[Mg²⁺]_e. The Var = f(I_mean) plot was obtained by pooling the results from five different experiments during which ACh release was evoked by paired-pulse stimulations and under different [Ca²⁺]/[Mg²⁺]_e (0.14, 0.21, 0.42, 0.84, and 2.1). After each change in [Ca²⁺]/[Mg²⁺]_e and stabilization of IPSC amplitude, I_mean PPR and Var were determined of at least 20 subsequent IPSCs. For more detail, see Materials and Methods. The probability of release was deduced from each point in this plot, and associated with the corresponding value of PPR. B, Plots of PPR against the probability after changes in [Ca²⁺]/[Mg²⁺]_e. The probability was calculated from the Var = f(I_mean) plot (A). The solid black line represents the linear function fitted to the data. C, D, Comparison of the effects of a change in [Ca²⁺]/[Mg²⁺]_e with LFD on PPR and IPSC amplitude. C, Typical experiment during which PPR (gray-filled symbols) and IPSC amplitude (open squares and filled circles, respectively) were probed successively during a change in [Ca²⁺]/[Mg²⁺]_e (left) or during LFD (right). The values of the [Ca²⁺]/[Mg²⁺]_e and of the stimulation frequency are represented by the horizontal gray bars and the horizontal black bars, respectively. Note that the extent of the blockage of ACh release was approximately identical after the two treatments. The thin solid black lines correspond to the mean value of PPR calculated from three successive paired stimuli. D, Plots of PPR against I₁ amplitude after changes in [Ca²⁺]/[Mg²⁺]_e or during LFD. The solid black line represents the linear function fitted to the data after changes in [Ca²⁺]/[Mg²⁺]_e. E, Averaged values of Var/I_mean obtained at the plateau of 0.025 Hz stimulation (open bar), at the plateau of LFD (black-filled bar) and after a change in [Ca²⁺]/[Mg²⁺]_e (from 2.1 to 0.42; gray-filled bar). The dashed lines represent the expected values of Var/I_mean that should be observed if the ∼43% decrease in IPSC amplitude during LFD or after a change in [Ca²⁺]/[Mg²⁺]_e were simply attributable to a change in Q, N, or P. ***p < 0.001; n.s. denotes no significant difference (i.e., p > 0.05). F, Minor PPR changes during LFD; each point corresponds to the mean value of I₁ (black-filled circles) or PPR (gray-filled circles) from 11 experiments. The black-filled square and the gray-filled square correspond to the mean values of IPSC amplitude and PPR respectively calculated during the plateau at 0.025 Hz. Stimulus 1 corresponds to the first response at 1 Hz. Error bars indicate SEM.

Data presentation

In some cases, values obtained from various neurons were averaged and, unless otherwise stated, presented as mean ± SEM. In several experiments, data were normalized using the average value observed under control conditions (i.e., before any treatment). When appropriate (normally distributed data with equal variance), the significance between mean differences was tested by a one-way ANOVA or the Student's t test. Asterisks denote the following: *p < 0.05, **p < 0.01, and ***p < 0.001. n.s. denotes no significant difference (i.e., p > 0.05). If not stated otherwise, the number n, mentioned when analyzing the statistical significance of the comparison, refers to the number of independent sets of experiments.

Results

Low-frequency depression does not result from a depletion of ready-to-fuse synaptic vesicles

In the buccal ganglion of Aplysia, the twin B4 and B5 cholinergic neurons make well established inhibitory synapses on the same set of postsynaptic neurons. Evoked release level remains stable for very long time when the stimulation rate is maintained at a given frequency, but any increase, even moderate, in the stimulation frequency reproducibly decreases synaptic efficacy (Doussau et al., 1998; Humeau et al., 2001a,b, 2002). As shown in Figure 1A, increasing the stimulation rate from 0.025 to 1 Hz quickly induced an onset of depression reaching a plateau (at 43.16 ± 1.79% from control amplitude) in ∼30 min. Because of its induction at a low frequency (i.e., 1 Hz), we termed it LFD and investigated the underlying mechanisms.

At many synapses, synaptic depression occurring on repetitive activity arises from depletion of the RRP of SVs, possibly because of incomplete refilling at each stimulus (for review, see Kavalali, 2006). Accordingly, provided the interpulse interval is shorter than the time needed to refill all the empty release sites (we expected this is the case using a 1 Hz frequency), an increase in the output release probability P should produce faster depletion of the RRP on repetitive stimulation. Experimentally, P can be easily manipulated by changing the concentration of extracellular Ca²⁺ (Silver et al., 1998; Humeau et al., 2002). Under such conditions, we determined (see Materials and Methods, and below) an average p = 0.26 when [Ca²⁺]/[Mg²⁺]_e = 0.42 and p = 0.62 when [Ca²⁺]/[Mg²⁺]_e = 2.1. LFD was elicited under two conditions, namely in low and high [Ca²⁺]/[Mg²⁺]_e-containing medium (Fig. 1A₁). Although the average IPSC amplitude was greatly modified by ∼2.4-fold (at 0.025 Hz) because of the increase in P between the low and high [Ca²⁺]/[Mg²⁺]_e conditions, the time courses of LFD were very similar (Fig. A₃): in both conditions, the delay (d) before the actual induction of depression (8.4 s at low P and 7.4 s at high P) and the relative extents of depression (43.16 ± 1.79% at low P and 44.22 ± 1.39% at high P) were similar. In addition, the fast (τ_I) and slow (τ_II) time constants, and the relative weight of the decay components were all in the same range of magnitude (Table 1, Fig. 1B). Overall, these findings indicate that the kinetics and extent of LFD are independent of initial P, suggesting that changes in refilling of empty release sites or replacement of consumed SVs is unlikely to be the main cause of LFD.

Table 1.

Time constants of LFD, LFD_AR, and PTP_LFD were obtained by fitting mean amplitude values of IPSC (I) at any stimulus from n experiments (see Materials and Methods)

	Stim.	n	ωfast (%)	τfast (s)	ωI (%)	τI (s)	ωII (%)	τII (min)
LFD low P	S	9			54.6 ± 4.9	54.5 ± 6.9	45.4 ± 2.3	8.9 ± 1.0
LFD high P	S	7			51.9 ± 3.3	39.1 ± 9.7	48.1 ± 5.5	8.1 ± 0.9
Stat. with LFD low P					*	*	NS	NS
LFD low P + ApSynAla	S	4			64.3 ± 2.1	39.1 ± 7.1	35.7 ± 3.9	10.2 ± 2.8
Stat. versus LFD low P					*	NS	NS	NS
LFD low P + PKAi6-22	S	4			57.2 ± 3.8	18.7 ± 2.9	42.8 ± 3.9	6.8 ± 1.7
Stat. with LFD low P					NS	**	NS	NS
LFD high P	PP	10			43.3 ± 4.1	26.8 ± 4.5	56.7 ± 5.8	10.4 ± 1.1
LFDAR rest 10 s	PP	4	100	1.2 ± 0.2
LFDAR rest 15 s	PP	4	100	1.6 ± 0.4
LFDAR rest 20 s	PP	6	85.8 ± 5.8	1.0 ± 0.1	14.2 ± 2.0	19.8 ± 6.1
Stat. with LFD high P			—	—	—	NS
LFDAR rest 40 s	PP	5	86.3 ± 13.5	1.5 ± 0.2	13.7 ± 1.7	70.8 ± 12.0
Stat. with LFD high P			—	—	—	**
LFDAR rest 60 s	PP	4	76.7 ± 9.7	1.4 ± 0.4	23.3 ± 10.3	34.3 ± 10.2
Stat. with LFD high P			—	—	—	NS
LFDAR rest 90 s	PP	6	69.0 ± 12.0	1.0 ± 0.2	18.4 ± 7.8	13.2 ± 3.9	12.6 ± 0.6	2.3 ± 0.6
Stat. with LFD high P			—	—	—	NS	—	***
LFDAR rest 120 s	PP	5	65.0 ± 12.2	1.4 ± 0.2	22.1 ± 6.0	24.3 ± 8.3	12.1 ± 0.5	2.2 ± 0.1
Stat. with LFD high P			—	—	—	NS	—	**
LFDAR rest 240 s	PP	4	63.1 ± 3.6	1.6 ± 0.4	23.3 ± 6.1	22.8 ± 5.5	13.6 ± 1.4	3.4 ± 0.3
Stat. with LFD high P			—	—	—	NS	—	**
LFDAR rest 900 s	PP	7	49.0 ± 8.9	1.3 ± 0.2	29.2 ± 6.1	17.8 ± 2.7	21.8 ± 3.0	4.3 ± 0.3
Stat. with LFD high P			—	—	—	NS	—	***
PTPLFD rest 20 s	PP	5	60.3 ± 12.7	1.0 ± 0.1	27.7 ± 5.3	6.6 ± 0.1	12.0 ± 2.7	5.5 ± 0.8
Stat. with LFD high P			—	—	—	**	—	**
PTPLFD rest 120 s	PP	3	59.1 ± 6.9	1.6 ± 0.4	26.1 ± 4.1	9.4 ± 3.8	14.8 ± 2.7	3.4 ± 1.2
Stat. with LFD high P			—	—	—	**	—	**
Stat. with PTPLFD rest 20 s			NS	NS	—	NS	—	NS

Low P and high P correspond to [Ca²⁺]/[Mg²⁺]_e = 0.42 and [Ca²⁺]/[Mg²⁺]_e = 2.1, respectively. LFD_AR and PTP_LFD were probed at [Ca²⁺]/[Mg²⁺]_e = 2.1. LFD, LFD_AR, and PTP_LFD were probed using either a single stimulus (denoted as S) or a paired-pulse stimulation (interval, 40 ms; denoted as “PP”). The statistical differences (mentioned as “Stat.”) in the weights (ω_I and ω_II) and in the time constants (τ_I and τ_II) of the exponential decays were tested for two different conditions using either the t test or the Mann–Whitney rank sum test. The statistical difference in τ_fast calculated during LFD_AR and PTP_LFD at any rest period was probed using a one-way ANOVA. This test did not detect any statistical difference in τ_fast (p = 0.64).

*p < 0.05,

**p < 0.01, and

***p < 0.001. NS denotes no significant difference (i.e., p > 0.05).

Changes in the release probability or in quantal size do not mediate LFD

The use of the PPR as an index to detect change in P, although widely used in many works, has been challenged by several studies showing that modification of postsynaptic receptors properties may also induce change in PPR (Akopian and Walsh, 2002; Heine et al., 2008). At Aplysia cholinergic synapses, PPR has been shown to be inversely proportional to [Ca²⁺]/[Mg²⁺]_e (Doussau et al., 1998; Humeau et al., 2001a, 2007) and a change in [Ca²⁺]/[Mg²⁺]_e induces a change in P (Humeau et al., 2002). However, a direct correlation between PPR and P has never been established. In a series of five experiments, ganglia were superfused using different [Ca²⁺]/[Mg²⁺]_e ratios (0.14, 0.21, 0.42, 0.84, and 2.1) and ACh release was evoked using twin stimuli (interval, 40 ms). When a stable plateau was reached, PPR, I_mean, and Var were determined for at least 20 subsequent IPSCs [for a rationale, see Materials and Methods and Humeau et al. (2002, 2007)]. To pool the data, Var = f(I_mean) data were fitted using a simple parabola and then normalized to the fitted maximum Var and the corresponding I_mean (Fig. 2A). From the pooled parabola, average P were deduced from each point in this plot and associated with the corresponding PPR value. As shown in Figure 2B, a linear relationship between PPR and P can be established as follows: PPR = 1.6 − 1.2 · P (r² = 0.86).

These results confirm that, at these synapses, PPR is actually proportional to P. Therefore, PPR was used to determine whether LFD results from a decrease in P. The mean values of IPSC amplitude and PPR were determined before LFD by applying twin stimuli (40 ms interval) at 0.025 Hz, and after the induction of LFD by increasing the paired-pulse stimulation frequency to 1 Hz. To allow a comparison with the effect of manipulating P, we also monitored PPR when [Ca²⁺]/[Mg²⁺]_e was progressively reduced. Although IPSC amplitude was markedly reduced at the plateau of LFD (I₁ of the pair reduced by ∼40%), PPR was only slightly increased (Fig. 2C, right) compared with the PPR enhancement observed on decreasing ACh release to a similar extent (by ∼40%) by lowering [Ca²⁺]/[Mg²⁺]_e (Fig. 2C, left). The PPR = f(I₁) relationship obtained by manipulating [Ca²⁺]/[Mg²⁺]_e was satisfactorily fitted using a linear function with a negative slope of the following form: PPR = 1.4 − 4.9*I₁ (r² = 0.91) (Fig. 2D). In contrast, changes in I₁ were not correlated with changes in PPR (a linear relationship between PPR and I₁ cannot be established, r² = 0.15) when PPR was determined during LFD (Fig. 2D). This lack of a significant change in PPR during the course of LFD indicates that a reduction in P cannot directly contribute to LFD.

Next, we investigated whether changes in the number of the functional release sites, N, or in the quantal size, Q, may underlie LFD. Assuming that I_mean = N · P · Q and Var = N · P · (1 − P) · Q² (see Materials and Methods), the ratio Var/I_mean = Q · (1 − P) between the initial conditions (i.e., at 0.025 Hz, before LFD) and plateau of LFD (i.e., at 1 Hz) can be used to identify which of N, Q, and P is modified and responsible for the reduction in I_mean during LFD. Figure 2E presents the calculated values of Var/I_mean that we should have observed if the ∼44% decrease in IPSC amplitude during LFD were attributable to a pure change in Q, N, or P (dashed lines). Note that modification of N leaves Var/I_mean unmodified, whereas this ratio changes in opposite ways when Q or P is modified. We found no significant difference between the Var/I_mean determined before LFD or at its plateau (Fig. 2E, compare open and black-filled bars). However, when [Ca²⁺]/[Mg²⁺]_e was decreased from 2.1 to 0.42 (i.e., a P decrease from 0.62 to 0.26), Var/I_mean was significantly enhanced (Fig. 2E, compare open and gray-filled bars). These findings pinpoint that LFD mainly results from a decrease in N, indicating a silencing of release sites. However, these data cannot distinguish whether this results from a permanent or long-lasting (1) block of the refilling at certain release sites, (2) blockage of the priming process for a subpopulation of SVs, (3) or from an inactivation of the fusion competence of plasma membrane at a subpopulation of release sites.

Minor PPR changes during LFD indicate concomitant expression of opposite forms of synaptic plasticity

Although, overall, PPR does not change at the plateau of LFD compared with the control before LFD, minor changes in PPR (ranging between 0.97 and 1.12) reproducibly occurred at the same stimulus number during the course of LFD (Fig. 2F). When the stimulation rate was raised from 0.025 to 1 Hz, PPR was slightly, but significantly (p = 0.01), increased at the first stimulus, whereas the depression in I₁ amplitude was barely apparent. Surprisingly, over the subsequent ∼200–250 stimuli, PPR decreases concomitantly with I₁ (Fig. 2F) pinpointing a puzzling situation during which the decline in I₁ is associated with an increase in P. Then, during the last phase of LFD (after stimulus 250), there was again a slight increase in PPR, whereas the amplitude of I₁ continued to decrease. Overall, this suggests that several opposite forms of synaptic plasticity are operating during the early phase of LFD; after an initial decrease in P observed at the first stimulus, the reduction in N, which underlies LFD, is temporarily compensated by a concomitant short-term synaptic enhancement because of an increase in P (decrease of both I₁ and PPR for the first 200–250 stimuli). This is likely to account for the observed delay that occurs after the 1 Hz stimulation is initiated. This may also explain why, in some preparations, a transient potentiation of IPSC amplitude could be observed during the earliest phase of LFD (data not shown).

Recovery from depression after variable periods of inactivity implicates the awakening of silenced release sites

To investigate the recovery from LFD, we first examined the kinetics by which depressed synapses at rest (i.e., without stimulation) recovered their initial release capacity. LFD was induced, and after the plateau was reached (after ∼30 min at 1 Hz), the stimulation was stopped for varying periods of rest (of duration Δt), before resuming the stimulation (paradigm displayed on Fig. 3A). After a rest period of ∼60 s, the amplitude of the first IPSC reached the value of the plateau determined before induction of LFD (Fig. 3B). However, compared with control conditions (i.e., when LFD was elicited after a plateau at 0.025 Hz), the capacity to sustain repetitive stimulation after a rest period was very low. Indeed, for the shortest rest periods, resuming the 1 Hz stimulation led to a depression with a very fast decay (τ_fast ranging from 1 to 1.6 s) (Table 1), which reached the plateau of LFD observed before rest with just few stimuli (Fig. 3B) (see below). We will refer to this as LFD_AR. LFD_AR displayed a fast monoexponential decay for Δt <20 s, and clearly a triexponential decay for Δt >40 s (Fig. 3C,D). The two slowest decay components of LFD_AR were in the same order of magnitude (tens of seconds for τ_I and several minutes for τ_II) as those determined for control LFD. Overall, regardless of the rest periods, the time constant τ_I of LFD_AR was not significantly changed as compared with τ_I of LFD (Table 1). In contrast, the time constant τ_II of LFD_AR was markedly faster at all rest periods tested (Fig. 3E, Table 1). Even if τ_II of LFD_AR tended to increase proportionally with the length of the rest period (Fig. 3E), at the longest rest period tested (15 min) this kinetic component was more than twofold faster than the τ_II of LFD. This indicates that a residual form of depression induced during LFD was not still present after 15 min of rest.

Figure 3.

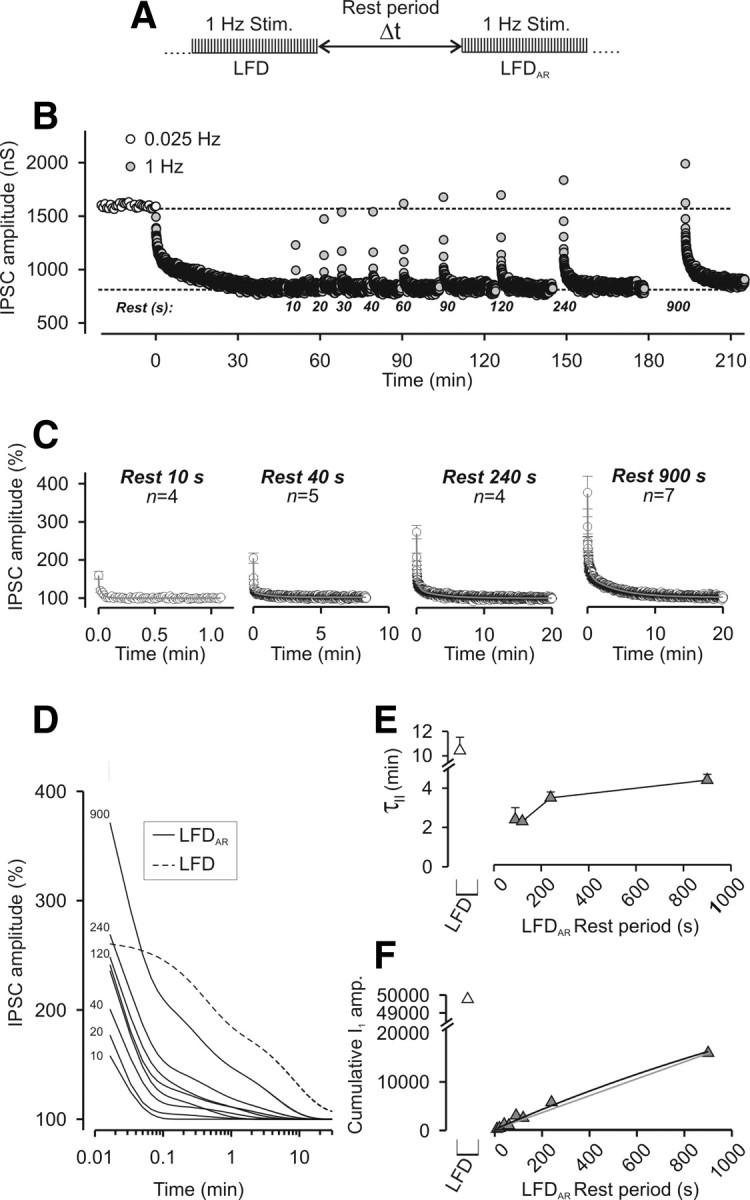
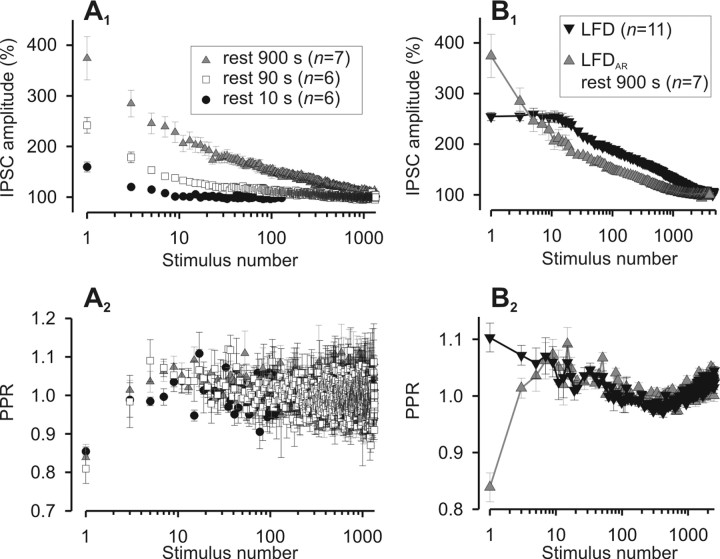
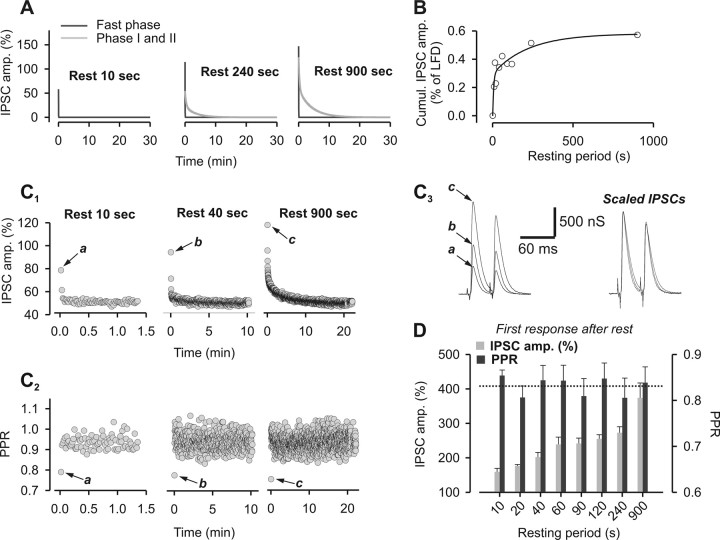
Recovery from LFD after variable rest periods. A, Paradigm of stimulation used to elicit LFD_AR. B, Typical experiment performed at the same synapse during which LFD_AR was probed after different duration of the rest periods. Time 0 denotes the start of 1 Hz stimulation. Note that the plateaus of LFD and LFD_AR are identical. C, The time course of LFD_AR was determined by averaging IPSCs at any stimulus from n experiments as indicated on the graphs. The solid gray lines represent the exponential decay curves fitted to the data. Only four representative rest periods are shown. D, Superimposition of the fitted decay curves to the data obtained for all the tested rest periods. The number indicated on the left of curves corresponds to the respective duration of the rest period. For C and D, IPSC amplitudes were normalized to the average IPSC amplitude determined during the plateau of LFD. E, The slowest time constants (τ_II) of LFD_AR (gray-filled triangles) that were obtained by fitting mean amplitude values of IPSC (Table 1) were plotted against the length of the rest periods and compared with the slowest time constant of LFD (open triangle). F, Cumulative plots of IPSC amplitude were calculated from the fits obtained in D over a period of 30 min (same symbols as in E). Error bars indicate SEM.

The cumulative IPSC amplitude can be used as an index of the total number of quanta released during a sustained stimulation (Schneggenburger et al., 1999). Since the above data suggest that, after short rest periods, the capacity to sustain ACh release at depressed synapses is far from being fully recovered, we calculated the cumulative IPSC amplitude over the first 30 min of LFD or LFD_AR (either from LFD_AR data or extrapolating their fit to 30 min). Figure 3F shows that the initial release capacity calculated during LFD (Fig. 3F, gray-filled triangle) was not yet recovered after rest periods as long as Δt = 900 s. Extrapolation of the “cumulative IPSC amplitude = f(Δt)” relationship using either a monoexponential function rising to a maximum (Fig. 3F, solid black line) or a linear function (Fig. 3F, solid gray line) indicated that spontaneous full recovery of release capacity is expected between 40 min and 3 h. Similarly as the deduction made when examining τ_II of LFD_AR, these data indicate that recovery from LFD is a slow process, which is not complete after 15 min of rest (Fig. 3, compare E, F). Together, this suggests that LFD is a form of presynaptic long-term depression.

To investigate the mechanisms underlying the spontaneous recovery from LFD, we analyzed the PPR changes that occurred during LFD_AR. Although increasing the duration of the rest period at the plateau of LFD greatly increased the extent of recovery in the IPSC amplitude (see above) (Fig. 4A₁), the average PPR remained unchanged (Fig. 4A₂). Except for the PPR determined for the first two IPSCs corresponding to the very fast phase of LFD_AR, the time course of minor PPR changes occurring during LFD_AR and LFD were indistinguishable (Fig. 4B₂). Together, these findings suggest that, except for the early phase, LFD_AR and LFD and their underlying mechanisms are similar. The fact that the changes in IPSC amplitude during LFD or LFD_AR were not associated with PPR changes (except for stimuli 1 and 2 corresponding to the fast early phase) indicates that synaptic depression is in both cases attributable to a decrease in N (i.e., release site silencing). By inference, this suggests that the recovery of synaptic efficacy during the rest periods is attributable to the reactivation of a fraction of release sites that were turned off during LFD, and that the number of sites that switch on during rest is somehow proportional to the duration of the rest period. However, both the persistence of a faster kinetic component and an incomplete restoration of the release capacity (Fig. 3E,F) indicate that the functioning of these sites was not reinitiated to initial conditions at the end of the rest periods tested.

Figure 4.

Effects of the duration of the rest period on IPSC amplitude and PPR. A, PPR change during LFD_AR is independent of the duration of the rest period. A₁, Mean values of I₁ from n experiments plotted against the stimulus number during LFD_AR after three distinct rest periods. A₂, Corresponding values of PPR. B, Minor PPR changes during LFD_AR are similar to those observed during LFD (except for the first response) and appear fixed to stimulus number. B₁, Mean values of I₁ from n experiments plotted against the stimulus number during LFD (same data as in Fig. 2D) and LFD_AR (rest, 900 s; same data as in Fig. 5A₁). B₂, Corresponding values of PPR. For A₁ and B₁, IPSC amplitudes were normalized to the average IPSC amplitude determined during the plateau of LFD. Error bars indicate SEM.

Next, we investigated the early fast depression phase that characterizes LFD_AR and contributes mostly to the first two IPSCs recorded after resuming the 1 Hz stimulation. The fastest exponential decay component of LFD_AR (τ_fast) was isolated by a fitting procedure (Fig. 5A) and the number of quanta released during this phase was estimated in function of the duration of the rest period (Fig. 5B). The function “cumulative IPSC amplitude = f(Δt)” could be fitted by a biexponential rising a maximum with time constants of 7.9 s and 4 min. This fit indicates that the capacity to sustain release during the fast phase promptly reached saturation. In contrast to the slower decay components of LFD_AR and LFD (τ_I and τ_II), the early fast decay phase of LFD_AR was associated with a very low value of PPR (Fig. 5C), which indicates that the probability of release (P) is high during this early short-lived phase. Importantly, the particular value of PPR determined at stimulus 1 (denoted as a, b, or c in Fig. 5C₂) was constant and independent of the duration of the rest period (Fig. 5D). After several minutes of rest, cytosolic [Ca²⁺] should have returned to basal levels and thus the acquisition of a high P status cannot be accounted for by a high amount of Ca²⁺ in the presynaptic terminal at the time of resuming the 1 Hz stimulation. However, this does not rule out a role for Ca²⁺ in this process. Indeed, a rise in cytosolic [Ca²⁺], which is likely to occur at naive synapses during the first stimulation at 1 Hz, may induce a switch of active releases sites to a high P status that persists for minutes (at least 15 min) after stopping stimulation. In any cases, the fast saturation of the early fast phase (Fig. 5B) clearly indicates that the high P status is acquired for rest periods too short to allow the awakening of silenced release sites. Therefore, the acquired high P is likely to apply to release sites that had not been turned off during LFD (i.e., release sites still active at the plateau of depression, or a subset of them). Overall, this high P phase is the expression of a peculiar form of presynaptic plasticity that superimposes on the awakening of release sites. This superimposed facilitation required a rest period to be expressed, is preserved whatever the length of the rest period is, and fades only after reactivation of the release machinery. The fact that the kinetics of LFD_AR was the result of the superimposition of two different forms of synaptic depression (the fast decaying component τ_fast and the components τ_I and τ_II of LFD) probably explains the absence of a delay in the onset of depression observed at naive synapse (Fig. 1B).

Figure 5.

Characterization of the fast decay phase of LFD_AR. A, Exponential decay curves of LFD_AR for all rest period tested could be decomposed into a monoexponential decay function (solid black line) with a fast component τ_fast (0.9 s < τ_fast < 1.7 s) and a biexponential decay function (solid gray line) with two components τ_I and τ_II (15 s < τ_I < 70 s and τ_II > 2 min). Only three representative rest periods are displayed. IPSC amplitudes were normalized to the average IPSC amplitude determined during the plateau of LFD. B, Cumulative plots of IPSCs during the fast phases of LFD_AR were calculated from the fits of these fast phases (represented by the solid black lines in A) were plotted against the duration of the rest period. Values of the cumulative plots were normalized with respect to the value of the cumulative plot of IPSC amplitude calculated during LFD. C, Representative experiments showing the time course of I₁ (C₁) and of the corresponding values of PPR (C₂) during LFD_AR elicited after three distinct rest periods. C₃, The left traces represent the first pairs of IPSCs recorded after the indicated rest period and correspond to the black arrow in C₁. The right traces represent the same pairs of IPSCs normalized with respect to the amplitude of I₁. For C₁, IPSC amplitudes were normalized with respect to the mean IPSC value recorded during the plateau at 0.025 Hz. D, Mean values of the amplitude of the first response and the corresponding PPR as a function of the duration of the rest period. The dashed line represents the mean value of PPR of the first response calculated independently of the duration of the rest period. IPSC amplitudes were normalized to the average IPSC amplitude determined during the plateau of LFD. Error bars indicate SEM.

An application of high-frequency trains rapidly switches on the release sites silenced during LFD and allows fast resetting of neurotransmitter release

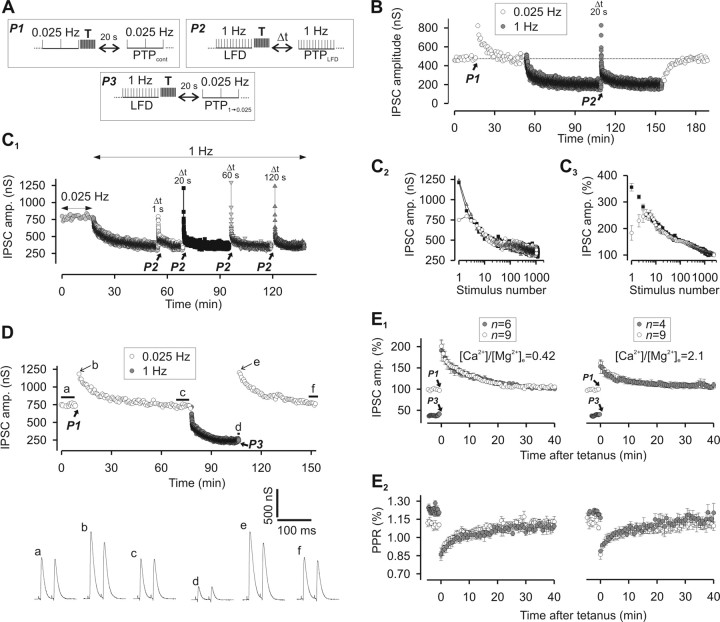
We previously reported that silencing of release sites because of inactivation of Rac-GTPase can be relieved by a high-frequency stimulation (or “tetanus”), which activates a bypass pathway (Doussau et al., 2000; Humeau et al., 2002, 2007). We examined whether a similar stimulation paradigm accelerates the reactivation of the sites switched off by the 1 Hz stimulation. However, as a tetanus induces PTP (Doussau et al., 1998, 2000; Humeau et al., 2001a, 2007), the concomitant acceleration of recovery from LFD must be separated from the overlapping PTP. First, PTP characteristics were determined under control conditions before induction of LFD (Fig. 6A, paradigm P1). This classical form of PTP is termed PTP_cont. Consistent with previous reports (Doussau et al., 1998; Humeau et al., 2001a, 2002, 2007), PTP_cont peaked at 73% above the basal amplitude and recovered to basal levels with a monoexponential decay (with a time constant of 11 min) (Fig. 6B). After LFD was induced and had reached plateau, the PTP paradigm was applied (Fig. 6A, paradigm P2), inducing a PTP termed PTP_LFD (Fig. 6B). The 1 Hz stimulation was then resumed to induce LFD. With a delay of 20 s between the 50 Hz trains and this stimulation, the IPSC amplitudes at peaks of both PTP_LFD and PTP_cont were found to be identical (peak of PTP_cont = 822 nS and peak of PTP_LFD = 827 nS) (Fig. 6B). Since the stimulation rates used to monitor PTP_LFD and PTP_cont were different (0.025 vs 1 Hz), their time courses were also different. This apparent recovery from LFD after the 50 Hz trains (Fig. 6B) is probably the consequence of a combination of different forms of synaptic plasticity that act either additively or synergistically. For release sites silenced during LFD, 50 Hz trains may act by immediately switching them on by either bypassing the mechanism underlying their silencing or accelerating their spontaneous recovery. Fifty hertz trains may also induce a classical form of PTP (i.e., PTP_cont) that acts on release sites still active at the plateau of LFD, on release sites that were reactivated by these trains, and on release sites with a high intrinsic P. Interestingly after delays longer than 10 s, the peak and time courses of PTP_LFD were found to be independent of the duration of the rest period (Fig. 6C₁,C₂). Note the perfect superimposition of IPSC amplitudes for PTP_LFD elicited after rest periods of 1, 20, and 120 s on Figure 6C₂. When PTP_LFD was probed 1 s after the 50 Hz train, a marked reduction of IPSC amplitude at stimuli 1 and 2 was observed (Fig. 6C₂,C₃), but the amplitudes of IPSCs at any other stimulus number were identical with the amplitudes of corresponding IPSCs measured during PTP_LFD with longer rest periods (Fig. 6C₃). This short-term depression, which overlaps PTP_LFD only during the first 5 s that follow the 50 Hz trains, may be attributable to a 50-Hz-induced depletion of the RRP as previously reported for PTP_cont at these synapses (Humeau et al., 2007). Alternatively, this short-term depression may be the consequence of a transient activation of a Ca²⁺-activated K⁺ current induced by Ca²⁺ accumulation during the tetanus as previously shown for PTP at another Aplysia synapse (Kretz et al., 1982). In any case, regardless of the mechanisms underlying PTP_LFD, the process is initiated during or immediately after the 50 Hz train.

Figure 6.

Recovery from LFD after a tetanus. A, Paradigms of stimulation used to elicit PTP_cont, PTP_LFD, and PTP_1→0.025. Tetanus (T) corresponds to two trains of APs at 50 Hz for 1 s each produced at 1 s interval. B, Representative experiment showing that the peaks of PTP_cont and PTP_LFD are identical. PTP_cont and PTP_LFD were elicited at the times indicated by the black arrows. P1 and P2 denote the stimulation paradigm illustrated in A. For B and C₁, the times mentioned above the peaks of PTP_LFD indicate the duration of the rest period after the conditioning trains (i.e., Δt in the paradigm P2). C₁, Typical experiment performed at the same synapse during which PTP_LFD was probed after different duration of the rest period after the conditioning trains. Conditioning trains were applied at the times indicated by the black arrows. C₂, The superimposition of IPSC amplitude from C₁ obtained during PTP_LFD elicited after rest periods after the conditioning train of 1 s (open circles), 20 s (black-filled squares), and 120 s (gray-filled triangles) shows that the time course of PTP_LFD was independent of the duration of the rest period after the conditioning trains. C₃, The time courses of PTP_LFD probed after rest periods after the conditioning trains of 1 s (open circles) and 20 s (black-filled squares) were obtained by averaging IPSCs amplitude recorded at the same stimulus number from four and five experiments, respectively. D, E, Resetting of ACh release after a tetanus. D, Representative experiment from a series of four, showing that the peak and time course of PTP_cont and PTP_1→0.025 are identical. Traces a, c, d, and f represent average traces of at least 10 successive IPSCs recorded during the period indicated by the thick horizontal lines. Traces b and e correspond to IPSCs recorded at the peaks of PTP_cont and PTP_1→0.025, respectively, as indicated by the thin black arrow. E₁, Superimposition of the time courses of PTP_cont (open circles) and PTP_1→0.025 (gray-filled circles) elicited at low and high [Ca²⁺]/[Mg²⁺]_e (left and right panels, respectively). Conditioning trains were applied at the times denoted by the black arrows. Mean values of IPSCs (from n experiments as indicated on the graphs) were expressed as a percentage of basal values (i.e., mean values of at least 10 successive IPSCs monitored during 0.025 Hz stimulation). E₂, Corresponding values of PPR. Note that the values of PPR were slightly higher at the plateau of LFD (gray-filled circles, before tetanus) as already shown in Figure 2C. Error bars indicate SEM.

Since PTP_LFD and PTP_cont were not monitored at the same stimulation frequency, an evaluation of the release capacity of the synapses (as defined above) could not be performed. Thus, we compared the time course of PTP_cont with the time course of a PTP elicited during a plateau of LFD, but this time probed with a 0.025 Hz stimulation frequency (Fig. 6A, paradigm P3). This PTP was termed PTP_1→0.025 (Fig. 6D). Since we previously established that PTP_cont at these Aplysia synapses is attributable to a transient increase in P, we also monitored PPR. As shown in Figure 6E, the amplitudes of IPSCs at any stimulus number, as well as the extent of PPR (monitored in the same neuron) were identical during PTP_cont and PTP_1→0.025. This was also independent of the initial release probability P (i.e., at various [Ca²⁺]/[Mg²⁺]_e) (Fig. 6E). These experiments indicate that the 50 Hz stimulus can relieve LFD, and suggest that, after a train of high-frequency stimulation, the release parameters are fixed to values that are independent of the history of the synapse.

Next, we determined the release component contributing to PTP_LFD. Given the paradigm used to induce PTP_LFD, this latter is likely to result from a combination of PTP_cont and LFD_AR. Decay of PTP_LFD recorded after a delay ≥20 s after the 50 Hz train was well fitted by a triexponential function with time constants close to those reported for LFD_AR (Table 1). To separate the contribution of PTP_LFD from spontaneous recovery from depression attributable to the rest period between the 50 Hz train and resuming stimulation (Fig. 6A), the amplitudes of IPSCs recorded during LFD_AR were subtracted from those corresponding to the same stimulus number during PTP_LFD (Fig. 7A₁ for Δt = 20 s; B₁ for Δt = 120 s). These differences were still well fitted by a triexponential function, confirming that the 50 Hz trains act on all release sites participating in LFD_AR.

Figure 7.

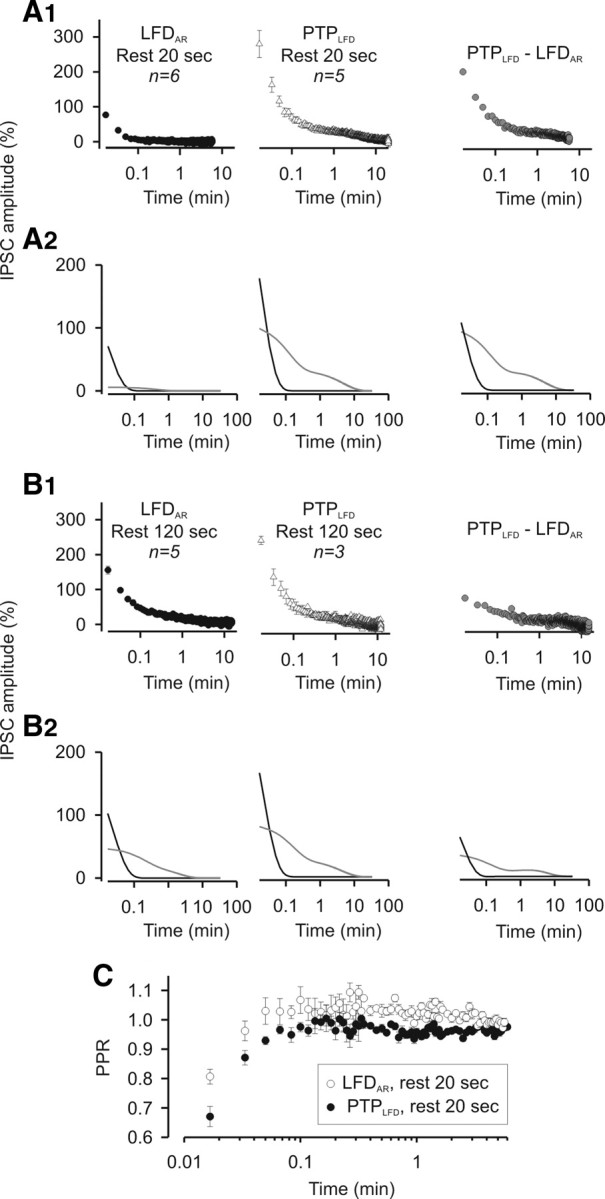
High-frequency stimulations accelerate the reactivation of the same population of release sites that were reactivated during period of inactivity. A₁, Left and middle, Mean values of IPSCs recorded during LFD_AR and PTP_LFD after a rest period of 20 s. Each point corresponds to the mean value of n experiments as indicated on the graphs. Right, Subtraction of the mean values of IPSCs recorded during LFD_AR after a rest period of 20 s from the corresponding IPSCs (i.e., at the same stimulus number) recorded during PTP_LFD after a rest period of 20 s. A₂, The time courses of LFR_AR, PTP_LFD, and the difference between PTP_LFD and LFR_AR could be fitted by a triexponential decay curve, which can be decomposed into a monoexponential decay with a fast component (0.9 s < τ_fast < 1.7 s; black lines) and a biexponential decay with time constants τ_I and τ_II close to the ones found in LFD (gray lines). B, Same measurements as in A, but for a rest period of 120 s. C, Superimposition of the mean values of PPR calculated for each stimulus during PTP_LFD and during LFD_AR after a rest period of 20 s. For A₁ and B₁, IPSC amplitudes were normalized to the average IPSC amplitude determined during the plateau of LFD. Error bars indicate SEM.

Determination of the relative weights of the three decay components revealed that, after the 50 Hz tetanus, the extents of the very fast phase (Fig. 7A₂,B₂, black line) and phases I and II (Fig. 7A₂,B₂, gray line) were increased in comparison with spontaneous recovery after a period of rest. This effect was less marked after a Δt = 120 s (Fig. 7B₂), suggesting that the subsets of release sites reactivated by 50 Hz trains and release sites that spontaneously switched on during a period of inactivity are the same.

If a transient increase in P also contributes to PTP_LFD (as in PTP_cont), PPR should transiently decrease as observed during PTP_1→0.025 or PTP_cont. To visualize an eventual increase in P during PTP_LFD, we superimposed the mean values of PPR obtained during PTP_LFD from the corresponding PPR values obtained during LFD_AR. Indeed, an increase in P was found to contribute to a much higher extent to PTP_LFD than during LFD_AR because PPR was significantly lower during PTP_LFD than during LFD_AR (Fig. 7C).

Together, these data indicate that trains of high-frequency stimulation are able to induce a rapid, nearly complete recovery from LFD, notably by accelerating the kinetics of spontaneous recovery from LFD. This raises the question of the synaptic mechanisms that allow immediate “resetting” of release characteristics to the level observed before LFD was induced.

Phosphorylation of synapsin at its P-site 1 is implicated in LFD and resetting

Phosphorylation of synapsin at its phosphorylation site 1 (P-site 1) by PKA has been shown to be essential in several forms of short-term plasticity including synaptic depression and PTP (Angers et al., 2002; Chi et al., 2003; Fiumara et al., 2004, 2007; Bonanomi et al., 2005; Hilfiker et al., 2005; Menegon et al., 2006).

We tried to determine whether phosphorylation of synapsin by PKA plays a role in LFD, PTP, and the resetting of synaptic strength at Aplysia cholinergic synapses. Presynaptic neurons were injected with either a recombinant Aplysia synapsin bearing a Ser⁹→Ala mutation (ApSynAla) that suppresses its ability to be phosphorylated by PKA (Fiumara et al., 2004, 2007) or a highly specific inhibitor of PKA (peptide 6–22 amide; PKAi_6–22) (Hilfiker et al., 2001).

As shown in Figure 8A, neither ApSynAla nor PKAi_6-22 had any effect on the basal release of ACh monitored at 0.025 Hz, but they both strongly affected the amplitude and the time course of LFD elicited at 1 Hz (Fig. 8B). The delay (d) that precedes the onset of depression was virtually abolished, and a significant depression was detected (by ∼20%) already at the first stimulus at 1 Hz. Analysis of the decay of LFD revealed that, after intracellular application of ApSynAla or PKAi_6-22, LFD was best fitted by a biexponential decay with phases I and II similar to phase I and II measured under control conditions (Table 1). Moreover, the plateau of LFD was diminished (26.32 and 30.26% with ApSynAla and PKAi_6-22, respectively), compared with the control plateau (43.16 ± 1.79%).

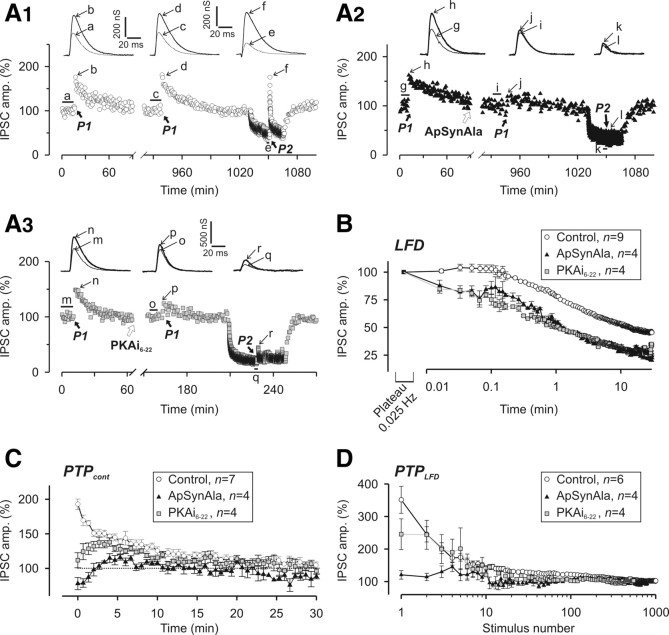
Figure 8.

Phosphorylation of synapsin at P-site 1 by PKA is involved in LFD, PTP_cont, and PTP_LFD. A₁, A₂, Representative experiment from a series of three during which PTP_cont (paradigm P1) (Fig. 6A) and PTP_LFD (paradigm P2) (Fig. 6A) (rest period of 20 s) were elicited in a mock-injected presynaptic neuron (A₁) or in a neuron injected with ApSynAla (A₂). Conditioning trains were applied at times indicated by the thick black arrows. A₃, PTP_cont and PTP_LFD probed before and after microinjection of PKAi_6-22, an inhibitor of PKA. ApSynAla (A₂) and PKAi_6-22 (A₃) were injected at the time indicated by the white arrows. Traces a, c, e, g, i, k, m, o, and q correspond to the mean traces of at least 10 successive IPSCs recorded before the conditioning train as indicated by the thick horizontal black lines, whereas traces b, d, f, h, j, l, n, p, and r were recorded at the peak of PTP_cont or PTP_LFD as indicated by the thin black arrows. B, Phosphorylation of synapsin at P-site 1 by PKA is involved in LFD. Comparison of the time course of LFD (mean values of IPSCs from n experiments as indicated on the graph) elicited in control condition (open circles, same values as in Fig. 1B₁) and neurons injected with either ApSynAla (black-filled triangles) or PKAi_6-22 (gray-filled squares), respectively. C, D, Changes in IPSC amplitude during PTP_cont (C) and PTP_LFD probed after a rest period of 20 s (D). PTP was determined in control neurons (open circles) and in neurons injected with either ApSynAla (black-filled triangles) or PKAi_6-22 (gray-filled squares). Each point corresponds to mean values of IPSCs from n experiments as indicated on the graphs. Note that intracellular injections of ApSynAla and PKAi_6-22 greatly altered the PTP_cont and PTP_LFD. For A–C, IPSC amplitudes were normalized to the average IPSC amplitude determined during the plateau at 0.025 Hz. For D, IPSC amplitudes were normalized to the average IPSC amplitude determined during the plateau of LFD. Error bars indicate SEM.

Intracellular injections of ApSynAla and PKAi_6-22 greatly altered both PTP_cont (Fig. 8C) and PTP_LFD (Fig. 8D). In this series of experiments ([Ca²⁺]/[Mg²⁺]_e = 0.42), the PTP_cont peaked at 92% (±7.6%; n = 7) above basal IPSC amplitude, and decayed monoexponentially (time constant of 11 min). After ApSynAla microinjections, PTP was abolished, creating instead a marked posttetanic depression (by 22.1 ± 8.9%; n = 3) (Fig. 8A₂,C). PKAi_6-22 microinjections reduced and delayed the peak of PTP_cont; indeed, the peak was reached only after five to six stimulations and PTP_cont peaked only at 38% (±6%; n = 4) above basal release (Fig. 8A₃,C). Consistent with their effects on PTP_cont, ApSynAla also abolished PTP_LFD and PKAi_6-22 strongly reduced it (Fig. 8D). This difference in the efficacy of PKAi_6-22 and ApSynAla to affect PTP_LFD may be attributable to a progressive degradation of PKAi_6-22 in the cell. Indeed, we observed that, several hours after its injection, PKAi_6-22 lost its effects on both PTP_cont and LFD. Since PTP_LFD was elicited at least 1 h after PKAi_6-22 injection, we cannot exclude that the lack of efficacy of this peptide is attributable to its partial degradation in the cell. In any case, these data indicate that, at this Aplysia synapse, the fast recovery from LFD induced by tetanus requires phosphorylation of synapsin at its P-site 1.

Discussion

Comparison of LFD with other forms of homosynaptic depression

The form of LFD described here is clearly reminiscent of the synaptic fatigue or LFD reported at other invertebrate and mammalian synapses (Silver et al., 1998; Saviane et al., 2002; Abrahamsson et al., 2005; Silverman-Gavrila et al., 2005; Silverman-Gavrila and Charlton, 2009). In all cases, LFD is induced at the same rate of stimulation (1 Hz) and stabilizes at a plateau-fixed level. However, the underlying mechanisms of LFD probably depend on the type of synapse. At Aplysia cholinergic synapses, several important findings indicate that LFD mainly results from an activity-dependent silencing of a fraction of release sites. First, LFD is independent of the initial synaptic strength. In addition, there are changes neither in Var/I_mean nor in PPR during the course of LFD. Finally, at rest, the restoration of the full capacity of release is achieved with a time constant much larger than the time constant of SV recycling. Interestingly, during the first minutes at 1 Hz, the depression attributable to the silencing of release sites is temporally counterbalanced by a quasi-immediate increase in P induced by the acceleration in stimulation frequency. Our results clearly implicate the PKA–synapsin pathway in this form of short-term synaptic enhancement as both ApSynAla and PKA inhibitor eliminated the delay in the onset of LFD. This is consistent with previous studies showing that a synapsin-dependent mobilization of SVs supports exocytosis during repetitive activity (Humeau et al., 2001a; Chi et al., 2003; Fassio et al., 2006; Menegon et al., 2006).

LFD differs from depression induced by high-frequency stimulation, which is the consequence of the rate-limiting kinetics of the refilling mechanisms and therefore related to RRP depletion (Wang and Kaczmarek, 1998; Wu and Borst, 1999; Schneggenburger et al., 2002; Zucker and Regehr, 2002; Foster and Regehr, 2004). LFD shares obvious similarities with homosynaptic depression described at Aplysia sensorimotor synapses (Royer et al., 2000; Gover et al., 2002). Both are induced at a low rate of stimulation, are independent of the release probability, and are the consequence of synapse silencing (Jiang and Abrams, 1998; Gover et al., 2002). In addition, these forms of depression are not related to RRP depletion. Full recovery of synaptic strength after LFD or after homosynaptic depression requires a very long rest period (Gover et al., 2002; this study). However, the finding of a release component characterized by a high intrinsic release probability and a limited capacity that allows fast, yet labile (lost in two to three stimuli at 1 Hz), recovery from LFD is a unique feature of the synapse studied here. At sensorimotor synapses, homosynaptic depression is relieved by serotonin application (Gover et al., 2002), whereas in our model serotonin by itself induces depression (data not shown), and very fast recovery can be induced by trains of high-frequency stimulation.

Mechanisms underlying the switching off of release sites

The mechanisms involved in the silencing of release sites during LFD were not identified. In theory, any event controlling the availability of readily releasable SVs on a release site in an all-or-none manner may determine the functional status of the site (see also Introduction and Materials and Methods). Since coactivation of several Ca²⁺ channels is likely to be required for inducing SV fusion in our model (Fossier et al., 1999; Humeau et al., 2007), we can exclude an activity-dependent inactivation of presynaptic Ca²⁺ channels during LFD, because this inactivation would have been detected as a decrease in P, rather than site silencing. Our data do not distinguish between selective long-lasting blockage of refilling at certain release sites, inactivation of fusion competence of plasma membrane at subpopulation of release sites, or complete blockage of priming events at a subset of sites or docked SVs. Interestingly, at mammalian synapses, the all-or-none feature of presynaptic adaptation has been proposed to result from changes in SV priming (Moulder et al., 2006). Moreover, at phasic synapses of a crayfish motoneuron, LFD is induced by an activity-dependent dephosphorylation of proteins involved in neurotransmitter release (Silverman-Gavrila et al., 2005). Therefore, a progressive and activity-dependent dephosphorylation of proteins involved in priming may lead to a silencing of presynaptic release sites.

Mechanisms underlying the switching on of release sites and resetting

Release site silencing is reversible. Indeed, sites can be reactivated either spontaneously with a slow time constant (∼40 min) or in an accelerated manner after a burst of high-frequency activity. PKA inhibition or microinjection of a nonphosphorylable synapsin mutated at its P-site 1 does not affect spontaneous recovery but compromises the accelerated recovery from LFD after application of 50 Hz trains. Hence, tetanus acts by activating the PKA–synapsin pathway probably via an elevation of cAMP concentration in the vicinity of release sites. Additional investigations should be done to establish the link between an application of 50 Hz trains and the activation of a synaptic adenylate cyclase. At its P-site 1, Aplysia synapsin can also be phosphorylated by Ca²⁺/calmodulin-dependent protein kinases I and IV (Angers et al., 2002; Fiumara et al., 2004); thus, our results do not permit to exclude the recruitment of these kinases in the pathway that controls the functional status of release sites even if all calmodulin inhibitors tested in our model were unable to affect LFD (data not shown).

Once again, this study is consistent with the finding that serotonin recruits the cAMP–PKA–synapsin pathway to switch on release sites silenced by repetitive activity at Aplysia sensorimotor synapses (Angers et al., 2002; Gover et al., 2002; Fioravante et al., 2007). Since synapsin also operates during the post-docking/priming events of exocytosis at invertebrate and vertebrate synapses (Hilfiker et al., 1998, 2005; Humeau et al., 2001a; Fassio et al., 2006), it may activate a pathway that bypasses the molecular events underlying silencing of release sites. The recruitment of this cascade for the reactivation of silent release sites at Aplysia synapses may be the functional equivalent of the cAMP–PKA–RIM1α pathway involved in presynaptic forms of long-term potentiation at both the hippocampal mossy fiber–CA3 synapses (Lonart et al., 2003) and the corticolateral amygdala synapses (Fourcaudot et al., 2008). Interestingly, the cAMP–PKA–RIM1α pathway is also implicated in the recovery from long-term depression at the mossy fiber-to-stratum lucidum synapses in the hippocampus (Pelkey et al., 2008).

Strikingly, bursts of high-frequency activity occurring at depressed synapses are able to reset all parameters of neurotransmitter release to the values observed before induction of LFD. At depressed synapses, resetting is illustrated by the induction of a form of PTP (PTP_1→0.025), which is indistinguishable from PTP induced before LFD (PTP_cont). The fact that the PKA–synapsin pathway is also involved in PTP_cont does not necessarily mean that the mechanisms underlying PTP_1→0.025 (or PTP_LFD) and PTP_cont are identical. PTP_cont is related to an increase in P (which is detected as a decrease in PPR) (Fig. 6E) (Humeau et al., 2007), whereas PTP_LFD and PTP_1→0.025 are related to synapse awakening combined with an increase in P that applies to all classes of release sites (i.e., release sites with a high intrinsic P, release sites reactivated by the tetanus, and release sites that remained active before the tetanus). The mechanisms underlying this reactivation and the increase in P are probably different even if they are initiated by the same molecular cascades.

In addition to the activation of the PKA–synapsin pathway, the key event for resetting is the involvement of a subset of release sites that have acquired a high release probability status (as detected by a very small PPR) during LFD. This subset of release sites, which cannot by itself reconstitute full release capacity, can be maintained without any decline during long rest periods, and shapes the peak and the first phase of PTP_LFD and PTP_1→0.025. Along the same line, cAMP also selectively increases P at the calyx of Held synapses (Sakaba and Neher, 2001). In addition, at hippocampal synapses, the phosphorylation of synapsin by PKA counteracts synaptic depression and accelerates recovery from depression when neurons are challenged with sustained stimulation (Menegon et al., 2006).

In conclusion, we have explored the interplay between various forms of short-term synaptic plasticity involving either an activity-dependent regulation of the on/off functional status of release sites or a change in the probability of release. Although the molecular mechanisms involved are not completely elucidated, the PKA–synapsin pathway appears to be involved. The timing and the interplay of multiple forms of short-term plasticity allow fine-tuning of synaptic efficacy in response to changes in the stimulation rate and also confer surprising properties to the synapse. The most striking is the possibility of the synapse to “forget” its recent history (i.e., history of synaptic activity) and reset synaptic strength to a value that is fixed and independent of the status of release sites.