Mechanistically Guided Predictive Models for Ligand and Initiator Effects in Copper-Catalyzed Atom Transfer Radical Polymerization (Cu-ATRP)

Abstract

Copper-catalyzed atom transfer radical polymerization (Cu-ATRP) is one of the most widely used controlled radical polymerization techniques. Notwithstanding the extensive mechanistic studies in the literature, the transition states of the activation/deactivation of the growing polymer chain, a key equilibrium in Cu-ATRP, have not been investigated computationally. Therefore, the understanding of the origin of ligand and initiator effects on the rates of activation/deactivation is still limited. Here, we present the first computational analysis of Cu-ATRP activation transition states to reveal factors that affect the rates of activation and deactivation. The Br atom transfer between the polymer chain and the Cu catalyst occurs through an unusual bent geometry that involves pronounced interactions between the polymer chain end and the ancillary ligand on the Cu catalyst. Therefore, the rates of activation/deactivation are determined by both the electronic properties of the Cu catalyst and the ligand-initiator steric repulsions. In addition, our calculations revealed the important role of ligand backbone flexibility on the activation. These theoretical analyses led to the identification of three chemically meaningful descriptors, namely HOMO energy of the catalyst (E_HOMO), percent buried volume (V_bur%), and distortion energy of the catalyst (ΔE_dist), to describe the electronic, steric, and flexibility effects on reactivity, respectively. A robust and simple predictive model for ligand effect on reactivity is thereby established by correlating these three descriptors with experimental activation rate constants using multivariate linear regression. Validation using a structurally diverse set of ligands revealed the average error is less than ±2kcal/mol compared to the experimentally derived activation energies. The same approach was also applied to develop a predictive model for reactivity of different alkyl halide initiators using R–X bond dissociation energy (BDE) and Cu–X halogenophilicity as descriptors.

Graphical Abstract

1. Introduction

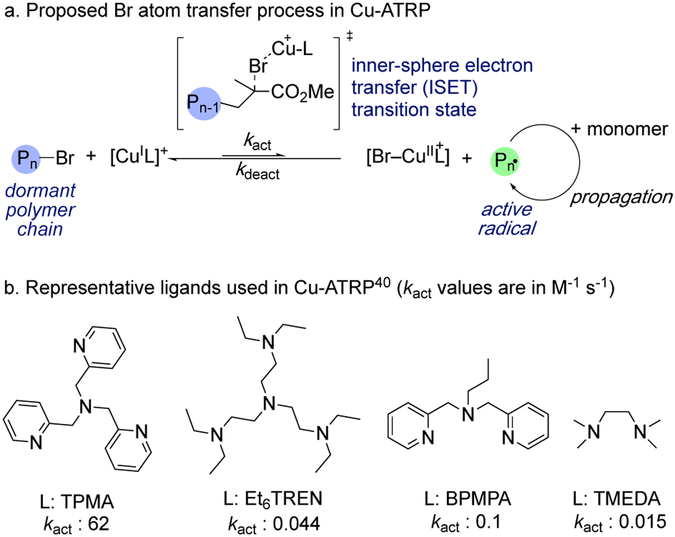
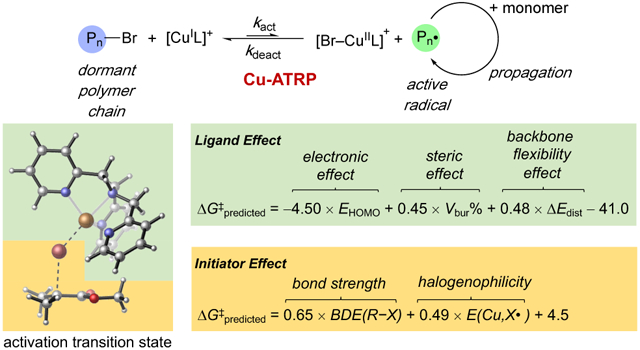
Atom transfer radical polymerization (ATRP) is among the most powerful and robust controlled radical polymerization techniques that facilitate macromolecular engineering by synthesis of polymers with precise molecular weights, low dispersities, and well-controlled architectures.¹ Although ATRP has been achieved with diverse transition metal² and photoredox catalysts,^3,4 copper-catalyzed ATRP (Cu-ATRP) is still the most extensively used and investigated ATRP^1a,5 with a wide range of compatible monomers, initiators, and solvents. Control of polymer chain growth via Cu-ATRP is largely attributed to the dynamic activation/deactivation equilibrium between a [Cu^IL]⁺/[Br-Cu^IIL]⁺ couple where L represents a multidentate nitrogen-donor ligand (Figure 1).^6,7 The [Cu^IL]⁺ catalyst activates the dormant alkyl bromide chain end (P_n–Br) to form the [Br-Cu^IIL]⁺ complex and a propagating alkyl radical (P_n•). The alkyl radical continues to grow by adding a few monomers before it abstracts the Br from [Br-Cu^IIL]⁺ to reform an alkyl bromide. A successful ATRP catalyst system should have a large activation rate constant (k_act) and an even larger deactivation rate constant (k_deact) to provide good control over the polymerization while maintaining a reasonable polymerization rate.

Figure 1.

Ligand effects on the activation/deactivation of Cu-ATRP.

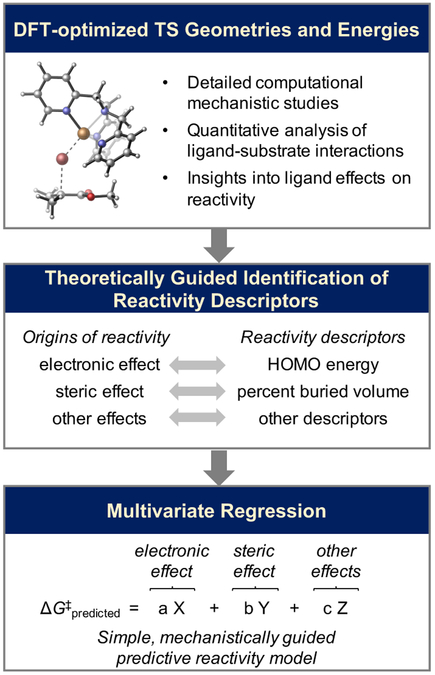
Previous mechanistic studies from Coote, Gennaro, and Matyjaszewski indicated that Cu-ATRP occurs via a concerted inner-sphere electron transfer (ISET) process in which the Br atom is transferred from the alkyl bromide to the [Cu^IL]⁺ catalyst (Figure 1a), because the predicted outer-sphere electron transfer (OSET) barriers are much higher than experimental data.⁸ However, the geometry and energy of this Br atom transfer transition state have not been explored by computations so far. Although a few computational studies demonstrated that the reactivity of alkyl halide initiators is affected by their bond dissociation energies^8,9 and LUMO energies,¹⁰ it remains challenging to understand and computationally predict the reactivities of Cu-ATRP catalysts with the structurally-diverse ligands (Figure 1b). The lack of theoretical insights into the origins of ligand effects hinders the rational catalyst design for Cu-ATRP. Herein, we describe a workflow to establish mechanistically guided predictive models for the reactivity of Cu-ATRP catalysts. Inspired by the elegant work from Sigman,¹¹ Doyle,¹² and Paton¹³‘s groups that utilizes a multivariate regression approach to predict ligand effects in transition metal catalyzed reactions using steric and electronic parameters, we surmised such parameterization approach may be facilitated by mechanistic insights from DFT calculations. In particular, in-depth analysis of factors that stabilize the rate-determining transition state may offer the theoretical basis for the rational selection of ligand parameters.¹⁴ Our workflow to establish the predictive mathematical equation is summarized in Figure 2. First, we applied DFT calculations to obtain the geometries and energies of Cu-ATRP activation transition sates. Detailed investigations of the transition states revealed key factors that control catalyst and initiator reactivities. These theoretical insights were then utilized to rationally select a set of chemically meaningful descriptors to define effects of different factors on the reactivity. Finally, a simple mathematical equation for predicting ligand effect was established by correlating these descriptors with experimental reactivities using a multivariate regression approach. Similarly, a predictive equation was developed for the reactivity of different alkyl halide initiators. These predictive models can be used to guide rational catalyst design¹⁵ and computational ligand discovery for Cu-ATRP reactions.

Figure 2.

Workflow of establishing predictive models for reactivity of Cu-ATRP catalysts.

2. Computational Methods

All geometry optimizations and single point energy calculations were performed with the Gaussian 09 software package.¹⁶ Geometries were optimized in the gas phase using the ω-B97XD¹⁷ functional and a mixed basis set of SDD¹⁸ for Cu and 6-31G(d)¹⁹ for other atoms. Single point energies were calculated using ω-B97XD and the def2-TZVP²⁰ basis set in acetonitrile using the CPCM solvation model.²¹ Reported Gibbs free energies and enthalpies in solution include thermal corrections computed at 298 K and are computed at the standard concentration (1 mol/L). The activation free energies of the outer-sphere single electron transfer reactions were calculated using modified Marcus theory (see SI for details).^22,23 Parameters used in the predictive models for initiator and ligand effects (eqs. 3 and 4), including bond dissociation energies (BDE), halogenophilicity (E(Cu, X•)), HOMO energies (E_HOMO), and catalyst distortion energies (ΔE_dist(TS) and ΔE_{dist(BrCu^IIL)}), were also calculated at the ω-B97XD/def2-TZVP level of theory in acetonitrile using the CPCM solvation model. Distortion/interaction model and energy decomposition analysis (EDA) calculations in Figure 5 were performed to dissect the computed gas-phase activation energy (ΔE^‡). The activation energy was first decomposed into the distortion energy of the two reactive fragments, i.e. the [Cu^IL]⁺ catalyst and the alkyl halide, to reach their transition state geometries (ΔE_dist = ΔE_dist(CuL) + ΔE_dist(RX)) and the interaction energy (ΔE_int) between these two fragments (eq. 1).^24,25

$$\mathrm{\Delta }{E}^{‡}=\mathrm{\Delta }{E}_{\text{dist}}+\mathrm{\Delta }{E}_{\text{int}}$$ (eq.1)

Figure 5.

The origin of the bent geometry in TS1.

Here, the distortion energies were calculated from the energy difference between the distorted fragment in the transition state geometry and the same fragment in the fully optimized ground state geometry. Then, ΔE_int is calculated from ΔE_int = ΔE^‡ – ΔE_dist. Next, ΔE_int was further dissected into chemically meaningful terms using the second-generation EDA based on absolutely-localized molecular orbitals (ALMO-EDA2)^26,27 in Q-Chem 5.0 (eq. 2).²⁸

$$\mathrm{\Delta }{E}_{\text{int}}=\mathrm{\Delta }{E}_{\text{pauli}}+\mathrm{\Delta }{E}_{\text{elstat}}+\mathrm{\Delta }{E}_{\text{disp}}+\mathrm{\Delta }{E}_{\text{orb}}$$ (eq.2)

Here, ΔE_pauli is the Pauli repulsion, ΔE_elstat is the electrostatic interactions, ΔE_disp is the dispersion interaction, and ΔE_orb is the orbital interaction energy that consists of interfragment charge transfer energy and intrafragment polarization energy.

3. Results and Discussion

3.1. Activation mechanisms in Cu-ATRP

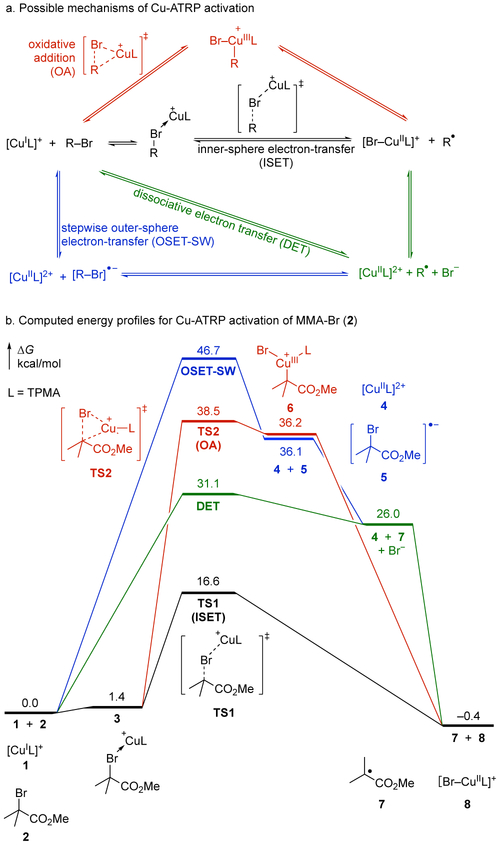
In previous studies, several possible mechanisms have been proposed for the activation/deactivation process in Cu-ATRP (Figure 3a), including inner-sphere single electron transfer (ISET), stepwise outer-sphere single electron transfer (OSET-SW), and dissociative electron transfer (DET).⁸ Here, we used DFT and Marcus theory to investigate these previously proposed pathways, as well as the oxidative addition (OA) of alkyl bromide to the Cu^I catalyst to form a Cu^III intermediate (Figure 3b). The barrier for the concerted DET to form the MMA radical 7 and a bromide was estimated using the “sticky model”, a modification of the Marcus theory.^8,23 The calculations were performed using a model system that consists of [Cu^I(TPMA)]⁺ (TPMA: tris(2-pyridylmethyl)amine), one of the most popular ATRP catalysts, and a widely used initiator α-bromoisobutyrate (i.e. a mimic of a dormant chain end in ATRP of methyl methacrylate, MMA-Br, 2). In agreement with previous computational studies,⁸ the OSET-SW and DET processes both involve very high barriers that are inconsistent with experimental data. The oxidative addition of the sterically crowded tertiary alkyl bromide (TS2) also requires a very high barrier.²⁹ The most favorable activation mechanism is the concerted ISET (TS1), which requires a substantially lower barrier (ΔG^‡ = 16.6 kcal/mol in MeCN) than other processes considered.³⁰

Figure 3.

Computed energy profiles of Cu-ATRP activation pathways in MeCN at 25 °C with tris(2-pyridylmethyl)amine (TPMA) ligand.

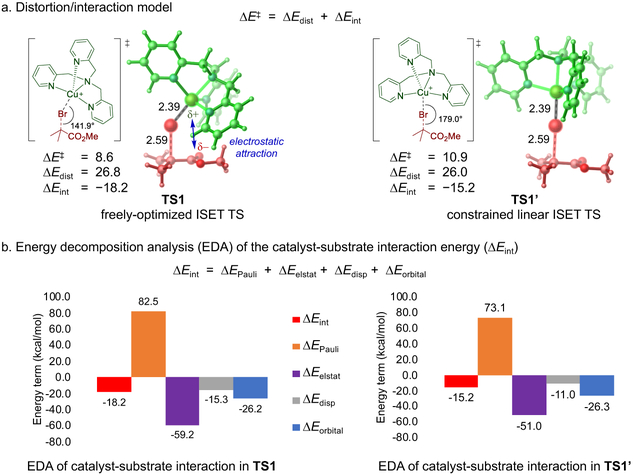
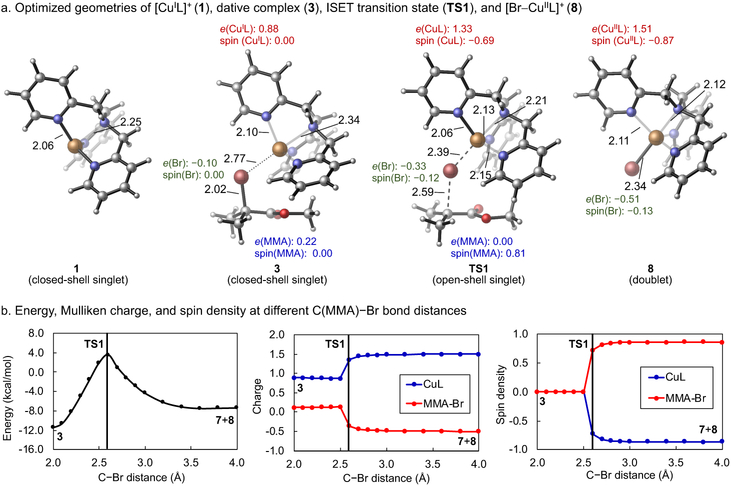
The optimized geometries, Mulliken atomic charges, and spin densities of the Cu^I and Cu^II complexes and transition state involved in the ISET pathway are shown in Figure 4.³¹ The analysis of charge and spin density at different C(MMA)–Br bond distances (Figure 4b) indicates a dramatic change of charge and spin density before TS1, while both quantities remain almost constant after the transition state. The computed Mulliken charge of the CuL fragment in TS1 is +1.33, indicating a considerable amount (0.33 e) of charge transfer from the [Cu^IL]⁺ catalyst to the alkyl bromide in the ISET transition state. Nonetheless, since the charge transfer in TS1 is much less than unity and the Cu is less positively charged than that in the [Br-Cu^IIL]⁺ complex 8, the Cu...Br interaction in TS1 has a significant covalent character. The much-shortened Cu–Br bond distance (2.39 Å) and the elongated C–Br bond distance (2.59 Å) in TS1, along with the relatively large spin densities on the Cu catalyst and the MMA, indicate the ISET process involves a late transition state that structurally resembles the [Br-Cu^IIL]⁺ product. Furthermore, the computed Wiberg bond indices³² of the Cu–Br bond in TS1 and 8 are 0.386 and 0.574, respectively, which is consistent with a late transition state with a substantial bonding interaction between the Cu and Br in TS1.

Figure 4.

Optimized geometries, energies, Mulliken charges, and spin densities of computed structures in the ISET pathway.

The optimized geometry of TS1 has a substantially bent Cu–Br–C bond angle (141.9°).³³ This is rather surprising considering most known halogen atom transfer processes involve a linear transition state structure.^3,34,35 The bent geometry means a closer distance between the ancillary ligand and the substrate (i.e. the alkyl halide initiator or the dormant chain end). As such, the non-covalent interactions between the ligand and the substrate, a previously underappreciated effect, may play a significant role on the activation/deactivation reactivity. Because of its potential impacts on the catalyst reactivity, we have undertaken a detailed computational analysis to investigate the origin of the bent geometry. We performed a constrained optimization of the ISET transition state by forcing a linear geometry, fixing the Cu–Br–C bond angle at 179° (Figure 5a). It was found that the freely optimized bent transition state was 2.3 kcal/mol lower in energy than the linear transition state. The distortion/interaction model analysis indicates the bent TS geometry has 3.0 kcal/mol more favorable interaction energy (ΔE_int) between the CuL catalyst and the MMA-Br. We then applied the energy decomposition analysis methods to dissect the interaction energy (Figure 5b). Although the bent transition state is disfavored by Pauli repulsion (ΔΔE_Pauli = +9.4 kcal/mol), it has stronger attractive electrostatic interaction (ΔΔE_elstat = −8.2 kcal/mol) and dispersion interaction (ΔΔE_disp = −4.3 kcal/mol) between the catalyst and the substrate than linear transition state. While the increased dispersion is expected to partially compensate the Pauli repulsion effect, the stronger electrostatic interaction is attributed to the attraction between the positively charged Cu catalyst and the partial negatively charged ester group of the substrate. DFT calculations using other alkyl halides also provided bent ISET transition state structures (see Figure S6 in the SI). The bent TS structures are stabilized by either electrostatic attraction with the Cu catalyst when an electron-withdrawing group is present in the chain end or attractive London dispersion forces in reactions with benzylic halides (see SI for details).

Collectively, the computational data indicate the ISET involves a late, open-shell singlet transition state that is consistent with a concerted bromine atom transfer^3,34,35 process. The substantial C–Br bond stretch and Cu–Br interactions in the late TS implies that the BDE of the carbon-halogen bond and the halogen binding energy to Cu both play a significant role on the reaction rate.³⁶ In addition, the charge transfer from the Cu catalyst to the alkyl bromide in the ISET TS suggests a more electron-rich ligand would promote the reaction. The bent transition state geometry suggests the ligand-substrate non-bonding interactions are expected to affect the stability of the transition state. These mechanistic insights were used to develop the predictive models for reactivity between different alkyl halide initiators and the Cu ATRP catalysts (vide infra).

3.2. Predictive Model for Initiator Effects on Reactivity

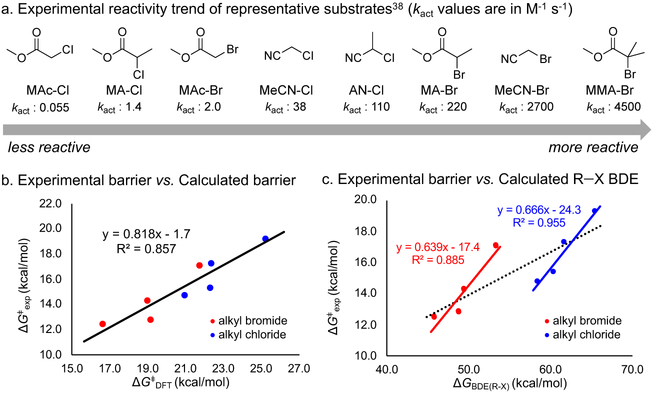
Over the past decades, Cu-ATRP was successfully employed with a variety of initiators, which activation rate constants (k_act) have been determined by experimental kinetic studies with different catalysts (Figure 6a).^37,38 Herein, we report the first computational prediction of activation barriers for a representative set of alkyl bromide and alkyl chloride initiators (R–X, Figure 6a) using transition state calculations. The DFT-computed barriers of the ISET transition states (ΔG^‡_DFT) with the [Cu^I(TPMA)]⁺ catalyst in acetonitrile provided a good agreement with the experimentally determined reactivity trend (ΔG^‡_exp)³⁹ for both alkyl bromide and alkyl chloride initiators, which validates the robustness and reliability of the computational methods and computed transition state models. To further explore the origin of reactivity of the different initiators, we performed distortion/interaction model analysis for the computed ISET transition states. The results indicate the activation energies correlates well with the distortion energies of the R–X initiators (see Figure S1 in SI). Furthermore, ISET transition states with alkyl bromides are stabilized by stronger interaction energies between the Cu catalyst and the halide compared to those with alkyl chlorides (see Figure S2 in SI). Therefore, the distortion/interaction model analysis reaffirmed the significant roles of both the R–X bond strength and Cu–X interactions on the stability of the transition state.

Figure 6.

Initiator effect in Cu-ATRP with the [Cu^I(TPMA)]⁺ catalyst.

Because the transition state analysis discussed above indicated the R–X bond strength and the Cu–X covalent interactions are both important factors for the transition state energy, we surmised the R–X BDE and the halogenophilicity⁸ (i.e. the binding ability of X• to [Cu^IL]⁺) can be used as two appropriate descriptors for the initiator reactivity model. Although it has been widely recognized that the R–X BDE plays a significant role on the activation rate,^8,9 the computed BDEs do not have a good overall correlation with experimental barriers for the entire set of alkyl bromide and chloride initiators (Figure 6c, dashed line). However, within the same type of halides (X =Br or C1), R–X BDEs are good indicators of their reactivities (Figure 6c, solid red and blue lines). This indicates the halogenophilicity is another important factor impacting the reactivity. Indeed, when combining R–X BDE with Cu–X halogenophilicity (E(Cu, X•)), the two-parameter equation (eq. 3) provides an excellent correlation with the experimentally observed activation rate

$$\mathrm{\Delta }{G^{‡}}_{\text{predicted}}=0.56\times \text{BDE(R-X)}+0.39\times E(\text{Cu,X}•)+4.8$$ (eq.3)

constants. (Figure 7). Previous studies have revealed a good correlation between the activation rate constant and the activation/deactivation equilibrium constant (K_ATRP).^38,40c Because K_ATRP is determined by both R–X BDE and Cu–X halogenophilicity, our two-parameter equation is consistent with the experimentally observed effects of K_ATRP on the activation rate.

Figure 7.

Predictive model for initiator reactivity in Cu-ATRP.

3.3. Predictive Model for Ligand Effects on Reactivity

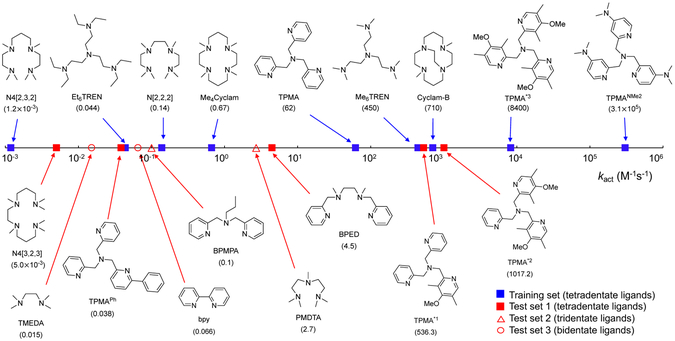
The reactivities of Cu-ATRP catalysts can be significantly impacted by altering the structures of their N-donor ligands. In the past decades, a structurally diverse set of multidentate N-donor ligands have been used experimentally, including bi-, tri-, and tetradentate ligands with either sp² or sp³ N atoms (Figure 8).⁴⁰ The reactivity of the Cu-ATRP catalyst appears to be affected by a combination of a few different types of ligand effects, including electronic, steric, denticity, hybridization, and other factors. As such, rational ligand design for efficient Cu-ATRP catalysts remains challenging. Here, we use the three-step approach described in the Introduction (Figure 2) to establish a simple mathematical equation for the prediction of the activation rate of Cu-ATRP catalysts. We selected 9 representative ligands with distinct electronic and steric properties (blue squares in Figure 8) as a training set to understand the factors controlling the ATRP activation rate constants, and to identify suitable descriptors for the predictive model. The rest of the ligands (red squares, circles, and triangles) are used as test sets to validate the reliability of the predictive model. All of ISET transition states were calculated with the same initiator MMA-Br.

Figure 8.

Representative ligands for Cu-ATRP catalyst. Experimentally determined activation rate constants are provided in parentheses.⁴⁰

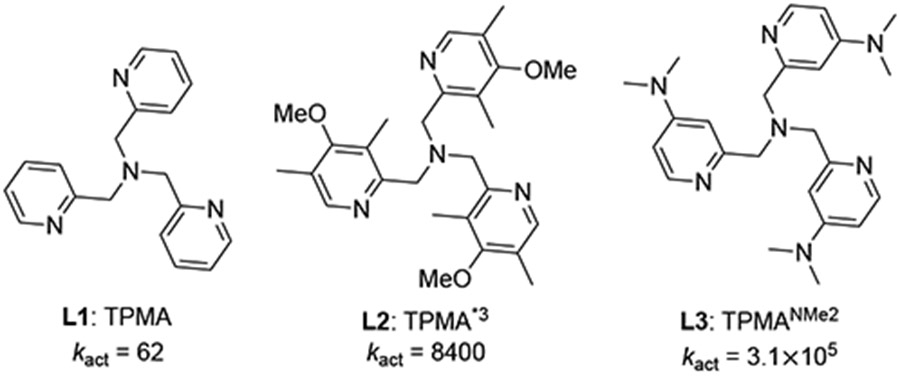
3.3.1. Ligand Electronic Effect

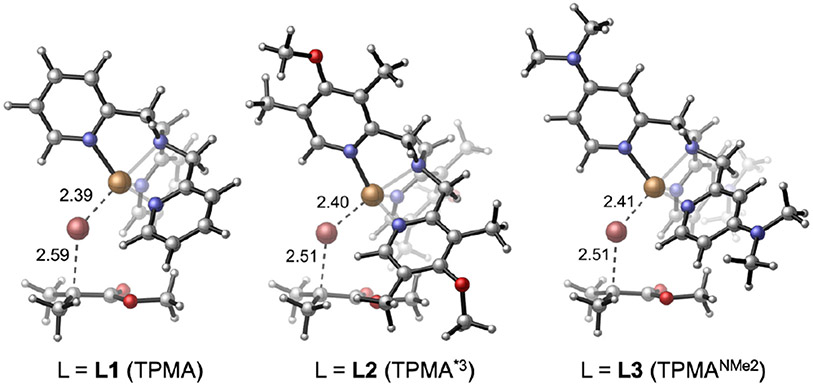
Three TPMA derivatives (L1-L3) with similar steric properties were chosen to investigate the electronic effects of the ancillary ligands. Recently, Matyjaszewski group discovered that incorporation of electron-donating groups in the pyridine ring of TPMA profoundly increased the ATRP catalyst activity (Table 1).^40c Notably, the dimethyl amino (−NMe₂) substituted TPMA (L3, TPMA^NMe2) ligand forms the most reactive Cu-ATRP catalyst reported to date. We performed DFT calculations to locate the ISET transition states for these three Cu-ATRP catalysts in Figure 9. The DFT-predicted activation barriers (ΔG^‡_DFT) were consistent with the experimental reactivity trend. The computed percent buried volume (V_bur%)⁴¹ and the catalyst distortion energy in the transition state (ΔE_dist(TS)) are similar for all three catalysts, which confirmed the ligand steric properties and the distortion of the Cu catalysts are comparable among this group of ligands. As such, their reactivity difference is expected to be mainly controlled by inductive electronic effects of the ligand. A good correlation between the activation energies and the computed HOMO energy of the Cu^I catalyst (E_HOMO) was observed (see Figure S3 in SI). Thus, E_HOMO was chosen as an appropriate descriptor to describe the electronic effects of the ancillary ligand.^13a,b

Table1.

Electronic effects of the TPMA family ligands.^a

ligand	ΔG‡exp	ΔG‡DFT	EHOMOb	Vbur%c	ΔEdist(TS)d	ΔEdist(BrCuIIL)e
TPMA	15.0	16.6	−7.66	39.2	2.1	4.0
TPMA*3	12.0	14.6	−7.41	40.3	2.0	3.6
TPMANMe2	10.0	13.0	−7.36	39.0	1.8	3.7

^ak_act values are in M⁻¹ s⁻¹. All Gibbs free energies and distortion energies are in kcal/mol; E_HOMO is in eV. All energies and E_HOMO are computed in acetonitrile using the CPCM solvation model.

^bHOMO energy of [Cu^IL]⁺.

^cPercent buried volume of the ligand computed from the DFT-optimized geometry of [Cu^IL]⁺.⁴¹

^dDistortion energy of the CuL catalyst in the ISET transition state with respect to the ground state [Cu^IL]⁺.

^eDistortion energy of the CuL catalyst in the [BrCu^IIL]⁺ complex with respect to the ground state [Cu^IL]⁺.

Figure 9.

Optimized geometries of ISET transition states with TPMA family ligands.

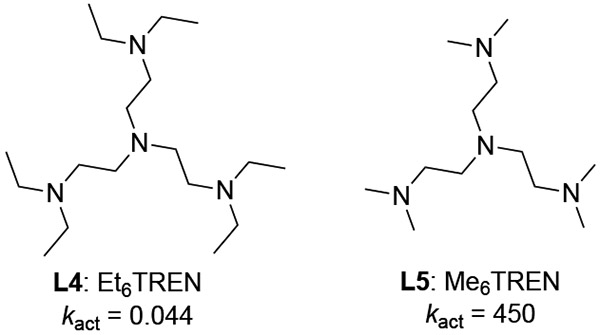
3.3.2. Ligand Steric Effect

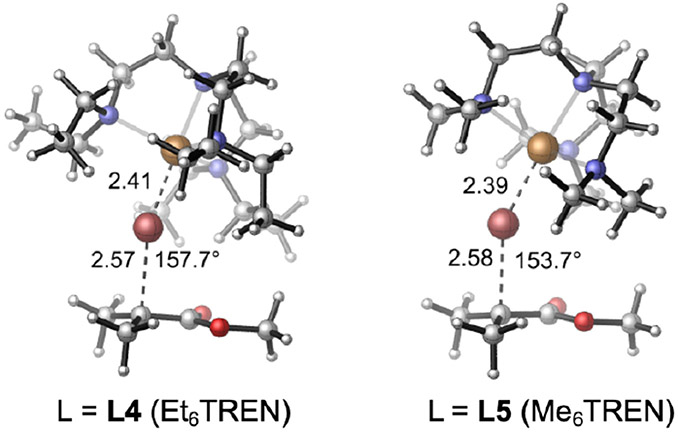
Me₆TREN (L5) is another highly effective and commonly employed ligand in Cu-ATRP.⁴² When replacing all N-methyl substituents with ethyl groups (L4, Et₆TREN), the ATRP reactivity dramatically decreases (Table 2). Considering their similar electronic properties, this series of ligands was chosen to study the ligand steric effect on reactivity. The optimized ISET transition states with both ligands have a greater Cu—Br—C bond angle than that of TS1, indicating greater steric repulsions than with the TPMA ligand (Figure 10). The computationally predicted barrier with Et₆TREN is more than 4 kcal/mol higher than that with Me₆TREN (Table 2), in agreement with the experimental reactivity trend (ΔΔG_exp^‡ = 5.5 kcal/mol).^40a The decreased reactivity with the Et₆TREN ligand is mostly due to the greater steric hindrance of the ligand as evidenced by the less bent geometry in the ISET transition state (Figure 10). As shown in Table 2, the widely used percent buried volume (V_bur%)⁴¹ is an appropriate descriptor to distinguish the ligand steric properties. Et₆TREN has a much larger V_bur% than Me₆TREN (56.5% versus 45.7%), while the less hindered TPMA has a smaller V_bur% (39.2%) than both ligands. As expected, the computed HOMO energies for L4 and L5 are similar, which confirmed the similar electronic properties of these ligands. Although the transition state with Et₆TREN has greater distortion energy (ΔE_dist(TS)) than that with Me₆TREN, the relatively small distortion energy difference between the two transition states suggests the ligand distortion may not strongly correlate with the steric effects of ligands. Effects of ligand distortion on reactivity are discussed in more detail below.

Table2.

Steric effects of the TREN family ligands.^a

ligand	ΔG‡exp	ΔG‡DFT	EHOMOb	Vbur%c	ΔEdist(TS)d	ΔEdist(BrCuIIL)e
Et6TREN	19.3	18.5	−7.33	56.5	3.5	5.1
Me6TREN	13.8	14.3	−7.34	45.7	2.2	4.0

^ak_act values are in M⁻¹ s⁻¹. All Gibbs free energies and distortion energies are in kcal/mol; E_HOMO is in eV. All energies and E_HOMO are computed in acetonitrile using the CPCM solvation model.

^bHOMO energy of [Cu^IL]⁺.

^cPercent buried volume of the ligand computed from the DFT-optimized geometries of [Cu^IL]⁺.⁴¹

^dDistortion energy of the CuL catalyst in the ISET transition state with respect to the ground state [Cu^IL]⁺.

^eDistortion energy of the CuL catalyst in the [BrCu^IIL]⁺ complex with respect to the ground state [Cu^IL]⁺.

Figure 10.

Optimized geometries of ISET transition states with TREN family ligands.

3.3.3. Ligand Backbone Flexibility Effect

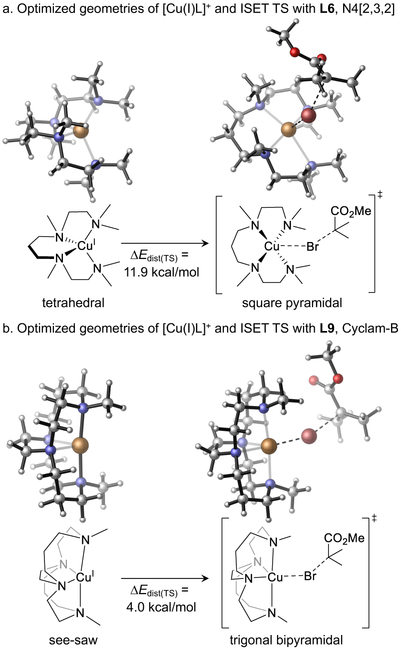
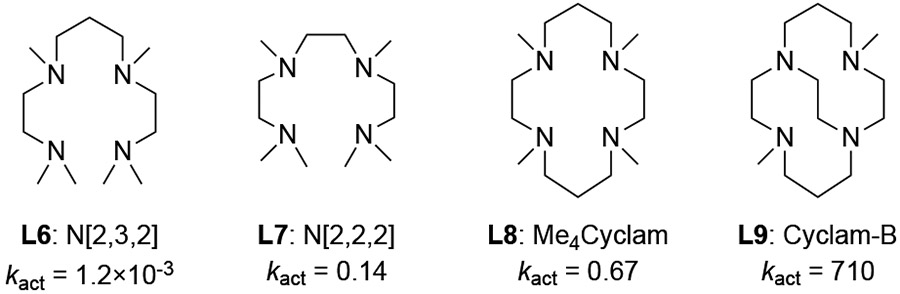
Finally, we considered a series of tetradentate Cyclam family ligands (L6-L9) to investigate the effect of ligand backbone flexibility (Table 3). Albeit their similar donor abilities, these ligands have significantly different reactivities in Cu-ATRP. Experimental kinetic data showed that the reactivity decreases with augmented backbone flexibility.^40a For example, the Cu complex with the most rigid ligand, Cyclam-B, is among the most active catalysts for Cu-ATRP, while the complex with structurally-similar acyclic ligand N[2,3,2] is six orders of magnitude less reactive. This reactivity trend was successfully reproduced by the computed transition state energies (ΔG^‡_DFT). The computed distortion energies (ΔE_dist(TS)) indicated the low reactivities with the more flexible ligands (L6 and L7) are mainly due to the high distortion energy of the CuL catalyst in the ISET transition state. In reactions with L6, L7, and L8, the CuL catalyst is distorted from a tetrahedral geometry in the Cu^I ground state to a square pyramidal geometry in the ISET transition state (Figure 11 and Figure S4 in the SI). In contrast, the ligand conformation remains similar in reaction with the more rigid ligand L9, leading to a much smaller distortion energy.

Table3.

Flexibility effects of the Cyclam family ligands.

ligand	ΔG‡exp	ΔG‡DFT	EHOMOb	Vbur%c	ΔEdist(TS)d	ΔEdist(BrCuIIL)e
N[2,3,2]	21.5	27.5	−7.12	48.4	11.9	14.4
N[2,2,2]	18.6	26.4	−7.26	45.6	14.2	17.0
Me4Cyclam	17.7	20.3	−6.92	49.6	7.0	9.0
Cyclam-B	13.6	16.8	−6.81	47.6	4.0	5.2

^ak_act values are in M⁻¹ s⁻¹. All free energies and distortion energies are in kcal/mol; E_HOMO is in eV. All energies and E_HOMO are computed in acetonitrile using the CPCM solvation model.

^bHOMO energy of [Cu^IL]⁺.

^cPercent buried volume of the ligand computed from the DFT-optimized geometries of [Cu^IL]⁺.⁴¹

^dDistortion energy of the CuL catalyst in the ISET transition state with respect to the ground state [Cu^IL]⁺.

^eDistortion energy of the CuL catalyst in the [BrCu^IIL]⁺ complex with respect to the ground state [Cu^IL]⁺.

Figure 11.

Optimized geometries of Cu^I catalysts and ISET transition states with Cyclam family ligands.

Because of its significant role on reactivity, a specific parameter should be included in the predictive model to describe the effect of ligand backbone flexibility.^5a Here, we found the computed distortion energy of CuL in the ISET transition state (ΔE_dist(TS)) and in the [Br-Cu^IIL]⁺ product (ΔE_{dist(BrCu^IIL)}) can both adequately describe the ligand flexibility effect. Because the ISET transition states are late (vide supra) and product-like, an excellent linear correlation between ΔE_dist(TS) and ΔE_{dist(BrCu^IIL)} for all 9 aforementioned ligands is observed (See Figure S5 in SI). Because the computation of ΔE_{dist(BrCu^IIL)} does not require optimization of the ISET transition state geometry and thus is much more feasible, ΔE_{dist(BrCu^IIL)} was chosen as a parameter to describe the ligand flexibility effect.

3.3.4. Predictive Model for Ligand Effect on Reactivity

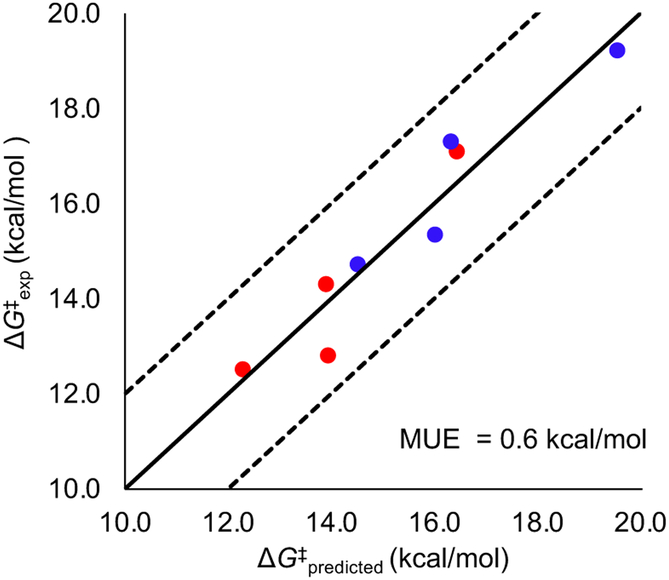
Through the detailed analysis of computed transition state structures and energies, we not only uncovered the factors that affect reactivity, but also identified appropriate parameters to describe each type of ligand effects. Therefore, these theoretical insights allowed us to establish a simple mathematical equation using only three parameters to predict the reactivity of the structurally diverse Cu-ATRP catalysts, namely, the HOMO energy of the [Cu^IL]⁺ catalyst (E_HOMO), the percent buried volume (V_bur%), and the distortion energy of CuL in the [BrCu^IIL]⁺ complex (ΔE_dist). Using the nine ligands discussed above (L1-L9) as the training set, eq. 4 was developed using multivariate linear regression by correlating the experimental activation free energies with these three calculated parameters (Figure 12). The rest of the ligands in Figure 8 were then used as test sets to validate the predictive model.

Figure 12.

Predictive model for ligand effect on Cu-ATRP reactivity.

Overall, a good correlation between the predicted activation free energies (ΔG^‡_predicted) and the experimentally derived activation free energies (ΔG^‡_exp). For all 18 ligands studied, the mean unsigned error (MUE) of the predicted activation free energy is 1.1 kcal/mol. Although the training set only contains tetradentate ligands, eq. 4

$$\mathrm{\Delta }{G^{‡}}_{\text{predicted}}=-4.50\times E_{\text{HOMO}}+0.45\times V_{\text{bur}}\%+0.48\times \mathrm{\Delta }{E}_{\text{dist}}-41.0$$ (eq.4)

performed well for tetradentate as well as tridentate ligands in the test set. The barriers for all tetradentate and tridentate ligands from either the training set or the test set were correctly predicted within ±2 kcal/mol error ranges (between the two dash lines). This is very promising to Cu-ARTP ligand discovery since tetra- and tridentate ligands form the most reactive Cu catalysts for ATRP. The less accurate prediction for the bidentate bpy ligand⁴³ might be due to the fact that a tetradentate coordinated Cu catalyst with two bpy ligands is considered in the modeling while other Cu complexes with one bpy ligand may also exist under the reaction conditions.

To further understand the impact of each factor on the reactivity, the computed parameters of all 18 ligands are shown using the green-yellow-red color scale in Table 4. Here, green indicates a positive effect to enhancing the reactivity, while red indicates a negative effect as compared with other investigated ligands. In terms of electronic effect, ligands with a greater number of chelating sp³ N atoms are generally more effective due to their stronger donicity. For example, the all-sp³ N cyclam-family ligands (Cyclam-B, Me₄Cylam, N[2,2,2], N[2,3,2], and N[3,2,3])) have HOMO values between −6.81 eV to −7.26 eV, while the sp³/sp² hybrid ligands such as TPMA ligands have lower HOMO values ranging from −7.36 eV to −7.66 eV. Similarly, two TREN-type ligands (Me₆TREN and Et₆TREN) have higher HOMO than TPMA ligands. Although not among the most electronically activated ligands, TPMA ligands are advantageous due to their less steric repulsions and high rigidity with low V_bur% and ΔE_dist values. Therefore, five of the seven most reactive ligands (ΔG^‡_exp≤15.0 kcal/mol) are TPMA derivatives. In fact, we found steric effect (V_bur%) and backbone flexibility effect (ΔE_dist) have greater contribution to the reactivity than the electronic effect (E_HOMO) from the standardized multivariate linear equation (see eq. S6 in SI). Furthermore, the electronic properties of TPMA ligands can be easily tuned by substitution on the pyridine rings. As such, TPMA^NMe2 is the most reactive ligand discovered so far because it has low steric repulsion and distortion penalty, and favorable electronic effect via incorporation of strong electron-donating groups.

Table 4.

Calculated electronic (E_HOMO), steric (V_bur%), and backbone flexibility (ΔE_dist) parameters for all 18 ligands.^a

ligand	ΔG‡exp	ΔG‡predicted	EHOMO	Vbur%	ΔEdist
TPMANMe2	10.0	11.5	−7.36	39.0	3.7
TPMA*3	12.1	12.2	−7.41	40.3	3.6
TPMA*2	13.4	12.6	−7.49	40.0	3.8
Cyclam-B	13.6	13.6	−6.81	47.6	5.2
TPMA*1	13.7	12.9	−7.57	39.6	4.0
Me6TREN	13.8	14.5	−7.34	45.7	4.0
TPMA	15.0	13.0	−7.66	39.2	4.0
BPED	16.6	18.5	−7.48	41.8	14.7
PMDTA	16.9	18.2	−7.46	40.9	14.9
Me4Cyclam	17.7	16.8	−6.92	49.6	9.0
N[2,2,2]	18.6	20.3	−7.26	45.6	17.0
BPMPA	18.8	17.7	−7.82	37.5	13.9
bpy	19.1	16.3	−7.78	38.6	10.2
Et6TREN	19.3	19.9	−7.33	56.5	5.1
TPMAPh	19.4	18.1	−7.62	47.7	7.0
TMEDA	20.0	20.5	−7.39	47.4	14.4
N[3,2,3]	20.6	21.0	−7.21	51.1	13.6
N[2,3,2]	21.5	19.7	−7.12	48.4	14.4

^aAll calculated parameters are color-coded. Green indicates quantities that are favorable for reactivity, and red indicates quantities that lead to lower reactivity. All energies are in kcal/mol. E_HOMO are in eV.

4. Conclusion

In this study, we demonstrate a computational approach to develop predictive mathematical equations for the reactivity of catalysts and initiators in Cu-ATRP, a widely used controlled radical polymerization reaction. We report the first DFT calculations of the inner-sphere electron transfer transition state, which involves a halogen atom transfer between a dormant alkyl halide chain end and the Cu^I catalyst. An in-depth computational analysis revealed a few key factors controlling the stability of the ISET transition state, and thus the activation rate constant. The ISET transition state involves a bent geometry of the Cu∙∙∙Br∙∙∙R bond, which leads to an enhanced non-covalent interaction between the ancillary N-donor ligand and the alkyl halide chain end. As such, the stability of the ISET transition state is sensitive to the steric properties of the ligand. A substantial amount of charge transfer from the Cu^I catalyst to the alkyl halide is observed in the transition state, which indicates the ISET process can be facilitated by stronger donor ligands. In addition, ISET transition states with flexible multidentate ligands, such as the acyclic ligand N[2,3,2], suffer from a high catalyst distortion energy due to the different ligand conformations in the [Cu^IL]⁺ resting state and the ISET transition state. With these mechanistic insights into the factors controlling reactivity, we identified three parameters, namely the percent buried volume, HOMO energy of the [Cu^IL]⁺ catalyst, and the catalyst distortion energy of the [Br-Cu^IIL]⁺ complex, to describe the steric, electronic, and flexibility effects of ligand, respectively. We developed a three-variable linear equation using these three DFT-computed parameters to predict the reactivity of a structurally diverse set of Cu-ATRP catalysts. The predicted activation barriers are within ±2 kcal/mol of the experimental values for 17 out of 18 ligands used in the training and test sets.

The same computational approach was used to develop a predictive equation for initiator effects on reactivity. Since the DFT calculations indicated a late ISET transition state with a substantial R–X bond stretch and a strong X∙∙∙Cu interaction, the stability of the transition state is expected to be affected by both the R–X bond dissociation energy (BDE) and the halogenophilicity of the [Cu^IL]⁺ complex. These conclusions were reaffirmed by a distortion/interaction model analysis, which indicated the activation energy is affected by both the R–X distortion energies and the interaction energies between R–X and Cu in the ISET transition state. Using these mechanistic insights, a two-variable linear equation was developed using R–X BDE and Cu–X halogenophilicity as parameters to describe the effects of R–X bond stretch and Cu–X interactions, respectively.

Taken together, we demonstrated the use of mechanistic insights derived from transition state calculations to guide the development of predictive mathematical equations for reactivities of Cu-ATRP. We expect our models to shed light on the rational ligand design and discovery for Cu-ATRP. Similar approaches may be employed to benefit the ligand design in other transition metal-catalyzed reactions.