Measuring and analyzing length of stay in critical care trials

Abstract

Background:

In randomized clinical trials (RCTs) among critically ill patients, it is uncertain how choices regarding the measurement and analysis of nonmortal outcomes measured in terms of duration, such as intensive care unit (ICU) length of stay (LOS), affect studies’ conclusions.

Objectives:

Assess the definitions and analytic methods used for ICU LOS analyses in published RCTs.

Research Design:

Systematic review and statistical simulation study.

Results:

Among the 80 of 150 trials providing sufficient information regarding the chosen definition of ICU LOS, three different start-times (ICU admission, trial enrollment/randomization, receipt of intervention) and two end-times (discharge readiness, actual discharge) were used. In roughly three-quarters of these studies, ICU LOS was compared using approaches that did not explicitly account for death, either by ignoring it entirely or stratifying the analyses by survival status. The remaining studies used time-to-event (discharge) models censoring at death or applied a fixed LOS value to patients who died. In statistical simulations, we showed that each analytic approach tested a different question regarding ICU LOS, and that approaches that do not explicitly account for death often produce misleading or ambiguous conclusions when treatments produce small effects on mortality, even if those are not detected as significant in the trial.

Conclusions:

There is considerable variability in how ICU LOS is measured and analyzed which impairs the ability to compare results across trials and can produce spurious conclusions. Analyses of duration-based outcomes such as LOS should jointly assess the impact of the intervention on mortality to yield correct interpretations.

INTRODUCTION

Length of stay (LOS) in the intensive care unit (ICU) is a common randomized clinical trial (RCT) endpoint used to quantify the duration of time that ICU-level care is needed for acutely ill patients. It has several attractive qualities as an endpoint including its ease of measurement in health records. It is also relevant to all ICU patients, in contrast to other common nonmortal outcomes, such as ventilator- or organ failure-free days, which are most applicable to patients with specific illnesses. Despite widespread use in RCTs, LOS and other nonmortal, duration-based outcomes (e.g., time requiring mechanical ventilation) raise several analytic and definitional challenges that cloud their interpretation. One such challenge is that many critically ill patients die. As a result, the observed ICU LOS represents a composite summary of at least two processes: the time until either a patient’s death or discharge. Thus, investigators must consider how to handle LOS values for those who died when comparing nonmortal endpoints between study arms. Because the truncation of follow-up (frequently called “censoring from death”) is a post-randomization event that may be impacted by the intervention, biased or ambiguous conclusions regarding the interventions’ effects may result despite the randomized design (1-4).

Though statistical frameworks have been proposed to support statistical inference with outcome data censored due to death in critical care settings (5-13) uptake of these methods has been limited and may be challenging to implement or interpret. Therefore, in this manuscript we sought to identify and examine the inferential consequences of different approaches chosen by researchers to compare ICU LOS. To accomplish these aims we performed a systematic review, conducted a statistical simulation study, and, based on our findings, generated recommendations for reporting and analyzing ICU LOS and other duration-based, nonmortal outcomes in RCTs.

METHODS

Systematic review

We extended a previously described database of critical care RCTs published in 16 high-impact journals (14) by two years, such that it spanned January 2007 through June 2015. For each trial, two abstractors identified the definition of ICU LOS provided by the authors, the statistical methodology used to compare ICU LOS between study arms, and how the ICU LOS distribution was reported.

Simulation study

We designed a statistical simulation study to assess how mortality-specific responses to an intervention could impact the statistical comparison of a duration-based outcome such as LOS. Our simulation study does not focus on model performance or estimate precision. Rather, we are interested in the clinical conclusions of harm (longer required duration of critical care) or benefit (shorter duration of critical care) for a duration-based outcome in the presence of small, potentially non-significant, intervention-associated mortality effects. Though we refer to our simulated values as ICU LOS, any duration-based outcome is applicable.

We outline the data generation process and our conceptual framework in the Supplementary Digital Content online and briefly provide our rationale for analytic decisions here. First, we designed a simulation study of LOS where an intervention would only impact the rate of mortality, and not discharge. Though unlikely in reality, this ‘test tube’ approach allows us to isolate our manipulation to only one part of the observed ICU LOS distribution, and thus gain insight into the potential inferential consequences of each manipulation. Second, we considered several ways to simulate hypothetical ICU LOS distributions and acknowledge that different researchers could approach this question differently. Ultimately, for this Monte Carlo experiment, we simulated hypothetical RCTs from a competing risks model using the survsim package in Stata 15 with two cause-specific hazards: time-to-death and time-to-discharge, following the methodology outlined by Beyersmann and colleagues (4, 15-17).

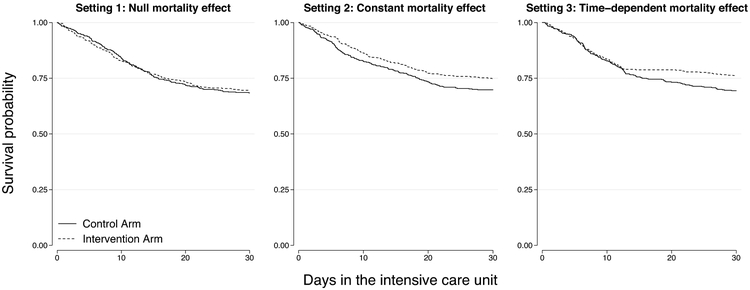
In our data generation model a hypothetical patient could be in one of three states at any given time: alive in the ICU, dead, or discharged, with the latter two as absorbing states (i.e., we did not allow for readmissions). In all settings, the true intervention effect on the discharge-specific hazard rate was 0 (i.e., null). Three varying intervention-associated mortality effects were applied in the mortality-specific hazard model. These scenarios summarize the majority of observed survival functions in published RCTs, with real-world examples shown in Figure E1. Simulated survival functions matching those in Figure E1 are displayed visually in Figure 1 and summarized below.

Figure 1.

Example Kaplan-Meier curves from the three simulated mortality settings. The three panels show one replicate from each setting randomly generated using an average 30% control arm mortality rate and 5% absolute treatment-associated mortality reduction.

Setting 1: Null mortality effect: in this setting, there was no intervention-associated mortality reduction (i.e., no treatment effect on mortality).

Setting 2: Constant mortality effect: in this setting, the intervention imposed a constant effect on the mortality rate over time (i.e., proportional hazards). As a result, the intervention impacted both early and late ICU mortality in the simulated trials.

Setting 3: Time-dependent mortality effect: in this setting, we model an intervention that only impacts late ICU mortality. To do so, we generated data using a time-dependent effect on the mortality rate such that there was no intervention-associated mortality reduction during the first two-thirds of the simulated sample’s ICU LOS, but there was a constant intervention effect on the mortality rate in the final one-third of the LOS distribution. This setting, observed for example in the ACURASYS trial (18), reflects the possibility that a treatment might help only the sickest patients who tend to have a longer LOS (19, 20).

Although we simulate beneficial intervention-associated mortality effects, identical results would manifest had we imposed the mortality reduction on the control arm. Thus, the results of the simulation study also apply to cases of harmful intervention effects.

By restricting the impact of the intervention to the mortality rate in our data generation process, any observed effect of the intervention on LOS must be due to the intervention-associated mortality effects or chance (i.e., stochastic error). Such effects could arise if an intervention extended patients’ LOS by saving them, or lengthened time-to-death (i.e., postponed death), because the intervention helped but did not save patients who nonetheless die. To assess the mechanistic consequence of intervention-associated mortality effects in the statistical frameworks identified in our systematic review, we summarize the percentage of 1,000 Monte Carlo replicates that reported a statistically significant difference in LOS between the intervention and comparator arms, and the direction of this effect. Administrative censoring occurred at 30-days to reflect common follow-up periods in published studies (14) and we used a two-sided alpha ( α)=0.05 to determine statistical significance, which is conventional in ICU-based RCTs. Based on our review of published RCTs (detailed in the results), we examined the following statistical approaches for comparing ICU LOS between study arms: linear regression and a Wilcoxon rank-sum test among all patients (ignoring mortality) and then among survivors only (stratified analysis), a Cox Proportional Hazards model for time-to-discharge with censoring at the time of death, ICU-free days (defined as 0 for a patient who died before day 30, and 30-ICU LOS for others) and a competing risks model (as used for our data generation).

We systematically adjusted four parameters in each of the three mortality settings outlined above. First, the control arm 30-day mortality was set to 30% or 10% (i.e., a probability of death of 0.30 and 0.10), representing relatively high and low in-hospital mortality rates for modern RCTs (14). Second, we imposed an absolute mortality reduction of 2.5% or 5.0% (i.e., an average probability difference of −0.025 and −0.050) in the intervention arm. We chose these effect sizes because they would be clinically important, and reflect actual differences observed in published RCTs, but most critical care RCTs would fail to detect them as statistically significant (14). Third, we examined short (e.g., median of 3 days, interquartile range [IQR]=1.5 to 4.5) and long (e.g., median of 10 days, IQR=5 to 17) LOS distributions, guided by RCTs where LOS was the primary outcome (21-23). Finally, we simulated the total sample size as 250 or 1,000 patients (125 or 500 patients per arm) as we sought to examine the potential impact of small intervention-associated mortality effects in the finite sample sizes of the vast majority of modern critical care RCTs (14, 24).

RESULTS

We identified 193 eligible RCTs among ICU patients from 2007 to 2015. Of these, 150 (78%) RCTs reported a statistical test comparing ICU LOS. In 132 of these trials, ICU LOS was specified as an a priori primary outcome (n=6) or secondary outcome (n=126).

Definition and measurement of LOS

In 70 (47%) RCTs reporting on ICU LOS, insufficient details were provided to determine how ICU LOS was measured. Of the remaining 80 (53%) RCTs, at least the start or the end time was reported by the authors (n=54, 36%), or one of these times could be reasonably deduced based on the descriptions of the study design or other trial outcomes (n=26, 17%). In 70 trials with reported or deducible “start times,” LOS measurement began at: a) the time of ICU admission (47%), b) the time of randomization or trial enrollment (34%), or c) the time of intervention initiation (7%). In the remaining 11% of trials, more than one start time was reported or two or more of these times appeared to overlap. In 70 trials with reported or deducible LOS “end times,” these times were specified as: a) ICU discharge and/or death (93%), or b) time of critical illness resolution (7%). As a result, current ICU RCTs report LOS as one of six distinct durations. The reported units of LOS also varied, with 60 trials (40%) reporting LOS in 24-hour periods without rounding to the nearest day, 77 trials (51%) reporting LOS as “days” without clarifying if days were calendar days or 24-hour periods, and 13 (9%) reporting LOS in hours.

Statistical analysis of ICU LOS

The analytic approach used by authors to compare ICU LOS between trial arms was generally poorly reported. Based on the published trial reports we concluded that 92 (61%) RCTs compared ICU LOS between study arms in all patients without discussion or statistical consideration of mortality. An additional 13 (9%) RCTs assessed a stratified sample of survivors, and 4 (3%) reported both stratified and all patients results. The remaining 41 (27%) trials reported at least one approach that we infer to have been chosen to account for the potential effects of mortality. These approaches, summarized in Table E1, may be categorized as follows: (a) an event-free outcome (e.g., ICU-free days), (b) changing the value of LOS to be the longest LOS for patients who die, or (c) using a time-to-event (e.g., time-to-discharge) model.

Simulation study

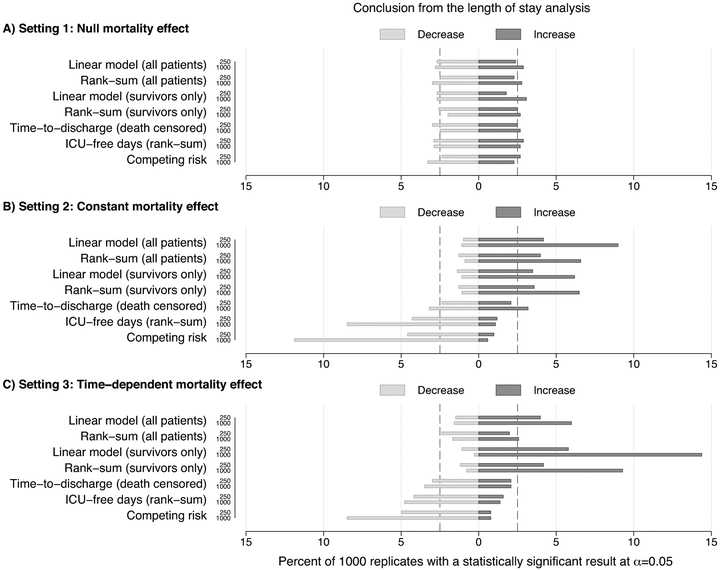
In setting 1, where the true treatment effect for both the mortality and discharge hazard was 0, we observed a similar percentage of replicates concluding harm or benefit across all approaches, aligning nearly symmetrically with the two-sided α value of 0.05/2 (Figure 2 and E2). That is, the presence of high mortality (and thus censoring) alone did not impact the results of any statistical method. In contrast, in settings 2 and 3, when there was a true simulated beneficial intervention-associated mortality effect, but none on time-to-discharge, we observed disparate conclusions between approaches (Figure 2, E2-E5). Thus, only simulations with a differential mortality rate due to the intervention impacted clinical conclusions regarding ICU LOS.

Figure 2.

Percent of simulations suggesting clinical harm (i.e., an increase in intensive care unit (ICU) length of stay (LOS)) or benefit (i.e., a decrease in ICU LOS). These results correspond to the simulation settings with n = 250 or n = 1,000 patients (with 1:1 randomization) and a 30% control arm mortality rate. On average, setting 1 (Panel A) had no treatment-associated mortality reduction, whereas settings 2 (Panel B) and 3 (Panel C) had an absolute treatment-associated mortality reduction of 2.5%. Setting 3 restricted the treatment-associated mortality effect to simulated patients who survived beyond the longest tertile of their hypothetical ICU LOS. Additional details of the Monte Carlo simulation study are summarized in the EMethods.

The difference in the percent of replicates suggesting harm or benefit alongside the underlying hypothesis that is tested by each analytic approach showed that an intervention can impact ICU LOS comparisons through three mechanisms: (i) incidence, (ii) duration (i.e., distribution of observed LOS), or (iii) the rate of an event (i.e., discharge). For example, approaches that compared observed LOS durations (i.e., rank-sum and linear models) were the most susceptible to misleading conclusions of harm in our simulated settings. Specifically, both the linear regression models as well as the Wilcoxon rank-sum tests identified longer overall LOS times (suggesting a negative or harmful effect) in the intervention arms that had reduced mortality. In contrast, the competing risk model showed that the declines in mortality we imposed resulted in a statistically significant increase in the probability of discharge in several replicates. The increased incidence of discharges in the intervention arm corresponded to fewer individuals dying, and thus more ICU-free days. As a result, the competing risk and ICU-free days approach to comparing LOS more frequently suggested a beneficial treatment effect. The time-to-event (discharge) analyses with censoring for death produced the lowest rates of perceived harm or benefit. These results reflect the increase in the incidence of discharge due to the beneficial intervention effect on mortality, while there was no direct effect on the rate of discharge in our data generation.

The magnitude of the intervention-associated mortality effects on the conclusions from different approaches to comparing ICU LOS in the presence of differential mortality depended on the total sample size, magnitude of the mortality effect, and time dependency of the mortality effect (i.e., constant versus time-dependent intervention effects) (Figure 2, E2-E5). When the mortality intervention effect was constant (setting 2, Figure 1), we found that summary comparisons of the entire sample (which ignore differences between deaths and discharges) were most likely to suggest harmful (longer) LOS treatment effects, with small differences between parametric and non-parametric comparisons. While we found high rates of harmful LOS treatment effects when only survivors were evaluated in setting 2, this effect was most pronounced when the intervention-associated mortality effect was isolated to the sickest patients (setting 3, Figure 1).

DISCUSSION

This study demonstrates considerable variability in how ICU LOS is measured and analyzed in critical care RCTs, and reveals the importance of how investigators account for mortality when analyzing this endpoint. Several specific results yield recommendations for future measurement, analysis, and reporting of ICU LOS.

In regards to measuring ICU LOS, the considerable variability we identified limits the ability to compare interventions’ effects on LOS across trials. Similar problems arise from the noted variability across trials in the start and stop times of ICU LOS, and in the scale of LOS reporting (i.e., calendar days, 24-hour periods without rounding, or hours), which may also influence the magnitude of measurement errors (25). Therefore, we recommend a standardized measurement of ICU LOS that begins with receipt of a trial intervention and ends when a patient is deemed clinically ready for discharge (26) (Table 1).

Table 1.

Recommendations for reporting and analyzing nonmortal endpoints in critical care trials, using intensive care unit (ICU) length of stay (LOS) as an example.

Domain	Problem identified in review	Recommendations
Measurement	Trials reporting start and end times for LOS varied in their definitions, and many do not report definitions.	Clearly indicate the LOS start and end times. Give special consideration to using the start of an intervention and the time when patients are deemed clinically ready for discharge for these times.
	Trials predominantly report LOS in "days." Calendar days and 24-hour periods are different, and can further vary based on the above-mentioned issue of start and end times. This potentially adds measurement error.	Measure LOS in hours or 24-hour periods with decimal places.
Analysis	Many trials simply state that nonparametric or parametric statistical models were used without any further detail. It is unclear in some trials which model was used to generate the reported p-value.	Clearly report the statistical method used to compare LOS between study arms.
	The treatment of LOS among those who died is often unclear, but is important to the interpretation of the effect estimate presented.	Clearly indicate how LOS values among decedents were coded. For example, indicate if LOS was censored at the time-of-death in a time-to-event model or when reporting composite outcomes that include LOS (e.g., event-free days), clearly define the value for LOS used for those who die (e.g., zero free days).
	The analytic sample that was used to estimate the effect of an intervention on LOS is not always clear or well-defined.	Cleary state the analytic sample (e.g., survivors only) and sample size for each statistical analysis that is conducted.
	Mortality is often reported at a few discrete time points (e.g., 28 or 60 days) or without a specific follow-up period (e.g., ICU mortality). This makes it difficult or impossible to assess trials for interpretive bias in the reporting of nonmortal endpoints if non-differential mortality occurs between study arms.	Include a Kaplan-Meier survival probability figure that reports mortality rates at regular and frequent time periods (e.g., 7, 14, 21, and 28 days) that complement the follow-up time of the LOS analysis.
	Most trials do not execute sensitivity analyses using advanced statistical methods.	Although the ideal or “correct” method for statistical inference may be uncertain, using secondary methods such as competing risk, principal stratification, or joint statistical models can help researchers assess both the impact of their assumptions and the robustness of their results.

We also identified at least four distinct analytic approaches that were commonly used to compare LOS between study arms (Table 2). These variations in statistical methods lead to the testing of fundamentally different research questions. The most common approach is to contrast overall LOS distributions in each study arm without accounting for mortality. Our simulations suggest that this approach commonly generated misleading results in the context of even small intervention-associated mortality effects. This limits the ability to differentiate interventions that seem to lengthen LOS due to beneficial, albeit perhaps underpowered mortality effects, versus those that truly lengthen LOS without such corresponding benefits.

Table 2.

Common approaches used to account for mortality in the analysis of intensive care unit (ICU) length of stay (LOS).

Approach	Conceptual and empirical issues
Contrast a pooled LOS distribution of survivors and decedents together without acknowledging death.	LOS treatment effects for survivors and decedents may differ both in magnitude and direction. Patients saved by a treatment may experience longer LOS.
Contrast the LOS distribution among survivors only.	Survival may be affected by the intervention. Thus, it is a post-randomization variable. Conditioning on survival reduces statistical power and can erode randomization inference.
Contrast time-to-discharge in a time-to-event model and treat mortality as a form of non-administrative censoring.	• Risk set subsequent to the first death comprises a new subset of patients who have not previously died or been censored. Thus, the balance of confounders assumed by randomization is potentially eroded. • Statistical model assumes LOS at the time of death is not related to the intervention.
Contrast a composite endpoint that includes both a value for death and LOS (e.g., ICU-free day metric where those who died are assumed to have zero ICU-free days or changing LOS to the longest value).	• Valuing death inserts subjectivity into the statistical analysis and changes the causal question. • Composite outcome (e.g., ICU-free day) may summarize the net effect of an intervention but does not have a real-world translation.

The other three approaches attend to mortality in different ways, with some raising greater interpretive challenges than others. First, assessment of LOS among survivors reduces analytic sample sizes, which may be small in critical care trials to begin with (14, 27, 28). Additionally, such restriction can yield misleading results if an intervention shifts very sick patients from the “deceased” cohort to the “survived” cohort, where they may contribute an unusually long LOS (20). Setting 3 of the simulation study showed that this approach can be especially problematic in RCTs in which the benefit of an intervention is largest among relatively sicker patients (29).

Second, investigators may use time-to-event models that estimate time-to-discharge. Although censoring on death is likely superior to ignoring it altogether, such censoring assumes that death is random and non-informative. This assumption is almost certainly untenable, as patients’ acuities and comorbid conditions are related to both their probability of dying and their LOS if they survive (30). Thus, the probability of censoring may be time-dependent, and thus introduce bias despite randomization (31). Therefore, the observation that time-to-event analyses produced the fewest instances of bias in our simulations should not necessarily be interpreted as a reason to advocate using this approach, because the validity of the results rests upon the untestable and unlikely assumption that death is non-informative.

The final approach values death as a fixed LOS for decedents, most commonly using an ICU-free day method where LOS is set equal to the maximum follow-up time minus ICU LOS for live discharges and zero for decedents (10). Another valuation approach changes the LOS of those who died to the longest LOS but does not transform to ICU-free days. A prior simulation study suggested that when non-parametric tests are used to compare LOS distributions among treatment and control groups, this latter approach to valuing LOS can accommodate a range of values for death, such as coding it at the 80^th percentile of the LOS distribution or as the worst possible LOS (20). Wang and colleagues have also proposed recent innovations to composite outcome measurement and analysis, focusing on approaches to ranking death and nonmortal outcomes in critical care (9, 11). Combining death and a nonmortal outcome is an attractive approach as it preserves a study’s sample size (and thus supports an intention to treat analysis). However, combining outcomes into a composite rank provides little insight about an intervention’s direct impact on mortality or LOS. Instead, this approach gauges an intervention’s “net” impact on both morbidity and mortality. Thus, the approach is unbiased, but proper interpretation is dependent on the value given to those who died being acceptable to and understood by key stakeholders. A benefit of testing a range of death values (20) is that it enables investigators to assess whether the conclusions drawn are sensitive to how patients value death versus prolonged ICU stays.

In practice, researchers must find a balance between acceptability and potential bias. That is, while more complex analytic methods exist (5-9, 12) for contrasting “truncated by death” outcomes, they may not be well received by regulatory agencies, journal editors, or reviewers. Testing for the stability of an observed treatment effect using more than one approach in sensitivity analyses may be infeasible for every secondary outcome, but we recommend that multiple methods be examined for concordance in the results of contrasts between at least the primary, and ideally key secondary trial outcomes. In addition to the traditional ICU-free days (or an alternative rank-based method) and competing risk method we assessed, we believe two other methods should be utilized by researchers if their data permits. The first is a joint longitudinal and survival model, which provides an effect estimate specific to the nonmortal outcome through the end of the study period (i.e., longitudinal submodel) that accounts for missing outcome data due to death (survival submodel) (12, 13, 32). In addition, a principal stratification approach can estimate the survivor average causal effect if certain data elements and follow-up are available (5-7, 11).

Limitations

The categorization of each RCT’s methods in the systematic review was limited by differential reporting practices by authors as well as standards and requirements at different journals (e.g., publication of trial protocols). It is possible that many trials utilized detailed and standardized definitions, measurements, and contrasts of LOS, but did not report them, particularly when LOS was a secondary outcome. However, it is unlikely that more complete reporting would have reduced the considerable variability in the measurement and comparison methods we identified. Second, it is possible that our search did not identify some trials published in the 16 target journals. Such omissions are unlikely to have been systematic, and would not be expected to alter our conclusions.

Third, our simulation study did not address all potential ICU trial settings. Instead, we chose a limited set of scenarios to illustrate how missing or truncated outcome data may alter the conclusions formed in studies of ICU interventions. We did not model other scenarios, such as those in which treatments directly affect LOS, because we sought to highlight problems that may result due to small mortality changes resulting from an intervention, rather than to provide an exhaustive accounting of the magnitudes of these problems in all possible scenarios.

Conclusion

This study reveals that although ICU LOS is a commonly used outcome in contemporary critical care RCTs, tremendous variability exists among trials in how it is reported and analyzed. Similar heterogeneity of outcome use and definition have been documented in trials of patients requiring mechanical ventilation and other fields of clinical research (33-35). However, the present study extends this descriptive literature by illustrating how these choices may impact the interpretation of trial results. While we chose to focus on ICU LOS, our results are likely applicable to most duration-based outcomes measured among critically ill patients. We therefore provide recommendations to help investigators measure and report trial results that will aid in their interpretation and synthesis. Specifically, employing primary, or at least predefined secondary, analyses with novel statistical approaches, such as the aforementioned rank-based method (20) and joint modeling approaches (12, 13), would enable experience to be gained with these methods to determine whether they ought to become standard. Although it is possible that no single method will solve the analytic challenges that arise in duration-based outcomes in which substantial portions of patients die during longitudinal evaluation, this work will help researchers consider, when designing their protocols and reporting their results, the advantages and disadvantages of different approaches to evaluating trial outcomes.