ESTIMATING BREAST CANCER SURVIVAL BY MOLECULAR SUBTYPE IN THE ABSENCE OF SCREENING AND ADJUVANT TREATMENT

Abstract

As molecular subtyping of breast cancer influences clinical management, evaluation of screening and adjuvant treatment interventions at the population level needs to account for molecular subtyping. Performing such analyses are challenging because molecular-subtype-specific long-term outcomes are not readily accessible as these markers were not historically recorded in tumor registries. We present a modeling approach to estimate historical survival outcomes by estrogen-receptor (ER) and human epidermal growth factor 2 (HER2) status. Our approach leverages a simulation model of breast cancer outcomes and integrates data from two sources: the Surveillance Epidemiology and End Results (SEER) databases and the Breast Cancer Surveillance Consortium (BCSC). We not only produce ER,HER2-specific estimates of breast cancer survival in the absence of screening and adjuvant treatment, but we also estimate mean tumor volume doubling time (TVDT) and mean mammographic detection threshold by ER/HER2-status. In general, we found that tumors with ER-negative and HER2-positive status are associated with more aggressive growth, have lower TVDTs, are harder to detect by mammography and have worse survival outcomes in the absence of screening and adjuvant treatment. Our estimates have been used as inputs into model-based analyses that evaluate the effects of screening and adjuvant treatment interventions on population outcomes by ER and HER2 status developed by the Cancer Intervention and Surveillance Modeling Network (CISNET) Breast Cancer Working Group. In addition, our estimates enable a re-assessment of historical trends in breast cancer incidence and mortality in terms of contemporary molecular tumor characteristics. Our approach can be generalized beyond breast cancer and to more complex molecular profiles.

INTRODUCTION

Advances in the molecular characterization of breast cancer have allowed researchers to recognize and study the highly heterogeneous nature of this disease. Currently, several molecular markers and genetic signatures have been identified that are predictive of survival, response to molecularly targeted therapies, and the likelihood of recurrence (1–10). As the understanding of this heterogeneity becomes increasingly relevant in clinical practice, population surveillance models will need to evaluate the population impact of current and emerging screening and adjuvant treatment (hereafter referred to as “treatment”) patterns by accounting for this molecular heterogeneity.

Simulation-based analyses provide a means to synthesize the available clinical and population-level data to quantify the effects of cancer control interventions. In prior work (11), a consortium of independent investigators from the Cancer Intervention and Surveillance Modeling Network (CISNET) reported on the use of several simulation-based models to assess the relative contributions of screening mammography and adjuvant treatment on the reduction in breast-cancer mortality for the overall U.S. population. In that analysis, all CISNET models began by recreating incidence and mortality trends in the absence of screening and adjuvant treatment interventions. Then, these interventions were superimposed based on their dissemination and efficacies across calendar years to assess the effect of the presence of interventions relative to their absence on outcomes. For this reason, possessing molecular-subtype data in the absence of screening and treatment are necessary to estimate the impact of these interventions by molecular-subtype using similar simulation-based approaches. Assessing molecular-subtype data in the absence of screening and treatment, however, poses a significant challenge. Given the relatively novel nature of clinically-relevant molecular markers such as estrogen receptor (ER), and human epidermal growth factor 2 (HER2), historical surveillance data reporting them are rare. Therefore, using existing methods to infer the impact of screening and treatment on breast cancer trends by ER and HER2 status is not straightforward.

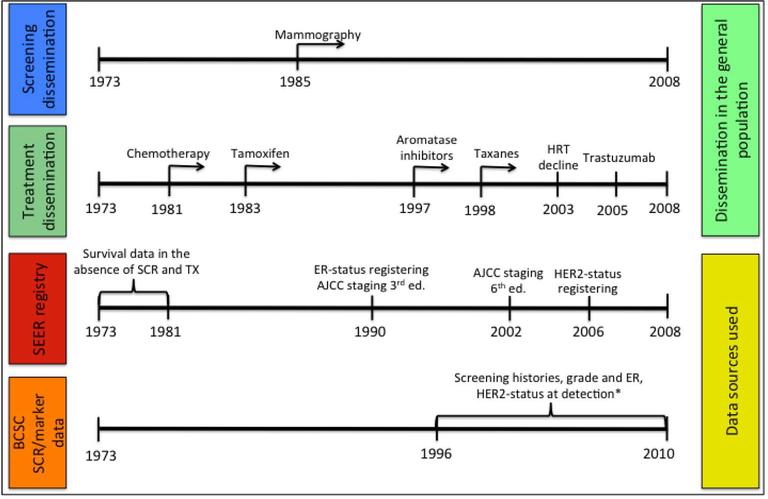
In this work, we focus on ER and HER2 molecular markers because of their clinical relevance. ER-status serves as a predictor of patient response to systemic therapies (1, 2), such as hormonal therapy (i.e. tamoxifen). Additionally, when compared to its ER-positive counterpart, ER-negative breast cancer is also associated with higher tumor aggressiveness and lower screening benefits due to length time biases (12–14). Although registries such as Surveillance Epidemiology and End Results (SEER) report breast cancer specific survival dating back several decades, collection of ER-status began by 1990 in an era where mammographic screening and treatment were widespread. Hence, ER-specific data that can be used to estimate underlying survival by these molecular subtypes in the absence of screening or adjuvant treatment is not readily available. Similarly, acquisition of HER2-status, which is a strong predictor of tumor aggressiveness and response to trastuzumab (15–17), only started in the early 2000s and the SEER cancer registries began reporting this data in 2010. To illustrate this point, Figure 1 presents a timeline showing when screening mammography and different types of treatment became widely disseminated compared to when records in the SEER registry were annotated by ER and HER2 status.

Figure 1.

Timeline showing when screening mammography and different types of treatment became widespread in the general population compared to data available in the Surveillance Epidemiology and End Results (SEER) registry and incidence records with screening histories provided by the Breast Cancer Surveillance Consortium (BCSC). * Estrogen-receptor (ER) status and human epidermal growth factor 2 (HER2) status were available in the Breast Cancer Surveillance Consortium (BCSC) data for women diagnosed between 1996–2010 and 1999–2010, respectively.

We present a modeling approach to estimate several population-level breast cancer survival by ER and HER2 status, in the absence of screening and treatment. Our approach makes use of a previously developed natural history model of breast cancer (18–20) to integrate data from two distinct sources: 1) SEER and 2) Breast Cancer Surveillance Consortium (BCSC). Data on women detected with breast cancer between 1996–2010 provided by the BCSC includes ER/HER2, mode of detection and screening histories (note the BSCS data source in Figure 1). Our method not only produces ER/HER2-specific breast cancer survival cases in the absence of screening and adjuvant, we simultaneously produce several other ER/HER2-specific estimates, including: the distribution of ER/HER2-subtypes by age in the absence of screening, ER/HER2-specific tumor volume doubling times and tumor-size specific mammography threshold by ER/HER2.

The estimates presented herein have been recently incorporated into the current versions of the CISNET breast cancer models (21, 22). Furthermore, the CISNET modeling groups have already used them to evaluate the relative contributions of screening and adjuvant treatment by ER-subtype (23) and by ER/HER2-subtypes (24,25).

MATERIALS AND METHODS

This study makes use of a previously developed model (Model S, also referred to as BCOS for “Breast Cancer Outcomes Simulator”) to simulate the natural history of breast cancer in the average-risk U.S. population, incorporating the effect of screening and treatment (18–20). We modify Model S to estimate underlying breast cancer progression and survival by ER/HER2-status. Specifically, we stratify the natural history of breast cancer by tumor grade, low (grade I+II) versus high (grade III), following an approach used in our prior work (26, 27). The inclusion of grade into our natural history model serves to leverage this feature’s relationship with ER and HER2 status. In addition, it expands the model’s ability to capture a broader spectrum of tumor aggressiveness (27). In this regard, Model S is well suited for this work because its underlying natural history model is easily adaptable in the manner (19, 20).

Broadly, our methodology for estimating ER/HER2-specific breast cancer survival in the absence of screening and treatment consists of several steps. First, we constructed ER-specific and ER/HER2-specific classifiers that are capable of inferring these molecular markers based on a patient’s mode of detection, screening history and tumor features at detection. Then, we simulated an enhanced virtual SEER breast cancer registry that includes patient-level information not found in SEER such as: the mode of detection, screening history, tumor features and survival in the presence and absence of screening. We use the molecular classifier (from the first step) to assign the molecular profile for each individual patient. In essence, this procedure may be conceptualized as an imputation of molecular-specific markers run across a virtual patient registry. Later, we demonstrate how this virtual, enhanced database allows us to evaluate population-level outcomes by ER and HER2 subtypes as if these were measured directly in the general population. Table 1 shows an overview of our estimation procedure indicating inputs and outputs for each step.

Table 1.

List of steps involved in the estimation procedure indicating inputs, a brief description and outputs for each.

Estimation Step	Input	Description	Output
1. Train ER/HER2-Classifiers	BCSC data consisting of 13,900 patient records labeled with ER/HER2-status	Build a classification model (LADTree) to predict ER/HER2-status based on other tumor features, screening history and mode of detection	ER/HER2-status based on: 1) detection age, 2) tumor grade, 3) tumor size, 4) tumor stage, 5) screening history and 6) mode of detection.
2. Estimate BCOS’s Natural History Model Parameters	SEER Incidence data from 1975–1981	Fit maximum likelihood estimates of the natural history model parameters using data on tumor size, stage and grade at diagnosis.	BCOS with grade-specific natural history model parameters
3. Run BCOS to construct an enhanced, virtual SEER registry	- Natural history model parameters (Step 2) - SEER survival curves from pre-screening period (1975–1981)	Generate samples of simulated women across different cohorts and calendar years	Virtual registry of 180 million women with their tumor features, screening history, detection age and survival. Generate these features both in the presence and absence of screening and treatment for all calendar years.
4. Predict ER/HER2status for women in the virtual SEER registry	- Virtual cancer registry (Step 3) - ER/HER2-status classifier (Step 1)	Input each of the simulated tumor features (in the presence of screening) to the classifier to predict the ER/HER2-status for each simulated patient	Virtual registry of 180 million women labeled with their predicted ER/ HER2-status
5. Compute desired estimates by ER/HER2-status	Virtual registry of 180 million women (Step 3) with their predicted ER/HER2-status (Step 4)	Compute several ER/HER2-specific estimates.	All the following are computed by ER/HER2-status: 1) Survival in the absence of screening and treatment, 2) Distribution of ER/HER-status at clinical detection, 3) Mean tumor doubling time (TVDT) 4) Mean mammography detection thresholds.

Abbreviations: BCOS: Breast Cancer Outcomes Simulator, aka Model S.

To more fully describe our estimation methodology, we introduce some notation. For each simulated woman, we define the following features:

ER ER-status, which may be positive or negative.

HER HER2-status, which may be positive or negative.

g Tumor grade, which may be low-grade (I+II) or high-grade (III) (28).

A: (A_A, A_P) Age at detection in the absence (A) and presence (P) of screening, respectively.

V: (V_A, V_P) Size at detection in the absence (A) and presence (P) of screening, respectively.

N: (N_A, N_P) Stage at detection in the absence (A) and presence (P) of screening, respectively.

We used SEER historical stages of local (L), regional (R) and distant (D). (Note that SEER historical stage combined with tumor size can be used to approximate AJCC stages.)

M Screening history, which includes the mode of detection and the interval between the last screening examination and breast cancer detection. We consider seven possible scenarios for this feature:

1. Prevalence detected (S_P): patient was screen-detected during her first screening examination.

2. Screen detected-Annual (S_A): patient was screen-detected and the time since her last screen was between 0 to 17 months.

3. Screen detected-Biannual (S_B): patient was screen-detected and the time since her last screen was between 18 to 30 months.

4. Screen detected-Other (S_O): patient was screen-detected and the time since her last screen was > 30 months ago.

5. Clinically detected-No Screening (C₀): patient was clinically detected and never underwent screening.

6. Clinical detected-6 months (C₁): patient was clinically detected and the last time since her previous screen was <= 6 months. These cases correspond to interval cases detected at most 6 months after the last screen.

7. Clinical detected-6+ months (C2): patient was clinically detected and the last time since her previous screen was > 6 months. These cases correspond to interval cases detected with more than 6 months transpired since the last screen.

λ₀ Survival time in the absence of screening

Note that for A_A, V_A, N_A and λ₀ the term ‘absence of screening’ refers to the age, size and stage at detection, respectively, for a woman that has never undergone a screening examination. Alternatively, parameters A_P, V_P and N_P refer to the age, size and stage at detection, respectively, for a woman who has had at least one screening. Both sets of parameters may be equal if a woman is screened but the disease is not detected before symptoms arise; in fact, these cases correspond to interval cancers. It is relevant to note that the inclusion of mode of detection as a feature to the classifiers was necessary to account for the significant length-time biases associated with differences in tumor growth across different molecular subtypes.

BCSC data used to determine grade dependent on model of detection

In addition to the inputs required for our natural history model that have been described in previous work (18–20, 27), our estimation also relies on new inputs obtained from data provided by the Breast Cancer Surveillance Consortium (BCSC) and the SEER registry. The BCSC provided individual level patient records from breast cancer cases detected between 1996–2010, which include the following features: age, stage and size at detection (A, V and N), mode of detection, time between the last screen and invasive BC detection (M), tumor grade (τ), ER-status (ER) and HER2-status (HER). We removed cases that possessed missing information, assuming it was missing at random, and worked only with the remaining 13,900 complete records.

The BCSC data is used in several ways. First, we used it to calculate the probability of an individual woman’s cancer being low or high-grade conditioned on age of clinical detection:

$$P\left(g|A_A\right)$$

This parameter is a direct input used by the model to determine the tumor grade of every simulated woman. To avoid potential length time biases, we only use BCSC records for women who did not undergo screening to estimate the distribution of grade.

BCSC data used to build ER/HER2-classifier

We also used BCSC data to build two classifiers: one to infer ER-status and the other to infer ER/HER2-status jointly. In the case of ER-status, we are making a two class prediction: (1) ER-positive versus (2) ER-negative; whereas for the joint ER/HER2-status we make a prediction across four different classes: (1) ER-positive, HER2-positive, (2) ER-positive, HER2-negative, (3) ER-negative, HER2-positive and (4) ER-negative, HER2-negative.

We compared the performance of several different machine learning techniques and chose to use Alternating Decision Trees (ADTree) (29) for the ER-status classifier and its multiclass counterpart, LADTree (30), for the joint ER/HER2-status classifier, as these performed best in terms of predictive power (comparisons across other types of classifiers are not shown). ADTree is a classifier that combines decision trees, voted decision trees, and voted decision stumps based on the concept of boosting, which produces accurate predictions by combining a series of “weak” learners together (29). The LADTree algorithm produces a multi-class prediction alternating decision tree and uses the LogitBoost strategy, which performs additive logistic regression (30). A graphical representation of the ER/HER2-status classifiers are provided in the supplemental material Figures S.1 and S.2 for high and low-grade tumors, respectively. To predict the molecular markers based on a woman’s tumor features, the tree is traversed adding a different score at each decision stump. The final prediction is made by choosing the molecular-marker with the highest score after reaching the lowest leaf. Supplemental tables S.1 and S.2 show the scores associated to each molecular-marker for each decision stump of the alternating decision tree.

We constructed two separate classifiers corresponding to low and high-grade tumors, and all classifiers use the following features to determine the molecular subtype of each woman: (A_P, V_P, N_P,M). Given these classifiers and the distribution of women with different combinations of features, let us denote P(ER, HER|g, A_P, V_P,N_P,M) as the probability of a particular ER/HER-2 status given (g, A_P, V_P,N_P,M).

SEER survival in pre-screening period defines the baseline survival curves

To ultimately determine ER/HER2-specific survival for patients in the absence of screening mammography and adjuvant treatment, we leverage SEER survival curves for cases detected between 1975–1981, when use of screening and adjuvant treatment were not widespread in the general population. We define a survival curve as a function S(t, θ) such that:

$$S(t,\theta )=\frac{P(\lambda \ge t|\theta )}{P(\theta )}$$

where t and λ are survival times, and θ is the set of parameters that describe the patient’s breast tumor characteristics. These survival curves are stratified by tumor grade (low: I+II and high: III), age (<=50, >50), tumor size (<=2cm, 2–5cm and >=5cm) and SEER historic stage (local, regional and distant), and were fit to parametric cure models using CANSURV, a statistical software developed by the NCI to analyze population-based survival data. (31).

Molecular-specific Parameter Estimation

The premise behind our estimation is to generate the individual-level characteristics of each woman’s breast cancer during its pre-clinical course and at the time of clinical detection in the absence of screening, and then use this information to determine ER/HER2-status by applying the molecular-subtype classifiers. Note that adjuvant treatment or survival outcomes are not used to assign molecular subtype at detection. Instead, the breast tumor’s features at clinical detection are used to determine survival in the absence of screening and treatment by sampling from the 1975–1981 SEER survival curves. In this manner, we can compute (or “back-calculate”) survival curves for each molecular subtype. In essence, by following this procedure, we are generating a “virtual population” of women, conditioning each of the tumor features and outcomes to form a sample from a distribution:

$$\begin{gathered} P\left({\lambda }_0,g,A_P,V_P,N_P,ER,HER,M,A_A,V_A,N_A\right)=P\left({\lambda }_0|g,A_A,V_A,N_A\right)\ast \\ P\left(ER,HER|g,A_P,V_P,N_P,M\right)\ast P^{SCR}\left(A_P,V_P,N_P,M|A_A,V_A,N_A,g\right)\ast \\ {P}^{NH}\left(V_A,N_A|g,A_A\right)\ast P\left(g|A_A\right)\ast P\left(A_A\right) \end{gathered}$$

derived by applying the chain rule using conditional probabilities for each set of random variables.

To obtain stable estimates, we simulated the outcomes of 2,000,000 women for each of the 90 birth cohorts from 1891–1981. Let & be the complete set of simulated women, this implies that we construct a “virtual population” of over & =180,000,000 women with data on their breast cancer tumor features and outcomes. In the following subsections, we detail the modeling of each component of this joint distribution.

Probability of age at clinical detection P(A_A)

As described in previous work (19, 20), our simulation model begins generating the life history of an individual patient by determining: date at birth, date of death from other-cause mortality, and age of clinical detection for the first invasive breast cancer in the absence of screening (A_A). For the latter, we sample from a distribution function of the clinical detection age at symptomatic detection:

$$P\left(A_A\le a\right)=1-\prod _{i=25}^a\left(1-h_i\right)/100000$$

where age a is an integer and ℎ_i is the hazard rate per 100,000 women at age i. Incidence rates are provided from a prior CISNET’s base case input, commonly referred to as the “secular trend in breast cancer incidence” from 1975–2000 (32).

Probability of grade, volume and grade at clinical detection, P(g|A_A)

Given A_A, we then determine the woman’s tumor grade by sampling from the distribution P(g|A_A) derived from BCSC data. Subsequently, we use the natural history model to determine each woman’s tumor volume doubling time (TVDT) conditional on age and grade and use it to model tumor size (V_A) and stage (N_A) at symptomatic detection in the absence of screening and treatment (18, 19). Specifically, let us denote P^NH(V_A,N_A| g, A_A), as the set of distributions that characterize the natural history by modeling V_A and N_A, given g and A_A.

Probability of grade, volume and grade at screen detection

Having each woman’s parameters in the absence of screening (A_A, V_A,N_A), we now superimpose screening to obtain the set of parameters in the presence of screening (A_P, V_P,N_P) (19). In other words, we denote P^SCR (A_P, V_P,N_P,M| A_A, V_A,N_A) as the screening function that determines the age (A_P), size (V_P) and stage (N_P) at detection in the presence of screening, as well as the mode of detection and the interval between the last screening examination and breast cancer detection (M).

Determining molecular-subtype and survival at clinical detection

To determine each patient’s molecular status, we use the features (g, A_P, V_P,N_P,M) as inputs to our ER/HER2-status classifiers. Then, to determine survival time, we use survival curves from SEER 1975–1981 stratified by tumor grade, age, size and stage; in other words, we sample from P(λ₀|g, A_A, V_A,N_A) to determine the survival time for clinical detection, λ₀. Note that we specifically condition our survival time on (A_A, V_A,N_A), instead of (A_P,V_P,N_P), because our ultimate objective is to estimate survival curves by ER/HER2-status in the absence of screening and adjuvant treatment. Hence, we assume these molecular markers remain unchanged during the pre-clinical course of the disease; in other words, a tumor will not change molecular subtype during its natural history.

Using the joint distribution to estimate molecular-specific parameters

Having simulated the large cohort of women, we utilize the joint distribution of their tumor features to calculate molecular-specific parameters. For instance, we calculate underlying survival as follows:

$$S(t|\left(A_A,V_A,N_A,ER\right)=\frac{P\left({\lambda }_0\ge t,A_A,V_A,N_A,ER\right)}{P\left(A_A,V_A,N_A,ER\right)}$$

where P(λ₀ ≥ t, A_A, V_A,N_A, ER) and P(A_A, V_A,N_A, ER) are the marginal distributions:

$$\begin{gathered} P\left({\lambda }_0\ge t,A_A,V_A,N_A,ER\right)=\sum _{{\lambda }_0\ge t}\sum _M\sum _g\sum _{\left(A_P,V_P,N_P\right)}P\left({\lambda }_0,g,A_P,V_p,N_P,ER,M,A_A,V_A,N_A\right) \\ P\left(A_A,V_A,N_A,ER\right)=\sum _{{\lambda }_0}\sum _M\sum _g\sum _{\left(A_P,V_P,N_P\right)}P\left({\lambda }_0,g,A_P,V_P,N_P,ER,M,A_A,V_A,N_A\right) \end{gathered}$$

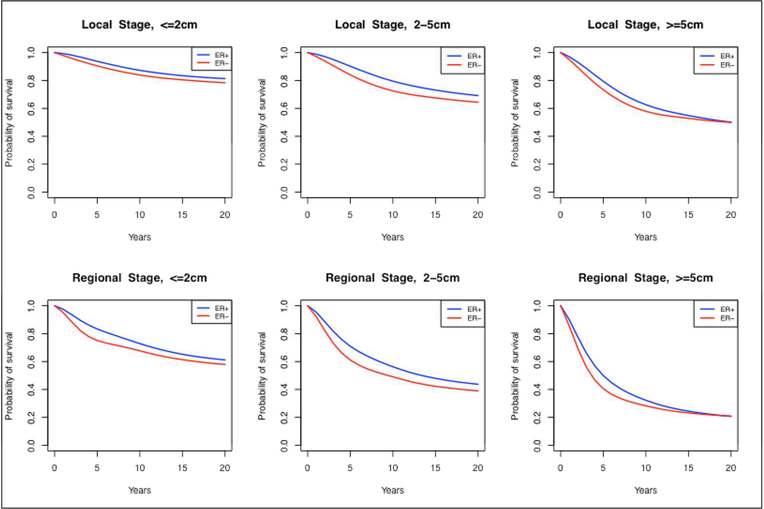
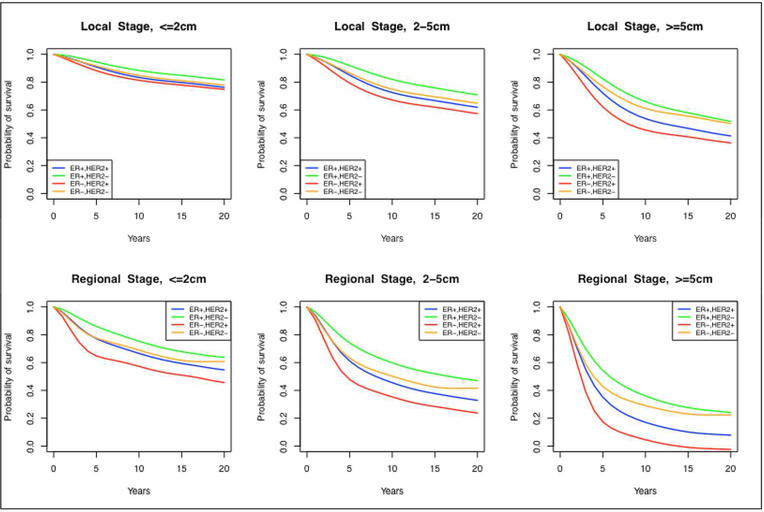
We only show the derivation for calculating ER-specific estimates, but the ER/HER2 case is analogous. Note that these survival curves are conditioned on (A_A, V_A,N_A, ER), which make them ER−, age-, size- and stage-specific in the absence of screening and treatment. Since age and size are continuous variables, we aggregate the survival curves for ages <40, 40–49, 50–59, 60–69 and 70+ and three different size groups: <2cm, 2–5cm and >5cm. These size groups roughly correspond to AJCC stages (28), facilitating use in models that rely on this stage classification. A subset of the estimated ER-status and ER/HER2-status showing the underlying survival curve differences across subtypes is shown in Figure 2 and Figure 3, respectively; the numerical values of the complete set of curves may be found in supplemental spreadsheet S.1.

Figure 2.

Estimated survival curves by estrogen-receptor (ER) status, stage (local and regional), and tumor size (<=2cm, 2–5cm, >=5cm) in the absence of screening and adjuvant treatment.

Figure 3.

Estimated annual mortality hazards by joint estrogen-receptor and human epidermal growth factor 2 (HER2) status, stage (local and regional), and tumor size (<=2cm, 2–5cm, >=5cm) in the absence of screening and adjuvant treatment.

Working with the feature estimates of each woman in the virtual population, we also computed mean tumor volume doubling times (TVDT), mean mammography detection thresholds and mean sojourn times for each combination of molecular subtype as described below.

Mean tumor volume doubling times (TVDT)

$$TVD{T}_{ER}=\frac{{\sum }_{i=1}^W{1}_{E{R}_i}TVD{T}_i}{{\sum }_{i=1}^W{1}_{E{R}_i}}$$

where 1_ER is an indicator function for a given ER-status and TVDT_i is the tumor volume doubling time of simulated woman i.

Mean mammography detection thresholds

$$M{T}_{ER}=min\left\{V_P\right\}$$

across all cases with a given ER-status and with A_P < A_A (i.e., the detection was done due to screening).

Mean sojourn time

$$TVD{T}_{ER}=\frac{{\sum }_{i=1}^W{1}_{E{R}_i}{f}_T\left(V_A-V_P\right)}{{\sum }_{i=1}^W{1}_{E{R}_i}}$$

where 1_ER is an indicator function for a given ER-status and f_T is a function that relates tumor volume and time that is used as a base assumption for Model S (see (19) for more details).

Once again, we only show the derivation for calculating ER-specific estimates for these parameters, but the ER/HER2 case is analogous.

Lastly, to quantify tumor growth relative to molecular-subtype, we also calculate the distributions of ER and ER/HER2-status conditioned on different ages at clinical detection, P(ER|A_A) and P(ER, HER2|A_A), respectively, and the distribution of ER/HER2-status conditioned on TVDT, age, stage and size at clinical detection, P(ER, HER2|TVDT, A_A, V_A,N_A). In the latter case, we aggregate age and size in the same groups used for the survival curves, but with the addition of 16 different TVDT groups in increments of 4 months ranging from 0–4 to 56+ months.

RESULTS

Molecular-specific modeling parameters

Table 2 shows the estimated mean tumor volume doubling time (TVDT) by ER and HER2 status. The fastest growing subtype is ER−, HER2+ with a mean TVDT of 6.8 months. The slowest growing is ER+, HER2− with a mean TVDT of 9.8 months. Table 3 shows the estimated mean tumor size mammography detection thresholds by ER and HER2 status. The mean mammography detection threshold was highest for ER−/HER2+ disease, at 1.05 cm, and lowest for ER+,HER2− disease, at 0.89 cm. Note that the difference between the smallest and largest mean threshold is 1.6mm. To put this difference into context, consider a spherical tumor of diameter 0.8cm, a 1.6mm increase in diameter size would be achieved, on average, between 4.9 months (for a ER−, HER2+ tumor) and 7.1 months (for a ER+, HER2− tumor). Table 4 shows the distribution of ER/HER2 status by age at detection, in the presence of screening. For validation purposes, this table compares the distribution of joint ER/HER2-status by different ages estimated through our modeling approach versus those found in the SEER. Consistent with SEER, our modeling results show that the proportion of ER− tumors is higher for younger women and, in fact, decreases as women age. For instance, the percent difference between the proportion of women with ER/HER2-status across the youngest group (<40 years) and the eldest group (70+) was approximately 10%. Lastly, Table 5 shows the distribution of ER/HER2 status by size at detection, in the presence of screening, comparing the estimates estimated with the model versus those observed in SEER. As a form of validation, we show that our estimates follow a similar pattern to that observed in SEER: for example, the more aggressive cancer subtypes (ER− or HER2+ subtypes) had a higher likelihood of presenting as larger tumors at detection.

Table 2.

Mean Tumor Volume Doubling Times (months) by ER/HER2-status

Subtype	TVDT (months)
All women	9.0
ER+, HER2+	7.9
ER+, HER2−	9.8
ER−, HER2+	6.8
ER−, HER2−	7.5

Table 3.

Mean Mammography Detection Thresholds (cm) by ER/HER2-status

Subtype	Mean Mammography Detection Threshold (cm)
All women	0.92
ER+, HER2+	0.96
ER+, HER2−	0.89
ER−, HER2+	1.05
ER−, HER2−	0.99

Table 4.

Comparison of the modeled distribution of ER/HER2-status stratified by age at detection versus data observed in SEER.^*

	Model				SEER
Age	ER+, HER2+	ER+, HER2−	ER−, HER2+	ER−, HER2−	ER+, HER2+	ER+, HER2−	ER−, HER2+	ER−, HER2−
All Ages	0.11	0.70	0.07	0.14	0.10	0.74	0.04	0.12
Age < 40	0.15	0.58	0.09	0.18	0.19	0.55	0.08	0.18
Age 40–49	0.12	0.64	0.08	0.16	0.13	0.70	0.05	0.13
Age 50–59	0.11	0.68	0.07	0.14	0.12	0.70	0.06	0.13
Age 60–69	0.10	0.74	0.06	0.10	0.08	0.77	0.04	0.10
Age 70+	0.10	0.76	0.05	0.09	0.07	0.81	0.03	0.10

^*SEER estimates are obtained from the incidence observed between the calendar years 2010–2012, excluding unknown cases. Model estimates are provided for the same time period, in the presence of screening, to enable comparison to SEER.

Table 5.

Comparison of the modeled distribution of ER/HER2-status stratified by size at detection versus data observed in SEER.^*

	Model				SEER
Age	ER+, HER2+	ER+, HER2−	ER−, HER2+	ER−, HER2−	ER+, HER2+	ER+, HER2−	ER−, HER2+	ER−, HER2−
All Sizes	0.11	0.70	0.07	0.14	0.10	0.74	0.04	0.12
0–2cm	0.09	0.76	0.04	0.11	0.08	0.80	0.03	0.09
2–5cm	0.12	0.64	0.06	0.18	0.12	0.67	0.05	0.16
5+cm	0.17	0.57	0.08	0.18	0.14	0.61	0.09	0.16

^*SEER estimates are obtained from the incidence observed between the calendar years 2010–2012, excluding unknown cases. Model estimates are provided for the same time period, in the presence of screening, to enable comparison to SEER.

Underlying breast-cancer specific survival by ER-status and ER/HER2-status

Figure 2 and Figure 3 show the estimated survival curves by ER status and ER/HER2-status, respectively, in the absence of screening and treatment. We found that both ER and HER2 status were strong predictors of prognosis. Specifically, in the absence of adjuvant therapy, ER+,HER2− cases had better survival compared to ER−, HER2+ cases, independent of stage or size at detection.

In the Supplemental spreadsheet, we present all the estimated survival curves stratified by ER-status only, ER/HER-status, stage (local and regional), tumor size (<2cm, 2–5cm and 5+cm) and age at detection (<40, 40–49, 50–59, 60–69 and 70+). It is important to note that, since the sample size was not sufficient to support estimation for all age and size combinations for patients with distant-stage disease at initial diagnosis, we chose to group these cases into a single survival curve for all ages and sizes.

When comparing the survival curves in the absence of screening and adjuvant treatment, we find that, the breast cancer subtype with the worst survival is ER−, HER2+ with a 5-year survival ranging from 70.5% to 89.3% across different tumor sizes, ages and local/regional stages. On the other hand, the best survival is seen for is ER+, HER2− cases, with a 5-year survival ranging from 80.7% to 94.4% across different tumor sizes, ages and local/regional stages. Incorporating these survival curves into BSOC, we simulate ER/HER2-specific survival curves in the presence of screening and treatment, and where sufficient data is available, we demonstrate consistency with SEER (20). It is relevant to note that there exist important differences when comparing the survival curves in absence of screening and treatment to contemporary survival data in the presence of screening and treatment. In particular, our results demonstrated that the effect of trastuzumab improve the outcomes of ER−,HER2+ patients to the point in which they have better outcomes than ER−,HER2− patients, for which there is yet no targeted treatment.

In supplemental Figure S.3 and S.4, we also show the annual hazards associated with the underlying breast cancer survival curves. Interestingly, we found that there is exists a cross-over between ER+ and ER− annual hazards in the absence of screening and adjuvant. Compared to ER+ disease, ER− disease exhibits a higher risk of death in the first 5 years but has lower risk afterwards (Figure S.3).

DISCUSSION

We present a modeling approach to estimate ER and HER2-specific breast cancer features and survival in the absence of screening and treatment. Our methodology is data-driven as it leverages data from two large sets, SEER and BCSC, and builds a link between them by making use of a model of the natural history of breast cancer. The results provide insights into the nature of ER/HER2-subtypes. In general, ER-negative status and HER2-positive status are associated with higher tumor aggressiveness, are harder to detect by mammography and are more frequent (percent-wise) among younger women. The underlying survival estimated through this approach suggests that both ER and HER2-status are strong predictors of long-term prognosis, even in the absence of screening and treatment. Our analysis also revealed a crossover between ER+ and ER− annual hazards of breast cancer death, where the latter exhibits a much higher risk of death in the first 5 years but has lower risk afterwards. This result is consistent with two other studies that have analyzed clinical data with definite local regional therapy but without systemic therapy (33) and with only low-doses of cyclosphosphamide, doxorubicin or fluorouracil regimens (2).

Our ER, HER2 estimates can serve as input for simulation models aimed at recreating incidence and mortality trends by molecular-subtype. All models in the CISNET Breast Cancer Working Groups have already implemented these estimates to model molecular-specific incidence and mortality trends (22). The analyses include comparing modeled ER-specific trends to SEER data have been presented elsewhere (23–25).

Although our method is computationally intensive, it has several advantages. First, it is data-driven and it maintains the observed correlations between patient age, stage, survival and ER-status. Second, it enables us to associate molecular subtypes with the probability of being screen detected, correcting for the length bias induced over-sampling of ER+ by screen detection. Finally, our approach is flexible enough to account for new evidence that may demonstrate a different relationship between age, stage, survival and molecularly-specific subgroups.

Our approach has some limitations. First, it does not account for DCIS. DCIS was not considered in Model S due to issues of nonidentifiability concerning the estimation of natural history parameters that describe the progression of DCIS to invasive disease. We assume that ER-status, HER-status and tumor grade remain unchanged during the preclinical course of the disease because we do not have data to inform the model under what conditions these molecular marker might transition. This particular assumption adds a degree of uncertainty to our approach that is not trivial to evaluate, as it would elicit quantifying its impact on several other modeling assumptions including the secular trend of breast cancer, the natural history model of breast cancer and the detection characteristics of screening mammography.

Despite the limitations, our approach is validated against SEER. We generate estimates of ER/HER2-specific characteristics in the absence of screening and adjuvant treatment that are modeled in the presence of these interventions to produce results consistent with ER/HER2 observations found in contemporary cancer registries (in the presence of screening and adjuvant treatment). In this manner, we produce a virtual SEER registry with historic ER/HER2-specific characteristics well before these molecular markers were collected in SEER. More generally, our approach offers a means to integrate long-term historical cancer registry observations with contemporary molecular-specific data. With the emergence of precision medicine, deeper molecular characterization of breast cancer, and all diseases, is imminent. Our approach may be extended to any disease where molecular markers influence clinical intervention and there is a need to understand how these markers affect cancer outcomes by assessing outcomes both in the presence and absence of clinical intervention by the molecular markers.