Abstract
Predicting pathologic fractures in femora with metastatic lesions remains a clinical challenge. Currently used guidelines are inaccurate, especially to predict non-impeding fractures. This study evaluated the ability of a nonlinear quantitative computed tomography (QCT)-based homogenized voxel finite element (hvFE) model to predict patient-specific pathologic fractures. The hvFE model was generated highly automated from QCT images of human femora. The femora were previously loaded in a one-legged stance setup in order to assess stiffness, failure load, and fracture location. One femur of each pair was tested in its intact state, while the contralateral femur included a simulated lesion on either the superolateral- or the inferomedial femoral neck. The hvFE model predictions of the stiffness (0.47 < R2 < 0.94), failure load (0.77 < R2 < 0.98), and exact fracture location (68%) were in good agreement with the experimental data. However, the model underestimated the failure load by a factor of two. The hvFE models predicted significant differences in stiffness and failure load for femora with superolateral- and inferomedial lesions. In contrast, standard clinical guidelines predicted identical fracture risk for both lesion sites. This study showed that the subject-specific QCT-based hvFE model could predict the effect of metastatic lesions on the biomechanical behaviour of the proximal femur with moderate computational time and high level of automation and could support treatment strategy in patients with metastatic bone disease.
Subject terms: Bone metastases, Experimental models of disease
Introduction
Today, life expectancy of cancer patients is increasing. As a result, there is a higher prevalence of metastatic bone disease that affects patients with a rather good prognosis1. Metastatic cancer with skeletal involvement can result in a pathologic bone fracture, often in absence of a traumatic event and during everyday activities. Despite multiple treatment options, surgical intervention is often required due to poor bone healing and the patient’s limited life expectancy2. The proximal femur is among the most affected anatomical sites3. When diagnosed, bone metastases present a great challenge in choosing the appropriate treatment strategy. Prophylactic fixation is generally preferred to pathologic fracture and its subsequent treatment4,5. However, current clinical guidelines and methodologies for fracture risk prediction, such as the Mirels’ scoring system6 are not specific enough, particularly in non-impending fracture prediction7.
In summary, by defining patient-specific fracture risk, patients with an impending pathologic fracture would benefit from a prophylactic intervention, while patients with a non-impending fracture could be spared from unnecessary treatment.
Assessing strength of a metastatic bone requires information on its geometry, three-dimensional distribution of density8, the size9, shape10, site11, and nature of the lesion6,12, as well as on the patient’s loading regimen and activity level.
The finite element analysis (FEA) is a computer simulation method which has been recognized as a powerful tool for bone fragility prediction13–20. FEA considers both, the individual geometric and densitometric parameters retrieved from computed tomography imaging. In homogenized continuum level voxel based FE (hvFE) models, voxels are directly converted to hexahedral elements with specific homogenized material properties depending on local bone density.
Several authors have applied FEA to predict fracture loads of femora with metastatic lesions and reported good correlations to in vitro testing21–25. However, these data have often been based on a small number of specimens, mostly with one specimen per specific site of the metastatic lesion. More importantly, most modeling has been performed using fine finite element meshes associated with high computational resources and longer analysis time. A single finite element analysis of a femoral fracture was recently estimated to take four to ten hours24,26. Furthermore, the model generation and analysis requires profound technical knowledge of the operator and, thus, specially trained personnel becomes inevitable. As a result, increasing the level of automation is mandatory to make this method time- and cost-effective, and finally, to include it in the clinical routine.
The objective of the present study was to introduce QCT-based finite element models to predict patient-specific pathologic fracture loads of proximal femora in a clinical context. We hypothesized that the FE models allow predicting the fracture load of pathologic femora just as well as fracture load of intact femora. Model validation was performed on a large number of specimens (n > 30) using previously collected in vitro experimental data. To meet clinical demands, patient-specific models were generated with a high level of automation and simplified to minimize analysis time.
Methods
Study outline
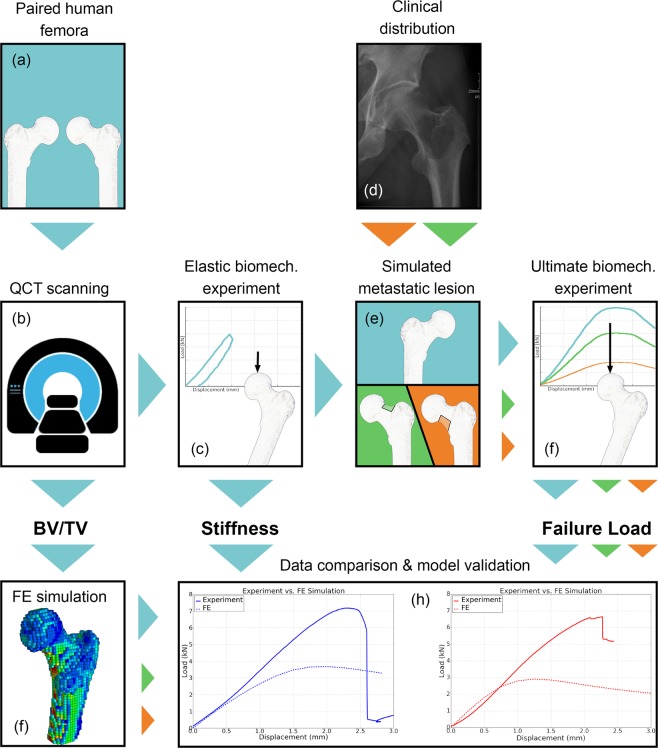
As illustrated in the graphical abstract, (Fig. 1) first, QCT image sequences of human femoral specimens were acquired. Thereafter, the specimens were subjected to mechanical compression in stiffness- and failure load tests. Tests were performed on intact specimens as well as on specimens with simulated metastatic lesions. The results of the mechanical experiments were published previously11. Nonlinear hvFE models were generated from QCT images and validated with data assessed in mechanical experiments on specimens under careful consideration of experimental boundary conditions. The study was approved by the Ethics Committee of the Medical University of Vienna (1400/2013). The specimens were obtained from voluntary donors to the Center for Anatomy and Cell Biology, Medical University of Vienna, who consented in written form during their lifetime to the use of their bodies for research and education. All study procedures were conducted in accordance with the guidelines approved by the Ethics Committee and the Declaration of Helsinki.
Figure 1.
Graphical abstract of the project: Thirty-two paired femora (a) underwent QCT scanning (b) and elastic biomechanical experiments to determine stiffness (c). Based on clinical distribution in patients who suffered a pathologic fracture (d), metastatic lesions were simulated in either the superolateral or inferomedial neck in one femur of each pair (e), followed by a second QCT scan and stiffness test. All femora were then subjected to an ultimate biomechanical test to determine failure load11 (f). A FE model was generated based on geometry and bone density distribution (BV/TV) retrieved from QCT images (g). Experimental data were used to evaluate the QCT-based FE model (h).
QCT scanning and mechanical testing
For the direct validation of the FEA, the authors used QCT-images from anatomic specimens, previously loaded in mechanical experiments. For a detailed description of the experiments, the reader is referred to this previous work11. In short, a total of 32 paired fresh frozen human femoral anatomic specimens (9 female, 7 male, mean age 79.7 ± 10.7 years) were used. The sample size and age were restricted by limited availability of human anatomic specimens. One femur of each pair remained intact, while the contralateral femur was assigned to the metastatic group, in which a simulated metastatic lesion was created on either the superolateral- or inferomedial femoral neck. One specimen from the group with superolateral lesions was excluded due to severe head necrosis. The simulated lesions occupied one third of the cortical circumference over the whole length of the specified neck site including the underlying cancellous bone and were created using a milling-cutter. These regions were chosen based on retrospective clinical data of patients who suffered a pathologic fracture11.
The most distal part of each femur was dissected. QCT image sequences were acquired with the Brilliance CT 64-channel scanner (Philips, Amsterdam, Netherlands) with a voxel size of 0.33 mm × 0.33 mm × 1 mm. The samples were scanned in 0.9% saline solution on top of a calibration phantom, BDC Phantom (QMR GmbH, Möhrendorf, Germany).
Additionally, the centrum-collum-diaphyseal (CCD) angle was measured from original uncropped QCT image sequences using ImageJ (developed by Wayne Rasband at NIH). Also, the volumetric bone mineral density (vBMD) and bone mineral content (BMC) were retrieved from the scans for the masked proximal part of each specimen before and after creating the lesion in one region of interest including head, neck, trochanter, and intertrochanteric region, using Medtool v.4.0 software (Dr. Pahr Ingenieurs e.U., Pfaffstätten, Austria).
Following imaging, the specimens were embedded, rigidly fixed in the experimental setup, and loaded in a quasi-static mode, mimicking one-legged stance. One-legged stance is not representative for all real life fracture mechanisms, which are inherently different from one patient to another. Nevertheless, pathologic fractures predominantly occur during non-traumatic everyday activities. The assessment of femoral mechanics in one-legged stance hase been previously used to study the incidence of spontaneous27,28 and pathologic fractures21, the behavior of the hip during daily activities29 or the load sharing between cortical and trabecular bone30. Initially, the stiffness was quantified by applying compressive load to induce axial displacement from 0 to 1 mm in all specimens in their intact condition. After creating a lesion in one specimen of each femoral pair, these specimens underwent additional QCT scanning for purposes of model generation, followed by another elastic test to assess the stiffness of the pathological bone. A second compression cycle was finally performed on all specimens until failure to determine the failure load.
Homogenized voxel FE models
A homogenized continuum level voxel based FE model, previously developed for prediction of biomechanical behavior of the femur in different loading scenarios16, was adapted for the purpose of the present study. In short, QCT images were processed and voxels were directly converted into FE hexahedral model elements. The bone contour was segmented using the fill algorithm, as already described in previous studies for the human vertebrae31 and femora16. For each sample, the Hounsfield unit (HU) scale of the corresponding QCT image sequence was converted to the equivalent bone mineral density (BMD) scale (in mg HA/cm3) using a linear calibration law, computed from the two scales for the phantom inserts with known BMD values. The BMD range was limited to −100 and 1,400 mg HA/cm3 to restrict the effect of residual air and other artefacts. Due to the limited resolution of the QCT scans, no fabric measurement could be done and bone was therefore considered isotropic. The bone material was modelled using an isotropic elastic-damage constitutive law adapted16 from Garcia et al.32. Material nonlinearity was applied when bone was loaded beyond a yield limit, defined by a piecewise Hill criterion33, in which the inelastic behavior was driven by a damage scalar variable (between 0 and 1), that represents the reduction of the material elastic modulus34. The assigned material properties originate from preceding studies. Briefly summarized, multi-axial mechanical testing on a large number of human trabecular bone specimens was performed to assess the elastic and strength properties35. Due to the fact that those material parameters were measured in trabecular bone samples, a correction was defined for the poreless bone (BV/TV = ρ = 1) to provide the elastic modulus, compression ultimate stress, and tension ultimate stress for cortical bone16, considering previously published ultimate values36,37. Utilizing cement markers incorporated in the distal embedding, each specimen was positioned in a one-legged stance alignment, where the angle between the loading axis and the proximal shaft was equal to 20 degrees. This alignment was identical to the experimental condition. The images were cut proximally up to the polyurethane embedding. A polyurethane embedding layer (Poisson ratio: 0.3, Young’s modulus: 1.36 GPa) and a steel plate (Poisson ratio: 0.3, Young’s modulus: 210 GPa) were modelled isotropically at the cranial portion of the femoral head to exactly mimic the experimental setup16. The external bone contour was found with a filling algorithm, as already described in a previous study for the human vertebrae31 and femora16, followed by image coarsening to 3 mm × 3 mm × 3 mm voxel size. Image coarsening aimed to simulate QCT image resolution, requiring a minimum of radiation exposure in clinical routine. The FE mesh was generated by converting all voxels to hexahedral elements. In the next step the BMD scale was converted to a bone volume to total volume (BV/TV) scale with the linear equation BV/TV = 0.093*BMD + 1.077 as described previously38. Loading was imposed as vertical displacement of a reference node, located at the mean position of the most cranial voxel layer of the femoral head. All translations and rotations of the reference node except for vertical translation were unconstrained. Unconstrained in-plane translations should mimic the axle bearing used in the experimental setup, while unconstrained rotations should simulate motions between the proximal embedding and the femoral head. The translations of the nodes at the most distal portion of the shaft, starting at the polyurethane embedding, were fully constrained. Compression was simulated using a −5 mm vertical displacement of the reference node.
Model simulation
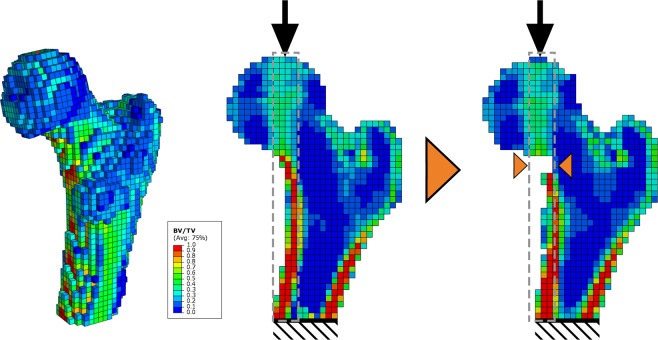
The generated QCT-based FE model (Fig. 2) had an average number of approximately 11,000 nodes and 13,000 elements. The models were generated in less then 30 minutes, including all necessary manual inputs. Following manual user inputs were needed: selection of four regions of interest: the proximal femur and three different phantom inserts, annotation of cement markers in the distal embedding, and selection of a threshold for the segmentation algorithm39. The models were solved on a conventional four CPU desktop PC with 3.4 GHz, in an average CPU time of 27 min with average necessary memory of 390 MB using Abaqus v.6.14-5. (Dassault Systemes Simulia Corp., Johnston, RI, USA).
Figure 2.
QCT-based finite element model with a voxel size of 3 mm × 3 mm × 3 mm in 3D and midplanes for intact- and specimen with a simulated inferomedial lesion (from left to the right). Specimen is positioned in one-legged stance. Values of highest BV/TV are in line with the vertical force vector (grey rectangle). Destroying the cortex in this region will result in redistribution of load and premature failure.
Image processing, modelling and data evaluation were performed in a highly automated manner using the Medtool software.
Statistical analysis
Pearsons product-moment correlation coefficient (R) was computed to investigate linear correlations between experimental and simulation data. Differences in mean stiffness and mean failure load between the three different groups (intact femora and femora with simulated lesions in two different sites) were investigated using the ANOVA and a post-hoc Tukey Honest Significant Difference Comparison. Differences with p-values lower than 0.05 were considered statistically significant. Each group was tested for normal distribution using Shapiro-Wilk test. The analysis was performed using IBM SPSS Statistics 24 (IBM Corp., Armonk, NY, USA).
Results
Stiffness and failure load
The correlations between the experimental and computed stiffness for the three groups: (1) intact-, (2) specimens with superolateral-, and (3) inferomedial lesion, were (1) R2 = 0.75 (p < 0.00005, 95% CI: 0.770–0.970), (2) R2 = 0.94 (p < 0.0005, 95% CI: 0.829–0.996), and (3) R2 = 0.47 (p = 0.058, 95% CI: −0.026–0.938), respectively. The correlations (1) and (2) were statistically significant. Strong correlations were found between the experimental- and computed failure loads in all three groups: (1) R2 = 0.83 (p < 0.00001, 95% CI: 0.77–0.97), (2) R2 = 0.77 (p < 0.01, 95% CI: 0.381–0.982), and (3) R2 = 0.98 (p < 0.00001, 95% CI: 0.966–0.998) (Figs 3 and 4). However, the failure load was underestimated approximately by a factor of 2. As expected a strong correlation was also found between the simulated stiffness and simulated failure load for all three groups ((1) R2 = 0.88 (p < 0.00001, 95% CI: 0.835–0.979), (2) R2 = 0.93 (p < 0.0005, 95% CI: 0.799–0.995), and (3) R2 = 0.98 (p < 0.00001, 95% CI: 0.955–0.998)).
Figure 3.
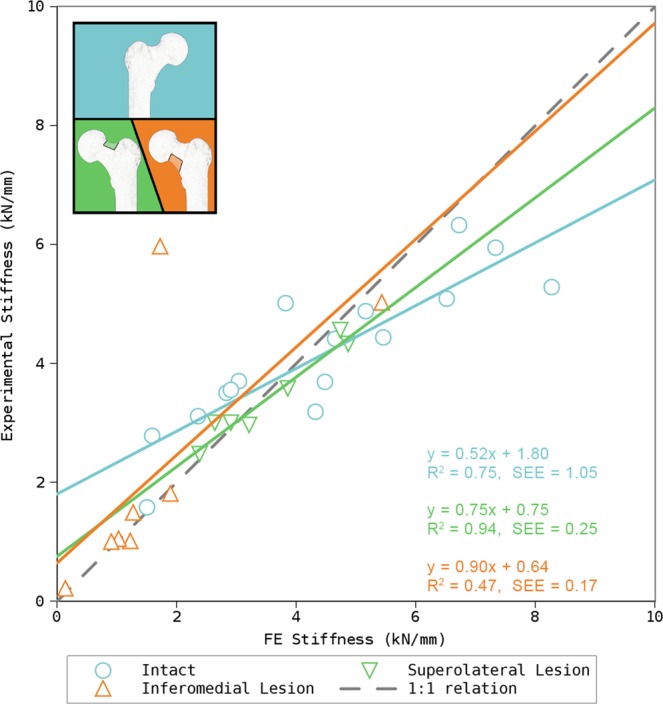
Results for prediction of stiffness in intact- and femora with simulated metastatic lesion in two different regions of the femoral neck. The ideal correlation (1:1 relation) is represented by the dashed line. The moderate correlation of femora with an inferomedial lesion is likely a result of a single outlier.
Figure 4.
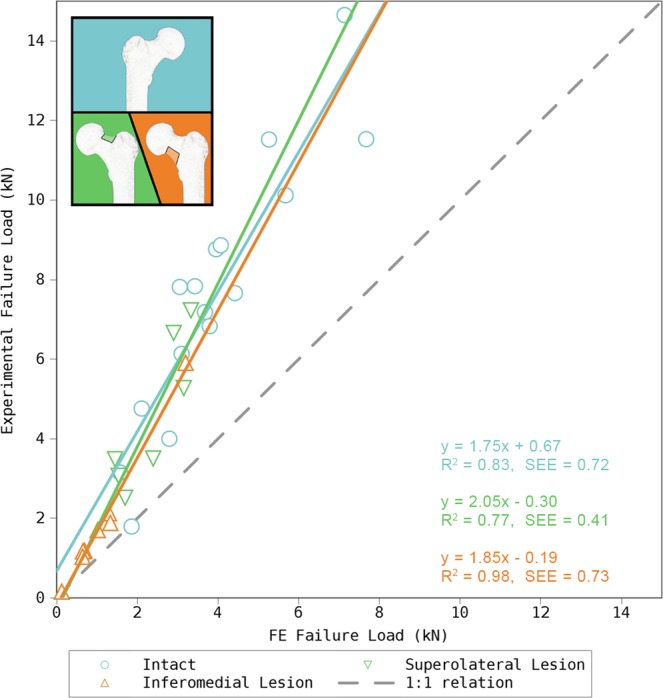
Results for prediction of failure load in intact- and femora with metastatic lesion in two different regions of the femoral neck. The ideal correlation (1:1 relation) is represented by the dashed line.
The mean simulated stiffness was 4.44 ± 2.04 kN/mm (mean ± SD) (range: 1.50–8.27 kN/mm) for intact specimens, 3.52 ± 0.99 kN/mm (range: 2.47–4.55 kN/mm) for specimens with the superolateral lesion, and 1.70 ± 1.59 kN/mm (range: 0.14–5.43 kN/mm) for specimens with the inferomedial lesion. The mean simulated failure load was 3.91 ± 1.89 kN (range: 1.06–7.81 kN) for intact specimens, 2.35 ± 0.79 kN (range: 2.51–7.22 kN) for specimens with the superolateral lesion and 1.12 ± 0.92 kN (range: 0.12–3.20 kN) for specimens with the inferomedial lesion. A clear load maximum was seen in all load-displacement curves before the maximum displacement was reached. Fracture occurred at the simulated mean displacement of −1.40 mm in compression. Statistically significant differences were found between the mean stiffnesses of the intact- and specimens with the simulated inferomedial lesion (p < 0.005, 95% CI: 0.849–4.614) and between mean failure loads of intact- and specimens with the simulated superolateral and inferomedial lesion (p < 0.05, 95% CI: 0.045–3.201 and p < 0.0005, 95% CI: 1.347–4.362, respectively), which was in accordance with the experimental data.
Fracture location
The QCT-based FE model predicted most fractures to occur in the subcapital region for intact specimens and in the femoral neck in specimens with simulated lesions. The model predicted the exact fracture location correctly in the majority of cases (21 out of 31 or in 68% of all specimens) (Table 1). The fracture location was correctly predicted in 56% of the intact specimens, in 100% in the superolateral-, and in 63% in the inferomedial-lesion group.
Table 1.
Fracture locations recorded in the experiments and as predicted by the QCT-based FE model.
| Specimen | Lesion | Fracture location | |
|---|---|---|---|
| Experiment | FE | ||
| 01R | superolateral | neck | neck |
| 01L | intact | subcapital | subcapital |
| 02R | superolateral | neck | neck |
| 02L | intact | subcapital | neck |
| 03R | superolateral | intertrochanteric | intertrochanteric |
| 03L | intact | intertrochanteric | subcapital |
| 04R | intact | subcapital | subcapital |
| 04L | superolateral | subcapital | subcapital |
| 05L | intact | subcapital | subcapital |
| 05R | excluded specimen | ||
| 06R | intact | subcapital | subcapital |
| 06L | superolateral | subcapital | subcapital |
| 07R | intact | subcapital | subcapital |
| 07L | superolateral | neck | neck |
| 08R | intact | subcapital | subcapital |
| 08L | inferomedial | subcapital | neck |
| 09R | inferomedial | neck | subcapital |
| 09L | intact | neck | subcapital |
| 10R | inferomedial | neck | neck |
| 10L | intact | subcapital | subcapital |
| 11R | intact | subcapital | subcapital |
| 11L | superolateral | neck | neck |
| 12R | inferomedial | neck | neck |
| 12L | intact | subcapital | subcapital |
| 13R | inferomedial | neck | neck |
| 13L | intact | subcapital | neck |
| 14R | inferomedial | neck | neck |
| 14L | intact | intertrochanteric | subcapital |
| 15R | intact | subcapital | neck |
| 15L | inferomedial | neck | neck |
| 17R | intact | neck | subcapital |
| 17L | inferomedial | subcapital | neck |
Correlation with vBMD, BMC, and CCD angle
Mean volumetric bone mineral density (vBMD) of all included specimens was 218.60 ± 53.70 mg/cm3 (range 82.97–336.56) and mean bone mineral content (BMC) was 35.39 ± 13.98 g (range 12.68–74.75). Neither the assessed densitometric (vBMD and BMC) nor geometric (CCD angle) parameters showed a significant correlation with the ultimate loads for any specimen group (Table 2).
Table 2.
Pearson’s Correlation Coefficient R2 between volumetric bone mineral density (vBMD), bone mineral content (BMC), caput-collum-diaphyseal (CCD) angle, as well as failure load from simulation (FE Fu) and failure load from biomechanical experiments.
| vBMD (mg/cm3) | BMC (g) | CCD (degree) | FE Fu (kN) | |
|---|---|---|---|---|
| Intact | 0.75 | 0.68 | 0.15 | 0.83 |
| Superolateral lesion | 0.25 | 0.10 | 0.08 | 0.77 |
| Inferomedial lesion | 0.75 | 0.74 | 0.14 | 0.98 |
Discussion
This study aimed to introduce a QCT-based finite element model to predict the biomechanical behavior of intact- and femora with metastatic lesions. To meet the demands of clinical applicability, the model was required to be easy to generate, fast to solve.
Simulation data provided statistically significant correlations for all biomechanical parameters, except for the stiffness in specimens with inferomedial lesions. This observation was very likely based on one single outlier (specimen 12R), which showed unusually high stiffness. While the stiffness was in range with other specimens in the simulation, it reached an unusually high value in the experiment. Possible causes could have been interlocking of the proximal setup, which, however, could have not been identified in recorded video or in video extensometer data or a not-visible pathologic alteration of bone tissue. Correlation of failure loads between models and experimental data was significant for all specimen groups. However, the failure load was underestimated by a factor of 2. These findings are similar to previously published data16, and can likely be attributed to limitations of coarsened QCT voxels in capturing the correct bone morphology. Luisier et al.40 showed a significantly improvement of fracture load prediction from QCT-based FE models using a high-resolution peripheral quantitative computed tomography (HR-pQCT)-based FE model and using a fabric-based orthotropic material model. However, given the strong and statistically significant validation of the QCT-based model, but also from clinical perspective these results alone are not sufficient to justify the higher radiation dose needed to reach such resolution in a central anatomical site, like the femur and in patients, who undergo frequent QCT-scanning due to rapid growth of the bone metastases. The authors of the present study also used rather large elements to reduce preprocessing and analysis time in order for the technique to be clinically applicable. Using such coarse models, the thin cortical shell cannot be resolved adequately, introducing geometrical artifacts and also discrepancies in fracture site prediction. It is important to stress that the bone material properties were obtained from previous research35 without any further internal calibration or tuning of the values. Even though tuning of the material properties would probably lead to improved predictions closer to the 1:1 relation, this was not the purpose of the present study. Nevertheless, the presented model showed strong correlation between the experimental and simulated data and proved its ability to reliably and fast predict the failure load for both the intact and the pathological femora. Despite the mentioned underestimation of the failure loads, the slopes of the regression lines were nearly identical for all three groups underlying the reliability of used methodology. In other words, structural variations (large geometrical changes) of bone due to metastases had limited influence on the model robustness. Pooled simulated data sets from all three groups correlated strongly with the experimental data (R2 = 0.91 (p < 0.00001, 95% CI: 0.913–0.979)). Improved modelling approaches will be necessary to further increase the correlation to the experimental data. Alternatively, linear FE models (e.g.17,20) have shown promising potential for clinical applications because of their faster simulation and could possibly be useful in pathologic fracture load prediction as well. Nishimaya et al.17 reported mesh generation and simulation of a femur in less than twelve minutes. While studies using linear FE models have reported more favorable correlation to the experimental data, they also have not reached 1:1 relation, similar to the present study. Finally, despite their advantages and robustness, linear models still have to be applied and validated for pathological bone. Present data have confirmed the well known linear relationship between stiffness and ultimate load in intact bone. This observation was, however, not made for pathological bone and could affect the accuracy of linear FE models.
The experiments were able to show that simulated metastatic lesions in the femoral neck lead to reduction in both, stiffness and failure load and in addition that the site of the lesion had a great effect on the reduction magnitude. While the finite element analysis correspondingly found significant differences in failure load between groups with different sites of the metastases, all specimens would be considered for prophylactic surgery according to Mirels’ scoring system. Mirels’ scoring system combines four radiographic and clinical risk factors: degree of pain, lesional size or its cortical involvement, osteolytic versus osteoblastic nature, and anatomic location (upper limb, lower limb, peritrochanter). It represents the standard method for pathologic fracture prediction. Another common clinical methodology would not recommend any specimen for prophylactic stabilization, since less than 50% of its cortex were affected by the presented lesions41–43. The discrepancy between different clinical guidelines, as well as their insufficient sensitivity, again underlines the necessity for a more sensitive patient-specific solution.
As previously shown in biomechanical in vitro experiments11, a lesion in the inferomedial femoral neck produces significantly greater deterioration of biomechanical properties of the femur compared to a lesion in the superolateral neck. One-legged stance induces a considerable bending moment at the femoral neck21, with maximum value at the neck’s distal base. Also, the highest compressive stresses occur in the medial portion of the neck44. This results in the highest cortical thickness being present in the inferior neck, while the thinnest lies in the superior region (Fig. 2). Destroying the inferior cortex will eliminate the capacity of the femur to support the stress at the base of the medial femoral neck, while the remaining load must then be redistributed to adjacent regions, subjecting them to greater stresses, leading to premature failure. None of the established clinical methods for fracture risk prediction takes this effect into account11.
The present work has two major limitations. First, the use of QCT data, coarse voxel, and simplified model assumptions (isotropic bone material behavior, similar damage behavior for trabecular and cortical bone, isotropic damage, no softening in compression) have resulted in inaccurate failure load predictions in the hvFE model despite high correlations. However, there is still no reliable and clinically available imaging method to measure the trabecular orientation and bone anisotropy. The second limitation arises from the lesions, which were simulated by total bone removal and do not exactly represent metastatic geometries observed in clinical routine. Metastatic lesions often affect multiple bone regions and the cortex by spreading from the bone marrow. The aim of this study was not the perfect match with an individual pathology but the systematic validation of the QCT-based FEA for representative anatomies, pathologies, and loading conditions. Simulating metastatic lesions by total bone removal is common in the literature11,23,24, but it assumes the lesion to be fully osteolytic, affecting the total width of the cortical bone and would represent the clinical worst case scenario. Osteolytic lesions have poor mechanical properties, justifying their simulation by total bone removal, while at the same time there are no data on material properties of mixed or purely osteoblastic lesions. Further research is required on this topic. The focus of the present study was mainly the destruction of the cortex, which was shown to be subjected to highest strains44 in one-legged stance and which contributes to over 90% of bone’s strength30. In addition, high age of the donors does not adequately represent patients, who typically suffer a pathologic fracture.
In conclusion, this study showed the ability of the subject-specific QCT-based FE model to predict of the biomechanical behavior for both, the intact and pathological femur. Considering the usage of QCT data with low level of complexity and moderate computational resources needed for analysis performance and the high level of automation applied in this study, as well as the strong correlation with experimental data, the presented model could qualify as a good candidate for clinical applications. In order to make this model clinically applicable as a decision support system in prediction of pathologic fractures its reliability has to be evaluated in in situ scanning conditions for various loading scenarios. Finally, the image segmentation and model generation should be performed fully automated.
Acknowledgements
The authors gratefully acknowledge Ms. Sonja Plischke and Ms. Ingrid März for numerous, but brilliant QCT scans, Enrico Dall’Ara, PhD for his previous work and insight, and Claudia Fischer, PhD for statistical support and revision.
Author Contributions
L.H. collected anatomical specimens. F.K. supervised QCT scanning. E.B., A.S., M.A., R.W. and W.M. conceived, developed, and adopted the finite element model. E.B., M.A. and D.H.P. analyzed the data. E.B. and D.H.P. wrote the manuscript. E.B., A.S., M.A., F.K., L.H., R.W., W.M. and D.H.P. approved the submitted and final version.
Competing Interests
D.H.P. is the CEO of Dr. Pahr Ingenieurs e.U., which distributes the Medtool software commercially). Other than that the authors declare no conflict of interest regarding the presented work.
Footnotes
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Weber KL, Randall RL, Grossman S, Parvizi J. Management of lower-extremity bone metastasis. The J. Bone & Jt. Surg. 2006;88:11–19. doi: 10.2106/JBJS.F.00635. [DOI] [PubMed] [Google Scholar]
- 2.Healey JH, Brown HK. Complications of bone metastases. Cancer. 2000;88:2940–2951. doi: 10.1002/1097-0142(20000615)88:12+<2940::AID-CNCR10>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 3.Sim, F. Instructional course lectures: metastatic bone disease. In Instructional course lectures, vol. 49 (American Academy of Orthopaedic Surgeons, Anaheim, CA, 1999).
- 4.Cheal E, Hipp J, Hayes W. Evaluation of finite element analysis for prediction of the strength reduction due to metastatic lesions in the femoral neck. J. biomechanics. 1993;26:251–264. doi: 10.1016/0021-9290(93)90363-J. [DOI] [PubMed] [Google Scholar]
- 5.Dijkstra P, Oudkerk M, Wiggers T. Prediction of pathological subtrochanteric fractures due to metastatic lesions. Arch. orthopaedic trauma surgery. 1997;116:221–224. doi: 10.1007/BF00393714. [DOI] [PubMed] [Google Scholar]
- 6.Mirels H. Metastatic disease in long bones a proposed scoring system for diagnosing impending pathologic fractures. Clin. Orthop. Relat. Res. 1989;249:256–264. [PubMed] [Google Scholar]
- 7.Benca E, Patsch JM, Mayr W, Pahr DH, Windhager R. The insufficiencies of risk analysis of impending pathological fractures in patients with femoral metastases: A literature review. Bone Reports. 2016;5:51–56. doi: 10.1016/j.bonr.2016.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Michaeli D, Inoue K, Hayes W, Hipp J. Density predicts the activity-dependent failure load of proximal femora with defects. Skeletal radiology. 1999;28:90–95. doi: 10.1007/s002560050480. [DOI] [PubMed] [Google Scholar]
- 9.Amanatullah DF, Williams JC, Fyhrie DP, Tamurian RM. Torsional properties of distal femoral cortical defects. Orthopedics. 2014;37:158–162. doi: 10.3928/01477447-20140225-51. [DOI] [PubMed] [Google Scholar]
- 10.Kaneko TS, Pejcic MR, Tehranzadeh J, Keyak JH. Relationships between material properties and CT scan data of cortical bone with and without metastatic lesions. Med. engineering & physics. 2003;25:445–454. doi: 10.1016/S1350-4533(03)00030-4. [DOI] [PubMed] [Google Scholar]
- 11.Benca Emir, Reisinger Andreas, Patsch Janina M., Hirtler Lena, Synek Alexander, Stenicka Sandra, Windhager Reinhard, Mayr Winfried, Pahr Dieter H. Effect of simulated metastatic lesions on the biomechanical behavior of the proximal femur. Journal of Orthopaedic Research. 2017;35(11):2407–2414. doi: 10.1002/jor.23550. [DOI] [PubMed] [Google Scholar]
- 12.Keene J, Sellinger D, McBeath A, Engber W. Metastatic breast cancer in the femur a search for the lesion at risk of fracture. Clin. orthopaedics related research. 1986;203:282–288. [PubMed] [Google Scholar]
- 13.Mirzaei M, Zeinali A, Razmjoo A, Nazemi M. On prediction of the strength levels and failure patterns of human vertebrae using quantitative computed tomography (qct)-based finite element method. J. biomechanics. 2009;42:1584–1591. doi: 10.1016/j.jbiomech.2009.04.042. [DOI] [PubMed] [Google Scholar]
- 14.Varga P, Dall’Ara E, Pahr DH, Pretterklieber M, Zysset PK. Validation of an HR-pQCT-based homogenized finite element approach using mechanical testing of ultra-distal radius sections. Biomech. modeling mechanobiology. 2011;10:431–444. doi: 10.1007/s10237-010-0245-3. [DOI] [PubMed] [Google Scholar]
- 15.Pahr DH, Dall’Ara E, Varga P, Zysset PK. HR-pQCT-based homogenised finite element models provide quantitative predictions of experimental vertebral body stiffness and strength with the same accuracy as μfe models. Comput. methods biomechanics biomedical engineering. 2012;15:711–720. doi: 10.1080/10255842.2011.556627. [DOI] [PubMed] [Google Scholar]
- 16.Dall’Ara E, et al. A nonlinear QCT-based finite element model validation study for the human femur tested in two configurations in vitro. Bone. 2013;52:27–38. doi: 10.1016/j.bone.2012.09.006. [DOI] [PubMed] [Google Scholar]
- 17.Nishiyama KK, Gilchrist S, Guy P, Cripton P, Boyd SK. Proximal femur bone strength estimated by a computationally fast finite element analysis in a sideways fall configuration. J. biomechanics. 2013;46:1231–1236. doi: 10.1016/j.jbiomech.2013.02.025. [DOI] [PubMed] [Google Scholar]
- 18.Zysset, P. K., Dall’Ara, E., Varga, P. & Pahr, D. H. Finite element analysis for prediction of bone strength. BoneKEy reports2 (2013). [DOI] [PMC free article] [PubMed]
- 19.Mirzaei M, Keshavarzian M, Naeini V. Analysis of strength and failure pattern of human proximal femur using quantitative computed tomography (qct)-based finite element method. Bone. 2014;64:108–114. doi: 10.1016/j.bone.2014.04.007. [DOI] [PubMed] [Google Scholar]
- 20.Schileo E, Balistreri L, Grassi L, Cristofolini L, Taddei F. To what extent can linear finite element models of human femora predict failure under stance and fall loading configurations? J. biomechanics. 2014;47:3531–3538. doi: 10.1016/j.jbiomech.2014.08.024. [DOI] [PubMed] [Google Scholar]
- 21.Keyak JH, Kaneko TS, Skinner HB, Hoang BH. The effect of simulated metastatic lytic lesions on proximal femoral strength. Clin. orthopaedics related research. 2007;459:139–145. doi: 10.1097/BLO.0b013e3180514caa. [DOI] [PubMed] [Google Scholar]
- 22.Tanck E, et al. Pathological fracture prediction in patients with metastatic lesions can be improved with quantitative computed tomography based computer models. Bone. 2009;45:777–783. doi: 10.1016/j.bone.2009.06.009. [DOI] [PubMed] [Google Scholar]
- 23.Derikx L, et al. The assessment of the risk of fracture in femora with metastatic lesions comparing case-specific finite element analyses with predictions by clinical experts. J. Bone & Jt. Surgery, Br. Vol. 2012;94:1135–1142. doi: 10.1302/0301-620X.94B8.28449. [DOI] [PubMed] [Google Scholar]
- 24.Anez-Bustillos L, et al. Finite element analysis and CT-based structural rigidity analysis to assess failure load in bones with simulated lytic defects. Bone. 2014;58:160–167. doi: 10.1016/j.bone.2013.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yosibash Z, et al. Predicting the stiffness and strength of human femurs with real metastatic tumors. Bone. 2014;69:180–190. doi: 10.1016/j.bone.2014.09.022. [DOI] [PubMed] [Google Scholar]
- 26.Keyak J. Improved prediction of proximal femoral fracture load using nonlinear finite element models. Med. engineering & physics. 2001;23:165–173. doi: 10.1016/S1350-4533(01)00045-5. [DOI] [PubMed] [Google Scholar]
- 27.Cristofolini L, Juszczyk M, Martelli S, Taddei F, Viceconti M. In vitro replication of spontaneous fractures of the proximal human femur. J. biomechanics. 2007;40:2837–2845. doi: 10.1016/j.jbiomech.2007.03.015. [DOI] [PubMed] [Google Scholar]
- 28.Viceconti M, et al. Are spontaneous fractures possible? an example of clinical application for personalised, multiscale neuro-musculo-skeletal modelling. J. biomechanics. 2012;45:421–426. doi: 10.1016/j.jbiomech.2011.11.048. [DOI] [PubMed] [Google Scholar]
- 29.Juszczyk MM, Cristofolini L, Viceconti M. The human proximal femur behaves linearly elastic up to failure under physiological loading conditions. J. biomechanics. 2011;44:2259–2266. doi: 10.1016/j.jbiomech.2011.05.038. [DOI] [PubMed] [Google Scholar]
- 30.Holzer G, von Skrbensky G, Holzer LA, Pichl W. Hip fractures and the contribution of cortical versus trabecular bone to femoral neck strength. J. bone mineral research. 2009;24:468–474. doi: 10.1359/jbmr.081108. [DOI] [PubMed] [Google Scholar]
- 31.Dall’Ara E, Pahr D, Varga P, Kainberger F, Zysset P. QCT-based finite element models predict human vertebral strength in vitro significantly better than simulated DEXA. Osteoporos. Int. 2012;23:563–572. doi: 10.1007/s00198-011-1568-3. [DOI] [PubMed] [Google Scholar]
- 32.Garcia D, Zysset PK, Charlebois M, Curnier A. A three-dimensional elastic plastic damage constitutive law for bone tissue. Biomech. modeling mechanobiology. 2009;8:149–165. doi: 10.1007/s10237-008-0125-2. [DOI] [PubMed] [Google Scholar]
- 33.Zysset, P. & Rincón, L. An alternative fabric-based yield and failure criterion for trabecular bone. In Mechanics of biological tissue, 457–470 (Springer, 2006).
- 34.Zysset P, Curnier A. A 3D damage model for trabecular bone based on fabric tensors. J. biomechanics. 1996;29:1549–1558. doi: 10.1016/S0021-9290(96)80006-6. [DOI] [PubMed] [Google Scholar]
- 35.Rincón-Kohli L, Zysset PK. Multi-axial mechanical properties of human trabecular bone. Biomech. modelling mechanobiology. 2009;8:195–208. doi: 10.1007/s10237-008-0128-z. [DOI] [PubMed] [Google Scholar]
- 36.Bayraktar HH, et al. Comparison of the elastic and yield properties of human femoral trabecular and cortical bone tissue. J. biomechanics. 2004;37:27–35. doi: 10.1016/S0021-9290(03)00257-4. [DOI] [PubMed] [Google Scholar]
- 37.Öhman C, et al. Compressive behaviour of child and adult cortical bone. Bone. 2011;49:769–776. doi: 10.1016/j.bone.2011.06.035. [DOI] [PubMed] [Google Scholar]
- 38.Dall’Ara E, Pahr D, Zysset P. Proceedings of esb2012 - 18th congress of the european society of biomechanics QCT-BMD to microCT-BV/TV calibration relationships are similar for human vertebra and femur. J. Biomech. 2012;45:S450. doi: 10.1016/S0021-9290(12)70451-7. [DOI] [Google Scholar]
- 39.Pahr DH, Zysset PK. From high-resolution ct data to finite element models: development of an integrated modular framework. Comput. methods biomechanics biomedical engineering. 2009;12:45–57. doi: 10.1080/10255840802144105. [DOI] [PubMed] [Google Scholar]
- 40.Luisier B, et al. Orthotropic hr-pqct-based fe models improve strength predictions for stance but not for side-way fall loading compared to isotropic qct-based fe models of human femurs. journal mechanical behavior biomedical materials. 2014;32:287–299. doi: 10.1016/j.jmbbm.2014.01.006. [DOI] [PubMed] [Google Scholar]
- 41.Fidler M. Incidence of fracture through metastases in long bones. Acta Orthop. 1981;52:623–627. doi: 10.3109/17453678108992157. [DOI] [PubMed] [Google Scholar]
- 42.Menck H, Schulze S, Larsen E. Metastasis size in pathologic femoral fractures. Acta Orthop. 1988;59:151–154. doi: 10.3109/17453678809169697. [DOI] [PubMed] [Google Scholar]
- 43.Van der Linden Y, et al. Comparative analysis of risk factors for pathological fracture with femoral metastases. J. Bone & Jt. Surgery, Br. Vol. 2004;86:566–573. doi: 10.1302/0301-620X.86B4.14703. [DOI] [PubMed] [Google Scholar]
- 44.Van Rietbergen B, Huiskes R, Eckstein F, Rüegsegger P. Trabecular bone tissue strains in the healthy and osteoporotic human femur. J. Bone Miner. Res. 2003;18:1781–1788. doi: 10.1359/jbmr.2003.18.10.1781. [DOI] [PubMed] [Google Scholar]