Relative efficiency of unequal cluster sizes in stepped wedge and other trial designs under longitudinal or cross‐sectional sampling

Abstract

Background: A cluster trial with unequal cluster sizes often has lower precision than one with equal clusters, with a corresponding inflation of the design effect. For parallel group trials, adjustments to the design effect are available under sampling models with a single intracluster correlation. Design effects for equal clusters under more complex scenarios have appeared recently (including stepped wedge trials under cross‐sectional or longitudinal sampling). We investigate the impact of unequal cluster size in these more general settings.

Results: Assuming a linear mixed model with an exchangeable correlation structure that incorporates cluster and subject autocorrelation, we compute the relative efficiency (RE) of a trial with clusters of unequal size under a size‐stratified randomization scheme, as compared to an equal cluster trial with the same total number of observations. If there are no within‐cluster time effects, the RE exceeds that for a parallel trial. In general, the RE is a weighted average of the RE for a parallel trial and the RE for a crossover trial in the same clusters. Existing approximations for parallel designs are extended to the general setting. Increasing the cluster size by the factor (1 + CV²), where CV is the coefficient of variation of cluster size, leads to conservative sample sizes, as in a popular method for parallel trials.

Conclusion: Methods to assess experimental precision for single‐period parallel trials with unequal cluster sizes can be extended to stepped wedge and other complete layouts under longitudinal or cross‐sectional sampling. In practice, the loss of precision due to unequal cluster sizes is unlikely to exceed 12%.

1. BACKGROUND AND SCOPE

In a cluster trial, the presence of unequally sized clusters can affect the precision of the treatment effect estimate. Suggested modifications to the equal cluster design effects (DEs) to account for this have focussed mostly on the parallel group trial under a simplified statistical model with a single intracluster correlation coefficient (ICC).1, 2, 3, 4 In this case the, precision is reduced compared to a trial in which the same total number of observations is equally distributed across the clusters.

Alternatives to the parallel group design include cluster crossover designs and stepped wedge designs in both of which the experimental condition (ie, treatment/control status) is varied during the course of the study. For such designs, it is natural to consider more complex statistical models in which subject and cluster effects vary over time.5, 6, 7 In a recent paper,8 Hooper et al have presented DEs for “complete” cluster designs, including parallel, crossover, and stepped wedge layouts, under either cross‐sectional or longitudinal sampling and with allowance for within‐cluster variation over time. This work encompasses a wide range of possibilities, in particular, the model of Hussey and Hughes9 is subsumed as a special case, but the results apply only to designs in which the clusters are equal in size. Here, we consider the impact of variable cluster size on these DEs. We give expressions for the relative efficiency (RE) of the treatment effect estimate relative to that for the equal cluster design with the same total number of observations, which can then be used to modify the equal cluster DE.

The RE is derived under a stratified cluster randomization scheme for which the distribution of cluster sizes is the same within each design sequence (study arm). This is the same condition under which standard modifications to the parallel group DE have been derived.4

Throughout this work, “cluster size” refers to the total number of subjects (or observations) in a cluster and is allowed to vary between but not within clusters, so that a constant rate of sampling within each individual cluster is assumed. This corresponds to a (common) practical situation in which the clusters in a study can be identified with institutions of different sizes (eg, hospitals, care homes, general practices) with different capacities for recruitment. We do not consider the implications of uneven sampling within individual clusters.

The statistical model is described in Section 2. The main results on the RE of designs with unequal cluster sizes are presented in Section 3. Section 4 describes some practical implications with calculations for two recent trials. Conclusions and limitations are discussed in Section 5.

2. STATISTICAL MODEL

We introduce unequally sized clusters into an existing linear mixed effects model(8, 10 for closed‐cohort trials, in which the same subjects are observed at each timepoint under an exchangeable correlation structure. Results for cross‐sectional trials (where observations at different times are made on different subjects) can be obtained by reducing the subject‐level variation to zero in this model.

We assume that a fixed number of clusters is observed over T epochs. There are two experimental conditions indexed by the binary array X _l j, l = 1, …, L; j = 1,…. ,T, where X _lj = 0 or 1 indicates “control” or “treated” conditions and L denotes the number of treatment sequences (or “arms”) in the trial. There are N (= rL) clusters divided by size into r strata of L clusters each and allocated to treatment arms according to a stratified scheme, which ensures that the size distribution is the same in each arm. In any given cluster, the number of subjects (m _k) is a constant which depends only on the stratum k (= 1, …,r) to which the cluster belongs. The observations are generated by a linear mixed model of the form

$$Y_{\mathit{\text{ijkl}}}={\beta }_j+\mathrm{\theta }{X}_{\mathit{lj}}+c_{\mathit{kl}}+s_{\mathit{ikl}}+{\left(\mathit{ct}\right)}_{\mathit{jkl}}+{\left(\mathit{st}\right)}_{\mathit{\text{ijkl}}}.$$ (1)

Here, Y _ijkl is the outcome at time j (j = 1, …,T) for the ith subject (i = 1, …,m _k) in the cluster from stratum k in arm l; β ₁, …,β _T are fixed time effects and θ is the treatment effect whose estimation is the purpose of the study. The other terms in (1) represent independent random effects: c, between clusters; s, between subjects; (ct), cluster by time interaction; and (st), subject by time interaction (including measurement error). These have variances η _C, η _S, η _CT, and η _ST respectively, with η _C + η _S + η _CT + η _ST =σ ² = varY _ijkl.

2.1. Correlation structure

We follow an established notation8 to characterize the correlation structure:

$$\begin{array}{lll}\left(\mathit{ICC}\right)& \mathrm{\rho }=\frac{{\eta }_C+{\eta }_{\mathit{CT}}}{{\eta }_C+{\eta }_S+{\eta }_{\mathit{CT}}+{\eta }_{\mathit{ST}}}& \left(0\le \mathrm{\rho }<1\right)\\ \left(\mathrm{\text{cluster autocorrelation}}\right)& \mathrm{\pi }=\frac{{\eta }_C}{{\eta }_C+{\eta }_{\mathit{CT}}}& \left(0\le \mathrm{\pi }\le 1\right)\\ \left(\mathrm{\text{individual autocorrelation}}\right)& \mathrm{\tau }=\frac{{\eta }_S}{{\eta }_S+{\eta }_{\mathit{ST}}}& \left(0\le \mathrm{\tau }<1\right)\end{array}$$

(It is assumed throughout that η _ST > 0).

In a cross‐sectional study, each subject contributes data only at a single timepoint so that a cluster of “size” m _k will contain a total of Tm _k subjects overall. A model for this scenario is obtained by setting the between subject effect, s, to zero in (1), whereupon η _S = 0 and τ = 0. The Hussey and Hughes model9 omits both subject‐level effects and cluster by period effects and relies on a single ICC to characterize the correlation structure. This corresponds to the particular case, where τ = 0 and π= 1.

2.2. The experimental layout

For the results given here, the experimental layout (X _lj) is characterized by two coefficients: $A=\frac{1}{\mathit{LT}}{\sum }_{j=1}^T{\sum }_{l=1}^L$ ${\left(X_{lj}-{\bar{X}}_{•j}-{\bar{X}}_{l•}+{\bar{X}}_{••}\right)}^2$ and $B=\frac{1}{L}{\sum }_{l=1}^L{\left({\bar{X}}_{l•}-{\bar{X}}_{••}\right)}^2$. These coefficients are given elsewhere10 for some standard designs, including those in Table 1.

Table 1.

Coefficients A, B for four standard design layouts (illustrated in Figure 1) taken from table 1 of Girling and Hemming,10 with B ≡ b and A ≡ a – b, in their notation

Design Layout	A	B
(a) Crossover	¼	0
(b) Parallel	0	¼
(c) g‐Step Wedge (SWg)	$\frac{1}{12}\left(1-\frac{2}{g\left(g+1\right)}\right)$	$\frac{1}{12}\left(1-\frac{2}{g+1}\right)$
(d) Delay‐control design (DCDp,q,r)	$\frac{1}{4}q\left(1-q\right)$	$\frac{1}{4}{q}^2$

The values of these coefficients depend only on the “geometry” of the layout, ie, the pattern of light and shade in Figure 1, and not on the numbers of clusters or time periods in the design. For instance, a parallel cluster trial over a single time period has exactly the same coefficient values as a parallel trial with observations taken over several time periods; an SW_g design with a single cluster randomized at each step has the same coefficients as an SW_g design with several clusters at each step provided this number is the same for all steps. Most existing work on the efficiency of unequal cluster designs applies only to two‐arm, single‐period parallel layouts, a special case of layout (b) in Figure 1 with T = 1.

Figure 1.

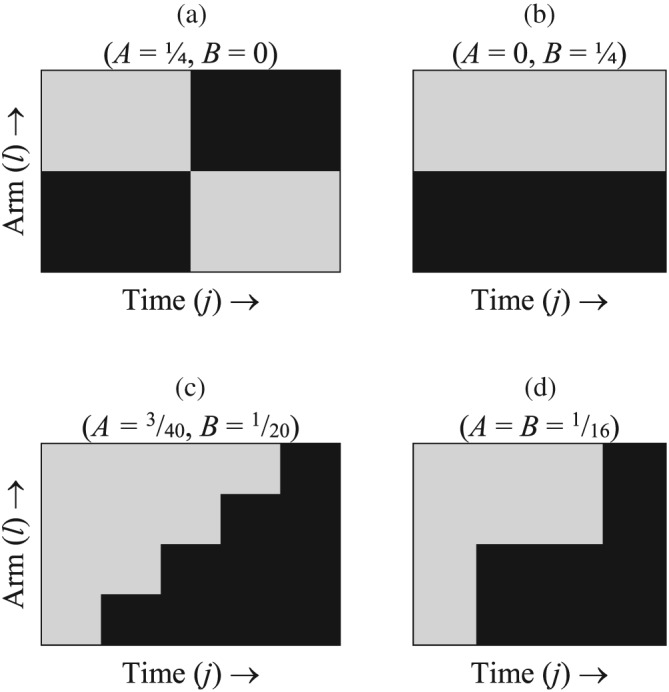
Diagrammatic representation of four experimental layouts (X _lj; 1 ≤ l ≤ L, 1 ≤ j ≤ T). Light‐shading indicates X _lj = 0, dark‐shading indicates X _lj = 1. The values of the coefficients A and B depend only on the patterns of light and shade in these figures and not on the dimensions L and T. (a) Crossover; (b) Parallel; (c) SW₄; (d) DCD_{0.25, 0.5, 0.25}

3. RELATIVE EFFICIENCY OF UNEQUAL CLUSTER DESIGNS

Let $\mathrm{var}\left(\widehat{\mathrm{\theta }};m_1,m_2,\text{…},m_r\right)$ denote the sampling variance of the best linear unbiased estimate of θ in model (1) with (possibly unequal) cluster sizes m ₁, …,m _r. The RE of this design compared to the equal cluster design with the same total number of observations is defined as

$$\mathrm{RE}=\frac{\mathrm{var}\left(\widehat{\mathrm{\theta }};m,m,\text{…},m\right)}{\mathrm{var}\left(\widehat{\mathrm{\theta }};m_1,m_2,\text{…},m_r\right)},$$

where $m=\frac{1}{r}{\sum }_{k=1}^r{m}_k$, the mean cluster size.

Our main result states that

$$\mathrm{RE}=\frac{A\mathrm{\Psi }\left({\lambda }_0{m}^{\left(\mathrm{\rho }\right)}\right)+\mathit{B}\nu \mathrm{\Psi }\left({\lambda }_1{m}^{\left(\mathrm{\rho }\right)}\right)}{A+\mathit{B}\nu },$$ (2)

where

$$\begin{array}{ll}{m}^{\left(\mathrm{\rho }\right)}& =m\frac{\mathrm{\rho }}{1-\mathrm{\rho }}\left(m^{\left(\mathrm{\rho }\right)}\ge 0\right)\\ {\lambda }_0& ={\lambda }_0\left(\mathrm{\pi },\mathrm{\tau }\right)=\frac{1-\mathrm{\pi }}{1-\mathrm{\tau }}\left({\lambda }_0\ge 0\right)\\ {\lambda }_1& ={\lambda }_1\left(\mathrm{\pi },\mathrm{\tau }\right)=\frac{1+\left(T-1\right)\mathrm{\pi }}{1+\left(T-1\right)\mathrm{\tau }}\left({\lambda }_1\ge 0\right)\\ \nu & =\frac{1-\mathrm{\tau }+m^{\left(\mathrm{\rho }\right)}\left(1-\mathrm{\pi }\right)}{1+\left(T-1\right)\mathrm{\tau }+m^{\left(\mathrm{\rho }\right)}\left(1+\left(T-1\right)\mathrm{\pi }\right)}\left(0\le \nu \le 1\right)\end{array}.$$

(The parameterν can be interpreted as 1 minus the cluster‐mean correlation10 for a cluster of size m – ie, with Tm observations overall.)

The function $\mathrm{\Psi }$(.) is defined as

$$\mathrm{\Psi }\left(\alpha \right)=\left(1+\alpha \right)\times \frac{1}{r}\sum _{k=1}^r\frac{m_k}{m+\alpha m_k},\text{for}\alpha \ge 0.$$ (3)

The functional form of Ψ is determined by the distribution of cluster sizes relative to the mean cluster size, ie, on the distribution of z _k = m _k/m. In the case of equal clusters (ie, z _k ≡1), $\mathrm{\Psi }$(α) = 1 for all α, as expected. For clusters unequal in size, $\mathrm{\Psi }$(0) = 1, and $\mathrm{\Psi }$(α) ≤ 1 for α> 0, with a unique minimum in the range (0, ∞], as shown in the appendix. In general, $\mathrm{\Psi }$(∞) equals the proportion of nonzero clusters in the design. In most practical applications, $\mathrm{\Psi }$(∞) = 1 and the impact of cluster inequality is low when the scaled mean cluster size, m ^(ρ) = mρ/(1 −ρ), is either very small or very large.

The DE for the unequal cluster design is given by

$$\mathrm{DE}={\mathrm{DE}}_0÷\mathrm{RE},$$ (4)

where the equal cluster DE is

$${\mathrm{DE}}_0=\frac{\mathit{T}\nu \left(1+\left(m-1\right)\mathrm{\rho }\right)}{4\left(1+\left(T-1\right)\nu \right)\left(A+\mathit{B}\nu \right)}.$$ (5)

Alternatively, DE₀ may be obtained using the more transparent approach given by Hooper et al.8

3.1. Relative efficiency for parallel and crossover layouts

Under a parallel layout, the coefficients from Table 1 are A = 0, B = ¼, and (2) reduces to

$${\mathrm{RE}}_{\text{Parallel}}=\mathrm{\Psi }\left({\lambda }_1{m}^{\left(\mathrm{\rho }\right)}\right)\equiv \frac{1+\left({\lambda }_{1}m-1\right)\mathrm{\rho }}{\mathit{mr}}\sum _{k=1}^r\frac{m_k}{1+\left({\lambda }_1{m}_k-1\right)\mathrm{\rho }}.$$ (6)

This equation generalizes the result4 for single‐period parallel designs, for which T = 1 and λ ₁ = 1.

For any given set of relative cluster sizes (z _k), RE_Parallel depends only on a scaled version of the mean cluster size, m, namely, ${\lambda }_1{m}^{\left(\mathrm{\rho }\right)}=m\times \frac{{\lambda }_1\mathrm{\rho }}{1-\mathrm{\rho }}$. In principle, this means that the behavior of the RE as a function of the mean cluster size under a complex correlation structure can be read from a plot of $\mathrm{\Psi }$(α) with an appropriate scaling of the α‐axis. For example, in Figure 2, the value α= ⅓ (corresponding to 0.25 on the horizontal scale) gives the RE when λ ₁ m ^(ρ) = ⅓, ie, when the mean cluster size m is equal to $\frac{1-\mathrm{\rho }}{3{\lambda }_1\mathrm{\rho }}$.

Figure 2.

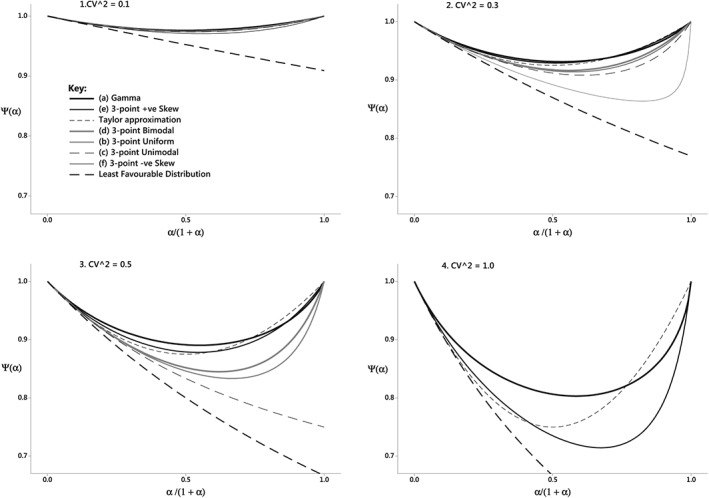
The function Ψ(α) for a selection of cluster size distributions, together with the Taylor approximation due to van Breukelen. The argument of Ψ(α) is given on the transformed scale u = α/(1 + α), which enables the complete range of α‐values to be plotted on a bounded interval, with u =1 when α = ∞. The key is the same in all 4 panels and is ordered according to ordinate values in the middle of the range. The three‐point specimen distributions (b), (c), (d), (e), and (f) are available only at lower CV‐values (see Table 2): so (f) is missing from panel 3 (CV² = 0.5) and only (e) appears in panel 4 (CV² = 1)

Similarly, in a crossover layout, A = ¼, B = 0 and

$${\mathrm{RE}}_{\text{Cross}‐\text{over}}=\mathrm{\Psi }\left({\lambda }_0{m}^{\left(\mathrm{\rho }\right)}\right).$$

This has the same form as RE_Parallel with λ ₁ replaced by λ ₀. If λ ₁ and λ ₀ are both positive (ie, π < 1), then RE_Parallel and RE_Crossover run through exactly the same range of values as m ^(ρ) varies. Effectively RE_Crossover is just the RE for a parallel study with different values (π′,τ′) for the two autocorrelation parameters chosen so that λ₁(π′,τ′) = λ₀(π,τ). In the (admittedly unusual) case that π = τ< 1, then λ ₁ = λ ₀ = 1 and the RE is independent of T and is the same for both parallel and crossover layouts, and indeed for any complete layout whatsoever (from Equation (2)). An important special case arises when π = 1. This corresponds to a complete absence of cluster‐level time effects, as in the Hussey and Hughes model. Here, λ ₀ = 0, RE_Crossover ≡ 1, and there is no loss of precision associated with unequal cluster sizes.

The general behavior of the function Ψ is illustrated in Figure 2 by sampling the relative cluster sizes z _k (=m _k/m) from several different probability distributions with mean 1 and specified coefficient of variation (CV = standard deviation ÷ mean). These include (a) a Gamma distribution with shape parameter = 1/CV², and five three‐point distributions, labeled (b) to (f) in Table 2, based on those suggested by van Breukelen et al4 for a similar purpose. Plots of the expected value of $\mathrm{\Psi }$(α) are shown in Figure 2 for CV² = 0.1, 0.3, 0.5, and 1.0.

Table 2.

Some specimen distributions to illustrate the impact of varying CV on the relative efficiency. Each distribution has mean 1 and is fully specified once the CV is given. The final column shows the greatest value of the CV² for which the distribution is available (given that z _i ≥ 0 necessarily). The Least Favorable Distribution minimizes Ψ(α) for all α≥ 0 over all such distributions with nonnegative support

	Support	Probabilities	Range	CV2	Max CV2
Three‐point symmetrical distributions
(b) Uniform (p = ⅓)	{a, 1, 2 – a}	{p, 1 – 2p, p}	2(1 – a)	2p(1 – a)2	0.6667
(c) Unimodal (p = ¼)					0.5000
(d) Bimodal (p = 2 / 5)					0.8000
Three‐point skew distributions
(e) Positive skew	{1 −S/3, 1 + S/6, 1 + 2S/3}	{½, ⅓, 1 / 6}	S	5S2/36	1.2500
(f) Negative skew	{1 −2S/3, 1 −S/6, 1 + S/3}	{1 / 6, ⅓, ½}	S	5S2/36	0.3125
Least Favorable Distribution (LFD)	{0, 1 + c 2}	$\left\{\frac{c^2}{1+c^2},\frac{1}{1+c^2}\right\}$	1 + c 2	c 2	∞

Other things being equal, Ψ(α), and hence the RE, is smaller for higher values of the CV. The Gamma and three‐point positive skew distributions give similar results for Ψ(α) over values of the CV most likely to be encountered in practice (ie, CV² = 0.1, 0.3, 0.5 in panels 1, 2, 3). The other three‐point distributions are associated with more extreme (ie, lower) values as α increases. Notice that the three‐point unimodal distribution with CV² = 0.5 entails a finite probability for clusters of size zero so that Ψ(α) does not return to 1 as α→∞. In general, Ψ(∞) = the proportion of nonzero clusters in the design.

For any cluster size distribution with CV = c,

$$\mathrm{\Psi }\left(\alpha \right)\ge {\mathrm{\Psi }}_{\mathrm{LFD}}\left(\alpha \right)=\frac{1+\alpha }{1+\alpha +\alpha {\mathrm{c}}^2}>\frac{1}{1+c^2},\text{for}\alpha \ge 0.$$ (7)

The expression after the “=” is the actual value of Ψ(α) under a particular two‐point distribution for relative cluster sizes. This “Least Favorable Distribution” (LFD) is given by $\mathrm{Pr}\left\{z_k=1+c^2\right\}=\frac{1}{1+c^2}=1-\mathrm{Pr}\left\{z_k=0\right\}$ and included in Figure 2. Although the LFD is unlikely to be a realistic model in practice (because it involves clusters of size 0), it provides an absolute bound on the possible loss of efficiency under any distribution whatsoever.

3.2. General layouts, including stepped wedge and delay‐control designs

For a layout with both A > 0 and B > 0 the RE in (2) is a weighted average of RE_Parallel and RE_Crossover with weights in the ratio A:Bν. As noted above, RE_Crossover is itself the RE for a parallel design under a modified correlation structure. In general, the weights depend on the experimental layout (through A and B), the mean cluster size (m), and the correlations ρ, π, and τ but not on the distribution of the relative cluster sizes z _k. The CV of the cluster size distribution and the shape of that distribution influence the RE only through their impact on the form of the function Ψ(.).

In the absence of cluster‐specific time effects (ie, π = 1, Ψ(λ₀m^(ρ)) = 1), the RE cannot be less than that under a parallel layout. This no longer holds when π < 1. Nevertheless, for any layout with a specified distribution of relative cluster sizes, the RE is bounded below by the (unique) minimum value of Ψ(α) over the range 0 < α ≤ ∞. This bound is also the least RE attainable under any parallel layout. In this sense, the loss of efficiency can be no worse than the worst‐case associated with a parallel group design.

For a stepped wedge design with g = T – 1 steps, the RE depends on the number of measurement periods, T. However, as T increases, ν → 0, $\frac{A}{B}=1+\frac{2}{T-1}\to 1$ and the ratio of weights A:Bν → ∞. It follows that the RE for a stepped wedge design approaches that of the crossover design when T is large.

Following the work of Girling and Hemming,10 we use the term delay‐control design (DCD_p,q,r) for a design in which a parallel study runs for a proportion q of the study duration, preceded by a baseline control period (proportion p), and followed by a postimplementation period (proportion r) in which the treatment is present in all clusters (p + q + r = 1). Instances include parallel designs with baseline observations6 for which r = 0, and “delayed start designs”11 for which p = 0. In any case, the coefficients A and B depend only on the proportion of time (q) spent under the parallel regime (see Table 1) with $\frac{A}{B}=q^{-1}-1$. If q is fixed, this implies that the RE again approaches the crossover result as T increases, although less rapidly than for a stepped wedge design.

3.3. Numerical results: CV² = 0.5

We present some detailed results for cluster size distributions with CV² = 0.5, a value at the higher end of those commonly encountered in cluster studies.12

3.3.1. The Hussey and Hughes model (π = 1, τ= 0)

Under this model, λ ₀ = 0, λ ₁ = T, $\nu =\frac{1}{1+{\mathit{Tm}}^{\left(\mathrm{\rho }\right)}}$ and the RE can be written as $\frac{A+\mathit{B}\nu \mathrm{\Psi }\left({\nu }^{-1}-1\right)}{A+\mathit{B}\nu }$. Here, the parallel design (with A = 0) has the worst (ie, least) RE among all complete layouts; the best RE ( ≡ 1) is achieved by the crossover design under which there is no loss of efficiency at all. The behavior of the RE as a function of m ^(ρ)/(1 + m ^(ρ)) for crossover, parallel, and stepped wedge layouts (with T = 4 and 10) is shown in Figure 3, for Gamma‐distributed cluster sizes with CV² = 0.5. In general, the efficiency loss for a stepped wedge design is much less than that for the corresponding parallel design.

Figure 3.

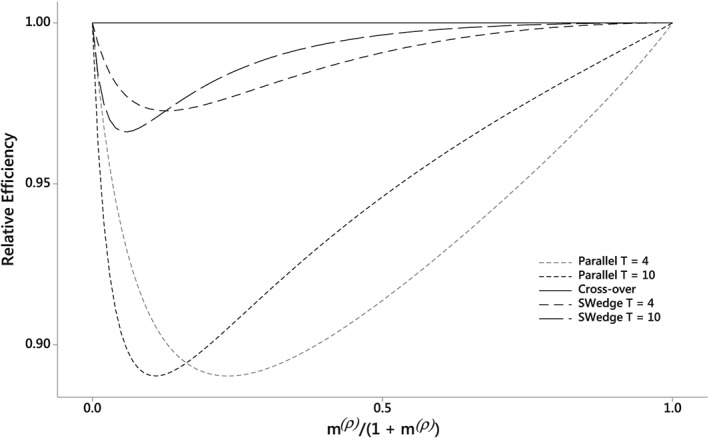
Relative efficiency (of unequal clusters) for a crossover layout (solid line) and some parallel (dotted lines) and stepped wedge (broken lines) layouts for the Hussey and Hughes model (π = 1, τ = 0) under a Gamma distribution for cluster size with CV² = 0.5. The horizontal axis represents a transformed version of the average cluster size (m) and ICC (ρ), as described in the text

3.3.2. General correlation structure

Results for some representative values of π ( = 1, 0.95, 0.75, 0.50) and τ ( = 0, 0.25, 0.5) are shown in Figure 4, under a Gamma distribution for cluster size with CV² = 0.5. In panel 3 of Figure 4, π = τ and the RE is the same for all layouts and independent of the actual value of π (and τ). In the remaining panels, the autocorrelation parameters have been chosen so that 0 ≤ τ< π ≤ 1. A value of π close to 1 corresponds to slowly varying cluster effects consistent with a small perturbation from traditional ICC models. In addition, the value of τ is attenuated by the inclusion of measurement error in the subject x time variance component, η _ST. Nonetheless, the assumption that τ ≤ π may not be appropriate in settings where the cluster effects are highly volatile.

Figure 4.

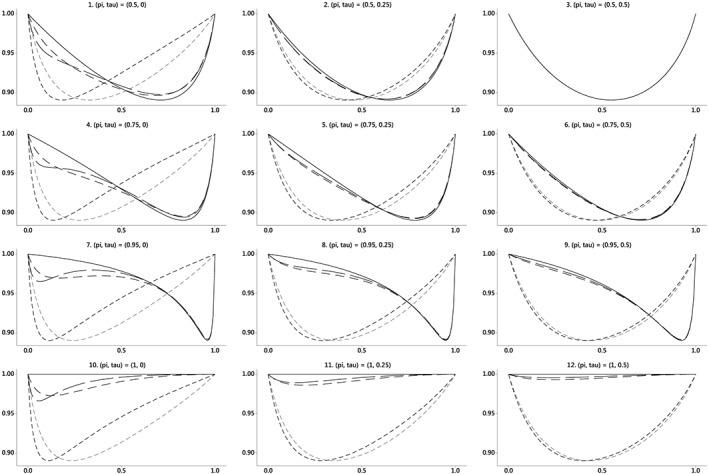
Relative efficiency and a transformed version of average cluster size for a crossover layout (solid line) and some parallel (dotted lines) and stepped wedge (broken lines) layouts for π = (0.5, 0.75, 0.95, 1.0) and τ = (0, 0.25, 0.5). The axes and line types are the same as those in Figure 3, which is reproduced for completeness in panel 10 here. Panels in the first column (1, 4, 7, 10) correspond to cross‐sectional studies with individual autocorrelation = 0. The cluster size distribution is Gamma with CV² = 0.5

The results are based on model (1), which applies explicitly to a longitudinal study where the same subjects are observed at every observation time. By reducing the subject variance η _S to 0, a model for cross‐sectional studies is obtained in which effectively different subjects are measured at each timepoint. Thus, REs for cross‐sectional studies appear as special cases by setting τ = 0 in (2), giving rise to the results in the first column of Figure 4 (panels 1, 4, 7, 10).

In general, the RE for any layout is bounded below by the minimum value of the function Ψ(α), which is ≈ 0.89 under the Gamma distribution considered here. Its actual value must lie between the RE for a cross‐sectional layout and that for a parallel layout with the same number of observation times T. Although the function Ψ(α) has a unique minimum, this property does not necessarily extend to the behavior of the RE as a function of m ^(ρ), as in panel 7 where a pair of minima is visible for the stepped wedge layout with T = 10. Nevertheless, when T is large, the RE for a stepped wedge layout approximates to that of the crossover design with the same correlation parameters. Once again, if π = 1, the loss of efficiency for a stepped wedge design is necessarily less than for the corresponding parallel design (panels 10, 11, 12), but this is not so if temporal variation within clusters is present (π < 1, panels 1 to 9).

Corresponding results for parallel designs with baseline observations are presented in an online appendix in Supp Figure 1 (for T = 4) and Supp Figure 2 (T = 10). Two exemplars of such designs are shown, namely, where the baseline runs for exactly half of the study period, (ie, DCD_0.5,0.5,0) as in the work of Teerenstra et al6 and a design with a single baseline time epoch (DCD_{1/T,1−1/T,0}).

4. PRACTICAL CONSEQUENCES

If the cluster sizes are known, Equations (2) and (4) can be used directly to obtain an explicit form for the DE that generalizes the known result (eg, equation 15 in the work of Rutterford et al13) for single‐period parallel designs.

Where only the mean and standard deviation of the cluster sizes are known, several methods have been proposed to approximate the unequal cluster DE for single‐period parallel studies.3, 14 Because each method entails a particular approximation to the function Ψ(α) in equation (6) they can all be extended to any of the designs considered here.

The method due to van Breukelen et al4 uses a Taylor approximation of the form

$$\mathrm{\Psi }\left(\alpha \right)\approx {\mathrm{\Psi }}_{\mathit{BC}}\left(\alpha \right)=1-\frac{\alpha }{{\left(1+\alpha \right)}^2}{c}^2,$$

(where c = CV of cluster size) which is illustrated in Figure 2. It works well over a wide range of parameter values particularly for the positively skewed distributions of cluster size likely to be encountered in practice. Since, in practice, c ² seldom exceeds 0.5, it has been suggested that the RE will be no less than $\underset{\alpha }{\min }{\mathrm{\Psi }}_{\mathit{BC}}\left(\alpha \right)=88\%$ for most parallel studies.12 The same remark is equally applicable in the general setting.

Another popular method13 for single‐period parallel studies replaces m with m(1 + c ²) in the equal cluster DE, ie, 1 + (m −1)ρ, to give DE = 1 + {(1 + c²)m − 1}ρ. This amounts to using the LFD in place of the actual distribution of cluster sizes and entails the approximation

$$\mathrm{\Psi }\left(\alpha \right)\approx {\mathrm{\Psi }}_{\mathrm{LFD}}\left(\alpha \right)=\frac{1+\alpha }{1+\left(1+{\mathrm{c}}^2\right)\alpha }.$$

The LFD method necessarily underestimates the RE of the unequal cluster design, but it can be useful for exploring the potential impact of unequal cluster sizes. For example, it shows that Ψ(α) > 0.95 for all α whenever c < 0.23, giving an RE in (2) of at least 95%. Thus, the suggestion2 that cluster inequality can be ignored in parallel studies unless the CV exceeds 0.23 is equally applicable to any design layout.

In practice, conservative sample size calculations based on the LFD can be made without recourse to detailed computation of relative efficiencies. For a given CV = c, the LFD entails a mixture of null clusters (of size 0) and nonnull clusters of size m(1 + c ²), in the ratio c ²: 1. Since the null clusters contribute nothing to the experimental precision, the precision under the LFD is equal to that of a design in which the observations are divided equally between the nonnull clusters, which would constitute a fraction 1/(1 + c ²) of the clusters in the study. It follows that a conservative estimate for the total number of observations required under any layout can be made by applying equal cluster methods8 with an assumed cluster size = m(1 + c ²).

4.1. Two examples

In the examples below, power is estimated from the standard formula Φ (|θ ₀| × (Precision)^½ −1.96), where θ₀ is the hypothesized value of the treatment effect and Φ is the cumulative standard normal distribution function.

The EPOCH trial15 aims to evaluate an intervention to improve mortality from emergency laparotomy in 90 hospitals. The design was based on six replicates of an SW₁₅ design with cross‐sectional data collected in 16 consecutive five‐week periods. The average number of subjects per period over all hospitals was assumed to be 18, with variation between hospitals characterized by a CV² of 0.5 (from a preliminary subsample of hospitals). The study was powered to detect a reduction in 30‐day mortality from 25% to 22% (ie, θ ₀ = −3%). We illustrate the calculations using an approximate linear mixed model for binomial data9 with ICC ρ = 0.0075, π = 1 and τ = 0. (The details differ slightly from the published protocol, which incorporates allowance for transition periods between treatment conditions and an ad hoc adjustment for geographical clustering of hospitals.) For SW₁₅, the design coefficients from Table 1 are A = 0.0826 and B = 0.0729. Hence, for equal clusters of size m = 18, we have ν = 0.3148 and DE₀ = 2.3508 (from Equation (5)). The precision of the estimated change in percentage mortality in an individually randomized trial with the same total number (6 × 15 × 16 × 18 = 25 920) of observations is 3.4560. Thus, the equal cluster precision is given by 3.4560 ÷ 2.3508 = 1.4710, which translates to a power of 95.3%.

From Section 3.3.1, the RE due to unequal cluster sizes is

$$\mathrm{RE}=\frac{A+\mathit{B}\nu \mathrm{\Psi }\left({\nu }^{-1}-1\right)}{A+\mathit{B}\nu }=0.783+0.217\times \mathrm{\Psi }\left(2.177\right).$$

Simulating a Gamma distribution of cluster sizes, we find Ψ(2.177) = 0.896 ( ± 0.002), and RE = 0.977; whereas, Ψ_BC(2.177) = 0.892, RE = 0.976. The resulting DE ( = DE₀ ÷ RE) is similar in both cases with power = 94.9%.

The LFD (“worst‐case”) adjustment for CV² = 0.5 can be achieved by assuming equal clusters in a design with m = 18(1 + 0.5) = 27 subjects per period in each of 90 ÷ (1 + 0.5) = 60 hospitals, ie, with the same total number of observations. To do this, ν is recalculated: ν = 0.2345, and the equal cluster DE = 2.4885, yielding a precision of 3.4560 ÷ 2.4885 = 1.3888. The corresponding RE = 2.3508 ÷ 2.4885 = 0.945, with power 94.2%.

Hooper et al8 present calculations for a longitudinal SW₃ trial16 incorporating subject and cluster autocorrelations under model (1). They assume ρ = 0.33, π = 0.9, τ = 0.7, σ= 5, with the study powered to detect an improvement in outcome of two units on a 10‐point ordinal scale. With m = 10 subjects per cluster, they conclude that a minimum of 93 subjects is required, which (after rounding up to whole numbers of clusters) translates to four clusters in each arm, ie, 120 subjects in total. The resulting precision of the effect estimate is 2.5673, giving a power of 89.3%. In the actual trial, between 8 and 12 subjects were recruited in each cluster, consistent with a cluster size CV of the order of 0.1. Here, allowance for unequal cluster size would have had a negligible effect on precision and power. The “worst‐case” is computed by assuming 10 × (1 + 0.1²) = 10.1 subjects per cluster in an SW₃ study with 4 ÷ (1 + 0.1²) = 3.96 clusters per arm. This has precision of 2.5512 and estimated power of 89.1%.

5. CONCLUSIONS AND LIMITATIONS

We have obtained the RE for a design with unequal cluster sizes under an exchangeable correlation structure that encompasses both cross‐sectional and longitudinal studies, with and without cluster‐level time effects. The RE can be used to adjust existing DEs for stepped wedge and cluster crossover studies to take account of cluster inequality. In general, the RE must lie between the RE for a parallel layout and the RE for a crossover layout with the same set of observation times. In the absence of cluster‐level time effects, as in the Hussey and Hughes model, there is no loss of efficiency in a crossover study, implying that the RE for an arbitrary layout is never less than that for a parallel design. Even when cluster‐level time effects are present, it remains true that the loss of efficiency under the worst‐case configuration of parameters for any layout (eg, stepped wedge, crossover) is never more than that in the worst‐case for a parallel design. A consequence is that results for parallel layouts that rely on worst‐case scenarios will often carry over to more general designs. For example, the statements “when the coefficient of variation is <0.23, the effect of adjustment for variable cluster size on sample size is negligible”2 and “the loss of efficiency due to variation in cluster sizes rarely exceeds 10%”4 apply equally well to stepped wedge and other designs.

When the CV of cluster sizes is known, an upper bound on the unequal cluster DE (or sample size) can be obtained by inflating the average cluster size in the corresponding calculation with equal clusters. For parallel studies, this has been a popular method for dealing with clusters of unequal size, and it applies equally well for the more general designs considered here. It can be implemented using existing methodology for equal clusters.

We treat only rectangular (ie, “complete”) design layouts under linear mixed models with an exchangeable correlation structure for subject and cluster effects, but these are precisely the conditions under which explicit general formulae for the equal cluster DEs are known. Thus, our work complements these formulae8 but does not consider more general autocorrelation structures. For example, the exponential correlation model discussed by Kasza et al7 leads to unmanageable algebraic forms even for the equal cluster DEs. This would likely rule out a simple expression for the RE, although the impact of unequally sized clusters could be investigated numerically.

The RE computed here refers to the sampling behavior of an (asymptotically) efficient estimator of the treatment effect, such as would be obtained by maximum likelihood. For parallel studies, this is equivalent (asymptotically) to a cluster‐level estimator using inverse‐variance weighting of the cluster means. In practice, alternative analyses are sometimes specified based on equally weighted or size‐weighted cluster means. When the clusters are equal in size, all three weightings are equivalent; but the equivalence no longer holds for unequally sized clusters, and the alternative estimators are technically inefficient. It follows that, for these estimators, the RE due to cluster inequality is necessarily less than that computed here. Indeed, this property has been used to derive lower bounds for the RE in parallel studies.4 Some alternative estimators have been proposed for stepped wedge designs, eg, the vertical estimators of Matthews and Forbes,17 but these are not efficient estimators even when the clusters are of equal size. Thus, the current work seems to have no direct implications for the impact of cluster inequality on the precision of such estimators.

This paper concerns the consequences of inequality between the clusters within the arms of a trial, not inequality between different arms, which, in principle, can be randomized away. Indeed, the formulae for the RE are strictly valid only for size‐stratified randomization schemes under which the precision of the trial is the same irrespective of the outcome of the cluster randomization. This limitation is shared by most, but not all,18 published adjustments to the DEs for parallel group designs where it is explicitly (or implicitly) assumed that the distribution of cluster sizes is identical in the two arms of the trial. Such adjustments are asymptotically valid (and commonly used) even under unrestricted randomization schemes if the number of clusters is large. A similar asymptotic argument applies for more general designs, including the stepped wedge, although it may be a less reliable guide to finite sample behavior when balance over several treatment sequences (arms) is required.

In practice, stepped wedge designs are sometimes used for very small numbers of clusters, perhaps with only one or two clusters allocated to each sequence. In such cases, the current analysis is incomplete: the RE given here provides a sensible average adjustment, but a full treatment of the problem may be more complex. The realized precision of the trial can vary with the particular outcome of the randomization. Further work is needed to explore the implications for trial design.

Supporting information

SIM_7943‐Supp‐0001‐Supp Figs.docx

APPENDIX A.

RELATIVE EFFICIENCY OF STRATIFIED UNEQUAL CLUSTER DESIGNS

1.

An outline of the argument leading to Equation (2) is given here. The following notation is used: for any n > 0, 1_n is the (n ×1) vector of 1s; I_n is the (n × n) identity matrix; ${\mathrm{J}}_n=\frac{1}{n}{1}_n{1}_n^T$; and Π_n = I_n − J_n. The matrices J_n and Π_n are mutually orthogonal projection matrices (ie, J² = J, Π² = Π, JΠ = ΠJ = 0). For any two matrices A and B, A ⊕ B denotes the direct sum and A ⊗ B the direct (Kronecker) product.

1. Since the subjects within a cluster are exchangeable, the BLUE for θ in model (1) will depend only on the means of the observations in each cluster at each timepoint, ie, the “cell means,” ${\bar{Y}}_{•\mathit{jkl}}$. The array of cell means may be vectorized as $y={\left({\left(\mathrm{vec}{\bar{Y}}_{•j1l}\right)}^T\left|{\left(\mathrm{vec}{\bar{Y}}_{•j2l}\right)}^T\right|\text{…}{\left(\mathrm{vec}{\bar{Y}}_{•\mathit{jrl}}\right)}^T\right)}^T$, a column vector consisting of r blocks, one for each stratum, with entries within blocks ordered by time within clusters. With this notation, model (1) may be written in the form

   $$y=\mathrm{Z}\beta +\mathrm{\theta }\mathit{x}+\epsilon .$$ (A1)

   Here, Z = 1_r ⊗ 1_L ⊗ I_T; x = 1_r ⊗ x₀ with x₀ = vec(X^T); β is the (T × 1) vector of time effects; and ε is a random (rLT × 1) vector with zero mean and variance‐covariance matrix of the form V = V(m ₁) ⊕ V(m ₂) ⊕… ⊕ V(m _r), where V (m _k) is the variance‐covariance matrix of the T cell means from a cluster of size m _k, namely,

   $$\mathrm{V}\left(m_k\right)=\left({\eta }_C+\frac{{\eta }_S}{m_k}\right)1_T{1}_T^T+\left({\eta }_{\mathit{CT}}+\frac{{\eta }_{\mathit{ST}}}{m_k}\right){\mathrm{I}}_T.$$
2. From the theory of weighted least squares estimation, the precision of the BLUE of θ in model (A1) is ${\left(\mathrm{var}\widehat{\mathrm{\theta }}\right)}^{-1}=x^T\mathrm{P}x$, with

   $$\mathrm{P}={\mathbf{V}}^{-1}-{\mathbf{V}}^{-1}Z{\left(Z^T{\mathbf{V}}^{-1}Z\right)}^{-1}{Z}^T{\mathbf{V}}^{-1}.$$ (A2)
3. To compute the matrix P, we must find the inverse of V. To do this, note that V can be expressed as

   $$\mathbf{V}=\text{Diag}{\left(\zeta \right)}^{-1}\otimes {\mathrm{I}}_L\otimes {\mathrm{\Pi }}_T+\text{Diag}{\left(\xi \right)}^{-1}\otimes {\mathrm{I}}_L\otimes {\mathrm{J}}_T,$$

   where the (r × 1) vectors ζ and ξ have components ${\zeta }_k=\zeta \left(m_k\right)={\left({\eta }_{\mathit{CT}}+\frac{{\eta }_{\mathit{ST}}}{m_k}\right)}^{-1}$ and ${\xi }_k=\xi \left(m_k\right)=\left(T{\eta }_C+\frac{T{\eta }_S}{m_k}+\right.$ ${\left.{\eta }_{\mathit{CT}}+\frac{{\eta }_{\mathit{ST}}}{m_k}\right)}^{-1}$. It follows from the properties of J_T and Π_T that

   $${\mathbf{V}}^{-1}=\text{Diag}\left(\zeta \right)\otimes {\mathrm{I}}_L\otimes {\mathrm{\Pi }}_T+\text{Diag}\left(\xi \right)\otimes {\mathrm{I}}_L\otimes {\mathrm{J}}_T.$$ (A3)
4. From (A3),

   $$Z^T{\mathbf{V}}^{-1}Z=\left(1_r^T\text{Diag}\left(\zeta \right)1_r\right)·\left(1_L^T{1}_L\right)·{\mathrm{\Pi }}_T+\left(1_r^T\text{Diag}\left(\zeta \right)1_r\right)·\left(1_L^T{1}_L\right)·{\mathrm{J}}_T=\mathit{rL}\left(\bar{\zeta }{\mathrm{\Pi }}_T+\bar{\xi }{\mathrm{J}}_{\mathrm{T}}\right),$$

   with $\bar{\zeta }=\frac{1}{r}\sum _1^r{\zeta }_k$ and $\bar{\xi }=\frac{1}{r}\sum _1^r{\xi }_k$. Moreover, ${\left(Z^T{\mathbf{V}}^{-1}Z\right)}^{-1}=\frac{1}{\mathit{rL}}\left({\bar{\zeta }}^{-1}{\mathrm{\Pi }}_T+{\bar{\xi }}^{-1}{\mathrm{J}}_{\mathrm{T}}\right)$. On substituting this inverse into (A2) and using (A3), we have

   $$\mathrm{P}=\text{Diag}\left(\zeta \right)\otimes {\mathrm{I}}_L\otimes {\mathrm{\Pi }}_T-\frac{1}{\mathit{rL}\bar{\zeta }}{\zeta \zeta }^T\otimes 1_L{1}_L^T\otimes {\mathrm{\Pi }}_T+\text{Diag}\left(\xi \right)\otimes {\mathrm{I}}_L\otimes {\mathrm{J}}_T-\frac{1}{\mathit{rL}\bar{\xi }}{\xi \xi }^T\otimes 1_L{1}_L^T\otimes {\mathrm{J}}_T.$$
5. From the fact that $1_r^T\text{Diag}\left(\omega \right)1_r=1_r^T\omega =\frac{1}{1_r^T\omega }{1}_r^T{\omega \omega }^T{1}_r$ for any (r ×1) vector, ω (= ζ or ξ here), it follows that

   $$x^T\mathrm{P}x=\left(1_r^T\otimes x_0^T\right)\mathrm{P}\left(1_r\otimes x_0\right)={\mathit{rx}}_0^T\left({\mathrm{\Pi }}_L\otimes {\mathrm{\Pi }}_T\right)x_0\times \bar{\zeta }+{\mathit{rx}}_0^T\left({\mathrm{\Pi }}_L\otimes {\mathrm{J}}_T\right)x_0\times \bar{\xi }=\mathit{rLT}\left(A\bar{\zeta }+B\bar{\xi }\right),$$ (A4)

   where $A\left[={\left(\mathit{LT}\right)}^{-1}{x}_0^T\left({\mathrm{\Pi }}_L\otimes {\mathrm{\Pi }}_T\right)x_0\right]$ and $B\left[={\left(\mathit{LT}\right)}^{-1}{x}_0^T\left({\mathrm{\Pi }}_L\otimes {\mathrm{J}}_T\right)x_0\right]$ are the coefficients that characterize the design layout, as defined in the main text of the paper (see Table 1).
6. The expression (A4) gives the precision of the θ‐estimate for a (stratified) design in which m _k subjects are observed in the clusters in stratum k. In the equal cluster case, m _k = m for each k so that $\bar{\zeta }$ and $\bar{\xi }$ are replaced by ζ(m) and ξ(m), respectively. Thus, the relative efficiency (unequal vs equal clusters) is

   $$\mathrm{RE}=\frac{\mathit{rLT}\left(A\bar{\zeta }+B\bar{\xi }\right)}{\mathit{rLT}\left(\mathit{A}\zeta \left(m\right)+\mathit{B}\xi \left(m\right)\right)}=\frac{A\frac{\bar{\zeta }}{\zeta \left(m\right)}+B\frac{\xi \left(m\right)}{\zeta \left(m\right)}·\frac{\bar{\xi }}{\xi \left(m\right)}}{A+B\frac{\xi \left(m\right)}{\zeta \left(m\right)}}.$$ (A5)

   Some elementary algebra shows that (A5) is equivalent to Equation (2), ie, $\frac{\bar{\zeta }}{\zeta \left(m\right)}=\mathrm{\Psi }\left({\lambda }_0{m}^{\left(\mathrm{\rho }\right)}\right)$, $\frac{\bar{\xi }}{\xi \left(m\right)}=\mathrm{\Psi }\left({\lambda }_1{m}^{\left(\mathrm{\rho }\right)}\right)$, and $\frac{\xi \left(m\right)}{\zeta \left(m\right)}=\nu$.
7. Using (A4), the precision in the equal cluster case can be expressed as

   $$\mathit{rLT}\left(\mathit{A}\zeta \left(m\right)+\mathit{B}\xi \left(m\right)\right)=\frac{\mathit{\text{rLTm}}}{4{\sigma }^2}·\frac{4\left[1+\left(T-1\right)\nu \right]\left(A+\mathit{B}\nu \right)}{\mathit{T}\nu \left(1+\left(m-1\right)\mathrm{\rho }\right)}.$$ (A6)

   The first factor on the right‐hand side is the precision for a randomized controlled trial with the same total number of observations, (= rLTm). Thus, the second factor is the inverse of the equal cluster DE given in (5).

APPENDIX B.

PROPERTIES OF Ψ(α)

1.

In this appendix, we use a more general definition of the function Ψ(α) than in Equation (3), in terms of an expected value over a general probability distribution. Namely,

$\mathrm{\Psi }\left(\alpha \right)=\mathrm{E}\left[\frac{\left(1+\alpha \right)Z}{1+\alpha \mathit{Z}}\right]$, where Z is a nonnegative random variable with E (Z) = 1.

1. Ψ(0) = 1, from the definition.

2. Ψ(∞) = Pr {Z > 0}. This follows because $\mathrm{\Psi }\left(\infty \right)={\lim }_{\alpha \to \infty }\mathrm{E}\left[\frac{\left(1+\alpha \right)Z}{1+\alpha \mathit{Z}}\right]=\mathrm{E}\left[{\lim }_{\alpha \to \infty }\frac{\left(1+\alpha \right)Z}{1+\alpha \mathit{Z}}\right]$.

3. Ψ(α) ≤ 1, from Jensen's inequality since $\frac{\left(1+\alpha \right)Z}{1+\alpha \mathit{Z}}$ is a convex function of Z.

4. Either Ψ(α) is constant (= 1) or it has a unique minimum in the range 0 < α≤ ∞. Putting $u=\frac{\alpha }{1+\alpha }$, we have $\frac{{\partial }^2}{\partial u^2}\mathrm{\Psi }\left(\alpha \right)=\mathrm{E}\left[\frac{Z{\left(Z-1\right)}^2}{{\left(1-u+\mathit{uZ}\right)}^2}\right]\ge 0$ so that Ψ(α) is convex when considered as a function of u. The result follows because u is strictly increasing in α.

5. (Least Favorable Distribution) Suppose that Z has discrete support $\mathit{S}$ with probability distribution $\{p_z;z\in \mathit{S}\}$. Let $\{q_z;z\in \mathit{S}\}$ be the “size‐biased” distribution defined by q _z = zp _z for $z\in \mathit{S}$. This is a proper distribution because ${\sum }_{z\in \mathrm{S}}{q}_z={\sum }_{z\in \mathrm{S}}{\mathit{zp}}_z=\mathrm{E}\left(Z\right)=1$. Now, apply Jensen's inequality to the convex function (of Z): $\frac{1+\alpha }{1+\alpha \mathit{Z}}$, over the size‐biased distribution {q _z}. This yields ${\mathrm{E}}_q\left[\frac{1+\alpha }{1+\alpha \mathit{Z}}\right]\ge \frac{1+\alpha }{1+\alpha {\mathrm{E}}_q\left(Z\right)}$, where E_q denotes an expectation over the q‐distribution, ie, E_q f (Z) = E[Zf (Z)] for any function f ().

Hence, $\mathrm{\Psi }\left(\alpha \right)=\mathrm{E}\left[\frac{\left(1+\alpha \right)Z}{1+\alpha \mathit{Z}}\right]={\mathrm{E}}_q\left[\frac{1+\alpha }{1+\alpha \mathit{Z}}\right]\ge \frac{1+\alpha }{1+\alpha \mathrm{E}\left(Z^2\right)}=\frac{1+\alpha }{1+\alpha \left(1+c^2\right)}$, where c is the CV of Z. It is straightforward to show that the bound is attained under the LFD defined in Section 3.1.

Girling AJ. Relative efficiency of unequal cluster sizes in stepped wedge and other trial designs under longitudinal or cross‐sectional sampling. Statistics in Medicine. 2018;37:4652–4664. 10.1002/sim.7943