Abstract
A correct estimate of ligand binding modes and a ratio of their occupancies is crucial for calculations of binding free energies. The newly developed method BLUES combines molecular dynamics with nonequilibrium candidate Monte Carlo. Nonequilibrium candidate Monte Carlo generates a plethora of possible binding modes and molecular dynamics enables the system to relax. We used BLUES to investigate binding modes of caffeine in the active site of its metabolizing enzyme Cytochrome P450 1A2 with the aim of elucidating metabolite-formation profiles at different concentrations. Because the activation energies of all sites of metabolism do not show a clear preference for one metabolite over the others, the orientations in the active site must play a key role. In simulations with caffeine located in a spacious pocket above the I-helix, it points N3 and N1 to the heme iron, whereas in simulations where caffeine is in close proximity to the heme N7 and C8 are preferably oriented toward the heme iron. We propose a mechanism where at low caffeine concentrations caffeine binds to the upper part of the active site, leading to formation of the main metabolite paraxanthine. On the other hand, at high concentrations two molecules are located in the active site, forcing one molecule into close proximity to the heme and yielding metabolites theophylline and trimethyluretic acid. Our results offer an explanation of previously published experimental results.
Introduction
Human cytochromes P450 (CYP) are oxidoreductases with a heme cofactor that are responsible for the Phase I metabolism of 75% of drugs in the human body.1−3 There are 57 mammalian isoforms known and their inhibition, induction, or allosteric effects by various small molecules often lead to a number of drug–drug interactions. Cytochromes P450 catalyze a wide variety of reactions, that are in general improving the water solubility either of their endogenous substrates or xenobiotics. These reactions take place at the functional groups of the molecules, also known as sites of metabolism (SOM). A general rule-of-thumb is that poses for which the distance between a SOM of a molecule to the heme iron is not more than 6 Å are considered to be active binding modes.4,5 Here, we chose the 1A2 isoform, which metabolizes caffeine in four positions. Caffeine is a methylxanthine neurostimulant, acting as a competitive antagonist of adenosine receptors, that most Europeans consume every day.6−8 Caffeine, like many other aromatic and heterocyclic amines, is metabolized by CYP1A2.9 CYP1A2 has a relatively narrow and planar binding site (375 Å3) suitable for accommodation of such amines. The active site is formed by the I-helix situated above a cysteine-bound heme with residues Phe226 and Asp320 playing a crucial role in the kinetics of the chemical reaction.10,11
The exact binding modes of caffeine are unknown, however the main metabolites are known and NMR studies investigating the binding modes and their ratios have been reported.12 The main metabolites of caffeine are paraxanthine (PX) accounting for about 80% of product formation, theobromine (TB) with about 10%, theophylline (TP) with about 5%, and 1,3,7-trimethyluretic acid (TMU) with only 1%, all of which are biologically active and further metabolized by cytochrome P450s,13−16 shown in Figure 1.
Figure 1.
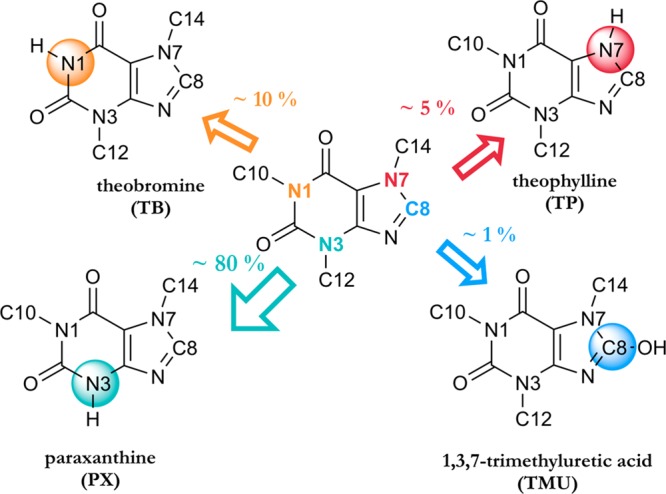
Main metabolites of caffeine. Caffeine is in the middle and the SOM are depicted in colorful spheres. The main metabolite PX is shown in cyan.
Regal and Nelson12 observed a shift in the metabolite ratio with increasing caffeine concentration, making theophylline the main metabolite at higher caffeine concentrations. CYP1A2 in its resting state is in the high spin state (HS) which is typically associated with a penta-coordinated heme iron in its ferric form.17 For other CYPs, the resting state involves coordination of a water molecule as sixth ligand to the heme iron, leading to a (measurable) low spin state (LS). The lack of a sixth-coordinating water molecule in the resting state of CYP1A2 might be caused by the narrow hydrophobic active site of CYP1A2, which might to some degree hamper coordination of a water molecule with the heme iron.
A potential substrate binds to the active site in the resting state, potentially in a fixed orientation. For CYP1A2, it was shown that in the presence of higher concentrations of substrate there was an incomplete shift (∼28%) from the high spin to the low spin state.18 Regal and Nelson12 showed that average distances of caffeine SOMs to the heme iron are approximately 2 Å shorter for CYP1A2 in a 100% low spin state than in a 100% high spin state. Nevertheless, the distances of all three nitrogens N1, N3, and N7 to the iron atom differ less than 0.2 Å in both spin states, see Table S1. Similar distances of all SOMs to the heme iron do not indicate a clear binding mode leading to the known main metabolites in human.
After substrate binding, diffusion of molecular oxygen to the heme iron leads to the formation of compound one (CPDI) with one oxygen atom bound to the iron in its ferryl state. CPDI is a highly reactive species responsible for product formation.
The aim of our work is to elucidate the binding modes of caffeine with the CYP1A2 isoform by using the package BLUES, which can by NCMC lead to a better sampling of ligand orientations.
Activation Energy
The activation energy of the oxidation reaction at each SOM determines the reactivity. Previous studies show that the rate-limiting step in aliphatic oxidation is the creation of a radical intermediate, that is, hydrogen abstraction. The rate-limiting step for aromatic oxidation is the creation of the bond between the oxygen bound to the iron and the aromatic carbon. Rydberg and co-workers19 proposed a method predicting these activation energies for potential SOMs based on the effect of their surrounding atoms. This method consists of a number of rules that are derived from high-level density functional theory (DFT) calculations. The calculated activation energies from Rydberg et al.19 are shown in Table 1. The aliphatic oxidation on N7–C14 and aromatic oxidation on C8 yielded the lowest activation energies, both 52 kJ/mol. The aliphatic oxidations on N3–C12 and N1–C10, were slightly higher, ranging from 57 to 62 kJ/mol.
Table 1. Activation Energies for SOM of Caffeine Taken from Rydberg et al.19 at Given SOMsa.
| SOM | E [kJ/mol] |
|---|---|
| Aliphatic Oxidations | |
| N1–C10 (TB) | 61.7 |
| N3–C12 (PX) | 57.3 |
| N7–C14 (TP) | 52.1 |
| Aromatic Oxidation | |
| C8 (TMU) | 52.2 |
Abbreviations of the formed products in brackets.
Despite the lower activation energies of N7–C14 and C8, the overall energies differ by less than 10 kJ/mol, which does not imply a distinctly higher reactivity of one SOM over the others. Apparently, the activation energies alone do not explain the preferred formation of PX (metabolism at N3–C12) but rather suggest a preference for TP or TMU. Caffeine’s orientation with respect to the heme might have a stronger impact on its metabolism than its intrinsic reactivity.
Ligand Sampling
Enzymes catalyze chemical reactions typically through a stabilization of the transition state in the active site. The active site might be located on the surface of the protein but might be also buried in the protein interior. In those cases, a ligand or a substrate is steered by nonbonded interactions through the protein along its binding path, passing by potential subpockets until it reaches a reactive binding mode in the protein active site. Assessing the correct ligand binding modes and the ratios of their occurrences is essential for the estimate of ligand binding strength and, for enzyme–substrate complexes, the proper orientation of the substrate.
Binding modes play an important role in drug design where one aims to predict the binding characteristics of a large number of potential drug molecules to the target of interest. Probably the most frequently used and the fastest method for selection of the most likely binders is molecular docking. Molecular docking positions a ligand into multiple binding modes and selects the one with the lowest score (hopefully roughly corresponding to a binding enthalpy) which can be calculated in various ways.20 Docking can reach high computational speed by neglecting the protein motion and solvation. These factors have, however, a negative impact on the accuracy of the results, which makes docking a “guiding filter” to refine ligand libraries and select potentially active binders. Docking does not accurately predict free-energies and occupancies of different binding modes because of the lack of physically accurate sampling.21 There are several more extensive methods, employing molecular dynamics (MD) simulations, that address these topics, such as replica exchange,22−24 umbrella sampling with potential of mean force25−27 and others.28−30 These methods are, however, often rather laborious and need a significant amount of preparation for individual systems. Alchemical methods that focus on the relative free energies between individual ligands are often initiated from a single binding pose for multiple ligands. This way they ignore possible orientational differences between ligands which might lead to higher errors and inconsistencies with simulations that start from a different binding pose.31,32
A recently developed method, binding modes of ligands using enhanced sampling (BLUES),33 addresses these issues. The uniqueness of the BLUES method lies in the combination of MD with a nonequilibrium candidate Monte Carlo (NCMC) approach. The NCMC approach is based on the naïve Monte Carlo method while yielding higher acceptance probabilities with shorter correlation times.34 NCMC introduces a nonequilibrium phase, which consists of a number of instantaneous perturbation steps separated by short relaxation periods. Afterward the entire series is accepted or rejected. In the particular implementation of NCMC used in BLUES, the perturbations scale down the interactions, that is, the potential energy of the ligand with its surroundings is gradually changed to zero, followed by a ligand rotation around its center of mass (COM) into a new orientation without changing the potential energy of the system. After the ligand rotation, the interactions are gradually turned on again (Figure 2). Coulombic interactions are turned off before the van der Waals interactions, and after rotation interactions are turned on in reverse order to avoid numerical instabilities and to ensure reversibility.35
Figure 2.
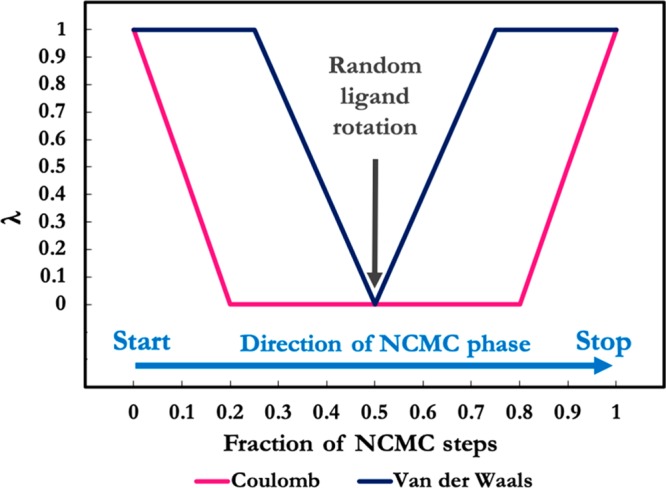
Scaling of nonbonded interactions of the ligand with respect to λ over the course of NCMC steps. At λ = 1 the ligand is fully interacting, whereas at λ = 0 the interactions of the ligand are turned off completely. The relaxation MD part is not included in this figure. Adapted from Gill et al.33
The acceptance criterium for the entire NCMC procedure is derived from the Metropolis-Hastings criterium.36 The acceptance probability of process X, A[X] is computed as
| 1 |
where w is the protocol work of the procedure, estimated as
| 2 |
where xt is a microstate at a given simulation step and ut is the reduced potential energy. Because a Langevin integrator is used, w in eq 1 is complemented with the appropriate shadow work.37 After each accepted or rejected move, the momenta are randomly reassigned based on the Maxwell–Boltzmann distribution in order to keep detailed balance.38 The NCMC stage is followed by a series of conventional MD steps, using a Langevin integrator to relax the entire system. BLUES creates a trajectory of MD and accepted moves, which can be subsequently clustered and used for estimating populations of binding modes.
Methods
The crystal structure of CYP1A2 with the PDB code 2HI4(39) with a resolution of 1.95 Å was used as an input structure for all MD simulations. The crystallized ligand α-naphthoflavone was subsequently removed and caffeine was docked into the active site using the AutoDock Vina tool and AutoDock Vina scoring function.40 The active site was defined as a cube with an edge length of 13 Å, centered at the heme iron. Figure S1 shows the docking setup for both receptors. The flexibility of the receptor was not considered. The nine best scored docking poses were saved for further simulations.
Hydrogens were added to the protein using tleap from AmberTools1741,42 and the protein was parametrized using the ff99SB force field.43 The parameters for heme in the ferric form, compound I, and neighboring cysteine were adopted from Shahrokh et al.44 In a classical force field, no differences between ferric high spin or low spin states are described. Hydrogens were added to caffeine using AutoDockTools445 and caffeine was parametrized using the GAFF46 force field with AM1-BCC charges.47 The docked proteins were solvated in a rectangular box with TIP3P water molecules48 with 13 Å as the minimal protein-wall distance and 6 Cl– counterions were added. The system was minimized and equilibrated for 6.2 ns using OpenMM 7.1.149 under constant pressure at 1 atm with 300 K. A Monte Carlo barostat and Langevin integrator were used with a 4 fs time step while setting the hydrogen mass to 3.024 Da and using 1 ps–1 collision rate. The bond distance between hydrogen and heavy atoms was constrained while using the hydrogen mass repartitioning scheme.50 The particle Mesh Ewald method51 was used to calculate the long-range electrostatics.
To generate reasonable starting structures for the simulations with the ferric heme, all poses from the last 6 ns of equilibration were merged and analyzed by time-structure-independent component analysis (tICA) using PyEMMA 2.5.2.52,53 tICA was performed on the pairwise-distances of the caffeine atoms and the alpha carbons of the binding site with a lagtime of 200 ps and the frames were clustered by PCCA.54,55 Four of the five most stable clusters were used for standard MD and BLUES simulations. Note that the sole purpose of the tICA analysis and clustering was to obtain initial structures for the production simulations; from such short simulations, no conclusions with respect to the orientational preferences of the substrate can be deduced. Although tICA is also used in the context of building Markov State Models for analysis of long MD simulations, that was not our focus here; instead, we simply sought to identify potential stable or metastable binding modes for further analysis via additional simulations. For the CPDI simulations we did not perform clustering but directly used the rather diverse original docking poses for standard MD and BLUES simulations.
The production runs of standard MD with ferric heme and CPDI were performed by OpenMM in the NVT ensemble without use of a barostat. We have found that running BLUES with a barostat can impair acceptance rates and, for a buried binding site like this, ligand placement is unlikely to affect the pressure of the system. For consistency, the standard MD simulations were also performed without a barostat. In all cases, equilibration brought the systems to the correct pressure prior to these production runs. The production simulations were performed for 1 μs per docked pose.
BLUES version 0.1.3 was used. The BLUES calculations were performed using openmmtools 0.13.056 to annihilate caffeine Coulombic and van der Waals interactions. The MD part was performed as described above by OpenMM’s Langevin integrator and the NCMC part by the BAOAB integrator for Langevin dynamics.57 The protein and water residues further than 5 Å from the ligand were constrained during the NCMC phase (though these are fully flexible during the conventional MD phase) to improve acceptance, as in previous work.33 For every perturbation step performed, three additional propagation (or relaxation) steps were applied between λ = 0.2 and 0.8. BLUES runs consisted of 1000 iterations, each of which consisted of 10 000 NCMC steps and 10 000 MD steps. Thus, the total simulation time of one BLUES run is equivalent to 20 × 106 force evaluations. The general scheme of the BLUES workflow is depicted in Figure S2.
Results and Discussion
In order to investigate binding modes of caffeine we included two heme states of the CYP1A2 catalytic cycle. The first of them was heme in its ferric resting state to which the substrate binds and the second was CPDI, which plays a key role in the actual substrate metabolism.
Heme with Ferric Iron
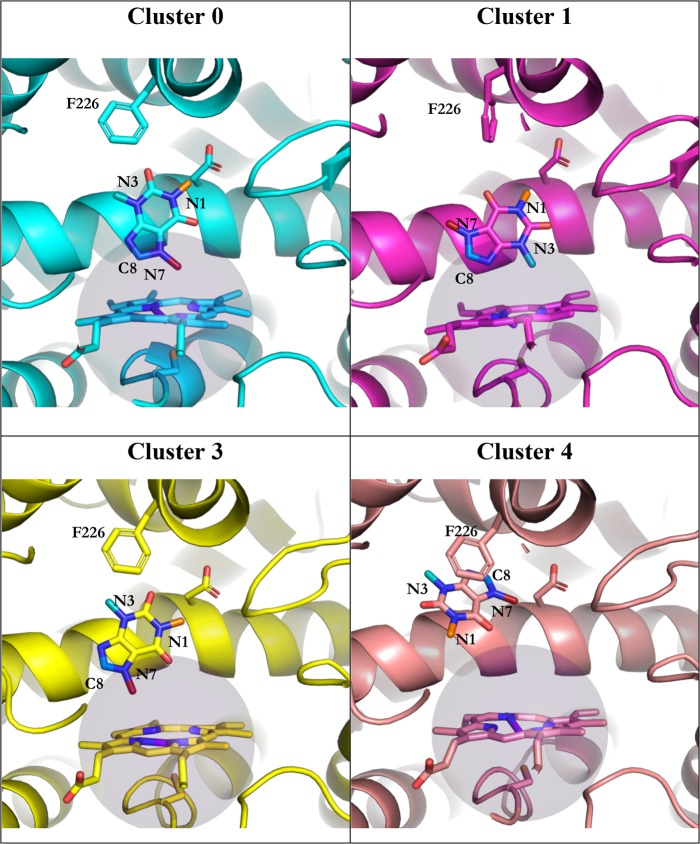
After the removal of the α-naphthoflavone molecule from the crystal structure, caffeine was docked into the active site of CYP1A2. The docking process resulted in multiple docking poses where at least one functional moiety of caffeine would fulfill the 6 Å rule. Nine well-scoring poses were selected for further simulations. After the minimization and equilibration of docked poses, the feature coordinates were transformed using tICA and subsequently assigned to clusters using PCCA. From five suggested clusters, four were chosen, because the representative structures of clusters 2 and 3 were, based on visual inspection, almost identical. The remaining four clusters were used to start standard MD and BLUES simulations and are shown in Figure 3.
Figure 3.
Starting poses for MD and BLUES simulations. The amino acids in sticks are he226 and Asp320, the purple sphere represents a sphere of 6 Å around the heme iron. Caffeine SOMs C10 is in orange, C12 is in cyan, C14 is in dark red, and C8 is in marine blue. The nitrogen atoms to which C10, C12, and C14 are bound, as well as C8, are labeled as well as Phe226.
We measured distances of the four sites of metabolism, depicted as C10 (neighboring N1), C12 (neighboring N3), C14 (neighboring N7), and C8, as well as the running average of the distance of the center of mass of caffeine depicted as COM, all to the heme iron of the ferric state.
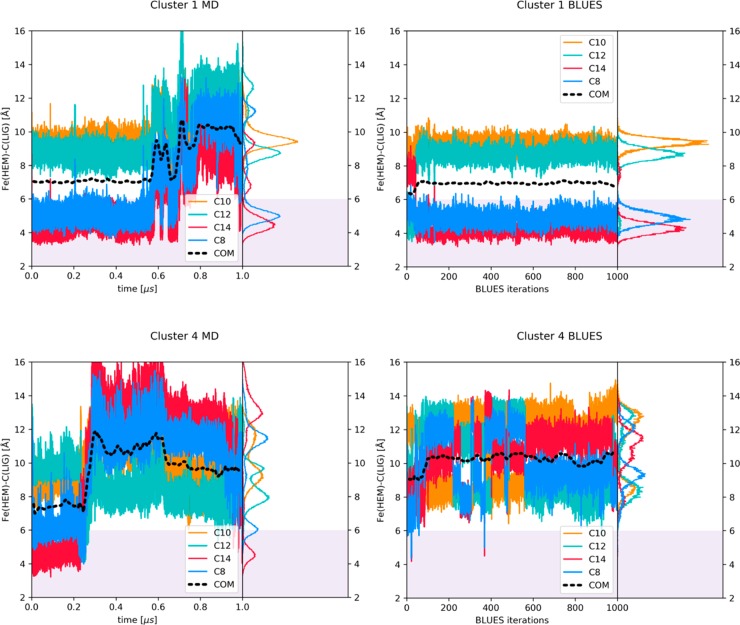
For the sake of clarity we compare in Figure 4 these distances during standard MD and BLUES simulations of cluster 1 and 4, as the behavior of caffeine in simulations starting from clusters 0 and 3 resemble the data in cluster 1 (Figure S3). For clusters 0, 1, and 3, in BLUES we observed binding modes consistent with a clear preference for metabolism at C8 and C14, because these SOMs were pointing to the heme iron for more than 90% of simulation frames, see Table S3 and Figure 5. This trend can be seen in MD simulations as well; however, in clusters 1 and 3 caffeine tends to leave the close vicinity of the heme and reaches distances around 10 Å from the heme iron. Because in BLUES the trajectory is divided by the NCMC phase, caffeine does not have the chance for bigger translational moves and remains at a constant distance around 7 Å from the heme. Table S2 shows the percentages of frames, in which the distance between the caffeine SOMs and the heme iron is less than 6 Å. In BLUES simulations, we could not observe any transitions between different binding poses, leading to an average acceptance rate of ∼3% in all cluster simulations. Table S1 summarizes average distances of the carbon atoms from the heme iron as ⟨r⟩ and as ⟨r–6⟩–1/6 which are more representative to the distances that are derived from NMR experiments.
Figure 4.
Time series of the distance from the heme iron (ferric state) to indicated atoms in caffeine and its center of mass (COM). The right-hand-side panels show the corresponding histograms.
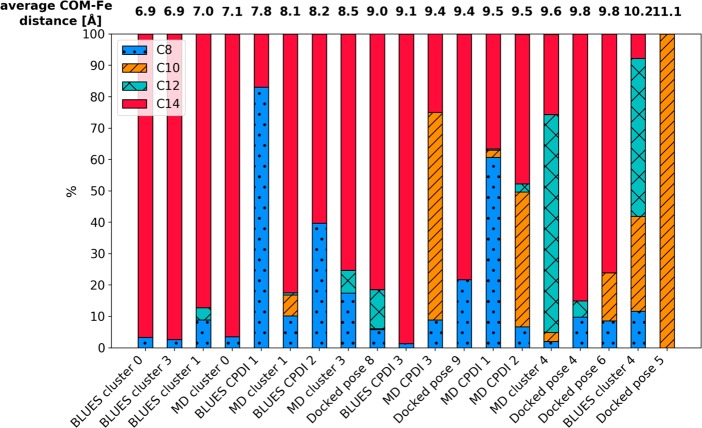
Figure 5.
Ratio of the closest SOMs to the heme iron in all simulations. The bars are ordered according to the average COM-Fe distance. We can observe an orientational change in the position where the COM-Fe distance is larger than 9 Å. The exact values and error estimates are shown in Table S7.
Unlike simulations of clusters 0, 1, and 3, simulations of cluster 4 started from a position where the COM of caffeine was 10 Å from the heme iron. In BLUES simulations of cluster 4, we observe a higher number of transitions, repeatedly placing all four SOMs of caffeine toward the heme, shown in Figure 4. In MD simulations of cluster 4, caffeine first comes closer to the heme to around 8 Å, then leaves the active site and rotates. In both simulations, MD and BLUES, caffeine reaches a metastable pose where C12, which is the methyl group that when cleaved yields the main metabolite PX, is oriented toward the heme iron in more than 50% of simulation frames. It is important to note that in both simulations of cluster 4, C12 does not reach the distance of 6 Å to the heme iron, which is considered to be necessary for the SOM metabolism to take place.
To obtain a better view of the different binding modes, we measured distances from the center of mass of the aromatic cluster (Phe226, Phe256, and Phe260) and the ligand, see Figure S6. We note that when caffeine leaves the close vicinity of the heme, which is the case for clusters 1, 3, and 4, it approaches this aromatic cluster. Favorable aromatic interactions can be the cause of caffeine movement during the MD simulations.
Several factors may cause the differences between BLUES and MD simulations. In BLUES simulations, caffeine does not leave the close vicinity of the heme, because the simulation is constantly interrupted by a series of NCMC steps where it can adjust its orientation. The MD simulations on the other hand, offer a long continuous run where the caffeine molecule has a chance to diffuse away from the direct vicinity of the heme, from which we learn that a single caffeine molecule prefers to bind further away from the heme. The strength of BLUES, however, lies in the effective sampling of all relevant binding modes, where it surpasses standard MD simulations (e.g., cluster 4 in Figure 4).
Measured distances of MD simulations of four additional docked poses that were not used in BLUES are in the Supporting Information (Figure S4), most of them with C14 and C8 oriented toward the heme.
Compound I
Starting poses for simulations with Compound I (CPDI) were obtained from docking using the same procedure as described for the ferric state of the enzyme. These were, however, not clustered, yet the three most distinct docking poses, each orienting a different SOM (C10, C12, and C14) to the heme iron, were chosen for further study. While the binding of the substrate takes place with the enzyme in the ferric resting state, the actual reaction is performed by CPDI. Therefore, we investigated if CPDI affects the orientation of caffeine. During the equilibration run all of them reoriented such that C8 and C14 were pointing to the heme iron. In these MD simulations, the COM of caffeine was at a distance of around 9 Å from the heme iron and C8 and C14 were at 7–8 Å, which was again higher than in BLUES, where these average distances were 8 and 5–6 Å, respectively, see Figure S5 and Table S4. In contrast to the simulation with the ferric iron, the standard MD CPDI simulations showed distances of the SOMs to the heme iron smaller than 6 Å for less than 9% of the frames (Table S5). Interestingly, we observe a stronger preference for C8 than in the ferric heme simulations for both standard MD and BLUES (see Table S6). However, these SOMs are located closely to each other suggesting only a minor difference between heme and CPDI poses. The larger distances are probably caused by the oxygen atom bound to the heme iron and a reduced net charge of the iron-center. These larger distances from the heme iron are correlated with shorter distances to the aromatic cluster (Figure S6).
Figure 5 summarizes the percentages of simulation frames in which each SOM was closest to the heme iron for all simulations. The simulations are ordered by the distance of the COM of the ligand from the heme iron. In binding poses where the COM is located more than 9 Å from the heme iron, a clear shift toward C12(N3) and C10(N1) is observed. This might suggest that for the binding poses, where the ligand is located further from the heme iron, the metabolite distribution changes and favors formation of PX and TB, while at closer distances TP and TMU are expected as main metabolites.
Two Spin States–Two Mechanisms?
The work of Regal et al.12 suggests a more complicated picture of caffeine dynamics onto which our simulations may shed light. At low caffeine concentrations, PX is the main metabolite and the protein is observed to be in a high spin state. They determined an average distance for all aromatic nitrogens at roughly 7.3 Å, suggesting a favored binding mode that is too far from the heme iron to explain metabolism. Indeed, in many of the MD simulations that start with the caffeine close to the heme, it is seen to move further away, toward the aromatic cluster (Figure 4, Figure S6, Tables S1–3). In the MD and BLUES simulations that place the caffeine at a larger distance, we observe orientations of the substrate, which point C12 toward the heme iron for appreciable amounts of time which is in agreement with the experimentally observed product formation. This binding mode does not only provide caffeine favorable interactions with Phe226 via π–π stacking, see Figure S6, but also places it in a more spacious cavity above the I-helix giving it a higher conformational freedom to rotate.
At high caffeine concentrations, Regal et al.12 observe a shift in the product formation and in the spin-state of the enzyme to 72% high spin and 28% low spin, see Table 2. We propose that the 28% of low spin corresponds to a situation in which two caffeine molecules bind to the active site forcing one molecule closer to the heme. In Table 2, we compute the normalized product formation for the 100% low spin state as the distribution that would lead to the observed product formation at 25 mM, taking into account the mixed spin state and increased activity (approximately by a factor of 2.112) at the higher concentration. For a 100% low spin state, a 69% preference for product TP with C14 pointing toward the heme and a 5-fold increase in activity relative to the 100% high spin state would be necessary to lead to the observed product formation.
Table 2. Observed Product Formation (Normalized) As Described by Regal et al.12 at 5 and 25 mM Caffeinea.
| normalized product formation | ||||
|---|---|---|---|---|
| SOM | 5 mM (100% HS) | 25 mM (72% HS + 28% LS) | 100% high spin | 100% low spin |
| N1-C10 (TB) | 0.11 | 0.22 | 0.11 | 0.25 |
| N3-C12 (TX) | 0.78 | 0.17 | 0.78 | 0 |
| N7-C14 (TP) | 0.12 | 0.56 | 0.12 | 0.69 |
| C8 (TMU) | 0 | 0.05 | 0 | 0.07 |
We propose that the data at 25 mM with an increased overall turnover by a factor 2.1 is the weighted average of an HS product formation and an LS product formation at fivefold increased activity.
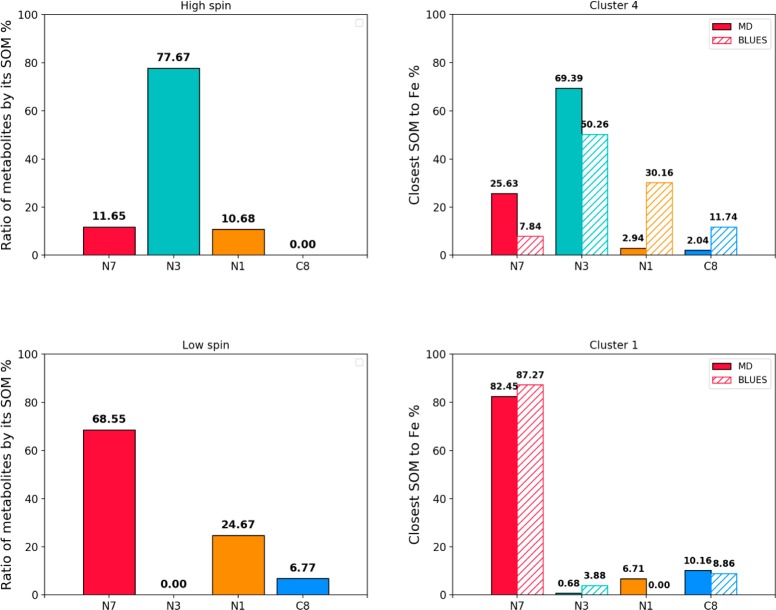
In Figure 6, we summarize the renormalized metabolite yields corresponding to different spin states in Table 2 and compare them to the percentages of the closest SOM to the heme iron throughout our simulations. The main SOM of caffeine in CYP1A2 in its high spin state is N3, which is also the SOM oriented toward the heme iron for more than 50% of the time in both MD and BLUES simulations. In the low spin state, which is present during 28% of time at high caffeine concentrations, the main SOM is N7, corresponding to the most preferred SOM in the simulations, where caffeine is in close vicinity to the heme.
Figure 6.
(Left) Renormalized metabolite formation at different spin states, where the bars indicate which SOM has to be the closest to the heme in order for the SOM’s metabolism to take place. (Right) Percentages of the corresponding orientation of caffeine during MD (full) and BLUES (striped) simulations. The labels above bars show the percentages of corresponding orientation rounded to two decimal places.
Summarizing, a single substrate molecule in the active site prefers to bind close to the aromatic cluster and relatively far away from the heme group. The orientations that are observed for simulations at this distance agree with the experimentally observed product formation at low concentrations. At higher concentrations, a spin shift is experimentally observed, resulting from a shorter substrate-heme distance. Simultaneously, a shift in the product formation is observed. The orientation of the substrate in simulations at shorter distances agrees with this altered product formation. We propose that a second caffeine molecule in the active site could be the cause for placing the first substrate molecule closer to the heme iron.
MD Simulation with Two Ligands in the Active Site
In order to explore the possibility of simultaneous binding of two ligands in the active site of CYP1A2, we simulated such a complex with standard MD for 1 μs. The initial structure was created from the initial binding poses of caffeine in cluster 1 and cluster 4 with the enzyme in the ferric state. Both structures were overlaid and the caffeine molecule in the binding mode from cluster 1 was added to the starting structure of cluster 4. This approach was preferred over a new ab initio docking of the two molecules, as, for example, described for Aflatoxin B1 in Cytochrome P450 3A4,58 as the two poses represented by clusters 1 and 4 were naturally observed in MD simulations previously and seemed to be readily accommodated in the structure. The system was initially minimized in MOE,59 and subsequently the complex was minimized, equilibrated, and simulated as described above for the simulations of CYP1A2 with one ligand.
In the production run, both ligands were very stable; the COM of the caffeine molecule closer to the heme iron (Caffeine 1) was located 7 Å from the heme iron whereas the COM of the second molecule (Caffeine 2) was located around 13–14 Å from the heme iron. These distances did not change significantly during the simulation, see Figure S7. Caffeine 1 in the beginning of the production run rotates which results in an orientation that resembles simulations of clusters 0, 1, and 3, that is, with C8 and C14(N7) pointing toward the heme iron. Caffeine 1 stays in this orientation for more than 98% of simulation time with the C8, C14(N7) within 5 Å from the heme iron (Tables S2–3). Caffeine 2 is stabilized by aromatic stacking with Phe226 and Phe260 from both sides and Phe256 from the top. It remains in the same orientation throughout the simulation. The importance of aromatic interactions in CYPs is demonstrated in the defense mechanism of Antarctic sponges.60 Here, two small molecules inhibit CYP315a1 and CYP314a1 by aromatic interactions within the active site. Figure 7 shows a snapshot from this simultaneous binding of two caffeine molecules into CYP1A2.
Figure 7.
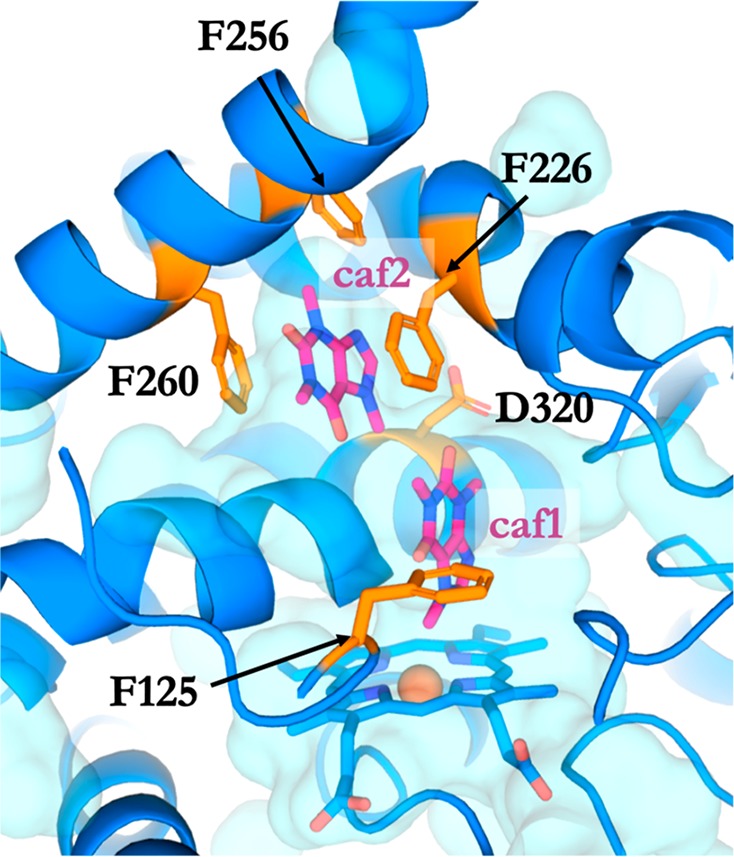
A snapshot of the simulation of simultaneous binding of two caffeine molecules to CYP1A2 after 1000 ns. Caffeine molecules are in magenta, and residues accommodating the caffeine molecules are in orange.
The stability of the protein conformation with two ligands bound was monitored in order to investigate possible effects on the protein upon binding of two caffeine molecules. Figure S8 shows the backbone root-mean-square-deviation (RMSD) curves for this simulation and for the simulations of cluster 1 and cluster 4. Despite the steeper increase of the RMSD curve of protein with two ligands bound, the overall value does not exceed the RMSD from the simulations starting from Cluster 1 and 4. This suggests that simultaneous binding of two caffeine molecules does not have a negative impact on the CYP1A2 stability and in fact may be thermodynamically reasonable. A similar simultaneous binding of two pyrene molecules to the active site of CYP1A2 has been previously suggested by Sohl et al.61,62
Under physiological conditions in humans, much lower concentrations of caffeine (<100 μM) are usually present, and paraxanthine remains the main metabolite, supporting the proposed mechanism with one caffeine molecule in the active site. On the other hand, a double occupancy of the active site might be responsible for the caffeine-induced enhanced metabolism of several druglike compounds.63 Cameron et al.64 described heterotropic cooperativity of acetaminophen and caffeine binding in CYP3A4, leading to enhanced metabolism of caffeine. Multiple molecules binding to the active site of CYP3A4 has been described for ketoconazole experimentally65 and computationally66 and was postulated for aflatoxin B158 based on observed homotropic cooperativity.67
Conclusion
In this work, we investigated the binding modes of caffeine to its metabolizing enzyme CYP1A2 via standard molecular dynamics and the enhanced ligand sampling method BLUES. We observed a clear preference of orientation of the N7–C14 and C8 sites of metabolism toward the heme iron, when the center of mass of the ligand was in the vicinity of the active site. This is in agreement with previously published experimental results showing an altered rate of metabolism and shorter caffeine–iron distances at high caffeine concentrations. Preference of N7–C14 and C8 metabolism is also expected from quantum mechanically derived activation energies from literature, which were slightly lower than the activation energies for other SOMs.
In case of caffeine bound further from the heme, we could see a more pronounced conformational freedom due to a larger cavity, where BLUES was able to sample binding poses with all SOMs oriented toward the heme. Additionally, this was the only case where we could observe the N3–C12 moiety facing the heme iron for a significant amount of time. This binding mode still requires the substrate to transiently approach the heme before metabolism takes place. We suggest that the further removed binding mode corresponds to the binding mode of caffeine when it is present in lower concentrations, where the main metabolite, paraxanthine, is formed. We propose a mechanism, where at higher concentrations two caffeine molecules are accommodated in the active site, forcing one caffeine molecule to be in close vicinity (<6 Å) of the heme iron, leading to formation of theophylline as the main metabolite. To confirm our theory, we simulated simultaneous binding of two caffeine molecules bound to CYP1A2, which indeed lead to stable binding poses with N7–C14 and C8 SOM oriented toward the heme. Moreover, such binding did not disrupt the overall stability of the protein and both caffeine molecules were very stably interacting with the key active site residues. Taken together, the work of Regal et al.,12 complemented by the simulations described in this work, draw a complex but consistent picture of caffeine metabolism by CYP1A2, which might shed more light on caffeine-drug interactions in humans.
Acknowledgments
We thank Prof. Thomas Poulos for inspiring and helpful discussions regarding Cytochromes P450. Financial support of the Austrian Science Fund (FWF) through project I 1999 and the FWF-funded doctoral school BioToP (W1224) is gratefully acknowledged.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.chemrestox.9b00030.
Docking setup for ferric heme and Compound I; BLUES scheme; time series of heme iron to SOM distances for additional simulations; time series of distances from the substrate to the aromatic cluster; atom-positional root-mean-square deviations for selected simulations; average distances and preferred orientations in the various simulations; orientational preferences for all simulations (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Evans W. E.; Relling M. V. (1999) Pharmacogenomics: Translating functional genomics into rational therapeutics. Science 286 (5439), 487–491. 10.1126/science.286.5439.487. [DOI] [PubMed] [Google Scholar]
- Guengerich F. P. (2008) Cytochrome P450 and chemical toxicology. Chem. Res. Toxicol. 21 (1), 70–83. 10.1021/tx700079z. [DOI] [PubMed] [Google Scholar]
- Guengerich F. P. (1992) Characterization of human cytochrome-p450 enzymes. FASEB J. 6 (2), 745–748. 10.1096/fasebj.6.2.1537465. [DOI] [PubMed] [Google Scholar]
- de Graaf C.; Oostenbrink C.; Keizers P. H. J.; van der Wijst T.; Jongejan A.; Vemleulen N. P. E. (2006) Catalytic site prediction and virtual screening of cytochrome P450 2D6 substrates by consideration of water and rescoring in automated docking. J. Med. Chem. 49 (8), 2417–2430. 10.1021/jm0508538. [DOI] [PubMed] [Google Scholar]
- de Graaf C.; Pospisil P.; Pos W.; Folkers G.; Vermeulen N. P. E. (2005) Binding mode prediction of cytochrome P450 and thymidine kinase protein-ligand complexes by consideration of water and rescoring in automated docking. J. Med. Chem. 48 (7), 2308–2318. 10.1021/jm049650u. [DOI] [PubMed] [Google Scholar]
- Nehlig A.; Daval J. L.; Debry G. (1992) Caffeine and the central-nervous-system - mechanisms of action, biochemical, metabolic and psychostimulant effects. Brain Res. Rev. 17 (2), 139–169. 10.1016/0165-0173(92)90012-B. [DOI] [PubMed] [Google Scholar]
- Fisone G.; Borgkvist A.; Usiello A. (2004) Caffeine as a psychomotor stimulant: mechanism of action. Cell. Mol. Life Sci. 61 (7–8), 857–872. 10.1007/s00018-003-3269-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fredholm B. B.; Battig K.; Holmen J.; Nehlig A.; Zvartau E. E. (1999) Actions of caffeine in the brain with special reference to factors that contribute to its widespread use. Pharmacol. Rev. 51 (1), 83–133. [PubMed] [Google Scholar]
- Guengerich F. P.Human Cytochrome P450 Enzymes, 3rd ed.; Kluwer Academic/Plenum Publishers: New York, 2005; p 689. [Google Scholar]
- Yun C. H.; Miller G. P.; Guengerich F. P. (2001) Oxidations of p-alkoxyacylanilides catalyzed by human cytochrome P450 1A2: Structure-activity relationships and simulation of rate constants of individual steps in catalysis. Biochemistry 40 (14), 4521–4530. 10.1021/bi002906n. [DOI] [PubMed] [Google Scholar]
- Yun C. H.; Miller G. P.; Guengerich F. P. (2000) Rate-determining steps in phenacetin oxidations by human cytochrome P450 1A2 and selected mutants. Biochemistry 39 (37), 11319–11329. 10.1021/bi000869u. [DOI] [PubMed] [Google Scholar]
- Regal K. A.; Nelson S. D. (2000) Orientation of caffeine within the active site of human cytochrome P450 1A2 based on NMR longitudinal (T-1) relaxation measurements. Arch. Biochem. Biophys. 384 (1), 47–58. 10.1006/abbi.2000.2073. [DOI] [PubMed] [Google Scholar]
- Nehlig A. (2018) Interindividual Differences in Caffeine Metabolism and Factors Driving Caffeine Consumption. Pharmacol. Rev. 70 (2), 384–411. 10.1124/pr.117.014407. [DOI] [PubMed] [Google Scholar]
- Martinez-Lopez S.; Sarria B.; Baeza G.; Mateos R.; Bravo-Clemente L. (2014) Pharmacokinetics of caffeine and its metabolites in plasma and urine after consuming a soluble green/roasted coffee blend by healthy subjects. Food Res. Int. 64, 125–133. 10.1016/j.foodres.2014.05.043. [DOI] [PubMed] [Google Scholar]
- Arnaud M. J.Metabolism of Caffeine and Other Components of Coffee; Raven Press, Ltd.: New York, 1993. [Google Scholar]
- Kot M.; Daniel W. A. (2008) Caffeine as a marker substrate for testing cytochrome P450 activity in human and rat. Pharmacological Reports 60 (6), 789–797. [PubMed] [Google Scholar]
- Sotokawa H.; Shimizu T.; Furuya H.; Sadeque A. J. M.; Hatano M.; Ohba Y.; Iwaizumi M.; Fujiikuriyama Y. (1990) Electron-spin resonance studies of wild-type and mutant cytochromes-p-450d - Effects of mutations at proximal, aromatic and distal sites on g-values. Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol. 1037 (1), 122–128. 10.1016/0167-4838(90)90110-2. [DOI] [PubMed] [Google Scholar]
- Tamburini P. P.; White R. E.; Schenkman J. B. (1985) Chemical characterization of protein-protein interactions between cytochrome-p-450 and cytochrome-b5. J. Biol. Chem. 260 (7), 4007–4015. [PubMed] [Google Scholar]
- Rydberg P.; Vasanthanathan P.; Oostenbrink C.; Olsen L. (2009) Fast Prediction of Cytochrome P450 Mediated Drug Metabolism. ChemMedChem 4 (12), 2070–2079. 10.1002/cmdc.200900363. [DOI] [PubMed] [Google Scholar]
- Sliwoski G.; Kothiwale S.; Meiler J.; Lowe E. W. (2014) Computational Methods in Drug Discovery. Pharmacol. Rev. 66 (1), 334–395. 10.1124/pr.112.007336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaput L.; Mouawad L. (2017) Efficient conformational sampling and weak scoring in docking programs? Strategy of the wisdom of crowds. J. Cheminf. 9, 37. 10.1186/s13321-017-0227-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostermeir K.; Zacharias M. (2017) Accelerated flexible protein-ligand docking using Hamiltonian replica exchange with a repulsive biasing potential. PLoS One 12 (2), e0172072. 10.1371/journal.pone.0172072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Ruiter A.; Oostenbrink C. (2013) Protein-Ligand Binding from Distancefield Distances and Hamiltonian Replica Exchange Simulations. J. Chem. Theory Comput. 9 (2), 883–892. 10.1021/ct300967a. [DOI] [PubMed] [Google Scholar]
- Wang K.; Chodera J. D.; Yang Y. Z.; Shirts M. R. (2013) Identifying ligand binding sites and poses using GPU-accelerated Hamiltonian replica exchange molecular dynamics. J. Comput.-Aided Mol. Des. 27 (12), 989–1007. 10.1007/s10822-013-9689-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastug T.; Chen P. C.; Patra S. M.; Kuyucak S. (2008) Potential of mean force calculations of ligand binding to ion channels from Jarzynski’s equality and umbrella sampling. J. Chem. Phys. 128 (15), 155104. 10.1063/1.2904461. [DOI] [PubMed] [Google Scholar]
- Nagy G.; Oostenbrink C.; Hritz J. (2017) Exploring the binding pathways of the 14–3-3zeta protein: Structural and free-energy profiles revealed by Hamiltonian replica exchange molecular dynamics with distancefield distance restraints. PLoS One 12 (7), e0180633 10.1371/journal.pone.0180633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okumura H.; Gallicchio E.; Levy R. M. (2009) Conformational Populations of Ligand-Sized Molecules by Replica Exchange Molecular Dynamics and Temperature Reweighting. J. Comput. Chem. 31 (7), 1357–1367. 10.1002/jcc.21419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaus J. W.; McCammon J. A. (2015) Enhanced Ligand Sampling for Relative Protein-Ligand Binding Free Energy Calculations. J. Phys. Chem. B 119 (20), 6190–6197. 10.1021/acs.jpcb.5b02348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E.; Lapelosa M.; Levy R. M. (2010) Binding Energy Distribution Analysis Method (BEDAM) for Estimation of Protein Ligand Binding Affinities. J. Chem. Theory Comput. 6 (9), 2961–2977. 10.1021/ct1002913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capoferri L.; Leth R.; ter Haar E.; Mohanty A. K.; Grootenhuis P. D. J.; Vottero E.; Commandeur J. N. M.; Vermeulen N. P. E.; Jorgensen F. S.; Olsen L.; Geerke D. P. (2016) Insights into regioselective metabolism of mefenamic acid by Cytochrome P450 BM3 mutants through crystallography, docking, molecular dynamics, and free energy calculations. Proteins: Struct., Funct., Genet. 84 (3), 383–396. 10.1002/prot.24985. [DOI] [PubMed] [Google Scholar]
- Mobley D. L.; Klimovich P. V. (2012) Perspective: Alchemical free energy calculations for drug discovery. J. Chem. Phys. 137 (23), 230901. 10.1063/1.4769292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobley D. L.; Dill K. A. (2009) Binding of Small-Molecule Ligands to Proteins: ″What You See″ Is Not Always ″What You Get″. Structure 17 (4), 489–498. 10.1016/j.str.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gill S. C.; Lim N. M.; Grinaway P. B.; Rustenburg A. S.; Fass J.; Ross G. A.; Chodera J. D.; Mobley D. L. (2018) Binding Modes of Ligands Using Enhanced Sampling (BLUES): Rapid Decorrelation of Ligand Binding Modes via Nonequilibrium Candidate Monte Carlo. J. Phys. Chem. B 122 (21), 5579–5598. 10.1021/acs.jpcb.7b11820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilmeier J. P.; Crooks G. E.; Minh D. D. L.; Chodera J. D. (2011) Nonequilibrium candidate Monte Carlo is an efficient tool for equilibrium simulation (vol 108, pg E1009, 2011). Proc. Natl. Acad. Sci. U. S. A. 108 (45), E1009. 10.1073/pnas.1106094108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J. Y.; Deng Y. Q.; Roux B. (2006) Absolute binding free energy calculations using molecular dynamics simulations with restraining potentials. Biophys. J. 91 (8), 2798–2814. 10.1529/biophysj.106.084301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastings W. K. (1970) Monte-Carlo Sampling Methods Using Markov Chains And Their Applications. Biometrika 57 (1), 97. 10.1093/biomet/57.1.97. [DOI] [Google Scholar]
- Sivak D. A.; Chodera J. D.; Crooks G. E. (2013) Using Nonequilibrium Fluctuation Theorems to Understand and Correct Errors in Equilibrium and Nonequilibrium Simulations of Discrete Langevin Dynamics. Phys. Rev. X 3 (1), 011007. 10.1103/PhysRevX.3.011007. [DOI] [Google Scholar]
- Horowitz A. M. (1991) A generalized guided Monte-Carlo algorithm. Phys. Lett. B 268 (2), 247–252. 10.1016/0370-2693(91)90812-5. [DOI] [Google Scholar]
- Sansen S.; Yano J. K.; Reynald R. L.; Schoch G. A.; Griffin K. J.; Stout C. D.; Johnson E. F. (2007) Adaptations for the oxidation of polycyclic aromatic hydrocarbons exhibited by the structure of human P450 1A2. J. Biol. Chem. 282 (19), 14348–14355. 10.1074/jbc.M611692200. [DOI] [PubMed] [Google Scholar]
- Trott O.; Olson A. J. (2010) Software News and Update AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 31 (2), 455–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case D. A., Cerutti D. S., Cheatham T. E., Darden I. T.A., Duke R. E., T.J. Giese H. G., Goetz A.W., Greene D., Homeyer N., Izadi S., Kovalenko A., Lee T.S., LeGrand S., Li P., Lin C., Liu J., Luchko T., Luo R., Mermelstein D., Merz K.M., Monard G., Nguyen H., Omelyan I., Onufriev A., Pan F., Qi R., Roe D. R., Roitberg A., Sagui C., Simmerling C. L., Botello-Smith W. M., Swails J., Walker R. C., Wang J., Wolf R. M., Wu X., Xiao L., York D. M., and Kollman P.A.. AMBER 2017; University of California: San Francisco, 2017.
- Case D. A.; Cheatham T. E.; Darden T.; Gohlke H.; Luo R.; Merz K. M.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. (2005) The Amber biomolecular simulation programs. J. Comput. Chem. 26 (16), 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornak V.; Abel R.; Okur A.; Strockbine B.; Roitberg A.; Simmerling C. (2006) Comparison of multiple amber force fields and development of improved protein backbone parameters. Proteins: Struct., Funct., Genet. 65 (3), 712–725. 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahrokh K.; Orendt A.; Yost G. S.; Cheatham T. E. (2012) Quantum Mechanically Derived AMBER-Compatible Heme Parameters for Various States of the Cytochrome P450 Catalytic Cycle. J. Comput. Chem. 33 (2), 119–133. 10.1002/jcc.21922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris G. M.; Huey R.; Lindstrom W.; Sanner M. F.; Belew R. K.; Goodsell D. S.; Olson A. J. (2009) AutoDock4 and AutoDockTools4: Automated Docking with Selective Receptor Flexibility. J. Comput. Chem. 30 (16), 2785–2791. 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J. M.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. (2004) Development and testing of a general amber force field. J. Comput. Chem. 25 (9), 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Jakalian A.; Jack D. B.; Bayly C. I. (2002) Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 23 (16), 1623–1641. 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. (1983) Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79 (2), 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Eastman P.; Friedrichs M. S.; Chodera J. D.; Radmer R. J.; Bruns C. M.; Ku J. P.; Beauchamp K. A.; Lane T. J.; Wang L. P.; Shukla D.; Tye T.; Houston M.; Stich T.; Klein C.; Shirts M. R.; Pande V. S. (2013) OpenMM 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation. J. Chem. Theory Comput. 9 (1), 461–469. 10.1021/ct300857j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopkins C. W.; Le Grand S.; Walker R. C.; Roitberg A. E. (2015) Long-Time-Step Molecular Dynamics through Hydrogen Mass Repartitioning. J. Chem. Theory Comput. 11 (4), 1864–1874. 10.1021/ct5010406. [DOI] [PubMed] [Google Scholar]
- Darden T.; York D.; Pedersen L. (1993) Particle Mesh Ewald - An N.log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 98 (12), 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Scherer M. K.; Trendelkamp-Schroer B.; Paul F.; Perez-Hernandez G.; Hoffmann M.; Plattner N.; Wehmeyer C.; Prinz J. H.; Noe F. (2015) PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 11 (11), 5525–5542. 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
- Perez-Hernandez G.; Paul F.; Giorgino T.; De Fabritiis G.; Noe F. (2013) Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 139 (1), 015102. 10.1063/1.4811489. [DOI] [PubMed] [Google Scholar]
- Roblitz S.; Weber M. (2013) Fuzzy spectral clustering by PCCA plus: application to Markov state models and data classification. Advances in Data Analysis and Classification 7 (2), 147–179. 10.1007/s11634-013-0134-6. [DOI] [Google Scholar]
- Noe F.; Wu H.; Prinz J. H.; Plattner N. (2013) Projected and hidden Markov models for calculating kinetics and metastable states of complex molecules. J. Chem. Phys. 139 (18), 184114. 10.1063/1.4828816. [DOI] [PubMed] [Google Scholar]
- Chodera J., Rizzi A., Naden L., Beauchamp K., Grinaway P., Fass J., Rustenburg B., Ross G. A., Macdonald H. B., Swenson D. W. H., and Simmonett A.. OpenMMTools 0.13.0, 2017, 10.5281/ZENODO.844926 with https://github.com/choderalab/openmmtools/tree/master/openmmtools. [DOI]
- Leimkuhler B.; Matthews C. (2013) Robust and efficient configurational molecular sampling via Langevin dynamics. J. Chem. Phys. 138 (17), 174102. 10.1063/1.4802990. [DOI] [PubMed] [Google Scholar]
- Bren U.; Fuchs J. E.; Oostenbrink C. (2014) Cooperative Binding of Aflatoxin B-1 by Cytochrome P450 3A4: A Computational Study. Chem. Res. Toxicol. 27 (12), 2136–2147. 10.1021/tx5004062. [DOI] [PubMed] [Google Scholar]
- Chemical Computing Group ULC Molecular Operating Environment (MOE), 2013.08; 1010 Sherbooke St. West, Suite #910, Montreal, QC, Canada, H3A 2R7, 2017. [Google Scholar]
- Vankayala S. L.; Kearns F. L.; Baker B. J.; Larkin J. D.; Woodcock H. L. (2017) Elucidating a chemical defense mechanism of Antarctic sponges: A computational study. J. Mol. Graphics Modell. 71, 104–115. 10.1016/j.jmgm.2016.11.004. [DOI] [PubMed] [Google Scholar]
- Sohl C. D.; Isin E. M.; Eoff R. L.; Marsch G. A.; Stec D. F.; Guengerich F. P. (2008) Cooperativity in oxidation reactions catalyzed by cytochrome P450 1A2 - Highly cooperative pyrene hydroxylation and multiphasic kinetics of ligand binding. J. Biol. Chem. 283 (11), 7293–7308. 10.1074/jbc.M709783200. [DOI] [PubMed] [Google Scholar]
- Isin E. M.; Guengerich F. P. (2008) Substrate binding to cytochromes P450. Anal. Bioanal. Chem. 392 (6), 1019–1030. 10.1007/s00216-008-2244-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrillo J. A.; Benitez J. (2000) Clinically significant pharmacokinetic interactions between dietary caffeine and medications. Clin. Pharmacokinet. 39 (2), 127–153. 10.2165/00003088-200039020-00004. [DOI] [PubMed] [Google Scholar]
- Cameron M. D.; Wen B.; Roberts A. G.; Atkins W. M.; Campbell A. P.; Nelson S. D. (2007) Cooperative binding of acetaminophen and caffeine within the P450 3A4 active site. Chem. Res. Toxicol. 20 (10), 1434–1441. 10.1021/tx7000702. [DOI] [PubMed] [Google Scholar]
- Ekroos M.; Sjogren T. (2006) Structural basis for ligand promiscuity in cytochrome P450 3A4. Proc. Natl. Acad. Sci. U. S. A. 103 (37), 13682–13687. 10.1073/pnas.0603236103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bren U.; Oostenbrink C. (2012) Cytochrome P450 3A4 Inhibition by Ketoconazole: Tackling the Problem of Ligand Cooperativity Using Molecular Dynamics Simulations and Free-Energy Calculations. J. Chem. Inf. Model. 52 (6), 1573–1582. 10.1021/ci300118x. [DOI] [PubMed] [Google Scholar]
- Ueng Y. F.; Kuwabara T.; Chun Y. J.; Guengerich F. P. (1997) Cooperativity in oxidations catalyzed by cytochrome P450 3A4. Biochemistry 36 (2), 370–381. 10.1021/bi962359z. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.