First clinical retrospective investigation of limited projection CBCT for lung tumor localization in patients receiving SBRT treatment

Abstract

To clinically investigate the limited-projection CBCT (LP-CBCT) technology for daily positioning of patients receiving breath-hold lung SBRT radiation treatment and to investigate the feasibility of reconstructing fast 4D-CBCT from 1 min 3D-CBCT scan.

Eleven patients who underwent breath-hold lung SBRT radiation treatment were scanned daily with on-board full-projection CBCT (CBCT) using half-fan scan. A subset of the CBCT projections and the prior planning CT were used to estimate the LP-CBCT images using the weighted free-form deformation method. The limited projections are clusteringly sampled within fifteen sub-angles in 360° in order to simulate the fast 1 min scan for 4D-CBCT. The estimated LP-CBCTs were rigidly registered to the planning CT to determine the clinical shifts needed for patient setup corrections, which were compared with shifts determined by the CBCT for evaluation. Both manual and automatic registrations were performed in order to compare the systematic registration errors. Fifty CBCT volumes were obtained from the eleven patients in fifty fractions for this pilot clinical study.

For the CBCT images, the mean (±standard deviation) shifts between CBCT and planning CT from manual registration in left–right (LR), anterior–posterior (AP), and superior–inferior (SI) directions are 1.1 ± 1.2 mm, 2.1 ± 1.9 mm, 5.2 ± 3.6 mm, respectively. The mean deviation difference between shifts determined by CBCT and LP-CBCT images are 0.3 ± 0.5 mm, 0.5 ± 0.8 mm, 0.4 ± 0.3 mm, in LR, AP, and SI directions, respectively. The mean vector length of CBCT shift for all fractions is 6.1 ± 3.6 mm, and the mean vector length difference between CBCT and LP-CBCT for all fractions studied is 1.0 ± 0.9 mm. The automatic registrations yield similar results as manual registrations.

The pilot clinical study shows that LP-CBCT localization offers comparable accuracy to CBCT localization for daily tumor positioning while reducing the projection number to 1/10 for patients receiving breath hold lung radiation treatment. The cluster projection sampling in this study also shows the feasibility of reconstructing fast 4D-CBCT from 1 min 3D-CBCT scan.

1. Introduction

Four-dimensional cone-beam CT (4D-CBCT) is essential for many clinical tasks in radiotherapy, such as image guidance, marker-less tumor tracking, volume assessment of moving targets, and 4D dose reconstruction. It has also been demonstrated that 4D-CBCT can reduce setup errors when compared with normal 3D-CBCT (Sweeney et al 2012, Thengumpallil et al 2016, Tan et al 2017). For hypo-fractionated treatment regimens, such as stereotactic body radiation therapy (SBRT), accurate target localization using 4D-CBCT is especially critical, due to its high fractional dose and tight PTV margin (Shah et al 2013). However, long scan time, poor image quality, and high imaging dose remain a challenge for widespread clinical use of 4D-CBCT (Santoso et al 2016, Nakamura et al 2018). Additionally, dedicated 4D protocols typically have poorer 3D image quality due to reduced tube current (Thengumpallil et al 2016).

Previously, we developed a structural motion modeling (SMM) and weighted free form deformation (WFD) method to estimate on-board CBCT using projections acquired in limited angles (Harris et al 2017, Zhang et al 2018). Principle component based SMM is used to model the patient respiratory motion and WFD is used to correct the patient anatomical and breathing pattern changes from CT simulation to treatment. From our previous simulation study, we found that SMM-WFD method was able to estimate the limited angle CBCT accurately using ~50 projections with orthogonal 15° view for full fan scan. However, such acquisition scheme requires slow gantry rotation and does not acquire images while rotating to the orthogonal angle, which is not clinically optimized. To make it more feasible and effective, the patient study in this work focused on evaluating limited projection CBCT (LP-CBCT) accuracy estimated from a subset of projections acquired from 60 s fast gantry rotation acquisitions with full 360° rotation angle.

One challenge with the patient study is to obtain the ground truth images for evaluating the accuracy of the method. Onboard 4D-CBCT estimated from fully sampled 4D cone-beam projections can be potentially used as the ground truth. However, typical clinical 4D-CBCT scans have limited projections for each respiratory phase, and its image quality is far from enough to be used as the ground truth for the evaluation. In addition, to simulate a set of free breathing 60 s scan with fast gantry rotation, it has very strict requirement for the original 4D-CBCT scanning in order to select the projections at right angle and right phase (Sonke et al 2005). Alternatively, this study used the breath hold patient data to evaluate the accuracy of the limited projection technique. During the breath-hold scan, patient has minimal respiratory motion and the patient images can be considered as one static phase of 4D-CBCT. As a result, all projections (around 900 projections) acquired in the breath hold scan can be used to reconstruct the ground truth images for evaluation of the technique. It uses the weighted free-form deformation to estimate the LP-CBCT images from planning CT and under sampled projections. The under sampled projections (around 90 projections per phase) were selected clusteringly as the patient is free breathing during CBCT scan. This is the first study to use task oriented matrix, i.e. the patient shifts determined from the CT-CBCT registration, to evaluate the clinical efficacy of the technique. These shifts are used to correct the setup differences between treatment and planning positions, to make sure the patient position during the treatment is as same as the position defined in the treatment plan system.

2. Methods and materials

2.1. Weighted free form deformation technique

This study uses the patient planning CT images as prior knowledge (CT_prior), and considers the on-board volumetric images (CBCT) to be estimated as a deformation of the prior images based on a deformation field map D:

$$\text{CBCT}(i,j,k)=C{T}_{prior}(i+D_x(i,j,k),j+D_y(i,j,k),k+D_z(i,j,k))$$ (1)

where D_x, D_y, and D_z represent the deformation fields along the three canonical directions (i, j, k) of the Cartesian coordinate system. It converts the CBCT estimation problem to a problem of solving the deformation field map D. The data fidelity constraint requires digitally reconstructed radiographs (DRRs) generate by prior CT match to on-board projections. On-board projections were acquired with default CBCT thorax technique (125 kVp, 20 mA, half-fan mode). The half-fan mode was achieved by shifting the detector 16 cm laterally, and the full projections were acquired using a gantry rotation speed of 6 ° s⁻¹, with frame rate of 15 fps in 360° scan angle. The data fidelity constraint requires the simulated cone beam projections of the estimated CBCT to match with the actual projection data acquired. For real clinical images, it may not be satisfied due to errors between DRRs and on-board kV projections. Normalized cross correlation (NCC) is used to account the gray level difference between DRRs and on-board kV projections (Zhang et al 2015):

$$\text{NCC}(\text{DRR},\text{onboard kV projection})=1-\epsilon .$$ (2)

ε here accounts for the fact that DRRs cannot be exactly matched to on-board projections. Many factors could contribute to this, including impaction of deformation fields, the existence of data inconsistencies such as imaging artifacts and noise, spectral and other hardware differences between prior and on-board images. It was empirically set to 0.05 and is same for all the datasets in this study.

The weighted free-form deformation model has been employed to regulate the variables in D. The weighting was added within a region of interest (ROI) around the tumor in the on board projections:

$$\text{NCC}=(1-w)*{\text{NCC}}_{global}+w*{\text{NCC}}_{ROI}.$$ (3)

Where NCC_global is the normalized cross correlation calculated using the entire image, NCC_ROI is the normalized cross correlation calculated using ROI, w is the weighting factor. It gives more flexibility in adjusting the importance of matching to different regions in the projection data in the data fidelity constraint based on the clinical interests. The weighting factor was empirically set to 0.05 and is same for all the datasets in this study as well. Details about solving D based on the data fidelity and energy constraints using the WFD model can be found in Harris et al (2017) and Zhang et al (2017). After the deformation field map D is solved, the on-board volume is obtained by deforming the prior volumes based on the D according to equation (1).

2.2. Design and procedure

The primary objective of this study is to compare the clinical use of LP-CBCT versus state-of-art CBCT for target location. Figure 1 shows the work flow of this study. Patient planning CT, CBCT, and kilovoltage (kV) projections used to reconstruct the CBCT were extracted from the breath hold lung patient SBRT treatment. A subset of the CBCT projections and the planning CT were used to estimate the LP-CBCT images. Shifts between on-board volume and planning CT determined by CBCT and LP-CBCT were recorded, and the deviations between these shifts were analyzed at the end to compare the difference.

Figure 1.

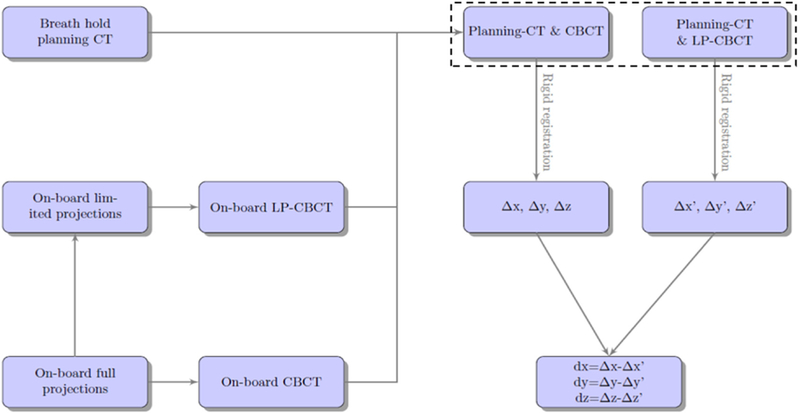
Work flow for the clinical evaluation of the weighted free-form deformation LP-CBCT technique.

The limited projections were selected to simulate a 1 min CBCT scan with patient under free breathing, as shown in figure 2. The purpose of this selection is to demonstrate the feasibility of using this fast scan to reconstruct 4D-CBCT for patient positioning guidance.

Figure 2.

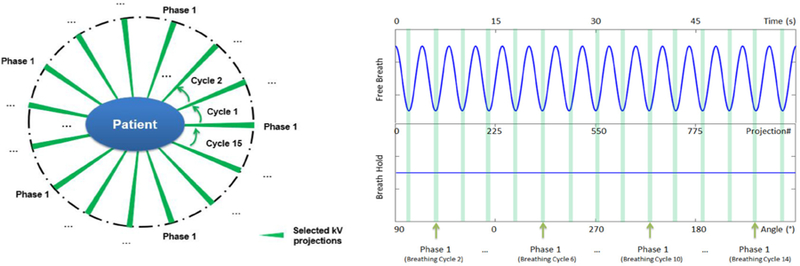
Diagram for selection of limited projections for LP-CBCT reconstruction. The breath hold projections were clustering sampled to simulate a free breath patient. The projections falls into the light green region were selected to reconstruct one phase of 4D-CBCT. The patient breath period was 4 s and gantry rotation speed was 6 ° s⁻¹. Totally 15 breath periods were included in a 1 min scan with 10 phases each period. The green cluster stands for the projection selecting for phase 1. Each cluster has 6 projections.

2.3. Patient data

Eleven patients with lung cancer were retrospectively enrolled in this study, under a protocol (Pro00058148) approved by the institutional review board at Duke University. Each patient has one planning CT set and multiple daily CBCT set. The planning CT were acquired with the default CT thorax scan technique (120 kVp, auto mA) and the CBCT were acquired with the default CBCT thorax scan technique (120 kVp, 20 mA). Before the CBCT scan, the couch was centered to prevent collision during gantry rotation. To increase the field of view, a half-fan mode was used for the CBCT scan with the detector shifted laterally by 16 cm. For each full-projection scan, the projections were acquired using a gantry rotation speed of 6 ° s⁻¹, with frame rate of 15 fps. Totally ~900 projections were acquired in 360° scan angle for daily CBCT reconstruction. Each on-board projection contains 1024 × 768 pixels, with each pixel measuring 0.388 × 0.388 mm². In total, there are 50 daily CBCT projection sets from the 11 patients. In order to be consistent with the clinical CBCT volume and resolution, all CT and CBCT image data were set to have a volume of 512 × 512 × 88 voxels with voxel size of 0.9 × 0.9 × 2.0 mm³.

2.4. CBCT and LP-CBCT reconstruction

On-board CBCT images were reconstructed using the clinical ‘gold standard’ Feldkamp–Davis–Kress (FDK) algorithm (Feldkamp et al 1984) by Varian clinical software (Varian Medical Systems, Palo Alto, CA) embedded in our treatment consoles. Pre and post processing steps were conducted by this clinical software to remove the CBCT artifacts (beam hardening, scattering etc). A subset of each CBCT scan was created to include approximately 90 projections each over 360° scan angle as shown in figure 2. The patient breath period was 4 s and gantry rotation speed was 6 ° s⁻¹. Totally 15 breath periods were included in a 1 min scan with 10 phases each period. These subsets of scans were used to reconstruct LP-CBCT images for each phase, using the weighted free form deformation method as introduced in section 2.1.

2.5. Projection number study for LP-CBCT reconstruction

The projection number/frame rate was further reduced to investigate the projection number dependent of WFD technique, as shown in table 1.

Table 1.

Projection numbers used in estimating LP-CBCT for a 10-phase binned patient. The frame rates were rounded to integers.

Frame rate (/s)	15	13	10	8	5	3
Proj#	900	750	600	450	300	150
Proj#/phase	90	75	60	45	30	15
Proj#/phase/cycle	6	5	4	3	2	1

2.6. 3D image registration

CBCT and LP-CBCT were registered to planning CT separately. Shift-only rigid registration was performed for tumor localization in Eclipse (Varian Medical Systems, Palo Alto, CA) using manual and automatic matches independently. Specifically, for manual match, the registration was performed manually to align the tumor. For auto match, a coarse registration was performed based on the whole 3D image volume, a second registration encompassing the tumor was further performed automatically to fine tune the results. Both registrations were performed by one clinician and checked by the second clinician independently.

2.7. Statistical analysis for registration accuracy and evaluation metrics

The CBCT detected shifts were considered as the ‘gold standard’. Registration differences were calculated for each pair of CBCT and LP-CBCT registration results. A localization error metric was defined to quantitatively compare the registered tumor shifts of each LP-CBCT to the ‘standard’ localization results. For each method, each data point consists of three position corrections, i.e. along the x (left–right), y (anterior–posterior), z (inferior–superior) axis respectively. The means set-up error in each direction over the course of treatment is:

$$\overline{dx}=\frac{\sum \left|{(\mathrm{\Delta }{x}_{FP}-\mathrm{\Delta }{x}_{LP})}_{ij}\right|}{n}$$ (4)

$$\overline{dy}=\frac{\sum \left|{(\mathrm{\Delta }{y}_{FP}-\mathrm{\Delta }{y}_{LP})}_{ij}\right|}{n}$$ (5)

$$\overline{dz}=\frac{\sum \left|{(\mathrm{\Delta }{z}_{FP}-\mathrm{\Delta }{z}_{LP})}_{ij}\right|}{n}$$ (6)

where i stands for the patient number, j stands for the treatment fraction for each patient, and n stands for the total treatment fractions over all patients. The vector correction (center of mass shift) for each fraction is:

$$\text{COMS}=\sqrt{{(\mathrm{\Delta }{x}_{FP}-\mathrm{\Delta }{x}_{LP})}^2+{(\mathrm{\Delta }{y}_{FP}-\mathrm{\Delta }{y}_{LP})}^2+{(\mathrm{\Delta }{z}_{FP}-\mathrm{\Delta }{z}_{LP})}^2}.$$ (7)

And the mean overall vector correction is:

$$\overline{\text{COMS}}=\frac{{\sum \text{COMS}}_{ij}}{n}.$$ (8)

The consistence of the position correction is described by the standard deviation of each correction data.

3. Results

3.1. Image quality comparisons between LP-CBCT and CBCT

Figure 3 shows the slice cuts from the prior CT image, the LP-CBCT image reconstructed by FDK, the LP-CBCT image estimated by WFD technique, and the reference CBCT image reconstructed by FDK, respectively. The LP-CBCT is reconstructed using 90 half fan projections by WFD technique and the reference CBCT is reconstructed using full sampled 900 half fan projections by FDK.

Figure 3.

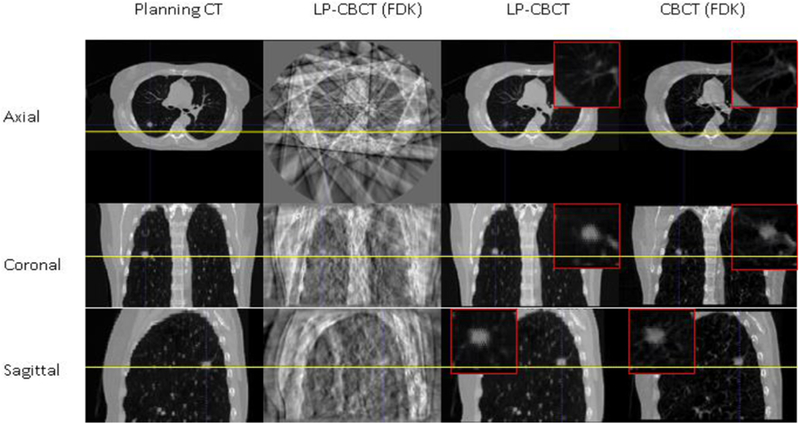
Slice cuts from the prior CT image, the LP-CBCT image reconstructed by FDK, the LP-CBCT image estimated by WFD technique, and the reference CBCT image reconstructed by FDK. The LP-CBCT is estimated/reconstructed using 90 half fan projections and the reference CBCT is reconstructed using full sampled 900 half fan projections. Zoom in figures for LP-CBCT and CBCT are placed on the corners of images.

3.2. Positioning differences between LP-CBCT and CBCT

For the CBCT images, the mean (±standard deviation) shifts between CBCT and planning CT from manual registration in left–right (LR), anterior–posterior (AP), and superior–inferior (SI) directions are 1.1 ± 1.2 mm, 2.1 ± 1.9 mm, 5.2 ± 3.6 mm, respectively. The corresponding maximum shifts are 4.1 mm, 5.1 mm and 13.4 mm. Note that the maximum shifts for LR, AP and SI are from different fractions. For the LP-CBCT images, the mean (±standard deviation) shifts between LP-CBCT and planning CT from manual registration in LR, AP, and SI directions are 1.1 ± 1.3 mm, 1.6 ± 1.3 mm, 5.1 ± 3.5 mm, respectively. The corresponding maximum shifts are 4.6 mm, 5.0 mm, 12.8 mm. The mean deviation difference between shifts determined by CBCT and LP-CBCT images are 0.3 ± 0.5 mm, 0.5 ± 0.8 mm, 0.4 ± 0.3 mm, in LR, AP, and SI directions, respectively. The corresponding maximum deviations are 2.0 mm, 1.9 mm, 1.0 mm. The mean vector length of CBCT shift for all fractions is 6.1 ± 3.6 mm, and the corresponding value for LP-CBCT is 5.7 ± 3.6 mm. The mean vector length set up error between CBCT and LP-CBCT for all fractions studied is 1.0 ± 0.9 mm. The max vector length set up error between CBCT and LP-CBCT among all fractions studied is 2.5 mm. The automatic registrations yield similar results as manual registrations.

3.3. Projection number dependence of LP-CBCT

Figure 4 shows the image quality and accuracy comparison among planning CT, LP-CBCT reconstructed from 90, 60, 30 projections, respectively, and CBCT reconstructed by FDK. The baseline of the lesion is shown with yellow lines. Table 3 shows the positioning differences between different LP-CBCTs estimated from different projection numbers.

Figure 4.

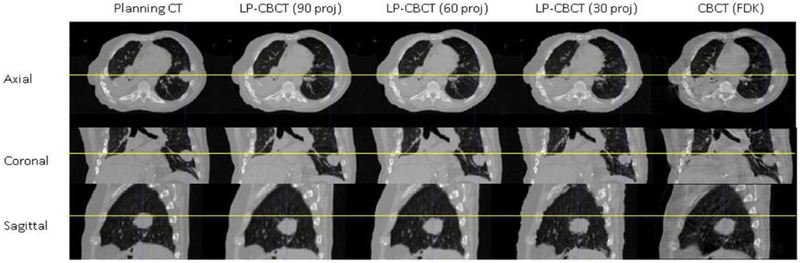
Slice cuts from the prior CT image, the LP-CBCT image estimated by WFD technique with 90, 60, 30 half fan projections, respectively, and the reference CBCT image reconstructed by FDK. The reference CBCT is reconstructed using full sampled 900 half fan projections.

Table 3.

Registered shifts (in millimeters) using LP-CBCTs estimated from different projections (registered to planning CT).

	Proj#	90	78	60	48	30	18	FDK (900)
Manual Registration	∆x (mm)	−0.8	−0.8	−0.6	−0.7	−0.7	−1.0	−0.7
	∆y (mm)	−1.0	−0.8	−0.9	−1.4	−1.3	−0.7	−1.6
	∆z (mm)	11.8	11.6	11.2	11.2	10.8	10.9	11.5
	Vector (mm)	11.9	11.7	11.3	11.3	10.9	11.0	11.6
Automatic Registration	∆x (mm)	−1.2	−1.6	−1.4	−1.3	−1.6	−1.6	−1.3
	∆y (mm)	−1.2	−1.2	−1.2	−1.6	−1.2	−1.6	−1.5
	∆z (mm)	12.9	12.9	12.3	12.0	12.0	11.3	12.5
	Vector (mm)	13.0	13.1	12.4	12.2	12.2	11.5	12.7

4. Discussions

4.1. Image quality of LP-CBCT

As shown in figure 3, the quality of LP-CBCT images estimated from WFD technique is comparable to the planning CT and full sampled FDK reconstructed CBCT images. In contrast, the LP-CBCT images reconstructed from FDK has a lot of artifacts using 90 half fan projections and it is hard to visualize the tumor.

4.2. Positioning differences between LP-CBCT and CBCT

Results in table 2 showed that the mean positioning differences between CBCT and LP-CBCT from manual registration for all fractions studied in this work are 0.3 ± 0.5 mm, 0.5 ± 0.8 mm, 0.4 ± 0.3 mm, in LR,AP, and SI directions, respectively. The mean vector positioning difference between CBCT and LP-CBCT are 1.0 ± 0.9 mm. For patient receiving lung irradiation, LP-CBCT localization offers comparable accuracy to CBCT for daily patient positioning while reducing the projection numbers. On the other hand, LP-CBCT localization has the potential to do 4D-verification while using all the projections from 1 min scan. This allows us to significantly reduce the imaging dose and time to achieve ultra-fast 4D-CBCT imaging for intra-fraction verification to improve the treatment accuracy, which is especially critical for SBRT treatments.

Table 2.

Positioning differences (in millimeters) between CBCT and LP-CBCT for all fractions studied in this work.

		CBCT	LP-CBCT	Difference
Manual Registration	$\overline{dx}\pm std(\text{LR})$	1.1 ± 1.2	1.1 ± 1.3	0.3 ± 0.5
	$\overline{dy}\pm std(\text{AP})$	2.1 ± 1.9	1.6 ± 1.3	0.5 ± 0.8
	$\overline{dx}\pm std(\text{SI})$	5.2 ± 3.6	5.1 ± 3.5	0.4 ± 0.3
	$\overline{coms}\pm std(\text{vector})$	6.1 ± 3.6	5.7 ± 3.6	1.0 ± 0.9
Automatic Registration	$\overline{dx}\pm std(\text{LR})$	1.2 ± 0.9	1.0 ± 1.1	0.2 ± 0.4
	$\overline{dy}\pm std(\text{AP})$	2.0 ± 1.8	1.8 ± 1.2	0.5 ± 0.6
	$\overline{dx}\pm std(\text{SI})$	5.0 ± 3.7	5.0 ± 3.6	0.4 ± 0.4
	$\overline{coms}\pm std(\text{vector})$	5.9 ± 3.7	5.7 ± 3.6	0.7 ± 0.7

4.3. Projection number dependence of LP-CBCT

Results in figure 4 and table 3 showed that the WFD method is robust against reduction of the projection numbers. The positioning differences between different LP-CBCTs estimated from different projection numbers are within 1 mm. The FDK technique had a significant decrease in image quality when the Nyquist frequency requirement does not meet, as shown in figure 3. In contrast, the WFD technique is robust against reduction of projection numbers down to only 18 projections per phase for 4D-LP-CBCT estimation. This brings projection number down significantly in comparison to clinical 4D-CBCT scans (Santoso et al 2016). Note that the LP-CBCT images estimated from 18 projections are noisier than those estimated from 90 projections, as shown in figure 4. But the tumor locations are similar, and it affected the positioning little, as shown in table 3.

4.4. Clinical implementation

The WFD technique is validated via breath hold patient in this study using a subset of projections from simulated projection angles. In clinical practice, the pre-treatment 4D-CT can be used as prior images, the on-board 4D-CBCT can be obtained by deforming the corresponding phases of 4D-CT to 4D-CBCT using the 1 min scan projections. The maximum vector shift difference in this study was 2.5 mm. This maximum error is still acceptable considering the 5–7 mm margin typically used to account for set up errors in SBRT. In addition, the LP-CBCT provides additional values for intrafraction verification. A study conducted by Purdie et al found that the target intra-fraction motion can be as much as 1 cm for lung SBRT (Purdie et al 2007). However, currently fully sampled CBCT cannot be used multiple times for intrafraction verification due to its long scanning time and high imaging dose. In contrast, our study demonstrated that the weight free-form deformation technique is enable to estimate on-board 4D-CBCT images with as less as 18 projections per phase, which reduces the imaging dose dramatically. Using this method, multiple fast 4D-CBCT scans can be taken with comparable imaging dose to regular CBCT and can be used for intra-fraction verification during the patient treatment. As a result, the localization errors can be reduced from as large as 1cm without intrafraction verification to within 2.5 mm with intrafraction verification based on LP-CBCT.

4.5. Limitation of this study

Due to the strict requirement for the original 4D-CBCT scanning in order to select the projections at right angle and right phase, this study used the breath hold patient data to evaluate the accuracy of the limited projection technique. Ideally the fully sampled 4D cone-beam projections need to be used to obtain the ground truth images for evaluating the accuracy of the method. However, typical clinical 4D-CBCT scans have limited projections for each respiratory phase, and they do not meet the requirement for selecting the projections for 1 min scan. One possible solution is using two sets of 4D-CTs. The first set of 4D-CT can be used as the prior images. The second set of 4D-CT can be used as the ground truth, and the projections used for LP-CBCT estimation can be simulated from the second set of 4D-CT (Jia et al 2012). This approach will be investigated in the future study.

5. Conclusion

The pilot clinical study shows that for patients receiving breath hold lung radiation treatment, LP-CBCT localization offers comparable accuracy to CBCT localization for daily patient positioning while reducing the projection number to 1/10. The preliminary results from breath hold patient studies demonstrated the potential of the WFD technique for reconstructing 4D-CBCT from a 1 min 3D-CBCT scan for fast low dose 4D intrafraction verification of lung SBRT.