The Augmentation of Retinogeniculate Communication during Thalamic Burst Mode

Abstract

Retinal signals are transmitted to cortex via neurons in the lateral geniculate nucleus (LGN), where they are processed in burst or tonic response mode. Burst mode occurs when LGN neurons are sufficiently hyperpolarized for T-type Ca²⁺ channels to deinactivate, allowing them to open in response to depolarization, which can trigger a high-frequency sequence of Na⁺-based spikes (i.e., burst). In contrast, T-type channels are inactivated during tonic mode and do not contribute to spiking. Although burst mode is commonly associated with sleep and the disruption of retinogeniculate communication, bursts can also be triggered by visual stimulation, thereby transforming the retinal signals relayed to the cortex. To determine how burst mode affects retinogeniculate communication, we made recordings from monosynaptically connected retinal ganglion cells and LGN neurons in male/female cats during visual stimulation. Our results reveal a robust augmentation of retinal signals within the LGN during burst mode. Specifically, retinal spikes were more effective and often triggered multiple LGN spikes during periods likely to have increased T-type Ca²⁺ channel activity. Consistent with the biophysical properties of T-type Ca²⁺ channels, analysis revealed that effect magnitude was correlated with the duration of the preceding thalamic interspike interval and occurred even in the absence of classically defined bursts. Importantly, the augmentation of geniculate responses to retinal input was not associated with a degradation of visual signals. Together, these results indicate a graded nature of response mode and suggest that, under certain conditions, bursts facilitate the transmission of visual information to the cortex by amplifying retinal signals.

SIGNIFICANCE STATEMENT The thalamus is the gateway for retinal information traveling to the cortex. The lateral geniculate nucleus, like all thalamic nuclei, has two classically defined categories of spikes—tonic and burst—that differ in their underlying cellular mechanisms. Here we compare retinogeniculate communication during burst and tonic response modes. Our results show that retinogeniculate communication is enhanced during burst mode and visually evoked thalamic bursts, thereby augmenting retinal signals transmitted to cortex. Further, our results demonstrate that the influence of burst mode on retinogeniculate communication is graded and can be measured even in the absence of classically defined thalamic bursts.

Introduction

The lateral geniculate nucleus (LGN) of the dorsal thalamus is the primary source of visual signals sent to primary visual cortex, receiving monosynaptic input from retinal ganglion cells (RGCs) and projecting directly to cortical target neurons. Despite being labeled a relay nucleus, the LGN serves to transform retinal signals in several significant and dynamic ways (Dan et al., 1996; Usrey et al., 1998, Martinez et al., 2014; Fisher et al., 2017; Alitto et al., 2019), including changes in the temporal domain that accompany tonic and burst activity modes (for review, see Sherman and Guillery, 2009; Usrey and Alitto, 2015). During tonic mode, LGN neurons respond to excitatory input with regularly spaced action potentials, the rate of which is proportional to the strength of the stimulus (Llinás and Jahnsen, 1982; Huguenard and McCormick, 1992). By contrast, LGN spike trains during burst mode are irregular and include tight clusters of spikes known as “bursts,” and the firing rate becomes uncoupled from stimulus strength. Although geniculate bursts are generally associated with periods of low arousal and sleep, when LGN neurons are thought to be dissociated from the periphery, they can also occur during sensory processing and have been shown to be particularly effective in evoking cortical responses (Reinagel et al, 1999; Swadlow and Gusev, 2001; Weyand et al., 2001; Lesica and Stanley, 2004; Alitto et al., 2005, 2011; Bezdudnaya et al., 2006; Bereshpolova et al., 2011). Determining how burst mode affects retinogeniculate communication is therefore important for understanding the transmission of visual information to the cortex.

Across thalamic nuclei the transition from tonic to burst mode depends on a common mechanism, the deinactivation of T-type Ca²⁺ channels (or T-channels) that occurs when neurons are sufficiently hyperpolarized for a sufficient duration of time (Llinás and Jahnsen, 1982; Huguenard and McCormick, 1992; Wei et al., 2011). When this occurs, depolarizing stimuli can activate T-channels to generate a Ca²⁺ potential (T-potential), which can then trigger a short train of high frequency, Na⁺-based action potentials. It is important to note that the magnitude of the T-potential and subsequently the number of spikes it triggers depend on the percentage of T-channels in the deinactivated versus the inactivated state, which, in turn, depends on the depth and duration of the preceding hyperpolarization (Deschênes et al., 1984; Destexhe and Sejnowski, 2002; Hong et al., 2014).

Here, we explore the influence of thalamic response mode on retinogeniculate communication by performing simultaneous extracellular recordings of monosynaptically connected pairs of RGCs and LGN neurons in the anesthetized cat. Although the occurrence of T-potentials is best determined with intracellular recording methods, past work has shown that bursts can be identified by applying a previously established set of statistical criteria to extracellular records of LGN spike trains (Lu et al., 1992; see Materials and Methods). Using these criteria, we calculated retinal efficacy (the percentage of RGC spikes that triggered LGN cell spikes) and retinal contribution (the percentage of LGN spikes evoked by a simultaneously recorded RGCs) during tonic and burst response modes. Our results reveal a fundamental change in retinogeniculate communication during burst mode and suggest an augmentation of visual signals by T-potentials. We found that individual retinal spikes arriving during epochs supportive of T-channel activity were more effective in evoking LGN responses and often triggered multiple spikes. We also found an increased variability in the temporal relationship between retinal spikes and evoked LGN spikes during thalamic bursts; however, this variability was not associated with a degradation of visual signals within the LGN. Consistent with the biophysical properties of T-channels, the modulation of retinogeniculate communication was proportional to the duration of the preceding interspike interval (ISI) of the LGN neuron and was evident even in the absence of classically defined thalamic bursts. These results reveal how retinal signals are transformed by the transition between tonic and burst modes and, importantly, suggest that the influence of thalamic response mode on retinogeniculate communication is a continuous process.

Materials and Methods

Animal preparation.

Sixteen adult cats of either sex were used for this study. All experimental procedures were conducted with the consent of the Animal Care and Use Committee at the University of California, Davis and followed National Institutes of Health guidelines. Some of the data analyzed in this study contributed to previous unrelated studies on the retinogeniculate pathway (Usrey et al., 1998, 1999; Rathbun et al., 2010, 2016).

Surgical procedures were performed while animals were anesthetized. Surgical anesthesia was induced with ketamine (10 mg/kg, i.m.) and maintained with thiopental sodium (20 mg/kg, i.v., supplemented as needed). A tracheotomy was performed, and animals were placed in a stereotaxic apparatus where they were mechanically ventilated. EEG, EKG, CO₂, and temperature were monitored throughout the experiment. A scalp incision was made, and wound edges were infused with lidocaine. A craniotomy was made over the LGN, the dura was removed, and the craniotomy was filled with agarose to protect the underlying brain. Eyes were adhered to metal posts, fitted with contact lenses, and focused on a tangent screen located 172 cm in front of the animal. Phenylephrine (10%) was administered to retract the nictitating membranes and flurbiprofen sodium drops were administered (1.5 mg/h) to prevent miosis. The positions of area centralis and the optic disk were mapped by back-projecting the retinal vasculature of each eye onto a tangent screen. After the completion of surgical procedures, maintenance anesthesia (thiopental sodium, 2–3 mg/kg/h, i.v.) was administered for the remaining duration of the experiment. Supplemental thiopental was given, and the rate of infusion was increased if physiological monitoring indicated a decrease in the level of anesthesia. Once a steady plane of maintenance anesthesia was established, animals were paralyzed with vecuronium bromide (0.2 mg/kg/h, i.v.). Animals were killed with Euthasol (100 mg/kg; Virbac Animal Health) at the conclusion of each experiment.

Electrophysiological recording and visual stimuli.

Simultaneous extracellular recordings were made from LGN cells in layers A and A1 and RGCs. For thalamic recordings, the LGN was first located using single, parylene-coated tungsten electrodes (AM Systems). After the preferred retinotopic position was located in the LGN, a seven-channel multielectrode array (Thomas Recording) was positioned into the LGN. RGCs were recorded from using a tungsten-coated microelectrode inserted into the eye through an intraocular guide tube and maneuvered via a custom-made manipulator. Neural responses were amplified, filtered, and recorded to a computer equipped with a Power 1401 data acquisition interface and the Spike 2 software package (Cambridge Electronic Design). Spike isolation was based upon waveform analysis (parameters established independently for each cell) and the presence of a refractory period, as indicated in the autocorrelogram (Usrey et al., 2000, 2003; Kiley and Usrey, 2017).

Visual stimuli were generated using a VSG2/5 visual stimulus generator (Cambridge Research Systems) and presented on a gamma-calibrated Sony monitor running at 140 Hz. The mean luminance of the monitor was 38 cd/m². Visual responses of LGN neurons and RGCs were mapped and characterized using drifting sine-wave gratings and white-noise stimuli. The white-noise stimulus consisted of a 16 × 16 grid of black and white squares. Each square was temporally modulated according according to a 2¹⁵-1 length m-sequence (Sutter, 1987; Reid and Shapley, 1992; Reid et al., 1997). Individual squares in the stimulus were updated with each monitor frame for 2¹⁵-1 frames (∼4 min). Approximately 4–16 squares of the stimulus overlapped receptive field center of each neuron. Drifting sine-wave grating stimuli (4 Hz, 100% contrast) were presented at the preferred spatial frequency for the recorded cells.

Identification of LGN bursts and tonic spikes.

We used two well established criteria to identify bursts in the spike trains of LGN neurons (Lu et al., 1992; Swadlow and Gusev, 2001; Weyand et al., 2001; Lesica and Stanley, 2004; Alitto et al., 2005, 2011; Denning and Reinagel, 2005; Bezdudnaya et al., 2006; Bereshpolova et al., 2011). These criteria were as follows: (1) an ISI of >100 ms that preceded the first spike in a sequence; and (2) one or more subsequent spikes that followed with ISIs of <4 ms (Fig. 1A). Past studies applying these criteria to intracellular recordings show that events defined as bursts co-occur with T-channel plateau potentials (Lu et al., 1992). For this study, the first spike in the burst is referred to as the cardinal spike, and each additional spike is referred to by its ordinal position (e.g., secondary, tertiary).

Figure 1.

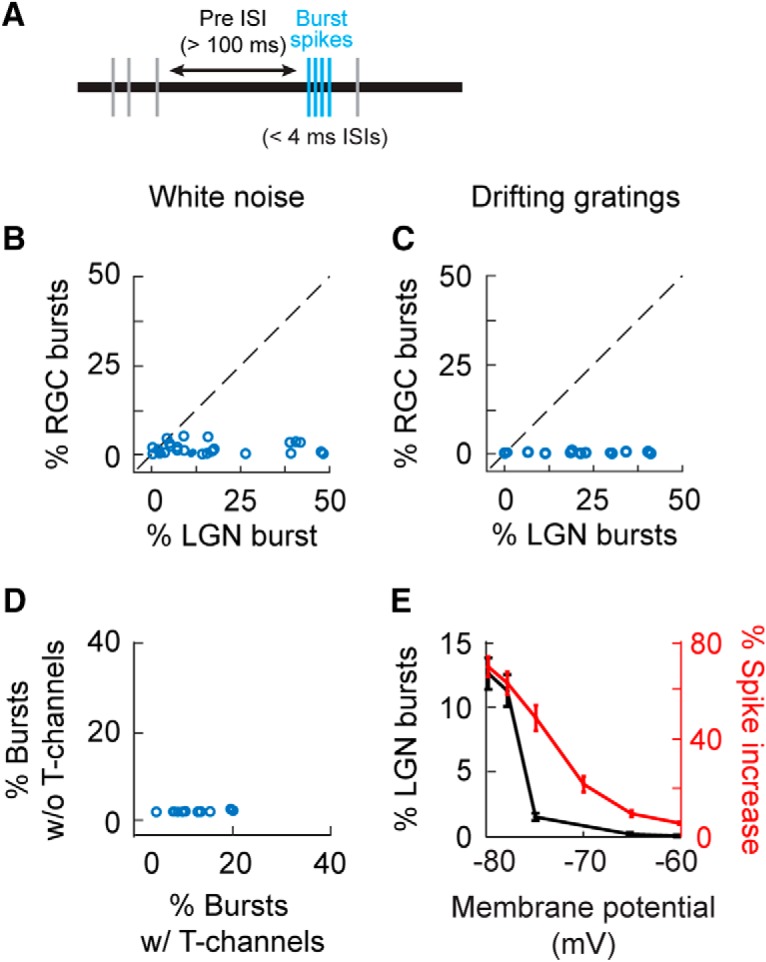
Comparison of burst frequency in the retina and LGN. A, Bursts (blue tick marks) were identified by applying the following criteria to extracellular recordings: (1) the first spike was preceded by an ISI >100 ms (horizontal arrow) and (2) subsequent spikes followed with ISIs of <4 ms. B, C, Scatterplot showing the percentage of RGC and LGN cell spikes that were identified as part of a burst, during white noise (B) and drifting grating (C) stimulation. D, Scatterplot showing the percentage of simulated LGN spikes that were identified as part of a burst when a leaky integrate-and-fire mode either included or did not include T-channels. E, Line graph showing the influence of membrane potential on the percentage of LGN spikes that were identified as part of a burst when the simulation included T-channels (left y-axis, black line) and the increase in simulated LGN spike count due to the addition of T-channels to the model (right y-axis, red line). Error bars indicate SE.

Simulation of T-type Ca⁺² channels.

Given the critical role that T-type Ca⁺² channels play in the generation of thalamic bursts and that the biophysical properties of these channels have been extensively characterized, we simulated the interaction of T-type Ca⁺² channels and synaptic EPSPs. We used a leaky integrate-and-fire model neuron and a series of previously published equations that quantify the voltage and time dependence of both the deinactivation and inactivation of T-Channels (Huguenard and McCormick, 1992). There is at least one other variation of this series of equations (Wang et al., 1991); however, the two versions produce equivalent results within the scope of the current study. The membrane potential (V_m) of the model neuron was simulated as follows:

Here, E_Leak, E_Ex, and E_Ca are the reversal potentials for the leak current, excitatory input, and T-channels, respectively. g_Leak, g_Ex, and g_T are the conductance values for the leak current, the excitatory inputs, and the T-channels. Synaptic inhibition was not necessary to produce thalamic bursts, so they were not included in this simulation. Excitatory input was simulated using the retinal spike trains recorded in vivo. When the V_m exceeded −35 mV, an action potential was recorded and V_m was reset to −60 mV. Maximum g_Ex was selected to generate biologically reasonable firing rates and retinal spike-efficacy curves (Usrey et al., 1998) with a −60 mV resting membrane potential. g_T was controlled by the following voltage- and time-dependent equations:

Here, G_T is the maximum T-channel conductance, T_m is the activation gate, and T_h is the inactivation gates for the T-channels.

The activation states of T_m and T_h were determined by the following equations:

Here τ_m and τ_h are the time constants for the activation and inactivation gates, respectively.

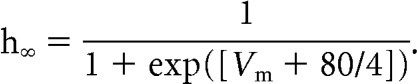Here, m_∞ and h_∞ are the steady-state activation levels for the activation and inactivation gates, respectively. While this model is a simplified representation of a thalamic neuron that lacks important details of the underlying biological processes such as the dendritic T-channel distribution (Destexhe et al., 1998), the phosphorylation-dependent potentiation of T-channels (Leresche et al., 2004), and the interplay between T-channels and other active currents (Huguenard and McCormick, 1992), it clearly illustrates the voltage and time dependence of T-channels that will form the basis for the interpretation of the current dataset. For more details on simulating T-channels, see Huguenard and McCormick (1992), Smith et al. (2000), and Destexhe and Sejnowski (2001).

Cross-correlation analysis.

Cross-correlograms between retinal and geniculate spike trains were made to assess connectivity between pairs of cells (Fig. 2). Cross-correlograms were calculated by generating histograms of LGN spikes relative to each retinal spike and retinal spikes relative to each LGN spike (Fig. 2A,B). Peaks indicative of monosynaptic connectivity were narrow (<1.5 ms, full-width at half-height), short latency (<5 ms), and exceeded 5× the SD of the baseline (Cleland et al., 1971; Usrey et al., 1998). For quantitative analysis, bins contributing to the peak were identified using a bin size of 0.5 ms. The peak bin was first identified, and all neighboring bins >3 SDs above the baseline mean were considered part of the peak, where the baseline consisted of bins ranging from 30 to 50 ms on either side of the peak bin.

Figure 2.

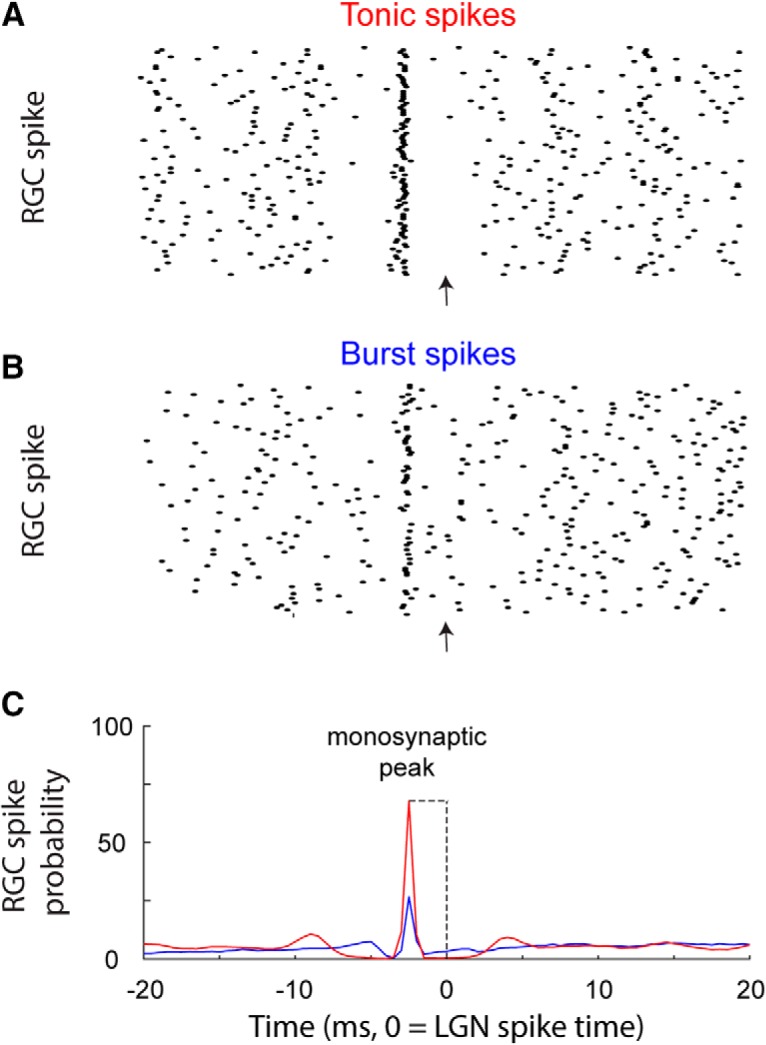
Cross-correlation analysis to identify monosynaptic connections between RGCs and LGN neurons. A, Raster plot showing the timing of RGC action potentials relative to the tonic action potentials of a simultaneously recorded LGN (time = 0, indicated with arrow). B, A similar plot for LGN burst action potentials. C, A clear, narrow, short-latency peak can be seen in both of the example cross-correlograms (red, tonic spikes; blue, burst spikes), indicating a monosynaptic connection between the two neurons. Note: cross-correlation analysis can be performed using either the presynaptic spikes or postsynaptic spikes as the reference events. Here, we use the postsynaptic spikes for the reference to illustrate differences in retinal activity preceding burst and tonic spikes (see Materials and Methods).

Retinal spike contribution and efficacy.

Cross-correlation analysis was used to assess connectivity between cell pairs as well as strength of connection. The monosynaptic peak in a cross-correlogram (Fig. 2C) was used to calculate two measures of correlation strength: efficacy and contribution (Cleland et al., 1971; Usrey et al., 1998). Efficacy is the number of spikes in the monosynaptic peak divided by the total number of retinal spikes; contribution is the number of spikes in the peak divided by the total number of LGN spikes. To the extent that peaks were caused by monosynaptic connections, efficacy and contribution have very simple interpretations. Efficacy represents the fraction of the retinal spikes that evoked geniculate spikes, and contribution represents the fraction of the geniculate spikes that were caused by a spike from the RGC. Given that LGN neurons receive convergent input from two to six RGCs (Cleland, 1986; Hamos et al., 1987; Reid and Usrey, 2004), it is worth noting that this measure of retinal contribution quantifies the influence of the simultaneously recorded RGC on the spiking behavior of the LGN neuron and not the combined influence of all the RGCs that provide convergent input to the LGN neuron. Contribution and efficacy were estimated separately for tonic and burst spikes via separate cross-correlograms (Fig. 2A,B). Differences in the amplitudes of tonic and burst correlograms, as quantified by contribution and efficacy, are presented in the Results section.

When applicable we calculated the expected retinal spike efficacy for each recorded cell pair as follows (Alitto et al., 2019). First, we calculated the average spike efficacy across a range of ISIs, estimated independently for responses driven by drifting gratings and white-noise stimuli. We then modeled the expected spike efficacy by assigning each retinal spike the efficacy value calculated for the corresponding ISI. Thus, the spike efficacy became the value expected if retinogeniculate transmission did not systematically depend upon a given independent variable.

Interactions of EPSPs and T-potentials.

The tight temporal relationship between retinal spikes and evoked LGN action potentials (Fig. 2) depends, to a large extent, on the amplitude and fast rise times of retinogeniculate EPSPs. Even when two or more retinal EPSPs interact through temporal summation, the tight temporal relationship is maintained because of the fast rise time of the triggering EPSP. A similar tight temporal relationship is expected if the retinal EPSP occurs during an ongoing T-potential. However, there may be a significant increase in the latency between retinal spikes and subsequent geniculate spikes if a subthreshold retinogeniculate EPSP initiates a suprathreshold T-potential. Here, the increased latency follows the comparatively slow activation of T-channels in response to depolarization (Huguenard and McCormick, 1992). We therefore also examined retinogeniculate interactions over a time window of 10 ms (T-potential delay window), which past work indicates captures the variable delay between EPSP and resulting T-potential (Wang et al., 2007). Specifically, we used a 10 ms window immediately preceding LGN spike onset, excluding the monosynaptic window to avoid redundant counting of spikes, to determine the delayed contribution. Using this value, we calculated the total retinal contribution for cardinal LGN spikes, which is the sum of the contribution value calculated from the short-latency monosynaptic window and the T-potential delay window. Because of the relatively long duration of the T-potential delay window, contribution values calculated from drifting grating data were corrected with a shuffle subtraction to remove stimulus-dependent correlations (Usrey et al., 1998; Wang et al., 2007) before calculating total contribution. It was not possible to perform the same correction on m-sequence data; therefore, m-sequence data were excluded from this analysis.

Additionally, T-potentials may allow single retinal spikes to evoke multiple LGN spikes, leading to an amplification of the retinal signal within the LGN. This would cause a decrease in the measured retinal contribution because the time delay from the triggering retinal spike increases with each subsequent LGN spike. Consequently, only the first spike would fall into the monosynaptic window and thus be counted as triggered by the retina. To determine the extent to which this occurred, we calculated retinal augmentation, which is here defined as the average retinal contribution to secondary burst spikes minus the conditional contribution given that the previous spike (i.e., cardinal burst spike) was directly evoked by the recorded RGC. Effectively, this quantifies the relative change in contribution following an evoked spike. Considering this influence, we calculated total retinal contribution for secondary LGN spikes as the sum of standard retinal contribution, delayed retinal contribution (based on the T-potential delay window of the partnered cardinal spike), and retinal augmentation.

Spatiotemporal receptive field maps.

Spatiotemporal receptive fields (STRFs) were calculated from LGN spike trains evoked during the presentation of a binary white-noise stimulus, as described above. To determine whether LGN burst spikes were driven by visual stimulation, LGN STRFs were calculated using either the full spike trains (all spikes) or spike count-matched subsets of data (e.g., only cardinal burst spikes). Spike count matching was performed on a cell-by-cell basis by determining which subset had the least number of spikes and then randomly subsampling the other subsets to have the same total. This was done so that the signal-to-noise ratios (SNR) were comparable within a given cell. The signal was estimated as the amplitude of the 2D Gaussian fit (Matlab function fmincon) to the frame of the STRF containing the peak pixel. The Gaussian receptive field estimate is described by the following equation: G_ij = K × exp[ − (x_i − x₀)²/2 × σ²] × exp[ − (y_i − y₀)²/2 × σ2], where K is the amplitude, x₀ and y₀ are the coordinates of the center of the receptive field, and σ is the SD. Noise was estimated as the mean value for three frames centered at t = +100 ms.

Experimental design and statistical analysis.

To quantify the relationship between retinogeniculate communication and thalamic response mode, we used generalized linear mixed effect (GLME) models (Matlab function fitglme; Raudenbush and Bryk, 2002) using a Laplace fit method. This is done to take full advantage of the number of data points collected (e.g., hundreds of thousands of retinal and thalamic spikes) while accounting for differences between cells. The general form of a GLME is as follows:

Here y is the outcome being modeled, x is matrix of fixed-effects variables, β is a vector of fixed-effects coefficients, z is a matrix of random-effects variables, μ is a vector of random-effects coefficients, ε is the residual error, and f is the identity link function. β₀ is the y-intercept, while β_{variable name} is the coefficient of a specific variable (e.g., β_ISI). When analyzing the percentage of high-frequency spikes, these values were modeled using the identify function and as arising from a normal distribution. In this case, the β-coefficients represent the linear slope between the predicted outcome and the fixed-effect variable. When analyzing the percentage of spikes per burst, these values were modeled using a log link function and as arising from a Poisson process. When analyzing retinal contribution and retinal spike efficacy, these values were modeled using a logit link function and as arising from a Bernoulli process (0 and 1 s). For example, retinal spikes were assigned values of 1 and 0 based on whether they triggered an LGN action potential (1) or did not (0), as described above. In this case, the β-coefficients represent the influence of the fixed-effect variable on the log of the odds ratio of the predicted outcome. For each GLME model, cell identity was set as a random effect to account for differences between cells. For illustrative purposes, data were binned and normalized (see Fig. 7). Normalization was performed such that the average value (efficacy or contribution) was set to 1.0. It is important to note that these transformations were done to represent effects graphically that are difficult to directly represent based on Bernoulli variables; however, the GLMEs models were fit to the raw values that were neither binned nor normalized.

Figure 7.

Retinal spike efficacy is influenced by a preceding LGN ISI. A, To quantify the influence of an preceding LGN ISI on retinal spike efficacy, and time = 0 was set to 4.0 ms after the cardinal spike in a burst or the referenced tonic spike (black arrow). B, C, Line plot showing that retinal spike efficacy is enhanced following both burst spikes (blue line) and tonic spikes with a preceding ISI of >100 ms (red line). The expected values given the preceding retinal ISIs are plotted as a baseline comparison (black line). Shaded areas indicate SE. D, E, Line plots showing the influence of preceding ISI on retinal spike efficacy for 4–10 ms following time 0, as indicated in A.

When simpler statistical analyses were sufficient to compare two distributions, we first tested the normality of the distributions using Lilliefors modification of the Kolmogorov–Smirnov test. If it was determined that both distributions were not significantly different from normal distributions, then a t test was used to compare the means of the two samples, otherwise a Wilcoxon rank sum test or a sign test was used. X and Y cells were classified based on the latency of the monosynaptic peak (Usrey et al., 1999). Using this measure, of the 29 cell pairs examined in this study, 7 were X cell pairs and 22 were Y cell pairs. Results did not differ for these cell groups; thus, the 29 cell pairs were treated as a single group for the statistical analyses presented. It should be noted that small differences between X and Y cells may have gone undetected because of the small sample sizes inherent to studying monosynaptic connections in vivo.

Results

To quantify retinogeniculate communication during tonic and burst activity modes in the LGN, we made simultaneous recordings of synaptically connected RGCs and LGN neurons in the anesthetized cat. Retinal and geniculate neurons were excited with white-noise stimuli (n = 29 cell pairs) and/or drifting sinusoidal gratings (n = 15 cell pairs; see Materials and Methods). As will be expounded upon in the Discussion section, these stimuli were chosen because of how their spatiotemporal profiles are predicted to differentially interact with geniculate response mode. Geniculate bursts were identified using established criteria for extracellularly recorded spikes (Lu et al., 1992). Specifically, a burst was defined as a sequence of spikes that met the following two criteria (Fig. 1A): (1) the first spike in the sequence followed an ISI of >100 ms, and (2) one or more subsequent spikes followed with ISIs of <4 ms. Across 29 monosynaptically connected pairs of RGCs and LGN neurons, we recorded 1,394,029 retinal spikes and 530,428 LGN spikes, including 54,482 geniculate bursts (≥2 spikes). As expected, burst frequency was significantly greater for LGN neurons than for RGCs (Fig. 1B,C; during white-noise stimulation: RGC = 1.5 ± 0.3%; LGN = 16.1% ± 2.8%, p < 10⁻⁵; during drifting grating stimulation: RGC = 0.24 ± 0.6%, LGN = 26.2 ± 4.7%, p < 10⁻⁵).

Simulating thalamic bursts involving T-potentials

Given that the biophysical properties of T-channels are well characterized, simulations can be used to illustrate how T-channels and retinal spikes are predicted to interact and transform retinogeniculate communication (see Materials and Methods). In particular, leaky integrate-and-fire neuronal models generate bursts with the simple addition of T-channels based on published equations (Fig. 1D; percentage bursts with T-channels, 11.5 ± 0.3%; percentage bursts without T-channels, 0.1 ± 0.05%; p < 10⁻⁵, see Materials and Methods; Huguenard and McCormick, 1992). Similarly, the addition of T-channels increased the number of geniculate spikes evoked from the same excitatory input (Fig. 1E, blue line and axis). Interestingly, the increase in geniculate spike count remained elevated at higher resting membrane potentials where the percentage of burst spikes was greatly reduced (Fig. 1E, black line and axis). This suggests that the influence of T-channels on geniculate activity can be measured even in the absence of classically defined bursts.

We hypothesized that visually evoked T-potentials augment the transmission of visual signals through the LGN because of the summation of retinal EPSPs with T-potentials. Specifically, T-potentials are predicted to increase the ability of retinal spikes to trigger geniculate spikes as well as cause single retinal spikes to trigger multiple LGN spikes. Further, given the voltage and time dependence of the deinactivation of T-channels, the influence of T-potentials on retinogeniculate communication should be dynamically regulated by the depth and duration of the preceding membrane hyperpolarization (Fig. 3).

Figure 3.

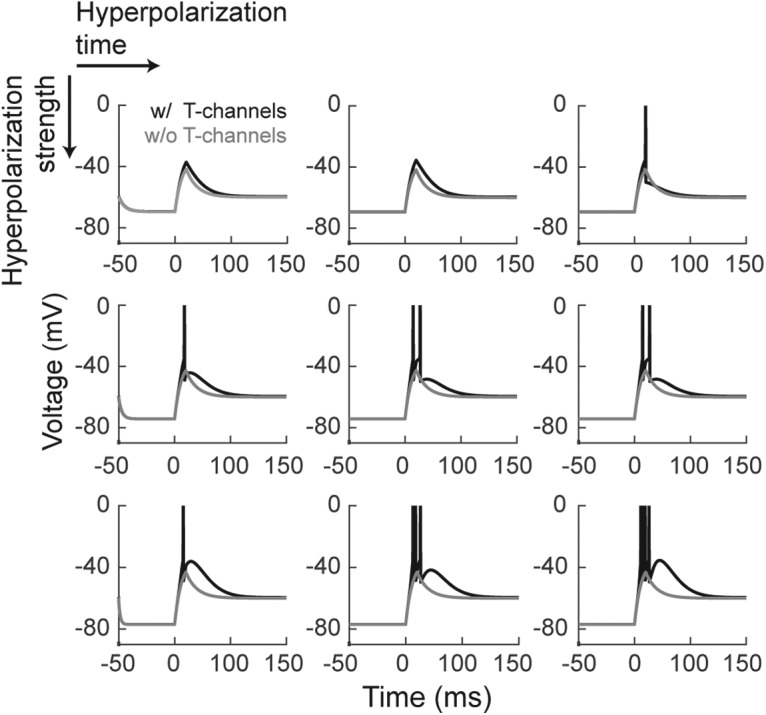
Leaky integrate-and-fire simulation of geniculate bursts. Simulation of T-potentials using a standard integrate-and-fire neural model. Using previously published equations (see Materials and Methods), we simulated the influence of increasing the amplitude (progressively stronger by row) and duration (progressively longer by column) of a hyperpolarization on T-channel activation in response to depolarization. Black lines, Model with T-channels; gray lines, model without T-channels.

Although membrane hyperpolarization cannot be directly measured from extracellular recordings, it is likely that its influence on T-channel activity is correlated with the length of the preceding ISI of the LGN cell—the longer the ISI, the greater the probability of T-channel deinactivation. To test this idea, we compared the probability that LGN cells generate high-frequency spikes (ISIs < 4 ms) as a function of the preceding ISI of the LGN cells. Results show that the percentage of high-frequency spikes from LGN cells increased dramatically as the preceding ISI increased beyond 50 ms (Fig. 4A,B; white noise: β_ISI = 0.59 ± 0.05, p < 10⁻⁵, dist. = distribution; drifting grating: β_ISI = 0.59 ± 0.15, p < 0.0005, dist. = distribution). This effect was not seen for RGCs. In addition, the number of spikes per burst was also directly dependent upon the preceding ISI (Fig. 4C,D; white noise: β_ISI = 0.65 ± 0.1, p < 10⁻⁵, dist. = Poisson; drifting grating: β_ISI = 0.29 ± 0.14, p < 0.053, dist. = normal). These findings are consistent with results showing that the number of spikes generated in a burst is directly proportional to the size of the underlying T-potential (Mease et al., 2017).

Figure 4.

The influence of the preceding ISI on high-frequency spiking in the retina and LGN. A, B, Line plots showing the influence of the preceding ISI on the percentage of high-frequency spikes (red line, RGC; blue line, LGN) during white-noise (A) and drifting grating (B) stimulation. High-frequency spikes are defined as two or more consecutive spikes with ISIs of <4 ms. C, D, Line plots showing the influence of a preceding LGN ISI on the number of spikes per burst. Shaded regions indicate SE.

Visually evoked geniculate bursts

The deinactivation of T-channels that is fundamental to thalamic bursts can occur via multiple mechanisms. During sleep and deep anesthesia, when thalamic neurons typically fire in burst mode, the deinactivating hyperpolarization is not associated with visual stimulation but rather involves intrinsic corticothalamic oscillations. Under these conditions, intrinsically generated bursts decouple the retina from the LGN and therefore do not convey visual information to the cortex. However, as we and others have shown previously, the hyperpolarization needed to deinactivate T-channels can also result from visual stimulation (Alitto et al., 2005; Denning and Reinagel, 2005; Ortuño et al., 2014). Under these conditions, bursts do not degrade visual signals, but instead relay retinal/visual information to the cortex. Given these very different mechanisms for burst production and the implications each mechanism would have on the interpretation of our data, we examined the spike trains of the cells in this study to determine whether or not the bursts conveyed visual information. To do so, we calculated space–time receptive fields from LGN responses to the white-noise stimulus using only burst spikes and compared these response maps to those computed using a spike count-matched subset of tonic spikes. As shown in Figure 5, A and B, burst and tonic maps had similar signal-to-noise ratios, indicating that the burst spikes were evoked by visual stimulation (tonic spikes, 9.5 ± 1.5; burst spikes, 10.6 ± 1.3; p = 0.54). Similarly, burst spikes recorded during visual stimulation with drifting gratings were tightly phase locked to the stimulus (Fig. 5C,D; tonic spikes circular variance, 0.12 ± 0.02; burst spikes, 0.03 ± 0.01; p = 0.001).

Figure 5.

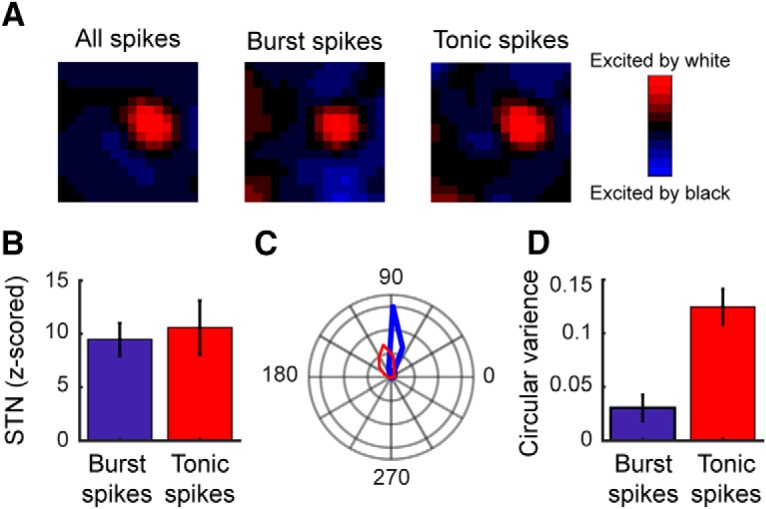
Geniculate bursts are evoked by visual stimulation. A, STRF maps from a representative LGN neuron calculated using specific subsets of spike count-matched geniculate spikes: all spikes (left), burst spikes (middle), and tonic spikes (right). B, Bar graph showing sample mean SNRs for tonic and burst STRFs. C, Polar plot illustrating the phase locking of LGN tonic (red line) and burst (blue line) spikes during visual stimulation with drifting gratings. D, Bar graph showing circular variance for tonic and burst spikes during visual stimulation with drifting gratings. Low circular variance values indicate that the spikes were phase locked to the visual stimulus, while a value of 1 indicates that the spikes occurred equally across all phases. Error bars indicate SE.

Augmentation of retinal signals during visually evoked geniculate bursts

To test the hypothesis that visually evoked geniculate bursts are associated with an amplification of the retinal signal within the LGN, we measured retinal spike efficacy as a function of time since the most recent LGN spike. Using the assumption that the probability of T-channel deinactivation increases as the LGN ISI increases in duration (see above), we calculated retinal spike efficacy as a function of the “ongoing” LGN ISI (Fig. 6A). For example, if a retinal spike occurred 10 ms after the most recent LGN spike, the ongoing LGN ISI is 10 ms, regardless of the timing of either the previous retinal spike or the next thalamic spike. If T-channels deinactivate during relatively long LGN ISIs, then retinal spikes that occurred during such ongoing LGN ISIs are predicted to trigger T-potentials and thus have an enhanced ability to evoke a geniculate response.

Figure 6.

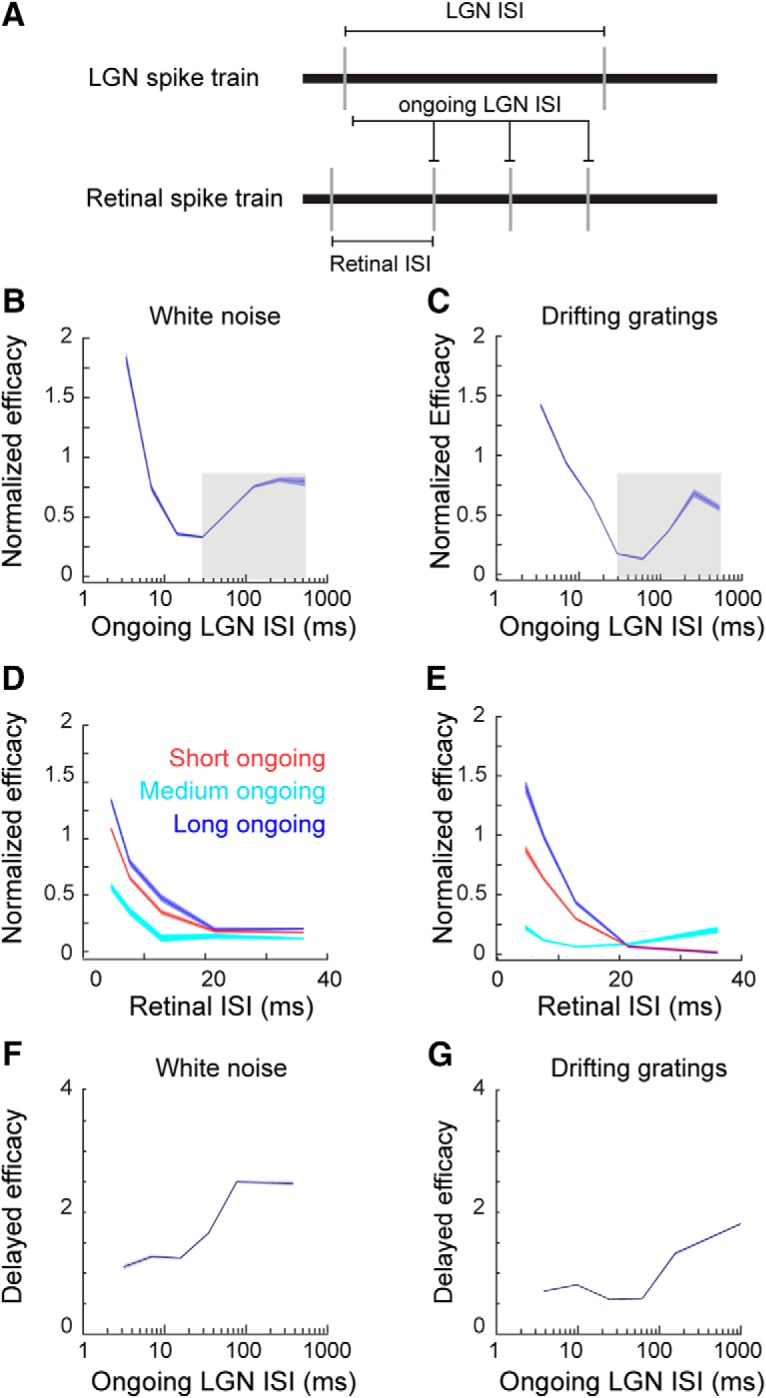
Retinal spike efficacy is influenced by ongoing LGN ISI. A, Ongoing LGN ISI is defined as the time since the most recent LGN spike at the occurrence of an RGC spike. This is in contrast to a retinal ISI, the interval between two consecutive RGC spikes, and an LGN ISI, the interval between two consecutive LGN spikes. B, C, Line plots showing the influence of an ongoing LGN ISI on retinal spike efficacy, during white-noise (B) and drifting grating (C) stimulation. The shaded areas around the line indicate SE. The gray boxes indicate the range of ISI values used for the GLME model (see Materials and Methods). D, E, Line plots showing the influence of retinal ISI on retinal spike efficacy (red, ongoing LGN ISI < 30 ms; light blue line, ongoing LGN ISI > 30 ms and < 100 ms; dark blue line, ongoing LGN ISI > 100 ms). F, G, Line plots showing the influence of an ongoing LGN ISI on delayed retinal spike efficacy.

Unsurprisingly, retinal spike efficacy was greatest during the shortest ongoing LGN ISIs and decreased as this value approached 30 ms (Fig. 6B,C). This is to be expected given that most LGN spikes are triggered by retinal EPSPs, and it takes ∼30 ms for the LGN membrane potential to return to baseline after these depolarizations occur (Usrey et al., 1998; Carandini et al., 2007). However, consistent with the deinactivation of T-channels during longer LGN ISIs, there was an increase in retinal spike efficacy during ongoing LGN ISIs of >50 ms that was maintained for the longest recorded values (> 300 ms; Fig. 6B,C; white noise: β_ISI = 2.11 ± 0.12, p < 10⁻⁵, dist. = binomial; drifting grating: β_ISI = 9.41 ± 0.15, p < 10⁻⁵, dist. = binomial). Consistent with past reports, retinal ISI also had a strong influence on retinal spike efficacy, reflecting the temporal summation of multiple retinal EPSPs in the thalamus (Usrey et al., 1998, Alitto et al., 2019; Carandini et al., 2007). To account for this effect, we calculated retinal ISI–spike efficacy for the following three categories of ongoing LGN ISIs: short (<30 ms), medium (>30 ms and <100 ms), and long (>100 ms). From this, it is evident that the two factors, retinal ISI and ongoing LGN ISI, interact to influence retinal spike efficacy (Fig. 6D,E).

While efficacy calculated from the monosynaptic peak is clearly influenced by an increased probability of T-potentials, this measure may not capture the ability of retinal EPSPs to trigger T-potentials because of the relatively slow activation kinetics of T-potentials. EPSCs can be modeled as an α function with a time constant of 0.5 ms (Koch, 1999), meaning that postsynaptic channels are fully open within <1 ms. By comparison, the activation kinetics of T-channels are slower and more variable. At a typical membrane potential range of −50 to −70 mV, the activation time constant is 6–14 ms (Huguenard and McCormick, 1992). When a retinogeniculate EPSP occurs during an ongoing T-potential, the slow activation kinetics does not alter the time between retinal spikes and triggered LGN spikes. However, when a subthreshold EPSP triggers a suprathreshold T-potential, there is an additional variable delay between retinal EPSP and LGN spike. Given that during longer ongoing LGN ISIs is precisely when an RGC spike may trigger a T-potential, we also measured “delayed efficacy” using an estimate of the temporal relationship between retinal EPSPs and T-potentials that was previously measured under similar experimental conditions (Wang et al., 2007; see Materials and Methods). Consistent with the increased ability of retinal EPSPs to trigger T-potentials during long ongoing LGN ISIs, we found a clear dependence between delayed efficacy and ongoing LGN ISIs (Fig. 6F,G; white noise: β_ISI = 0.91 ± 0.03, p < 10⁻⁵, dist. = binomial; drifting grating: β_ISI = 5.96 ± 0.05, p < 10⁻⁵, dist. = binomial).

Because T-potentials can last for tens of milliseconds (Destexhe and Sejnowski, 2001), we next quantified the time course of retinal spike efficacy modulation following relatively prolonged LGN ISIs (Fig. 7A). For this analysis, we plotted retinal spike efficacy as a function of time following the initiation of a geniculate burst. For each burst, time 0 was set 4 ms after the cardinal spike, thus excluding the increase in retinal spike efficacy caused by the definition of a thalamic burst (i.e., at least two spikes within 4 ms). Given the influence of the RGC ISI on retinal spike efficacy, we also calculated the “expected efficacy” as if retinal efficacy was not influenced by the preceding geniculate ISI, but was instead determined only by the retinal ISI (see Materials and Methods).

Across our dataset, there was a dramatic increase in retinal spike efficacy that lasted for ∼10 ms from the onset of a burst compared with the expected efficacy values (Fig. 7B,C; white noise: burst measured, β₀ = 0.55± = 0.34; burst expected, β₀ = −1.90 ± 0.36, p < 10⁻⁵, dist. = binomial; drifting gratings: burst measured, β₀ = 2.1± 0.40; burst expected, β₀ = −3.20 ± 0.43, p < 10⁻⁵, dist. = binomial). Importantly, a similar modulation was seen for individual tonic spikes that were preceded by an ISI of >100 ms (Fig. 7B,C; white noise: long ISI tonic, β₀ = −3.20 ± −0.11, p < 0.0005, dist. = binomial; drifting gratings: long ISI tonic, β₀ = 0.34 ± = 0.43, p < 10⁻⁵, dist. = binomial). Although, the increase in efficacy was greater following burst spikes compared with tonic spikes (white noise, p = 0.073; drifting gratings, p < 0.005), it is clear that the modulation of retinal efficacy is present even in the absence of classically defined bursts. As shown in Figure 7, D and E, the modulation of retinal spike efficacy is strongly dependent upon the preceding ISI of LGN cells (white noise: high-frequency spikes, β_ISI = 3.1 ± 0.5, p < 10⁻⁵; low-frequency spikes, β_ISI 3.4 ± 1.8, p = 0.047; drifting gratings: high-frequency spikes, β_ISI = 5.3 ± 0.3, p < 10⁻⁵; low-frequency spikes, β_ISI 4.0 ± 0.2, p < 10⁻⁵). Further, the modulation of retinal efficacy begins to occur following geniculate ISIs shorter than would constitute a classically defined thalamic burst (Lu et al., 1992).

Retinal contribution to geniculate burst spikes

Results presented above show that retinal spike efficacy is modulated by the preceding ISIs of LGN cells in a manner consistent with the involvement of T-channels and the amplification of visual signals within the LGN. To gain a comprehensive understanding of how response mode modulates retinogeniculate communication, we also quantified the influence of geniculate bursts on retinal contribution—the percentage of LGN spikes evoked from the recorded RGC. In general, geniculate bursts are expected to decrease retinal contribution by generating LGN spikes independent of retinal influence, therefore degrading the visual signal within the LGN. As described above, this is particularly true during geniculate bursts evoked by intrinsic corticothalamic oscillations. However, during visually driven geniculate bursts, such as the bursts examined in the current study (Fig. 5), one may detect a decrease in retinal contribution, as measured via correlation analysis, even when there is no corresponding degradation of visual processing and LGN activity remains reliant on retinal influences. Thus, in addition to quantifying the influence of response mode on retinal contribution, we also sought to gain deeper insight into its functional consequences on visual processing in the LGN.

Consistent with the ability of T-channels to modulate retinal contribution, there was a significant inverse relationship between preceding LGN ISI and retinal contribution during visual stimulation (Fig. 8A,B; white noise: β_ISI = −1.0 ± 0.1, p = 10⁻⁵, dist. = binomial; drifting grating: β_ISI = −8.6 ± 0.06, p < 10 ⁻⁵, dist. = binomial). This correlation was present even in the absence of high-frequency geniculate spikes (ISIs < 4 ms; white noise: β_ISI = −0.37 ± 0.09, p = 0.0001, dist. = binomial; drifting grating: β_ISI = −4.4 ± 1.2, p < 0.0001, dist. = binomial) and was evident for preceding ISIs of <100 ms during visual stimulation with drifting gratings (drifting grating: β_ISI = −2.2 ± 0.41, p < 10⁻⁵, dist. = binomial; white noise: β_ISI = −1.1 ± 0.65, p = 0.09, dist. = binomial), again reinforcing the conclusion that T-channel activity can influence geniculate activity even in the absence of classically defined bursts. For both white noise and grating stimulation, the decrease in retinal contribution lasted for several milliseconds following a prolonged LGN ISI (Fig. 8C,D; white noise = 6.1 ms; drifting gratings = 5.2 ms).

Figure 8.

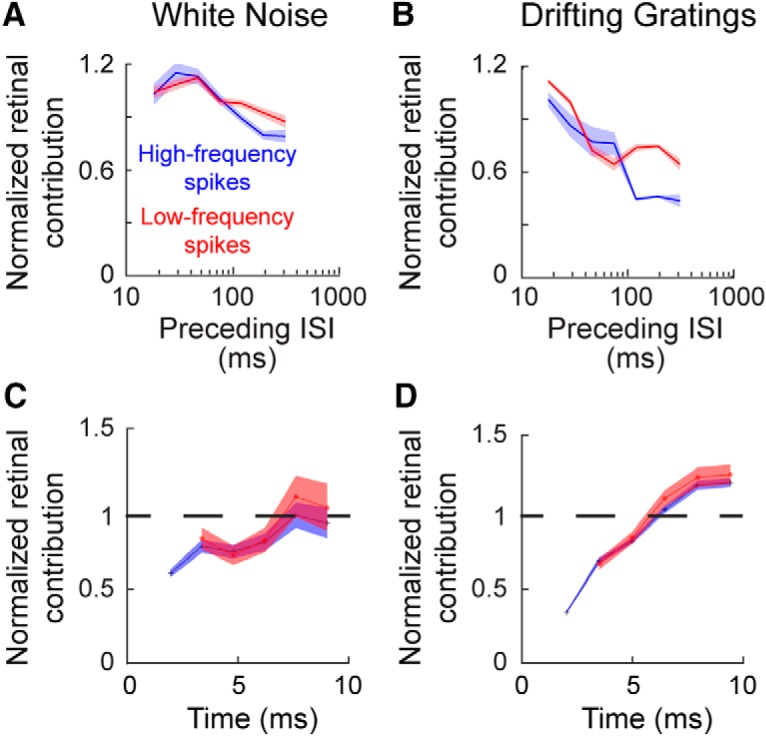
The influence of a preceding LGN ISI on retinal contribution. A, B, Line plot showing the influence of a preceding LGN ISI on retinal spike contribution (red line, low-frequency spikes, subsequent ISI of >4 ms; blue line, high-frequency spikes, subsequent ISI of ≤4 ms). Shaded area indicates SE. C, D, Line plots showing the temporal duration of the influence shown in A and B. Time = 0 is set as the occurrence of the initial spike following the referenced ISI (e.g., time of the cardinal spike in a burst).

We next wanted to determine whether the measured decrease in retinal contribution (Fig. 8A,B) was associated with the relatively slow activation kinetics of T-channels. If this is the case, then one would expect an increased probability of RGC spiking during the T-potential delay window for burst spikes not preceded by an RGC spike at the monosynaptic latency. Further, delayed retinal contribution measured in this manner should be dependent upon the preceding LGN ISI. We therefore looked at delay period activity in the following two separate categories of LGN spikes: (1) cardinal burst spikes and tonics spikes that were not triggered by the recorded RGC (no retinal spike in the monosynaptic window, Fig. 9A); and (2) cardinal burst spikes and tonic spikes that were triggered by the recorded RGC (retinal spike in the monosynaptic window; Fig. 9B).

Figure 9.

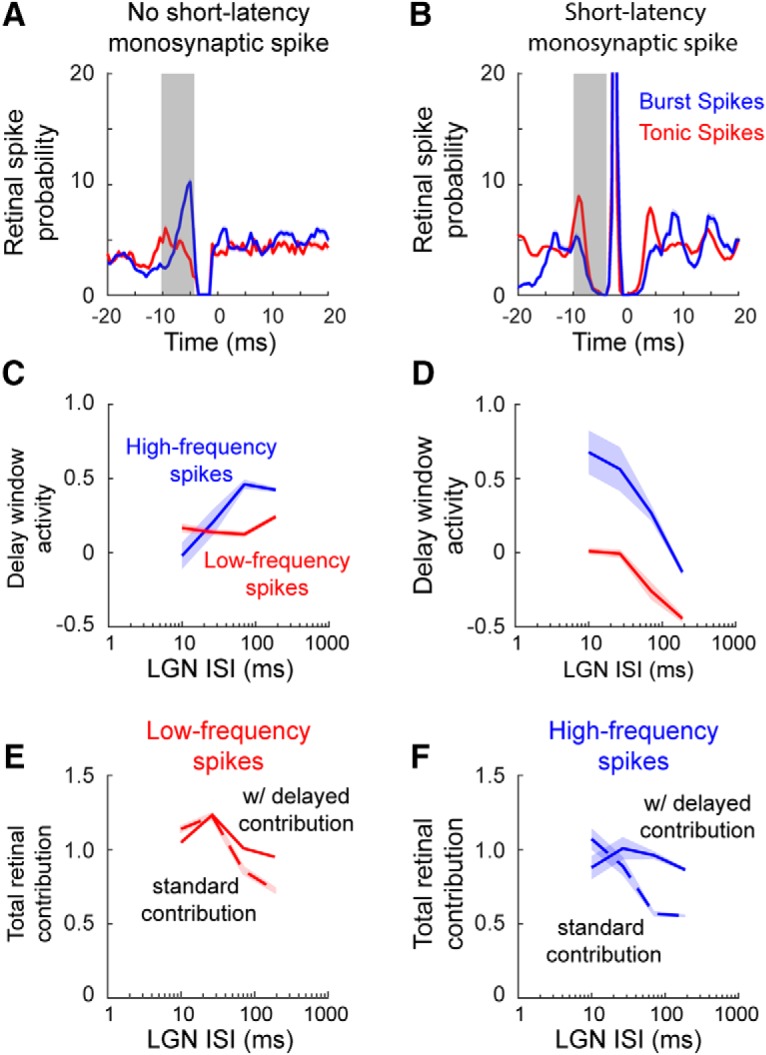
Cardinal burst spikes can be triggered by delayed retinal contribution. A, B, To quantify delayed retinal contribution, LGN spikes were divided into two categories: triggered by the recorded RGC (A) or not triggered by the recorded RGC (B). The window of delayed retinal contribution (gray box) was 0.5–10 ms before the monosynaptic peak. C, D, Delayed retinal contribution plotted as a function of a preceding LGN ISI. E, F, Total retinal contribution for cardinal burst spikes, plotted as a function of a preceding LGN ISI, is defined as classically defined retinal contribution (dashed lines) plus delayed retinal contribution.

Consistent with T-potential-dependent delayed retinal contribution, activity during the delay window preceding an LGN spike was clearly dependent upon the preceding LGN ISI (Fig. 9C,D). When an LGN spike was not triggered by the recorded RGC, there was a direct relationship between the delay window and the preceding LGN ISI (Fig. 9C; high-frequency spikes: β_ISI = −2.68 ± 0.53, p < 10⁻⁵, dist. = binomial; low-frequency spikes: β_ISI = −3.92 ± 0.35, p < 10⁻⁵, dist. = binomial). This is consistent with T-potentials that are triggered by RGC spikes and, in turn, trigger LGN spikes. By comparison, there was an inverse relationship between LGN ISI and delay window activity when an LGN spike was preceded by an RGC spike at the monosynaptic latency (Fig. 9D; high-frequency spikes: β_ISI = −1.54 ± 0.32, p < 10⁻⁵, dist. = binomial; low-frequency spikes: β_ISI = −0.38 ± 0.15, p = 0.078, dist. = binomial). Although the relationship between delay activity and LGN ISI is reversed, this is also consistent with the influence of T-potentials. When there is a low probability of a T-potential (e.g., short LGN ISI), the ability of an RGC spike to trigger LGN activity is highly dependent upon temporal summation. As the preceding LGN ISI increases, there is less need for temporal summation, presumably as a result of an increase in the probability of T-potentials that boost the efficacy of the retinal signal.

Considering delay window activity, the total retinal contribution can be calculated as a standard contribution, computed from the monosynaptic peak (Fig. 8), plus delayed contribution calculated from the delayed T-potential window. Consistent with the hypothesis that the decrease in retinal contribution is largely due to the relatively slow activation kinetics of T-channels, the addition of delayed retinal contribution removed the influence of preceding LGN ISI on retinal contribution (Fig. 9E,F). Indeed, normalized total retinal contribution remained close to 1.0 regardless of the preceding LGN ISI.

An additional mechanism that may contribute to the decrease in retinal contribution to burst spikes is the possibility that T-potentials allow single retinal spikes to evoke multiple LGN spikes, leading to an amplification of the retinal signal within the LGN. This would cause a decrease in the measured retinal contribution because the time delay from the triggering retinal spike increases with each subsequent LGN spike. Consequently, only the first spike would fall into the monosynaptic window and thus be counted as triggered by the retina. To determine the extent to which this occurred, we calculated retinal augmentation, which is defined here as the average retinal contribution minus the retinal contribution given that the previous spike was directly evoked by the recorded RGC. Effectively, this quantifies the relative change in contribution following an evoked spike. Positive values of retinal augmentation would be consistent with single retinal spikes triggering multiple LGN action potentials. Further, for retinal augmentation to be consistent with the involvement of T-potentials, then it should (1) increase with the preceding LGN ISI and (2) only be present during epochs containing relatively short subsequent LGN ISIs (e.g., high-frequency LGN spikes).

Retinal augmentation was significantly greater than zero during LGN bursts (white noise: retinal augmentation = 0.23 ± 0.1, p = 0.0027; drifting gratings: retinal augmentation = 0.77 ± 0.13, p < 0.0001). Further, this effect was dependent upon the preceding LGN ISI, as measured by the difference in the influence of LGN ISI when the retinal contribution of the cardinal spike is considered (Fig. 10A,B; white noise: cardinal contributed, β_ISI = −2.8 ± 0.3; cardinal not contributed, β_ISI = −1.7 ± 0.4, p = 0.017, dist. = binomial; drifting grating: cardinal contributed, β_ISI = −24.0 ± 0.8; cardinal not contributed, β_ISI = −3.6 ± 0.2, p < 10⁻⁵, dist. = binomial). By comparison, in the absence of high-frequency LGN spikes, there was no evidence of signal augmentation, regardless of the preceding ISI (Fig. 10C,D, red lines; white noise: retinal augmentation = 0.05 ± 0.06, p = 0.18; drifting gratings: retinal augmentation = −0.11 ± 0.12, p = 0.3). Finally, the total retinal contribution for secondary retinal burst spikes was calculated by adding standard contribution, augmented contribution, and delay-window contribution (Fig. 10E,F). Consistent with the measured decrease in retinal contribution being a result of the presence of T-potentials, total retinal contribution for secondary high-frequency spikes was largely independent of preceding LGN ISI and was close to 1.0 (Fig. 10F).

Figure 10.

Augmentation of retinal transmission during high-frequency LGN activity. A, B, The influence of a preceding LGN ISI on retinal contribution when the data are separated into two categories: cardinal spike was contributed by the recorded RGC (red line), and cardinal spike was not contributed by the recorded RGC (green). Shaded area indicates SE. C, D, Line plots showing retinal augmentation calculated from the data shown in A and B. E, F, Line plot showing standard retinal contribution (blue line), standard retinal contribution plus augmented contribution (orange line), and total retinal contribution augmentation (black line).

The above analyses recast the decrease in retinal contribution to burst spikes as a change in the temporal dynamics of retinogeniculate communication due to the inferred presence of T-potentials. However, given that these events occur outside of the typical window for monosynaptic communication and their influence is therefore more speculative, we asked whether there was a decrease in the visual signal conveyed by nontriggered versus triggered LGN spikes (as defined by the monosynaptic window). If our speculation concerning retinal augmentation and delayed T-channel dynamics is correct, then nontriggered burst and tonic spikes should both convey visual information. To determine whether LGN spikes that lacked a detectable triggering retinal spike encoded visual information, we calculated spike count-matched response maps for four categories of LGN spikes: contributed and noncontributed spikes during both tonic and burst response modes (Fig. 11). While there was an overall decrease in signal-to-noise ratios for noncontributed spikes compared with contributed spikes (all contributed SNR, 5.14 ± 0.54; all noncontributed SNR, 3.5 ± 0.41; p = 0.02), the decrease was present for both tonic spikes and burst spikes (noncontributed burst SNR, 4.2 ± 0.6; noncontributed tonic SNR, 2.8 ± 0.5; p = 0.1). Thus, burst spikes occurring outside of the short-latency monosynaptic window for retinogeniculate communication convey visual information to cortex.

Figure 11.

Burst spikes lacking a triggering RGC spike are nonetheless visually evoked. A–E, STRFs calculated from different subsets of spike count-matched LGN spikes: all spikes (A), tonic and burst spikes evoked by the recorded RGC (B, C), and tonic and burst spikes that were not evoked by the recorded RGC (D, E). F, G, Bar graphs showing signal-to-noise ratios for LGN spikes that were either evoked (F) or not evoked (G) by the recorded RGC (red, tonic spikes; blue, burst spikes). Error bars indicate SE.

Discussion

The goal of this study was to determine the influence of thalamic burst mode on retinogeniculate communication. By simultaneously recording the spiking activity of monosynaptically connected pairs of RGCs and LGN neurons, we show that retinal signals to the cortex are amplified by visually evoked bursts in the LGN. This amplification is the result of (1) an increase in the probability that a retinal spike will trigger a geniculate response and (2) an increase in the number of geniculate spikes that a single retinal spike can trigger. Further analysis demonstrates that the modulation of retinogeniculate communication increases as the preceding LGN ISI increases, and the amplification of retinal activity occurs even in the absence of traditionally defined thalamic bursts. These results are consistent with the known properties of T-type Ca²⁺ channels that underlie thalamic bursts (Llinás and Jahnsen, 1982; Destexhe, and Sejnowski, 2001; Babadi, 2005; Sherman and Guillery, 2009; Elijah et al., 2015; Zeldenrust et al., 2018). We propose that T-potentials amplify the transmission of visual signals to primary visual cortex, most likely during periods of low arousal. Given that this modulation can occur in the absence of thalamic bursts, T-potentials may also modulate retinogeniculate communication during behavioral conditions not typically associated with thalamic bursts.

Retinogeniculate communication during visually driven LGN bursts can be explained by the known properties of T-type Ca²⁺ channels

Thalamic bursts are generated by the deinactivation and subsequent activation of T-type Ca²⁺ channels (for review, see Destexhe and Sejnowski, 2001). This occurs when a strong hyperpolarization (deinactivation) is followed by rapid depolarization (activation). The depolarization can be active, as occurs with synaptic excitation, or passive, as occurs during the withdrawal of synaptic inhibition, or a combination of both (Andersen and Eccles, 1962; Llinás and Jahnsen, 1982; Hirsch et al., 1983; Deschênes et al., 1984; Destexhe, and Sejnowski, 2001; Wang et al., 2007). Importantly, the resulting Ca²⁺-mediated depolarizations (T-potentials) are dependent upon the depth and duration of the preceding hyperpolarization (Fig. 3). Because of this, we hypothesized that T-channel activity could be estimated from the preceding LGN ISI. Consistent with this hypothesis, we found an increase in the probability and duration of high-frequency spiking (ISIs < 4 ms; the second criterion of a burst) as the preceding LGN ISI increased in duration (Fig. 4). Likewise, there was a strong relationship between the preceding LGN ISI and the amplification of retinogeniculate transmission (Figs. 6, 7, 10).

During tonic response mode, it is generally assumed that each geniculate spike is triggered by a retinal action potential (Kaplan and Shapley, 1984; Sincich et al., 2007). As is common for monosynaptic interactions, and is particularly true at retinogeniculate synapses, cross-correlation indicates a precise monosynaptic window in which the triggering spike is found before the postsynaptic response (Fig. 2). Although previous work has shown that the latency and duration of the monosynaptic window is invariant to changes in the visual stimulus (Fisher et al., 2017; Alitto et al., 2019), T-potentials can alter this relationship in two important ways. First, the relatively slow activation kinetics of T-channels may introduce an initial, voltage-dependent delay in retinogeniculate communication. This would occur when a retinal EPSP triggers a suprathreshold T-potential. Under similar experimental conditions, this added variable delay between the retinal spike and the subsequent LGN response was reported to extend out to ∼10 ms. (Wang et al., 2007). Thus, a significant percentage of LGN burst spikes that occur outside of the monosynaptic delay can be still attributed to retinal activity. Second, T-potentials can cause single retinal EPSPs to trigger multiple LGN action potentials. In this case, there is a retinal EPSP in the monosynaptic window of the cardinal burst spike; however, for each subsequent LGN spike, the triggering retinal spike occurs outside of this window (Fig. 10). Importantly, burst spikes that are associated with retinal activity in either of these scenarios convey visual information (Fig. 11).

Stimulus-dependent amplification of visual signals

The biophysical properties of T-channels also explain stimulus-dependent differences in retinogeniculate communication during LGN bursts. In particular, the inferred influence of T-channels was greater with drifting grating stimulation compared with white-noise stimulation. This difference likely reflects the different spatiotemporal properties of drifting gratings and white-noise. Namely, the periodic nature of drifting gratings ensures that LGN neurons alternate between periods of strong excitation and strong inhibition, a pattern well suited for T-channel activity (Lu et al., 1992; Smith et al., 2000). By contrast, white-noise stimuli lack these correlations, leading to fewer and weaker T-potentials. Consistent with these differences, the amplification of visual signals was weaker and required longer geniculate ISIs during white-noise stimulation compared with drifting grating stimulation.

These stimulus-dependent effects may also align our results with those from a previous study in macaque monkeys (Sincich et al., 2007). In this study, results indicate that retinal activity, as assessed using geniculate S-potentials, drives nearly all geniculate burst spikes. Importantly, they did not find an increase in the latency or variability of communication during thalamic bursts. Similar to the white-noise stimulus used in the current study, the pink-noise stimulus used in the earlier study lacked the low temporal frequencies that strongly deinactivate T-channels, likely resulting in a greater percentage of subthreshold T-potentials that were more dependent upon retinal excitation to drive geniculate spikes. Although this study did not examine the influence of geniculate bursts on retinal spike efficacy, if our suggestion is correct, then similar increases in retinal spike efficacy should be present in their dataset. This would also indicate a shared mechanism across species to augment retinal signaling during geniculate bursts.

Thalamic burst mode and behavioral state

Visually evoked geniculate bursts are more likely to occur with inattentiveness or light anesthesia when the geniculate membrane potential is thought to be more hyperpolarized than in the alert state. Under these conditions, the type of visual signal that is most likely to trigger a T-potential is a strongly suppressive stimulus followed by a strongly excitatory stimulus (Alitto et al., 2005; Wang et al., 2007). Resulting bursts effectively amplify the geniculocortical transmission of retinal signals resulting from the onset of the preferred stimulus of a neuron (Guido et al., 1992; Sherman and Guillery, 2002). In contrast, sleep and deep anesthesia engage intrinsic corticothalamic oscillations that dominate geniculate activity and drive synchronous bursting activity that serves to decouple the thalamus and cortex from sensory activity (Steriade and Contreras, 1995; Timofeev et al., 1996; Elton et al., 1997; Steriade, 2003). Thus, depending on the state of the corticothalamic circuitry, bursts may serve very different purposes: they can amplify the communication of visual signals to cortex during inattentiveness or light anesthesia or decouple the thalamus and cortex during sleep and deep anesthesia.

Although bursts occur across all behavioral states, they occur most frequently during periods associated with diminished visual processing (Livingstone and Hubel, 1981; Bezdudnaya et al., 2006; Niell and Stryker, 2010). With this in mind, the amplification of retinal signals during geniculate bursts should not be taken as evidence that visual processing is enhanced during periods of low arousal relative to periods of more highly engaged sensory processing. Rather, T-potentials enhance the ability of retinal spikes to trigger LGN activity during periods of otherwise diminished visual processing. During comparable behavioral states, a retinal EPSP that occurs during a T-potential is more likely to trigger LGN spikes than the same retinal spike in isolation. Given the relative suppression of tonic LGN activity during periods associated with geniculate bursts, the burst-related retinal amplification functions as a contingency mechanism for the successful transmission of sensory signals to the cortex that would otherwise be lost.

Burst and tonic response modes are often described as binary states, which is an accurate description for the extreme ends of behavioral arousal: tonic mode during active sensory processing and burst mode during sleep and anesthesia. This hard distinction, however, fails to capture thalamic processing during the transition between the two response modes (Deleuze et al., 2012; Hong et al., 2014). In between the extremes of focused sensory processing and slow-wave sleep, the graded deinactivation of the T-channels of a cell may play a previously underappreciated role in visual processing (Mease et al., 2017). Under certain conditions, the transition between tonic and burst response modes may approach a step function (Bezdudnaya et al., 2006); however, more studies are required to understand the full dynamic range of state-dependent sensory processing. Finally, although bursts defined by classical criteria are less frequent in alert animals (Weyand et al., 2001; Ruiz et al., 2006; Weyand, 2007; Alitto et al., 2011), this does not exclude the influence of T-potentials on visual responses in the LGN. T-potentials that do not trigger classically defined thalamic bursts may make a significant contribution to sensory processing in the engaged state. Indeed, there are several mechanisms by which T-channels may be more active during alert sensory processing than was previously appreciated. This includes the phosphorylation-dependent potentiation of T-potentials by sustained depolarization, noise-sensitive T-channel dynamics, and T-channel window currents that result in the incomplete inactivation of T-channels near −60 mV (Leresche et al., 2004; Wolfart et al., 2005; Bessaïh et al., 2008; Dreyfus et al., 2010; Wijesinghe et al., 2013).