Modular FBG Bending Sensor for Continuum Neurosurgical Robot

Abstract

We present a modular sensing system to measure the deflection of a minimally invasive neurosurgical intracranial robot: MINIR-II. The MINIR-II robot is a tendon-driven continuum robot comprised of multiple spring backbone segments, which has been developed in our prior work. Due to the flexibility of the spring backbone and unique tendon routing configuration, each segment of MINIR-II can bend up to a large curvature (≥100 m⁻¹) in multiple directions. However, the shape measurement of the robot based on tendon displacement is not precise due to friction and unknown external load/disturbance. In this regard, we propose a bending sensor module comprised of a fiber Bragg grating (FBG) fiber, a Polydimethylsiloxane (PDMS) cylinder, and a superelastic spring. The grating segment of the FBG fiber is enclosed inside a PDMS cylinder (1 mm in diameter), and the PDMS cylinder is bonded with the superelastic spring in series. The deflection or bending of the robot backbone segment is translated into an axial loading in the superelastic spring, which applies tension to the FBG; therefore, by measuring the peak wavelength shift of the FBG, the bending angle can be estimated. This paper describes the design, fabrication, and kinematic aspects of the sensor module in detail. To evaluate the proposed concept, one such sensor module has been tested and evaluated on the MINIR-II robot.

I. Introduction

BRAIN tumors affect over 700,000 Americans today and are one of the leading causes of cancer-related deaths [1]. Furthermore, brain metastases occur in 20-40% of adult cancer patients [2]. When surgical resection is performed in addition to the standard whole brain radiation therapy, overall survival and freedom from local recurrence have been shown to improve [2]. Performing brain tumor resection with MRI guidance increases the surgeon’s ability to find residual tumor, maximizes normal tissue preservation, and can allow surgical planning to improve safety [3]. For these reasons, the MINIR-II, a magnetic resonance imaging (MRI) compatible continuum robot, has been previously developed [4], [5], as shown in Fig. 1. The goal of the MINIR-II robot is to enable the neurosurgeon to maneuver the robot inside the brain, under MRI guidance, to facilitate complete tumor removal [4]. The MINIR-II robot consists of three spring backbone segments. Four evenly spaced tendons are connected to the disk on the end of each segment for tendon-driven actuation. By using a central tendon routing configuration, each segment can be independently actuated with the minimum coupling effect with proximal segments [5].

fig. 1.

(a) Demonstration of MINIR-II robot manipulated within a human skull model, (b) close view of the robot.

Knowledge of the shape of this robot during operation can assist the surgeon to avoid important structures in tight anatomical confines, efficiently reach the target location, and successfully complete the surgery with minimal trauma to the patient. Also, MR imaging cannot provide real-time position information for a continually moving tool without lowering resolution and causing artifacts because of its relatively long imaging time [3]. Other possible methods to obtain required information for shape reconstruction of a continuum robot developed for minimally invasive surgery include FBG sensing, electromagnetic (EM) tracking, fluoroscopic imaging, and ultrasound imaging [6]. EM tracking suffers from errors caused by the magnetic and conductive objects used during diagnostic and therapeutic procedures [7], [8]. Fluoroscopic imaging is unsuited for continuous, real-time tracking as it exposes the patient to ionizing radiation. Ultrasound imaging suffers from low resolution and imaging artifacts [9]. Previous studies have attempted to use FBG fibers for the shape sensing of robotic and non-robotic surgical tools. Roesthuis et al. embedded three FBG fibers with four grating segments per fiber into grooves created in a flexible needle for reconstructing the 3D shape of the needle [10]. Park, Yong-Lae et al. proposed a MRI-compatible biopsy needle that consists of three identical grooves at 120 degree intervals, where three FBG sensors were bonded using a low-viscosity biocompatible cyanoacrylate adhesive [11]. An interesting helical wrapping of the FBG sensors over the continuum robot is proposed in [12]. The wrapped FBGs [12] measure curvature, force and torsion based on force-curvature-strain model. In another research [13], a polymer tube consisting of surface mounted FBG is proposed as an alternative substrate to bond between the FBG sensor and continuum robot. The shape sensing tube [13] separates the sensors from the robot structure. Araújo et al. fixed two D-shaped FBG sensors together to overcome temperature sensitivity of strained FBG during shape estimation [14]. Chen et al. offset the fiber core from the neutral axis of its coating and report the sensitivity of the device [15]. Liu et al. attached an FBG fiber along two superelastic nitinol wires in a triangular configuration and threaded the sensing assembly through a channel along the length of a continuum manipulator to measure its planar deflection [16]. The largest reported curvature found in previous studies is 66.6 m⁻¹, achieved by a sensing assembly formed by one FBG fiber and two superelastic nitinol wires encased in a polycarbonate tube [17].

The objective of this study is to develop an FBG-based sensing module to measure the deflection of the MINIR-II robot. MINIR-II is a unique robot [5] whose backbone is composed of multiple flexible springs. The combination of 1.5 mm pitch, 1.2 mm spring wire diameter, and 4.2 mm spring coil diameter, led the robot segment to have a flexural rigidity of 3.7 × 10⁻⁵ Nm² and axial stiffness of 46.6 N/m. These allow adequate flexibility for bending in universal directions. The central channel of MINIR-II segment is exploited for electrocautery and suction purposes. For the chosen structure of the MINIR-II, it is difficult to use conventional and potential approaches of shape sensing that have been explored in the above mentioned studies. Surface mounting of an FBG sensor to the flexible spring backbone of a MINIR-II segment with the help of a substrate or adhesive similar to the studies [10]–[12], [16], [17] will restrict the bending of the spring backbone. Shape sensing tube [13] separates the sensor from the robot, which is promising. However, the maneuverability of the MINIR-II depends on its flexible spring backbone segment. Therefore we propose a model (both analytical and fabricated) to develop bending sensor whose rigidity can be estimated explicitly and behavior can be characterized. Also the sensor should not need to be glued over the entirety of the robot segment. The design of the sensor proposed in this research allows the user to change its sensitivity, which is a major advantage compared to [13].

The rest of this paper is organized as follows. In Section II, the design and fabrication of the proposed sensor module are described. Section III explains the behavior modeling of the sensor module. Section IV covers the experimental details and analyzes the results. Finally, conclusions and future work are discussed in Section V.

II. Development of the Sensor Module

A. Design

The MINIR-II robot is comprised of multiple universal bending segments and each segment is comprised of a spring backbone integrated between a top disk and a base disk. By selectively pulling the four tendons attached to the top disks, the spring backbones can perform large-curvature deflection. In this research work, we focus on the development of a bending sensor for one segment of the MINIR-II robot, as shown in Fig. 2(a). Since the gap between two adjacent spring coils is zero, the neutral axis that keeps constant length is located at the spring circumference when the bending segment is deflected. According to the application and system design of the MINIR-II robot, the bending sensors should satisfy the following requirements: a) Sufficient space should be maintained inside the spring backbone to pass through surgical accessories; b) The sensors should not interfere with the tendon wires outside the spring backbone; c) The bending stiffness of the sensors should be low to maintain the essential flexibility of the robot; and d) If the sensors are integrated between two disks, the sensors should be able to accommodate to the axial length change during the segment deflection.

fig. 2.

Design of the bending sensor: (a) one segment of the MINIR-II robot, (b) four bending sensors integrated with the robot, (c) top view showing the placement of the bending sensors, and (d) design of the bending sensor and the points (shown as red) where the sensor is attached with Bottom and Top Disk, (e) cut cross-section of the MINIR-II segment and the location of the bending sensor investigated in this study.

Due to the aforementioned requirements, a sensing system is designed to measure the deflection of one robot segment, as shown in Fig. 2(b). Four sensor modules are fixed between the top disk and the base disk. The sensors are equally spaced inside the spring backbone at a 45° offset from the tendons, as shown in Fig. 2(c). As shown in Fig. 2(d), each sensor module is developed by combining a micro superelastic nitinol spring with a PDMS cylinder in series. An FBG fiber is employed as the sensing component by co-axially embedding the grating segment within the PDMS cylinder. Due to the reinforcing effect of the FBG fiber, the PDMS cylinder with the fiber has a much higher axial stiffness than the superelastic spring, while the bending stiffness of the spring is much higher. When the robot segment deflects, the two disks will apply a tensile force and a bending moment to the sensor module. As a result, the PDMS cylinder will be deflected and the superelastic spring will be extended. The tensile force applied to the PDMS cylinder by the superelastic spring will induce axial strain in the grating segment, resulting in wavelength shifts of the reflected light. The tensile force will be scaled according to the bending angle of the robot segment. The PDMS cylinder functions as a bonding layer between the FBG fiber and the superelastic spring, in addition to protecting the grating segment.

B. Fabrication Procedures

The sensor module is fabricated by curing a PDMS cylinder around the grating segment of an FBG fiber and attaching a superelastic nitinol spring to the top of the PDMS cylinder. To fabricate the PDMS cylinder, a set of mold pieces, shown in Figs. 3(a), 3(b), and 3(c), are 3D printed using a Projet MJP 5600 3D printer (3D Systems, Rock Hill, SC, USA) with Visijet CR-CL material. Once printed, the molds are heated at 65°C for 45 minutes to remove the supporting wax. They are then washed by an ultrasonic cleaner in a hot oil bath to remove any residual wax. Finally, the molds are allowed to sit in hot, soapy water for 10 minutes to remove any remaining oil before rinsing and drying. The oil and wax are completely removed by taking these measures to ensure the full curing of the PDMS cylinder. Meanwhile, a 13 mm long and 1 mm inner diameter (ID) Teflon tube is cut entirely down on one side to form a seam. On the opposite side, the tube is notched at the top and scored down the length.

fig. 3.

Fabrication of the bending sensor: (a) CAD drawing of the mold, (b) partially disassembled mold showing placement of Teflon tube and spring, (c) close view of the half of the mold, (d) removal of sensor from Teflon tube, and (e) bending sensor prototype.

Dow Corning Sylgard 184 is used to make the PDMS solution by mixing the pre-polymer base and cross-linking curing agent in a 10:1 ratio. The PDMS solution is then placed in a 5 Pa vacuum chamber for 15 minutes to remove air bubbles. As shown in Fig. 3(a), the two halves of the mold are assembled onto the mold base, while placing the FBG fiber inside the lower fiber channel. Afterwards, the bulk PDMS solution is pipetted into the cavity in the mold. The fiber is then adjusted to ensure the grating segment is located in the middle of the PDMS cavity. The top is left off and the filled mold is placed in the 5 Pa vacuum chamber for 30 minutes. The fiber is threaded through the Teflon tube which is then slowly inserted through the PDMS cavity, between the support arms of the mold, allowing time for the PDMS to fully fill the tube from the bottom up as it is pushed down. The mold is placed into the 5 Pa vacuum chamber until bubbles are no longer observed on the top of the PDMS. Afterwards, a 1 mm outer diameter (OD) superleastic nitinol spring is threaded over the fiber and inserted 1 mm into the top of the Teflon tube. Once the spring has been inserted, the two halves of the mold top are assembled to hold the spring and fiber in place so that the fiber remains centered in the Teflon tube (Fig. 3(b)). The fiber and mold assembly is then placed in an oven to cure at 65 °C for 24 hours. Once the PDMS has been cured, the fiber and mold assembly is naturally cooled to room temperature and then disassembled. The PDMS cylinder and the embedded FBG fiber form an FBG-substrate assembly. The sensor module is removed from the Teflon tube by peeling away the two sides so that the tube splits in half along the cut and the score made down its length (Fig. 3(c)). The spring is then gently removed from the PDMS cylinder, leaving the small protrusion of PDMS that filled the inside of the spring. This protrusion is then used to place the longer (15 mm) section of nitinol spring with correct center alignment when gluing it to the PDMS cylinder using super glue. As a result, the PDMS cylinder and superelastic spring of the developed sensor module are 12 mm and 15 mm long, respectively, and both of them are 1 mm in diameter. After integrating the sensor module onto the segment of the MINIR-II robot using super glue, the effective length of the PDMS cylinder and spring are 8.4 mm and 11.4 mm, respectively. The effective turns and wire diameter of the spring are equal to 45 and 0.25 mm, respectively.

III. Sensor Behavior Modeling

In this section, we describe the design principles that can be used to determine parameters of the bending sensor. Force and moment information are useful for measuring the bending stiffness of the sensor, and the analysis shown in this Section will provide the measure of rigidity which is going to impose on MINIR-II.

The wavelength of the light reflected by the grating segment is determined by its effective refractive index and grating period, both of which are linearly affected by axial normal strain and temperature. If the temperature is assumed to be constant, the wavelength shift is proportional to the axial normal strain in the fiber core. The FBG sensor itself is designed to be extended in the axial direction (strain ≤ 5%), and it has negligible bending stiffness due to its small diameter (195 μm). Hence the FBG sensor is required to bond with additional substrate to strengthen its bending stiffness (defined in this paper as the ratio between applied force F shown in Fig. 4(a) and the deflection, δ) to match with the bending stiffness of the spring in the sensor module. In an ideal design, the spring and the bonded FBG-substrate should have the same bending stiffness. To model this case, the substrate around the FBG fiber is assumed to have a significantly higher stiffness than the fiber. As mentioned, the sensor module consists of a spring connected to the bonded FBG-substrate. If both (FBG-substrate and spring) have different bending stiffnesses as shown in Fig. 4(c), the radii of curvature (R_p, R_s) due to a bending load will be different. In this regard, we report three possible outcomes for the sensor module design:

• Case 1: the bending stiffness of the bonded FBG-substrate is higher than that of the spring

• Case 2: the bending stiffness is equal for both

• Case 3: the bending stiffness of the spring is higher than that of the bonded FBG-substrate

fig. 4.

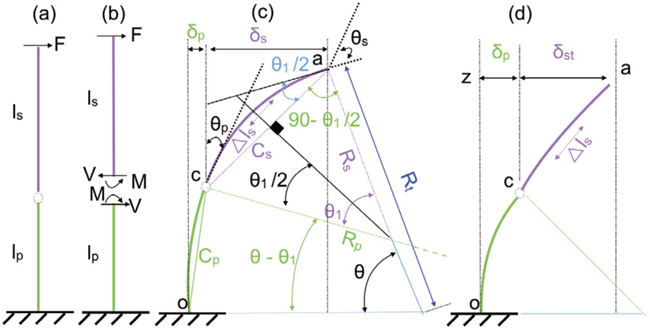
Simplified kinematics of the sensor module: (a) l_p and l_s are the bonded FBG-substrate and spring, (b) free body diagram of the sensor module, (c) deflection of the sensor module modeled as a cantilever beam, and (d) a case where deflection of spring cannot be modeled as cantilever beam.

A. Case 1

If the bending stiffness of the spring is smaller than that of the bonded FBG-substrate, the spring can be assumed to bend as a cantilever beam; the fixed end is c in Fig. 4(c). The deflection of the bonded FBG-substrate can be assumed to be insignificant.

B. Case 2

The deflection for the second case can also be made using the same rationale, except that the fixed end of the beam should be moved to o instead of c in Fig. 4(c). Therefore, for Case 1 and this case, the bending deflection of the sensor module can be modeled as a cantilever beam. In Case 1, the bending stiffness of the spring is much smaller than that of the bonded FBG-substrate. Therefore, the overall deflection of the module under a load at the tip (Fig. 4(a)) is mostly dependent on the shear and flexural effects of the spring. The slopes of the spring and the bonded FBG-substrate due to the load are described as θ_s and θ_p, respectively, as shown in Fig. 4(c). The bonded FBG-substrate is assumed to be a stiff rod in this modeling. The deflection angle, θ_p, will also be very small compared to θ_s based on our assumption. If F is the applied force at the tip of the sensor module, θ_s and θ_p can be written as:

$${\theta }_s=\frac{F{l}_s^2}{2E_s{I}_s};{\theta }_p=\frac{F{l}_p^2}{2E_p{I}_p}$$ (1)

where F, l_s, E_s, and I_s are applied force, length, Young’s modulus and area moment of inertia of the spring, respectively. l_p, E_p, and I_p are the length, Young’s modulus, and area moment of inertia of the bonded FBG-substrate, respectively. Fig. 4(c) illustrates this case where the spring-arc creates a larger angle (θ₁) than the comparatively stiffer bonded FBG-substrate (θ–θ₁). Thus, the arc ao is not continuous. To obtain a continuous arc, θ_s and θ_p must be equal. For θ_s and θ_p to be equal, the bending stiffness of the spring and bonded FBG-substrate must also be equal.

The contributions of spring and bonded FBG-substrate in the deflection quantity of the sensor module can be obtained by the following estimation. The spring deflection at its tip, δ_s, due to the shear force can be expressed as follows:

$${\delta }_s=\frac{F{l}_s^3}{3\beta }+\frac{F{l}_s}{\gamma }$$ (2)

where β and γ are the flexural and the shear rigidity of the spring, respectively. β and γ are given by [18]:

$$\beta =\frac{2l_s{E}_s{I}_s{G}_s}{\pi nR(2G_s+E_s)};\gamma =\frac{l_s{E}_s{I}_s}{\pi n{R}^3}$$ (3)

where G_s, R, and n are the shear modulus, mean spring coil radius, and number of active coils of the spring, respectively. The area moment of inertia of the spring is given by, $I_s=\frac{\pi r^4}{4}$,

where r is the wire radius of the spring. Substituting β and γ into Eq. (2), we obtain:

$${\delta }_s=F(\pi nR)\{\frac{l_s^2(2G_s+E_s)+6R^2{G}_s}{6E_s{I}_s{G}_s}\}$$ (4)

On the other hand, δ_s, can also be obtained from the kinematic relationship shown in Fig. 4(c). Chord length, C_s can be expressed as: C_s = 2R_s sin(θ₁/2), where R_s = l_s/θ₁ and δ_s = C_s sin(θ₁/2). Therefore:

$${\delta }_s=C_s\sin ({\theta }_1∕2)=\frac{2l_s}{{\theta }_1}si{n}^2({\theta }_1∕2)$$ (5)

From Eq. (4) and Eq. (5), θ₁ can be solved. According to the assumption, we get:

$${\delta }_p=\frac{F{l}_p^3}{3E_p{I}_p}+\frac{M{l}_p^2}{2E_p{I}_p}$$ (6)

where M = Fl_s. However similar to δ_s, δ_p can also be obtained from the kinematic relationship in Fig. 4(c). If the length of l_p and bending curvature are small, we can assume:

$${\delta }_p=l_{p}sin(\theta -{\theta }_1)∕2$$ (7)

Using Eqs. (4) to (7), θ, which is the deflected angle of the sensor module, can be solved from the below equations:

$$\theta -{\theta }_1={\sin }^{-1}(\frac{F{l}_p^2}{3E_p{I}_p}+\frac{F{l}_s{l}_p}{2E_p{I}_p})$$ (8)

where

$${\theta }_1=2{\sin }^{-1}F\pi nR(\frac{l_s^2(2G_s+E_s)+6R^2{G}_s}{6E_s{I}_s{G}_s{C}_s})$$ (9)

In the design perspective, the module is expected to bend with the robot curvature. Therefore, in the ideal case, l_s and l_p will follow with the robot curvature. Hence for this ideal case, the condition for designing the sensor module should be:

$$\frac{l_s}{l_p}=\frac{C_s}{C_p}=\frac{{\theta }_1}{\theta -{\theta }_1}$$ (10)

It is important to note that θ₁ contains the parameters related to the spring. R_t and θ in Fig. 4(c) are the radius of curvature and the deflected angle of the sensor module, respectively. We define K as:

$$K=\frac{\frac{l_s}{{\theta }_1}}{\frac{l_p}{\theta -{\theta }_1}}=x\frac{\theta -{\theta }_1}{{\theta }_1}$$ (11)

where x = l_s/l_p. To obtain a continuous arc oca, K should equal or be close to one. Eq. (11) can be used to map between the properties of spring and bonded FBG-substrate and vice-versa. Let us assume that the properties of the spring are known. The angle (θ — θ₁) can then be estimated for different values of K and x. Again, Eq. (8) states that (θ — θ₁) is a function of the Young’s modulus and the area moment of inertia of the FBG-substrate material. Therefore, the estimated quantity (θ — θ₁) derived from Eq. (11) can be used to obtain the Young’s modulus and area moment of inertia of the bonded FBG-substrate from the following:

$$E_p{I}_p=\frac{1}{\sin \frac{K{\theta }_1}{x}}(\frac{F{l}_p^2}{3}+\frac{xF{l}_p^2}{2})$$ (12)

where the variable K must be ≥ 1, to satisfy the cantilever beam assumption.

C. Case 3

In Case 3 the bending stiffness of the spring is higher compared to the bonded FBG-substrate, the spring deflection cannot be measured assuming it functions as a cantilever beam. We report that when force is applied at the tip, the bending sensor follows a characteristics similar shown in Fig. 4(d). It (Fig. 4(d)) has been seen both in simulation and experiment. The component (FBG-substrate here) which has lower bending stiffness compared to the remain component (in the series connection), typically shows greater deflection-response (compared to stiffer component, spring) when the module experiences a point load at the tip. Having said that, the total deflection quantity δ_t (= δ_s + δ_p) also consists a component which is governed by spring length. ANSYS simulation was conducted to investigate deflection at various force for a chosen module (Fig. 5, nitinol spring and PDMS). Table I shows the properties of the nitinol spring and substrate (PDMS) used in this simulation. For this properties (Table I), we observe that the spring does not deflect (see inset of Fig. 5) in response to a load, while the weaker component (FBG-PDMS) responses to the load. Since the spring is found relatively straight for large deflection in simulation, we measure the deflection (δ_p) at point c in Fig. 4(d) by using Eq. (6). By assuming the spring is tangential to the bonded FBG-substrate (inset of Fig. 5), the quantity δ_st becomes: l_s sin θ_p, where the slope θ_p is given in Eq. (1). We can then define the total deflection as δ_case3 = δ_p + l_s sin(θ_p + θ_c).

fig. 5.

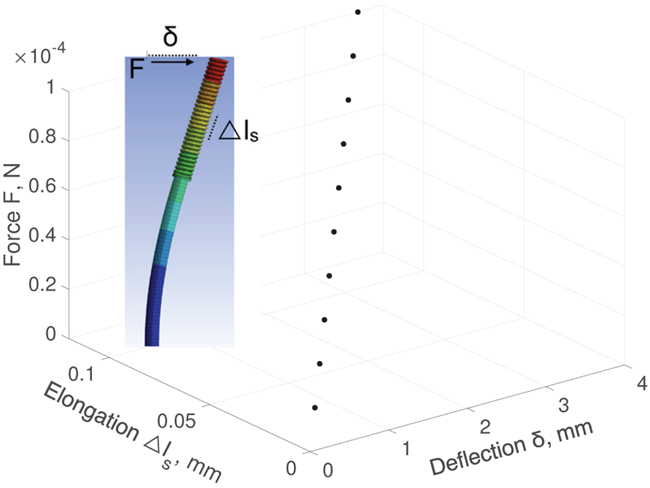
ANSYS simulation of the sensor module: deflection and elongation of the module increases as the force rises, and the elongation induces axial normal strain in the FBG grating segment.

tab. I.

Properties of the sensor module developed in this work

nitinol spring (D = 1 mm, turns = 60)	E = 55 GPa, G = 21 GPa [19]
PDMS cylinder (D = 1 mm, with 0.2 mm channel for FBG)	E=1.7 MPa, G=0.568 MPa [20]
ls = 15 mm	lp = 12 mm
m = 6.053× 104	C = −0.1073

where θ_c is a calibration factor that primarily depends on the ratio of the bending stiffness between the FBG-substrate and spring. However, we observe a linear relationship between θ_c and the applied force F in the finite element simulation using the chosen parameters detailed in Table I. We observe θ_c = mF + C approximately for the sensor module; the parameters are listed on Table I. The assumption drawn for measuring δ_case3 may not always be valid particularly if a constraint restricts and changes the shape of the segment. We think this problem can be addressed if the properties of the constraint are known.

IV. Experimental Evaluation

We describe the measurement procedure, prediction accuracy, and sensitivity of the proposed sensor in this section.

From the validation point of view of the bending sensor, it is adequate to investigate one sensor at an arbitrary location between S1, S2, S3 and S4 (Figs. 2(c)). The experimental setup is shown in Fig. 6, and the inset (Fig. 6) illustrates the location of the installed sensor in a cut cross-section of the segment. In this experiment, we positioned the sensor at S1 location and two tendons (T1, T3) were used to deflect the robot segment. In the Ideal case, T1 and T3 (assuming T2 and T4 are not actuated and at home configuration) are capable to bend the segment in a 2D plane. A sensor located at S1 moves in a plane which is parallel to the T1 −T3 plane (assuming T₂ = T₄ = 0 at home configuration). However, the installed sensor at S1 achieves better mobility when T3 only has been pulled, which is due to its position with respect to T3 (by mobility, we mean moving without colliding with the segment’s wall). On the other hand, the sensor at S1 does not have enough space to move when T1 has been pulled. These advantages and disadvantages are true for all locations of the sensor inside the segment, and can be addressed measuring alternate sensor such as considering S4 for T1.

fig. 6.

Setup detail: sensor module integrated MINIR-II is mounted with a fixed support where piezo linear actuator (SLC2490s-56, by SmarAct GmbH) operates the tendon, and MotionTracker 2 H40 tracks the reference markers, and wavelength shift is being recorded.

A. Measurement & Prediction Accuracy

Figures 7 and 8 illustrate the results obtained in this study. Figure 7(a) shows the wavelength changes for three angular cycles driven by T3 that run for a specific range of (−14 to −28). It has seen that the wavelength shift contains identical hysteresis pattern in the cycles. Due to this identical pattern, a polynomial fit is presented in Fig. 7(b) for the first half of the cycle shown in Fig. 7(a). The second half of the cycle can be fitted similarly (not shown). The polynomial fit (Fig. 7(b)) has been used to measure angle for 5 cycles that have run over the same angular range. We estimate the root-mean-square deviation between the predicted value (using Fig. 7(b)) and the actual angle measured by camera for five cycles as follows: 1.29, 0.92, 3.21, 1.01 and 0.86 degrees. The predictions are reasonable for MINIR-II, as an accuracy between 1 to 2 degree is sufficient.

fig. 7.

Experiments conducted on the MINIR-II robot segment: (a) angular cycles for T3, (b) polynomial fit for a first half of a chosen cycle, (c) response of the sensor module for small continuous angular loops, and (d) angular cycles for T1.

fig. 8.

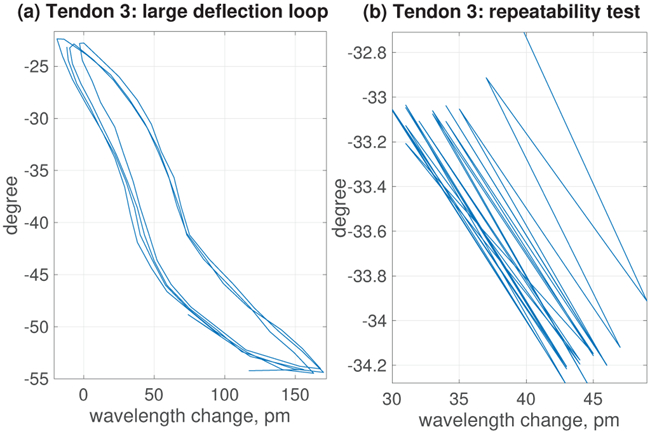
Experiments conducted on the MINIR-II robot segment: (a) response of the sensor module for large continuous angular loops and (b) repeatability test.

The sensor module has also been tested for measuring the deflection driven by T1 (Fig. 7(c)). The characteristics (Fig. 7(c)) were found to be repetitive in three consecutive cycles but different than the previous case (Fig. 7(a)). As explained previously, we assume that the sensor collides with the wall while it is pulled by T1. However Fig. 7(c) reveals that the wavelength shift initially reduces, and after an approximate angle of 12°, the wavelength shift starts increasing. We investigated this particular case in a cut cross-section of MINIR-II segment, to visually inspect the sensor and its reading while the bending is driven by T1. The sensor output dropped possibly due to the misalignment of the grating segment with the robot axis, which caused compression on the sensor when T1 was pulled to deflect the robot segment in the small range. The hysteresis was caused by the friction between the sensor module and wall segment. We assume a sensor located either at S3 or S4 will most likely show similar characteristics when T1 is being pulled.

We also demonstrate the wavelength shift for small (Fig. 7(d)) and large (Fig. 8(a)) deflection loops (continuous) and observe a hysteresis pattern. We observe the hysteresis pattern is approximately consistent for large deflection loops. However, for the smaller loops we found the wavelength shift reduces over time (Fig. 7(d)). Therefore, a test was conducted to observe continuous step response for multiple cycles of small angular deviation (Fig. 8(b)), while the wavelength shift readings were collected at intervals of 30 seconds. The shifts over test cycles in this test shows a damping pattern. The shifts over the test cycles are probably caused by the damping properties of the PDMS cylinder. By performing a fatigue test over 10 cycles, this can be alleviated for small-deflection measurements. The experimental results confirm the concept of the sensor module. However, if the robot segment operates in the range close to its initial configuration (for example: 0 to 10°), the wavelength shift of the sensor module will be relatively smaller. This phenomenon can be explained by observing Fig. 5. The shifts at this zone (0 to 10°) can be increased by using a spring of higher spring constant, k, or limiting the effective turns of the spring in the existing sensor module by using glue, which can increase the normal strain of the fiber to result a larger shift in wavelength. The choice of stiffness (k) of the spring in the sensor module is a tradeoff between the required sensitivity and the maximum normal strain allowed in the FBG fiber.

B. Sensitivity

We observe that sensitivity varies for different tendons and chosen angular range. It was found below 3pm/degree approximately for the range of 0 to 20°. As the MINIR-II segment deflects more, the sensor shows better sensitivity, Fig. 7(b) illustrates this fact. We report 5-7pm/degree for the range of 20 to 50° and an exponential increase later on.

V. Conclusions & Future works

We have proposed a sensor module of 1 mm in diameter to measure the bending deflection of the MINIR-II robot. The modelling and simulation results have shown that the sensor module possesses a negligible bending stiffness (≤×10⁻⁵ N/mm). Therefore, the module adds insignificant rigidity to the robot structure. Another advantage of such a sensor module lies in its potential re-usability, since the module does not need to be fixed along the entire length of the robot. The sensor design, fabrication, and kinematic modeling have been illustrated, and some experiments were conducted to prove the novel concept. The results obtained are satisfactory as the sensor is capable of measuring the required deflections of MINIR-II. However, the experimental results also show a hysteresis effect which we plan to model in our future work. The final aim is to integrate multiple sensor modules for 3D shape estimation of the MINIR-II robot, and focus to develop multi-DoF bending sensors for all three segments of MINIR-II robot. Hence, we consider them as future study of this work.