Self-Weighted Multi-Kernel Multi-Label Learning for Potential miRNA-Disease Association Prediction

Abstract

Researchers have realized that microRNAs (miRNAs) play significant roles in the pathogenesis of various diseases. Although many computational models have been proposed to predict the associations between miRNAs and diseases, prediction performance could still be improved. In this paper, we propose a novel self-weighted, multi-kernel, multi-label learning (SwMKML) method to predict disease-related miRNAs. SwMKML adaptively learns two optimal kernel matrices for both miRNAs and diseases from multiple kernels constructed from known miRNA-disease associations. Moreover, the miRNA-disease associations predicted from both spaces are updated simultaneously based on a multi-label framework. Compared with four state-of-the-art computational models, SwMKML achieved best results of 95.5%, 93.1%, and 84.1% in global leave-one-out cross-validation, 5-fold cross-validation, and overall prediction accuracy, respectively. A case study conducted on head and neck neoplasms further identified two potential prognostic biomarkers, hsa-mir-125b-1 and hsa-mir-125b-2, for the disease. SwMKML is freely available at Github, and we anticipate that it may become an effective tool for potential miRNA-disease association prediction.

Introduction

MicroRNAs (miRNAs) are a class of evolutionarily conserved, non-coding, small-molecule RNAs that have the function of regulating gene expression at the post-transcriptional level.¹ Recent studies have shown that miRNAs play crucial roles in various biological processes, such as cell growth and apoptosis, hemocyte differentiation, cardiac genesis, and late embryonic development.2, 3 Therefore, researchers have made great efforts to explore disease-related miRNAs by biological experiments to promote the understanding of the functional roles of miRNAs in the pathogenesis of human diseases and provide new clues for subsequent clinical treatment.⁴ Nevertheless, the experimental methods are usually costly and time-consuming, which hinders their applicability to large-scale prediction.⁵ Because of the relatively limited experimental data, recently, various studies regarding this topic have also been proposed to detect potential disease-related miRNAs based on computational biology methods.6, 7, 8

Existing computational models can be roughly divided into three categories: similarity-based approaches, network topology-based methods, and machine learning-based methods. Based on the assumption that functionally similar miRNAs are generally associated with phenotypically similar diseases, many similarity-based approaches have been developed.9, 10, 11, 12, 13, 14 For instance, Jiang et al.⁹ constructed a comprehensive human phenome-microRNAome network to prioritize the entire human microRNAome for diseases of interest. Chen et al.¹⁰ adopted global network similarity measures to infer potential disease-related miRNAs by implementing random walk with restart on the functional similarity network. Both Xuan et al.¹¹ and Liu et al.¹² constructed a bilayer heterogeneous network to effectively uncover miRNA-disease associations.

Another set of prediction methods utilized network topological characteristics and also achieved remarkable performance.15, 16, 17, 18, 19, 20 Zou et al.¹⁵ learned an integrated network similar to a social network composed of multiple heterogeneous networks to predict the potential associations between miRNAs and diseases. You et al.¹⁶ adopted a depth-first search algorithm to rank the associations between miRNAs and diseases in terms of their path length. Chen et al.¹⁹ used graphlet interaction to quantify the relationships between miRNAs and diseases. Qu et al.²⁰ developed a novel KATZ model-based computational method through a reliable heterogeneous network by integrating multiple data sources. Although these methods have achieved great performance, their prediction performance could be easily affected by a change in network topology.

In addition, with the rapid development of artificial intelligence techniques, increasing numbers of computational models based on machine learning have also been designed to solve the prediction problem.21, 22, 23, 24, 25, 26, 27 Chen and Yan²⁸ developed a regularized least-squares method to discover new disease-related miRNAs. Xiao et al.²⁹ proposed a graph-regularized, non-negative matrix factorization framework to discover potential associations between miRNAs and diseases. Chen et al.30, 31 presented a novel model of inductive matrix completion for miRNA-disease association prediction. Zeng et al.³² proposed a structural perturbation method based on the metric of structural consistency to predict potential new associations.

Despite the tremendous efforts made to identify the possible associations between miRNAs and diseases, most computational methods still suffer from several limitations that affect their prediction accuracy and scalability. For instance, the similarity matrices constructed for miRNAs and diseases might be sub-optimal because of data incompleteness. Moreover, the prediction process in miRNA space is usually separated from that in disease space. To conquer the aforementioned limitations, we propose a novel method to predict potential disease-related miRNAs based on a self-weighted, multi-kernel, multi-label learning (SwMKML) framework. Specifically, our method first constructs a set of kernel matrices by fully taking advantage of known miRNA-disease associations. We then adaptively learn two optimal kernel matrices for both miRNAs and diseases from multiple kernels. Finally, the predicted miRNA-disease associations are updated synchronously according to a graph-based, multi-label learning framework. To illustrate the effectiveness of the proposed method, we apply several evaluation metrics to systematically measure prediction performance. The experimental results show that our method achieves favorable performance compared with several state-of-the-art methods. We further implement a case study of head and neck neoplasms to identify potential diagnostic biomarkers for the disease. In summary, our method demonstrates a superior ability to predict candidate disease-related miRNAs for future clinical trials.

Results

Performance Evaluation

We compared the prediction performance of our method with four state-of-the-art computational models: L1-Norm, structural perturbation method for miRNA-disease association prediction (SPMMDA), path-based miRNA-disease association prediction (PBMDA), and extreme gradient boosting machine for miRNA-disease Association prediction (EGBMMDA). Specifically, L1-Norm is a graph-based, semi-supervised learning method that obtains sparse solutions for prioritizing disease-related miRNAs.³³ SPMMDA uses structural consistency to estimate the link probability between miRNAs and diseases.³² PBMDA measures the association scores of miRNA-disease pairs by calculating the accumulative contributions from all paths.¹⁶ EGBMMDA utilizes an extreme gradient-boosting machine model for predicting miRNA-disease associations.³¹ Several different evaluation metrics were employed to comprehensively verify the performance of our method.

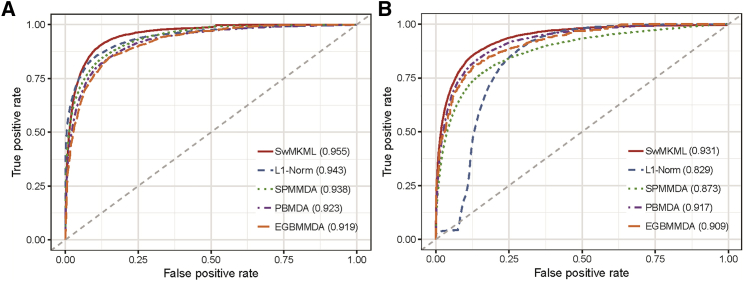
We first performed global leave-one-out cross-validation (LOOCV) and 5-fold cross-validation (CV) to evaluate our method based on the experimentally verified miRNA-disease association dataset from Human MicroRNA Disease Database (HMDD) v.2.0.³⁴ In particular, global LOOCV considered each association as the test set and the rest as the training set to iteratively obtain a predicted ranking.³⁵ For 5-fold CV, the entire miRNA-disease associations were randomly divided into five disjoint subsections, and then each part was selected as the test set, whereas the remaining parts were taken as the training set.³⁶ To intuitively demonstrate prediction performance, the receiver operating characteristic (ROC) curve was drawn by plotting the true positive rate (TPR) against the false positive rate (FPR) at varying thresholds.³⁷ Moreover, the area under the ROC curve (AUC) was calculated to quantitatively measure the performance of all methods.³⁸ AUC = 1 means that the method achieves a perfect performance, whereas AUC = 0.5 indicates that the method has a random prediction performance. Figure 1 shows in detail the performance of our method compared with the other four methods in terms of global LOOCV and 5-fold CV. It can be observed that our method obtained the best performance within both frameworks.

Figure 1.

Performance Comparison of SwMKML with the Other Four Methods

(A and B) Comparisons in terms of (A) global LOOCV and (B) 5-fold CV.

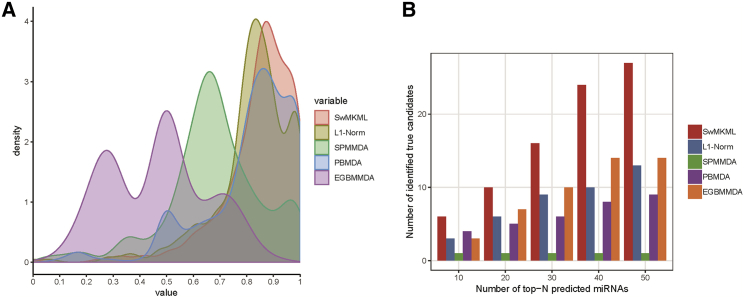
Next, a new evaluation metric, called leave-one-disease-out cross-validation (LODOCV) was adopted to assess the prediction power of our method in predicting diseases without known associated miRNAs. Specifically, for a given disease, LODOCV removed all miRNAs associated with this disease, and the predictions were carried out relying on the association information from other diseases. As shown in Figure 2A, our method also achieved the best performance among all methods. Furthermore, we also calculated the statistical significance of differences in performance obtained by our method and the other four methods (Table 1), and a Wilcoxon signed-rank test statistically confirmed the superiority of our method.

Figure 2.

Performance Comparison between SwMKML and the Other Methods under Two Different Evaluation Metrics

(A) Performance comparison of SwMKML with the other four methods in terms of LODOCV. (B) The number of predicted miRNAs that were confirmed in HMDD v.2.0.

Table 1.

Statistical Significance of Differences in Performance between SwMKML and the Other Four Methods in LODOCV

	L1-Norm	SPMMDA	PBMDA	EGBMMDA
p Value	3.99e−03	3.81e−37	4.01e−02	3.17e−87

We also selected four classical performance evaluation metrics—sensitivity (Sn), specificity (Sp), overall accuracy (Acc), and stability (Matthews correlation coefficient [MCC])—to objectively reflect the prediction performance of each method in a quantitative way.39, 40 The definitions of the four metrics are given as follows:41, 42

$$\{\begin{array}{l}Sn=1-\frac{N_{-}^{+}}{N^{+}}0\le Sn\le 1\\ Sp=1-\frac{N_{+}^{-}}{N^{-}}0\le Sp\le 1\\ Acc=1-\frac{N_{-}^{+}+N_{+}^{-}}{N^{+}+N^{-}}0\le Acc\le 1\\ MCC=\frac{1-\left(\frac{N_{-}^{+}}{N^{+}}+\frac{N_{+}^{-}}{N^{-}}\right)}{\sqrt{\left(1+\frac{N_{+}^{-}-N_{-}^{+}}{N^{+}}\right)\left(1+\frac{N_{-}^{+}-N_{+}^{-}}{N^{-}}\right)}}-1\le MCC\le 1\end{array},$$

where $N^{+}$ and $N^{-}$ represent the total number of positive samples and negative samples investigated, respectively. $N_{-}^{+}$ is the number of positive samples incorrectly predicted to be negative, whereas $N_{+}^{-}$ is the number of negative samples incorrectly predicted to be positive. According to the definitions above, we obtained the values of the four metrics for each disease following the same process as that of LODOCV and calculated their average as the final results for each method. As shown in Table 2, SwMKML achieved the best performance under all evaluation metrics except Sn.

Table 2.

Comparison of the Proposed Method with the Four State-of-the-Art Methods in Terms of Acc, MCC, Sn, and Sp

Method	Acc (%)	MCC	Sn (%)	Sp (%)
SwMKML	84.10	0.3059	63.79	85.30
L1-Norm	83.34	0.3005	51.37	84.87
SPMMDA	82.45	0.2932	38.43	84.34
PBMDA	79.37	0.2613	65.00	79.78
EGBMMDA	54.87	0.1845	38.04	56.58

Finally, to demonstrate the prediction power of our method on real datasets, we implemented our method on the HMDD v.1.0 dataset and verified the prediction results based on the HMDD v.2.0 dataset. The older version of HMDD v.1.0 contained 1,616 association pairs involving 129 diseases and 280 miRNAs after filtering. Specifically, we compared the number of validated miRNA-disease pairs among the top 50 associations predicted by each method. As shown in Figure 2B, our method identified more validated associations than the other computational methods. Taken together, all results demonstrated the superiority and reliability of our method in predicting potential miRNAs associated with diseases.

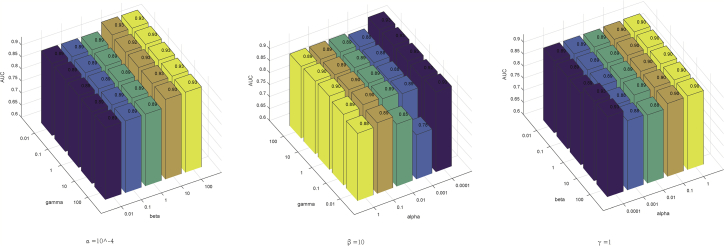
Parameter Analysis

There were three trade-off parameters in our objective function. In this section, we varied their values to see their effects on the final prediction accuracy of 5-fold CV. Specifically, we tested the effects of two parameters each time by fixing the other parameter (Figure 3). We found that our method achieved the best performance when α = 10⁻⁴, β = 10, and γ = 1.

Figure 3.

Effects of the Three Parameters α, β, and γ on the Prediction Performance of SwMKML in 5-Fold CV

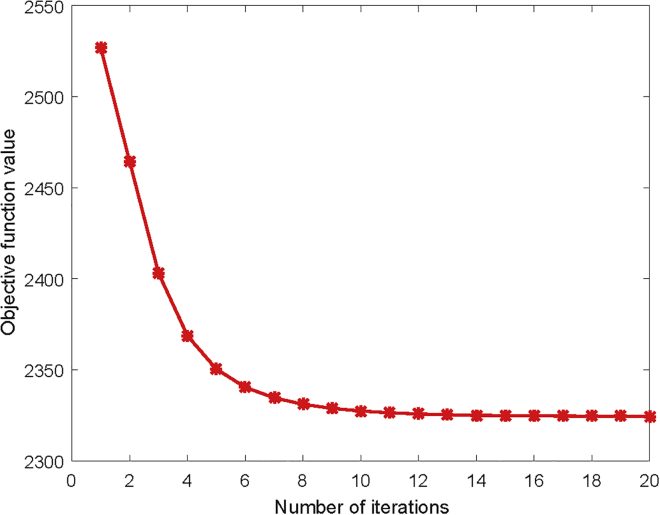
Convergence Analysis

In this section, we verified the convergence of our method in practice based on 5-fold CV. As shown in Figure 4, our method quickly reached a steady state within 15 iterations, which clearly demonstrated that our method has a fast convergence speed. This characteristic ensures the extendibility of our method on large-scale datasets.

Figure 4.

The Variations of the Objective Function Value of SwMKML with Respect to the Number of Iterations

Case Study

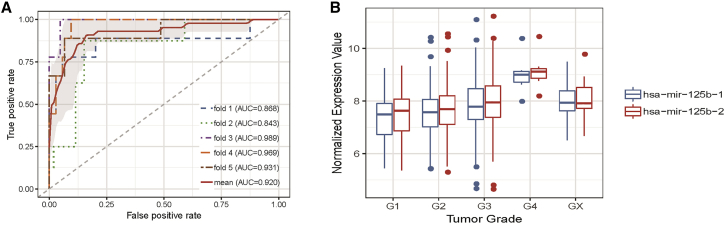
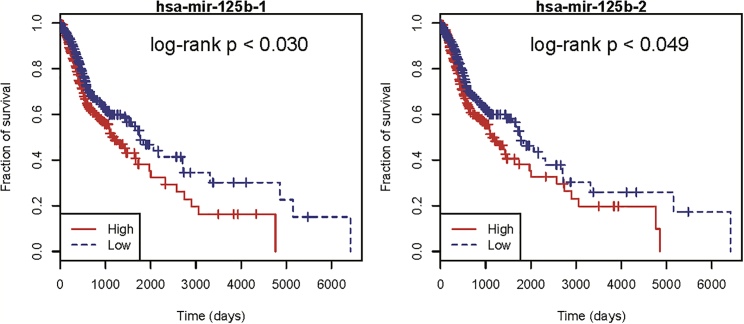
We conducted a case study analysis on head and neck neoplasms to further prove the reliability and prediction performance of our method. Head and neck squamous cell carcinoma (HNSC) is the sixth most common cause of cancer death worldwide, and the molecular mechanism of HNSC is not yet clear. In recent years, a handful of miRNAs were found to be differentially expressed in HNSC through clinical experiments, such as hsa-let-7a-1. The top10 miRNAs predicted to be related to HNSC by our method are listed in Table 3. Moreover, we downloaded miRNA expression data as well as clinical information of HNSC patients from The Cancer Genome Atlas (https://portal.gdc.cancer.gov/repository)⁴³ for further analysis. Concretely, the miRNA expression data contain 567 HNSC samples: 44 normal samples and 523 tumor samples. We first perform a 5-fold CV to assess the classification ability of the predicted miRNAs in differentiating the normal samples from tumor samples. As expected, these miRNAs achieved a mean classification accuracy of 0.92, indicating their strong classification power in HNSC (Figure 5A). We then carried out a differential expression analysis by using the R package edgeR.⁴⁴ As a result, we found that 2 of the top 3 predicted miRNAs, hsa-mir-125b-1 and hsa-mir-125b-2, were significantly differentially expressed (false discovery rate [FDR] < 0.05 and log fold-change [|logFC|] > 1). Therefore, we further tested whether these two miRNAs were also significantly differentially expressed at different tumor stages by one-way ANOVA. Specifically, 5 pathological stages—G1, G2, G3, G4, and GX—were recorded in the clinical information, and the test results confirmed that their expression levels were indeed altered at varying stages (Figure 5B). Last, we carried out a Kaplan-Meier survival analysis to assess their potential prognostic role for HNSC by using the R package survival (Figure 6). Intriguingly, we found that patients with a lower expression level have a higher survival rate. In summary, our analysis indicated that the two miRNAs were closely related to HNSC and that they could serve as potential prognostic markers for clinical diagnosis.

Table 3.

Top 10 miRNAs related to HNSC based on our method.

miRNA	p Value	logFC	FDR
hsa-mir-125b-1	2.59e−16	−1.001610441	5.23e−15
hsa-let-7a-1	2.50e−08	−0.606930394	2.13e−07
hsa-mir-125b-2	1.15e−17	−1.061612358	2.70e−16
hsa-let-7a-3	2.64e−08	−0.60496417	2.23e−07
hsa-let-7a-2	2.23e−08	−0.609628999	1.92e−07
hsa-let-7b	0.000766178	−0.367610987	3.24e−03
hsa-let-7e	0.606511339	−0.068722721	9.64e−01
hsa-mir-1-1	9.77e−27	−3.369305544	4.08e−25
hsa-mir-221	0.045288057	0.252113845	1.16e−01
hsa-mir-145	8.05e−06	−0.563207754	4.80e−05

The first column represents the miRNA names predicted by SwMKML. The second column represents the p value of the significance of differential expression for each miRNA. The third column represents the log2 fold change. The fourth column represents the adjusted p value of the differential analysis.

Figure 5.

Analysis for the Top 10 Predicted miRNAs

(A) Classification accuracy of the top 10 predicted miRNAs under 5-fold CV. (B) The expression level of has-mir-125b-1 and hsa-mir-125b-2 at different tumor stages.

Figure 6.

Kaplan-Meier Survival Analysis for hsa-mir-125b-1 and hsa-mir-125b-2, Identified as Prognostic Biomarkers in HNSC

As observed, patients with a lower expression level have a higher survival rate.

Discussion

It has been found that miRNAs play increasingly important roles in physiological processes and even complex human diseases. Researchers have attempted to make miRNAs valuable biomarkers for disease prevention, diagnosis, and treatment. Because of the inefficiency and high cost of experimental methods, many computational models have been developed to make effective predictions, such as graph-based methods, network topology-based methods, and the most widely used machine learning-based methods. In this paper, we propose a novel SwMKML method to predict potential miRNA-disease associations based on a miRNA functional similarity matrix, disease semantic similarity matrix, Gaussian interaction profile kernel similarity matrix, and association matrix between miRNAs and diseases. Specifically, our method learned an optimal kernel matrix adaptively from multiple kernel matrices for both miRNAs and diseases, respectively. We also propose a unified optimization process to update the predicted miRNA-disease association synchronously according to a graph-based, multi-label learning framework. As a result, comparative experiments conducted using our method and several state-of-the-art methods confirmed the superior performance and practicability of the proposed method. Last, the case study of head and neck neoplasms further validated the prediction ability of our method, and two miRNAs, hsa-mir-125b-1 and hsa-mir-125b-2, were identified as potential prognostic markers for HNSC.

The main reasons for the success of our model are 3-fold. First, the kernel matrices learned for both miRNAs and diseases during the optimization process were optimal kernels instead of a simple linear combination of base kernels. Moreover, the set of Gaussian kernels constructed with varying bandwidth parameters better characterized the known miRNA-disease associations from multiple views. Notably, our method is highly scalable because it only requires the miRNA-disease associations to fulfill the prediction task. Last but not least, the predictions of the miRNA-disease associations from both optimization spaces were unified by leveraging the multi-label learning framework. Nevertheless, there were also some limitations in our model. Because our method is a multi-kernel learning method, the given miRNA similarity matrix as well as disease similarity matrix has to be kernelized in advance, and different kernelization strategies might lead to different results. It remains a challenging task to balance the three trade-off parameters involved in our objective function to reach a global optimum.

Materials and Methods

Human miRNA-Disease Associations

The human miRNA-disease associations dataset used in this paper was downloaded from HMDD v.2.0, which includes 6,088 experimentally verified associations between 328 diseases and 550 miRNAs.⁴⁵ For simplicity, we use $Y\in {\mathbb{R}}^{nd\times nm}$ to represent the known miRNA-disease association matrix. If miRNA m_i is related to disease d_j, then the entry Y(m_i,d_j) is 1 and 0 otherwise. Furthermore, the variables nm and nd represent the number of miRNAs and diseases in the dataset, respectively.

Disease Semantic Similarity

The development of the Mesh database provides great convenience for studying the relationship among diseases.⁴⁶ Concretely, the relationship between different diseases in the database can be represented by a directed acyclic graph (DAG).⁴⁷ A disease D can be represented as DAG_(D) = (D,T(D),E(D)), where T(D) represents both D and its ancestor nodes, and E(D) represents all direct edges from parent nodes to child nodes. The contribution value of disease d to the semantic value of disease D can be formed as follows:

$$\{\begin{array}{l}{D}_D\left(d\right)=1ifd=D\\ D_D\left(d\right)=\max \left\{\Delta \ast D_D\left(d^{\text{'}}\right)|d^{\text{'}}\in childrenofd\right\}ifd\ne D\end{array},$$ (Equation 1)

where Δ = 0.5 is the semantic contribution factor. For disease D, the contribution value to itself can be set to 1. From the representation of DAG mentioned above, we can finally conclude the semantic value of disease D as

$$DV\left(D\right)={\sum }_{d\in T\left(D\right)}D{}_D\left(d\right).$$ (Equation 2)

Therefore, the semantic similarity between disease d_i and disease d_j can be calculated as follows:

$$S\left(d_i,d_j\right)=\frac{{\sum }_{d\in T\left(d_i\right)\cap T\left(d_j\right)}\left(D_{d_i}\left(d\right)+D_{d_j}\left(d\right)\right)}{DV\left(d_i\right)+DV\left(d_j\right)}.$$ (Equation 3)

According to Equation 3, we obtained the disease semantic similarity matrix$A_D\in {\mathbb{R}}^{nd\times nd}$.

miRNA Functional Similarity

Wang et al.⁴⁸ introduced a novel method to calculate miRNA functional similarity in terms of the associated disease terms. Here we directly downloaded the miRNA functional similarity score for the 550 miRNAs from http://www.cuilab.cn/files/images/cuilab/misim.zip.⁴⁵ We use $A_M\in {\mathbb{R}}^{nm\times nm}$ to denote the obtained similarity matrix for miRNAs, and (A_M)_ij measures the closeness between m_i and m_j.

Gaussian Interaction Profile Kernel Similarity

Based on the current miRNA-disease interaction prediction problem, we prefer the Gaussian kernel approach, which can construct a kernel matrix from the miRNA-disease interaction profiles. Gaussian interaction profile kernel similarity is the most popular method, and it has already been confirmed as an effective method for measuring similarities. For a given miRNA i or disease j, y(m_i) or y(d_j) is the interaction profile for the i-th row or the j-th column of the miRNA-disease association matrix. Therefore, the Gaussian interaction profile kernel similarity is defined as follows for both miRNA m_i and disease d_j:

$$K_{GIP,d}\left(d_i,d_j\right)=\exp \left(-{\gamma }_d{\Vert y\left(d_i\right)-y\left(d_j\right)\Vert }^2\right)\text{and}$$ (Equation4)

$$K_{GIP,m}\left(m_i,m_j\right)=\exp \left(-{\gamma }_m{\Vert y\left(m_i\right)-y\left(m_j\right)\Vert }^2\right),$$ (Equation 5)

where γ_d and γ_m are determined by the following transformation:

$${\gamma }_d={{\gamma }^{\prime }}_d/\left(\sum _{i=1}^{nd}\Vert y\left(d_i\right)\Vert /nd\right)\text{and}$$ (Equation 6)

$${\gamma }_m={{\gamma }^{\prime }}_m/\left(\sum _{i=1}^{nm}\Vert y\left(m_i\right)\Vert /nm\right),$$ (Equation 7)

where ${{\gamma }^{\prime }}_d$ and ${{\gamma }^{\prime }}_m$ are the kernel bandwidth. We denote $A_M^{\left(i\right)}\in {\mathbb{R}}^{nm\times nm}$ and$A_D^{\left(j\right)}\in {\mathbb{R}}^{nd\times nd}$ (i,j = 1,2,…,7) for the K_GIP,m, and K_GIP,d for both the miRNA space and disease space.

Kernelization

Because our method is based on multi-kernel learning, we first need to make the given miRNA similarity matrix A_M as well as the disease similarity matrix A_D positive semi-definite. As we know, a real symmetric matrix S could be decomposed into S = UΛU^T, where U is an orthogonal matrix, and Λ is a diagonal matrix of real eigenvalues with Λ = diag(λ₁,λ₂,…,λ_n). Previous studies have considered different spectrum modifications to make S positive semi-definite, such as spectral shift, flip, and clip. Here we adopted spectrum shift because it only strengthens the self-similarities and does not change the similarity between any two different samples:⁴⁹

$$S=U\left(\Lambda +\left|\min \left({\lambda }_{\min }\left(S\right),0\right)\right|I\right)U^T,$$ (Equation 8)

where λ_min(S) is the minimum eigenvalue of S. According to Equation 8, we converted A_M and A_D into the corresponding kernel matrices.

SwMKML

To fully understand the rationale behind our model, we first briefly introduced the single-kernel learning (SKL) framework on which SwMKML is based. In general, the SKL could be formulated as⁵⁰

$$\underset{S,F}{\min }Tr\left(K-2KS+S^{T}KS\right)+\gamma {\Vert S\Vert }_F^2+\alpha Tr\left(F^{T}LF\right),s.t.S\ge \text{0,}$$ (Equation 9)

where K represents the kernel matrix constructed from the input data, and S is the similarity matrix that will be learned from K. L = D-S is the Laplacian matrix, and D is the diagonal degree matrix, with its i-th diagonal element defined as $d_{ii}={\sum }_j\left(s_{ij}+s_{ji}\right)/2$. In particular, F could be the class indicator matrix or label matrix, depending on whether this framework is applied to unsupervised or semi-supervised problems.51, 52 Therefore, we can obtain the multi-kernel learning framework by extending Equation 9 as follows:

$$\underset{S,P,K}{\min }Tr\left(K-2KS+S^{T}KS\right)+\gamma {\Vert S\Vert }_F^2+\alpha Tr\left(F^{T}LF\right)+\beta \sum _{i=1}^l{w}_i{\Vert H^i-K\Vert }_F^2,s.t.S\ge 0,$$ (Equation 10)

where Hⁱ (i = 1,…,l) is one of the input kernel matrices. Specifically, the kernel weight parameter w_i is defined as

$$w_i=\frac{1}{2{\Vert H^i-K\Vert }_F}.$$ (Equation 11)

Although w_i is dependent on K, we could update its value alternatively after obtaining K. As a result, the weight assignment for each kernel matrix is totally self-weighted. According to Equation 10, we could obtain the optimization function in miRNA space by substituting the variables in Equation 10 with matrices constructed in miRNA space:

$$\begin{array}{l}\underset{S_M,F,K_M}{\min }Tr(K_M-2K_M{S}_M+S_M^T{K}_M{S}_M)+{\Vert S_M\Vert }_F^2+\alpha Tr\left(F{L}_{S_M}{F}^T\right)+\beta \sum _{v=1}^8{W}_M^{\left(v\right)}{\Vert A_M^{\left(v\right)}-K_M\Vert }_F^2\hfill \\ s.t.S_M\ge 0\hfill \end{array},$$ (Equation 12)

where$L_{S_M}=D_{S_M}-\left(S_M^T+S_M\right)/2$ is the Laplacian matrix, and the degree matrix $D_{S_M}\in {\mathbb{R}}^{nm\times nm}$ is defined as a diagonal matrix whose i-th diagonal element is ${\sum }_j\left({\left(S_M\right)}_{ij}+{\left(S_M\right)}_{ji}\right)/2$. Similarly, we define the objective function in the disease space as follows:

$$\begin{array}{l}\underset{S_D,F,K_D}{\min }Tr(K_D-2K_D{S}_D+S_D^T{K}_D{S}_D)+{\Vert S_D\Vert }_F^2+\alpha Tr\left(F^T{L}_{S_D}F\right)+\beta \sum _{v=1}^8{W}_D^{\left(v\right)}{\Vert A_D^{\left(v\right)}-K_D\Vert }_F^2\hfill \\ s.t.S_D\ge 0\hfill \end{array}.$$ (Equation 13)

The definition of variables in the disease space is equivalent to that in the miRNA space. Finally, instead of simply combining these two objective functions with equal weights, we integrate them into one overall optimization formulation in terms of the graph-based, multi-label learning framework:

$$\underset{S_M,S_D,F,K_M,K_D}{\min }Tr(K_M-2K_M{S}_M+S_M^T{K}_M{S}_M)+{\Vert S_M\Vert }_F^2+\alpha Tr\left(F{L}_{S_M}{F}^T\right)+\beta \sum _{v=1}^8{W}_M^{\left(v\right)}{\Vert A_M^{\left(v\right)}-K_M\Vert }_F^2+Tr(K_D-2K_D{S}_D+S_D^T{K}_D{S}_D)+{\Vert S_D\Vert }_F^2+\alpha Tr\left(F^T{L}_{S_D}F\right)+\beta \sum _{v=1}^8{W}_D^{\left(v\right)}{\Vert A_D^{\left(v\right)}-K_D\Vert }_F^2+\gamma {\Vert F-Y\Vert }_F^{2}s.t.S_M\ge 0,S_D\ge 0.$$ (Equation 14)

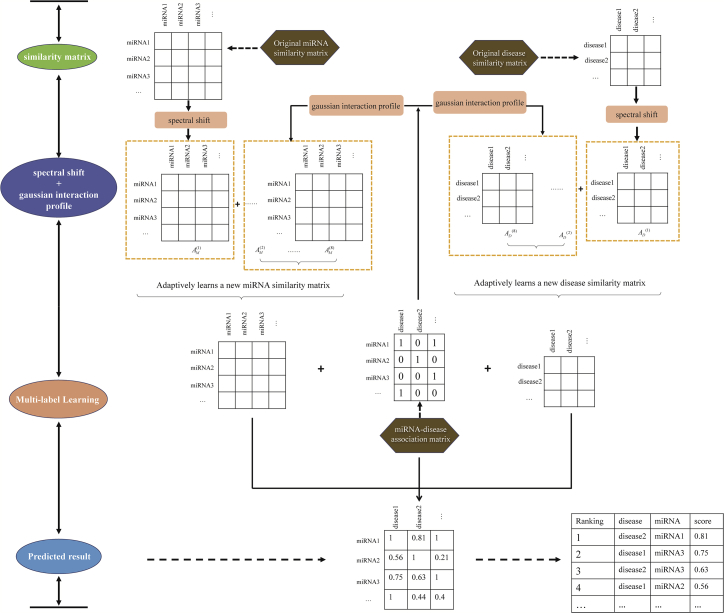
An overall workflow of the SwMKML method to predict the disease-related miRNAs is shown in Figure 7.

Figure 7.

Integrated Flow Chart of SwMKML to Predict Disease-Related miRNAs

Optimization

We divide the problem in Equation 14 into three subproblems with regard to miRNA space and disease space, respectively. We then develop an iterative algorithm to solve these problems alternatively.

Update S_M. By fixing the other variables, the optimization for S_M from Equation 14 can be derived as

$$\begin{array}{l}\underset{S_M}{\min }Tr\left(-2K_M{S}_M+S_M^T{K}_M{S}_M\right)+{\Vert S_M\Vert }_F^2+\alpha Tr\left(F{L}_{S_M}{F}^T\right)\hfill \\ s.t.S_M\ge 0\hfill \end{array}.$$ (Equation 15)

Note that the problem (Equation 15) is independent for different i; thus, we can solve the problem separately for each i. Based on ${\sum }_{ij}\left(1/2\right){\Vert F_i-F_j\Vert }_2^2{\left(S_M\right)}_{ij}=Tr\left(F{L}_{S_M}{F}^T\right)$, we can equivalently solve the following problem for each i individually:

$$-2{\left(K_M\right)}_i{\left(S_M\right)}_i+{\left(S_M\right)}_i^T{K}_M{\left(S_M\right)}_i+{\left(S_M\right)}_i^T{\left(S_M\right)}_i+\frac{\alpha }{2}{G}_i^T{\left(S_M\right)}_i,$$ (Equation 16)

where$G_i\in {\mathbb{R}}^{n\times 1}$ with $g_{ij}={\Vert F_i-F_j\Vert }_2^2$. By setting its first derivative with respect to (S_M)_i to zero, we can obtain

$${\left(S_M\right)}_i={\left(I+K_M\right)}^{-1}\left({\left(K_M\right)}_i-\frac{\alpha G_i}{4}\right).$$ (Equation17)

Update K_M. By fixing the other variables, Equation 14 can be rewritten as

$$\underset{K_M}{\min }Tr\left(K_M-2K_M{S}_M+S_M^T{K}_M{S}_M\right)+\beta \sum _{v=1}^m{W}_M^{\left(v\right)}{\Vert A_M^{\left(v\right)}-K_M\Vert }_F^2.$$ (Equation 18)

By differentiating Equation 18 with respect to K_M, we could obtain:

$$K_M=\frac{2S_M^T-S_M{S}_M^T-I+2\beta \sum _{v=1}^m{W}_M^{\left(v\right)}{A}_M^{\left(v\right)}}{2\beta \sum _{v=1}^m{W}_M^{\left(v\right)}}.$$ (Equation 19)

After we obtained K_M, we could update the weight value for each view as follows:

$$W_M^{\left(v\right)}=1/\left(2{\Vert K_M-A_M^{\left(v\right)}\Vert }_F\right).$$ (Equation 20)

Because the optimization in disease space is the same as that in miRNA space, we could derive the formulas to optimize S_D, K_D and $W_D^{\left(v\right)}$ as follows:

$${\left(S_D\right)}_i={\left(I+K_D\right)}^{-1}\left({\left(K_D\right)}_i-\frac{\alpha G_i}{4}\right),$$ (Equation 21)

$$K_D=\frac{2S_D^T-S_D{S}_D^T-I+2\beta \sum _{v=1}^d{W}_D^{\left(v\right)}{A}_D^{\left(v\right)}}{2\beta \sum _{v=1}^d{W}_D^{\left(v\right)}},\text{and}$$ (Equation 22)

$$W_D^{\left(v\right)}=1/\left(2{\Vert K_D-A_D^{\left(v\right)}\Vert }_F\right),$$ (Equation 23)

where $G_i\in {\mathbb{R}}^{n\times 1}$ with its j-th element defined as$g_{ij}={\Vert F_i-F_j\Vert }_2^2$.

Update F. Equation 14 is transformed into the following formula by fixing the other four variables:

$$\underset{F}{\min }\alpha Tr\left(F{L}_{S_M}{F}^T\right)+\alpha Tr\left(F^T{L}_{S_D}F\right)+\gamma \sum _{i=1}^n{\Vert F_i-Y_i\Vert }^2.$$ (Equation 24)

By differentiating Equation 24 with respect to F and setting it to zero, we could obtain the following formula:

$$\left(\alpha L_{S_M}+\gamma I\right)F+\alpha F{L}_{S_D}-\gamma Y=0.$$ (Equation 25)

Obviously, Equation 25 is a Sylvester equation and can be easily solved.⁵³ The overall procedure for solving Equation 14 is summarized in Box 1. The dataset used in this paper as well as the source code of SwMKML is available at https://github.com/JiaMuL/SwMKML.

Box 1. Algorithm to Solve Equation 14.

Input: miRNA similarity matrices of n views {$A_M^{\left(1\right)}$,$A_M^{\left(2\right)}$, …, $A_M^{\left(n\right)}$}, disease similarity matrices of m views {$A_D^{\left(1\right)}$, $A_D^{\left(2\right)}$, …, $A_D^{\left(m\right)}$}, known association matrix $Y\in {\mathbb{R}}^{nd\times nm}$, the parameters α, β and γ.

Output: Predicted association matrix F.

• 1. Initialize the weights of each view for both miRNAs and diseases with $W_M^{\left(v\right)}=1/n$, $W_D^{\left(u\right)}=1/m$.

• 2. Repeat:

• 3. Repeat:

• 4. Update S_M by solving problem (17).

• 5. Update K_M by solving problem (19).

• 6. Update S_D by solving problem (21).

• 7. Update K_D by solving problem (22).

• 8. Update F by solving problem (25).

• 9. Until convergence

• 10. Update $W_M^{\left(v\right)}$, $W_D^{\left(u\right)}$ according to Equation (20) and Equation (23).

• 11. Until convergence

• 12. Return S_M, K_M, S_D, K_D, F

Author Contributions

C.L. and Z.P. conceived the study. C.L., Z.P., and J.L. developed the algorithm and analyzed the results. C.L. and Z.P. wrote this paper. H.Z., G.L., Q.X., and P.D. supervised this study. All authors read and approved the final manuscript.

Conflicts of Interest

The authors declare no competing interests.