Advancing the Study of Adolescent Substance Use Through the Use of Integrative Data Analysis

Abstract

A wealth of information is currently known about the epidemiology, etiology, and evaluation of drug and alcohol use across the lifespan. Despite this corpus of knowledge, much has yet to be learned. Many factors conspire to slow the pace of future advances in the field of substance use including the need for long-term longitudinal studies of often hard-to-reach subjects who are reporting rare and episodic behaviors. One promising option that might help move the field forward is integrative data analysis, or IDA. IDA is a principled set of methodologies and statistical techniques that allow for the fitting of statistical models to data that have been pooled across multiple, independent samples. IDA offers a myriad of potential advantages including increased power, greater coverage of rare behaviors, more rigorous psychometric assessment of theoretical constructs, accelerated developmental time period under study, and enhanced reproducibility. However, IDA is not without limitations and may not be useful in a given application for a variety of reasons. The goal of this paper is to describe the advantages and limitations of IDA in the study of individual development over time, particularly as it relates to trajectories of substance use. An empirical example of the measurement of polysubstance use is presented and the paper concludes with recommendations for practice.

Introduction

Adolescent substance use has long been known to represent a significant, multifaceted problem in the United States. The most recent surveillance data for secondary school students shows that a high proportion of youth are using alcohol and illicit drugs. For example, in 2016 a national survey found that 22.8% of 8th graders, 43.4% of 10th graders, and 61.2% of 12th graders having initiated alcohol use; 8.6% of 8th graders, 26.0% of 10th graders, and 46.3% of 12th graders reported having been drunk at least once in their life; and 17.2% of 8th graders, 33.7% of 10th graders, and 48.3% of 12th graders reported having initiated the use of illicit drugs (Miech, Johnston, O’Malley, Bachman, Schulenberg, & Patrick, 2017). There is also the economic costs associated with underage youth drinking. Sacks, Gonzales, Bouchery, Tomedi, and Brewer (2015) estimated underage drinking cost the United States 24.3 billion dollars in 2010. Even more troubling is the strong relation between adolescent drug and alcohol use and car and motorcycle accidents, high risk sexual behavior, and even death (USDHHS, 2007). Evidence suggests that drug use during adolescence has longer-term negative impacts on various facets of functioning including biological and pubertal development (Emanuele, Wezeman, & Emanuele, 2002; Tapert, Caldwell, & Burke, 2004). There are also unambiguous negative psychosocial outcomes including lower educational status, challenges navigating the transition to emerging adulthood, and longer-term psychological impairments in adulthood (e.g., Hussong & Chassin, 2004; Trim, Meehan, King, & Chassin, 2007). There are clearly a myriad of negative sequelae associated with adolescent alcohol and drug use and abuse.

Given the critical importance of better understanding the course, causes, and consequences of adolescent substance use, there have been many recent advances in the theoretical conceptualization and empirical evaluation of developmental pathways leading to the onset and acceleration of drug and alcohol use. For example, models of deviance proneness posit that substance use occurs in parallel with the development of broad spectrum conduct problems (e.g., Sher, Grekin, & Williams, 2005). A number of related theories, including developmental cascade models, posit that substance use behavior arises from the continued interactions between deficits in multiple contexts – including parental competence and monitoring, behavioral control, and social competence – across development (Dodge et al., 2009; Haller, Handley, Chassin, & Bountress, 2010; Eiden et al., 2016). Further, models incorporating biological pathways hypothesize that children exposed to a family history of substance abuse and dependence are at an elevated risk for drug and alcohol use themselves (Chassin, Hussong, & Beltran, 2009; Chassin, Presson, Pitts, & Sherman, 2000). Thus much is known about both the epidemiology and etiology of child and adolescent substance use; however, a number of ongoing challenges exist that slow the rate of progress that might otherwise be made.

Common Challenges Encountered in Substance Use Research

It is a hopeful sign that alcohol and drug use is a relatively rare behavior in children and young adolescents. Notwithstanding, when youth behavior is surveyed this often results in low endorsement rates of substance use that in turn leads to low power and instability in model estimation. Similarly, high-risk samples of children and adolescents are difficult to obtain, and this may lead to decreased heterogeneity in the demographic and psychosocial characteristics of the sample that subsequently limits the generalizability of findings. Another significant challenge is the need to repeatedly assess individuals over time to allow for the important disaggregation of within-person and between-person influences on developmental change (Curran & Bauer, 2011). Finally, nearly all contemporary theories of etiology, risk, and resilience require the testing of sometimes complex mediating and moderating influences in models of individual stability and change over time, and this often requires high quality data drawn from moderate to large samples of individuals.

In addition to these study-specific challenges, there are a myriad of related difficulties stemming from the so-called “replicability crisis” in psychology (e.g., Maxwell, Lau, & Howard, 2015). There is a broadening consensus that the social, behavioral, and health sciences do not have a strong history of building a cumulative and reproducible science. More than four decades ago Paul Meehl famously wrote “It is simply a sad fact that in soft psychology theories rise and decline, come and go, more as a function of baffled boredom than anything else; and the enterprise shows a disturbing absence of that cumulative character that is so impressive in disciplines like astronomy, molecular biology, and genetics.” (Meehl, 1978, p. 807, emphasis in original). More recent concerns have been voiced about the associated challenge of reproducibility or, more importantly, the failure to replicate prior findings (e.g., Cesario, 2014; Open Science Collaboration, 2012).

In some ways the “replicability crisis” may seem unsurprising because the empirical study of individual behavior is awash in small effect sizes and low statistical power that are naturally difficult to reproduce (Maxwell, 2004). Further, empirical results are largely driven by the idiosyncratic characteristics of a given set of items used in a single study (e.g., Curran, 2009). However, many of these issues can be resolved through the lens of moderation; that is, reframing the research question from “whether a hypothesized effect exists” to “for what type of person in what context and at what developmental stage” a hypothesized effect exists. The challenges of replication and moderation are particularly salient in the study of child and adolescent substance use and must be addressed if we are to progress as a field.

There are thus a plethora of challenges that potentially limit our development of a comprehensive understanding of the risk and protective factors that influence the etiology of child and adolescent substance use. However, several of these issues can be mitigated through the use of an exciting new set of methodologies that broadly referred to as integrative data analysis, or IDA. As we describe in detail below, IDA is a principled method that allows for the fitting of statistical models to data that have been pooled across multiple, independent samples. There are distinct advantages offered by IDA that are particularly relevant in the study of high-risk behavior such as drug and alcohol use, and these advantages extend to a broad array of other research settings as well. Nevertheless, there are also many challenges and potential limitations that have limited the use of IDA in practice. The goal of our article is to describe IDA and demonstrate its uses in the hope that these methods might be more widely used in future research applications.

We begin with an introduction to and definition of IDA; we then discuss the potential advantages and disadvantages of IDA in practice; next, we present a worked example of IDA as applied to the study of developmental trajectories of substance use ranging from childhood to young adulthood; finally, we describe potential limitations of IDA and offer recommendations about the use of these methods in practice.

Integrative Data Analysis

Integrative data analysis (IDA) is a set of methodologies that allow for the fitting of statistical models to data that have been pooled over multiple independent sources (Curran, 2009; Curran & Hussong, 2009; Hussong, Curran & Bauer, 2013). The core concepts underlying IDA are far from new and early examples include the use of individual patient data meta-analysis (e.g., Lambert, Sutton, Abrams & Jones, 2002) and “mega-analysis” that uses pooled raw data as an alternative to “meta-analysis” that is typically based on summary statistics (e.g., DeRubeis, Gelfand, Tang, & Simons, 1999; McArdle & Horn, 2002). IDA draws on this prior work to significantly extend the approach and use formal psychometric models that can address the critical issue of commensurate measurement (Bauer, 2017; Bauer & Hussong, 2009). More specifically, IDA provides a set of tools for computing psychometrically-informed scale scores based on items that may appear in some contributing studies but not others, and may differ in content, response scale, or both. Further, IDA has the potential to differentially weight these sets of items as a function of characteristics of the individual (e.g., gender, age) and of the contributing study (e.g., sampling design, ethnic composition).

There are numerous advantages associated with the use of IDA that apply to almost any research application. For example, a logical advantage is the increase in statistical power and precision resulting from the pooling of multiple independent samples (e.g., Curran & Hussong, 2009). Holding effect size constant, statistical power will increase given larger numbers of observations in the pooled sample. Similarly, the pooling of multiple samples will often result in greater between-subject heterogeneity in demographic and psychosocial characteristics that in turn enhance external validity and generalizability. Further, a key potential advantage is the broader psychometric assessment of theoretical constructs under study resulting from the use of different item sets across study. For example, internalizing symptomatology might be assessed using a combination of unique and shared items drawn across the set of contributing studies, and this enhances the psychometric assessment of depression and anxiety beyond what would be possible with fewer items obtained from just one study alone (e.g., Curran et al., 2014). Finally, IDA allows for the testing of novel hypotheses based on the pooled aggregate data that could not be evaluated within any of the individual contributing studies. IDA clearly has much promise in nearly any research application within the behavioral and health sciences.

However, there are several particularly salient advantages that IDA offers to the developmental study of high-risk behaviors such as adolescent substance use. First, it is increasingly clear that longitudinal data are the gold standard for inference about development as this allows for the disaggregation of between-person and within-person differences in traits as they unfold (e.g., Curran & Bauer, 2011). However, because of practical and financial limitations, most developmental studies are not able to follow a large sample of subjects at regular, frequently-spaced intervals across a broad span of development. Using concepts drawn from accelerated longitudinal designs, (e.g., Nesselroade & Baltes, 1979), IDA offers the possibility of pooling overlapping developmental cohorts that can “stretch” or elongate the developmental period under study (Hussong et al., 2013). For example, if one study followed children from ages five to 15, a second from ages 10 to 20, and a third from ages 15 to 25, the aggregate sample covers development from age five to 25. Having this wide an age range provides a significant advantage in any developmental research study but is particularly important for modeling developmental trajectories of substance use over time.

Second, as we noted earlier, drug use in childhood and early adolescence is often a rare behavior resulting in low observed endorsement rates across both individuals and time points. Although this may be an accurate reflection of the phenomena, these low endorsement rates also introduce low power, loss of efficiency, and significant instability in model estimation. These challenges combine to limit the types of models that can be estimated and the types of hypotheses that can be evaluated. While the pooling of multiple independent samples will not necessarily increase the marginal endorsement rates (e.g., each contributing study may only have 3% endorsement of rare behaviors), it does increase the actual number of respondents who endorse a given item. For example, five individual studies with sample sizes of 200 would each have six children endorsing an item with a base rate of 3%, but the aggregate sample would combine to have 30 children endorsing the same pooled item. These higher numbers of observed behaviors have significant advantages in the types of models that can be estimated and the confidence one has in the resulting findings.

Finally, a substantial challenge faced in any single-study design is the natural limitation of the generalizability of findings to individuals who are similar to those in the sample.¹ This not only restricts our ability to draw broader conclusions about the developmental and etiological processes at hand, but it also contributes to the contemporary problems of reproducibility described earlier. The pooling of multiple samples, each of which may reflect different study-specific characteristics such as sampling frame, demographic composition, geographic location, or any number of other factors, offers two distinct advantages. First, the aggregate sample is characterized by far greater between-subject heterogeneity than does any one of the contributing samples. Second, this heterogeneity allows for the testing of study-specific characteristics that might serve as moderators of the hypothesized developmental processes. These moderators thus provide a mechanism for internal replication in which the magnitude of the hypothesized effects are formally tested within and across the set of contributing studies. Though replicability is often conceptualized in terms of multiple, separate, independent studies obtaining the same result, pooling across multiple studies provides a much more rigorous test of the research hypotheses.

Current Uses of IDA in Practice

The National Institutes of Health (2003) actively endorses the sharing of extant datasets between research groups. Required to accomplish these goals are methods supporting principled analysis of pooled datasets. As such, IDA has seen recent applications in the study of developmental psychopathology and substance use including the development of internalizing symptomatology (Hussong et al., 2008; Hastings et al., 2015; Mills et al., 2012; Perrino et al., 2014) and externalizing symptomatology (Hussong, Huang, Curran, Chassin, & Zucker, 2010; Perrino et al., 2014). Additionally, IDA has helped to reconcile between-study differences in the measurement of a number of substance use-related constructs, including alcohol use (Witkiewitz, Hallgren, O’Sickey, Roos, & Maisto, 2016; Huh et al, 2016), marijuana use (Silins et al., 2014), tobacco use (Rose, Dierker, Hedeker, & Mermelstein, 2013), and general drug use involvement (Greenbaum et al., 2015). Outside of the study of substance use and developmental psychopathology, IDA has been applied to a wide range of phenomena such as health and personality in development (e.g., Pedersen et al., 2013; Kern, Hampson, Goldberg, & Friedman, 2014), aging (e.g., McArdle et al., 2009), and depression treatment (e.g., Brown et al., 2016; Gibbons, Brown, Hur, Davis, & Mann, 2012a, 2012b).

IDA has been especially useful in helping researchers address mismatches across studies in the measurement of substance use symptoms when pooling data. For instance, Rose et al. (2013) investigated differences between two independent studies in the measurement of nicotine dependence by DSM-IV criteria. Although these 14 diagnostic criteria (e.g., experiencing withdrawal, needing to smoke more to feel satisfied) are common to any study using the DSM-IV, they were assessed in these two studies using different instruments. Moreover, the studies relied on different item prompts and response options to assess the criteria. Using IDA, the researchers found that one of the items captured nicotine differentially well between the two studies and they were able to account for this difference when estimating individuals’ levels of nicotine dependence. Witkiewitz et al. (2016) used IDA to address a similar problem in the measurement of adult alcohol dependence. Using data from four studies, these authors successfully assessed whether a number of items, both within and outside of DSM-IV criteria, measured alcohol dependence equally well across different samples and instruments.

The evaluation of substance use prevention and treatment efforts is another area in which IDA has been applied to great effect (Greenbaum et al., 2015; Huh et al, 2015; Mun et al, 2015; Ray et al., 2014). For example, Mun et al. (2015) pooled across 24 studies of brief motivational interviewing (BMI) interventions for alcohol use disorders (AUD) in college students. Using a set of hierarchical IRT analyses, these researchers tested for differential item functioning in items used to assess AUD severity, allowing inferences about the effect of BMI on AUD symptoms to be made on the basis of all of the studies’ data (combined N = 12,360). Interestingly, this combined sample comprised studies that differed widely in their levels of AUD severity, including both volunteer and mandated samples; IDA allows for differences between these samples in AUD severity to be disaggregated from study-specific measurement differences. Similarly, Greenbaum et al. (2014) pooled across five independent studies to evaluate the effects of multidimensional family therapy (MDFT) on substance use disorder (SUD) severity in adolescents. As with Mun et al. (2015), the samples were highly heterogeneous, ranging from 16% to 100% of the sample meeting DSM-IV criteria for drug dependence, and 22% to 100% of the sample involved in the justice system. After measures of SUD severity were harmonized across studies, it was shown that the efficacy of MDFS differed across races and genders. These studies underscore the benefits of increased heterogeneity, as well as the ability to directly test hypotheses about measurement invariance, afforded by IDA.

Why is IDA Not More Widely Used?

Despite the many advantages IDA affords, this approach has not been as widely incorporated into substance use research as might be otherwise possible. Part of this is due to the natural limitations of the approach. For example, IDA may not be possible because there is incompatible measurement coverage across the set of contributing studies. It is a necessary condition that at least one or a small number of items be shared across contributing data sources; if this does not hold, then IDA is not possible. Similarly, if the goal of IDA is to accelerate the developmental span under study, the data sources must provide overlapping age cohorts, which then allows connections from study to study. Finally, in some applications the psychometric models become complex and simply fail to converge to appropriate solutions. In situations such as these, a number of options are available including a parallel analysis approach in which models are fit in each study individually and findings are compared with one another (Hofer & Piccinin, 2009; Hussong et al., 2013).

However, another factor that might serve to limit the broader use of IDA in practice is the relative newness of the methods and the associated lack of examples demonstrating applications of IDA in a given setting. IDA is a principled application of a set of existing and inter-related methods and techniques, yet as several articles in this Special Issue have pointed out, there are numerous steps that must be taken in terms of data management, variable scoring, and model fitting, the particular order of which can impact the subsequent results. We have described one possible ordering of steps in Curran et al. (2014) that includes the explication of the study hypotheses; the identification of potential contributing data sets; the development of a pool of items for each construct; the harmonization of item stems and responses when necessary (see Hansen et al. this issue); fitting psychometric models to test invariance within and between studies; and the estimation of scale scores to be used in subsequent pooled analyses. Additional or fewer steps may be required given the specifics of a given IDA application and are ultimately determined as a function of the research application and hypotheses at hand.

To highlight the potential that IDA offers to the study of high risk and maladaptive behaviors, we next turn to an example in which we combine subjects from three independent longitudinal samples and use eight items to create a measure of polysubstance use. Space constraints preclude a comprehensive presentation of all details of the analysis in this paper; instead, our intent is to provide a sufficiently clear description that highlights the many ways in which IDA might be used in similar research applications. Full details about all aspects of this modeling approach can be found elsewhere (Bauer, 2017; Bauer & Hussong, 2009; Curran et al., 2014, 2016; Hussong et al., 2013).

Example: Computing Polysubstance Use Scores Across Three Contributing Samples

Data for our example were drawn from three independent longitudinal studies of children of alcoholic parents and matched controls. These three studies are well suited for IDA due to the similar sampling of overlapping populations, the use of both unique and common items assessing alcohol and drug use, and the overlap in the developmental periods covered in each individual study. Further, each study is characterized by its own strong methodology including the use of community recruitments, the maintenance of high retention over time, and the incorporation of extensive assessment batteries. The contributing studies were the Michigan Longitudinal Study (MLS; Zucker et al., 2000), that contributed 634 individuals from ages 11 to 30; the Adolescent/Young Adult and Family Development Project (AFDP; Chassin, Barrera, Bech, & Kossak-Fuller, 1992), that contributed 847 individuals from ages 11 to 35; and the Alcohol and Health Behavior project (AHBP; Sher, Walitzer, Wood, & Brent, 1991), that contributed 485 individuals from ages 17 to 35. Taken together, the three studies administered multiple items assessing alcohol and drug use for 1,966 individuals providing 9,438 person-by-time observations spanning ages 11 to 35.

Covariates.

For the purpose of demonstration, we are selectively interested in a reduced set of items, although each study incorporated extensive assessment batteries. First, we consider four person-specific characteristics. These are status as a child of an alcoholic parent, or COA (0=neither biological nor custodial parent is alcoholic; 1=at least one biological and custodial parent is alcoholic); biological sex (0=female, 1=male); chronological age at time of assessment (in yearly integer increments centered at age 21)²; and study membership (1= MLS, 2=AFDP, 3=AHBP). In some models, study membership is captured via two dummy variables in which AFDP is the reference category. In the MLS, 71% of the sample were male and 76% were COA; in the AFDP, 52% were male and 51% were COA; in the AHBP, 47% were male and 49% were COA; and in the pooled sample, 57% were male and 58% were COA.

Assessment of substance use.

We considered eight items assessing substance use within a 12-month timespan: four items assessed different dimensions of alcohol use, and four measured the use of specific substances other than alcohol. Full details about item content, response options, and study contribution are presented in Table 1.³ Briefly, the four alcohol use items assessed the frequency of drunkenness, the consumption of five or more drinks in one sitting (i.e., binge drinking), the typical number of drinks consumed per occasion, and the typical frequency of drinking occasions; all items were assessed on an ordinal scale ranging from low to high (see Table 1). The four remaining items assessed past 12-month use of marijuana, stimulants, sedatives, and opiates/hallucinogens; all items were assessed on a binary scale indicating no use or at least some use. One alcohol item and all four illicit substance use items were present across all three contributing studies and the remaining three items were available in only two of the three studies. The partial availability of several items from a subset of contributing studies highlights a strength of IDA in that that entire set of items can be retained in the factor model given that that absent items are treated as missing at random (see Curran et al., 2014 for a description of how missing data are handled in IDA under various assumptions).

Table 1.

Item stems and response distributions for the calibration sample within each contributing study and for the pooled sample.

		Study
Item	Response	MLS	AFDP	AHBP	Pooled
1. Frequency of drunkenness in the past year	0=Never	432 (78%)	511 (60%)	--	943 (67%)
	1=1–5 times	66 (12%)	220 (26%)	--	286 (20%)
	2=6–11 times or 1–3 times per month	38 (7%)	87 (10%)	--	125 (9%)
	3=1–2 times a week or 3 times a week or more	21 (4%)	29 (3%)	--	50 (4%)
2. Frequency of drinking 5 or more drinks at one time in the past year	0=Never	--	470 (55%)	79 (32%)	549 (50%)
	1=1–5 times	--	213 (25%)	66 (27%)	279 (25%)
	2=6–11 times or 1–3 times per month	--	109 (13%)	61 (25%)	170 (16%)
	3=1–2 times a week or 3 times a week or more	--	55 (6%)	42 (17%)	97 (9%)
3. Number of drinks on one occasion in the past year	0=None or less than 1	--	265 (31%)	39 (8%)	304 (23%)
	1=1–2 total drinks	--	221 (26%)	122 (25%)	343 (26%)
	2=3–5 total drinks	--	308 (36%)	217 (45%)	525 (40%)
	3=6 or more total drinks	--	53 (6%)	104 (22%)	157 (12%)
4. Frequency of alcohol use (beer, wine, & liquor) in the past year	0=Never or less than once per month	426 (68%)	562 (72%)	112 (23%)	1100 (58%)
	1=1–3 times per month	120 (19%)	75 (10%)	144 (30%)	339 (18%)
	2=Weekly	85 (13%)	139 (18%)	226 (47%)	450 (24%)
5. Past year marijuana use	0=No	485 (77%)	686 (81%)	335 (69%)	1506 (77%)
	1=Yes	148 (23%)	160 (19%)	150 (31%)	458 (23%)
6. Past year stimulant use	0=No	598 (94%)	780 (92%)	427 (88%)	1805 (92%)
	1=Yes	35 (6%)	67 (8%)	58 (12%)	160 (8%)
7. Past year sedative use	0=No	613 (97%)	831 (98%)	463 (95%)	1907 (97%)
	1=Yes	18 (3%)	16 (2%)	22 (5%)	56 (3%)
8. Past year opiates/sedative use	0=No	606 (96%)	819 (97%)	438 (90%)	1863 (95%)
	1=Yes	26 (4%)	28 (3%)	47 (10%)	101 (5%)

Note: The response scales for the first four items were manually harmonized across the three studies to have the same ordinal structure.

Moderated nonlinear factor analysis.

Our motivating goal is to compute an individual- and age-specific scale score representing polysubstance use based on the responses to whichever of the eight items the individual was presented in their respective study. Importantly, we want to differentially weight the items in the composite as a function of age, sex, COA status, and study membership. To accomplish this, we will use the moderated nonlinear factor analysis (MNLFA) strategies first proposed by Bauer and Hussong (2009), demonstrated in Curran et al. (2014), evaluated in Curran et al. (2016), and expanded in Bauer (2017). The MNLFA draws on elements from nonlinear factor analysis and item response theory (IRT) models to build an integrated framework for incorporating a set of covariates that can influence the parameters that define the latent factor representing polysubstance use. These parameters include the mean and variance of the latent factors, and the factor loadings and intercepts for the set of items.⁴ Whereas an item intercept represents the predicted value of the item when the latent variable is held at zero, the factor loading represents the predicted increment in a subject’s response to the item associated with a one-unit increase in the latent variable.

Importantly, the MNLFA allows the covariates to exert direct influences on these factor- and item-specific parameters so that the estimated values can be systematically shifted as a function of the value of the covariates. For example, a given item might exert a stronger or weaker effect depending on whether the child is a COA, is female, is drawn from Study 1, and so on. This allows for the differential weighting of items as a function of the covariates when the scale scores are computed (Bauer, 2017).⁵ Comprehensive computer simulation studies have demonstrated that factor scores obtained in this way are psychometrically superior to those derived from more traditional methods that do not incorporate covariates (Curran et al., 2016).

The eight items will be used as multiple indicators to define the latent factor of polysubstance use. Because the items are discretely scaled (four are ordinal and four are binary) we will estimate the latent factor using maximum likelihood estimation with nonlinear link functions that relate each item to the underlying factor (Bauer & Hussong, 2009). However, at the same time we will include our set of covariates (age, sex, COA status, and study membership) to test for potential influences of the covariates on factor means and variances and item loadings and intercepts. The reason we do this is to “fine tune” the calculation of our polysubstance use scores. For example, if we were to find that several items were more strongly related to the latent factor at certain ages or for males or for subjects drawn from a given study, the influence of the covariates will correspondingly shift the estimated parameters to reflect this differential item functioning. These parameter shifts are then retained in the calculation of the scale scores. Figure 1 presents the summary path diagram for this comprehensive model.

Figure 1.

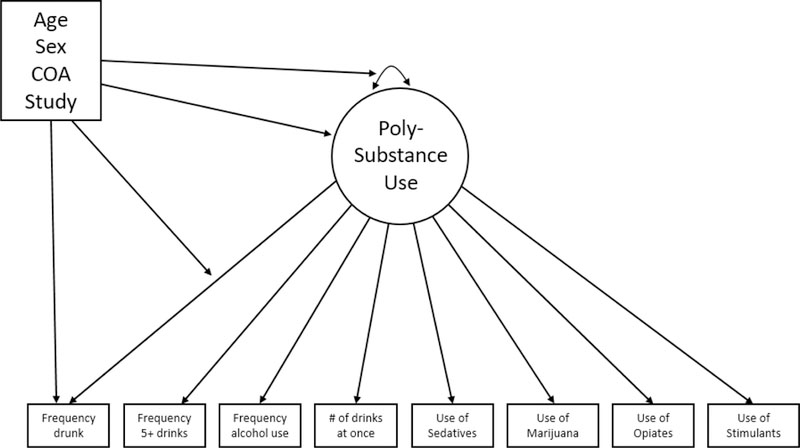
Conceptual path diagram of the moderated nonlinear factor analysis model for polysubstance use.

Note: Single-headed arrows linking the latent factor to the individual items represent the factor loadings; single-headed arrows linking the four predictor variables to the factor model indicate covariate effects on the factor mean and variance and on the item factor loadings and intercepts. This is a general depiction of the model and the specific effects identified in the final MNLFA model are described in the text.

Model building strategy.

We will follow the general model building strategy described in Curran et al. (2014). First, we select a calibration sample that represents a random draw of a single observation for each adolescent from the complete data file that will be used to build the scoring model; this is done to ensure independence among observations given that nearly all subjects provided multiple repeated assessments. For example, say an individual was assessed at five different occasions, a single one of these five assessments would be randomly selected and retained for the calibration sample. Second, we estimate an unconditional factor model within the calibration sample in which the eight items define the latent factor, but no covariates are included.⁶ Third, we include the set of covariates in the model and we regress the latent factor on the covariates to estimate mean impact. Fourth, we draw on the nonlinear constraints proposed in Bauer and Hussong (2009) to extend the factor model to estimate the covariate effect on the latent factor variance to evaluate variance impact. Fifth, we further extend the model to estimate the effects of the covariates on the factor loading and intercept for each item to evaluate differential item functioning, or DIF; covariate effects are estimated item-by-item and significant DIF is identified using a standard likelihood ratio test (or LRT) and all significant covariate effects are retained and non-significant effects are omitted. Sixth, once the final scoring model is determined, the resulting set of parameters are used to compute individual- and time-specific scale scores for all subjects at all time points in the full sample; these scores are called expected a posteriori estimates, or EAPs, and are then available for subsequent analyses.

Step 1: Calibration sample.

A calibration sample was selected in which a single random observation was drawn from each case in the sample. This resulted in a single assessment drawn from each of the 1,966 individuals pooling across all three studies. Table 1 presents summary statistics for the eight substance use items for each individual sample and for the calibration sample. It is immediately clear that the pooled sample results in substantially higher number of observed endorsements of the rare behaviors of hard drug use that will in turn help stabilize model estimation and improve precision in the calculation of scale scores. For example, for item 7 (past 12 month use of sedatives), 18 individuals endorsed this item in the MLS, 16 in the AFDP, and 22 in the AHBP, but this totaled 56 in the pooled calibration sample.

Step 2: Unconditional factor model.

An eight-item, one-factor model was estimated in which nonlinear link functions related each binary or ordinal item to the underlying latent factor. Omnibus measures of model fit (e.g., chi-square tests, fit indices) are not available in this type of nonlinear model. However, the factor model converged to a stable solution and factor loadings for all eight items were relatively large and significant indicating that the latent factor was well determined by the set of items.

Step 3: Mean impact.

The model obtained from Step 2 was then regressed on five covariates: age, sex, COA status, and two dummy variables that compared MLS to AFDP and AHBP to AFDP. Results indicated significantly higher means of polysubstance for children of alcoholics ($\widehat{\gamma }$= .39, se = .06), males ($\widehat{\gamma }$= .39, se = .06), older individuals ($\widehat{\gamma }$ = .04, se = .005), and individuals in AFDP relative to AHBP ($\widehat{\gamma }$= .38, se = .13). There were no significant mean differences between MLS and AFDP.

Step 4: Variance impact.

The model from Step 3 was then extended to include nonlinear constraints that linked the set of covariates to the variance of the latent factor. Whereas the mean impact model allowed for shifts in the latent mean as a function of the covariates, the variance impact model allows for shifts in the latent variance as a function of the same covariates. Results indicated that only one covariate was meaningfully related to the magnitude of the factor variance: subjects within the MLS had larger variances of polysubstance use compared to subjects within the AFDP ($\widehat{\gamma }$=.66, se=.16). There were no other covariate effects detected.

Step 5: Differential item functioning.

The model from Step 4 was then extended to allow for covariate effects on both the intercept and factor loadings for each of the eight items. As noted earlier, these were conducted in an item-by-item fashion (as detailed in Curran et al., 2014). For example, the five covariate effects would be introduced for just the first item and a likelihood ratio test would be computed to determine if the inclusion of the effects led to a significant improvement in model. Then these effects were removed and the process was repeated for the second item, and so on. For items with significant LRTs, the covariate effects were retained; for those with non-significant LRTs, the covariate effects were rejected. Of the eight items, three items were found to be invariant: frequency of drunkenness, frequency of binge drinking, and past year sedative use. A model positing invariance means that the item relates to the latent factor equivalently for levels of the covariate (e.g., it is equally strong for COAs and non-COAs, males and females, etc.). This is important to establish because these anchor items provided a strong basis for establishing a shared common metric of polysubstance use across the three contributing studies.

The remaining five items were non-invariant with varying degrees of loading and intercept DIF identified across the set of covariates. There were many identified covariate effects, and we do not detail these here; instead we will illustrate the findings by detailing the DIF found for the item past year stimulant use. Two covariate effects were found indicating that the factor loading for stimulant use was more strongly related to the polysubstance use factor for males and for subjects from the AHBP relative to females and subjects from the AFDP (the reference group). Further, two covariate effects were found for the item intercept indicating that stimulant use for males and for subjects from the AHBP had a higher item intercept relative to females and subjects from the AFPD (again the reference group). The set of covariate effects on all of the item loadings and intercepts will play an important role when computing scale scores for polysubstance use conducted in the sixth and final step.

Step 6: Scoring.

Once the final model was defined in Step 5, the resulting set of parameter estimates were used to compute factor scores for all individuals at all assessment periods. The technical details of this procedure are described in Bauer (2017) and Bauer and Hussong (2009). More colloquially, the final set of obtained parameter estimates from the MNLFA model are fixed as weights in what is functionally a highly complex calculator. Specifically, a numerical factor score is computed for each person at each age of assessment as a function of the scoring weights, the values on the covariates, and the observed responses on the set of eight substance use items. Importantly, the contribution of the individual items are up- or down-weighted as a function of the impact and DIF covariate effects that were identified in the prior steps. For example, in Step 5 it was determined that past year of marijuana use displayed age loading DIF while COA and AHBP displayed intercept DIF. The age loading DIF suggested that past year of marijuana use was less related to polysubstance use for older individuals and the intercept DIF suggested that children of alcoholics were more likely to endorse this item while individuals from AHBP were less likely to endorse this item. This information directly informs the calculation of the time-specific scale scores.

Results

Scores for polysubstance use were calculated for all 9,438 repeated assessments that were obtained from the 1,966 individuals spanning ages 11 to 35 based on the final parameter estimates obtained from the MNLFA that was fitted to the calibration sample. Although the developmental coverage spanned 25 years, no single individual provided more than eight repeated assessments (and most provided between four and six assessments). This is a clear example of how time can be “stretched” by pooling the overlapping cohorts drawn from the three contributing studies. Figure 2 presents the distribution of all polysubstance use scores across all possible ages in the form of a traveling boxplot. The length of the boxes represents the inter-quartile range of the scores; the width is proportional to the sample size at each age; the plus sign indicates the mean and the notch the median of the scores at that age; and the whiskers represent the 5th and 95th percentile of the scores.

Figure 2.

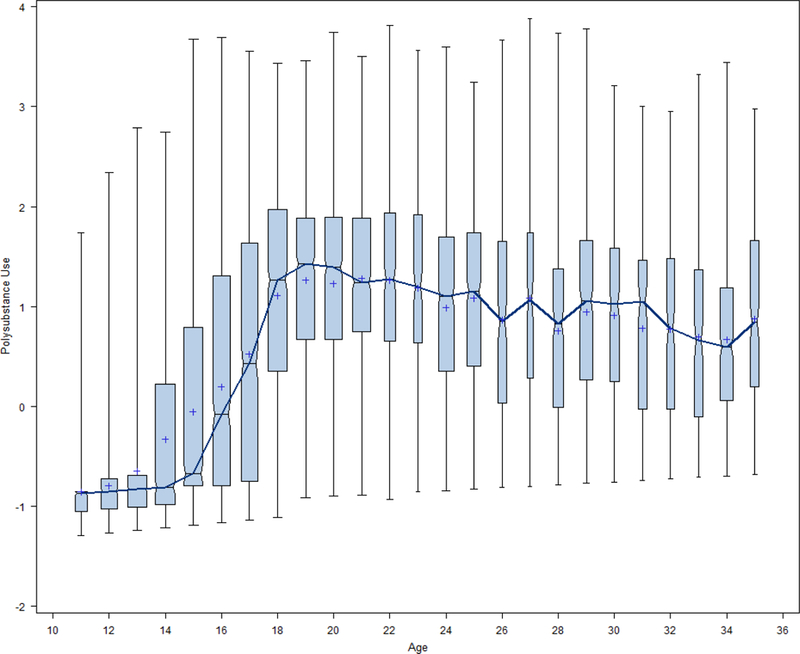
Age-specific distributions of polysubstance use factor scores for the pooled sample.

Note: Box length represents inter-quartile range of scores; box width is proportional to sample size; the notch indicates the age-specific median; the plus sign the age-specific mean; the dark line connects the sample medians over time.

Remember that these scores were obtained from eight discretely scaled items (four ordinal and four binary), yet the resulting scores approximate a continuous distribution. This is because, although the items are discretely scaled, the latent factor is assumed to be continuously distributed, and the scores are computed accordingly. This continuity in score distribution introduces important individual variability among the scores and allows us to fit a broad set of statistical models to these repeated measures (e.g., growth models, mixture models, etc.). Further, recall that five of the eight items were presented in all three contributing studies with the remaining three present in only two of the three studies, yet comparable scores are obtained for all subjects regardless of study membership. This is a key advantage of IDA when combined with MNLFA.

Second, Figure 3 presents the age-specific mean trends as a function of COA status (top panel) and biological sex (bottom panel), respectively. It can be seen that there are interesting differences in age trends such that COAs appear to accelerate more rapidly earlier in development and decelerate more slowly in later development relative to non-COAs. Similarly, although males and females show similar mean trajectories earlier in development, females peak at a lower level and decrease more rapidly than do males. Although these plots reflect potential age-specific trends in polysubstance use as a function of biological sex and COA status, they do not capture potential variability in the individual developmental trajectories over time. To provide a brief initial demonstration of whether this could be done, we estimated a two-level multilevel growth model of polysubstance use in which the repeated measures were nested within individual.

Figure 3.

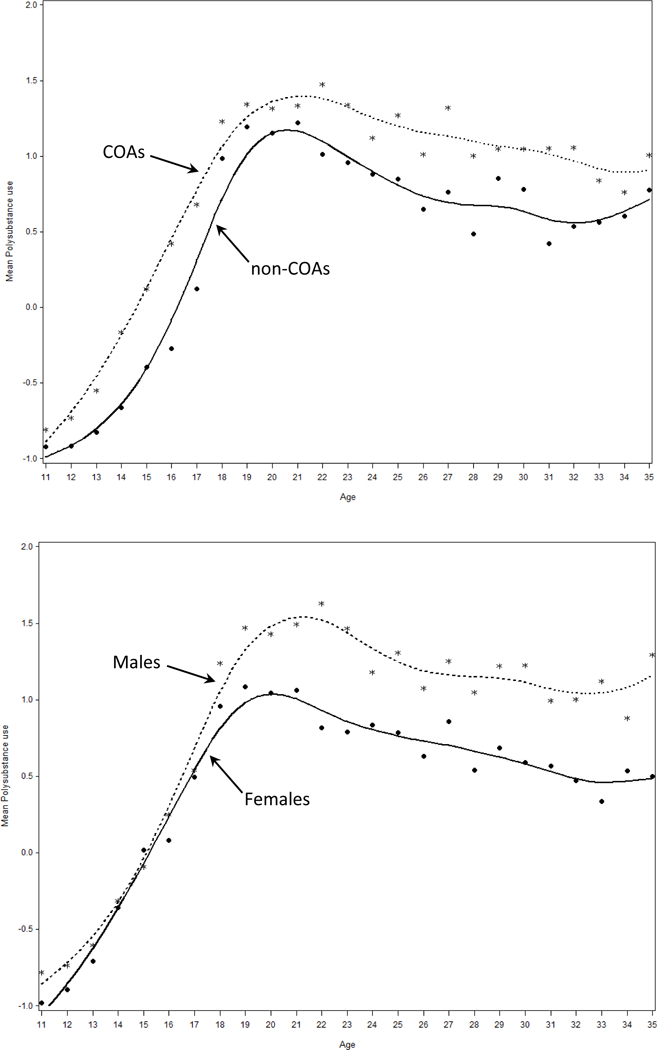
Age-specific mean scores of polysubstance use as a function of COA status (top panel) and biological sex (bottom panel) for the pooled sample.

Note: COA represents child of an alcoholic.

We fit a series of models of increasing complexity to capture the optimal functional form of growth over time that identified a growth trajectory best defined by a cubic function of age. There were significant fixed effects for all trajectory components (i.e., the intercept and the effects of age, age-squared, and age-cubed) suggesting a rapid acceleration in polysubstance use in adolescence, a peaking of use in the early 20’s, and a deceleration and stabilization of use in the late 20’s onward. Further, there was significant variability around all four trajectory components suggesting potentially important person-to-person variability in growth over time.

The growth model produced a plethora of numerical results, the tabling of which is less useful given our purposes here. Instead, we computed empirical Bayes estimates of individual trajectories for all 1,966 subjects in the pooled sample and these are plotted for a random subset of 300 cases in Figure 4; 100 cases were randomly drawn from each study. These plots convey a great deal of information about the estimated growth trajectories, both within each study separately and in the aggregate pooled sample. First, there is substantial individual variability in the starting point and rate of change in polysubstance use over time; this suggests that both time-invariant covariates (e.g., COA status, biological sex, parental diagnosis) or time-varying covariates (e.g., internalizing symptomatology, delinquency, school success) might help account for these observed differences. Second, the study-specific plots reflect that each study contributed different age periods that overlap in the pooled sample. That is, MLS covers earlier development, AHBP later development, and AFDP spans the full age range; when pooled, all three studies contribute to the understanding of continuous develop across the entire 11 to 35 year period. This cubic growth model would be the first step in a more comprehensive sequence of model building to test specific research hypotheses of interest, but that is beyond the scope of this article.

Figure 4.

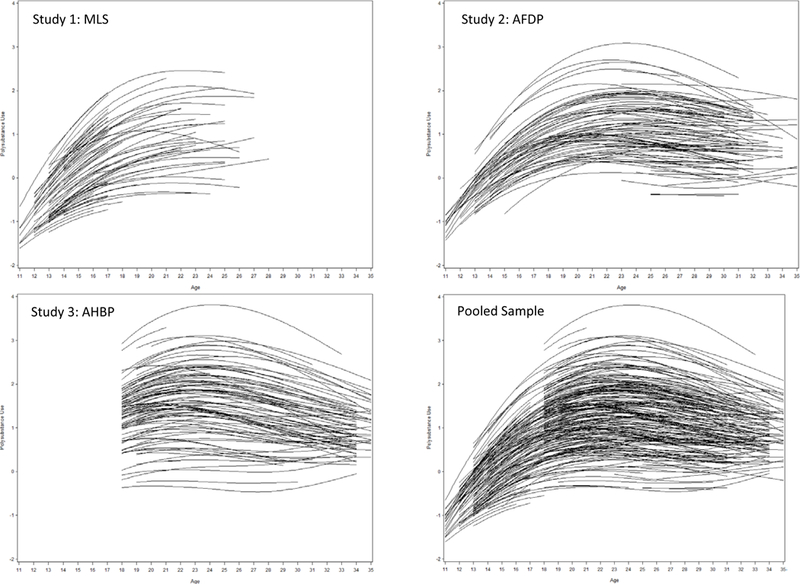
Empirical Bayes estimates of 300 randomly sampled trajectories plotted within each study and within the pooled sample.

Note: Individual trajectory estimates obtained from a multilevel growth model defined by a cubic trajectory of age.

Extensions Not Explored Here

Given space constraints, we simplified our demonstration in several ways so as to not hinder clear communication of the core concepts at hand. First, we only considered the main effects of our set of covariates in the MNLFA model for polysubstance use (biological sex, parental alcoholism status, age, and study membership). A more comprehensive analysis would follow procedures described in Curran et al. (2014) in which higher-order interactions were considered among the covariates, particularly between individual-difference measures and study membership. This is a more complex model that allows for the identification of conditional covariate effects on the measurement model. Second, four of the eight items assess alcohol use, and these might not meet the assumption of local independence (i.e., that the residuals for these four items are uncorrelated net the influence of the underlying factor). A more complicated bi-factor model could be estimated in which potential dependence among the alcohol use items could be captured and removed from the polysubstance use factor. Both of these extensions might further improve the psychometric quality of the estimated factor scores.

Potential Limitations of IDA

We hope that our example has highlighted the many exciting possibilities IDA offers a variety of potential research applications in the social, behavioral, and health sciences. Although here we focused on developmental trajectories of polysubstance use, these techniques can be applied across a myriad of experimental settings. The pooling of multiple independent samples of data offers many potential advantages including increased power and precision, higher observed cases of rare behaviors, greater psychometric coverage of theoretical constructs, acceleration of developmental period, and most importantly, the ability to test novel hypotheses in the pooled data that are not possible in any single contributing sample. However, there are a number of situations in which IDA might not be tractable within a given application.

First, it is critically important that at least one item within the measurement scale be invariant across the contributing studies. We were fortunate here in that three of the eight items were found to be invariant. This means that those three items related to the underlying factor in precisely the same way regardless of age, sex, COA status, or study membership, and these in turn provide a strong basis for establishing a common metric for the latent factor across the levels of the covariates. If at a minimum one item (and hopefully more) is not found to be invariant, then we cannot derive a single set of scores computed across all contributing studies. Instead, a “parallel analysis” approach might be needed in which models are fitted separately within each study and then compared with one another (e.g., Hofer & Piccinin, 2009; Hussong et al., 2013).

Second, it is important that the developmental age spans overlap by at least a single assessment point if the goal is to fit longitudinal trajectories that cover the entire span under study. Although applying IDA to non-overlapping assessment periods is analytically possible (that is, it can be done), this does not allow for important tests of study-by-age developmental effects. For example, in our IDA application the age spans for the three studies were 11 to 30, 11 to 35, and 17 to 35, thus allowing us to estimate trajectories spanning age 11 to 35. However, this allows us to explicitly test age-by-study interactions in our latent measurement model to determine if age is differentially related to polysubstance use in one study compared to another; omission of such a difference could result in a threat to internal validity.

Finally, we were fortunate in that the response scales for the substance use items could be manually harmonized so that the same ordinal values could be used in the calibration and scoring phase of the analysis. However, this is not always the case. For example, in other project work we considered an item assessing positive alcohol expectancies. In one study the response options were never, very rarely, rarely, etc.; in a second study the response options were strongly disagree, disagree, etc.; and in a third study the response options were not at all, a little bit, somewhat, etc. There is no rational way to bin these different ordinal categories into a single common response scale and we thus did not pursue this as a potential common item across the three studies. Care must always be taken when harmonizing response options to ensure comparability across contributing study (see Hansen et al., this issue).

Recommendations For Practice

There are as many potential IDA applications as there are research questions, so it is difficult to develop a fixed set of recommendations that cover all possible settings. However, we have learned several lessons from a decade of wrestling with IDA ourselves, and we share a few of these here.

Lesson 1: Focus on new and novel questions that can only be evaluated using the pooled data.

IDA can certainly be advantageous when applied to pooled data that have the same items and the same subject characteristics, particularly in terms of increased power and enhanced precision. However, IDA becomes truly advantageous when it is possible to evaluate new and exciting hypotheses within the pooled data that are not possible within one or a few contributing studies. We recommend that, when first approaching a possible IDA, focus on what unique novel types of questions might be evaluated within the pooled data that move beyond simple increases in statistical power.

Lesson 2: Never underestimate the time (or resources) an IDA will require.

At first blush, a potential IDA seems easy -- all of the data are already collected, right? However, this is overly simplistic given the complexity of IDA. Much work is needed to organize each data set individually, to manually harmonize individual items, to carefully merge multiple data sets, and to fit scoring models and subsequent tests of hypotheses. We recommend careful planning and allocation of time and effort, particularly if seeking external funding to support your work.

Lesson 3: Data management and documentation is your friend.

For IDA applications using multiple data sets with many measured variables, careful data management and detailed documentation is absolutely critical. We developed extensive tables that we called “cross walks” in which we can navigate from one item to another both within and across contributing studies that are absolutely invaluable.⁷ We also developed a work flow strategy to document extensive computer coding that manages the original data files and creates the newly pooled files for subsequent analysis. We have found that no detail is too small to document.

Lesson 4: You do not need a Ph.D. in statistics to conduct a meaningful IDA.

As is likely clear from our polysubstance use example, there are many steps in an IDA of varying degrees of complexity. However, it is important to realize that each individual component that makes up an IDA is both well developed and well understood. Most IDA applications do require knowledge about data management, factor analysis, and statistical modeling, but no more so than is needed for any typical single-study research application. At least as anecdotal evidence, not one of us holds a Ph.D. in statistics, yet we hope that we have collectively made meaningful contributions to both the fields of IDA itself and the use of IDA in the pursuit of important research questions and hypotheses, particularly as they bear on the field of substance abuse.

Lesson 5: Pick your battles.

Our final lesson is one that can be applied across many domains of our personal lives, and that is to pick your battles. More specifically, we often have to make concessions in our approach in which we invoke an assumption or accept a limitation so that we can focus greater attention on more important parts of the analysis. For example, the motivating goal in our example was to obtain a scale score representing polysubstance use for all subjects. These scores were then taken to a second-stage analysis where we fit the growth model. What we would ideally like to have done was to fit the measurement model and the growth model simultaneously, such as a second-order growth model in which we define a latent factor of substance use at each unique age (e.g., Hancock, Kuo, & Lawrence, 2001). Although this would be ideal, it is not tractable in that there are too many items and too many factors at too many individual ages to support model estimation. Instead, we conceded that the second-order growth model is not possible and we instead invoked the two-step procedure where we first computed scale scores to which we then fit a separate growth model. Decisions such as these must be made throughout any IDA and careful thought is needed when balancing multiple demands.

Conclusion

Integrative data analysis is a powerful methodology that allows for the fitting of statistical models to data that have been pooled over two or more contributing data sets. Although we focused on longitudinal data, IDA can equivalently be applied to cross-sectional data, or potentially some mix of cross-sectional and longitudinal applications. IDA offers many promising advantages that span a myriad of potential applications in the behavioral and health sciences. However, these advantages are particularly salient in the study of high-risk and rare behaviors, and we have demonstrated this application here through the measurement and modeling of polysubstance use across two decades of life. Although limitations exist that might preclude the use of IDA in some research settings, this remains an exciting new approach in many domains of empirical research.