Skip to main content
PMC home page
Molecular Plant Pathology logoLink to Molecular Plant Pathology
. 2018 Oct 25;19(12):2575–2589. doi: 10.1111/mpp.12730

Impact of genetic drift, selection and accumulation level on virus adaptation to its host plants

Elsa Rousseau 1,2,3,8,[Link], Lucie Tamisier 1,4,9,[Link], Frederic Fabre 5, Vincent Simon 1,6, Marion Szadkowski 4, Olivier Bouchez 7, Catherine Zanchetta 7, Gregory Girardot 1, Ludovic Mailleret 2,3, Frederic Grognard 2, Alain Palloix 4, Benoit Moury 1,✉
PMCID: PMC6638063  PMID: 30074299

SUMMARY

The efficiency of plant major resistance genes is limited by the emergence and spread of resistance‐breaking mutants. Modulation of the evolutionary forces acting on pathogen populations constitutes a promising way to increase the durability of these genes. We studied the effect of four plant traits affecting these evolutionary forces on the rate of resistance breakdown (RB) by a virus. Two of these traits correspond to virus effective population sizes (N e) at either plant inoculation or during infection. The third trait corresponds to differential selection exerted by the plant on the virus population. Finally, the fourth trait corresponds to within‐plant virus accumulation (VA). These traits were measured experimentally on Potato virus Y (PVY) inoculated to a set of 84 pepper doubled‐haploid lines, all carrying the same pvr23 resistance gene, but having contrasting genetic backgrounds. The lines showed extensive variation for the rate of pvr23 RB by PVY and for the four other traits of interest. A generalized linear model showed that three of these four traits, with the exception of N e at inoculation, and several pairwise interactions between them had significant effects on RB. RB increased with increasing values of N e during plant infection or VA. The effect of differential selection was more complex because of a strong interaction with VA. When VA was high, RB increased as the differential selection increased. An opposite relationship between RB and differential selection was observed when VA was low. This study provides a framework to select plants with appropriate virus evolution‐related traits to avoid or delay RB.

Keywords: effective population size, eIF4E, genetic drift, plant breeding, resistance breakdown, selection, viral load.

Introduction

Resistance to pathogens, defined as the capacity of a host to decrease its pathogen load (Råberg et al., 2007; Restif and Koella, 2004), is widespread in plants. However, resistance efficiency, specificity and genetic determinism are highly variable across genotypes of a given plant species. To date, plant breeders have mostly created resistant cultivars using resistance mechanisms showing monogenic inheritance and a high efficiency level, often called ‘qualitative resistance’. Unfortunately, the protection conferred by such resistance genes is often poorly durable, and resistance ‘breakdowns’ caused by pathogen evolution can be frequent and rapid (García‐Arenal and McDonald, 2003; McDonald and Linde, 2002). In the case of viruses, the breakdown of a major resistance gene recently introgressed into commercial plant cultivars and used by growers can be schematically divided into three major steps (Gómez et al., 2009; Moury et al., 2011). If we assume that no resistance‐breaking variant is initially present, the first step is the appearance of such variants from a wild‐type (WT) virus population. The second step is within‐plant colonization and accumulation of the resistance‐breaking variants in competition with the rest of the virus population (i.e. WT variants). The last step is the transmission of the resistance‐breaking variants to other plants, allowing epidemics to develop in plant cultivars carrying the resistance gene. Different evolutionary forces rule these three steps. The appearance of resistance‐breaking variants usually involves a small number of nucleotide substitutions in the so‐called avirulence factor encoded by the viral genome (Harrison, 2002; Moury et al., 2011). More rarely, recombination may be required for this step (Díaz et al., 2004; Miras et al., 2014). Then, the accumulation of resistance‐breaking variants within plants depends on selection and genetic drift. Selection favours the variants with highest fitness, i.e. growth rates when considering the within‐plant scale, increasing their frequency over time. This deterministic force is usually evaluated with the selection coefficient, defined as the difference in fitness between two variants. By contrast, genetic drift acts in the same way on all variants of the population, introducing random fluctuations in the dynamics of variant frequencies (Charlesworth, 2009). This stochastic force is commonly evaluated using the effective population size N e, defined as the size of an idealized population (i.e. a panmictic population of constant size with discrete generations), which would show the same degree of randomness in the evolution of variant frequencies as the observed population (Kimura and Crow, 1963; Wright, 1931). In plant viruses, the intensity of genetic drift is modulated by bottlenecks occurring at multiple steps of virus infection (French and Stenger, 2003; Gutiérrez et al., 2012, 2010 ; Sacristán et al., 2003; Zwart and Elena, 2015). Modelling approaches have estimated that the evolutionary forces acting at the within‐plant scale, especially the mutational pathway involved in resistance breakdown and the fitness cost associated with the resistance‐breaking mutation(s), account for about 50% of the risk of resistance breakdown in the field (Fabre et al., 2009, 2012b, 2015). Experimental data have shown that these two factors are indeed good predictors of the risk of resistance breakdown (Fabre et al., 2012a; Harrison, 2002; Janzac et al., 2009). The remaining 50% depend on factors related to virus epidemiology and thus mostly to the third step of resistance breakdown.

One way to avoid or delay the breakdown of monogenic qualitative resistance is to combine the resistance gene with a suitable genetic background. Combined with a partially resistant genetic background, a major resistance gene can show a significant increase in durability, as demonstrated experimentally for resistances targeting an RNA virus (Palloix et al., 2009), a fungus (Brun et al., 2010) and a nematode (Fournet et al., 2013). Indeed, the host genetic background can affect the level of resistance to pathogens and the intensity of different evolutionary forces undergone by pathogen populations (Lannou, 2012). In the case of the Potato virus Y (PVY, genus Potyvirus; family Potyviridae)–pepper (Capsicum annuum; family Solanaceae) pathosystem, Quenouille et al. (2013, 2015 ) showed a significant correlation between the breakdown frequency of a major resistance gene [the pvr23 gene, encoding a eukaryotic translation initiation factor 4E (eIF4E)] and the capacity of the virus to accumulate in the plant, i.e. the additional resistance level conferred by the plant genetic background. Assuming an identical virus mutation rate between plant genotypes, they hypothesized that within‐plant virus accumulation was linked to the total number of virus replications during plant infection and, consequently, to the probability of appearance of the resistance‐breaking mutations. Using a progeny of pepper genotypes carrying the same major resistance gene, but contrasting genetic backgrounds, Quenouille et al. (2014) mapped the quantitative trait loci (QTLs) controlling either within‐plant virus accumulation or the frequency of breakdown of the major resistance gene in the pepper genome. The two QTLs controlling virus accumulation co‐localized with some of the QTLs controlling the frequency of breakdown of the major resistance gene, which provided a genetic explanation for the observed correlation between the two traits. Further, by comparing two pepper genotypes carrying the same major resistance gene, associated with either a partially resistant or a susceptible genetic background, Quenouille et al. (2013) showed that the selection of the most adapted resistance‐breaking PVY mutants was slower and/or rarer in plants with a partially resistant genetic background than in those with a susceptible genetic background. This slower and/or rarer selection may result from: (i) the smaller selection coefficient of the adapted mutants; and/or (ii) a higher genetic drift in the plants with a partially resistant genetic background (Charlesworth, 2009; Feder et al., 2016; Quenouille et al., 2013; Rouzine et al., 2001).

The aim of this study was to disentangle the role and relative importance of the three factors, virus accumulation, selection coefficient between virus variants and virus effective population size, on the breakdown of the major resistance gene in order to foster the breeding of plant cultivars with durable virus resistance.

Results

The breakdown frequency of pvr23‐mediated resistance at the individual plant level [response variable resistance breakdown (‘RB’)] and several putative explanatory variables linked to within‐plant PVY evolutionary processes (mutation, selection and genetic drift) were estimated in 84 doubled‐haploid (DH) pepper lines. The terminology ‘resistance breakdown’ is frequently used to describe the increase in infection rates, and often of subsequent economic losses, at the field scale following the adaptation of pathogen populations to resistant cultivars. For simplicity, we use this term to describe pathogen adaptation at the individual plant level, regardless of its epidemiological consequences. The variable RB and the explanatory variables corresponding to within‐plant virus accumulation (variable ‘VA’) and to the PVY effective population size at the inoculation step (variable ‘N e inoc’) have been estimated previously (Quenouille et al., 2014; Tamisier et al., 2017) (Table 1 and Experimental procedures). In this study, two additional explanatory variables were estimated: PVY effective population size during plant infection from inoculation to 21 days post‐inoculation (dpi) and the differential selection exerted by the plant on the same PVY population (variables ‘N e’ and ‘σ r’, respectively; see below; Table 1). It should be noted that, in the following, N e and RB correspond to the names of the variables estimated in our experimental context, whereas the expressions ‘effective population size’ and ‘resistance breakdown’ are used to refer to the general concepts.

Table 1.

Description of the variables used in this study.

Variable Experiment Number of DH lines Plants per DH line PVY inoculum* Infection stage/date of measure Reference
RB: frequency of resistance breakdown 1 151 60 CI chimera Systemic/38 dpi† Quenouille et al. (2014)
VA: level of virus accumulation 2 151 10 Mutant N of CI chimera Systemic/36 dpi Quenouille et al. (2014)
N e inoc: virus effective population size at inoculation 3 151 10‡ Mutant K of SON41p‐GFP Inoculated cotyledon/5–6 dpi Tamisier et al. (2017)
N e: virus effective population size during infection from inoculation to 21 dpi 4 84 8 SON41p mutants G, N, K, GK and KN Systemic/21 dpi This study
σ r: differential selection exerted on the virus population 4 84 8 SON41p mutants G, N, K, GK and KN Systemic/21 dpi This study
Open in a new tab
*

One or two letter codes for mutants correspond to amino acid substitutions in Potato virus Y (PVY) VPg (viral protein genome‐linked) allowing infection of plants carrying the pvr2 3 resistance gene.

†

dpi, days post‐inoculation.

‡

10 plants × 2 cotyledons.

Estimates of N e and σr with a PVY composite population in 84 pepper DH lines

The intensities of genetic drift and selection operating on PVY during plant infection were estimated experimentally by studying the dynamics of an artificial population composed of five PVY variants from inoculation to 21 dpi. The inoculum was composed of a roughly similar amount of these five variants carrying one or two non‐synonymous substitutions (named variants G, K, N, GK and KN). These variants were chosen because they showed contrasting selection coefficients in plants belonging to the same progeny as that studied here, but none of the variants had been counter‐selected too rapidly, ensuring sufficient genetic diversity in the PVY populations to allow the estimation of N e and selection coefficients (Rousseau et al., 2017). The variant frequencies in the common inoculum and in pools of three systemically infected leaves at 21 dpi for each plant were accurately determined using MiSeq Illumina high‐throughput sequencing (HTS) of the VPg (viral protein genome‐linked) cistron region in which the mutations that distinguish the five variants were located. We also calculated the frequencies of de novo nucleotide substitutions in each sample and at each nucleotide position by comparison with the sequence of the PVY SON41p reference clone, as described in Rousseau et al. (2017). In all, PVY populations sampled from 30 plants (4.2%) presented one or several de novo substitution(s) (38 substitutions in total) with a frequency exceeding 7% (Methods S1 and Table S1, see Supporting Information). Thirty‐seven of these 38 substitutions were non‐synonymous and 34 involved codon positions 105, 115 or 119 which have been shown previously to determine PVY adaptation to pvr2‐mediated resistance in pepper (Ayme et al., 2006). Consequently, most of these mutations are certainly adaptive for PVY and were selected for during plant infection. Numerical simulations have shown that the presence of an additional, unaccounted for, virus variant present at a mean frequency of 7% had no significant impact on estimates of N e and selection coefficients (Rousseau et al., 2017). Moreover, this 7% frequency threshold is close to the expected error frequency as a result of reverse transcription‐polymerase chain reaction (RT‐PCR) and MiSeq Illumina sequencing (Rousseau et al., 2017). Consequently, these 30 PVY populations were removed from the analyses. In total, data from five or more plant replicates were available for 84 pepper DH lines, which were subsequently analysed.

The effective population size of the PVY population during plant infection from 0 to 21 dpi (N e) and the relative growth rates of the five PVY variants (ri with i ∈ {G, K, N, GK, KN}) were estimated for each DH line using a method developed recently (Rousseau et al., 2017). Briefly, this method allows the estimation of the Ne and r i parameters of a multi‐allelic Wright–Fisher model for haploids in the absence of neutral markers (Ewens, 2004). Before using the estimation method in our experimental context, we performed several batches of simulations to assess its ability to infer effective population sizes and selection coefficients accurately [see Experimental procedures and Fig. S1 (Supporting Information)]. Overall, these numerical simulations indicated that the σ r and N e estimates obtained are precise and accurate. Moreover, it is noteworthy that a Wright–Fisher model including selection and genetic drift fitted our dataset satisfactorily (Fig. 1). The best‐fit line between the observed and fitted mean variant frequencies was very close to the first bisector (Fig. 1a): the slope was close to 1.0 (0.92; standard deviation, 0.024) and the intercept was close to 0.0 (0.016; standard deviation, 0.007), with R 2 = 0.77. The fit was also satisfactory for the variability (i.e. standard deviation) of variant frequencies among the plants (Fig. 1b; slope of 0.89 with standard deviation of 0.08; intercept of 0.025 with standard deviation of 0.015; R 2 = 0.59).

Figure 1.

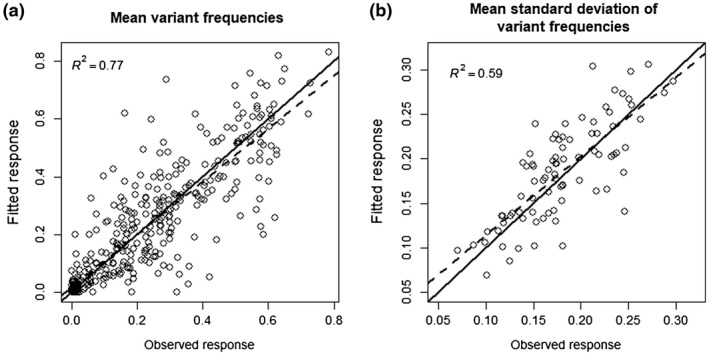
Figure 1

Open in a new tab

Goodness of fit of a Wright–Fisher model with selection and genetic drift with the experimental dataset. (a) Correlation between the observed mean frequencies of each of the five virus variants in the population and their fitted values [n = 420; 84 doubled‐haploid (DH) lines, five values per DH line]. (b) Correlation between the observed means of the standard deviation of variant frequencies and their fitted values (n = 84; one value per DH line). In both panels, the black line is the first bisector and the dashed line is the best‐fitting linear model for which the coefficient of determination R² is indicated.

The fitness (r i) ranks of the five PVY variants were similar amongst the 84 DH lines, as described previously on a set of 15 DH lines (Fig. 2; Rousseau et al., 2017). In 78 of the 84 lines, variant ‘G’ was the least fit. In the six remaining lines, variant ‘N’, which shows, on average, an intermediate fitness amongst the DH lines, was the least fit. The three variants possessing the ‘K’ mutation (i.e. variants ‘K’, ‘GK’ and ‘KN’) showed the highest fitness with small ri differences amongst them in 82 of the 84 lines. Because of this conserved fitness ranking among the 84 DH lines, we estimated the differential selection exerted by each DH line on the PVY population by the standard deviation of the growth rates ri of the five PVY variants, σ r. Amongst the 84 DH lines, σ r and N e showed unimodal distributions (Fig. 3). σ r varied from 0.041 to 0.156 (mean and median, 0.12) and presented a nearly Gaussian shape (Fig. 3b). N e varied from 15.4 to 293.6 (mean, 46.4; median, 35.9) and the DH line distribution was skewed towards small values (Fig. 3a). About two‐thirds of the lines (57 of 84) had N e < 50 and only six lines had N e > 100. Figure 3c shows a set of bar plots representing the frequencies of the five PVY variants in the sampled plants and their mean frequencies in four DH lines showing contrasted N e and σ r values.

Figure 2.

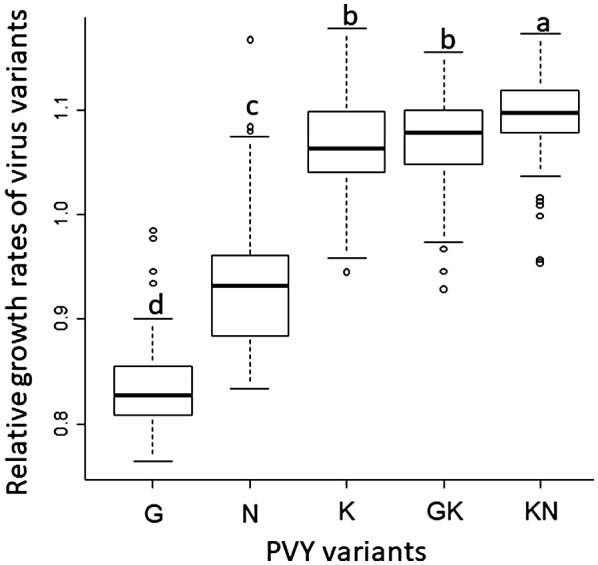
Figure 2

Open in a new tab

Distribution of the relative growth rates of the five Potato virus Y (PVY) variants in 84 pepper doubled‐haploid (DH) lines. Different letters indicate significantly different groups (P < 0.05) in Mann–Whitney–Wilcoxon tests with Bonferroni correction.

Figure 3.

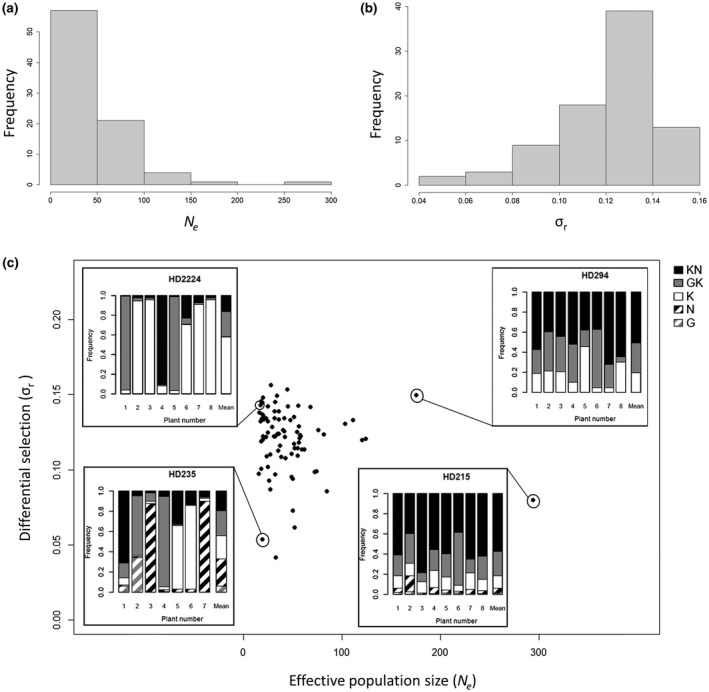
Figure 3

Open in a new tab

Distribution of differential selection and effective population size values in Potato virus Y (PVY) populations in 84 pepper lines. (a) Distribution of the effective population size (N e). (b) Distribution of differential selection (σ r). σ r is the standard deviation of the relative growth rates ri of the five variants composing the PVY population. (c) Distribution of the 84 pepper doubled‐haploid (DH) lines according to N e and σ r. For four DH lines with contrasted N e and σ r values, bar plots illustrating the composition of the PVY population at 21 days post‐inoculation are provided. For each DH line, each of the first seven or eight bars represents the frequencies of the five PVY variants (G, N, K, GK and KN) in a single plant initially inoculated with a similar amount of the five variants. The last bar represents the mean frequencies of the five PVY variants among plants.

Effect of evolutionary forces exerted on PVY populations on resistance breakdown

Weak or no correlation was observed amongst the explanatory variables N e, σ r, N e inoc and VA (Table 2; Fig S2, see Supporting Information). N e and VA showed a significant positive correlation (Pearson’s r = 0.31, P = 0.0045). However, this effect was mainly caused by an outlier DH line showing an extreme N e value and the highest VA value (Fig. S2). After withdrawing this DH line (or using the Spearman’s rank correlation test), no significant correlation was observed between N e and VA (P ≥ 0.072). With Spearman’s ρ test, a weakly significant correlation was observed between N e and σ r (ρ = –0.22, P = 0.048). Finally, a weakly significant correlation was also observed between VA and σ r, with both Pearson’s and Spearman’s tests (P = 0.041 and 0.028, respectively). No correlation was detected between N e and N e inoc or N e inoc and VA. Moreover, variance inflation factors (VIF) were calculated for each explanatory variable. All VIF values were below four, which ensures the lack of multi‐collinearity between explanatory variables in our analysis.

Table 2.

Pearson’s r (below the diagonal) and Spearman’s rank ρ (above the diagonal) correlation coefficients between the pvr23 resistance breakdown frequency (RB) and four variables linked to evolutionary forces characterizing Potato virus Y (PVY) populations in the different pepper genotypes: the differential selection (σ r), effective population size during plant colonization (N e), effective population size at inoculation (N e inoc) and viral accumulation (VA). Correlations that are significant with both Pearson’s and Spearman’s coefficients are shaded in grey.

RB σr Ne N e inoc VA
RB ρ = −0.32 ρ = 0.05 ρ = 0.31 ρ = 0.50
P †  = 0.003** P = 0.65 P = 0.0046** P = 1e‐06***
σr r = −0.32 ρ = −0.22 ρ = −0.044 ρ = −0.24
P = 0.003** P = 0.048* P = 0.69 P = 0.028*
Ne r = −0.05 r = −0.145 ρ = 0.067 ρ = 0.20
P = 0.65 P = 0.19 P = 0.55 P = 0.072
Neinoc r = 0.40 r = −0.063 r = −0.067 ρ = 0.14
P = 0.00014*** P = 0.57 P = 0.54 P = 0.20
VA r = 0.41 r = −0.22 r = 0.31 r = 0.15
P = 0.00013*** P = 0.041* P = 0.0045** P = 0.17
Open in a new tab
†

P values corresponding to H 0: r = 0 or ρ = 0. *, ** and *** correspond to 0.05, 0.01 and 0.001 significance thresholds, respectively.

In contrast, three explanatory variables were significantly and consistently correlated with the response variable RB: σ r, N e inoc and VA (Table 2). The correlation was positive and highly significant between RB and either N e inoc or VA. The correlation was negative and moderately significant between RB and σ r. Finally, no significant link was noticed between RB and N e. Pairwise plots of the variables for the 84 DH lines did not reveal particular relationships other than the linear or ranking relationships revealed by the correlation analyses (Figs S2 and S3).

Generalized linear model (GLM) analyses were performed to investigate the effect of the four explanatory variables, σ r, VA, N e and N e inoc, on RB. After a stepwise selection procedure, both forward and backward, based on Akaike’s information criterion (AIC), the retained model included three of the four explanatory variables (N e, VA and σ r) and four of the six pairwise interactions (Table 3). These factors and interactions had highly significant effects on RB. The model fit was quite good, with McFadden R 2 = 0.40.

Table 3.

Generalized linear model analysis of the frequency of pvr2 3 resistance breakdown (RB) with four explanatory variables linked to evolutionary forces characterizing Potato virus Y (PVY) populations in the different pepper genotypes. The explanatory variables are the differential selection σ r, the effective population size during plant colonization (N e), the effective population size at inoculation (N e inoc) and viral accumulation (VA). A stepwise selection procedure, both forward and backward, was applied using Akaike’s information criterion. The resulting model presented had a null deviance of 2264.3 on 83 degrees of freedom, whereas the residual deviance was 1287.7 on 75 degrees of freedom. McFadden’s R 2 was 0.40.

Explanatory variable Estimate Standard error z value P value†
Intercept 4.71 0.60 7.81 6e‐15***
σ r −56.32 4.02 −14.03 <2e‐16***
N e −3.6e‐02 6.7e‐03 −5.37 8e‐08***
VA −2.92 0.40 −7.26 4e‐13***
σ r × VA 28.44 2.97 9.56 <2e‐16***
N e × N e inoc 1.5e‐03 2.9e‐04 5.30 1.1e‐07***
N e × VA 7.8e‐03 1.8e‐03 4.26 2.1e‐05***
N e inoc × VA 2.5e‐02 9.3e‐03 2.73 0.0064**
Open in a new tab

†** and *** correspond to 0.01 and 0.001 significance thresholds, respectively.

Significant interactions revealed several synergistic effects on RB (Table 3 and Fig. 4). Indeed, the positive effect of N e inoc on RB increased with increasing values of VA, as attested by the higher slope value (Fig. 4a). The same trend was observed with N e inoc and N e, and with VA and N e (Fig. 4b,d). However, for the last significant pairwise interaction, σ r × VA, the effect on RB was dependent on the values of the variables (Fig. 4c). When VA was small, RB decreased with increasing σ r values, whereas, when VA was high, RB increased with increasing σ r values.

Figure 4.

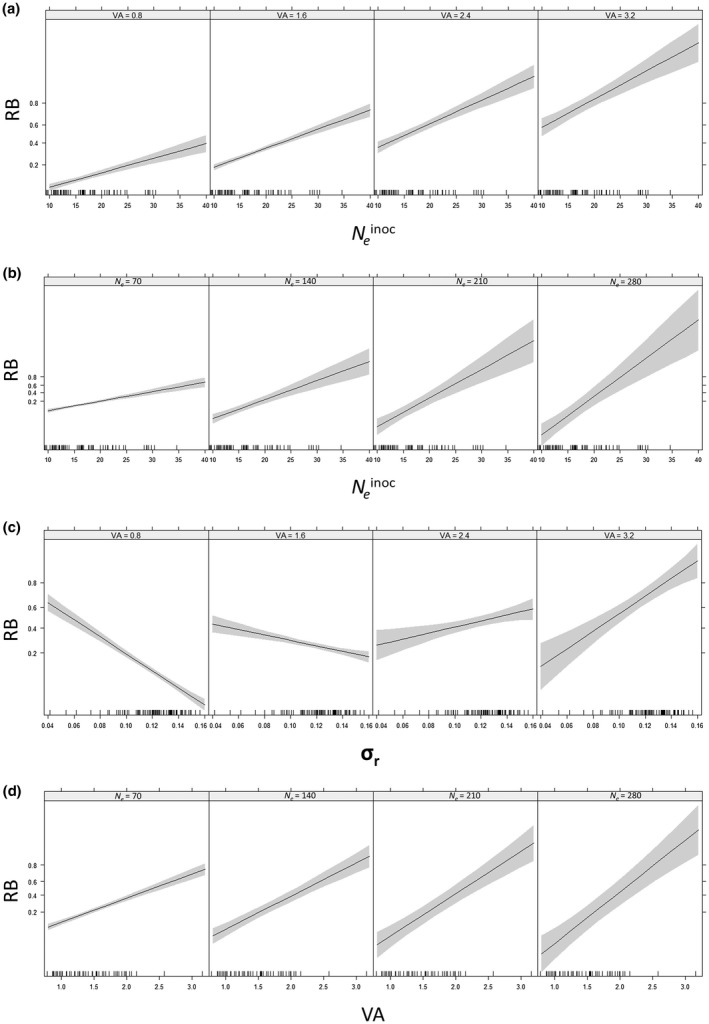
Figure 4

Open in a new tab

Response of RB to pairwise interactions between the four explanatory variables according to the generalized linear model (GLM). Only significant interactions are shown (Table 3). RB is the frequency of breakdown of pvr23‐mediated resistance in 84 pepper doubled‐haploid (DH) lines. The four explanatory variables considered were within‐plant virus accumulation (VA), effective population size at the plant inoculation step (N e inoc) or during plant colonization (N e) and differential selection exerted by the host plant on the composite Potato virus Y (PVY) population (σ r). (a) Pairwise interaction between N e inoc and VA. (b) Pairwise interaction between N e inoc and N e. (c) Pairwise interaction between σ r and VA (d) Pairwise interaction between VA and N e. Grey areas correspond to the 95% confidence intervals and black bars above the x axes correspond to the observed data.

We computed conditional inference regression trees to synthesize the effect of the four explanatory variables on RB (Fig. 5). Regression trees take into account the interactions between explanatory variables and identify combinations of their levels leading to higher or lower RB. The first dichotomy in the regression tree was linked to the variable VA, reflecting its strong influence on RB. The second dichotomies were linked to the variables σ r and N e inoc. The variable N e was not retained (Table 2). The best way to reduce RB is thus to combine a weak VA (≤1.474) and a high σ r (>0.117). When VA is higher (>1.474), a low N e inoc value (≤16) also contributes significantly to reduce RB.

Figure 5.

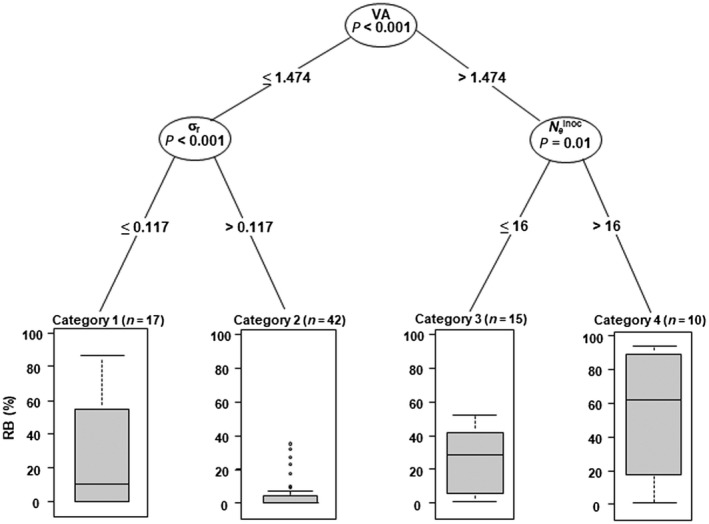
Figure 5

Open in a new tab

Conditional inference regression tree modelling RB with three explanatory variables. RB is the frequency of breakdown of pvr23‐mediated resistance in 84 pepper doubled‐haploid (DH) lines. Three explanatory variables representing evolutionary forces exerted by the host plant on Potato virus Y (PVY) populations were retained by the analysis: VA (within‐plant virus accumulation), N e inoc (effective population size at the plant inoculation step) and σ r (differential selection exerted by the host plant on the composite PVY population). Given the parameters of the analysis (minimum number of 10 DH lines in each terminal ‘leaf’ of the tree and default setting for other parameters), the fourth explanatory variable (N e, effective population size during plant colonization) was not found to determine significantly RB. The number of DH lines in each category is indicated in parentheses. P: P value indicating the significance of the variable.

Discussion

The main objective of this investigation was to study the relationships between the frequency of breakdown of the major resistance gene pvr23 (variable RB) and proxy variables quantifying the main evolutionary forces exerted by the host plants on the virus population, notably the intensities of genetic drift and selection (N e inoc, N e and σ r) and virus accumulation (VA).

Lack of strong relationships between Neinoc, Ne, σr and VA

No strong evidence of correlations between the four explanatory variables N e inoc, N e, σ r and VA were observed (Table 2). First, a positive correlation could have been expected between N e inoc and N e. Indeed, experiments with Tobacco etch virus (TEV; genus Potyvirus) in pepper or tobacco plants showed that within‐plant genetic drift was mostly determined by the inoculation step and not by the colonization of inoculated or apical leaves (Zwart et al., 2011, 2012 ). Second, a positive correlation could also have been expected between N e inoc and VA because, for potyviruses, a low N e inoc was shown to result in a delay in plant infection at the systemic level (Rodrigo et al., 2014; Zwart et al., 2012) or in a lower proportion of infected cells (Lafforgue et al., 2012), hence probably also in a lower VA. Importantly, Lafforgue et al. (2012) and Rodrigo et al. (2014) analysed potyvirus infection in one highly susceptible plant species, whereas we used a large number of pepper lines carrying different sets of resistance QTLs (Quenouille et al., 2014). As partial resistance mechanisms may act specifically on the virus local and/or systemic movement, they probably explain the absence of correlation between N e inoc and VA or between N e inoc and N e (Table 2; Fig. S2). The lack of correlation between N e inoc and N e is consistent with the narrow bottleneck observed between 6 and 10 dpi, i.e. at the onset of systemic infection, in the majority of the pepper DH lines (eight of 15 tested) (Rousseau et al., 2017). Moreover, if links between N e inoc and N e (or VA) occur early in the infection process, they may have blurred with time until disappearing at 21 dpi (for N e) or 36 dpi (for VA) (Table 1). The lack of (or low) correlation between N e and VA could similarly be a result of the bottleneck during systemic infection. As the effective population size N e corresponds to the harmonic mean of the effective population sizes over successive generations, a transient bottleneck could induce a strong reduction in N e, whereas its effect could be small on VA because of the subsequent growth of the virus population.

Which evolutionary forces contribute most to resistance breaking?

Relationships between the number of viral mutations required for host adaptation, their probabilities of appearance, the incurred fitness changes and genetic drift are complex (da Silva and Wyatt, 2014; Fabre et al., 2009; Iwasa et al., 2004; Quenouille et al., 2013). We thus also anticipated that complex interactions between VA, σ r, N e and N e inoc may determine RB.

The strong positive correlation between VA and RB, observed earlier (Quenouille et al., 2014), may result from the link between VA and the probability of appearance of the resistance‐breaking mutations in the inoculated plants (Quenouille et al., 2013). Indeed, VA is an estimate of the virus census population size at a given time point, which depends on the population growth rate and generation time. Assuming equal PVY mutation rates between DH lines, VA would be a proxy of the probability for a new mutation to occur during the experiment. This assumption also implies that the within‐plant accumulation of the resistance‐breaking variant (CI chimera carrying the ‘N’ substitution; Table 1), used to measure VA, is correlated with the residual accumulation of the WT variant (CI chimera), used to estimate RB. Unfortunately, we could not measure the accumulation of the WT variant in these plants. Indeed, even if the pvr23 resistance gene does not control completely PVY multiplication or even movement (Montarry et al., 2011), the WT viruses were outcompeted by the resistance‐breaking mutants that appeared stochastically and emerged rapidly in 99% of the infected plants. This scenario, in which resistance breakdown results from the residual replication of the WT PVY variant, was suggested by Montarry et al. (2011), who established that the PVY resistance‐breaking mutants did not pre‐exist in the inoculum.

The strong positive correlation between N e inoc and RB is expected if we consider, as mentioned above, that genetic drift frequently slows down adaptation. As the PVY resistance‐breaking mutants were most probably absent from the inoculum, low N e inoc is not likely to eliminate these putative resistance‐breaking mutants at the inoculation step, but rather to decrease their probabilities of appearance and slow down their subsequent increase in frequency during the early steps of infection.

Similarly, we anticipated a positive correlation between σ r and RB (Feder et al., 2016), as higher σ r values would accelerate the fixation of resistance‐breaking mutations in the PVY populations. Although the overall link between σ r and RB was negative (Table 2), the effect of σ r on RB was complex because of strong interaction with VA (Table 3). When VA was high, RB increased with increasing σ r values, which fits our expectations. However, when VA was small, RB decreased with increasing σ r values (Figs 4 and 5).

Our interpretation relies on the relationships between VA, σ r and the type of resistance‐breaking substitutions (transitions or transversions) (Fig. 6). Indeed, transitions are five to eight times more frequent than transversions in the PVY genome (Ayme et al., 2006). In the experiment performed to estimate RB, the resistance‐breaking PVY mutants were single mutants such as G, K and N (Montarry et al., 2011). Double mutants (GK and KN) would need much more time to appear and increase in frequency (Quenouille et al., 2013).

Figure 6.

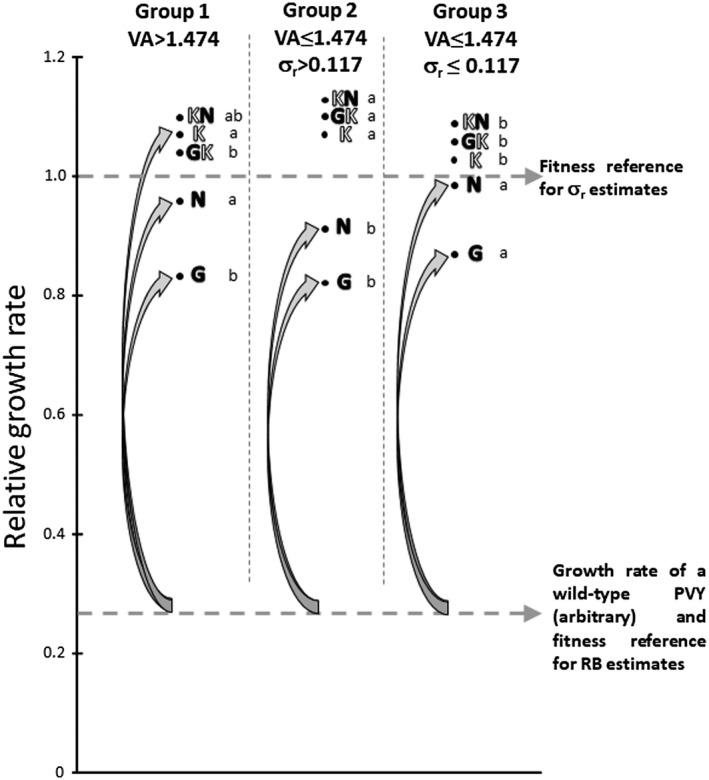
Figure 6

Open in a new tab

Interpretation of the combined effects of virus accumulation and differential selection on RB. The effects of virus accumulation (VA) and differential selection (σr) on RB, the frequency of resistance breakdown, were considered for the three groups of doubled‐haploid (DH) lines defined by the regression tree (Fig. 5). Represented are the mean relative growth rates of the five Potato virus Y (PVY) variants (uppercase single or double letters) used to estimate σ r in experiment 4 (Table 1) amongst each plant group. Letters filled in black correspond to transitions and letters filled in white to transversions. Lower case letters represent, for each PVY variant, significant differences in relative growth rates amongst plant groups (Kruskal–Wallis test, P < 0.05). Double mutants GK and KN did not appear in the resistance‐breaking experiments, but were used for the estimation of σ r. When VA is high (group 1), the K mutant, which confers a high fitness gain to PVY and requires a transversion, is likely to appear. When VA is lower, resistance breakdown involves more likely mutants which require a transition (G and N), but confer lower fitness gains. As RB was evaluated in experiment 1 (Table 1) with a wild‐type PVY, its initial fitness in pvr23‐carrying plants is low (fictitious lower broken line). Fitness gains associated with resistance‐breaking mutations G and N are higher for group 3 than for group 2, despite higher σ r values in the latter group. This may explain the negative effect of σ r on RB when VA is low (Fig. 4).

When VA is high (>1.474; plant group 1 in Fig. 6), the PVY population undergoes a large number of replication events and any kind of single mutant is likely to appear, issuing either from a transition (G and N mutants) or a transversion (K mutant). In particular, a high‐fitness, resistance‐breaking mutant (mutant K) is likely to appear rapidly. In this case, the higher the differential selection σ r, the faster this mutant will become fixed and the higher the RB. A synergistic effect between VA and σ r on RB is expected in this group of plants.

In contrast, when VA is low (≤1.474), the appearance of the N and G transitions remains almost certain, whereas the appearance of the K transversion may be stochastic. It is noteworthy that the relative growth rates of mutants N and G are significantly higher for group 3 than for group 2, whereas, in contrast, σ r values are higher for group 2 (σ r > 0.117) than for group 3 (σ r ≤ 0.117) (Fig. 6). Then, starting with a WT virus with a low fitness, as was the case in the experiment used to measure RB, the fitness gains provided by mutations G or N are higher for plants of group 3 than for plants of group 2, explaining the higher RB observed in this case (Fig. 6). In these two groups of plants with low VA, a negative correlation between σ r and RB is therefore expected.

This result underlines the risk of extrapolating selection coefficients from one experimental context to the other, as they may be strongly influenced by the composition of the considered population (kind, number and initial frequency of variants).

Applied consequences: breeding rules to improve the durability of major effect resistance genes

The breeding of cultivars with efficient and durable pathogen resistance frequently relies on the measurement of the pathogen load (VA in our case). Our results indicate, first, that independent mechanisms are likely to act on N e inoc, N e, σ r and VA, given the lack of (or low) correlation between them. Accordingly, these evolution‐related factors could also be considered as complementary breeding levers to control virus infection and evolution. Indeed, in addition to VA, the intensities of genetic drift and selection are relevant traits to promote the durability of plant resistance genes to viruses (Rousseau et al., 2017; Zhan et al., 2015), as proposed more generally to limit the emergence of microbe variants adapted to drug treatments (Abel et al., 2015). Accordingly, Lê Van et al. (2013) showed that the differential selection exerted by apple trees on a composite fungus population was inversely correlated with the spectrum of action of the resistance, and hence also inversely correlated with the expected durability of the resistance. From an applied point of view, the regression tree issued from this work can provide insightful decision rules for breeding strategies (Fig. 5). A reduction in RB is first achieved by reducing VA. Then, if VA is high, one can still reduce RB by favouring plants with low N e inoc values. Finally, low VA values can be combined with high σ r values to further improve resistance durability. It should be noted, however, that this latter effect should be taken with caution, being linked to the experimental context used to estimate σ r. One can argue, at least on a limited set of plant–virus genotype × genotype interactions, that N e inoc estimates and, to a lesser extent, VA estimates may be representative of various PVY population compositions. In contrast, the differential selection (σ r) estimates may vary strongly with the PVY population used (notably with different numbers and/or types of variants).

As a conclusion, we provide evidence that traits accounting for plant impact on virus evolution have great potential to reduce the risks of breakdown of major resistance genes. Phenotyping such traits becomes feasible with recent sequencing technologies and population genetics models. Hence, the conditions are met to include these, or similar, approaches in plant breeding programmes aimed to improve the resistance durability to pathogens.

Experimental Procedures

Previous data

Different variants of the WT PVY clone SON41p (Moury et al., 2004) were chosen to estimate the response variable RB (breakdown frequency of pvr23‐mediated resistance) and the explanatory variables corresponding to within‐plant PVY accumulation (VA) and PVY effective population size at inoculation (N e inoc). RB was previously evaluated after inoculation of each of the DH lines (60 plants per DH line) with the ‘CI chimera’, an artificial recombinant of SON41p carrying the cylindrical inclusion (CI) coding region of PVY isolate LYE84.2 (Table 1) (Montarry et al., 2011; Quenouille et al., 2014). This variant was preferred to SON41p because of its greater ability to break pvr23 resistance, providing a larger range of RB values amongst DH lines, and hence allowing a higher precision for genetic and statistical analyses. Nevertheless, RB obtained with SON41p was shown to be highly correlated with RB obtained with the CI chimera on a subset of 16 contrasted DH lines (Quenouille et al., 2013). RB corresponds to the frequency of plants showing virus infection at the systemic level around 1 month after inoculation, and has been shown to correspond to situations in which a non‐synonymous mutation in the VPg coding region became fixed in the PVY population, conferring adaptation to pvr23 resistance (Ayme et al., 2006; Montarry et al., 2011).

PVY accumulation in plants was measured by quantitative double antibody sandwich enzyme‐linked immunosorbent assay (DAS‐ELISA) (Quenouille et al., 2014). Mean relative virus accumulation (VA) was assessed in pools of three systemically infected leaves per plant at 36 dpi in 10 plants per DH line (Quenouille et al., 2014) (Table 1). For this, a mutant of the CI chimera carrying the aspartic acid to asparagine substitution at amino acid position 119 of the VPg (‘N’ substitution), which allowed the infection of plants carrying pvr23, was used.

Finally, the effective population size at plant inoculation (N e inoc) was estimated with a SON41p variant carrying a green fluorescent protein (GFP) reporter gene and a single amino acid substitution in VPg (threonine to lysine substitution at codon position 115; ‘K’ substitution), which allows the infection of plants carrying pvr23 (Tamisier et al., 2017) (Table 1). N e inoc corresponds to the mean number of PVY primary infection foci visualized by GFP fluorescence 5 or 6 days after mechanical inoculation of 20 pepper cotyledons per DH line.

Analysis of composite PVY populations infecting pepper DH lines

An experiment was dedicated to estimate two more explanatory variables for RB: the PVY effective population size during plant infection (N e) and the differential selection exerted by the host genotype on a composite PVY population (σ r). The experimental design was as in Rousseau et al. (2017), except for two main differences: (i) the experiment comprised initially 151 pepper DH lines instead of 15; and (ii) only one sampling date (21 dpi) was retained instead of six to keep the experimental size compatible with MiSeq Illumina sequencing capacity. The sampling date at 21 dpi was chosen based on the previous experiments (Rousseau et al., 2017) as a balance between the time for differential selection to operate on the PVY population and the risk of extinction of the less fit PVY variants with time. In the latter case (absence of a virus variant in all sampled plants), the lack of genetic information in the PVY populations would preclude the estimation of N e and σ r with the model of Rousseau et al. (2017). All 151 DH lines of C. annuum carried the PVY resistance allele pvr23 and differed in their genetic background (Quenouille et al., 2014). They were issued from the F1 hybrid between ‘Perennial’, a PVY‐resistant pepper line carrying the pvr23 allele, and ‘Yolo Wonder’, a PVY‐susceptible line (Quenouille et al., 2014). The five SON41p variants, named G, N, K, GK and KN based on their amino acid substitutions in VPg (i.e. the ‘K’ and ‘N’ mutations defined previously and the ‘G’ mutation corresponding to the serine to glycine substitution at codon position 101 of VPg), were mixed in similar amounts based on quantitative DAS‐ELISA and were mechanically inoculated onto the two cotyledons of eight plants per DH line. Each of these mutations or mutation pairs (double‐letter names) conferred to PVY the capacity to infect plants carrying pvr23. At 21 dpi, for each plant, all apical leaves were collected, pooled together and crushed in buffer before RNA purification as in Rousseau et al. (2017). One‐step RT‐PCR amplification was conducted for 1208 plants (8 plants × 151 DH lines), individually, in thirteen 96‐well PCR plates. The amplified region was 104 nucleotides long and corresponded to positions 5991–6094 of PVY SON41p (accession AJ439544).

In all, the sampling, RT‐PCR and sequencing procedures performed to obtain the viral sequences were essentially carried out as described in Rousseau et al. (2017). Eight differently tagged primers were used, corresponding to the eight different plant replicates of the same plant genotype. Three of the eight primers used by Rousseau et al. (2017) were poorly efficient in PCR (corresponding to primer tags 5′‐GGTCTAGTAC, 5′‐GAGGCTCTAC and 5′‐TGCTGATATC), and were thus replaced with primer tags 5′‐CGACGACTGC, 5′‐TGGAGTACGA and 5′‐GGAGCGTCAC. Amplified DNAs corresponding to the eight plant replicates were pooled together on the basis of their intensity on electrophoresis gels. To avoid opening the reaction microtubes and hence cross‐contamination between microtubes of the same RT‐PCR plate, single‐step RT‐PCRs were performed on RNA extracts on a first set of 13 PCR plates. For 66 DH lines, no RT‐PCR products were detected by agarose gel electrophoresis for at least four of the eight plants. A two‐step RT‐PCR protocol was thus carried out for all the samples of these 66 DH lines in six additional 96‐well PCR plates. This protocol usually provides a higher sensitivity than the first, but increases the risk of contamination (Bustin, 2000). Unfortunately, MiSeq sequencing results showed that significant contamination occurred in four of these six additional PCR plates (see below). As next‐generation sequencing data may be impacted by contamination, several controls were included as in Rousseau et al. (2017). These controls allowed the estimation of potential cross‐contamination amongst samples during the crushing step or during RT‐PCR. HTS was performed at the GeT‐PlaGe Genomic Platform of INRA Toulouse, France. For this purpose, 2 × 150 base‐pair libraries were prepared with multiplex adapters (12 PCR cycles), and all the RT‐PCR‐amplified products were pooled into a single large sample. This sample was run on a MiSeq Illumina paired‐end sequencer with the MiSeq Reagent Kit v2, for 500 cycles. By using tagged primers and subsequent multiplex adapters, we were able to assign a plant number and a plant genotype to each sequence.

After MiSeq sequencing, the number (counts) of reads detected in the negative controls of the former set of 13 PCR plates ranged from 0 to 100, with a mean number (± standard deviation) of 40 ± 24. This contrasts greatly with the number of reads per sample, which ranged from 201 to 11 052, with a mean read number of 4919 ± 1747. As mentioned above, the sequencing results confirmed the occurrence of high contamination levels on four plates in the second set of six PCR plates, with 1449 ± 1917 reads in the negative controls. All DH lines corresponding to these four PCR plates were removed from the dataset. Consequently, sequences corresponding to 89 DH lines were kept and analysed further. From these reads, counts of sequences corresponding to the five inoculated PVY variants in each individual plant were obtained as in Rousseau et al. (2017). The initial inoculum was also sequenced and the following frequencies were obtained for the five PVY variants: G (22%), N (15%), K (17%), GK (18%) and KN (28%). Counts of sequences corresponding to the five PVY variants in all sampled plants and in the inoculum are shown in Table S2 (see Supporting Information). Moreover, the presence of de novo nucleotide substitutions in the sequence dataset was checked as described in Rousseau et al. (2017) (Methods S1 and Table S1). A minimal threshold of 7% was considered for these de novo mutations, which accounts for: (i) potential errors caused by RT‐PCR and MiSeq Illumina sequencing; and (ii) potential impact on the precision of estimation of genetic drift (N e) and differential selection (σr) with the method of Rousseau et al. (2017). Consequently, we withdrew plants with de novo mutations exceeding 7% of the PVY population. For five DH lines, less than five plant replicates remained and these DH lines were removed before further analyses. We ended up with a dataset of 84 DH lines.

Inference of virus Ne and σ r

Estimation of the strength of genetic drift and the relative growth rates of PVY variants acting on the composite PVY population was performed with the method proposed by Rousseau et al. (2017). The estimated parameters are the relative growth rates ri of each PVY variant i (G, N, K, GK and KN) and the effective population size N e of the whole PVY population for each of the 84 DH lines considered. For a given DH line, the observed variables are the PVY variant sequence counts obtained from HTS data in the eight sampled plants. The differential selection (σ r) exerted by a pepper DH line on the whole PVY population composed of five variants was estimated as the standard deviation of the ri values of the five PVY variants.

The method of Rousseau et al. (2017) was validated for an experimental context involving the determination of virus variant frequencies by HTS in eight plants at each of six sampling dates. In contrast, the present experimental design involved a single sampling date. Before applying the method to the current dataset, we performed several batches of simulations to assess its efficiency to infer accurately virus effective population sizes and relative growth rates with a single sampling date. Briefly, we first simulated the changes in frequency of five virus variants under 400 selection and genetic drift regimes with a Wright–Fisher model for haploid individuals. The simulated datasets were generated as in Rousseau et al. (2017), except that a single sampling date (21 dpi with eight independent host plants sampled for each plant genotype) was considered and the criteria for accepting the simulated datasets differed as follows: (i) three of the five virus variants had to be present at a minimum frequency of 0.5% in at least 50% of the plants; and (ii) all variants had to be present in at least one of the eight plants at a minimum frequency of 0.1%. These criteria were met in 83 of the 84 DH lines analysed.

The genetic drift regimes were defined by a vector of effective population sizes varying every five generations (text S2 in Rousseau et al., 2017). For each of the 400 datasets obtained, the true parameters are known and can be compared with the estimated parameters (one growth rate for each variant; one effective population size corresponding to the harmonic mean of the effective population sizes over the successive generations).

Estimates of the relative growth rates ri were highly accurate, with an R 2 of the best‐fit line of 0.96, a slope close to 1.0 (0.98) and an intercept of 0.02 (Fig. S1a). Estimates of the harmonic mean of the effective population size N e h were also accurate with a best‐fit line, in logarithmic scale, close to the first bisector (R 2 = 0.86), a slope of 0.98 and an intercept of 0.05 (Fig. S1b). In both cases, the 95% confidence interval of the mean relative bias included zero. The 90% confidence interval was highly accurate for N e h as it included 89% of the true parameter values. However, the 90% confidence interval of ri was overestimated, the true parameter values being included in 98% of cases.

Statistical analyses of the links between variables related to the evolution of PVY populations

Statistical analyses were handled with R software version 3.0.2 (R Core Team, 2013; https://www.r-project.org/). We used GLMs to study the effects of N e, σ r, N e inoc and VA on the response variable RB, considered as a binary variable representing the occurrence (1) or absence (0) of infection in a total of 60 individual plants per DH line, except for seven DH lines for which only 30 plants were assayed (Quenouille et al., 2014). As a consequence, a binomial distribution was used in the GLMs for RB. The values of all variables for each DH line are shown in Table S3 (see Supporting Information). All explanatory variables (N e, σ r, N e inoc and VA) and their pairwise interactions were included in the full GLM, and stepwise model selection was performed using AIC (Akaike, 1974). GLMs were performed with the R packages ‘lme4’ and ‘MASS’. VIF was assessed with the R package ‘car’. In addition, conditional inference regression trees were realized using the method ‘ctree’ implemented in the package ‘party’. Such trees allow to explore the effects of the most significant explanatory variables on RB. Regression trees were computed with a minimum number of 10 DH lines in each terminal ‘leaf’ of the tree and default setting for other parameters to describe the conditional distribution of RB as a function of the four explanatory variables N e, σ r, N e inoc and VA.

Supporting information

Fig. S1 Inference of the relative growth rates of virus variants and of the effective population size of the virus population with 400 datasets simulated with five virus variants and a single sampling date with the method of Rousseau et al. (2017). (a) Correlation between true and estimated relative growth rates ri (all variants mixed). (b) Correlation between true and estimated harmonic means of effective population sizes Ne h (log‐scale). In both panels, the black line is the first bisector and the red dashed line is the best linear model fit.

Click here for additional data file. (192.3KB, tif)

Fig. S2 Pairwise relationships between the four explanatory variables related to PVY evolution: VA (within‐plant virus accumulation), σr (differential selection exerted on the virus population), Ne (virus effective population size during plant infection) and Neinoc (virus effective population size at virus inoculation). The arrow indicates the outlier for Ne.

Click here for additional data file. (81.1KB, tif)

Fig. S3 Pairwise relationships between the response variable RB (frequency of breakdown of the pvr23‐mediated resistance) and each of four explanatory variables related to PVY evolution: VA (within‐plant virus accumulation), σr (differential selection exerted on the virus population), Ne (virus effective population size during plant infection) and Neinoc (virus effective population size at inoculation).

Click here for additional data file. (66KB, tif)

Table S1 De novo mutations observed in PVY populations in inoculated plants in Illumina sequencing data. Only mutations representing >7% of the PVY populations are indicated.

Click here for additional data file. (14.2KB, xlsx)

Table S2 Number of sequences and composition of the virus populations in each plant sample. Columns indicate (i) the name of each DH line, (ii) the plant number, (iii) the infection status of each plant (0: not infected / 1: infected / 2: infected with a de novo substitution >7% of the virus population), (iv‐viii) the number of sequences for each inoculated viral variant (G, N, K, GK and KN). The last lines correspond to six independent sequencing replicas of the artificial PVY population used to inoculate all plants.

Click here for additional data file. (38.4KB, xlsx)

Table S3 Values of variables for each DH line. See main text for definition of variables. In experiments designed to estimate variable RB, the frequency of resistance breakdown, the number of infected plants was RB1 and the number of noninfected plants was RB2.

Click here for additional data file. (18.6KB, xlsx)

Methods S1 Analyses of Illumina sequences to detect de novo mutations in PVY populations.

Click here for additional data file. (18.3KB, docx)

Acknowledgements

The authors thank A. M. Sage‐Palloix and G. Nemouchi for providing pepper genetic resources and J. Béraud, N. Truglio and M. Pascal for plant care. They also thank H. M. Clause for support. L.T.’s PhD was supported by the department ‘Biologie et Amélioration des Plantes’ (BAP) of INRA and the Sustainable Management of Crop Health (SMaCH) INRA metaprogramme, and by the Région Provence‐Alpes‐Côte d’Azur (PACA). Experimental work was supported by the SMaCH metaprogramme and partly performed on the LBM platform of INRA Avignon. Simulations were carried out with the Avakas computer cluster at Bordeaux University. This work was performed in collaboration with the GeT core facility, Toulouse, France (https://get.genotoul.fr), and was supported by France Génomique National infrastructure, funded as part of the ‘Investissement d’avenir’ programme, managed by the Agence Nationale pour la Recherche (contract ANR‐10‐INBS‐09).

References

  1. Abel, S. , Abel zur Wiesch, P. , Davis, B.M. and Waldor, M.K. (2015) Analysis of bottlenecks in experimental models of infection. PLoS Pathog. 11, e1004823. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Akaike, H. (1974) A new look at the statistical model identification. IEEE Trans. Autom. Control, 19, 716–723. [Google Scholar]
  3. Ayme, V. , Souche, S. , Caranta, C. , Jacquemond, M. , Chadœuf, J. , Palloix, A. and Moury, B. (2006) Different mutations in the genome‐linked protein VPg of Potato virus Y confer virulence on the pvr2 3 resistance in pepper. Mol. Plant–Microbe Interact. 19, 557–563. [DOI] [PubMed] [Google Scholar]
  4. Brun, H. , Chèvre, A.‐M. , Fitt, B.D. , Powers, S. , Besnard, A.‐L. , Ermel, M. , Huteau, V. , Marquer, B. , Eber, F. , Renard, M. and Andrivon, D. (2010) Quantitative resistance increases the durability of qualitative resistance to Leptosphaeria maculans in Brassica napus . New Phytol. 185, 285–299. [DOI] [PubMed] [Google Scholar]
  5. Bustin, S.A. (2000) Absolute quantification of mRNA using real‐time reverse transcription polymerase chain reaction assays. J. Mol. Endocrinol. 25, 169–193. [DOI] [PubMed] [Google Scholar]
  6. Charlesworth, B. (2009) Fundamental concepts in genetics: effective population size and patterns of molecular evolution and variation. Nat. Rev. Genet. 10, 195–205. [DOI] [PubMed] [Google Scholar]
  7. Díaz, J.A. , Nieto, C. , Moriones, E. , Truniger, V. and Aranda, M.A. (2004) Molecular characterization of a Melon necrotic spot virus strain that overcomes the resistance in melon and nonhost plants. Mol. Plant–Microbe Interact. 17, 668–675. [DOI] [PubMed] [Google Scholar]
  8. Ewens, W.J. (2004) Mathematical Population Genetics. I. Theoretical Introduction, 2nd edn., Interdisciplinary Applied Mathematics, Vol. 27. New York: Springer‐Verlag. [Google Scholar]
  9. Fabre, F. , Bruchou, C. , Palloix, A. and Moury, B. (2009) Key determinants of resistance durability to plant viruses: insights from a model linking within‐ and between‐host dynamics. Virus Res. 141, 140–149. [DOI] [PubMed] [Google Scholar]
  10. Fabre, F. , Montarry, J. , Coville, J. , Senoussi, R. , Simon, V. and Moury, B. (2012a) Modelling the evolutionary dynamics of viruses within their hosts: a case study using high‐throughput sequencing. PLoS Pathog. 8, e1002654. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fabre, F. , Rousseau, E. , Mailleret, L. and Moury, B. (2012b) Durable strategies to deploy plant resistance in agricultural landscapes. New Phytol. 193, 1064–1075. [DOI] [PubMed] [Google Scholar]
  12. Fabre, F. , Rousseau, E. , Mailleret, L. and Moury, B. (2015) Epidemiological and evolutionary management of plant resistance: optimizing the deployment of cultivar mixtures in time and space in agricultural landscapes. Evol. Appl. 8, 919–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Feder, A.F. , Rhee, S.‐Y. , Holmes, S.P. , Shafer, R.W. , Petrov, D.A. and Pennings, P.S. (2016) More effective drugs lead to harder selective sweeps in the evolution of drug resistance in HIV‐1. Elife, 5, e10670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fournet, S. , Kerlan, M.‐C. , Renault, L. , Dantec, J.‐P. , Rouaux, C. and Montarry, J. (2013) Selection of nematodes by resistant plants has implications for local adaptation and cross‐virulence: local adaptation and cross‐virulence in Globodera pallida . Plant Pathol. 62, 184–193. [Google Scholar]
  15. French, R. and Stenger, D.C. (2003) Evolution of wheat streak mosaic virus: dynamics of population growth within plants may explain limited variation. Annu. Rev. Phytopathol. 41, 199–214. [DOI] [PubMed] [Google Scholar]
  16. Gago, S. , Elena, S.F. , Flores, R. and Sanjuán, R. (2009) Extremely high mutation rate of a hammerhead viroid. Science, 323, 1308–1308. [DOI] [PubMed] [Google Scholar]
  17. García‐Arenal, F. and McDonald, B.A. (2003) An analysis of the durability of resistance to plant viruses. Phytopathology, 93, 941–952. [DOI] [PubMed] [Google Scholar]
  18. Gómez, P. , Rodríguez‐Hernández, A. , Moury, B. and Aranda, M. (2009) Genetic resistance for the sustainable control of plant virus diseases: breeding, mechanisms and durability. Eur. J. Plant Pathol. 125, 1–22. [Google Scholar]
  19. Gutiérrez, S. , Michalakis, Y. and Blanc, S. (2012) Virus population bottlenecks during within‐host progression and host‐to‐host transmission. Curr. Opin. Virol. 2, 546–555. [DOI] [PubMed] [Google Scholar]
  20. Gutiérrez, S. , Yvon, M. , Thébaud, G. , Monsion, B. , Michalakis, Y. and Blanc, S. (2010) Dynamics of the multiplicity of cellular infection in a plant virus. PLoS Pathog. 6, e1001113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Harrison, B.D. (2002) Virus variation in relation to resistance‐breaking in plants. Euphytica, 124, 181–192. [Google Scholar]
  22. de la Iglesia, F. , Martínez, F. , Hillung, J. , Cuevas, J.M. , Gerrish, P.J. , Daròs, J.‐A. and Elena, S.F. (2012) Luria–Delbrück estimation of Turnip mosaic virus mutation rate in vivo. J. Virol. 86, 3386–3388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Iwasa, Y. , Michor, F. and Nowak, M.A. (2004) Stochastic tunnels in evolutionary dynamics. Genetics, 166, 1571–1579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Janzac, B. , Fabre, F. , Palloix, A. and Moury, B. (2009) Constraints on evolution of virus avirulence factors predict the durability of corresponding plant resistances. Mol. Plant Pathol. 10, 599–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Khelifa, M. , Massé, D. , Blanc, S. and Drucker, M. (2010) Evaluation of the minimal replication time of Cauliflower mosaic virus in different hosts. Virology, 396, 238–245. [DOI] [PubMed] [Google Scholar]
  26. Kimura, M. (1970) Stochastic processes in population genetics, with special reference to distribution of gene frequencies and probability of gene fixation In: Mathematical Topics in Population Genetics, pp. 178–209. Springer. [Google Scholar]
  27. Kimura, M. and Crow, J.F. (1963) The measurement of effective population number. Evolution, 17, 279–288. [Google Scholar]
  28. Lafforgue, G. , Tromas, N. , Elena, S.F. and Zwart, M.P. (2012) Dynamics of the establishment of systemic potyvirus infection: independent yet cumulative action of primary infection sites. J. Virol. 86, 12 912–12 922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lande, R. and Barrowclough, G.F. (1987) Effective population size, genetic variation, and their use in population management. Viable Popul. Conserv. 87, 124. [Google Scholar]
  30. Lanfear, R. , Kokko, H. and Eyre‐Walker, A. (2014) Population size and the rate of evolution. Trends Ecol. Evol. 29, 33–41. [DOI] [PubMed] [Google Scholar]
  31. Lannou, C. (2012) Variation and selection of quantitative traits in plant pathogens. Annu. Rev. Phytopathol. 50, 319–338. [DOI] [PubMed] [Google Scholar]
  32. Lê Van, A. , Caffier, V. , Lasserre‐Zuber, P. , Chauveau, A. , Brunel, D. , Le Cam, B. and Durel, C.‐E. (2013) Differential selection pressures exerted by host resistance quantitative trait loci on a pathogen population: a case study in an apple × Venturia inaequalis pathosystem. New Phytol. 197, 899–908. [DOI] [PubMed] [Google Scholar]
  33. Malpica, J.M. , Fraile, A. , Moreno, I. , Obies, C.I. , Drake, J.W. and García‐Arenal, F. (2002) The rate and character of spontaneous mutation in an RNA virus. Genetics, 162, 1505–1511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Martínez, F. , Sardanyés, J. , Elena, S.F. and Daròs, J.‐A. (2011) Dynamics of a plant RNA virus intracellular accumulation: stamping machine vs. geometric replication. Genetics, 188, 637–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. McDonald, B.A. and Linde, C. (2002) Pathogen population genetics, evolutionary potential, and durable resistance. Annu. Rev. Phytopathol. 40, 349–379. [DOI] [PubMed] [Google Scholar]
  36. Miras, M. , Sempere, R.N. , Kraft, J.J. , Miller, W.A. , Aranda, M.A. and Truniger, V. (2014) Interfamilial recombination between viruses led to acquisition of a novel translation‐enhancing RNA element that allows resistance breaking. New Phytol. 202, 233–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Montarry, J. , Doumayrou, J. , Simon, V. and Moury, B. (2011) Genetic background matters: a plant–virus gene‐for‐gene interaction is strongly influenced by genetic contexts: viral genetic background matters. Mol. Plant Pathol. 12, 911–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Moury, B. , Morel, C. , Johansen, E. , Guilbaud, L. , Souche, S. , Ayme, V. , Caranta, C. , Palloix, A. and Jacquemond, M. (2004) Mutations in Potato virus Y genome‐linked protein determine virulence toward recessive resistances in Capsicum annuum and Lycopersicon hirsutum . Mol. Plant–Microbe Interact. 17, 322–329. [DOI] [PubMed] [Google Scholar]
  39. Moury, B. , Fereres, A. , García‐Arenal, F. and Lecoq, H. (2011) Sustainable management of plant resistance to viruses In: Recent Advances in Plant Virology (Caranta C., Aranda M.A., Tepfer M., López‐Moya J.J. and eds), pp. 219–336. Norfolk, UK: Caister Academic Press. [Google Scholar]
  40. Palloix, A. , Ayme, V. and Moury, B. (2009) Durability of plant major resistance genes to pathogens depends on the genetic background, experimental evidence and consequences for breeding strategies. New Phytol. 183, 190–199. [DOI] [PubMed] [Google Scholar]
  41. Quenouille, J. , Montarry, J. , Palloix, A. and Moury, B. (2013) Farther, slower, stronger: how the plant genetic background protects a major resistance gene from breakdown: mechanisms of polygenic resistance durability. Mol. Plant Pathol. 14, 109–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Quenouille, J. , Paulhiac, E. , Moury, B. and Palloix, A. (2014) Quantitative trait loci from the host genetic background modulate the durability of a resistance gene: a rational basis for sustainable resistance breeding in plants. Heredity, 112, 579–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Quenouille, J. , Saint‐Felix, L. , Moury, B. and Palloix, A. (2015) Diversity of genetic backgrounds modulating the durability of a major resistance gene. Analysis of a core collection of pepper landraces resistant to Potato virus Y . Mol. Plant Pathol. 17, 296–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Råberg, L. , Sim, D. and Read, A.F. (2007) Disentangling genetic variation for resistance and tolerance to infectious diseases in animals. Science, 318, 812–814. [DOI] [PubMed] [Google Scholar]
  45. R Core Team (2013) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria: URL: https://www.R-project.org. [Google Scholar]
  46. Restif, O. and Koella, J.C. (2004) Concurrent evolution of resistance and tolerance to pathogens. Am. Nat. 164, E90–E102. [DOI] [PubMed] [Google Scholar]
  47. Rodrigo, G. , Zwart, M.P. and Elena, S.F. (2014) Onset of virus systemic infection in plants is determined by speed of cell‐to‐cell movement and number of primary infection foci. J. R. Soc. Interface, 11, 20140555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Rousseau, E. , Moury, B. , Mailleret, L. , Senoussi, R. , Palloix, A. , Simon, V. , Valière, S. , Grognard, F. and Fabre, F. (2017) Estimating virus effective population size and selection without neutral markers. PLoS Pathog. 13, e1006702. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Rouzine, I.M. , Rodrigo, A. and Coffin, J.M. (2001) Transition between stochastic evolution and deterministic evolution in the presence of selection: general theory and application in virology. Microbiol. Mol. Biol. Rev. 65, 151–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Sacristán, S. , Malpica, J.M. , Fraile, A. and García‐Arenal, F. (2003) Estimation of population bottlenecks during systemic movement of Tobacco mosaic virus in tobacco plants. J. Virol. 77, 9906–9911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. da Silva, J. and Wyatt, S. (2014) Fitness valleys constrain HIV‐1’s adaptation to its secondary chemokine coreceptor. J. Evol. Biol. 27, 604–615. [DOI] [PubMed] [Google Scholar]
  52. Tamisier, L. , Rousseau, E. , Barraillé, S. , Nemouchi, G. , Szadkowski, M. , Mailleret, L. , Grognard, F. , Fabre, F. , Moury, B. and Palloix, A. (2017) Quantitative trait loci in pepper control the effective population size of two RNA viruses at inoculation. J. Gen. Virol. 98, 1923–1931. [DOI] [PubMed] [Google Scholar]
  53. Tromas, N. and Elena, S.F. (2010) The rate and spectrum of spontaneous mutations in a plant RNA virus. Genetics, 185, 983–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Wright, S. (1931) Evolution in Mendelian populations. Genetics, 16, 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Zhan, J. , Thrall, P.H. , Papaïx, J. , Xie, L. and Burdon, J.J. (2015) Playing on a pathogen’s weakness: using evolution to guide sustainable plant disease control strategies. Annu. Rev. Phytopathol. 53, 19–43. [DOI] [PubMed] [Google Scholar]
  56. Zwart, M.P. , Daròs, J.‐A. and Elena, S.F. (2011) One is enough. In vivo effective population size is dose‐dependent for a plant RNA virus. PLoS Pathog. 7, e1002122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Zwart, M.P. , Daros, J.‐A. and Elena, S.F. (2012) Effects of potyvirus effective population size in inoculated leaves on viral accumulation and the onset of symptoms. J. Virol. 86, 9737–9747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Zwart, M.P. and Elena, S.F. (2015) Matters of size: genetic bottlenecks in virus infection and their potential impact on evolution. Annu. Rev. Virol. 2, 161–179. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Fig. S1 Inference of the relative growth rates of virus variants and of the effective population size of the virus population with 400 datasets simulated with five virus variants and a single sampling date with the method of Rousseau et al. (2017). (a) Correlation between true and estimated relative growth rates ri (all variants mixed). (b) Correlation between true and estimated harmonic means of effective population sizes Ne h (log‐scale). In both panels, the black line is the first bisector and the red dashed line is the best linear model fit.

Click here for additional data file. (192.3KB, tif)

Fig. S2 Pairwise relationships between the four explanatory variables related to PVY evolution: VA (within‐plant virus accumulation), σr (differential selection exerted on the virus population), Ne (virus effective population size during plant infection) and Neinoc (virus effective population size at virus inoculation). The arrow indicates the outlier for Ne.

Click here for additional data file. (81.1KB, tif)

Fig. S3 Pairwise relationships between the response variable RB (frequency of breakdown of the pvr23‐mediated resistance) and each of four explanatory variables related to PVY evolution: VA (within‐plant virus accumulation), σr (differential selection exerted on the virus population), Ne (virus effective population size during plant infection) and Neinoc (virus effective population size at inoculation).

Click here for additional data file. (66KB, tif)

Table S1 De novo mutations observed in PVY populations in inoculated plants in Illumina sequencing data. Only mutations representing >7% of the PVY populations are indicated.

Click here for additional data file. (14.2KB, xlsx)

Table S2 Number of sequences and composition of the virus populations in each plant sample. Columns indicate (i) the name of each DH line, (ii) the plant number, (iii) the infection status of each plant (0: not infected / 1: infected / 2: infected with a de novo substitution >7% of the virus population), (iv‐viii) the number of sequences for each inoculated viral variant (G, N, K, GK and KN). The last lines correspond to six independent sequencing replicas of the artificial PVY population used to inoculate all plants.

Click here for additional data file. (38.4KB, xlsx)

Table S3 Values of variables for each DH line. See main text for definition of variables. In experiments designed to estimate variable RB, the frequency of resistance breakdown, the number of infected plants was RB1 and the number of noninfected plants was RB2.

Click here for additional data file. (18.6KB, xlsx)

Methods S1 Analyses of Illumina sequences to detect de novo mutations in PVY populations.

Click here for additional data file. (18.3KB, docx)

Articles from Molecular Plant Pathology are provided here courtesy of Wiley

RESOURCES