Abstract
Introduction
Failure to properly account for normal systematic variations in OMICS datasets may result in misleading biological conclusions. Accordingly, normalization is a necessary step in the proper preprocessing of OMICS datasets. In this regards, an optimal normalization method will effectively reduce unwanted biases and increase the accuracy of downstream quantitative analyses. But, it is currently unclear which normalization method is best since each algorithm addresses systematic noise in different ways.
Objective
Determine an optimal choice of a normalization method for the preprocessing of metabolomics datasets.
Methods
Nine MVAPACK normalization algorithms were compared with simulated and experimental NMR spectra modified with added Gaussian noise and random dilution factors. Methods were evaluated based on an ability to recover the intensities of the true spectral peaks and the reproducibility of true classifying features from orthogonal projections to latent structures – discriminant analysis model (OPLS-DA).
Results
Most normalization methods (except histogram matching) performed equally well at modest levels of signal variance. Only probabilistic quotient (PQ) and constant sum (CS) maintained the highest level of peak recovery (> 67%) and correlation with true loadings (> 0.6) at maximal noise.
Conclusion
PQ and CS performed the best at recovering peak intensities and reproducing the true classifying features for an OPLS-DA model regardless of spectral noise level. Our findings suggest that performance is largely determined by the level of noise in the dataset, while the effect of dilution factors was negligible. A minimal allowable noise level of 20% was also identified for a valid NMR metabolomics dataset.
Keywords: Metabolomics, Normalization, Noise, NMR, Preprocessing Chemometrics
Introduction
High-throughput facilities continue to improve the acquisition and throughput of OMICS experiments (e.g., genomics, transcriptomics, proteomics, and metabolomics), which has resulted in the rapid accumulation of large amounts of data (Berger, Peng, Singh 2013). These massive datasets have enabled the detection and quantification of thousands of genes, proteins, and metabolites across various biological samples (Chawade, Alexandersson, Levander 2014). Accordingly, OMICs data has significantly contributed to a variety of fields including drug discovery, (Butcher, Berg, Kunkel 2004) personalized medicine, (Chen, Mias, Li-Pook-Than, Jiang, Lam, Chen, Miriami et al. 2012) nutrition (Wishart 2008) and environmental studies (Aardema, MacGregor 2002). Perturbations or variance are inherent to all experimental datasets and come from a variety of sources such as biological variability, instrument instability, and inconsistency in sample handling and preparation. For example, the number of cells harvested, the mass of tissue collected, or the amount of urine produced may vary significantly across all of the biological replicates. These unavoidable variations may mask the real biological signals present in the samples, which, in turn, complicates the reliability and accuracies of all downstream quantitative analyses (Kohl, Klein, Hochrein, Oefner, Spang, Gronwald 2012). Accordingly, the preprocessing of OMICs data is a critical step and involves minimizing undesirable noise to make all subsequent analyses more robust, accurate, and precise (Dieterle, Ross, Schlotterbeck, Senn 2006). One crucial preprocessing step is the normalization of data, which has been shown to effectively reduce systematic noise in OMICs datasets (Chawade, Alexandersson, Levander 2014).
Normalization of OMICS datasets can be accomplished using a variety of methods (Giraudeau, Tea, Remaud, Akoka 2014; Hochrein, Zacharias, Taruttis, Samol, Engelmann, Spang, Oefner et al. 2015). But, the proper choice depends on data characteristics and the sources of variation that needs correcting. How well a specific normalization technique performs in reducing these extraneous biases is still an open question. Accordingly, identifying an optimal normalization technique is still a common issue encountered throughout the OMICs fields. For example, in genomics, differences in sequencing length (library size), gene length, or guanine-cytosine content may lead to data variance and a false interpretation of gene expression variability (Zyprych-Walczak, Szabelska, Handschuh, Gorczak, Klamecka, Figlerowicz, Siatkowski 2015). Thus, an appropriate normalization method needs to eliminate these sources of variance to ensure an accurate measure of gene expression levels. To address this issue, Choe et al. examined four popular normalization methods routinely used in genomics that included: constant sum, rank-invariant, LOESS (LOcally Estimated Scatterplot Smoothing), and quantile (Choe, Boutros, Michelson, Church, Halfon 2005). The normalization algorithms were compared using RNA-microarray data. The LOESS normalization algorithm assumes a non-linear relationship and uses a local regression approach to adjust signal intensity and noise. Incorporating LOESS normalization into the analysis of the RNA-microarray data yielded superior results relative to the other normalization techniques. LOESS improved the detection of true differentially expressed genes as evident by the largest area under the receiver operating characteristic (ROC) curve. Similarly, Callister et al. evaluated four normalization techniques routinely used in proteomics (Callister, Barry, Adkins, Johnson, Qian, Webb-Robertson, Smith et al. 2006). Central tendency, linear regression, locally weighted regression, and quantile normalization algorithms were compared using three sets of samples representing different levels of data complexity. The linear regression normalization algorithm was identified as the top performer since it exhibited the largest reduction in extraneous variability while also maintaining the highest reproducibility as measured by both pooled estimate of variance and a median coefficient of variance.
Metabolomics characterizes both the identity and the quantity of metabolites present in a biological sample (Kohl, Klein, Hochrein, Oefner, Spang, Gronwald 2012). Since metabolites are a direct product of cellular processes, the metabolome is able to accurately capture the current state of the system. Thus, even subtle changes in metabolite concentrations may provide important insights into disease progression, (Cuykx, Claes, Rodrigues, Vanhaecke, Covaci 2018) drug resistance, (Thulin, Thulin, Andersson 2017) or a response to numerous stress factors (e.g., environmental toxins, nutrient limitation, genetic mutation, etc.)(Doran, Knee, Wang, Rzezniczak, Parkes, Li, Merritt 2017; Fukushima, Iwasa, Nakabayashi, Kobayashi, Nishizawa, Okazaki, Saito et al. 2017; Jung, Lee, Seo, Hwang 2017). Unfortunately, like genomics and proteomics, these metabolite differences are easily obscured by the natural variance that occurs between biological replicates or by inconsistencies in sample sizes. Furthermore, since nuclear magnetic resonance (NMR) spectroscopy (Kohl, Klein, Hochrein, Oefner, Spang, Gronwald 2012) is routinely used to monitor the metabolome, instrument instability and experimental factors such as changes in pH, temperature, ionic strength or even sample composition may lead to unintended signal variance (Dieterle, Ross, Schlotterbeck, Senn 2006). Such non-biologically induced perturbations are likely to mask the true biological signals in the data and complicate the data analysis process. Again, normalization is a necessary requirement to minimize these undesirable variations and to increase the accuracy and reliability of all subsequent data analyses.
A variety of procedures are currently available to normalize NMR metabolomics data (Fukushima, Iwasa, Nakabayashi, Kobayashi, Nishizawa, Okazaki, Saito et al. 2017; Hochrein, Zacharias, Taruttis, Samol, Engelmann, Spang, Oefner et al. 2015). Since each algorithm addresses systematic variations in a different manner, the correct choice of a normalization scheme can be challenging. For example, some normalization algorithms aim to remove unwanted noise by minimizing inter-sample variation such as probabilistic quotient (Dieterle, Ross, Schlotterbeck, Senn 2006) and cubic splines methods (Workman, Jensen, Jarmer, Berka, Gautier, Nielser, Saxild et al. 2002), while others such as unit variance or Pareto (often referred to as scaling), aim to adjust the variance of spectral features so that all peaks are equally weighted when used to construct multivariate models such as principal components analysis (PCA). Since these algorithms were developed with different underlying assumptions, each method confers a unique set of advantages and disadvantages. For example, Craig et al. (Craig, Cloarec, Holmes, Nicholson, Lindon 2006), demonstrated that while constant sum normalization adequately preserves signal quality, it can change the underlying correlations between peaks and generate artifacts. Thus, constant sum may confound interpretations when used incorrectly. A comparative analysis of normalization schemes by Kohl et al. (Kohl, Klein, Hochrein, Oefner, Spang, Gronwald 2012) determined that quantile normalization significantly outperforms other approaches in both minimizing inter-sample standard deviation and accurately preserving fold change information. However, it was also noted that the performance of quantile normalization was only truly realized for large datasets (n ≥ 50) and offers no significant performance benefits on more modestly sized datasets.
The diversity of normalization algorithms and the lack of a clear consensus has provided the motivation to conduct a thorough and quantitative evaluation of normalizing methods currently available to the metabolomics community through our MVAPACK software package (Worley, Powers 2014a). MVAPACK is open source software that includes a complete set of functions for data loading, preprocessing, modeling, and validation of NMR metabolomics datasets. MVAPACK also includes the following normalization methods: probabilistic quotient (PQ) (Dieterle, Ross, Schlotterbeck, Senn 2006), histogram matching (HM) (Torgrip, Åberg, Alm, Schuppe-Koistinen, Lindberg 2008), standard normal variate (SNV) (Barnes, Dhanda, Lister 1989), multiplicative scatter correction (MSC) (Windig, Shaver, Bro 2008), quantile (Q) (Kohl, Klein, Hochrein, Oefner, Spang, Gronwald 2012), natural cubic splines (CSpline) (Workman, Jensen, Jarmer, Berka, Gautier, Nielser, Saxild et al. 2002), smoothing splines (SSpline) (Fujioka, Kano 2005), constant sum (CS) and region of interest (ROI) (Dieterle, Ross, Schlotterbeck, Senn 2006). Our phase-scatter correction (PSC) algorithm is also available in MVAPACK, but was not included in this comparison since PSC was previously discussed in detail (Worley, Powers 2014b). The normalization methods were compared using simulated and experimental NMR datasets with various levels of added noise and dilution factors (Worley, Powers 2016). Their performances were evaluated based on an ability to recover the intensities of the true spectral peaks and the reproducibility of true classifying features from orthogonal projections to latent structures – discriminant analysis (OPLS-DA) model (Worley, Powers 2013). In this manner, the normalization methods were evaluated based upon expected outcomes for routine metabolomics study: (i) the ability to eliminate irrelevant signal variance due to dilution factors and noise; and (ii) the ability to produce a predictive model that correctly identifies the real group-dependent variants. Our analysis indicates that of the normalization algorithms evaluated, PQ and CS performed the best in the analysis of noisy one-dimensional (1D) NMR metabolomics datasets.
Materials and Methods
The performance of each normalization method was assessed using two distinct datasets: (i) simulated spectral data and (ii) a previously described experimental data set of 1D 1H NMR spectra of various coffee samples (Worley, Powers 2016). All of the analyses were conducted using our MVAPACK software package (Worley, Powers 2014a). All of the figures were generated using the R software package (R Development Core Team 2017).
Simulated 1D 1H NMR metabolomics dataset.
The simulated dataset consisted of 50 spectra in which each spectrum contained 901 spectral features. The set of spectra were divided into two separate groups. Each group consisted of 25 spectra that were randomly generated from a reference spectrum. The reference spectrum for each group was independently simulated from the Cauchy distribution (Weisstein), but with different parameters. Each reference spectrum contains four peaks located at chemical shifts of 3 ppm, 3.2 ppm, 3.5 ppm, and 8 ppm, respectively. The peak intensities differ between the four peaks and between the two reference spectra as illustrated in Figure 1.
Figure 1.
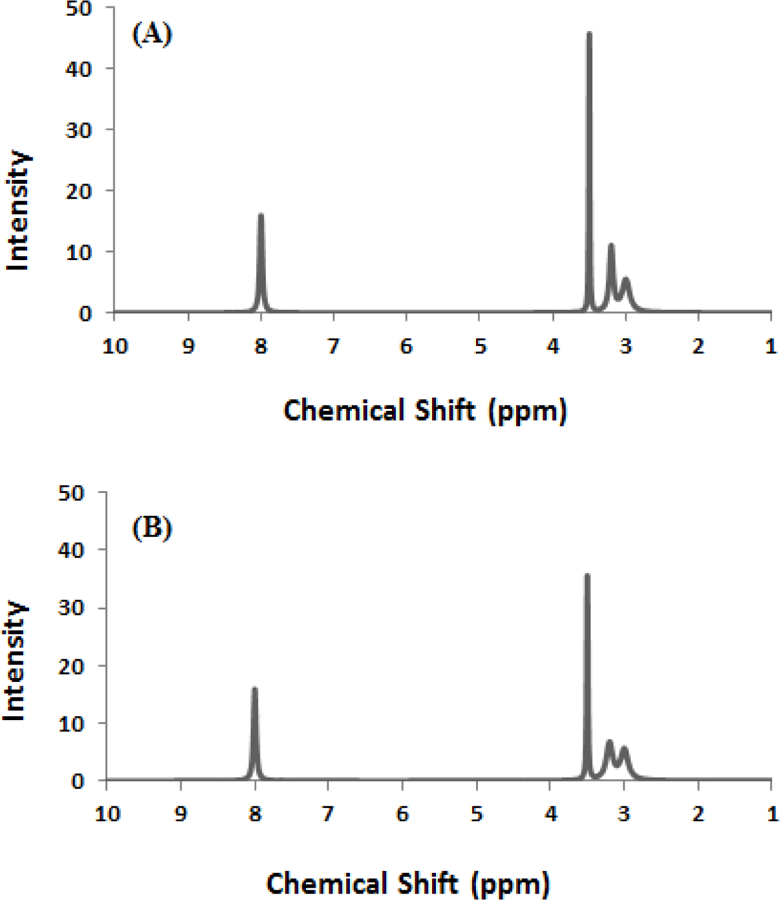
The simulated reference spectrum used for (A) group 1 and (B) for group 2. The two spectra contain the same number of peaks at the same chemical shifts. The only difference between the spectra is the relative peak intensities.
The 25 spectra per group were generated from the reference spectrum by the addition of a minimal amount of Gaussian noise (Mean = 0, SD = 0.001). These two sets of 25 spectra, which correspond to group 1 and group 2, were combined to define the simulated reference dataset (N = 50, K = 901). The simulated reference dataset was then used to generate eight noise-added simulated sets (Xi) (Figure S1) with (Table 1) according to equation (1):
| (1) |
where is a 50×1 vector of dilution factors generated from a uniform distribution for the set, is a matrix of independent Gaussian noise distributed with mean 0 and standard deviation for the set, and * presents element-wise multiplication. The value of ranged from 0.1 to 5 which produced a systematic increase in noise for the dataset.
Table 1:
Parameters used to generate the noise-added simulated spectra
| Set | Dilution Factors (F)a | Standard Deviation b | Percent Added Noise |
|---|---|---|---|
| S1 | 0.1 | 5% | |
| S2 | 0.2 | 10% | |
| S3 | 0.4 | 20% | |
| S4 | 1 | 50% | |
| S5 | 1.4 | 70% | |
| S6 | 1.8 | 90% | |
| S7 | 2.5 | 100% | |
| S8 | 4 | 200% |
A dilution factor was randomly selected from the indicated range of values.
The value of standard deviation used to generate a Gaussian distribution of noise.
The CS, PQ, HM, SNV, MSC, ROI, Q, CSpline, and SSpline normalization methods were then separately applied to each noise-added set to obtain normalized set . An OPLS-DA model was then generated from each normalized set . Two-component OPLS-DA models were calculated to obtain the first component loadings to compare the performance of the normalization approaches.
Experimental 1D 1H NMR metabolomics dataset.
A data matrix of 32 1D 1H NMR spectra from a publicly available coffees dataset was used to further evaluate the normalization algorithms (Worley, Powers 2016). The coffees dataset contains two groups defined as light and medium decaffeinated coffee consisting of 16 1D 1H NMR spectra per group. Each spectrum contains 284 spectral features.
We applied the same procedures as described above to generate the noise-added experimental dataset. Specifically, the original coffees dataset of 32 1D 1H NMR experimental spectra was designated as the reference data set (N = 32, K = 284). The reference data set was then used to generate seven simulated sets with (Table 2) according to equation 2:
| (2) |
where is a 32×1vector of dilution factors generated from a uniform distribution for the set, (N = 32, K = 284) is a matrix of independent Gaussian noise distributed with mean 0 and standard deviation for the set, and * presents element-wise multiplication. The value of ranged from to which produced a systematic increase in noise while also mimicking the relative variance in the noise present in the coffees dataset.
Table 2.
Parameters used to generate the noise-added coffees dataset
| Set | Dilution Factors a | Standard Deviation b | Percent Added Noise |
|---|---|---|---|
| C1 | 5% | ||
| C2 | 10% | ||
| C3 | 20% | ||
| C4 | 50% | ||
| C5 | 100% | ||
| C6 | 170% | ||
| C7 | 200% |
A dilution factor was randomly selected from the indicated range of values.
The value of standard deviation used to generate a Gaussian distribution of noise.
Summary of normalization procedures.
CS:
Each spectrum of the data matrix was divided by its own integral (Dieterle, Ross, Schlotterbeck, Senn 2006).
PQ:
The normalization factor was the most probable quotient between the signals of the corresponding spectrum and the reference spectrum (Dieterle, Ross, Schlotterbeck, Senn 2006). The reference spectrum was chosen as the median spectrum of the spectral set. Each spectrum in the dataset was divided by this normalization factor to obtain the normalized spectrum.
HM:
Raw spectra were log transformed prior to normalization. Similar to PQ, the target reference spectrum was the median spectrum of the dataset. Histograms for each sample spectrum and target spectrum were obtained on prespecified intensity intervals. A dilution factor was then chosen to minimize the differences between each sample spectrum histogram and the target histogram (Torgrip, Åberg, Alm, Schuppe-Koistinen, Lindberg 2008). The new normalized spectrum was generated by multiplying each original spectrum by the corresponding dilution factor.
SNV:
Each sample spectrum in the dataset was centered prior to normalization. The standard deviation of each spectrum was calculated as a normalization factor (Barnes, Dhanda, Lister 1989). A new normalized dataset was then obtained by dividing each original spectrum by its corresponding normalization factor.
MSC:
The normalization factors were least squares estimates obtained by regressing each sample spectrum onto the reference spectrum (Windig, Shaver, Bro 2008). The reference spectrum was the mean spectrum. The ordinary least squares of the regression parameters were used to correct the spectral intensities.
ROI:
Each sample spectrum of the dataset was normalized to a specified spectral region where its integral was set to one. Each sample spectrum was then normalized relative to the most intense peak in the spectrum.
Q:
The goal of this quantile normalization method was to obtain an identical distribution of intensities for all of the spectral features (Kohl, Klein, Hochrein, Oefner, Spang, Gronwald 2012). First, the mean spectrum was calculated for the data set. The intensities of all features in each sample spectrum were then replaced by the mean intensities in accordance with their quantile orders.
CSpline:
The CSpline method normalized each sample spectrum to the target spectrum. The target spectrum was calculated using the non-linear arithmetic mean of the data set. Depending on the type of data, a geometric mean may also be used (Kohl, Klein, Hochrein, Oefner, Spang, Gronwald 2012). A set of 100 quantiles was taken from both the sample spectrum and the target spectrum. The quantiles were then fitted to a natural cubic spline to obtain parameter estimates, which were used for interpolations. The process was repeated five times. For each iteration, a small offset was added to the quantiles before refitting with a natural cubic spline to obtain new interpolations. The set of interpolations were averaged to obtain the normalized spectrum.
SSpline:
SSpline is similar to CSpline, but the SSpline algorithm adds more quantiles toward the tail end of the spectrum. The most intense spectral features are located in this region of the spectrum. Moreover, the quantiles are fitted with a smoothing spline that includes a penalty parameter to avoid overfitting. The predicted feature intensities were then used as the normalized intensities.
Evaluation Criteria.
Regardless of the type of approach used to address dataset bias or variance, an optimal normalization procedure should reduce any unwanted noise while still preserving the true biological signals. In other words, a necessary condition to retain the true signals is the ability to recover the original peak intensities after removing noise. In this regards, it should be possible to evaluate the relative performance of normalization methods based on how well the algorithms handle increasingly noisy spectra. As the reference set is exposed to increasing amounts of noise, some (or all) of the normalization algorithms would be expected to fail to recover the original peaks intensities. Thus, the peak recovery criteria served as a means to filter-out poorly performing normalization procedures prior to proceeding with the second evaluation criteria.
A multivariate statistical model, such as PCA or OPLS, is typically employed to identify spectral features that separate the different groups in the dataset (Worley, Powers 2013). These spectral features are intrinsic to the dataset. Accordingly, any properly normalized dataset should reproduce these true set of features. The first component loadings extracted from an OPLS-DA model contains the weights of the spectral features that contribute the most to separating the groups. Simply, the first component loadings identify the most-important group-dependent features. Thus, an OPLS-DA model was generated to obtain the first component loadings associated with each normalization method. Only the top performing normalization methods were used to generate an OPLS-DA model. The top performing normalization methods were identified based on the peak recovery criteria. Pearson correlation coefficients were calculated between the loadings of each normalized dataset and the true loadings set. The Pearson correlation coefficients provide a means to measure the reproducibility of the true classifying spectral features produced by each normalization algorithm.
Peak Recovery:
After sequentially normalizing each noisy data matrix using the nine normalization methods, the intensity of each peak in each spectrum of the normalized set was compared to the true original spectrum to measure the recovery of peak intensities . For each spectrum from the normalized data matrix , the recovery of the peak was calculated according to this eqn. 3:
| (3) |
where and are the intensities of the peak from and , respectively. In this manner, will range from 0 to 1 regardless of the relative magnitudes of and . This process was repeated for every peak in each spectrum. The mean recovery and standard error were calculated and reported for each normalized set.
Pearson correlation coefficients:
The coffees noisy data matrix was only normalized using the top performing algorithms identified from the peak recovery criteria. An OPLS-DA model was generated for each normalized coffees data matrix and also the original coffees data set . The datasets were scaled with Pareto scaling prior to calculating the OPLS-DA models. The first component loadings from each OPLS-DA model were then used to calculate a Pearson correlation coefficient between the true backscale loadings vector from the original coffees data set and the backscale loadings vector from each normalized coffees noisy data matric . The Pearson correlation coefficients were calculated according to eqn. 4:
| (4) |
where K denotes the number of spectral features; is the mean loading of vector ; is the loading of vector ; is the mean loading of vector ; and is the loading of vector . This process was repeated 100 times. The mean correlation coefficients and standard error were calculated for each normalized set.
Results and Discussions
The two reference NMR spectra displayed in Figure 1 were used to generate eight noise-added simulated metabolomics datasets consisting of 25 spectra for each of the two groups (Figure S1). Accordingly, each simulated dataset contained a total of 50 spectra. The total signal variance in each dataset was defined by the amount of Gaussian noise added and by the dilution factors listed in Table 1. The simulated NMR metabolomics datasets were then normalized using each of the nine normalization methods (i.e., CS, CSpline, HM, MSC, PQ, Q, ROI, SNV, and SSpline). A peak recovery was calculated for each dataset according to eqn. 3. The peak recovery compares each of the normalized dataset to the original reference NMR spectra (Figure 1). The peak recoveries for each normalized dataset are plotted in Figures 2 and 3.
Figure 2.
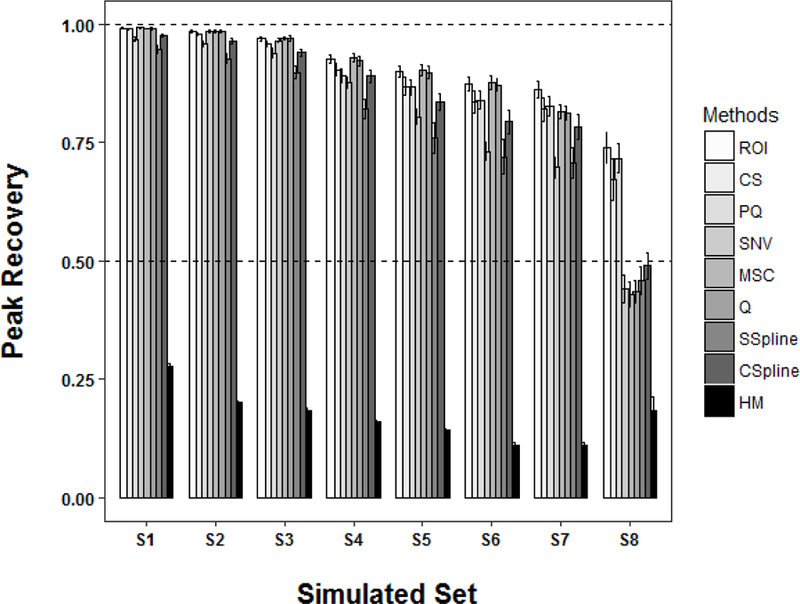
A plot of the recovery of peak intensities (eqn. 3) for the 9 normalization methods after being applied to the 8 (S1 to S8) simulated datasets listed in Table 1. The total signal variance due to the amount of added Gaussian noise and the magnitude of the dilution factor increases from S1 to S8. The horizontal dashed lines represent a full recovery at 100% and partial recovery at 50%. Each bar represents the mean peak recovery and the error bars represent ±2*standard error of the mean.
Figure 3.
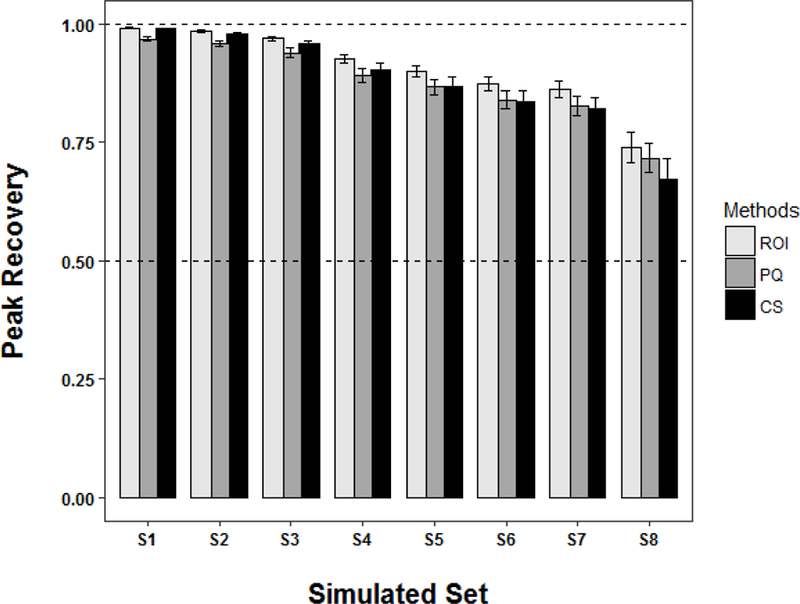
A plot of the recovery of peak intensities (eqn. 3) for the three top performing normalization methods after being applied to the 8 (S1 to S8) simulated datasets listed in Table 1. The total signal variance due to the amount of added Gaussian noise and the magnitude of the dilution factor increases from S1 to S8. The horizontal dashed lines represent a full recovery at 100% and partial recovery at 50%. Each bar represents the mean peak recover and the error bars represent ±2*standard error of the mean.
As expected, the efficiency of peak recovery decreases with increasing signal variance regardless of the normalization method. As illustrated in Figure 2, most of the normalization methods achieve nearly 100% peak recovery (96 to 99%) under conditions of modest signal variance (S1 and S2).
The most notable outlier is HM, which achieved a peak recovery of only 20% to 28%. This extremely poor performance suggests that HM should be avoided and not used for the normalization of NMR metabolomics data. While significantly better than HM, SSpline also performed consistently below average with a peak recovery range of 93% to 95%. PQ was modestly below the best performers with a peak recovery range of 96% to 97%. Conversely, ROI, CS, SNV, MSC, and Q, recovered at least 98% of the peak intensities under conditions of modest signal variance. A further separation in algorithm performance was apparent as the signal variance was progressively increased. SSpline continued to perform worse than average, but from simulated set S5 forward the performance of SNV had also significantly declined to match SSpline.
Similarly, from simulated set S6, CSpline had fallen below the average performance of the other normalization methods. In fact, as the amount of signal variance was increased to the highest level (S8), the peak recoveries for CSpline, HM, MSC, Q, and SSpline all fell below 50%. Conversely, CS, PQ and ROI maintained a peak recovery of around 70% (67% to 74%). Accordingly, the peak recovery results suggest that the CS, PQ and ROI were the most robust normalization methods and were able to maintain a maximal peak recovery as a function of signal variance (Figure 3). Pairwise Student’s t tests of the mean peak recovery values at the highest signal variance level (S8) yield a maximum p-value of < 2.8×10−13 between the CS, PQ, ROI algorithms and the other normalization methods.
To further investigate the individual impact of Gaussian noise and dilution factors on peak recovery, the simulation was repeated for the three top performing normalization methods (i.e., CS, PQ and ROI). Instead of simultaneously varying both Gaussian noise and the dilution factors as listed in Table 1, the simulation was repeated with either Gaussian noise or the dilution factor held constant at S1 values. The combined average peak recovery values for CS, PQ and ROI normalized datasets are plotted as a function of added Gaussian noise or dilution factor in Figure 4. This simulation yielded an unexpected result. The performance of the normalization method was essentially unaffected by the dilution factor. Near perfect peak recovery was obtained even for the highest dilution factor. Instead, the normalization performance was strictly dependent on the level of Gaussian noise add to the spectra. However, it is important to note that normalization methods also rely on good peak alignment, spectral phasing, baseline correction and solvent suppression in order to perform well. Accordingly, the simulations reported herein were restricted to well-behaved datasets.
Figure 4.
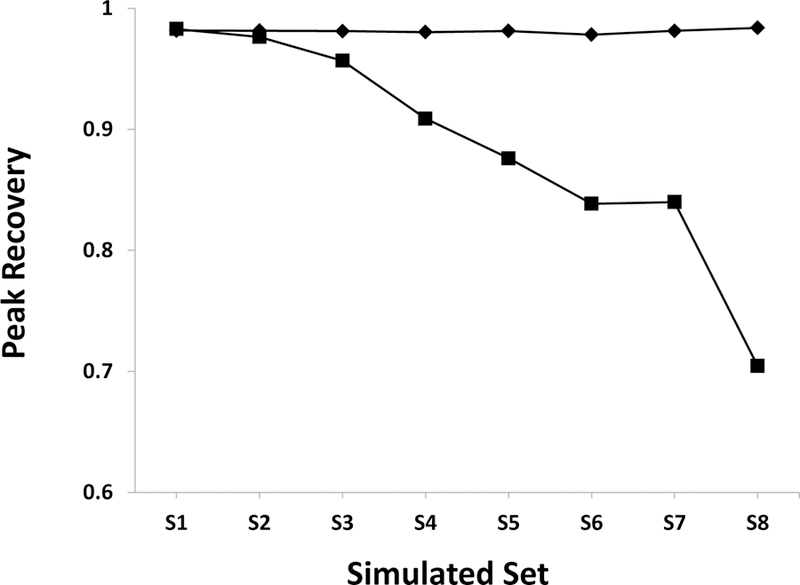
A plot of the average peak recovery calculated from the three top-performing normalization methods (CS, PQ, and ROI). Datasets were regenerated according to the scheme described in Table 1 but containing only a dilution factor (♦) or the addition of Gaussian noise (■). The dilution factor or added Gaussian noise was held constant at S1 values when the other parameter was varied. The peak recovery decreases with additive noise, but is unaffected by dilution factor.
While being able to accurately reconstitute peak intensity is an important attribute of a normalization algorithm, the proper identification of group-defining spectral features is still a vital necessity. In essence, are biologically-relevant metabolic differences still being correctly identified regardless of the natural signal variance? Does a PCA or OPLS scores plot yield statistically relevant group separations and do the loadings identify the “true” metabolic differences between the groups? To address this issue, the CS, PQ and ROI normalization methods were further evaluated based on the reproducibility of OPLS-DA models as a function of increasing signal variance. An experimental coffees dataset previously used to investigate PCA and OPLS model stability (Worley, Powers 2016), was employed to generate OPLS-DA models using the CS, PQ and ROI normalization methods. Specifically, the coffee dataset consists of 32 1D 1H NMR spectra for two groups of observations (light and medium decaffeinated coffees). The coffees dataset was modified with Gaussian noise and a dilution factor (Figure S2) as outlined in Table 2. Consistent with our prior observations (Worley, Powers 2016), the two coffee groups become indistinguishable with an increase in signal variance. Importantly, the estimated loadings from the corresponding OPLS-DA model are less correlated to the true loadings (Figure 5) with increasing signal variance. Notably, at minimal to moderate signal variance levels (C1 to C3), the PQ and ROI normalization methods perform almost identically and significantly better than CS. But, as the amount of signal variance increased significantly (C4 to C7), the OPLS-DA model was no longer valid with the ROI normalization technique; and the loadings correlation, not surprisingly, decreased dramatically.
Figure 5.
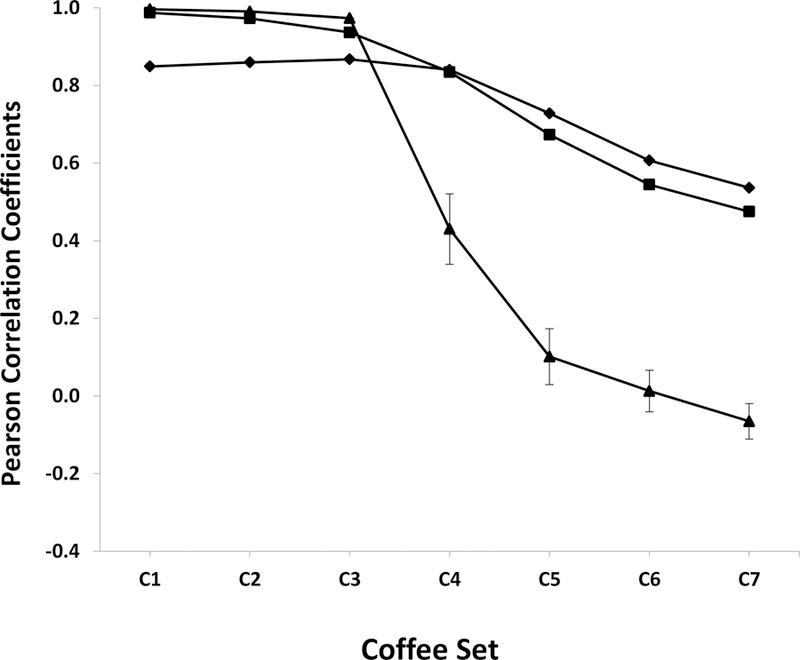
A plot of the average Pearson correlation coefficients (eqn. 4) calculated by comparing the true backscaled loadings from the original coffee dataset OPLS-DA model relative to the backscaled loadings from the CS (♦), PQ (■), and ROI (▲) normalized coffees noisy dataset OPLS-DA model. The amount of signal variance introduced into the coffees dataset is described in Table 2. The error bars represent ±2*standard error of the mean. Please note that most of the error bars are smaller than the size of the symbols.
Similarly, the standard errors of mean loadings correlation coefficients increased significantly for ROI compared to the negligible values observed for CS and PQ (ranged from 0.0003 to 0.008). Interestingly, despite CS initially performing worse than PQ, there was no difference in the loadings correlation between PQ and CS at C4. Furthermore, CS out-performed PQ at the highest signal variance levels (C5 to C7). But, the loadings correlations still decreased linearly with increasing signal variance following CS or PQ normalization. The loss of a correlation to the true loadings was still substantial and would likely lead to incorrect biological interpretations. A similar set of results was obtained for the simulated dataset (Figure S3). In total, our analysis suggest that CS and PQ are the most robust normalization techniques and are able to compensate, at least partly, for large signal variance. Both CS and PQ maintained the highest level of peak recovery and the highest correlation between backscaled loadings. Notably, PQ was the most robust normalization technique at low to moderate noise levels while CS was slightly better at compensating for larger signal variance.
A combined analysis of the peak recovery and OPLS-DA backscaled loadings data provides some further guidance for designing and executing an NMR metabolomics study. As we have noted previously (Halouska, Powers 2006; Halouska, Zhang, Gaupp, Lei, Snell, Fenton, Barletta et al. 2013; Worley, Powers 2016), noise is detrimental to the accurate and reliable analysis of metabolomics data using multivariate statistical techniques such as PCA and OPLS. The results reported herein further support the negative impact of noise on the analysis of NMR metabolomics data. As evident in Figure 4, a dilution factor had no appreciable impact on the performance of a normalization method. Instead, all variance in the performance of the normalization methods was due to noise. Furthermore, most of the normalization methods performed equally-well in regards to peak recovery and loadings correlation for added noise levels up to about 20%. The lone exception is HM, which should be avoided. A significant decay in performance occurred when more than 20% of noise was added to either the simulated or experimental dataset. Accordingly, an experimental NMR dataset that exhibits greater than 20% noise is a serious concern and the resulting chemometrics model is highly suspect. In essence, our analysis sets a minimum criterion for maintaining noise (defined by a standard Gaussian distribution) at below 20% for a valid metabolomics dataset.
Conclusion
The nine normalization methods available in our MVAPACK software package were evaluated for their ability to compensate for increasing signal variance. The performance of the normalization techniques were tested on simulated and experimental 1D 1H NMR datasets with the addition of Gaussian noise and dilution factors. However, it is important to keep in mind that the Gaussian noise and dilution factors used in model construction are only an approximation of non-biological variance. At low to moderate noise levels, all of the normalization methods, except HM, performed well in terms of peak recovery. Accordingly, HM should be avoided as a normalization technique for NMR. Notably, peak recovery performance was only dependent on added Gaussian noise, and independent of dilution factor. At high signal variance, most normalization procedures failed to recover true peak intensities except for CS, PQ, and ROI. Again, PQ and ROI normalization algorithms performed equally-well and significantly better than CS at low to moderate noise levels in reproducing the backscaled loadings from an OPLS-DA model. But, ROI generated statistically invalid OPLS-DA models and poor backscaled loadings correlations at higher-levels of noise. Interestingly, CS performed slightly better than PQ in reproducing the backscaled loadings at high noise levels. Thus, our results suggest that CS and PQ perform the best in regards to maintaining the true signal in noisy datasets. Consistent with our prior observations, groups become indistinguishable with increasing noise; and correlations to the true loadings are lost. In other words, an increasing level of additive Gaussian noise masks the true signals in the datasets. Accordingly, if this noise is not handled properly, it will lead to false conclusions and biologically irrelevant observations. In this regards, our analysis suggests that, at a minimum, noise needs to remain below 20% in order for an NMR metabolomics dataset to provide an accurate and biologically-relevant chemometrics model.
Supplementary Material
Acknowledgements
We thank Dr. Martha Morton, the Director of the Research Instrumentation Facility in the Department of Chemistry at the University of Nebraska-Lincoln for her assistance with the NMR experiments. This material is based upon work supported by the National Science Foundation under Grant Number (1660921). This work was supported in part by funding from the Redox Biology Center (P30 GM103335, NIGMS); and the Nebraska Center for Integrated Biomolecular Communication (P20 GM113126, NIGMS). The research was performed in facilities renovated with support from the National Institutes of Health (RR015468–01). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Abbreviations
- NMR
Nuclear Magnetic Resonance
- PCA
principal components analysis
- OPLS-DA
orthogonal projections to latent structures – discriminant analysis
- PQ
probabilistic quotient
- HM
histogram matching
- SNV
standard normal variate
- MSC
multiplicative scatter correction
- Q
quantile
- CSpline
natural cubic splines
- SSpline
smoothing splines
- CS
constant sum
- ROI
region of interest
- PSC
phase-scatter correction
- LOESS
LOcally Estimated Scatterplot Smoothing
- ROC
receiver operating characteristic curve
- 1D
one-dimensional
- SD
standard deviation
Footnotes
Compliance with Ethical Requirement
Conflict of Interest
Authors have no conflict of interest to declare.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
References
- Aardema MJ, MacGregor JT (2002). Toxicology and genetic toxicology in the new era of “toxicogenomics”: impact of “-omics” technologies. Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis 499, 13–25 doi: 10.1016/S0027-5107(01)00292-5 [DOI] [PubMed] [Google Scholar]
- Barnes RJ, Dhanda MS, Lister SJ (1989). Standard Normal Variate Transformation and De-Trending of Near-Infrared Diffuse Reflectance Spectra. Applied Spectroscopy 43, [Google Scholar]
- Berger B, Peng J, Singh M (2013). Computational solutions for omics data. Nature reviews Genetics 14, 333–346 doi: 10.1038/nrg3433 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butcher EC, Berg EL, Kunkel EJ (2004). Systems biology in drug discovery. Nature Biotechnology 22, 1253 doi: 10.1038/nbt1017 [DOI] [PubMed] [Google Scholar]
- Callister SJ, et al. (2006). Normalization approaches for removing systematic biases associated with mass spectrometry and label-free proteomics. J Proteome Res 5, 277–86 doi: 10.1021/pr050300l [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chawade A, Alexandersson E, Levander F (2014). Normalyzer: a tool for rapid evaluation of normalization methods for omics data sets. J Proteome Res 13, 3114–20 doi: 10.1021/pr401264n [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen R, et al. (2012). Personal Omics Profiling Reveals Dynamic Molecular and Medical Phenotypes. Cell 148, 1293–1307 doi: 10.1016/j.cell.2012.02.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choe SE, Boutros M, Michelson AM, Church GM, Halfon MS (2005). Preferred analysis methods for Affymetrix GeneChips revealed by a wholly defined control dataset. Genome Biology 6, R16 doi: 10.1186/gb-2005-6-2-r16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig A, Cloarec O, Holmes E, Nicholson JK, Lindon JC (2006). Scaling and Normalization Effects in NMR Spectroscopic Metabonomic Data Sets. Analytical Chemistry 78, 2262–2267 doi: 10.1021/ac0519312 [DOI] [PubMed] [Google Scholar]
- Cuykx M, Claes L, Rodrigues RM, Vanhaecke T, Covaci A (2018). Metabolomics profiling of steatosis progression in HepaRG® cells using sodium valproate. Toxicology Letters 286, 22–30 doi: 10.1016/j.toxlet.2017.12.015 [DOI] [PubMed] [Google Scholar]
- Dieterle F, Ross A, Schlotterbeck G, Senn H (2006). Probabilistic quotient normalization as robust method to account for dilution of complex biological mixtures. Application in 1H NMR metabonomics. Anal Chem 78, 4281–90 doi: 10.1021/ac051632c [DOI] [PubMed] [Google Scholar]
- Doran ML, et al. (2017). Metabolomic analysis of oxidative stress: Superoxide dismutase mutation and paraquat induced stress in Drosophila melanogaster. Free Radical Biology and Medicine 113, 323–334 doi: 10.1016/j.freeradbiomed.2017.10.011 [DOI] [PubMed] [Google Scholar]
- Fujioka H, Kano H (2005). Smoothing Spline curves and surfaces for sampled data. Int J Innov Comput 1, 429–449 [Google Scholar]
- Fukushima A, et al. (2017). Effects of Combined Low Glutathione with Mild Oxidative and Low Phosphorus Stress on the Metabolism of Arabidopsis thaliana. Frontiers in Plant Science 8, 1464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giraudeau P, Tea I, Remaud GS, Akoka S (2014). Reference and normalization methods: Essential tools for the intercomparison of NMR spectra. Journal of Pharmaceutical and Biomedical Analysis 93, 3–16 doi: 10.1016/j.jpba.2013.07.020 [DOI] [PubMed] [Google Scholar]
- Halouska S, Powers R (2006). Negative impact of noise on the principal component analysis of NMR data. Journal of Magnetic Resonance 178, 88–95 [DOI] [PubMed] [Google Scholar]
- Halouska S, et al. (2013). Revisiting Protocols for the NMR Analysis of Bacterial Metabolomes. Journal of Integrated OMICS 2, 120–137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochrein J, et al. (2015). Data Normalization of 1H NMR Metabolite Fingerprinting Data Sets in the Presence of Unbalanced Metabolite Regulation. Journal of Proteome Research 14, 3217–3228 doi: 10.1021/acs.jproteome.5b00192 [DOI] [PubMed] [Google Scholar]
- Jung Y-S, Lee J, Seo J, Hwang G-S (2017). Metabolite profiling study on the toxicological effects of polybrominated diphenyl ether in a rat model. Environmental Toxicology 32, 1262–1272 doi: 10.1002/tox.22322 [DOI] [PubMed] [Google Scholar]
- Kohl SM, Klein MS, Hochrein J, Oefner PJ, Spang R, Gronwald W (2012). State-of-the art data normalization methods improve NMR-based metabolomic analysis. Metabolomics 8, 146–160 doi: 10.1007/s11306-011-0350-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Thulin E, Thulin M, Andersson DI (2017). Reversion of High-level Mecillinam Resistance to Susceptibility in Escherichia coli During Growth in Urine. EBioMedicine 23, 111–118 doi: 10.1016/j.ebiom.2017.08.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torgrip RJO, Åberg KM, Alm E, Schuppe-Koistinen I, Lindberg J (2008). A note on normalization of biofluid 1D 1H-NMR data. Metabolomics 4, 114–121 doi: 10.1007/s11306-007-0102-2 [DOI] [Google Scholar]
- Weisstein EW Cauchy Distribution. In: MathWorld http://mathworld.wolfram.com/CauchyDistribution.html 2017
- Windig W, Shaver J, Bro R (2008). Loopy MSC: a simple way to improve multiplicative scatter correction. Appl Spectrosc 62, 1153–9 doi: 10.1366/000370208786049097 [DOI] [PubMed] [Google Scholar]
- Wishart DS (2008). Metabolomics: applications to food science and nutrition research. Trends in Food Science & Technology 19, 482–493 doi: 10.1016/j.tifs.2008.03.003 [DOI] [Google Scholar]
- Workman C, et al. (2002). A new non-linear normalization method for reducing variability in DNA microarray experiments. Genome Biology 3, research0048.1 doi: 10.1186/gb-2002-3-9-research0048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worley B, Powers R (2013). Multivariate Analysis in Metabolomics. Curr Metabolomics 1, 92–107 doi: 10.2174/2213235X11301010092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worley B, Powers R (2014a). MVAPACK: a complete data handling package for NMR metabolomics. ACS Chem Biol 9, 1138–44 doi: 10.1021/cb4008937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worley B, Powers R (2014b). Simultaneous Phase and Scatter Correction for NMR Datasets. Chemometr Intell Lab Syst 131, 1–6 doi: 10.1016/j.chemolab.2013.11.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worley B, Powers R (2016). PCA as a practical indicator of OPLS-DA model reliability. Curr Metabolomics 4, 97–103 doi: [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zyprych-Walczak J, et al. (2015). The Impact of Normalization Methods on RNA-Seq Data Analysis. Biomed Res Int 2015, 621690 doi: 10.1155/2015/621690 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


