‘Remember that all models are wrong; the practical question is how wrong do they have to be to not be useful.’ (George E. P. Box)
Introduction
In 2006, Jones and Dangl proposed a simple coevolutionary model of plant–pathogen interactions, called the ‘zigzag’ model, which encompasses two branches of the plant immune system (Jones and Dangl, 2006). The first branch recognizes conserved molecules shared by many classes of microbe (pathogen‐associated or microbe‐associated molecular patterns, PAMPs or MAMPs), and is now called pattern‐triggered immunity (PTI). The second branch recognizes and responds to virulence factors termed effectors that, in the model, serve to suppress PTI. This branch is called effector‐triggered immunity (ETI). The model has captured the imagination of plant pathology researchers and students alike, and has proved to be a powerful conveyor of the principal concepts in plant–pathogen interactions. Eight years on, we take a fresh look at the model to consider how well it fits its intended purpose, and how a model framework to inspire future researchers in the field of plant–microbe interactions might develop.
What Models Mean
Models in the scientific sense are abstract representations of reality. Their purpose is to reduce the complexity of a real‐world system to a manageable and understandable level. At its heart, any model simply acts as a logical machine for deducing conclusions from the restricted set of assumptions that define that model (Gunawardena, 2014). A model is, essentially, a microcosm of scientific hypothesis generation.
Some models are expository, in that they are intended to clarify principles so that they can be explained simply. Expository models are not usually intended to make quantitative predictions or to generate novel insights. Examples of expository models might include diagrams that represent protein complexes inferred from a protein–protein interaction experiment or schematics of dynamic processes, such as an organism's life cycle.
Other models, especially those based on physical laws or ones that are quantitative, are predictive. The aim of a predictive model is to represent complex systems in such a manner that new knowledge and understanding can be obtained by analysis of the model and not just by direct investigation of the real‐world system it represents. Models of this kind include Henri–Michaelis–Menten enzyme kinetics, the Lotka–Volterra model of predator–prey interactions and the Virtual Liver(Holzhütter et al., 2012).
It may not be important that an expository model is ‘wrong’ if the aim of transferring understanding is achieved. Predictive models can even achieve great utility and power when they are wrong because they are falsifiable: the assumptions that define the model can be tested experimentally and discarded if they are incorrect. Models of this kind can deliver great, and perhaps unanticipated, biological insight. As George Box pointed out, a model that has not (yet) been falsified is still likely to be wrong but, by a cycle of progressive improvement (revision of assumptions) and testing, our confidence in the model's output might be improved to the point that it is predictively useful. A quantitative, predictive model framework would be especially useful in the study of plant–microbe interactions, where so much can be measured in the context of the still‐expanding influence of the many ‘omics’ methods, but the complexity of the biological system ensures that much insight is currently derived from phenomenology and guesswork.
In this opinion piece we argue that the time has come for the study of plant–microbe interactions as a field to move beyond the dominant expository zigzag model of the plant immune system (Jones and Dangl, 2006) to embrace fully quantitative, predictive modelling. We want to encourage scientists in this field to adopt a diversity of model frameworks that are able to incorporate new and unexpected knowledge revealed by experiment, rather than risk moulding all interpretation into an expository model form that simply does not fit. To this end, we briefly describe a toy quantitative dynamic model that, while by no means complete or the only alternative or potentially useful model of the plant immune system, provides a basic dynamic representation of key behaviours of the plant immune system.
What are the Limitations of the Expository Zigzag Model?
The zigzag model of the plant immune system was introduced by Jones and Dangl in 2006 and was intended to ‘illustrate […] the quantitative output of the plant immune system’(Jones and Dangl, 2006). The model has an implied time component, because ordered phases [PTI, effector‐triggered susceptibility (ETS), ETI, ETS2, ETI2, etc.] are described, each following the other. As an expository model of (one possible realization of) the evolutionary history of the plant immune system, the zigzag model is difficult to criticize. However, the model has limitations that mean it is not a quantitative or predictive framework for the direct study of plant–microbe interactions.
Molecular scope.The zigzag model defined in Jones and Dangl (2006) is based only upon interactions between the host immune system and biotrophic microbes that impair plant growth and reproduction. The defined molecular participants in the model are: (1) on the plant's side, pattern recognition receptors (PRRs) and NB‐LRR proteins; and (2) on the pathogen's side, MAMPs or PAMPs and ‘effectors that interfere with PTI or otherwise enable pathogen nutrition and dispersal’. It has been noted previously that endogenous elicitors, or ‘damage‐associated molecular patterns’ (DAMPs) are not accounted for in the original zigzag model (Boller and Felix, 2009), though an attempt has been made to incorporate them (Hein et al., 2009). Other potential interactions, including nutrient exchange, are also likely to occur as part of the extensive natural association between plants and microbes (Knief, 2014). These interactions may also have an impact on the progress of disease but are, by definition, beyond the scope of the zigzag model, and it is not immediately clear how they might be integrated into that framework. Other productive and relevant interaction modes such as symbiosis and necrotrophy also occur, but are likewise not within the scope of the model. A severe ETI response from the plant is probably not a component in symbiosis (the plant ‘leaves the door open’). In necrotrophy, plant cell death might be seen as a favourable outcome for the microbe, thereby reversing the usual interpretation of induced cell death in ETI from ‘immunity’ to something more like ‘susceptibility’ (Dickman and de Figueiredo, 2013). Also, despite the definition of effector function including the possibility that they may otherwise enable pathogen nutrition and dispersal (Jones and Dangl, 2006), this too lies outside the model's intentionally restricted scope.
Absence of environmental context.Over the lifetime of any organism, its environmental context and history influence which molecular processes are active, and to what degree. Prosaically, a plant's immune response is dependent on its previous and current experiences, whether biotic or abiotic—drought or flood; heat or cold; dark or light; whether there has been prior exposure to pathogens and beneficial microorganisms, or sterile growth. Assuming that the genotypes of an interacting host and pathogen are constant and fixed, the outcome of the interaction in terms of resistance or susceptibility may nevertheless be influenced by environmental factors. These may have a negative impact (e.g. abiotic stresses) or a positive impact [e.g. factors promoting systemic acquired resistance or induced systemic resistance (‘priming’)] on the host's expression of immunity. The zigzag model was never intended to reflect these possibilities or their potential influences, and it is not clear how they might be incorporated.
Ordering of events.The zigzag model describes four phases: phase 1 (PAMPs detected by PRRs) is followed by phase 2 (pathogens deliver effectors to interfere with PTI), which is in turn followed by phase 3 (effectors recognized by NB‐LRRs, ETI) then phase 4 (loss/gain of effectors over evolutionary time). In the original model description this was not intended to be a physical description of cell–cell interaction during infection time‐scales (Jones and Dangl, 2006). Recent literature indicates strongly that plant innate immunity is an integrative and essentially stochastic process combining the detection and action of effectors, MAMPs and damage‐associated signals, and casts doubt on the validity of a conceptual division between PTI and ETI, when considered at a molecular or systems level in the plant (Thomma et al., 2011). The strongly ordered nature of the zigzag model does not capture behaviour that is useful for predictive or quantitative modelling of a system where these interactions occur concurrently.
Time‐scale.Most of the molecular processes described in the zigzag model are likely to occur during a single plant interaction with one or more biotrophic pathogens. It can be tempting to attempt to interpret the model on the time‐scale of a single interaction. However, phase 4 (ETS2) of the original model description (loss and/or gain of effectors) occurs in the zigzag model explicitly as a result of selection pressure, which would act at a population level and over longer time‐scales. The zigzag model was clearly not intended to represent an ordered set of occurrences during a single infection event or to describe the processes that occur during infection in such a way as to be an interpretative framework for direct experiment, in that context.
Physical scale.The original formulation of the zigzag model is ambiguous about the physical scale it describes. The evolutionary events of phase 4 (effector loss/gain) necessarily transpire at the population level, but the molecular processes being described occur in only some proportion of cells in a plant currently being challenged by a pathogen. Although some might succumb to the temptation, again it seems we ought not to interpret the zigzag model to represent events in a single cell, or even a single organism.
The model is qualitative.Although the original presentation of the zigzag model states that it ‘illustrates the quantitative output of the plant immune system’, this is not the case. The quantitative term ‘amplitude’ (meaning breadth, range, physical extent or magnitude) is used in the model, and an expression is presented as representing the ‘ultimate amplitude of disease resistance or susceptibility proportional to [PTI – ETS + ETI]’, but it is not indicated what measurements these values might represent, what units they may have, or whether a linear summation of the values is valid. Instead, the host response is subdivided into three qualitative states, delimited either by a ‘threshold for effective resistance’ and a ‘threshold for HR [the hypersensitive cell death response]’ (Jones and Dangl, 2006). At no point is the model actually made quantitative.
The zigzag model is extremely widely used. It is a good pedagogical and expository model and maybe even an accurate approximation to the evolutionary order of development of components of the plant immune system. It illustrates well the broad nature of some types of plant–microbe molecular interactions, but it does not describe them in a way that is useful for quantification or prediction.
With the advent of faster, cheaper, high‐throughput ‘omics’ methods, the ability to acquire large amounts of quantitative data is transforming and accelerating research in plant science, and in plant–microbe interactions (Knief, 2014). To integrate and analyse these data in a productive way, molecular plant pathologists need not just one model, or even a single overarching model framework, but many models—predictive, quantitative, qualitative and expository—for a range of systems and interactions. Influential as the zigzag model has been, it cannot be the whole story for plant–microbe interactions.
What Other Models might be Useful?
Molecular plant pathology has been relatively underserved in terms of modelling effort, particularly when compared with studies associated with similar human–microbial pathosystems. The current representation of models associated with plant pathology in the BioModels repository (http://www.ebi.ac.uk/biomodels‐main/; Li et al., 2010), for example, is disappointingly sparse. This is surprising given the many natural advantages of working in this area for model validation and hypothesis generation. Plants and their pathogens, particularly microbial pathogens, are of much less ethical concern than are animal models of disease. Also, there are some well‐understood pathosystems, such as Arabidopsis thaliana with Pseudomonas syringae or Hyaloperonospora arabidopsidis, that have a wide range of useful genomic resources and experimental toolkits for targeted and genome‐wide knockout and RNA interference studies, and also large collections for investigation of the effects of both host and pathogen diversity. Plant pathosystems offer unparalleled opportunities for large‐scale validation of biological modelling, systems biology and translation of the resulting insights into solutions to problems of food security that could potentially benefit many across the globe.
Contributions of existing modelling and systems biology to plant–microbe interactions include: mathematical modelling of subcellular metabolic pathways in A. thaliana (Nägele and Weckwerth, 2013); flux‐balance analysis and Boolean modelling of plant–pathogen interactions (Pinzón et al., 2010); metabolic reconstruction and modelling of nitrogen fixation (Resendis‐Antonio et al., 2007); kinetic modelling of mitogen‐activated protein kinase signalling in response to biotic stress (Pathak et al., 2013); and semi‐quantitative models of plant signalling (Sankar et al., 2011). We have also previously proposed a quantitative framework for understanding plant–pathogen molecular interactions as changes of ‘state’ of the pathosystem (Pritchard and Birch, 2011), which is capable of integrating multiple sources of high‐throughput experimental data and may also enable falsification and hypothesis generation for the complete interacting system and its interaction with the environment. Significant progress has been made in modelling (and subsequent experimental validation) of the interplay of ethylene, salicylic acid and jasmonic acid signalling pathways in PTI (e.g. Kim et al., 2014).
For this discussion, we have prepared a dynamic and quantitative model of the plant immune system. This model was deposited in the BioModels database (Li et al., 2010) and assigned the identifier MODEL1408280000. The model abstracts key features of the plant–pathogen molecular interactions that feature in the zigzag model: PAMP detection and PTI; effector action to suppress PTI, with corresponding effector detection by an R protein and ETI (Figure 1, Figure S1 in Supporting Information). This model is clearly not a highly detailed, or perhaps even very accurate, representation of the plant immune system; nor are the model parameters optimized in any way to represent any biological system or reproduce experimentally acquired data. It is noted that although this model contains only nine differential equations (Figure S2) and is extremely simple in relation to the actual complexities of plant–pathogen molecular interactions, it still contains 15 reactions with 19 kinetic parameters and would require some effort to parameterize to any particular pathosystem.
Figure 1.
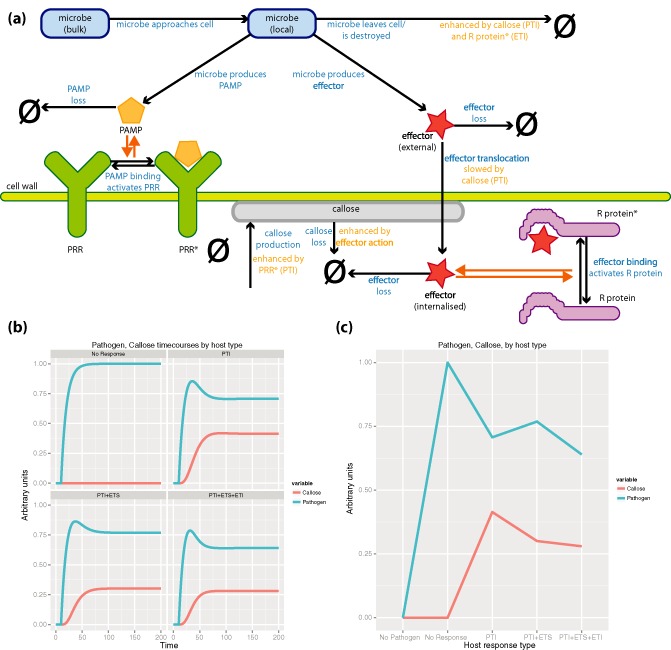
(a) Schematic diagram of the model plant immune system (BioModels: MODEL1408280000). The system is divided into two ‘compartments’: extracellular (external to the cell wall) and intracellular (internal to the cell wall). In the extracellular compartment the local microbial population is drawn from a remote bulk population and is also ‘destroyed’, as indicated by the arrow pointing to the empty set symbol (ϕ). The rate at which the microbe is ‘destroyed’, which may be interpreted, for example, as microbial movement or death, is enhanced by pattern‐triggered immunity (PTI) and effector‐triggered immunity (ETI). While local to the plant, the microbe produces two species: pathogen‐associated molecular patterns (PAMP) and effector; both species can be lost (e.g. by diffusion or destruction) in the extracellular compartment. The PAMP may interact reversibly with plant pattern‐recognition receptor (PRR) to produce an activated PRR* species. The effector may be internalized to the cell (translocation), where it may interact reversibly with plant R protein to produce an activated R protein* species. Within the cell compartment, if there is activated PRR*, the plant also produces callose, as a proxy for PTI activity. This is degraded within the plant cell. As a proxy for PTI, callose also increases the rate at which local microbe populations decline, and acts to reduce the rate at which effector is translocated into the cell. Activated R protein* also increases the rate at which the local microbial population is depleted, as an abstraction of ETI. (b), (c) Quantitative output of the immune system model. (b) Levels of callose and pathogen (arbitrary units) over 200 time units of simulation, for systems where the host shows: no resistance response: PTI, host shows PTI only; PTI+ETS, host shows PTI only but the pathogen suppresses PTI by effector production; PTI+ETS+ETI, host exhibits PTI and ETI, but the pathogen suppresses PTI by effector production. (c) Levels of callose and pathogen (arbitrary units) after 200 time units, when a steady state has been reached, demonstrating the influence of PTI, ETI and effector action with respect to the absence of a host immune response. The profile of steady‐state pathogen levels resembles the profile of the expository zigzag model.
Despite its relative simplicity, and the complete lack of parameterization to a real system, the model broadly reproduces the expected features of interaction between a host cell and an invading pathogen (Figure 1). In the absence of a host immune response, the pathogen reaches an arbitrary level of one unit, and no callose deposition occurs. If only PTI is active, callose deposition occurs and the pathogen fails to reach as high a level. If the pathogen is able to introduce an effector to suppress callose deposition, the steady‐state level of pathogen is increased and the amount of callose deposition reduced. Finally, a host having both PTI and ETI systems active supports the presence of the pathogen even if it introduces a PTI‐suppressing effector—but in this case the amount of callose deposition is also reduced with respect to the system in which the host does not have an active ETI response. In all cases where there is a host immune response, the pathogen briefly reaches elevated levels in the locality of the cell before this level is seen to fall (due to the action of resistance mechanisms). Each alternative scenario above leads to a different steady‐state level of the pathogen as an outcome. These predictive outcomes represent falsifiable hypotheses that cannot be suggested by a purely expository model such as the zigzag.
The toy model additionally overcomes several limitations of the zigzag model indicated above: the time‐scale and nature of interactions is explicit in the model definition; events take place concurrently during the interaction; the results are quantitative (though due to the structure of the model, and in the absence of parameter optimization, they currently have arbitrarily values). The molecular scope of the basic assumptions of this toy model, and treatment of context, is no greater than that for the zigzag model, but it is clear how further processes (such as production of host nutrient and its effect on local pathogen levels) can be integrated into the model by the addition of further terms in the model, and how parameters might be modified to reflect the immediate history of either the plant host or pathogen. Most significantly, unlike the zigzag model, the qualitative and quantitative outcomes of interaction, i.e. ETI, ETS and PTI, are not specified directly in the model description. Instead, these outcomes are predictions of the model, which may be obtained by parameterizing the model in different ways to reflect changes in the system.
There are many opportunities for improvement to the model: parameterization to reflect a ‘real’ pathosystem; dependency of pathogen propagation on host nutrient production; introduction of a panel of effector proteins (possibly with different functions, such as the promotion of pathogen growth) and corresponding R genes; competition for resources; spatial elements such as pathogen mobility and an array of host cells; integration with more complex models of PTI and signalling; environmental context and influence; and so on. Even in this simplistic form, however, it still represents a tangible basis for posing reasonable hypotheses, some of which may be answered in silico and some in vitro or in vivo, that cannot be framed at all in the context of the expository zigzag model. To investigate complex, dynamic processes we will probably always benefit from having a dynamic model for the interpretation and guidance of experiment.
Models such as these can guide future research towards the most critical components of dynamic systems as we best understand them at the current moment. Any reductionist investigation of a single component of even this simple model cannot give us more than a focused, fragmentary account of the host response. Understanding and interpreting the result of a reductionist experiment may itself be dependent on the behaviour of the rest of the interacting components. The implication is clear: we need to consider the biology of the system, and dynamic modelling can be a powerful tool for achieving this goal.
Conclusion
Dynamic, quantifiable and predictive models of host–pathogen interactions, like all models, will be wrong. They are bound to be incomplete, given our current levels of understanding, but they can form the basis for asking new questions that improve our understanding and the quality of the models themselves. Expository models such as the zigzag model have great value in conceptualizing and communicating aspects of host–pathogen interactions, but they should not form the limit of our representation or understanding. In order to understand and investigate complex dynamic processes like host–microbe interactions sufficiently well, we will need to develop dynamic models of these systems and move beyond static, expository models.
Supporting information
Figure S1 Systems Biology Graphical Notation (SBGN, http://www.sbgn.org/) representation of the toy immune system model (BioModels accession no. MODEL1408280000 http://www.ebi.ac.uk/biomodels‐main/).
Figure S2 Ordinary differential equation (ODE) representation of the immune system model (BioModels accession no. MODEL1408280000 http://www.ebi.ac.uk/biomodels‐main/). By convention, the terms in square brackets (e.g. [PRR]) represent a nominal concentration—or, if modelled stochastically, a count—of the entity represented within the brackets. For the simulations represented in this paper, kinetic parameters (k1, k2, etc. for each model step) were set to an arbitrary value of 0.1. In this model, time, volume and concentration were set to be dimensionless, so these parameters also have no units.
References
- Boller, T. and Felix, G. (2009) A renaissance of elicitors: perception of microbe‐associated molecular patterns and danger signals by pattern‐recognition receptors. Annu. Rev. Plant. Biol. 60, 379–406. [DOI] [PubMed] [Google Scholar]
- Dickman, M.B. and de Figueiredo, P. (2013) Death be not proud–cell death control in plant‐fungal interactions. PLoS Pathog. 9, e1003542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunawardena, J. (2014) Models in biology: ‘accurate descriptions of our pathetic thinking.’ BMC Biol. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hein, I. , Gilroy, E.M. , Armstrong, M.R. and Birch, P.R.J. (2009) The zig‐zag‐zig in oomycete‐plant interactions. Mol Plant Pathol. 10, 547–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzhütter, H.‐G. , Drasdo, D. , Preusser, T. , Lippert, J. and Henney, A.M. (2012) The virtual liver: a multidisciplinary, multilevel challenge for systems biology. Wiley Interdiscip Rev Syst Biol Med. 4, 221–235. [DOI] [PubMed] [Google Scholar]
- Jones, J.D.G. and Dangl, J.L. (2006) The plant immune system. Nature. 444, 323–329. [DOI] [PubMed] [Google Scholar]
- Kim, Y. , Tsuda, K. , Igarashi, D. , Hillmer, R.A. , Sakakibara, H. , Myers, C.L. and Katagiri, F. (2014) Mechanisms underlying robustness and tunability in a plant immune signaling network. Cell Host Microbe. 15, 84–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knief, C. (2014) Analysis of plant microbe interactions in the era of next generation sequencing technologies. Front Plant Sci. 5, 216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, C. et al (2010) BioModels Database: An enhanced, curated and annotated resource for published quantitative kinetic models. BMC systems biology. 4, 92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nägele, T. and Weckwerth, W. (2013) A workflow for mathematical modeling of subcellular metabolic pathways in leaf metabolism of Arabidopsis thaliana. Front Plant Sci. 4, 541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pathak, R.K. , Taj, G. , Pandey, D. , Arora, S. and Kumar, A. (2013) Modeling of the MAPK machinery activation in response to various abiotic and biotic stresses in plants by a system biology approach. Bioinformation. 9, 443–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinzón, A. , Rodríguez‐R, L.M. , González, A. , Bernal, A. and Restrepo, S. (2010) Targeted metabolic reconstruction: a novel approach for the characterization of plant‐pathogen interactions. Brief Bioinformatics. [DOI] [PubMed] [Google Scholar]
- Pritchard, L. and Birch, P. (2011) A systems biology perspective on plant‐microbe interactions: Biochemical and structural targets of pathogen effectors. Plant Science. 180, 584–603. [DOI] [PubMed] [Google Scholar]
- Resendis‐Antonio, O. , Reed, J.L. , Encarnación, S. , Collado‐Vides, J. and Palsson, B.Ø. (2007) Metabolic reconstruction and modeling of nitrogen fixation in Rhizobium etli. PLoS Comp Biol. 3, 1887–1895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankar, M. , Osmont, K.S. , Rolcik, J. , Gujas, B. , Tarkowska, D. , Strnad, M. , Xenarios, I. and Hardtke, C.S. (2011) A qualitative continuous model of cellular auxin and brassinosteroid signaling and their crosstalk. Bioinformatics. 27, 1404–1412. [DOI] [PubMed] [Google Scholar]
- Thomma, B.P.H.J. , Nurnberger, T. and Joosten, M.H.A.J. (2011) Of PAMPs and Effectors: The Blurred PTI‐ETI Dichotomy. Plant Cell. 23, 4–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1 Systems Biology Graphical Notation (SBGN, http://www.sbgn.org/) representation of the toy immune system model (BioModels accession no. MODEL1408280000 http://www.ebi.ac.uk/biomodels‐main/).
Figure S2 Ordinary differential equation (ODE) representation of the immune system model (BioModels accession no. MODEL1408280000 http://www.ebi.ac.uk/biomodels‐main/). By convention, the terms in square brackets (e.g. [PRR]) represent a nominal concentration—or, if modelled stochastically, a count—of the entity represented within the brackets. For the simulations represented in this paper, kinetic parameters (k1, k2, etc. for each model step) were set to an arbitrary value of 0.1. In this model, time, volume and concentration were set to be dimensionless, so these parameters also have no units.


