Small ion effects on self-coacervation phenomena in block polyampholytes

Abstract

Self-coacervation is a phenomenon in which a solution of polyampholytes spontaneously phase separates into a dense liquid coacervate phase, rich in the polyampholyte, coexisting with a dilute supernatant phase. Such coacervation results in the formation of membraneless organelles in vivo and has further been applied industrially as synthetic encapsulants and coatings. It has been suggested that coacervation is primarily driven by the entropy gain from releasing counter-ions upon complexation. Using fully fluctuating field-theoretic simulations employing complex Langevin sampling and complementary molecular dynamics simulations, we have determined that the small ions contribute only weakly to the self-coacervation behavior of charge-symmetric block polyampholytes in solution. Salt partitioning between the supernatant and coacervate is also found to be negligible in the weak-binding regime at low electrostatic strengths. Asymmetries in charge distribution along the polyampholytes can cause net-charges that lead to “tadpole” configurations in dilute solution and the suppression of phase separation at low salt content. The field and particle-based simulation results are compared with analytical predictions from the random phase approximation (RPA) and postulated scaling relationships. The qualitative trends are mostly captured by the RPA, but the approximation fails at low concentration.

I. INTRODUCTION

Both simple and complex coacervates, ubiquitous throughout nature from membraneless organelles^1–11 to the wet-adhesion^12–14 of mussels and sandcastle worms, have found numerous applications in the food industry,^15–17 drug delivery,^18–21 and organic electronics.²² Simple, single-component, or self-coacervation of polyampholytes and complex coacervation in the case of mixtures of oppositely charged polyelectrolytes arise from liquid–liquid phase separations that produce a polymer-rich coacervate in coexistence with a polymer-depleted supernatant comprised of primarily salt ions in solution. The broad interest in applications and their fundamental polymer physics has spurred parameterization of their structures and phase diagrams^23–31 as well as numerous theories for predicting the richness of coacervation phenomena.

The first theoretical description was proposed by Voorn and Overbeek^32,33 by expanding a Flory–Huggins mixing free energy expression to include a Debye–Hückel treatment of disconnected charges. While the Voorn–Overbeek model is often used, it has multiple significant deficiencies through failures to account for charge connectivity to the polymers and the simplistic treatment of the electrostatic interactions. Subsequent theories have focused on correcting these deficiencies through incorporation of charge connectivity and correlations^27,34–56 and rigorous handling of electrostatic and dipolar interactions.^50–56

However, an accurate and predictive universal model has been elusive due to limitations in computational implementation and in model assumptions about relevant molecular parameters. Scaling, mean-field, and random phase approximation (RPA) approaches have resulted in a thorough understanding of the salient features of coacervation and their dependence on a number of molecular parameters^{41–47,53,56} but are often limited to certain concentration and solvent quality regimes. Similarly, transfer matrix and counter-ion release models have developed comprehensive models as a function of sequence and other molecular details but have thus far focused on strongly charged polyelectrolytes in the strong-ion binding regime.^{27,38–40,46,57–59} Other theories, particularly those based on PRISM or liquid state theories, should, in principle, span multiple regimes but rely on closure or other approximations in their analytical or numerical implementation, as well as other mean-field or density functional approximations to address inhomogeneous structures.^34–38

Monte Carlo (MC) and molecular dynamics (MD) simulations of coarse-grained particle models^28,60–63 have been used to understand the structure and thermodynamics of coacervation phenomena more accurately. However, these approaches are plagued by difficulties in simulating the phase coexistence between the dilute and concentrated phases. In particular, the polymer chemical potential of the concentrated phase is difficult to obtain, so the typical approach is to assume that the dilute phase is infinitely dilute in polymer, thus providing a criterion to determine the concentrated (coacervate) phase boundary. These assumptions further make it difficult to explore the region near the critical point, where the polymer concentration in the dilute phase starts to approach that in the concentrated phase. The inability to accurately locate the dilute branch is particularly problematic for biopolymer systems, where the phase coexistence envelope is experimentally accessed by concentrating ultra-dilute solutions.

A more elegant and numerically efficient approach is to mathematically (and exactly) transform the coarse-grained molecular model into a field theory.⁶⁴ The field theory can then be solved analytically using the random phase approximation (RPA).^45–47 While this allows for access to thermodynamic and structural parameters in the supernatant and coacervate, it is well known that the RPA suffers catastrophic failures on predictions for the dilute phase, missing the binodal concentrations by many orders of magnitude. This failure can be partially mitigated through self-consistently renormalizing the chain statistics using a recently developed renormalized Gaussian fluctuation theory (RGF)^48,49 although the resulting theory becomes numerically complicated to implement and relies on a chain of approximations. Alternatively, approximation-free phase diagrams including the full phase coexistence window of the field-theoretic model can be simulated in an efficient manner using field-theoretic simulations (FTSs) employing complex Langevin sampling.^50–55

The focus of the present work is on understanding the relative importance of small ions to self-coacervation phenomena. Here, we use field-theoretic simulations to construct the phase diagrams of block polyampholytes, specifically elucidating self-coacervation phenomena as a function of net polymer charge as well as excess salt and multivalency of counter-ions. Our field-theoretic approach yields phase diagrams of both the dilute and concentrated branches of the coexistence curves without any uncontrolled approximations or limitations to specific charge association regimes. In this study, we restrict ourselves to a diblock polyampholyte, but as shown elsewhere, the sequence of the polymer is an important parameter on the phase diagrams, structure, and accessible chain conformations in solution.^{27,40,54,55,65–67}

The inclusion of explicit counter-ions and/or low concentrations of salt is shown to have only a weak effect on the phase diagrams and structure of charge-neutral polyampholytes in solution. The small ions are shown to renormalize the effective electrostatic strength affecting the accessibility of phase coexistence regions. However, multivalent small counter-ions are shown to strongly suppress the phase separation due to competition between the condensation of the polyampholyte self-coacervate and the complexation of the polyampholyte with the multivalent ions. Charge asymmetric polyampholytes possessing a net-charge are shown to resist coacervation at a critical fractional net-charge where the polyelectrolyte effect dominates over the polyampholyte effect resulting in “tadpole” chain conformations in dilute solution.

II. MODEL AND METHODOLOGY

A. Molecular model

We extend a coarse-grained, implicit solvent model^50–55,64 of polyelectrolytes as continuous Gaussian chains to include small ions, both counter-ions and optionally salt. All segments (inclusive of polymer statistical segments and small ions) interact through a weak contact excluded-volume parameter, $v$, and charged segments interact via a Coulomb potential screened by a uniform background dielectric of Bjerrum length, l_B. The interaction energy is

$$\beta \overline{U}=\frac{v}{2}\int d\mathbf{r}{\overline{\rho }}^2\left(\mathbf{r}\right)+\frac{l_B}{2}\int d\mathbf{r}\int d{\mathbf{r}}^{\prime }\frac{{\overline{\rho }}_e\left(\mathbf{r}\right){\overline{\rho }}_e\left({\mathbf{r}}^{\prime }\right)}{|\mathbf{r}-{\mathbf{r}}^{\prime }|},$$ (1)

with microscopic density of segment centers $\widehat{\rho }\left(\mathbf{r}\right)={\sum }_{\alpha =1}^{n_p}\int ds\delta \left(\mathbf{r}-{\mathbf{r}}_{\alpha }\left(s\right)\right)+{\sum }_{i=1}^{n_{s,+}}\delta \left(\mathbf{r}-{\mathbf{r}}_i\right)+{\sum }_{j=1}^{n_{s,-}}\delta \left(\mathbf{r}-{\mathbf{r}}_j\right)$for n_p, n_s,+, and n_s,− polymer, small cation, and small anion species. The electrostatic charge density is ${\widehat{\rho }}_e\left(\mathbf{r}\right)={\sum }_{\alpha =1}^{n_p}\int ds{\sigma }_{\alpha }\left(s\right)\delta \left(\mathbf{r}-{\mathbf{r}}_{\alpha }\left(s\right)\right)+{\sum }_{i=1}^{n_{s,+}}{\sigma }_i\delta \left(\mathbf{r}-{\mathbf{r}}_i\right)+{\sum }_{j=1}^{n_{s,-}}{\sigma }_j\delta \left(\mathbf{r}-{\mathbf{r}}_j\right)$. $\overline{\rho }\left(\mathbf{r}\right)$ and ${\overline{\rho }}_e\left(\mathbf{r}\right)$ are spatially smeared versions of $\widehat{\rho }\left(r\right)$ and ${\widehat{\rho }}_e\left(r\right)$, respectively, as described below. r_α(s) is a space curve encoding the configuration of chain α, where s is a continuous backbone contour variable and σ_α(s) is the signed charge valency density at position s on polymer chain α. σ_α(s) is normalized so that its integral along the contour is the total charge per chain in units of the elementary charge. Throughout this study, the charge density is set to |σ| = 1, i.e., there is a fully ionized residue per statistical segment. r_i and r_j are the positions of small ions i and j of signed valence σ_i and σ_j.

To ensure that the chemical potentials and pressures calculated in the field-theoretic simulations are insensitive to the computational grid and are free of ultraviolet divergences,^68,69 the segment and ion coordinates are smeared over a finite volume by convolution with a normalized Gaussian profile, $\mathrm{\Gamma }\left(r\right)={\left(2\pi a^2\right)}^{-3/2}\exp \left(-r^2/2a^2\right)$ of width a. The Gaussian smearing is a model definition corresponding to a soft repulsive Gaussian pair potential acting among all polymer segments and small ions [Eq. (2)]. For weakly charged polyelectrolytes with charge spacing greater than the Bjerrum length, this aspect of the model should not impact the presented results as electrostatic and structural correlations occur on length scales larger than the segment size b, smearing length a, and Bjerrum length l_B. Here, all segments and ions are given the same smearing width, a, but this model can be readily extended to different smearing widths for different species types (i.e., polymer chain segments vs small ion particles). The smeared microscopic density is then $\overline{\rho }\left(\mathbf{r}\right)=\int d{\mathbf{r}}^{\prime }\mathrm{\Gamma }\left(|\mathbf{r}-{\mathbf{r}}^{\prime }|\right)\widehat{\rho }\left({\mathbf{r}}^{\prime }\right)$, and the smeared electrostatic charge density is likewise denoted by ${\overline{\rho }}_e\left(\mathbf{r}\right)$.

This interaction energy can be equivalently written in a particle-based representation of bead–spring chains with a nonbonded pair potential between beads separated by a distance r as

$$\beta u_{ij}\left(r\right)=\frac{v}{8{\pi }^{3/2}{a}^3}{e}^{-r^2/4a^2}+\frac{l_B{\sigma }_i{\sigma }_j}{r}\mathrm{e}\mathrm{r}\mathrm{f}\left(\frac{r}{2a}\right).$$ (2)

The Gaussian smearing in the field theory is seen to translate to a particle model with a soft Gaussian repulsion on the scale of the smearing length a and a Coulomb interaction that is cutoff at short distances by an error function with the same range.^70,71 In this implicit solvent model, the $v$ parameter characterizes the solvent quality (larger $v$ implies better solvent quality), while l_B is a measure of the electrostatic strength and is inversely proportional to the solvent dielectric constant. Field-theoretic (FTS-CL) and molecular dynamics (MD) simulations of the corresponding field theory and particle models, respectively, are used to sample the energetic landscape prescribed by the interaction energy of Eqs. (1) and (2) and provide a framework for examining the importance of small ions on the structure and thermodynamics of block polyampholytes.

B. Field theory

The canonical partition function of the model specified in Eq. (1), augmented by the canonical stretching energy of continuous Gaussian chains and integrated over segment and ion coordinates, can be converted via an exact Hubbard–Stratonovich transformation to a complex-valued statistical field theory.⁶⁴ The nonbonded interactions among segments are consequently decoupled and the segments interact only with auxiliary fields, representing the fluctuating excluded-volume and electrostatic potentials.^53,55

In the field theory, the model parameters are scaled by the statistical segment size b to yield the following dimensionless parameters: $\overline{a}=a/b$, a smearing scale for segments; $v$b⁻³, an excluded-volume parameter; l_Bb⁻¹, a measure of electrostatic interaction strength; ρ₀b³, a total number density of polymer segments and small ions; ${\varphi }_l=\frac{n_l{N}_l}{{\sum }_m{n}_m{N}_m}$, a number fraction of species l of length N_l; and ${\rho }_l={\rho }_0\frac{{\varphi }_l}{N_l}$, a number density of ions or chains. Small ions are represented with N_s,± = 1 and polymers with N_p = 100 throughout.

The resulting field theory can be approximated through a Gaussian approximation (RPA) formalism^51–53,55 (the Appendix) or investigated numerically through field-theoretic simulations that fully sample the field configurations and capture all higher-order fluctuation and correlation effects.^53,55 We use the complex Langevin equations of motion to perform approximation-free importance sampling of the field theory including calculation of field-theoretic thermodynamic operators (osmotic pressure and chemical potentials) and structure factors [total density structure factor, $S_n\left(k\right)=⟨\delta \widehat{\rho }\left(\mathbf{r}\right)\delta \widehat{\rho }\left({\mathbf{r}}^{\prime }\right)⟩$, and charge-weighted structure factor, $S_e\left(k\right)=⟨\delta {\widehat{\rho }}_e\left(\mathbf{r}\right)\delta {\widehat{\rho }}_e\left({\mathbf{r}}^{\prime }\right)⟩$], as described in Refs. 53 and 55.

In all field-theoretic simulations, the fields were sampled with a spatial collocation mesh of resolution Δx = 0.8b, which was found to be sufficient to fully resolve chemical potentials and pressures across a wide range of l_B and ρ₀ values. The segment smear scale was fixed to a = 0.8b throughout. The FTS-CL results reported here were generated using a periodically repeated cubic simulation cell of side L = 20b. Tests were conducted with simulations in smaller and larger cells to ensure that the data reported here are not affected by finite size errors.

The modified diffusion equations were solved using a pseudospectral approach with operator splitting^72–74 and fixed contour step size Δs = 1. The exponential time difference (ETD) algorithm^75,76 with time step t = 0.1 was used to numerically propagate the CL equations of motion.^53,55 All FTS-CL simulations were performed on NVIDIA Tesla M2075, K80, or P100 GPUs.⁷⁷

C. Determination of multicomponent phase equilibrium conditions

Phase equilibrium conditions can be constructed through the explicit computation of the osmotic pressure Π(ρ) and multiple chemical potentials μ(ρ) for a range of species densities (ρ_p, ρ_s,−, and ρ_s,+) and determination of the densities at which chemical and mechanical equilibrium conditions can be established between coexisting coacervate and supernatant phases.⁵³ However, root-finding in a multicomponent system with a mixture of polymeric and small ion species can prove tedious and challenging; a more efficient determination of the phase equilibrium conditions utilizes the Gibbs ensemble (Fig. 1).^41,78–84

FIG. 1.

Schematic of the Gibbs ensemble. The volume is partitioned into two simulation cells corresponding to a dense and a dilute phase. Particle concentrations are exchanged to achieve chemical equilibrium and phase volumes are exchanged to achieve mechanical equilibrium.

The Gibbs ensemble enables direct calculations of phase coexistence, from which the binodal concentrations and thermodynamic properties can be calculated in an efficient manner.^78–81 The main advantage of this method comes from eliminating interfaces between coexisting phases from the calculations. The coexisting phases are instead placed in separate simulation cells, which significantly suppress finite-size errors and allow rapid convergence to the thermodynamic limit with cell volume. The overall Gibbs ensemble forms a canonical ensemble; the distribution of mass and volume is constrained by the total mass and volume specified for the system. The partition function can be decomposed into contributions from each phase resulting in an overall Helmholtz free energy density that is the volume-weighted sum of the Helmholtz energy densities of each phase,

$$F\left(\left[{\rho }_i\right]\right)=\frac{V^I}{V}{F}^I\left(\left[{\rho }_i^I\right]\right)+\frac{V^{II}}{V}{F}^{II}\left(\left[{\rho }_i^{II}\right]\right),$$ (3)

with number densities ${\rho }_i^I$, ${\rho }_i^{II}$ and volumes V^I, V^II of boxes I and II. Variable elimination upon applying the constraint, V = V^I + V^II, gives $\nu =\frac{V^I}{V}$ and $1-\nu =\frac{V^{II}}{V}$. The mass conservation balance can further be expressed as ${\rho }_i^{II}=\frac{{\rho }_i-\nu {\rho }_i^I}{1-\nu }$. This results in coexistence conditions for chemical and mechanical equilibrium,

$$\frac{\partial F}{\partial {\rho }_i^I}=\nu \left({\mu }_i^I-{\mu }_i^{II}\right)=0,$$ (4)

$$\frac{\partial F}{\partial \nu }=F^I-F^{II}+\sum _i{\mu }_i^{II}\left(\frac{{\rho }_i-{\rho }_i^I}{1-\nu }\right)={\mathrm{\Pi }}^{II}-{\mathrm{\Pi }}^I=0,$$ (5)

which is achieved by doing mass and volume swaps between the coexisting phases, respectively, resulting in the Gibbs ensemble equations of motion,

$${\rho }_i^I\left(k+1\right)={\rho }_i^I\left(k\right)-\mathrm{\Delta }{t}_{\mu }\left({\mu }^I\left(k\right)-{\mu }^{II}\left(k\right)\right),$$ (6)

$$\nu \left(k+1\right)=\nu \left(k\right)-\mathrm{\Delta }{t}_{\mathrm{\Pi }}\left({\mathrm{\Pi }}^{II}\left(k\right)-{\mathrm{\Pi }}^I\left(k\right)\right),$$ (7)

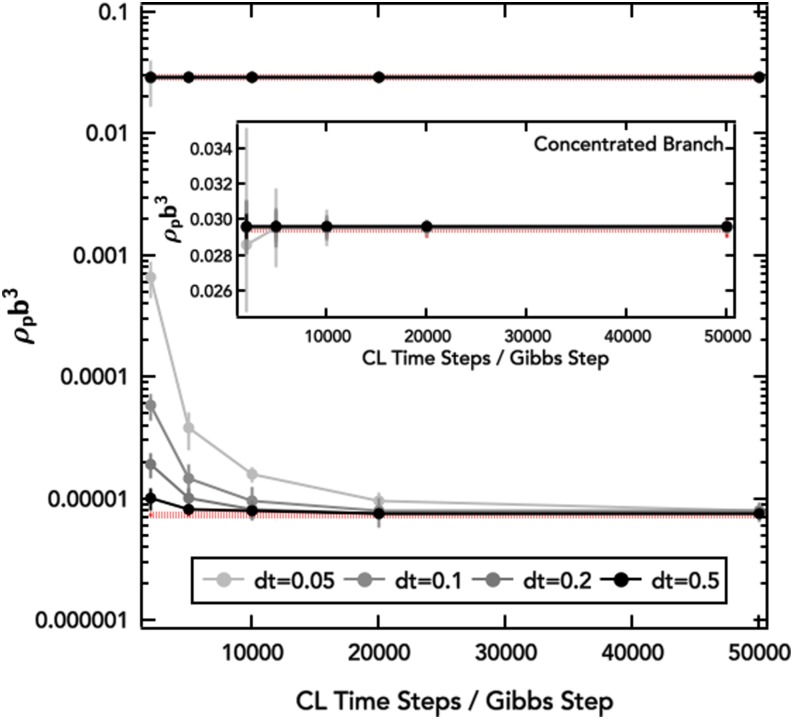
where the discrete time index is denoted k and the Gibbs time step size for densities, Δt_μ, and for phase volume fractions, Δt_Π. For stability, it is important to update the densities faster than the phase volume fraction (i.e., Δt_μ > Δt_Π) due to a sensitivity of small changes in volume fraction causing large differences in overall segment density. Here, we set Δt_μ = 0.1 and Δt_Π = 0.01. Furthermore, charge neutrality imposes the condition, ∑_iσ_iρ_i = 0 in each macrophase, I and II, which is imposed by restricting Gibbs density moves to charge-neutral pairs of molecular species (i.e., pairs of small ions or a polyampholyte chain and minimum required number of counter-ions for charge neutrality). More general cases are easily handled by incorporating a Lagrange multiplier into the Gibbs update equations of motion. The Gibbs procedure for finding multicomponent phase coexistence conditions can be repeated using RPA estimates (the Appendix) of the chemical potential and pressure in an analogous manner. The Gibbs ensemble equations of motion use the real components of the block-averaged thermodynamic operators, i.e., $\mu =\mathfrak{R}\left(⟨\tilde{\mu }⟩\right)$ and $\mathrm{\Pi }=\mathfrak{R}\left(⟨\tilde{\mathrm{\Pi }}⟩\right)$, discarding the residual (after a block of FTS-CL time steps) imaginary component. Employing long blocks with a large number of FTS-CL time steps between Gibbs updates serves to minimize the bias from the discarded imaginary parts of the thermodynamic operators but also lengthens the calculation. As shown in Fig. 2, an optimal balance between speed and accuracy can be achieved by adjusting both the FTS-CL time step and number of CL steps per Gibbs move.

FIG. 2.

Convergence of Gibbs ensemble calculations for the phase coexistence binodal curves (l_B/b = 0.13, $v$/b³ = 0.0068, a/b = 0.8) to prior results^53,55 (red dashed lines) for the diblock polyampholyte at different numbers of FTS-CL time steps per Gibbs step (symbols and connecting solid lines). Inset: expansion of the high density region to show the narrowing of error bars at different block averaging conditions.

It should be noted that while the removal of interfaces by the Gibbs ensemble method has reduced statistical uncertainty in determination of the phase coexistence conditions, the precise determination of the critical point is still challenging in the FTS-CL simulations due to increasing fluctuation strength in $\beta \tilde{\mu }$ and $\beta \tilde{\mathrm{\Pi }}$ operators and increasing correlation lengths and thus finite-size errors as the critical point is approached. The critical point is estimated by extrapolating the FTS-CL binodal curves to intersection with imposition of a polynomial form locally near the extrapolated critical point. The size of the critical point markers reflects the uncertainty associated with this fitting procedure.

D. Molecular dynamics

The coarse-grained molecular model used for the field-theoretic simulations can be used to construct corresponding molecular dynamics simulations.^54,55 Single chain simulations of the polyampholyte with commensurate number of small ions in the dilute phase (ρ_pb³ = 7.35 × 10⁻⁷, the same as used in FTS-CL dilute structure factors) are implemented using the Large Atomic/Molecular Massively Parallel Simulation (LAMMPS) software,⁸⁵ with bond, excluded-volume, and electrostatic interaction potentials, as described in Refs. 54 and 55.

As explored in detail elsewhere, particle MD simulation provides an opportunity to supplement the FTS-CL simulations with structural information regarding single chain conformations.^54,55 The single-chain structure factor is given by

$$P\left(\mathbf{k}\right)=\frac{1}{N^2}\sum _{j=1}^N\sum _{i\ne j}^N⟨\exp \left(-i\mathbf{k}\cdot {\mathbf{r}}_{i,j}\right)⟩,$$ (8)

with quantized wave vectors k = 2π(n_x, n_y, n_z)/L of integers n_x, n_y, and n_z, periodic boundary conditions, and r_i,j denoting the separation vector between monomers i and j.

Here, a single chain and a stoichiometric number of counter-ions were simulated in a periodically repeated cubic simulation cell of side L = 110b, corresponding to a polymer number density of ρ_pb³ = 7.35 × 10⁻⁷ as used in the dilute phase FTS-CL structure factors. The same random initial configuration is used for all systems, corresponding to an initial Gaussian walk for the polyampholyte and random distribution of counter-ions throughout the cell. A time step of δt = 0.001 was chosen to maximize both numerical stability and number of accessed conformations in ∼5 000 000 time steps. The temperature was controlled through a Langevin thermostat.⁸⁶ Particle trajectories are visualized using OVITO,⁸⁷ with counter-ions omitted from snapshots for clarity. Simulations were performed on a single Intel X5650 processor.

III. RESULTS AND DISCUSSION

We begin by comparing the inclusion of explicit counter-ions for a diblock polyampholyte to see the sensitivity on the phase coexistence behavior and structures in the dilute and concentrated phases, before focusing on the effects of manipulating the valency, charge asymmetry, and excess of small ions in more detail.

A. Explicit counter-ions

Prior field-theoretic studies have focused on charge-neutral pairs of polyelectrolytes or charge-neutral block polyampholytes as a minimal model to understand the thermodynamics of coacervation and structure of both the dense coacervate and dilute supernatant phases.^53,55 For such charge-neutral systems, the counter-ions can be treated implicitly, such as in acid–base polyelectrolytes, where the counter-ions join to form implicit water. Here, we include explicit small ions (with one counter-ion of opposite valence per polymeric charge) and show their weak effects compared to prior results for the diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$).^53,55 To simplify descriptions of the polyampholyte charge patterns, we use a nomenclature where $\mathcal{A}$ represents the negatively charged block and $\mathcal{C}$ the positively charged block and the subscripts are the length of the like-charged block in statistical segment units with the entire chain comprising 100 statistical segments. ${\mathcal{A}}_{50}{\mathcal{C}}_{50}$ is thus a charge-neutral diblock polyampholyte of uniform and opposite valence on the two blocks.

Figure 3 shows the effects of the inclusion of explicit ions on the phase diagram for the diblock polyampholyte. This phase diagram is presented in an analogous manner to the E vs C phase diagrams previously published,^53,55 where l_B/b is a scaled electrostatic strength and ρ_pb³ is a scaled polymer chain number density.

FIG. 3.

Phase diagram showing the relatively weak effects of including explicit counter-ions on the phase diagram of a diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$). Symbols are binodal points obtained from FTS-CL and lines are RPA predictions. The Gaussian smearing width is set at a/b = 0.8 and the excluded-volume parameter at $v$/b³ = 0.0068.

Importantly, l_B/b for many polymer systems in H₂O is $\sim \mathcal{O}\left(1\right)$, but here we have zoomed in on the critical point to carefully assess small changes to the phase diagram. The phase diagrams are then in a weak association regime, where ion binding and Manning ion condensation are not predicted to occur.⁸⁸ This weak association regime for the collapse of flexible block polyampholytes is driven by fluctuation-induced electrostatic attraction.^41,42,89 Shen and Wang have shown that even at these relatively mild conditions, field fluctuations of highly charged chains renormalize the chain structure significantly altering the correlation energies and thermodynamics.⁴⁸ The fully fluctuating FTS-CL simulations conducted in this work should capture these effects, while the Gaussian approximation inherent in the RPA leads to catastrophic failure at low concentrations.^48,49,53,55

Figure 3 shows the inclusion of explicit counter-ions leads to only a minor shift in the critical electrostatic strength (Δl_B ≈ 0.004b) due to the additional screening from the additional ionic strength imposed by the added ions; a remarkably weak effect given the equivalent numbers of small ions and polymer segments and thus large increase in total charge in the system. The added small ions increase the osmotic pressure in the coacervate, causing a decrease in the polymer number density ρ_p of the coacervate and an equivalent increase in ρ_p on the dilute branch to compensate for mechanical equilibrium.

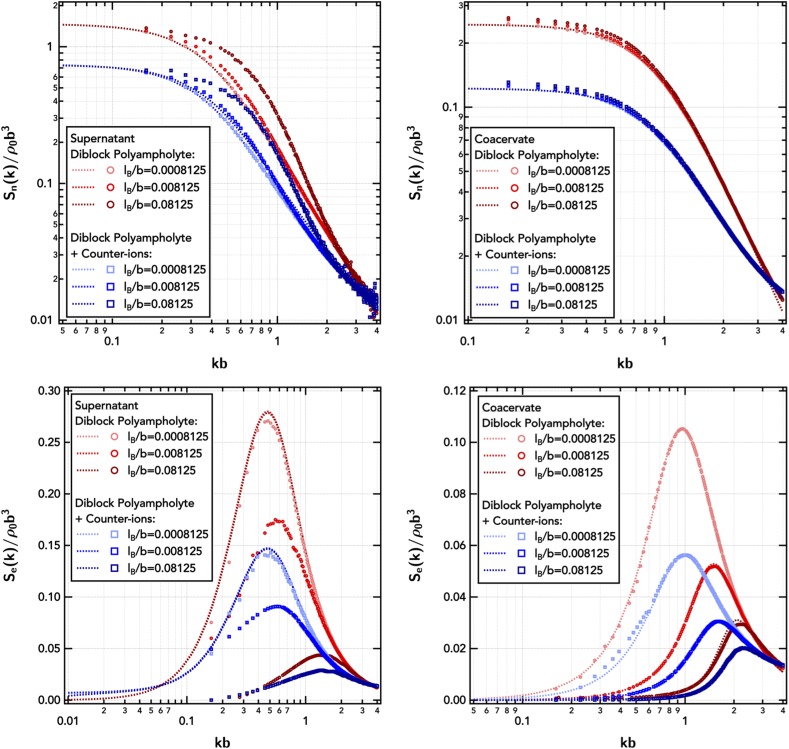
The added ions also increase the total density (ρ₀) at fixed polymer concentration (ρ_p), which decreases the isothermal compressibility [S_n(0); Fig. 4] in both phases. Since the small ion particles are pointlike before smearing, their inclusion into the solution causes the total-density structure factor, S_n(k), to increase at high-k reflecting increased structural correlations at small length scales. The Edwards correlation length, ${\xi }_E\sim \frac{b}{{\left(N_p{\rho }_{p}v\right)}^{1/2}}$, the length scale for independent density fluctuations in the concentrated polymer solution is at first-order not affected by the small ions.

FIG. 4.

Total-density structure factor, S_n(k), and charge-weighted structure factor, S_e(k), of the diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$) in the dilute supernatant and coacervate as a function of the electrostatic strength, l_B/b, with and without explicit counter-ions. The supernatant is at a polymer number density of ρ_pb³ = 7.35 × 10⁻⁷, and the coacervate is at ρ_pb³ = 0.0735. Symbols are obtained from FTS-CL, and lines are RPA predictions. The Gaussian smearing width is set at a/b = 0.8 and the excluded-volume parameter is set at $v$/b³ = 0.0068.

These small ion effects are qualitatively well captured by the RPA, but the enhanced density–density fluctuations manifest in S_n(k) due to charge correlation couplings at high electrostatic strengths are still not quantitatively described, particularly in the dilute phase. The failure of RPA is even more evident in the charge-weighted structure factor, S_e(k), of Fig. 4, where the electrostatic correlations are strongly overpredicted. These two failures of the RPA in inaccurately capturing the electrostatic and chain correlations in dilute solution further translate into very poor predictions of the location of the dilute branch of the binodal coexistence curve.

The inclusion of explicit counter-ions does not significantly affect the electrostatic correlation length, ξ_e, reflecting the peak in S_e(k) in Fig. 4, in either the dilute or dense phases [${\xi }_e\sim {\left(l_B{\sigma }^2{b}^{-2}{N}_p{\rho }_p\right)}^{-1/4}$ in the coacervate], likely due to the only marginal difference in effective electrostatic strength by incorporating the small ions. Increasing the electrostatic strength (i.e., increasing l_B/b by altering temperature or solvent) shifts the peak in S_e(k) to higher k, decreasing the electrostatic correlation length to smaller distances, as the electrostatics become stronger relative to the thermal energy, k_BT. Only at high salt (${\rho }_{s,+}+{\rho }_{s,-}>N_p^2{\rho }_p$) does the RPA predict a transition to a different scaling relationship for the electrostatic correlation length, namely, the Debye–Hückel scaling ${\xi }_e\sim {\left(l_B{\sigma }^2{\rho }_{salt}\right)}^{-1/2}$, as the salt begins to significantly dominate the structure and thermodynamics of the solution. Furthermore, it should be noted that both the FTS-CL and RPA results are sensitive to the polymer degree of polymerization N_p (with fixed N_s,± = 1), and N_p = 100 is long enough to reproduce characteristic polymeric behavior (Fig. S1). The computational effort of FTS-CL simulations scales linearly with N_p, making a field-theoretic approach to polyelectrolytes and polyampholytes advantageous over particle or lattice based simulations, which are limited to small N_p and thus may not be representative.

B. Excess salt

In order to understand the solubilization of polyampholytes with increased salt, we have studied the effects of salt on the phase diagram and the structure of the dilute and concentrated phases. The influence of excess salt on the binodal coexistence curves and critical electrostatic strength of the diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$) is shown in Fig. 5. Here, the different salt conditions are presented as number fractions ϕ_salt,±; the concentration (number density) of both polymer and salt increases along the horizontal axis (i.e., with increasing total density ρ₀). Recall, the number density of small anions is ρ_s− = ρ₀ϕ_s− = ρ₀(ϕ_salt,± + f₋ϕ_PA), and the number density of small cations is ρ_s+ = ρ₀ϕ_s+ = ρ₀(ϕ_salt,± + f₊ϕ_PA), where f₋ and f₊ are the fraction of charged segments of sign −, + along the polyampholyte; f₋ = f₊ = 0.5 for ${\mathcal{A}}_{50}{\mathcal{C}}_{50}$.

FIG. 5.

Phase diagram showing the modulation of critical electrostatic strength with inclusion of excess salt on the phase diagram of a diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$). Symbols are binodal points obtained from FTS-CL, and lines are RPA predictions. The Gaussian smearing width is set at a/b = 0.8 and the excluded-volume parameter is set at $v$/b³ = 0.0068. The different salt conditions are presented as number fractions ϕ_salt,±; the concentration (number density) of both polymer and salt increases along the horizontal axis.

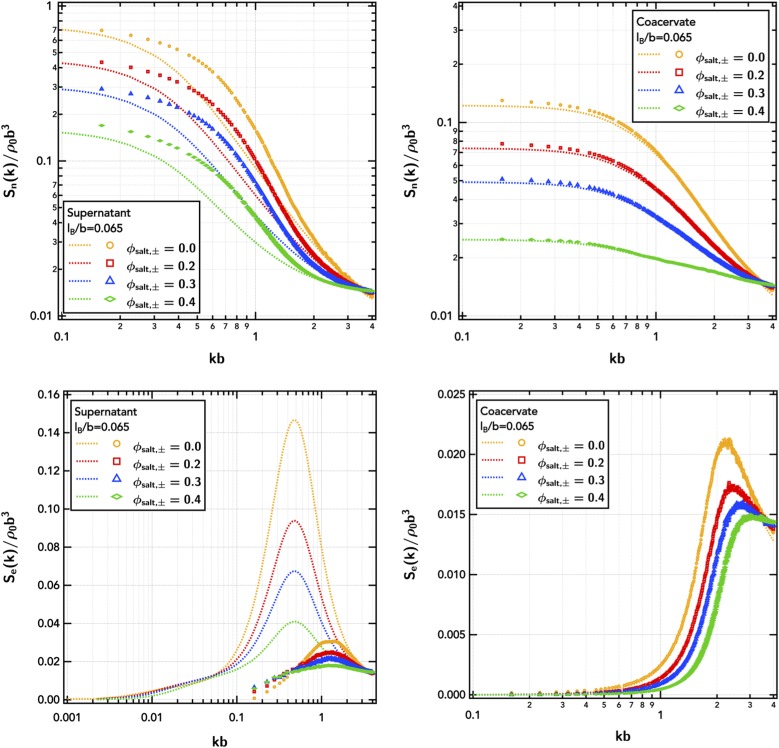
The narrowing of the phase coexistence window at both low and high polymer concentrations with increasing salt concentration is again related to increased osmotic pressure penalties and reduced isothermal compressibility [S_n(0); Fig. 6] as seen with the inclusion of explicit counter-ions. There is a dramatic increase in the critical electrostatic strength as the salt concentration is increased, particularly at high number fractions of the excess salt [for ϕ_salt,± = 0.4, the polyampholyte is only 20% of the (explicit) species in the system]. Increasing the fraction of excess salt primarily shifts the phase diagram by adjusting the effective electrostatic strength due to additional screening from the increased density of charges at equivalent polymer concentrations. This increased electrostatic screening results in decreased intensity of charge–charge correlations with increased salt content [S_e(k), Fig. 6] in both the dilute and concentrated phases. In the coacervate, the electrostatic correlation length, reciprocally related to the wavevector at the peak in S_e(k), decreases with excess salt. The RPA (the Appendix) predicts ξ_e to transition from $\sim {\left(l_B{\sigma }^2{b}^{-2}{\rho }_p\right)}^{-1/4}$ to $\sim {\left(l_B{\sigma }^2{\rho }_{salt}\right)}^{-1/2}$ with increasing salt content (as ${\rho }_{s,+}+{\rho }_{s,-}>N_p^2{\rho }_p$). Deep in the dilute phase, ξ_e remains effectively constant with increasing salt as the electrostatic correlations are primarily intramolecular and dictated by the physical chain size and geometry of the polymer.^53,55 Figure 6 again shows that the RPA significantly overestimates both S_e(k) and ξ_e in the dilute regime, both with and without salt.

FIG. 6.

Total-density structure factor, S_n(k), and charge-weighted structure factor, S_e(k), of the diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$) in the dilute supernatant and coacervate as a function of the number fraction of excess salt, ϕ_salt,±. Symbols are obtained from FTS-CL, and lines are RPA predictions. The supernatant is at a polymer number density of ρ_pb³ = 7.35 × 10⁻⁷, and the coacervate is at ρ_pb³ = 0.0735. The Gaussian smearing width is set at a/b = 0.8, the excluded-volume parameter is set at $v$/b³ = 0.0068, and the electrostatic strength is set at l_B/b = 0.065.

Overall, the salt trends are consistent with the weaker effects caused by the inclusion of explicit counter-ions. This is to be expected as there is no difference between counter-ions and co-ions (i.e., excess salt) in our coarse-grained model; both are small ions that affect the ionic strength (and for many experimental systems even have the same chemical identity). This is particularly true in the low-electrostatic-strength limit (l_B/b ≤ 1), where there is no ion condensation, and the ions distribute throughout both the dilute and concentrated phases.

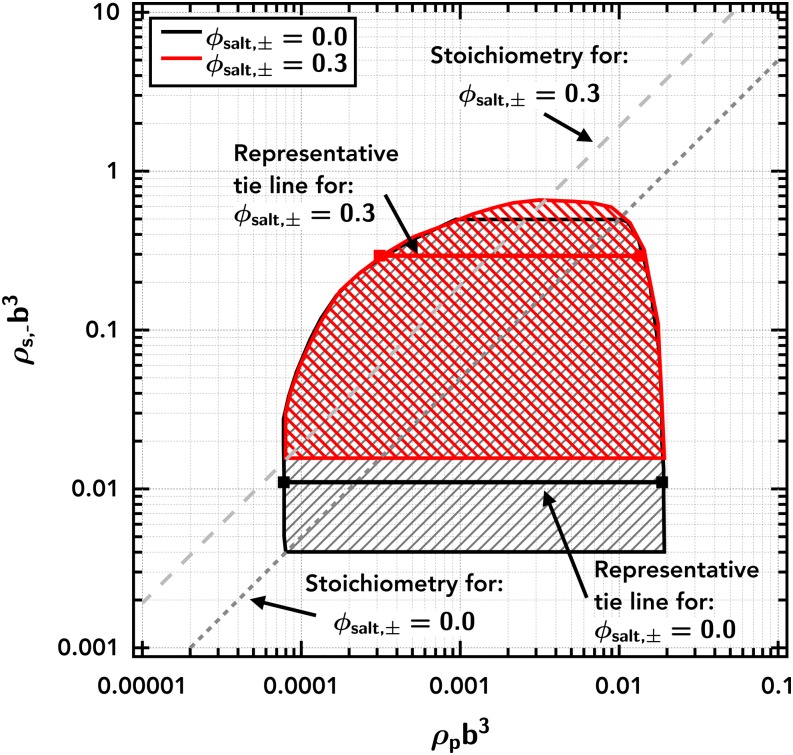
It should be emphasized that the simulation results reflect a three-component phase equilibrium—polyampholyte, small cation, and small anion (with implicit solvent)—while the phase diagrams shown thus far (Figs. 3 and 5) are pseudo-two-component by flattening l_B/b vs composition coordinates to two variables. Since the phase diagram behaves in a predictable manner with l_B/b, the compositional partitioning can be revealed in two dimensional phase diagrams at fixed electrostatic strength, here l_B/b = 0.065, and presented as polymer number density ρ_p vs small anion number density ρ_s,−. This representation of the phase diagrams for a diblock polyampholyte with excess salt number fraction ϕ_salt,± = 0 (i.e., no excess salt, just counter-ions) and ϕ_salt,± = 0.3 is shown in Fig. 7.

FIG. 7.

Phase diagram showing excess salt shifting the location of the two-phase region for the diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$). The shaded region is the region between the binodal curves. Representative tie lines are shown as horizontal solid lines. Dotted (ϕ_salt,± = 0.0) and dashed (ϕ_salt,± = 0.3) diagonal lines show stoichiometry constraints (i.e., concentration of small ions corresponding to the polymer concentration for each salt condition.) The Gaussian smearing width is set at a/b = 0.8, the excluded-volume parameter is set at $v$/b³ = 0.0068, and the electrostatic strength is set at l_B/b = 0.065.

This representation is similar to commonly presented phase diagrams in the literature (i.e., small ion concentration vs polymer concentration), with a few key differences in presentation to highlight salient features: logarithmic scaling of both the polymer and salt concentration axes and the specific choice for the salt axis to be a single valence of small ions (inclusive of both counter- and co-ions). The logarithmic scaling of the polymer concentration axis (ρ_pb³) emphasizes the key features occurring on the dilute branch. This is particularly important as the dilute branch is ignored or constrained to have zero polymer in most theories and simulations of coacervation; yet, the dilute branch is important for both fundamental studies and industrial applications as coacervates are often prepared by entering the phase coexistence window from dilute conditions.^20,22

A single valence of small ions is chosen rather than the total salt concentration (ρ_s) or the ionic strength, $I={\sum }_{i=\pm }{q}_i^2{\rho }_i$ to highlight the importance of charge neutrality and partitioning with asymmetries, discussed in Secs. III C–III E. Counter-ions of the polyampholyte are included in ρ_s (and thus in the ρ_s,− axis). This emphasizes the equivalency of the counter-ions and co-ions. Importantly, this also sets upper and lower bounds to the phase coexistence window, based on the stoichiometry. The dotted and dashed lines in Fig. 7 show stoichiometry constraints (i.e., concentration of small ions corresponding to the polymer concentration for each salt condition.) Experimentally, as the polymer content is increased, one would follow the dotted and dashed stoichiometry lines. At a constant polymer number density, one could add or remove salt and move vertically through the phase diagram. This reinforces that with the addition of excess salt the stoichiometry between small ions and the polymer shifts, allowing the accessibility of different regions of composition space. While not shown here, the equivalent shift in accessible composition space would occur by shifting the stoichiometry in the other direction by removing small ions (experimentally accessed by dialyzing out some fraction of the small ions).

The representative tie lines for the diblock polyampholyte in Fig. 7 are nearly flat, but very weakly positively sloped (<1% enrichment of small ions in the coacervate phase). The negligible partitioning at different overall levels of salt indicates the dominance of the translational entropy in dictating into which phase the small ions phase separate.⁹⁰ This equipartitioning highlights the large amount of counter-ions that have been “released” from the polyampholyte as the polymer number density in the coacervate is much higher than the supernatant phase, yet the number density of small ions are effectively equivalent. (If the counter-ions were not released, the concentration of small ions in the dense coacervate would be stoichiometrically equivalent to the density of polymeric charges.) The slight positive enrichment of small ions in the coacervate phase is indicative of the net attractive charge correlation energy produced by the higher density of charges.

This tie line behavior is in contrast to a number of theories that predict rather strong partitioning $\left({\rho }_s^{II}/{\rho }_s^I>1\right)$ although it is unclear from both experiments^24,28,32 and theories into which phase the small ions should selectively partition. To our knowledge, there have been no studies on the salt partitioning of polyampholytes, which may not behave in an equivalent manner to mixtures of oppositely charged polyelectrolytes. Original studies of the complex coacervation of weakly charged gum arabic by Voorn and Overbeek found partitioning into the concentrated phase.³² More recent studies by Wang and Schlenoff and Radhakrishna et al. have found enrichment of small ions into the dilute phase for mixtures of strongly charged polyelectrolytes at high salt conditions.^37,58 Li et al. recently showed the same enrichment at high salt conditions but found partitioning into the dilute phase for low salt conditions.²⁸

Prior field-theoretic simulations⁵² as well as the commonly used the Voorn–Overbeek model³³ and associated extensions⁵⁷ predict partitioning into the coacervate phase due to the increased electrostatic screening, while particle²⁸ and lattice simulations^39,62 that focus on connectivity effects predict partitioning into the dilute phase, apparently due to excluded-volume penalties in the coacervate.⁹¹ We note that while Gaussian excluded-volume repulsions are included in our model, they are softer than the hard core potentials typically used in particle simulations. A number of approximate analytical theories incorporating the RPA formalism,^46,47 renormalized Gaussian fluctuation theory,⁹² or liquid state theories^34,35 predict both behaviors depending on molecular weight and location within the phase diagram: partitioning into the coacervate at low salt conditions and partitioning into the supernatant as the critical salt concentration is approached.

Overall, it is apparent that the inclusion of explicit counter-ions and small amounts of salt has only a weak effect on the thermodynamics and structure of near-symmetric block polyampholyte solutions, as seen in associative charging models in the weak association regime of polyelectrolyte complexation.^93,94 The small effects are largely predictable, such as renormalizing the electrostatic strength l_B/b due to the additional charge screening by the small ions. The structures of the coacervate and supernatant are similarly weakly affected, even with dramatic increases in the levels of added small ions, in stark contrast to the large influence that sequence and molecular architecture have on the self-coacervation behavior and accessible chain conformations.⁵⁵

C. Charge asymmetric polyampholytes

Experimentally, the chain conformations and solution properties of polyampholytes seem to be controlled by two main parameters: the net charge on the polymer and the ionic strength of the medium. Both are important as pH changes (for weak polyelectrolytes) and synthetic dispersity can cause varying amounts of charge asymmetry. Net-charge-neutral polyampholytes are often insoluble in water, which is thought to be due to the strong electrostatic attractions between oppositely charged polymer segments;⁹⁵ the polymers can be solubilized through the addition of salt, which screens the electrostatic interactions and weakens the attractions (as seen in Fig. 7). We now consider polyampholytes with net-charge to explore the transition when the electrostatic repulsions (polyelectrolyte effect) begin to dominate over the electrostatic attractions (polyampholyte effect).⁹⁵ It should be expected that the specific placement of the excess charge along the backbone will affect the accessible chain conformations and phase separation tendencies,⁵⁵ but we will restrict our study to the diblock polyampholyte.

The excess charge per copolymer is conveniently measured by an average net-charge per statistical segment,

$$f_{\pm }^{ex}=\left|\frac{N_{+}-N_{-}}{N}\right|,$$ (9)

where N_i is the number of statistical segments of charge i, a simplification of the average net-charge, q, discussed by Castelnovo and Joanny,⁴¹ given the present assumption of strong electrolytes/full dissociation. We find that even very small amounts of charge asymmetry, resulting in a net charge on the polyampholyte, shift the location of the binodal coexistence curves and shrinks the unstable region (Fig. 8). The concentrated branch shifts inward to lower salt and polyampholyte concentrations. This shift is caused by the increased osmotic pressure and loss of translational entropy from the additional small ions that are constrained to be localized in the coacervate to satisfy charge neutrality. The increased osmotic pressure competes against the electrostatic attractions responsible for the condensation of the dense phase.⁴¹ While this nonmonotonic effect was predicted by Castelnovo and Joanny, it was predicted to occur at $f_{ex}^{\pm }\approx 1$ for strongly charged chains, but phase separation is suppressed at much smaller fractions of net-charge ($f_{ex}^{\pm }=\mathrm{0,0.02},0.04,0.06$ for ${\mathcal{A}}_{50}{\mathcal{C}}_{50}$, ${\mathcal{A}}_{49}{\mathcal{C}}_{51}$, ${\mathcal{A}}_{48}{\mathcal{C}}_{52}$, and ${\mathcal{A}}_{47}{\mathcal{C}}_{53}$).

FIG. 8.

Phase diagram showing charge asymmetry shrinking phase coexistence and shifting binodal boundaries to lower polyampholyte and higher salt concentrations. The shaded region is the region between the binodal curves. Representative tie lines are shown as solid lines. The Gaussian smearing width is set at a/b = 0.8, the excluded-volume parameter is set at $v$/b³ = 0.0068, and the electrostatic strength is set at l_B/b = 0.065.

For small charge asymmetries, the dilute branch shifts to lower polymer concentration, but a narrower range of small ion concentration. Likely this is due to the small net-charge causing electrostatic repulsion in the cationic block that cannot be adequately compensated by the shorter anionic block; it is more energetically favorable to condense into the dense phase due to the increased screening and smaller electrostatic correlation length from higher density of charges. The salt dependence of these changes to the binodal curves leads to the emergence of closed-loop unstable regions: salting-out–salting-in behavior, as seen in polyelectrolytes.^48,96

The solubility of the non-neutral polyampholyte at low salt is due to the entropic penalty of phase separating out the counter-ions required for charge neutralization. Adding salt reduces this entropic penalty; once the supernatant salt concentration no longer changes appreciably upon phase separation, the polyampholyte becomes unstable.⁴⁸ As seen with the net-charge-neutral polyampholyte, at high salt concentrations, the added salt reduces the polymer concentration in the coacervate and the polyampholyte “salts in” due to the increasingly screened electrostatic interactions.

At the l_B/b = 0.065, $v$/b³ = 0.0068 conditions of Fig. 8 (weak electrostatic strength, slightly good solvent conditions), there exists no thermodynamic instability for charge asymmetries past ${\mathcal{A}}_{47}{\mathcal{C}}_{53}$ ($f_{\pm }^{ex}=.06$) without the addition of excess salt. At small asymmetries, the tie lines are weakly sloped but are increasingly positive with increasing asymmetry, as with asymmetric mixtures of oppositely charged polyelectrolytes.³⁵ The increased partitioning in the coacervate phase is due to the requirement for counter-ions to be localized for charge neutrality: increased local screening at the cost of less translational entropy for the small ions.⁴¹ Above that charge asymmetry, the localization of counter-ions is too energetically unfavorable, and net electrostatic repulsions begin to outweigh the electrostatic attractions between oppositely charged blocks of the polyampholyte.

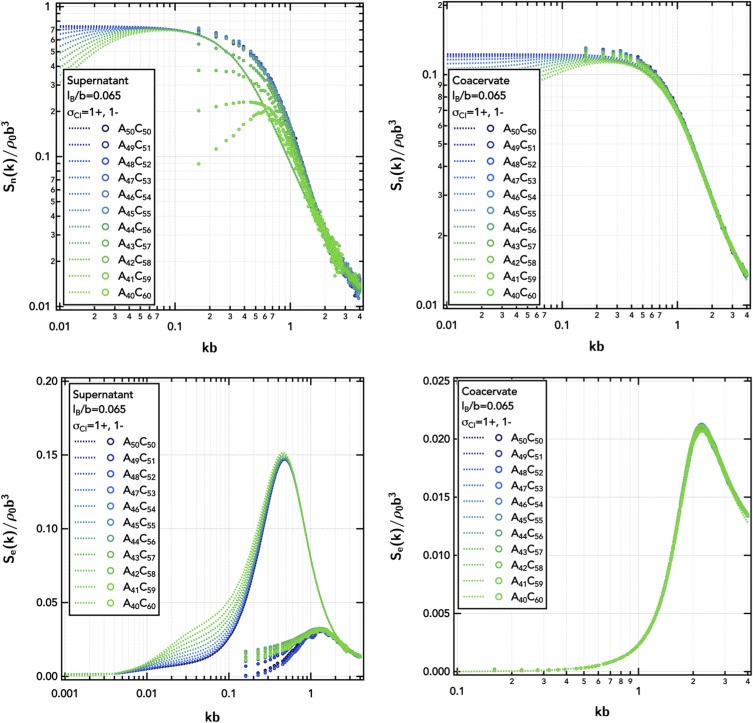
The charge asymmetry strongly affects the structure of the diblock polyampholyte solutions (Fig. 9). It is important to note that these structure factors highlight the collective structure of all polyampholytes and small ions in the system. The density–density correlations show a marked decrease in isothermal compressibility [S_n(0)] as the level of net-charge is increased on the polyampholyte. The RPA qualitatively captures this feature but severely underestimates the effects in the dilute supernatant by miscapturing both the intensity and the length scale where deviations from the charge-neutral diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$) begin. This reduction in compressibility arises from electrostatic repulsions between chains due to their net-charge and the resulting localization of counter-ions to maintain charge neutrality, as also seen in asymmetric mixtures of oppositely charged polyelectrolytes.⁴³ With increasing asymmetry (in both concentration limits), S_n(0) trends smaller, with the development of a finite wavevector for maximal density fluctuations, indicative of the polyelectrolyte peak and the appearance of a characteristic length scale of electrostatic repulsion between polymer segments.

FIG. 9.

Total-density structure factor, S_n(k), and charge-weighted structure factor, S_e(k), of the diblock polyampholyte in the dilute supernatant and coacervate as a function of charge asymmetry. Symbols are obtained from FTS-CL, and lines are RPA predictions. The supernatant is at a polymer number density of ρ_pb³ = 7.35 × 10⁻⁷, and the coacervate is at ρ_pb³ = 0.0735. The Gaussian smearing width is set at a/b = 0.8, the excluded-volume parameter is set at $v$/b³ = 0.0068, and the electrostatic strength is set at l_B/b = 0.065.

In the dense coacervate, there are negligible effects of charge asymmetry on the electrostatic correlations; the intensity of the electrostatic fluctuation correlations remains nearly constant, and the electrostatic screening lengths ξ_e are nearly unchanged. This behavior is well captured, quantitatively, by the RPA. In the dilute solution, however, electrostatic correlations are strongly dependent on the charge asymmetry. Analogous to the coacervate, there is only a weak effect of charge asymmetry on ξ_e or the intensity of correlations, except for the growth of a shoulder at small kb indicating long length scale electrostatic correlations at scales exceeding the molecular size—the isolated polyampholytes begin to “feel” the presence of the excess charge on other polyampholytes. This shoulder exists for net-charge-neutral polyampholytes (and has been attributed to the polarizability of the polyampholyte and associated counter-ion cloud), grows slightly at small asymmetries, but begins to grow more significantly at $f_{\pm }^{ex}\approx 0.1$.

The imbalance in net-charge should also influence the accessible chain conformations of an isolated polyampholyte. As seen in asymmetric mixtures of oppositely charged polyelectrolytes,⁴⁴ charge asymmetric polyampholytes exhibit asymmetry-conferred stability of finite-sized conformations that affect the transition to condensation. With increasing asymmetry, there is the development of “tadpole” configurations (Fig. 10) at $f_{\pm }^{ex}\approx 0.1$ (${\mathcal{A}}_{45}{\mathcal{C}}_{55}$) as predicted by Rubinstein.^42,89 These configurations arise from fluctuations in globular conformations but are distinct and persistent, with structural signatures of a globular “head” and extended “tail” over long MD simulation times for levels of charge asymmetry exceeding $f_{\pm }^{ex}\approx 0.1$. Above this critical charge asymmetry, single-chain structure factors, P(k), obtained from MD show the presence of a k⁻¹ scaling region in the structure of the isolated polyampholyte indicating extended rodlike or polyelectrolytelike contribution to the chain conformation. Such “tadpole” configurations are also seen qualitatively in MD snapshots (${\mathcal{A}}_{40}{\mathcal{C}}_{60}$ shown for clarity in Fig. 10 due to increased persistence and more visible/obvious “tail”).

FIG. 10.

Single chain structure factor, P(k), in the dilute supernatant (ρ_pb³ = 7.35 × 10⁻⁷) as a function of charge asymmetry. The Gaussian smearing width is set at a/b = 0.8, the excluded-volume parameter is set at $v$/b³ = 0.0068, and the electrostatic strength is set at l_B/b = 0.065. Insets: Snapshots from the MD simulations showing globular chain conformations at zero net-charge and the emergence of “tadpole” conformations with increasing charge asymmetry.

However, the non-neutral polyampholyte can also form aggregates in dilute solution that are soluble due to their net-charge. Multiple chain aggregates are possible in either restricted⁴¹ or disproportionated⁴² micelles or more exotic conformations. These mesoscopic structures in dilute solution (if they exist) are embedded in the fully fluctuating FTS-CL simulations but are finite-amplitude structures not captured in the RPA formalism. The structure of such aggregates could be investigated in multichain MD simulations, but we have not pursued that topic here.

D. Multivalent ions

It is well known that polyelectrolytes frequently precipitate with the addition of multivalent salts due to the complexation of the polyelectrolyte with the multivalent species, causing a combination of intrachain and interchain bridging attractions. Such condensation is further complicated by the possibility of the multivalent species to cause local “charge inversion” yielding polyampholytic solution properties, attributable to Debye–Hückel-like polarization interactions.^97–101 However, the effects of multivalent ions on a polyampholyte are largely unexplored. This is surprising as interactions between divalent ions like Ca²⁺ or Mg²⁺ and polyampholytic biomacromolecules (e.g., proteins) are crucial signal intermediates in biological regulation.²

Here, we focus on the valency of only one species of small ion to probe the asymmetry in altering the number of counter-ions present in the system. Increasing the valency of one type of counter-ions shrinks the phase coexistence window (Fig. 11). The binodal boundaries are primarily suppressed on the low salt and high salt borders. Since the diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$) used in the simulations is charge neutral, the present results are insensitve to which counter-ion is multivalent. The role of multivalent ions in charge asymmetric systems will be discussed below.

FIG. 11.

Phase diagram showing multivalent counter-ions shrinking the region for phase coexistence. The shaded region is the region between the binodal curves. Representative tie lines are shown as solid lines. The Gaussian smearing width is set at a/b = 0.8, the excluded-volume parameter is set at $v$/b³ = 0.0068, and the electrostatic strength is set at l_B/b = 0.065.

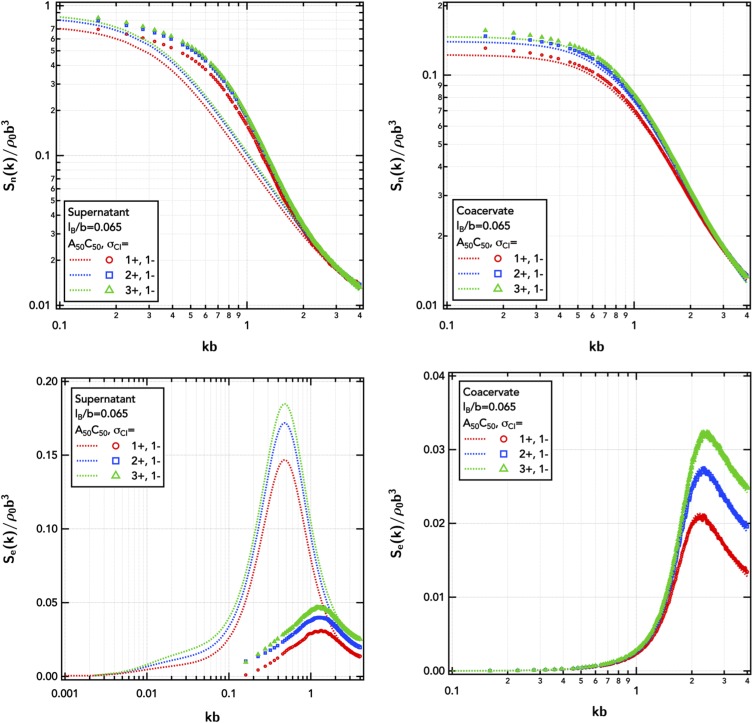
The influence of divalent counter-cations on symmetric polyampholyte phase behavior is primarily on the concentrated branch, with only a minor decrease in the concentration of the polyampholyte in the coacervate and a negligible effect on the concentration of isolated polyampholytes in the dilute solution. However, with trivalent ions, the concentrated branch shifts inward drastically causing a commensurate increase in the dilute phase.

This is a strong influence on the thermodynamics of phase coexistence, yet we find only minimal effects on the structure of the dilute or concentrated phases (Fig. 12). The total-density structure factors indicate nearly unchanged structure in the coacervate and supernatant with the increasing valency of the counter-cations. There is a small difference in the isothermal compresssibility [S_n(0)] due to the difference in the total number of total ions (there are fewer multivalent ions than monovalent counter-ions for equivalent polyampholyte charge).

FIG. 12.

Total-density structure factor, S_n(k), and charge-weighted structure factor, S_e(k), of the diblock polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$) in the dilute supernatant and coacervate as a function of counter-cation valency. Symbols are obtained from FTS-CL, and lines are RPA predictions. The supernatant is at a polymer number density of ρ_pb³ = 7.35 × 10⁻⁷, and the coacervate is at ρ_pb³ = 0.0735. The Gaussian smearing width is set at a/b = 0.8, the excluded-volume parameter is set at $v$/b³ = 0.0068, and the electrostatic strength is set at l_B/b = 0.065.

The multivalent ions intensify the electrostatic fluctuation correlations, but the effects on the charge–charge correlation length are weak. In the coacervate, ξ_e decreases with multivalency as there is stronger screening from the higher charge density of the ion particle. In the dilute supernatant, ξ_e increases as there are fewer small ions and the charged counter-ion cloud surrounding the polyampholyte is more discrete, with fewer numbers of more concentrated charges. Since the polyampholyte (${\mathcal{A}}_{50}{\mathcal{C}}_{50}$) considered in Figs. 11 and 12 is charge neutral, the charge–charge correlations here are due to charge distribution changes within the fluctuating polyampholyte globule and the associated counter-ions. The counter-ion cloud surrounding the polyampholyte manifests as a low-k shoulder in the dilute phase charge–charge structure factor [S_e(k), Fig. 12]. Ion-bridging, such as seen in polyelectrolyte solutions, causing aggregates in the supernatant is also possible, but there does not appear to be structural evidence for these species at the low polymer concentrations in the dilute phase (ρ_pb³ = 7.35 × 10⁻⁷).

E. Polyampholyte charge asymmetry and multivalent ions

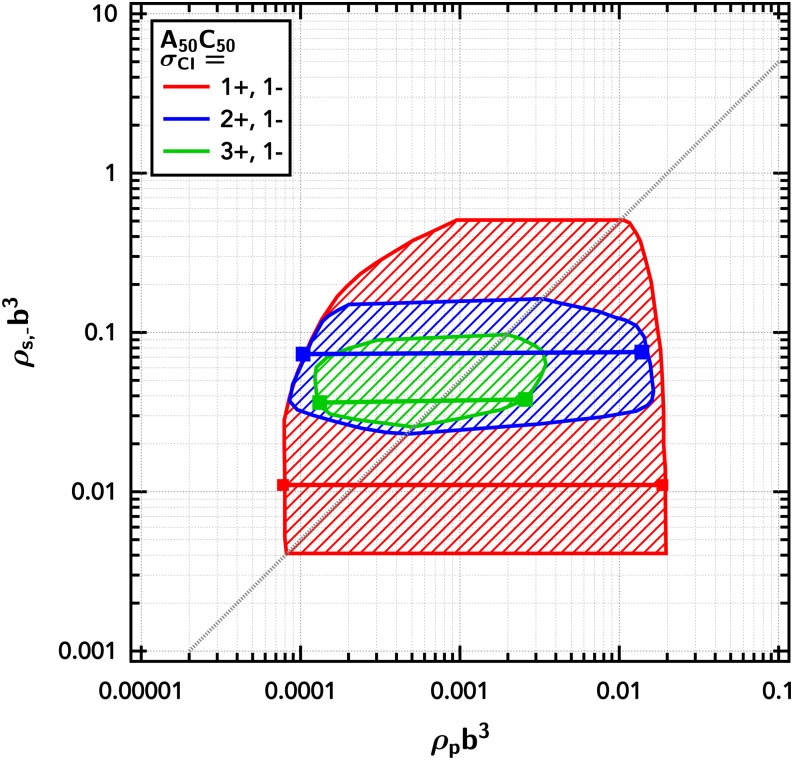
Up to this point, we have studied polyampholyte charge asymmetry and multivalency of counter-ions in isolation. We now consider the behavior of a charge asymmetric polyampholyte (${\mathcal{A}}_{48}{\mathcal{C}}_{52}$) and change the valency of the counter-cations and the counter-anions independently. The multivalent ions were found to shrink the phase coexistence window in the symmetric case of ${\mathcal{A}}_{50}{\mathcal{C}}_{50}$ but shift and weakly increase the two-phase region for the charge asymmetric ${\mathcal{A}}_{48}{\mathcal{C}}_{52}$ (Fig. 13).

FIG. 13.

Phase diagram showing the importance of charge neutrality in dictating partitioning and phase coexistence of a charge asymmetric diblock polyampholyte (${\mathcal{A}}_{48}{\mathcal{C}}_{52}$) with multivalent counter-ions. The shaded region is the region between the binodal curves. Representative tie lines are shown as solid lines. The Gaussian smearing width is set at a/b = 0.8, the excluded-volume parameter is set at $v$/b³ = 0.0068, and the electrostatic strength is set at l_B/b = 0.065.

When the divalent counter-ions are of the same sign as the net-charge on the polyampholyte and thus are not required for charge neutrality, there is only a weak effect, causing a minor shift of the dilute branch of the binodal curve to higher concentration and a small expansion of the phase coexistence window at high polymer concentrations. A much more significant disruption in the phase diagram is realized when the divalent counter-ion is of the opposite sign as the net-charge on the polyampholyte and thus is the counter-ion species required for charge neutrality. Interestingly, in this scenario, the divalent ions partition selectively into the dilute phase, as evidenced by the negative slope of the tie line shown in Fig. 13.

Nonetheless, we find that the structures of both of the phases are only weakly perturbed by a coupling between the presence of multivalent counter-ions and polyampholyte net-charge—for the charge asymmetric polyampholytes with divalent counter-ions, the trends of the structures with increasing polymer net-charge remain qualitatively the same as in the monovalent case (Figs. S2 and S3).

IV. CONCLUSIONS

Coarse-grained models of polyelectrolytes and polyampholytes accounting for chain connectivity, excluded-volume interactions representing a good solvent, and Coulomb interactions between charges are capable of predicting trends in coacervation phenomena that are seemingly in agreement with experiments conducted on synthetic polyelectrolytes and even biomacromolecules.^28,102 Field-theoretic simulations using complex Langevin sampling are an efficient strategy for numerical simulation of such models^53–55 due to no uncontrollable approximations, highly efficient sampling of the concentrated coacervate phase, and the semilocal nature of the Coulombic kernel in the field-theoretic representation. In particular, utilization of the Gibbs ensemble in tandem with the FTS-CL approach provides direct access to phase coexistence even in multicomponent mixtures of polymers and small ions. Molecular dynamics particle simulations were shown to further complement the field theory by providing information about single chain conformations using the same molecular model.^54,55 This tandem framework can be readily extended to explore more complex architectures, dissimilar excluded-volume interactions between chemically dissimilar species, and self-consistent polarizability for nanostructures arising from inclusion of hydrophobic segments.

The incorporation of explicit small ions is shown to have only a weak effect on the self-coacervation behavior of block polyampholytes; the phase diagrams and structures of charge-neutral block polyampholytes are dominated primarily by their charge patterns and sequence.⁵⁵ As in the case without explicit counter-ions, we find that RPA expressions for counter-ion containing models provide qualitatively correct trends but have limited quantitative ability to predict the dilute phase structure and consequently the dilute branch of the phase diagrams.

Excess salt reduces the critical electrostatic strength for self-coacervation due to additional screening. The small ions only minimally perturb the correlation lengths and structures of the phases, primarily affecting the accessibility of the phase coexistence region. The tie lines, representing the partitioning of salt between the supernatant and coacervate phases, are nearly flat but can be both positively and negatively sloped depending on the salt conditions, ion valency, and polyampholyte charge asymmetry. This points to relative equipartitioning of the small ions and confirms the translational entropy of the small ions as the dominant force in salt partitioning.

Even small amounts of charge asymmetry on the polyampholytes can lead to nonmonotonic features in the phase diagram. Initially, small amounts of net polymer charge are tolerated in the phase-separated coacervate by swelling with additional counter-ions to maintain charge neutrality. Increasing net-charge, however, results a critical loss of counter-ion translational entropy and increase in coacervate osmotic pressure that breaks apart the dense phase. This manifests as a closed-loop coexistence region with the emergence of salt-out–salt-in behavior, similar to that seen with polyelectrolytes.

At intermediate asymmetries, the disappearance of the two-phase region coincides with the emergence of “tadpole” configurations in dilute solution—the transition from the polyampholyte effect to the polyelectrolyte effect, as electrostatic repulsions begin to dominate over the electrostatic correlation attractions between oppositely charged blocks. This transition occurs at $f_{\pm }^{ex}\approx 0.1$ as predicted from scaling arguments and as seen in experiments on solutions of diblock polyampholytes.^41,42 Multivalent counter-ions suppress phase separation for charge-neutral polyampholytes but shift and expand the two-phase region in asymmetric polyampholytes for even small amounts of net polymer charge. This effect is most pronounced when the charge on the multivalent counter-ion is opposite to the excess charge on the chain and thereby compensating.

SUPPLEMENTARY MATERIAL

See supplementary material for dependence of molecular weight and counter-ion valence on the total density and charge-weighted structure factors of diblock polyampholyte solutions.

APPENDIX: RANDOM PHASE APPROXIMATION

Here, we pursue expressions for βFb³, βμ, and βΠb³ that result from a Gaussian approximation for ${\mathcal{Z}}_C$. The analysis proceeds by expanding the single-chain partition functions, Q_l, to second order in field fluctuations around the homogeneous saddle point configuration.⁶⁴ The resulting Helmholtz free energy density for the overall charge-neutral block polyampholyte is given by

$$\beta F^{RPA}{b}^3={\rho }_p{b}^3\ln {\rho }_p{b}^3+{\rho }_{s,+}{b}^3\ln {\rho }_{s,+}{b}^3+{\rho }_{s,+}{b}^3\ln {\rho }_{s,+}{b}^3-{\rho }_0{b}^3+\frac{v{\left({\rho }_0{b}^3\right)}^2}{2}$$ (A1)

$$+\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\ln \left(1+v\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{+}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)\right),$$ (A2)

$$+\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\ln \left(1+\frac{2\pi }{3}{l}_B{\sigma }^2{b}^2{k}^{-2}\left(\right.{\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{-}\left(k\right)\left)\right.V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)\right),$$ (A3)

where k is in b⁻¹ units, $V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)=e^{-{ā}^2{k}^2}$, and we have used Fourier conventions $f\left(\mathbf{r}\right)={\sum }_{\mathbf{k}}\widehat{f}\left(\mathbf{k}\right)e^{i\mathbf{k}\cdot \mathbf{r}}$, ${\widehat{f}}_k=V^{-1}\int d\mathbf{r}f\left(\mathbf{r}\right)e^{-i\mathbf{k}\cdot \mathbf{r}}$. In this RPA free energy expansion, the first five terms describe the mean-field free energy, including ideal-gas entropy, of an homogeneous solution of polymer chains of length N_p and positive and negative small ions at fixed concentration. The final two terms are the RPA corrections to the free energy density accounting for excluded-volume and electrostatic fluctuations. Chemical potentials and pressures can be obtained from the Helmholtz free energy as

$$\beta {\mu }_p^{RPA}=\ln {\rho }_p{b}^3+N_{p}v{\rho }_0{b}^3,$$ (A4)

$$+\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\left[\frac{v{b}^{-3}{N}_p^2{ĥ}_{+}\left(k\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}{1+v\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{+}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}\right],$$ (A5)

$$+\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\left[\frac{\frac{2\pi }{3}\frac{l_B}{b}{\sigma }^2{N}_p^2{ĥ}_{-}\left(k\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}{k^2+\frac{2\pi }{3}{l}_B{\sigma }^2{b}^2\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{-}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}\right],$$ (A6)

$$\beta {\mu }_{s,\pm }^{RPA}=\ln {\rho }_{s,\pm }{b}^3+v{\rho }_0{b}^3,$$ (A7)

$$+\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\left[\frac{v{b}^{-3}{V}^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}{1+v\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{+}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}\right],$$ (A8)

$$+\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\left[\frac{\frac{2\pi }{3}\frac{l_B}{b}{\sigma }^2{V}^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}{k^2+\frac{2\pi }{3}{l}_B{\sigma }^2{b}^2\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{-}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}\right],$$ (A9)

$$\beta {\mathrm{\Pi }}^{RPA}{b}^3={\rho }_0{b}^3+\frac{v{\left({\rho }_0{b}^3\right)}^2}{2},$$ (A10)

$$+\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\left[\frac{v\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{+}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}{1+v\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{+}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}\right],$$ (A11)

$$+\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\left[\frac{\frac{2\pi }{3}{l}_B{\sigma }^2{b}^2\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{-}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}{k^2+\frac{2\pi }{3}{l}_B{\sigma }^2{b}^2\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{-}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}\right],$$ (A12)

$$-\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\ln \left(1+v\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{+}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)\right),$$ (A13)

$$-\frac{1}{4{\pi }^2}{\int }_0^{\infty }dk{k}^2\ln \left(1+\frac{2\pi }{3}{l}_B{\sigma }^2{b}^2{k}^{-2}\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{-}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)\right).$$ (A14)

In all of the above expressions, the Debye pair correlations in reciprocal space between blocks i and j of uniform species index are

$${ĝ}_{ij}=\left\{\begin{array}{cc}ĝ\left(k,f_i\right),\hfill & i=j,\hfill \\ ĥ\left(k,f_i\right)ĥ\left(k,f_j\right)\widehat{l}\left(k,d_{ij}\right),\hfill & i\ne j,\hfill \end{array}\right.$$ (A15)

with

$$ĝ\left(k,f\right)=\frac{2}{{\left(\frac{N}{6}\right)}^2{k}^4}\left(\exp \left(-\frac{fN}{6}{k}^2\right)+\frac{fN}{6}{k}^2-1\right),$$ (A16)

$$ĥ\left(k,f\right)=\frac{6}{N{k}^2}\left(\exp \left(-\frac{fN}{6}{k}^2\right)-1\right),$$ (A17)

$$\widehat{l}\left(k,d\right)=\exp \left(-\frac{Nd}{6}{k}^2\right),$$ (A18)

where f_i is the normalized contour length (such that ∑_if_i = 1) of a sequential block of species i and d_ij is the sum of all normalized block lengths between but not including blocks i and j along the chain contour. Thus, the overall pair correlation functions used in thermodynamic observables and structure factors are

$${ĥ}_{+}\left(k\right)=\sum _i\sum _j{ĝ}_{ij},$$ (A19)

$${ĥ}_{-}\left(k\right)=\sum _i\sum _j{\sigma }_i{\sigma }_j{ĝ}_{ij},$$ (A20)

$${ĥ}_x\left(k\right)=\sum _i\sum _j{\sigma }_i{ĝ}_{ij},$$ (A21)

which can be used for any arbitrary block polyampholyte.

The RPA estimate of the total density [$S_n\left(k\right)=⟨\delta \widehat{\rho }\left(\mathbf{r}\right)\delta \widehat{\rho }\left({\mathbf{r}}^{\prime }\right)⟩$] and electrostatic [$S_e\left(k\right)=⟨\delta {\widehat{\rho }}_e\left(\mathbf{r}\right)\delta {\widehat{\rho }}_e\left({\mathbf{r}}^{\prime }\right)⟩$] structure factors are given below for the case of the charge-neutral block polyampholyte and explicit counter-ions.

For density–density correlations, the total-density structure factor is

$$\frac{S_n^{RPA}\left(k\right)}{{\rho }_0{b}^3}=\frac{{\varphi }_{s,+}+{\varphi }_{s,-}+{\varphi }_p{ĥ}_{+}\left(k\right)}{1+v{b}^{-3}\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{+}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}.$$ (A22)

In the k = 0 limit (isothermal osmotic compressibility),

$$\frac{S_n^{RPA}\left(0\right)}{{\rho }_0{b}^3}=\frac{{\varphi }_{s,+}+{\varphi }_{s,-}+{\varphi }_p}{1+v{b}^{-3}\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p\right)}.$$ (A23)

In the kb > 2π limit:for ${\rho }_{s,+}+{\rho }_{s,-}>N_p^2{\rho }_p{ĥ}_{+}\left(k\right)$,

$$\frac{b^3}{S_n^{RPA}\left(k\right)v}=V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)+{\left\{\left({\rho }_{s,+}+{\rho }_{s,-}\right)v\right\}}^{-1},$$ (A24)

for ${\rho }_{s,+}+{\rho }_{s,-}<N_p^2{\rho }_p{ĥ}_{+}\left(k\right)$,

$$\frac{b^3}{S_n^{RPA}\left(k\right)v}=V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)+k^2{\xi }_E^2,\text{where\hspace{0.17em}}{\xi }_E=\frac{b}{2\sqrt{3}{\left(N_p{\rho }_{p}v\right)}^{1/2}}.$$ (A25)

For the charge–charge correlations, the electrostatic structure factor is

$$\frac{S_e^{RPA}\left(k\right)}{{\rho }_0{b}^3}=\frac{k^2\left({\varphi }_{s,+}+{\varphi }_{s,-}+{\varphi }_p{ĥ}_{-}\left(k^2\right)\right)}{k^2+\frac{2}{3}\pi l_b{b}^2{\sigma }^2\left({\rho }_{s,+}+{\rho }_{s,-}+N_p^2{\rho }_p{ĥ}_{-}\left(k\right)\right)V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)}.$$ (A26)

In the k = 0 limit (charge neutrality),

$$\frac{S_e^{RPA}\left(0\right)}{{\rho }_0{b}^3}=0.$$ (A27)

In the kb > 2π limit:for ${\rho }_{s,+}+{\rho }_{s,-}>N_p^2{\rho }_p{ĥ}_{-}\left(k\right)$,

$$\begin{array}{l}\hfill \begin{array}{c}\frac{k^2}{S_e^{RPA}\left(k\right)\left(\frac{2\pi }{3}\frac{l_B}{b}{\sigma }^2\right)}=V^2{\widehat{\mathrm{\Gamma }}}^2\left(k\right)+k^2{\xi }_e^2,\\ \text{where\hspace{0.17em}}{\xi }_e={\left(\frac{2\pi }{3}{l}_B{\sigma }^2\left({\rho }_{s,+}+{\rho }_{s,-}\right)\right)}^{-1/2},\end{array}\end{array}$$ (A28)

for ${\rho }_{s,+}+{\rho }_{s,-}<N_p^2{\rho }_p{ĥ}_{-}\left(k\right)$,

$$\begin{array}{l}\hfill \begin{array}{c}\frac{k^2}{S_e^{RPA}\left(k\right)\left(\frac{2\pi }{3}\frac{l_B}{b}{\sigma }^2\right)}=V^2{\widehat{\mathrm{\Gamma }}}^2\left(\mathbf{k}\right)+k^4{\xi }_e^4,\\ \text{where\hspace{0.17em}}{\xi }_e={\left(\frac{4\pi }{3}{l}_B{\sigma }^2{b}^{-2}{N}_p{\rho }_p\right)}^{-1/4}.\end{array}\end{array}$$ (A29)