Solubility of Tris(hydroxymethyl)aminomethane in Water-Methanol Solvent Mixtures and Medium Effects in the Dissociation of the Protonated Base

Abstract

The dissociation constant of the protonated form of tris(hydroxymethyl)aminomethane has been measured at 25 °C in water-methanol solvents containing 30, 50, 70, and 90 wt percent methanol by means of potentiometric titrations. The solubility of tris(hydroxymethyl)aminomethane at 15, 25, and 35 °C in water-methanol solvents containing from 0 to 100 percent methanol has been determined. The results are discussed in terms of free energies of transfer and “medium effects” for hydrochloric acid, tris(hydroxymethyl)aminomethane, and tris(hydroxymethyl)aminomethane hydrochloride.

1. Introduction

The dissociation of an acid of the charge type A⁺B°, such as the ammonium ion or the protonated form of tris(hydroxymethyl)aminomethane,

$${\text{BH}}^{+}+{\text{H}}_2\text{O}\to {\text{H}}_3{\text{O}}^{+}+\text{B},$$

is a process in which a solvated hydrogen ion and an uncharged basic molecule are produced from a positively charged acid ion. The process in aqueous solution can be characterized by a dissociation constant, _wK:

$${}_{\text{w}}K=\frac{m_{{\text{H}}^{+}}\cdot m_{\text{B}}}{m_{{\text{BH}}^{+}}}{\cdot }_{{}_{\text{w}}}\left(\frac{{\gamma }_{{\text{H}}^{+}}\cdot {\gamma }_{\text{B}}}{{\gamma }_{{\text{BH}}^{+}}}\right)$$ (1)

where _wγ designates an activity coefficient. For aqueous solutions, it is convenient to refer these activity coefficients to the hypothetical molal standard state in water; thus the activity coefficients approach unity as the aqueous solution becomes more dilute. The subscript w indicates this choice of the standard state.

In aqueous solution at 25 °C, − log _wK for the protonated form of tris³ has been found [1, 2]⁴ to be 8.072. The increase in free energy corresponding to the reaction:

$${\text{BH}}^{+}+{\text{H}}_2\text{O}\to {\text{H}}_3{\text{O}}^{+}+\text{B}$$

is:

$${\Delta }_{\text{w}}{G}^{°}=G_{\text{H}}^{°}+G_{\text{B}}^{°}-G_{{\text{BH}}^{+}}^{°}=-RT\ln {}_{\text{\hspace{0.17em}w}}K$$ (2)

the free energies of the reactants and the products being measured in their standard states in water. At 25 °C, therefore, Δ_wG° is 46.07 kJ mol⁻¹.

If the dissociation constant is determined in another solvent medium, 50 wt percent water-methanol, for example, we have:

$${}_{\text{s}}K=\frac{m_{{\text{H}}^{+}}\cdot m_{\text{B}}}{m_{{\text{BH}}^{\text{+}}}}{\cdot }_{\text{s}}\left(\frac{{\gamma }_{{\text{H}}^{+}}\cdot {\gamma }_{\text{B}}}{{\gamma }_{{\text{BH}}^{\text{+}}}}\right)$$ (3)

where the subscript s denotes that the activity coefficients are referred to the hypothetical molal standard state in this solvent and approach unity as the solution becomes more dilute without change in the composition of the solvent. It has been found [3] that − log _SK = 7.818 for the protonated form of tris at 25 °C in 50 percent methanol. The reaction is:

$${\text{BH}}^{+}+\text{S}\to {\text{SH}}^{+}+\text{B}$$

where S is a solvent molecule and SH⁺ a solvated hydrogen ion. It is not necessary at this point to distinguish between solvation by water and by methanol molecules. The free energy change corresponding to this reaction is 44.62 kJ mol⁻¹.

The two processes, one in aqueous solution and the other in 50 percent methanol, can be regarded as a single transfer process

$${\text{BH}}^{+}(\text{s})+{\text{H}}^{+}(\text{w})+\text{B}(\text{w})\to {\text{BH}}^{+}(\text{w})+{\text{H}}^{+}(\text{s})+\text{B}(\text{s}),$$

in which the protonated form of tris is transferred from 50 percent methanol to water and solvated hydrogen ions and tris molecules are transferred in the opposite direction. The change in Gibbs free energy when this process occurs is the difference between the separate free energy changes, or Δ_mG° = −1.45 kJ mol⁻¹. The subscript m is used to indicate that the process is a “medium effect,” being the composite effect of transferring three species from one solvent medium to another. As each species is in its standard state in each solvent, the free energy change is not concentration-dependent.

It is convenient to define medium effects for each species separately,

$${}_{\text{m}}{G}_i^{°}=RT\ln {}_{\text{\hspace{0.17em} m}}{\gamma }_i$$ (4)

so that

$${\Delta }_{\text{m}}{G}^{°}=RT\left(\ln {}_{\text{\hspace{0.17em}m}}{\gamma }_{\text{B}}+\ln {}_{\text{\hspace{0.17em}m}}{\gamma }_{{\text{H}}^{+}}-\ln {}_{\text{\hspace{0.17em}m}}{\gamma }_{{\text{BH}}^{+}}\right).$$ (5)

This can be expressed in terms of the pK values:

$$p_{\text{s}}K-p_{\text{w}}K=\log {}_{\text{\hspace{0.17em}m}}{\gamma }_{\text{B}}+\log {}_{\text{\hspace{0.17em}m}}{\gamma }_{{\text{H}}^{+}}-\log {}_{\text{\hspace{0.17em}m}}{\gamma }_{{\text{BH}}^{+}}.$$ (6)

Hereafter, the terms ${\Delta }_{\text{m}}{G}_i^{°}$ will be termed “free energies of transfer,” and the quantities _mγ_i will be designated “medium effects.”

Of these three medium effects, two are concerned with the transfer of charged particles from one solvent to another of different dielectric constant (ϵ). The Born equation [4]:

$$G^{el}=\frac{N{e}^2}{2ϵr}$$ (7)

should, therefore, give at least an approximation to the energy of transfer of an ion from water (ϵ_w= 78.3) to 50 percent methanol (ϵ_s = 56.3):

$${\Delta }_{\text{m}}{G}_i^{°}{\approx }_{\text{s}}{G}_i^{el}{-}_{\text{w}}{G}_i^{el}=\frac{N{e}^2}{2}\left(\frac{1}{{ϵ}_{\text{s}}}-\frac{1}{{ϵ}_{\text{w}}}\right)\frac{1}{r_i}$$ (8)

where the superscript el indicates that the calculation is based on electrostatic considerations alone. The useful application of eq (8) requires that the radius, r_i, of the ion be known.

The radius of the tris cation was estimated [3] from atom models to be about 4 Å so that, from eq (8), the transfer of a tris cation from water to 50 percent methanol is accompanied by an increase in electrostatic free energy of 0.87 kJ mol⁻¹. There is some difficulty in assigning a radius to the solvated hydrogen ion, but it was estimated [3] that the radius is about 2.8 Å. Hence the transfer of hydrogen ion from water to 50 percent methanol involves an increase of 1.24 kJ mol⁻¹ in free energy.

We now have

	ΔmG°
BH+(s)+ H+(w)+ B(w)→ BH+(w) + H+(s)+ B(s)	−1.45 kJ mol−1
H+(w) → H+(s)	+1.24 kJ mol−1
BH+(s) →BH+(w)	−0.87 kJ mol−1

and hence,

$$\text{B}(\text{w})\to \text{B}(\text{s}),{\Delta }_{\text{m}}{G}^{°}=-1.82\text{\hspace{0.17em} kJ \hspace{0.17em}}{\text{mol}}^{-1}.$$

These results suggest, therefore, that there is a rather large effect, amounting to about 2 kJ mol⁻¹, accompanying the transfer of a mole of the neutral tris molecules between water and 50 percent methanol. A more refined treatment by Hepler [5] of a variable dielectric constant in the close vicinity of an ion reinforces the existence of this large transfer energy term for the uncharged base.

In the earlier study [3] of the pK of protonated tris at several temperatures in 50 wt percent methanol, the discrepancy of about 2 kJ mol⁻¹ between the calculated and “observed” free energies of dissociation was attributed to a “basicity effect” of the solvent, which was thought to be superimposed on the medium effects calculated from electrostatic considerations alone. This view was taken in the belief that the medium effect of an uncharged species would be so small as to be unable to account for the differences observed between the experimental and calculated free energies of dissociation.

In the present work, the free energy of transfer and the medium effect for the free base have been determined and found to account reasonably well for the “basicity effect” identified in the prior investigation. These conclusions are based on measurements of the solubility of tris in water and in water-methanol solvents and upon a determination of the pK of protonated tris at 25 °C in 30, 50, 70, and 90 wt percent methanol.

2. Outline of Present Method

The condition for equilibrium between solid tris and its saturated aqueous solution is:

$$G\left(\text{solid}\right){=}_{\text{w}}{G}^{°}+RT\ln {}_{\text{\hspace{0.17em}w}}\gamma \cdot m_{\text{w}},$$ (9)

where m_w is the molality of the saturated solution and _wγ is the activity coefficient of tris at this molality relative to unity in the standard state in water. The condition for equilibrium between solid tris and its saturated solution in a water-methanol mixture is:

$$G\left(\text{solid}\right){=}_{\text{w}}{G}^{°}+RT\ln {}_{\text{\hspace{0.17em}m}}\gamma {\cdot }_{\text{s}}\gamma \cdot m_{\text{s}},$$ (10)

where m_s is the molality of the saturated solution in the mixed solvent and _sγ is the activity coefficient of tris at this molality relative to unity in the standard state in the mixed solvent. The proof of eq (10) is given in the appendix to this paper.

It follows from eq (9) and (10) that

$$\ln {}_{\text{\hspace{0.17em}m}}\gamma =\ln m_{\text{w}}/m_{\text{s}}+\ln {}_{\text{\hspace{0.17em}w}}\gamma {/}_{\text{s}}\gamma$$ (11)

and hence that the medium effect, _mγ, can be obtained from the ratio of the solubilities of tris in water and in the mixed solvent, provided that _sγ/_wγ is unity. The latter condition will hold to a good approximation if the solute is only slightly soluble in each solvent medium. This would be true, for example, for silver chloride in water and water-methanol mixtures, for in dilute solutions _wγ and _sγ are, in the main, expressions of the Debye-Hückel (interionic) forces, and these become more nearly negligible as the solution becomes more dilute. A fortiori, this is true of the ratio ln _wγ/_sγ. Although tris is uncharged, it is very soluble, especially in water, and it might seem that this condition would not apply. It has, however, been shown [6] that the activity coefficient of tris does not depart much from unity even in concentrated solutions. Similar data are not available for water-methanol mixtures, but there is no reason to believe that _sγ will depart much from unity in these solvents. As will be shown later, m_w/m_s is large, and it would require values of _sγ very different from unity to reduce _mγ to a negligible quantity. In the absence of any proof that that _sγ is markedly different from unity, it will be assumed that m_w/m_s gives an approximation to the medium effect, _mγ. In order to obtain values of _mγ, the solubility of tris in a number of water-methanol mixtures has been measured at 15, 25, and 35 °C and the results are reported in this paper.

Equation (6) can be recast as follows:

$$p_{\text{s}}K-p_{\text{w}}K=\log {}_{\text{\hspace{0.17em}m}}{\gamma }_{\text{B}}+2\log {}_{\text{\hspace{0.17em}m}}{\gamma }_{\text{HCl}}-2\log {}_{\text{\hspace{0.17em}m}}{\gamma }_{\text{B}\cdot \text{HCl}}$$ (12)

The terms on the left and the first term on the right are obtained from measurements to be described later in this paper. The term in _mγ_HCl corresponds to the free energy change in the transfer of hydrochloric acid from water to a water-methanol mixture and can be obtained from the standard emf of the cell with hydrogen and silver-silver chloride electrodes in water and in the water-methanol mixtures, determined by emf measurements of solutions of hydrochloric acid:

Pt; H₂, HCl in water or water-methanol, AgCl: Ag.

Values of these standard electromotive forces have been tabulated [7]. Accordingly, the remaining term in eq (12), _mγ_{B· HCl}, the medium effect for the transfer of tris hydrochloride from water to water-methanol mixtures can be calculated and compared with similar free energy changes for other salts.

3. Experimental Procedures

3.1. Dissociation Constants

The dissociation constant of the protonated form of tris was determined in 30, 50, 70, and 90 wt percent methanol at 25 °C by potentiometric titration. The cell:

Glass electrode; HCl (0.01 m) in water-methanol, AgCl; Ag

was set up and its emf (E₁) measured when the silver-silver chloride electrode had come to equilibrium. A solution consisting of (0.01 m HCl + 0.1 m tris) in the same water-methanol mixture was then added in measured amounts and the emf (E₂) measured after each addition. Under these conditions of constant chloride concentration and constant total ionic strength (but varying ratio of tris to tris hydrochloride), the electrode comes to equilibrium quickly [8, 9]. Then,

$$p_{\text{s}}K=\left(E_2-E_1\right)/k+\log \frac{m_{{\text{BH}}^{+}}}{0.01m_{\text{B}}}+\log \frac{{}_{\text{s}}{\gamma }_{{\text{BH}}^{\text{+}}}{\cdot }_{\text{s}}{\gamma }_{\text{C}{1}^{-}}}{{}_{\text{s}}{\gamma }_{\text{B}}{\cdot }_{\text{s}}{{\gamma }^{\prime }}_{{\text{H}}^{+}}{+}_{\text{s}}{{\gamma }^{\prime }}_{\text{C}{1}^{-}}}$$ (13)

where k = (RT ln 10)/F and the primed quantities refer to the initial solution to which no tris had been added. A number of determinations of p_sK can be made, one corresponding to each addition of the (HCl + tris) solution. The last term of eq (13) should be negligible for solutions of these low ionic strengths and we can write:

$$pK=\left(E_2-E_1\right)/k+\log m_{{\text{BH}}^{+}}/\left(0.01m_{\text{B}}\right).$$ (14)

This neglect of the activity coefficient term in eq (13) appears justifiable because, omitting this term, we find p_sK = 7.825 in 50 percent methanol. This value compares well with p_sK = 7.818 obtained earlier [3] using an emf method in which the activity coefficient term was eliminated by extrapolating the data to zero ionic strength.

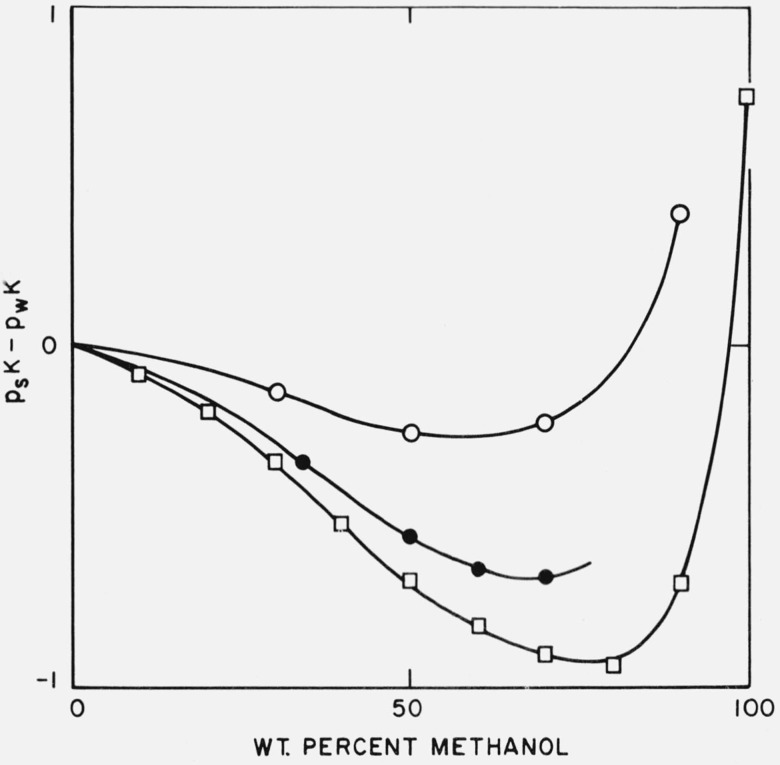
The results of these potentiometric titrations are given in table 1. They are compared, in figure 1, with similar data for the ammonium ion [10] and the o-chloroanilinium ion [11]. It is apparent that the effect of solvent composition on p_sK is specific to each acid, but there is a general resemblance between the three curves insofar as the effect of adding methanol to the solvent medium is concerned. Addition of methanol first reduces the value of p_sK. A minimum is reached between 60 and 80 percent methanol, after which p_sK rises to high values when the methanol content is large. There is evidence, for two of the acids, that the value of p_sK in solvents of high methanol content can exceed the pK value in water; this is probably true also for the ammonium ion.

Table 1.

Values of p_sK for the dissociation of the protonated form of tris(hydroxymethyl)aminomethane in water-methanol mixtures at 25 °C

Wt percent methanol	psK	psK–pwK
0	a (8.072)
30	7.940	−0.132
50	7.825	−.247
70	7.855	−.217
90	8.462	+ .390

^aFor this value of p_wK, see ref. [1] and [2].

Figure 1. Difference between the pK value in water-methanol mixtures and in water (p_sK − p_wK), for three acids.

O, Protonated form of tris(hydroxymethyl)aminomethane.

●, Ammonium ion.

□, o-Chloroanilinium ion.

3.2. Solubility

Tris is a very soluble substance which readily supersaturates; moreover, its solubility is highly temperature-sensitive. Solubility measurements were, therefore, made in a constant temperature bath. The solutions were shaken at frequent intervals, but vigorous shaking was avoided. The solutions were analyzed by acidimetric titration at intervals of 24 hr. The solutions were assumed to be in equilibrium with the solid phase if no change in concentration was found over a period of 72 hr. The equilibration time was between two and three weeks.

Table 2 gives the solubilities (in moles per kilogram of solvent) at 15, 25, and 35 °C. Table 3 records the medium effect, log _mγ_B, calculated from these solubility values with the aid of the equation:

$$\log {}_{\text{\hspace{0.17em}m}}{\gamma }_{\text{B}}\approx \log m_{\text{w}}/m_{\text{s}}$$ (15)

and also the corresponding free energy changes, ${\Delta }_{\text{m}}{G}_{\text{B}}^{°}=RT$ ln _mγ_B. From the temperature coefficient of the free energy change, it is possible to calculate the enthalpy and entropy changes accompanying the transfer process. Values of ${\Delta }_{\text{m}}{H}_{\text{B}}^{°}$ and ${\Delta }_{\text{m}}{S}_{\text{B}}^{°}$ are given in table 4. These were calculated by assuming that over this 20 °C temperature range:

$${\Delta }_{\text{m}}{G}_{\text{B}}^{°}=A+BT+C{T}^2.$$ (16)

Then, it can be shown that:

$${\Delta }_{\text{m}}{H}_{\text{B}}^{°}=g_2-0.05\left(g_3-g_1\right)T_0$$ (17)

and

$${\Delta }_{\text{m}}{S}_{\text{B}}^{°}=0.05\left(g_1-g_3\right),$$ (18)

for the enthalpy and entropy changes at the middle temperature (T₀ = 298.15 °K), where g₁, g₂, and g₃ are the values of ${\Delta }_{\text{m}}{G}_{\text{B}}^{°}$ at 15, 25, and 35 °C, respectively.

Table 2.

Solubility of tris(hydroxymethyl)aminomethane in water-methanol mixtures at 15, 25, and 35 °C

Wt percent methanol	15 °C		25 °C		35 °C
	S	σ	S	σ	S	σ
0	4.593	0.001	5.780	0.008	7.261	0.004
10	3.940	.001	5.092	.003	6.550	.010
20	3.363	.002	4.450	.010	5.827	.003
30	2.845	.004	3.821	.027	5.087	.003
40	2.382	.004	3.223	.027	4.366	.003
50	1.920	.005	2.622	.002	3.610	.004
60	1.455	.001	2.009	.011	2.813	.001
70	1.022	.001	1.440	.003	2.503	.006
80	0.6727	.0007	0.9359	.0007	1.356	.008
90	.3700	.0003	.5368	.0006	0.8443	.0021
100	.2186	.0001	.2918	.0007	.4266	.0007

S = solubility in moles per kilogram of solvent.

σ = standard deviation.

Table 3.

Medium effects and free energy changes in the transfer of tris(hydroxymethyl)aminomethane from water to water-methanol solvents

Wt percent methanol	15 °C		25 °C		35 °C
	log mγB	${\Delta }_{\text{m}}{G}_{\text{B}}^{°}$	log mγB	${\Delta }_{\text{m}}{G}_{\text{B}}^{°}$	log mγB	${\Delta }_{\text{m}}{G}_{\text{B}}^{°}$
10	0.0667	0.368	0.0550	0.314	0.0445	0.263
20	.135	.745	.114	.651	.0955	.563
30	.208	1.15	.180	1.03	.154	.909
40	.285	1.57	.254	1.45	.221	1.30
50	.379	2.09	.343	1.96	.303	1.79
60	.499	2.75	.459	2.62	.412	2.43
70	.653	3.60	.604	3.45	.549	3.24
80	.834	4.60	.791	4.52	.729	4.30
90	1.094	6.04	1.032	5.89	.935	5.52
100	1.322	7.29	1.297	7.40	1.231	7.26

Values of ${\Delta }_{\text{m}}{G}_{\text{B}}^{°}$ are expressed in kJ mol⁻¹.

Table 4.

Enthalpy and entropy changes in the transfer of tris(hydroxymethyl)aminomethane from water to water-methanol solvents at 25 °C

Wt percent methanol	${\Delta }_{\text{m}}{H}_{\text{B}}^{°}$	${\Delta }_{\text{m}}{S}_{\text{B}}^{°}$
10	1.9	5
20	3.4	9
30	4.6	12
40	5.5	14
50	6.5	15
60	7.4	16
70	8.8	18
80	9.0	15
90	13.6	26
100	7.9	2

${\Delta }_{\text{m}}{H}_{\text{B}}^{°}$ is given in kJ mol⁻¹ and ${\Delta }_{\text{m}}{S}_{\text{B}}^{°}$ in J deg⁻¹ mol⁻¹.

4. Discussion

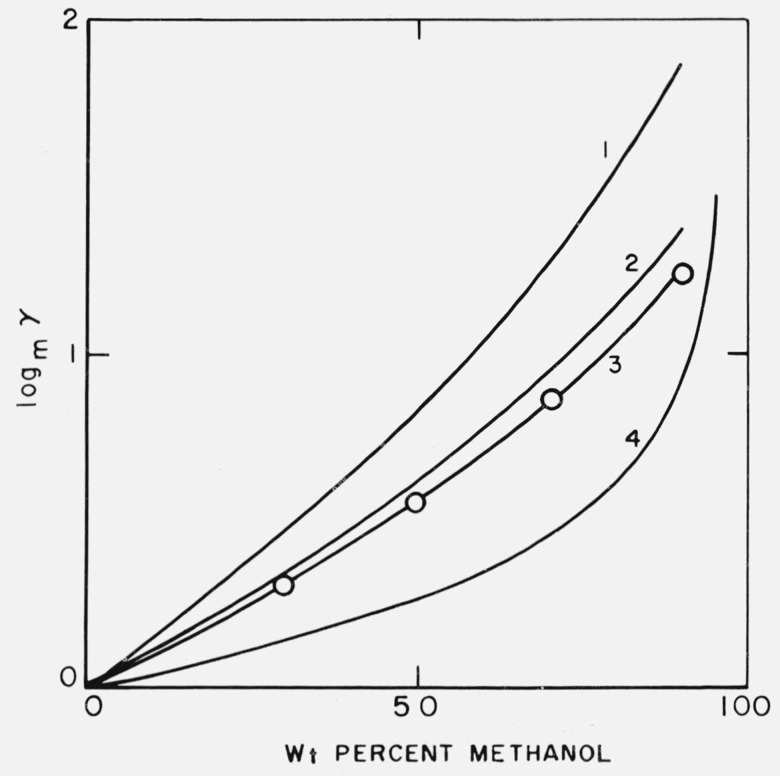
We now have the three quantities necessary to calculate log _mγ_{B· HCl} by means of eq (12). Values of (p_sK − p_wK) are given in table 1, log _mγ_B appears in table 3, and 2 log _mγ_HCl is calculated from the standard potentials of cells containing hydrochloric acid [7, 12]. All of these values are collected in table 5 along with log _mγ_{B · HCl} calculated with the aid of eq (12). The latter have also been expressed in terms of the free energy of transfer of tris hydrochloride from water to water-methanol. Table 5 also contains values of log _mγ_LiCl for the transfer of lithium chloride from water to water-methanol [13]. It can be seen, especially if the data are plotted as in figure 2, that the energies of transfer between water and water-methanol solvents of the same composition are similar for lithium chloride and for tris hydrochloride.

Table 5.

Medium effects involved in the dissociation of protonated tris(hydroxymethyl)aminomethane in water-methanol solvents at 25 °C

Wt percent methanol	30	50	70	90
psK — pwK	−0.132	−0.247	−0.217	+ 0.390
log mγB	.180	.343	.604	1.032
log mγHCl	.162	.268	.456	0.920
log mγB·HCl	.319	.563	.867	1.240
log mγLiCl	.361	.620	.936	1.369
${\Delta }_{\text{m}}{G}_{\text{B·HCl}}^{°}\left(\text{kJ\hspace{0.17em}}{\text{mol}}^{-1}\right)$	3.64	6.43	9.90	14.16

Figure 2. Medium effects for the transfer of electrolytes from water to water-methanol solvents.

1 NaCl,

2 LiCl,

3 Tris · HCl,

4 HCl.

The present picture of the transfer process is different from that discussed earlier [3|, as shown by the following résumé of the free energies of transfer (in kJ mol⁻¹) from water to 50 percent methanol:

The small difference between the two values given for the energy of process (i) arises from the difference between the values of p_sK recorded in table 1 and that given earlier [3]. As already indicated, the calculations of the earlier study gave only the free energy of transfer of the solvated hydrogen ion (1.24 kJ mol⁻¹) and that of the B · H⁺ ion (0.87 kJ mol⁻¹) for the transfer from water to 50 percent methanol. Therefore, for the comparisons shown above we have also used eq (7) to calculate a value of 1.91 kJ mol⁻¹ for the transfer of a mole of chloride ion from water to 50 percent methanol, assuming a radius of 1.81 Å for this ion. The calculated values for the processes (ii) and (iii) accordingly become −2.78 and 3.15 kJ mol⁻¹.

	ΔmG°
	Ref 3	This paper
(i) B HCl (s)+HCl (w)+B (w)→ B HCl (w)+HCl (s) + B (s)	−1.45	−1.41
(ii) B HCl (s) → B HCl (w)	−2.78	(−6.43)
(iii) HCl (w) → HCl (s)	3.15	3.06
(iv) B(w) → B(s)		1.96
(v) “Basicity effect”	(−1.82)
	−1.45	−1.41

Although specific interactions and selective solvation might be expected to have a stronger influence in solutions of hydrochloric acid than in solutions of tris hydrochloride, it is interesting to note that the transfer free energy for hydrochloric acid computed from purely electrostatic considerations is close to the experimental value given in the last column, while the differences for tris hydrochloride are considerable. In the earlier work, no attempt was made to estimate the free energy of process (iv). Instead, the discrepancy between the known value for process (i) and the sum of the calculated energies of processes (ii) and (iii) was attributed to a basicity effect (v), considered to be superimposed on the electrostatic energies, calculated from the Born model, eq (7). A more detailed analysis based on the concept of a variable dielectric constant in the vicinity of the ion affects the numerical values of the transfer energies but does not change the conclusions [3].

In this paper, however, we have described how transfer energies for tris can be determined experimentally by means of solubility measurements. The value of 1.96 kJ mol⁻¹ in the above tabulation, therefore, is an experimental quantity. Furthermore, the energy of transfer of hydrochloric acid, 3.06 kJ mol⁻¹, has been derived from emf measurements. The approximate agreement with the value of 3.15 kJ mol⁻¹ calculated by means of the Born equation, assuming a reasonable value of the ionic radius, suggests that the electrostatic effect is the main one in this instance.

The value of −6.43 kJ mol⁻¹ for the transfer energy of tris hydrochloride has not been derived by independent means but is based on the experimental values for processes (i), (iii), and (iv). The pertinent relationship among these quantities is set forth in eq (12). The discrepancy between the two values for the tris.H⁺ ion arises from the fact that Woodhead et al. [3] , ascribed a reasonable value of 4 Å to the radius of the tris cation and assumed that the electrostatic effect, as calculated by means of eq (7), gives a complete account of the transfer process. It is now found that the energy of transfer of tris hydrochloride from water to 50 percent methanol is 3.7 kJ mol⁻¹ larger than that so calculated.

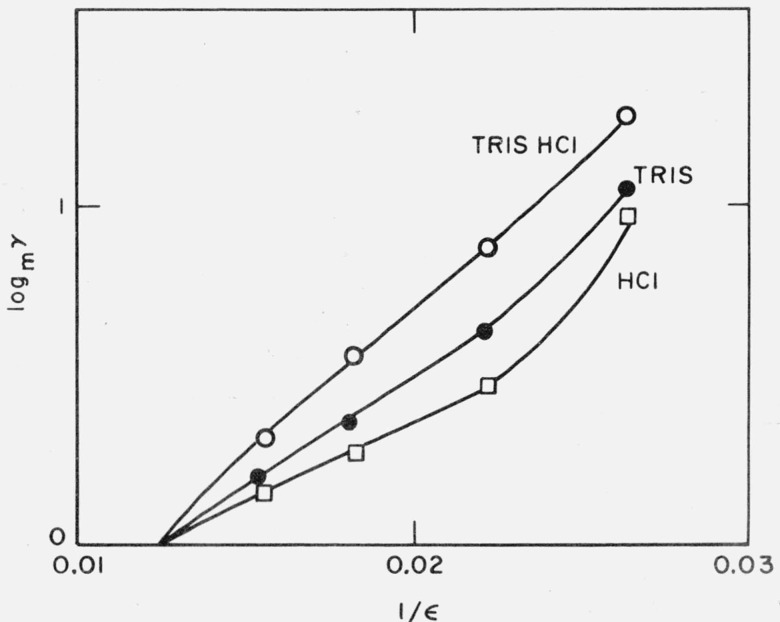
Figure 3 is a plot of log _mγ for three transfer processes from water to water-methanol against the reciprocal of the dielectric constant of the solvent. According to eq (7), two of these should be straight lines; it is curious that the best approximation to a straight line is found for the nonelectrolyte, tris. Nevertheless, up to a solvent composition of 70 percent methanol, the plots for hydrochloric acid and tris hydrochloride are almost linear and therefore satisfy one requirement of eq (7). According to this equation, however, if we take 1.91 kJ mol⁻¹ for the energy of transfer of the chloride ion from water to 50 percent methanol, the radius of the cation is given by the equation:

$$r_{+}=\frac{N{e}^2}{2{\Delta }_{\text{m}}{G}_{+}^{°}}\left(\frac{1}{{ϵ}_{\text{S}}}-\frac{1}{{ϵ}_{\text{W}}}\right)$$ (19)

Or

$$r_{+}=3.466{\left({\Delta }_{\text{m}}{G}_{+}^{\circ }\right)}^{-1}$$ 19a

if r₊ is expressed in Å and ${\Delta }_{\text{m}}{G}_{\text{+}}^{°}$ in kJ mol⁻¹, and the transfer process occurs between water (ϵ_w = 78.3) and 50 percent methanol (ϵ_s = 56.3).

Figure 3. Medium effects for the transfer from water to water-methanol solvents, as a function of the reciprocal of the dielectric constant of the medium.

O, Tris(hydroxymethyl)aminomethane hydrochloride.

●, Tris(hydroxymethyl)aminomethane.

□, Hydrochloric acid.

Åkerlöf [13] has determined log _mγ for the transfer of potassium chloride, sodium chloride, and lithium chloride and, if his data for the transfer of these salts from water to 50 percent methanol are used, values of r₊ = 0.40, 0.44, and 0.67 Å are obtained for the potassium, sodium, and lithium cations, respectively, assuming a radius of 1.81 Å for the chloride ion. Similarly, from the values of Δ_mG° for tris hydrochloride and hydrochloric acid, we find r₊ = 0.77 and 3.02 Å for protonated tris and hydrogen ions, respectively. Of these five cationic radii, only one, that of the hydrogen ion, is reasonable; the others are much too small. The anomaly is all the more curious because there is every reason to believe that the Debye-Hückel theory gives the correct values of the activity coefficients _sγ in 50 percent methanol just as it does for water as solvent, provided that the macroscopic dielectric constant is used in the Debye-Hückel equation and a reasonable value of the ion-size parameter is introduced. The use of the macroscopic dielectric constant, therefore, explains the concentration dependence of the activity coefficient in both solvent media but fails to account for the energy of transfer from one solvent to the other.

The standard state used in this discussion is that for the molal scale of concentration, both in water and in water-methanol. It is possible that the standard state on the mole-fraction scale would be a better choice. Equations for the conversion from one scale to the other can be found elsewhere [14]; the energy of transfer of the hydrogen ion from water to 50 percent methanol is lower by 0.61 kJ mol⁻¹ on the mole-fraction scale than on the molality scale, and the same is true of the chloride ion. Thus the energy of transfer of hydrochloric acid is 1.84 kJ mol⁻¹ on the mole-fraction scale and 3.06 kJ mol⁻¹ on the molality scale. Nevertheless, the adoption of the mole-fraction scale does not lead to a more reasonable set of ionic radii.

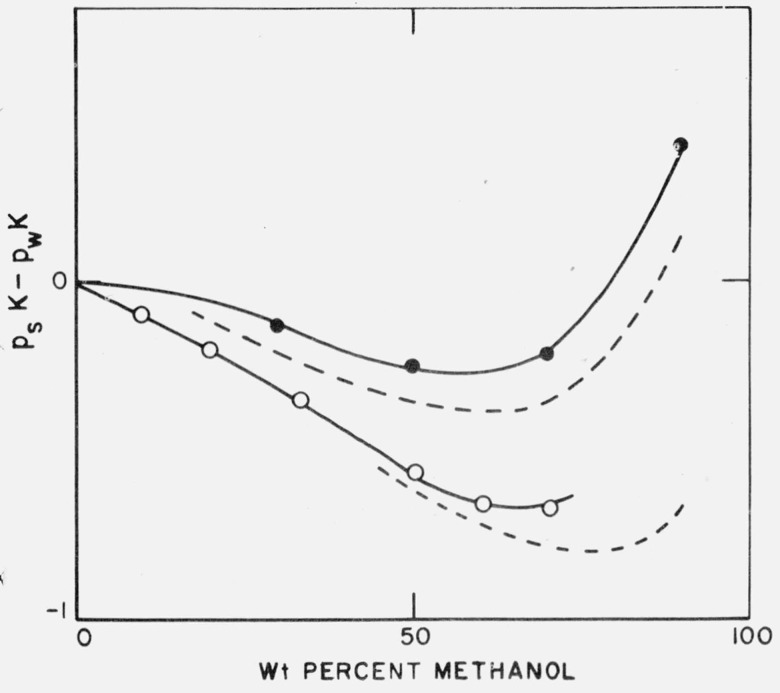
It is clear that there are difficulties in reconciling the transfer processes with a purely electrostatic theory. Nevertheless, if the experimental finding that the transfer process for tris hydrochloride is about equal in magnitude to that for lithium chloride is accepted, the diminution in the value of pK of the tris cation on addition of methanol (except for those solutions very high in methanol content) is seen to be due to the much higher transfer energy of tris hydrochloride (or lithium chloride) over that of hydrochloric acid. Assuming that the transfer energy of tris hydrochloride is identical with that of lithium chloride and using values of the latter taken from the work of Åkerlöf [13], p_sK values of the protonated form of tris can be calculated. Figure 4 compares such calculated values with the observed.

Figure 4. Comparison of experimental and calculated values of (p_sK − p_wK) in water-methanol mixtures.

____________________________, experimental.

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _, calculated.

●, Protonated tris(hydroxvmethyl)aminomethane.

O, Ammonium ion.

A similar calculation can be made for the dissociation constant of the ammonium ion; this has been measured in water-methanol mixtures [10, 15], and the energy of transfer of uncharged ammonia can be calculated from the known ammonia vapor pressure over the solutions [10, 16]. Again assuming that the energy of transfer of ammonium chloride is equal to that of lithium chloride, the comparison shown in figure 4 is obtained. It is evident that this approximation gives a good account of the experimental findings.

Finally, a comment on the high value of the energy of transfer of the neutral tris molecule from water to water-methanol is in order. The tris molecule has three hydroxymethyl groups, the hydroxyl radicals being terminal. The molecule, therefore, has hydrophilic character. From the known vapor pressures of ammonia over water and 50 percent methanol [10, 16], it is possible to show that the medium effect for ammonia is log _mγ = 0.131 or Δ_mG° = 0.75 kJ mol⁻¹. The transfer energy of tris is thus nearly three times as large as that for ammonia in 50 percent methanol.

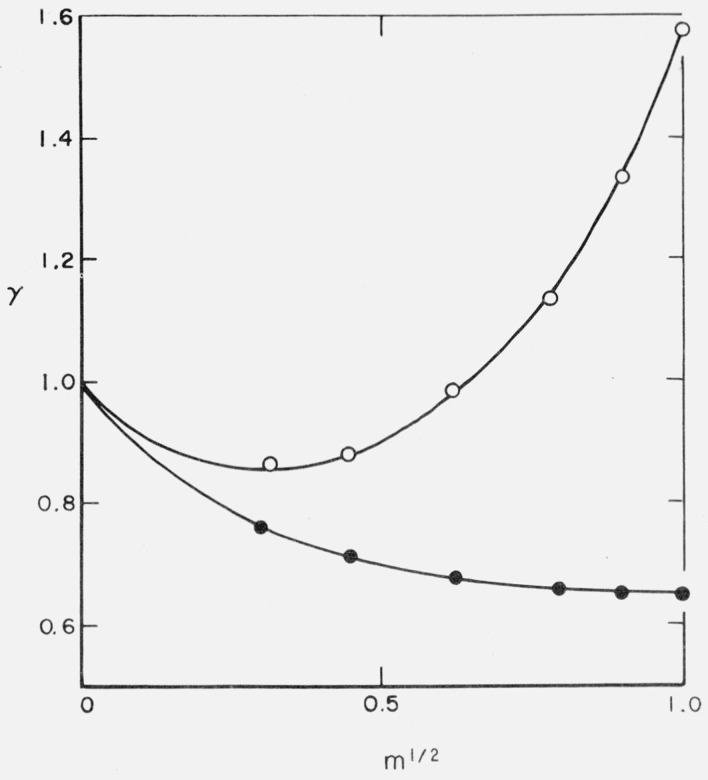
Figure 5 is a plot of the activity coefficients of tetrapropylammonium fluoride [17] and tetra(2-hydroxyethyl) ammonium fluoride [18] in aqueous solution against the square root of the molality. The contrast is remarkable. The tetraalkylammonium halides have many properties which are difficult to explain, but it has been suggested [18], very reasonably, that the tetra(hydroxyethyl)ammonium ion, (HOCH₂ · CH₂)₄N⁺, because of its four hydroxyl groups, can readily enter into the cluster structure of water. On the contrary, the tetrapropylammonium ion, (CH₃CH₂CH₂)₄N⁺, with its four terminal methyl groups, is hydrophobic and so less suited for participation in the water structure. Thus the (HOCH_2-CH₂)₄N⁺ ion is in a state of lower free energy than the (CH₃CH₂CH₂)₄N⁺ at the same concentration. In the same way, the tris molecule, (HOCH₂)₃C · NH₂, because of its three hydroxyl groups, can easily participate in the water structure, and is, in aqueous solution, in a state of comparatively low free energy.

Figure 5. Activity coefficients in aqueous solution as a function of the square root of the molality.

O, Tetrapropylammonium fluoride.

●, Tetra(hydroxyethyl)ammonium fluoride.

As methanol is added to the solvent, the amount of water structure is diminished, simply because there is less water to form structure. Consequently, in water-methanol solvents the tris molecule finds less solvent structure in which to accommodate itself and is in a state of higher free energy. This is equally true of the tris cation. It is thus evident, at least qualitatively, why both tris and its hydrochloride have high energies of transfer into water-methanol solvents.

5. Appendix

The proof of eq (10) necessitates a more complicated notation than has been used in the rest of this paper. The free energy of a (nonelectrolyte) solute in a mixed solvent can be measured relative to the hypothetical standard state in that solvent:

$$G{=}_{\text{s}}{G}^{°}+RT\ln {}_s^s\gamma \cdot m_{\text{s}},$$ (20)

where m_s is the molality of the solution, _sG° is the free energy of the solute in the standard state in this solvent mixture, and ${}_{\text{s}}{}^s\gamma$ is the activity coefficient of the solute referred to the standard state in this solvent.

The free energy could, however, be referred to the hypothetical standard state in water as solvent:

$$G{=}_{\text{w}}{G}^{°}+RT\ln {}_{\text{\hspace{0.17em}w}}^s\gamma \cdot m_{\text{s}},$$ (21)

where _wG° is the free energy of the solute in the standard state in water and ${}_{\text{w}}{}^s\gamma$ is the activity coefficient of the solute in the mixed solution (s) but referred to the standard state in water (w).

We now consider the limit when m_s → 0 and ${}_{\text{s}}{}^s\gamma \to 1$. Under these circumstances,

$${}_{\text{s}}{G}^{°}{-}_{\text{w}}{G}^{°}=RT\underset{m_{\text{s}}\to 0}{\text{L}im}\ln {}_{\text{\hspace{0.17em}w}}^s\gamma .$$ (22)

This is an expression for the free energy change in transferring the solute from water to the mixed solvent in the limit of extreme dilution when tshe concentration effects on the free energy change are absent. It is, therefore, the free energy change for the transfer from one hypothetical standard state to another, where also concentration effects are absent. Consequently,

$$\underset{m_{\text{s}}\to 0}{\text{L}im}\ln {}_{\text{\hspace{0.17em}w}}^s\gamma =\ln {}_{\text{\hspace{0.17em}m}}\gamma ,$$ (23)

from which follows the important relation:

$${}_{\text{w}}^s\gamma {=}_{\text{m}}\gamma {\cdot }_{\text{s}}^s\gamma \cdot$$ (24)

Equation (24) is sometimes abbreviated to:

$${}_{\text{w}}\gamma {=}_{\text{m}}\gamma {\cdot }_{\text{s}}\gamma ,$$ (25)

but when this is done care should be taken to note that here _wγ is an activity coefficient in the mixed solvent relative to the standard state in water, whereas in eq (1) _wγ designates an activity coefficient in aqueous solution relative to the standard state in water.

We next consider the equilibrium between a solid and its saturated solution. The condition for equilibrium between a solid and its saturated solution in a mixed solvent is:

$$G\left(\text{solid}\right){=}_{\text{w}}{G}^{°}+RT\ln {}_{\text{\hspace{0.17em}m}}\gamma {\cdot }_{\text{s}}^s\gamma \cdot m_{\text{s}}$$ (26)

and the condition for equilibrium between the solid and its saturated aqueous solution is:

$$G\left(\text{solid}\right)={}_{\text{w}}G{}^{°}+RT\ln {}_{\text{w}}{}^w\gamma \cdot m_{\text{w}}.$$ (27)

Hence,

$$\ln m_{\text{w}}/m_{\text{s}}=\ln {}_{\text{m}}\gamma +\ln {}_{\text{s}}{}^s\gamma /{}_{\text{w}}{}^w\gamma ,$$ (28)

which is sometimes abbreviated to:

$$\ln m_{\text{w}}/m_{\text{s}}=\ln {}_{\text{m}}\gamma +\ln {}_{\text{s}}\gamma /{}_{\text{w}}\gamma ,$$ (29)

which is eq (11). It should be noted that _wγ is now used, as in the body of the text, to denote an activity coefficient in aqueous solution relative to the standard state in water.