Subgroup-specific dose finding in phase I clinical trials based on time to toxicity allowing adaptive subgroup combination

Abstract

A Bayesian design is presented that does precision dose-finding based on time to toxicity in a phase I clinical trial with two or more patient subgroups. The design, called Sub-TITE, makes sequentially adaptive subgroup-specific decisions while possibly combining subgroups that have similar estimated dose-toxicity curves. Decisions are based on posterior quantities computed under a logistic regression model for the probability of toxicity within a fixed follow up period, as a function of dose and subgroup. Similarly to the time-to-event continual reassessment method (TITE-CRM, Cheung and Chappell), the Sub-TITE design downweights each patient’s likelihood contribution using a function of follow up time. Spike-and-slab priors are assumed for subgroup parameters, with latent subgroup combination variables included in the logistic model to allow different subgroups to be combined for dose finding if they are homogeneous. This framework can be used in trials where clinicians have identified patient subgroups but are not certain whether they will have different dose-toxicity curves. A simulation study shows that, when the dose-toxicity curves differ between all subgroups, Sub-TITE has superior performance compared to applying the TITE-CRM while ignoring subgroups, and has slightly better performance than applying the TITE-CRM separately within subgroups or using the two-group maximum likelihood approach of Salter et al. that borrows strength among the two groups. When two or more subgroups are truly homogeneous but differ from other subgroups, the Sub-TITE design is substantially superior to either ignoring subgroups, running separate trials within all subgroups, or the maximum likelihood approach of Salter et al. Practical guidelines and computer software are provided to facilitate application.

1 |. INTRODUCTION

Most phase I clinical trial designs use adaptive rules to choose doses for successive patient cohorts based on a binary indicator of toxicity ^1–5. In practice, toxicity is evaluated for each patient over a follow up period of specified length, T. If T is large relative to the trial’s accrual rate, then a severe logistical problem may arise when attempting to apply adaptive rules that use the (dose, toxicity) data of previous patients to choose doses for new patients. This sometimes is called a “late onset toxicity” setting. For example, suppose T = 12 weeks, the accrual rate is one patient per week, and the cohort size is three. Since a patient’s outcome can be scored definitively as “No toxicity” only if the patient is followed for 12 weeks, roughly nine to 12 patients may be accrued before the first cohort’s toxicity outcomes are fully evaluated. The question arises of how to treat each of patients #4 through #12 when they are enrolled. If some previously treated patients’ outcomes have not been fully evaluated when a new patient is enrolled, possible approaches include making each cohort wait until all previous patients’ toxicity outcomes have been evaluated before choosing their dose, not waiting and treating the new patient at the current recommended dose, not waiting and treating the new patient one dose level below the current recommended dose, or treating newly accrued patients off protocol. A discussion of problems with these approaches is given by Jin et al. ⁶, in the phase I-II dose-finding setting. Thall et al. ⁷ proposed a very simple approach, the so-called “look ahead” method, wherein if the outcomes of patients treated but not yet evaluated will not alter the adaptive rule’s decision, then that decision is made immediately. In practice, however, the look-ahead rule is of little use early in the trial. Bekele et al. ⁸ proposed a Bayesian method based on predictive probabilities of toxicity, but this approach is impractical because it may require repeatedly suspending accrual.

Cheung and Chappell ⁹ provided a practical solution to the late onset toxicity problem in phase I trials by proposing the time-to-event continual reassessment method (TITE-CRM). This method generalizes the CRM introduced by O’Quigley, Pepe and Fisher ¹⁰ by accounting for patients who have been treated recently but whose outcomes have not been fully evaluated as either time of toxicity, or last follow up time without toxicity. Since its introduction, the TITE-CRM has been studied and extended in several ways, including evaluation of model sensitivity ¹¹, refinement to accommodate both early and late onset toxicities ¹², use of the EM algorithm to predict future toxicities ¹³, called the EM-CRM, and a computer simulation study ¹⁴.

The current paper was motivated by the desire to account for patient heterogeneity in trials with late onset toxicity. If patients are classified into putatively heterogeneous subgroups and the dose-toxicity relationship may differ between subgroups, the adaptive dose finding problem becomes more complex, since the optimal dose may differ between subgroups. If so, then simply ignoring heterogeneity and applying the TITE-CRM to select one “optimal” dose risks choose a suboptimal dose in one or more subgroups. If, instead, the TITE-CRM is used to conduct separate trials within the subgroups, this may be inefficient due to small subgroup sample sizes, particularly if two or more subgroups are truly homogeneous in that they have the same dose-toxicity curves. Our proposed method is similar to that of Salter et al. ^20,21, who generalized the TITE-CRM by proposing a maximum likelihood-based method assuming a two parameter model, with the goal to choose subgroup-specific doses in the case of two subgroups.

For short term binary toxicity outcomes, methods that account for settings where the probability of toxicity increases with risk subgroup have been proposed by Mehta et al.¹⁵, O’Quigley and Paoletti ¹⁶, Yuan and Chappell ¹⁷, and Ivanova and Wang ¹⁸. O’Quigley and Paeletti ¹⁶ included an additional subgroup-specific intercept parameter in the usual TITE-CRM skeleton parameterization to perform dose-finding in a priori ordered subgroups. Morita, et al. ¹⁹ provided a simulation study of hierarchical and non-hierarchical model based subgroup-specific versions of the CRM.

In the late onset toxicity setting, we propose a method that deals with the problem that prespecified subgroups may have either different or similar dose-toxicity curves. To do this, we extend the TITE-CRM to do subgroup-specific dose selection while also possibly combining subgroups found to have the same dose-toxicity curve. The method, which we call the Sub-TITE design, is based on a working likelihood and down-weighting scheme similar to that of Cheung and Chappell ⁹. We assume a Bayesian logistic regression model for the probability of toxicity by follow up time T, with a linear component including effects of dose, subgroup, and dose-subgroup interaction. We assume spike-and-slab priors on subgroup-specific parameters to allow adaptive dose selection to be done within all subgroups, or for sets of subgroups combined if they are found to be homogeneous. This model provides a formal basis for implementing the Sub-TITE method’s main practical generalization, which is to choose optimal subgroup-specific doses while permitting some subgroups to be pooled if the data suggest it is appropriate. This provides a method for conducting a single trial that borrows strength between subgroups, rather than conducting separate trials within the subgroups. We also include safety rules that suspend accrual within a subgroup for which the lowest dose is found to be too toxic, but continue accrual in the other subgroups where the lowest dose is considered safe. To facilitate application, we provide algorithms for using elicited toxicity probabilities for each dose within each subgroup to calibrate prior means and variances, and we use simulation to determine subgroup specific cutoffs for stopping accrual in a subgroup. Computer code to simulate and conduct a trial using Sub-TITE is available on CRAN in the package SubTite.

While both our proposed method and that of Salter et al. ^20,21 generalize the TITE-CRM to choose subgroup-specific doses, there are several important differences. Our proposed method (1) adaptively combines subgroups that have empirically similar dose-toxicity curves, thus choosing the same dose for the combined subgroups, (2) accommodates more than two subgroups, (3) includes rules to stop accrual and choose no dose in subgroups for which the lowest dose is found to be excessively toxic, and (4) is based on Bayesian model and computational algorithms.

This research was motivated by a phase I trial to select subgroup-specific optimal doses of radiation therapy (RT) for advanced non small cell lung cancer. The subgroups in this trial corresponded to two different radiation modalities: proton beam or non-proton beam (conventional). The modality was chosen for each patient by the attending physician based on the patient’s insurance coverage and the location, type, and extent of disease. The clinician hypothesized that patients receiving proton beam RT might have lower toxicity probabilities, but was not certain that this was true and did not want to impose this as a restriction in the trial. Ideally, it would have been desirable to allow the design to either choose different optimal doses within the modality subgroups, or combine the modalities and choose one optimal dose if they were found to have the same dose-toxicity curve. No methodology for doing this existed at the time of the trial, however. The patient’s nodal mediastinal disease, located in the esophagus, spinal cord, or large blood vessels surrounding the heart, was to be treated with a RT dose chosen from the set of five possible levels {10, 20, 30, 50, 70 } Gy, where Gy denotes a Gray unit, which is 1 Joule of radiation absorbed per kilogram of the tumor. Toxicity was defined as any of several common adverse effects due to the RT, occurring over a T = 6 month follow up period, with target toxicity probability .30. We developed the Sub-TITE methodology with this trial in mind.

We compared the operating characteristics (OCs) of Sub-TITE to either using the TITE-CRM while ignoring subgroups, or the approach of using a TITE-CRM design to conduct a separate trial within each subgroup, which we call Sep-TITE. Our simulations showed that, when the true dose-toxicity curves differ substantively between subgroups, the Sub-TITE design has superior OCs compared to the TITE design that ignores subgroups and slightly better OCs than the Sep-TITE approach. When two or more subgroups are truly homogeneous, the Sub-TITE design is substantially superior to running separate trials within subgroups. In the case of two subgroups, we also compared our method to the maximum likelihood based approach of Salter et al.^20,21, which we refer to as SOCA-TITE. We also performed a robustness study to examine the performance of Sub-TITE and its comparators under different time-to-toxicity distributions, and to evaluate each design’s sensitivity to the number of subgroups, maximum sample size, and proportions of patients within subgroups. Our simulations, presented in Section 4, show that Sub-TITE provides more reliable within-subgroup decisions than either ignoring heterogeneity or conducting separate trials within subgroups.

The remainder of the paper is organized as follows. The probability model and prior distributions for time to toxicity as a function of dose and subgroup are given in Section 2. Section 3 describes how to elicit expected toxicity probabilities from clinicians for each subgroup and dose considered in the trial. It also describes how to use these expected toxicity probabilities to obtain the hyperparameters used for the design. Section 4 describes how the trial is designed and conducted using Sub-TITE, including step-by-step guidelines. The simulation study is presented in Section 5, including comparison of Sub-TITE to the three alternative approaches. We close with a brief discussion in Section 6.

2 |. DOSE-TOXICITY MODEL

Let d₁ < d₂ < ... < d_K denote the raw doses to be studied in the trial, and define the standardized doses $x_j=\left(d_j-\overline{\mathit{d}}\right)/s(\mathit{d}),$ for j = 1, …, K, where $\overline{\mathit{d}}$ is the mean and s(d) is the standard deviation of the raw doses. We denote $\mathcal{X}=\left\{x_1,\cdots ,x_K\right\}$ and an arbitrary standardized dose by unsubscripted x. We index subgroups by g = 0, ..., G − 1, with g = 0 an arbitrarily chosen baseline subgroup, and consider settings where K ≥ 3 and G = 2, 3,…,6. Let T denote a fixed follow up time for evaluating toxicity, specified by the clinical investigators. At trial time t, let a_i ≤ t denote the accrual time of the i^th patient, with follow up time $u_i(t)=\min \left\{t-a_i,T\right\},$ and define Y_i(u_i(t)) to be the binary indicator that patient i has experienced toxicity by t. Thus, Y_i(T) = Y_i is the indicator that the i^th patient has toxicity within the specified follow up period.

Let W_i ∈ {0, 1, …, G − 1} denote the i^th patient’s subgroup. We define a latent patient subgroup variable Z_i ∈ {0, …, G − 1}, and use Z_i in the likelihood in place of W_i. The Markov chain Monte Carlo (MCMC) posterior sampling scheme uses (Z₁, ..., Z_n) as a device to allow different subgroups to be combined for dose finding. We define Z_i = 0 if W_i = 0, and for G ≥ 2,

$$Z_i=\sum _{g=1}^{G-1}I\left[W_i=g\right]{\zeta }_g.$$ (1)

This definition implies that the baseline group is always included in the likelihood, although other subgroups may be combined with it. The elements of the vector $\mathit{\zeta }=\left({\zeta }_1,\dots ,{\zeta }_{G-1}\right)$ are random latent variables taking on values in {0, 1, …, G − 1}, with each ζ_g endowed with a prior, given below. In the MCMC algorithm, ζ is used to determine what other subgroups, if any, with which each subgroup should be combined for dose finding via the likelihood. Since Z_i is a function of W_i and ζ, as ζ changes throughout the MCMC, so does Z_i via (1). If ζ_g = g then the logistic model used for dose finding includes subgroup specific parameters for g, but if ζ_g = k for some k ≠ g, then for any W_i = g, in the likelihood Z_i = k.

Since phase I sample sizes are limited, we require a model that is reasonably parsimonious and tractable. It also must include appropriate regression structure to account for the effects of dose, subgroup, and dose-subgroup interactions as a basis for adaptive subgroup-specific decision making. Temporarily suppressing the patient index i for simplicity, let $\eta (x,Z,\mathit{\theta })={\text{logit}}^{-1}\{\pi (x,Z,\mathit{\theta })\}$ denote the linear term in a logistic regression model with parameter vector θ, where $\pi (x,Z,\theta )=Pr(Y=1|x,Z,\theta ).$ We assume that

$$\eta (x,Z,\mathit{\theta })=\alpha +\sum _{g=1}^{G-1}{\alpha }_{g}I(Z=g)+\exp \left[\beta +\sum _{g=1}^{G-1}{\beta }_{g}I(Z=g)\right]x,$$ (2)

so α and β are the intercept and dose effect parameters for subgroup g = 0, and α_g and β_g are the subgroup g–versus–0 intercept and dose effects. Thus, the 2G dimensional model parameter vector is $\mathit{\theta }=\left(\alpha ,{\alpha }_1,\dots ,{\alpha }_{G-1},\beta ,{\beta }_1,\dots ,{\beta }_{G-1}\right).$ This model is invariant to the choice of the baseline subgroup 0 and the operating characteristics do not change for the trial for different baseline subgroups. We parameterize the linear component in this way so that the model borrows strength across both subgroups and dose levels. We exponentiate β and β + β_g to ensure that the probability of toxicity increases with dose for each subgroup.

For priors, we assume that α ~ N($\tilde{\alpha }$, σ_α) and β ~ N($\tilde{\beta }$, σ_β). We introduce a binary random variable ρ_g to allow for the possibility that the subgroups are truly homogeneous and place a spike and slab prior on (α_g, β_g), of the form

$$\begin{gathered} {\alpha }_g~{\rho }_{g}N\left({\tilde{\alpha }}_g,{\sigma }_{\alpha }\right)+\left(1-{\rho }_g\right){\delta }_0\left({\alpha }_g\right) \\ {\beta }_g~{\rho }_{g}N\left({\tilde{\beta }}_g,{\sigma }_{\beta }\right)+\left(1-{\rho }_g\right){\delta }_0\left({\beta }_g\right) \\ P\left[{\rho }_g=1\right]=.9, \end{gathered}$$ (3)

where δ₀(·) denotes the probability function with point mass at {0}. We set the prior probability of heterogeneous subgroups to .9 to favor subgroup specific dose finding, while allowing the possibility that some subgroups are homogeneous.

We define a prior on each latent subgroup parameter ζ_g as follows. Denote $S=\left\{0\right\}\cup \left\{{\zeta }_g:{\rho }_g=1\right\},$ with |S| its cardinality.

1. If ρ_g = 1, then Pr(ζ_g = g) = 1.

2. If ρ_g = 0, then Pr(ζ_g = k) = 1/|S| for each k ∈ S.

That is, if ρ_g = 0, then the probability that subgroup g is truly a member of any other current latent subgroup is uniform on S. This construction allows two or more subgroups to be combined adaptively during the trial. If, for example, ${\zeta }_1={\zeta }_2={\zeta }_3=1$ then subgroups 1, 2, and 3 are combined. Thus, the parameter vector used in the likelihood is $\mathit{\theta }=\left(\alpha ,\beta ,{\left\{\left({\alpha }_g,{\beta }_g\right)\right\}}_{g=1}^{G-1}\right),$ while ζ determines the values of Z given the observed subgroups W.

To illustrate how the parameters θ, ζ, ρ work together in the likelihood, for example, suppose that G = 3 and ${\rho }_1={\rho }_2=0.$ By definition of the conditional prior, S = {0} hence both ${\zeta }_1={\zeta }_2=0$ and the subgroup parameters are ${\alpha }_1={\alpha }_2={\beta }_1={\beta }_2=0.$ If ρ₁ = 0 and ρ₂ = 1, then ζ₂ = 2, α₂ ≠ 0 and β₂ ≠ 0, and α₁ = β₁ = 0. In this case, S = {0, 2}. If ζ₁ = 0, then patients in subgroup W_i = 1 will have latent subgroup Z_i = 0, while if ζ₂ = 2, patients in subgroup W_i = 1 will have latent subgroup Z_i = 2.

A key point is that the subgroup combination algorithm is applied at every iteration of the MCMC. Thus, for example, two different subgroups g = 2 and g = 3 be may combined but later separated in the course of the MCMC. Consequently, the resulting posterior sample may have subgroups g = 2 and g = 3 combined as {2, 3} for, say, 90% of the posterior sample values and distinct for the remaning 10%. This reflects the stochastic nature of (ρ_g, ζ_g), for g = 0, ..., G − 1. Hyperparameter calibration including prior elicitation from clinicians is discussed in section 3 in detail.

Let n_t denote the number of patients enrolled and treated up to study time t, and index patients by i = 1, ..., n_t. To choose each patient’s dose adaptively, at study time t when a new patient is enrolled, a personalized dose is chosen based on that patient’s subgroup and the posterior distribution for θ, ζ given the current data

$${\mathcal{D}}_{n_t}=\left\{Y_i\left(u_i(t)\right),W_i,u_i(t),i=1,\cdots ,n_t\right\}$$

for all previously enrolled patients. We follow the approach of Cheung and Chappell⁹ by including the weight function ${\omega }_i(t)=u_i(t)/T$ in the likelihood for patients who have been partially followed but not experienced toxicity, resulting in the approximate (working) likelihood

$$\mathcal{L}\left(\mathit{\theta },\mathit{\zeta },{\mathcal{D}}_{n_t}\right)=\prod _{i=1}^{n_t}{\left\{\pi \left(x_{[i]},Z_i,\mathit{\theta }\right)\right\}}^{Y_i\left(u_i(t)\right)}{\left\{1-{\omega }_i(t)\pi \left(x_{[i]},Z_i,\mathit{\theta }\right)\right\}}^{1-Y_i\left(u_i(t)\right)}$$ (4)

where x_[i] denotes the standardized dose given to patient i. The weights {ω_i(t)} serve the purpose of downweighting censored outcomes for patients who have not been followed for long past their accrual in the study. Without this weighting scheme, dose escalation would be far too aggressive. We did not consider other forms of weights because it has been shown that using different weighting schemes does not improve the TITE-CRM design’s performance²². Additionally, we did not use subgroup specific weight functions because preliminary simulations showed that this causes some subgroups to have too much influence on dose finding decisions in the other subgroups, and it also disrupts the subgroup combination process, producing a design with poor properties.

We also considered using a full likelihood for the time to toxicity distribution as a function of subgroup and dose. However this decreased accuracy in the estimation of π(x, Z, θ), and the design performed poorly in settings with increasing hazards. For example, assuming either a lognormal or Weibull time-to-toxicity distribution, if the true distribution is Weibull with increasing hazard, so that toxicities are likely to occur late in the follow up interval [0, T], the design performs poorly compared to the downweighting approach. Since the posterior distribution for θ under the logistic model (2) does not have a closed form, we perform Metropolis Hastings steps for each θ_m within the MCMC sampling scheme including moves on ρ, ζ and on ζ|ρ. The posterior distribution for α, β, α_g, β_g are functions of the latent subgroup vector ζ and posterior toxicity probability estimates are computed using both the posterior parameter vector θ and the posterior latent subgroup vector ζ. Details are described in Web Appendix A.

3 |. ESTABLISHING PRIORS

In this section, we explain how one may obtain numerical values of the hyperparameters $\tilde{\mathit{\theta }}$ that characterize the prior $p(\mathit{\theta }|\tilde{\mathit{\theta }})$ of the logistic regression model parameter vector θ. We write $\tilde{\mathit{\theta }}=\left({\tilde{\mathit{\theta }}}_1,{\tilde{\mathit{\theta }}}_2\right)$ where ${\tilde{\mathit{\theta }}}_1=\left(\tilde{\alpha },\tilde{\beta },{\tilde{\alpha }}_1,\cdots ,{\tilde{\alpha }}_{G-1},{\tilde{\beta }}_1,\cdots ,{\tilde{\beta }}_{G-1}\right)$ is the subvector of 2G hypermeans and ${\tilde{\mathit{\theta }}}_2=\left({\sigma }_{\alpha }^2,{\sigma }_{\beta }^2\right)$ is the subvector of two hypervariances. The first step is to elicit the prior mean probability of toxicity, π^e(x, W), for each combination of dose x and subgroup W. This may be done by providing the clinician with a table with dose and subgroup cross-classified that has empty cells, and asking them to fill in their expected toxicity probability for each cell. The physician should be reminded that π(x, W) increases with x. When collaborating with two or more physicians, a consensus may be reached in various ways, with the simplest approach being to ask the physicians to work together to provide a table of values that they agree upon. In practice, we have found that this works quite well. Once the JG values {π^e(x, W)} are elicited, a general approach for establishing $\tilde{\mathit{\theta }}$ is to proceed in two steps. First, since JG > 2G for J > 2 dose levels, one may treat the π^e(x, W)’s like outcomes and ${\tilde{\mathit{\theta }}}_1$ like the parameter vector in a conventional nonlinear regression model, and use nonlinear least squares (NLS) to solve for ${\tilde{\mathit{\theta }}}_1$. Given these values, the hypervariances then may be calibrated to obtain a suitably non-informative prior $p(\mathit{\theta }|\tilde{\mathit{\theta }}).$

For our application, prior mean toxicity probabilities for each dose and subgroup were elicited from a single radiation oncologist at M.D. Anderson. Table 1 displays elicited prior expected π^e(x, W) for each dose and subgroup. For the sub-TITE model, we assume that the hypermeans ${\tilde{\mathit{\theta }}}_1$ satisfy the equation

$$logit\left\{{\pi }^e(x,W)\right\}=\tilde{\alpha }+\sum _{g=1}^{G-1}{\tilde{\alpha }}_{g}I(W=g)+\exp \left[\tilde{\beta }+\sum _{g=1}^{G-1}{\tilde{\beta }}_{g}I(W=g)\right]x$$

for all (x, W) pairs. We use the Newton-Raphson method to solve for the NLS estimates, although other iterative procedures, such as the Nelder-Mead algorithm, could be used. This computation is done using the function GetPriorMeans(). A key point here is that these hypermeans are based on the patient subgroups and not latent patient subgroups.

TABLE 1.

Elicited Prior Mean Dose-Toxicity Probabilities for each Subgroup.

Subgroup	Elicited Toxicity Probabilities
0	(.10, .25, .35, .50, .60)
1	(.04, .15, .20, .30, .40)
2	(.04, .10, .15, .25, .35)
3	(.01, .05, .10, .22, .32)

We then calibrate the hypervariances ${\tilde{\mathit{\theta }}}_2=\left({\sigma }_{\alpha }^2,{\sigma }_{\beta }^2\right)$ iteratively by first fixing them at some initial values, subject to the constraint ${\sigma }_{\alpha }^2>{\sigma }_{\beta }^2,$ such as ${\sigma }_{\alpha }^2=2\text{and}{\sigma }_{\beta }^2=1.$ The current prior $p(\mathit{\theta }|\tilde{\mathit{\theta }})$ then is used to generate a sample of $(\alpha ,\beta ,{\{{\alpha }_g,{\beta }_g\}}_{g=1}^{G-1})$ values, and we compute the resulting prior sample of π(x, W, θ) values for each (x, W). We then approximate the prior effective sample size (ESS) of the distribution of π(x, W, θ) by matching the sample mean ${\mu }_{x,W}$ and sample variance ${\sigma }_{x,W}^2$ of the π(x, W, θ) values to the corresponding values of a beta(a, b) distribution, which has ESS = a + b. This gives the approximate ESS of the prior on π(x, W, θ) as

$$\frac{{\mu }_{x,W}\left(1-{\mu }_{x,W}\right)}{{\sigma }_{x,W}^2}-1.$$

We then obtain an overall approximate ESS for $p(\mathit{\theta }|\tilde{\mathit{\theta }}),$ corresponding to the assumed fixed ${\sigma }_{\alpha }^2\text{and}{\sigma }_{\beta }^2,$ as the average over (x, Z) of these JG prior ESS values,

$$\frac{1}{G}\frac{1}{J}\sum _{x\in \mathcal{X}}\sum _{W=0}^{G-1}\left(a_{x,W}+b_{x,W}\right)=\frac{1}{G}\frac{1}{J}\sum _{x\in \mathcal{X}}\sum _{W=0}^{G-1}\left\{\frac{{\mu }_{x,W}\left(1-{\mu }_{x,W}\right)}{{\sigma }_{x,W}^2}-1\right\}.$$

We iterate this process using different numerical values of $({\sigma }_{\alpha }^2,{\sigma }_{\beta }^2)$ until we obtain an average ESS of about 1. Generally it only takes a few minutes to calibrate the two hypervariances using the function GetPriorESS(), which does the above steps and returns a single value for the approximate prior effective sample size.

4 |. TRIAL DESIGN AND CONDUCT

4.1 |. Trial Design

Computer software that implements the proposed methodology is available in the package SubTite on CRAN at http://cran.r-project.org. To start the design process, the physician must define toxicity and specify T, the doses to be studied, the starting dose, and a fixed target toxicity probability π*, or possibly different subgroup-specific targets ${\left\{{\pi }_g^{*}\right\}}_{g=0}^{G-1}.$ Additionally, prior means of π(x_j, g, θ) must be elicited from the physician for all GK pairs of (x_j, g) in order to determine prior hyperparameters, as described above. Our proposed design generalizes the TITE-CRM by determining, for each subgroup g = 0,1,..., G − 1 the dose $x_g^{opt}\text{such that}\pi \left(x_g^{opt},g,\mathit{\theta }\right)$ has posterior mean closest to the target ${\pi }_g^{*}.$ Formally, given the data ${\mathcal{D}}_{n_t},$ if the newly accrued patient at t has W = g, we choose the optimal dose so that

$$x_g^{opt}\left({\mathcal{D}}_{n_t}\right)=\underset{x\in \mathcal{X}}{\text{argmin}}\left|E\left\{\pi (x,g,\mathit{\theta })|{\mathcal{D}}_{n_t}\right\}-{\pi }_g^{*}\right|.$$ (5)

If desired, different starting doses may be used within the subgroups. Although in our simulations we consider the case where all ${\pi }_g^{*}={\pi }^{*},$ with the same starting dose x₁ in each subgroup, the package SubTite accommodates the more general design features given above. For each g, computation of the posterior optimality criterion (5), as well as the posterior safety stopping criterion, given below, reflect the possibility that some subgroups may be combined in some proportions of the MCMC sample.

To apply Sub-TITE to design and conduct a phase I trial, there must be sufficient evidence of subgroup heterogeneity to warrant the increased sample size in order to avoid the small loss in reliability in the truly homogeneous case. The prior parameter means are computed using the GetPriorMeans() function in the SubTite package, which applies non-linear least squares to the elicited toxicity probabilities. After the prior means are obtained, these are used in the function GetPriorESS() to calibrate ${\sigma }_{\alpha }\text{and}{\sigma }_{\beta }$ to obtain a desired approximate prior ESS.

Before conducting the trial, a simulation study should be done to calibrate design parameters to ensure desirable OCs. This requires an expected accrual rate and proportion of patients in each subgroup to be elicited from the clinician. Depending on the number of doses, K, several potential values of N_Max may be evaluated to assess the design’s sensitivity to sample size. N_Max should be large enough so that the trial would assign at least one cohort of patients in each subgroup and dose if they were completely randomized. This ensures that there will be enough exploration among the doses within each subgroup. During the trial, accrual is suspended in a subgroup if the lowest dose is found to be too toxic. Formally, if at least three patients have been treated at the lowest dose x₁ and been fully evaluated in subgroup g and

$$\text{Pr}\left\{\pi \left(x_1,g,\mathit{\theta }\right)>{\pi }^{*}|{\mathcal{D}}_{n_t}\right\}>p_{g,U},$$

then accrual is suspended in that subgroup. If all subgroups are suspended at any interim time, then the trial is terminated.

Calibrating N_Max and the cutoffs $p_{g,U},g=0,\cdots ,G-1,$ for suspending accrual within subgroups is done via simulation using the function SimTrial() in the SubTite package. This should be done under a reasonably wide range of different true dose-toxicity-subgroup scenarios and time-to-toxicity distributions. This function supports the gamma, Weibull, lognormal, exponential, and uniform distributions for time to toxicity. Calibration of the p_g,U’s should include simulation of the trial under a scenario where one subgroup is excessively toxic at x₁. The design should stop this subgroup early with high probability, but without stopping safe subgroups too frequently.

In summary, the following steps should be taken when designing a trial using Sub-TITE:

1. Working with the physician(s) planning the trial, establish (a) the K doses to be evaluated, (b) definition of toxicity (c) follow up time T, (d) anticipated accrual rate (d) definitions of the subgroups, (e) anticipated subgroup proportions, (f) the starting dose for each subgroup, and (g) the target toxicity probability π*, or subgroup-specific targets.

2. Elicit the GK prior subgroup-specific mean dose-toxicity probabilities from the physician(s), and input these to compute the hyper parameter means $\tilde{\alpha },\tilde{\beta },{\left\{{\tilde{\alpha }}_g,{\tilde{\beta }}_g\right\}}_{g=1}^{G-1}$ using the GetPriorMeans() function. Calibrate ${\sigma }_{\alpha }\text{and}{\sigma }_{\beta }$ with the function GetPriorESS() to obtain approximate prior effective sample size 1.

3. Calibrate N_Max and ${\left\{p_{g,U}\right\}}_{g=0}^{G-1},$ by simulation.

4.2 |. Trial Conduct

The steps for trial conduct are as follows. While these are given in terms of the initial G distinct subgroups, the posterior dose selection and stopping criteria reflect the subgroup combination process in the MCMC sample.

1. Treat the first patient in each subgroup enrolled into the trial at that subgroup’s starting dose.

2. In each subgroup g, for each successive patient enrolled after the first patient, choose $x_g^{opt}({\mathcal{D}}_{n_t}),$ subject to the additional constraints given in the steps below.

3. In each subgroup, an untried dose may not be skipped when escalating.

4. In each subgroup g, after at least three patients have been enrolled and fully evaluated at the lowest dose, if the lowest dose is unacceptably toxic in the sense that

   $$\text{Pr}\left\{\pi \left(x_1,g,\mathit{\theta }\right)>{\pi }^{*}|{\mathcal{D}}_{n_t}\right\}>p_{g,U}$$ (6)

   then accrual to subgroup g is temporarily suspended with no dose selected for patients accrued in that subgroup until (6) does not hold. In practice, it may be more appropriate to treat these patients off protocol rather than delaying therapy. We fully evaluate the first subgroup cohort at the lowest dose to avoid stopping due to chance if the lowest dose is not truly toxic.

   If at some point during the trial, (6) holds for all $g=0,\cdots ,G-1,$ then (6) is re-evaluated for each g based on the data in that subgroup only before subgroup the trial is stopped. This mitigates the possibility that x₁ is so toxic for one subgroup g that all subgroups are stopped, when in fact not all of the other subgroups $g^{\prime }\ne g$ are truly excessively toxic at x₁.

5. Unless the trial is terminated early, it ends after N_Max patients have been enrolled and evaluated. The final optimal dose for each subgroup g that has not been terminated is $x_g^{opt}\left({\mathcal{D}}_{N_{\text{Max}}}\right).$

In practice, the values p_g,U = .90 to .99 typically work well for the safety stopping rule (6). The Sub-TITE methodology does not impose the constraint that π(x, W, θ) is increasing in subgroup W, although this can be done by adding additional constraints.

5 |. SIMULATION STUDY

In this section, we describe a simulation study conducted to evaluate the Sub-TITE method, and to compare it to using the TITE-CRM while ignoring subgroups, the approach of running separate trials using the TITE-CRM within each subgroup (Sep-TITE), and the two group maximum likelihood method introduced by Salter et al ¹⁹ (SOCA-TITE). We designed the simulations to mimic the motivating RT trial, hence T = 6 months, π* = .30, the maximum sample size is N_Max = 60, we assume an accrual rate of 2 patients per month, the subgroups are equally likely, and all designs considered start at x₁. For the true time to toxicity distribution, we assumed a Weibull parameterized as $-\log \{\text{Pr}(\text{time to toxicity}>t)\}={(t/\lambda )}^{\varphi },$ with shape parameter $\varphi =4$ to ensure late onset toxicities, and scale parameter λ set in each scenario to give the assumed true toxicity probability π(x, Z) at the reference time T. Recall that the raw dose levels in consideration for the radiation therapy are {10, 20, 30, 50, 70 } Gy, where Gy denotes a Gray unit, which is 1 Joule of radiation absorbed per kilogram of the tumor. Elicited toxicity probabilities for each subgroup and dose obtained from the clinician are listed in Table 1.

The hypermeans for the Sub-TITE prior based on the clinician elicited toxicity probabilities were $\tilde{\alpha }=-.70,\tilde{\beta }=-.04,{\tilde{\alpha }}_1=-.81\text{and}{\tilde{\beta }}_1=.009,$ with variances ${\sigma }_{\alpha }^2=5\text{and}{\sigma }_{\beta }^2=1$ giving approximate prior ESS = 1. We used the baseline subgroup’s elicited dose-specific toxicity probabilities as the prior dose-toxicity skeleton in the TITE-CRM design and the subgroup specific elicited dose-specific toxicity probabilities for each subgroup’s dose-toxicity skeleton for the Sep-TITE design. The model assumed for the TITE-CRM design was ${\text{logit}}^{-1}\left(\pi \left(x_j,\beta \right)\right)=3+\exp (\beta )D_{1,j}$ and for the Sep-TITE trial designs was ${\text{logit}}^{-1}\left(\pi \left(x_j,g,\beta \right)\right)=3+\exp (\beta )D_{g,j},\text{where}{D}_{g,j}={\text{logit}}^{-1}\left(s_{g,j}\right)-3,$ with $s_{g,j}$ is the elicited prior reference probability for subgroup g and dose level j. We assumed that $\beta ~N\left(0,{\tilde{\sigma }}^2\right).$ To ensure comparability to the Sub-TITE design in terms of prior information, we calibrated this hypervariance to obtain approximate prior ESS = 1, which resulted in ${\tilde{\sigma }}^2=\mathrm{.86.}$

We used the titecrm function from the dfcrm package ²³ in R to perform the comparative simulations for the TITE and Sep-TITE designs using the logit link function with the default parameter value for the intercept of 3. Since the Sub-TITE design has within-subgroup early stopping rules, again for comparability, when implementing the TITE-CRM and Sep-TITE designs we used the lower credible interval (ci) bound on the lowest dose toxicity probability to stop a subgroup or trial if this value was greater than the target toxicity probability. For the Sep-TITE design, these ci’s were constructed such that if the .90 ci lower bound on the probability of toxicity at x₁ was greater than π*, that subgroup was stopped. If all subgroups in the Sep-TITE trial were stopped after fully evaluating a cohort at the lowest dose in each subgroup, the trial was ended. For the TITE design, only the one group considered needs to be stopped for the trial to end. We calibrated the early stopping cut-offs for Sub-TITE {p_g,U} under scenario 5 so that subgroup 0 has a stopping probability and each subgroup $g\ne 0$ has a optimal dose selection probability near the values seen for the Sep-TITE trial. This upper cutoff vector was determined to be (.95, .99) for G = 2 and (.95, .99, .99, .99) for G = 4. Since the available SAS software for the SOCA-TITE design does not allow one to simulate trials as done in our simulation study, we implemented this design in R using C++ with an efficient grid search to find maximum likelihood estimates, assuming the logistic link function and linear term with intercept parameter equal to 3, to ensure comparability to Sep-TITE.

We studied five different simulation scenarios. The first four were defined by specifying four different dose-toxicity probability curves, one corresponding to each subgroup. Only two dose-toxicity curves are displayed for scenario 5, which is differs from the other scenarios in that we do not examine this scenario in the vase of G = 4 subgroups. The dose-toxicity probability curves for scenarios 1,2,3 and 5 are given graphically in Figure 1, and the numerical toxicity probabilities are given in Web Table 1.

FIGURE 1.

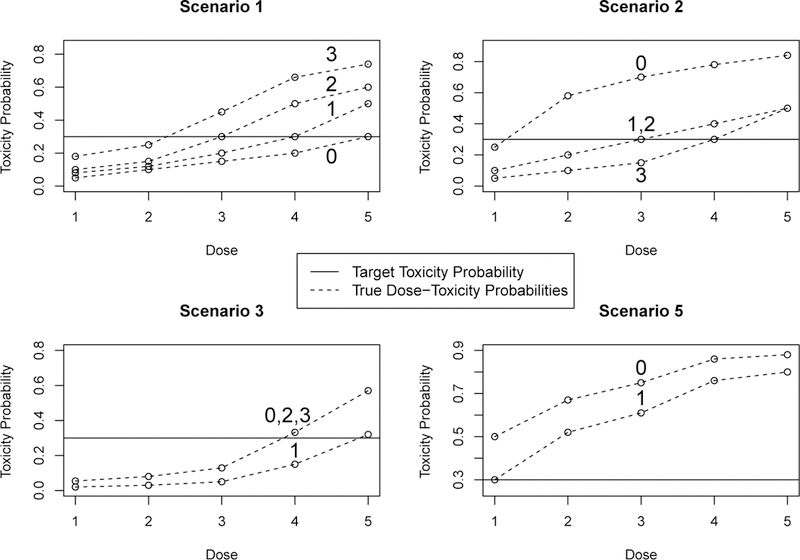
Simulation Study: Assumed dose-toxicity probability curves for the four subgroup design. The first two subgroups are used in trials with two subgroups. The horizontal solid line is the targeted probability π*. Solid dots represent that two or more subgroups share that dose-toxicity curve. Scenario 4 is not shown, since all subgroups in this scenario have the same toxicity probability vector, (.05, .10, .15, .30, .50). Only two subgroups are shown for scenario 5 since we do not investigate this scenario’s operating characteristics with four subgroups.

The five scenarios represent a variety of possible subgroup-specific dose-toxicity probability functions that may be seen in practice. In scenario 1, the optimal dose vector for the two subgroup case is (2,3). The average probability of toxicity across subgroups for dose 2 is .20 while this average for dose 3 is .375. We expect the TITE-CRM to do well in this case, but we note that the TITE-CRM can never pick the optimal dose for both subgroups, since the true optimal within-subgroup doses are different. Scenario 5 represents a case where the lowest dose is unacceptably toxic for subgroup 0, with true toxicity probability .50, but in subgroup 1 the lowest dose is optimal. In this scenario, the SOCA-TITE design will continue to treat patients at the excessively toxic lowest dose for subgroup 0 since this method does not have a subgroup-specific stopping rule.

When looking at the four subgroup scenarios in Figure 1, which have solid dots when two or more subgroups share a toxicity, we see that scenario 1 represents a case where all four patient subgroups have different dose-toxicity probabilities, with optimal doses (2, 3, 4, 5). In scenario 2, subgroups 1 and 2 are homogeneous, while subgroups 0 and 3 are different from the other subgroups, with optimal doses (1, 3, 3, 4). In scenario 3, subgroups 0, 2 and 3 are truly homogeneous and subgroup 1 has a different dose-toxicity probability vector, with optimal doses (4, 5, 4, 4). Again, scenario 4 is not depicted because all four subgroups have the same dose-toxicity curves. In an additional set of simulations, we evaluated the sensitivity of the Sub-TITE design to the proportions of patients in the subgroups, different families of time to toxicity distributions, and maximum sample size of the trial. All simulations were based on 5,000 replications.

5.1 |. Simulation Results for Trials With Two Subgroups

We first compare the Sub-TITE design to the TITE-CRM design that ignores subgroups, the Sep-TITE design, and the SOCA-TITE design, in the case of two subgroups (G=2). For each subgroup g = 0,1, we evaluated the average absolute difference Δ_g between the toxicity probabilities of the selected and optimal doses, the proportion of times P sel_g that each method selected the optimal dose, the number of toxicities N tox_g, and the stopping probability P stop_g. Let π^true(x, g, θ) denote the true toxicity probability by time T for subgroup W = g and dose x and $x_g^{\text{opt}}$ denotes the truly optimal dose for subgroup W = g. If we run B simulations and for the bth iteration $x_g^b$ is the dose chosen for subgroup g then we calculate Δ_g as

$${\mathrm{\Delta }}_g=\frac{1}{B}\sum _{b=1}^B\left|{\pi }^{\text{true}}\left(x_g^b,g,\theta \right)-{\pi }^{\text{true}}\left(x_g^{\text{opt}},g,\theta \right)\right|.$$

Larger values of P sel₀ + P sel₁ and smaller values of Δ₀ + Δ₁ and N tox₀ + N tox₁ indicate superior design performance. The results of the simulation study with two subgroups and a late onset Weibull distribution for time to toxicity are given in Table 2. Figure 2 displays the dose selection probability for each dose within each subgroup across scenarios 1–4. In Figure 2, the symbol * denotes the optimal dose within the (PTox) parenthesis. This facilitates evaluating how frequently each method selects the optimal dose within each subgroup under each scenario. In scenario 1, the Sep-TITE and TITE designs pick the optimal dose for subgroup 0 most often, but the Sub-TITE design picks the optimal dose for subgroup 1 with a much higher probability than all other competitors. In scenario 2, the optimal dose for subgroup 0 is picked by the Sep-TITE design most often, but, again, the Sub-TITE design performs best for subgroup 1. The TITE design that ignores patient heterogeneity here does a very poor job of picking the optimal dose for both subgroups in scenario 2. In scenario 3, the TITE design picks the optimal dose for subgroup 0 with the highest probability, slightly higher than the Sub-TITE design. However, for subgroup 1 the TITE design performs poorly and the SOCA-TITE design performs best. We note the important point that, when considering both subgroups, the total probability of selecting the optimal dose for the two subgroups, denoted by the sum P sel₀ + P sel₁, is higher for the Sub-TITE design than for all of the three competitors across all scenarios 1–3. In scenario 4, where the subgroups are homogeneous, the TITE design performs best in each subgroup, followed closely by the Sub-TITE design. The TITE design performs better in scenario 4 because it correctly assumes one dose toxicity curve for the trial.

TABLE 2.

Simulation study with two subgroups comparing the Sub-TITE, TITE, Sep-TITE and SOCA-TITE designs. For each subgroup g = 0,1, Δ_g is the mean absolute difference between the true toxicity probabilities of the optimal dose and the selected dose, P sel_g is the probability of selecting the optimal dose, N tox_g is the mean number of toxicities, and P stop_g = P[Stop subgroup g]. Dur is the average trial duration, in years. In Scenario 5, where the lowest dose is too toxic for subgroup 0, the symbol ‘—’ is used for Δ₀ and P sel₀ since no optimal dose exists.

Scen	Method	Δ0	Δ1	P sel0	P sel1	N tox0	N tox1	P stop0	P stop1	Dur
1	Sub-TITE	.07	.06	.53	.64	11.7	10.4	0	0	2.96
	Sep-TITE	.06	.09	.59	.47	10.9	10.2	< .01	< .01	2.96
	TITE	.08	.09	.59	.39	12.2	8.3	0	0	2.95
	SOCA-TITE	.07	.08	.49	.32	10.4	10.3	0	0	2.96
2	Sub-TITE	.04	.06	.86	.46	13.4	9.5	.01	0	2.97
	Sep-TITE	.04	.07	.88	.39	12.1	10.1	.03	0	2.97
	TITE	.19	.14	.42	.02	15.7	6.7	< .01	< .01	2.96
	SOCA-TITE	.03	.07	.91	.38	12.1	10.1	0	0	2.97
3	Sub-TITE	.05	.05	.75	.74	10.3	7.1	0	0	2.96
	Sep-TITE	.09	.05	.60	.74	9.4	7.6	0	0	2.97
	TITE	.05	.14	.79	.19	12.5	6.5	0	0	2.96
	SOCA-TITE	.13	.05	.38	.75	9.4	7.7	0	0	2.96
4	Sub-TITE	.04	.04	.75	.76	9.2	9.8	0	0	2.96
	Sep-TITE	.07	.08	.61	.54	9.2	9.4	0	0	2.95
	TITE	.04	.04	.77	.77	9.2	9.3	0	0	2.95
	SOCA-TITE	.10	.10	.40	.42	9.3	9.3	0	0	2.95
5	Sub-TITE	—	.04	—	.84	13.5	14.6	.72	.04	3.42
	Sep-TITE	—	.04	—	.85	14.2	14.0	.69	.08	3.32
	TITE	—	.17	—	.43	15.6	10.6	.57	.57	2.35
	SOCA-TITE	—	.02	—	.92	16.6	12.9	0	0	2.96

FIGURE 2.

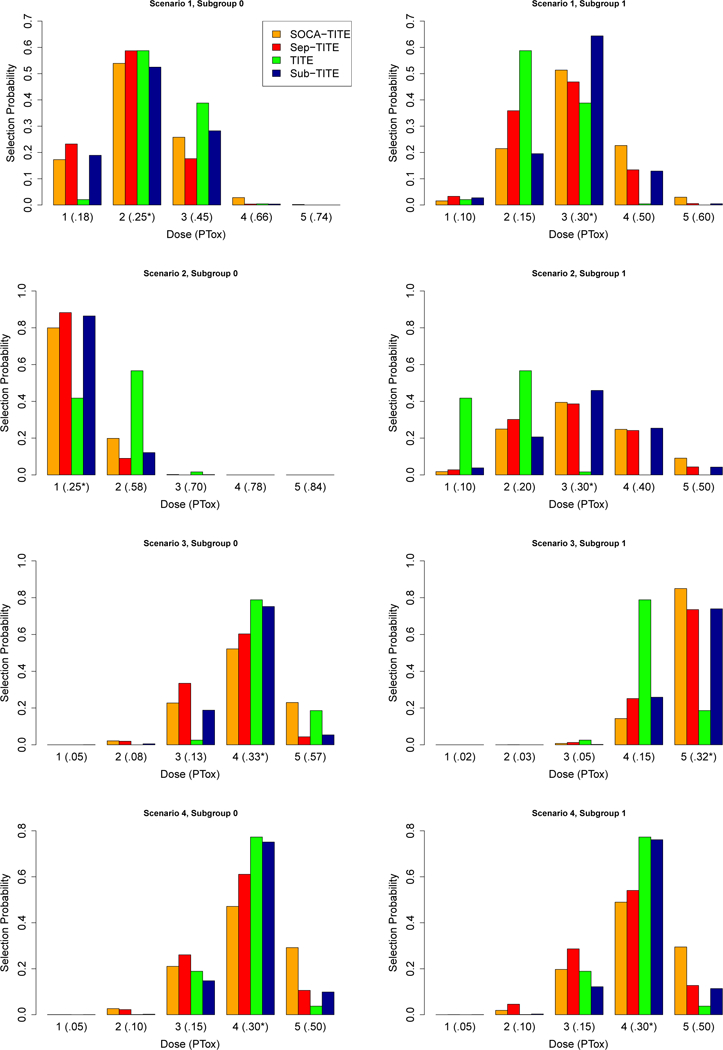
Simulation Study: Dose selection probabilities in each of the two subgroups in scenarios 1–4. PTox denotes the true toxicity probability for each dose within each subgroup and * denotes the dose toxicity probability closest to the target of .3.

In the case of G = 2 subgroups, across all five scenarios, the Sub-TITE design performed better than all three comparators in terms of P sel₀ + P sel₁, the probability of selecting the optimal dose for both subgroups, with the exception that the TITE-CRM has superior performance in scenario 4, where the subgroups are truly homogeneous. In scenario 1, where the optimal doses are 2 and 3, respectively, the Sub-TITE design has a smaller P sel₀ than the Sep-TITE and TITE designs, but has larger values of P sel₁, with sum P sel₀ + P sel₁ that is at least .11 higher than any of the three comparators. Similarly, the value of Δ₁ + Δ₂ for the Sub-TITE design is at least .02 smaller than each of the other designs. In scenario 2, where the optimal doses are 1 and 3, respectively, the SOCA-TITE method has the highest optimal dose selection probability for subgroup 0 with P sel₀ = .91, due in part to the SOCA-TITE design’s inability to stop subgroup 0. The Sub-TITE method has a value of P sel₀ + P sel₁ that is .03 higher than it’s closest competitor, SOCA-TITE. In scenario 3, where the optimal doses are 4 and 5, the Sub-TITE design provides improvements of .15, .36, and .52 in P sel₀ + P sel₁ compared to the Sep-TITE, SOCA-TITE, and TITE designs, respectively. Similarly, the Sub-TITE design provides improvements of .04, .08 and .09 in Δ₀ + Δ₁ compared to the Sep-TITE, SOCA-TITE and TITE designs.

Scenarios 4 and 5 are important special cases. In scenario 4, the two subgroups are truly homogeneous, and in scenario 5 the lowest dose is too toxic for subgroup 0 but not for subgroup 1. In scenario 4, the Sub-TITE design accurately combines the two subgroups, thus providing improvements in P sel₀ + P sel₁ of .36 and .69, and in Δ₀ + Δ₁ of .07 and .12, compared to the Sep-TITE and SOCA-TITE designs, respectively. As may be expected in this scenario, the Sub-TITE design does not perform as well as the TITE-CRM design, which ignores patient heterogeneity, losing by .03 in terms of P sel₀ + P sel₁. However, this loss in total optimal dose selection probability is not nearly as large as those of two competing designs that account for subgroups. This indicates that the Sub-TITE design provides a good compromise between running separate trials within subgroups and ignoring heterogeneity. In scenario 5, the SOCA-TITE design has the highest optimal dose selection probability P sel₁, with advantages of .07 and .08 compared to the Sep-TITE and Sub-TITE designs, respectively. It also has the lowest value of Δ₁ by .02. However, again, SOCA-TITE can not stop accrual to subgroup 0, which has a toxicity probability of .50 at the lowest dose in scenario 5, resulting in SOCA-TITE having 3.1 more patient toxicities on average than the Sub-TITE design.

5.2 |. Sensitivity to trial design parameters

We also examined sensitivity of the Sub-TITE design’s OCs to N_max = 30, 60, 90, and the expected proportions of patients in each subgroup. Here we only consider scenarios 1–4 since scenario 5 represents a special case where the lowest dose is too toxic for subgroup 0 but not for subgroup 1. Figure 3 displays plots of the differences DPsel, defined as P sel₀ + P sel₁ for the Sub-TITE design minus this sum for each of the TITE, SOCA-TITE and Sep-TITE designs. Since Sub-TITE sometimes outperforms Sep-TITE or SOCA-TITE in one subgroup but not the other, DPsel provides a useful overall index of the Sub-TITE design’s ability to select optimal doses within subgroups compared to each of the other designs.

FIGURE 3.

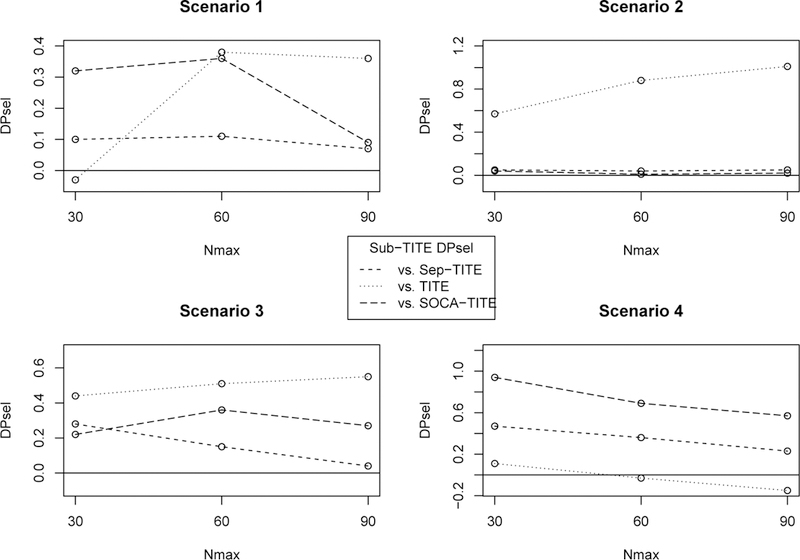
Total difference in optimal dose selection probability, DPsel, of Sep-TITE versus each comparator, for different maximum sample sizes.

When comparing the three designs as a function of N_max, Sub-TITE design outperforms the TITE design further as the sample size increases, except in scenario 4 where the subgroups are homogeneous. The Sep-TITE and SOCA-TITE designs have improved operating characteristics as the sample size increases compared to the Sub-TITE design. However, the sum of the optimal dose selection probabilities is never greater than that of Sub-TITE for any sample size or scenario. In a small sample size of N_max = 30, where we expect about 15 patients in each subgroup, we see large improvements in P sel₀ + P sel₁ of at least .10, .04, .22 and .47 for scenarios 1–4, respectively, compared to the SOCA-TITE and Sep-TITE designs. In scenario 4, where the subgroups are homogeneous, the Sub-TITE design has D P sel values at least .23 greater than that of the Sep-TITE design and .57 of that of the SOCA-TITE design for any sample size. Here the D P sel values for the comparison to the TITE design are (.11, –.03, –.15), so the Sub-TITE design loses some efficiency in larger trials in the homogeneous case, but not nearly as badly as the Sep-TITE design.

Figure 4 shows the differences in P sel₀ + P sel₁ for the Sub-TITE design compared to the Sep-TITE, SOCA-TITE and TITE designs for scenarios 1–4, for different subgroup proportions. Other than scenario 2 for P(Subgroup 0) = .20, the Sub-TITE design has substantially larger total optimal dose selection probability compared to the SOCA-TITE and Sep-TITE designs. In scenario 2, the two subgroup specific optimal doses are not adjacent, so the Sub-TITE method has a harder time recognizing this with only 12 patients, on average, in subgroup 0. In scenario 4, we see that when the subgroups are homogeneous the Sub-TITE design outperforms the Sep-TITE and SOCA-TITE designs regardless of the proportions of patients in the subgroups. In this scenario, the Sub-TITE design D P sel ≥ .35 compared to the Sep-TITE design and D P sel ≥ .59 compared to the SOCA-TITE design. These results suggest that, for large or small trials, and for balanced or unbalanced subgroups, the Sub-TITE design provides a desirable compromise between the TITE-CRM that ignores subgroups and the Sep-TITE or SOCA-TITE design.

FIGURE 4.

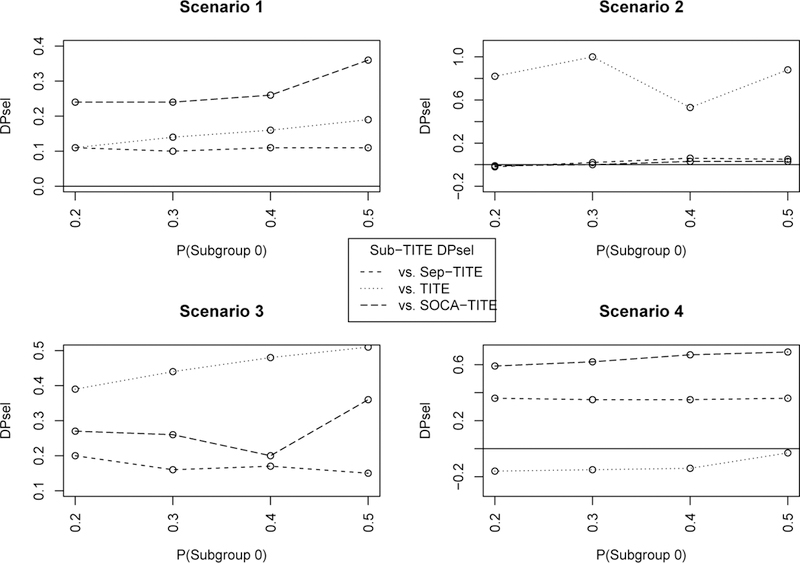
Total difference in optimal dose selection probability, DPsel, of Sep-TITE versus each comparator, for different proportions of patients in subgroup 0.

5.3 |. Robustness study

To assess robustness, in addition to the late onset Weibull distribution, we examined the OCs of the Sub-TITE design in each scenario for an exponential, uniform, and a lognormal distribution. For the uniform distribution, indicators of toxicity first were generated from the scenario subgroup specific dose-toxicity probabilities, and if a patient experienced a toxicity their toxicity time was generated from a Uniform[0, T] distribution. For the exponential distribution, the rate parameters were calibrated to give the simulation scenario’s cumulative toxicity probabilities at the reference time T. For the lognormal distribution, we simulated data with variance parameter σ² = 1 and calibrated the mean for each dose and subgroup to have each scenario’s specified cumulative toxicity probabilities by time T. No other aspects of the trial were changed, in order to isolate the effects of different time-to-toxicity distributions. The results for the Sub-TITE design are given in Web Table 2, with the results for the Sep-TITE, TITE and SOCA-TITE designs shown in Web Tables 3, 4 and 5, respectively.

In general, the OCs of the Sub-TITE design change very little for the different distributions considered. The values for (Δ₀, Δ₁) differ by at most .01 while the largest difference in selection probability for one subgroup is .06 which took place in subgroup 1 in scenarios 1 and 2 for the Weibull increasing and exponential. Since the two subgroup probabilities of optimal dose selection do not differ by more than .01 between the two subgroups in the homogeneous case for any distribution considered, it appears that the Sub-TITE design is likely to correctly identify that only one subgroup is needed. The average trial times for the different distributions considered were about the same except for in scenario 5, where the lowest dose is too toxic, with a difference of about 1.8 months between the Weibull increasing hazard and the uniform distribution. In general, the exponential distribution had the fewest patient toxicities while the Weibull distribution with an ncreasing hazard had the most toxicities in each scenario.

When comparing the results for Sub-TITE to the Sep-TITE and TITE designs for different distributions, we see the same results as in Table 2, namely that Sub-TITE has superior performance compared to the TITE design when patient heterogeneity is present, and is superior to Sep-TITE and SOCA-TITE designs when subgroups are homogeneous. This is shown by the D P sel values since, as in the homogeneous case, D P sel ≥ .15 when comparing Sub-TITE to either Sep-TITE or SOCA-TITE.

For scenario 3, where doses 4 and 5 are optimal, for g = 0 and 1, the Sub-TITE design had a slight decrease in performance compared to the Sep-TITE design for other distributions considered, having D P sel values of − .04 and −.02 for the exponential and uniform distributions. In these cases the values of Δ₁ + Δ₀ were the same and the Sub-TITE design had about .8 less patient toxicities. The average D P sel values comparing Sub-TITE to Sep-TITE for scenarios (1,2,3,4) are (.15, .07, .03, .21) and comparing Sub-TITE to SOCA-TITE are (.17, .08, .13, .42). For scenario 5, where subgroup 0 is too toxic, the Sep-TITE design stopped this subgroup (.04, .01, .05, −.03) more often than the Sub-TITE design for the exponential, uniform, lognormal and Weibull increasing hazards, respectively, but chose the optimal dose for subgroup 1 with the same probability on average as the Sep-TITE design. For subgroup 1, SOCA-TITE picked the optimal dose .06,06, .06, and .04 more often than Sep-TITE, but never stopped the truly toxic subgroup 0, resulting in 3.9 more toxicities for this subgroup on average over the four extra distributions considered. Thus, across all scenarios and time-to-toxicity distributions,in general the Sub-TITE design has superior performance compared to both the Sep-TITE and SOCA-TITE designs. The Sub-TITE design is greatly superior to the TITE design that ignores subgroups in terms of D P sel in all scenarios, except in the homogeneous case, losing by an average of .15. The Sub-TITE design had about .4 more total patient toxicities in each scenario compared to the TITE and Sep-TITE designs, and had similar trial durations in all but scenario 5, with about a month longer trial duration than the Sep-TITE design due to skipping more patients in subgroup 0.

5.4 |. Simulation results for four subgroups

We next performed a simulation study to evaluate the Sub-TITE method in the case of G = 4 subgroups for scenarios 1–4 compared to the Sep-TITE and TITE designs. Scenario 5 was not used because it is a special case where subgroup 0 has an unacceptably high toxicity probability at the lowest dose. The SOCA-TITE design was not included because it cannot accommodate more than two patient subgroups. The four assumed true subgroup-specific dose-toxicity vectors are given in Figure 1 and listed numerically in Web Table 1. We assumed that a patient was equally likely to be in any of the four subgroups. We increased N_max to 90 to ensure a sufficient number of patients to do dose finding reasonably reliably in each subgroup. The simulation results for the Sub-TITE, Sep-TITE, and TITE designs are summarized in Table 3. The additional hypermeans here are ${\tilde{\alpha }}_2=-1.77,{\tilde{\beta }}_2=-.05,{\tilde{\alpha }}_3=-2.35\text{and}{\tilde{\beta }}_3=\mathrm{.35.}$

TABLE 3.

Simulation study with four subgroups. For each g = 0,1,2,3, Δ_g is difference between the true optimal dose toxicity probability and the true toxicity probability of the dose chosen, P sel_g is the probability of selecting the optimal dose and N tox_g is the mean number of toxicities.

	Seb-TITE			Sep-TITE			TITE
g	Δg	P selg	N toxg	Δg	P selg	N toxg	Δg	P selg	N toxg
Scenario 1
0	.09	.46	8.4	.07	.53	7.6	.23	.05	11.6
1	.07	.60	7.9	.10	.43	7.1	.04	.77	8.5
2	.06	.55	6.6	.08	.45	6.7	.09	.18	5.7
3	.05	.53	4.9	.06	.61	5.1	.09	0	4.0
Scenario 2
0	.07	.80	9.5	.05	.84	8.6	.38	< .01	14.7
1	.06	.48	7.1	.08	.34	7.0	.06	.41	14.7
2	.06	.45	7.1	.08	.37	7.1	.06	.41	6.4
3	.07	.58	6.1	.08	.55	6.6	.18	.01	4.1
Scenario 3
0	.07	.68	6.4	.13	.57	6.6	.01	.94	8.1
1	.06	.67	5.1	.05	.73	5.3	.17	.03	4.0
2	.06	.72	7.4	.10	.55	6.9	.01	.94	8.1
3	.05	.75	7.3	.09	.56	6.8	.01	.94	8.1
Scenario 4
0	.05	.67	6.0	.08	.53	6.4	.02	.90	7.1
1	.06	.68	7.0	.09	.52	6.6	.02	.90	7.1
2	.05	.69	7.0	.08	.53	6.7	.02	.90	7.1
3	.05	.69	7.0	.08	.54	6.5	.02	.90	7.1

Let $Pse{l}^{+}(\text{Method})={\sum }_{g=0}^{G-1}P{sel}_g(\text{Method})$ denote the sum of the optimal dose selection probabilities and ${\mathrm{\Delta }}^{+}(\text{Method})={\sum }_{g=0}^{G-1}{\mathrm{\Delta }}_g(\text{Method})$ denote the sum of the Δ_g’s for a given Method ∈ {Sub-TITE,Sep-TITE,TITE}. Larger values of P sel⁺(Method) and smaller values of Δ⁺(Method) are more desirable. In each of the four scenarios considered, the smallest difference

$$Pse{l}^{+}(\text{Sub-TITE})-Pse{l}^{+}(\text{Sup-TITE})$$

was .12 in scenario 1, where all subgroups are heterogeneous, and the largest difference of .61 was in scenario 4, where the subgroups are homogeneous. On average, P sel⁺(Sub-TITE) − P sel⁺(Sep-TITE) = .34 over the four scenarios considered, and Δ⁺(Sub-TITE) − Δ⁺(Sep-TITE) = −.08, with a maximum value of −.03 in scenario 2 and minimum value of −.12 in scenarios 3 and 4. The Sub-TITE design again had slightly more total toxicities over the four scenarios, with an average .5 more toxicities than Sep-TITE. In scenarios 1, 2, and 3, where at least two subgroups are heterogeneous, the Sub-TITE design had much better OCs than the TITE design, with P sel⁺(Sub-TITE) − P sel⁺(TITE) = 1.14, 1.82 and .58 and, Δ⁺(Sub-TITE) − Δ⁺(TITE) of −.24, −.52 and −.13, respectively.

In scenarios 3 and 4, where three and four subgroups are homogeneous, respectively, the P sel⁺(Sub-TITE) − P sel⁺(TITE) values are −.23 and −.47, and values of Δ⁺(Sub-TITE) − Δ⁺(TITE) values are .04 and .13. In scenario 4, where all four subgroups are homogeneous, we see the same qualitative result as with two subgroups, namely that the TITE design outperforms the Sub-TITE design. However, in the heterogeneous subgroups cases, again, the TITE design has extremely small P sel_g values for some subgroups, e.g. P sel₀ = .05 and P sel₃ = 0 in scenario 1. In scenarios 3 and 4, the differences P sel⁺(Sub-TITE) − P sel⁺(Sep-TITE) were .32 and .61, and Δ⁺(Sub-TITE) − Δ⁺(Sep-TITE) were −.13 and −.12.

These results indicate that, when two, three, or four of G = 4 subgroups are homogeneous, because the Sub-TITE design can accurately combine these subgroups for dose selection, it greatly outperforms Sep-TITE. This advantage also is seen in scenario 2, where two subgroups are homogeneous, and in scenario 1, where all four subgroups are different, demonstrating how Sub-TITE borrows strength flexibly among subgroups. In general, although the values of P stop_g are not listed, they are all 0 or < .01, except for in scenario 2, subgroup 0, where the stopping probability is .02 for both the Sub-TITE and Sep-TITE designs. Similarly, the average durations of the trials did not differ by more than .01 between the three competing methods.

We also compared the three methods for N_max = 60 and 120 in the four subgroup case. When comparing the Sub-TITE and Sep-TITE designs, we see the same trend, namely that increasing the sample size decreases the margin of advantage for Sub-TITE in terms of the P sel⁺, but Sub-TITE always outperforms Sep-TITE, regardless of sample size. This difference is striking in scenario 4, where all subgroups are homogeneous, with a difference P sel⁺(Sub-TITE) − P sel⁺(Sep-TITE) = .73 for N_max = 60 and P sel⁺(Sub-TITE) − P sel⁺(Sep-TITE) = .18 for N_max = 120. Likewise, in scenario 3, where 3 of the subgroups are homogeneous, P sel⁺(Sub-TITE) − P sel⁺(Sep-TITE) = .51 for N_max = 60 and .27 for N_max = 120. In scenarios 1 and 2, where none and two of the subgroups are homogeneous, respectively, we see a substantial improvement for both sample sizes, with respective differences P sel⁺(Sub-TITE) − P sel⁺(Sep-TITE) = .18 and .21 for N_max = 60, and .06 and .13 for N_max = 120. Thus the Sub-TITE design provides large improvements with any sample size compared to the Sep-TITE design and compared to the TITE design with heterogeneous subgroups.

6 |. DISCUSSION

We have presented a subgroup specific phase I dose finding design based on a time-to-toxicity outcome that adaptively allows some subgroups to be combined if they are found to have similar dose-toxicity probability curves. This is implemented as part of the MCMC posterior computation using latent subgroup membership variables and spike-and-slab priors. This methodology provides a compromise between the Sep-TITE design, that applies the TITE design to do dose-finding separately in the sub-groups, and the TITE design that ignores subgroups. In cases where some subgroups are heterogeneous, the Sub-TITE design performs at least as well as running separate trials, outperforms the TITE design that ignores subgroups. In the two subgroup case, Sep-TITE performs favorably compared to the two group maximum likelihood approach of Salter et al., with values of P sel_g and Δ_g that are either similar or greatly superior to those of SOCA-TITE, depending on scenario and subgroup. When the subgroups are homogeneous, the Sub-TITE design selects the correct dose much more frequently than Sep-TITE, and performs nearly as well as the TITE design that ignores subgroups.

In cases where some but not all subgroups have the same dose-toxicity curve, the ability of Sub-TITE to combine some subgroups provides a substantial advantage over SOCA-TITE in the two subgroup case (scenario 4 in Table 2) and the Sep-TITE approach in the four subgroup case (scenarios 3 and 4, Table 3). Essentially, this is because these two comparators do not have the ability to combine homogeneous subgroups. This seems to be a generally desirable property of any adaptive precision medicine design, since subgroups identified at the start of a trial may in fact not differ with regard to the distribution of outcome as a function of treatment. Thus, this is an important area for future research in other precision medicine settings.