Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2016 Oct 19;1(4):620–625. doi: 10.1021/acsomega.6b00170

Theoretical Investigation of Promising Molecules for Obtaining Complexes with Planar Tetracoordinate Carbon

Congjie Zhang †,*, Dongxia Ma †, Shaoni Yang †, Jinxia Liang ‡,*
PMCID: PMC6640768  PMID: 31457151

Abstract

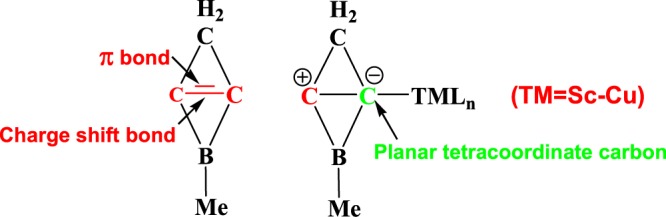
graphic file with name ao-2016-001702_0008.jpg

We have theoretically investigated the stability, chemical bonding, and coordination ability of the 2-Me-2-borabicyclo[1.1.0]but-1(3)-ene (2-Me-2BB) molecule using density functional theory and ab initio molecular dynamics (AIMD) simulations. Calculated results indicated that 2-Me-2BB is both thermodynamically and kinetically stable. The C=C bonds in 2-Me-2BB contain a π bond and a charge shift (CS) bond, different from those in 1-Me-borirene and cyclopropylene. Moreover, 2-Me-2BB can be a σ donor, leading to the formation of TM(2-Me-2BB)Ln complexes containing planar tetracoordinate carbon (ptC) with transition metals (TM = Sc–Cu), in which the lone electron pair of 2-Me-2BB results from its ionic resonance form. The lengths and Wiberg bond indices of the TM-ptC bond in TM(2-Me-2BB)Ln (TM = Sc–Cu) reveal that 2-Me-2BB can be a ligand similar to N-heterocyclic carbene. Therefore, 2-Me-2BB and its derivatives are promising molecules to obtain complexes with ptC. The natural charges on TM atoms in TM(2-Me-2BB)Ln (TM = Sc–Cu) complexes range from −0.97 to 1.54e, indicating that such complexes with ptC might have potential applications in catalytic chemistry.

Introduction

Since Hoffmann theoretically proposed the molecules containing the planar tetracoordinate carbon (ptC) to be stable in 1970,1 plenty of stable molecules,2−8 clusters,9−13 and nanotubes,14−17 as well as transition metal complexes18−23 have been theoretically found to contain one or more ptCs. However, only a few compounds with ptC were experimentally observed.24−28 Hence, obtaining more compounds containing ptC is a challenging work. In general, electronic and mechanical strategies are used to stabilize the main group element compounds with ptC. The electronic approach is that the ptC is placed on aromatic systems, in which the lone electron pair on ptC is delocalized.29−31 The mechanical strategy is that the ptC atom is confined within a ring or a cage.20,32−34 In addition to the main group element compounds with ptC, many stable complexes with ptC are also considered to adopt the electronic approach.19−21 Recently, we have theoretically obtained some silver and gold complexes containing ptC, supported by the derivatives of 2-borabicyclo[1.1.0]but-1(3)-ene (2BB).22,35−37 Moreover, the gold complexes Au(2BB)+ were used to catalyze the rearrangement reaction of allylic acetates, and the free-energy barriers were lower than that of the [Au(NHC)]+-catalyzed reaction by about 2 kcal/mol.37 The ptCs in these stable silver and gold complexes do not adopt the previous electronic and mechanical strategies, but adopt a σ coordination bond between ptC and Ag (or Au). To better understand the fact that the derivative of 2BB can act as a σ donor, we have investigated the chemical bonding, stability, and isomerization of 2-Me-2-borabicyclo[1.1.0]but-1(3)-ene (2-Me-2BB, as shown in Scheme 1). Moreover, nine complexes composed of transition metals Sc to Cu supported by 2-Me-2BB were designed. The structures, stability, and Wiberg bond indices (WBIs) of the nine complexes were theoretically investigated.

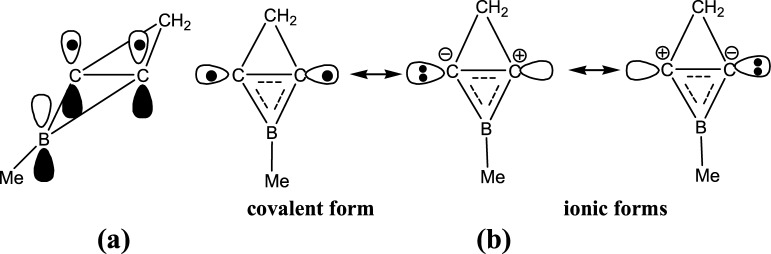
Scheme 1. Conjugation π Bond (a) and Resonance Structures (b) of the Horizontal C–C Bond in 2-Me-2BB.

Scheme 1

Open in a new tab

Computational Methods

The possible isomers of C3BH2CH3 were constructed and optimized at the B3LYP/6-31+G** level, and the structures of 1-Me-borirene and cyclopropylene were optimized at the same level of theory. The vibrational frequencies and WBIs of C3BH2CH3, 1-Me-borirene, and cyclopropylene were calculated using the B3LYP/6-31+G** approach. The structures, vibrational frequency calculations, and WBIs of the complexes of the Sc–Cu-bearing 2-Me-2BB ligand were obtained using the B3PW91 functional in combination with LANL2DZ(f) basis sets38−41 for transition metals Sc to Cu, LANL2DZ(dp) ECP basis sets42 for the I atom, and standard 6-31+G** basis sets for other atoms. Intrinsic reaction coordinates were calculated to confirm the calculated transition structures involved in the isomerization of 2-Me-2BB. WBIs as well as natural charges of transition metals in the compounds studied here were computed by the natural bond orbital methods.43 All the above calculations in this article were performed with the Gaussian 09 program.44 The electron density and Laplacian values of 2-Me-2BB, 1-Me-borirene, and cyclopropylene were calculated using the Atoms In Molecule program.45

To confirm the dynamical stability of 2-Me-2BB, ab initio molecular dynamics (AIMD) simulations of 2-Me-2BB were carried out using the Vienna ab initio simulation package program.46,47 The core and valence electrons were represented by using the projector augmented wave48 method and plane-wave basis functions with a kinetic energy cutoff of 400 eV. The generalized gradient approximation with the Perdew–Burke–Ernzerhof49 exchange-correlation functional was used in the calculations. The finite temperature simulation of the dynamical properties was performed at temperatures ranging from 373 to 1273 K using the exact Hellman–Feynman forces and applying the statistics of the canonical ensemble to the motion of atomic nuclei by means of a Nosé–Hoover thermostat.50 Newton’s equations of motion were integrated using the Verlet algorithm51 with a time step of 1 fs. 2-Me-2BB molecules were calculated in a cubic box of 10 × 15 × 10 Å3. A vacuum distance of more than 8 Å was set to maintain a negligible interaction between molecules in the adjacent boxes. The Brillouin-zone sampling was restricted to the Γ-point. The optimization of atomic geometries was performed via a conjugate-gradient algorithm until residual forces acting on atoms were less than 0.1 eV Å–1.

Results and Discussion

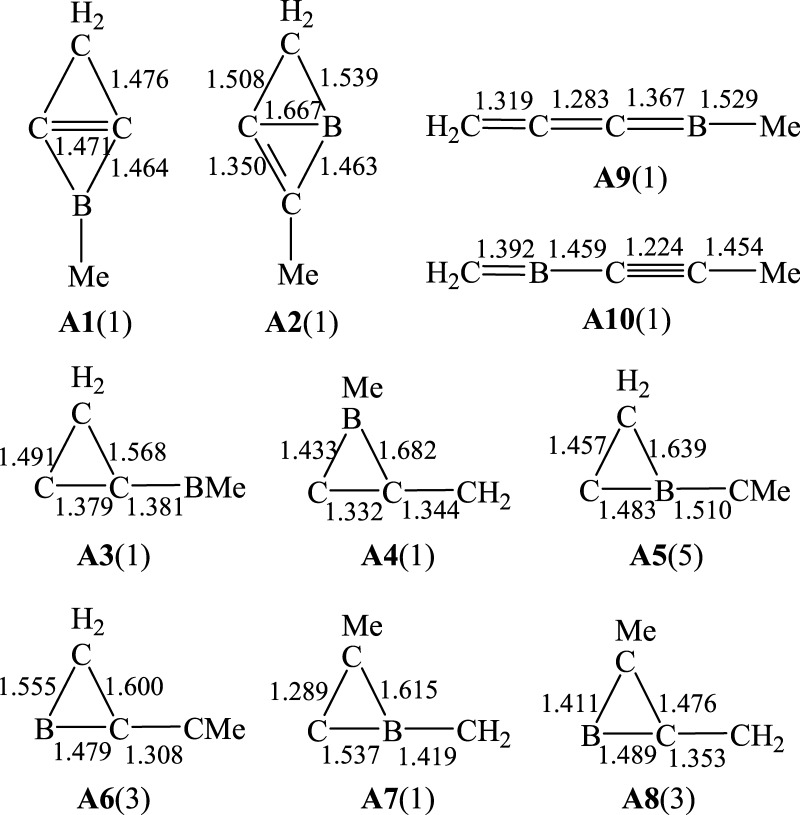
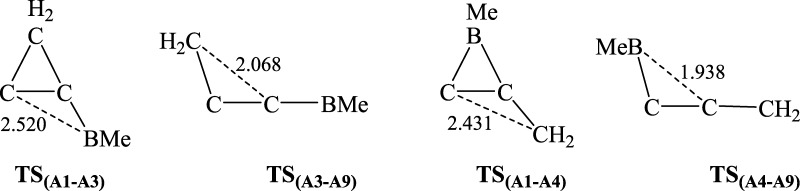
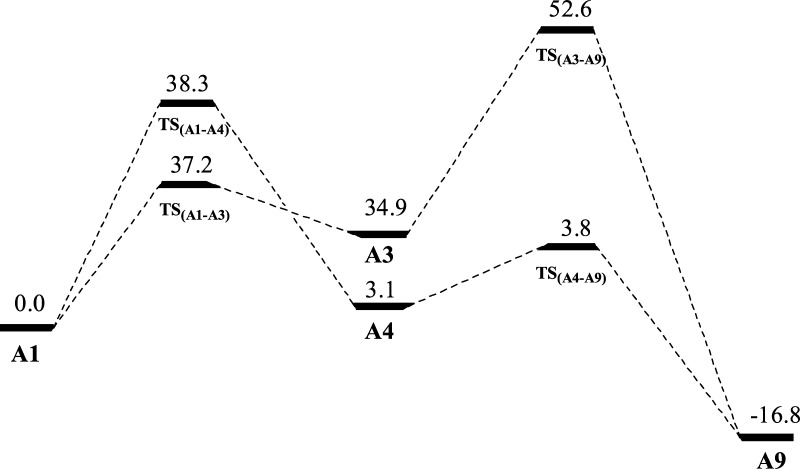
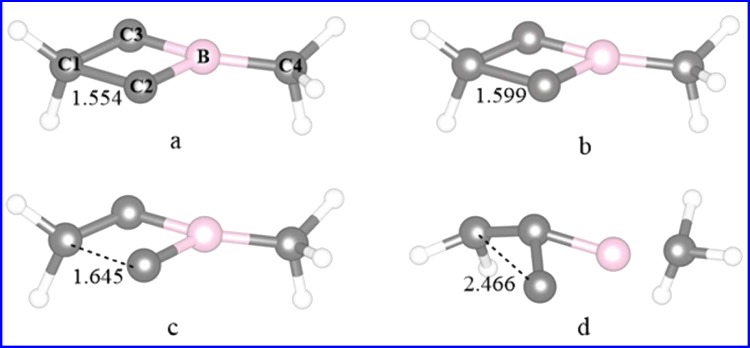
The possible isomers of C3BH2CH3 in which CH2 and CH3 units remain unchanged were considered. The reason for that is the fact that the structure of 2-Me-2BB, as shown in Scheme 1, can contain the structures of 1-Me-borirene and cyclopropylene. Accordingly, 10 possible isomers were constructed, as shown in Figure 1 (A1–A10). Calculated energies and relative energies of A1–A10 are listed in Table S1 of the Supporting Information. As seen from Table S1, the lower energy structures of A5, A6, and A8 are quintuplet, triplet, and triplet, respectively, whereas the other isomers have a singlet structure. The most stable structure of C3BH2CH3 is A9, in which the carbon and boron atoms are arranged in line. The lengths of the C–C (left), C–C (middle), C–B (middle), and B–C (right) bonds in A9 are 1.319, 1.283, 1.367, and 1.529 Å, respectively, in which B–C (right) is a single bond, whereas the remaining C–C and C–B bonds are double bonds. Isomer A10 is an isoenergetic structure of A9 because the difference in energy between them is only 0.5 kcal/mol. A1, 2-Me-2BB, is the most stable among the nonlinear structures. The lengths of the horizontal C–C, C–B, and C–C(H2) bonds are 1.471, 1.464, and 1.476 Å, respectively. The lengths of the horizontal C–C and C–C(H2) bonds are between those of single and double bonds, in which the short C–C(H2) bond results from a hyperconjugation effect. The relative energy of A1 is higher than that of A9 by 16.4 kcal/mol. Then, is it easy for A1 to isomerize to A9? Thus, we have considered the isomerization processes from A1 to A9. There are two kinds of paths for A1 → A9 according to the symmetry of A1: one is the cleavage of the C–B bond in A1 (A1 → A3 → A9), and the other is the breaking of the C–C(H2) bond in A1 (A1 → A4 → A9). The transition structures involved in the two reactions are illustrated in Figure 2 (TSA1–A3, TSA3–A9, TSA1–A4, and TSA4–A9). The distances of C···B(Me) in TSA1–A3, C···C(H2) in TSA3–A9, C···C(H2) in TSA1–A4, and C···B(Me) in TSA4–A9 are 2.520, 2.068, 2.431, and 1.938 Å, respectively. The single imaginary frequency of TSA1–A3, TSA3–A9, TSA1–A4, and TSA4–A9 are 135i, 774i, 448i, and 228i, respectively. The reaction profiles of the two paths are given in Figure 3. The free-energy barriers of A1 → A3 and A3 → A9 via TSA1–A3 and TSA3–A9 are 37.2 and 17.7 kcal/mol, respectively. The free-energy barriers of A1 → A4 → A9 via TSA1–A4 and TSA4–A9 are 38.3 and 0.7 kcal/mol, respectively. Thus, the C–C(H2) bond in A1 is more easy to break than the C–B bond. However, the free-energy barriers of both paths for A1 → A9 are very high, indicating that it is very difficult for A1 to isomerize to A9. Thus, 2-Me-2BB is kinetically stable.

Figure 1.

Figure 1

Open in a new tab

Selected bond lengths and multiplicity (in parentheses) of the lower energy isomers of 2-Me-2BB.

Figure 2.

Figure 2

Open in a new tab

Optimized geometries of the transition states involved in the isomerization of A1 to A9.

Figure 3.

Figure 3

Open in a new tab

Profiles of the potential energies (in kcal/mol) of the isomerization of A1 → A9.

We further determined the dynamical stability of 2-Me-2BB with temperature in the range of 373–1273 K using the AIMD method. The structure of 2-Me-2BB remains unchanged below 1173 K, whereas one C–C bond in 2-Me-2BB begins to break at 1273 K. Thus, we display four structures (at 8651, 8652, 8653, and 16 000 fs) and selected bond lengths of 2-Me-2BB at T = 1273 K in Figure 4. As can be seen from Figure 4, the structure of 2-Me-2BB has no significant change before 8651 fs, whereas the C1–C2 bond begins to increase after 8651 fs and the entire molecule is dissociated into small fragments at 16 000 fs, which is consistent with ab initio calculations by which the cleavage of the C–C(H2) bond in A1 is favorable. In addition, detailed variations of the C1–C2 bond in A1 versus time at 1273 K are given in Figures S1 and S2, indicating that the C1–C2 bond breaks after 8651 fs. Thus, 2-Me-2BB is confirmed to be kinetically stable.

Figure 4.

Figure 4

Open in a new tab

Selected molecules and bond lengths of C1–C2 and B–C4 of 2-Me-2BB from AIMD simulations at T = 1273 K: (a) at 8651 fs; (b) at 8652 fs; (c) at 8653 fs; and (d) at 16 000 fs.

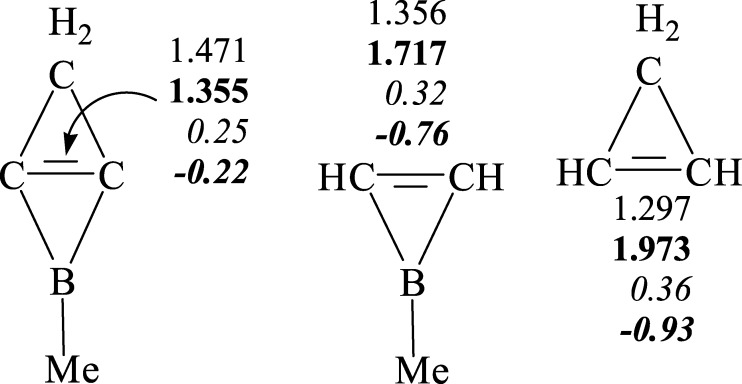
Previous studies showed that 2-Me-2BB can be a σ donor to coordinate with silver and gold ions to form complexes.22,35−37 We focus on the structure of 2-Me-2BB here and analyze its chemical bonding. The HOMO of the derivatives of 2BB is contributed by the occupied sp2 hybrid orbitals of carbon atoms, which are very similar to that of [1.1.1]propellane.52,53 On the basis of the bonding properties of [1.1.1]propellane, we illustrate the electronic structures of 2-Me-2BB in Scheme 1. As seen from Scheme 1a, the three-membered ring formed by two carbon atoms and a boron atom contains a conjugate bond (Π32) contributed by their 2pz orbitals, obeying the 4n + 2 rule. The sp2 hybrid orbitals of the two horizontal carbons are situated in opposite directions. According to the characteristic of the charge shift (CS) bonding of [1.1.1]propellane,52−54 the two sp2 hybrid orbitals from the two horizontal carbons will form a CS bond, and its resonance structures (covalent and ionic forms) are shown in Scheme 1b. Moreover, the ionic structures can serve as a σ donor when they come into contact with a transition metal. To further understand the CS bonding of C=C in 2-Me-2BB, we have optimized structures of 1-Me-borirene and cyclopropylene and calculated their WBIs, density, and Laplacian values. The lengths, WBIs, density, and Laplacian values of C–C bonds in 2-Me-2BB, 1-Me-borirene, and cyclopropylene are illustrated in Figure 5. The lengths, WBIs, and density of C–C bonds show that the strength of C–C bonds is in the order of 2-Me-2BB < 1-Me-borirene < cyclopropylene, indicating that the C=C bond in 2-Me-2BB is the weakest. The C=C bond in cyclopropylene is a double bond, which contains a 2c–2e σ bond and a 2c–2e π bond. The C=C bond in 1-Me-borirene is also a double bond, which results from a 2c–2e σ bond and a 3c–2e π bond, thus, the C=C bond is weaker than that in cyclopropylene. In addition, the Laplacian values of the C=C bond in 1-Me-borirene and cyclopropylene are very negative, indicating that the C=C bond is a covalent bond. In contrast, the Laplacian values of the C=C bond in 2-Me-2BB are significantly higher than those in 1-Me-borirene and cyclopropylene; thus, the C=C bond in 2-Me-2BB is different from that in 1-Me-borirene and cyclopropylene. The C=C bond in 2-Me-2BB is a weak double bond, which arises from a 2c–2e CS bond and a 3c–2e π bond. Therefore, the lengths, WBIs, density, and Laplacian values of the C=C bond in 2-Me-2BB are very consistent with the description in Scheme 1.

Figure 5.

Figure 5

Open in a new tab

Lengths (in plain, in Å), WBIs (in bold), electron density (in italic), and Laplacian values (in bold and italic) of the C–C bond in 2-Me-2BB, 1-Me-borirene, and cyclopropylene.

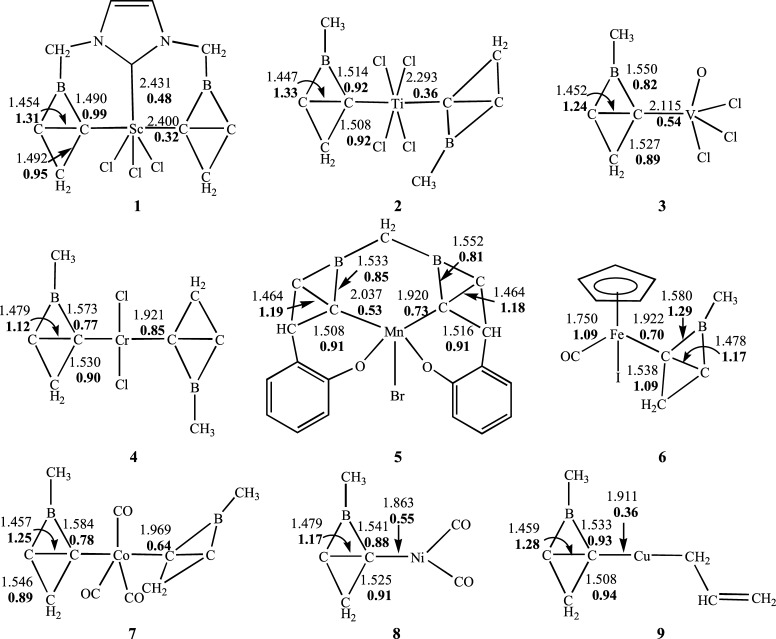
As discussed above, 2-Me-2BB is not only both thermodynamically and kinetically stable, but also its ionic resonance structure can serve as a σ ligand at carbon atoms to form complexes. Here, we have designed Sc–Cu complexes supported by a 2-Me-2BB ligand to investigate the coordination ability of 2-Me-2BB. The lowest energy structures of Sc–Cu complexes (1–9) are displayed in Figure 6. As seen from Figure 6, the lengths of Sc–C(carbene) and Sc–C(2BB) bonds in 1 are 2.431 and 2.400 Å, respectively. Sc–C bonds in 1 are slightly longer than the Sc–C bonds in the η3-2,6-bis(imidazole-2-ylidene)pyridineScCl3 complex,55 which might arise from the tension of the bis-2-Me-2BB ligand. The WBIs of Sc–C(carbene) and Sc–C(2BB) in 1 are 0.48 and 0.32, respectively, indicating that the ability of the donating electron of 2-Me-2BB is slightly weaker than that of NHC.

Figure 6.

Figure 6

Open in a new tab

Optimized geometries of the lowest energy structures of Sc–Cu complexes (1–9).

The two 2-Me-2BB ligands in complex 2 are perpendicular, and the distance of the Ti–C bond in 2 are 2.293 Å, which is very consistent with the Ti–C bond in 1,3,4,5-tetramethylimidazol-2-ylideneTiF4.56 The WBI of the Ti–C bond in 2 is 0.36, showing that Ti–C is a weak coordinate bond.

The structure of complex 3 is similar to that of 1,3-dimesitylimidazol-2-ylideneV(O)Cl3.5 The length and WBI of the V–C bond in complex 3 are 2.115 Å and 0.54, respectively, in which the V–C bond length in 3 is almost close to that in 1,3-dimesitylimidazol-2-ylideneV(O)Cl3.57 This indicates that 2-Me-2BB is similar to NHC.

The Cr–C bond length in 4 is 1.921 Å and is shorter than that of Cr(Cl2)(NHC)2 by ca. 0.280 Å;58 in addition, the WBI of the Cr–C bond in 4 is 0.85, thus, the Cr–C bond in 4 is a strong coordinate bond.

The distances of two Mn–C bonds in 5 are 2.037 and 1.920 Å, respectively, which are consistent with the Mn–C bond length (2.015 and 1.984 Å) in the Mn(III) complex with a tetradenate NHC ligand.59

In complex 6, the length and WBI of the Fe–C bond are 1.922 Å and 0.70, indicating that the Fe–C bond is a strong coordinate bond. The Fe–C bond in 6 is shorter than that in CpFe(CO)(H2-IMes) by about 0.06 Å,60 which is similar to that in complex 4.

The lengths of TM–C (TM = Co, Ni, and Cu) bonds in complexes 7, 8, and 9 are 1.969, 1.863, and 1.911 Å, respectively, which are very consistent with the distances of TM–C bonds in [Co(CO)3(IMes)2]+, Ni(CO)2(NHC), and 1,3-bis(2′,6′-diisopropylphenyl)imidazole-2-ylideneCu(CH2CH=CH2).61−63

Therefore, 2-Me-2BB is a kind of σ donor at carbon atoms, similar to NHC. The boron and carbon atoms of 2-Me-2BB and the transition metals in complexes 1–9 locate on a plane. Thus, 2-Me-2BB can also be a kind of novel σ donor to form complexes with ptC. In addition, on the basis of the previous results,22,35−37 it can be concluded that the derivatives of 2-Me-2BB can also coordinate with transition metals to form complexes with ptC. The natural charges on the TM in complexes 1–9 are 0.37, 1.54, 0.07, 0.03, 0.25, −0.84, −0.97, −0.22, and 0.54e, respectively, indicating that the TM can bond both electrophilic and nucleophilic molecules. Therefore, we suggest that these complexes with ptC have potential applications in the field of catalysis.

Conclusions

The stability and chemical bonding of the 2-Me-2BB molecule as well as the structures of the complexes of Sc–Cu bearing 2-Me-2BB have been investigated using density functional theory. The following conclusions were drawn: (1) 2-Me-2BB is both thermodynamically and kinetically stable. (2) The C=C bond in 2-Me-2BB is a CS bonding and significantly different from the C=C bonds in 1-Me-borirene and cyclopropylene. (3) 2-Me-2BB can form complexes containing ptC with transition metals Sc to Cu. (4) The natural charges on the TM in Sc–Cu complexes bearing 2-Me-2BB ligands vary from −0.97 to 1.54e. Therefore, 2-Me-2BB or its derivatives can form complexes with ptC, and the complexes have potential applications in the field of catalysis.

Acknowledgments

The authors thank the National Natural Science Foundation of China for financial support (No. 21373133).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.6b00170.

  • Cartesian coordinates and electronic energies of the compounds and the transition states (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao6b00170_si_001.pdf (560.5KB, pdf)

References

  1. Hoffmann R.; Alder R. W.; Wilcox C. F. J. Am. Chem. Soc. 1970, 92, 4992–4993. 10.1021/ja00719a044. [DOI] [Google Scholar]
  2. Roettger D.; Erker G.; Fröhlich R.; Grehl M.; Silverio S. J.; Hyla-Kryspin I.; Gleiter R. J. Am. Chem. Soc. 1995, 117, 10503–10512. 10.1021/ja00147a011. [DOI] [Google Scholar]
  3. Boldyrev A. I.; Simons J. J. Am. Chem. Soc. 1998, 120, 7967–7972. 10.1021/ja981236u. [DOI] [Google Scholar]
  4. Perez N.; Heine T.; Barthel R.; Seifert G.; Vela A.; Mendez-Rojas M. A.; Merino G. Org. Lett. 2005, 7, 1509–1512. 10.1021/ol050170m. [DOI] [PubMed] [Google Scholar]
  5. Keese R. Chem. Rev. 2006, 106, 4787–4808. 10.1021/cr050545h. [DOI] [PubMed] [Google Scholar]
  6. Xie H. B.; Ding Y. H. J. Chem. Phys. 2007, 126, 184302 10.1063/1.2723109. [DOI] [PubMed] [Google Scholar]
  7. Merino G.; Méndez-Rojas M. A.; Vela A.; Heine T. J. Comput. Chem. 2007, 28, 362–372. 10.1002/jcc.20515. [DOI] [PubMed] [Google Scholar]
  8. Sun W. X.; Zhang C. J.; Cao Z. X. J. Phys. Chem. C 2008, 112, 351–357. 10.1021/jp0771522. [DOI] [Google Scholar]
  9. Li S. D.; Ren G. M.; Miao C. Q.; Jin Z. H. Angew. Chem., Int. Ed. 2004, 43, 1371. 10.1002/anie.200353068. [DOI] [PubMed] [Google Scholar]
  10. Li S. D.; Ren G. M.; Miao C. Q. J. Phys. Chem. A 2005, 109, 259. 10.1021/jp040259u. [DOI] [PubMed] [Google Scholar]
  11. Castro A. C.; Audiffred M.; Mercero J. M.; Ugalde J. M.; Mendez-Rojas M. A.; Merino G. Chem. Phys. Lett. 2012, 519–520, 29–33. 10.1016/j.cplett.2011.11.030. [DOI] [Google Scholar]
  12. Tam N. M.; Pham H. T.; Nguyen M. T. Chem. Phys. Lett. 2014, 608, 255–263. 10.1016/j.cplett.2014.05.098. [DOI] [Google Scholar]
  13. Cui Z. H.; Ding Y. H.; Cabellos J. L.; Osorio E.; Islas R.; Restrepo A.; Merino G. Phys. Chem. Chem. Phys. 2015, 17, 8769–8775. 10.1039/C4CP05707D. [DOI] [PubMed] [Google Scholar]
  14. Zhang C. J.; Sun W. X.; Cao Z. X. J. Am. Chem. Soc. 2008, 130, 5638–5639. 10.1021/ja800540x. [DOI] [PubMed] [Google Scholar]
  15. Wu M. H.; Pei Y.; Zeng X. C. J. Am. Chem. Soc. 2010, 132, 5554–5555. 10.1021/ja1002026. [DOI] [PubMed] [Google Scholar]
  16. Xiao B.; Ding Y. H.; Sun C. C. Phys. Chem. Chem. Phys. 2011, 13, 2732–2737. 10.1039/C0CP01498B. [DOI] [PubMed] [Google Scholar]
  17. Chai G. L.; Lin C. S.; Cheng W. D. J. Mater. Chem. 2012, 22, 11303–11309. 10.1039/c2jm31593a. [DOI] [Google Scholar]
  18. Binger P.; Sandmeyer F.; Kruger C.; Erker G. Tetrahedron 1995, 51, 4277–4290. 10.1016/0040-4020(94)01118-J. [DOI] [Google Scholar]
  19. Huang J. H.; Luci J. J.; Lee T. Y.; Swenson D. C.; Jensen J. H.; Messerle L. J. Am. Chem. Soc. 2003, 125, 1688–1689. 10.1021/ja020369j. [DOI] [PubMed] [Google Scholar]
  20. Roy D.; Corminboeuf C.; Wannere C. S.; King R. B.; Schleyer P. V. R. Inorg. Chem. 2006, 45, 8902–8906. 10.1021/ic060802g. [DOI] [PubMed] [Google Scholar]
  21. Suresh C. H.; Frenking G. Organometallics 2010, 29, 4766–4769. 10.1021/om100260p. [DOI] [Google Scholar]
  22. Zhang C. J.; Li F. F. J. Phys. Chem. A. 2012, 116, 9123–9130. 10.1021/jp305871m. [DOI] [PubMed] [Google Scholar]
  23. Yang L. M.; Ganz E.; Chen Z. F.; Wang Z. X.; Schleyer P. V. Angew. Chem., Int. Ed. 2015, 54, 9468–9501. 10.1002/anie.201410407. [DOI] [PubMed] [Google Scholar]
  24. Binger P.; Sandmeyer F.; Krueger C. Organometallics 1995, 14, 2969–2976. 10.1021/om00006a047. [DOI] [Google Scholar]
  25. Röttger D.; Pflug J.; Erker G.; Kotila S.; Fröhlich R. Organometallics 1996, 15, 1265–1267. 10.1021/om950651h. [DOI] [Google Scholar]
  26. Choukroun R.; Donnadieu B.; Zhao J. S.; Cassoux P.; Lepetit C.; Silvi B. Organometallics 2000, 19, 1901–1911. 10.1021/om0001218. [DOI] [Google Scholar]
  27. Averkiev B. B.; Wang L. M.; Huang W.; Wang L. S.; Boldyrev A. I. Phys. Chem. Chem. Phys. 2009, 11, 9840–9849. 10.1039/b908973j. [DOI] [PubMed] [Google Scholar]
  28. Cooper O. J.; Wooles A. J.; McMaster J.; Lewis W.; Blake A. J.; Liddle S. T. Angew. Chem., Int. Ed. 2010, 49, 5570–5573. 10.1002/anie.201002483. [DOI] [PubMed] [Google Scholar]
  29. Suresh C. H.; Frenking G. Organometallics 2013, 32, 1531–1536. 10.1021/om301037a. [DOI] [Google Scholar]
  30. Fias S.; Geerlings P.; De Proft F. Comput. Theor. Chem. 2013, 1022, 108–114. 10.1016/j.comptc.2013.08.010. [DOI] [Google Scholar]
  31. Zhao H.; Zhang C. J. Comput. Theor. Chem. 2015, 1055, 42–50. 10.1016/j.comptc.2014.12.009. [DOI] [Google Scholar]
  32. Wang Y. J. Comput. Chem. 2009, 30, 2122–2126. 10.1002/jcc.21213. [DOI] [PubMed] [Google Scholar]
  33. Wu Y. B.; Jiang J. L.; Zhang R. W.; Wang Z. X. Chem. – Eur. J. 2010, 16, 1271–1280. 10.1002/chem.200901983. [DOI] [PubMed] [Google Scholar]
  34. Tam N. M.; Ngan V. T.; Nguyen M. T. Chem. Phys. Lett. 2014, 595–596, 272–276. 10.1016/j.cplett.2014.02.015. [DOI] [Google Scholar]
  35. Zhang C. J.; Zhao H.; Li J. X. Comput. Theor. Chem. 2015, 1054, 22–28. 10.1016/j.comptc.2014.12.002. [DOI] [Google Scholar]
  36. Jia X. F.; Zhang C. J. Comput. Theor. Chem. 2016, 1075, 47–53. 10.1016/j.comptc.2015.11.010. [DOI] [Google Scholar]
  37. Jia X. F.; Zhang C. J. Acta Phys.-Chim. Sin. 2016, 32, 1434–1438. 10.3866/PKU.WHXB201603101. [DOI] [Google Scholar]
  38. Hay P. J.; Wadt W. R. J. Chem. Phys. 1985, 82, 270–283. 10.1063/1.448799. [DOI] [Google Scholar]
  39. Hay P. J.; Wadt W. R. J. Chem. Phys. 1985, 82, 299–310. 10.1063/1.448975. [DOI] [Google Scholar]
  40. Ehlers A. W.; Bohme M.; Dapprich S.; Gobbi A.; Hollwarth A.; Jonas V.; Kohler K. F.; Stegmann R.; Veldkamp A.; Frenking G. Chem. Phys. Lett. 1993, 208, 111–114. 10.1016/0009-2614(93)80086-5. [DOI] [Google Scholar]
  41. Roy L. E.; Hay P. J.; Martin R. L. J. Chem. Theory Comput. 2008, 4, 1029–1031. 10.1021/ct8000409. [DOI] [PubMed] [Google Scholar]
  42. Wadt W. R.; Hay P. J. J. Chem. Phys. 1985, 82, 284–298. 10.1063/1.448800. [DOI] [Google Scholar]
  43. Reed A. E.; Curtiss L. A.; Weinhold F. Chem. Rev. 1988, 88, 899–926. 10.1021/cr00088a005. [DOI] [Google Scholar]
  44. Frish M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; et al. Gaussian 09, revision C.01; Gaussian: Wallingford, CT, 2009.
  45. Bader R. F. W.Atoms In Molecules: A Quantum Theory; Clarendon Press: Oxford, U.K., 1990. [Google Scholar]
  46. Kresse G.; Hafner J. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  47. Kresse G.; Joubert D. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  48. Blöchl P. E. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  49. Perdew J. P.; Burke K.; Ernzerhof M. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  50. Nosé S. J. Chem. Phys. 1984, 81, 511–519. 10.1063/1.447334. [DOI] [Google Scholar]
  51. Verlet L. Phys. Rev. 1967, 159, 98–103. 10.1103/PhysRev.159.98. [DOI] [Google Scholar]
  52. Wu W.; Gu J.; Song J.; Shaik S.; Hiberty P. C. Angew. Chem., Int. Ed. 2009, 48, 1407. 10.1002/anie.200804965. [DOI] [PubMed] [Google Scholar]
  53. Shaik S.; Danovich D.; Wu W.; Hiberty P. C. Nat. Chem. 2009, 1, 443. 10.1038/nchem.327. [DOI] [PubMed] [Google Scholar]
  54. Zhang C. J.; Ning L.; Li J. Organometallics 2013, 32, 7083–7089. 10.1021/om400807w. [DOI] [Google Scholar]
  55. Maron L.; Bourissou D. Organometallics 2009, 28, 3686–3690. 10.1021/om9000988. [DOI] [Google Scholar]
  56. Nikiforov G. B.; Roesky H. W.; Jones P. G.; Magull J.; Ringe A.; Oswald R. B. Inorg. Chem. 2008, 47, 2171–2179. 10.1021/ic701751r. [DOI] [PubMed] [Google Scholar]
  57. Abernethy C. D.; Codd G. M.; Spicer M. D.; Taylor M. K. J. Am. Chem. Soc. 2003, 125, 1128–1129. 10.1021/ja0276321. [DOI] [PubMed] [Google Scholar]
  58. Ai P. F.; Danopoulos A. A.; Braunstein P. Organometallics 2015, 34, 4109–4116. 10.1021/acs.organomet.5b00547. [DOI] [Google Scholar]
  59. Yagyu T.; Yano K.; Kimata T.; Jitsukawa K. Organometallics 2009, 28, 2342–2344. 10.1021/om900007b. [DOI] [Google Scholar]
  60. Buchgraber P.; Toupet L.; Guerchais V. Organometallics 2003, 22, 5144–5147. 10.1021/om034056o. [DOI] [Google Scholar]
  61. van Rensburg H.; Tooze R. P.; Foster D. F.; Otto S. Inorg. Chem. 2007, 46, 1963–1965. 10.1021/ic062368o. [DOI] [PubMed] [Google Scholar]
  62. Dorta R.; Stevens E. D.; Hoff C. D.; Nolan S. P. Stable. J. Am. Chem. Soc. 2003, 125, 10490–10491. 10.1021/ja0362151. [DOI] [PubMed] [Google Scholar]
  63. Russo V.; Herron J. R.; Ball Z. T. Org. Lett. 2010, 12, 220–223. 10.1021/ol902458v. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao6b00170_si_001.pdf (560.5KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES