Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2016 Nov 7;1(5):837–842. doi: 10.1021/acsomega.6b00231

Fe(II)/Fe(III) Redox Process Can Significantly Modulate the Conformational Dynamics and Electrostatics of Pirin in NF-κB Regulation

Arghya Barman 1, Donald Hamelberg 1,*
PMCID: PMC6640773  PMID: 31457166

Abstract

graphic file with name ao-2016-00231e_0005.jpg

Pirin is an iron (Fe)-dependent regulatory protein of nuclear factor κB (NF-κB) transcription factors. Binding studies have suggested that the oxidative state of iron plays a crucial role in modulating the binding of Pirin to NF-κB p65, in turn enhancing the binding of p65 to DNA. The Fe(III) form of Pirin is the active form and binds to NF-κB, whereas the Fe(II) form does not bind to NF-κB. However, the surprising consequence of a single charge perturbation in the functional modulation of NF-κB is not well understood. Here, we use quantum mechanical calculations and microsecond-long molecular dynamics simulations to explore the free-energy landscapes of the Fe(II) and Fe(III) forms of Pirin. We show that the restricted conformational space and electrostatic complementarity of the Fe(III) form of Pirin are crucial for binding and regulation of NF-κB. Our results suggest that a subtle single-electron redox trigger could significantly modulate the conformational dynamics and electrostatics of proteins in subcellular allosteric regulatory processes.

Introduction

Nuclear factor κB (NF-κB) is a class of ubiquitous cellular regulatory transcription factors that modulate the intracellular signaling cascade for immune response, inflammatory response, cell growth, and apoptosis.1−5 Their uncontrolled regulation could lead to several life-threatening diseases, such as cancer, diabetes, and acquired immune deficiency syndrome.6−8 In response to activating external stimuli, NF-κB proteins are translocated from the cytoplasm to the nucleus, where they bind and activate several κB genes. Inside the nucleus, the activity of NF-κB proteins is tightly controlled by a number of regulatory proteins and cofactors, collectively known as co-regulators.9−11 Although the exact role of these co-regulators is not well understood, experiments suggest that one such co-regulator, Pirin, interestingly plays a crucial role in regulating the activity of NF-κB proteins via a single-electron redox process at the iron center.

Pirin is a nonheme iron-binding nuclear protein composed of 290 amino acid residues.12,13 The iron is located in an open cleft near an R-shaped loop (Figure 1).14 A recent study has suggested that Pirin binds and activates NF-κB in a redox-dependent manner, although the mechanism of the redox reaction is not completely known.14 It has been suggested that the Fe(III) form of Pirin is the active form and the Fe(II) form of Pirin is the resting form. Quartz crystal microbalance with dissipation, surface plasmon resonance, and fluorescence spectroscopy have shown that Pirin in its Fe(III) form significantly enhances the binding of the NF-κB p65 homodimer to the κB DNA.14 High-resolution crystal structures of the Fe(II) form (PDB ID: 1J1L) and Fe(III) form (PDB ID: 4GUL) of Pirin show that the metal is located near the R-shaped loop region and is coordinated to three histidines (His56, His58, His101), one glutamate (Glu103), and two water molecules. The crystal structures of Pirin in the Fe(II) and Fe(III) forms show subtle differences in the conformations at the R-shaped Fe center, but these differences are significant enough at the R-shaped region that is suggested to directly interact with the outer surface of the NF-κB p65 protein.14 Although the X-ray structures show subtle differences between the Fe(II) and Fe(III) forms of Pirin, the effect of Pirin binding to NF-κB is dramatic, and Pirin significantly enhances the binding of NF-κB to the κB DNA. Additionally, very little is known about the effect of a single-electron redox process on the conformational dynamics of Pirin and on the regulation of NF-κB.

Figure 1.

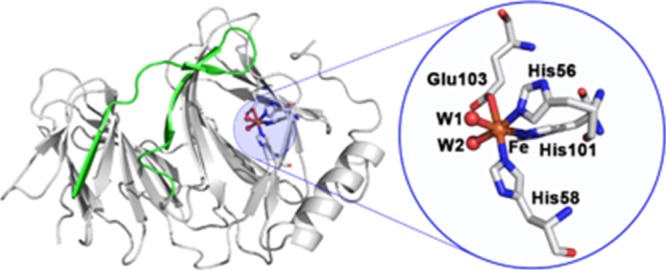
Figure 1

Open in a new tab

Crystal structure of the Fe(II) form of Pirin (PDB ID: 1J1L). The green region (residues Val7–Lys34) represents the R-shaped loop. A zoomed-in image of the Fe-binding site, with an octahedral geometry and coordinating residues, is presented.

Results and Discussion

Conformational Dynamics of the Fe(II) and Fe(III) Forms of Pirin

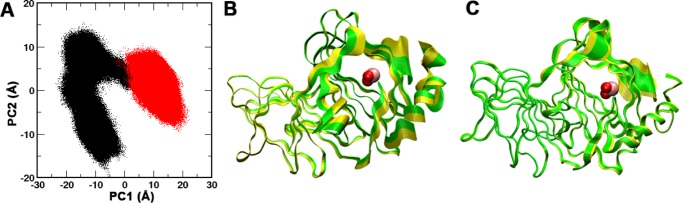
We initially study the conformational dynamics of the Fe(II) and Fe(III) forms of Pirin using principal component analysis (PCA) on the Cartesian coordinates of the backbone Cα atoms to determine the principal eigenvectors that represent the dominant motions (Figure 2A).

Figure 2.

Figure 2

Open in a new tab

PCA of the Fe(II) and Fe(III) forms of Pirin. (A) Projection of principal component 1 (PC1) and PC2 of Fe(II) (black) and Fe(III) (red). PC1 contributes 62% and PC2 contributes 18% among the top five components. (B) Dominant motions contributed by PC1: Fe(III), green; Fe(II), yellow. (C) Major fluctuations contributed by PC2: Fe(III), green; Fe(II), yellow. Fe and waters are shown as pink and red spheres, respectively. Movies of PC1 and PC2 fluctuations are provided in the Supporting Information.

The majority of the total fluctuations of the two forms is captured by the top two PCs: PC1 and PC2. PC1 clearly separates the Fe(II) and Fe(III) forms of Pirin, with little overlap between the two forms (Figure 2A). The ensemble of conformations of the Fe(III) form of Pirin is restricted to a single energy basin. On the other hand, the ensemble of the Fe(II) form of Pirin is relatively broader than that of the Fe(III) form, sampling multiple basins. Therefore, the results suggest that binding of the Fe(III) form of Pirin to NF-κB would be entropically more favorable than that of the Fe(II) form, losing less conformational entropy upon binding. The dominant motions contributed by PC1 are primarily observed near the R-shaped loop region (residues Ala74–Gly83), residues Pro249–Phe256, the C-terminus, and the terminal helix of Pirin (Figure 2B). The major contributions from PC2 were also observed in the R-shaped loop region, mainly residues Ala74–Gly83. The R-shaped region has been suggested to be the binding interface of Pirin when interacting with NF-κB p65, using mutagenesis experiments.14

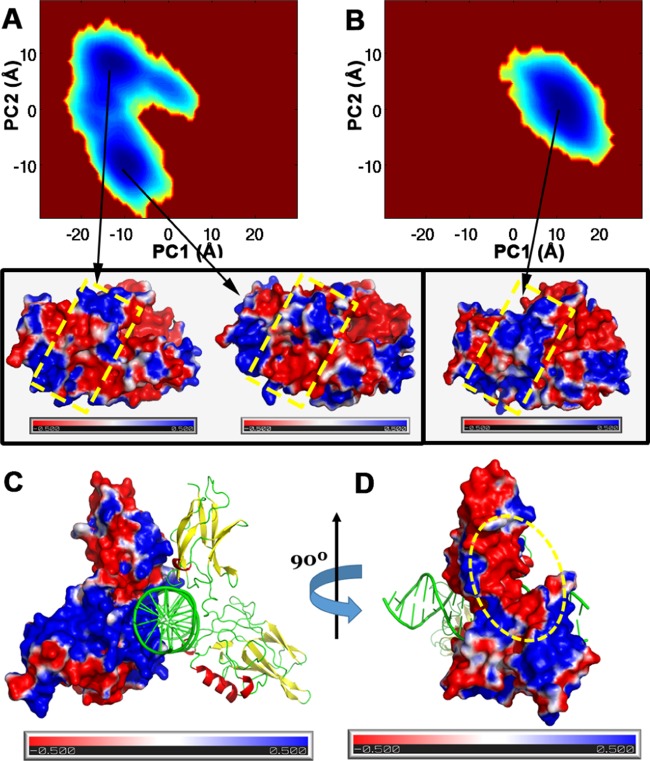
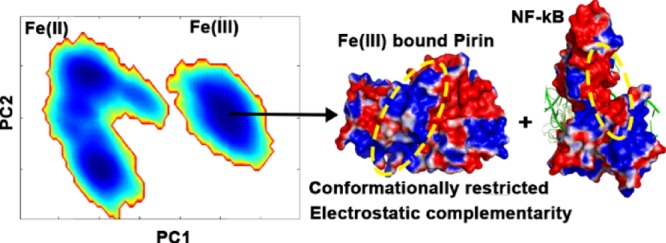
The probability densities of the distributions of the conformations projected on PC1 and PC2 were calculated to identify the prevalent conformations of Pirin in the different oxidation states of iron (Figure 3). In the Fe(II) form of Pirin, two dominant conformational states were observed (Figure 3A). The Fe(III) form of Pirin is localized to a single free-energy basin (Figure 3B), as shown in Figure 2. The conformations at the center of the free-energy basins were isolated, and the electrostatic potentials for each conformation were calculated using the Adaptive Poisson–Boltzmann Solver (APBS)15 and projected onto their respective molecular surfaces. The electrostatic potential shows that in the Fe(II) form of Pirin the R-shaped loop region is a patchwork of electropositive and electronegative regions. On the other hand, the electrostatic potential of the Fe(III) form shows a significant concentration of electropositive regions on the proposed binding surface of Pirin. Most interestingly, the distribution of the electropositive environment was observed in the R-shaped loop region and its surroundings. These results clearly show that a single-electron redox process in the metal center can significantly modulate the conformational dynamics and electrostatics of proteins. We hypothesized that electrostatic modulation by the Fe(III) of Pirin could provide a better electrostatic complementarity with NF-κB p65.

Figure 3.

Figure 3

Open in a new tab

Conformational space and electrostatic potential of Pirin and NF-κB. (A) Probability density map of conformational space projected on PC1 and PC2 of the Fe(II) form of Pirin. Two wells with lower energy conformations are observed (two deep blue wells). The electrostatic potential maps are portrayed on the surfaces of the two representative snapshots from the two wells (indicated with two arrows and shown below). (B) Density contour projection of PC1 and PC2 of Fe(III)-bound Pirin. Electrostatic potential map of a single representative snapshot from the high-density restricted conformational space explored for Fe(III)-bound Pirin (a representative snapshot is shown below and indicated by an arrow). The R-shaped loop and neighboring regions on the surface of Pirin are indicated by dotted rectangular boxes in yellow. (C) NF-κB and DNA complex; the electrostatic potential is projected onto the surface of one of the NF-κB monomers. The other NF-κB monomer and DNA are shown as cartoons. Highly dense electropositive region near the DNA (green) binding region. (D) Rotation (90°) of NF-κB and the DNA complex. The red electronegative patch on the surface of NF-κB (shown by the dotted oval in yellow) is the complementary binding region of the R-shaped loop region of Pirin. The electrostatic map is shown from −0.5 kT (red) to 0.5 kT (blue).

Role of Electrostatics in the Pirin–NF-κB Association

To test the electrostatic complementarity hypothesis, we calculated the electrostatic potential of the NF-κB p65 protein obtained from the Protein Data Bank, with PDB ID 2RAM.16Figure 3C shows the electrostatic potentials on the molecular surface of the NF-κB p65 monomer bound to DNA. As expected, the DNA-binding region of NF-κB has a high density of electropositive potential. On the other hand, the region suggested to interact with Pirin has a high density of electronegative potential (Figure 3D), suggesting electrostatic complementarity with the binding surface of Pirin. Unlike the Fe(II) form, the Fe(III) form of Pirin provides the positive environment necessary to complement the negative potential of the interaction site on NF-κB p65.

Estimating the electrostatic interaction free energy between Pirin and the NF-κB–DNA complex further assessed the contribution of electrostatics. The initial coordinates of the NF-κB–DNA complex were obtained from the Protein Data Bank, with PBD ID 2RAM. The initial Pirin–NF-κB–DNA supercomplex was obtained by docking the Pirin onto the NF-κB–DNA complex using ZDOCK,17 applying constraints based on mutagenesis results, as previously described.14 Molecular dynamics (MD) simulations were then performed on the Pirin–NF-κB–DNA supercomplexes of the Fe(III) form of Pirin. More details of the simulations can be found in the Computational Methods section. The molecular mechanics (MM)/Poisson–Boltzmann surface area approach was used to estimate the electrostatic contribution to the binding free energy (ΔGbinding) of Pirin within the supercomplex. The binding free energies were calculated using snapshots from the MD trajectories. Using the snapshots of the Fe(III) form of the Pirin supercomplex, the partial charges of the iron center and surrounding residues were replaced with the partial charges corresponding to the system in the Fe(II) state, and the binding free energies were recomputed. This was done to assess the immediate effect of changing from Fe(III) to Fe(II) on the binding free energy before any conformal change. The electrostatics component of the binding free energy for the binding of the Fe(III) form of Pirin to the supercomplex has a much lower value (ΔGbinding(electrostatic)), −444.5 ± 2.4 kcal/mol, compared to the ΔGbinding(electrostatic) for the Fe(II) form, −216.6 ± 2.2 kcal/mol, corresponding to a significant reduction. These results also suggest a significant role for electrostatics in the association between Pirin and NF-κB. It can be concluded that the Fe(III) form of Pirin has a stronger affinity to the NF-κB–DNA complex also due to the more favorable electrostatic interaction free energy. Taken together, the results suggest that the Fe(III) form of Pirin is entropically preorganized to bind with better electrostatic free energy, losing less entropy upon binding compared with Fe(II). The Fe(III) form of Pirin could therefore bind more tightly to the NF-κB–DNA complex compared with the Fe(II) form, in agreement with the spectroscopic assays.14

Reorganization of Residue–Residue Contact Dynamics

It is clear from the current studies that a single-electron redox process can significantly alter the dynamics and electrostatics of Pirin. How does this subtle redox process dramatically alter the dynamics? We can answer this question by investigating the ensuing rearrangements of the residue–residue contact dynamics and how this information is propagated away from the iron center. In general, proteins with N number of residues can have N(N – 1)/2 possible residue–residue contacts. The majority of these residue–residue contacts are never formed, and a small amount of contacts are always formed or dynamically form and break in the ensemble of native conformations. Analysis of residue–residue contacts between the active and inactive forms of protein structures from the Protein Data Bank suggested that the network of residue–residue contacts can describe functional modulation of proteins.18

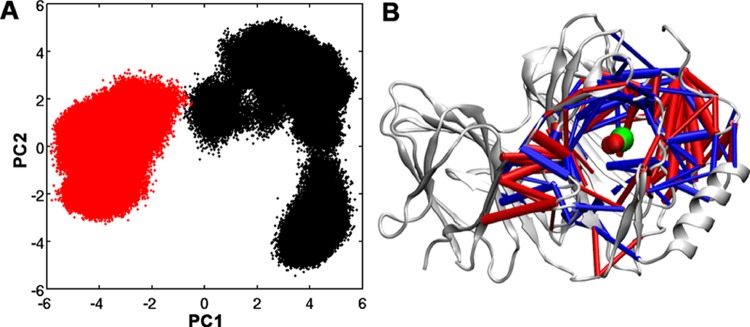
In this study, we define a residue–residue contact as having been formed when any two of the inter-residue heavy atoms are within 4.5 Å. Only non-neighboring residue–residue contacts are considered. A contact is defined as a part of the “dynamic contacts” if the average percentage of contact formation is between 10 and 90% over the entire microsecond-long simulations of the Fe(II) and Fe(III) forms of Pirin. A total of 594 dynamic contacts were considered. Details of the method have been described previously.19,20 Perturbation of the contact dynamics between the Fe(II) and Fe(III) forms of Pirin is analyzed by carrying out PCA on the contact trajectories of the dynamic contacts. A contact trajectory is a time-dependent trajectory of all of the dynamic contacts defined as 0 or 1 to signify broken or formed, respectively. Projections of the top two PCs are shown in Figure 4A. The projection in the residue–residue contact space explored by the Fe(II) form of Pirin shows an extended distribution of loosely forming and breaking contacts relative to the Fe(III) form.

Figure 4.

Figure 4

Open in a new tab

Residue–residue contact dynamics of the Fe(II) and Fe(III) forms of Pirin. Projection of the top two PCs of dynamic contacts in the residue–residue contact space for Fe(II) (black) and Fe(III) (red). PC1 contributes 54.5% and PC2 contributes 25.7% among the top five components (A). The residue–residue contacts that are more formed and more broken in the Fe(III) form are represented in blue and red, respectively. The width of the cylinder represents the magnitude of the difference. Residue–residue contacts, with an absolute difference greater than 30% (B) of all of the dynamics contacts, are shown. Iron and waters are shown as green and red van der Waals spheres, respectively.

On the other hand, a more restricted residue–residue contact space is seen in the Fe(III) form of Pirin, which is completely shifted away from that of the Fe(II) form, suggesting tighter residue–residue contacts. The separation between the Fe(II) and Fe(III) forms of Pirin is along the PC1 component. We take a closer look at those dynamic contacts that largely contribute to PC1. The percent difference in dynamic contact is calculated by subtracting the fraction of formed contact in the Fe(II) form of Pirin from that for the Fe(III) form, that is, (Fe(III) – Fe(II)); therefore, contacts that are more formed in Fe(III) are positive (shown in blue) and contacts that are less formed in the Fe(III) form are negative (shown in red). The difference in the fractions between the Fe(II) and Fe(III) forms of Pirin is shown in Figure 4B. Figure 4B shows the residue–residue contact statistics when the difference is more than 30%. Figure 4B clearly shows significant residue–residue contact rearrangement around the R-shaped region, the loop region, and the N-terminal region of Pirin, mainly the proposed interaction site with NF-κB p65. More precisely, more number of contacts are formed at the R-shaped region as the oxidative state of iron changes from Fe(II) to Fe(III). The residue–residue interactions tighten up in the Fe(III) form, restricting the conformational space. Interestingly, rearrangement of the residue–residue contacts due to the subtle redox trigger is shown to propagate far beyond the iron center, accompanied by changes in the backbone dynamics. These results therefore suggest that such a subtle change in the oxidation state of metal ions could significantly alter the dynamics of proteins distal to the metal center.

Conclusions

We have investigated a plausible role of Fe(II)/Fe(III) redox-dependent activation of Pirin in the regulation of NF-κB transcription factors. In the Fe(III) form, Pirin explores a more restricted conformational space compared to that in the Fe(II) form, which explores multiple conformational states, suggesting a possible role of entropy in the Pirin–NF-κB association. Preorganization of the Fe(III) form of Pirin would be entropically more favorable upon binding to the NF-κB protein due to the less loss in entropy compared to that for the Fe(II) form of Pirin. In addition to the entropic contribution, the charge distribution associated with the Fe(III) form induces a more electropositive environment at the R-shaped region, creating an electrostatic complementary surface for its binding partner, NF-κB p65. The electrostatic contribution of the binding free energy between the Fe(III) form of Pirin and NF-κB p65 is found to be significantly more favorable than that for the Fe(II) form. This study provides substantive evidence for the pivotal role of entropy and electrostatics in iron redox-dependent activation of Pirin in NF-κB regulation. These results provide a new outlook and perspective on redox activation of metalloproteins in complex biological systems. A single redox trigger could allosterically regulate subcellular processes. We can therefore speculate that many other cellular processes are possibly regulated by subtle changes in the oxidative state of metal centers, cofactors, or amino acid residues.

Computational Methods

Here, we have used quantum mechanical/molecular mechanical (QM/MM) methods to calculate partial charges and microsecond-long MD simulations (a total 5 μs) of the Fe(II) and Fe(III) forms of Pirin to explore the free-energy landscape and provide a detailed atomistic description of the dynamical response as a result of the redox process.

Calculation of the Partial Charge of Iron-Coordinating Residues

The initial structure of the iron (Fe)-bound Pirin (obtained from PDB ID: 1J1L(13)) was processed using the xleap module in AmberTools12. Two systems, one for Fe(II) and one for Fe(III), were solvated in octahedron periodic boxes using the TIP3P21 explicit water model. The overall charge of the system was neutralized by adding counter ions for electrostatic neutrality. The Fe(II)- and Fe(III)-bound forms of Pirin were optimized using the QM/MM method incorporated in the AMBER14 package22 and using the external Gaussian0323 program for the quantum mechanical calculations. The QM region consisted of His56, His58, His101, Glu103, Gln115, two water molecules, and the Fe atom (Figure S1A,B). The histidine residues coordinated to the Fe atom are treated as monoprotonated HID residues. The QM/MM minimization was performed with the QM region treated at the B3LYP level of theory and the LANL2DZ Hay–Wadt effective core potential as the basis set. The rest of the protein was treated with the AMBER14 ff14sb force-field parameters.24−27 On the basis of previous experiments, the spin states of Fe(III) and Fe(II) were considered as high spin and low spin, respectively.14 In addition to the minimized geometries in the QM/MM region, two additional residues, Pro57 (connecting His56 and His58) and Ala102 (connecting His101 and Glu103), were considered in calculating the electrostatic potential, preceding the restrained electrostatic potential (RESP)28 charge-fitting procedure (Figure S1C). Only subtle structural changes in the iron centers and to the distal regions were observed after the QM/MM minimization (see Figure S2). The RESP partial charges were calculated for ∼150 atoms from the electrostatic potential calculated at the M06 level of theory and all-electron 6-31G(d) basis set.29 The partial charges obtained from the RESP fitting procedure (see Table S1 for detail) were used for the microsecond-long MD simulations.

MD Simulations

All MD simulations were performed with the CUDA version of the AMBER1422 program, using the ff14SB30 force field. Each simulation was run using a single NVIDIA GeForce GTX 980 GPU. The overall charge of the system was neutralized by adding counter ions for electrostatic neutrality. The SHAKE algorithm31 was implemented to constrain all of the bonds involving hydrogen. The systems were equilibrated at 300 K, and the Langevin thermostat, with a collision frequency of 1 ps–1, was used to maintain the temperature.32 The long-range electrostatic interactions were calculated using the particle mesh Ewald summation method,33 and a cutoff of 9 Å was used for the nonbonded interactions. All simulations were carried out using the NPT ensemble at a constant pressure of 1 bar, and a time step of 2 fs was used to integrate the equation of motion. The optimized nonbonded parameters for Fe(II) and Fe(III) by Merz et al. were used.34,35 After a series of minimizations (500 step conjugate gradient method followed by 500 step steepest descent method) and MD simulations with constraints on the protein (slowly releasing the force constant from 250 to 10 kcal/mol/Å2), the production simulations were run for 2.5 μs, considering the first 500 ns of simulation as equilibration. The crystallographic coordination bonds from the Fe to the coordinating atoms were maintained by applying harmonic bonds with a force constant of 150.0 kcal/mol Å2 throughout the simulation. The root-mean-square deviation (RMSD) over the trajectory indicates equilibration of the trajectory. The RMSDs of the Cα atoms of both systems suggested that each system had reached equilibrium (Figure S3) and therefore all of the analyses were performed during the last 2 μs of the simulations. VMD36 and PyMOL37 visualization programs were used for graphical representations.

Calculation of Electrostatic Potentials

The electrostatic potentials of Pirin and NF-κB were determined using numerical solutions to the Poisson–Boltzmann equation using the APBS package.15 Atomic charges were obtained from the AMBER force field and parameterized partial charges for the iron center. A low dielectric constant of 2.0 was assigned to the protein interior, whereas a dielectric of 78.0 was assigned to the solvent. Multigrid solutions with grid dimensions of 161 × 131 × 161 and 161 × 225 × 161, with a solvent radius of 1.4 Å, were used for Pirin and NF-κB, respectively. The salt concentration of 150 mM was used as the ionic strength for the calculations. The temperature was set to 310 K.

Acknowledgments

The National Science Foundation (MCB-1517617) supported this research. We also acknowledge support from Georgia State University.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.6b00231.

  • Crystal structure and QM/MM model for Pirin and the Fe center; structural superposition of the Fe(II) and Fe(III) forms of Pirin after QM/MM minimizations; RMSD of the Cα atoms of the Fe(II) and Fe(III) forms of Pirin during the MD simulations (Figures S1–S3); partial charges for the Fe center and coordinated residues of the Fe(II) and Fe(III) forms of Pirin (Table S1) (PDF)

  • Movies of the fluctuations of the backbone along PC1 and PC2 shown in Figure 2 (GIF, GIF)

The authors declare no competing financial interest.

Supplementary Material

ao6b00231_si_001.pdf (490.5KB, pdf)
ao6b00231_si_002.zip (1.1MB, zip)
ao6b00231_si_003.zip (1.1MB, zip)

References

  1. Romashkova J. A.; Makarov S. S. NF-[kappa]B is a target of AKT in anti-apoptotic PDGF signalling. Nature 1999, 401, 86–90. 10.1038/43474. [DOI] [PubMed] [Google Scholar]
  2. Li Q.; Verma I. M. NF-[kappa]B regulation in the immune system. Nat. Rev. Immunol. 2002, 2, 725–734. 10.1038/nri910. [DOI] [PubMed] [Google Scholar]
  3. Hayden M. S.; Ghosh S. Shared Principles in NF-κB Signaling. Cell 2008, 132, 344–362. 10.1016/j.cell.2008.01.020. [DOI] [PubMed] [Google Scholar]
  4. Schreiber J.; Jenner R. G.; Murray H. L.; Gerber G. K.; Gifford D. K.; Young R. A. Coordinated binding of NF-κB family members in the response of human cells to lipopolysaccharide. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 5899–5904. 10.1073/pnas.0510996103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Hoffmann A.; Natoli G.; Ghosh G. Transcriptional regulation via the NF-[kappa]B signaling module. Oncogene 2006, 25, 6706–6716. 10.1038/sj.onc.1209933. [DOI] [PubMed] [Google Scholar]
  6. Baldwin A. S. Jr. Series Introduction: The transcription factor NF-κB and human disease. J. Clin. Invest. 2001, 107, 3–6. 10.1172/JCI11891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Kumar A.; Takada Y.; Boriek A. M.; Aggarwal B. B. Nuclear factor-κB: its role in health and disease. J. Mol. Med. 2004, 82, 434–448. 10.1007/s00109-004-0555-y. [DOI] [PubMed] [Google Scholar]
  8. Lee C. H.; Jeon Y.-T.; Kim S.-H.; Song Y.-S. NF-κB as a potential molecular target for cancer therapy. BioFactors 2007, 29, 19–35. 10.1002/biof.5520290103. [DOI] [PubMed] [Google Scholar]
  9. Näär A. M.; Lemon B. D.; Tjian R. Transcriptional Coactivator Complexes. Annu. Rev. Biochem. 2001, 70, 475–501. 10.1146/annurev.biochem.70.1.475. [DOI] [PubMed] [Google Scholar]
  10. Jeong K. W.; Kim K.; Situ A. J.; Ulmer T. S.; An W.; Stallcup M. R. Recognition of enhancer element–specific histone methylation by TIP60 in transcriptional activation. Nat. Struct. Mol. Biol. 2011, 18, 1358–1365. 10.1038/nsmb.2153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bergqvist S.; Alverdi V.; Mengel B.; Hoffmann A.; Ghosh G.; Komives E. A. Kinetic enhancement of NF-κB·DNA dissociation by IκBα. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 19328–19333. 10.1073/pnas.0908797106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Wendler W. M. F.; Kremmer E.; Förster R.; Winnacker E.-L. Identification of Pirin, a Novel Highly Conserved Nuclear Protein. J. Biol. Chem. 1997, 272, 8482–8489. 10.1074/jbc.272.13.8482. [DOI] [PubMed] [Google Scholar]
  13. Pang H.; Bartlam M.; Zeng Q.; Miyatake H.; Hisano T.; Miki K.; Wong L.-L.; Gao G. F.; Rao Z. Crystal Structure of Human Pirin: An Iron-binding Nuclear Protein And Transcription Cofactor. J. Biol. Chem. 2004, 279, 1491–1498. 10.1074/jbc.M310022200. [DOI] [PubMed] [Google Scholar]
  14. Liu F.; Rehmani I.; Esaki S.; Fu R.; Chen L.; de Serrano V.; Liu A. Pirin is an iron-dependent redox regulator of NF-κB. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 9722–9727. 10.1073/pnas.1221743110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Baker N. A.; Sept D.; Joseph S.; Holst M. J.; McCammon J. A. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 10037–10041. 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Chen Y.-Q.; Ghosh S.; Ghosh G. A novel DNA recognition mode by the NF-[kappa]B p65 homodimer. Nat. Struct. Mol. Biol. 1998, 5, 67–73. 10.1038/nsb0198-67. [DOI] [PubMed] [Google Scholar]
  17. Pierce B. G.; Wiehe K.; Hwang H.; Kim B.-H.; Vreven T.; Weng Z. ZDOCK server: interactive docking prediction of protein–protein complexes and symmetric multimers. Bioinformatics 2014, 30, 1771–1773. 10.1093/bioinformatics/btu097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Daily M. D.; Upadhyaya T. J.; Gray J. J. Contact rearrangements form coupled networks from local motions in allosteric proteins. Proteins: Struct., Funct., Bioinf. 2008, 71, 455–466. 10.1002/prot.21800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Barman A.; Hamelberg D. Coupled Dynamics and Entropic Contribution to the Allosteric Mechanism of Pin1. J. Phys. Chem. B 2016, 120, 8405–8415. 10.1021/acs.jpcb.6b02123. [DOI] [PubMed] [Google Scholar]
  20. Doshi U.; Holliday M. J.; Eisenmesser E. Z.; Hamelberg D. Dynamical network of residue–residue contacts reveals coupled allosteric effects in recognition, catalysis, and mutation. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, 4735–4740. 10.1073/pnas.1523573113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Jorgensen W. L. Revised TIPS for simulations of liquid water and aqueous solutions. J. Chem. Phys. 1982, 77, 4156–4163. 10.1063/1.444325. [DOI] [Google Scholar]
  22. Case D. A.; Cheatham T. E.; Darden T.; Gohlke H.; Luo R.; Merz K. M.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Frisch M. J.; et al. Gaussian 03, revision C.02; Gaussian Inc.: Wallingford, CT, 2004.
  24. Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  25. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  26. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  27. Hay P. J.; Wadt W. R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. 10.1063/1.448799. [DOI] [Google Scholar]
  28. Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
  29. Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  30. Hornak V.; Abel R.; Okur A.; Strockbine B.; Roitberg A.; Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins: Struct., Funct., Bioinf. 2006, 65, 712–725. 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
  32. Izaguirre J. A.; Catarello D. P.; Wozniak J. M.; Skeel R. D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. 10.1063/1.1332996. [DOI] [Google Scholar]
  33. Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  34. Li P.; Song L. F.; Merz K. M. Parameterization of Highly Charged Metal Ions Using the 12-6-4 LJ-Type Nonbonded Model in Explicit Water. J. Phys. Chem. B 2015, 119, 883–895. 10.1021/jp505875v. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Li P.; Merz K. M. Taking into Account the Ion-Induced Dipole Interaction in the Nonbonded Model of Ions. J. Chem. Theory Comput. 2014, 10, 289–297. 10.1021/ct400751u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Humphrey W.; Dalke A.; Schulten K. VMD: Visual molecular dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  37. DeLano W. L.The PyMOL Molecular Graphics System, version 1.1r1; DeLano Scientific: Palo Alto, CA, 2002.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao6b00231_si_001.pdf (490.5KB, pdf)
ao6b00231_si_002.zip (1.1MB, zip)
ao6b00231_si_003.zip (1.1MB, zip)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES